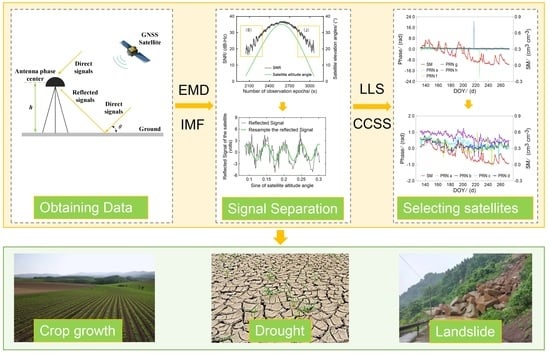
Soil Moisture Retrieval Using GNSS-IR Based on Empirical Modal Decomposition and Cross-Correlation Satellite Selection
Abstract
1. Introduction
2. Site and Data
2.1. GNSS Site Description
2.2. SM and Precipitation Data
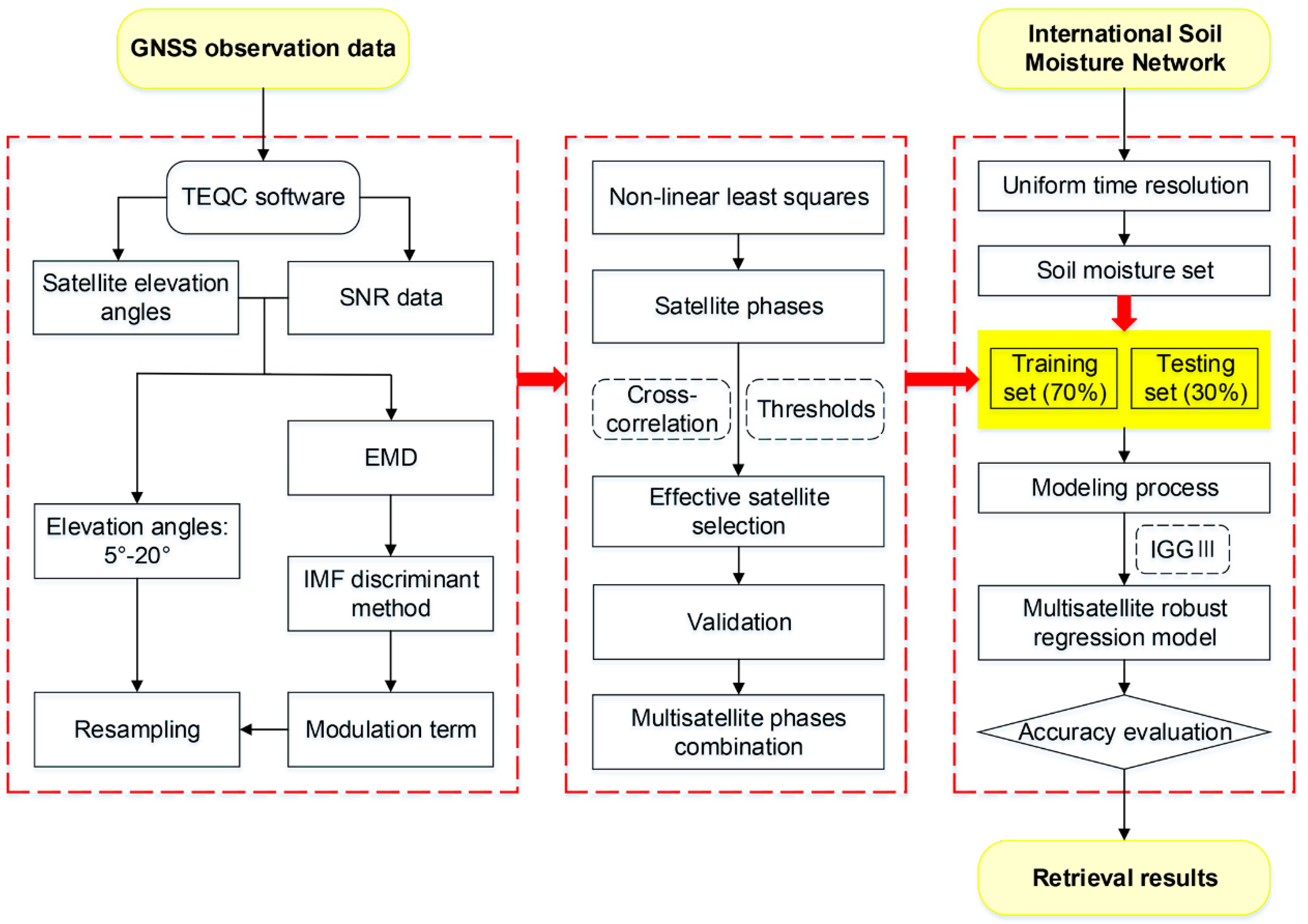
3. Methodology
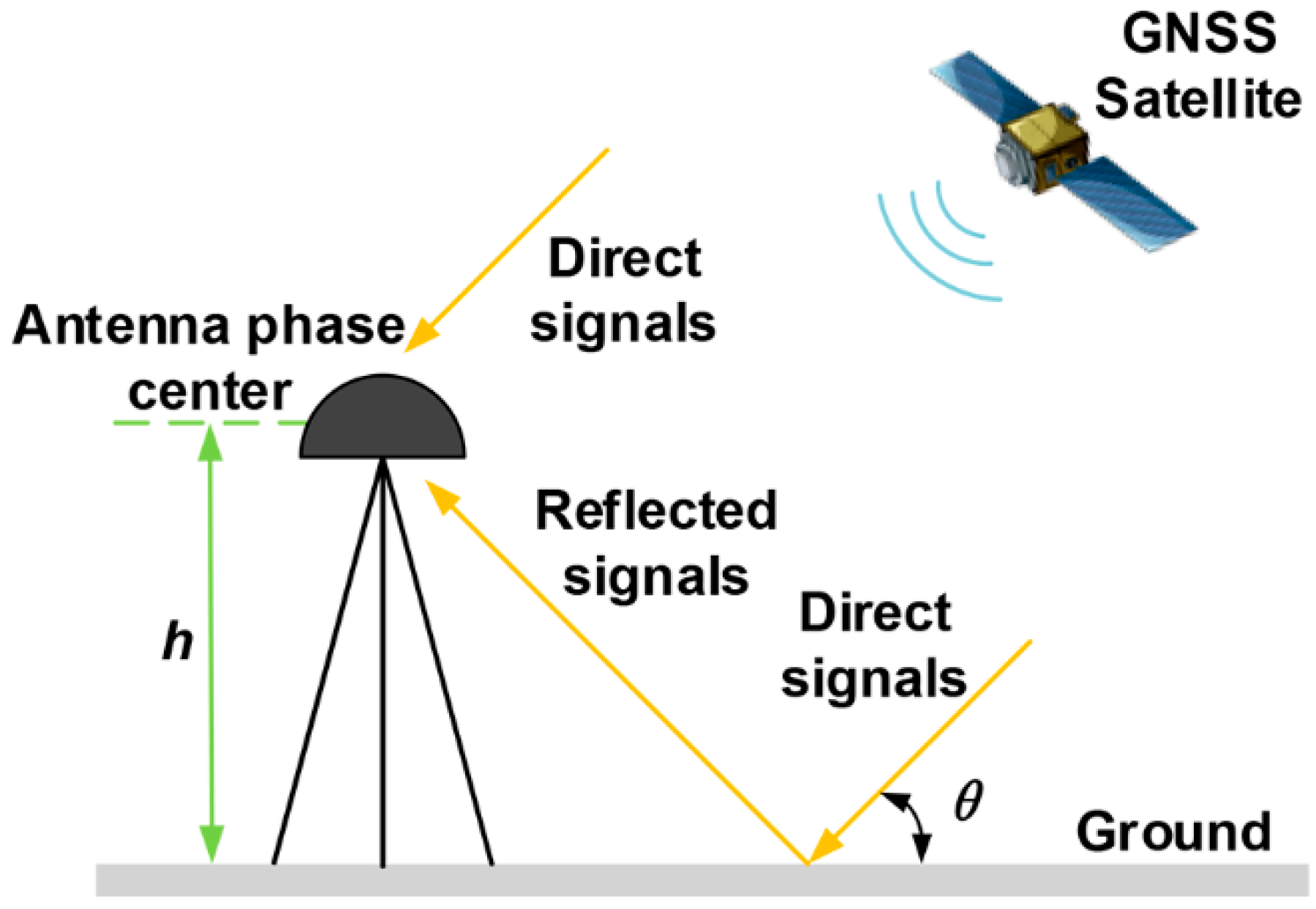
3.1. GNSS Satellite Reflected Signal
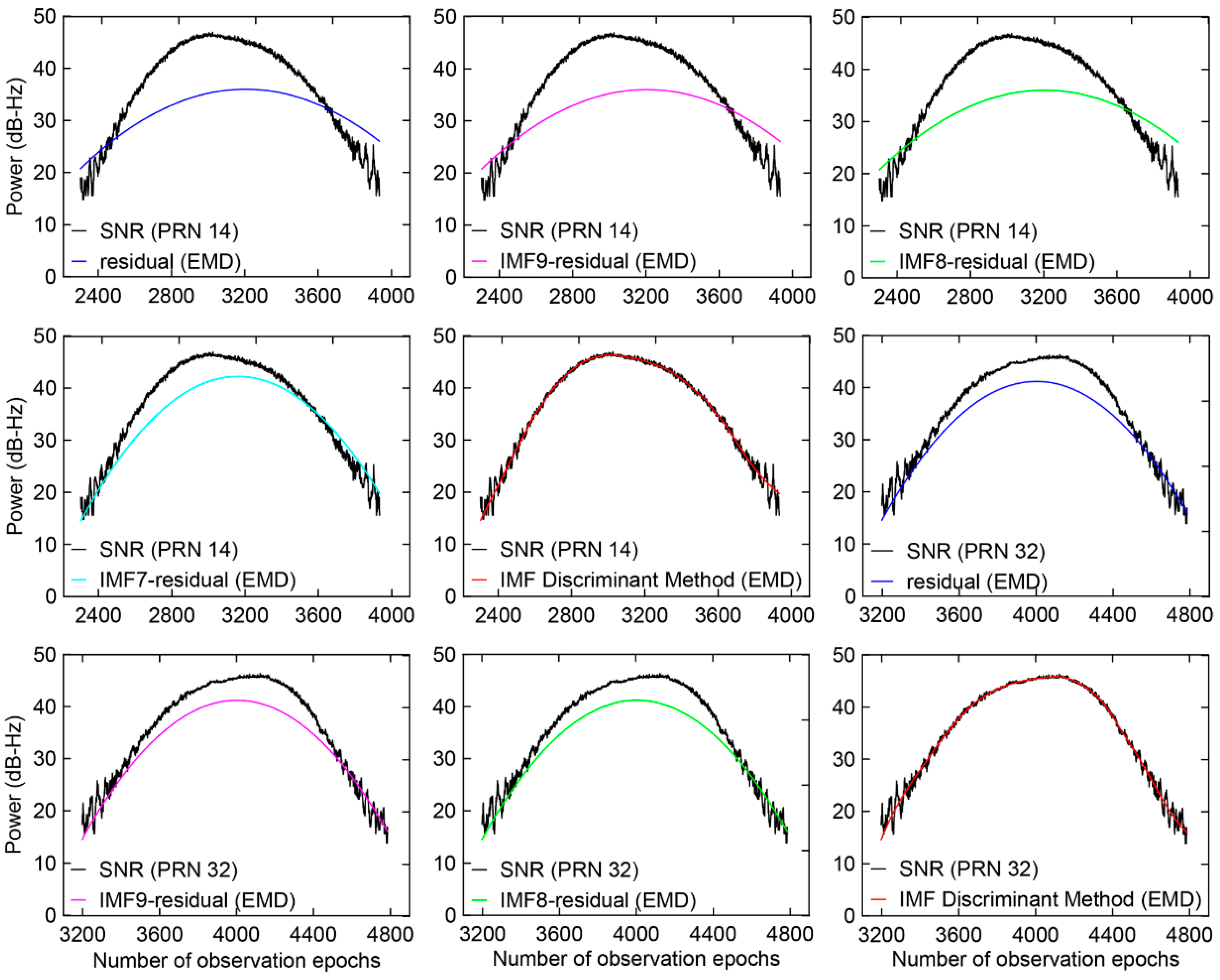
3.2. EMD for Separating the Modulation Terms
3.3. CCSS Method
- During the experiment, the satellites with relatively complete phase data (more than 95% of the total data) were selected preliminarily. Because for the multisatellite combination retrieval mode, the selected satellite data needed to meet the requirement of continuous and consistent reflection trajectories within the range of satellite interception elevation, the continuous phase could be generated throughout the annual product day observation period.
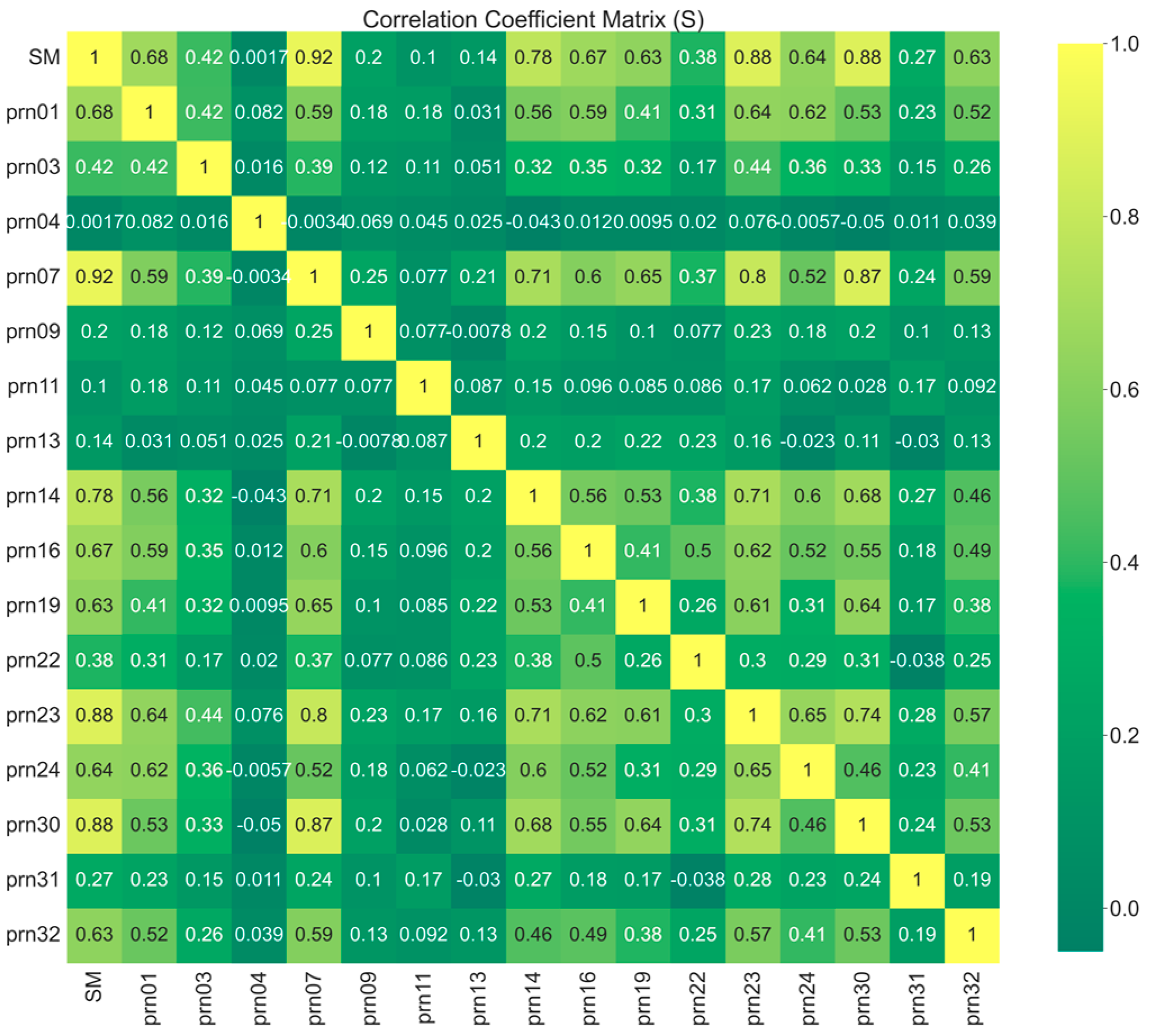
- Based on the satellites selected in step ➀, the cross-correlation coefficient () between each satellite phase and other satellite phases was calculated separately. Then, considering the medium correlation as the initial reference condition according to the cross-correlation threshold range in Table 2, the satellites with greater than 0.400 were selected as long as they existed, and the satellites without greater than 0.400 were excluded.where and correspond to different (PRN) numbers of GNSS satellites, is the covariance corresponding to and , represents the variance of , and represents the variance of .
- The cross-correlation coefficient () and its average value () for each satellite selected in step ➁ were calculated. Then, the threshold ranges () of different gradients were set for the cross-correlation coefficient average, and the satellites with larger than were selected. Among them, the setting of started from a value greater than 0.400 and increased at intervals of 0.1 each time. Moreover, in every screening process, it was necessary first to eliminate the satellites with smaller than , then continue to calculate and for the remained satellites, and only later compare the updated with the newly set threshold . This way, the accurate selection of satellites with different precision was realized:where is the sum of the correlation values between satellite and other satellites.
- Based on the satellites selected in step ➂, effective satellites within different ranges were obtained. We continued to select and process them, eliminating satellites with duplicate ascending and descending segments. For the same satellite, if there was no ascending segment (S), the phase of the descending segment (J) was used; if there was no descending segment, the phase of the ascending segment was used; if both the ascending and the descending segments existed, the satellite within the higher CCSS threshold range was selected.
3.4. MRER Model
4. GNSS-IR SM Retrieval
5. Results and Discussion
5.1. Separation of the Modulation Terms
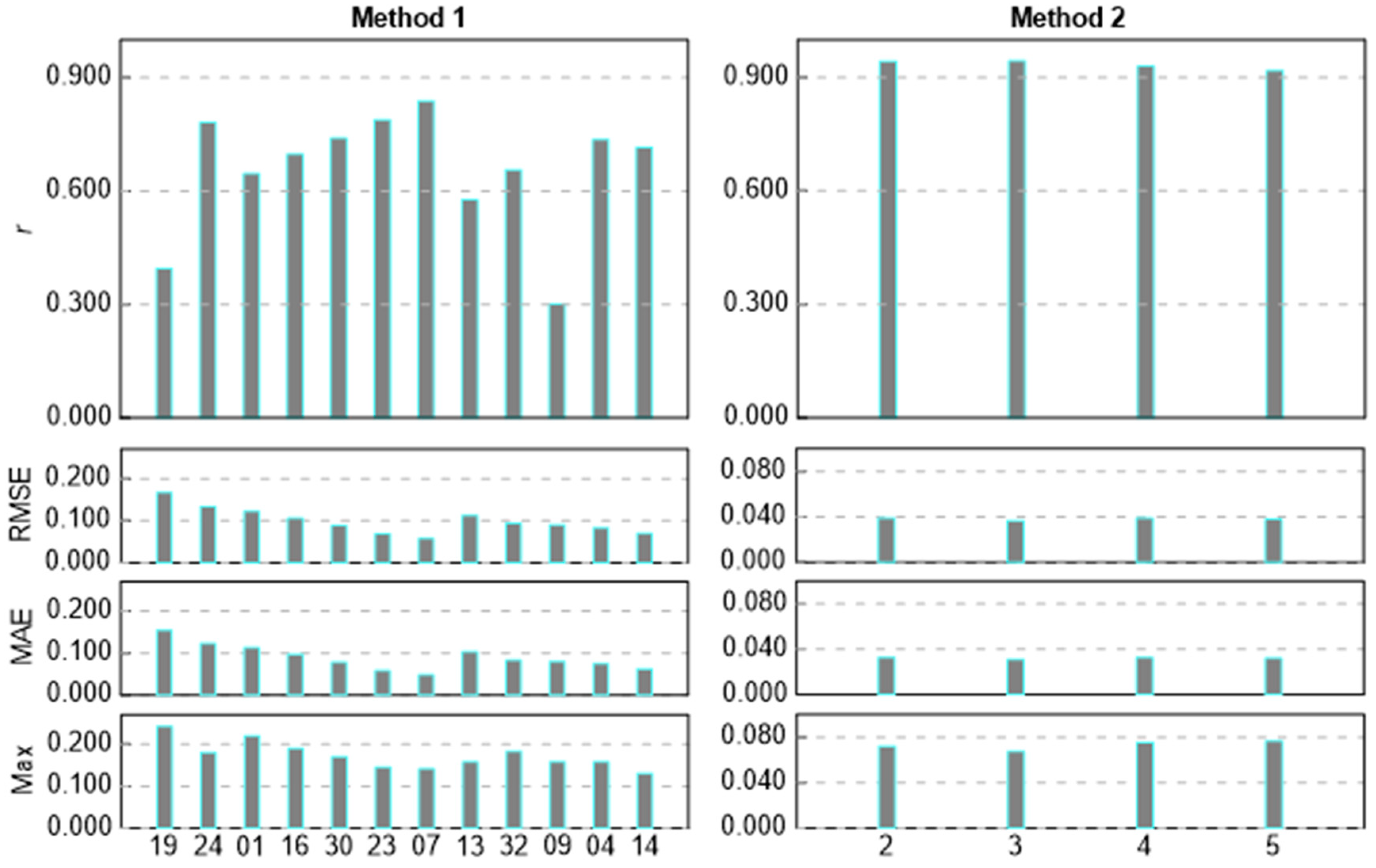
5.2. Selection of Available Satellites
5.3. Retrieval of SM
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bastiaanssen, W.; Molden, D.J.; Makin, I.W. Remote sensing for irrigated agriculture: Examples from research and possible applications. Agric. Water Manag. 2000, 46, 137–155. [Google Scholar] [CrossRef]
- Xu, Y.; Dong, K.; Jiang, M.; Liu, Y.; He, L.; Wang, J.; Zhao, N.; Gao, Y. Soil moisture and species richness interactively affect multiple ecosystem functions in a microcosm experiment of simulated shrub encroached grasslands. Sci. Total Environ. 2022, 803, 149950. [Google Scholar] [CrossRef] [PubMed]
- Saadatabadi, A.R.; Izadi, N.; Karakani, E.G.; Fattahi, E.; Shamsipour, A.A. Investigating relationship between soil moisture, hydro-climatic parameters, vegetation, and climate change impacts in a semi-arid basin in Iran. Arab. J. Geosci. 2021, 14, 1796. [Google Scholar] [CrossRef]
- Mohanty, B.P.; Cosh, M.; Lakshmi, V.; Montzka, C. Remote sensing for vadose zone hydrology—A synthesis from the vantage point. Vadose Zone J. 2013, 12, 128. [Google Scholar] [CrossRef]
- Brocca, L.; Ciabatta, L.; Massari, C.; Camici, S.; Tarpanelli, A. Soil moisture for hydrological applications: Open questions and new opportunities. Water 2017, 9, 140. [Google Scholar] [CrossRef]
- Ochsner, T.E.; Cosh, M.H.; Cuenca, R.H.; Dorigo, W.A.; Draper, C.S.; Hagimoto, Y.; Kerr, Y.H.; Larson, K.M.; Njoku, E.G.; Small, E.E.; et al. State of the art in large-scale soil moisture monitoring. Soil Sci. Soc. Am. J. 2013, 77, 1888–1919. [Google Scholar] [CrossRef]
- Xu, L.; Chen, N.; Zhang, X.; Moradkhani, H.; Zhang, C.; Hu, C. In-situ and triple-collocation based evaluations of eight global root zone soil moisture products. Remote Sens. Environ. 2021, 254, 112248. [Google Scholar] [CrossRef]
- Barre, H.M.; Duesmann, B.; Kerr, Y.H. SMOS: The mission and the system. IEEE Trans. Geosci. Remote Sens. 2008, 46, 587–593. [Google Scholar] [CrossRef]
- Entekhabi, D.; Njoku, E.G.; Oneill, P.; Spencer, M.; Jackson, T.; Entin, J.; Im, E.; Kellogg, K. The soil moisture active passive mission (SMAP). In Proceedings of the IGARSS 2008–2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; Volume 3, pp. 1–4. [Google Scholar] [CrossRef]
- Burgin, M.S.; Colliander, A.; Njoku, E.G.; Chan, S.K.; Cabot, F.; Kerr, Y.H.; Bindlish, R.; Jackson, T.J.; Entekhabi, D.; Yueh, S.H. A comparative study of the smap passive soil moisture product with existing satellite-based soil moisture products. IEEE Trans. Geosci. Remote Sens. 2017, 55, 2959–2971. [Google Scholar] [CrossRef]
- Xu, H.; Yuan, Q.; Li, T.; Shen, H.; Zhang, L.; Jiang, H. Quality improvement of satellite soil moisture products by fusing with in-situ measurements and GNSS-R estimates in the Western Continental US. Remote Sens. 2018, 10, 1351. [Google Scholar] [CrossRef]
- Hein, G.W. Status, perspectives and trends of satellite navigation. Satell. Navig. 2020, 1, 22. [Google Scholar] [CrossRef]
- Jin, S.; Cardellach, E.; Xie, F. GNSS Remote Sensing, Theory, Methods and Applications; Springer: Amsterdam, The Netherlands, 2014; Volume 19, pp. 241–249. [Google Scholar] [CrossRef]
- Nievinski, F.G.; Larson, K.M. Forward modeling of GPS multipath for near-surface reflectometry and positioning applications. GPS Solute. 2014, 18, 309–322. [Google Scholar] [CrossRef]
- Wu, X.; Jin, S.; Chang, L. Monitoring Bare Soil Freeze-Thaw Process Using GPS-Interferometric Reflectometry: Simulation and Validation. Remote Sens. 2018, 10, 14. [Google Scholar] [CrossRef]
- Chew, C.C.; Small, E.E. Soil Moisture Sensing Using Spaceborne GNSS Reflections: Comparison of CYGNSS Reflectivity to SMAP Soil Moisture. Geophys. Res. Lett. 2018, 45, 4049–4057. [Google Scholar] [CrossRef]
- Munoz-Martin, J.F.; Llaveria, D.; Herbert, C.; Pablos, M.; Park, H.; Camps, A. Soil moisture estimation synergy using gnss-r and l-band microwave radiometry data from fsscat/fmpl-2. Remote Sens. 2021, 13, 994. [Google Scholar] [CrossRef]
- Nievinski, F.G.; Hobiger, T.; Haas, R.; Liu, W.; Strandberg, J.; Tabibi, S.; Vey, S.; Wickert, J.; Williams, S. SNR-based GNSS reflectometry for coastal sea-level altimetry: Results from the first IAG inter-comparison campaign. J. Geod. 2020, 94, 70. [Google Scholar] [CrossRef]
- Zhang, S.; Liu, K.; Liu, Q.; Zhang, C.; Zhang, Q.; Nan, Y. Tide variation monitoring based improved GNSS-MR by empirical mode decomposition. Adv. Space Res. 2019, 63, 3333–3345. [Google Scholar] [CrossRef]
- Larson, K.M.; Nievinski, F.G. GPS snow sensing: Results from the earthscope plate boundary observatory. GPS Solut. 2013, 17, 41–52. [Google Scholar] [CrossRef]
- Li, Y.; Chang, X.; Yu, K.; Wang, S.; Li, J. Estimation of snow depth using pseudorange and carrier phase observations of GNSS single-frequency signal. GPS Solut. 2019, 23, 118. [Google Scholar] [CrossRef]
- Lei, J.; Li, W.; Zhang, S. Improving Consistency of GNSS-IR Reflector Height Estimates between Different Frequencies Using Multichannel Singular Spectrum Analysis. Remote Sens. 2023, 15, 1779. [Google Scholar] [CrossRef]
- Su, M.; Zheng, F.; Shang, J.; Qiao, L.; Qiu, Z.; Zhang, H.; Zheng, J. Influence of flooding on GPS carrier-to-noise ratio and water content variation analysis: A case study in Zhengzhou, China. GPS Solut. 2023, 27, 21. [Google Scholar] [CrossRef]
- Wan, W.; Larson, K.M.; Small, E.E.; Chew, C.C.; Braun, J.J. Using geodetic GPS receivers to measure vegetation water content. GPS Solut. 2015, 19, 237–248. [Google Scholar] [CrossRef]
- Camps, A.; Alonso-Arroyo, A.; Park, H.; Onrubia, R.; Pascual, D.; Querol, J. L-band vegetation optical depth estimation using transmitted gnss signals: Application to gnss-reflectometry and positioning. Remote Sens. 2020, 12, 2352. [Google Scholar] [CrossRef]
- Martin-Neira, M. A passive reflectometry and interferometry system (PARIS): Application to ocean altimetry. ESA J. 1993, 17, 331–355. [Google Scholar]
- Lowe, S.T.; Zuffada, C.; Chao, Y.; Kroger, P.; Young, L.E.; LaBrecque, J.L. 5-cm-Precision aircraft ocean altimetry using GPS reflections. Geophys. Res. Lett. 2002, 29, 13-1–13-4. [Google Scholar] [CrossRef]
- Li, W.; Yang, D.; D’Addio, S.; Martín-Neira, M. Partial Interferometric Processing of Reflected GNSS Signals for Ocean Altimetry. IEEE Geosci. Remote Sens. Lett. 2014, 11, 1509–1513. [Google Scholar] [CrossRef]
- Clarizia, M.P.; Ruf, C.; Cipollini, P.; Zuffada, C. First spaceborne observation of sea surface height using GPS-reflectometry. Geophys. Res. Lett. 2016, 43, 767–774. [Google Scholar] [CrossRef]
- Ban, W.; Yu, K.; Zhang, X. GEO-satellite-based reflectometry for soil moisture estimation: Signal modeling and algorithm development. IEEE Trans. Geosci. Remote Sens. 2018, 56, 1829–1838. [Google Scholar] [CrossRef]
- Calabia, A.; Molina, I.; Jin, S. Soil moisture content from GNSS reflectometry using dielectric permittivity from Fresnel reflection coefficients. Remote Sens. 2020, 12, 122. [Google Scholar] [CrossRef]
- Yan, Q.; Huang, W.; Jin, S.; Jia, Y. Pan-tropical soil moisture mapping based on a three-layer model from CYGNSS GNSS-R data. Remote Sens. Environ. 2020, 247, 111944. [Google Scholar] [CrossRef]
- Munoz-Martin, J.F.; Rodriguez-Alvarez, N.; Bosch-Lluis, X.; Oudrhiri, K. Analysis of polarimetric GNSS-R Stokes parameters of the Earth’s land surface. Remote Sens. Environ. 2023, 287, 113491. [Google Scholar] [CrossRef]
- Yu, K.; Li, Y.; Jin, T.; Chang, X.; Wang, Q.; Li, J. GNSS-R-based snow water equivalent estimation with empirical modeling and enhanced SNR-based snow depth estimation. Remote Sens. 2020, 12, 3905. [Google Scholar] [CrossRef]
- Hu, Y.; Yuan, X.; Liu, W.; Hu, Q.; Wickert, J.; Jiang, Z. An SVM-based snow detection algorithm for GNSS-R snow depth retrievals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2022, 15, 6046–6052. [Google Scholar] [CrossRef]
- Guo, W.; Du, H.; Guo, C.; Southwell, B.J.; Cheong, J.W.; Dempster, A.G. Information fusion for GNSS-R wind speed retrieval using statistically modified convolutional neural network. Remote Sens. Environ. 2022, 272, 112934. [Google Scholar] [CrossRef]
- Rodriguez-Alvarez, N.; Bosch-Lluis, X.; Camps, A.; Vall-Llossera, M.; Valencia, E.; Marchan-Hernandez, J.F.; Ramos-Perez, I. Soil moisture retrieval using GNSS-R techniques: Experimental results over a bare soil field. IEEE Trans Geosci. Remote Sens. 2009, 47, 3616–3624. [Google Scholar] [CrossRef]
- Larson, K.M.; Small, E.E.; Gutmann, E.; Bilich, A.; Axelrad, P.; Braun, J. Using GPS multipath to measure soil moisture fluctuations: Initial results. GPS Solut. 2008, 12, 173–177. [Google Scholar] [CrossRef]
- Chew, C.C.; Small, E.E.; Larson, K.M.; Zavorotny, V.U. Effects of Near-Surface Soil Moisture on GPS SNR Data: Development of a Retrieval Algorithm for Soil Moisture. IEEE Trans. Geosci. Remote Sens. 2014, 52, 537–543. [Google Scholar] [CrossRef]
- Roussel, N.; Frappart, F.; Ramillien, G.; Darrozes, J.; Baup, F.; Lestarquit, L.; Ha, M.C. Detection of Soil Moisture Variations Using GPS and GLONASS SNR Data for Elevation Angles Ranging From 2 degrees to 70 degrees. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4781–4794. [Google Scholar] [CrossRef]
- Chew, C.C.; Small, E.E.; Larson, K.M. An algorithm for soil moisture estimation using GPS-interferometric reflectometry for bare and vegetated soil. GPS Solut. 2016, 20, 525–537. [Google Scholar] [CrossRef]
- Small, E.E.; Larson, K.M.; Chew, C.; Dong, J.; Ochsner, T.E. Validation of GPS-IR soil moisture retrievals: Comparison of different algorithms to remove vegetation effects. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 9, 4759–4770. [Google Scholar] [CrossRef]
- Zhang, S.; Calvet, J.C.; Darrozes, J.; Roussel, N.; Frappart, F.; Bouhours, G. Deriving surface soil moisture from reflected GNSS signal observations from a grassland site in southwestern France. Hydrol. Earth Syst. Sci. 2018, 22, 1931–1946. [Google Scholar] [CrossRef]
- Lv, J.; Zhang, R.; Tu, J.; Liao, M.; Pang, J.; Yu, B.; Li, K.; Xiang, W.; Fu, Y.; Liu, G. A GNSS-IR Method for Retrieving Soil Moisture Content from Integrated Multi-Satellite Data That Accounts for the Impact of Vegetation Moisture Content. Remote Sens. 2021, 13, 2442. [Google Scholar] [CrossRef]
- Ran, Q.; Zhang, B.; Yao, Y.; Yan, X.; Li, J. Editing arcs to improve the capacity of GNSS-IR for soil moisture retrieval in undulating terrains. GPS Solut. 2022, 26, 19. [Google Scholar] [CrossRef]
- Tabibi, S.; Nievinski, F.G.; van Dam, T.; Monico, J.F. Assessment of modernized GPS L5 SNR for ground-based multipath reflectometry applications. Adv. Space Res. 2015, 55, 1104–1116. [Google Scholar] [CrossRef]
- Vey, S.; Güntner, A.; Wickert, J.; Blume, T.; Ramatschi, M. Long-term soil moisture dynamics derived from GNSS interferometric reflectometry: A case study for Sutherland, South Africa. GPS Solut. 2016, 20, 641–654. [Google Scholar] [CrossRef]
- Yang, T.; Wan, W.; Chen, X.; Chu, T.; Qiao, Z.; Liang, H.; Wei, J.; Wang, G.; Hong, Y. Land surface characterization using BeiDou signal-to-noise ratio observations. GPS Solut. 2019, 23, 32. [Google Scholar] [CrossRef]
- Chen, K.; Cao, X.; Shen, F.; Ge, Y. An Improved Method of Soil Moisture Retrieval Using Multi-Frequency SNR Data. Remote Sens. 2021, 13, 3725. [Google Scholar] [CrossRef]
- Nie, S.; Wang, Y.; Tu, J.; Li, P.; Xu, J.; Li, N.; Wang, M.; Huang, D.; Song, J. Retrieval of Soil Moisture Content Based on Multisatellite Dual-Frequency Combination Multipath Errors. Remote Sens. 2022, 14, 3193. [Google Scholar] [CrossRef]
- Liang, Y.; Lai, J.; Ren, C.; Lu, X.; Zhang, Y.; Ding, Q.; Hu, X. GNSS-IR multisatellite combination for soil moisture retrieval based on wavelet analysis considering detection and repair of abnormal phases. Measurement 2022, 203, 111881. [Google Scholar] [CrossRef]
- Han, M.; Zhu, Y.; Yang, D.; Hong, X.; Song, S. A semi-empirical SNR model for soil moisture retrieval using GNSS SNR data. Remote Sens. 2018, 10, 280. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Q.; Zhang, S. Water levels measured with SNR using wavelet decomposition and Lomb-Scargle periodogram. GPS Solut. 2018, 22, 22. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, T.; Wang, L.; Zhang, J. Evaluation of GNSS-IR for retrieving soil moisture and vegetation growth characteristics in wheat farmland. J. Surv. Eng. 2021, 147, 04021009. [Google Scholar] [CrossRef]
- Dunn, M.J. Global Positioning Systems Wing (GPSW) Systems Engineering & Integration, Interface Specification IS-GPS-200. 2010; pp. 1–226. Available online: http://www.gps.gov/technical/icwg/IS-GPS-200E.pdf (accessed on 5 May 2023).
- Zavorotny, V.U.; Larson, K.M.; Braun, J.J.; Small, E.E.; Gutmann, E.D.; Bilich, A.L. A Physical Model for GPS Multipath Caused by Land Reflections: Toward Bare Soil Moisture Retrievals. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 100–110. [Google Scholar] [CrossRef]
- Schwarz, G.E.; Alexander, R.B. Soils Data for the Conterminous United States Derived from the NRCS State Soil Geographic (STATSGO) Data Base. US Geological Survey Open-File Report. 1995; pp. 95–449. Available online: https://water.usgs.gov/lookup/getspatial?ussoils (accessed on 5 May 2023).
- Bilich, A.; Larson, K.M. Correction to “mapping the GPS multipath environment using the signal to noise ratio (SNR)”. Radio Sci. 2008, 43, 3442–3446. [Google Scholar] [CrossRef]
- Tong, Z.; Su, M.; Zheng, F.; Shang, J.; Wu, J.; Shen, X.; Chang, X. Accurate Retrieval of the Whole Flood Process from Occurrence to Recession Based on GPS Original CNR, Fitted CNR, and Seamless CNR Series. Remote Sens. 2023, 15, 2316. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.S.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-siteary time series analysis. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1988, 454, 903–995. [Google Scholar] [CrossRef]
- Beckheinrich, J.; Hirrle, A.; Schön, S.; Beyerle, G.; Semmling, M.; Wickert, J. Water level monitoring of the Mekong Delta using GNSS reflectometry technique. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 3798–3801. [Google Scholar] [CrossRef]
- Johnson, M.L.; Correia, J.J.; Yphantis, D.A.; HalvorSON, H.R. Analysis of data from the analytical ultracentrifuge by nonlinear least-squares techniques. Biophys. J. 1981, 36, 575–588. [Google Scholar] [CrossRef]
- Jing, L.; Yang, L.; Yang, W.; Xu, T.; Gao, F.; Lu, Y.; Sun, B.; Yang, D.; Hong, X.; Wang, N.; et al. Robust Kalman Filter Soil Moisture Inversion Model Using GPS SNR Data—A Dual-Band Data Fusion Approach. Remote Sens. 2021, 13, 4013. [Google Scholar] [CrossRef]
- Huber, P.J.; Ronchetti, E.M. Robust Statistics. In Wiley Series in Probability and Statistics, 2nd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Yang, Y. Robust Estimation for Dependent Observations. Manuscr. Geod. 1994, 19, 10–17. [Google Scholar]
- Yang, Y.; Song, L.; Xu, T. Robust estimator for correlated observations based on bifactor equivalent weights. J. Geod. 2002, 76, 353–358. [Google Scholar] [CrossRef]






| Location | Receiver Type | Antenna Type | Sampling Rate |
|---|---|---|---|
| 43°52′52″N, 104°11′09″W | Trimble NERT9 | TRM59800.80 SCIT | 30 Hz |
| Degree of Cross-Correlation | Very Weak Correlation | Weak Correlation | Medium Correlation | Strong Correlation | Very Strong Correlation |
|---|---|---|---|---|---|
| correlation coefficient | 0~0.2 | 0.2~0.4 | 0.4~0.6 | 0.6~0.8 | 0.8~1 |
| IMF | r | |
|---|---|---|
| PRN14 | PRN32 | |
| SNR | 1 | 1 |
| IMF1 | 0.064 | 0.015 |
| IMF2 | 0.065 | 0.050 |
| IMF3 | 0.013 | 0.053 |
| IMF4 | 0.174 | 0.051 |
| IMF5 | 0.018 | 0.056 |
| IMF6 | 0.703 | 0.208 |
| IMF7 | 0.989 | 0.925 |
| IMF8 | 0.989 | 0.989 |
| IMF9 | 0.989 | 0.989 |
| residual | 0.905 | 0.988 |
| Satellite Number | Number of Decomposition Layers of EMD | Number of Layers of Combined Modulation Term | Number of Layers of Combined Trend Term |
|---|---|---|---|
| PRN 01 | 10 | IMF1–4 | IMF5–10 |
| PRN 02 | 10 | IMF1–8 | IMF9–10 |
| PRN 03 | 10 | IMF1–8 | IMF9–10 |
| PRN 04 | 10 | IMF1–8 | IMF9–10 |
| PRN 05 | 10 | IMF1–9 | IMF10 |
| PRN 06 | 10 | IMF1–8 | IMF9–10 |
| PRN 07 | 10 | IMF1–9 | IMF10 |
| PRN 09 | 10 | IMF1–6 | IMF7–10 |
| PRN 10 | 10 | IMF1–7 | IMF8–10 |
| PRN 11 | 9 | IMF1–6 | IMF7–10 |
| PRN 12 | 10 | IMF1–7 | IMF8–10 |
| PRN 13 | 10 | IMF1–7 | IMF8–10 |
| PRN 14 | 10 | IMF1–6 | IMF7–10 |
| PRN 15 | 10 | IMF1–8 | IMF9–10 |
| PRN 16 | 10 | IMF1–6 | IMF7–10 |
| PRN 18 | 10 | IMF1–8 | IMF9–10 |
| PRN 19 | 9 | IMF1–8 | IMF9–10 |
| PRN 20 | 10 | IMF1–5 | IMF6–10 |
| PRN 21 | 10 | IMF1–8 | IMF9–10 |
| PRN 22 | 10 | IMF1–8 | IMF9–10 |
| PRN 23 | 10 | IMF1–8 | IMF9–10 |
| PRN 24 | 10 | IMF1–6 | IMF7–10 |
| PRN 25 | 10 | IMF1–8 | IMF9–10 |
| PRN 27 | 10 | IMF1–7 | IMF8–10 |
| PRN 28 | 10 | IMF1–6 | IMF7–10 |
| PRN 29 | 10 | IMF1–8 | IMF9–10 |
| PRN 30 | 9 | IMF1–8 | IMF9 |
| PRN 32 | 10 | IMF1–6 | IMF7–10 |
| Satellite Number | (S/J) | Satellite Number | (S/J) | ||
|---|---|---|---|---|---|
| PRN 04 | S | <0.4 | PRN 01 | J | <0.4 |
| PRN 09 | S | <0.4 | PRN 03 | J | <0.4 |
| PRN 11 | S | <0.4 | PRN 11 | J | <0.4 |
| PRN 13 | S | <0.4 | PRN 16 | J | <0.4 |
| PRN 27 | S | <0.4 | PRN 22 | J | <0.4 |
| PRN 31 | S | <0.4 | PRN 23 | J | <0.4 |
| PRN 22 | S | <0.4 | PRN 27 | J | <0.4 |
| PRN 03 | S | <0.4 | PRN 18 | J | <0.4 |
| PRN 32 | S | 0.4–0.5 | PRN 21 | J | <0.4 |
| PRN 19 | S | 0.4–0.5 | PRN 24 | J | <0.4 |
| PRN 24 | S | 0.5–0.6 | PRN 31 | J | <0.4 |
| PRN 01 | S | 0.5–0.6 | PRN 15 | J | <0.4 |
| PRN 16 | S | 0.5–0.6 | PRN 13 | J | 0.5–0.6 |
| PRN 14 | S | 0.6–0.7/0.7–0.8 | PRN 32 | J | 0.5–0.6 |
| PRN 30 | S | 0.6–0.7/0.7–0.8 | PRN 09 | J | 0.6–0.7 |
| PRN 23 | S | 0.6–0.7/0.7–0.8 | PRN 04 | J | 0.6–0.7 |
| PRN 07 | S | 0.6–0.7/0.7–0.8 | PRN 14 | J | 0.7–0.8 |
| Scheme | Method 2 | |
|---|---|---|
| 2 | >0.4 | PRN 19, 24, 01, 16, 30, 23, 07,13, 32, 09, 04, 14 |
| 3 | >0.5 | PRN 24, 01, 16, 30, 23, 07, 13, 32, 09, 04, 14 |
| 4 | >0.6 | PRN 30, 23, 07, 09, 04, 14 |
| 5 | >0.7 | PRN 30, 23, 07, 14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ding, Q.; Liang, Y.; Liang, X.; Ren, C.; Yan, H.; Liu, Y.; Zhang, Y.; Lu, X.; Lai, J.; Hu, X. Soil Moisture Retrieval Using GNSS-IR Based on Empirical Modal Decomposition and Cross-Correlation Satellite Selection. Remote Sens. 2023, 15, 3218. https://doi.org/10.3390/rs15133218
Ding Q, Liang Y, Liang X, Ren C, Yan H, Liu Y, Zhang Y, Lu X, Lai J, Hu X. Soil Moisture Retrieval Using GNSS-IR Based on Empirical Modal Decomposition and Cross-Correlation Satellite Selection. Remote Sensing. 2023; 15(13):3218. https://doi.org/10.3390/rs15133218
Chicago/Turabian StyleDing, Qin, Yueji Liang, Xingyong Liang, Chao Ren, Hongbo Yan, Yintao Liu, Yan Zhang, Xianjian Lu, Jianmin Lai, and Xinmiao Hu. 2023. "Soil Moisture Retrieval Using GNSS-IR Based on Empirical Modal Decomposition and Cross-Correlation Satellite Selection" Remote Sensing 15, no. 13: 3218. https://doi.org/10.3390/rs15133218
APA StyleDing, Q., Liang, Y., Liang, X., Ren, C., Yan, H., Liu, Y., Zhang, Y., Lu, X., Lai, J., & Hu, X. (2023). Soil Moisture Retrieval Using GNSS-IR Based on Empirical Modal Decomposition and Cross-Correlation Satellite Selection. Remote Sensing, 15(13), 3218. https://doi.org/10.3390/rs15133218