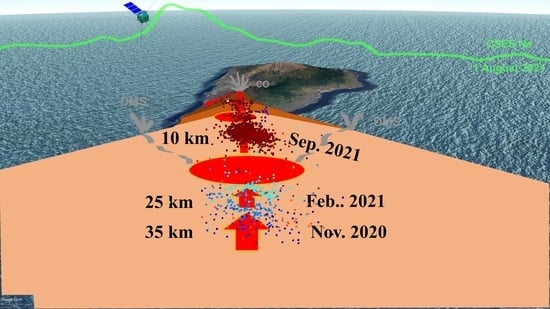
Clues of Lithosphere, Atmosphere and Ionosphere Variations Possibly Related to the Preparation of La Palma 19 September 2021 Volcano Eruption
Abstract
1. Introduction
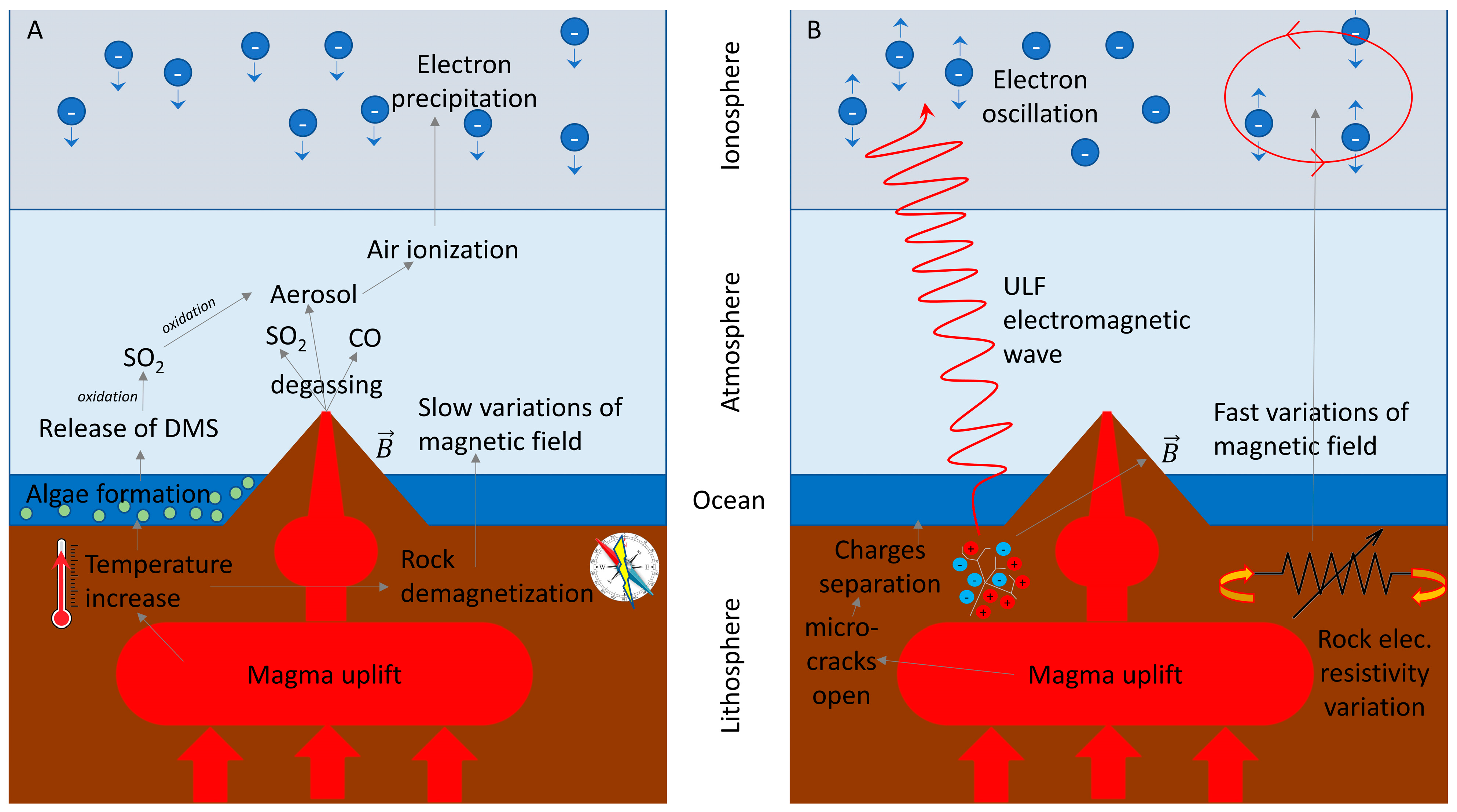
Bottom-Up Lithosphere–Atmosphere–Ionosphere Coupling Interaction Mechanisms
2. Materials and Methods
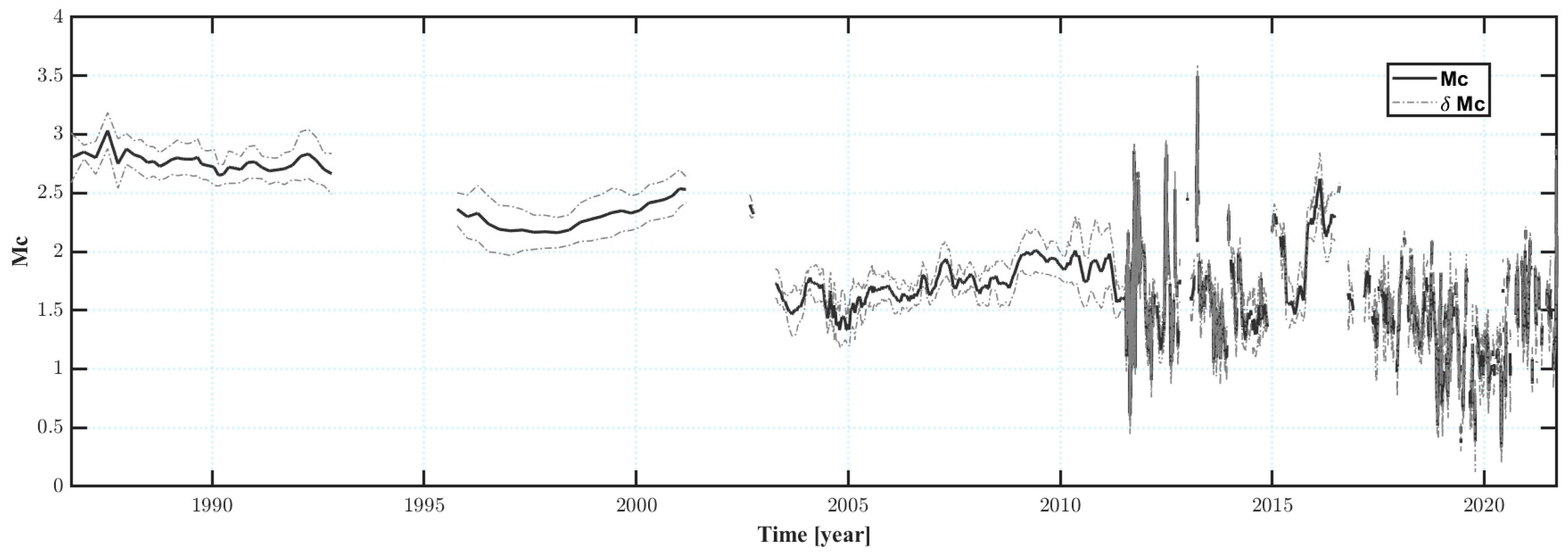
2.1. Earthquake Catalogue
2.2. Atmospheric Data and Methodologies
2.3. Ionospheric Data and Methodologies
2.3.1. CSES Electron Density Data Processing
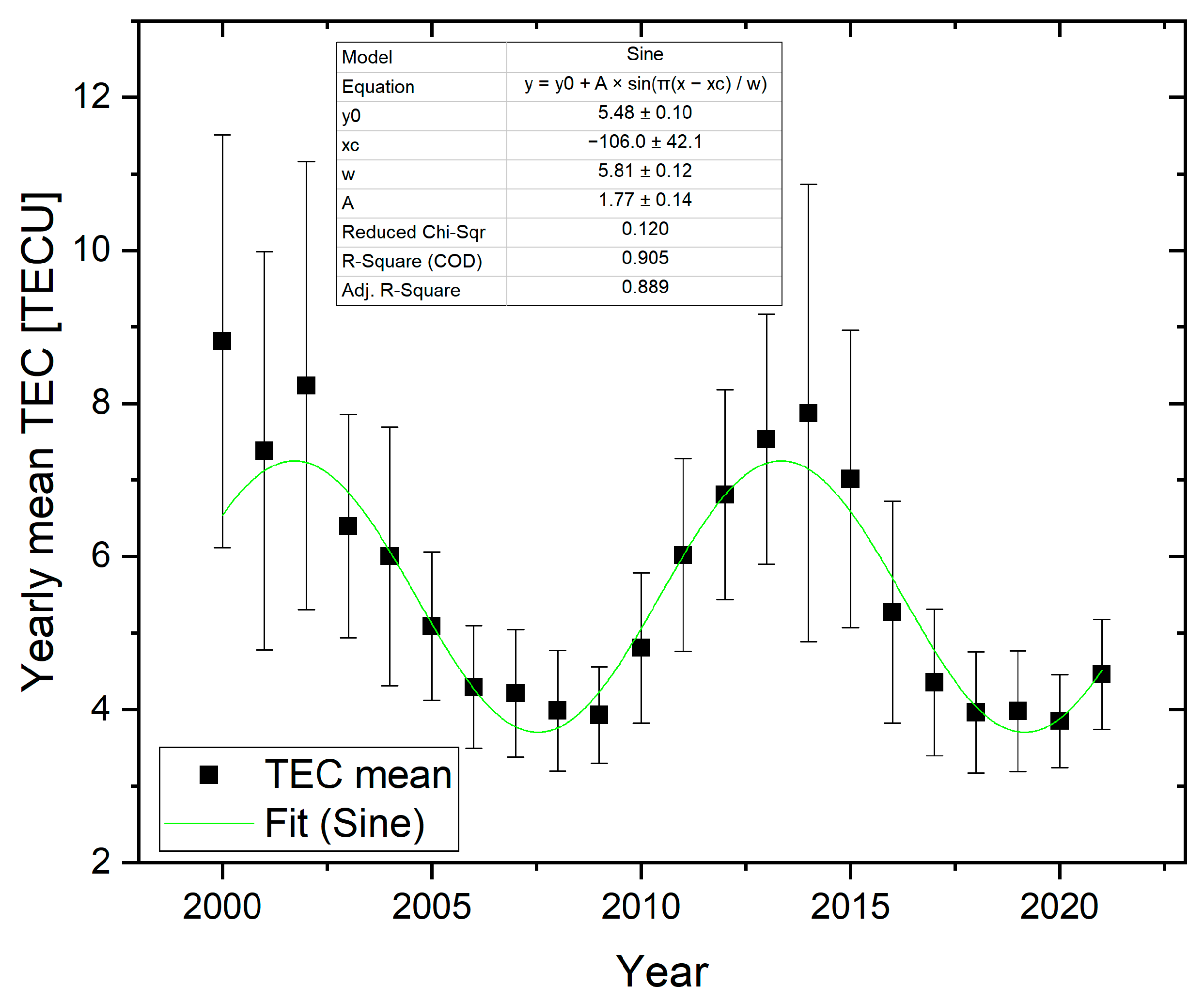
2.3.2. Total Electron Content Data Processing
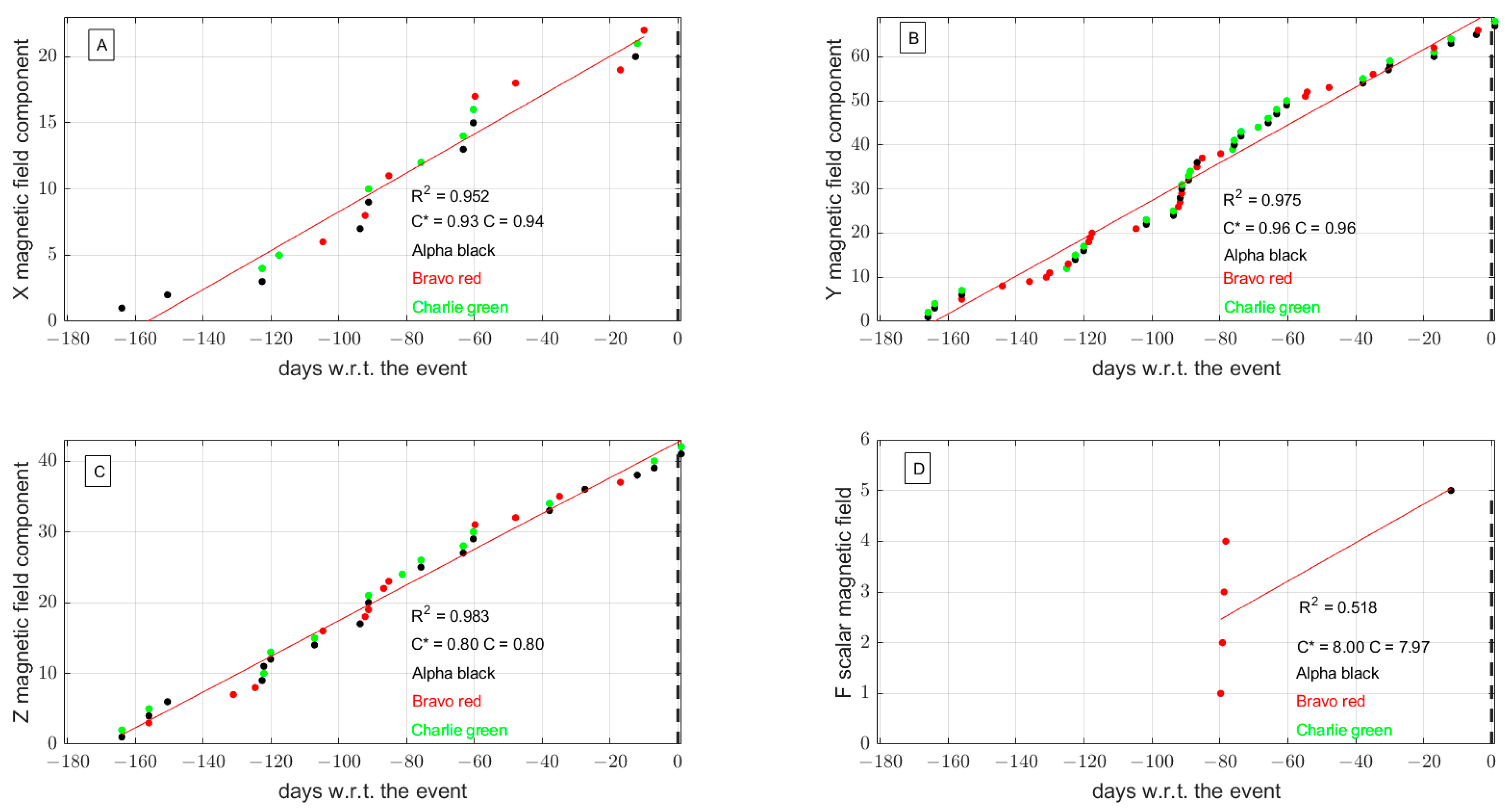
2.3.3. Swarm Magnetic Data Processing
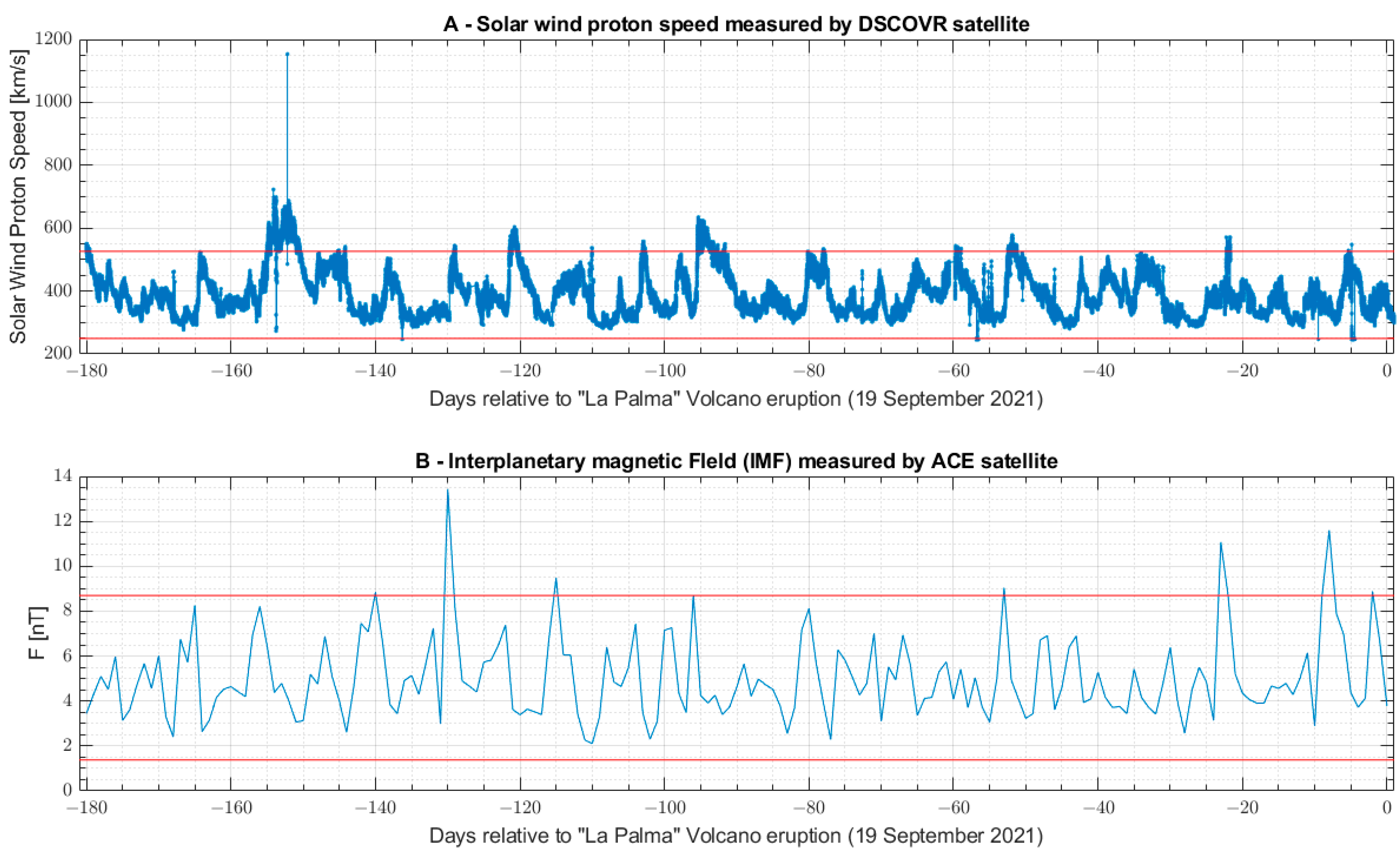
2.3.4. Monitor the Solar Activity
3. Results
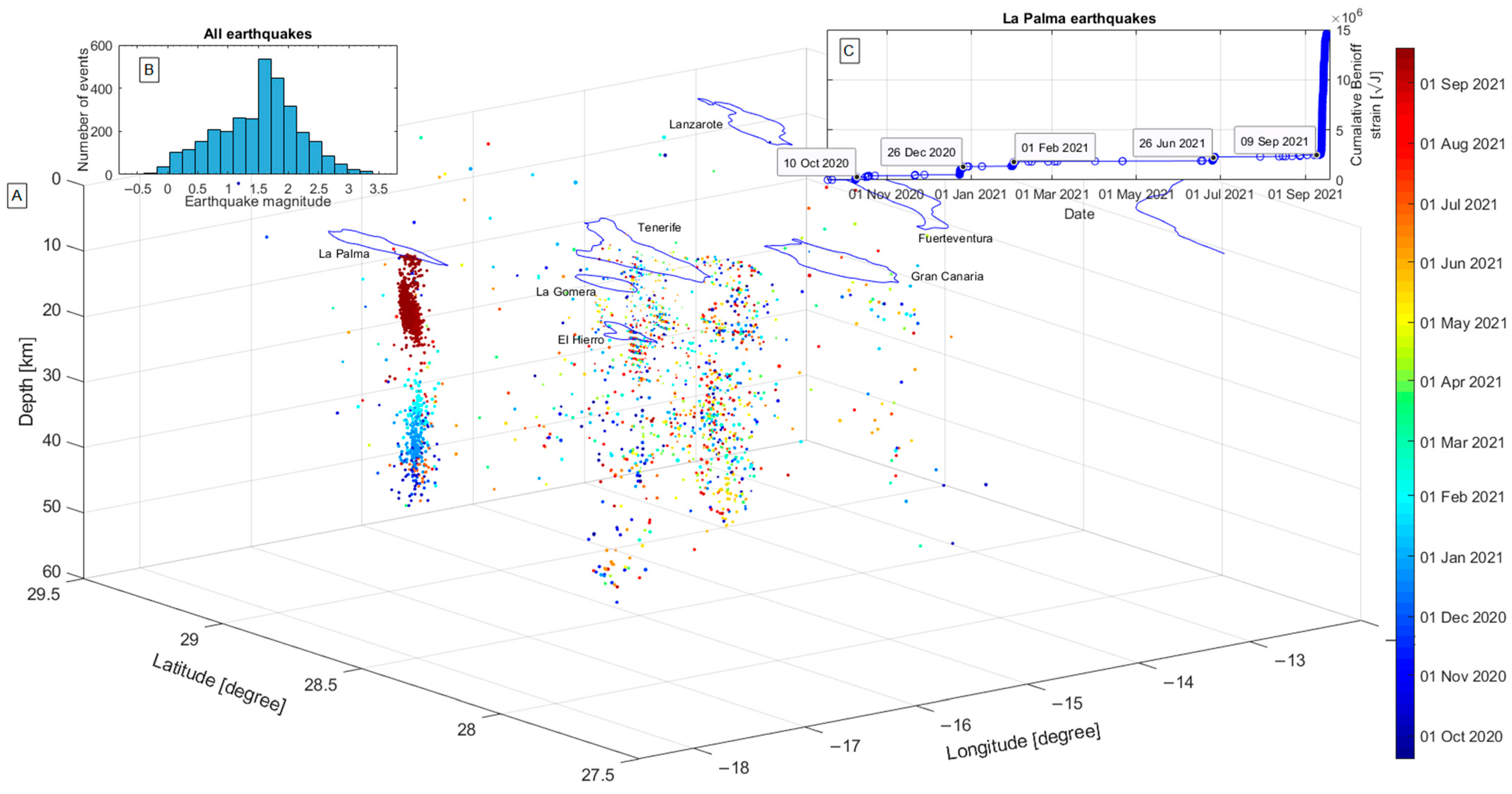
3.1. Seismicity Investigation
3.2. Atmospheric Investigation
3.2.1. Ground Geomagnetic Field
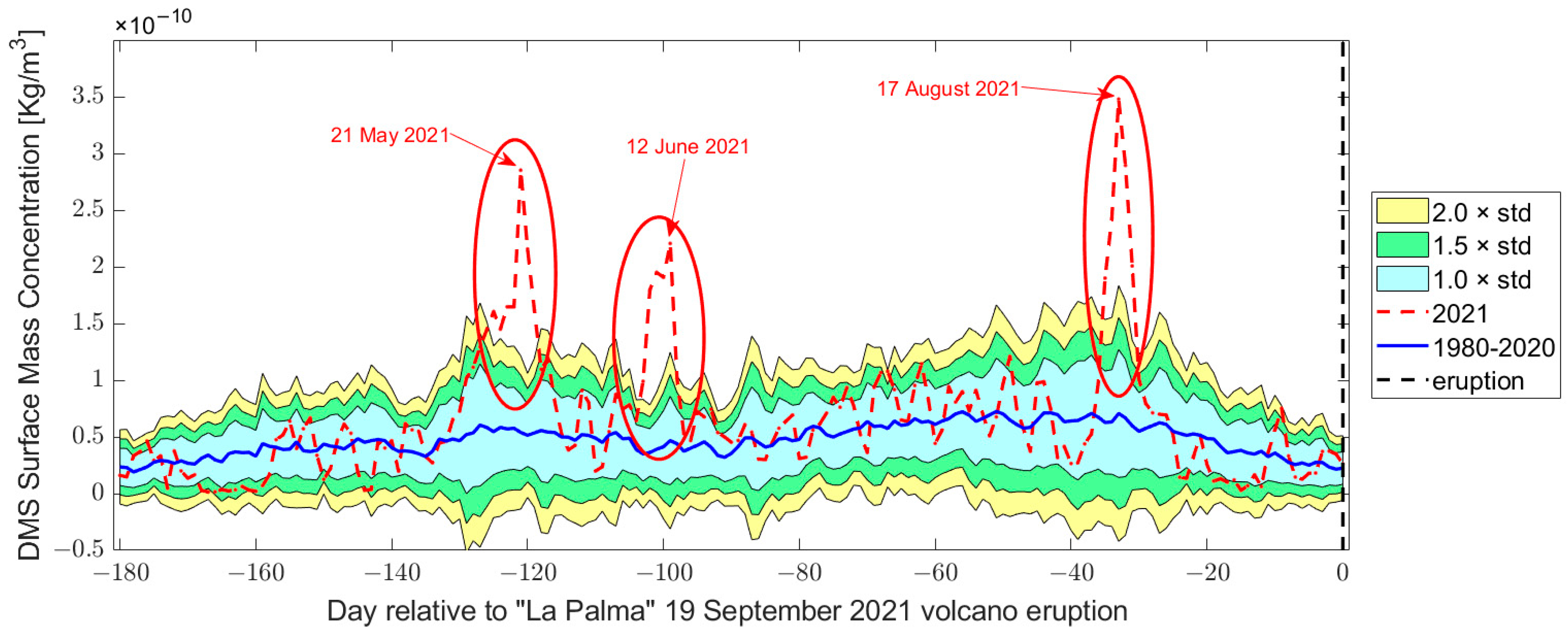
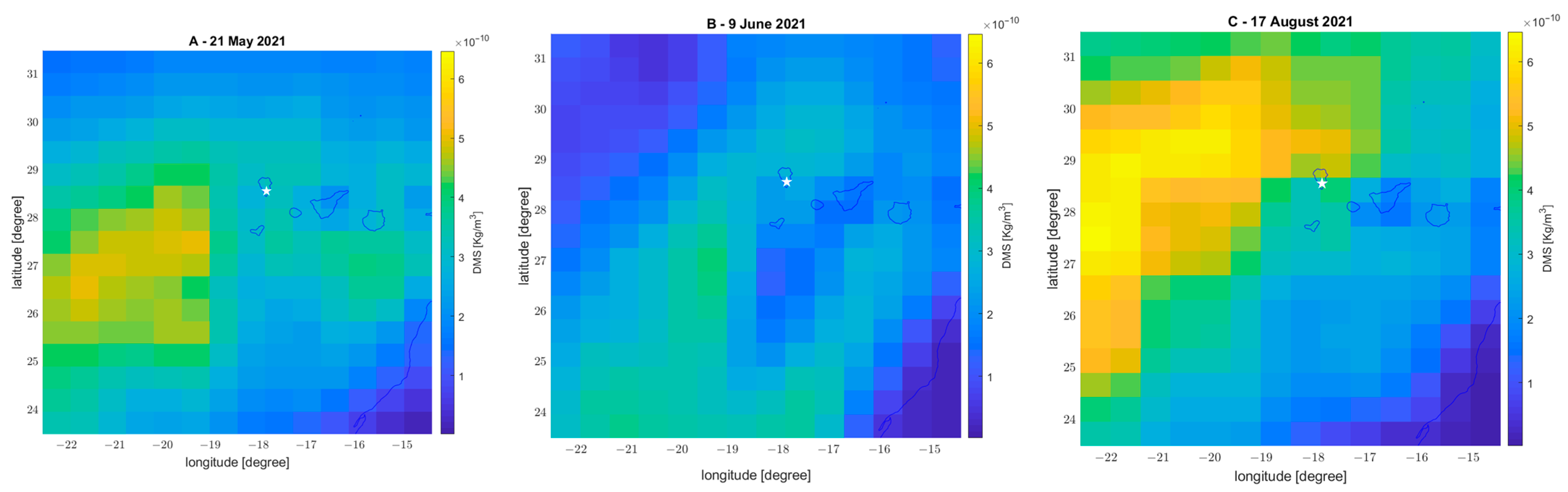
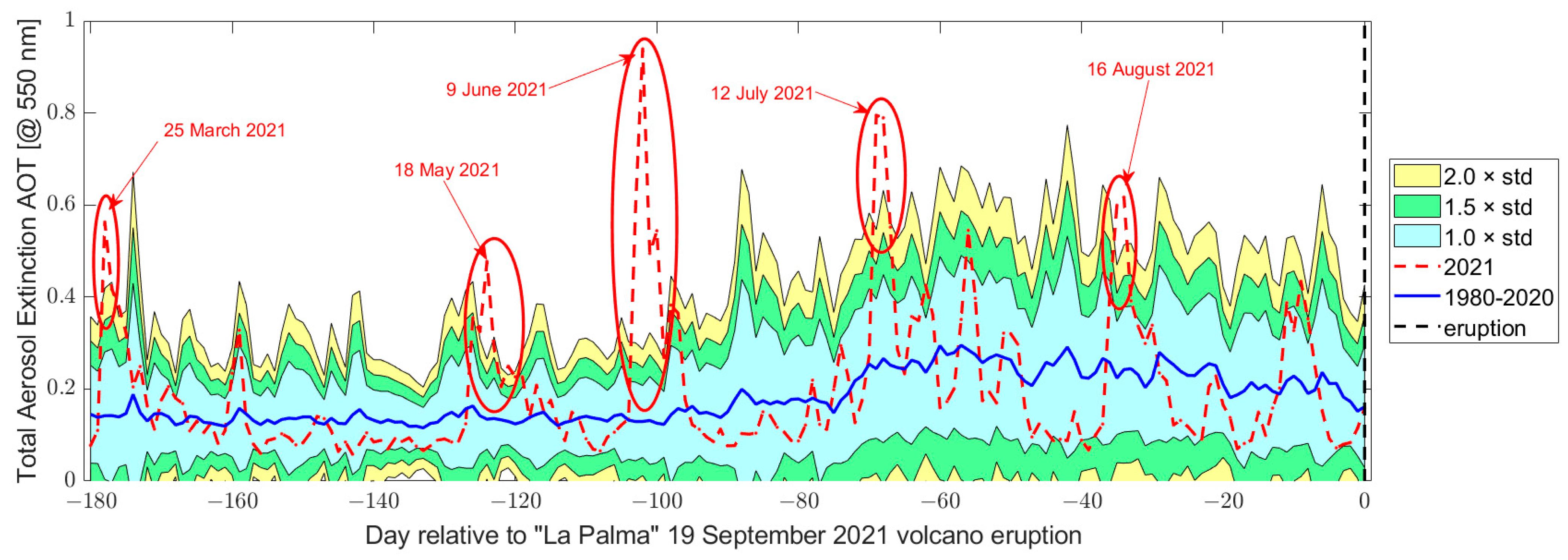
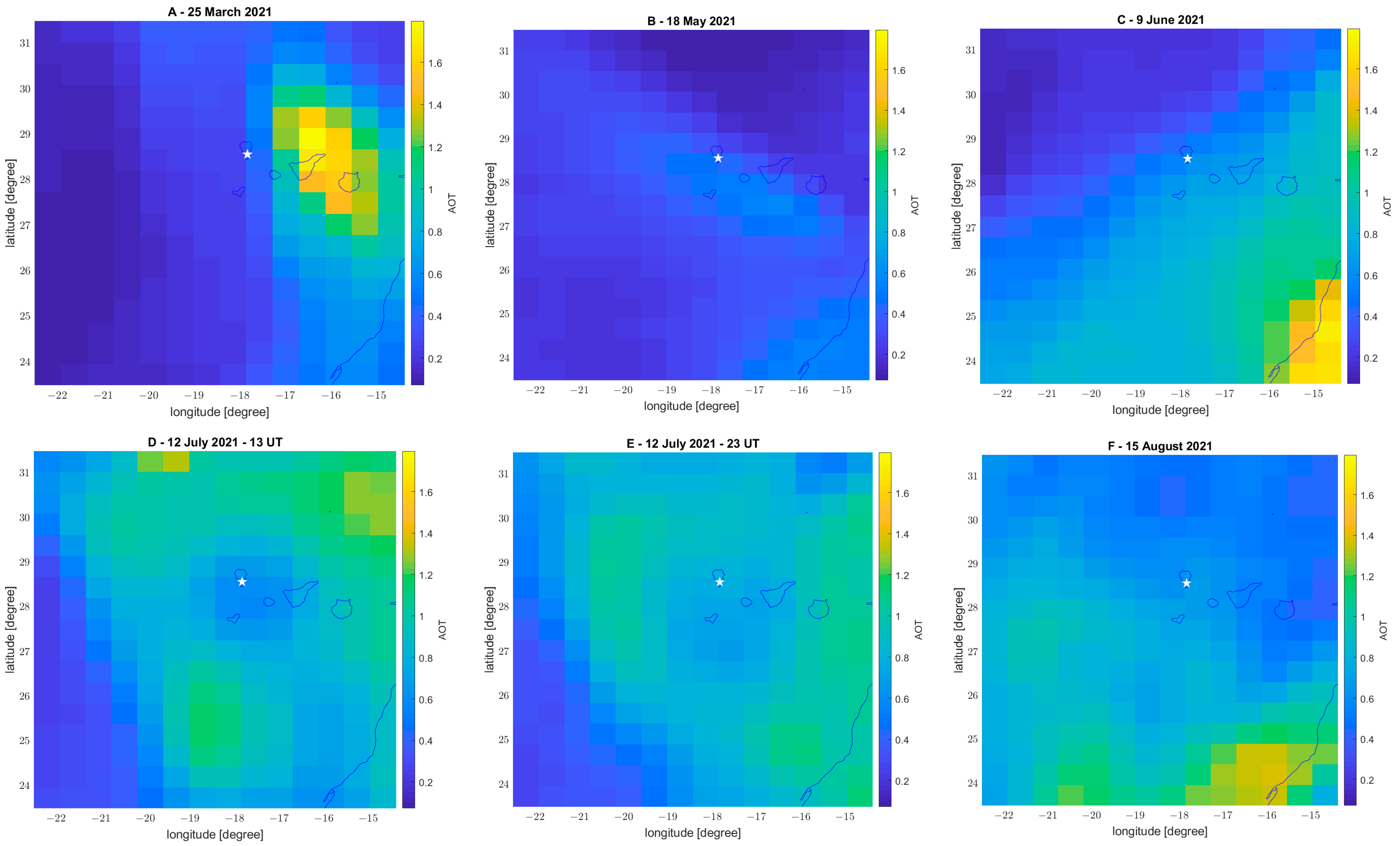
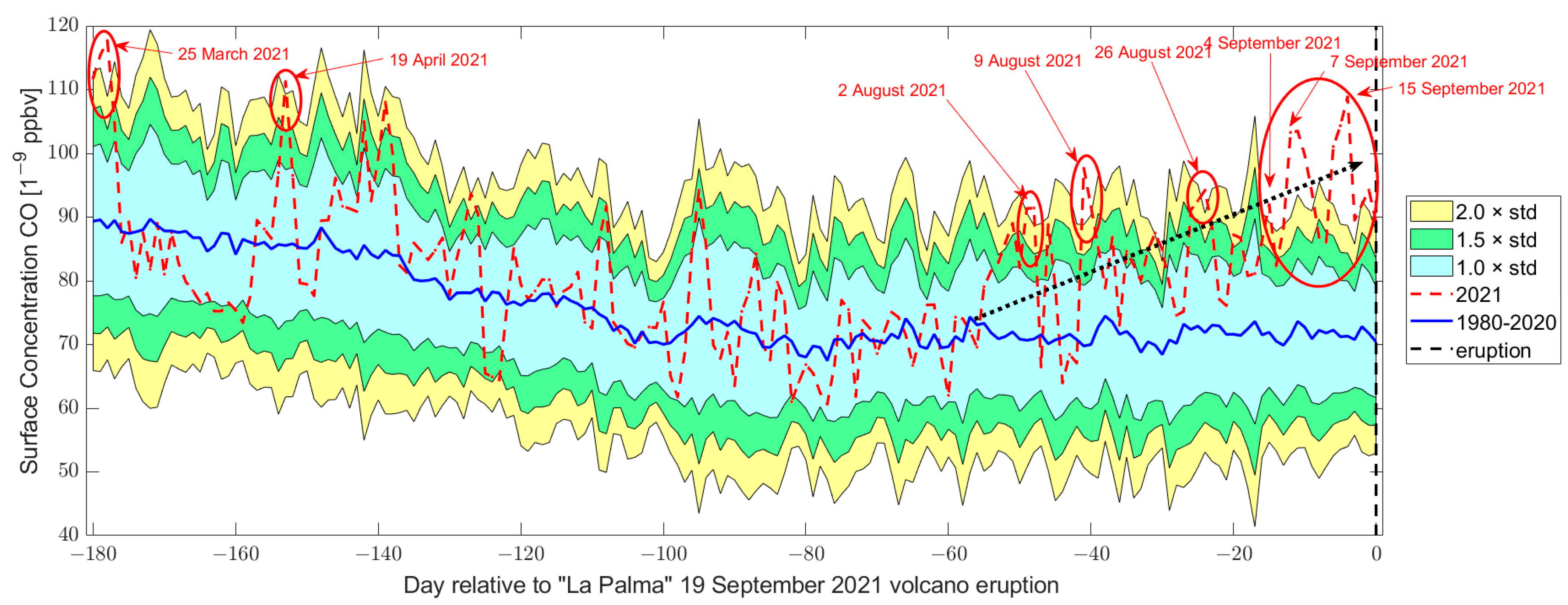
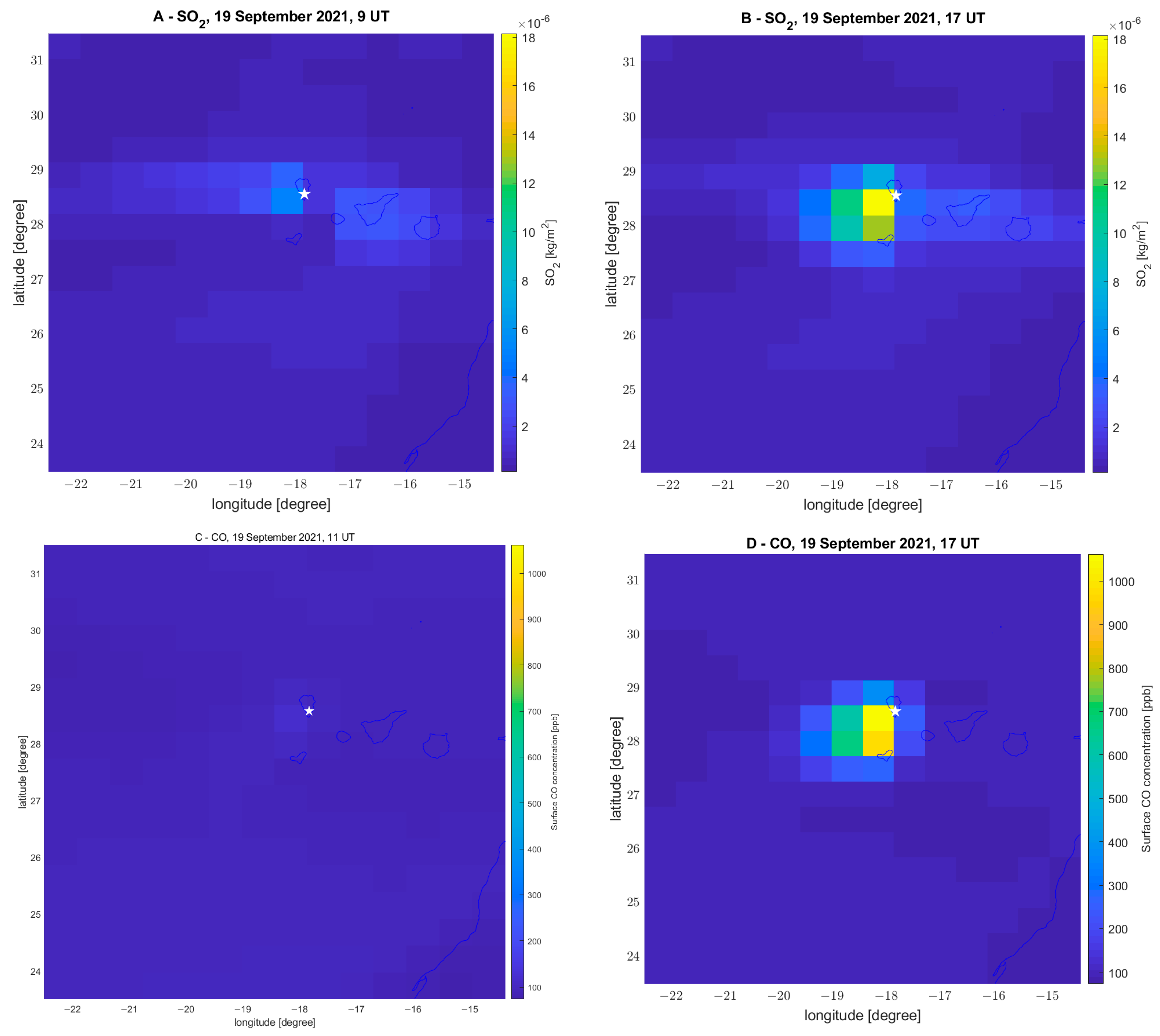
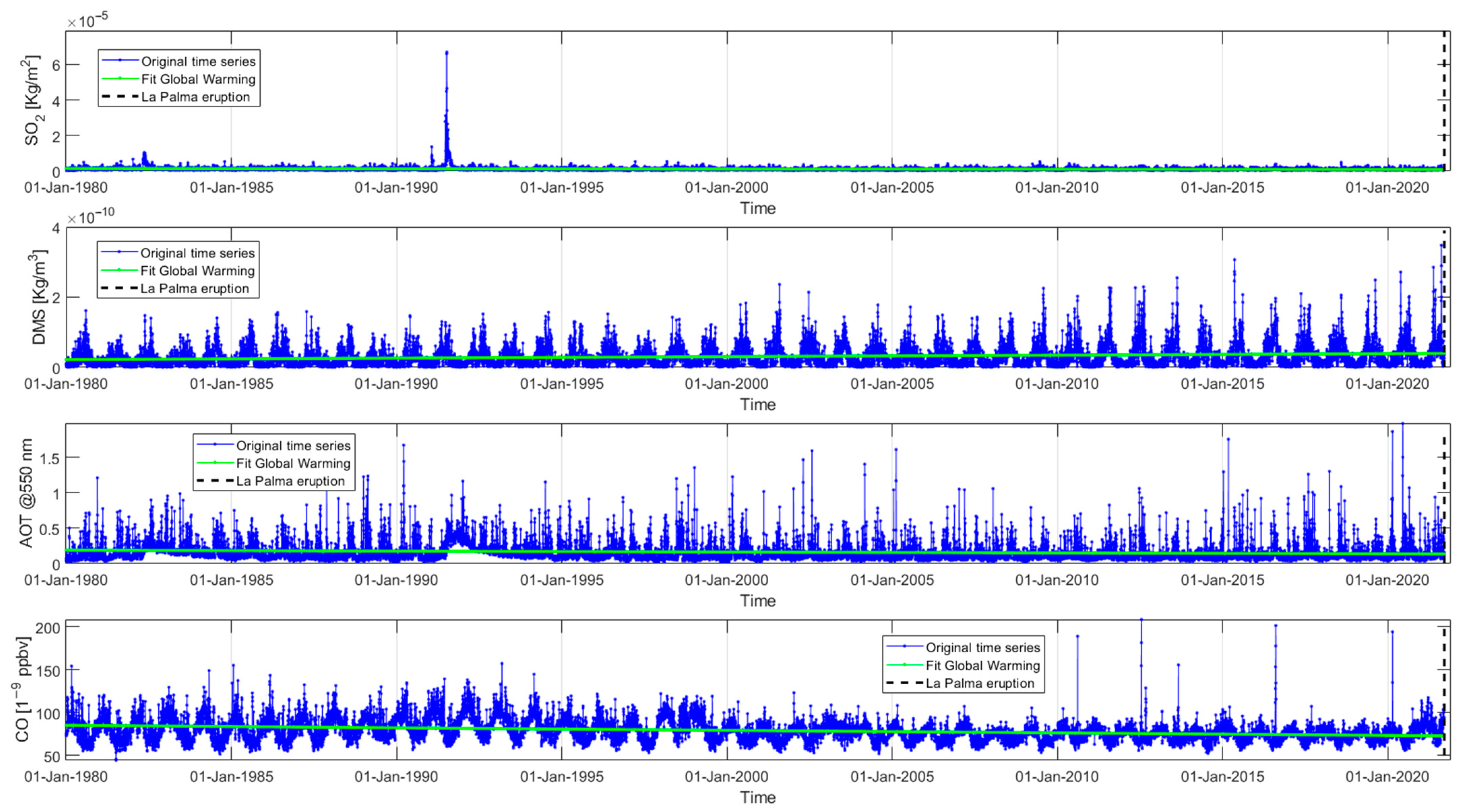
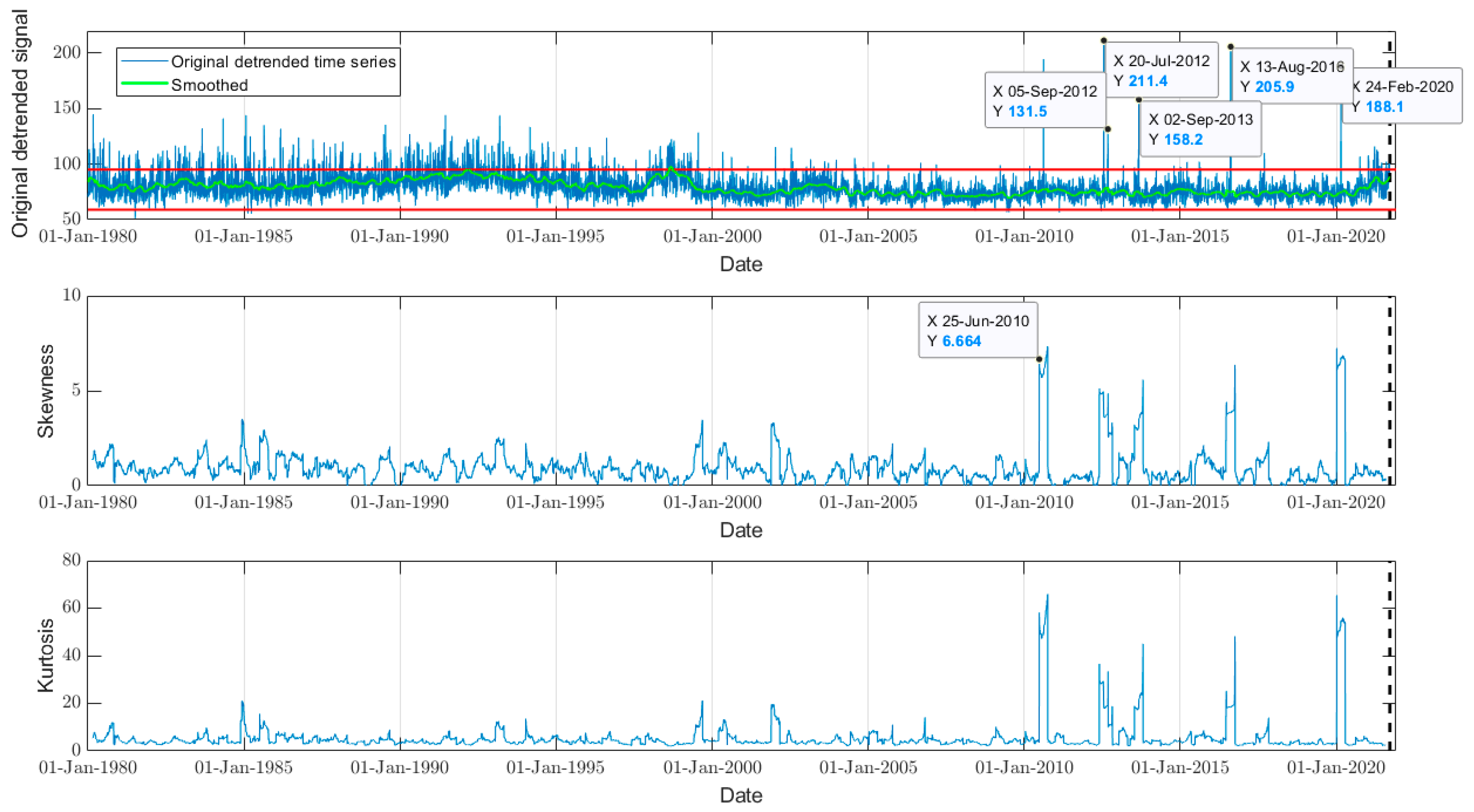
3.2.2. Atmospheric Composition Investigation (SO2, DMS, Aerosol and CO)
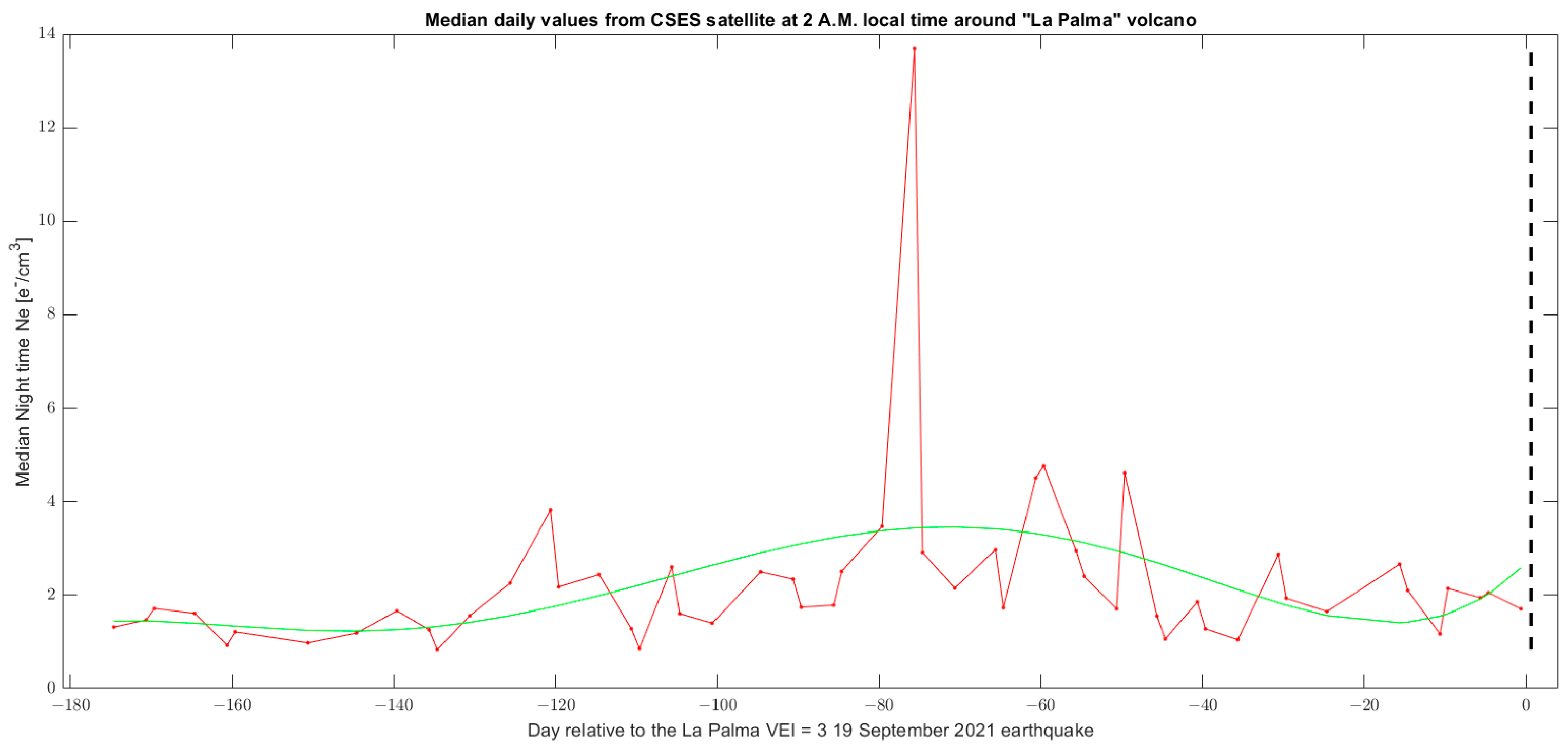
3.3. Ionospheric Investigation
4. Discussion
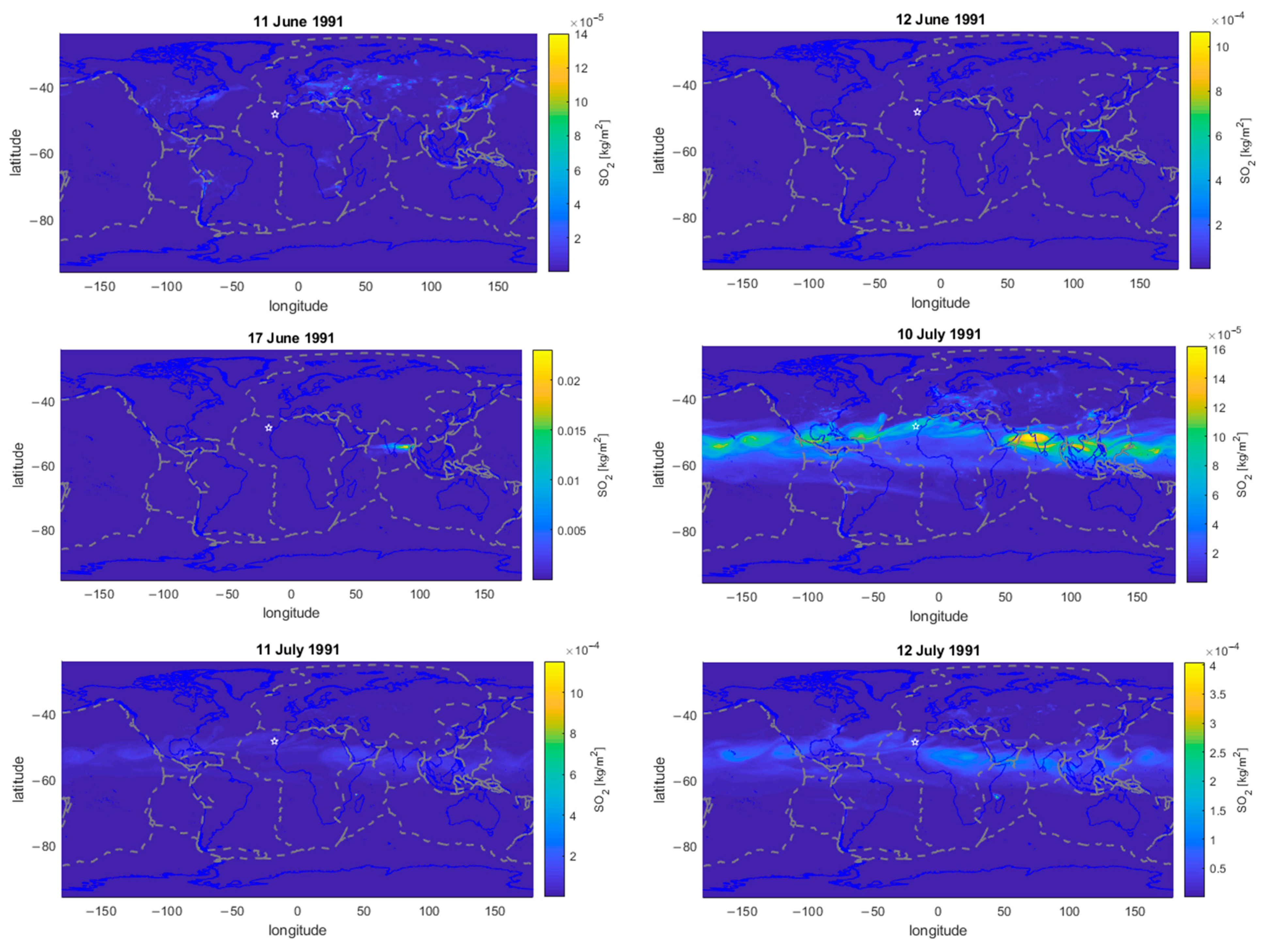
4.1. Source of the High Amount of SO2 Detected in 1991
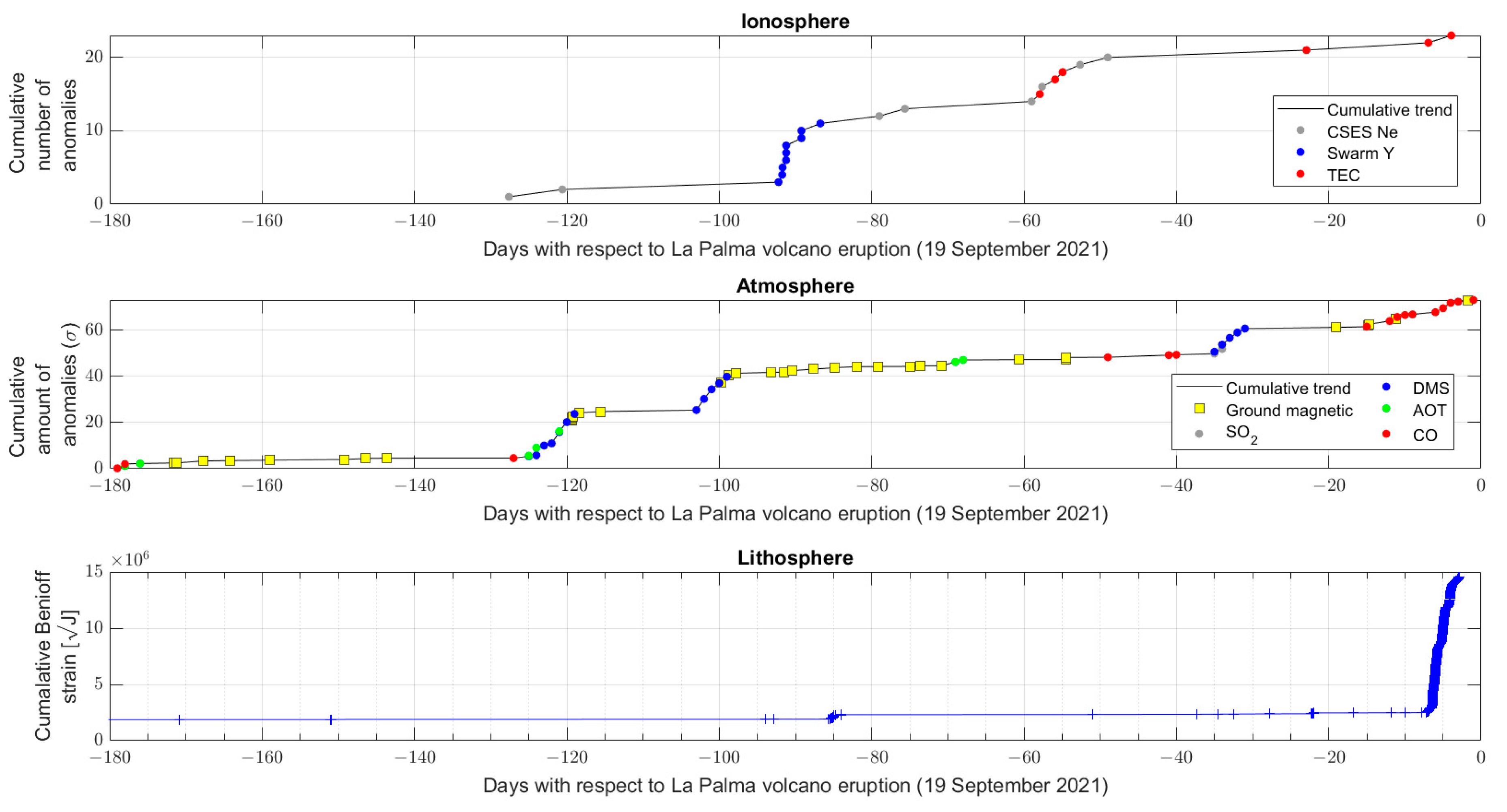
4.2. Lithosphere, Atmosphere, and Ionosphere Bottom-Up Interactions in the Six Months Preceding the 19 September 2021 La Palma Volcano Eruption
4.3. Comparison with Other Works and Longer Term Preparation Effects of the Eruption of 19 September 2021
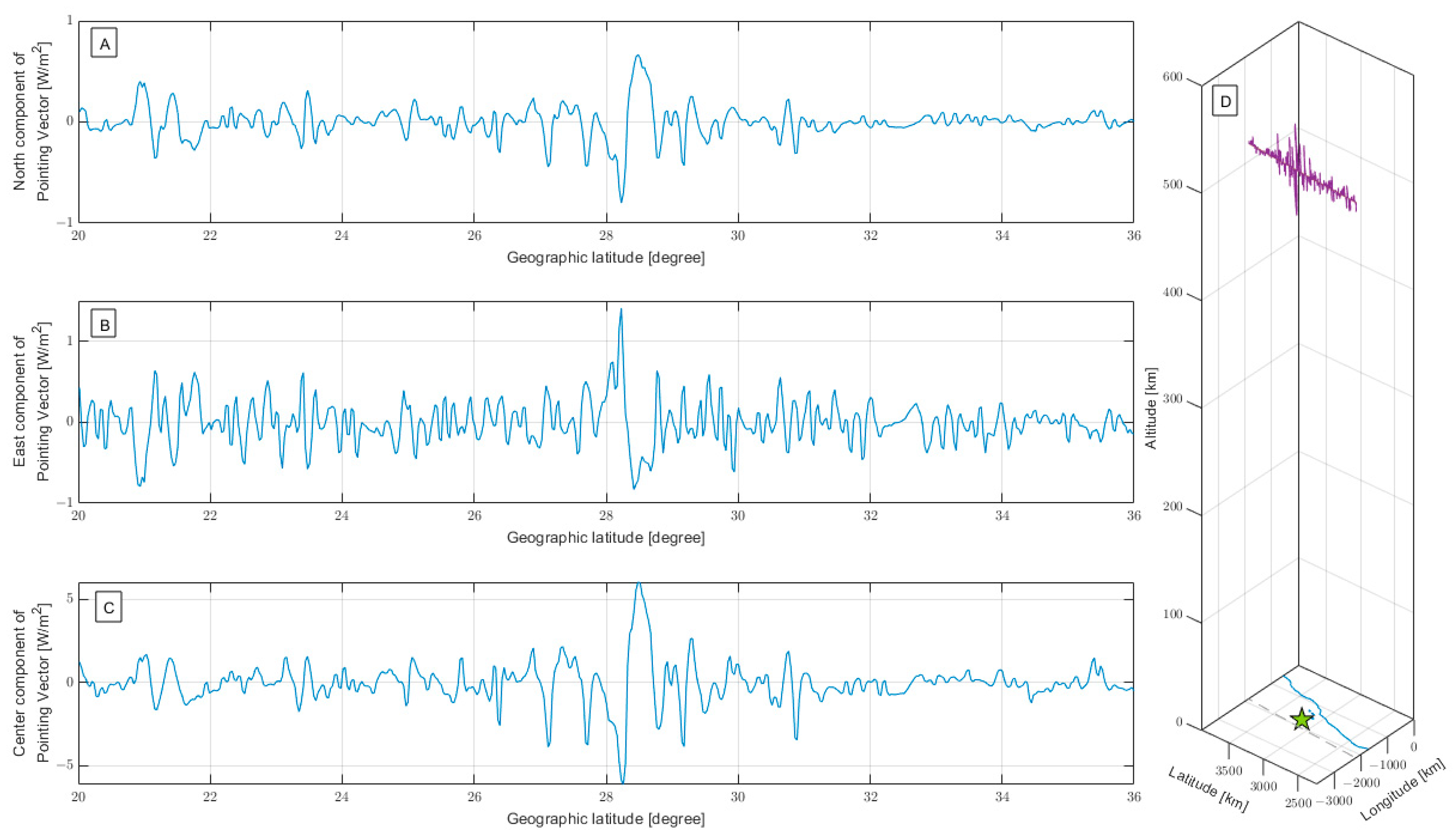
4.4. Investigation of the Possible Direction of Propagation of the Electromagnetic Waves by Calculating the Pointing Vector
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Detailed Description of CSES Electron Density Data Processing

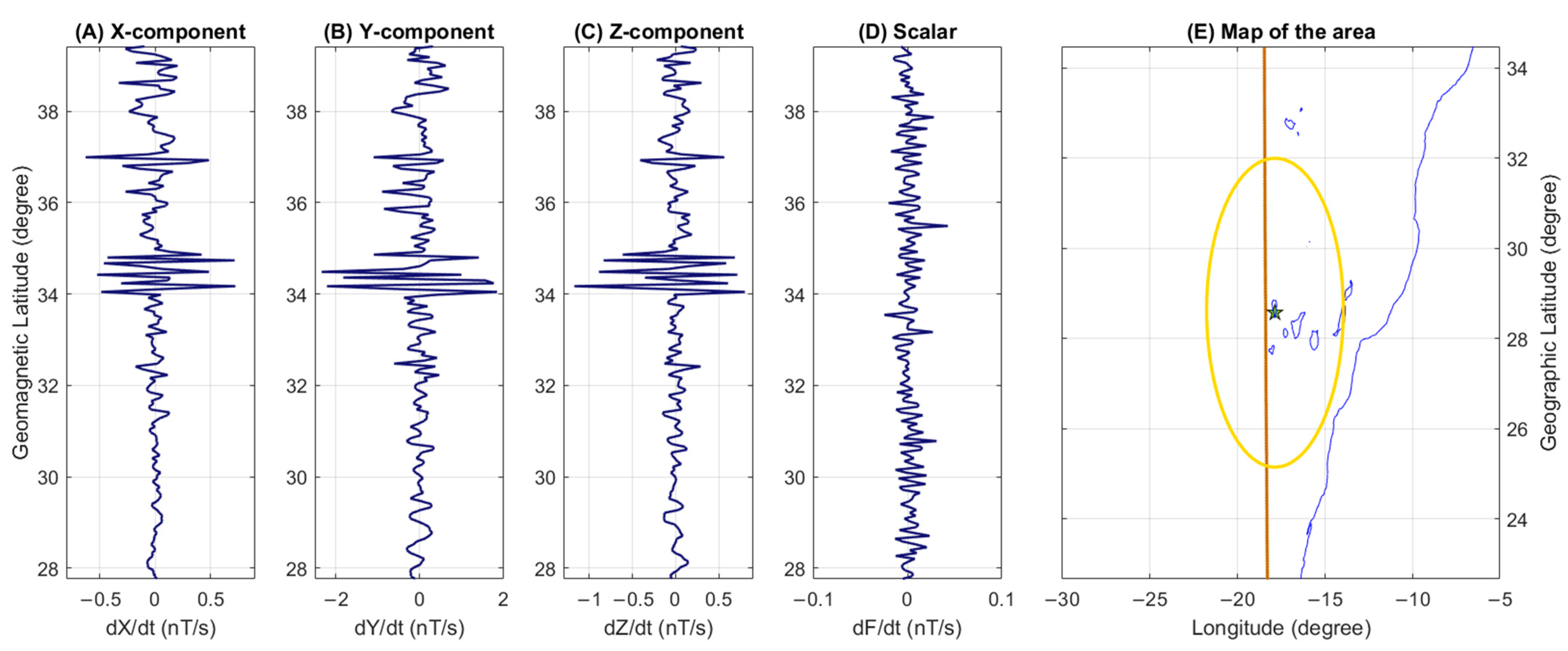
Appendix B. Detailed Description of Swarm Magnetic Data Analysis
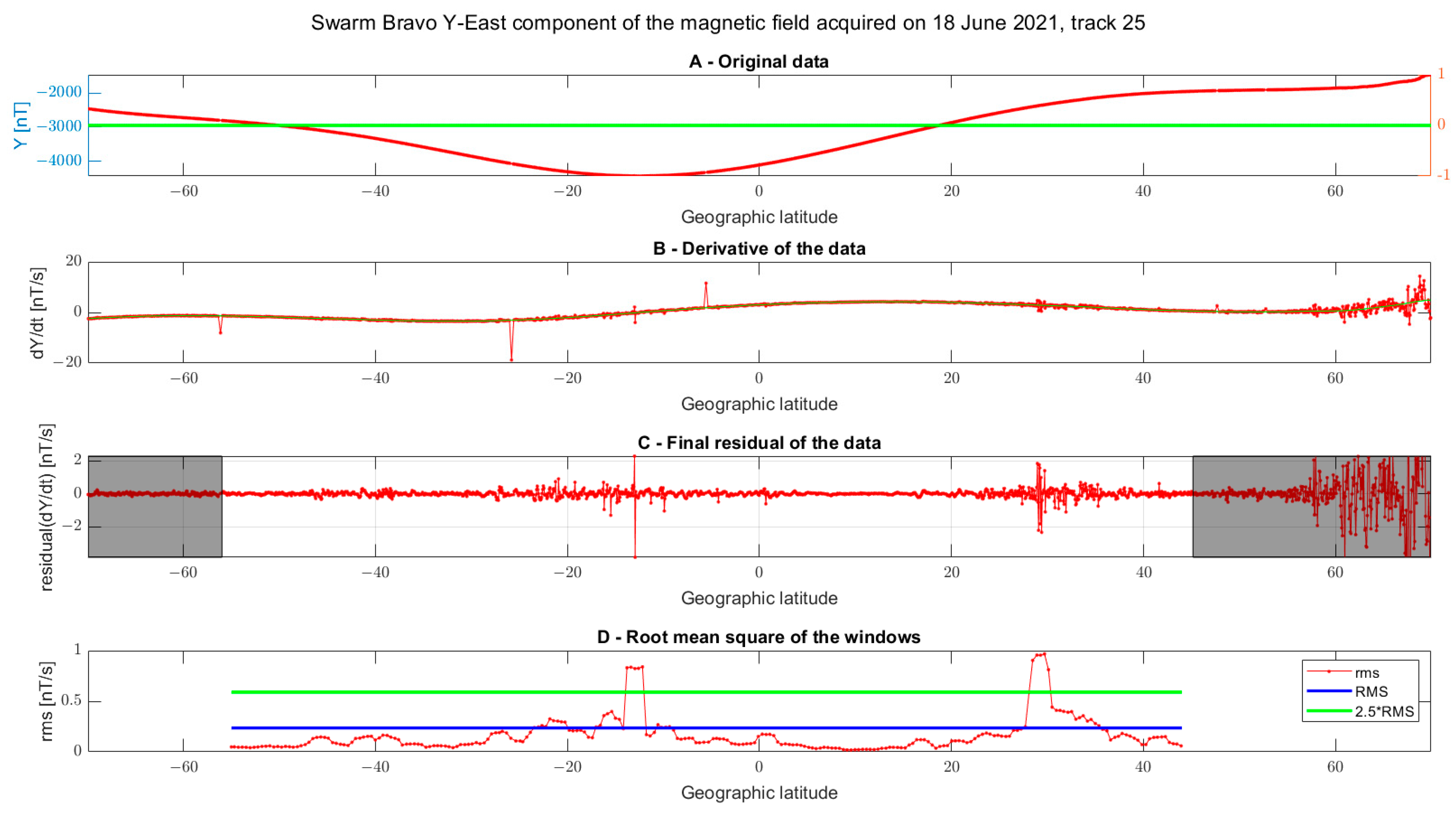
- Estimation of the numerical first order derivative of the original data . This step is done by calculating the differences sample by sample (S) and dividing the result by the time “t” (i.e., the time difference between the two consecutive data):
- In order to remove the further trend from the data, a cubic spline S(t) was fitted on , setting the knock points every 20 samples:
- The geomagnetic latitude of each sample was computed considering the position of the magnetic pole provided by the IGRF-13 geomagnetic model [96], and the samples outside the range [−50, +50] of geomagnetic latitude were rejected.
- The Root Mean Square “RMS” of the whole track is calculated and compared with the root mean square “rms” of a moving window with a length for this work of 2.0° latitude. Ifthe window is defined as anomalous. “kt” is a threshold to define the anomalies and, in this work, has been set to 2.5.
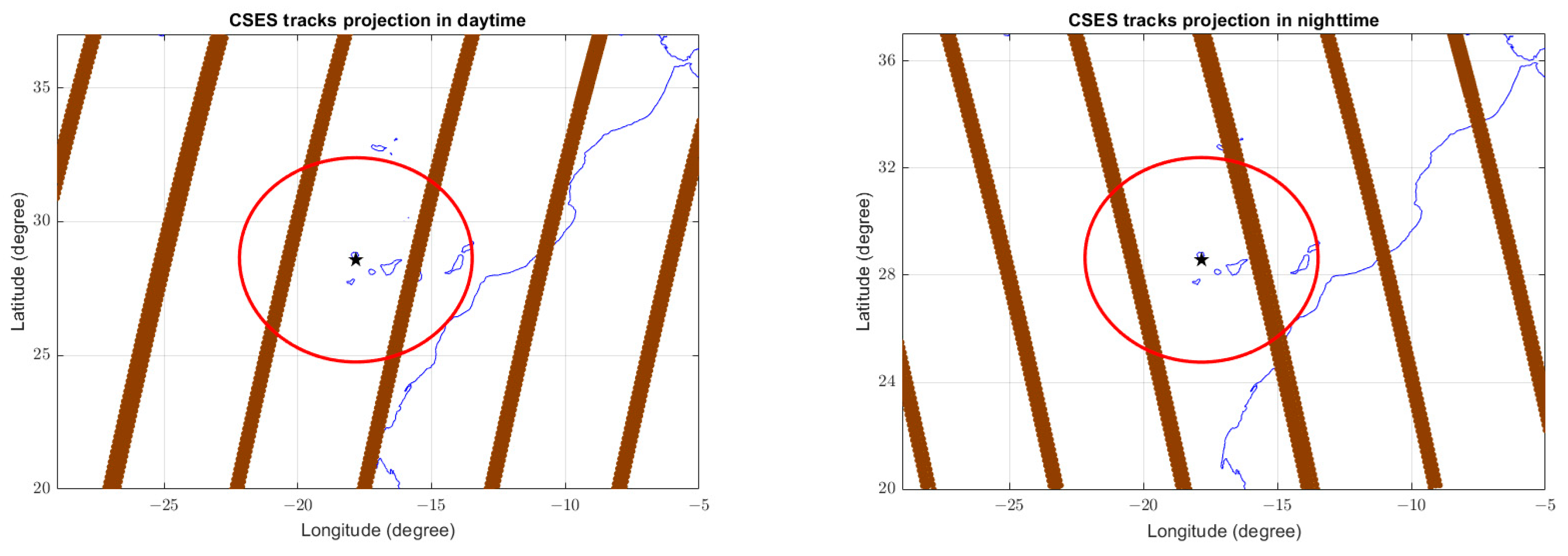
- A track is classified as anomalous if it contains at least one anomalous window whose centre falls inside the research area (a circle of 420 km of radius), and geomagnetic conditions were quiet (|Dst| ≤ 20 nT and ap ≤ 10 nT).
- The cumulative curve of all the identified anomalous tracks was computed for each component of the geomagnetic field, combining the three satellites together.
Appendix C. Global Distributions of TEC and Electron Density from CSES-01 Satellite
| Figure | Day [2021] | Parameter | Notes |
|---|---|---|---|
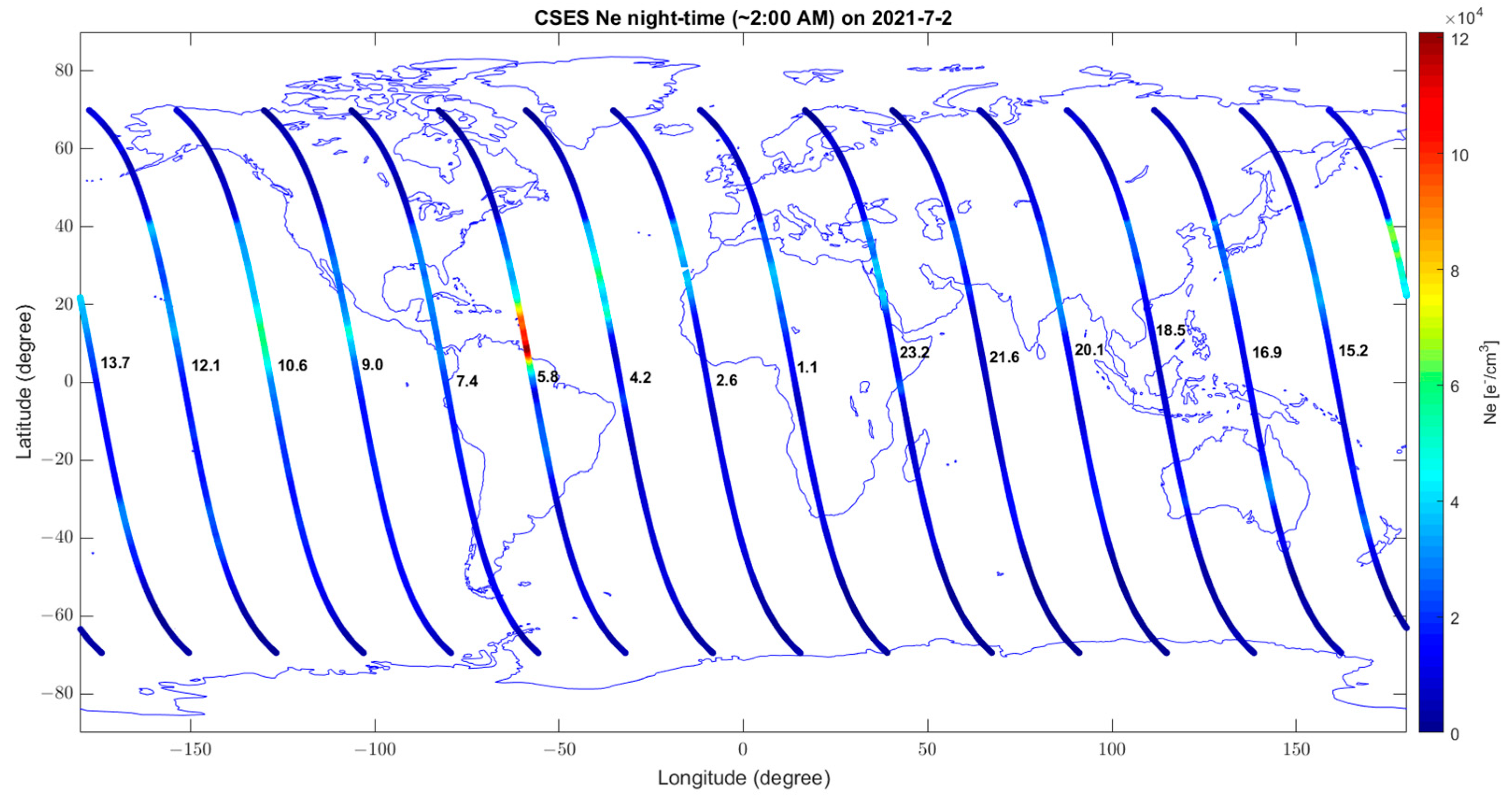
| Figure A5 | 2 July | TEC | TEC and CSES Ne are well in agreement. The high value of Ne over La Palma seems more a global disturbance. |
| Figure A6 | Ne (CSES-01) | ||
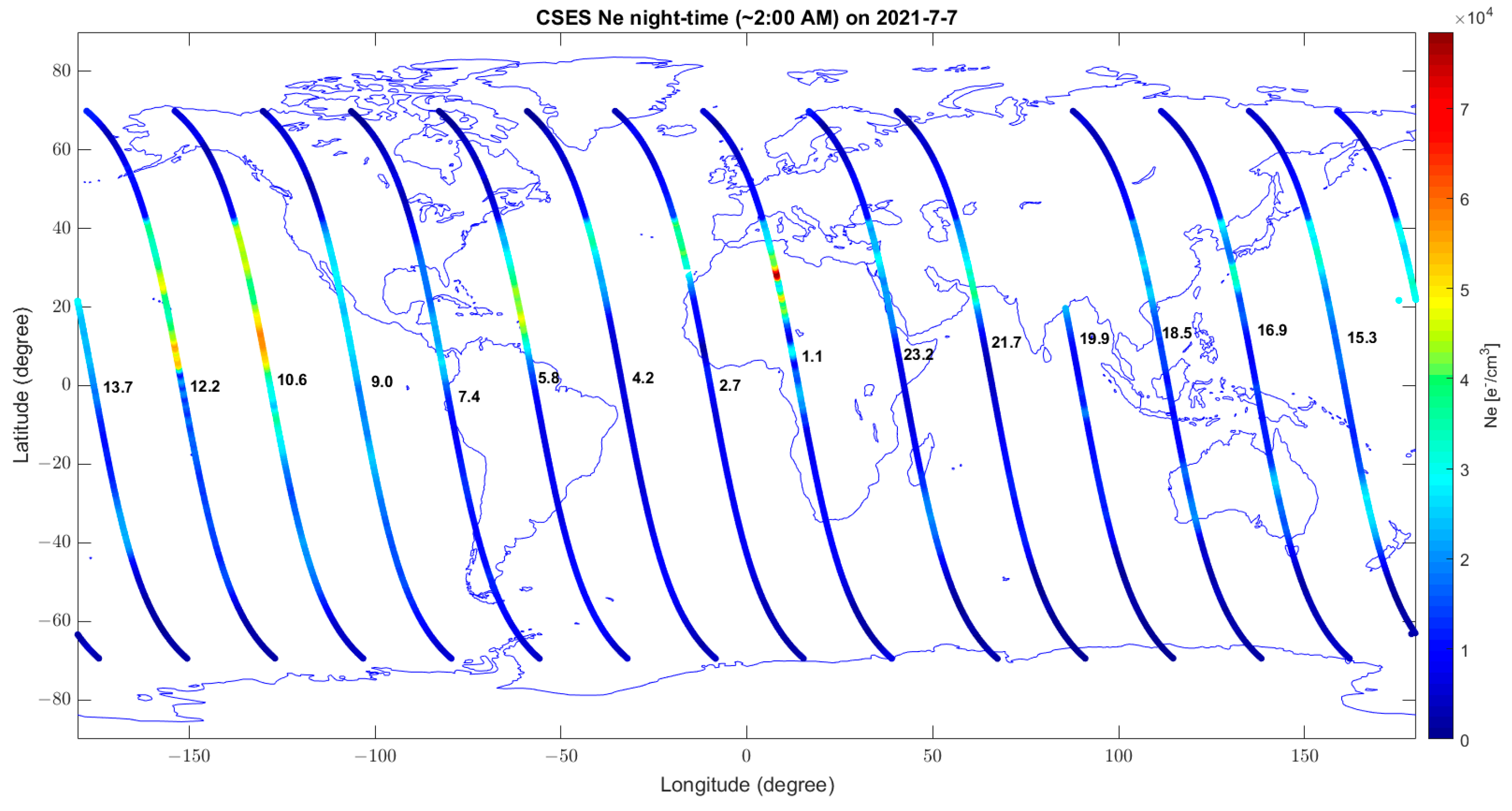
| Figure A7 | 7 July | TEC | Global distribution of TEC and Ne from CSES present the same structures. The disturbance seems global. |
| Figure A8 | Ne (CSES-01) | ||
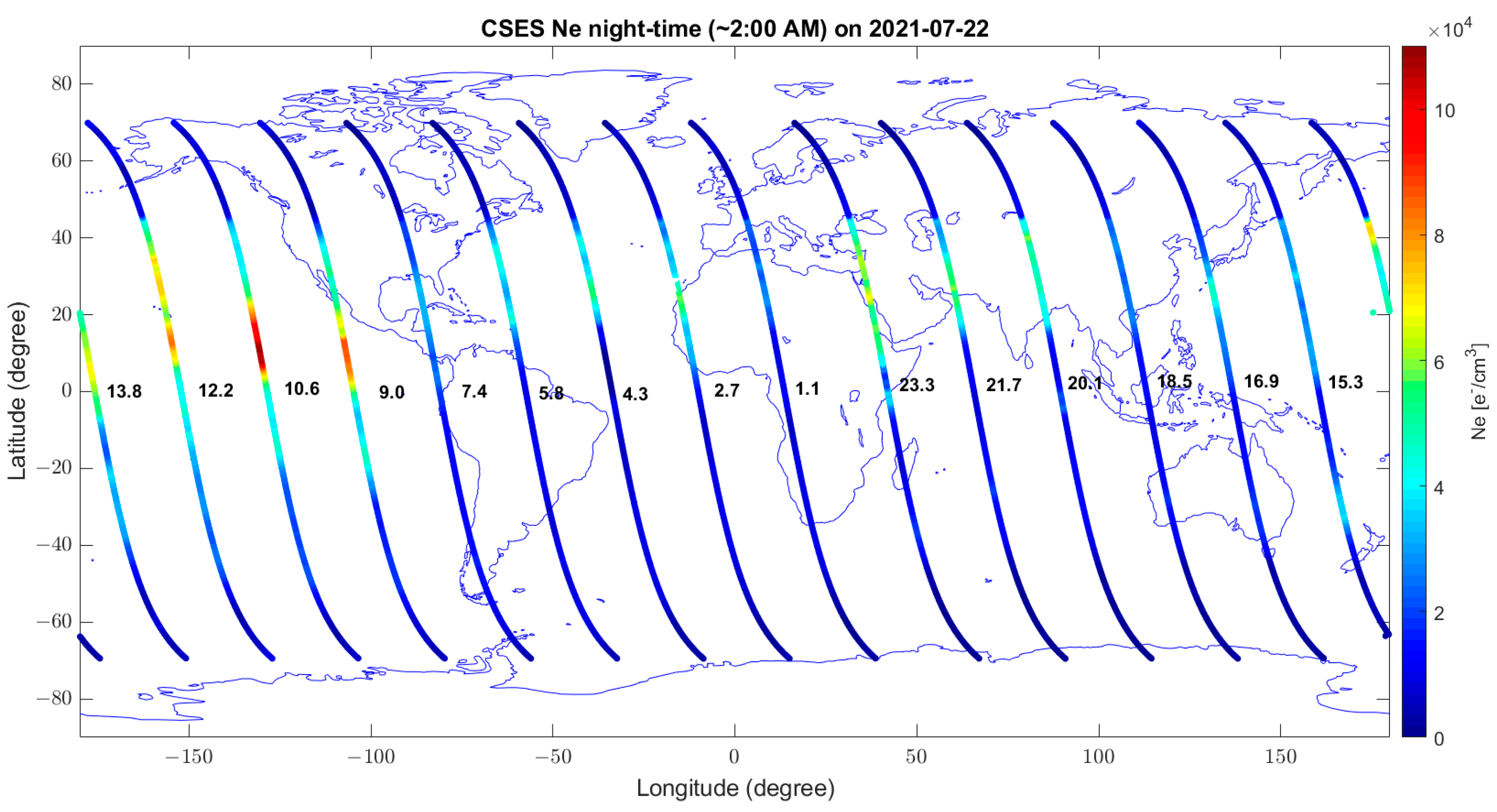
| Figure A9 | 22 July | TEC | The structures in TEC and CSES Ne are compatible, even if the localizations of maximum are different |
| Figure A10 | Ne (CSES-01) | ||
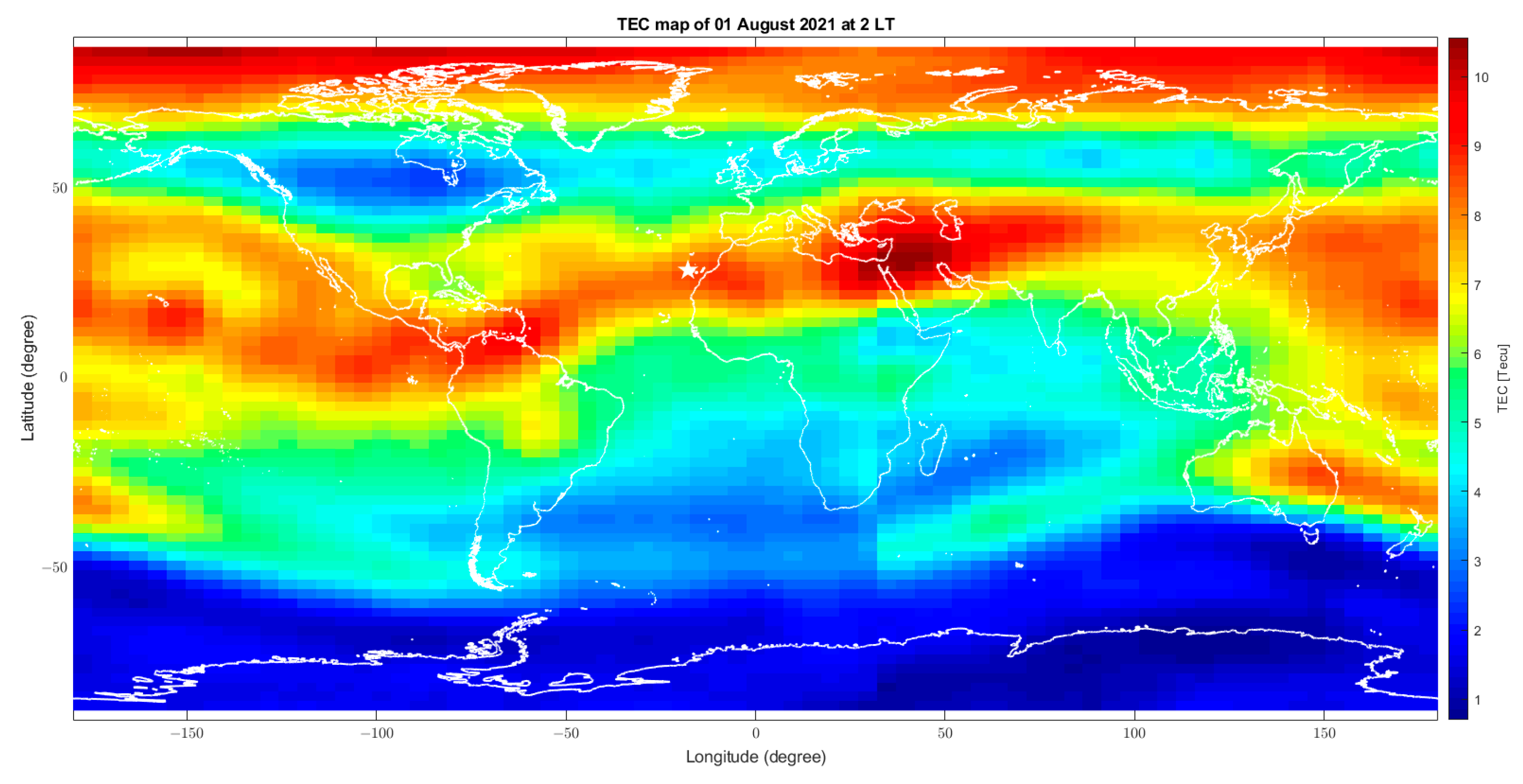
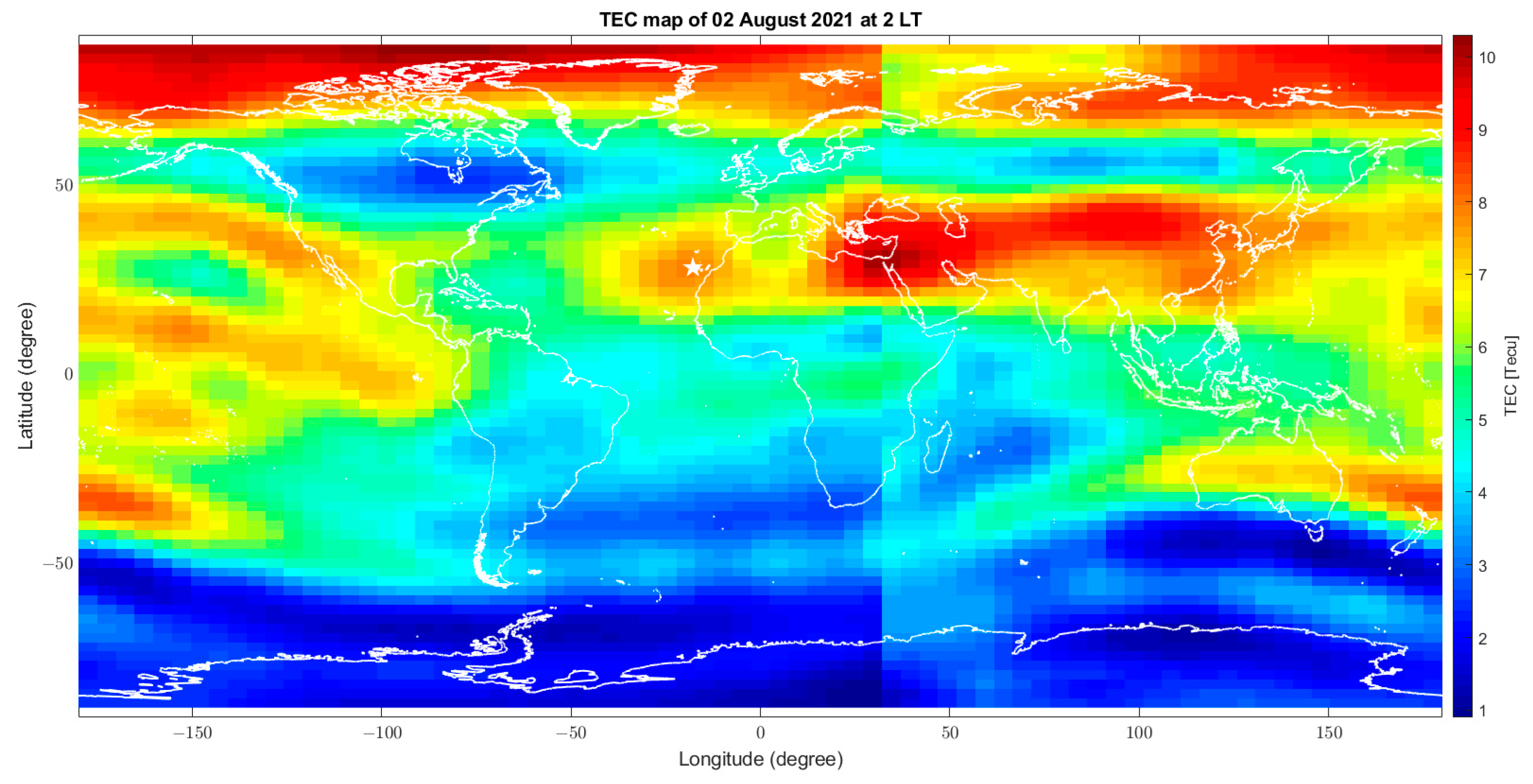
| Figure A11 | 1 and 2 August | TEC | The distributions of TEC and CSES Ne are well in agreement. The enhancement above “La Palma” volcano seems a local anomaly. |
| Figure A12 | |||
| Figure A13 | Ne (CSES-01) | ||
| Figure A14 | |||
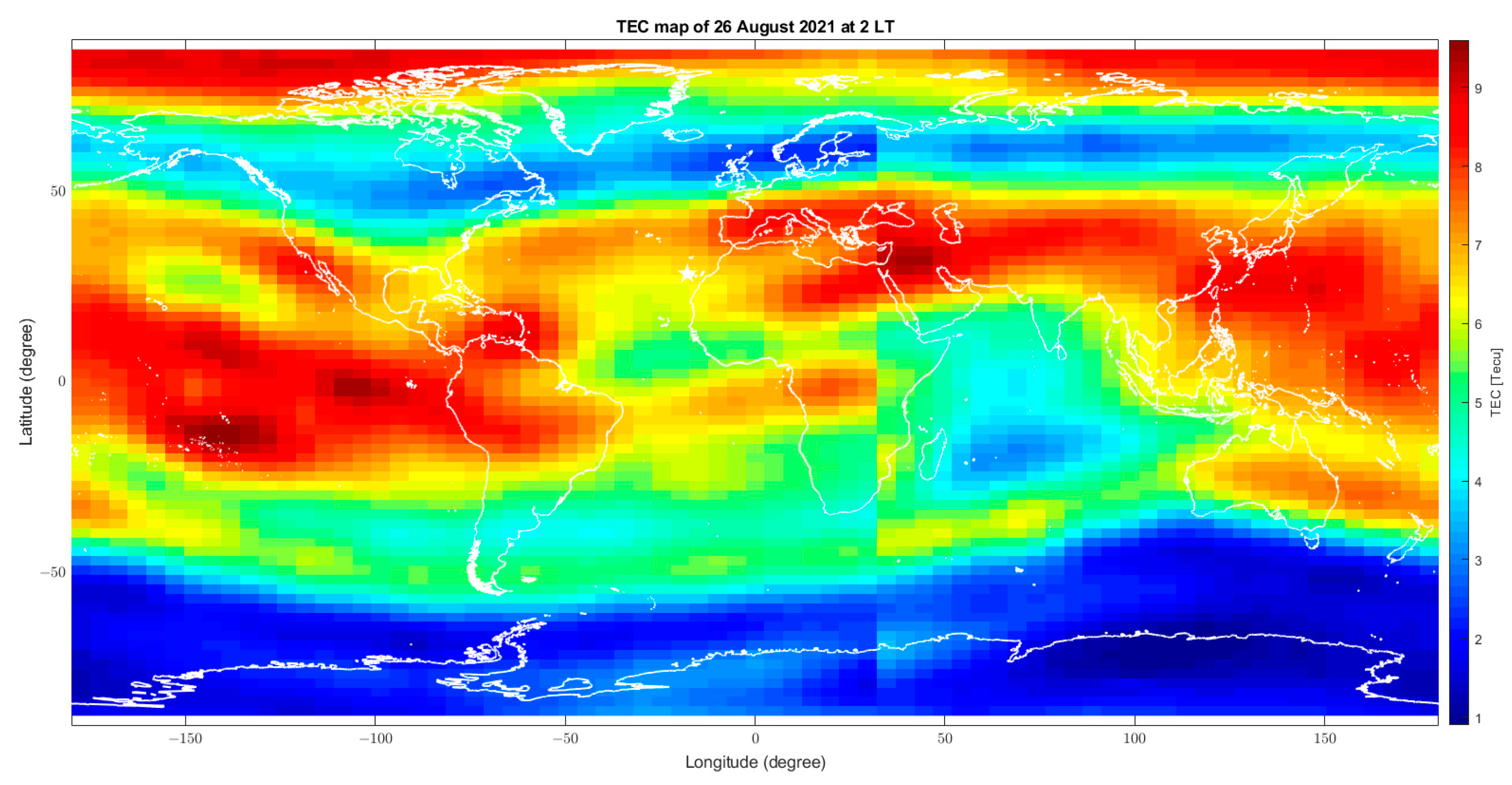
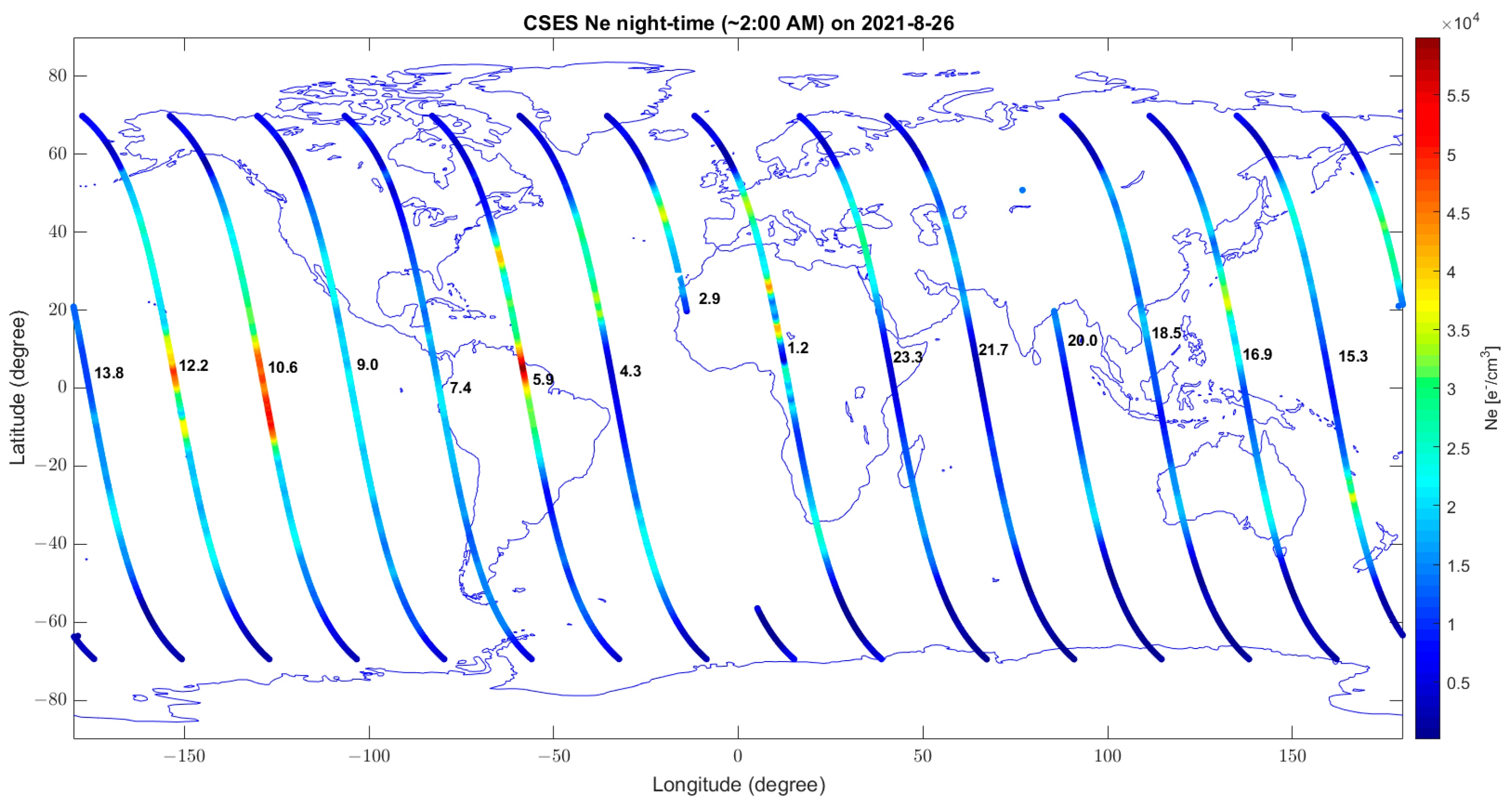
| Figure A15 | 26 August | TEC | Ionospheric structures are more complex and they are well depicted by both TEC and CSES Ne satellite. Disturbance seems global phenomenon |
| Figure A16 | Ne (CSES-01) |





Appendix D. Comparison of Carbon Monoxide Measured from Ground Station IZO and the Value Obtained from the MERRA-2 Archive

Appendix E. Calculus of the Point Vector with Swarm Data
References
- Parrot, M.; Tramutoli, V.; Liu, T.J.Y.; Pulinets, S.; Ouzounov, D.; Genzano, N.; Lisi, M.; Hattori, K.; Namgaladze, A. Atmospheric and Ionospheric Coupling Phenomena Associated with Large Earthquakes. Eur. Phys. J. Spec. Top. 2021, 230, 197–225. [Google Scholar] [CrossRef]
- Pulinets, S.; Ouzounov, D. Lithosphere–Atmosphere–Ionosphere Coupling (LAIC) Model—An Unified Concept for Earthquake Precursors Validation. J. Asian Earth Sci. 2011, 41, 371–382. [Google Scholar] [CrossRef]
- American Geophysical Union. Pre-Earthquake Processes: A Multidisciplinary Approach to Earthquake Prediction Studies; Geophysical Monograph Series; American Geophysical Union: Washington, DC, USA; Hoboken, NJ, USA, 2018; ISBN 978-1-119-15694-9. [Google Scholar]
- De Santis, A.; Marchetti, D.; Pavón-Carrasco, F.J.; Cianchini, G.; Perrone, L.; Abbattista, C.; Alfonsi, L.; Amoruso, L.; Campuzano, S.A.; Carbone, M.; et al. Precursory Worldwide Signatures of Earthquake Occurrences on Swarm Satellite Data. Sci. Rep. 2019, 9, 20287. [Google Scholar] [CrossRef]
- Marchetti, D.; De Santis, A.; Campuzano, S.A.; Zhu, K.; Soldani, M.; D’Arcangelo, S.; Orlando, M.; Wang, T.; Cianchini, G.; Di Mauro, D.; et al. Worldwide Statistical Correlation of Eight Years of Swarm Satellite Data with M5.5+ Earthquakes: New Hints about the Preseismic Phenomena from Space. Remote Sens. 2022, 14, 2649. [Google Scholar] [CrossRef]
- Pergola, N.; Marchese, F.; Tramutoli, V. Automated Detection of Thermal Features of Active Volcanoes by Means of Infrared AVHRR Records. Remote Sens. Environ. 2004, 93, 311–327. [Google Scholar] [CrossRef]
- Filizzola, C.; Corrado, A.; Genzano, N.; Lisi, M.; Pergola, N.; Colonna, R.; Tramutoli, V. RST Analysis of Anomalous TIR Sequences in Relation with Earthquakes Occurred in Turkey in the Period 2004–2015. Remote Sens. 2022, 14, 381. [Google Scholar] [CrossRef]
- Crisp, N.H.; Roberts, P.C.E.; Livadiotti, S.; Oiko, V.T.A.; Edmondson, S.; Haigh, S.J.; Huyton, C.; Sinpetru, L.A.; Smith, K.L.; Worrall, S.D.; et al. The Benefits of Very Low Earth Orbit for Earth Observation Missions. Prog. Aerosp. Sci. 2020, 117, 100619. [Google Scholar] [CrossRef]
- Scarino, B.; Minnis, P.; Palikonda, R.; Reichle, R.; Morstad, D.; Yost, C.; Shan, B.; Liu, Q. Retrieving Clear-Sky Surface Skin Temperature for Numerical Weather Prediction Applications from Geostationary Satellite Data. Remote Sens. 2013, 5, 342–366. [Google Scholar] [CrossRef]
- Uyeda, S.; Hayakawa, M.; Nagao, T.; Molchanov, O.; Hattori, K.; Orihara, Y.; Gotoh, K.; Akinaga, Y.; Tanaka, H. Electric and Magnetic Phenomena Observed before the Volcano-Seismic Activity in 2000 in the Izu Island Region, Japan. Proc. Natl. Acad. Sci. USA 2002, 99, 7352–7355. [Google Scholar] [CrossRef]
- Marchese, F.; Filizzola, C.; Mazzeo, G.; Paciello, R.; Pergola, N.; Tramutoli, V. Robust Satellite Techniques for Thermal Volcanic Activity Monitoring, Early Warning and Possible Prediction of New Eruptive Events. In Proceedings of the 2009 IEEE International Geoscience and Remote Sensing Symposium, Cape Town, South Africa, 12–17 July 2009; IEEE: Cape Town, South Africa, 2009; Volume II, pp. 953–956. [Google Scholar]
- Marchese, F.; Filizzola, C.; Lacava, T.; Falconieri, A.; Faruolo, M.; Genzano, N.; Mazzeo, G.; Pietrapertosa, C.; Pergola, N.; Tramutoli, V.; et al. Mt. Etna Paroxysms of February–April 2021 Monitored and Quantified through a Multi-Platform Satellite Observing System. Remote Sens. 2021, 13, 3074. [Google Scholar] [CrossRef]
- Pulinets, S.; Davidenko, D. Ionospheric Precursors of Earthquakes and Global Electric Circuit. Adv. Space Res. 2014, 53, 709–723. [Google Scholar] [CrossRef]
- Pulinets, S.; Khachikyan, G. The Global Electric Circuit and Global Seismicity. Geosciences 2021, 11, 491. [Google Scholar] [CrossRef]
- Parrot, M. Events Linked to the Lithosphere-Atmosphere-Ionosphere Coupling Observed by DEMETER. URSI Radio Sci. Bull. 2017, 2017, 75–79. [Google Scholar] [CrossRef]
- Tramutoli, V.; Marchese, F.; Falconieri, A.; Filizzola, C.; Genzano, N.; Hattori, K.; Lisi, M.; Liu, J.-Y.; Ouzounov, D.; Parrot, M.; et al. Tropospheric and Ionospheric Anomalies Induced by Volcanic and Saharan Dust Events as Part of Geosphere Interaction Phenomena. Geosciences 2019, 9, 177. [Google Scholar] [CrossRef]
- Pulinets, S.; Davidenko, D.; Pulinets, M. Atmosphere-Ionosphere Coupling Induced by Volcanoes Eruption and Dust Storms and Role of GEC as the Agent of Geospheres Interaction. Adv. Space Res. 2022, 69, 4319–4334. [Google Scholar] [CrossRef]
- Voight, B. A Method for Prediction of Volcanic Eruptions. Nature 1988, 332, 125–130. [Google Scholar] [CrossRef]
- Matoza, R.S.; Fee, D.; Assink, J.D.; Iezzi, A.M.; Green, D.N.; Kim, K.; Toney, L.; Lecocq, T.; Krishnamoorthy, S.; Lalande, J.-M.; et al. Atmospheric Waves and Global Seismoacoustic Observations of the January 2022 Hunga Eruption, Tonga. Science 2022, 377, 95–100. [Google Scholar] [CrossRef]
- Heki, K. Ionospheric Signatures of Repeated Passages of Atmospheric Waves by the 2022 Jan. 15 Hunga Tonga Eruption Detected by QZSS-TEC Observations in Japan. Earth Planets Space 2022, 74, 112. [Google Scholar] [CrossRef]
- D’Arcangelo, S.; Bonforte, A.; De Santis, A.; Maugeri, S.R.; Perrone, L.; Soldani, M.; Arena, G.; Brogi, F.; Calcara, M.; Campuzano, S.A.; et al. A Multi-Parametric and Multi-Layer Study to Investigate the Largest 2022 Hunga Tonga–Hunga Ha’apai Eruptions. Remote Sens. 2022, 14, 3649. [Google Scholar] [CrossRef]
- Barbieri, C. The Galileo Italian National Telescope and Its Instrumentation. Exp. Astron. 1997, 7, 257–279. [Google Scholar] [CrossRef]
- Aleksić, J.; Ansoldi, S.; Antonelli, L.A.; Antoranz, P.; Babic, A.; Bangale, P.; Barceló, M.; Barrio, J.A.; Becerra González, J.; Bednarek, W.; et al. The Major Upgrade of the MAGIC Telescopes, Part I: The Hardware Improvements and the Commissioning of the System. Astropart. Phys. 2016, 72, 61–75. [Google Scholar] [CrossRef]
- Martí, J.; Pinel, V.; López, C.; Geyer, A.; Abella, R.; Tárraga, M.; Blanco, M.J.; Castro, A.; Rodríguez, C. Causes and Mechanisms of the 2011–2012 El Hierro (Canary Islands) Submarine Eruption: EL HIERRO ERUPTION. J. Geophys. Res. Solid Earth 2013, 118, 823–839. [Google Scholar] [CrossRef]
- Venzke, E.; Smithsonian Institution. Volcanoes of the World, v. 4.3.4; Smithsonian Institution: Washington, DC, USA, 2013. [Google Scholar]
- López, C.; Blanco, M.J.; Abella, R.; Brenes, B.; Cabrera Rodríguez, V.M.; Casas, B.; Domínguez Cerdeña, I.; Felpeto, A.; de Villalta, M.F.; del Fresno, C.; et al. Monitoring the Volcanic Unrest of El Hierro (Canary Islands) before the Onset of the 2011–2012 Submarine Eruption: Monitoring El Hierro prior 2001 eruption. Geophys. Res. Lett. 2012, 39, L13303. [Google Scholar] [CrossRef]
- De Luca, C.; Valerio, E.; Giudicepietro, F.; Macedonio, G.; Casu, F.; Lanari, R. Pre- and Co-Eruptive Analysis of the September 2021 Eruption at Cumbre Vieja Volcano (La Palma, Canary Islands) Through DInSAR Measurements and Analytical Modeling. Geophys. Res. Lett. 2022, 49, e2021GL097293. [Google Scholar] [CrossRef]
- Schekotov, A.; Hayakawa, M.; Potirakis, S.M. Does Air Ionization by Radon Cause Low-Frequency Atmospheric Electromagnetic Earthquake Precursors? Nat. Hazards 2021, 106, 701–714. [Google Scholar] [CrossRef]
- Liperovsky, V.A.; Pokhotelov, O.A.; Meister, C.-V.; Liperovskaya, E.V. Physical Models of Coupling in the Lithosphere-Atmosphere-Ionosphere System before Earthquakes. Geomagn. Aeron. 2008, 48, 795–806. [Google Scholar] [CrossRef]
- Yi, J.; Wang, P.; Shan, X.; Ventura, G.; Wu, C.; Guo, J.; Liu, P.; Li, J. Modeling the Multi-Level Plumbing System of the Changbaishan Caldera from Geochemical, Mineralogical, Sr-Nd Isotopic and Integrated Geophysical Data. Geosci. Front. 2021, 12, 101171. [Google Scholar] [CrossRef]
- Di Paolo, F.; Ledo, J.; Ślęzak, K.; Martínez van Dorth, D.; Cabrera-Pérez, I.; Pérez, N.M. La Palma Island (Spain) Geothermal System Revealed by 3D Magnetotelluric Data Inversion. Sci. Rep. 2020, 10, 18181. [Google Scholar] [CrossRef] [PubMed]
- Kanda, W.; Utsugi, M.; Tanaka, Y.; Hashimoto, T.; Fujii, I.; Hasenaka, T.; Shigeno, N. A Heating Process of Kuchi-Erabu-Jima Volcano, Japan, as Inferred from Geomagnetic Field Variations and Electrical Structure. J. Volcanol. Geotherm. Res. 2010, 189, 158–171. [Google Scholar] [CrossRef]
- Alcolombri, U.; Ben-Dor, S.; Feldmesser, E.; Levin, Y.; Tawfik, D.S.; Vardi, A. Identification of the Algal Dimethyl Sulfide–Releasing Enzyme: A Missing Link in the Marine Sulfur Cycle. Science 2015, 348, 1466–1469. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, B.C.; Gaudry, A.; Bonsang, B.; Lambert, G. Reevaluation of the Role of Dimethyl Sulphide in the Sulphur Budget. Nature 1978, 275, 637–639. [Google Scholar] [CrossRef]
- Loyola, D.; van Geffen, J.; Valks, P.; Erbertseder, T.; Van Roozendael, M.; Thomas, W.; Zimmer, W.; Wißkirchen, K. Satellite-Based Detection of Volcanic Sulphur Dioxide from Recent Eruptions in Central and South America. Adv. Geosci. 2008, 14, 35–40. [Google Scholar] [CrossRef]
- Wallace, J.M.; Hobbs, P.V. Atmospheric Chemistry. In Atmospheric Science; Elsevier: Amsterdam, The Netherlands, 2006; pp. 153–207. ISBN 978-0-12-732951-2. [Google Scholar]
- Cadle, R.D. A Comparison of Volcanic with Other Fluxes of Atmospheric Trace Gas Constituents. Rev. Geophys. 1980, 18, 746. [Google Scholar] [CrossRef]
- Pulinets, S.A. Physical Mechanism of the Vertical Electric Field Generation over Active Tectonic Faults. Adv. Space Res. 2009, 44, 767–773. [Google Scholar] [CrossRef]
- Ouzounov, D.; Pulinets, S.; Davidenko, D.; Rozhnoi, A.; Solovieva, M.; Fedun, V.; Dwivedi, B.N.; Rybin, A.; Kafatos, M.; Taylor, P. Transient Effects in Atmosphere and Ionosphere Preceding the 2015 M7.8 and M7.3 Gorkha–Nepal Earthquakes. Front. Earth Sci. 2021, 9, 757358. [Google Scholar] [CrossRef]
- Marchetti, D.; De Santis, A.; Shen, X.; Campuzano, S.A.; Perrone, L.; Piscini, A.; Di Giovambattista, R.; Jin, S.; Ippolito, A.; Cianchini, G.; et al. Possible Lithosphere-Atmosphere-Ionosphere Coupling Effects Prior to the 2018 Mw = 7.5 Indonesia Earthquake from Seismic, Atmospheric and Ionospheric Data. J. Asian Earth Sci. 2020, 188, 104097. [Google Scholar] [CrossRef]
- Molchanov, O.A.; Hayakawa, M. Generation of ULF Electromagnetic Emissions by Microfracturing. Geophys. Res. Lett. 1995, 22, 3091–3094. [Google Scholar] [CrossRef]
- Molchanov, O.A.; Hayakawa, M. On the Generation Mechanism of ULF Seismogenic Electromagnetic Emissions. Phys. Earth Planet. Inter. 1998, 105, 201–210. [Google Scholar] [CrossRef]
- Hattori, K.; Han, P.; Yoshino, C.; Febriani, F.; Yamaguchi, H.; Chen, C.-H. Investigation of ULF Seismo-Magnetic Phenomena in Kanto, Japan During 2000–2010: Case Studies and Statistical Studies. Surv. Geophys. 2013, 34, 293–316. [Google Scholar] [CrossRef]
- Hattori, K.; Serita, A.; Gotoh, K.; Yoshino, C.; Harada, M.; Isezaki, N.; Hayakawa, M. ULF Geomagnetic Anomaly Associated with 2000 Izu Islands Earthquake Swarm, Japan. Phys. Chem. Earth Parts A/B/C 2004, 29, 425–435. [Google Scholar] [CrossRef]
- Ouyang, X.Y.; Parrot, M.; Bortnik, J. ULF Wave Activity Observed in the Nighttime Ionosphere Above and Some Hours Before Strong Earthquakes. J. Geophys. Res. Space Phys. 2020, 125, e2020JA028396. [Google Scholar] [CrossRef]
- Ouyang, X.-Y.; Wang, Y.-F.; Zhang, X.-M.; Wang, Y.-L.; Wu, Y.-Y. A New Analysis Method for Magnetic Disturbances Possibly Related to Earthquakes Observed by Satellites. Remote Sens. 2022, 14, 2709. [Google Scholar] [CrossRef]
- Enomoto, Y. Coupled Interaction of Earthquake Nucleation with Deep Earth Gases: A Possible Mechanism for Seismo-Electromagnetic Phenomena: Coupled Interaction of Earthquake Nucleation. Geophys. J. Int. 2012, 191, 1210–1214. [Google Scholar] [CrossRef]
- Korepanov, V.; Hayakawa, M.; Yampolski, Y.; Lizunov, G. AGW as a Seismo-Ionospheric Coupling Responsible Agent. Phys. Chem. Earth Parts A/B/C 2009, 34, 485–495. [Google Scholar] [CrossRef]
- Wiemer, S. A Software Package to Analyze Seismicity: ZMAP. Seismol. Res. Lett. 2001, 72, 373–382. [Google Scholar] [CrossRef]
- Mignan, A.; King, G.C.P.; Bowman, D. A Mathematical Formulation of Accelerating Moment Release Based on the Stress Accumulation Model. J. Geophys. Res. 2007, 112, B07308. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Piscini, A.; Marchetti, D.; De Santis, A. Multi-Parametric Climatological Analysis Associated with Global Significant Volcanic Eruptions During 2002–2017. Pure Appl. Geophys. 2019, 176, 3629–3647. [Google Scholar] [CrossRef]
- Whitcher, B.; Guttorp, P.; Percival, D.B. Wavelet Analysis of Covariance with Application to Atmospheric Time Series. J. Geophys. Res. 2000, 105, 14941–14962. [Google Scholar] [CrossRef]
- Shen, X.; Zong, Q.-G.; Zhang, X. Introduction to Special Section on the China Seismo-Electromagnetic Satellite and Initial Results. Earth Planet. Phys. 2018, 2, 439–443. [Google Scholar] [CrossRef]
- Yang, Y.; Hulot, G.; Vigneron, P.; Shen, X.; Zhima, Z.; Zhou, B.; Magnes, W.; Olsen, N.; Tøffner-Clausen, L.; Huang, J.; et al. The CSES Global Geomagnetic Field Model (CGGM): An IGRF-Type Global Geomagnetic Field Model Based on Data from the China Seismo-Electromagnetic Satellite. Earth Planets Space 2021, 73, 45. [Google Scholar] [CrossRef]
- Friis-Christensen, E.; Lühr, H.; Knudsen, D.; Haagmans, R. Swarm—An Earth Observation Mission Investigating Geospace. Adv. Space Res. 2008, 41, 210–216. [Google Scholar] [CrossRef]
- Regi, M.; Di Mauro, D.; Lepidi, S. The Location of the Earth’s Magnetic Poles From Circum-Terrestrial Observations. J. Geophys. Res. Space Phys. 2021, 126, e2020JA028513. [Google Scholar] [CrossRef]
- Matzka, J.; Stolle, C.; Yamazaki, Y.; Bronkalla, O.; Morschhauser, A. The Geomagnetic Kp Index and Derived Indices of Geomagnetic Activity. Space Weather 2021, 19, e2020SW002641. [Google Scholar] [CrossRef]
- Nose, M.; Sugiura, M.; Kamei, T.; Iyemori, T.; Koyama, Y. Dst Index; WDC Geomagnetism: Kyoto, Japan, 2015. [Google Scholar]
- Cianchini, G.; Piscini, A.; De Santis, A.; Campuzano, S.A. Fast Dst Computation by Applying Deep Learning to Swarm Satellite Magnetic Data. Adv. Space Res. 2022, 69, 837–855. [Google Scholar] [CrossRef]
- Yang, Y.; Zhou, B.; Hulot, G.; Olsen, N.; Wu, Y.; Xiong, C.; Stolle, C.; Zhima, Z.; Huang, J.; Zhu, X.; et al. CSES High Precision Magnetometer Data Products and Example Study of an Intense Geomagnetic Storm. JGR Space Phys. 2021, 126, e2020JB020466. [Google Scholar] [CrossRef]
- Akhoondzadeh, M.; De Santis, A.; Marchetti, D.; Shen, X. Swarm-TEC Satellite Measurements as a Potential Earthquake Precursor Together with Other Swarm and CSES Data: The Case of Mw7.6 2019 Papua New Guinea Seismic Event. Front. Earth Sci. 2022, 10, 820189. [Google Scholar] [CrossRef]
- Kuo, C.L.; Huba, J.D.; Joyce, G.; Lee, L.C. Ionosphere Plasma Bubbles and Density Variations Induced by Pre-Earthquake Rock Currents and Associated Surface Charges: Pre-Earthquake Ionospheric Effect. J. Geophys. Res. 2011, 116, A10. [Google Scholar] [CrossRef]
- Kuo, C.L.; Lee, L.C.; Huba, J.D. An Improved Coupling Model for the Lithosphere-Atmosphere-Ionosphere System. J. Geophys. Res. Space Phys. 2014, 119, 3189–3205. [Google Scholar] [CrossRef]
- Tornatore, V.; Cesaroni, C.; Pezzopane, M.; Alizadeh, M.M.; Schuh, H. Performance Evaluation of VTEC GIMs for Regional Applications during Different Solar Activity Periods, Using RING TEC Values. Remote Sens. 2021, 13, 1470. [Google Scholar] [CrossRef]
- De Santis, A.; Balasis, G.; Pavón-Carrasco, F.J.; Cianchini, G.; Mandea, M. Potential Earthquake Precursory Pattern from Space: The 2015 Nepal Event as Seen by Magnetic Swarm Satellites. Earth Planet. Sci. Lett. 2017, 461, 119–126. [Google Scholar] [CrossRef]
- De Santis, A.; Marchetti, D.; Spogli, L.; Cianchini, G.; Pavón-Carrasco, F.J.; Franceschi, G.D.; Di Giovambattista, R.; Perrone, L.; Qamili, E.; Cesaroni, C.; et al. Magnetic Field and Electron Density Data Analysis from Swarm Satellites Searching for Ionospheric Effects by Great Earthquakes: 12 Case Studies from 2014 to 2016. Atmosphere 2019, 10, 371. [Google Scholar] [CrossRef]
- Marchetti, D.; De Santis, A.; Campuzano, S.A.; Soldani, M.; Piscini, A.; Sabbagh, D.; Cianchini, G.; Perrone, L.; Orlando, M. Swarm Satellite Magnetic Field Data Analysis Prior to 2019 Mw = 7.1 Ridgecrest (California, USA) Earthquake. Geosciences 2020, 10, 502. [Google Scholar] [CrossRef]
- Prado, F.B.A. Traveling between the Lagrangian Points and the Earth. Acta Astronaut. 1996, 39, 483–486. [Google Scholar] [CrossRef]
- Stone, E.C.; Frandsen, A.M.; Mewaldt, R.A.; Christian, E.R.; Margolies, D.; Ormes, J.F.; Snow, F. The Advanced Composition Explorer. Space Sci. Rev. 1998, 86, 1–22. [Google Scholar] [CrossRef]
- Burt, J.; Smith, B. Deep Space Climate Observatory: The DSCOVR Mission. In Proceedings of the 2012 IEEE Aerospace Conference, Big Sky, MT, USA, 3–10 March 2012; pp. 1–13. [Google Scholar]
- Endo, E.T.; Murray, T. Real-Time Seismic Amplitude Measurement (RSAM): A Volcano Monitoring and Prediction Tool. Bull. Volcanol. 1991, 53, 533–545. [Google Scholar] [CrossRef]
- Tan, Y.J.; Waldhauser, F.; Ellsworth, W.L.; Zhang, M.; Zhu, W.; Michele, M.; Chiaraluce, L.; Beroza, G.C.; Segou, M. Machine-Learning-Based High-Resolution Earthquake Catalog Reveals How Complex Fault Structures Were Activated during the 2016–2017 Central Italy Sequence. Seism. Rec. 2021, 1, 11–19. [Google Scholar] [CrossRef]
- Klügel, A.; Hansteen, T.H.; Schmincke, H.-U. Rates of Magma Ascent and Depths of Magma Reservoirs beneath La Palma (Canary Islands). Terra Nova 1997, 9, 117–121. [Google Scholar] [CrossRef]
- Fritsch, F.N.; Carlson, R.E. Monotone Piecewise Cubic Interpolation. SIAM J. Numer. Anal. 1980, 17, 238–246. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P. Generalizations of the Sampling Theorem: Seven Decades after Nyquist. IEEE Trans. Circuits Syst. I 2001, 48, 1094–1109. [Google Scholar] [CrossRef]
- Yamazaki, Y.; Maute, A. Sq and EEJ—A Review on the Daily Variation of the Geomagnetic Field Caused by Ionospheric Dynamo Currents. Space Sci. Rev. 2017, 206, 299–405. [Google Scholar] [CrossRef]
- Marchetti, D.; De Santis, A.; D’Arcangelo, S.; Poggio, F.; Piscini, A.; Campuzano, S.A.; De Carvalho, W.V.J.O. Pre-Earthquake Chain Processes Detected from Ground to Satellite Altitude in Preparation of the 2016–2017 Seismic Sequence in Central Italy. Remote Sens. Environ. 2019, 229, 93–99. [Google Scholar] [CrossRef]
- Andreae, M.O.; Raemdonck, H. Dimethyl Sulfide in the Surface Ocean and the Marine Atmosphere: A Global View. Science 1983, 221, 744–747. [Google Scholar] [CrossRef]
- Prospero, J.M. Saharan Dust Transport Over the North Atlantic Ocean and Mediterranean: An Overview. In The Impact of Desert Dust Across the Mediterranean; Guerzoni, S., Chester, R., Eds.; Springer: Dordrecht, The Netherlands, 1996; Volume 11, pp. 133–151. ISBN 978-90-481-4764-9. [Google Scholar]
- Piscini, A.; De Santis, A.; Marchetti, D.; Cianchini, G. A Multi-Parametric Climatological Approach to Study the 2016 Amatrice–Norcia (Central Italy) Earthquake Preparatory Phase. Pure Appl. Geophys. 2017, 174, 3673–3688. [Google Scholar] [CrossRef]
- De Santis, A.; Cianchini, G.; Marchetti, D.; Piscini, A.; Sabbagh, D.; Perrone, L.; Campuzano, S.A.; Inan, S. A Multiparametric Approach to Study the Preparation Phase of the 2019 M7.1 Ridgecrest (California, United States) Earthquake. Front. Earth Sci. 2020, 8, 540398. [Google Scholar] [CrossRef]
- Akhoondzadeh, M.; De Santis, A.; Marchetti, D.; Wang, T. Developing a Deep Learning-Based Detector of Magnetic, Ne, Te and TEC Anomalies from Swarm Satellites: The Case of Mw 7.1 2021 Japan Earthquake. Remote Sens. 2022, 14, 1582. [Google Scholar] [CrossRef]
- Lu, G.; Huba, J.D.; Valladares, C. Modeling Ionospheric Super-Fountain Effect Based on the Coupled TIMEGCM-SAMI3: Ionospheric Super-Fountain Effect. J. Geophys. Res. Space Phys. 2013, 118, 2527–2535. [Google Scholar] [CrossRef]
- Pitari, G.; Mancini, E. Short-Term Climatic Impact of the 1991 Volcanic Eruption of Mt. Pinatubo and Effects on Atmospheric Tracers. Nat. Hazards Earth Syst. Sci. 2002, 2, 91–108. [Google Scholar] [CrossRef]
- Torres, R.; Mouginis-Mark, P.; Self, S.; Garbeil, H.; Kallianpur, K.; Quiambao, R. Monitoring the Evolution of the Pasig–Potrero Alluvial Fan, Pinatubo Volcano, Using a Decade of Remote Sensing Data. J. Volcanol. Geotherm. Res. 2004, 138, 371–392. [Google Scholar] [CrossRef]
- Bluth, G.J.S.; Doiron, S.D.; Schnetzler, C.C.; Krueger, A.J.; Walter, L.S. Global Tracking of the SO 2 Clouds from the June, 1991 Mount Pinatubo Eruptions. Geophys. Res. Lett. 1992, 19, 151–154. [Google Scholar] [CrossRef]
- Ghamry, E.; Marchetti, D.; Yoshikawa, A.; Uozumi, T.; De Santis, A.; Perrone, L.; Shen, X.; Fathy, A. The First Pi2 Pulsation Observed by China Seismo-Electromagnetic Satellite. Remote Sens. 2020, 12, 2300. [Google Scholar] [CrossRef]
- Torres-González, P.A.; Luengo-Oroz, N.; Lamolda, H.; D’Alessandro, W.; Albert, H.; Iribarren, I.; Moure-García, D.; Soler, V. Unrest Signals after 46 Years of Quiescence at Cumbre Vieja, La Palma, Canary Islands. J. Volcanol. Geotherm. Res. 2020, 392, 106757. [Google Scholar] [CrossRef]
- Aiuppa, A.; Casetta, F.; Coltorti, M.; Stagno, V.; Tamburello, G. Carbon Concentration Increases with Depth of Melting in Earth’s Upper Mantle. Nat. Geosci. 2021, 14, 697–703. [Google Scholar] [CrossRef]
- Fernández, J.; Escayo, J.; Hu, Z.; Camacho, A.G.; Samsonov, S.V.; Prieto, J.F.; Tiampo, K.F.; Palano, M.; Mallorquí, J.J.; Ancochea, E. Detection of Volcanic Unrest Onset in La Palma, Canary Islands, Evolution and Implications. Sci. Rep. 2021, 11, 2540. [Google Scholar] [CrossRef] [PubMed]
- Pankhurst, M.J.; Scarrow, J.H.; Barbee, O.A.; Hickey, J.; Coldwell, B.C.; Rollinson, G.K.; Rodríguez-Losada, J.A.; Martín Lorenzo, A.; Rodríguez, F.; Hernández, W.; et al. Rapid Response Petrology for the Opening Eruptive Phase of the 2021 Cumbre Vieja Eruption, La Palma, Canary Islands. Volcanica 2022, 5, 1–10. [Google Scholar] [CrossRef]
- Rees, D.; Fuller-Rowell, T.J.; Quegan, S.; Moffett, R.J.; Bailey, G.J. Simulations of the Seasonal Variations of the Thermosphere and Ionosphere Using a Coupled, Three-Dimensional, Global Model, Including Variations of the Interplanetary Magnetic Field. J. Atmos. Terr. Phys. 1988, 50, 903–930. [Google Scholar] [CrossRef]
- Balan, N.; Bailey, G.J. Equatorial Plasma Fountain and Its Effects: Possibility of an Additional Layer. J. Geophys. Res. 1995, 100, 21421–21432. [Google Scholar] [CrossRef]
- Marchetti, D.; De Santis, A.; D’Arcangelo, S.; Poggio, F.; Jin, S.; Piscini, A.; Campuzano, S.A. Magnetic Field and Electron Density Anomalies from Swarm Satellites Preceding the Major Earthquakes of the 2016–2017 Amatrice-Norcia (Central Italy) Seismic Sequence. Pure Appl. Geophys. 2020, 177, 305–319. [Google Scholar] [CrossRef]
- Alken, P.; Thébault, E.; Beggan, C.D.; Amit, H.; Aubert, J.; Baerenzung, J.; Bondar, T.N.; Brown, W.J.; Califf, S.; Chambodut, A.; et al. International Geomagnetic Reference Field: The Thirteenth Generation. Earth Planets Space 2021, 73, 49. [Google Scholar] [CrossRef]
- De Santis, A.; De Franceschi, G.; Spogli, L.; Perrone, L.; Alfonsi, L.; Qamili, E.; Cianchini, G.; Di Giovambattista, R.; Salvi, S.; Filippi, E.; et al. Geospace Perturbations Induced by the Earth: The State of the Art and Future Trends. Phys. Chem. Earth Parts A/B/C 2015, 85–86, 17–33. [Google Scholar] [CrossRef]
- De Santis, A.; Abbattista, C.; Alfonsi, L.; Amoruso, L.; Campuzano, S.A.; Carbone, M.; Cesaroni, C.; Cianchini, G.; De Franceschi, G.; De Santis, A.; et al. Geosystemics View of Earthquakes. Entropy 2019, 21, 412. [Google Scholar] [CrossRef] [PubMed]
- Bilitza, D. Comparison of Measured and Predicted F2 Peak Altitude. Adv. Space Res. 1985, 5, 29–32. [Google Scholar] [CrossRef]
- Knudsen, D.J.; Burchill, J.K.; Buchert, S.C.; Eriksson, A.I.; Gill, R.; Wahlund, J.-E.; Åhlen, L.; Smith, M.; Moffat, B. Thermal Ion Imagers and Langmuir Probes in the Swarm Electric Field Instruments. J. Geophys. Res. Space Phys. 2017, 122, 2655–2673. [Google Scholar] [CrossRef]


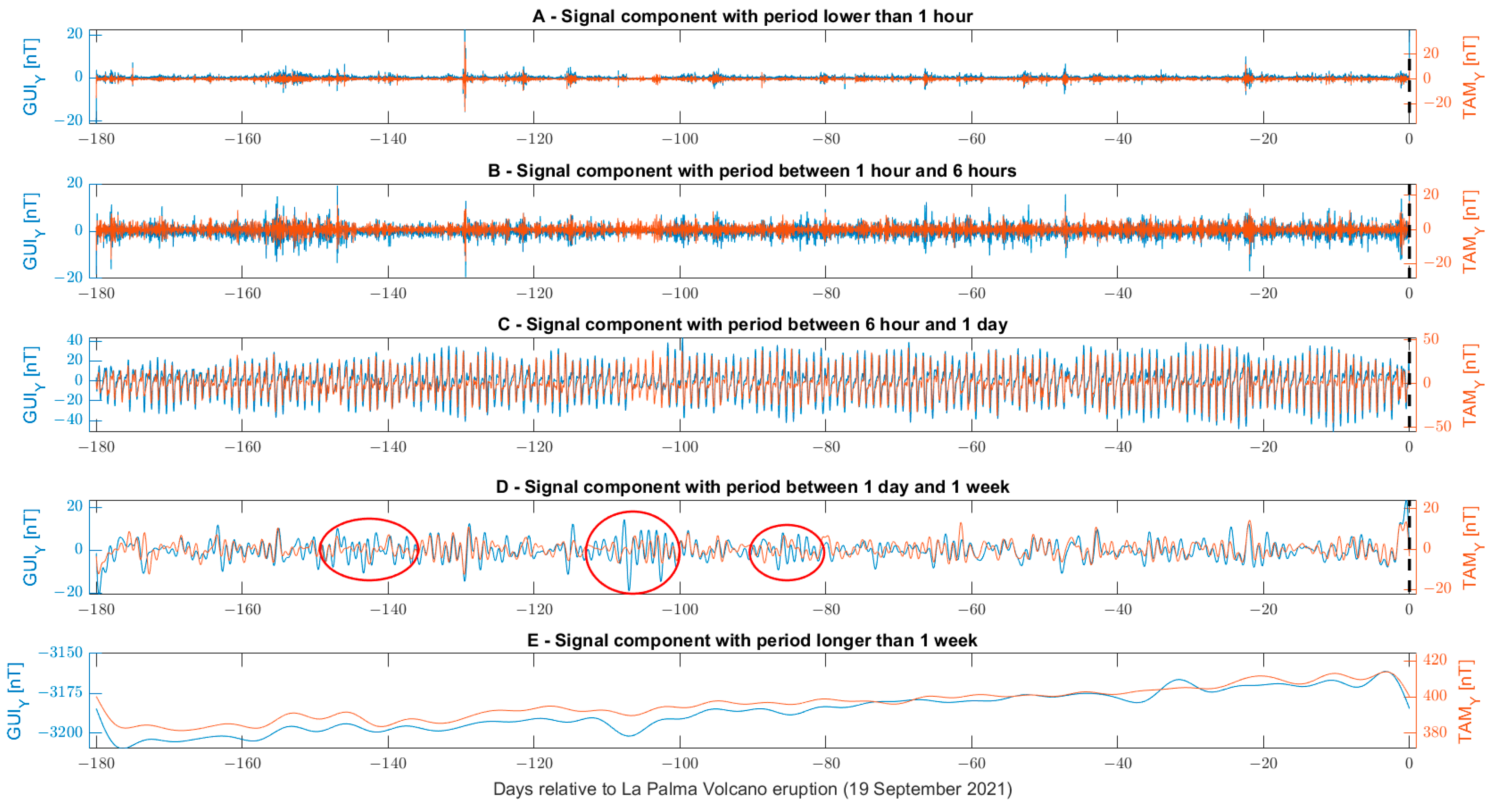
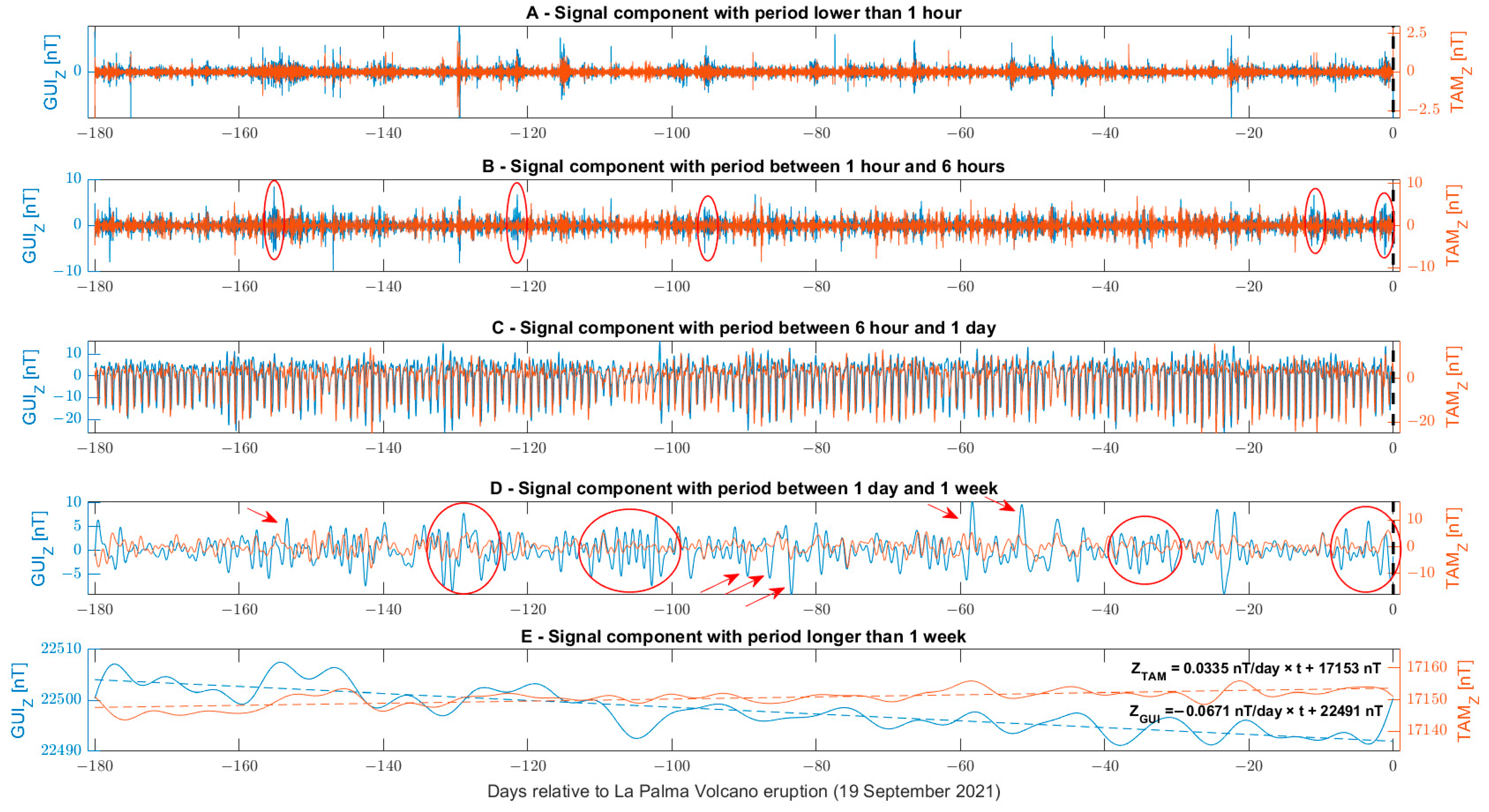
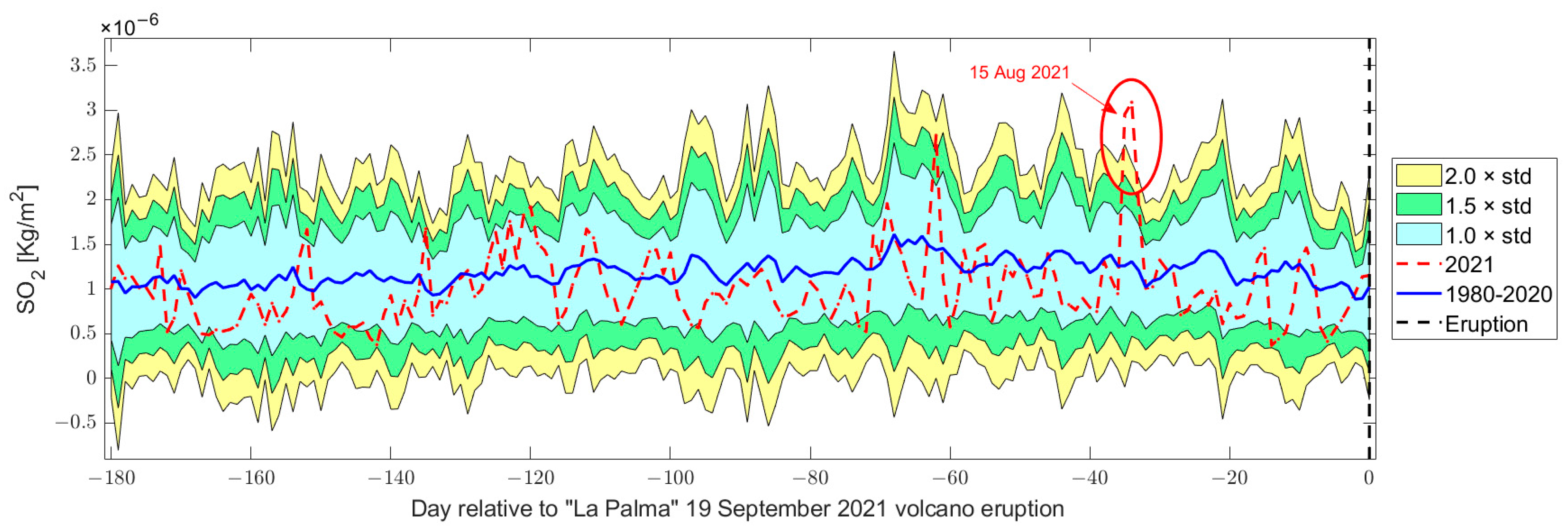
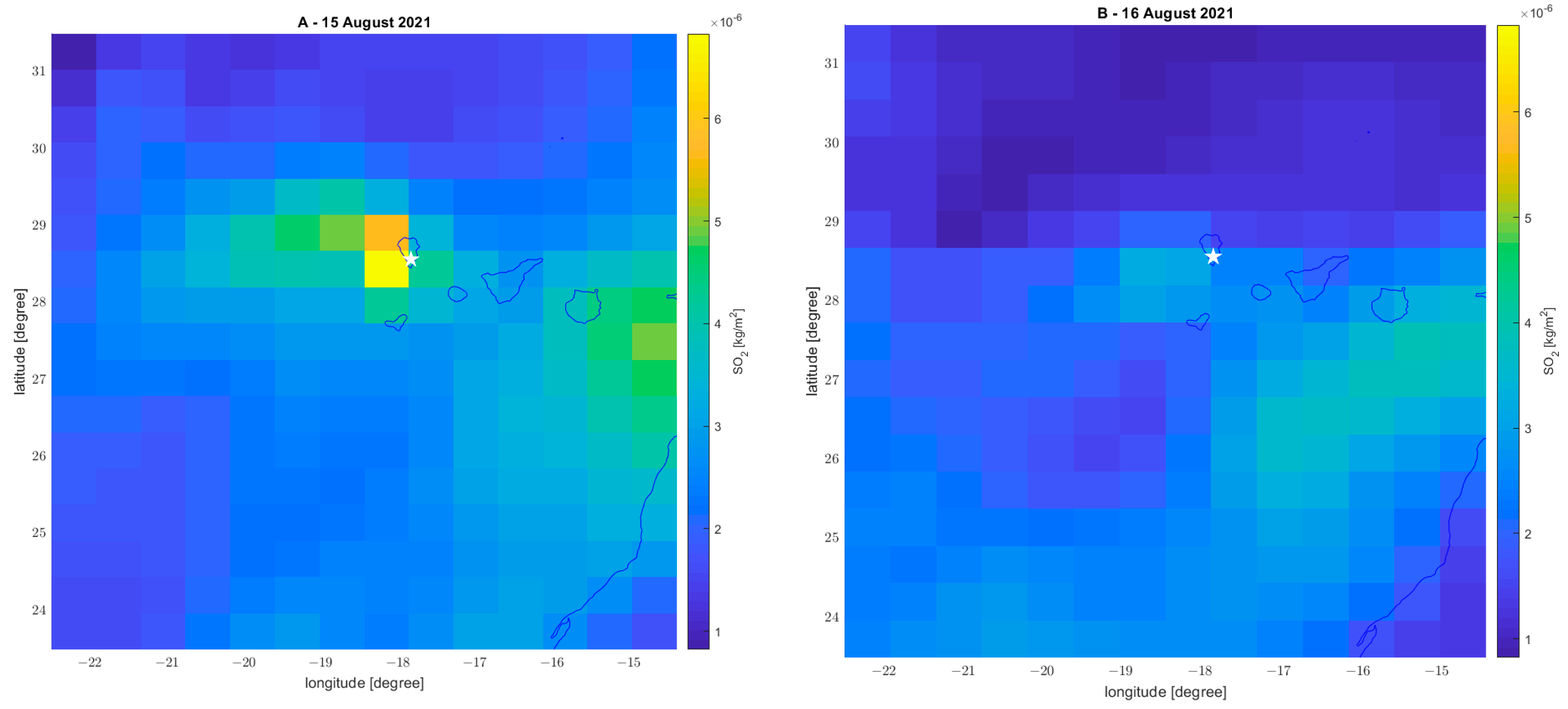

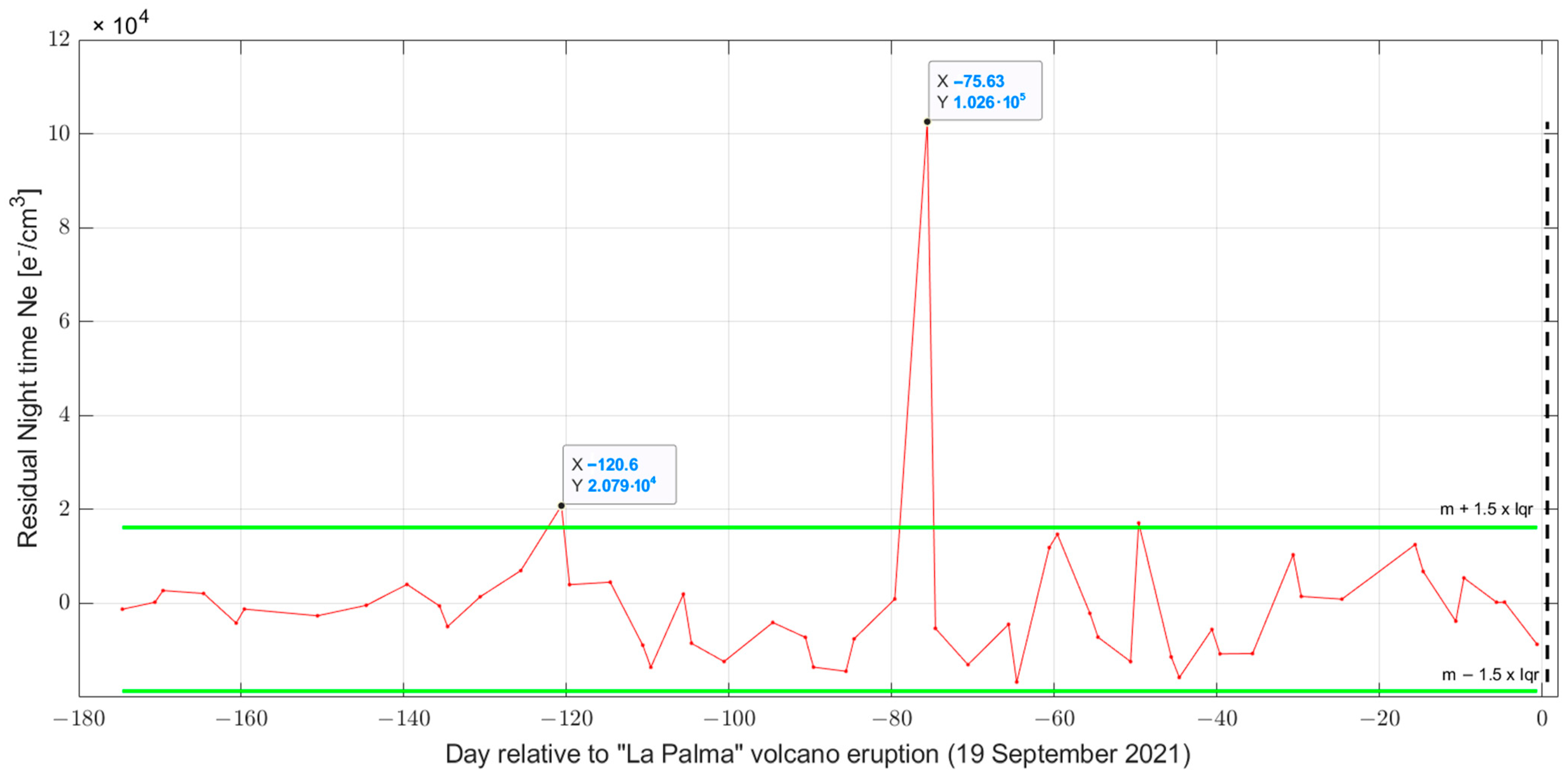
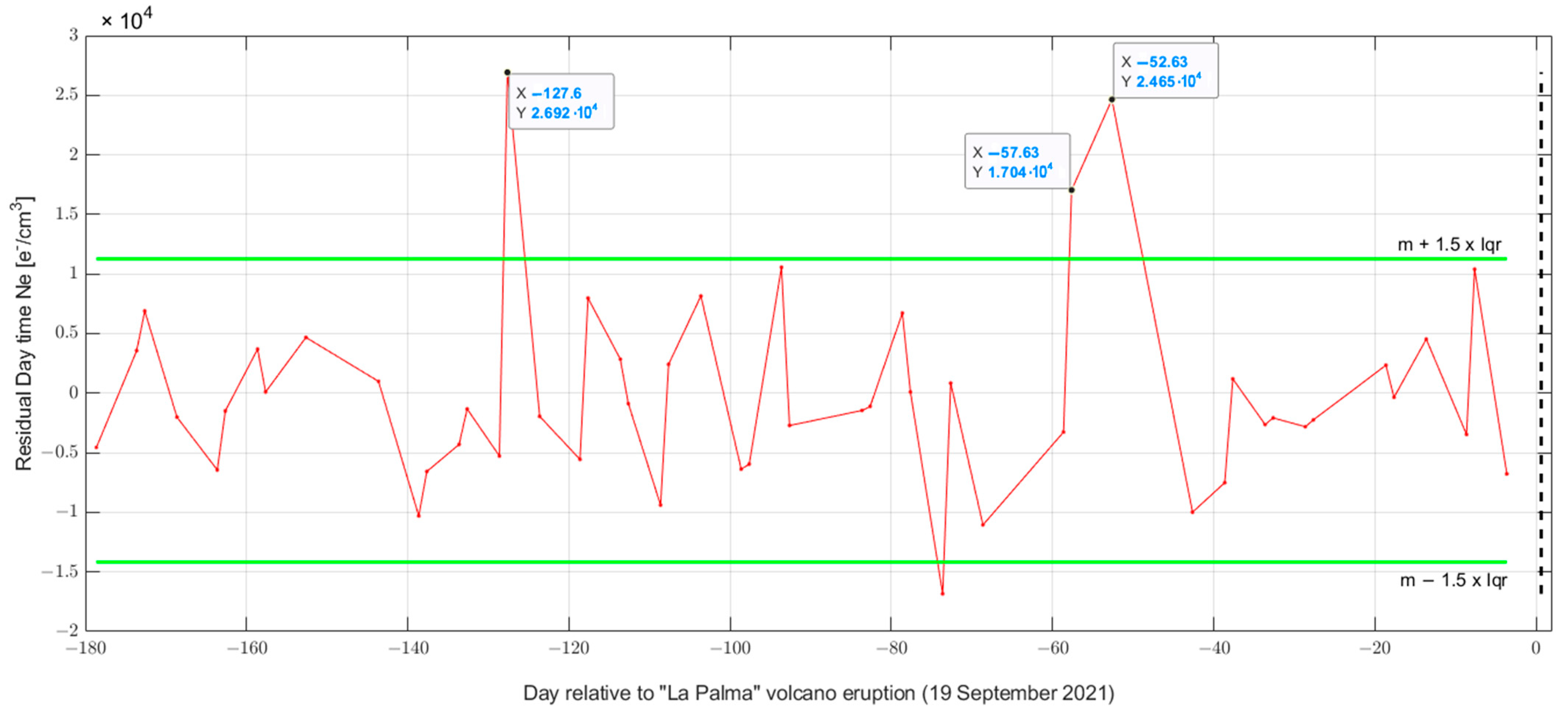
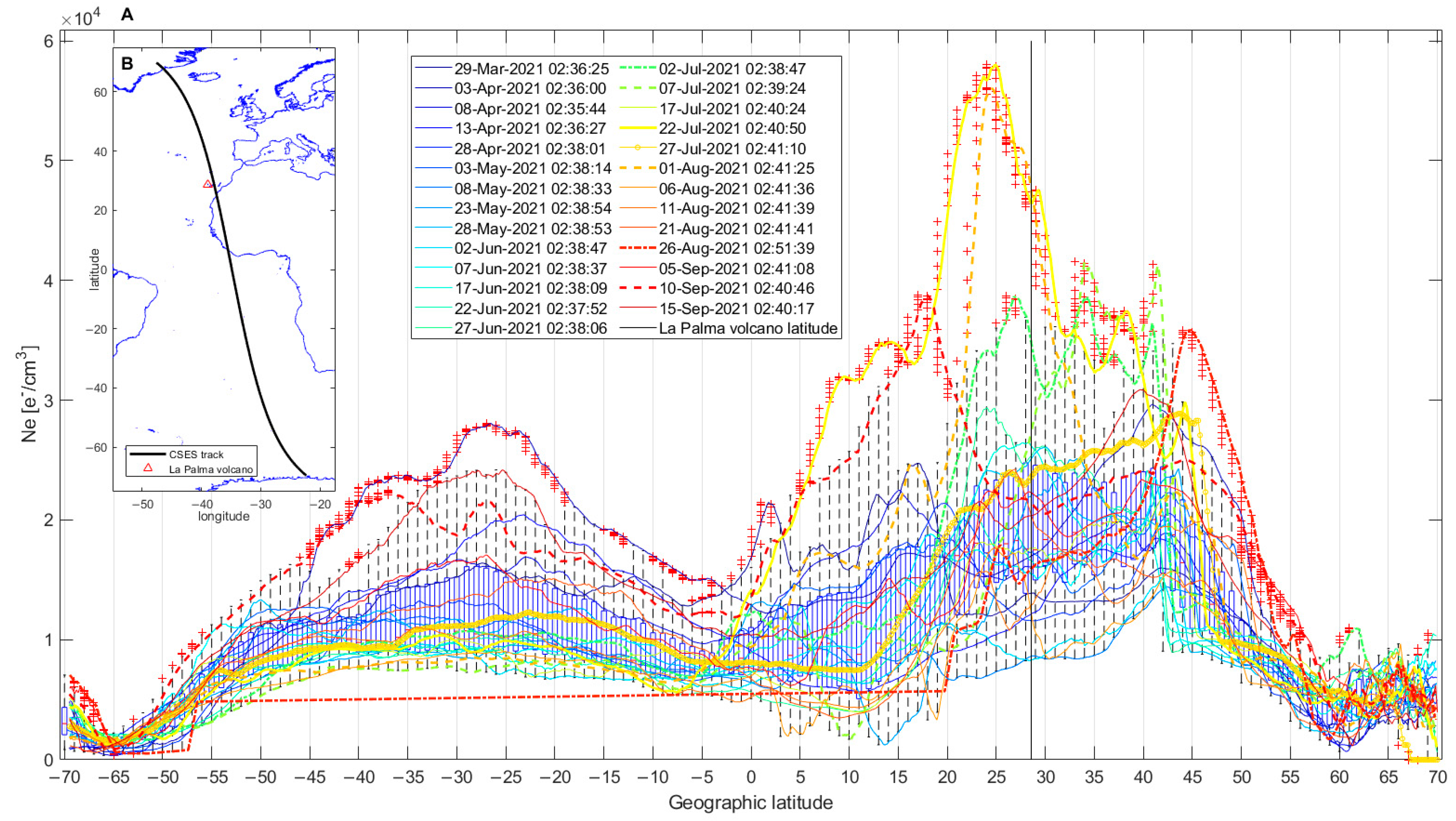
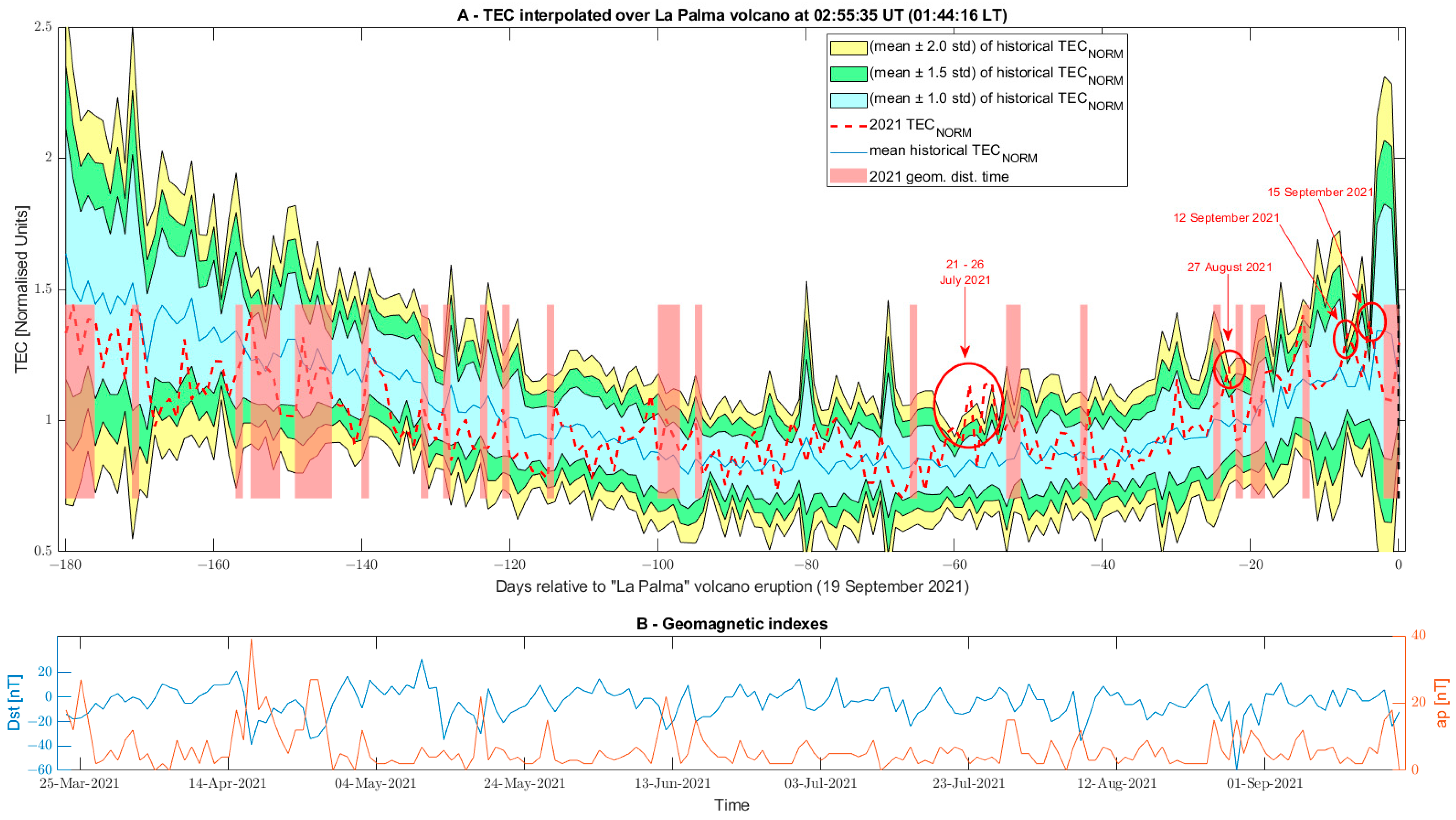

| Parameter | Anomalous Day [2021] | Amount of the Anomaly 1 | Visual Check of the Anomaly |
|---|---|---|---|
| SO2 | 15 August | 50.00% | They seem emitted by the volcano (anomaly clearly above volcano) |
| 16 August | 120.55% | ||
| DMS | 17 May | 79.76% | Not emitted by the volcano. It could be a secondary effect. |
| 18 May | 20.81% | ||
| 19 May | 97.22% | ||
| 20 May | 95.44% | ||
| 21 May | 484.99% | ||
| 22 May | 400.04% | ||
| 23 May | 130.18% | ||
| 8 June | 66.11% | Not emitted by the volcano, but value closer to the island. It could be a secondary effect. | |
| 9 June | 484.08% | ||
| 10 June | 417.27% | ||
| 11 June | 270.24% | ||
| 12 June | 246.10% | ||
| 15 August | 80.31% | Not emitted by the volcano. It could be a secondary effect. | |
| 16 August | 190.41% | ||
| 17 August | 291.80% | ||
| 18 August | 231.11% | ||
| 19 August | 174.06% | ||
| Aerosol | 25 March | 103.88% | Spatially coincide with the caldera of the Canarias volcano system |
| 27 March | 19.38% | ||
| 17 May | 19.38% | Spatially coincide with the caldera of the Canarias volcano system | |
| 18 May | 325.26% | ||
| 21 May | 38.09% | ||
| 8 June | 346.98% | It seems to be a sandstorm from the Sahara desert. | |
| 9 June | 834.43% | ||
| 10 June | 180.31% | ||
| 11 June | 285.23% | ||
| 12 June | 4.29% | ||
| 12 July | 164.26% | It is not centred on the volcano, but an indirect effect cannot be totally excluded. | |
| 13 July | 86.10% | ||
| 15 August | 105.87% | It seems not related to the volcano | |
| 16 August | 76.08% | ||
| CO | 24 March | 16.85% | Emission close to the volcano |
| 25 March | 84.75% | ||
| 19 April | 16.61% | It seems to be due to another source and later transported over the research area | |
| 15 May | 3.59% | Not clear as there is another phenomenon but also emission potentially related to the volcano | |
| 1 August | 7.30% | The emission seems to come from the volcano. | |
| 2 August | 30.76% | Not related to the volcano. | |
| 9 August | 93.07% | It could be related to the volcano. | |
| 10 August | 13.09% | ||
| 19 August | 2.88% | It does not seem to be related to the volcano | |
| 20 August | 24.88% | ||
| 26 August | 38.37% | Spatially not localised above the volcano. | |
| 4 September | 32.02% | It could be related to other volcanoes in the area. | |
| 7 September | 143.52% | It could be related to the volcano even if it is a very wide anomaly | |
| 8 September | 100.41% | ||
| 9 September | 85.10% | ||
| 10 September | 29.40% | ||
| 13 September | 91.86% | Some days are spatially well related to the volcano. | |
| 14 September | 174.76% | ||
| 15 September | 232.07% | ||
| 16 September | 50.25% | ||
| 18 September | 33.58% | ||
| 19 September 2 | 15.27% | “Co-eruption” emission. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marchetti, D.; Zhu, K.; Zhang, H.; Zhima, Z.; Yan, R.; Shen, X.; Chen, W.; Cheng, Y.; He, X.; Wang, T.; et al. Clues of Lithosphere, Atmosphere and Ionosphere Variations Possibly Related to the Preparation of La Palma 19 September 2021 Volcano Eruption. Remote Sens. 2022, 14, 5001. https://doi.org/10.3390/rs14195001
Marchetti D, Zhu K, Zhang H, Zhima Z, Yan R, Shen X, Chen W, Cheng Y, He X, Wang T, et al. Clues of Lithosphere, Atmosphere and Ionosphere Variations Possibly Related to the Preparation of La Palma 19 September 2021 Volcano Eruption. Remote Sensing. 2022; 14(19):5001. https://doi.org/10.3390/rs14195001
Chicago/Turabian StyleMarchetti, Dedalo, Kaiguang Zhu, Hanshuo Zhang, Zeren Zhima, Rui Yan, Xuhui Shen, Wenqi Chen, Yuqi Cheng, Xiaodan He, Ting Wang, and et al. 2022. "Clues of Lithosphere, Atmosphere and Ionosphere Variations Possibly Related to the Preparation of La Palma 19 September 2021 Volcano Eruption" Remote Sensing 14, no. 19: 5001. https://doi.org/10.3390/rs14195001
APA StyleMarchetti, D., Zhu, K., Zhang, H., Zhima, Z., Yan, R., Shen, X., Chen, W., Cheng, Y., He, X., Wang, T., Wen, J., Zhang, D., & Zhang, Y. (2022). Clues of Lithosphere, Atmosphere and Ionosphere Variations Possibly Related to the Preparation of La Palma 19 September 2021 Volcano Eruption. Remote Sensing, 14(19), 5001. https://doi.org/10.3390/rs14195001