Design and Analysis of a New Deployable Docking Mechanism for Microsatellites
Abstract
1. Introduction
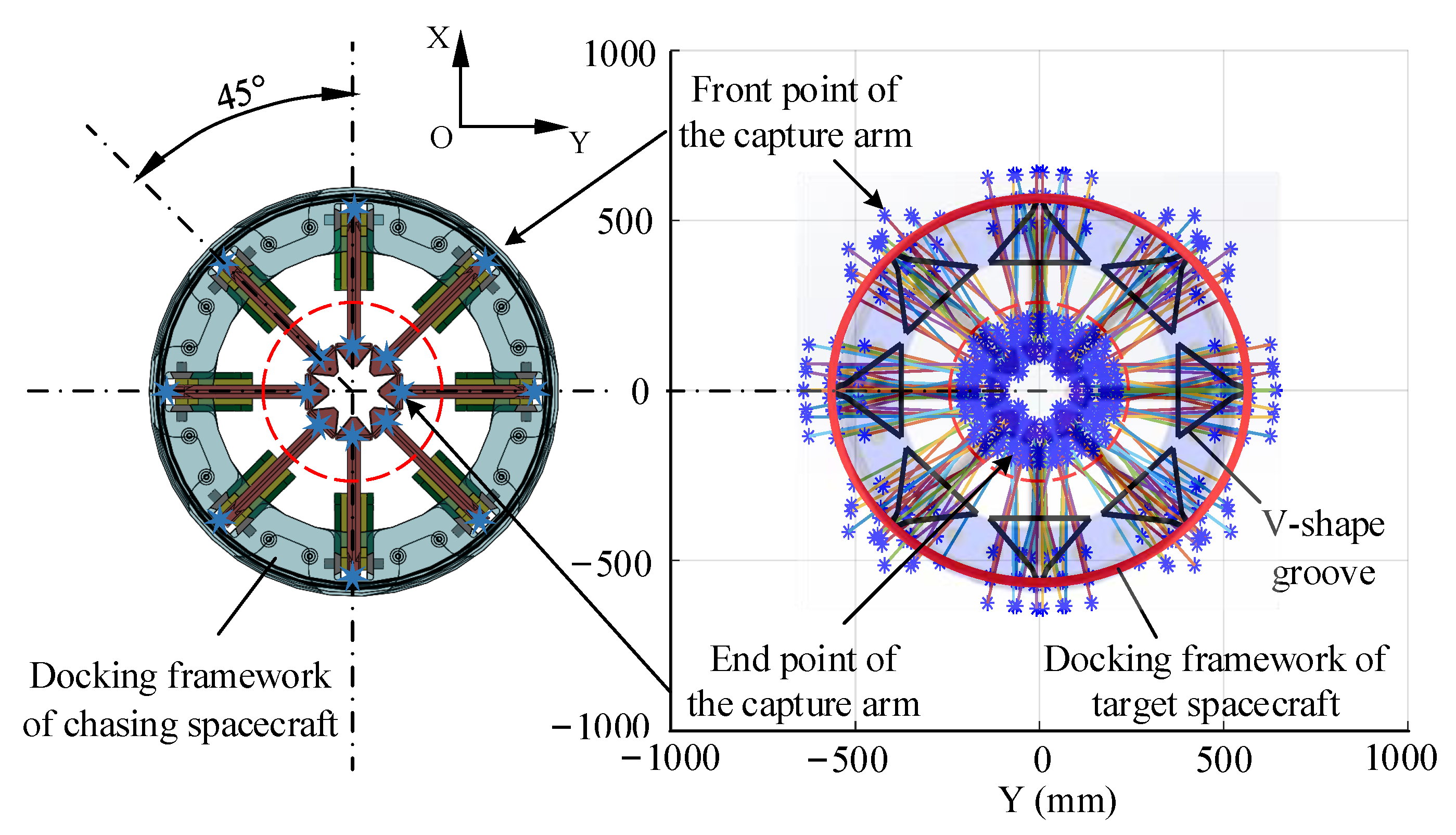
2. Structure and Working Principle
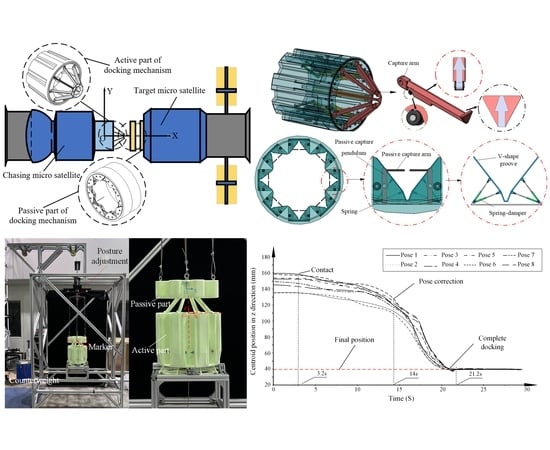
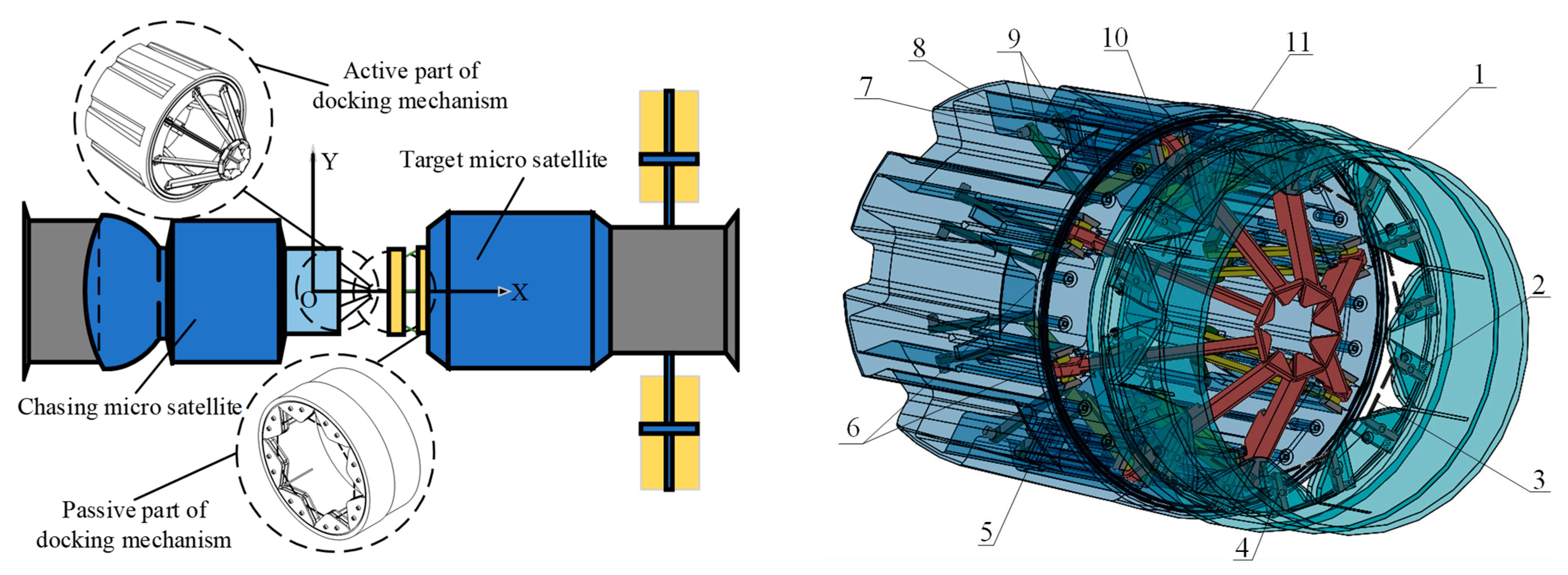
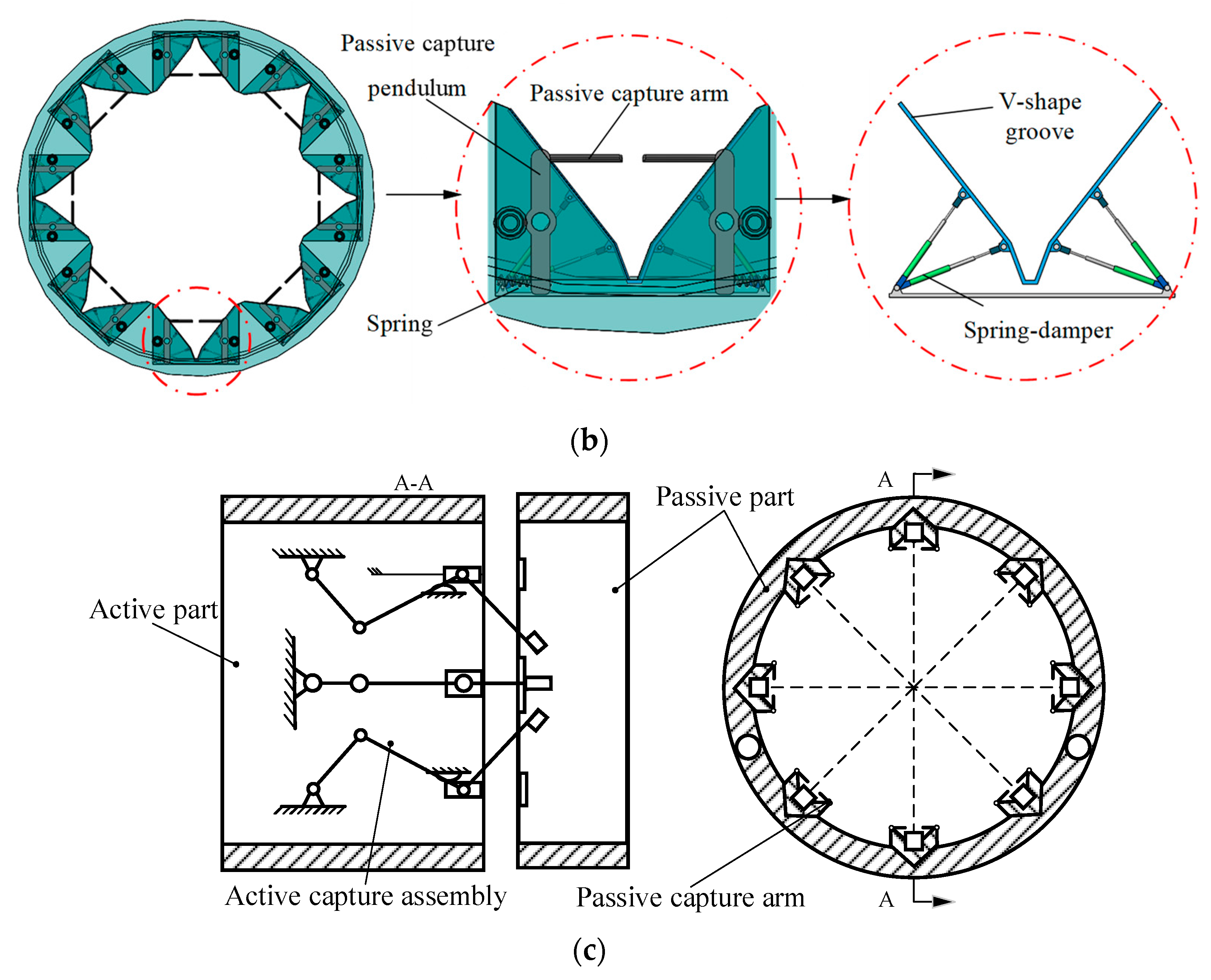
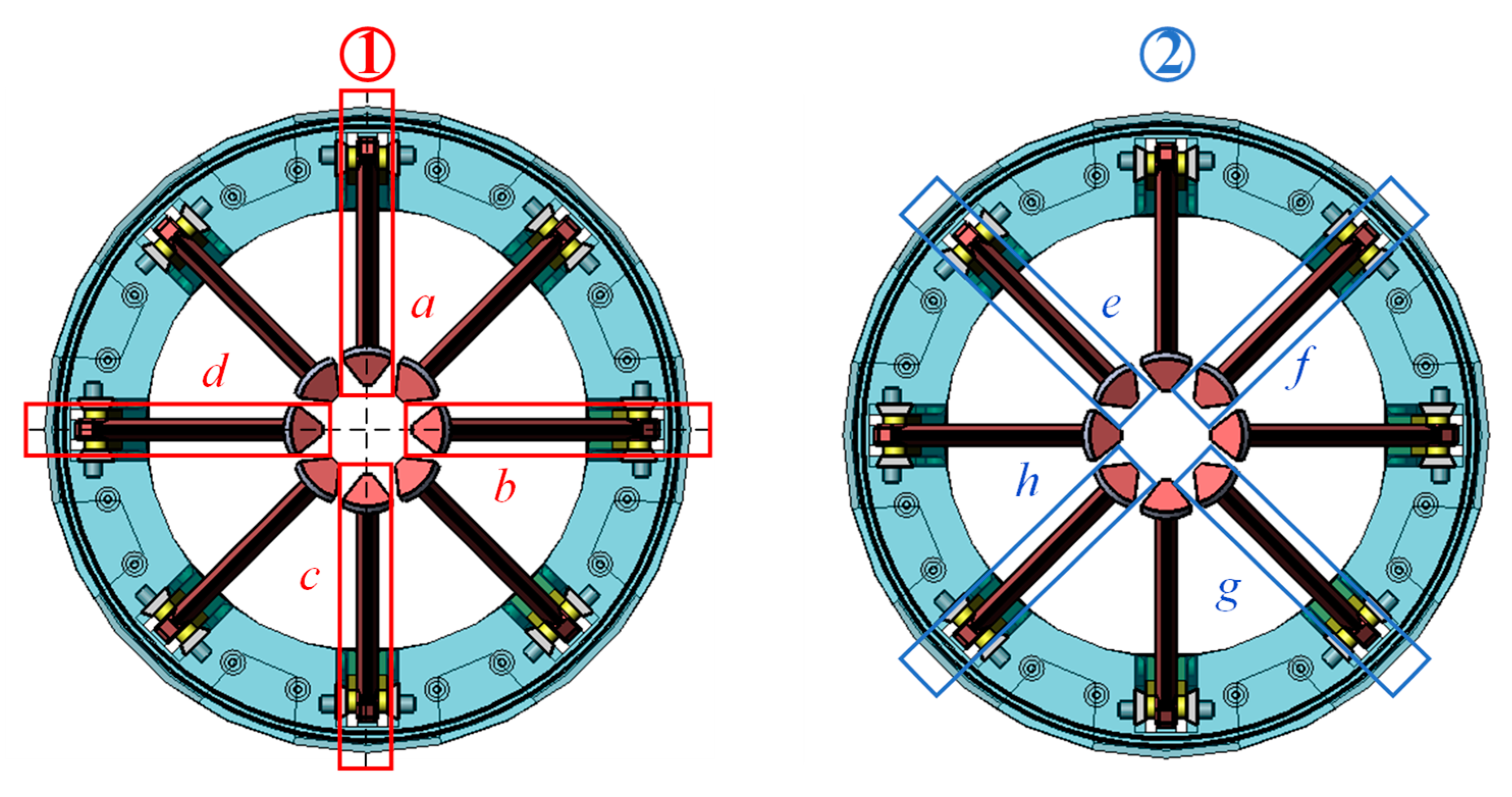
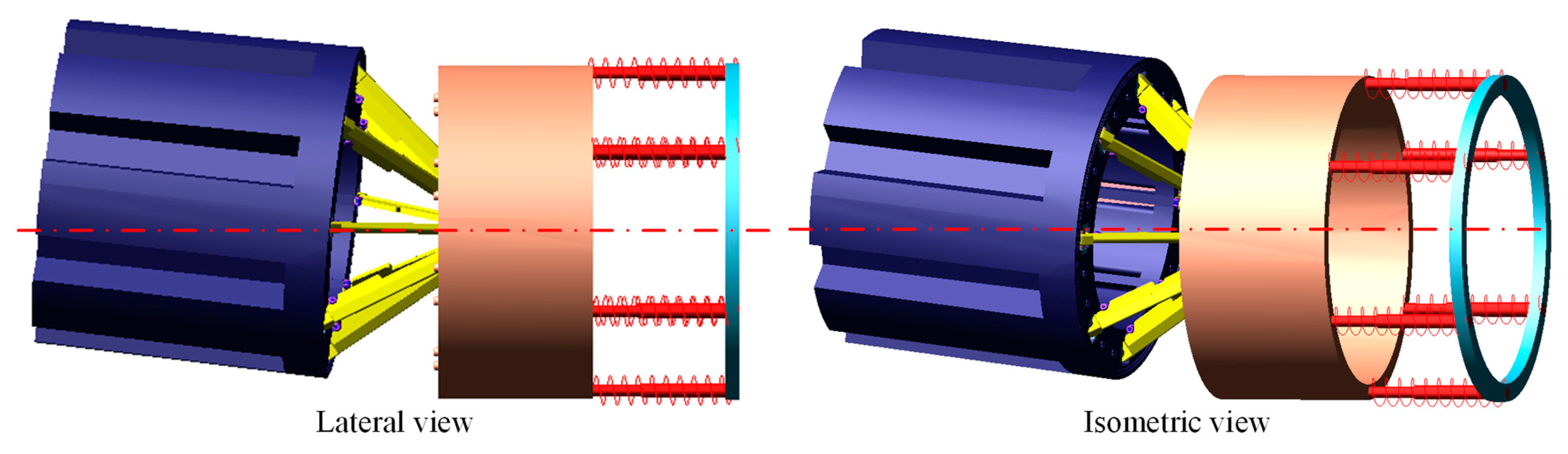
2.1. System Composition
2.2. Working Principle
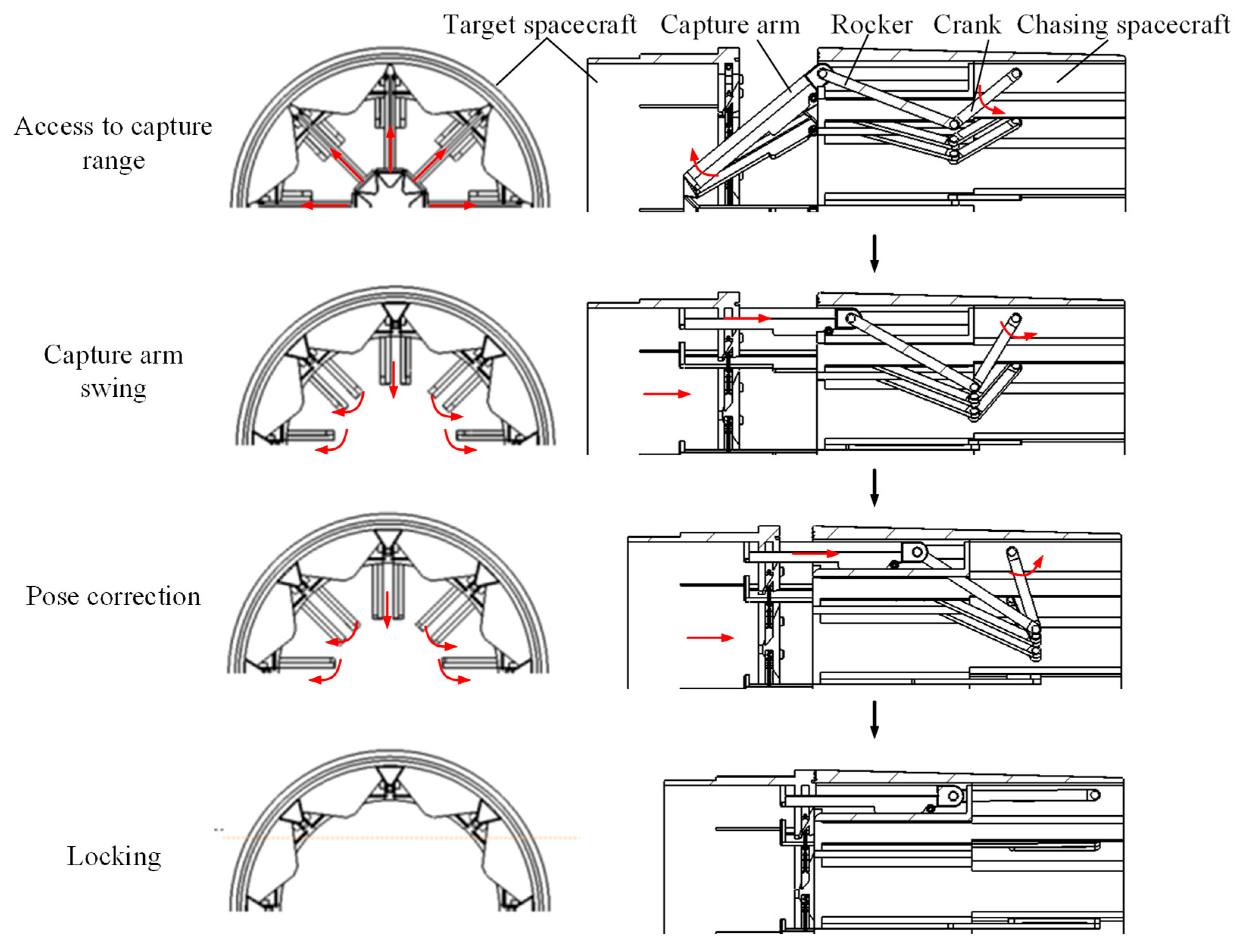
- (a)
- Access to the capture range. The capture arms are arranged at a fixed angle to the docking axis. And the passive part of the docking mechanism is extended by a six-degree-of-freedom platform. So, the capture arm of the active part is placed within the tolerance space at the passive part of the docking mechanism.
- (b)
- Capture arm swing. The crank slider module starts to work and all capture arms are simultaneously aligned along the direction away from the axis. Then, the capture arms are first in contact with the passive part of the docking mechanism on the target satellite.
- (c)
- Posture correction and approach. As the bevel of the capture arm squeezes the spring after contacting the bevel of the passive rocker, the passive rocker moves closer to the sides of the V-shape groove. When the capture arm ends contact with the bevel of the passive rocker, the spring springs back and the passive rocker catches the capture arm to achieve reliable capture. The capture arm is in continuous contact with the V-shape groove to achieve attitude correction between the two satellites.
- (d)
- Capture locking stage. The crank continues to rotate under the action of the motor, and the capture arm moves backward following the slider. The capture arm drives the target satellite to approach the chasing satellite. The seal ring on the docking frame of the chasing satellite contacts the docking frame of the target satellite and continuously squeezes the seal ring and the axially arranged disc spring on the docking frame to complete the application and sealing of the locking force between the two satellites. The six-degree-of-freedom docking platform at the end of the passive part is simultaneously retracted into the satellite, and the crank-slider mechanism achieves reliable self-locking.
3. Collaborative Capture Strategy
3.1. Positional Posture Error Analysis
3.2. Capture Arm Deployment Speed Analysis
3.3. Cooperative Capture Action Matching
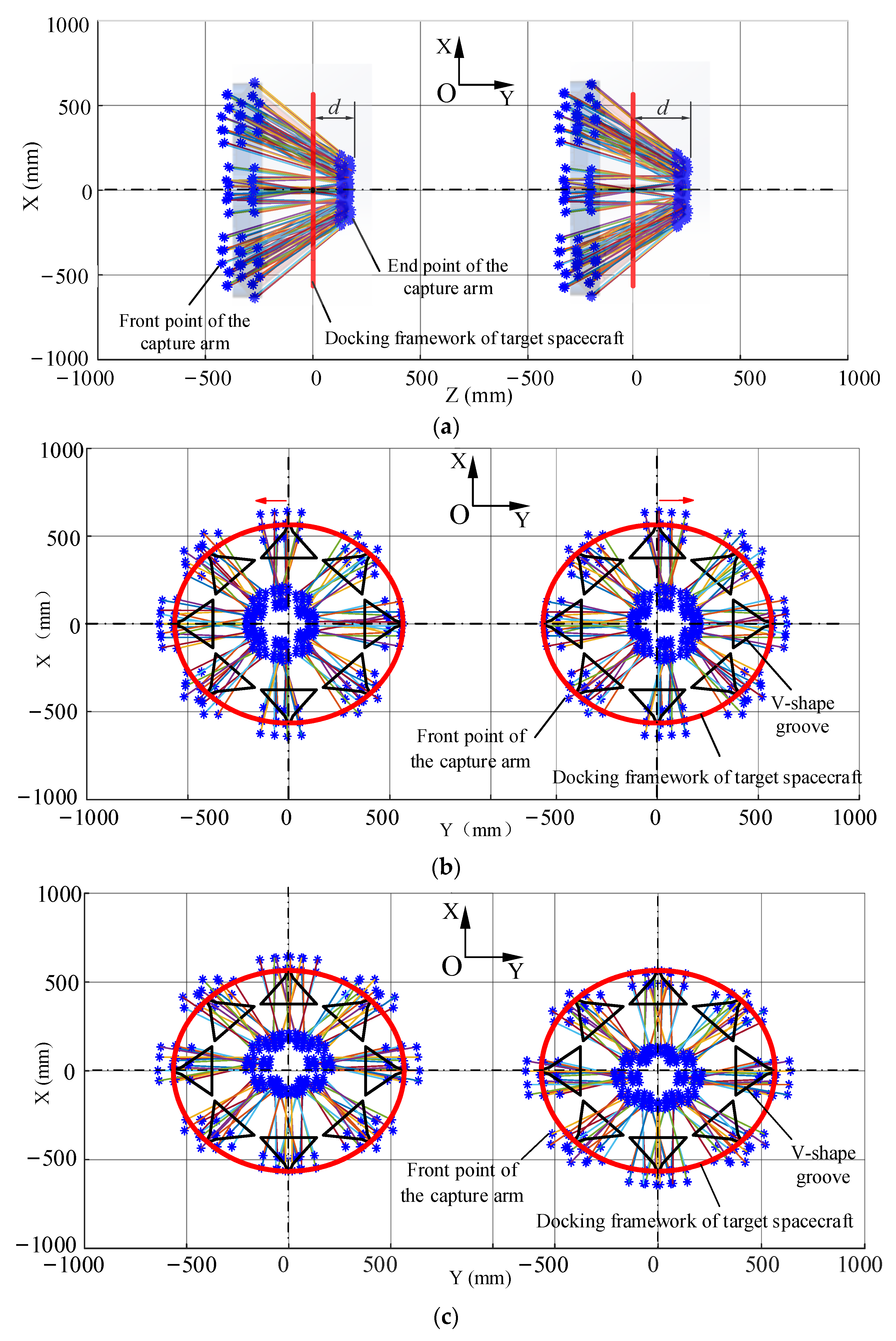
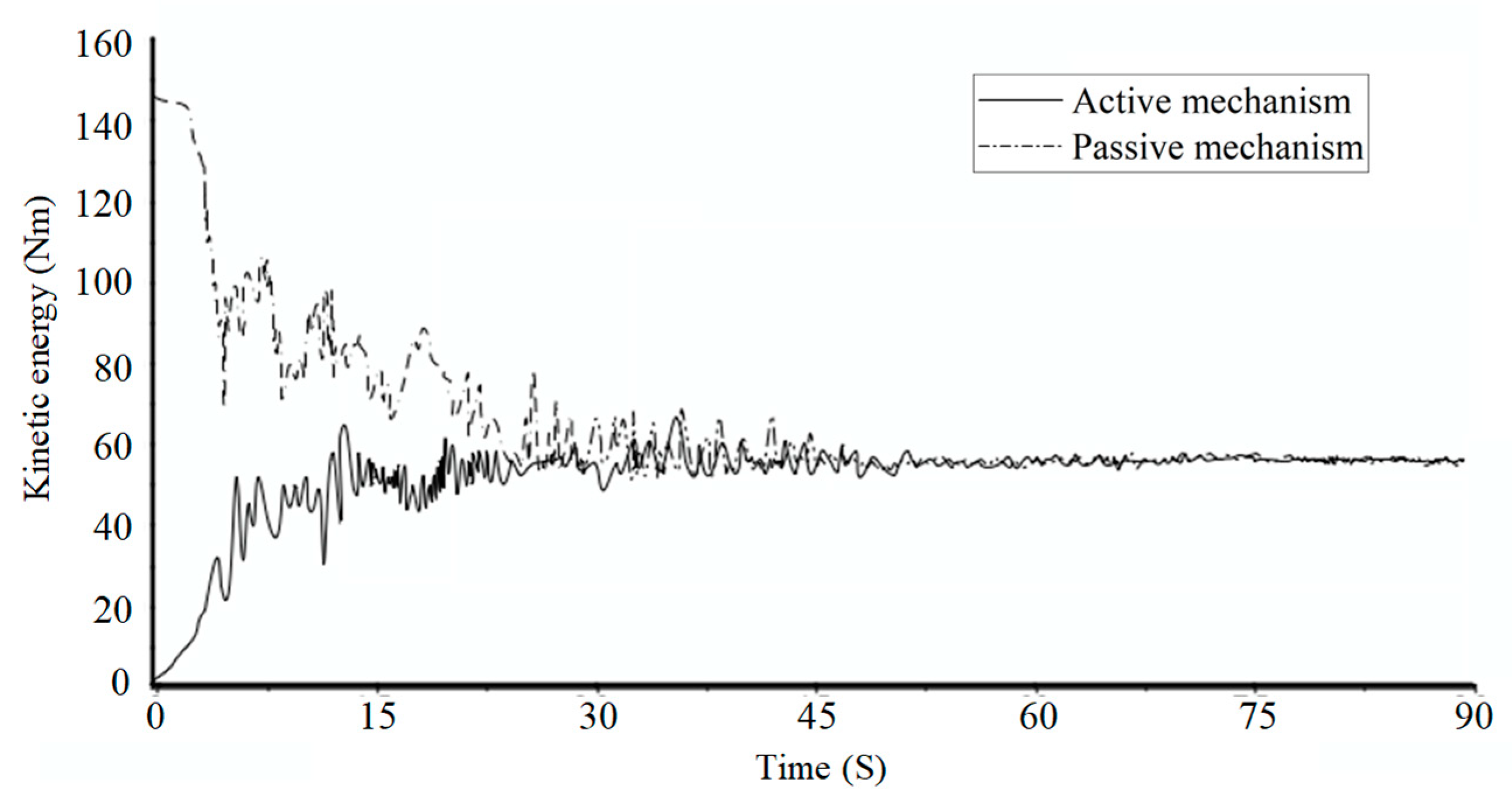
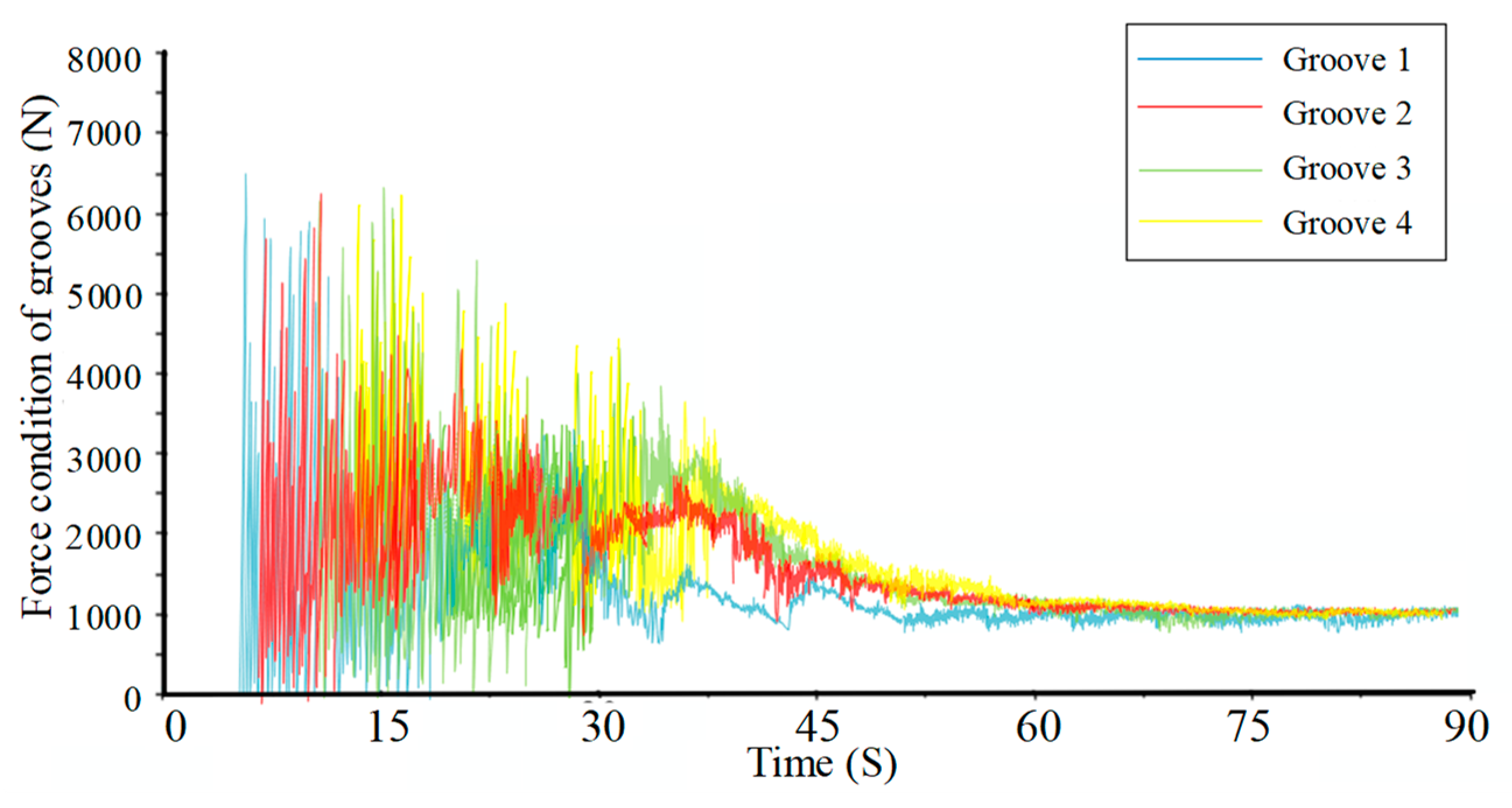
4. Simulation and Experiment Investigation
4.1. Positive Bump Docking
4.2. Error Position
4.3. Capture Strategy Analysis
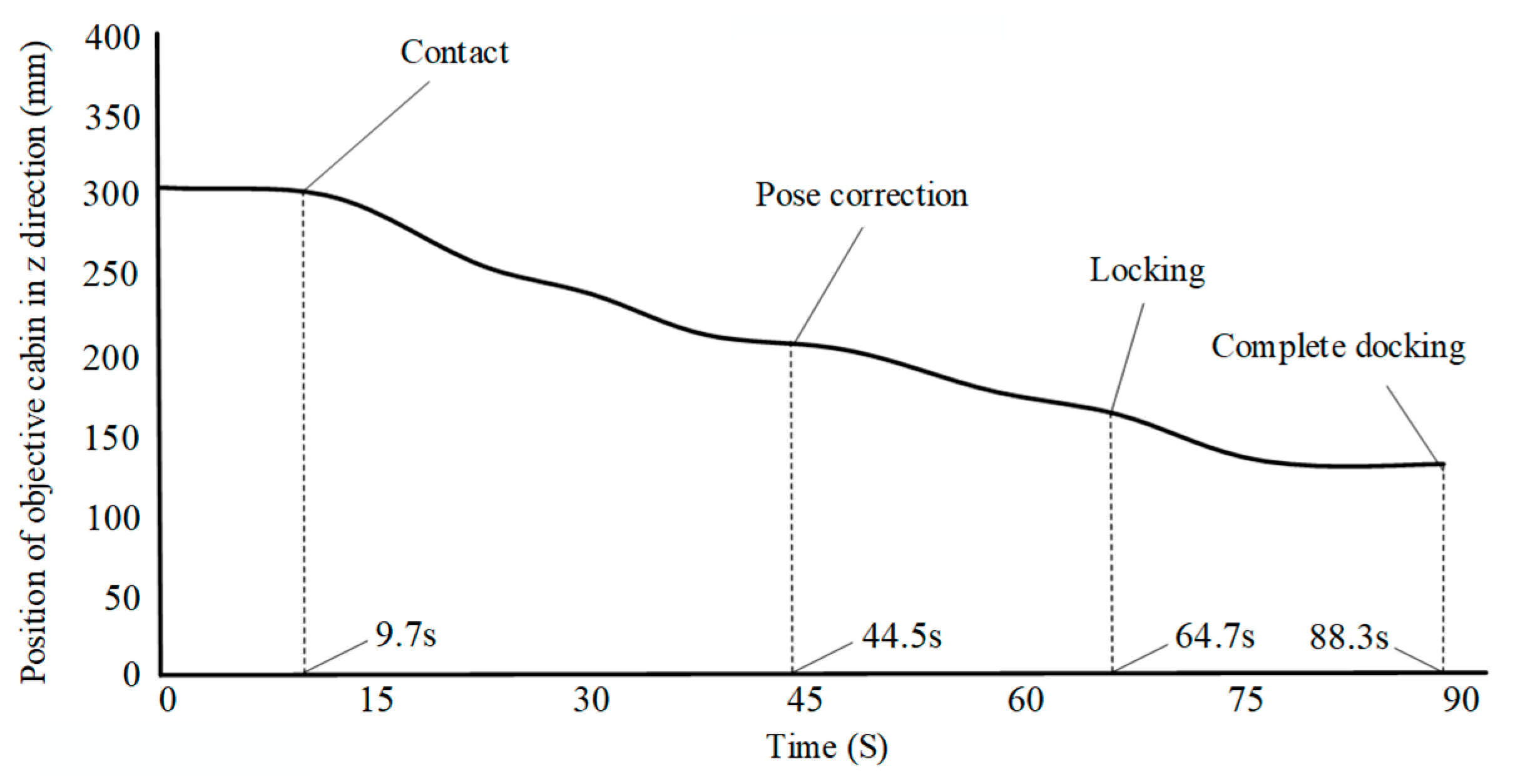
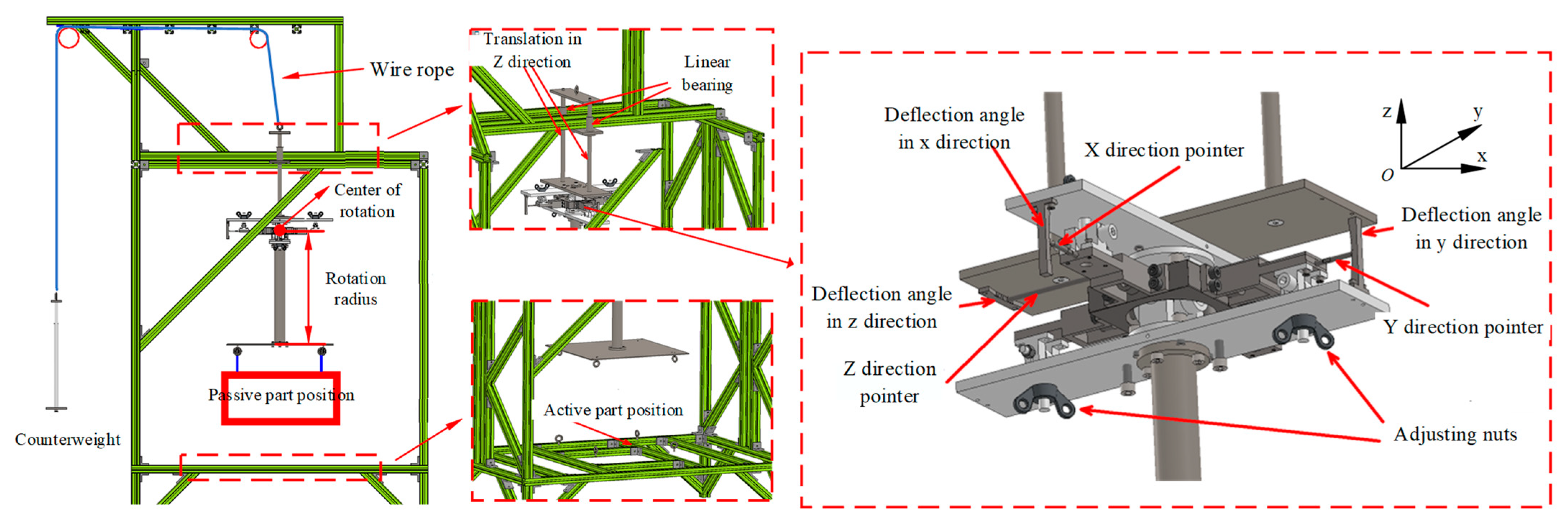
4.4. Experimental Verification
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Battistini, S.; De Angelis, G.; Pontani, M.; Graziani, F. An Iterative Guidance and Navigation Algorithm for Orbit Rendezvous of Cooperating CubeSats. Appl. Sci. 2022, 12, 9250. [Google Scholar] [CrossRef]
- Underwood, C.; Pellegrino, S.; Lappas, V.J. Using CubeSat/micro-satellite technology to demonstrate the Autonomous Assembly of a Reconfigurable Space Telescope (AAReST). Acta Astronaut. 2015, 114, 112–122. [Google Scholar] [CrossRef]
- Stesina, F. Tracking Model Predictive Control for Docking Maneuvers of a CubeSat with a Big Spacecraft. Aerospace 2021, 8, 197. [Google Scholar] [CrossRef]
- Zhao, X.; Zhang, S. Adaptive saturated control for spacecraft rendezvous and docking under motion constraints. Aerosp. Sci. Technol. 2021, 114, 106739. [Google Scholar] [CrossRef]
- Yan, W.; Bo, G.; Xiaodong, W.; Junde, W.; Chaoze, Z. Simulation of Spacecraft Cabin Automatic Docking. In Proceedings of the 2021 4th International Conference on Robotics, Control and Automation Engineering (RCAE), Wuhan, China, 4–6 November 2021; pp. 356–361. [Google Scholar] [CrossRef]
- Breeden, J.; Panagou, D. Guaranteed Safe Spacecraft Docking with Control Barrier Functions. IEEE Control Syst. Lett. 2021, 6, 2000–2005. [Google Scholar] [CrossRef]
- Yu, D.; Liu, P.; Qiao, D.; Tang, X. A Safety Prediction System for Lunar Orbit Rendezvous and Docking Mission. Algorithms 2021, 14, 188. [Google Scholar] [CrossRef]
- Hinkel, H.; Zipay, J.J.; Strube, M.; Cryan, S. Technology development of automated rendezvous and docking/capture sensors and docking mechanism for the Asteroid Redirect crewed mission. In Proceedings of the 2016 IEEE Aerospace Conference, Big Sky, MT, USA, 5–12 March 2016; pp. 1–8. [Google Scholar] [CrossRef][Green Version]
- Luo, Y.; Sun, Z. Safe rendezvous scenario design for geostationary satellites with collocation constraints. Astrodynamics 2017, 1, 71–83. [Google Scholar] [CrossRef]
- Choi, J.; Jung, J.; Lee, D.; Kim, B. Articulated linkage arms based reliable capture device for janitor satellites. Acta Astronaut. 2019, 163, 91–99. [Google Scholar] [CrossRef]
- Shi, K.; Liu, C.; Biggs, J.D.; Sun, Z.; Yue, X. Observer-based control for spacecraft electromagnetic docking. Aerosp. Sci. Technol. 2020, 99, 105759. [Google Scholar] [CrossRef]
- Olivieri, L.; Francesconi, A. Design and test of a semiandrogynous docking mechanism for small satellites. Acta Astronaut. 2016, 122, 219–230. [Google Scholar] [CrossRef]
- Shi, K.; Liu, C.; Biggs, J.D.; Sun, Z.; Yue, X. Coupled orbit-attitude dynamics and trajectory tracking control for spacecraft electromagnetic docking. Appl. Math. Model. 2022, 101, 553–572. [Google Scholar] [CrossRef]
- Stamm, S.; Motaghedi, P. Orbital express capture system: Concept to reality. Int. Soc. Opt. Photonics 2004, 5419, 78–91. [Google Scholar] [CrossRef]
- Motaghedi, P. On-orbit performance of the Orbital Express Capture System. In Sensors and Systems for Space Applications II, Proceedings of the SPIE Defense and Security Symposium, Orlando, FL, USA, 16–20 March 2008; SPIE: Bellingham, WA, USA, 2008; Volume 6958. [Google Scholar]
- Ui, K.; Matunaga, S. Identification of Docking Possibility Criteria Including Recovery from Incomplete Grasping of Docking Mechanism for Nanosatellite. J. Space Eng. 2009, 2, 1–11. [Google Scholar] [CrossRef]
- Boesso, A.; Francesconi, A. ARCADE small-scale docking mechanism for micro-satellites. Acta Astronaut. 2013, 86, 77–87. [Google Scholar] [CrossRef]
- Barbetta, M.; Boesso, A.; Branz, F.; Carron, A.; Olivieri, L.; Prendin, J.; Rodeghiero, G.; Sansone, F.; Savioli, L.; Spinello, F.; et al. ARCADE-R2 experiment on board BEXUS 17 stratospheric balloon. CEAS Space J. 2015, 7, 347–358. [Google Scholar] [CrossRef]
- Bowen, J.; Villa, M.; Williams, A. CubeSat based rendezvous, proximity operations, and docking in the CPOD mission. In Proceedings of the 29th Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 8–15 August 2015. [Google Scholar]
- Jianbin, H.; Zhi, L.; Bo, M.; Xu, H.; Yujia, P.; Longfei, H. Dynamic modeling and analysis of docking the GEO satellite interface ring. In Proceedings of the 2017 IEEE International Conference on Robotics and Biomimetics (ROBIO), Macau, Macao, 5–8 December 2017; IEEE: Piscataway Township, NJ, USA, 2017; pp. 2105–2110. [Google Scholar] [CrossRef]
- Branz, F.; Olivieri, L.; Sansone, F.; Francesconi, A. Miniature docking mechanism for CubeSats. Acta Astronaut. 2020, 176, 510–519. [Google Scholar] [CrossRef]
- Takao, Y.; Mori, O.; Kawaguchi, J. Analysis and design of a spacecraft docking system using a deployable boom. Acta Astronaut. 2021, 179, 172–185. [Google Scholar] [CrossRef]







| Number | x/mm | y/mm | z/mm | α/° | β/° | φ/° |
|---|---|---|---|---|---|---|
| 1 | −40 | 40 | 40 | 6 | 6 | 6 |
| 2 | −40 | 40 | 40 | −6 | 6 | 6 |
| 3 | −40 | 40 | 40 | 6 | −6 | 6 |
| 4 | −40 | 40 | 40 | 6 | 6 | −6 |
| 5 | −40 | 40 | 40 | −6 | −6 | 6 |
| 6 | −40 | 40 | 40 | 6 | −6 | −6 |
| 7 | −40 | 40 | 40 | −6 | 6 | −6 |
| 8 | −40 | 40 | 40 | −6 | −6 | −6 |
| Position Deviation/mm | Angular Deviation/° | Linear Velocity/mm·s−1 | Angular Velocity/°·s−1 |
|---|---|---|---|
| dy = 100 | 0 | vy = 100 | ω = 0.2 |
| Position Deviation/mm | Linear Velocity/mm·s−1 | Angular Velocity/°·s−1 |
|---|---|---|
| dy = 100 | vy = 100 | ω = 0.2 |
| Position Deviation/mm | Angular Deviation/° | Linear Velocity/mm·s−1 | Angular Velocity/°·s−1 |
|---|---|---|---|
| dx = dy = dz = 100 | φx = φy = φy = 6 | vy = vy = 100 | ω = 0.2 |
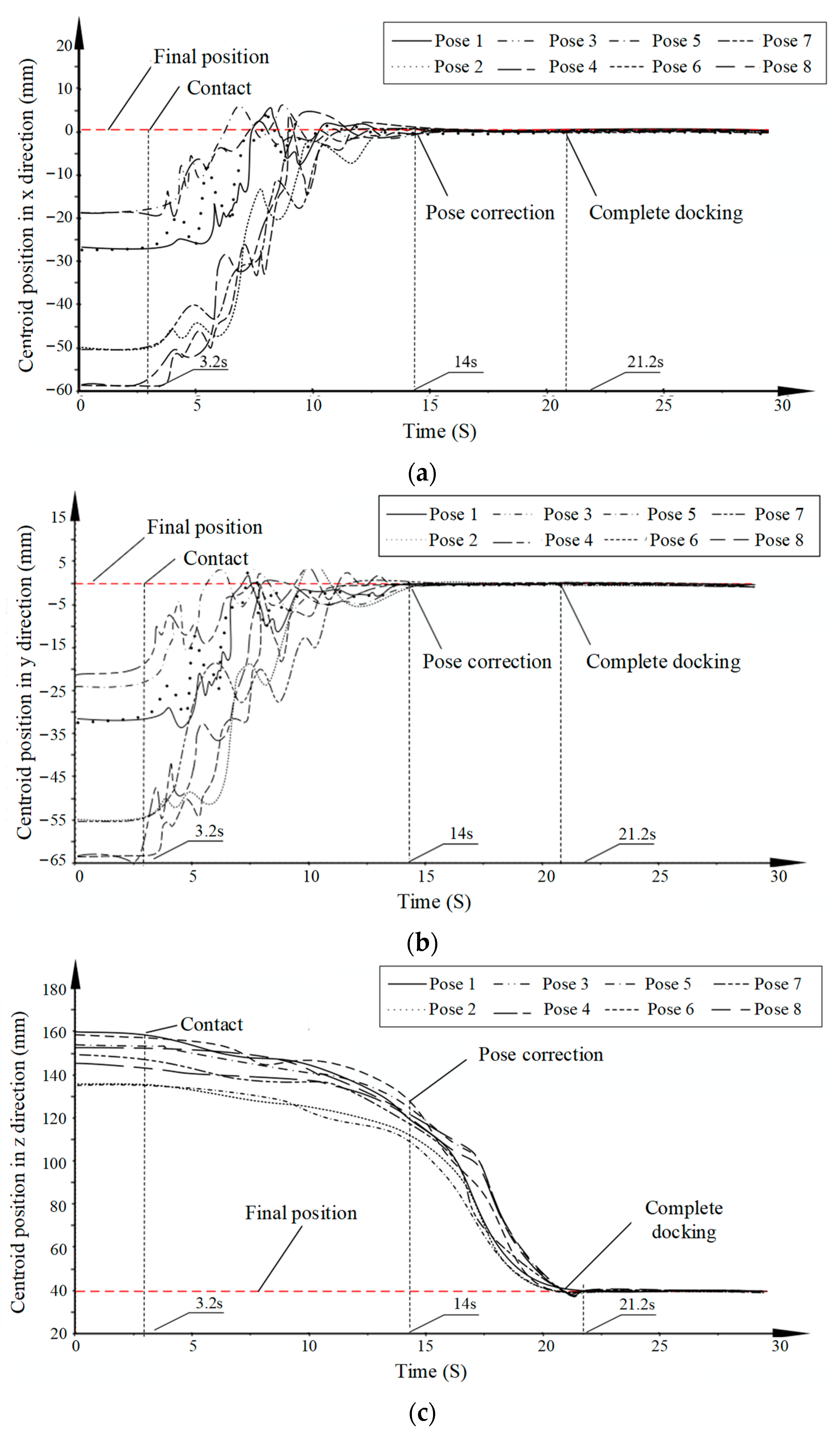
| Number | x/mm | y/mm | z/mm | /° | /° | /° |
|---|---|---|---|---|---|---|
| 1 | −27.6 | 18.8 | 161.6 | 6 | 6 | 6 |
| 2 | −27.5 | 52.0 | 154.2 | −6 | 6 | 6 |
| 3 | −59.9 | 19.8 | 145.4 | 6 | −6 | 6 |
| 4 | −19.2 | 27.2 | 161.6 | 6 | 6 | −6 |
| 5 | −59.9 | 51.0 | 135.0 | −6 | −6 | 6 |
| 6 | −51.6 | 28.0 | 154.2 | 6 | −6 | −6 |
| 7 | −19.2 | 60.2 | 145.4 | −6 | 6 | −6 |
| 8 | −51.6 | 59.4 | 135.1 | −6 | −6 | −6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, Y.; Yang, T.; Yue, H.; Yang, X.; Bai, D.; Yang, F. Design and Analysis of a New Deployable Docking Mechanism for Microsatellites. Remote Sens. 2022, 14, 5002. https://doi.org/10.3390/rs14195002
Zhao Y, Yang T, Yue H, Yang X, Bai D, Yang F. Design and Analysis of a New Deployable Docking Mechanism for Microsatellites. Remote Sensing. 2022; 14(19):5002. https://doi.org/10.3390/rs14195002
Chicago/Turabian StyleZhao, Yong, Tao Yang, Honghao Yue, Xiaoze Yang, Dong Bai, and Fei Yang. 2022. "Design and Analysis of a New Deployable Docking Mechanism for Microsatellites" Remote Sensing 14, no. 19: 5002. https://doi.org/10.3390/rs14195002
APA StyleZhao, Y., Yang, T., Yue, H., Yang, X., Bai, D., & Yang, F. (2022). Design and Analysis of a New Deployable Docking Mechanism for Microsatellites. Remote Sensing, 14(19), 5002. https://doi.org/10.3390/rs14195002