Quantifying the Response of German Forests to Drought Events via Satellite Imagery
Abstract
1. Introduction
2. Material and Methods
2.1. Materials
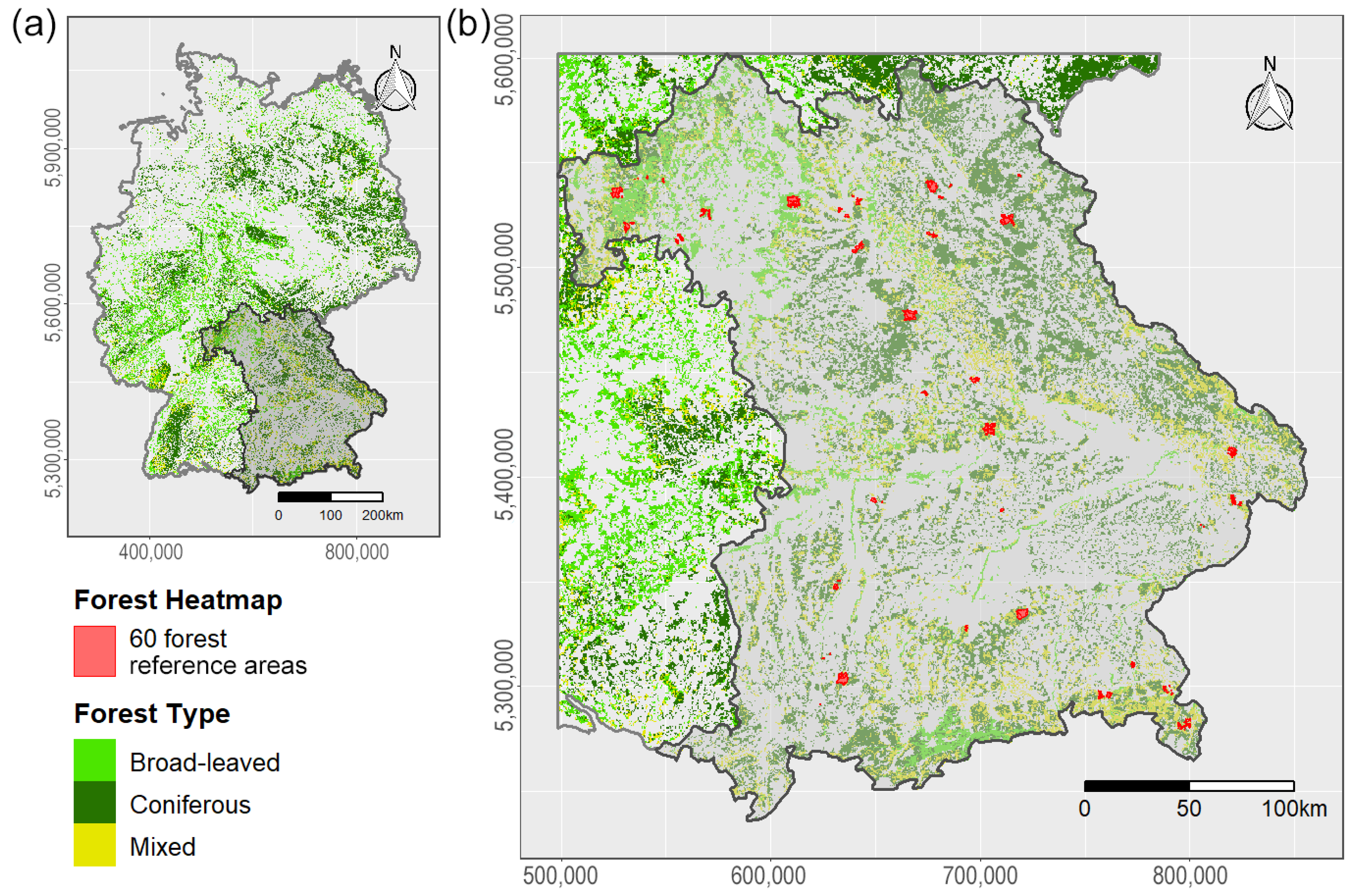
2.1.1. Forest Data
2.1.2. Meteorological Data
2.1.3. Soil Type Data
2.1.4. Topographic Data
2.1.5. Remote Sensing Data
2.2. Data Preprocessing
2.2.1. Calculation of the Self-Calibrated Palmer Drought Severity Index (scPDSI)
2.2.2. Cloud Masking and Calculation of Monthly Median Satellite Images
2.2.3. Calculation of Vegetation Indices
2.3. Capturing the Vegetation Response to Drought Events
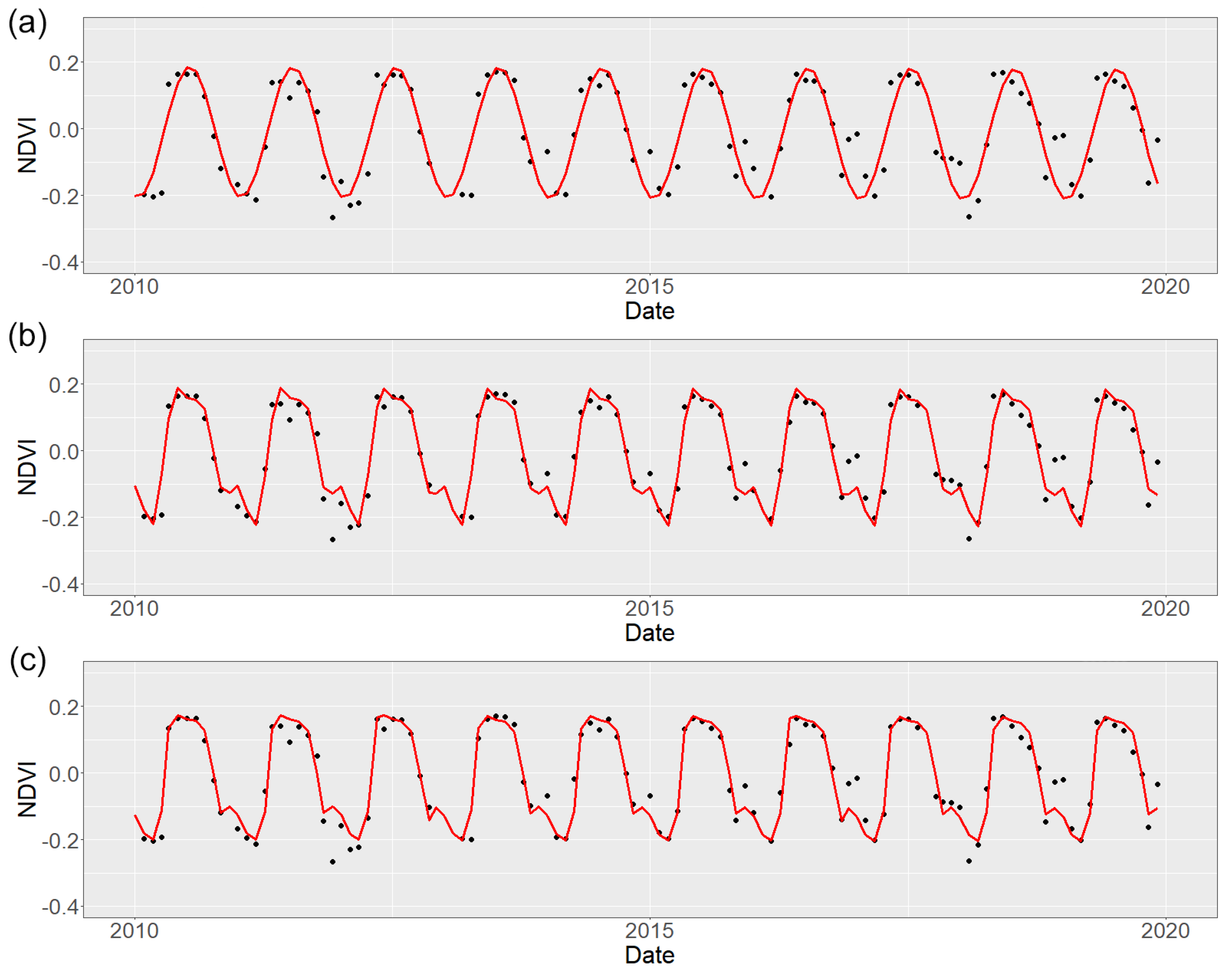
2.3.1. Harmonic Modelling
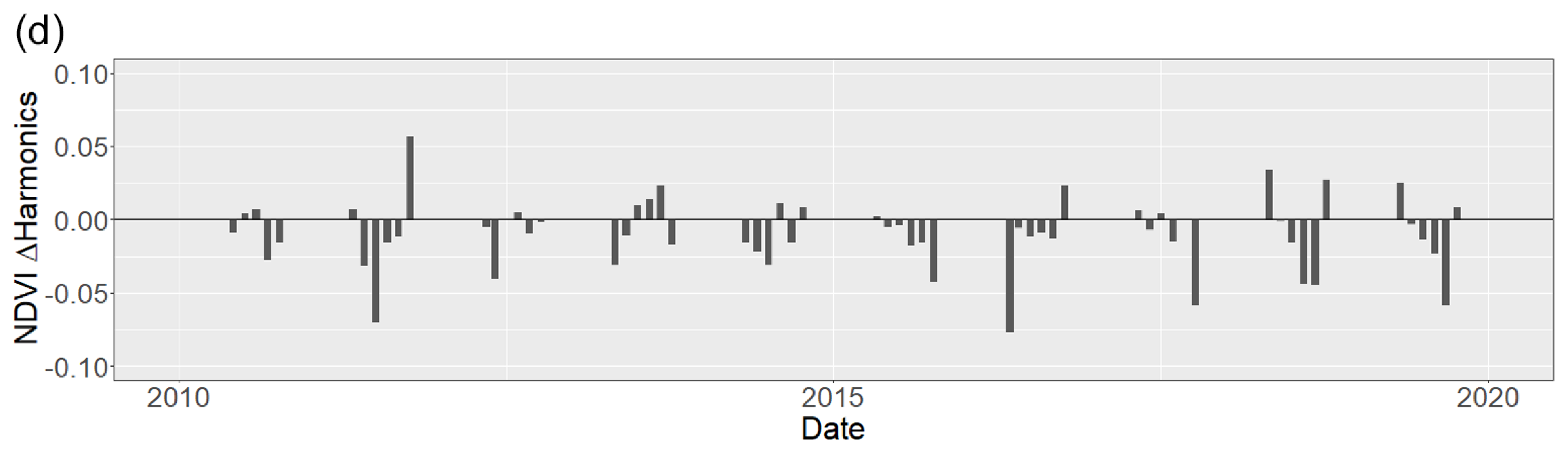
2.3.2. z-Score Analysis
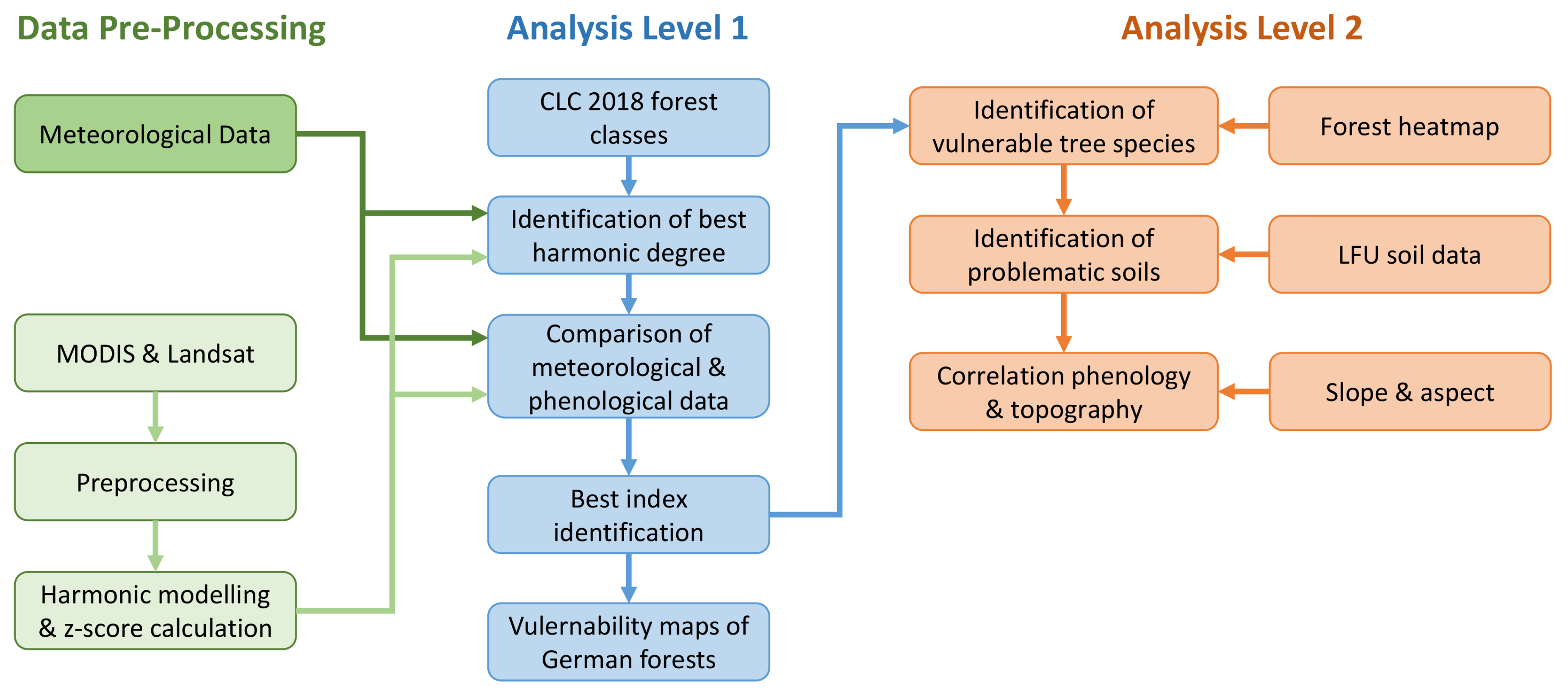
2.4. Analysis Level 1: Best Predictor Combination
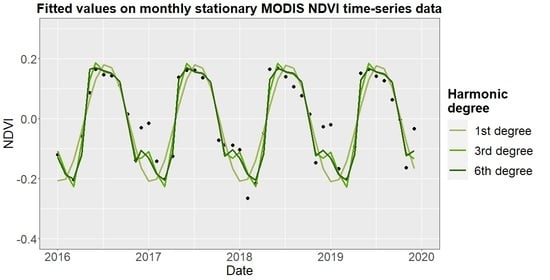
2.4.1. Harmonic Degree Comparison
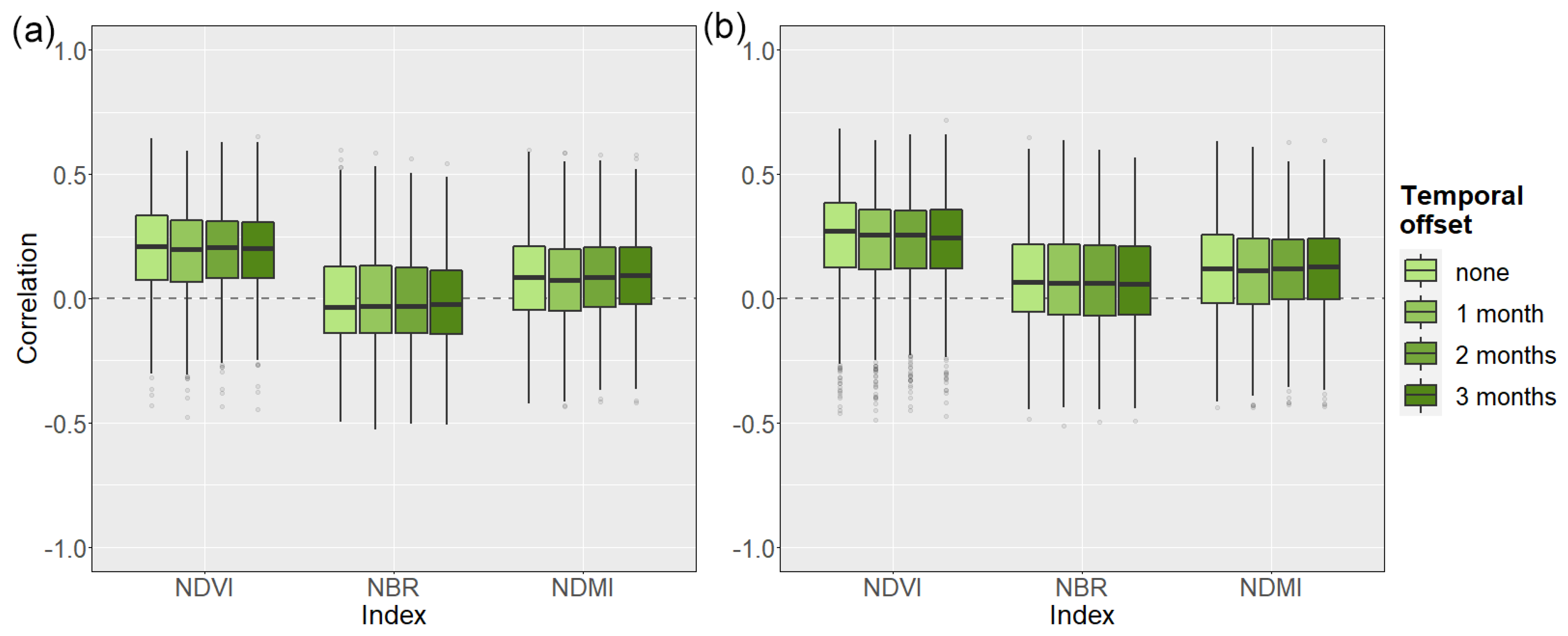
2.4.2. Comparison between Meteorological Drought and Spectral Characteristics of Forests
2.5. Analysis Level 2: Forest Type Vulnerability
2.5.1. Tree Species Vulnerability
2.5.2. Impact of Soil Types on Drought Vulnerability
2.5.3. Topographic Influence on Drought Vulnerability
3. Results
3.1. Analysis Level 1: Best Predictor Combination
3.1.1. Harmonic Degree Comparison
3.1.2. Comparison between Meteorological Drought and Spectral Characteristics of Forests
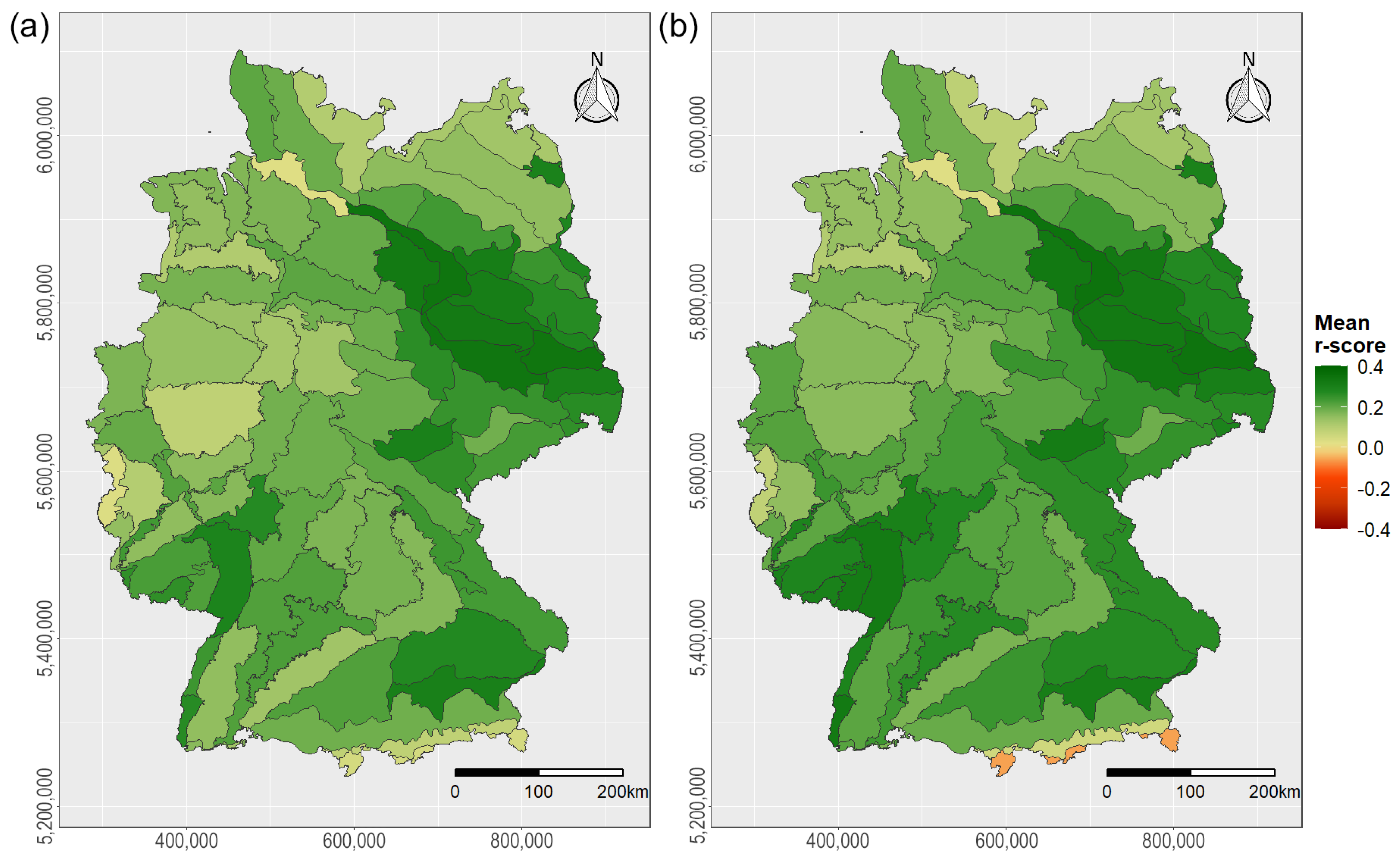
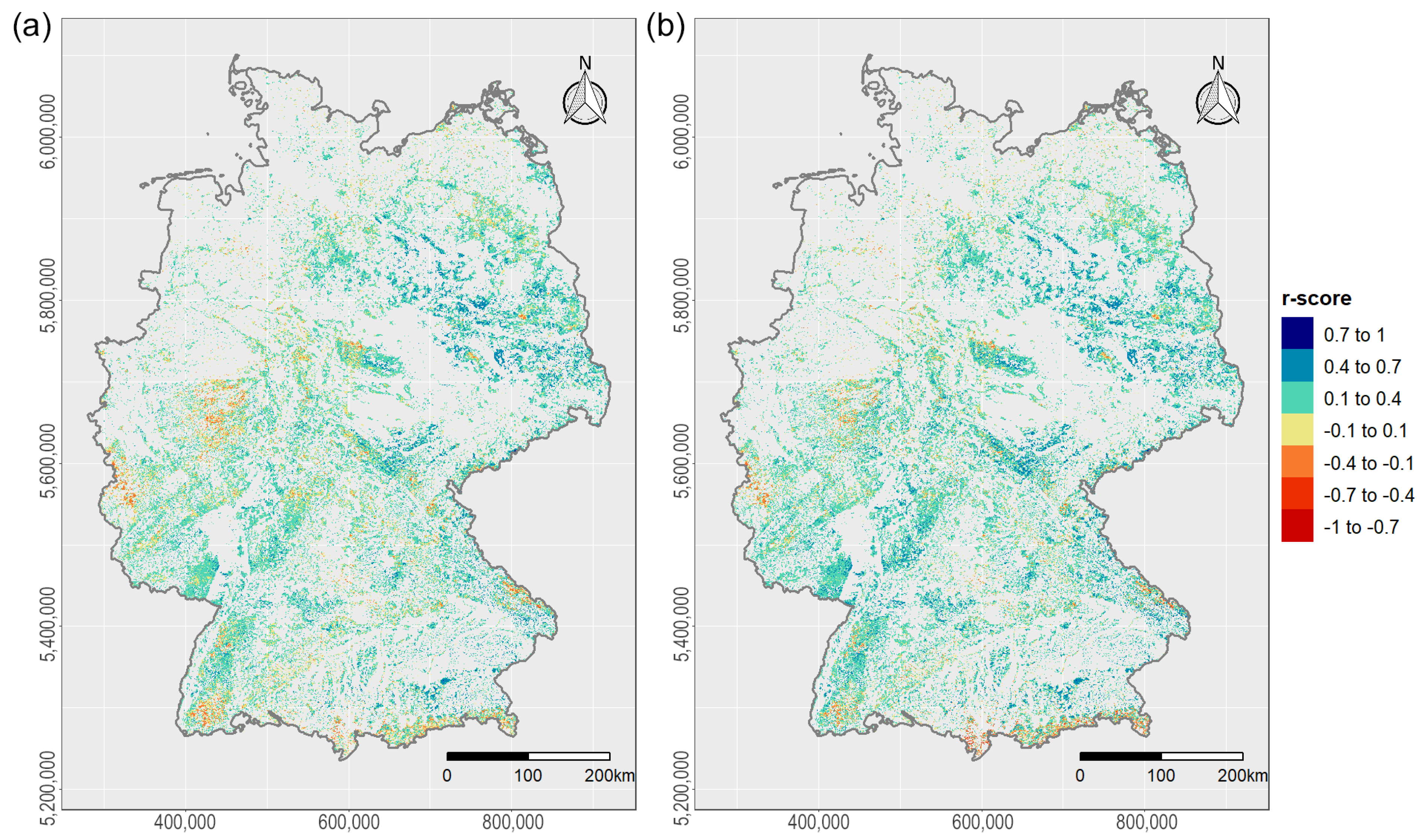
3.1.3. Vulnerability Maps of German Forests
3.2. Analysis Level 2: Forest Type Vulnerability
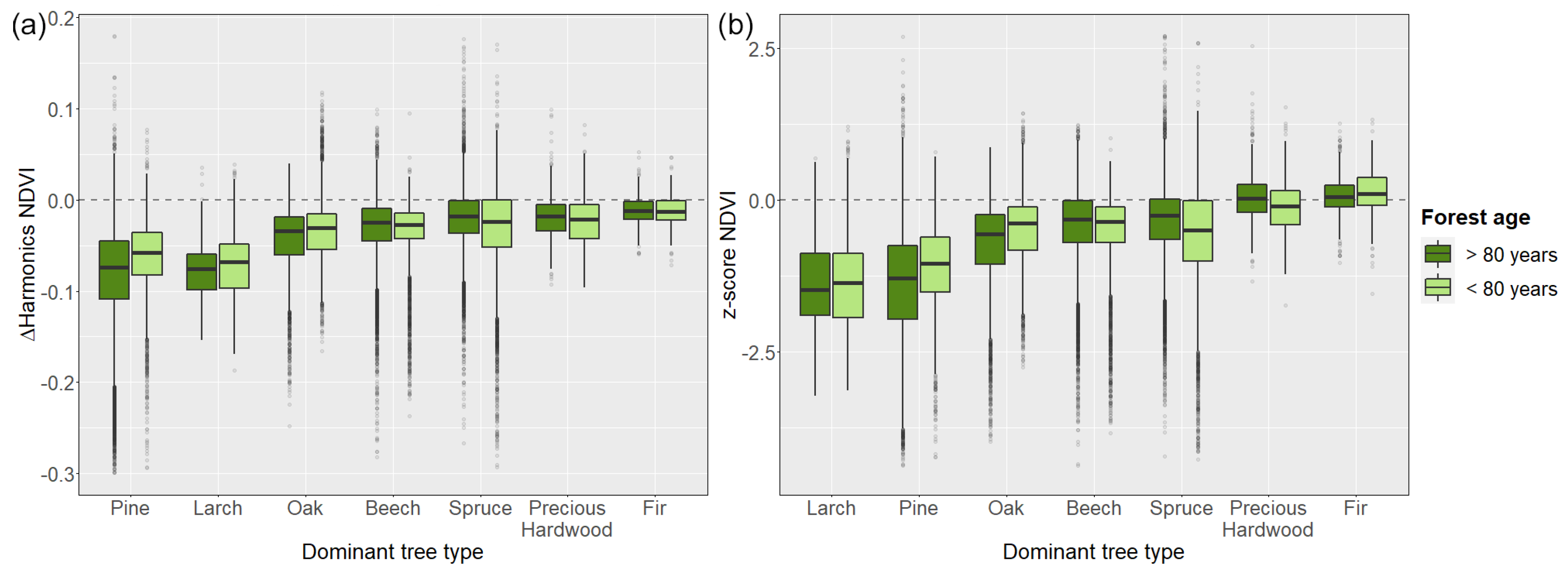
3.2.1. Tree Species Vulnerability
3.2.2. Influence of Soils on Drought Vulnerability
3.2.3. Topographic Influence on Drought Vulnerability
4. Discussion
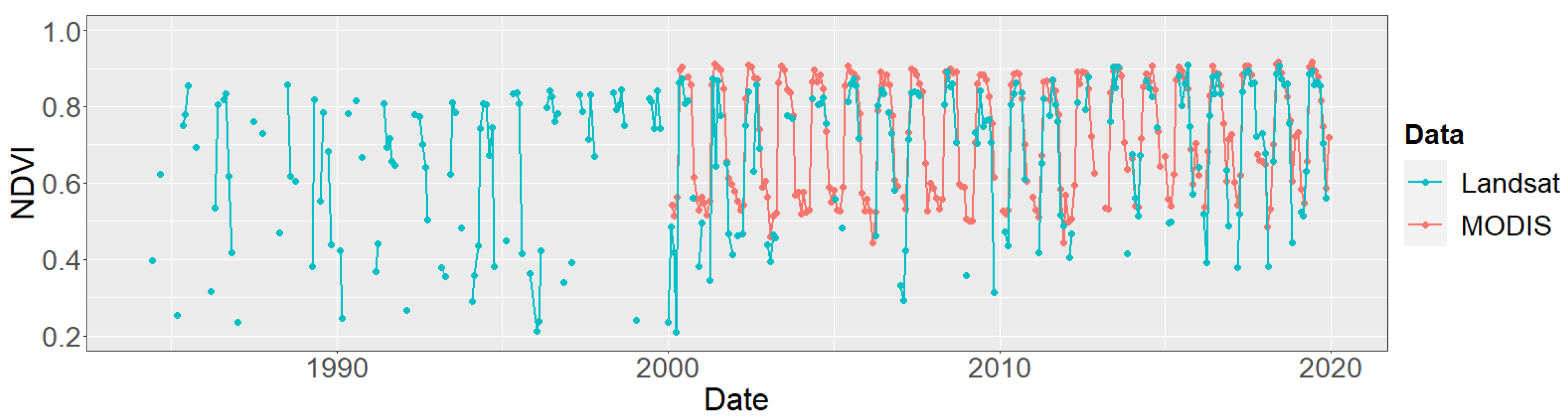
4.1. Spatio-Temporal Availability of Applied Satellite Data
4.2. Analysis Level 1: Best Predictor Combination
4.3. Analysis Level 2: Forest Type Vulnerability
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Acronyms
| BKG | Bundesamt für Kartographie und Geodäsie |
| BaySF | Bayerische Staatsforsten |
| CDC | Climate Data Center |
| CLC | Corine Land Cover |
| DTM | Digital Terrain Model |
| DWD | Deutscher Wetterdienst |
| EEC | existing climatic conditions |
| ETM+ | Enhanced Thematic Mapper Plus |
| GEE | Google Earth Engine |
| IDW | inverse distance weighting |
| LaSRC | Land Surface Reflectance Code |
| LEDAPS | Landsat Ecosystem Disturbance Adaptive Processing System |
| LFU | Landesamt für Umwelt |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
| NBR | Normalized Burn Ratio |
| NDMI | Normalized Difference Moisture Index |
| NDVI | Normalized Difference Vegetation Index |
| NDWI | Normalized Difference Water Index |
| NIR | Near Infrared |
| OLI | Operational Land Imager |
| OLS | Ordinary Least Squares |
| PDSI | Palmer Drought Severity Index |
| RGB | Red-Green-Blue |
| scPDSI | self-calibrated Palmer Drought Severity Index |
| SLC | Scan Line Corrector |
| SR | Surface Reflectance |
| SWIR | Short Wavelength Infrared |
| TM | Thematic Mapper |
| TOA | Top-of-Atmosphere |
| UTM | Universal Transverse Mercator |
| WRS | Worldwide Reference System |
Appendix A


References
- Sykes, M.T. Climate change impacts: Vegetation. eLS 2009. [Google Scholar] [CrossRef]
- Lindner, M.; Maroschek, M.; Netherer, S.; Kremer, A.; Barbati, A.; Garcia-Gonzalo, J.; Seidl, R.; Delzon, S.; Corona, P.; Kolström, M.; et al. Climate change impacts, adaptive capacity, and vulnerability of European forest ecosystems. For. Ecol. Manag. 2010, 259, 698–709. [Google Scholar] [CrossRef]
- Statistisches Bundesamt (Destatis). Forest Damage Due to Drought: Trees Logged Because of Insect Infestation Nearly Tripled in 2019 Compared with 2018. 2020. Available online: https://www.destatis.de/EN/Press/2020/07/PE20_N041_412.html (accessed on 12 April 2021).
- Reif, A.; Brucker, U.; Kratzer, R.; Schmiedinger, A.; Bauhus, J. Waldbau und Baumartenwahl in Zeiten des Klimawandels aus Sicht des Naturschutzes. BfN-Skripten 2010, 272, 1–125. [Google Scholar]
- Milad, M.; Schaich, H.; Bürgi, M.; Konold, W. Climate change and nature conservation in Central European forests: A review of consequences, concepts and challenges. For. Ecol. Manag. 2011, 261, 829–843. [Google Scholar] [CrossRef]
- Pause, M.; Schweitzer, C.; Rosenthal, M.; Keuck, V.; Bumberger, J.; Dietrich, P.; Heurich, M.; Jung, A.; Lausch, A. In situ/remote sensing integration to assess forest health—A review. Remote Sens. 2016, 8, 471. [Google Scholar] [CrossRef]
- Etzold, S.; Waldner, P.; Thimonier, A.; Schmitt, M.; Dobbertin, M. Tree growth in Swiss forests between 1995 and 2010 in relation to climate and stand conditions: Recent disturbances matter. For. Ecol. Manag. 2014, 311, 41–55. [Google Scholar] [CrossRef]
- Kölling, C. Wälder im Klimawandel: Die Forstwirtschaft muss sich anpassen. In Warnsignal Klima: Gesundheitsrisiken-Gefahren für Menschen, Tiere und Pflanzen; Lozán, J.L., Graßl, H., Jendritzky, G., Karbe, L., Reise, K., Maier, W.A., Eds.; GEO/Wissenschaftliche Auswertungen: Hamburg, Germany, 2008; pp. 357–361. [Google Scholar]
- Deutsche Welle. German Forest Decline Hits Record Levels. 2021. Available online: https://p.dw.com/p/3ppD4 (accessed on 14 April 2021).
- Caudullo, G.; Tinner, W.; de Rigo, D. Picea abies in Europe: Distribution, habitat, usage and threats. In European Atlas of Forest Tree Species; San-Miguel-Ayanz, J., de Rigo, D., Caudullo, G., Houston Durrant, T., Mauri, A., Eds.; Publication Office of the European Union: Luxembourg, 2016; pp. 114–116. [Google Scholar]
- Andersch AG. SECTOR UPDATE: Between Drought and COVID-19—Multiple Economic Strains on Agricultural, Food and Timber Industries. 2020. Available online: https://cms.andersch-ag.de/storage/uploads/2020/09/16/5f622f6070368200916_Andersch_Branchen-Update_Agrar_Ernahrungs_Holzindustrien_en.pdf (accessed on 15 April 2021).
- Jäger, R. Holzpreis für Fichte im Freien Fall. 2019. Available online: https://www.landwirt-media.com/holzpreis-fuer-fichte-im-freien-fall/ (accessed on 29 March 2021).
- Wald-Prinz. Holzpreise und Holzpreisentwicklung Fichte. 2020. Available online: http://www.wald-prinz.de/holzpreise-und-holzpreisentwicklung-fichte/383#Nadelholz (accessed on 5 April 2021).
- Karlsruhe: Stadtzeitung. Umwelt: Trockener Sommer lässt Bäume Sterben. 2018. Available online: https://presse.karlsruhe.de/db/stadtzeitung/jahr2018/woche51/umwelt_trockener_sommer_lasst_baume_sterben.html (accessed on 20 April 2021).
- Jacoby, O. Borkenkäfer im Klimawandel. 2015. Available online: https://www.ethz.ch/de/news-und-veranstaltungen/eth-news/news/2015/08/borkenkaefer-im-klimawandel.html (accessed on 5 April 2021).
- Tomiczek, C.; Pfister, A. Was bedeutet der Klimawandel für die Borkenkäfer. BFW-Praxisinf. 2008, 17, 23. [Google Scholar]
- Hlásny, T.; Krokene, P.; Liebhold, A.; Montagné-Huck, C.; Müller, J.; Qin, H.; Raffa, K.; Schelhaas, M.J.; Seidl, R.; Svoboda, M.; et al. Living with Bark Beetles: Impacts, Outlook and Management Options; Technical Report; European Forest Institute: Joensuu, Finland, 2019. [Google Scholar]
- Cwienk, J. German Forest Fire Risk Spikes Amid High Temperatures, Drought. 2019. Available online: https://www.dw.com/en/german-forest-fire-risk-spikes-amid-high-temperatures-drought/a-48422025 (accessed on 15 April 2021).
- Netherer, S.; Panassiti, B.; Pennerstorfer, J.; Matthews, B. Acute drought is an important driver of bark beetle infestation in Austrian Norway spruce stands. Front. For. Glob. Chang. 2019, 2, 39. [Google Scholar] [CrossRef]
- Seidl, R.; Thom, D.; Kautz, M.; Martin-Benito, D.; Peltoniemi, M.; Vacchiano, G.; Wild, J.; Ascoli, D.; Petr, M.; Honkaniemi, J.; et al. Forest disturbances under climate change. Nat. Clim. Chang. 2017, 7, 395–402. [Google Scholar] [CrossRef] [PubMed]
- Lausch, A.; Erasmi, S.; King, D.; Magdon, P.; Heurich, M. Understanding forest health with remote sensing-part II—A review of approaches and data models. Remote Sens. 2017, 9, 129. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Huang, C.; Goward, S.N.; Masek, J.G.; Thomas, N.; Zhu, Z.; Vogelmann, J.E. An automated approach for reconstructing recent forest disturbance history using dense Landsat time series stacks. Remote Sens. Environ. 2010, 114, 183–198. [Google Scholar] [CrossRef]
- Hansen, M.C.; Roy, D.P.; Lindquist, E.; Adusei, B.; Justice, C.O.; Altstatt, A. A method for integrating MODIS and Landsat data for systematic monitoring of forest cover and change in the Congo Basin. Remote Sens. Environ. 2008, 112, 2495–2513. [Google Scholar] [CrossRef]
- Asner, G.P.; Knapp, D.E.; Balaji, A.; Páez-Acosta, G. Automated mapping of tropical deforestation and forest degradation: CLASlite. J. Appl. Remote Sens. 2009, 3, 033543. [Google Scholar] [CrossRef]
- Miettinen, J.; Stibig, H.J.; Achard, F. Remote sensing of forest degradation in Southeast Asia—Aiming for a regional view through 5–30 m satellite data. Glob. Ecol. Conserv. 2014, 2, 24–36. [Google Scholar] [CrossRef]
- Kübert, C.; Conrad, C.; Klein, D.; Dech, S. Land Surface Phenology from MODIS data in Germany. In Proceedings of the MultiTemp 2013: 7th International Workshop on the Analysis of Multi-temporal Remote Sensing Images, Banff, AB, Canada, 25–27 June 2013; pp. 1–4. [Google Scholar]
- Bochenek, Z.; Ziolkowski, D.; Bartold, M.; Orlowska, K.; Ochtyra, A. Monitoring forest biodiversity and the impact of climate on forest environment using high-resolution satellite images. Eur. J. Remote Sens. 2018, 51, 166–181. [Google Scholar] [CrossRef]
- Lewińska, K.; Ivits, E.; Schardt, M.; Zebisch, M. Alpine forest drought monitoring in south tyrol: PCA based synergy between scPDSI data and modis derived NDVI and NDII7 time series. Remote Sens. 2016, 8, 639. [Google Scholar] [CrossRef]
- Holzwarth, S.; Thonfeld, F.; Abdullahi, S.; Asam, S.; Da Ponte Canova, E.; Gessner, U.; Huth, J.; Kraus, T.; Leutner, B.; Kuenzer, C. Earth Observation Based Monitoring of Forests in Germany: A Review. Remote Sens. 2020, 12, 3570. [Google Scholar] [CrossRef]
- Verbesselt, J.; Zeileis, A.; Herold, M. Near real-time disturbance detection using satellite image time series. Remote Sens. Environ. 2012, 123, 98–108. [Google Scholar] [CrossRef]
- De Jong, R.; de Bruin, S.; de Wit, A.; Schaepman, M.E.; Dent, D.L. Analysis of monotonic greening and browning trends from global NDVI time-series. Remote Sens. Environ. 2011, 115, 692–702. [Google Scholar] [CrossRef]
- Wilson, B.T.; Knight, J.F.; McRoberts, R.E. Harmonic regression of Landsat time series for modeling attributes from national forest inventory data. ISPRS J. Photogramm. Remote Sens. 2018, 137, 29–46. [Google Scholar] [CrossRef]
- Jakubauskas, M.E.; Legates, D.R.; Kastens, J.H. Crop identification using harmonic analysis of time-series AVHRR NDVI data. Comput. Electron. Agric. 2002, 37, 127–139. [Google Scholar] [CrossRef]
- Moody, A.; Johnson, D.M. Land-surface phenologies from AVHRR using the discrete Fourier transform. Remote Sens. Environ. 2001, 75, 305–323. [Google Scholar] [CrossRef]
- Landmann, T.; Eidmann, D.; Cornish, N.; Franke, J.; Siebert, S. Optimizing harmonics from Landsat time series data: The case of mapping rainfed and irrigated agriculture in Zimbabwe. Remote Sens. Lett. 2019, 10, 1038–1046. [Google Scholar] [CrossRef]
- Chen, J.; Chen, J.; Liu, H.; Peng, S. Detection of Cropland Change Using Multi-Harmonic Based Phenological Trajectory Similarity. Remote Sens. 2018, 10, 1020. [Google Scholar] [CrossRef]
- Rocchini, D.; Metz, M.; Ricotta, C.; Landa, M.; Frigeri, A.; Neteler, M. Fourier transforms for detecting multitemporal landscape fragmentation by remote sensing. Int. J. Remote Sens. 2013, 34, 8907–8916. [Google Scholar] [CrossRef]
- Jung, M.; Chang, E. NDVI-Based Land-Cover Change Detection Using Harmonic Analysis. Int. J. Remote Sens. 2015, 36, 1097–1113. [Google Scholar] [CrossRef]
- Philipp, M. rHarmonics V.1.0. 2020. Available online: https://doi.org/10.5281/zenodo.3994381 (accessed on 16 April 2021).
- Department of the Interior—U.S. Geological Survey. MOD09A1 v006. Available online: https://lpdaac.usgs.gov/products/mod09a1v006/ (accessed on 15 February 2021).
- Department of the Interior—U.S. Geological Survey. Landsat 4-7 Surface Reflectance Code LEDAPS Product Guide. 2019. Available online: https://www.usgs.gov/media/files/landsat-4-7-surface-reflectance-code-ledaps-product-guide (accessed on 9 April 2021).
- Department of the Interior—U.S. Geological Survey. Land Surface Reflectance Code LaSRC Product Guide. 2019. Available online: https://www.usgs.gov/media/files/land-surface-reflectance-code-lasrc-product-guide (accessed on 20 April 2021).
- Deutscher Wetterdienst. CDC-OpenData Area. 2019. Available online: https://opendata.dwd.de/climate_environment/CDC/Readme_intro_CDC_ftp.pdf (accessed on 12 April 2021).
- Bayerisches Landesamt für Umwelt. Details zu Download-Dienst Übersichtsbodenkarte von Bayern 1:25.000 (ÜBK25)—Downloaddienst des LfU. Available online: https://www.lfu.bayern.de/umweltdaten/geodatendienste/index_detail.htm?id=052f9934-dd4b-4d3e-86d2-2c9eb6372e4e&profil=Download (accessed on 22 March 2021).
- Bundesamt für Kartographie und Geodäsie. Digitales Geländemodell Gitterweite 25 m (DGM25). 2019. Available online: https://gdz.bkg.bund.de/index.php/default/digitale-geodaten/digitale-gelandemodelle/digitales-gelandemodell-gitterweite-25-m-dgm25.html (accessed on 12 April 2021).
- Copernicus Land Monitoring Service. CLC 2018 Metadata. 2019. Available online: https://land.copernicus.eu/pan-european/corine-land-cover/clc2018?tab=metadata (accessed on 14 March 2021).
- Bayerische Staatsforsten. 2021. Available online: https://www.baysf.de/de.html (accessed on 12 April 2021).
- Deutscher Wetterdienst. DATA SET DESCRIPTION: Grids of Monthly Total Precipitation over Germany. 2018. Available online: https://opendata.dwd.de/climate_environment/CDC/grids_germany/monthly/precipitation/DESCRIPTION_gridsgermany_monthly_precipitation_en.pdf (accessed on 15 April 2021).
- Fenn, M.E.; Perea-Estrada, V.; De Bauer, L.; Perez-Suarez, M.; Parker, D.; Cetina-Alcalá, V. Nutrient status and plant growth effects of forest soils in the Basin of Mexico. Environ. Pollut. 2006, 140, 187–199. [Google Scholar] [CrossRef]
- Onyekwelu, J.C.; Mosandl, R.; Stimm, B. Tree species diversity and soil status of two natural forest ecosystems in lowland humid tropical rainforest region of Nigeria. Utilisation of diversity inland use systems: Sustainable and organic approaches to meet human needs. In Tropentag 2007; Cuvillier Verlag Göttingen: Göttingen, Germany, 2007; pp. 1–4. [Google Scholar]
- Department of the Interior—U.S. Geological Survey. Landsat Surface Reflectance Data. 2015. Available online: https://pubs.usgs.gov/fs/2015/3034/pdf/fs20153034.pdf (accessed on 19 April 2021).
- Roy, D.P.; Wulder, M.; Loveland, T.R.; Woodcock, C.; Allen, R.; Anderson, M.; Helder, D.; Irons, J.; Johnson, D.; Kennedy, R.; et al. Landsat-8: Science and product vision for terrestrial global change research. Remote Sens. Environ. 2014, 145, 154–172. [Google Scholar] [CrossRef]
- Irons, J.R.; Dwyer, J.L.; Barsi, J.A. The next Landsat satellite: The Landsat data continuity mission. Remote Sens. Environ. 2012, 122, 11–21. [Google Scholar] [CrossRef]
- Storey, J.; Choate, M.; Lee, K. Landsat 8 Operational Land Imager on-orbit geometric calibration and performance. Remote Sens. 2014, 6, 11127–11152. [Google Scholar] [CrossRef]
- Roger, J.C.; Vermote, E.F.; Ray, J.P. MODIS Surface Reflectance User’s Guide. 2019. Available online: https://modis-land.gsfc.nasa.gov/pdf/MOD09_UserGuide_v1.4.pdf (accessed on 20 April 2021).
- Palmer, W.C. Meteorological Drought; Research Paper No. 45; US Weather Bureau: Washington, DC, USA, 1965; Volume 58. [Google Scholar]
- Zargar, A.; Sadiq, R.; Naser, B.; Khan, F.I. A review of drought indices. Environ. Rev. 2011, 19, 333–349. [Google Scholar] [CrossRef]
- Wells, N.; Goddard, S.; Hayes, M.J. A self-calibrating Palmer drought severity index. J. Clim. 2004, 17, 2335–2351. [Google Scholar] [CrossRef]
- Alley, W.M. The Palmer drought severity index: Limitations and assumptions. J. Clim. Appl. Meteorol. 1984, 23, 1100–1109. [Google Scholar] [CrossRef]
- Büntgen, U.; Trouet, V.; Frank, D.; Leuschner, H.H.; Friedrichs, D.; Luterbacher, J.; Esper, J. Tree-ring indicators of German summer drought over the last millennium. Quat. Sci. Rev. 2010, 29, 1005–1016. [Google Scholar] [CrossRef]
- Scharnweber, T.; Manthey, M.; Criegee, C.; Bauwe, A.; Schröder, C.; Wilmking, M. Drought matters–Declining precipitation influences growth of Fagus sylvatica L. and Quercus robur L. in north-eastern Germany. For. Ecol. Manag. 2011, 262, 947–961. [Google Scholar] [CrossRef]
- Gillner, S.; Vogt, J.; Roloff, A. Climatic response and impacts of drought on oaks at urban and forest sites. Urban For. Urban Green. 2013, 12, 597–605. [Google Scholar] [CrossRef]
- Zhong, R.; Chen, X.; Wang, Z.; Lai, C.; Goddard, S.; Wells, N.; Hayes, M. scPDSI: Calculation of the Conventional and Self-Calibrating Palmer Drought Severity Index. 2019. Available online: https://rdrr.io/cran/scPDSI/ (accessed on 14 April 2021).
- Rousseeuw, P.J.; Hubert, M. Robust statistics for outlier detection. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2011, 1, 73–79. [Google Scholar] [CrossRef]
- Markham, B.L.; Barker, J.L. Spectral characterization of the Landsat Thematic Mapper sensors. Int. J. Remote Sens. 1985, 6, 697–716. [Google Scholar] [CrossRef]
- Barsi, J.A.; Lee, K.; Kvaran, G.; Markham, B.L.; Pedelty, J.A. The spectral response of the Landsat-8 operational land imager. Remote Sens. 2014, 6, 10232–10251. [Google Scholar] [CrossRef]
- Maselli, F. Monitoring forest conditions in a protected Mediterranean coastal area by the analysis of multiyear NDVI data. Remote Sens. Environ. 2004, 89, 423–433. [Google Scholar] [CrossRef]
- Birky, A.K. NDVI and a simple model of deciduous forest seasonal dynamics. Ecol. Model. 2001, 143, 43–58. [Google Scholar] [CrossRef]
- Reid, S.L.; Walker, J.L.; Schaaf, A. Using multi-spectral landsat imagery to examine forest health trends at Fort Benning, Georgia. In Proceedings of the 18th Biennial Southern Silvicultural Research Conference; e-General Technical Report SRS-212; US Department of Agriculture, Forest Service, Southern Research Station: Asheville, NC, USA, 2016; Volume 212, pp. 601–603. [Google Scholar]
- Tucker, C.J. Red and photographic infrared linear combinations for monitoring vegetation. Remote Sens. Environ. 1979, 8, 127–150. [Google Scholar] [CrossRef]
- García, M.L.; Caselles, V. Mapping burns and natural reforestation using Thematic Mapper data. Geocarto Int. 1991, 6, 31–37. [Google Scholar] [CrossRef]
- McCarley, T.R.; Kolden, C.A.; Vaillant, N.M.; Hudak, A.T.; Smith, A.M.; Wing, B.M.; Kellogg, B.S.; Kreitler, J. Multi-temporal LiDAR and Landsat quantification of fire-induced changes to forest structure. Remote Sens. Environ. 2017, 191, 419–432. [Google Scholar] [CrossRef]
- Hoy, E.E.; French, N.H.; Turetsky, M.R.; Trigg, S.N.; Kasischke, E.S. Evaluating the potential of Landsat TM/ETM+ imagery for assessing fire severity in Alaskan black spruce forests. Int. J. Wildland Fire 2008, 17, 500–514. [Google Scholar] [CrossRef]
- Escuin, S.; Navarro, R.; Fernandez, P. Fire severity assessment by using NBR (Normalized Burn Ratio) and NDVI (Normalized Difference Vegetation Index) derived from LANDSAT TM/ETM images. Int. J. Remote Sens. 2008, 29, 1053–1073. [Google Scholar] [CrossRef]
- Philipp, M.B.; Levick, S.R. Exploring the potential of C-Band SAR in contributing to burn severity mapping in tropical savanna. Remote Sens. 2020, 12, 49. [Google Scholar] [CrossRef]
- Langner, A.; Miettinen, J.; Stibig, H.J. Monitoring Forest Degradation for a Case Study in Cambodia: Comparison of Landsat 8 and Sentinel-2 Imagery. In Proceedings of the Living Planet Symposium, Prague, Czech Republic, 9–13 May 2016; Volume 740, p. 200. [Google Scholar]
- Morresi, D.; Vitali, A.; Urbinati, C.; Garbarino, M. Forest Spectral Recovery and Regeneration Dynamics in Stand-Replacing Wildfires of Central Apennines Derived from Landsat Time Series. Remote Sens. 2019, 11, 308. [Google Scholar] [CrossRef]
- Langner, A.; Miettinen, J.; Kukkonen, M.; Vancutsem, C.; Simonetti, D.; Vieilledent, G.; Verhegghen, A.; Gallego, J.; Stibig, H.J. Towards operational monitoring of forest canopy disturbance in evergreen rain forests: A test case in continental Southeast Asia. Remote Sens. 2018, 10, 544. [Google Scholar] [CrossRef]
- Gao, B.C. NDWI—A normalized difference water index for remote sensing of vegetation liquid water from space. Remote Sens. Environ. 1996, 58, 257–266. [Google Scholar] [CrossRef]
- Jin, S.; Sader, S.A. Comparison of time series tasseled cap wetness and the normalized difference moisture index in detecting forest disturbances. Remote Sens. Environ. 2005, 94, 364–372. [Google Scholar] [CrossRef]
- Wilson, E.H.; Sader, S.A. Detection of forest harvest type using multiple dates of Landsat TM imagery. Remote Sens. Environ. 2002, 80, 385–396. [Google Scholar] [CrossRef]
- Stych, P.; Lastovicka, J.; Hladky, R.; Paluba, D. Evaluation of the Influence of Disturbances on Forest Vegetation Using the Time Series of Landsat Data: A Comparison Study of the Low Tatras and Sumava National Parks. ISPRS Int. J. Geo-Inf. 2019, 8, 71. [Google Scholar] [CrossRef]
- Shahabfar, A.; Eitzinger, J. Spatio-temporal analysis of droughts in semi-arid regions by using meteorological drought indices. Atmosphere 2013, 4, 94–112. [Google Scholar] [CrossRef]
- Housman, I.; Chastain, R.; Finco, M. An Evaluation of Forest Health Insect and Disease Survey Data and Satellite-Based Remote Sensing Forest Change Detection Methods: Case Studies in the United States. Remote Sens. 2018, 10, 1184. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Newnham, G.; Culvenor, D. Detecting trend and seasonal changes in satellite image time series. Remote Sens. Environ. 2010, 114, 106–115. [Google Scholar] [CrossRef]
- Han, P.; Wang, P.X.; Zhang, S.Y.; Zhu, D.H. Drought forecasting based on the remote sensing data using ARIMA models. Math. Comput. Model. 2010, 51, 1398–1403. [Google Scholar] [CrossRef]
- Shumway, R.H.; Stoffer, D.S. Time Series Analysis and Its Applications: With R Examples; Springer: Cham, Switzerland, 2017; p. 168. [Google Scholar]
- Google. EE—Arrays & Time Series. 2017. Available online: http://goo.gl/8TKA6F (accessed on 14 April 2021).
- Google. Glossary. 2019. Available online: https://developers.google.com/earth-engine/glossary (accessed on 12 April 2021).
- Brooks, E.B.; Thomas, V.A.; Wynne, R.H.; Coulston, J.W. Fitting the multitemporal curve: A Fourier series approach to the missing data problem in remote sensing analysis. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3340–3353. [Google Scholar] [CrossRef]
- Hermance, J.F. Stabilizing high-order, non-classical harmonic analysis of NDVI data for average annual models by damping model roughness. Int. J. Remote Sens. 2007, 28, 2801–2819. [Google Scholar] [CrossRef]
- Shannon, C.E. Communication in the presence of noise. Proc. IRE 1949, 37, 10–21. [Google Scholar] [CrossRef]
- Nyquist, H. Certain topics in telegraph transmission theory. Trans. Am. Inst. Electr. Eng. 1928, 47, 617–644. [Google Scholar] [CrossRef]
- Ficker, T.; Martišek, D. 3D image reconstructions and the Nyquist–Shannon theorem. 3D Res. 2015, 6, 23. [Google Scholar] [CrossRef]
- Kreyszig, E. Advanced Engineering Mathematics, 10th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2016; p. 1014. [Google Scholar]
- Peters, A.J.; Walter-Shea, E.A.; Ji, L.; Vina, A.; Hayes, M.; Svoboda, M.D. Drought monitoring with NDVI-based standardized vegetation index. Photogramm. Eng. Remote Sens. 2002, 68, 71–75. [Google Scholar]
- Mutlu, E. What Is Robustness in Statistics? A Brief Intro to Robust Estimators. 2019. Available online: https://towardsdatascience.com/what-is-robustness-in-statistics-a-brief-intro-to-robust-estimators-e926d74d1609 (accessed on 11 April 2021).
- Schmithüsen, J.; Meynen, E. Handbuch der naturräumlichen Gliederung Deutschlands; Bundesanstalt für Landeskunde und Raumforschung: Bad Godesberg, Germany, 1962. [Google Scholar]
- Ad-hoc-Arbeitsgruppe Boden. Bodenkundliche Kartieranleitung. KA5; Bundesanstalt für Geowissenschaften und Rohstoffe in Zusammenarbeit mit den Staatlichen Geologischen Diensten; E. Schweizerbart’sche: Stuttgart, Germany, 2005. [Google Scholar]
- Scaramuzza, P.; Barsi, J. Landsat 7 scan line corrector-off gap-filled product development. Proc. Pecora 2005, 16, 23–27. [Google Scholar]
- Foga, S.; Scaramuzza, P.L.; Guo, S.; Zhu, Z.; Dilley, R.D., Jr.; Beckmann, T.; Schmidt, G.L.; Dwyer, J.L.; Hughes, M.J.; Laue, B. Cloud detection algorithm comparison and validation for operational Landsat data products. Remote Sens. Environ. 2017, 194, 379–390. [Google Scholar] [CrossRef]
- Department of the Interior—U.S. Geological Survey. Landsat Collection 1 Surface Reflectance. Available online: https://www.usgs.gov/land-resources/nli/landsat/landsat-collection-1-surface-reflectance (accessed on 20 April 2021).
- Li, P.; Jiang, L.; Feng, Z. Cross-comparison of vegetation indices derived from Landsat-7 enhanced thematic mapper plus (ETM+) and Landsat-8 operational land imager (OLI) sensors. Remote Sens. 2014, 6, 310–329. [Google Scholar] [CrossRef]
- Xu, D.; Guo, X. Compare NDVI extracted from Landsat 8 imagery with that from Landsat 7 imagery. Am. J. Remote Sens. 2014, 2, 10–14. [Google Scholar] [CrossRef]
- Roy, D.P.; Kovalskyy, V.; Zhang, H.; Vermote, E.F.; Yan, L.; Kumar, S.; Egorov, A. Characterization of Landsat-7 to Landsat-8 reflective wavelength and normalized difference vegetation index continuity. Remote Sens. Environ. 2016, 185, 57–70. [Google Scholar] [CrossRef]
- Zhang, H.; Roy, D.P. Landsat 5 Thematic Mapper reflectance and NDVI 27-year time series inconsistencies due to satellite orbit change. Remote Sens. Environ. 2016, 186, 217–233. [Google Scholar] [CrossRef]
- Geerken, R.A. An algorithm to classify and monitor seasonal variations in vegetation phenologies and their inter-annual change. ISPRS J. Photogramm. Remote Sens. 2009, 64, 422–431. [Google Scholar] [CrossRef]
- Baniya, B.; Tang, Q.; Huang, Z.; Sun, S.; Techato, K.A. Spatial and temporal variation of ndvi in response to climate change and the implication for carbon dynamics in nepal. Forests 2018, 9, 329. [Google Scholar] [CrossRef]
- Hao, F.; Zhang, X.; Ouyang, W.; Skidmore, A.K.; Toxopeus, A. Vegetation NDVI linked to temperature and precipitation in the upper catchments of Yellow River. Environ. Model. Assess. 2012, 17, 389–398. [Google Scholar] [CrossRef]
- Gu, Y.; Brown, J.F.; Verdin, J.P.; Wardlow, B. A five-year analysis of MODIS NDVI and NDWI for grassland drought assessment over the central Great Plains of the United States. Geophys. Res. Lett. 2007, 34. [Google Scholar] [CrossRef]
- Chuai, X.; Huang, X.; Wang, W.; Bao, G. NDVI, temperature and precipitation changes and their relationships with different vegetation types during 1998–2007 in Inner Mongolia, China. Int. J. Climatol. 2013, 33, 1696–1706. [Google Scholar] [CrossRef]
- Ding, M.; Zhang, Y.; Liu, L.; Zhang, W.; Wang, Z.; Bai, W. The relationship between NDVI and precipitation on the Tibetan Plateau. J. Geogr. Sci. 2007, 17, 259–268. [Google Scholar] [CrossRef]
- Deutsche Welle. Stürme, Dürre, Borkenkäfer: Größte Holzernte Seit 2007 in Deutschland. 2019. Available online: https://p.dw.com/p/3HCgC (accessed on 19 April 2021).
- Kortmann, M.; Müller, J.; Thorn, S. 100 Jahre Kampf gegen den Borkenkäfer. Anliegen Natur 2018, 40, 29–32. [Google Scholar]
- Langer, G.; Bressem, U.; Habermann, M. Diplodia-Triebsterben der Kiefer und Endophytischer Nachweis des Erregers Sphaeropsis sapinea. AFZ-Der Wald 2011, 11, 28–31. [Google Scholar]
- Sebald, C. Sommerhitze Macht den Kiefern zu Schaffen. 2016. Available online: https://www.sueddeutsche.de/bayern/klimawandel-sommerhitze-macht-den-kiefern-zu-schaffen-1.3078376 (accessed on 21 April 2021).
- Pâques, L.E. Forest Tree Breeding in Europe; Springer: Dordrecht, The Netherlands, 2013; pp. 13–122. [Google Scholar]
- Eilmann, B.; Rigling, A. Tree-growth analyses to estimate tree species’ drought tolerance. Tree Physiol. 2012, 32, 178–187. [Google Scholar] [CrossRef] [PubMed]
- Lévesque, M.; Saurer, M.; Siegwolf, R.; Eilmann, B.; Brang, P.; Bugmann, H.; Rigling, A. Drought response of five conifer species under contrasting water availability suggests high vulnerability of Norway spruce and European larch. Glob. Chang. Biol. 2013, 19, 3184–3199. [Google Scholar] [CrossRef]
- Obojes, N.; Meurer, A.; Newesely, C.; Tasser, E.; Oberhuber, W.; Mayr, S.; Tappeiner, U. Water stress limits transpiration and growth of European larch up to the lower subalpine belt in an inner-alpine dry valley. New Phytol. 2018, 220, 460–475. [Google Scholar] [CrossRef]
- Bottero, A.; D’Amato, A.W.; Palik, B.J.; Bradford, J.B.; Fraver, S.; Battaglia, M.A.; Asherin, L.A. Density-dependent vulnerability of forest ecosystems to drought. J. Appl. Ecol. 2017, 54, 1605–1614. [Google Scholar] [CrossRef]
- Bessie, W.; Johnson, E. The relative importance of fuels and weather on fire behavior in subalpine forests. Ecology 1995, 76, 747–762. [Google Scholar] [CrossRef]
- Héon, J.; Arseneault, D.; Parisien, M.A. Resistance of the boreal forest to high burn rates. Proc. Natl. Acad. Sci. USA 2014, 111, 13888–13893. [Google Scholar] [CrossRef]
- Niklasson, M.; Granström, A. Numbers and sizes of fires: Long-term spatially explicit fire history in a Swedish boreal landscape. Ecology 2000, 81, 1484–1499. [Google Scholar] [CrossRef]
- Oberdorfer, E.; Schwabe, A.; Müller, T. Pflanzensoziologische Exkursionsflora für Deutschland und Angrenzende Gebiete; Verlag Eugen Ulmer: Stuttgart, Germany, 2001; pp. 93–94. [Google Scholar]
- Hawthorne, S.; Miniat, C.F. Topography may mitigate drought effects on vegetation along a hillslope gradient. Ecohydrology 2018, 11, e1825. [Google Scholar] [CrossRef]





| Name | Spatial Resolution | Temporal Resolution | Temporal Range | Analysis Level | Ref. |
|---|---|---|---|---|---|
| Satellite Data | |||||
| MODIS Terra (product MOD09A1) | 500 m | 8 days (aggregated to monthly medians) | since 2000 (subsetted to 2000–2019) | Analysis Level 1 | [41] |
| Landsat-4, -5, -7, -8 (surface reflectance products) | 30 m (resampled to 60 m) | 16 days (aggregated to monthly medians) | since 1982 (focus on August 2018) | Analysis Level 2 | [42,43] |
| Meteorological Data | |||||
| Precipitation | 1 km | monthly | since 1881 (subsetted to match MODIS) | Analysis Level 1 | [44] |
| Potential evapotranspiration | 1 km | monthly | since 1991 (subsetted to match MODIS) | Analysis Level 1 | [44] |
| Maximum air temperature | 1 km | monthly | since 1901 (subsetted to match MODIS) | Analysis Level 1 | [44] |
| Soil Data | |||||
| Soil moisture | 1 km | monthly | since 1991 (subsetted to match MODIS) | Analysis Level 1 | [44] |
| Soil types | scale of 1:25.000 | unitemporal | 2019 | Analysis Level 2 | [45] |
| Topographic Data | |||||
| Slope and aspect derived from a Digital Terrain Model (DTM) | 25 m (resampled to Landsat data) | unitemporal | 2019 | Analysis Level 2 | [46] |
| Forest Data | |||||
| Corine Land Cover (CLC) | 100 m | unitemporal | 2018 | Analysis Level 1 | [47] |
| Forest heatmap (60 forest reference areas in Bavaria) | scale of 1:10.000 | unitemporal | 2003–2018 | Analysis Level 2 | [48] |
| scPDSI Values | scPDSI Category |
|---|---|
| Above 4.00 | Extreme wet spell |
| 3.00 to 3.99 | Severe wet spell |
| 2.00 to 2.99 | Moderate wet spell |
| 1.00 to 1.99 | Mild wet spell |
| 0.50 to 0.99 | Incipient wet spell |
| 0.49 to −0.49 | Normal |
| −0.50 to −0.99 | Incipient drought |
| −1.00 to −1.99 | Mild drought |
| −2.00 to −2.99 | Moderate drought |
| −3.00 to −3.99 | Severe drought |
| Below −4.00 | Extreme drought |
| Bands | TM | ETM+ | OLI | MOD09A1 |
|---|---|---|---|---|
| Blue | 450–520 nm | 450–515 nm | 450–515 nm | 459–479 nm |
| Green | 520–600 nm | 525–605 nm | 525–600 nm | 545–565 nm |
| Red | 630–690 nm | 630–690 nm | 630–680 nm | 620–670 nm |
| NIR1 | 760–900 nm | 775–900 nm | 845–885 nm | 841–876 nm |
| NIR2 | – | – | – | 1230–1250 nm |
| SWIR1 | 1550–1750 nm | 1550–1750 nm | 1560–1660 nm | 1628–1652 nm |
| SWIR2 | 2080–2350 nm | 2090–2350 nm | 2100–2300 nm | 2105–2155 nm |
| Soil | Description |
|---|---|
| 401a | Almost exclusively regosol from gravel leading sand to sandy loam, poorly distributed over sandstone. |
| 405a | Predominantly brown earth, poorly distributed pseudogley brown soil, in forest areas poorly distributed podsol made out of (gravel-leading) sand (surface layer or sandstone) over (gravel leading) clay (sedimentary rock). |
| 524b | Almost exclusively brown earth (containing podsol), rarely podsol brown earth from skeletal-leading sand (surface layer) over (skeletal-leading) sand (sandstone). |
| 529a | Predominantly pseudogley, poorly distributed brown earth and podsol pseudogley from gravel leading sand to sandy loam (surface layer, sedimentary rock). |
| 529b | Predominantly pseudogley, poorly distributed brown earth and podsol pseudogley from (skeletal-leading) sand to sandy foam (surface layer, sedimentary rock) over clay (sedimentary rock). |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Philipp, M.; Wegmann, M.; Kübert-Flock, C. Quantifying the Response of German Forests to Drought Events via Satellite Imagery. Remote Sens. 2021, 13, 1845. https://doi.org/10.3390/rs13091845
Philipp M, Wegmann M, Kübert-Flock C. Quantifying the Response of German Forests to Drought Events via Satellite Imagery. Remote Sensing. 2021; 13(9):1845. https://doi.org/10.3390/rs13091845
Chicago/Turabian StylePhilipp, Marius, Martin Wegmann, and Carina Kübert-Flock. 2021. "Quantifying the Response of German Forests to Drought Events via Satellite Imagery" Remote Sensing 13, no. 9: 1845. https://doi.org/10.3390/rs13091845
APA StylePhilipp, M., Wegmann, M., & Kübert-Flock, C. (2021). Quantifying the Response of German Forests to Drought Events via Satellite Imagery. Remote Sensing, 13(9), 1845. https://doi.org/10.3390/rs13091845