Abstract
The diversity of change detection (CD) methods and the limitations in generalizing these techniques using different types of remote sensing datasets over various study areas have been a challenge for CD applications. Additionally, most CD methods have been implemented in two intensive and time-consuming steps: (a) predicting change areas, and (b) decision on predicted areas. In this study, a novel CD framework based on the convolutional neural network (CNN) is proposed to not only address the aforementioned problems but also to considerably improve the level of accuracy. The proposed CNN-based CD network contains three parallel channels: the first and second channels, respectively, extract deep features on the original first- and second-time imagery and the third channel focuses on the extraction of change deep features based on differencing and staking deep features. Additionally, each channel includes three types of convolution kernels: 1D-, 2D-, and 3D-dilated-convolution. The effectiveness and reliability of the proposed CD method are evaluated using three different types of remote sensing benchmark datasets (i.e., multispectral, hyperspectral, and Polarimetric Synthetic Aperture RADAR (PolSAR)). The results of the CD maps are also evaluated both visually and statistically by calculating nine different accuracy indices. Moreover, the results of the CD using the proposed method are compared to those of several state-of-the-art CD algorithms. All the results prove that the proposed method outperforms the other remote sensing CD techniques. For instance, considering different scenarios, the Overall Accuracies (OAs) and Kappa Coefficients (KCs) of the proposed CD method are better than 95.89% and 0.805, respectively, and the Miss Detection (MD) and the False Alarm (FA) rates are lower than 12% and 3%, respectively.
Keywords:
remote sensing; change detection; deep learning; CNN; hyperspectral; multispectral; polarimetric SAR 1. Introduction
The Earth’s surface is constantly changing due to numerous factors, such as natural events (e.g., earthquakes and floods) and human activities (e.g., urban development) [1,2]. The detection of these changes is necessary for better management of resources [3]. An efficient approach for monitoring these changes, especially over large inaccessible areas is remote sensing (RS) technology [4]. RS imagery can cover a wide area at different times and can be acquired in a very cost- and time-efficient manner [5].
Change detection (CD) using RS methods refers to the process of measuring the difference in objects in the same region of interest over time using earth observation imagery. CD based on RS imagery is used in many applications, including disaster assessment [2], fire detection [6], Land Cover/Land Use (LCLU) CD, updating LCLU maps [7], and urban development monitoring [8]. The accurate and timely detection of changes is the most important aspect of this process. Recently, due to the importance of CD and with increasing availably of the archived open-source multi-temporal dataset, many CD methods have been developed [9,10]. However, the accurate CD remains challenging, and, therefore, the development of more accurate CD methods using the most recent image processing and machine learning algorithms is required.
Recently, deep learning algorithms have become the most popular methods in the image processing field [11,12]. Deep learning methods automatically discover the representations of input data required for the CD. Generally, various deep learning methods have been proposed for CD in RS imagery, including CNN, deep belief networks (DBNs), recurrent neural networks (RNN), and auto-encoder (AE). Among these deep learning methods, CNN has drawn intensive attention and has proved for many RS applications, including CD [13]. Although many studies analyzed remote CD using CNN, developing a general CNN structure for CD in RS datasets is challenging due to the diversity of CNN architectures and their dependence on the characteristics of datasets. For example, the diversity in the types of remote sensing sensors (e.g., multispectral, hyperspectral, and PolSAR) has led researchers to propose different CD algorithms for various types of remote sensing datasets [2,8,9,10]. The details of these methods are discussed in more detail below.
Multispectral images have been widely used in CD applications due to the diversity of the type of sensors used to collect the data and the high temporal resolution of datasets [14]. However, low spectral resolution is one of the main disadvantages of CD using multispectral RS imagery. For example, this issue caused similar spectral responses for different LCLU classes to be detected due to the coarser bandwidths collected by multispectral sensors. In response, many statistical and deep learning-based multispectral CD methods have been developed. For example, Wu et al. [15] developed a slow feature analysis (SFA) CD method. The SFA extracted the most temporally invariant components from the bi-temporal datasets to transform the data into a new feature space to produce the change/no-change map in this feature space. Additionally, Wu et al. [16] proposed a CD framework based on low-rank sparse representation and nearest neighbor classifiers. Specifically, their proposed framework was developed based on low-rank matrix representation or low-rank sparse decomposition for change feature exaction. Finally, the change map was obtained based on the nearest neighbor classifier by predicted changes. Chen et al. [17] also developed a CD framework based on multiple levels of future fusion and two-level clustering. The gradient feature and spectral features were initially extracted and predicted in the changed regions. The binary change map was then produced based on two-level clustering by fuzzy-c-means and nearest neighbor rule classification. Furthermore, Zhang et al. [18] proposed a spectral-spatial joint learning network for a multispectral CD that was implemented in three phases: (1) extracting spatial and spectral features using network similar to the Siamese architecture, (2) fusing these features to represent the difference information, and (3) utilizing discrimination learning to explore the underlying information of the obtained fused features for better discrimination. Moreover, Papadomanolaki et al. [19] proposed a hybrid CD framework for urban areas. In their CD method, fully convolutional networks (U-Net) and powerful recurrent networks (LSTM) were subsequently utilized for feature representation and temporal modeling. Lv et al. [20] also proposed a new land cover CD method based on the integration of k-means clustering and adaptive majority voting that was implemented in three steps: (1) using contextual information adaptively based on calculating a change magnitude image, preparing training sample, and extension of an adaptive region surrounding of a central pixel, (2) determining the label of each pixel within the adaptive region by k-means, and (3) refining the label of the central pixel of the adaptive region by adaptive majority voting. Finally, Du et al. [21] proposed a CD framework that is applied in three main parts: (1) prediction by change vector analysis, (2) automated sample selection, and (3) refined modification based on SVM posterior probability comparison in temporal space.
The hyperspectral RS imagery contains many spectral bands (e.g., hundreds of bands), by which CD of similar targets can be potentially improved [3]. However, CD in hyperspectral datasets is a relatively challenging task due to the specific characteristics of these datasets, such as noise conditions and data redundancy [22]. Another issue is the low temporal resolution of most the hyperspectral RS systems, however, it is expected this issue will be resolved to some degrees with the implementation of new hyperspectral sensors such as the Environmental Mapping and Analysis Program (EnMAP), PRecursore IperSpettrale della Missione Applicativa (PRISMA), and Hyperspectral Infrared Imager (HyspIRI). So far, several CD methods for hyperspectral RS datasets have been proposed, some of which are discussed here. Nielsen et al. [23] introduced the multivariate alteration detection (MAD) transformation CD method. This method is based on finding differences between linear combinations of the spectral bands of the bi-temporal dataset. Wu et al. [24] proposed a hyperspectral CD method based on forming a sub-space and measuring spectral distance within this space. They also improved the performance of the proposed algorithm using several ancillary datasets. Additionally, Yuan et al. [25] investigated a semi-supervised CD method based on the distance metric learning method. This framework had two main steps: the first phase predicted the change areas via the distance metric, and the second phase involved binary classification using the Support Vector Machine (SVM) algorithm. Furthermore, Liu et al. [26] developed an unsupervised CD method based on spectral unmixing. Wang et al. [27] improved the performance of unsupervised CD based on minimizing registration errors. This method is applied in two main phases: (1) synthetically fused images are obtained based on block-based fusion method, and (2) iteratively regularized multivariate alteration detection (IR-MAD) is applied to synthetically fused images to reduce the falsely detected changes. Moreover, Song et al. [28] presented an unsupervised framework for binary and multiple CD of hyperspectral images. The proposed framework was implemented in two main steps: (1) sample generation based on principle component analysis (PCA) and spectral correlation analysis (SCA), and (2) the multiple and binary change maps are obtained by recurrent 3D fully convolutional network (Re3FCN). Wang et al. [29] proposed a CD method based on a 2D conventional neural network (CNN) and spectral unmixing. This method was implemented in two steps: a mixed-affinity matrix was first formed for each pixel by spectral unmixing and image differencing and the binary change map was then obtained by the CNN algorithm. Besides, Marinelli et al. [30] developed an unsupervised framework based on a discrete representation of the change information. In this method, binary change vector analysis was first employed and, then, a tree representation was then defined to discriminate changes. Li et al. [31] also developed unsupervised deep noise modeling for CD in hyperspectral datasets. The proposed framework was implemented in three main steps: (1) fully convolutional network (FCN) was used to learn discriminative features from high-dimensional data, (2) the two-stream feature fusion module was utilized for fusing feature maps, and (3) the unsupervised noise modeling module applied to tackle the influence of noise and to robustly train the proposed network. Seydi et al. [32] proposed a deep learning-based framework based on 3D-CNN and image differencing. This method is applied in two main steps: (1) the change areas are predicted by image differencing algorithm, and (2) make a decision on predicted area based on 3D-CNN. Huang et al. [33] also proposed a CD framework based on deep learning and the tensor model. The proposed method was implemented in two main phases: (1) the change features were extracted by the tensor model and the 3D change features (spectral, spatio-temporal, and wavelet texture) were combined. Subsequently, unsupervised learning was applied for feature extraction, in which the features were extracted based on the restricted Boltzmann machine and three-order tensor (Tensor3-RBM). The final change map was produced based on a deep belief network with multi-layer Tensor3-RBM and STM (TRS-DBN).
PolSAR data have several advantages for CD over other RS imagery. For instance, they can operate almost in any weather conditions (e.g., cloudy and rainy), which guarantees the acquisition of the area of interest. However, the existence of speckle-noise causes CD a challenging task using these types of datasets. To date, many polarimetric CD methods have been proposed by researches to improve the accuracy of CD using these datasets [34]. For example, Qi et al. [35] proposed a three-component polarimetric change method (1) a bi-temporal PolSAR dataset is segmented hierarchically to extract land parcels, (2) parcel-based change vector analysis (CVA) along with the coherency matrices of the PolSAR data are applied to predict changed parcels, and (3) post-classification comparison are employed based on a parcel-based classification algorithm that integrates polarimetric decomposition, SVM, and decision tree algorithms, to detect the type of change for the changed parcels. Furthermore, Liu et al. [13] developed a new version of CNN, which was named local restricted CNN (LRCNN). This CD method was implemented in two steps: (1) a similarity measure for the polarimetric was proposed and several layered difference maps were generated using PolSAR images transformed into discriminative enhanced LDI, and (2) CNN/LRCNN was trained for the tuning hyperparameter. Finally, the change map was obtained based on the optimized trained model. Ghanbari et al. [36] also proposed an unsupervised PolSAR CD method based on the Hotelling-Lawley Trace Statistic and Minimum-Error Thresholding. This method was implemented in two main steps: (1) the Hotelling–Lawley trace statistic was applied to predict the change area, (2) a generalized Kittler and Illingworth minimum-error thresholding algorithm was used for thresholding. Additionally, Cui et al. [37] proposed an unsupervised stochastic subspace ensemble learning method that was implemented in two main steps: (1) automatic determination of high-confidence samples, which were included in the refinement process and fusion strategy, and (2) implementing a stochastic subspace ensemble learning module that uses three phases: acquiring the subsample sets, building and training a two-channel network, and applying the prediction results and ensemble strategy. Moreover, Najafi et al. [38] investigated the potential distance-based algorithms for CD using PolSAR data. The CD framework in this study was implemented in two main steps: (1) the change area was predicted using the distance similarity measure method, and (2) decisions on predicted areas were made using the supervised thresholding. Mahdavi et al. [2] also proposed a polarimetric index-based CD method. In this study, a polarimetric index was developed based on the ratio of span values and the neighborhood information was investigated based on the weight parameter. Finally, Zhao et al. [39] presented a new CD framework based on statistical distribution characteristics. This method was implemented in two main steps: (1) change areas were predicted based on an image differencing algorithm, and (2) thresholding was conducted using an improved Kittler and Illingworth algorithm based on either the Weibull or gamma distribution.
Although there are many RS CD methods, they generally have one of the following limitations: (1) some of the proposed methods are implemented in two phases (i.e., predictor and decision), the combination of which can affect the accuracy of the CD algorithm, (2) some of the CD methods only utilize the spectral information and ignored the advantage of spatial features, (3) some handcrafted-based spatial/spectral features produced by conventional methods (e.g., texture feature and vegetation indices) may fail to extract the details embedded in the dataset and thus significant expertise is required to design an appropriate structure, (4) some of the methods are complex to implement, (5) several CNN-based CD methods are applied to two phases: predictor phase and decision phase. These CD techniques are not End-to-End because additional processing steps are required, (6) although an automatic sample generation framework through traditional CD methods, the extraction of training data is usually employed with low reliability due to several factors, such as noise and atmospheric conditions, (7) many methods are only used for one type of RS data and do not support other datasets, and (8) the current state-of-the-art CNN-based CD methods use a 2D convolution layer and ignore the relation of spectral bands, while a combination of 3D and 2D deep features can improve the performance results [40].
The main objective of this study is therefore to propose a new deep learning framework for CD in RS datasets to minimize some of the above-mentioned shortcomings. The main contributions of this study and the proposed CD method can be summarized as follows: (1) it can be effectively applied to different types of RS datasets, (2) it can potentially utilize all of the main information in a RS dataset for CD by extracting deep features within a multi-dimensional convolution layer, (3) it has an End-to-End framework as it does not require additional processing for CD, and (4) it is sensitive to subtle changes with high accuracy and low False Alarm (FA) rates.
2. Datasets
In this study, three different remote sensing datasets (i.e., multispectral, hyperspectral, and PolSAR) were applied to evaluate the performance of the proposed CD method. These datasets are illustrated in Figure 1, Figure 2 and Figure 3 (available from https://rslab.ut.ac.ir and https://rcdaudt.github.io/oscd/) and discussed in Section 2.1, Section 2.2 and Section 2.3. One of the important factors for assessing different types of remote sensing CD methods is the quality of the corresponding ground truth data. Therefore, the main reason for choosing these datasets was the availability of proper ground truth data. Additionally, these datasets are employed in many change detection studies (e.g., [3,29,38,41,42]) and, thus, the accuracies of the corresponding CD methods can be equally compared with those of the proposed method in this study.

Figure 1.
Multispectral datasets: (a) and (b) show the false-color composite of the multispectral images acquired over Abudhabi City, in United Arab Emirates (UAE) on 20 January 2016, and 28 March 2018, respectively, and (c) is the corresponding binary ground truth data which illustrates the change and no-change areas. (d) and (e) are the false-color composites of the multispectral images acquired over the Saclay area on 15 March 2016, and 29 October 2017, respectively, and (f) is the corresponding ground truth data, which white and black colors indicate the change and no-change areas, respectively.
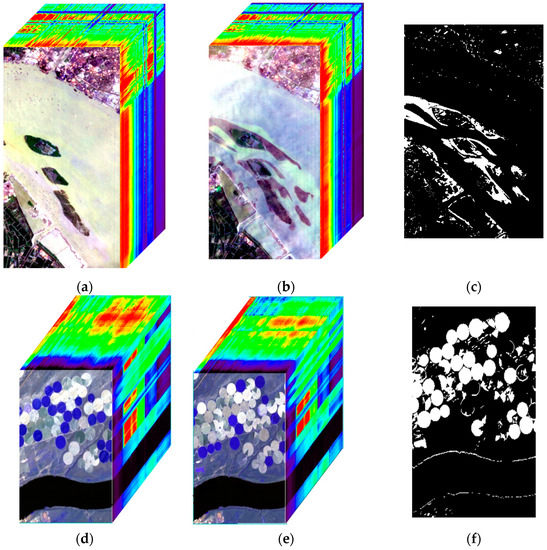
Figure 2.
Hyperspectral datasets: (a) and (b) are a false-color composite of the Hyperspectral-River images acquired over a river in Jiangsu province, China on 3 May 2013, and 31 December 2013, respectively, and (c) is the corresponding binary ground truth data, which white and black colors indicate the change and no-change areas, respectively. (d) and (e) are a false-color composite of the Hyperspectral-Farmland images acquired over farmland in the USA on 1 May 2004, and 8 May 2007, respectively, and (f) is the corresponding ground truth data in binary format, which white and black colors indicate the change and no-change areas, respectively.

Figure 3.
PolSAR dataset: (a) and (b) are the RGB composites generated from the Pauli decomposition (Red: |HH − VV|; Green: 2|HV|; Blue: |HH + VV|) for the PolSAR-San Francisco1 datasets, and (c) shows the corresponding binary ground truth data, which white and black colors indicate the change and no-change areas, respectively. (d) and (e) are Pauli RGB composite of the PolSAR-San Francisco2 images, and (f) shows the corresponding ground truth data in binary format, which white and black colors indicate the change and no-change areas, respectively. Note that (a) and (d) were acquired on 18 September 2009, and (b) and (e) were captured on 11 May 2015.
2.1. Multispectral Datasets
The multispectral CD was conducted using the Onera Satellite Change Detection Dataset (OSCD), which consists of Sentinel-2 satellite images [41]. The first image pairs (Figure 1a–c), which were acquired over Abudhabi, United Arab Emirates (UAE) on 20 January 2016, and 28 March 2018, respectively, were named Multispectral-Abudhabi. The second multispectral datasets, which were captured over the Saclay region in Paris, France on 15 March 2016, and 29 October 2017, respectively, were named Multispectral-Saclay. As demonstrated in Figure 1, the main changes over these areas are related to man-made objects. Table 1 provides more information about the multispectral datasets used in this study to evaluate the performance of the CD methods.

Table 1.
Description of multispectral datasets (italic characters are the name of datasets).
2.2. Hyperspectral Dataset
The hyperspectral CD was conducted using the two types of hyperspectral datasets acquired by the Hyperion sensor (see Table 2 and Figure 2). The first images (Figure 2a–c), which illustrates a river, was named Hyperspectral-River. These images were acquired over Jiangsu Province, China on 3 May 2013, and 31 December 2013, respectively. The main change type on these datasets is the disappearance of substance in the river. The second hyperspectral dataset, which illustrates farmland, was named Hyperspectral-Farmland. These images depict an irrigated agricultural field in Hermiston City in Umatilla County, Oregon, OR, USA, and were acquired on 1 May 2004, and 8 May 2007, respectively.

Table 2.
Description of hyperspectral datasets (italic characters are the name of datasets).
2.3. PolSAR Datasets
The polarimetric CD was conducted using the two PolSAR datasets acquired over the San Francisco city (Figure 3). These L-band PolSAR images were acquired by the Jet Propulsion Laboratory/National Aeronautics and Space Administration UAVSAR on 18 September 2009, and 11 May 2015. These datasets were named PolSAR-San Francisco1 and PolSAR-San Francisco2. Table 3 provides the characteristics of the PolSAR datasets used in this study. The main properties of these datasets are the existence of speckle noise. Additionally, the main purpose of using these images was to analyze the performance of the CD methods in terms of noise. It is also worth noting that although the urban areas in the PolSAR datasets had strong backscattering responses, the CD was a challenge due to several conditions such as noise, wind, and vegetation cover.

Table 3.
The description of the Polarimetric Synthetic Aperture RADAR (PolSAR) datasets (italic characters are the name of datasets).
3. Method
The general overview of the proposed CD method for RS datasets is illustrated in Figure 4 and is discussed in more detail in the following subsections. The proposed method has a supervised binary CD framework that receives two images acquired from a specific area at different times and produces a change map in a binary format (i.e., change/no-change map).
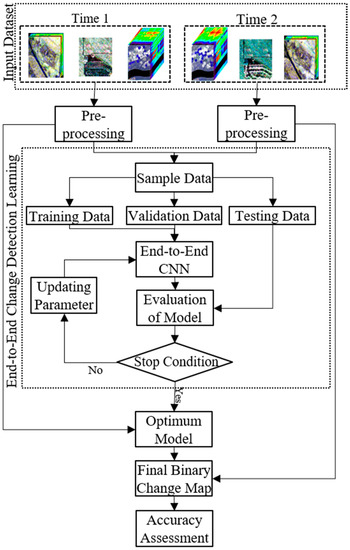
Figure 4.
General flowchart of the proposed supervised binary change detection (CD) method.
3.1. Pre-Processing
As clear from Figure 4, the input data should first be pre-processed. Data pre-processing plays an important role in CD methods and can be divided into two categories: spectral and spatial corrections. Spectral correction for the multispectral dataset included de-noising, radiometric correction, and atmospheric correction. Additionally, the spatial resolution of all spectral bands was resampled to 10 m. The pre-processing of the hyperspectral dataset included removing data bands that contain no data, shifting the pixels in sample 129, and all lines to sample 256 in SWIR spectral bands, de-striping, and removing the zero-line, and implementing radiometric and atmospheric corrections. The initial pre-processing of the PolSAR dataset included multi-looking and de-speckling. The second step was a geometric correction, for which relative registration was used. Then, several GCP points were selected and a second-order polynomial was utilized for modeling, and the bi-linear method was used for resampling gray values. The final accuracy of the geometric correction (i.e., RMSE) was approximately 0.4 pixels.
3.2. The Proposed End-to-End CD Network Based on CNN
The End-to-End CD network (indicated with the dashed box in Figure 4) is the main part of the proposed method developed based on a new CNN algorithm (see Figure 5). According to Figure 5, the proposed CNN architecture does not require predictors for CD. The process is applied by differencing and staking deep features. The proposed architecture is different from other previously developed CNN CD architectures because it uses (1) multi-dimensional convolution kernels, (2) a dilated convolution layer, (3) stacking and differencing layers.
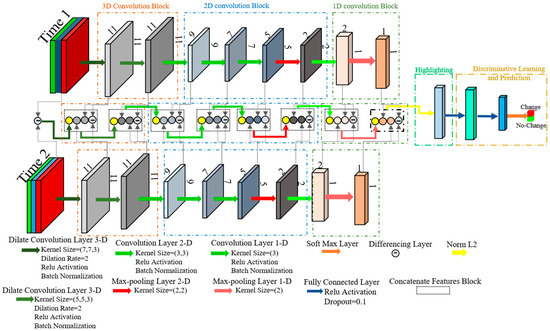
Figure 5.
The proposed End-to-End convolutional neural network (CNN) architecture for CD of remote sensing datasets.
As it is clear from Figure 5, the proposed CNN network employs bi-temporal datasets as inputs. The network has three channels of convolution layers where the first and third channels are related to the first- and second-time datasets, respectively. The second channel is related to the differencing and stacking convolution layers. Each convolution block includes an activation function (i.e., Rectified Linear Unit (ReLU)), batch normalization, and many convolution filters that extract deep features. The size and number of kernel convolutions for each channel is constant. The proposed CNN network is implemented using the following four steps:
(1) The deep feature generation commences with 3D-dilated convolution layers with a size of 7 × 7 × 3 and a dilation rate of 2 that investigates the relationship of the spectral bands. The second channel starts by differencing input datasets and, the deep feature is then extracted. The second convolution layer of this channel is a 3D-dilated convolution with a size of 7 × 7 × 3, and a dilation rate of 2. The input in the second channel is differencing, stacking of obtained deep features from the first and second layers, and the deep features extracted from the previous layer.
(2) The 3D features are reshaped to 2D features and the deep features are extracted by the 2D convolution layer in this step. This process is repeated as the number of filters increases. Finally, a max-pooling with a downsampling size of 2 is applied to three channels.
(3) The final convolution layer is 1D and requires features to be reshaped to 1D. A 1D convolution kernel with a size of 3 is applied to extract deep features. Finally, the 1D max pooling with a downsampling rate of 2 is applied for extraction deep features.
(4) The output of the third channel is the final extracted deep feature that is used for the subsequent analyses. The norm l2 is applied to these deep features and batch normalization is then performed. These features are transformed into a subset of fully connected layers to the final outputs of the network. To this end, two fully connected layers with the activation function of ReLU are utilized. In the dropout process, the randomly selected neurons are ignored during training to prevent overfitting. The first fully connected layer has 150 neurons and the dropping out units (dropout) rate is 0.1. The second fully connected layer has 15 neurons and the dropout rate is 0.1. The last layer of this network is the Softmax layer.
Figure 6 presents the structures of the three state-of-the-art CD framework based on the deep learning method. The proposed CNN architecture has a different network structure as follows:
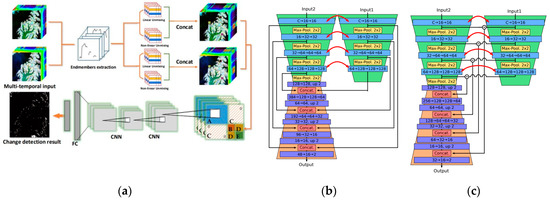
Figure 6.
Overview of the three state-of-the-art CD frameworks based on deep learning. (a) General End-to-end Two-dimensional CNN Framework (GETNET) [29], (b) Siamese-concatenate network [44], and (c) Siamese-differencing network [44].
(1) Most CD architectures extract deep features based on only a 2D convolution, in which the relationship between spectral bands is ignored. However, the proposed method is developed based on a combination of the 3D/2D/1D convolution layers.
(2) Most of the CNN-based CD methods only utilize stacking or differencing deep features. However, the proposed method considers both of them for the extraction of deep features.
(3) Most of the deep learning methods for CD require a predictor (e.g., image differencing, image ratio, and PCA). However, the proposed method does not need a predictor.
(4) The proposed CD method highlights deep features by adding the norm l2 and, thus, can increases the separability of the deep features.
(5) The proposed method utilizes the 3D-Dilated convolution for deep feature extraction.
In Figure 5, the proposed End-to-End CNN CD method has three main steps, including (1) convolution and pooling layers, (2) highlighting deep features, and (3) discriminative learning and prediction, and the details of each are discussed in the following subsections.
3.2.1. The Convolution and Pooling Layers
The main task of a convolution layer is to automatically extract spatial and spectral features from input data [43,45]. The convolution layer includes a combination of linear and nonlinear operations [45]. The dimensional kernel of convolution layers can be 1D, 2D, or 3D, the main differences of which are presented in Figure 7.
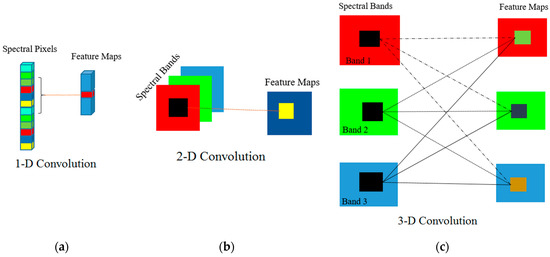
Figure 7.
Comparison of (a) 1-D, (b) 2-D, and (c) 3-D convolution layers.
For a convolutional layer in the lth layer, the computation is expressed according to Equation (1) [46].
where x is the neuron input from the previous layer, l−1, g is the activation function, is the weight template, and b is the bias vector of the current layer, l.
The main purpose of the 3D convolution layer is to investigate the relationship between spectral bands so that all of the content of the spectral information is fully used [46,47]. The value () at position (x,y,z) on the jth feature ith layer for the 3D-Dilated convolution layer is given by Equation (2) [46,48,49].
where b denotes bias, g is the activation function, m is the feature cube connected to the current feature cube in the (i − 1)th layer, W is the (r, s, t)th value of the kernel connected to the mth feature cube in the preceding layer, and R, S, and T are the length, width, and depth of the convolution kernel size, respectively. ,, and are also dilate convolution rates in length, width, and depth, respectively.
The 2D convolution layer is concentrated on spatial dimensions and is unable to handle spectral information [47,50]. In 2D convolution, the output of jth feature map in ith layer at the spatial location of (x,y) can be computed using Equation (3).
The 1D convolution layer is a modified version of the 2D convolution layer that has recently been developed [51,52]. The computational complexity of the 1D convolution layer is significantly lower than the 2D and 3D convolution layers, and it can also learn challenging tasks [53]. Additionally, this convolution is faster than others due to its structure and can considerably increase the speed of the network training. In 1D convolution, the activation value at spatial position x in the jth feature map of the ith layer is generated using Equation (4) [51].
In the proposed architecture, each convolution layer employs a ReLU activation function for nonlinear responses [54,55]. The ReLU function can be formulated as Equation (5) [54,55].
The pooling operation also plays an important role, contributing to invariance to data variation and perturbation [56]. The main task of the pooling layer is to reduce the in-plane dimensionality of the feature maps and, as a result, increase the speed of the convergence rate [45]. The max-pooling layer is the most popular pooling layer operated based on the maximum activation over non-overlapping rectangular regions [57]. It is worth noting that all the downsampling rates in the proposed network are set to 2.
3.2.2. Highlighting Deep Feature
Several mathematical operators, such as logarithmic ratio and power 2 are usually utilized in different CD methods to improve the separability of different LCLU classes. It was observed in this study (see Figure 8) that the norm l2 can increases the separability of the change and no-change areas. Moreover, CVA has a better performance compared to simple differencing in CD applications [35,58]. The main reason for this is the discriminating features in this space is easier. The use of norm l2 highlighted features that this process can increase, such as the discriminating deep features.

Figure 8.
The difference between (a) simple differencing and (b) norm l2 in discriminating change and no-change areas for Hyperspectral-Farmland datasets.
3.2.3. Discriminative Learning and Prediction
The fully connected layer is connected to all the activations in the upper extracted features to combine activations that lead to a meaningful prediction about the inputs [59]. The proposed network uses two fully connected layers with the ReLU activation function. The latest layer resolves the binary classification problem, in which the Softmax output activation function is used. This activation function is generally used for modeling categorical probability distributions and can be expressed by Equation (6) for input x and output y [60,61]:
The dropout rate is used widely in deep learning methods and improves the performance of deep learning methods [62]. Its main objective is to randomly ignore some sample neurons to prevent overfitting [62,63].
3.2.4. Updating Hyperparameter
The weight of CNN cannot be calculated using an analytical method instead the hyperparameter is tuned to achieve the solution with the lowest cost performs. To this end, the Adam optimizer is utilized that is based on adaptive estimates of lower-order moments. This optimizer compares to other optimizers has many advantages that are as follows: computationally efficient, requires little memory, is invariant to the diagonal rescaling of the gradients, and is well suited for problems that are large in terms of parameters, straightforward to implement. The weights of the network are tuned by Adam optimizer as iteratively based on calculation error of network on input data by the cost function. To this end, the sample datasets are divided into three categories: (1) training data, (2) validation data, and (3) testing data. The network is learned and evaluated by the training and validation datasets, respectively. It is worth noting that the best weight for the selection of parameters is based on the performance of the network on validation data. The learning phase continues until all epochs are finished.
The loss function is measured by the compatibility of the network with respect to the predicted output and ground-truth label. This research used binary cross-entropy as the loss function of the proposed architecture and is expressed mathematically in Equation (7):
where y is a binary indicator and p is related to the predicted probability observation.
3.2.5. Evaluation of Model and Stop Condition
Besides tuning the weight of CNN, other parameters should be tuned. These parameters are the input patches size, dropout rate, number of neurons, layers, dilation rate, mini-batch size, initial learning rate, number of the epoch. In this study, these parameters are started with an initial value for the configuration of the network and, then, the network is evaluated using accuracy indices, such as calculating the overall accuracy using test data. Finally, the parameters are updated and new values are assigned. The stopping criteria are defined based on achieving acceptable accuracy. It is also worth noting that the optimal values of these parameters are selected based on the experiments conducted on all three types of datasets (e.g., multispectral, hyperspectral, and SAR).
3.3. Optimum Model
The optimum model is obtained by tuning the weight of the network, as well as other parameters discussed in Section 3.2.5. To this end, the network is trained using the training data and the error of the network is calculated by the evaluation of the network using the validation dataset. Finally, the performance of the network is assessed using test data. This process is continued until the stopping condition is reached. Subsequently, the hyperparameters of the network are tuned, and an optimum model is created to produce the binary CD map. In this step, the final change map is directly produced by the proposed CD method and does not require additional processing (e.g., normalization, feature extraction, and threshold selection).
3.4. Accuracy Assessment
Accuracy assessment is the final step in any RS analysis. In this study, the final results of the proposed CD method were compared with both ground truth data the results from other state-of-the-art CD methods. These are explained in the following two subsections.
3.4.1. Comparison with Ground Truth Data
The results were compared with ground truth data through calculating several evaluation metrics, most of which are extracted from a confusion matrix which has four components: (1) True Positive (TP), (2) True Negative (TN), (3) False Positive (FP), and (4) False Negative (FN) (see Table 4). The formulae for the evaluation metrics used to assess the results are provided in Table 5 and include the Overall Accuracy (OA), precision, sensitivity, specificity, Balanced Accuracy (BA), F1-Score, Miss-Detection (MD), FA rate, and Kappa Coefficient (KC).

Table 4.
Confusion matrix (TP: True Positive, TN: True Negative, FP: False Positive, and FN: False Negative).

Table 5.
Different types of indices that were used for accuracy assessment of the change map produced using the proposed method by components TP, TN, FP, and FN (TP: True Positive, TN: True Negative, FP: False Positive, and FN: False Negative).
3.4.2. Comparison with Other CD Methods
It is also important to compare the proposed CD method with other state-of-the-art techniques. In this study, the results of the proposed CD method were compared with those of the slow feature analysis (SFA) [15], image differencing-principle component analysis (ID-PCA) [64,65], multivariate alteration detection (MAD) [23], iteratively reweighted multivariate alteration detection (IR-MAD) [27], change vector analysis (CVA) [21,30,66], and 3D-convolution neural network (3D-CNN) [32].
4. Results
4.1. Setting Parameters
Excluding 3D-CNN and the proposed method, the remaining CD methods compared in this study require a threshold selection, and so SVM was employed. The SVM classifier has two parameters: kernel parameters and the penalty coefficient. In this study, the radial basis function (RBF) kernel, which is widely utilized in the remote sensing community [67,68], was employed. These parameters are required for optimization, and their optimum values are obtained by a Grid Search (GS) algorithm [69].
In this study, 65%, 15%, and 20% of the sample datasets are selected as the training, validation, test data, respectively. Table 6 provides more information about each of these datasets.

Table 6.
Numbers of samples for change detection in the six datasets used in this study.
An imbalanced dataset is one of the most important challenges in supervised learning methods [70,71,72,73]. Class weight is one of the simplest techniques to address the class imbalance, providing a weight for each class. The weight class is automatically defied based on inversely adjusting weights proportional to class frequencies. All weights are initialized by the Glorot normal initializer [74] and are trained using a back-propagation algorithm with Adam optimizer by using the softmax loss function [72,75]. Table 7 provides information about the optimum values for the parameters of the proposed CNN network. It is worth noting that the selection of some of these parameters, which were related to hardware (e.g., increasing mini-batch size) quickly filled up the RAM of the system. Moreover, the weight initializer by the Glorot normal initializer increased the speed of network convergence compared to the random initializer. Among these parameters, patch size plays a key role in the performance of the proposed CD method. For example, decreasing the number of the patch size from 13 to 11 improved the OA of CD by approximately 3% for the test dataset.

Table 7.
The optimum values for the training parameters of the proposed CNN network.
The SVM algorithm has two main parameters: kernel parameter (gamma ) and penalty coefficient (C). These parameters were different for each dataset. These parameters were evaluated in the range of [10−5,105] and [10−3,103] for gamma and penalty coefficient, respectively.
The MAD, PCA, IR-MAD, and SFA methods produce a cube of change information, not a single band. The PCA algorithm has sorting criteria of component based on eigenvalue and, thus, change components with content information above 95% are selected in this study. The other methods do not have any criteria and, therefore, the high content of change information is selected based on visual analysis.
4.2. CD of Multispectral Datasets
4.2.1. Multispectral-Abudhabi Data
The CD maps for the Multispectral-Abudhabi dataset produced using different methods are illustrated in Figure 9. As is clear, the results are considerably different. The result of CVA is not accurate due to the high FP pixels. The results of the MAD, IR-MAD, SFA, and 3D-CNN are also inaccurate due to considerable FN pixels. However, the proposed CD method performs well when compared to ground truth data.

Figure 9.
The change detection maps produced by different CD methods for the Multispectral-Abudhabi dataset. (a) CVA-SVM, (b) MAD-SVM, (c) PCA-SVM, (d) IR-MAD -SVM, (e) SFA-SVM, (f) 3D-CNN, (g) Proposed Method, and (h) Ground Truth. White and black colors indicate the change and no-change areas, respectively.
The errors using different CD methods for the Multispectral-Abudhabi dataset are illustrated in Figure 10. As is clear, the amount of FP and FN pixels (i.e., red and blue colors, respectively) are significant for all CD methods excluding the proposed in this study. The CVA and PCA algorithms had high FP pixels while MAD, IR-Mad, SFA, and 3D-CNN had high FN pixels. The detection of main changes is a large challenge by these methods. However, the proposed method (Figure 10g) had the lowest error in terms of FP and FN pixels compared to the others.

Figure 10.
The errors in change detection using different methods for the Multispectral-Abudhabi dataset. (a) CVA-SVM, (b) MAD-SVM, (c) PCA-SVM, (d) IR-MAD -SVM, (e) SFA-SVM, (f) 3D-CNN, and (g) Proposed Method. Black, red, and blue colors indicate TP and TN, FN, and FP respectively.
The statistical accuracy assessments of the various CD methods for the Multispectral-Abudhabi dataset are provided in Table 8. As can be seen, the presented numerical results in this table have high variations. This issue originated from performance CD methods that are more methods sensitive to extract no-change pixels while they cannot detect more change pixels. According to Table 8, the proposed method had the best performance compared to the other methods. Although the OAs are considerably high for all methods, the KC values are significantly low for all CD methods except for the proposed method, confirming its high performance for CD of multispectral remote sensing datasets.

Table 8.
The accuracy of different change detection methods for the Multispectral-Abudhabi dataset (the best performance for each method appears in bold).
The confusion matrices for CD using different methods over the Multispectral-Abudhabi dataset are demonstrated in Figure 11. As can be seen, most methods have low performance in detecting change pixels compared to no-change pixels. The highest accuracy in detecting change areas are obtained by the proposed method.
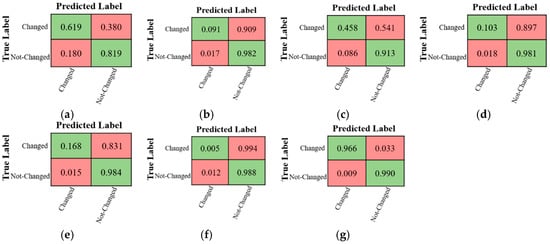
Figure 11.
The confusion matrices of different CD methods for the Multispectral-Abudhabi dataset. (a) CVA-SVM, (b) MAD-SVM, (c) PCA-SVM, (d) IR-MAD -SVM, (e) SFA-SVM, (f) 3D-CNN, and (g) Proposed Method.
4.2.2. Multispectral-Saclay Data
Based on the original Multispectral-Saclay data, the diversity of the change areas is high and there are several small changed regions in these datasets, making the detection of the changes relatively challenging. For instance, based on the results illustrated in Figure 12, there are several non-target change areas, which were wrongly detected as changed areas by most of the CD methods. However, the deep learning CD methods (i.e., 3D-CNN and the proposed method) provided acceptable accuracies. In total, the proposed method had the best performance on CD.

Figure 12.
The change detection maps produced by different methods for the Multispectral-Saclay dataset. (a) CVA-SVM, (b) MAD-SVM, (c) PCA-SVM, (d) IR-MAD -SVM, (e) SFA-SVM, (f) 3D-CNN, (g) Proposed Method, and (h) Ground Truth. White and black colors indicate the change and no-change areas, respectively.
According to the results demonstrated in Figure 13, although the FN pixels are significant in all CD methods, this is relatively low for the method proposed in this study. Additionally, the non-deep learning CD methods had high FP pixels, while this is significantly lower for the deep learning-based CD methods.
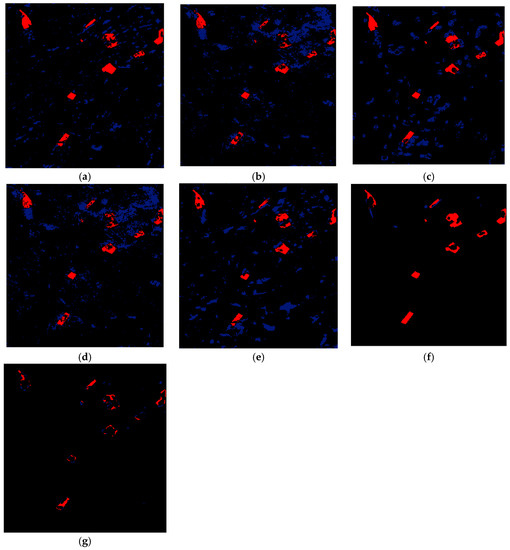
Figure 13.
The change detection errors of different methods for the Multispectral-Saclay dataset. (a) CVA-SVM, (b) MAD-SVM, (c) PCA-SVM, (d) IR-MAD -SVM, (e) SFA-SVM, (f) 3D-CNN, and (g) Proposed Method. Black, red, and blue colors indicate TP and TN, FN, and FP pixels, respectively.
The statistical evaluation metrics obtained for different CD methods applied to the Multispectral-Saclay dataset are presented in Table 9. Based on this table, all methods provided better performance compared to the results obtained for the Multispectral-Abudhabi dataset. Although most of the evaluation metrics indicate the high performance of all CD methods (e.g., high values of OA Precision, F1-score, and Sensitivity), several issues are notable. For instance, all the MD values are under 2%. Overall, the proposed CD method has the highest accuracy. For instance, the KC index of the proposed method is considerably higher than that of other methods. The BA index, which indicates the trade-off between change and no-change pixels, is also higher for the proposed CD method compared to the other methods.

Table 9.
The accuracy of different change detection methods for the Multispectral-Saclay dataset (the best performance for each method appears in bold).
The confusion matrices for CD using different methods over the Multispectral-Saclay dataset are demonstrated in Figure 14. Based on these results and the numerical analysis provided in Table 9, the performance of all methods in detecting change pixels is lower compared to those obtained for the Multispectral-Abudhabi. This issue originated from the complexity of change areas for this dataset.
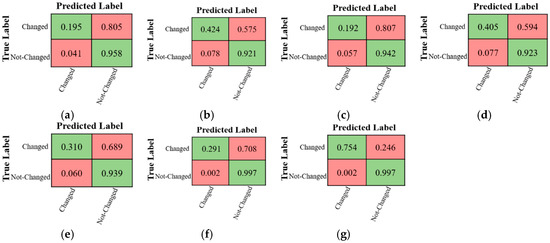
Figure 14.
The confusion matrices of different CD methods for the Multispectral-Saclay dataset. (a) CVA-SVM, (b) MAD-SVM, (c) PCA-SVM, (d) IR-MAD -SVM, (e) SFA-SVM, (f) 3D-CNN, and (g) Proposed Method.
4.3. CD of Hyperspectral Datasets
4.3.1. Hyperspectral-River Data
The visual comparison between the results of different CD methods for the Hyperspectral-River dataset is provided in Figure 15. The detection of changes within water bodies is generally difficult due to the complexity of these regions. It was challenging for all CD methods investigated here to detect changes within the river and surrounding areas (center of the dataset). The main difference in CD methods is related to the changes concentrated around the river. For example, there are many noisy pixels in the results of the CD by the IR-MAD and MAD algorithms. However, these areas are correctly identified using the proposed CD method (Figure 15g).

Figure 15.
The change detection maps obtained by different methods for the Hyperspectral-River dataset. (a) CVA-SVM, (b) MAD-SVM, (c) PCA-SVM, (d) IR-MAD -SVM, (e) SFA-SVM, (f) 3D-CNN, (g) Proposed Method, and (h) Ground Truth. White and black colors indicate the change and no-change areas, respectively.
The errors in CD using different methods for the Hyperspectral-River data were also evaluated, and the results are demonstrated in Figure 16. As can be seen, all CD methods have high FN pixels and more FN pixels most of which are related to the edges. The IR-MAD and MAD algorithms had the highest MD rates, whereas the SFA algorithm had the highest FA rate. Moreover, the FP and FN pixels of most CD methods cover a small region of the image, whereas this is not an issue in the result of the proposed method, where the error of the CD can be seen as a thin line (Figure 16g).
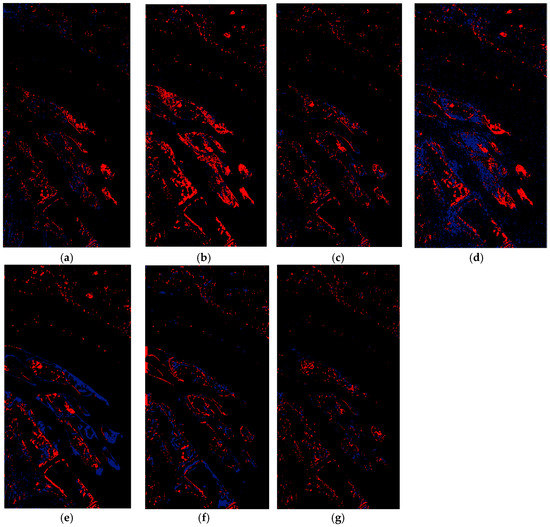
Figure 16.
The change detection errors of different methods for the Hyperspectral-River dataset. (a) CVA-SVM, (b) MAD-SVM, (c) PCA-SVM, (d) IR-MAD -SVM, (e) SFA-SVM, (f) 3D-CNN, and (g) Proposed Method. Black, red, and blue colors indicate TP and TN, FN, and FP pixels respectively.
Table 10 shows the statistical accuracies obtained for different CD methods applied to the Hyperspectral-River dataset. Based on this table, the OA of most of the CD methods is more than 92% and the BA is more than 80%. The MAD algorithm has the highest MD rate and the lowest BA value. Additionally, the IR-MAD method has the highest FA rate compared to the other methods.

Table 10.
The accuracy of different change detection methods for the Hyperspectral-River dataset (the best performance for each method appears in bold).
The Specificity index, which is sensitive to no-change pixels is more than 95% for all methods included in this study. Additionally, Sensitivity, which indicates the change rates, is a low value for all methods. Regardless, the proposed method has the best performance considering all the accuracy indices.
The confusion matrices in CD using different methods over the Hyperspectral-River dataset are illustrated in Figure 17. As can be seen, the performance of the CD method respect to no-change pixels is better than change pixels. All methods had high performance compared to those obtained for the multispectral dataset. These results show that the spectral information can affect the performance of CD algorithms.
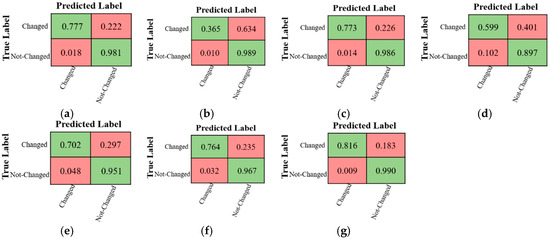
Figure 17.
The confusion matrices of different CD methods for the Hyperspectral-River dataset. (a) CVA-SVM, (b) MAD-SVM, (c) PCA-SVM, (d) IR-MAD -SVM, (e) SFA-SVM, (f) 3D-CNN, and (g) Proposed Method.
4.3.2. Hyperspectral-Farmland Data
In the Hyperspectral-Farmland dataset, there are more uniform land cover change areas than in the previous datasets. Based on the results of the CD for these datasets (see Figure 18), all methods correctly detected the main changes (i.e., circle areas). The visual analysis shows that the main differences between CD methods originate from the changes on the edge of the river and several small agriculture regions. In general, the MAD CD method (Figure 18b) has the poorest performance, followed by the SFA (Figure 18e). Finally, the best performance is observed for the CD method proposed in this study.


Figure 18.
The change detection maps of different methods for the Hyperspectral-Farmland dataset. (a) CVA-SVM, (b) MAD-SVM, (c) PCA-SVM, (d) IR-MAD -SVM, (e) SFA-SVM, (f) 3D-CNN, (g) Proposed Method, and (h) Ground Truth. White and black colors indicate the change and no-change areas, respectively.
The change detection errors using different CD methods for the Hyperspectral-Farmland datasets are demonstrated in Figure 19. As is clear, the main error of all CD methods originated from the edge of the river within the study area. Furthermore, the FN pixels are considerably more than the FP pixels and, thus, the FP pixels is very low. Among the CD methods, the MAD algorithm has the highest FN and FP pixels and several obvious changes are not detected by this method. Overall, the proposed method (Figure 19g) has the lowest MD rate compared to other methods.

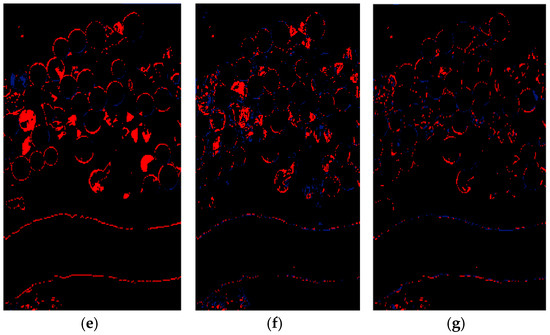
Figure 19.
The error in change detection maps obtained by different methods for the Hyperspectral-Farmland dataset. (a) CVA-SVM, (b) MAD-SVM, (c) PCA-SVM, (d) IR-MAD -SVM, (e) SFA-SVM, (f) 3D-CNN, and (g) Proposed Method. Black, red, and blue colors indicate TP and TN, FN, and FP pixels, respectively.
The evaluation metrics obtained from different CD methods for the Hyperspectral-Farmland dataset are provided in Table 11. The OAs of all methods are more than 91% excluding the MAD algorithm. Based on the results, most indices were improved compared to the case where the Hyperspectral-River dataset is used. The performance of the PCA and the proposed CD method are very close, although the former has a lower FA and higher Precision and Specificity compared to the proposed method. Since the Specificity and Precision of PCA are more than that of the proposed method and, also, the Sensitivity of the proposed method is more than PCA, the PCA tends to detect change pixels as no-change pixels that do not detect some change pixels. Overall, the proposed method has the highest OA, Sensitivity, KC, F1-Score, and lowest MD rate.

Table 11.
The accuracy of the different change detection methods applied to the Hyperspectral-Farmland dataset (the best performance for each method appears in bold).
The confusion matrices of CD using different methods over the Hyperspectral-Farmland dataset are demonstrated in Figure 20. Based on the results, the performance of the CD methods in detecting change pixels has the same trend as other datasets. The performance of detecting change pixels are lower than that of the no-change pixels. However, this issue for the Hyperspectral-Farmland dataset is less serious compared to other datasets.
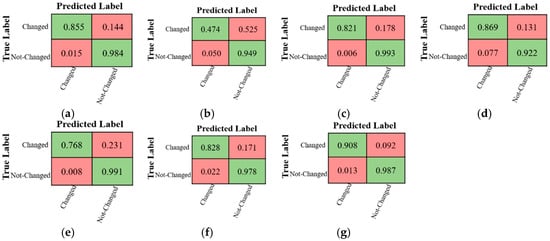
Figure 20.
The confusion matrices of different CD methods for the Hyperspectral-Farmland dataset. (a) CVA-SVM, (b) MAD-SVM, (c) PCA-SVM, (d) IR-MAD -SVM, (e) SFA-SVM, (f) 3D-CNN, and (g) Proposed Method.
4.4. CD of Polarimetric Datasets
4.4.1. PolSAR-San Francisco-1 Data
The results of the CD methods applied to the PolSAR-San Francisco1 dataset are presented in Figure 21. The CAV, MAD, PCA, and IR-MAD algorithms are sensitive to noise and therefore provided noisy results. Furthermore, these methods fail to detect several change areas in the image. The SFA, 3D-CNN, and the proposed methods provide promising results without noisy pixels. However, among these three methods, the IR-MAD method has the highest MD rate. Overall, the proposed method (Figure 21g) detects the changes with the highest accuracy.

Figure 21.
The change detection maps of different methods for the PolSAR-San Francisco1 dataset. (a) CVA-SVM, (b) MAD-SVM, (c) PCA-SVM, (d) IR-MAD -SVM, (e) SFA-SVM, (f) 3D-CNN, (g) Proposed Method, and (h) Ground Truth. White and black colors indicate the change and no-change areas, respectively.
Figure 22 shows the error of different CD methods for the PolSAR-San Francisco1 dataset. It is clear that most of the CD methods are unable to detect the main changes and have high FN pixels. This theme is evident in two large regions of the image that contain the main changes. Overall, the proposed CD method had the lowest error pixels.

Figure 22.
The errors in change detection of different methods for the PolSAR-San Francisco1 dataset. (a) CVA-SVM, (b) MAD-SVM, (c) PCA-SVM, (d) IR-MAD -SVM, (e) SFA-SVM, (f) 3D-CNN, and (g) Proposed Method. Black, red, and blue colors indicate TN and TP, FN, and FP pixels, respectively.
Based on statistical accuracy assessment using different indices for the PolSAR-San Francisco-1 data (see Table 12), all of the CD methods have OA over 91%. Moreover, the Precision, Sensitivity, and F1-Score values are generally more than 95%. The FA of CD methods is also significantly higher compared to their respective MDs. Overall, the proposed method provides the highest accuracy and lowest error.

Table 12.
The accuracy of different change detection methods for the PolSAR-San Francisco1 dataset (the best performance for each method appears in bold).
The confusion matrices in CD using different methods for the PolSAR-San Francisco1 dataset are demonstrated in Figure 23. All methods have high performance in detecting no-change pixels. For example, the accuracy is more than 96%. Although detecting change pixels by most of the CD methods is a challenge, the proposed method has better performance in this regard.
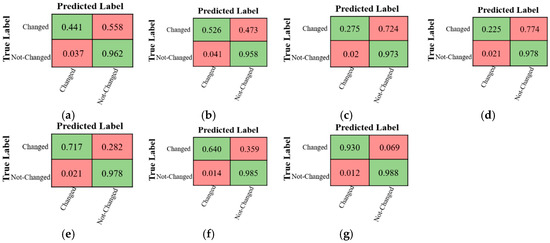
Figure 23.
The confusion matrices of different CD methods for the PolSAR-San Francisco1 dataset. (a) CVA-SVM, (b) MAD-SVM, (c) PCA-SVM, (d) IR-MAD -SVM, (e) SFA-SVM, (f) 3D-CNN, and (g) Proposed Method.
4.4.2. PolSAR-San Francisco-2 Data
The results of the different CD methods applied to the PolSAR-San Francisco-2 datasets are illustrated in Figure 24. The results are generally similar to those of the PolSAR-San Francisco-1 dataset. All CD methods are unable to detect the main changes, but their results contain low noise compared to the PolSAR-San Francisco-1 dataset. The CVA and the proposed CD methods have the lowest and highest accuracies, respectively.

Figure 24.
The change detection maps of different methods for the PolSAR-San Francisco2 dataset. (a) CVA-SVM, (b) MAD-SVM, (c) PCA-SVM, (d) IR-MAD -SVM, (e) SFA-SVM, (f) 3D-CNN, (g) Proposed Method, and (h) Ground Truth. White and black colors indicate the change and no-change areas, respectively.
The performances of the CD methods for the PolSAR-San Francisco2 dataset in terms of FP and FN pixels are presented in Figure 25. Based on the visual comparison, the FN pixels are generally higher than FP pixels. CNN based methods performed better compared to other CD methods. The 3D-CNN CD has low FP pixels and significantly high FN pixels. The error of the proposed method is mainly related to the edge of the changed objects. Moreover, the proposed method contains lower noise compared to the other CD methods.

Figure 25.
The errors in change detection using different methods for the PolSAR- Francisco2 dataset. (a) CVA-SVM, (b) MAD-SVM, (c) PCA-SVM, (d) IR-MAD -SVM, (e) SFA-SVM, (f) 3D-CNN, and (g) Proposed Method. Black, red, and blue colors indicate TP and TN, FN, and FP pixels, respectively.
The results of the different evaluation metrics for the CD methods applied to the PolSAR-San Francisco2 dataset are provided in Table 13. Their performance is generally lower compared to those when they were applied to the PolSAR-San Francisco1 dataset. In this dataset, however, the CVA method has the lowest FA rate and the highest Specificity value but it has poor performance in detecting change pixels. Moreover, the 3D-CNN has a high Precision value compared to the proposed method. Overall, the proposed method has the highest performance considering the values of the F1-Score, Sensitivity, BA, KC, and MD rates indices. The lowest MD rate is also related to the proposed method, while other methods have considerably higher MD rates. Finally, the KC for the proposed method is significantly higher than those of other CD methods.

Table 13.
The accuracy of different change detection methods for the PolSAR-San Francisco2 dataset (the best performance for each method appears in bold).
The confusion matrices in CD using different methods for the PolSAR-San Francisco2 dataset are illustrated in Figure 26. As can be seen, most of the CD methods have low performance in detecting change pixels compared to no-change pixels.
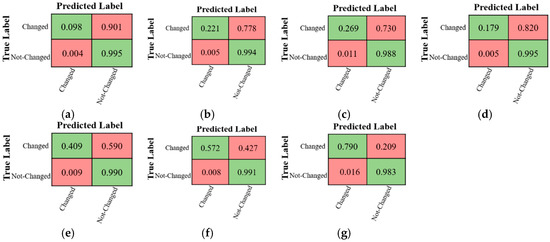
Figure 26.
The confusion matrices of different CD methods for the PolSAR-San Francisco2 dataset. (a) CVA-SVM, (b) MAD-SVM, (c) PCA-SVM, (d) IR-MAD -SVM, (e) SFA-SVM, (f) 3D-CNN, and (g) Proposed Method.
5. Discussion
In this section, the advantages of the proposed method are compared to other CD methods in terms of various factors, including accuracy, complexity, and diversity of classes, training data, and parameter setting, and its End-to-End framework.
5.1. Experimental Setup
The performance of the proposed method was evaluated using three different types of remote sensing datasets (i.e., multispectral, hyperspectral, and PolSAR). Based on the results presented in Figure 9, Figure 10, Figure 11, Figure 12, Figure 13, Figure 14, Figure 15, Figure 16, Figure 17, Figure 18, Figure 19 and Figure 20 and statistical accuracy assessments provided in Table 8, Table 9, Table 10, Table 11, Table 12 and Table 13, the proposed method has generally the best performance considering all types of datasets and accuracy indices. The proposed method maintains its high performance for different types of remote sensing datasets, indicating its robustness to all datasets. This fact is important because most statistics perform differently depending on the type of dataset and there is usually high variation between the results. Most of the CD methods have low performance in detecting change pixels. In other words, the poor value of some indices such as Precision, KC, and Sensitivity originated from the low performance of the CD algorithms in detecting change pixels. Furthermore, this increased the MD rate, which is reflected in all numerical values provided in Table 8, Table 9, Table 10, Table 11, Table 12 and Table 13. The CD methods have a reasonable performance in detecting no-change pixels, resulting in high OA, Specificity, F1-Score, and Precision values. Therefore, the FA rate is very low for most of the CD methods. The BA is a metric for evaluating the accuracy of the CD methods because it considers both change and no-change pixels. Sensitivity is a metric that is defined based on the number of TP pixels. Thus, the low value of this metric originated from the weak performance of the CD method in detecting change areas. The MD and Sensitivity is investigated the change pixels and their errors. Therefore, the high MD shows the method has low performance in detecting change pixels that led to low Sensitivity.
Multispectral imagery contains lower spectral bands compared to hyperspectral imagery, which causes difficulties in detecting changes in similar objects. The results presented in Figure 9, Figure 10, Figure 11, Figure 12, Figure 13 and Figure 14 and in Table 8 and Table 9 show that the accuracy of CD by the statistical methods is significantly low, the main reason for which is the low spectral information in the imagery. However, the proposed method compensates for this deficiency by utilizing both spatial and spectral features. This can be observed for the Multispectral-Abudhabi dataset.
Based on Table 11 and Figure 18, Figure 19 and Figure 20, although most of the CD methods are compared with the proposed method for the Hyperspectral-Farmland dataset, they differ in their abilities to detect subtle changes. Furthermore, based on the results for the Hyperspectral-River dataset, the proposed method has considerably higher performance compared to the other CD methods. The difference between the results of the proposed method and those of the other CD methods mainly relates to changes in water bodies. Water bodies contain low reflectance and the occurrence of high evaporation and fog over water areas usually causes a negative effect on spectral response. This issue decreased accuracies of all hyperspectral CD methods, except the proposed method when hyperspectral datasets are utilized. Finally, although hyperspectral imagery contains a high amount of spectral information, thus facilitating change detection, utilizing spatial information should also further improve accuracy. This is evident when the more accurate results of the proposed method and 3D-CNN are compared with those of the other methods.
As illustrated, the accuracy of the 3D-CNN method was lower than that of the proposed CD method when hyperspectral imagery was used. This can originate from two factors: (1) 3D-CNN algorithm requires a robust predictor, and (2) 3D-CNN algorithm only uses a 3D convolution and, thus, cannot provide excellent performance. The hybrid convolution can improve accuracy [40].
PolSAR datasets are another type of remote sensing imagery that is widely utilized in LCLU CD because they have several advantages. However, the PolSAR data suffer from speckle noise, and interpretation is difficult due to the special physics of PolSAR data compared to other kinds of remote sensing data which makes CD challenges. As illustrated in Figure 21, Figure 22, Figure 23, Figure 24, Figure 25 and Figure 26, CD in PolSAR data using the statistical CD methods is relatively difficult. However, the proposed method proved to be robust and accurate. The performance of CD methods is more evident on the PolSAR-Francisco2 dataset that more methods have high FN pixels. However, the PolSAR data has significant speckle noise but we expect the CD methods to handle this issue and provide a change map with minimum noise. The presented CD results in Figure 21 and Figure 22 of the PolSAR-Francisco1 dataset show the speckle noise cannot be controlled by statistical CD methods while the proposed method can also be handled.
Table 14 provides the best accuracies obtained for the hyperspectral datasets. The proposed method in [29] was evaluated by Hyperspectral-River dataset and the OA of 95% was reported. However, the proposed method results in an accuracy of 97% for the same dataset and similar conditions. Additionally, the Hyperspectral-Farmland dataset was used in [3] and an OA of 92% was obtained. However, the proposed method provided an OA of 97% for this dataset.

Table 14.
Comparison between the accuracies of the CD methods for CD in the Hyperspectral datasets (italic characters are the name of datasets).
The PolSAR datasets were utilized in [38,42], in which the highest OAs were 96%, and 97% for the PolSAR-Francisco1 and PolSAR-Francisco2 datasets, respectively (Table 15). Although these CD methods provided promising results in terms of OA, they utilized ground truth data for the selection of the threshold selection, making them less applicable to most of the studies.

Table 15.
Comparison between the accuracies of the CD methods for CD in the PolSAR datasets (italic characters are the name of datasets).
Based on the results, the proposed method has higher accuracy compared to the 3D-CNN and other CD methods. This is because (1) it uses multi-dimensional kernel convolution to improve the capability of the extraction type of deep features and (2) it does not need a predictor. However, the 3D-CNN and other CD methods need a predictor, which can negatively affect the CD results. Thus, the proposed method can effectively separate change and no-change pixels without any predictor.
5.2. Complexity and Diversity of Classes
One of the limitations of traditional CD methods is their low accuracy when the LCLU classes are complex and diverse. For this purpose, the multispectral dataset was implemented to evaluate the complexity of objects for CD. In this case, the change areas were related not only to built-up areas, but there were also many non-target change areas, such as farmland. It is evident that if object diversity was low, more methods provide good results, but they perform poorly when object diversity is high. In this case, the model should be deeply learned not only based on the unique characteristics of changes but also based on the structure of changed objects. Based on the presented results in this study, the proposed method can effectively handle this issue by extraction suitable deep features.
5.3. Training Data and Parameter Setting
The supervised CD methods require large amounts of training data to provide high accuracy. For example, when the deep learning algorithm and SVM classifier are used with the same amount of training data, they provide different results. Thus, the performance of the supervised CD methods depends on the size of the training dataset. The performance of these methods originated from two main factors: potential predictor and performance thresholding method. Generally, a weak predictor results in low accuracy even using a robust classifier. It should be noted that an accurate CD requires both a robust predictor and a classifier.
Recently, several automatic CD frameworks have been proposed [28,76,77]. Mainly, these methods employ the CVA, PCA, and thresholding methods for pseudo sample generation. However, based on the results of the CD by the CVA and PCA obtained in this study, these types of CD frameworks do not generate high-confidence training samples. Training a classifier using the low-confidence training sample leads to weak results. Finally, although unsupervised change detection methods require parameter setting, tuning these parameters is sometimes time-consuming.
5.4. Spatial and Spectral Features
Several studies have argued that incorporating spatial information can improve the result of CD [18,43,47,78,79,80]. The generation of suitable spatial features is one of the main challenges in this regard [79,80,81]. However, this is not a challenge for deep learning CD methods because they automatically employ both spatial and spectral features. This is one of the main reasons that deep learning CD methods have higher accuracies and are more robust compared to other CD methods.
One of the main differences of the proposed method compared to other CD architecture, such as the Siamese neural network, is using multi-dimensional convolution filters. The use of multi-dimensional convolution instead of single convolution can potentially improve the performance of CNN-based CD methods. To clarify this fact, the proposed method was compared to the 3D-CNN method, and it is observed that the proposed method has a better performance.
5.5. End-to-End Framework
Most remote sensing CD frameworks contain two main phases, although these frameworks have several limitations. First, their accuracy depends on the potential of the predictor and classifier. Consequently, both predictor and classifier algorithms must perform well to obtain high accuracy; however, improving both is a challenging task. Second, implementing and applying these two-phase frameworks for practical applications is time-consuming, and requires high computation, especially over large areas. While some CNN-based CD methods require pre-processing steps or predictors [29,32], one of the most important advantages of the proposed method is its End-to-End framework. The advantage of the proposed method in this regard is that it is not negatively impacted by other factors (e.g., the effect of predictor phase, informative features extraction, or classifier) and the accuracy of the CD only depends on the performance of the proposed architecture. Identifying components with the highest information content is also a substantial challenge for some of the statistical CD methods, such as MAD, IR-MAD, and SFA, causing these processes to be time-consuming. However, the proposed deep learning method. The main difference of its CD architecture network is related to how deep features are used for CD. There are usually two approaches for End-to-End CD methods: staking and differencing of deep features. The proposed method utilizes the advantages of both to improve the level of accuracy.
6. Conclusions and Future Work
In this study, a novel End-to-End framework based on deep learning was proposed for CD in remote sensing datasets. The proposed method utilizes a multi-dimensional convolution layer framework. Furthermore, the proposed method utilizes the benefits of both staking and differencing deep features. The performance of the proposed method was evaluated using three different types of remote sensing datasets. Moreover, the results of the proposed method were compared to other state-of-the-art CD methods. Both visual and statistical accuracy assessments show that the proposed method has the best performance for all the RS datasets and different study areas. Regarding hyperspectral datasets, although most of the CD methods provide acceptable results, their accuracies are lower compared to those of the method proposed in this study. The difference between the accuracies of the proposed method and other CD algorithms are more obvious in multispectral datasets due to the limited spectral information. In this regard, the proposed method can extract the changes information from a few spectral bands. The PolSAR datasets are considerably different from the two aforementioned datasets. The main challenge in CD in PolSAR datasets is the presence of speckle noise. It was observed that the statistical CD methods cannot identify changes in PolSAR data, however, the deep learning methods have relatively better performance. Most change detection methods have a reasonable performance in detecting no-change pixels. However, there were several challenges in detecting change pixels. Overall, the proposed CD method has good performance in detecting both change and no-change pixels. In summary, the proposed method has many advantages compared to other CD algorithms including (1) it provides higher accuracy compared to other state-of-the-art CD methods, (2) it is robust against noise and complex changed objects, (3) its End-to-End framework does not require pre-processing, (4) it is accurate for different types of remote sensing datasets with different characteristics, and (5) it has high generalization capabilities due to its excellent performance on different types of RS datasets over various study areas. It is expected that using a combination of multiple types of remote sensing datasets can improve the performance of the proposed CD method. Thus, future studies will investigate the performance of the proposed CNN-based CD method when a fusion of multi-source datasets is utilized.
Author Contributions
S.T.S. and M.H. did preprocess and prepare datasets. S.T.S., M.H. and M.A. designed modeling concepts and implemented change detection process. S.T.S., M.H. and M.A. wrote and checked the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Acknowledgments
We thank Rodrigo Caye Daudt, a Ph.D. student at ONERA and Télécom ParisTech, for providing a multispectral change detection dataset. We also would like to thank all the developers of Keras for providing such powerful frameworks.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Peduzzi, P. The Disaster Risk, Global Change, and Sustainability Nexus. Sustainability 2019, 11, 957. [Google Scholar] [CrossRef]
- Mahdavi, S.; Salehi, B.; Huang, W.; Amani, M.; Brisco, B. A PolSAR Change Detection Index Based on Neighborhood Information for Flood Mapping. Remote Sens. 2019, 11, 1854. [Google Scholar] [CrossRef]
- Hasanlou, M.; Seydi, S.T.; Shah-Hosseini, R. A Sub-Pixel Multiple Change Detection Approach for Hyperspectral Imagery. Can. J. Remote Sens. 2018, 44, 601–615. [Google Scholar] [CrossRef]
- Wang, M.; Tan, K.; Jia, X.; Wang, X.; Chen, Y. A Deep Siamese Network with Hybrid Convolutional Feature Extraction Module for Change Detection Based on Multi-sensor Remote Sensing Images. Remote Sens. 2020, 12, 205. [Google Scholar] [CrossRef]
- Zhang, Y.; Kerle, N. Satellite remote sensing for near-real time data collection. In Geospatial Information Technology for Emergency Response; CRC Press: Boca Raton, FL, USA, 2008; pp. 91–118. [Google Scholar]
- Liu, S.; Zheng, Y.; Dalponte, M.; Tong, X. A novel fire index-based burned area change detection approach using Landsat-8 OLI data. Eur. J. Remote Sens. 2020, 53, 104–112. [Google Scholar] [CrossRef]
- Demir, B.; Bovolo, F.; Bruzzone, L. Updating land-cover maps by classification of image time series: A novel change-detection-driven transfer learning approach. IEEE Trans. Geosci. Remote Sens. 2012, 51, 300–312. [Google Scholar] [CrossRef]
- Leichtle, T. Change Detection for Application in Urban Geography based on Very High Resolution Remote Sensing. Ph.D. Thesis, Humboldt-Universität zu Berlin, Berlin, Germany, 2020. [Google Scholar]
- Saha, S.; Bovolo, F.; Bruzzone, L. Unsupervised deep change vector analysis for multiple-change detection in VHR images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3677–3693. [Google Scholar] [CrossRef]
- López-Fandiño, J.; Heras, D.B.; Argüello, F.; Dalla Mura, M. GPU framework for change detection in multitemporal hyperspectral images. Int. J. Parallel Program. 2019, 47, 272–292. [Google Scholar] [CrossRef]
- Parikh, H.; Patel, S.; Patel, V. Classification of SAR and PolSAR images using deep learning: A review. Int. J. Image Data Fusion 2020, 11, 1–32. [Google Scholar] [CrossRef]
- Carranza-García, M.; García-Gutiérrez, J.; Riquelme, J.C. A framework for evaluating land use and land cover classification using convolutional neural networks. Remote Sens. 2019, 11, 274. [Google Scholar] [CrossRef]
- Liu, F.; Jiao, L.; Tang, X.; Yang, S.; Ma, W.; Hou, B. Local restricted convolutional neural network for change detection in polarimetric SAR images. IEEE Trans. Neural Netw. Learn. Syst. 2018, 30, 818–833. [Google Scholar] [CrossRef] [PubMed]
- Kwan, C. Methods and Challenges Using Multispectral and Hyperspectral Images for Practical Change Detection Applications. Information 2019, 10, 353. [Google Scholar] [CrossRef]
- Wu, C.; Du, B.; Zhang, L. Slow feature analysis for change detection in multispectral imagery. IEEE Trans. Geosci. Remote Sens. 2013, 52, 2858–2874. [Google Scholar] [CrossRef]
- Wu, S.; Bai, Y.; Chen, H. Change detection methods based on low-rank sparse representation for multi-temporal remote sensing imagery. Clust. Comput. 2019, 22, 9951–9966. [Google Scholar] [CrossRef]
- Chen, Z.; Leng, X.; Lei, L. Multiple features fusion change detection method based on Two-Level Clustering. In Proceedings of the 2019 International Conference on Robotics, Intelligent Control and Artificial Intelligence, Shanghai, China, 20–22 September 2019; pp. 159–165. [Google Scholar]
- Zhang, W.; Lu, X. The spectral-spatial joint learning for change detection in multispectral imagery. Remote Sens. 2019, 11, 240. [Google Scholar] [CrossRef]
- Papadomanolaki, M.; Verma, S.; Vakalopoulou, M.; Gupta, S.; Karantzalos, K. Detecting urban changes with recurrent neural networks from multitemporal Sentinel-2 data. In Proceedings of the IGARSS 2019—2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 28 July–2 August 2019; pp. 214–217. [Google Scholar]
- Lv, Z.Y.; Liu, T.F.; Zhang, P.; Benediktsson, J.A.; Lei, T.; Zhang, X. Novel adaptive histogram trend similarity approach for land cover change detection by using bitemporal very-high-resolution remote sensing images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9554–9574. [Google Scholar] [CrossRef]
- Du, P.; Wang, X.; Chen, D.; Liu, S.; Lin, C.; Meng, Y. An improved change detection approach using tri-temporal logic-verified change vector analysis. ISPRS J. Photogramm. Remote Sens. 2020, 161, 278–293. [Google Scholar] [CrossRef]
- Liu, S.; Marinelli, D.; Bruzzone, L.; Bovolo, F. A review of change detection in multitemporal hyperspectral images: Current techniques, applications, and challenges. IEEE Geosci. Remote Sens. Mag. 2019, 7, 140–158. [Google Scholar] [CrossRef]
- Nielsen, A.A.; Conradsen, K.; Simpson, J.J. Multivariate alteration detection (MAD) and MAF postprocessing in multispectral, bitemporal image data: New approaches to change detection studies. Remote Sens. Environ. 1998, 64, 1–19. [Google Scholar] [CrossRef]
- Wu, C.; Du, B.; Zhang, L. A subspace-based change detection method for hyperspectral images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 815–830. [Google Scholar] [CrossRef]
- Yuan, Y.; Lv, H.; Lu, X. Semi-supervised change detection method for multi-temporal hyperspectral images. Neurocomputing 2015, 148, 363–375. [Google Scholar] [CrossRef]
- Liu, S.; Bruzzone, L.; Bovolo, F.; Du, P. Unsupervised multitemporal spectral unmixing for detecting multiple changes in hyperspectral images. IEEE Trans. Geosci. Remote Sens. 2016, 54, 2733–2748. [Google Scholar] [CrossRef]
- Wang, B.; Choi, S.-K.; Han, Y.-K.; Lee, S.-K.; Choi, J.-W. Application of IR-MAD using synthetically fused images for change detection in hyperspectral data. Remote Sens. Lett. 2015, 6, 578–586. [Google Scholar] [CrossRef]
- Song, A.; Choi, J.; Han, Y.; Kim, Y. Change detection in hyperspectral images using recurrent 3D fully convolutional networks. Remote Sens. 2018, 10, 1827. [Google Scholar] [CrossRef]
- Wang, Q.; Yuan, Z.; Du, Q.; Li, X. GETNET: A general end-to-end 2-D CNN framework for hyperspectral image change detection. IEEE Trans. Geosci. Remote Sens. 2018, 57, 3–13. [Google Scholar] [CrossRef]
- Marinelli, D.; Bovolo, F.; Bruzzone, L. A novel change detection method for multitemporal hyperspectral images based on binary hyperspectral change vectors. IEEE Trans. Geosci. Remote Sens. 2019, 57, 4913–4928. [Google Scholar] [CrossRef]
- Li, X.; Yuan, Z.; Wang, Q. Unsupervised deep noise modeling for hyperspectral image change detection. Remote Sens. 2019, 11, 258. [Google Scholar] [CrossRef]
- Seydi, S.T.; Hasanlou, M. Hperspectral change detection based on 3D covolution deep learning. In Proceedings of the International Society for Photogrammetry and Remote Sensing (ISPRS) Congress, Nice, France, 14–20 June 2020. [Google Scholar]
- Huang, F.; Yu, Y.; Feng, T. Hyperspectral remote sensing image change detection based on tensor and deep learning. J. Vis. Commun. Image Represent. 2019, 58, 233–244. [Google Scholar] [CrossRef]
- Slagter, B.; Tsendbazar, N.-E.; Vollrath, A.; Reiche, J. Mapping wetland characteristics using temporally dense Sentinel-1 and Sentinel-2 data: A case study in the St. Lucia wetlands, South Africa. Int. J. Appl. Earth Obs. Geoinf. 2020, 86, 102009. [Google Scholar] [CrossRef]
- Qi, Z.; Yeh, A.G.-O.; Li, X.; Zhang, X. A three-component method for timely detection of land cover changes using polarimetric SAR images. ISPRS J. Photogramm. Remote Sens. 2015, 107, 3–21. [Google Scholar] [CrossRef]
- Ghanbari, M.; Akbari, V. Unsupervised Change Detection in Polarimetric SAR Data with the Hotelling-Lawley Trace Statistic and Minimum-Error Thresholding. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 4551–4562. [Google Scholar] [CrossRef]
- Cui, B.; Zhang, Y.; Yan, L.; Wei, J.; Wu, H.a. An Unsupervised SAR Change Detection Method Based on Stochastic Subspace Ensemble Learning. Remote Sens. 2019, 11, 1314. [Google Scholar] [CrossRef]
- Najafi, A.; Hasanlou, M.; Akbari, V. Change detection using distance-based algorithms between synthetic aperture radar polarimetric decompositions. Int. J. Remote Sens. 2019, 40, 6084–6097. [Google Scholar] [CrossRef]
- Zhao, J.; Chang, Y.; Yang, J.; Niu, Y.; Lu, Z.; Li, P. A Novel Change Detection Method Based on Statistical Distribution Characteristics Using Multi-Temporal PolSAR Data. Sensors 2020, 20, 1508. [Google Scholar] [CrossRef] [PubMed]
- Roy, S.K.; Krishna, G.; Dubey, S.R.; Chaudhuri, B.B. Hybridsn: Exploring 3-d-2-d cnn feature hierarchy for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2019, 17, 277–281. [Google Scholar] [CrossRef]
- Daudt, R.C.; Le Saux, B.; Boulch, A.; Gousseau, Y. Urban change detection for multispectral earth observation using convolutional neural networks. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 2115–2118. [Google Scholar]
- Seydi, S.T.; Shahhoseini, R. Transformation Based Algorithms for Change Detection in Full Polarimetric Remote Sensing Images. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, 42, 963–967. [Google Scholar] [CrossRef]
- Hu, W.-S.; Li, H.-C.; Pan, L.; Li, W.; Tao, R.; Du, Q. Feature extraction and classification based on spatial-spectral convlstm neural network for hyperspectral images. arXiv 2019, arXiv:1905.03577. [Google Scholar]
- Daudt, R.C.; Le Saux, B.; Boulch, A. Fully convolutional siamese networks for change detection. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; pp. 4063–4067. [Google Scholar]
- Yamashita, R.; Nishio, M.; Do, R.K.G.; Togashi, K. Convolutional neural networks: An overview and application in radiology. Insights Imaging 2018, 9, 611–629. [Google Scholar] [CrossRef]
- Ji, S.; Zhang, C.; Xu, A.; Shi, Y.; Duan, Y. 3D convolutional neural networks for crop classification with multi-temporal remote sensing images. Remote Sens. 2018, 10, 75. [Google Scholar] [CrossRef]
- Feng, F.; Wang, S.; Wang, C.; Zhang, J. Learning Deep Hierarchical Spatial–Spectral Features for Hyperspectral Image Classification Based on Residual 3D-2D CNN. Sensors 2019, 19, 5276. [Google Scholar] [CrossRef]
- Du, J.; Wang, L.; Liu, Y.; Zhou, Z.; He, Z.; Jia, Y. Brain MRI Super-Resolution Using 3D Dilated Convolutional Encoder–Decoder Network. IEEE Access 2020, 8, 18938–18950. [Google Scholar] [CrossRef]
- Chen, C.; Liu, X.; Ding, M.; Zheng, J.; Li, J. 3D dilated multi-fiber network for real-time brain tumor segmentation in mri. In Proceedings of the International Conference on Medical Image Computing and Computer-Assisted Intervention, Shenzhen, China, 13–17 October 2019; pp. 184–192. [Google Scholar]
- Hu, Z.; Hu, Y.; Liu, J.; Wu, B.; Han, D.; Kurfess, T. 3D separable convolutional neural network for dynamic hand gesture recognition. Neurocomputing 2018, 318, 151–161. [Google Scholar] [CrossRef]
- Kiranyaz, S.; Avci, O.; Abdeljaber, O.; Ince, T.; Gabbouj, M.; Inman, D.J. 1D convolutional neural networks and applications: A survey. arXiv 2019, arXiv:1905.03554. [Google Scholar]
- Chen, X.; Kopsaftopoulos, F.; Wu, Q.; Ren, H.; Chang, F.-K. A Self-Adaptive 1D Convolutional Neural Network for Flight-State Identification. Sensors 2019, 19, 275. [Google Scholar] [CrossRef]
- Li, J.; Cui, R.; Li, B.; Song, R.; Li, Y.; Du, Q. Hyperspectral Image Super-Resolution with 1D–2D Attentional Convolutional Neural Network. Remote Sens. 2019, 11, 2859. [Google Scholar] [CrossRef]
- Eckle, K.; Schmidt-Hieber, J. A comparison of deep networks with ReLU activation function and linear spline-type methods. Neural Netw. 2019, 110, 232–242. [Google Scholar] [CrossRef]
- Agarap, A.F. Deep learning using rectified linear units (relu). arXiv 2018, arXiv:1803.08375. [Google Scholar]
- Chetouani, A.; Treuillet, S.; Exbrayat, M.; Jesset, S. Classification of engraved pottery sherds mixing deep-learning features by compact bilinear pooling. Pattern Recognit. Lett. 2020, 131, 1–7. [Google Scholar] [CrossRef]
- Christlein, V.; Spranger, L.; Seuret, M.; Nicolaou, A.; Král, P.; Maier, A. Deep Generalized Max Pooling. arXiv 2019, arXiv:1908.05040. [Google Scholar]
- Hussain, M.; Chen, D.; Cheng, A.; Wei, H.; Stanley, D. Change detection from remotely sensed images: From pixel-based to object-based approaches. ISPRS J. Photogramm. Remote Sens. 2013, 80, 91–106. [Google Scholar] [CrossRef]
- Alexandari, A.M.; Shrikumar, A.; Kundaje, A. Separable Fully Connected Layers Improve Deep Learning Models for Genomics. BioRxiv 2017, 146431. [Google Scholar]
- Kanai, S.; Fujiwara, Y.; Yamanaka, Y.; Adachi, S. Sigsoftmax: Reanalysis of the softmax bottleneck. In Proceedings of the Advances in Neural Information Processing Systems, Montréal, QC, Canada, 3–8 December 2018; pp. 286–296. [Google Scholar]
- Oland, A.; Bansal, A.; Dannenberg, R.B.; Raj, B. Be careful what you backpropagate: A case for linear output activations & gradient boosting. arXiv 2017, arXiv:1707.04199. [Google Scholar]
- Srivastava, N.; Hinton, G.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Li, Z.; Gong, B.; Yang, T. Improved dropout for shallow and deep learning. In Proceedings of the Advances in Neural Information Processing Systems, Barcelona, Spain, 9 December 2016; pp. 2523–2531. [Google Scholar]
- Qahtan, A.A.; Alharbi, B.; Wang, S.; Zhang, X. A pca-based change detection framework for multidimensional data streams: Change detection in multidimensional data streams. In Proceedings of the 21th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Sydney, Australia, 10–13 August 2015; pp. 935–944. [Google Scholar]
- Deng, J.; Wang, K.; Deng, Y.; Qi, G. PCA-based land-use change detection and analysis using multitemporal and multisensor satellite data. Int. J. Remote Sens. 2008, 29, 4823–4838. [Google Scholar] [CrossRef]
- Pirrone, D.; Bovolo, F.; Bruzzone, L. A Novel Framework Based on Polarimetric Change Vectors for Unsupervised Multiclass Change Detection in Dual-Pol Intensity SAR Images. IEEE Trans. Geosci. Remote Sens. 2020. [Google Scholar] [CrossRef]
- Hasanlou, M.; Seydi, S.T. Automatic change detection in remotely sensed hyperspectral imagery (Case study: Wetlands and waterbodies). Earth Obs. Geomat. Eng. 2018, 2, 9–25. [Google Scholar]
- Yekkehkhany, B.; Safari, A.; Homayouni, S.; Hasanlou, M. A comparison study of different kernel functions for SVM-based classification of multi-temporal polarimetry SAR data. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 40, 281. [Google Scholar] [CrossRef]
- Lameski, P.; Zdravevski, E.; Mingov, R.; Kulakov, A. SVM parameter tuning with grid search and its impact on reduction of model over-fitting. In Rough Sets, Fuzzy Sets, Data Mining, and Granular Computing; Springer: Cham, Switzerland, 2015; pp. 464–474. [Google Scholar]
- Kotsiantis, S.; Kanellopoulos, D.; Pintelas, P. Handling imbalanced datasets: A review. Gests Int. Trans. Comput. Sci. Eng. 2006, 30, 25–36. [Google Scholar]
- Lin, Z.; Hao, Z.; Yang, X.; Liu, X. Several SVM ensemble methods integrated with under-sampling for imbalanced data learning. In Proceedings of the International Conference on Advanced Data Mining and Applications, Beijing, China, 17–19 August 2009; pp. 536–544. [Google Scholar]
- Longadge, R.; Dongre, S. Class imbalance problem in data mining review. arXiv 2013, arXiv:1305.1707. [Google Scholar]
- Ramyachitra, D.; Manikandan, P. Imbalanced Dataset Classification and Solutions: A Review. 2014. Available online: https://www.semanticscholar.org/paper/IMBALANCED-DATASET-CLASSIFICATION-AND-SOLUTIONS-%3A-A-Ramyachitra-Manikandan/3e8ea23ec779f79c16f8f5402c5be2ef403fe8d3?citationIntent=background#citing-papers (accessed on 19 June 2020).
- Glorot, X.; Bengio, Y. Understanding the difficulty of training deep feedforward neural networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, 13–15 May 2010; pp. 249–256. [Google Scholar]
- Huang, W.; Song, G.; Li, M.; Hu, W.; Xie, K. Adaptive Weight Optimization for Classification of Imbalanced Data. In Proceedings of the International Conference on Intelligent Science and Big Data Engineering, Beijing, China, 31 July–2 August 2013; pp. 546–553. [Google Scholar]
- Shah-Hosseini, R.; Homayouni, S.; Safari, A. A hybrid kernel-based change detection method for remotely sensed data in a similarity space. Remote Sens. 2015, 7, 12829–12858. [Google Scholar] [CrossRef]
- Song, A.; Kim, Y. Transfer Change Rules from Recurrent Fully Convolutional Networks for Hyperspectral Unmanned Aerial Vehicle Images without Ground Truth Data. Remote Sens. 2020, 12, 1099. [Google Scholar] [CrossRef]
- Zhao, W.; Du, S. Spectral–spatial feature extraction for hyperspectral image classification: A dimension reduction and deep learning approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, Q.; Du, B.; Huang, X.; Tang, Y.Y.; Tao, D. Simultaneous spectral-spatial feature selection and extraction for hyperspectral images. IEEE Trans. Cybern. 2016, 48, 16–28. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Xiang, S.; Zhong, Z.; Ding, K.; Pan, C. Multicluster spatial–spectral unsupervised feature selection for hyperspectral image classification. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1660–1664. [Google Scholar]
- Solberg, A.S.; Jain, A.K. Texture fusion and feature selection applied to SAR imagery. IEEE Trans. Geosci. Remote Sens. 1997, 35, 475–479. [Google Scholar] [CrossRef]
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).