Abstract
Nowadays, the high rate GNSS (Global Navigation Satellite Systems) positioning methods are widely used as a complementary tool to other geotechnical sensors, such as accelerometers, seismometers, and inertial measurement units (IMU), to evaluate dynamic displacement responses of engineering structures. However, the most common problem in structural health monitoring (SHM) using GNSS is the presence of surrounding structures that cause multipath errors in GNSS observations. Skyscrapers and high-rise buildings in metropolitan cities are generally close to each other, and long-span bridges have towers, main cable, and suspender cables. Therefore, multipath error in GNSS observations, which is typically added to the measurement noise, is inevitable while monitoring such flexible engineering structures. Unlike other errors like atmospheric errors, which are mostly reduced or modeled out, multipath errors are the largest remaining unmanaged error sources. The high noise levels of high-rate GNSS solutions limit their structural monitoring application for detecting load-induced semi-static and dynamic displacements. This study investigates the estimation of accurate dynamic characteristics (frequency and amplitude) of structural or seismic motions derived from multipath-affected high-rate GNSS observations. To this end, a novel hybrid model using both wavelet-based multiscale principal component analysis (MSPCA) and wavelet transform (MSPCAW) is designed to extract the amplitude and frequency of both GNSS relative- and PPP- (Precise Point Positioning) derived displacement motions. To evaluate the method, a shaking table with a GNSS receiver attached to it, collecting 10 Hz data, was set up close to a building. The table was used to generate various amplitudes and frequencies of harmonic motions. In addition, 50-Hz linear variable differential transformer (LVDT) observations were collected to verify the MSMPCAW model by comparing their results. The results showed that the MSPCAW could be efficiently used to extract the dynamic characteristics of noisy dynamic movements under seismic loads. Furthermore, the dynamic behavior of seismic motions can be extracted accurately using GNSS-PPP, and its dominant frequency equals that extracted by LVDT and relative GNSS positioning method. Its accuracy in determining the amplitude approaches 91.5% relative to the LVDT observations.
1. Introduction
Recently, the relative and precise point positioning (PPP) GNSS techniques have been intensively developed and used in structural health monitoring and detection of crustal movement applications [1,2,3,4]. By using high-rate sampling, amplitudes and frequencies of strong movements can be accurately detected in the position and frequency domains. As the cost of the monitoring system is an important factor, many researchers evaluated the measurement accuracy of the PPP technique, which uses only one receiver, for estimating the dynamic properties of measurements compared to the relative GNSS technique, which uses two receivers and shows appropriate accuracy. In addition, the PPP results were compared to results from other instruments, such as accelerometers, seismometers, inertial measurement units (IMU), or linear variable differential transformers (LVDT). For example, Li [5] evaluated the accuracy of the PPP technique for monitoring seismic motion using an integration method and compared its results with accelerator measurements, and it was realized that a few centimeters accuracy could be obtained for the displacement waveforms and permanent coseismic offsets. In addition, the method can reliably recover the moment magnitude and fault slip distribution of the motion. Xu et al. [3] experimentally compared the accuracy of PPP for the detection of seismic motions to that by IMU measurements, and a small discrepancy was found between PPP and IMU displacements. Xu et al. [3] also found that PPP is capable of detecting seismic displacement at the same level as the relative GNSS method. Furthermore, Alcay et al. [1] compared PPP solutions with relative GNSS positioning considering different session lengths (24, 12, 8, 4, and 2 h) for monitoring permanent (static) displacement in the horizontal and vertical directions. The study showed that 24 to 8 h observation durations for both methods have high consistency in detecting actual displacement in the horizontal direction. The authors also demonstrated that the relative GNSS method is superior to PPP when the observation duration is less than 4 h. Moreover, Yigit et al. [2,6] experimentally evaluated the performance of high-rate GPS/GNSS PPP for capturing dynamic structural displacements in both the horizontal and vertical directions. The authors demonstrated that the high rate GNSS-PPP could be successfully used to capture dynamic responses of engineering structures and to estimate their dynamic characteristics. More evaluations for the GNSS-PPP method are presented in [7,8].
However, although previous studies accepted the accuracy of GNSS-PPP for estimating the dynamic components of motions, there is a lack of studies on the effect of multipath errors and observation noises on the results, as most of the PPP method testing was conducted in open sky areas [6,9,10]. The GNSS multipath errors and noises for static and dynamic movements are presented and discussed in [11,12,13], where the geometry of satellites and reflective surfaces are the main parameters affecting the multipath [14,15]. For vibration monitoring, multipath errors and GNSS observation noise are characterized by a frequency of less than 0.2 Hz [11,14,16]. These errors influence the accuracy of amplitude and frequency of measurements. For the high rate GNSS relative positioning solution, the multipath errors and measurement noise effects are evaluated and tested for the dynamic measurements [14,17]. However, the evaluation of the GNSS-PPP solution for seismic motions that are contaminated by multipath errors and dynamic noises is still limited. For the latter, results of previous studies showed that signal processing or filtering methods are a reliable tool to eliminate the observations errors and noises of vibration measurements [15,18].
The GNSS-derived displacements of seismic motions comprise three components of movements: static, semi-static, and dynamic movement components. The semi-static and dynamic components of movement are embodied in the time series of the apparent displacements, which comprises the movement (signal) components and noises in each coordinate direction after removing the mean of collected coordinates [19]. Accordingly, to extract the signal dynamic characteristics, the noises and semi-static (low frequency) components should be removed. On the other hand, the accelerometer and LVDT are widely used to estimate the frequency and amplitude of the vibration motions, respectively [20,21]. Therefore, both sensors are used to assess the accuracy of GNSS relative and PPP solutions [19,21].
The wavelet transform or wavelet analysis has been applied to extract the dynamic characteristics of structures movements and denoise GNSS results [22,23]. The wavelet transform and principal component analysis (PCA) can be integrated to estimate the semi-static movement component of GNSS observations [24,25], where theoretically, the PCA and wavelet are able to denoise low and high frequencies noises, respectively [24]. Bakshi [26] merged both methods to develop multiscale PCA (MSPCA) and reported its efficiency for the multivariate monitoring process. The drawback of MSPCA in GNSS denoising is that it considers only the correlation between the same coordinate components of different stations, whereas it ignores the correlation among different coordinate components as it is used for one-dimensional signals [24]. Therefore, Le et al. [24,25] introduced multiscale multiway PCA (MSMPCA) to overcome the MSPCA disadvantages for the GPS measurements. The MSPCA and MSMPCA were performed to extract the semi-static movement component for one-dimension (1D) and two-dimension (2D) measurements, respectively. Thus, they can be used to estimate time-series movement components as measured by GNSS positioning. In addition, the wavelet-based MSPCA and wavelet package PCA were developed to improve the denoising results of MSPCA [27,28], and this approach outperformed other methods to smooth one coordinate or 1D of GNSS-derived displacements [24]. More details on the wavelet-based MSPCA and MSMPCA can be found in [24,26].
The wavelet transform is a powerful tool that can be used to evaluate the use of GNSS derived-displacements for monitoring vibration behaviors [29]. It can be used to extract the movement components, whereas the wavelet can divide the frequencies of measurements into low and high frequencies [30]. In addition, it can be integrated with other smoothing methods to improve the denoising outputs of sensors’ measurements [31,32]. The energy of wavelet decompositions is the main parameter for signal denoising [33,34]. The analyzed signal can be decomposed into high and low wavelet energy components according to the oscillatory behavior of the signal components. Because the dynamic characteristic of the signals has a powerful energy component, the wavelet decomposition that has high energy comprises high-frequency contents and vice versa. Kaloop et al. [35] evaluated the acceleration measurements of buildings under seismic effects using wavelet power energy, and the authors concluded that the wavelet energy could be used to classify the frequency contents of building performances. Hussan et al. [36] utilized a wavelet transform to assess the use of GPS data for monitoring movements of a long-span bridge, and they showed that the high energy reflects the dominant frequencies components of the bridge movements. Further applications for wavelet analysis into dynamic evaluation can be found in [37,38].
In structural health monitoring (SHM) applications, selecting a favorable environment to reduce the reflections surrounding the GNSS receiver is quite limited. The most common problem in SHM is the structural element and the other structures surrounding the GNSS receiver attached to the engineering structure being monitored, as they cause noise and multipath errors in GNSS observations. Since high-rise buildings in metropolitan cities are close to each other, and long-span bridges have many cables, pylons, and passing vehicles, multipath error in GNSS observations is inevitable when monitoring such flexible structures. Therefore, this leads to a low signals-to-noise ratio of GNSS-derived displacement time series obtained from both the relative positioning and PPP solutions. The main objective of this study is to simulate such a real situation and to investigate the effectiveness and efficiency of the proposed denoising method for capturing mm-level displacements. For this purpose, a shaking table was set up near a building with reflective surfaces to collect noisy GNSS observations, including multipath. A 10° elevation cut-off angle was implemented when collecting the observations to exclude the satellites of low elevation angles during the experiment. The solution precision is not affected by only the number of satellites but also constrained by the spatial geometric distribution of these satellites [39]. A series of harmonic motions with various amplitudes and frequencies were generated by the shaking table. In addition to the GNSS system, the observations collected during the experiment from an LVDT attached to the table were treated as ground truth to validate the proposed denoising method. A hybrid method of wavelet-based MSPCA, wavelet transform (MSPCAW), with a novel filtration model for the dynamic component of GNSS, was designed and assessed to estimate the amplitude of a filtered displacement time series. Additionally, Fast Fourier transform (FFT) was used to extract the movements’ frequency. The study aims to:
(1) Evaluate dynamic noises, including those from multipath of GNSS measurements, that could contaminate monitoring the vibration behaviors of engineering structures under dynamic loads and wave-motions of the ground caused by an earthquake.
(2) Study the influence of wavelet energy of GNSS-derived displacement series to extract the dynamic characteristics of harmonic/seismic motions of structures.
(3) Assess the MSPCAW method for denoising high-rate relative- and PPP-derived displacement series for dynamic motions.
2. Materials and Methods
The wavelet-based MSPCA and wavelet transform are presented and evaluated for the use of GNSS in [22,24,25]. Herein, a summary of these methods is first presented. Wavelet transform is a powerful tool used to smooth GNSS derived-displacement components [40]. Lau [41], Mosavi et al. [42], and Yu et al. [43] utilized wavelet transform to extract the semi-static and dynamic components of GNSS measurements. The main advantage of wavelet transform is its ability to separate the signals based on frequency bands, which allows the extraction of the smoothed signal using these bands and by reconstruction of the signal [37]. In this study, the wavelet packet transforms (WPT) was used, which possesses further decomposition information of the signal in the high-frequency regions. The process of wavelet transform is presented in Lau [41] as follows.
(i) Transform the measurement to the wavelet domain using a wavelet mother transform:
The wavelet coefficients are generated from a mother wavelet scaling and translation. The standard wavelet transform can be expressed as [42]:
where, S(t) is the measured signals to be transformed at time t, ψ(t) is the mother wavelet, s is the dilation factor, and τ is the translation parameter, * symbolizes the complex conjugate. Wavelet, in general, should be defined on a compact set. The selection of the mother wavelet is dependent on the properties of the wavelet and its similarity with collected signals. In this study, Symlets 6 (Sym6) mother wavelet was selected because it can reduce the phase distortion in signal analysis and reconstruction [44], and it is suitable for the characteristics of GNSS measurements [24]. Figure 1a illustrates the scaling and function of the Sym6 wavelet. The symmetry of function reduces the phase distortion in signal analysis and reconstruction. In addition, the scale is used to normalize the signal energy at every scale, which produces a wavelet that possesses the same energy at every scale. Thus, the scale is used to represent the wavelet results in the columns of the time-scale plane. Hence, the signals that have a high energy can be detected. More details about utilizing the wavelet scale and function can be found in Merry and Steinbuch [45].
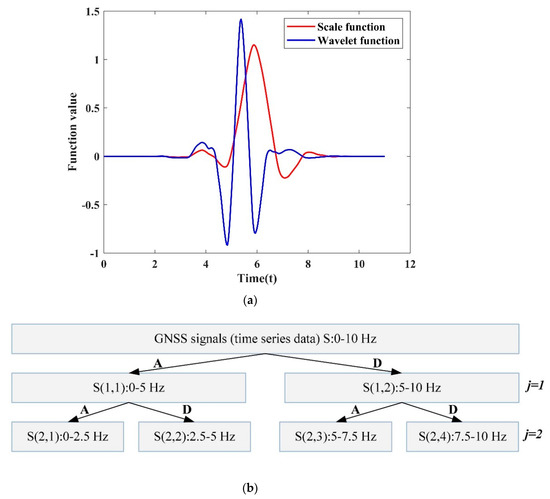
Figure 1.
(a) Scale and wavelet functions of Sym6, (b) two decomposition level of 10 Hz Global Navigation Satellite System (GNSS) results.
(ii) Decompose all wavelet coefficients using a design-level wavelet:
The original signal is decomposed into approximate (A) and detail (D) coefficients at each level designed. The decomposition of the signal based on WPT can be presented as follows [30]:
where n is the number of decomposition tree nodes, j denotes the jth decomposition level, and there will be 2j wavelet packet bases at the jth level. P is the parameter position, h(i) and g(i) represent the low (A components) and high (D components) passes filters of the signal, respectively. Here, the decomposition levels are selected based on the frequency range of wavelet decomposition, applying a threshold to remove the noise. As an example, Figure 1b shows a diagram of a two-level WPT of a GNSS signal (S) for a sampling frequency of 10 Hz.
(iii) Apply a threshold to remove the noise:
A threshold is used to remove the measurement noise by comparing the magnitude of signal decomposition with the threshold (λ). Hard, soft, and mid thresholding methods are utilized. The hard threshold, statistically investigated in Equation (4) [41], was selected in this study, as it is suitable for GNSS signals [24,41].
where m denotes the number of samples in the Gaussian distributed noise vector N.
(iv) Inverse the denoised wavelet coefficient to obtain the signal in its original domain:
The inverse transform is the reverse process of the direct transform presented for the given example in Figure 1b. This step reconstructs the denoised wavelet decompositions to estimate the denoised signals.
The wavelet-based MSPCA was defined as a wavelet decomposing method used to re-represent signals in a smooth shape. As mentioned above, the wavelet is used to separate low and high frequencies of the signals into wavelet decompositions that have approximate and detailed components. For smoothing, the GNSS results at static points, the approximate decomposition is only used to extract the point positioning. Similarly, when extracting the semi-static component of dynamic movements from GNSS observations, the approximate decomposition is only utilized. In the MSPCA, the PCA is used to select the useful detail and approximate decomposition of GNSS results. A reduced set of multichannel signals are proposed with a reduced set of principal components (PC). Additional matrices are proposed with all remaining number of PCs. After applying the multiscale matrices from A and D wavelet decompositions for MSPCA by calculating the covariance matrices from multiscale matrices of PCs and estimating the Eigen-decomposition of these matrices, the eigenvalues and eigenvectors are arranged for each matrix, and the PCs are selected for the chosen matrices. Finally, the mean of data removed from the GNSS data in the PCA space is transformed for denoising the signals based on the selection decompositions [24]. The smoothed signal is reconstructed from the selected detail and approximate decompositions.
The MSPCA steps that were used in the current study can be summarized as follows: (i) Transform the 2D data matrix of GNSS results (x and y coordinate directions) into a 1D signal (horizontal dynamic motion), which represents the dynamic motions. (ii) Apply j level of wavelet transform of the signal, which yields j + 1 matrices that include the D and A coefficients. (iii) For each level j, perform multiway PCA (MPCA) of the Dj and Aj + 1 matrices and select an approximate number of useful PC, respectively; (iv) reconstruct the signal using the inverse of wavelet transform. (v) Perform MPCA of the reconstructed signal to obtain the smoothed signal.
In this study, a hybrid of the two methods, denoted as MSPCAW (MSPCA and WPT), is used to estimate the dynamic characteristics of the vibration motions. MSPCAW is coded in the MATLAB 2016 software package. First, a comparison is conducted between the wavelet denoising and MSPCA to compare the performance of the two methods when applied in our case. From the evaluation, results showed that the performance of MSPCA is slightly better, as will be presented in the next sections. Therefore, the MSPCA is used to extract the semi-static components of the apparent displacement. The dynamic component of movements and noises, including multipath, which are characterized by a short-period movement component, can be presented by removing the semi-static component from the apparent displacements of movements. Previous studies showed that the energy of the wavelet power of GNSS derived-displacements and dynamic noises is small [11,14,20]. In this study, the energy percentage of wavelet components of the short-period component has been calculated to estimate a signal with a significant impact. Significant energy of wavelet decompositions of a short-period is considered and selected to build the dynamic movement component. Herein, the wavelet energy is used to extract the dynamic component of GNSS derived-displacements. The wavelet energy of the wavelet decomposition, which has a time interval [0 t], of the short-period component can be estimated as follows:
where E is the wavelet total energy, Sj is j decomposition level of short-period movement components; and n is the number of decomposition levels. Figure 2 illustrates the development model and processing. To evaluate the performance of MSPCAW in extracting the dynamic component, their results were compared with LVDT observations.
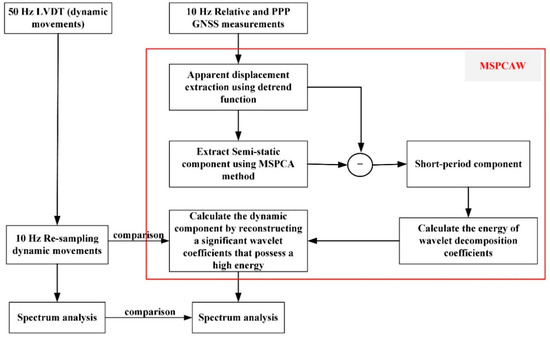
Figure 2.
Multiscale principal component analysis and wavelet transform (MSPCAW) model diagram and study process.
3. Test Description
This section describes the test performed to evaluate the proposed method and describes how GNSS data was processed.
3.1. Data Collection
For implementation and testing of the proposed method, a rover GNSS receiver/antenna was installed on a shaking table, which was placed near a building, as illustrated in Figure 3. The building façade consists of glass and metal, which are reflective surfaces, causing multipath for GNSS observations. The shaking table was set up about 8.30 m away from the long side of the building. The height and width of the building are 16.0 and 78.1 m, respectively. The height of the GNSS antenna from the ground is 0.7 m. The building also blocks signals from some satellites, which will result in a degraded satellite geometry with high PDOP values.
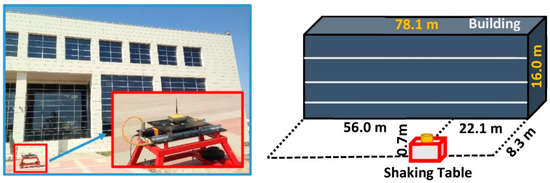
Figure 3.
Location of the shaking table with respect to the building.
The shaking table used in the experiments has a flat plate, where the GNSS receiver was mounted on. The movement of the shaking table is provided by an electric motor connected to this plate, and the stability of the table is maintained on a metal frame under high rate motions by placing weights on both sides of the platform. The position of the plate on the rails is controlled by software running on a Windows computer platform, where the control unit verifies the position using an LVDT, which measures the position of the table with mm accuracy at 50 Hz output rate. A large set of harmonic oscillations with different amplitudes and frequencies were generated. Four experiments with different harmonic oscillations were selected to evaluate the effectiveness of the filtered method used in this study. The frequency and amplitude of the selected events are 0.5 Hz/15 mm, 1 Hz/5 mm, 1 Hz/10 mm, and 1 Hz/15 mm denoted as events 1, 2, 3, and 4, respectively. Durations of sinusoidal oscillations are 100 s for event 1 and 50 s for the events 2, 3, and 4.
Two dual-frequency (L1 and L2) Topcon ™ HiPer-Pro GNSS receivers were used in this experiment. GPS and GLONASS observations were collected at a 10 Hz (0.1 s) sampling interval. A 10° elevation cut-off angle was used when collecting the observations from the satellites during the experiment. One GNSS receiver was mounted on the table, whereas the second receiver was installed approximately 100 m away from the rover at a known point, and it served as a base station for the relative positioning. The experiment was carried out on 17 September 2017 at the Gebze Technical University, Turkey. The experiment (GNSS session) lasted about 40 min. An average of 16 GPS and GLONASS satellites were observed at the base station, and 12 satellites were visible at the rover during the experiment. Figure 4 shows the sky-view of GNSS observations at both receivers. As can be seen, 4 satellites, 1 GPS, and 3 GLONASS were blocked by the building at the rover location.
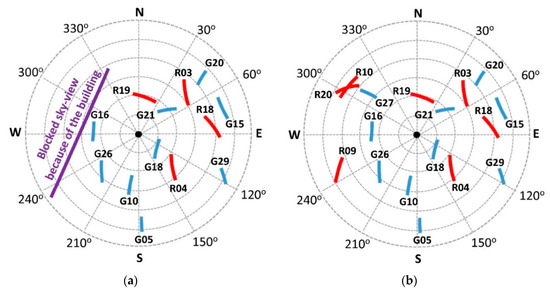
Figure 4.
Satellite sky-view at the rover (a) and the base station (b).
3.2. Multipath
In order to demonstrate multipath effects on satellite observations collected by the rover receiver, the GPS satellites on L1 frequency were analyzed as a representative example. Since the estimation of multipath of phase measurements is a complex process, only the multipath of code observations was analyzed [46]. The satellite-specific P-code (L1) pseudorange multipath pattern for visible GPS satellites traces were generated using TEQC software and plotted for both the rover and base stations in Figure 5. In general, the multipath of all satellites at the rover station are larger than those at the base station. The multipath noises of satellite G15, G20, and G29 for both stations are relatively more than others due to having lower elevation angles [47]. Worth noting, due to the signal reflected from the building surface, some satellites, such as G16, which has a relatively high elevation angle of about 53°, experienced L1 pseodorange multipath at the rover station similar to other low elevation-angle satellites (e.g., G15, G20, and G29). To further analyze this phenomenon, L1 multipath traces of satellite G16 for both the rover and the base station are plotted as a superimposed time series (Figure 6). As can be seen from the figure, L1 multipath for the rover station is higher than that of the base station. The standard deviation of the L1 multipath of satellite G16 for the rover was 0.74 m, whereas it was only 0.27 m at the base station.
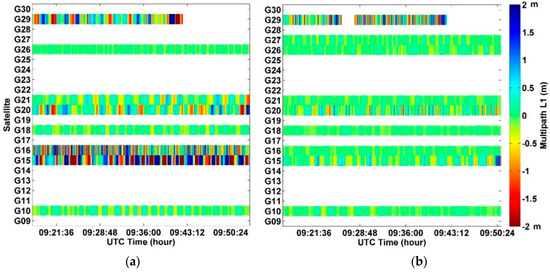
Figure 5.
L1 multipath satellite-specific patterns for the rover (a) and base station (b).
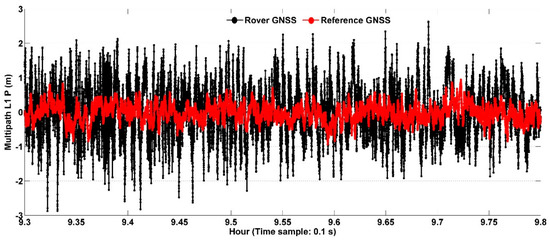
Figure 6.
L1 Multipath superimposed time series of Satellite G16 for rover (black) and base station (red).
3.3. GNSS Data Processing
In this study, GNSS data were processed by both relative positioning and PPP methods. The GPS and GLONASS observations were processed in the relative positioning mode using the Leica Geo Office (LGO) 3.0 software. In the process, dual frequency (L1 and L2) phase measurements and IGS final precise ephemeris were used. The Hopfield tropospheric model was implemented to model out the tropospheric dry delay. Double differences of the carrier phase signal were employed to eliminate the influence of ionospheric delay, orbit errors, and clock errors. The GNSS integer ambiguity-fixed solution was computed.
Compared to conventional PPP with float ambiguity solution, ambiguity resolution (AR) in PPP requires not only precise satellite orbit and clocks, but also phase bias corrections. The integer carrier-phase ambiguities are mixed with the code and phase biases to capture the integer property of the ambiguities; therefore, these biases should be accounted for. The purpose of PPP-AR is to shorten the solution convergence time and to improve the precision and accuracy of the estimated coordinates. The GNSS-PPP-AR solution of the rover GNSS data on the shaking table was processed in the post-mission kinematic PPP mode using SPARK (formerly known as CSRS-PPP) software developed by NRCan GSD (Geodetic Survey Division of the Natural Resource Canada). IGS final 5 min precise orbit and 30 s clock products were used. Dual frequency (L1 and L2) code and phase measurements were used to mitigate the first-order ionospheric error. Global mapping function (GMF) model was used as the troposphere mapping function, and zenith tropospheric delay (ZTD) was estimated alongside with the unknown position.
With respect to the relative and PPP kinematic processing, the precision of the epoch-by-epoch obtained coordinates in both horizontal directions varies between 0.8 and 2.7 cm for the relative solution and between 1.9 and 2.5 cm for the PPP solution. The coordinates obtained from both relative and PPP solutions were converted to the local topocentric Cartesian system. Then, the topocentric coordinates were projected onto the movement direction of the shaking table.
4. Results and Discussion
This section presents the test results, data analysis, and discussion of results.
4.1. Denoising and Noise Evaluation
Figure 7 demonstrates observations of the four events that are tested in this study. The re-sampling of 10 Hz LVDT is shown in the top panel, and the detrend relative and PPP GNSS results are presented in the bottom panel. From Figure 7, it can be seen that the dominant frequencies of the four events are 0.5 and 1.0 Hz, as extracted from the LVDT and GNSS results. However, the amplitudes of the GNSS movements for the relative and PPP techniques are not clear, as the displacements are contaminated by semi-static movement components and noise. The frequencies extracted from LVDT are primarily dynamic frequencies, while the signals obtained from GNSS contain semi-static and dynamic frequencies. The figure shows that the amplitudes estimated from the PPP and relative positioning methods are correlated and, likewise, their frequencies. Figure 7 also depicts that the semi-static frequency of the whole movements is 0.008 Hz. Herein, it can be noted that the displacements and frequencies obtained from LVDT can be effectively used as a reference value for evaluating the displacement measured using GNSS devices since the amplitudes and frequencies of the four events are approximately the same with the generated motions properties, which are 0.5 Hz/15 mm, 1 Hz/5 mm, 1 Hz/10 mm, and 1 Hz/15 mm for the events 1, 2, 3, and 4, respectively.

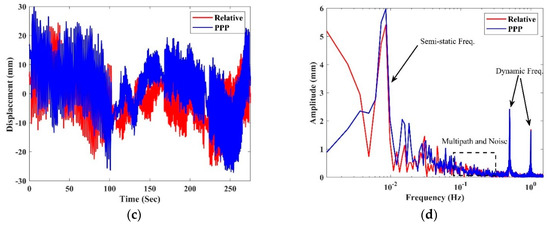
Figure 7.
Four events amplitude (a) and frequency (b) for LVDT and amplitude (c) and frequency (d) for both GNSS solutions.
Previous results of GNSS/GPS noises and errors that were presented in Han and Rizos [48] and Moschas and Stiros [11,14] showed that the frequencies of multipath and colored noises of GNSS results could be observed up to 0.05 and 0.2 Hz, respectively. Furthermore, the dynamic multipath, which has no systematical frequency peaks and is induced by changes in the geometry of the receiver and reflecting surfaces, has a small effect on the horizontal coordinates [14]. The contaminated noises of the observations included multipath errors and dynamic noises; therefore, a double filter and spectral analysis is used to evaluate the effect of these errors on the dynamic motion’s properties. Figure 8 illustrates the movement component of PPP, relative GNSS positioning, and LVDT measurements for event 1. A comparison between the displacements of the three methods presented in Figure 8a shows that the amplitude of the dynamic movements cannot be extracted from the apparent displacement of GNSS results. Therefore, the semi-static movements must be removed first. The MSPCA and wavelet filters were implemented and compared here. Figure 8b shows the movement of relative GNSS for event 1 and both filter results. To extract the semi-static movement by the MSPCA method, the detailed decompositions of movements are removed and used with the approximate wavelet coefficients to extract the smoothed signals [25]. Herein, five levels are selected based on the frequency range of wavelet decomposition, and with Symlets 6 mother wavelet, are used to extract the semi-static movement by the MSPCA and wavelet denoise methods. The whole data of the four events are used in the smoothing process since the length of the signal influences the filter accuracy. In addition, the hard threshold (Equation (4)) is used in the wavelet, and just one of the approximate coefficients of wavelet decomposition is used to estimate the semi-static component [43].

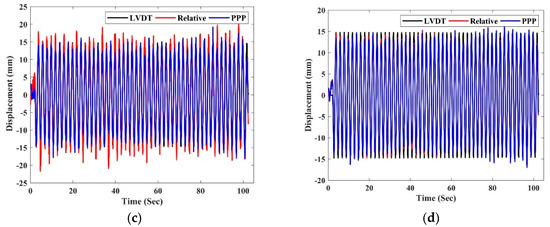
Figure 8.
MSPCAW evaluation in amplitude, (a) apparent displacement, (b) relative measurement filter, (c) short-period component, and (d) dynamic component.
A high correlation (0.99) between the semi-static movements of MSPCA and wavelet filters is observed in Figure 8b. Furthermore, the accuracy of both methods is almost the same. Thus, because of the filter design concept of the MSPCA, all approximate wavelet coefficients are utilized to reconstruct the smoothed signals. Consequently, no information losses are expected from the extracted signals; therefore, this method is used in the current study. Figure 8c shows the short-period component (dynamic movement + errors and noises) of the vibration motion. This movement is extracted after removing the semi-static component from the apparent displacements. From Figure 8c, it can be seen that the noise affected both GNSS techniques. Therefore, the wavelet packets decomposition is used to extract the dynamic components, as presented in Figure 9a, based on the wavelet energy of the wavelet tree. Here, three levels are used to eliminate the remaining noises and errors of the signal. Figure 9b illustrates the wavelet energy of each node for the PPP and the relative GNSS positioning methods. From Figure 9b, it can be seen clearly that the nodes (3,4), (3,5), and (3,7) are insignificant statistically at the 95% level. Therefore, these coefficients are removed from the wavelet reconstruction process to estimate the dynamic movements of the GNSS antenna, which are presented in Figure 8d.
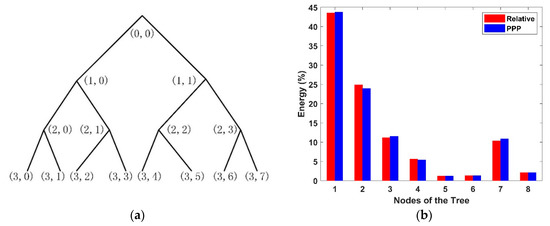
Figure 9.
Wavelet tree and energy, (a) wavelet tree, (b) energy of nodes.
For the statistical evaluation of results, the descriptive statistics, including the mean and standard deviation (std) of the absolute movement and the range of displacements, of the apparent, short-period and dynamic displacements extracted by MSPCAW using the three methods (LVDT, relative GNSS, and PPP) are presented in Table 1. From Table 1 and Figure 8, it can be clearly seen that the apparent displacement does not reflect the accurate amplitude performance of the movement; the variation between the statistical parameters of displacements that extracted by PPP- and relative-GNSS results and displacement of LVDT is high. In addition, no constant amplitudes for the PPP- and relative-GNSS are observed. Furthermore, with references to the LVDT measurements, the short-period component can be used to extract the insignificant amplitude of the dynamic movement. The accuracy of displacement range for the short-period component is 55.93% and 73.76% for the extracted displacement by the relative- and PPP-GNSS techniques, respectively. The dynamic component of the GNSS derived-displacements can be accurately obtained by the MSPCAW method. Thus, it can be used to study the dynamic behavior. The accuracy of the range of the extracted dynamic displacement was 90.5% and 86.54% for the relative- and PPP-GNSS, respectively, compared to the measurement dynamic behavior of the movement by LVDT. In addition, it can be seen that the displacement standard deviation and mean improved for the relative- and PPP-GNSS results for short-period and dynamic cases, are both approximately the same. Moreover, the range of errors of the relative- and PPP-GNSS techniques is 10.1 and 9.8 mm, respectively. More discussion of measurement errors is presented in the next section. From the above, it can be concluded that the proposed method (MSPCAW) can be used to improve extracting the amplitude of the dynamic movements of the GNSS-based method for structures analyses.

Table 1.
Statistical analysis of the development model (unit: mm).
To assess the performance of the proposed method in the evaluation of structures in the frequency domain, the spectrum is analyzed to check the accuracy of movement detection by GNSS. The FFT is used to extract the frequency contents of the measurements. Figure 10 illustrates this frequency content of event 1 as a representative example. The comparison between LVDT and GNSS frequencies (Figure 10a) shows that the dominant frequency of the measurements of both sensors is 0.5 Hz, but the frequency of semi-static movement clearly affected the cross-correlation between the LVDT and GNSS results. The correlation of the absolute frequency amplitude between the relative GNSS positioning and PPP techniques is high (0.98). This means that the PPP method can be used to extract the dominant frequencies of movements. In addition, the semi-static frequency of the relative and PPP results is presented in Figure 10b. These are calculated using semi-static movements extracted by the MSPCA filter. The figure shows that the dominant frequency of semi-static movement for the relative GNSS positioning, and PPP is 0.008 Hz. Furthermore, the frequency contents of a semi-static component can reach 0.16 Hz. Therefore, the multipath errors can be removed by using a low-pass filter, and the remaining frequency contents will be due to the dynamic and background noises. The background noise is the main noise of stationary GNSS measurements, and their frequency power is small [43]. Herein, the frequency of the short-period component is presented in Figure 10c. From the figure, one can see that the frequency components improved for the GNSS methods, but some noise still influences the frequency contents. For that, the last step of MSPCAW is applied, which is reconstructing the signal based on the wavelet energy contents, leading to an improvement of the frequencies contents of the signals, as depicted in Figure 10d. The correlation of the absolute frequency amplitude between relative GNSS positioning and LVDT also improved from 0.95 to 0.99 for the short-period and dynamic components, respectively. Consequently, this proves that the use of MSPCAW enhances the detection of the signal’s characteristics in terms of amplitude and frequency contents of dynamic motions.
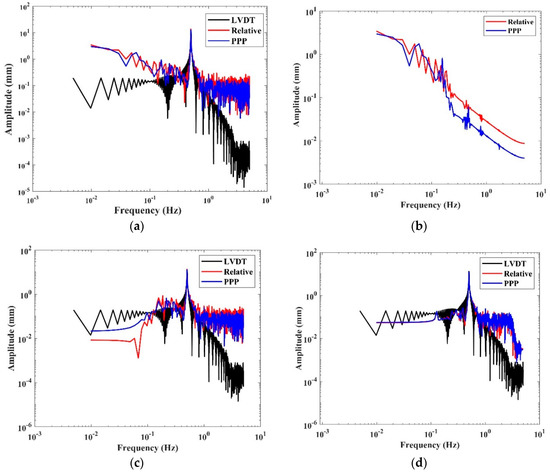
Figure 10.
MSPCAW evaluation in frequency, (a) measurement frequency, (b) semi-static frequency, (c) short-period frequency, (d) dynamic frequency.
It is worth mentioning that the number of observations is an essential factor that affects the energy of wavelet decompositions and the accuracy of results. In the case of using event 1 data only, the significant wavelet nodes based on the calculation wavelet energy were (3,0) and (3,1), and this affected the accuracy of the GNSS results. The range of dynamic displacement is calculated and found to be 38.08 and 33.89 mm for the relative- and PPP-GNSS methods, respectively. This means that some information is lost due to removing the nodes (3,2), (3,3), and (3,6), and the length of data is a significant parameter for the proposed method accuracy.
4.2. Motions’ Characteristics
The characteristics of the four events are extracted and presented using the proposed MSPCAW method (cf. Figure 2). Recall that Figure 8d shows the amplitudes of the apparent displacements of the LVDT measurement and GNSS relative positioning and PPP results for the first event, Figure 11 shows these amplitudes for the three remaining events.

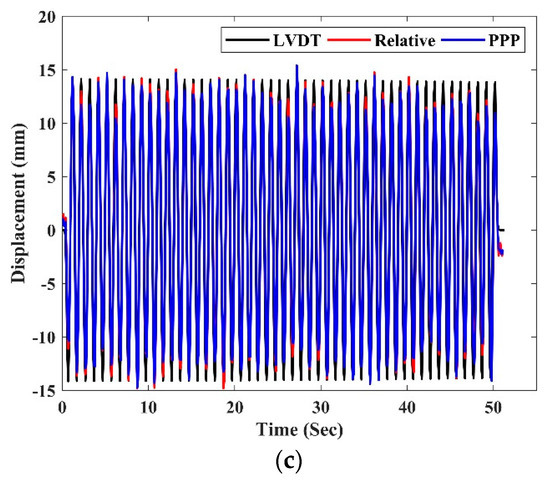
Figure 11.
Dynamic movements of seismic movement of events: (a) event 2, (b) event 3, and (c) event 4.
From Figure 8d and Figure 11, it can be seen that the correlation between GNSS techniques and LVDT observations is high. The ranges of displacements for the LVDT, GNSS relative positioning, and PPP in event 1 are 29.5, 32.4, and 33.5 mm, respectively. In event 2, the ranges are 9.4, 13.8, and 14.0 mm for the three methods. Moreover, the ranges of displacements of these methods (LVDT, relative GNSS positioning, and PPP) are 18.5, 21.1, and 20.6 mm, respectively, for event 3, and are 28.3, 29.8, and 30.2 mm, respectively, for event 4. The average accuracy of the range of GNSS relative positioning and PPP techniques is 80.94% and 79.77%, respectively, taking the LVDT measurements as the reference. Furthermore, the correlation between the dynamic movements extracted by the proposed method from GNSS and LVDT observations are calculated and presented in Table 2. From the table, a high correlation of the extracted dynamic component between LVDT and GNSS relative positioning and PPP results is observed. Therefore, the amplitude values can be extracted from the GNSS-derived displacement series using the proposed MSPCAW method, and one can conclude that the accuracy of the PPP method is suitable enough to extract the dynamic behavior of seismic motions.

Table 2.
The correlation coefficient of dynamic movements extracted from GNSS with LVDT measurements.
To study the type of the noise that affects high-rate GNSS observation used for detection of the dynamic motion of structures, the measurement’s residuals of GNSS techniques relative to LVDT measurements are computed and presented in Figure 12 and Table 3 for the four events. The quantile–quantile plot (Q-Q plot) is presented in the figure for the four events, where the standard normal quantile of the normal distribution was empirically plotted against the residuals of the events. The Q-Q plot is used to assess if a set of data plausibly came from some theoretical distribution such as a normal or exponential; more details can be found in Dodge [49]. In this plot, a reference fitting line is used to test the quartile of the data, a solid reference line connects the first and third quartiles (Q1 and Q3) of the data, and a dashed reference line extends the solid line to the ends of the data (see zoom-in in Figure 12a). To illustrate the quartiles, box-plots of events 2 and 4 are presented in the Figure 12e,f. In addition, Table 3 summarizes the statistical analysis of the GNSS errors for the four events in terms of the minimum (Min), maximum (Max), mean, std, skewness, and kurtosis of these errors. For all four cases, the differences were generally in the range of −9 to 8 mm, and the range of residuals of PPP is almost close to the range of the residuals of the relative positioning residuals.
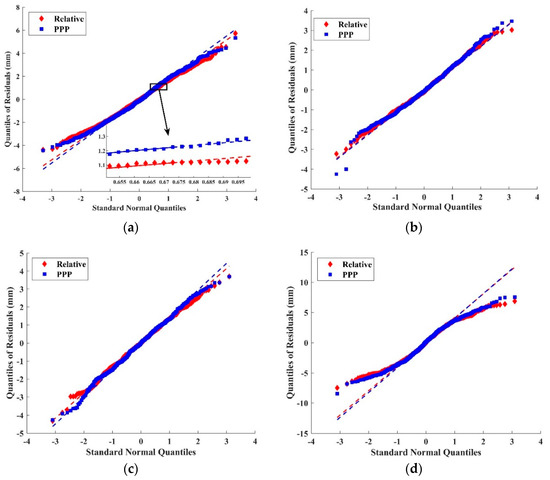
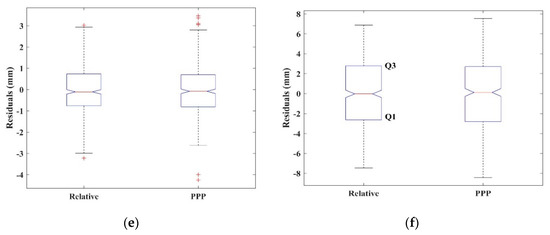
Figure 12.
Residual Q-Q plot of events 1 (a), 2(b), 3 (c), and 4 (d) and box-plots of events 2 (e) and 4 (f).

Table 3.
Statistical results of GNSS residuals.
The residuals of both techniques approximately followed a normal distribution, where the relationship between quantiles, as presented in the Q-Q and box plots, of the residuals and standard normal is approximately linear for the four events, and small outliers are observed in events 1, 2, and 3 for both measurement techniques. Furthermore, the distribution of the PPP residuals is approximately similar to the distribution of the residuals of the relative GNSS positioning, and the outliers of PPP are slightly higher than those of the relative GNSS technique (Figure 12e). In addition, the actual median of the residuals for PPP and relative results is different with a 95% confidence level, as presented in the box-plot, since the difference of the median is small, and the notches do not overlap. Also, asymmetry of data around their mean is measured by skewness; if it is negative, the data spread out more to the left of the mean than to the right, and vice versa if it is positive. Moreover, kurtosis is a measure of the outliers of distribution. If kurtosis is three, it implies that the distribution of the errors is normal, and distributions that have more or less outliers than the normal distribution have kurtosis greater or less than three, respectively. From Table 3, it can be seen that the skewness and kurtosis values reveal that the distributions of the events errors for the relative GNSS positioning and PPP techniques are not-exactly Gaussian. This indicates that the errors that contaminated GNSS results are not background noise only, but dynamic noises also affected the measurement signals. Also, the number of observations affected the GNSS measurements, while the standardization of the Q-Q plot for the events 1 (top-left) and 4 (middle-right) that approximately have the same amplitude are different since the number of observations is not equal. Furthermore, the figure shows that the accuracy of GNSS results in the extraction of deformation characteristics of structures is high in the case of low amplitude events. However, from Figure 12, it can be seen that the standard Gaussian distributions capture the majority of these noises and provide a conservative measure of the noise spread. Therefore, although the fluctuation of background and dynamic noises contaminates the GNSS results, the Gaussian assumption is adequate to estimate the distribution of these noises at 99.7% probability (three std).
The spectrum evaluation of the four events is calculated and presented in Figure 13 and Table 4. The signals collected by the LVDT sensor and that calculated by the proposed method (MSPCAW) form the GNSS results are used. From the figure and the table, it can be seen that the GNSS methods provided high accuracy for estimation of the dominant frequency and amplitude when compared with the LVDT results. A significant frequency domain is clear for the three methods (LVDT, relative GNSS positioning, and PPP). The dominant frequency of movements measured by LVDT and GNSS is equal for all four events. In addition, the average variation of the amplitude of the movement, relative to LVDT measurements, is 0.54 and 0.62 mm for the GNSS relative positioning and PPP, respectively. Moreover, the correlation between the spectrum of the LVDT and GNSS results is high (an average of 0.97 for the four events). Likewise, the correlation between the spectrum of relative GNSS positioning and PPP techniques is also high (on average 0.99 for the four events). These results demonstrate that MSPCAW is an efficient denoising method for the extraction of the dynamic characteristics of motions from noisy GNSS data. Furthermore, similar to the relative GNSS positioning method, the PPP method can provide sufficient accuracy for the extraction of the dynamic behavior of strong motions.
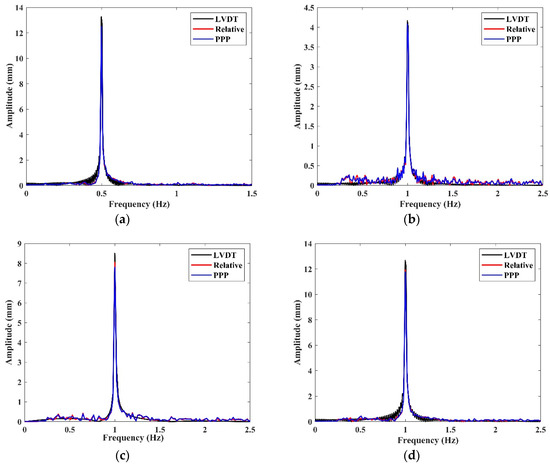
Figure 13.
Spectrum diagram of the four events: (a) event 1, (b) event 2, (c) event 3, and (d) event 4.

Table 4.
Summary of characteristics of the four events.
5. Conclusions
High-rate GNSS receivers in structural health monitoring have been widely used as a complementary sensor to other geotechnical sensors. In GNSS-based or aided SHM applications, the structural element and the other structures surrounding the GNSS receiver attached to the engineering structure being monitored cause noise and multipath errors in GNSS observations. The main objective of this study is to simulate a real situation and to investigate the effectiveness and efficiency of the proposed denoising method for capturing mm-level displacement and estimating the dynamic characteristics of an engineering structure. In this study, a novel hybrid MSPCA and wavelet transform (MSPCAW) method was designed and evaluated to denoise a GNSS-derived displacement time series used to extract and estimate the dynamic characteristics of an engineering structure or seismic ground motions in the horizontal directions. To simulate the real-world situation in structural monitoring, in which the surrounding environment of the monitoring GNSS receiver may include several reflective surfaces causing multipath, a series of harmonic motions were generated using a shaking table installed near a building. The GNSS data were processed using the relative positioning and PPP methods to obtain time series of displacements. These GNSS-derived time series were filtered by the proposed method to extract the dynamic characteristics of motions tested using the shaking table. The efficiency of the method was evaluated by referencing GNSS results to those obtained from an LVDT system. The results of the study show that:
- -
- The multipath error and measurement noise have affected the amplitude accuracy of the displacement obtained from GNSS results. The multipath contaminates the semi-static component and can be removed using a low-pass filter. The background and dynamic noises contaminate the GNSS results, and the Gaussian assumption is adequate to describe the distribution of these noises at a probability of 99.7%.
- -
- The comparison between the short-period and dynamic component wavelet energy in the current study shows that the low energy wavelet affects the accuracy of the dynamic properties of movements by 90.5% and 86.54% for the relative GNSS positioning and PPP methods, respectively. The amplitude and the frequency contents of GNSS-measured displacement are equal and are similar to the frequencies that are estimated by the LVDT. Furthermore, the number of observations in the time series is an essential factor for the extraction of the wavelet energy impact in the GNSS results.
- -
- Evaluation of the four events shows that the MSPCAW model can be used to estimate an accurate performance of GNSS-derived displacements in terms of the time and frequency domains. The evaluation of motion amplitudes for these events assessed by LVDT and extracted by MSPCAW from GNSS results show that the average accuracy of extracting the amplitude of movements is 80.94% and 79.77% for the relative GNSS positioning and PPP techniques, respectively. Meanwhile, the spectrum analysis of extracted displacement from GNSS results shows that the average variation of errors in computing the amplitude of the movements, relative to LVDT measurements, is 0.54 mm and 0.62 mm for the relative GNSS positioning and PPP, respectively. Results also show that the extracted dominant frequency of movements by both GNSS methods and LVDT is equal. From these results, it is concluded that the proposed hybrid method can be used to extract the accurate dynamic characteristic of engineering structures, such as high-rise buildings and suspended bridges, where the GNSS observations are subject to harsh environments.
Author Contributions
M.R.K. and C.O.Y. conceived and designed the research; C.O.Y., A.A.D. and M.B. collected the data; M.R.K. designed and performed the computational implementation of the model and contributed with analyses; M.R.K. and C.O.Y. wrote the manuscript and evaluated overall model results; A.E.-M. reviewed and edited the manuscript, and M.R.K., C.O.Y., A.E.-M., and J.W.H. revised the manuscript. All authors have read and agreed to the published version of the manuscript.
Funding
This research was supported by a grant (2019-MOIS41-002) from National Demand Customized Life Safety R&D Project funded by Korean Ministry of Interior and Safety (MOIS, Korea).
Acknowledgments
The second author would like to thank the TUBITAK (Scientific and Technological Research Council of Turkey) Science Fellowships and Grant Programs Department for awarding him a grant to perform research on the High-rate GNSS-PPP Method for GNSS seismology and structural health monitoring applications, including this study, at the School of Earth and Planetary Sciences, Curtin University, Australia. The authors would also like to thank Natural Resources Canada for providing CSRS-PPP service.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alcay, S.; Ogutcu, S.; Kalayci, I.; Yigit, C.O. Displacement monitoring performance of relative positioning and Precise Point Positioning (PPP) methods using simulation apparatus. Adv. Space Res. 2019, 63, 1697–1707. [Google Scholar] [CrossRef]
- Yigit, C.O.; Dindar, A.A.; Bezcioglu, M.; El-Mowafy, A. Evaluation of High-Rate GNSS-PPP for Monitoring Structural Health and Seismogeodesy Applications. In Proceedings of the XXVI FIG Congress 2018, Istanbul, Turkey, 6–11 May 2018. [Google Scholar]
- Xu, P.; Shi, C.; Fang, R.; Liu, J.; Niu, X.; Zhang, Q.; Yanagidani, T. High-rate precise point positioning (PPP) to measure seismic wave motions: An experimental comparison of GPS PPP with inertial measurement units. J. Geod. 2013, 87, 361–372. [Google Scholar] [CrossRef]
- Tang, X.; Roberts, G.W.; Li, X.; Hancock, C.M. Real-time kinematic PPP GPS for structure monitoring applied on the Severn Suspension Bridge, UK. Adv. Space Res. 2017, 60, 925–937. [Google Scholar] [CrossRef]
- Li, X. Real-Time High-Rate GNSS Techniques for Earthquake Monitoring and Early Warning. Ph.D. Thesis, Der Technische Universität Berlin, Berlin, Germany, 2015; p. 139. [Google Scholar]
- Yigit, C.O.; Gurlek, E. Experimental testing of high-rate GNSS precise point positioning (PPP) method for detecting dynamic vertical displacement response of engineering structures. Geomat. Nat. Hazards Risk 2017, 8, 893–904. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Yigit, C.O.; Hu, J.W. Analysis of the dynamic behavior of structures using the high-rate GNSS-PPP method combined with a wavelet-neural model: Numerical simulation and experimental tests. Adv. Space Res. 2018, 61, 1512–1524. [Google Scholar] [CrossRef]
- Dawidowicz, K. Sub-hourly precise point positioning accuracy analysis—Case study for selected ASG-EUPOS stations. Surv. Rev. 2019, in press. [Google Scholar] [CrossRef]
- Quesada-Olmo, N.; Jimenez-Martinez, M.; Farjas-Abadia, M. Real-time high-rise building monitoring system using global navigation satellite system technology. Measurement 2018, 123, 115–124. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, Y.; Li, B.; Qiu, G. GNSS-Based Verticality Monitoring of Super-Tall Buildings. Appl. Sci. 2018, 8, 991. [Google Scholar] [CrossRef]
- Moschas, F.; Stiros, S. Noise characteristics of high-frequency, short-duration GPS records from analysis of identical, collocated instruments. Measurement 2013, 46, 1488–1506. [Google Scholar] [CrossRef]
- Pirsiavash, A.; Broumandan, A.; Lachapelle, G.; O’Keefe, K. GNSS Code Multipath Mitigation by Cascading Measurement Monitoring Techniques. Sensors 2018, 18, 1967. [Google Scholar] [CrossRef]
- Zheng, K.; Zhang, X.; Li, X.; Li, P.; Chang, X.; Sang, J.; Ge, M.; Schuh, H. Mitigation of Unmodeled Error to Improve the Accuracy of Multi-GNSS PPP for Crustal Deformation Monitoring. Remote Sens. 2019, 11, 2232. [Google Scholar] [CrossRef]
- Moschas, F.; Stiros, S. Dynamic multipath in structural bridge monitoring: An experimental approach. GPS Solut. 2014, 18, 209–218. [Google Scholar] [CrossRef]
- Quan, Y.; Lau, L.; Roberts, G.W.; Meng, X.; Zhang, C. Convolutional Neural Network Based Multipath Detection Method for Static and Kinematic GPS High Precision Positioning. Remote Sens. 2018, 10, 2052. [Google Scholar] [CrossRef]
- Ogaja, C.; Satirapod, C. Analysis of high-frequency multipath in 1-Hz GPS kinematic solutions. GPS Solut. 2007, 11, 269–280. [Google Scholar] [CrossRef]
- Wang, D.; Meng, X.; Gao, C.; Pan, S.; Chen, Q. Multipath extraction and mitigation for bridge deformation monitoring using a single-difference model. Adv. Space Res. 2017, 60, 2882–2895. [Google Scholar] [CrossRef]
- Ogundipe, O.; Lee, J.K.; Roberts, G.W. Wavelet De-noising of GNSS Based Bridge Health Monitoring Data. J. Appl. Geod. 2014, 8, 273–281. [Google Scholar] [CrossRef]
- Moschas, F.; Stiros, S. Dynamic Deflections of a Stiff Footbridge Using 100-Hz GNSS and Accelerometer Data. J. Surv. Eng. 2015, 141, 04015003. [Google Scholar] [CrossRef]
- Moschas, F.; Avallone, A.; Saltogianni, V.; Stiros, S. Strong motion displacement waveforms using 10-Hz precise point positioning GPS: An assessment based on free oscillation experiments Fanis. Int. Assoc. Earthq. Eng. 2015, 44, 657–675. [Google Scholar] [CrossRef]
- Koo, G.; Kim, K.; Chung, J.Y.; Choi, J.; Kwon, N.-Y.; Kang, D.-Y.; Sohn, H. Development of a High Precision Displacement Measurement System by Fusing a Low Cost RTK-GPS Sensor and a Force Feedback Accelerometer for Infrastructure Monitoring. Sensors 2017, 17, 2745. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Yigit, C.O.; Dindar, A.A.; ElSharawy, M.; Hu, J.W. Evaluation of the high-rate GNSS-PPP method for vertical structural motion. Surv. Rev. 2018, in press. [Google Scholar] [CrossRef]
- Wu, H.; Li, K.; Shi, W.; Clarke, K.C.; Zhang, J.; Li, H. A wavelet-based hybrid approach to remove the flicker noise and the white noise from GPS coordinate time series. GPS Solut. 2014, 19, 511–523. [Google Scholar] [CrossRef]
- Li, Y.; Xu, C.; Yi, L. Denoising effect of multiscale multiway analysis on high-rate GPS observations. GPS Solut. 2017, 21, 31–41. [Google Scholar] [CrossRef]
- Li, Y.; Xu, C.; Yi, L.; Fang, R. A data-driven approach for denoising GNSS position time series. J. Geod. 2018, 92, 905–922. [Google Scholar] [CrossRef]
- Bakshi, B.R. Multiscale PCA with application to multivariate statistical process monitoring. AIChE J. 1998, 44, 1596–1610. [Google Scholar] [CrossRef]
- Aminghafari, M.; Cheze, N.; Poggi, J.-M. Multivariate denoising using wavelets and principal component analysis. Comput. Stat. Data Anal. 2006, 50, 2381–2398. [Google Scholar] [CrossRef]
- Xiuxi, L.; Qian, Y.; Wang, J. Process Monitoring Based on Improved Principal Component Analysis. Comput. Aided Chem. Eng. 2003, 14, 455–460. [Google Scholar]
- Kaloop, M.R.; Hussan, M.; Kim, D. Time-series analysis of GPS measurements for long-span bridge movements using wavelet and model prediction techniques. Adv. Space Res. 2019, 63, 3505–3521. [Google Scholar] [CrossRef]
- Sayed, M.A.; Kaloop, M.R.; Kim, E.; Kim, D. Assessment of Acceleration Responses of a Railway Bridge using Wavelet Analysis. KSCE J. Civ. Eng. 2017, 21, 1844–1853. [Google Scholar] [CrossRef]
- Ke, L. Denoising GPS-Based Structure Monitoring Data Using Hybrid EMD and Wavelet Packet. Math. Probl. Eng. 2017, 2017, 1–7. [Google Scholar] [CrossRef]
- M’Ng, J.C.P.; Mehralizadeh, M. Forecasting East Asian Indices Futures via a Novel Hybrid of Wavelet-PCA Denoising and Artificial Neural Network Models. PLoS ONE 2016, 11, 1–29. [Google Scholar]
- Jing-Yi, L.; Hong, L.; Dong, Y.; Yan-Sheng, Z. A New Wavelet Threshold Function and Denoising Application. Math. Probl. Eng. 2016, 2016, 1–8. [Google Scholar] [CrossRef]
- Srivastava, M.; Anderson, C.L.; Freed, J.H. A New Wavelet Denoising Method for Selecting Decomposition Levels and Noise Thresholds. IEEE Access 2016, 4, 3862–3877. [Google Scholar] [CrossRef] [PubMed]
- Kaloop, M.R.; Hu, J.W.; Sayed, M.A.; Seong, J. Structural Performance Assessment Based on Statistical and Wavelet Analysis of Acceleration Measurements of a Building during an Earthquake. Shock Vib. 2016, 2016, 1–13. [Google Scholar] [CrossRef]
- Hussan, M.; Kaloop, M.R.; Sharmin, F.; Kim, D. GPS Performance Assessment of Cable-Stayed Bridge using Wavelet Transform and Monte-Carlo Techniques. KSCE J. Civ. Eng. 2018, 22, 4385–4398. [Google Scholar] [CrossRef]
- Taha, M.M.R.; Noureldin, A.; Lucero, J.L.; Baca, T.J. Wavelet Transform for Structural Health Monitoring: A Compendium of Uses and Features. Struct. Health Monit. 2006, 5, 267–295. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Hu, J.W. Damage Identification and Performance Assessment of Regular and Irregular Buildings Using Wavelet Transform Energy. Adv. Mater. Sci. Eng. 2016, 2016, 1–11. [Google Scholar] [CrossRef]
- Gao, Z.; Shen, W.; Zhang, H.; Niu, X.; Ge, M. Real-time Kinematic Positioning of INS Tightly Aided Multi-GNSS Ionospheric Constrained PPP. Sci. Rep. 2016, 6, 30488. [Google Scholar] [CrossRef]
- Kaloop, M.R.; Elbeltagi, E.; Hu, J.W.; Elrefai, A. Recent Advances of Structures Monitoring and Evaluation Using GPS-Time Series Monitoring Systems: A Review. ISPRS Int. J. Geo Inf. 2017, 6, 382. [Google Scholar] [CrossRef]
- Lau, L. Wavelet packets based denoising method for measurement domain repeat-time multipath filtering in GPS static high-precision positioning. GPS Solut. 2017, 21, 461–474. [Google Scholar] [CrossRef]
- Mosavi, M.R.; Zebarjad, R.; Moazedi, M. Novel Anti-spoofing Methods Based on Discrete Wavelet Transform in the Acquisition and Tracking Stages of Civil GPS Receiver. Int. J. Wirel. Inf. Netw. 2018, 25, 449–460. [Google Scholar] [CrossRef]
- Yu, J.; Yan, B.; Meng, X.; Shao, X.; Ye, H. Measurement of Bridge Dynamic Responses Using Network-Based Real-Time Kinematic GNSS Technique. J. Surv. Eng. 2016, 142, 04015013. [Google Scholar] [CrossRef]
- Ma, J.; Yang, Z.; Shi, Z.; Zhang, X.; Liu, C. Application and Optimization of Wavelet Transform Filter for North-Seeking Gyroscope Sensor Exposed to Vibration. Sensors 2019, 19, 3624. [Google Scholar] [CrossRef] [PubMed]
- Merry, R.; Steinbuch, M. Wavelet Theory and Application: Literature Study; Eindhoven University of Technology, Department of Mechanical Engineering, Control Systems Technology Group: Eindhoven, The Netherlands, 2005. [Google Scholar]
- El-Mowafy, A.; Bilbas, E. Quality Control in Using GNSS CORS Network for Monitoring Plate Tectonics: A Western Australia Case Study. J. Surv. Eng. 2016, 142, 05015003. [Google Scholar] [CrossRef]
- Ogaja, C.; Hedfors, J. TEQC multipath metrics in MATLAB. GPS Solut. 2007, 11, 215–222. [Google Scholar] [CrossRef]
- Han, S.; Rizos, C. Multipath effects on GPS in mine environments. In Proceedings of the 10th International Congress of the International Society for Mine Surveying Fremantle, Fremantle, Australia, 2–6 November 1997. [Google Scholar]
- Dodge, Y. Q-Q Plot (Quantile to Quantile Plot). In The Concise Encyclopedia of Statistics; Springer: New York, NY, USA, 2008; pp. 437–439. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).