Estimating Forest Stock Volume in Hunan Province, China, by Integrating In Situ Plot Data, Sentinel-2 Images, and Linear and Machine Learning Regression Models
Abstract
1. Introduction
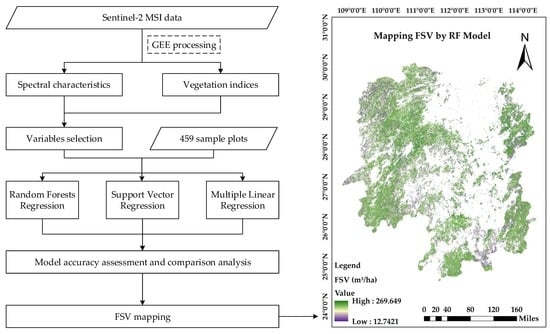
2. Materials and Methods
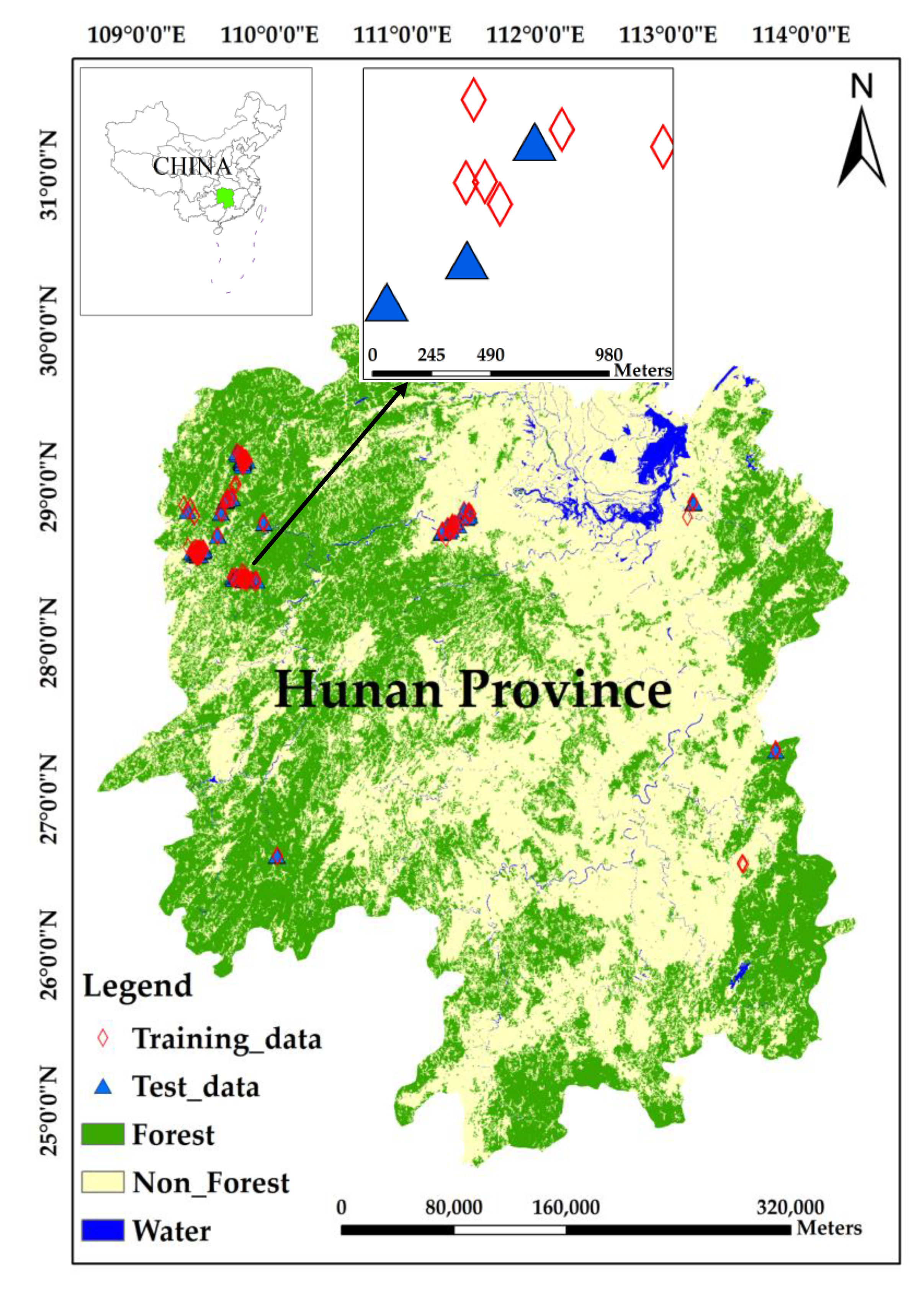
2.1. Study Area
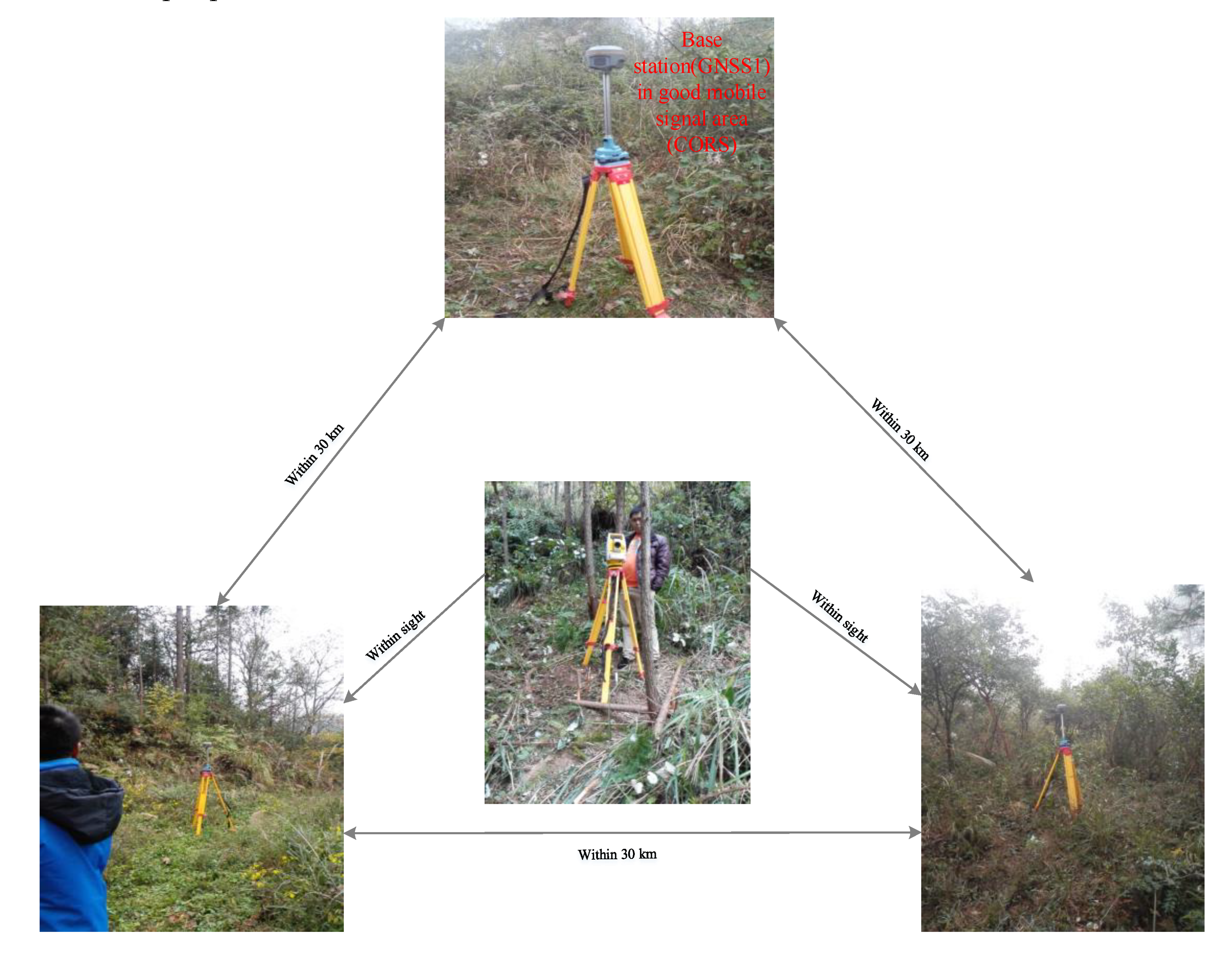
2.2. In situ Sample Plot Data Collection
2.3. Sentinel-2 Images Preprocessing and Variable Calculation
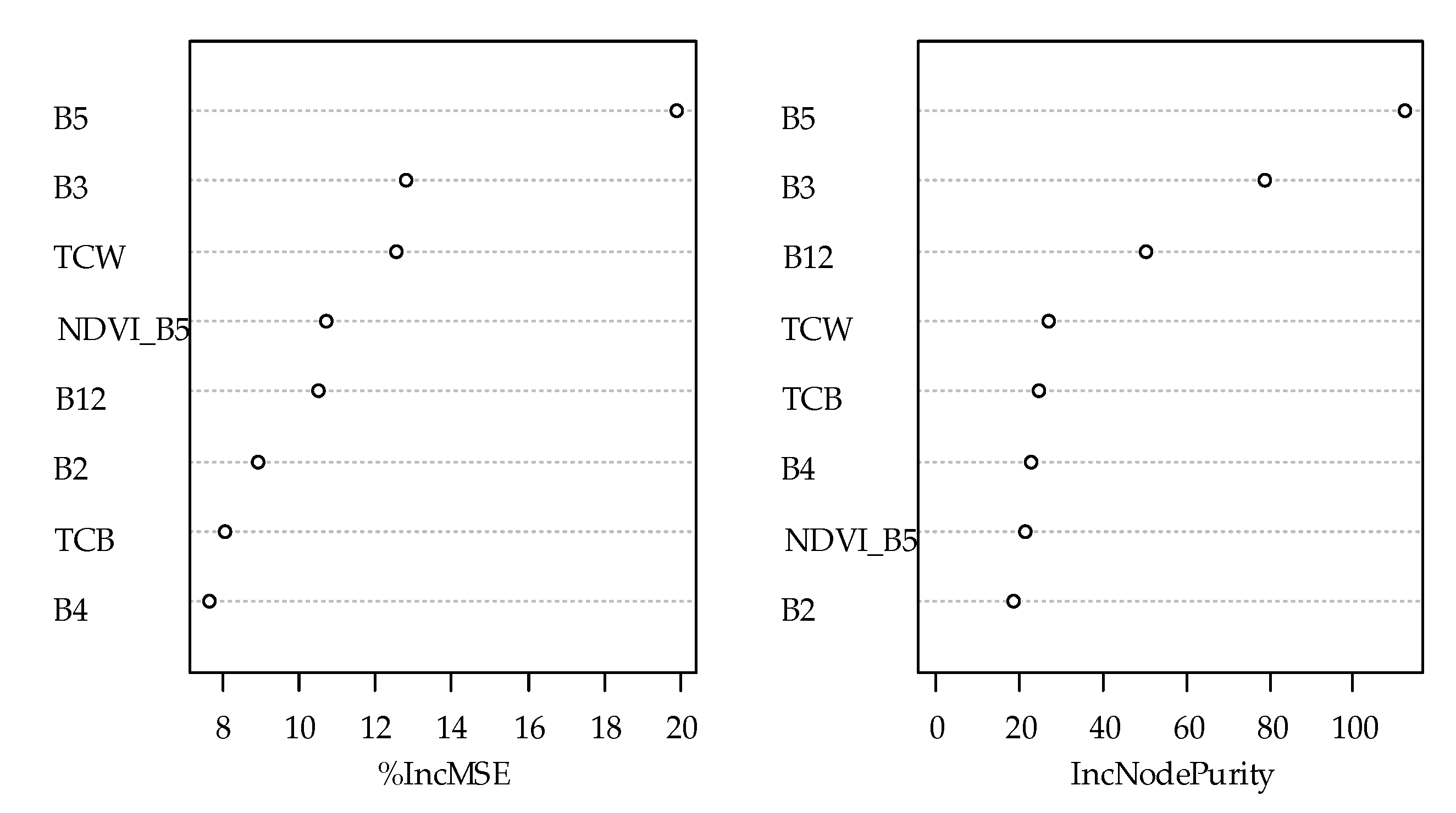
2.4. Selection of Relevant Variables for FSV Estimation
2.5. Statistical Models for Estimating the FSV
3. Results
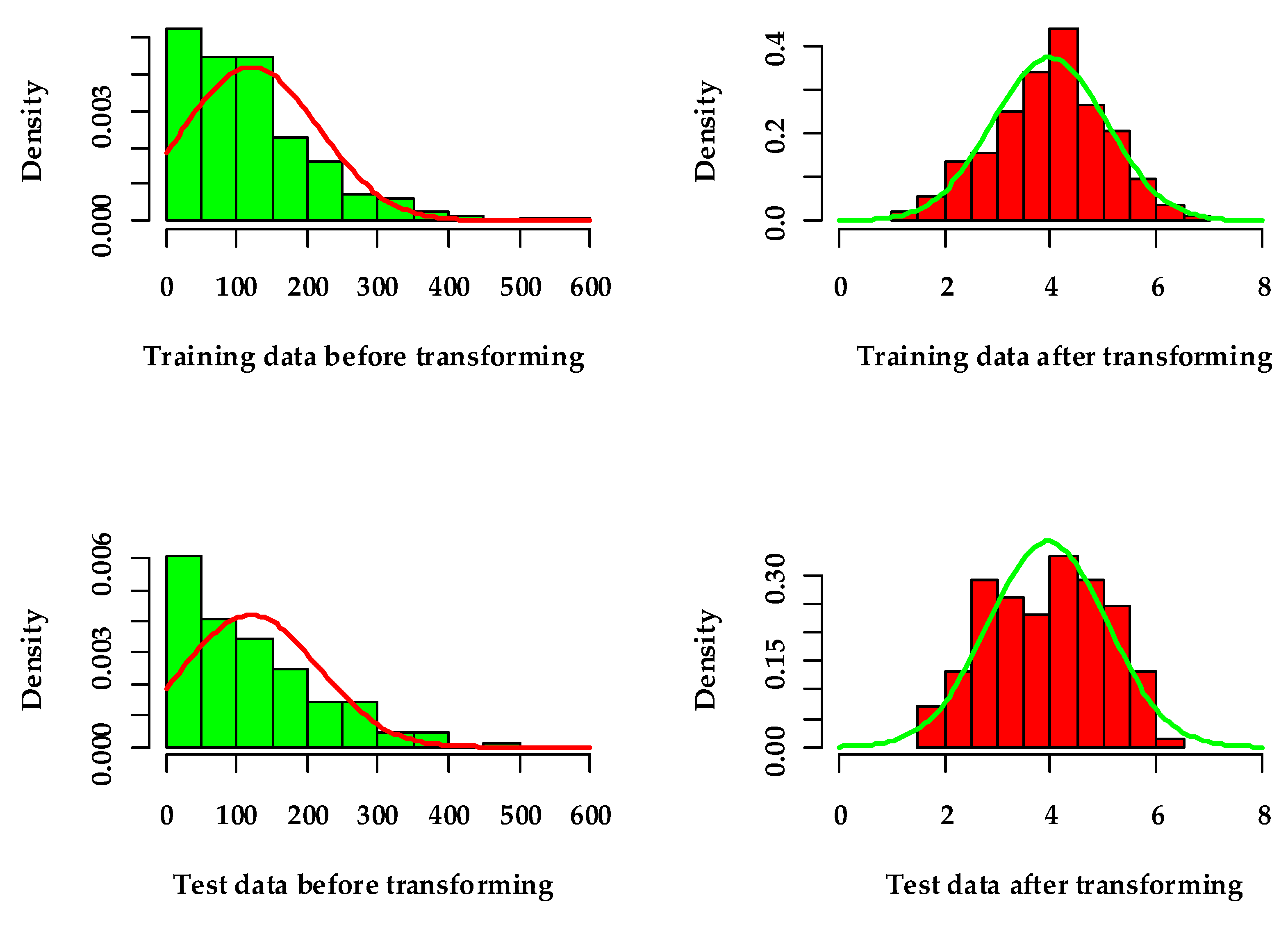
3.1. Characteristics of the in Situ FSV Data
3.2. Major Variables Related to the FSV Data
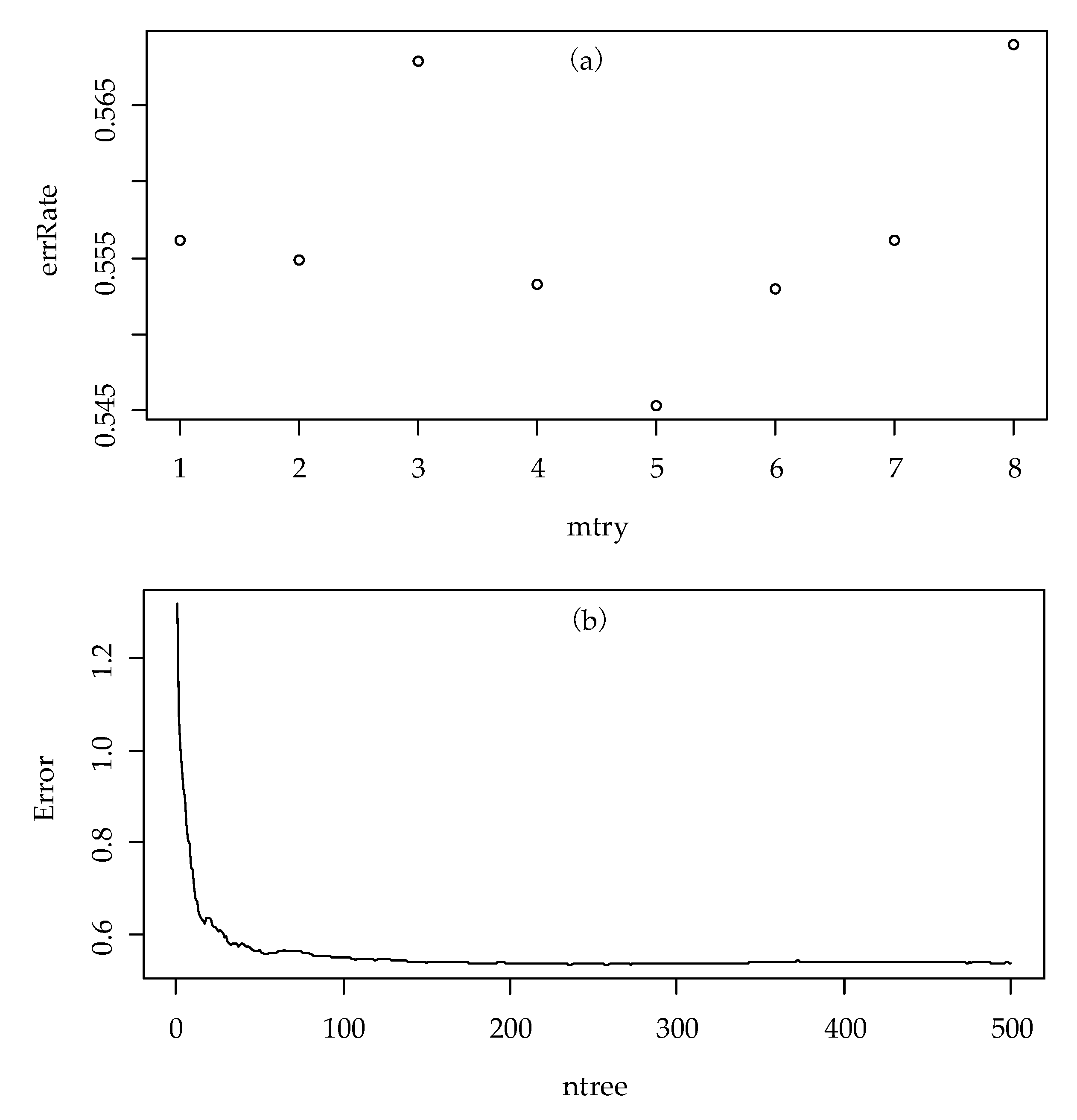
3.3. Optimal Regression Model for the RF, SVR, and MLR
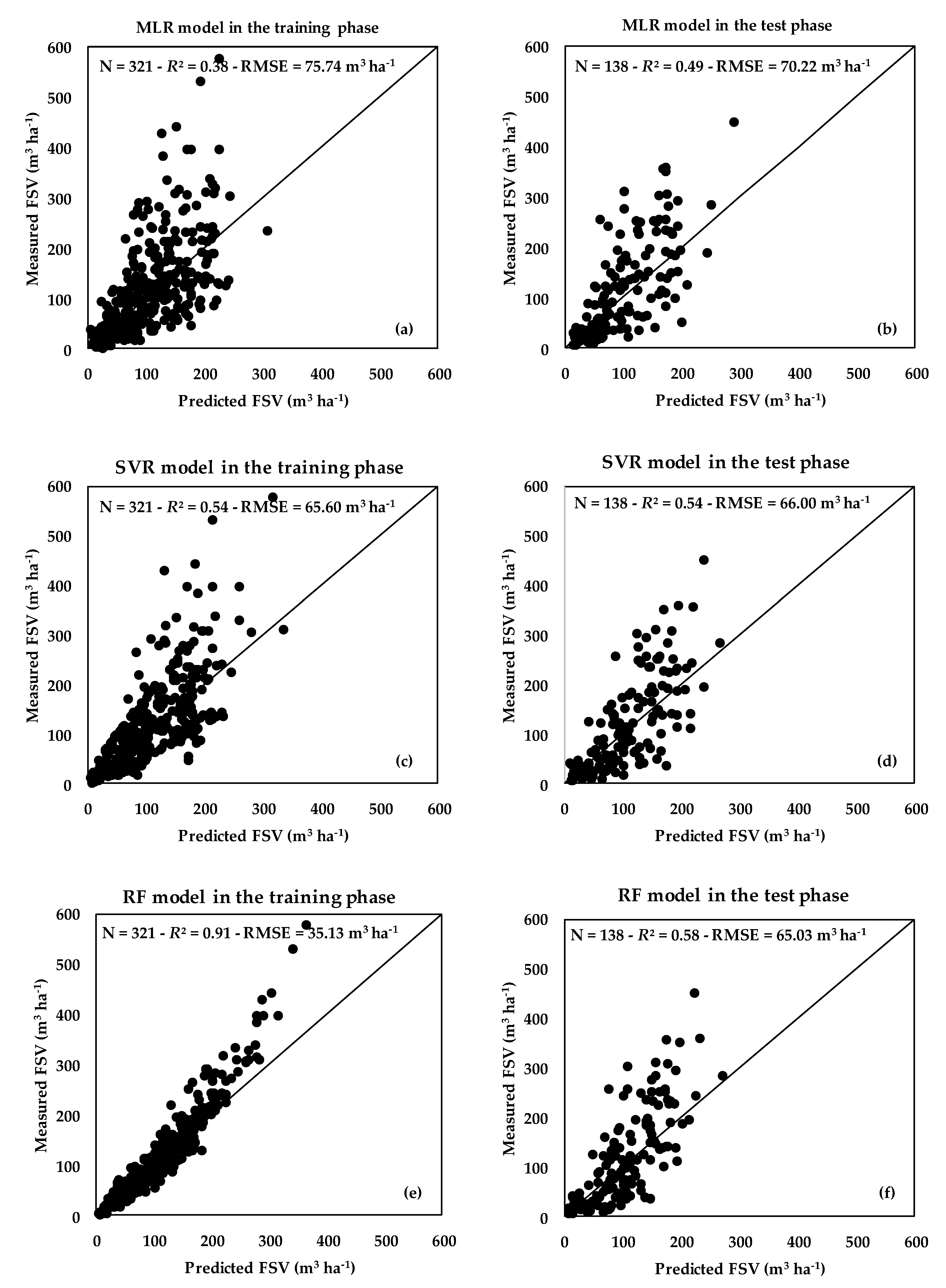
3.4. Comparison of the Predicted FSV Estimates among the Three Models (MLR, SVR, and RF)
3.5. Modeling Results Comparison between Selected Variables and all Variables
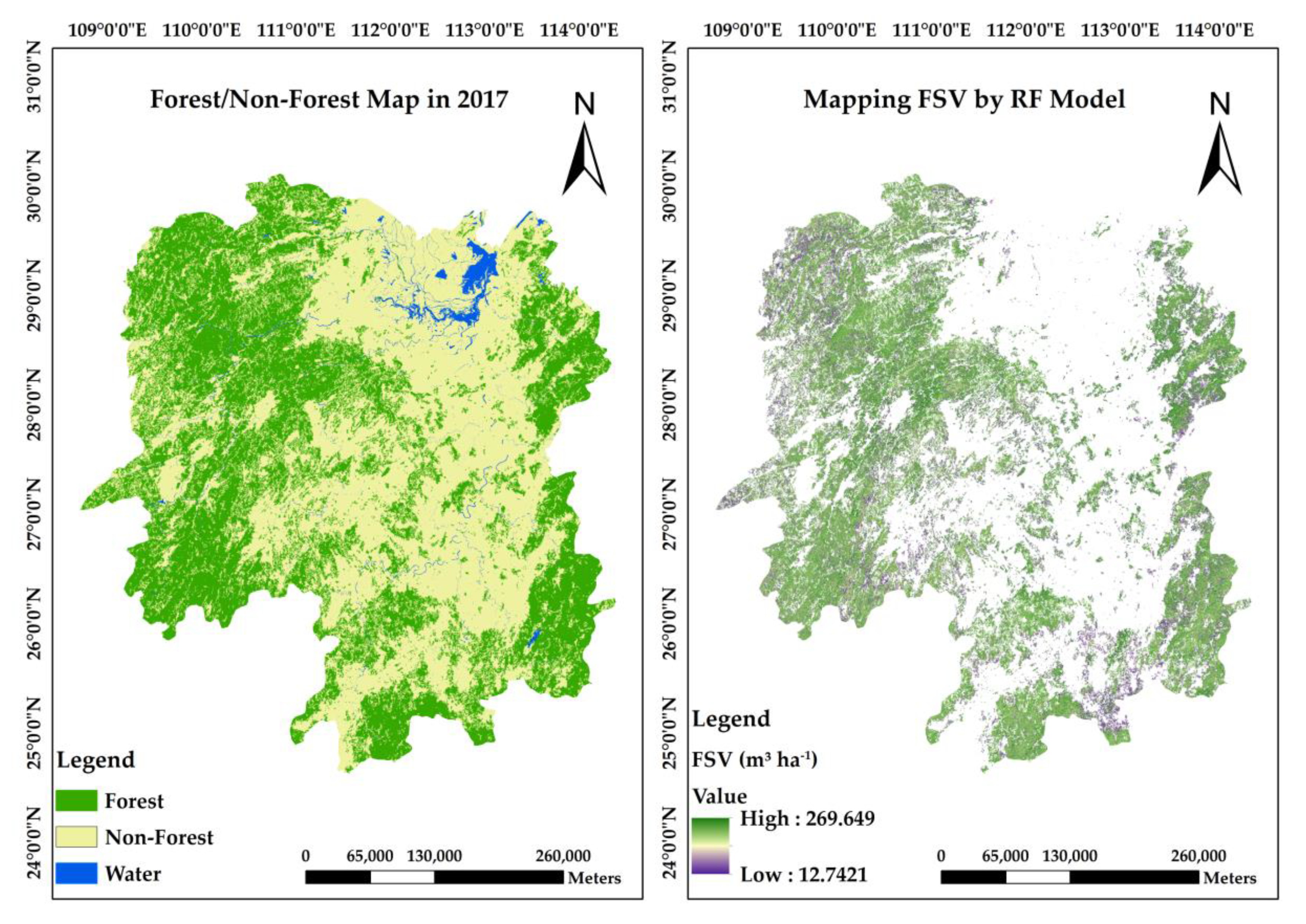
3.6. Map of the FSV Estimation in Hunan Province in 2017
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mura, M.; Bottalico, F.; Giannetti, F.; Bertani, R.; Giannini, R.; Mancini, M.; Orlandini, S.; Travaglini, D.; Chirici, G. Exploiting the capabilities of the Sentinel-2 multi spectral instrument for predicting growing stock volume in forest ecosystems. Int. J. Appl. Earth Obs. 2018, 66, 126–134. [Google Scholar] [CrossRef]
- Somogyi, Z.; Teobaldelli, M.; Federici, S.; Matteucci, G.; Pagliari, V.; Grassi, G.; Seufert, G. Allometric biomass and carbon factors database. iForest—Biogeosci. For. 2008, 1, 107–113. [Google Scholar] [CrossRef]
- Santoro, M.; Beaudoin, A.; Beer, C.; Cartus, O.; Fransson, J.E.S.; Hall, R.J.; Pathe, C.; Schmullius, C.; Schepaschenko, D.; Shvidenko, A.; et al. Forest growing stock volume of the northern hemisphere: Spatially explicit estimates for 2010 derived from Envisat ASAR. Remote Sens. Environ. 2015, 168, 316–334. [Google Scholar] [CrossRef]
- Astola, H.; Häme, T.; Sirro, L.; Molinier, M.; Kilpi, J. Comparison of Sentinel-2 and Landsat 8 imagery for forest variable prediction in boreal region. Remote Sens. Environ. 2019, 223, 257–273. [Google Scholar] [CrossRef]
- Boyle, S.A.; Kennedy, C.M.; Torres, J.; Colman, K.; Pérez-Estigarribia, P.E.; de la Sancha, N.U. High-resolution satellite imagery is an important yet underutilized resource in conservation biology. PLoS ONE 2014, 9, e86908. [Google Scholar] [CrossRef] [PubMed]
- Neigh, C.; Bolton, D.; Diabate, M.; Williams, J.; Carvalhais, N. An Automated Approach to Map the History of Forest Disturbance from Insect Mortality and Harvest with Landsat Time-Series Data. Remote Sens. 2014, 6, 2782–2808. [Google Scholar] [CrossRef]
- Zhu, Z.; Woodcock, C.E. Continuous change detection and classification of land cover using all available Landsat data. Remote Sens. Environ. 2014, 144, 152–171. [Google Scholar] [CrossRef]
- Griffiths, P.; Kuemmerle, T.; Baumann, M.; Radeloff, V.C.; Abrudan, I.V.; Lieskovsky, J.; Munteanu, C.; Ostapowicz, K.; Hostert, P. Forest disturbances, forest recovery, and changes in forest types across the Carpathian ecoregion from 1985 to 2010 based on Landsat image composites. Remote Sens. Environ. 2014, 151, 72–88. [Google Scholar] [CrossRef]
- Morresi, D.; Vitali, A.; Urbinati, C.; Garbarino, M. Forest Spectral Recovery and Regeneration Dynamics in Stand-Replacing Wildfires of Central Apennines Derived from Landsat Time Series. Remote Sens. 2019, 11, 308. [Google Scholar] [CrossRef]
- Wulder, M.A.; Masek, J.G.; Cohen, W.B.; Loveland, T.R.; Woodcock, C.E. Opening the archive: How free data has enabled the science and monitoring promise of Landsat. Remote Sens. Environ. 2012, 122, 2–10. [Google Scholar] [CrossRef]
- Banskota, A.; Kayastha, N.; Falkowski, M.J.; Wulder, M.A.; Froese, R.E.; White, J.C. Forest Monitoring Using Landsat Time Series Data: A Review. Can. J. Remote Sens. 2014, 40, 362–384. [Google Scholar] [CrossRef]
- Giree, N.; Stehman, S.; Potapov, P.; Hansen, M. A Sample-Based Forest Monitoring Strategy Using Landsat, AVHRR and MODIS Data to Estimate Gross Forest Cover Loss in Malaysia between 1990 and 2005. Remote Sens. 2013, 5, 1842–1855. [Google Scholar] [CrossRef]
- Clerici, N.; Weissteiner, C.J.; Gerard, F. Exploring the Use of MODIS NDVI-Based Phenology Indicators for Classifying Forest General Habitat Categories. Remote Sens. 2012, 4, 1781–1803. [Google Scholar] [CrossRef]
- Frantz, D.; Röder, A.; Udelhoven, T.; Schmidt, M. Forest Disturbance Mapping Using Dense Synthetic Landsat/MODIS Time-Series and Permutation-Based Disturbance Index Detection. Remote Sens. 2016, 8, 277. [Google Scholar] [CrossRef]
- Senf, C.; Pflugmacher, D.; van der Linden, S.; Hostert, P. Mapping Rubber Plantations and Natural Forests in Xishuangbanna (Southwest China) Using Multi-Spectral Phenological Metrics from MODIS Time Series. Remote Sens. 2013, 5, 2795–2812. [Google Scholar] [CrossRef]
- Chi, H.; Sun, G.; Huang, J.; Guo, Z.; Ni, W.; Fu, A. National Forest Aboveground Biomass Mapping from ICESat/GLAS Data and MODIS Imagery in China. Remote Sens. 2015, 7, 5534–5564. [Google Scholar] [CrossRef]
- Ehlers, S.; Saarela, S.; Lindgren, N.; Lindberg, E.; Nyström, M.; Persson, H.; Olsson, H.; Ståhl, G. Assessing Error Correlations in Remote Sensing-Based Estimates of Forest Attributes for Improved Composite Estimation. Remote Sens. 2018, 10, 667. [Google Scholar] [CrossRef]
- Meng, J.; Li, S.; Wang, W.; Liu, Q.; Xie, S.; Ma, W. Estimation of Forest Structural Diversity Using the Spectral and Textural Information Derived from SPOT-5 Satellite Images. Remote Sens. 2016, 8, 125. [Google Scholar] [CrossRef]
- Wolter, P.T.; Townsend, P.A.; Sturtevant, B.R. Estimation of forest structural parameters using 5 and 10 meter SPOT-5 satellite data. Remote Sens. Environ. 2009, 113, 2019–2036. [Google Scholar] [CrossRef]
- Bochenek, Z.; Ziolkowski, D.; Bartold, M.; Orlowska, K.; Ochtyra, A. Monitoring forest biodiversity and the impact of climate on forest environment using high-resolution satellite images. Eur. J. Remote Sens. 2018, 51, 166–181. [Google Scholar] [CrossRef]
- Racoviteanu, A.; Williams, M.W. Decision Tree and Texture Analysis for Mapping Debris-Covered Glaciers in the Kangchenjunga Area, Eastern Himalaya. Remote Sens. 2012, 4, 3078–3109. [Google Scholar] [CrossRef]
- Stournara, P.; Patias, P.; Karamanolis, D. Evaluating wood volume estimates derived from Quickbird imagery with GEOBIA for Pinus nigra trees in the Pentalofo forest, northern Greece. Remote Sens. Lett. 2017, 8, 96–105. [Google Scholar] [CrossRef]
- Li, W.; Dong, R.; Fu, H.; Yu, A.L. Large-Scale Oil Palm Tree Detection from High-Resolution Satellite Images Using Two-Stage Convolutional Neural Networks. Remote Sens. 2019, 11, 11. [Google Scholar] [CrossRef]
- Deutscher, J.; Perko, R.; Gutjahr, K.; Hirschmugl, M.; Schardt, M. Mapping Tropical Rainforest Canopy Disturbances in 3D by COSMO-SkyMed Spotlight InSAR-Stereo Data to Detect Areas of Forest Degradation. Remote Sens. 2013, 5, 648–663. [Google Scholar] [CrossRef]
- Hirata, Y.; Furuya, N.; Saito, H.; Pak, C.; Leng, C.; Sokh, H.; Ma, V.; Kajisa, T.; Ota, T.; Mizoue, N. Object-Based Mapping of Aboveground Biomass in Tropical Forests Using LiDAR and Very-High-Spatial-Resolution Satellite Data. Remote Sens. 2018, 10, 438. [Google Scholar] [CrossRef]
- Abdollahnejad, A.; Panagiotidis, D.; Shataee Joybari, S.; Surový, P. Prediction of Dominant Forest Tree Species Using QuickBird and Environmental Data. Forests 2017, 8, 42. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Wang, T.; Skidmore, A.; Vrieling, A.; O’Connor, B.; Gara, T.; Ens, B.; Paganini, M. Analysis of Sentinel-2 and RapidEye for Retrieval of Leaf Area Index in a Saltmarsh Using a Radiative Transfer Model. Remote Sens. 2019, 11, 671. [Google Scholar] [CrossRef]
- Wallner, A.; Elatawneh, A.; Schneider, T.; Knoke, T. Estimation of forest structural information using RapidEye satellite data. Forestry 2015, 88, 96–107. [Google Scholar] [CrossRef]
- Hojas Gascón, L.; Ceccherini, G.; García Haro, F.; Avitabile, V.; Eva, H. The Potential of High Resolution (5 m) RapidEye Optical Data to Estimate Above Ground Biomass at the National Level over Tanzania. Forests 2019, 10, 107. [Google Scholar] [CrossRef]
- Rana, P.; Tokola, T.; Korhonen, L.; Xu, Q.; Kumpula, T.; Vihervaara, P.; Mononen, L. Training Area Concept in a Two-Phase Biomass Inventory Using Airborne Laser Scanning and RapidEye Satellite Data. Remote Sens. 2014, 6, 285–309. [Google Scholar] [CrossRef]
- Schlund, M.; Davidson, M. Aboveground Forest Biomass Estimation Combining L- and P-Band SAR Acquisitions. Remote Sens. 2018, 10, 1151. [Google Scholar] [CrossRef]
- Tello, M.; Cazcarra-Bes, V.; Pardini, M.; Papathanassiou, K. Forest Structure Characterization From SAR Tomography at L-Band. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 3402–3414. [Google Scholar] [CrossRef]
- Brolly, M.; Woodhouse, I. Long Wavelength SAR Backscatter Modelling Trends as a Consequence of the Emergent Properties of Tree Populations. Remote Sens. 2014, 6, 7081–7109. [Google Scholar] [CrossRef]
- Ortiz, S.M.; Breidenbach, J.; Knuth, R.; Kändler, G. The Influence of DEM Quality on Mapping Accuracy of Coniferous- and Deciduous-Dominated Forest Using TerraSAR-X Images. Remote Sens. 2012, 4, 661–681. [Google Scholar] [CrossRef]
- Tian, J.; Wang, L.; Li, X.; Yin, D.; Gong, H.; Nie, S.; Shi, C.; Zhong, R.; Liu, X.; Xu, R. Canopy Height Layering Biomass Estimation Model (CHL-BEM) with Full-Waveform LiDAR. Remote Sens. 2019, 11, 1446. [Google Scholar] [CrossRef]
- González-Jaramillo, V.; Fries, A.; Zeilinger, J.; Homeier, J.; Paladines-Benitez, J.; Bendix, J. Estimation of Above Ground Biomass in a Tropical Mountain Forest in Southern Ecuador Using Airborne LiDAR Data. Remote Sens. 2018, 10, 660. [Google Scholar] [CrossRef]
- Pang, Y.; Li, Z.; Ju, H.; Lu, H.; Jia, W.; Si, L.; Guo, Y.; Liu, Q.; Li, S.; Liu, L.; et al. LiCHy: The CAF’s LiDAR, CCD and Hyperspectral Integrated Airborne Observation System. Remote Sens. 2016, 8, 398. [Google Scholar] [CrossRef]
- Chen, B.; Pang, Y.; Li, Z.; North, P.; Rosette, J.; Sun, G.; Suárez, J.; Bye, I.; Lu, H. Potential of Forest Parameter Estimation Using Metrics from Photon Counting LiDAR Data in Howland Research Forest. Remote Sens. 2019, 11, 856. [Google Scholar] [CrossRef]
- Hu, Y.; Wu, F.; Sun, Z.; Lister, A.; Gao, X.; Li, W.; Peng, D. The Laser Vegetation Detecting Sensor: A Full Waveform, Large-Footprint, Airborne Laser Altimeter for Monitoring Forest Resources. Sensors 2019, 19, 1699. [Google Scholar] [CrossRef]
- Drusch, M.; Del Bello, U.; Carlier, S.; Colin, O.; Fernandez, V.; Gascon, F.; Hoersch, B.; Isola, C.; Laberinti, P.; Martimort, P.; et al. Sentinel-2: ESA’s Optical High-Resolution Mission for GMES Operational Services. Remote Sens. Environ. 2012, 120, 25–36. [Google Scholar] [CrossRef]
- Persson, M.; Lindberg, E.; Reese, H. Tree Species Classification with Multi-Temporal Sentinel-2 Data. Remote Sens. 2018, 10, 1794. [Google Scholar] [CrossRef]
- Hościło, A.; Lewandowska, A. Mapping Forest Type and Tree Species on a Regional Scale Using Multi-Temporal Sentinel-2 Data. Remote Sens. 2019, 11, 929. [Google Scholar] [CrossRef]
- Pandit, S.; Tsuyuki, S.; Dube, T. Estimating Above-Ground Biomass in Sub-Tropical Buffer Zone Community Forests, Nepal, Using Sentinel 2 Data. Remote Sens. 2018, 10, 601. [Google Scholar] [CrossRef]
- Zarco-Tejada, P.J.; Hornero, A.; Beck, P.S.A.; Kattenborn, T.; Kempeneers, P.; Hernández-Clemente, R. Chlorophyll content estimation in an open-canopy conifer forest with Sentinel-2A and hyperspectral imagery in the context of forest decline. Remote Sens. Environ. 2019, 223, 320–335. [Google Scholar] [CrossRef] [PubMed]
- Lima, T.A.; Beuchle, R.; Langner, A.; Grecchi, R.C.; Griess, V.C.; Achard, F. Comparing Sentinel-2 MSI and Landsat 8 OLI Imagery for Monitoring Selective Logging in the Brazilian Amazon. Remote Sens. 2019, 11, 961. [Google Scholar] [CrossRef]
- Grabska, E.; Hostert, P.; Pflugmacher, D.; Ostapowicz, K. Forest Stand Species Mapping Using the Sentinel-2 Time Series. Remote Sens. 2019, 11, 1197. [Google Scholar] [CrossRef]
- Kumar, L.; Mutanga, O. Google Earth Engine Applications Since Inception: Usage, Trends, and Potential. Remote Sens. 2018, 10, 1509. [Google Scholar] [CrossRef]
- Mutanga, O.; Kumar, L. Google Earth Engine Applications. Remote Sens. 2019, 11, 591. [Google Scholar] [CrossRef]
- Amani, M.; Mahdavi, S.; Afshar, M.; Brisco, B.; Huang, W.; Mohammad Javad Mirzadeh, S.; White, L.; Banks, S.; Montgomery, J.; Hopkinson, C. Canadian Wetland Inventory using Google Earth Engine: The First Map and Preliminary Results. Remote Sens. 2019, 11, 842. [Google Scholar] [CrossRef]
- Lee, J.; Cardille, J.; Coe, M. BULC-U: Sharpening Resolution and Improving Accuracy of Land-Use/Land-Cover Classifications in Google Earth Engine. Remote Sens. 2018, 10, 1455. [Google Scholar] [CrossRef]
- Mahdianpari, M.; Salehi, B.; Mohammadimanesh, F.; Homayouni, S.; Gill, E. The First Wetland Inventory Map of Newfoundland at a Spatial Resolution of 10 m Using Sentinel-1 and Sentinel-2 Data on the Google Earth Engine Cloud Computing Platform. Remote Sens. 2019, 11, 43. [Google Scholar] [CrossRef]
- Ravanelli, R.; Nascetti, A.; Cirigliano, R.; Di Rico, C.; Leuzzi, G.; Monti, P.; Crespi, M. Monitoring the Impact of Land Cover Change on Surface Urban Heat Island through Google Earth Engine: Proposal of a Global Methodology, First Applications and Problems. Remote Sens. 2018, 10, 1488. [Google Scholar] [CrossRef]
- Sidhu, N.; Pebesma, E.; Câmara, G. Using Google Earth Engine to detect land cover change: Singapore as a use case. Eur. J. Remote Sens. 2018, 51, 486–500. [Google Scholar] [CrossRef]
- Sun, Z.; Xu, R.; Du, W.; Wang, L.; Lu, D. High-Resolution Urban Land Mapping in China from Sentinel 1A/2 Imagery Based on Google Earth Engine. Remote Sens. 2019, 11, 752. [Google Scholar] [CrossRef]
- Wang, Y.; Ma, J.; Xiao, X.; Wang, X.; Dai, S.; Zhao, B. Long-Term Dynamic of Poyang Lake Surface Water: A Mapping Work Based on the Google Earth Engine Cloud Platform. Remote Sens. 2019, 11, 313. [Google Scholar] [CrossRef]
- Zhang, K.; Dong, X.; Liu, Z.; Gao, W.; Hu, Z.; Wu, G. Mapping Tidal Flats with Landsat 8 Images and Google Earth Engine: A Case Study of the China’s Eastern Coastal Zone circa 2015. Remote Sens. 2019, 11, 924. [Google Scholar] [CrossRef]
- Hird, J.; DeLancey, E.; McDermid, G.; Kariyeva, J. Google Earth Engine, Open-Access Satellite Data, and Machine Learning in Support of Large-Area Probabilistic Wetland Mapping. Remote Sens. 2017, 9, 1315. [Google Scholar] [CrossRef]
- Hu, Y.; Hu, Y. Land Cover Changes and Their Driving Mechanisms in Central Asia from 2001 to 2017 Supported by Google Earth Engine. Remote Sens. 2019, 11, 554. [Google Scholar] [CrossRef]
- Aguilar, R.; Zurita-Milla, R.; Izquierdo-Verdiguier, E.; A De By, R. A Cloud-Based Multi-Temporal Ensemble Classifier to Map Smallholder Farming Systems. Remote Sens. 2018, 10, 729. [Google Scholar] [CrossRef]
- He, M.; Kimball, J.; Maneta, M.; Maxwell, B.; Moreno, A.; Beguería, S.; Wu, X. Regional Crop Gross Primary Productivity and Yield Estimation Using Fused Landsat-MODIS Data. Remote Sens. 2018, 10, 372. [Google Scholar] [CrossRef]
- Teluguntla, P.; Thenkabail, P.S.; Oliphant, A.; Xiong, J.; Gumma, M.K.; Congalton, R.G.; Yadav, K.; Huete, A. A 30-m landsat-derived cropland extent product of Australia and China using random forest machine learning algorithm on Google Earth Engine cloud computing platform. ISPRS J. Photogramm. 2018, 144, 325–340. [Google Scholar] [CrossRef]
- Tian, F.; Wu, B.; Zeng, H.; Zhang, X.; Xu, J. Efficient Identification of Corn Cultivation Area with Multitemporal Synthetic Aperture Radar and Optical Images in the Google Earth Engine Cloud Platform. Remote Sens. 2019, 11, 629. [Google Scholar] [CrossRef]
- Xiong, J.; Thenkabail, P.; Tilton, J.; Gumma, M.; Teluguntla, P.; Oliphant, A.; Congalton, R.; Yadav, K.; Gorelick, N. Nominal 30-m Cropland Extent Map of Continental Africa by Integrating Pixel-Based and Object-Based Algorithms Using Sentinel-2 and Landsat-8 Data on Google Earth Engine. Remote Sens. 2017, 9, 1065. [Google Scholar] [CrossRef]
- Liu, C.; Shieh, M.; Ke, M.; Wang, K. Flood Prevention and Emergency Response System Powered by Google Earth Engine. Remote Sens. 2018, 10, 1283. [Google Scholar] [CrossRef]
- Sazib, N.; Mladenova, I.; Bolten, J. Leveraging the Google Earth Engine for Drought Assessment Using Global Soil Moisture Data. Remote Sens. 2018, 10, 1265. [Google Scholar] [CrossRef]
- Sproles, E.A.; Crumley, R.L.; Nolin, A.W.; Mar, E.; Moreno, J.I.L. SnowCloudHydro—A New Framework for Forecasting Streamflow in Snowy, Data-Scarce Regions. Remote Sens. 2018, 10, 1276. [Google Scholar] [CrossRef]
- Condés, S.; McRoberts, R.E. Updating national forest inventory estimates of growing stock volume using hybrid inference. For. Ecol. Manag. 2017, 400, 48–57. [Google Scholar] [CrossRef]
- Chrysafis, I.; Chrysafis, I.; Mallinis, G.; Siachalou, S.; Patias, P. Assessing the relationships between growing stock volume and Sentinel-2 imagery in a Mediterranean forest ecosystem. Remote Sens Lett 2017, 8, 508–517. [Google Scholar] [CrossRef]
- Laurin, G.V.; Balling, J.; Corona, P.; Mattioli, W.; Papale, D.; Puletti, N.; Rizzo, M.; Truckenbrodt, J.; Urban, M. Above-ground biomass prediction by Sentinel-1 multitemporal data in central Italy with integration of ALOS2 and Sentinel-2 data. J. Appl. Remote Sens. 2018, 12, 1. [Google Scholar] [CrossRef]
- Torbick, N.; Ledoux, L.; Salas, W.; Zhao, M. Regional Mapping of Plantation Extent Using Multisensor Imagery. Remote Sens. 2016, 8, 236. [Google Scholar] [CrossRef]
- Vafaei, S.; Soosani, J.; Adeli, K.; Fadaei, H.; Naghavi, H.; Pham, T.; Tien Bui, D. Improving Accuracy Estimation of Forest Aboveground Biomass Based on Incorporation of ALOS-2 PALSAR-2 and Sentinel-2A Imagery and Machine Learning: A Case Study of the Hyrcanian Forest Area (Iran). Remote Sens. 2018, 10, 172. [Google Scholar] [CrossRef]
- Mauya, E.W.; Koskinen, J.; Tegel, K.; Hämäläinen, J.; Kauranne, T.; Käyhkö, N. Modelling and Predicting the Growing Stock Volume in Small-Scale Plantation Forests of Tanzania Using Multi-Sensor Image Synergy. Forests 2019, 10, 279. [Google Scholar] [CrossRef]
- Pham, T.; Yokoya, N.; Bui, D.; Yoshino, K.; Friess, D. Remote Sensing Approaches for Monitoring Mangrove Species, Structure, and Biomass: Opportunities and Challenges. Remote Sens. 2019, 11, 230. [Google Scholar] [CrossRef]
- Schepaschenko, D.; Chave, J.; Phillips, O.L.; Lewis, S.L.; Davies, S.J.; Réjou-Méchain, M.; Sist, P.; Scipal, K.; Perger, C.; Herault, B.; et al. The Forest Observation System, building a global reference dataset for remote sensing of forest biomass. Sci. Data 2019, 6, 198. [Google Scholar] [CrossRef]
- Abdi, E.; Mariv, H.S.; Deljouei, A.; Sohrabi, H. Accuracy and precision of consumer-grade GPS positioning in an urban green space environment. For. Sci. Technol. 2014, 10, 141–147. [Google Scholar] [CrossRef]
- Luo, K.; Tao, F. Monitoring of forest virtual water in Hunan Province, China, based on HJ-CCD remote-sensing images and pattern analysis. Int. J. Remote Sens. 2016, 37, 2376–2393. [Google Scholar] [CrossRef]
- Sun, X.; Li, B.; Du, Z.; Li, G.; Fan, Z.; Wang, M.; Yue, T. Surface Modelling of Forest Aboveground Biomass Based on Remote Sensing and Forest Inventory Data. Geocarto Int. 2019. [Google Scholar] [CrossRef]
- Liu, Q.; Meng, S.; Zhou, H.; Zhou, G.; Li, Y. Tree Volume Tables of China; China Forestry Publishing House: Beijing, China, 2017; p. 1107. [Google Scholar]
- Agency, E.S. Sentinel-2 User Handbook, Revision 2, ESA Standard Document; ESA: Paris, France, 2015; 64p. [Google Scholar]
- Xiao, X.; Boles, S.; Liu, J.; Zhuang, D.; Frolking, S.; Li, C.; Salas, W.; Moore, B. Mapping paddy rice agriculture in southern China using multi-temporal MODIS images. Remote Sens. Environ. 2005, 95, 480–492. [Google Scholar] [CrossRef]
- Wittke, S.; Yu, X.; Karjalainen, M.; Hyyppä, J.; Puttonen, E. Comparison of two-dimensional multitemporal Sentinel-2 data with three-dimensional remote sensing data sources for forest inventory parameter estimation over a boreal forest. Int. J. Appl. Earth Obs. 2019, 76, 167–178. [Google Scholar] [CrossRef]
- Xia, H.; Zhao, W.; Li, A.; Bian, J.; Zhang, Z. Subpixel Inundation Mapping Using Landsat-8 OLI and UAV Data for a Wetland Region on the Zoige Plateau, China. Remote Sens. 2017, 9, 31. [Google Scholar] [CrossRef]
- Shen, W.; Li, M.; Huang, C.; Tao, X.; Wei, A. Annual forest aboveground biomass changes mapped using ICESat/GLAS measurements, historical inventory data, and time-series optical and radar imagery for Guangdong province, China. Agric. For. Meteorol. 2018, 259, 23–38. [Google Scholar] [CrossRef]
- Adame-Campos, R.L.; Ghilardi, A.; Gao, Y.; Paneque-Gálvez, J.; Mas, J. Variables Selection for Aboveground Biomass Estimations Using Satellite Data: A Comparison between Relative Importance Approach and Stepwise Akaike’s Information Criterion. ISPRS Int. J. Geo-Inf. 2019, 8, 245. [Google Scholar] [CrossRef]
- Cho, J.; Lee, J. Multiple Linear Regression Models for Predicting Nonpoint-Source Pollutant Discharge from a Highland Agricultural Region. Water 2018, 10, 1156. [Google Scholar] [CrossRef]
- Niu, W.; Feng, Z.; Feng, B.; Min, Y.; Cheng, C.; Zhou, J. Comparison of Multiple Linear Regression, Artificial Neural Network, Extreme Learning Machine, and Support Vector Machine in Deriving Operation Rule of Hydropower Reservoir. Water 2019, 11, 88. [Google Scholar] [CrossRef]
- Wicki, A.; Parlow, E. Multiple Regression Analysis for Unmixing of Surface Temperature Data in an Urban Environment. Remote Sens. 2017, 9, 684. [Google Scholar] [CrossRef]
- Wang, J.; Xiao, X.; Bajgain, R.; Starks, P.; Steiner, J.; Doughty, R.B.; Chang, Q. Estimating leaf area index and aboveground biomass of grazing pastures using Sentinel-1, Sentinel-2 and Landsat images. ISPRS J. Photogramm. 2019, 154, 189–201. [Google Scholar] [CrossRef]
- Liu, J.; Zheng, H.; Zhang, Y.; Li, X.; Fang, J.; Liu, Y.; Liao, C.; Li, Y.; Zhao, J. Dissolved Gases Forecasting Based on Wavelet Least Squares Support Vector Regression and Imperialist Competition Algorithm for Assessing Incipient Faults of Transformer Polymer Insulation. Polymers 2019, 11, 85. [Google Scholar] [CrossRef]
- Omer, G.; Mutanga, O.; Abdel-Rahman, E.; Adam, E. Empirical Prediction of Leaf Area Index (LAI) of Endangered Tree Species in Intact and Fragmented Indigenous Forests Ecosystems Using WorldView-2 Data and Two Robust Machine Learning Algorithms. Remote Sens. 2016, 8, 324. [Google Scholar] [CrossRef]
- Silva, R.; Gomes, V.; Mendes-Faia, A.; Melo-Pinto, P. Using Support Vector Regression and Hyperspectral Imaging for the Prediction of Oenological Parameters on Different Vintages and Varieties of Wine Grape Berries. Remote Sens. 2018, 10, 312. [Google Scholar] [CrossRef]
- Tan, B.; Ke, X.; Tang, D.; Yin, S. Improved Perturb and Observation Method Based on Support Vector Regression. Energies 2019, 12, 1151. [Google Scholar] [CrossRef]
- Wu, C.; Shen, H.; Shen, A.; Deng, J.; Gan, M.; Zhu, J.; Xu, H.; Wang, K. Comparison of machine-learning methods for above-ground biomass estimation based on Landsat imagery. J. Appl. Remote Sens. 2016, 10, 35010. [Google Scholar] [CrossRef]
- Chen, L.; Wang, Y.; Ren, C.; Zhang, B.; Wang, Z. Optimal Combination of Predictors and Algorithms for Forest Above-Ground Biomass Mapping from Sentinel and SRTM Data. Remote Sens. 2019, 11, 414. [Google Scholar] [CrossRef]
- Dube, T.; Mutanga, O.; Elhadi, A.; Ismail, R. Intra-and-Inter Species Biomass Prediction in a Plantation Forest: Testing the Utility of High Spatial Resolution Spaceborne Multispectral RapidEye Sensor and Advanced Machine Learning Algorithms. Sensors 2014, 14, 15348–15370. [Google Scholar] [CrossRef]
- Kilham, P.; Hartebrodt, C.; Kändler, G. Generating Tree-Level Harvest Predictions from Forest Inventories with Random Forests. Forests 2019, 10, 20. [Google Scholar] [CrossRef]
- Ou, Q.; Lei, X.; Shen, C. Individual Tree Diameter Growth Models of Larch–Spruce–Fir Mixed Forests Based on Machine Learning Algorithms. Forests 2019, 10, 187. [Google Scholar] [CrossRef]
- Pullanagari, R.; Kereszturi, G.; Yule, I. Integrating Airborne Hyperspectral, Topographic, and Soil Data for Estimating Pasture Quality Using Recursive Feature Elimination with Random Forest Regression. Remote Sens. 2018, 10, 1117. [Google Scholar] [CrossRef]
- Soriano-Luna, M.; Ángeles-Pérez, G.; Guevara, M.; Birdsey, R.; Pan, Y.; Vaquera-Huerta, H.; Valdez-Lazalde, J.; Johnson, K.; Vargas, R. Determinants of Above-Ground Biomass and Its Spatial Variability in a Temperate Forest Managed for Timber Production. Forests 2018, 9, 490. [Google Scholar] [CrossRef]
- Breiman, L. RandomForests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Huang, W.; Swatantran, A.; Duncanson, L.; Johnson, K.; Watkinson, D.; Dolan, K.; O’Neil-Dunne, J.; Hurtt, G.; Dubayah, R. County-scale biomass map comparison: A case study for Sonoma, California. Carbon Manag. 2017, 8, 417–434. [Google Scholar] [CrossRef]
- Korhonen, L.; Hadib, P.P.A.; Rautiainen, M. Comparison of Sentinel-2 and Landsat 8 in the estimation of boreal forest canopy cover and leaf area index. Remote Sens. Environ. 2017, 195, 259–274. [Google Scholar] [CrossRef]
- Immitzer, M.; Vuolo, F.; Atzberger, C. First Experience with Sentinel-2 Data for Crop and Tree Species Classifications in Central Europe. Remote Sens. 2016, 8, 166. [Google Scholar] [CrossRef]
- Lin, S.; Li, J.; Liu, Q.; Li, L.; Zhao, J.; Yu, W. Evaluating the Effectiveness of Using Vegetation Indices Based on Red-Edge Reflectance from Sentinel-2 to Estimate Gross Primary Productivity. Remote Sens. 2019, 11, 1303. [Google Scholar] [CrossRef]
- Lu, D.; Mausel, P.; Brondı́zio, E.; Moran, E. Relationships between forest stand parameters and Landsat TM spectral responses in the Brazilian Amazon Basin. Forest Ecol. Manag. 2004, 198, 149–167. [Google Scholar] [CrossRef]
- Ou, G.; Li, C.; Lv, Y.; Wei, A.; Xiong, H.; Xu, H.; Wang, G. Improving Aboveground Biomass Estimation of Pinus densata Forests in Yunnan Using Landsat 8 Imagery by Incorporating Age Dummy Variable and Method Comparison. Remote Sens. 2019, 11, 738. [Google Scholar] [CrossRef]
- The Forestry Department of Hunan Province. Analysis Report of Hunan Forestry Statistics Annual Report 2017; Hunan, China, 2017; 11p. [Google Scholar]
- Ali, S.; Smith-Miles, K.A. Improved Support Vector Machine Generalization Using Normalized Input Space; Springer: Berlin/Heidelberg, Germany, 2006; Volume 4304, pp. 362–371. [Google Scholar]
- Payn, T.; Carnus, J.; Freer-Smith, P.; Kimberley, M.; Kollert, W.; Liu, S.; Orazio, C.; Rodriguez, L.; Silva, L.N.; Wingfield, M.J. Changes in planted forests and future global implications. Forest Ecol. Manag. 2015, 352, 57–67. [Google Scholar] [CrossRef]
- Zhang, L.; Shao, Z.; Liu, J.; Cheng, Q. Deep Learning Based Retrieval of Forest Aboveground Biomass from Combined LiDAR and Landsat 8 Data. Remote Sens. 2019, 11, 1459. [Google Scholar] [CrossRef]

| Sample Plot Type | Stock Volume (m³) | Proportion (%) |
|---|---|---|
| Total forest stock volume | 330,992,700 | 100.00 |
| Cunninghamia lanceolata | 109,035,700 | 32.94 |
| Pinus massoniana | 46,395,900 | 14.02 |
| Quercus sp. | 5,098,800 | 1.54 |
| Pinus elliottii | 3,020,400 | 0.91 |
| Populus sp. | 2,022,900 | 0.61 |
| Cinnamomum camphora | 2,244,100 | 0.68 |
| Cupressus funebris | 1,329,900 | 0.40 |
| Broad-leaved mixed forests | 84,515,000 | 25.53 |
| Coniferous and broad-leaved mixed forests | 36,681,900 | 11.08 |
| Coniferous mixed forests | 34,136,400 | 10.31 |
| Total | 324,481,000 | 98.00 |
| Tree Specie | Formula |
|---|---|
| Cunninghamia lanceolata | V = 0.000058777042D1.9699831H0.89646157 |
| Pinus massoniana | V = 0.000062341803D1.8551497H0.95682492 |
| Quercus sp. | V = 0.000050479055D1.9085054H0.99076507 |
| Pinus elliottii | V = 0.000086791543D(1.6638000575+0.0094299757(D+10H))H(0.9693404868-0.0292030826(D+2.5H)) |
| Populus sp. | V = 0.000041028005D1.8006303H1.13059897 |
| Cinnamomum camphora | V = 0.000050479055D1.9085054H0.99076507 |
| Cupressus funebris | V = 0.000058777042D1.9699831H0.89646157 |
| Characteristic Variable | Index Short Name | Calculation Method |
|---|---|---|
| Vegetation indices | NDVI_B5 | (B5 − B4)/(B5 + B4) |
| NDVI_B6 | (B6 − B4)/(B6 + B4) | |
| NDVI_B7 | (B7 − B4)/(B7 + B4) | |
| NDVI_B8 | (B8 − B4)/(B8 + B4) | |
| NDVI_B8A | (B8A − B4)/(B8A + B4) | |
| SAVI | 1.5*(B8 − B4)/(B8 + B4 + 0.5) | |
| RVI | B8/B4 | |
| MSI | B8/B11 | |
| EVI | 2.5*(B8 − B4)/(B8 + 6*B4 − 7.5*B2 + 1) | |
| EVI2 | 2.5*(B8 − B4)/(B8 + 2.4*B4 + 1) | |
| TCW | 0.1509*B2 + 0.1973*B3 + 0.3279*B4 + 0.3406*B8 + 0.7112*B11 + 0.4572*B12 | |
| TCB | 0.3037*B2 + 0.2793*B3 + 0.4734*B4 + 0.5585*B8 + 0.5082*B11 + 0.1863*B12 | |
| TCG | − 0.2848*B2 − 0.2435*B3 − 0.5436*B4 + 0.7243*B8 + 0.0840*B11 − 0.1800*B12 |
| Descriptive Statistics | Training Data | Transformed Training Data | Test Data | Transformed Test Data |
|---|---|---|---|---|
| Mean | 121.11 (m3 ha−1) | 3.98 | 120.53 (m3 ha−1) | 3.95 |
| Median | 103.33 (m3 ha−1) | 4.08 | 98.37 (m3 ha−1) | 4.02 |
| Minimum value | 1.42 (m3 ha−1) | 1.11 | 4.25 (m3 ha−1) | 1.55 |
| Maximum value | 577.49 (m3 ha−1) | 6.87 | 450.11 (m3 ha−1) | 6.37 |
| Variance | 9019.13 | 1.15 | 9053.02 | 1.24 |
| Kurtosis | 2.73 | −0.23 | 0.22 | −0.89 |
| Skewness | 1.40 | −0.18 | 0.89 | −0.11 |
| Number of sample plots | 321 | 321 | 138 | 138 |
| Estimate | Std. Error | t Value | P | |
|---|---|---|---|---|
| (Intercept) | 5.6320995 | 0.9240733 | 6.095 | 3.17e − 09 *** |
| B5 | −0.005478 | 0.0004089 | −13.397 | < 2e − 16 *** |
| MSI | 1.9034603 | 0.4423448 | 4.303 | 2.24e − 05 *** |
| Methods | Best Model Parameters | R2.training | RMSE.training (m3 ha−1) | R2.test | RMSE.test (m3 ha−1) | |
|---|---|---|---|---|---|---|
| Selected variables | RF | mtry = 5 | 0.91 | 35.13 | 0.58 | 65.03 |
| ntree = 257 | ||||||
| SVR | cost = 8 | 0.54 | 65.60 | 0.54 | 66.00 | |
| gamma = 0.125 | ||||||
| epsilon = 0.68 | ||||||
| All variables | RF | mtry = 7 | 0.92 | 34.83 | 0.58 | 66.04 |
| ntree = 495 | ||||||
| SVR | cost = 4 | 0.61 | 60.58 | 0.51 | 67.86 | |
| gamma = 0.04166667 | ||||||
| epsilon = 0.57 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, Y.; Xu, X.; Wu, F.; Sun, Z.; Xia, H.; Meng, Q.; Huang, W.; Zhou, H.; Gao, J.; Li, W.; et al. Estimating Forest Stock Volume in Hunan Province, China, by Integrating In Situ Plot Data, Sentinel-2 Images, and Linear and Machine Learning Regression Models. Remote Sens. 2020, 12, 186. https://doi.org/10.3390/rs12010186
Hu Y, Xu X, Wu F, Sun Z, Xia H, Meng Q, Huang W, Zhou H, Gao J, Li W, et al. Estimating Forest Stock Volume in Hunan Province, China, by Integrating In Situ Plot Data, Sentinel-2 Images, and Linear and Machine Learning Regression Models. Remote Sensing. 2020; 12(1):186. https://doi.org/10.3390/rs12010186
Chicago/Turabian StyleHu, Yang, Xuelei Xu, Fayun Wu, Zhongqiu Sun, Haoming Xia, Qingmin Meng, Wenli Huang, Hua Zhou, Jinping Gao, Weitao Li, and et al. 2020. "Estimating Forest Stock Volume in Hunan Province, China, by Integrating In Situ Plot Data, Sentinel-2 Images, and Linear and Machine Learning Regression Models" Remote Sensing 12, no. 1: 186. https://doi.org/10.3390/rs12010186
APA StyleHu, Y., Xu, X., Wu, F., Sun, Z., Xia, H., Meng, Q., Huang, W., Zhou, H., Gao, J., Li, W., Peng, D., & Xiao, X. (2020). Estimating Forest Stock Volume in Hunan Province, China, by Integrating In Situ Plot Data, Sentinel-2 Images, and Linear and Machine Learning Regression Models. Remote Sensing, 12(1), 186. https://doi.org/10.3390/rs12010186