Mask Sparse Representation Based on Semantic Features for Thermal Infrared Target Tracking

Abstract

Thermal infrared (TIR) target tracking is a challenging task as it entails learning an effective model to identify the target in the situation of poor target visibility and clutter background. The sparse representation, as a typical appearance modeling approach, has been successfully exploited in the TIR target tracking. However, the discriminative information of the target and its surrounding background is usually neglected in the sparse coding process. To address this issue, we propose a mask sparse representation (MaskSR) model, which combines sparse coding together with high-level semantic features for TIR target tracking. We first obtain the pixel-wise labeling results of the target and its surrounding background in the last frame, and then use such results to train target-specific deep networks using a supervised manner. According to the output features of the deep networks, the high-level pixel-wise discriminative map of the target area is obtained. We introduce the binarized discriminative map as a mask template to the sparse representation and develop a novel algorithm to collaboratively represent the reliable target part and unreliable target part partitioned with the mask template, which explicitly indicates different discriminant capabilities by label 1 and 0. The proposed MaskSR model controls the superiority of the reliable target part in the reconstruction process via a weighted scheme. We solve this multi-parameter constrained problem by a customized alternating direction method of multipliers (ADMM) method. This model is applied to achieve TIR target tracking in the particle filter framework. To improve the sampling effectiveness and decrease the computation cost at the same time, a discriminative particle selection strategy based on kernelized correlation filter is proposed to replace the previous random sampling for searching useful candidates. Our proposed tracking method was tested on the VOT-TIR2016 benchmark. The experiment results show that the proposed method has a significant superiority compared with various state-of-the-art methods in TIR target tracking.

1. Introduction

With the improvement of the imaging quality and resolution of thermal cameras, thermal infrared (TIR) target tracking has begun to attract many researchers’ attention in recent years. Compared with visual target tracking, TIR target tracking is capable of working in total darkness and is less susceptible to changes in external environment, such as lighting and shadows. Thus, it is important for both military and civil use [1,2]. However, there are some adverse factors that could influence the accuracy and robustness of the TIR target tracking. Firstly, the TIR images have the characteristics of low-contrast, low signal-to-noise ratio, low signal-to-clutter ratio and lack of color information [3,4], which cause a lot of difficulty in distinguishing the moving target from the background. Secondly, the deformation and scale change of the moving target also bring great challenges to the tracking task.

To handle these difficulties, several TIR tracking methods have been proposed, which can be categorized into discriminative tracking methods [5,6,7,8,9,10,11] and generative tracking methods [12,13,14,15,16,17,18]. Discriminative approaches formulate tracking as a classification task, which aims to find the target area whose features are most discriminative to the background. By comparison, generative approaches focus more on building an appearance model to describe the target. Accordingly, the final tracking result is determined by finding the candidate area with the maximum likelihood score. Sparse representation has drawn much attention in the generative tracking branch due to its good adaption to target appearance changes [13,14,17]. In the sparse representation-based method, the target templates are linearly combined to describe candidate images, while the negative templates are used to handle target partial occlusion, deformation, etc.

First, sparse representation-based tracking methods adopt a global model to describe the target, which is susceptible to target local appearance changes [17,19,20]. Afterwards, some local sparse models [21,22,23] are proposed successively, in which each target is divided into several rectangular image blocks by a sliding window. These local blocks are treated equally in the sparse coding process, regardless of the diverse discriminant capabilities of different object local parts. However, as shown in Figure 1, the human body wrapped by the yellow line is much easier to distinguish compared with the remaining area in the red bounding box, which is also annotated as the tracking target but actually belongs to the background. Current local sparse representation-based trackers neglect this problem and are prone to tracking drift when there are too many non-distinguishable pixels in some of the local patches.

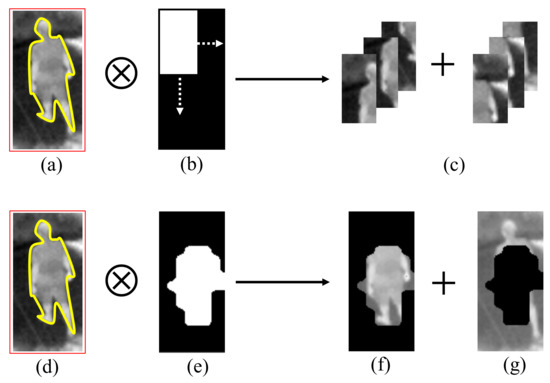
Figure 1. Comparison of the target partition using sliding window and semantic mask template. The upper part of the illustration shows the target partition approach using sliding window, and the lower part shows the target partition approach using semantic mask template: (a) tracking target area; (b) sliding window; (c) target local parts; (d) tracking target area; (e) semantic mask template; (f) reliable target partition; and (g) unreliable target partition.

This observation motivates an approach that can adaptively extract distinguishable/reliable pixels from the whole target area, and then use the reliable target part to refine the reconstruction output of the unreliable target part. Considering the benefit of strong discriminative ability of the deep convolutional neural networks (DCNN) [7,8,10,11,24], we propose a supervised learning manner to extract high-level semantic features of the target area. Based on the convolutional neural networks pre-trained for image classification, DCNN can learn information of salient objects at any position of the input image. In [25], a soft-mask module is added to an optical flow estimation network, which aims to mask out parts with consistency motions. The mask filters are trained by fixing the pre-trained weights. In this paper, we propose to add a channel selection layer after convolutional layers, which is more specific to the tracking task. With the pixel-wise labeling results of the target and its surrounding background in the last frame, the output channels are sorted and filtered to obtain target-specific features from DCNN.

The binarized semantic features are introduced as the mask template to extract reliable pixels with powerful discriminative capability, as shown in the lower part of Figure 1. In the proposed MaskSR model, the reliable target part (with label 1) and the unreliable target part (with label 0) correspond to their respective dictionary sets. For each candidate image, the MaskSR model enables representing its two local parts collaboratively by adding $l_1$ regularization to the difference between the sparse coefficients of the reliable part and unreliable part, aiming to preserve the category consistency of the same candidate area. On the other hand, the fidelity term of the reliable target part is assigned to a larger weight to ensure its superiority to the unreliable part in sparse coding. Therefore, our model fully considers the reliability of different target parts in distinguishing the target from the background. The multi-parameter problem is solved by a customized alternating direction method of multipliers (ADMM). The proposed mask sparse representation model is applied to achieve TIR object tracking under the particle filter framework. In the conventional particle filter method, the target motion parameters should be set in advance to perform Gaussian random sampling on the next frame. Moreover, to ensure efficient calculation, the number of particles cannot be too large, which makes it uncertain whether the scattered random particles cover the real target region. To solve the above two problems, we improve the random particle sampling strategy to discriminative particle selection, which is achieved by the kernel correlation filter method. Experiments on VOT-TIR2016 benchmark show that the developed method is effective for TIR object tracking.

In summary, the contributions of this paper include the following three points:

• To improve the ability of distinguishing the target from the clutter background, we propose a mask sparse representation method for target appearance modeling. In this model, the distinguishable and reliable pixels of the target are identified and are utilized to refine the reconstruction output of the unreliable target part.
• With the pixel-wise labeling results of the target and its surrounding background in the last frame, we develop a supervised manner to learn a high-level pixel-wise discriminative map of the target area. The binarized discrimination map is introduced in the MaskSR model to indicate discrimination capabilities of different object parts.
• The proposed MaskSR model is introduced in an improved particle filter framework to achieve TIR target tracking. We achieved state-of-the-art performance on VOT-TIR2016 benchmark, in terms of both robustness and accuracy evaluations.

The rest of this paper is organized as follows. In Section 2, some works that are closely related to ours are introduced. In Section 3, we present the details of our tracking framework. Section 4 shows the experiment results of the proposed tracker and the comparison results to other state-of-the-art tracking methods. Section 5 is the conclusion of the whole paper.

2. Related Work

Our work is focus on the formulation of the target appearance model and candidate searching strategy. Thus, we first review some TIR tracking methods based on deep learning and sparse representation. Then, the development of particle filter framework for object tracking is discussed afterwards.

2.1. Deep Learning-Based TIR Tracking Method

Deep convolutional neural networks (CNN) have made great progress in the visual classification task. However, there are some limitations for the usage of CNN in the TIR object tracking, which is mainly caused by the lack of labeled infrared image data and the unfitness of the location estimation task compared with label prediction. Many methods have been developed to address these two problems recently. In [11], an image-to-image transition model is employed to generate synthetic TIR data, on which they can train end-to-end optimal features for TIR tracking. By comparison, most existing methods directly adopt a pre-trained network on visual image set and transfer it to the TIR data. For example, in [8,26], a pre-trained Siamese network is utilized as a similarity function to evaluate the similarity between the initial target and candidates. To improve the accuracy of location estimation, some spatial related methods have been proposed [7,8,10] recently. The presented spatial-aware Siamese network in [8] combines spatial and semantic features of TIR object together to enhance the discriminative ability of the coalesced hierarchical feature. In [7], features are extracted from multiple convolutional layers and are used to construct multiple weak trackers to give response maps of the target’s location. The evaluation result in [27] has shown that the learned infrared features perform favorably against the hand-crafted features (HOG and Gist) in the correlation filter-based tracking framework.

2.2. Sparse Representation-Based TIR Tracking Method

From the presence of the $l_1$ tracker, the sparse representation model has been widely applied in object tracking, including the field of TIR object tracking. In [28], a discriminative sparse representation model is presented for infrared dim moving target tracking, in which the dictionary is composed of a target dictionary and a background dictionary. A sparsity-based discriminative classifier is proposed in [9] to evaluate the confidence of different target templates, of which the best template is used for calculating the convolution score of the candidate images. To explore the underlying relationship of multiple candidates, a low-rank sparse learning method is proposed in [13] that describes corruptions adaptively by finding the maximum-likelihood estimation solution of the residuals. Later, a multi-task Laplacian sparse representation is proposed in [1] to refine the sparse coefficients by deploying the similarity of each candidate pair. Due to the low-rank property of the infrared background, some decomposition-based methods have been proposed for TIR object tracking. A block-wise sparse representation-based tracker is proposed in [29], in which the infrared image is divided into overlapped blocks. These blocks are further decomposed into low-rank target components and sparse occlusion components with adaptive weighting parameters of different parts. A total variation term is further added to constrain the occlusion matrix in [18] to prevent the noise pixel from being separated into the occlusion term. Apart from the pure TIR object tracking, some methods integrate the RGB information of the corresponding visual data with the thermal information to achieve RGB-T object tracking [16,30,31,32,33]. In these methods, the joint sparse representation model is employed to ensure multiple modalities in appearance representation.

2.3. Particle Filter for Tracking

Particle filter framework models object tracking as a state estimation process, which is implemented by a Bayesian inference filter with Monte Carlo simulation. The dynamics between the states in two adjacent frames is usually modeled by a Brownian motion. In most tracking methods  [19,28,34], the state parameters are predicted independently by a Gaussian distribution. However, in these methods, many particles are needed to cover the states of the real target. In [15,35,36], the result of the saliency extraction is utilized as a prior knowledge of the transition probability model to limit the particle sampling process, which can improve the efficiency of particle sampling significantly. In [37], an improved particle filter framework is proposed to enhance the mean state estimation and resampling procedures, in which the number of high-weighted particles are determined adaptively by applying the k-means clustering over all particles’ weights. In [38], a multi-task correlation particle filter (MCPF) is proposed for object tracking, which can cover object state space well with a few particles. In this method, each particle corresponds to an image region enclosed by a bounding box instead of a single target state. The above-mentioned methods employ the particle filter approach to estimate the target space with affine space. In [39], Li et al. directly used it to infer whether the reliable patches are on the tracked object. In contrast to the traditional particle filters, they do not need to remove and resample particles at each frame. Instead, the posterior of each reliable patch can be employed to estimate the scale and position of the tracked target through a Hong Voting-like scheme.

3. Proposed Approach

In this section, we first introduce the method of building the target appearance model for TIR images, which is composed of two individual components, the target mask generation part in Section 3.1 and the mask sparse representation part in Section 3.2 and Section 3.3. Then, the proposed appearance model is applied to an improved particle filter framework with discriminative particle selection to achieve TIR object tracking, which is illustrated in Section 3.4. The algorithm overview and update strategy are shown in Section 3.5.

Besides, we use a uniform rule to define the notations in the following context. Capital letters are used to define matrices, bold lowercase letters are used to define vectors, and ordinary lowercase letters are used to define scalars.

3.1. Target Mask Generation

The network structure of the VGG-Net19 has received considerable attention in many CNN based trackers [7,24,40]. In this work, we adopt the popular VGG-Net19 pre-trained on the ImageNet dataset and transfer the first four convolutional layers of it to extract features of the TIR images. To obtain the high-level semantic attributes specific to the target area, we propose to add a channel selection layer after the layer of conv 4-4 to account for the channel entry with target area enhancement. This process is shown in Figure 2.

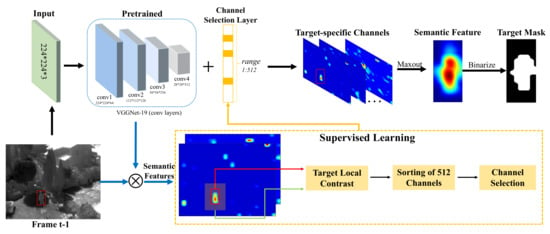
Figure 2. Illustration of generating binary mask template of the target based on CNN features.

In the online training stage, our goal is to use the given target and background classification labels to obtain high-level feature channels specific to the target area. The feature maps are firstly resized to the same size as the input image. Then, we use the local contrast value to evaluate the saliency of the target area in the feature maps. Denote $T_{x,y}\in R^{w\times h}$ as the target area, where $\left(x,y\right)$ and $\left(w,h\right)$ represent the target center position and target size, respectively, which are calibrated in the last frame. Its surrounding background is denoted as $B_{x,y}\in R^{w\left(1+s\right)\times h\left(1+s\right)}$, which is centered on $\left(x,y\right)$ and is s times larger than the target size. The average gray values of the target and its surrounding background are defined as follows:

$$t_{x,y}=\frac{1}{n_T}\sum T_{x,y}$$

(1)

$$b_{x,y}=\frac{1}{n_B}\left(\sum B_{x,y}-\sum T_{x,y}\right)$$

(2)

where $n_T$ and $n_B$ denote the target pixel number and background pixel number, respectively. The contrast value $c^j$ on the jth channel is defined as follows:

$$c^j=\frac{t_{x,y}^j}{b_{x,y}^j}$$

(3)

where $t_{x,y}^j$ and $b_{x,y}^j$ are the target area and background area extracted from the jth channel. After the local contrast values of all L channels are sorted, the indicating values of the first few channels are set to 1 and others are set to 0, which forms the channel selection layer. In this way, channels corresponding to larger local contrast are output as target-specific feature maps, while other entries are removed. Assuming that each feature map models a single part or multiple parts of the target, we adopt a maxout operation to extract useful target information among the output channels. The obtained feature map is further binarized to form a binary mask template of the target $\mathit{m}\in R^d$, where d is the dimension of the target.

3.2. Mask Sparse Representation Model

By adding the binary mask template $\mathit{m}$ to the input infrared image, the tracking object is divided into two partitions. Pixels corresponding to label 1 definitely belong to the reliable target part, while pixels corresponding to label 0 are denoted as the unreliable target part. Let $Y=\left\{{\mathit{y}}_1,{\mathit{y}}_2,\dots {\mathit{y}}_n\right\}\in R^{d\times n}$ denote the candidate target set, where d and n represent the dimension of the target and the number of candidates, respectively. Let $D=\left[D_{pos},D_{neg}\right]$ denote the dictionary base, which is composed of a positive dictionary set $D_{pos}=\left\{{\mathit{d}}_1,{\mathit{d}}_2,\dots {\mathit{d}}_p\right\}$ and a negative dictionary set $D_{neg}=\left\{{\mathit{d}}_{p+1},{\mathit{d}}_{p+2},\dots {\mathit{d}}_{p+q}\right\}$. Thus, the reliable candidate partition is denoted as $T_r=\left\{\mathit{m}\otimes {\mathit{y}}_1,\mathit{m}\otimes {\mathit{y}}_2,\dots \mathit{m}\otimes {\mathit{y}}_n\right\}$, the unreliable candidate partition is denoted as $T_{r^{\prime }}=\left\{\left(\mathbf{1}-\mathit{m}\right)\otimes {\mathit{y}}_1,\left(\mathbf{1}-\mathit{m}\right)\otimes {\mathit{y}}_2,\dots \left(\mathbf{1}-\mathit{m}\right)\otimes {\mathit{y}}_n\right\}$, the reliable dictionary partition is denoted as $D_r=\left\{\mathit{m}\otimes {\mathit{d}}_1,\mathit{m}\otimes {\mathit{d}}_2,\dots \mathit{m}\otimes {\mathit{d}}_{p+q}\right\}$, and the unreliable dictionary partition is denoted as $D_{r^{\prime }}=\left\{\left(\mathbf{1}-\mathit{m}\right)\otimes {\mathit{d}}_1,\left(\mathbf{1}-\mathit{m}\right)\otimes {\mathit{d}}_2,\dots \left(\mathbf{1}-\mathit{m}\right)\otimes {\mathit{d}}_{p+q}\right\}$. We use the reliable dictionary partition as the basis to reconstruct the reliable candidate partition. Meanwhile, the unreliable dictionary partition is utilized as the basis to reconstruct the unreliable candidate partition. The mask sparse representation model is shown as follows:

$$\underset{{\mathit{x}}_r,{\mathit{x}}_{r^{\prime }}}{argmin}\frac{w}{2}{∥D_r{\mathit{x}}_r-{\mathit{y}}_r∥}_2^2+\frac{1}{2}{∥D_{r^{\prime }}{\mathit{x}}_{r^{\prime }}-{\mathit{y}}_{r^{\prime }}∥}_2^2+{\lambda }_1{∥{\mathit{x}}_r∥}_1+{\lambda }_2{∥{\mathit{x}}_{r^{\prime }}∥}_1+{\lambda }_3{∥{\mathit{x}}_r-{\mathit{x}}_{r^{\prime }}∥}_1$$

(4)

where ${\mathit{x}}_r$ and ${\mathit{x}}_{r^{\prime }}$ are the sparse coefficient vectors corresponding to representation of the reliable target part and the unreliable target part, respectively. w is the reliable weight, which is a constant larger than 1. ${\lambda }_1$, ${\lambda }_2$ and ${\lambda }_3$ are balance parameters.

The first and second terms of Equation (4) represent the reconstruction error of the reliable target part and the unreliable target part, respectively. According to Section 3.1, the reliable part is the target area corresponding to more salient semantic features, which means this part has better discriminative ability on distinguishing the target from its surrounding background compared with the unreliable part. Therefore, a larger weight is assigned to the first penalty function to ensure a higher reconstruction accuracy of the reliable target part. When w is set to 1, these two terms can be combined together, and the mask sparse representation model is equal to the traditional sparse representation model.

For the representation of a single candidate, the obtained non-zero coefficients of the reliable part and the unreliable part may correspond to different dictionary subsets, which will cause ambiguity on deciding which category the candidate area belongs to. To solve this problem, a constraint term ${∥{\mathit{x}}_r-{\mathit{x}}_{r^{\prime }}∥}_1$ is added to the mask sparse representation model. The difference between the coefficients $x_r$ and $x_{r^{\prime }}$ is induced to be sparse by an $l_1$ norm, which aims to encourage one candidate target to share the same template basis d across different target partitions.

3.3. Optimization Approach

The objective function defined in Equation (4) is a convex problem which includes two variables ${\mathit{x}}_r$ and ${\mathit{x}}_{r^{\prime }}$ to be solved. We adopt the alternating direction method of multipliers (ADMM) to optimize one variable by fixing another one. More in detail, we first solve over ${\mathit{x}}_r^{\left(k+1\right)}$ given $\left({\mathit{x}}_{r^{\prime }}^{\left(k\right)},{\mathit{z}}_1^{\left(k\right)},{\mathit{z}}_3^{\left(k\right)},{\mathit{u}}_1^{\left(k\right)},{\mathit{u}}_3^{\left(k\right)}\right)$, and then for ${\mathit{x}}_{r^{\prime }}^{\left(k+1\right)}$ given $\left({\mathit{x}}_r^{\left(k+1\right)},{\mathit{z}}_2^{\left(k\right)},{\mathit{z}}_3^{\left(k\right)},{\mathit{u}}_2^{\left(k\right)},{\mathit{u}}_3^{\left(k\right)}\right)$. The algorithm flow of ADMM is summarized in Algorithm 1. See Appendix A for formula derivation.

Algorithm 1 Optimization approach for solving the proposed mask sparse representation model via ADMM

Input: dictionary $D_r$ and $D_{r^{\prime }}$, candidate ${\mathit{y}}_r$ and ${\mathit{y}}_{r^{\prime }}$, reliable weight w, regularized parameters ${\lambda }_1$, ${\lambda }_2$ and ${\lambda }_3$, penalty parameters ${\rho }_1$, ${\rho }_2$ and ${\rho }_3$, relaxation parameters $\alpha$, iteration number $MAX\_ITER$ 1.35  Initialize:${\mathit{x}}_{r^{\prime }}^{\left(k\right)}={\mathit{z}}_1^{\left(k\right)}={\mathit{z}}_2^{\left(k\right)}={\mathit{z}}_3^{\left(k\right)}={\mathit{u}}_1^{\left(k\right)}={\mathit{u}}_2^{\left(k\right)}={\mathit{u}}_3^{\left(k\right)}=0\in R^{\left(p+q\right)\times 1}$  while not converged do   Step 1: update variable $x_r^{\left(k+1\right)}$: ${\mathit{x}}_r^{\left(k+1\right)}=\underset{{\mathit{x}}_r}{argmin}{L}_{{\rho }_1,{\rho }_3}\left({\mathit{x}}_r;{\mathit{x}}_{r^{\prime }}^{\left(k\right)},{\mathit{z}}_1^{\left(k\right)},{\mathit{z}}_3^{\left(k\right)},{\mathit{u}}_1^{\left(k\right)},{\mathit{u}}_3^{\left(k\right)}\right)$   Step 2: update variable ${\mathit{x}}_{r^{\prime }}^{\left(k+1\right)}$: ${\mathit{x}}_{r^{\prime }}^{\left(k+1\right)}=\underset{{\mathit{x}}_{r^{\prime }}}{argmin}{L}_{{\rho }_2,{\rho }_3}\left({\mathit{x}}_{r^{\prime }};{\mathit{x}}_r^{\left(k+1\right)},{\mathit{z}}_2^{\left(k\right)},{\mathit{z}}_3^{\left(k\right)},{\mathit{u}}_2^{\left(k\right)},{\mathit{u}}_3^{\left(k\right)}\right)$   Step 3: update auxiliary variables ${\mathit{z}}_1^{\left(k+1\right)}$, ${\mathit{z}}_2^{\left(k+1\right)}$ and ${\mathit{z}}_3^{\left(k+1\right)}$: $$\begin{gathered} \begin{array}{c}{\mathit{z}}_1^{\left(k+1\right)}=\underset{{\mathit{z}}_1}{argmin}{L}_{{\rho }_1}\left({\mathit{z}}_1;{\mathit{x}}_r^{\left(k+1\right)},{\mathit{u}}_1^{\left(k\right)}\right) \\ {\mathit{z}}_2^{\left(k+1\right)}=\underset{{\mathit{z}}_2}{argmin}{L}_{{\rho }_2}\left({\mathit{z}}_2;{\mathit{x}}_{r^{\prime }}^{\left(k+1\right)},{\mathit{u}}_2^{\left(k\right)}\right) \\ {\mathit{z}}_3^{\left(k+1\right)}=\underset{{\mathit{z}}_3}{argmin}{L}_{{\rho }_3}\left({\mathit{z}}_3;{\mathit{x}}_r^{\left(k+1\right)},{\mathit{x}}_{r^{\prime }}^{\left(k+1\right)},{\mathit{u}}_3^{\left(k\right)}\right)\hfill \end{array} \end{gathered}$$   Step 4: update dual variables ${\mathit{u}}_1^{\left(k+1\right)}$, ${\mathit{u}}_2^{\left(k+1\right)}$, ${\mathit{u}}_3^{\left(k+1\right)}$: $$\begin{gathered} \begin{array}{c}{\mathit{u}}_1^{\left(k+1\right)}/\phantom{{\mathit{u}}_1^{\left(k+1\right)}{\rho }_1}{\rho }_1={\mathit{u}}_1^{\left(k\right)}/\phantom{{\mathit{u}}_1^{\left(k\right)}{\rho }_1}{\rho }_1+\left({\mathit{x}}_r^{\left(k+1\right)}-{\mathit{z}}_1^{\left(k+1\right)}\right) \\ {\mathit{u}}_2^{\left(k+1\right)}/\phantom{{\mathit{u}}_2^{\left(k+1\right)}{\rho }_2}{\rho }_2={\mathit{u}}_2^{\left(k\right)}/\phantom{{\mathit{u}}_2^{\left(k\right)}{\rho }_2}{\rho }_2+\left({\mathit{x}}_{r^{\prime }}^{\left(k+1\right)}-{\mathit{z}}_2^{\left(k+1\right)}\right) \\ {\mathit{u}}_3^{\left(k+1\right)}/\phantom{{\mathit{u}}_3^{\left(k+1\right)}{\rho }_3}{\rho }_3={\mathit{u}}_3^{\left(k\right)}/\phantom{{\mathit{u}}_3^{\left(k\right)}{\rho }_3}{\rho }_3+\left({\mathit{x}}_r^{\left(k+1\right)}-{\mathit{x}}_{r^{\prime }}^{\left(k+1\right)}-{\mathit{z}}_3^{\left(k+1\right)}\right)\hfill \end{array} \end{gathered}$$  end while  Output: sparse coefficient vectors ${\mathit{x}}_r^{\left(k+1\right)}$, ${\mathit{x}}_{r^{\prime }}^{\left(k+1\right)}$

3.4. Particle Filter Framework with Discriminative Particle Selection

In the particle filter-based tracking method, the posterior distribution of the target state $Z_t$ at time t is approximated by a finite set of particles $I^{1:t}$ via the Bayesian inference:

$$p\left(Z^t\left|I^{1:t}\right.\right)\propto p\left(I^t\left|Z^t\right.\right)\int p\left(Z^t\left|Z^{t-1}\right.\right)p\left(Z^{t-1}\left|I^{1:t-1}\right.\right)d{Z}^{t-1}$$

(5)

where $p\left(Z^t\left|Z^{t-1}\right.\right)$ represents the state transition model and $p\left(I^t\left|Z^t\right.\right)$ is the observation model. The optimal target state for time t is obtained from the maximal estimation of $p\left(Z^t\left|I^{1:t}\right.\right)$. Thus, the construction of these two models formulate the core problem of object tracking.

In our tracking approach, the mask sparse representation method is employed as the observation model, where reconstruction errors generated from two target partitions are adopted to calculate the likelihood probability of candidate samples:

$$p\left(I^t\left|Z^t\right.\right)=exp\left(-\frac{{∥D_r\left(:,1:p\right){\mathit{x}}_r\left(1:p\right)-{\mathit{y}}_r∥}_2^2+{∥D_{r^{\prime }}\left(:,1:p\right){\mathit{x}}_{r^{\prime }}\left(1:p\right)-{\mathit{y}}_{r^{\prime }}∥}_2^2}{{\sigma }^2}\right)$$

(6)

From Equation (6), we can see that the efficiency of the likelihood estimation is determined by the number of particles at time t. In the traditional particle filter framework, the state parameters of $Z^t$ are generally denoted as $\left(x,y,s,\theta ,\alpha ,\varphi \right)$, which represent displacement in x-axis, displacement in y-axis, scale, rotation, aspect ratio and skew angle, respectively [19]. In the conventional particle filter method, the state transition parameters between two frames are modeled by Gaussian distribution, with every state parameter being treated independently with each other:

$$p\left(Z^t\left|Z^{t-1}\right.\right)=N\left(Z^t;Z^{t-1},\Phi \right)$$

(7)

where $\Phi =\left({\sigma }_x,{\sigma }_y,{\sigma }_s,{\sigma }_{\theta },{\sigma }_{\alpha },{\sigma }_{\varphi }\right)$ represents the affine variance. To ensure that the real target state is covered in the state transition process, many particles are needed, which will increase the computation cost of solving the mask sparse model. The visualization of the random particle sampling modeled by Gaussian distribution is shown in Figure 3a. To address this contradictory issue, we propose a discriminative particle selection method to construct the state model more effectively.

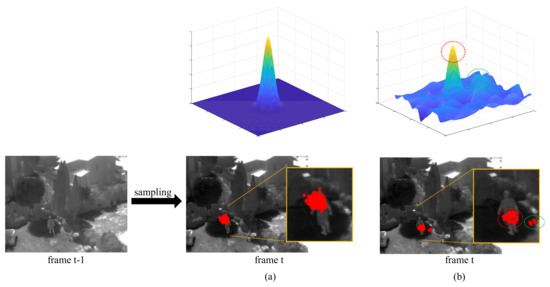
Figure 3. Visualization of particle distribution: (a) 300 particles are sampled, which are modeled by the Gaussian distribution; snf (b) 50 discriminative particles are drawn according to the peak values of the response map obtained from the correlation filter.

We note that the output of the correlation filter [41] can provide a rough prediction of the existence of the tracking object. On the other hand, the training of the correlation filter is very efficient, which can achieve millisecond order of magnitude. As shown in Figure 3b, the positions of the peak values appearing on the response map are selected as latent target states, to which the target areas correspond are further modeled by the mask sparse representation method. In the simple scenario, there is a single peak in the response map, which is the position of the target. In complex scenarios, multiple peaks appear in the response map, as shown in Figure 3. These local peaks have potential discriminative ability for the target and are selected to form the candidate set. After obtaining the placement state of the target, a scale filter is applied to obtain the optimal target scale, the details of which are described in [42].

3.5. Algorithm Overview and Update Strategy

The algorithm flow of our proposed tracking approach is shown in Algorithm 2. The method of obtaining the target mask has been described in Section 3.1. Detailed theory of the correlation filter and the scale filter can be found in [41,42]. Steps 1–5 of the tracking implementation process are described in Section 3.2 and Section 3.3. In this subsection, we first introduce the details on how to construct and update dictionary for target representation, and then present the update criteria for Steps 7–9.

Algorithm 2 The proposed approach for TIR object tracking

Input:   image sequence $\left\{f_1,f_2,\dots f_{frame\_end}\right\}$   target position in the first frame ${\mathit{s}}_{\mathbf{1}}$   target deep features in the first frame $featur{e}_1$  Initialize:   construct object dictionary D   obtain target mask $\mathit{m}$   correlation filter   scale filter  for$f=2$ to $frame\_end$ do   1. generate discriminative particles with correlation filter   2. construct the mask sparse representation model according to Eq (4)   3. compute the likelihood value of each particle (candidate) by Eq (14)   4. obtain the optimal target position   5. compute the optimal scale factor by scale filter   6. update object dictionary D   7. update target mask $\mathit{m}$   8. update correlation filter   9. update scale filter  end for  Output: target states: ${\mathit{s}}_2:{\mathit{s}}_{frame\_end}$

In this work, positive and negative dictionaries are constructed separately. The target state in the first frame is initialized by the ground truth data. Firstly, we adopt the areas surrounding the real target position as positive templates, and areas far away from the real target position as negative templates. Then, the eigenbasis vectors extracted from the positive template set are employed as the positive dictionary basis, which aims to preserve the information different observations have in common. The negative templates are directly utilized as the negative dictionary basis. Both the positive dictionary and the negative dictionary need to be updated in the tracking process to adapt to target appearance changes, as well as scene variations. For the positive dictionary, the target templates need to be updated frequently due to the inevitable appearance changes caused by target motion. However, if we update the templates too frequently, wrong tracking results may be introduced into the template set and cause tracking drift. Thus, we employ the cumulative probability-based method [21] to update the earlier accurate tracking results at a slow pace and update the newly entrant templates at a fast pace. The update probabilities for templates from older to newer ones are generated as:

$$L_p=\left\{0,\frac{1}{2^n-1},\frac{3}{2^n-1},\dots 1\right\}$$

(8)

The template to be replaced is determined by which interval the random number $r\in \left[0,1\right]$ lies in. The new positive dictionary is formulated by adding $\mathit{p}$ to the end of the old dictionary:

$$\mathit{q}=\underset{\mathit{q}}{argmin\frac{1}{2}}{∥\mathit{p}-\left[\begin{array}{cc}U& D_{neg}\end{array}\right]\left[\begin{array}{c}\mathit{q}\\ \mathit{e}\end{array}\right]∥}_2^2+\lambda {∥\left[\begin{array}{c}\mathit{q}\\ \mathit{e}\end{array}\right]∥}_1$$

(9)

where U represents the eigenbasis vectors and $\mathit{p}$ is the new observation. The new entrant $\mathit{q}$ is the target area removing noises and occlusion.

We propose a relatively strict criterion to update the negative dictionary with a slow pace to avoid bringing the target into it. The likelihood probability of the optimal observation in the second frame is denoted as a reference value ${conf}_{ref}$. When the maximum likelihood probability in the current frame exceeds $th\times {conf}_{ref}$, the current tracking result is regarded as a reliable new target. Then, the background areas extracted from this frame are used to form the new negative dictionary. Otherwise, the negative dictionary remains unchanged.

When the target result is considered to be reliable, the target mask, correlation filter and scale filter are updated with a fixed learning rate. Equation (10) takes the update for target mask as an example.

$$\mathit{m}=\left(1-\gamma \right){\mathit{m}}_{old}+\gamma {\mathit{m}}_{new}$$

(10)

4. Experiments

We first set the experiment environment in Section 4.1, including the parameters of our tracking approach and the testing dataset. The evaluation metrics for method comparison are introduced in Section 4.2. The parameter setting for optimization is discussed in Section 4.3. The quantitative and qualitative comparisons of our tracker with other state-of-the-art methods are given in Section 4.4 and Section 4.5, respectively.

4.1. Experiment Setup

The corresponding parameters of our tracker are given as follows. In the candidate searching stage, we crop a searching area which is 1.5 times larger than the size of the target in the last frame. The regularization parameter of the KCF tracker is set to ${10}^{-4}$. Fifty discriminative particles are drawn according to the peak values of the correlation filter response map. In the mask sparse representation stage, the infrared images are input into the VGG-Net19 pre-trained on the ImageNet dataset to extract deep features. Ten channels are selected from the convolution layer conv 4-4 as the output of target specific feature maps. The weight of the fidelity term for the reliable target part is set to $1.5$. The regularization parameters of the MaskSR model ${\lambda }_1$, ${\lambda }_2$ and ${\lambda }_3$ are set to $0.01$, $0.01$ and $0.005$, respectively. In the optimization stage, the penalty parameters ${\rho }_1$, ${\rho }_2$ and ${\rho }_3$ are set to 1. For the scale searching, we use the same parameters as DSST method [42], which includes 17 scales with a scale factor of $1.02$. The learning rates of the correlation filter and scale filter are set to $0.01$ and $0.1$, respectively. The update rate of the binary mask is set to $0.01$. We conducted the simulation experiments of our proposed method in Matlab 2017b combined with the Matconvnet toolbox. The proposed method ran at 1.2 fps averagely on a laptop with an Intel i7-6700HQ CPU at 2.60 GHz and 16.0 GB RAM.

We carried out the comparison experiment on the VOT-TIR2016 benchmark. This dataset includes 25 TIR sequences, with the minimum length of 92 frames and the maximum length of 1420 frames. The tracking objects include pedestrian, vehicle and animal with five challenging attributes annotated on each frame: camera motion, dynamics change, motion change, occlusion and size change.

4.2. Evaluation Metrics

The benchmark for VOT-TIR2016 has a re-start scheme, which means when the tracking fails, the tracker will be re-initialized after five frames. Accordingly, two performance measures, accuracy (A) and robustness (R), are used as evaluation metrics [43]. The accuracy is calculated by the overlap rate between the predicted bounding box and the ground truth during successful tracking period. The robustness measures the likelihood that the tracker will not fail in S frames, which is based on the number of tracking failures in a new sequence. It is calculated by:

$$\begin{array}{c}{R}_o={\displaystyle \sum _{j=0}^Q}{F}^j\hfill \\ R=e^{-S\frac{R_o}{Q}}\hfill \end{array}$$

(11)

where Q represents the sequence length on each attributes and $F^j$ is the failure number. Another measure called expected average overlap ($EAO$) is used to combine A and R together. To calculate this measure, the tracker is only initialized at the beginning of the sequence. When it drifts off the target, the remaining overlap rate is set to 0. Thus, the average overlap is computed by:

$${\mathrm{\Phi }}_{N_s}=\frac{1}{N_s}\sum _{i=1}^{N_s}{\Phi }_i$$

(12)

where ${\mathrm{\Phi }}_i$ is the per-frame overlap including the zero overlaps after failure. The $EAO$ measure $\Phi$ is calculated over an interval $\left[N_{lo},N_{hi}\right]$ as follows. The interval is provided by the benchmark.

$$\mathrm{\Phi }=\frac{1}{N_{hi}-N_{lo}}\sum _{N_s=N_{lo}:N_{hi}}{\mathrm{\Phi }}_{N_s}$$

(13)

4.3. Parameter Analysis

Several parameters play important roles in solving the MaskSR model. In this section, we set two comparison experiments to discuss the effect of the penalty parameter $\rho$ and the regularization parameter ${\lambda }_3$ on the convergence of ADMM.

(1)

Effect of ${\rho }_1$, ${\rho }_2$ and ${\rho }_3$

The penalty parameter $\rho$ is usually set to 1 in the standard ADMM algorithm. To test the effect of different $\rho$ on the convergence speed, we conducted several numerical examples. The convergence of ADMM was evaluated by the primal residuals ${∥r^{\left(k+1\right)}∥}_2$ and dual residuals ${∥s^{\left(k+1\right)}∥}_2$, which are denoted by:

$$\begin{array}{c}{r}^{\left(k+1\right)}=x^{\left(k+1\right)}-z^{\left(k+1\right)}\hfill \\ s^{\left(k+1\right)}=z^{\left(k+1\right)}-z^{\left(k\right)}\hfill \end{array}$$

(14)

Figure 4a shows the dual residuals and primal residuals when ${\rho }_1=0.8,1.0,1.2$, respectively. Similarly, Figure 4b,c shows the convergence performance with different ${\rho }_2$ and ${\rho }_3$. We can see that, with the increase of $\rho$, the convergence speed of dual residuals decreases; however, the convergence speed of primal residuals improves. Thus, we define $\rho =1$ to balance the convergence performance of these two characters.

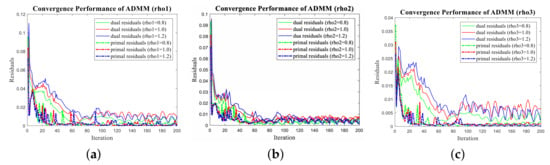
Figure 4. Convergence of primal residuals and dual residuals with different penalty parameters: (a) testing on penalty ${\rho }_1$; (b) testing on penalty ${\rho }_2$; and (c) testing on penalty ${\rho }_3$.

(2)

Effect of ${\lambda }_3$

The parameter ${\lambda }_3$ influences the sparseness degree of $x_r-x_r^{\prime }$. A larger ${\lambda }_3$ can lead to a better performance on refining the representation result of the unreliable target part. However, when ${\lambda }_3$ is set too large, the optimization process cannot converge. As shown in Figure 5, when ${\lambda }_3$ is set to 0.01, which is equal to the value of ${\lambda }_1$ and ${\lambda }_2$, both the dual residual plot (Figure 5a) and the primal residual plot (Figure 5b) diverge. Thus, we set ${\lambda }_3$ to 0.005 to guarantee the convergence of the optimization process.

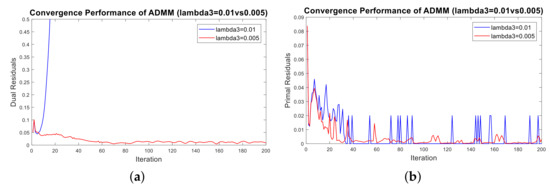
Figure 5. Convergence of primal residuals and dual residuals with different regularization parameters: (a) primal residuals of ${\lambda }_3=0.01$ vs. ${\lambda }_3=0.005$; and (b) dual residuals of ${\lambda }_3=0.01$ vs. ${\lambda }_3=0.005$.

4.4. Quantitative Comparison

We compared our tracker with other 19 state-of-the-art trackers on VOT-TIR2016 in the quantitative comparison experiment: two convolutional neural network based trackers, deepMKCF [44] and MDNet_NoTrain [43]; six discriminative correlation filter-based trackers, DSST [42], MvCFT [45], NSAMF [46], SKCF [47], SRDCF [48] and Staple+ [43]; seven part-based trackers, BDF [49], BST [43], DPCF [50], DPT [51], FCT [43], GGT2 [52] and LT_FLO [43]; one mean-shift based tracker, PKLTF [49]; one tracking-by-detection tracker, DAT [43]; and two fusion based trackers, LOFT_Lite [43] and MAD [43]. We removed the SRDCFir tracker [43] because it uses motion threshold to focus more on the performance evaluation of the target appearance model of different trackers.

There are three types of AR raw plot and AR rank plot in Figure 6. The mean AR raw plot and mean AR rank plot were obtained by the average values and averages ranks of seven attributes (including six challenging attributes and one empty tag). The weighted mean AR raw plot and weighted mean AR rank plot take the sequence length of each attribute into account. The pooled plots gather all frames and compute values and ranks on a single combined sequence. In all three rank plots, the proposed method achieves the best robustness, which means our tracker has the least failure probability on sequences with 100 frames. In the accuracy evaluation, the proposed tracker is not as good as the MDNet_NoTrain tracker, deepMKCF tracker, Staple+ and DSST tracker according to the pooled measurement. However, the accuracy difference between these trackers is very slight. On the other hand, the low failure number of our tracker will also influence the average value of the overlap rate. Thus, we further show the EAO comparison of 20 trackers in Figure 7 and Figure 8, which show the proposed tracker gives the best overall performance in the TIR object tracking.

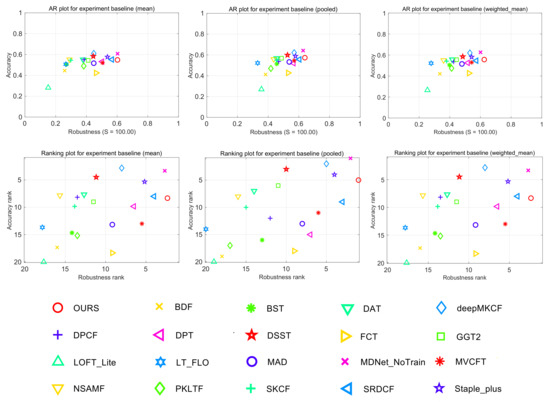
Figure 6. The overall AR raw plots and the AR rank plots of the 20 compared trackers on VOT-TIR2016.

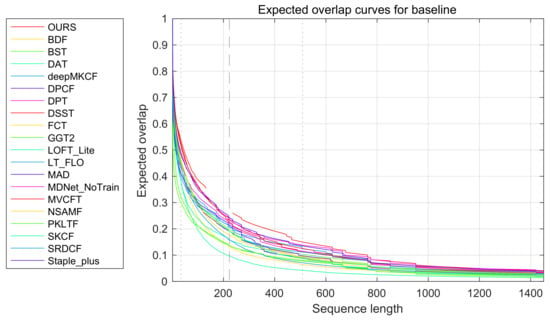
Figure 7. Expected overlap curves of the 20 compared trackers on VOT-TIR2016.

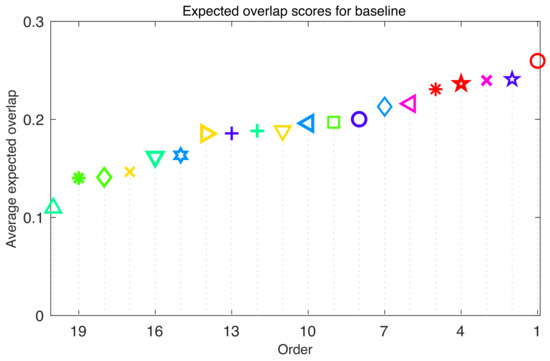
Figure 8. Expected overlap scores of 20 compared trackers on VOT-TIR2016 (see Figure 6 for legend).

To illustrate the tracking performance of trackers on different challenging scenarios, we show the accuracy ranking plot and robustness ranking plot with respect to six visual attributes in Figure 9: camera motion, dynamics change, empty tag, motion change, occlusion and size change. In the robustness evaluation, our tracker ranks first in the situation of camera motion, dynamics change, size change and empty. In the two other situations of occlusion and motion change, our tracker ranks fourth and sixth, respectively. The MDNet_NoTrain tracker and SRDCF tracker achieve the best performance in the occlusion and motion change scenarios, respectively. According to the accuracy ranking, our tracker achieves better performance in the situation of size change, motion change and empty. By comparison, two CNN based trackers, the MDNet tracker and deepMKCF tracker, locate the target more accurately in the tracking process. As shown in Table 1, the accuracy of the MDNet_NoTrain tracker is 1.8% and 9.7% higher than the proposed tracker in the situation of empty and size change, respectively. However, the robustness of the proposed tracker is 1.5% and 4.5% higher than the MDNet_NoTrain tracker, respectively. Similarly, the accuracy of the deepMKCF tracker is 20.5% and 17.2% higher than the proposed tracker, while the robustness of the proposed tracker is 19.6% and 211% higher than the deepMKCF tracker, respectively. Generally speaking, the correlation filter based trackers and CNN based trackers have better performance on the TIR object tracking.

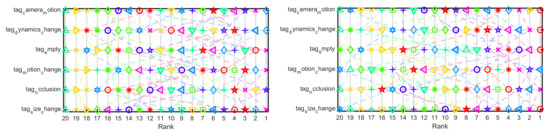
Figure 9. Accuracy ranking and robustness ranking of 20 trackers on six different attributes (see Figure 6 for legend).

Table 1. Quantitative results of expected average overlap (EAO), Accuracy (A) and Robustness (R) of the eight best trackers. The best, second best and the third best trackers in different situations are marked by */**/***, respectively.

Measurements		Staple+	MDNet_N	DSST	MVCFT	DPT	deepMKCF	MAD	Ours
ALL	EAO	0.241 **	0.240 ***	0.237	0.231	0.216	0.213	0.200	0.260 *
Camera Motion	A	0.584 ***	0.611 **	0.559	0.520	0.561	0.623 *	0.494	0.517
	R	0.517**	0.496***	0.410	0.465	0.418	0.490	0.382	0.586*
Dynamics Change	A	0.568 ***	0.518	0.574 **	0.467	0.523	0.612 *	0.483	0.522
	R	0.389 ***	0.532**	0.322	0.322	0.389 ***	0.182	0.266	0.576 *
Empty	A	0.544	0.624 *	0.579	0.522	0.585	0.589 ***	0.542	0.613 **
	R	0.460	0.473	0.404	0.480 *	0.480 *	0.422	0.480 *	0.480 *
Motion Change	A	0.514	0.613 *	0.551 ***	0.509	0.474	0.592 **	0.490	0.521
	R	0.867 *	0.848 **	0.684	0.789 ***	0.684	0.717	0.752	0.752
Occlusion	A	0.658 *	0.627 **	0.625 ***	0.562	0.573	0.607	0.570	0.520
	R	0.591 **	0.664 *	0.349	0.468	0.496	0.468	0.392	0.557 ***
Size Change	A	0.595	0.654 *	0.612 ***	0.544	0.474	0.643 **	0.520	0.596
	R	0.627	0.682 **	0.607	0.627	0.607	0.637 ***	0.560	0.713 *

4.5. Qualitative Comparison

To display the tracking results more intuitively, we give a qualitative comparison for eight trackers with better EAO ranks in the quantitative experiment, which is shown in Figure 10. Due to the re-start scheme in the VOT-TIR2016 benchmark, there is no sense in displaying the predicted bounding box for the sequence frames after re-initialization. Thus, when a tracker drifts off the target, the later tracker results are placed on top left corner of the images without re-initialization. Six representative sequences are selected in the qualitative experiment: “boat2”, “crouching”, “quadrocopter”, “car2”, “garden” and “excavator”. Generally speaking, the proposed method has a better performance than the seven other trackers. In Figure 10a (“boat2”); the predicted bounding boxes of the SRDCF and MvCFT tracker are far larger than the real target size. In the sequence “crouching” shown in Figure 10b, four trackers, namely Staple+, SRDCF, DPT, and deepMKCF, fail to locate the target when the target is occluded by another person. Targets in other two sequences, “car2” and “garden”, also suffer from severe occlusion; only the proposed method locates the target correctly among the eight trackers. For the sequence “quadrocopter” shown in Figure 10c, the appearance change of the target is slight, however the background around target has a dramatic variation in the tracking process. The proposed method uses the binary mask to extract reliable target part, which can improve the tracking performance in the situation of background clutter significantly. The target in Figure 10f is almost submerged in the background. Only the MDNet_NoTrain and the proposed trackers track the target successfully.

Figure 10. Visualized tracking results of several state-of-the-art trackers on representative sequences.

5. Conclusions

In this paper, we propose a MaskSR-based appearance model to achieve TIR target tracking in an improved particle filter framework. This model considers different discriminant capabilities of different target parts at a pixel level, which can enhance the importance of the distinguishable target pixels in the reconstruction process while weakening the diverse effect of target appearance changes and background clutters. Moreover, to improve the tracking efficiency, a discriminative particle selection strategy is proposed to replace the previous random sampling strategy, which can greatly reduce the number of represented particles and improve the tracking accuracy simultaneously. The proposed method was evaluated on the VOT-TIR2016 benchmark with a re-initialized scheme when tracking fails. The experiment results of accuracy, robustness and expected average overlap show that the proposed tracker is superior to 19 other state-of-the-art trackers for TIR object tracking. Future improvement can be made by applying a regression-based strategy to train the channel selection layer and using a more accurate segmentation method to divide the target.

Considering applying the proposed method to real applications, future improvement can be made by redesigning the program using C or C++, which are advantageous for running speed and are more convenient to be transplanted to the hardware platform. On the other hand, the improvement of sensors on imaging quality will significantly improve the accuracy and robustness of the proposed tracking in the real application.