Abstract
We present ground deformations in response to water level variations at the Toktogul Reservoir, located in Kyrgyzstan, Central Asia. Ground deformations were measured by Envisat Advanced Synthetic Aperture Radar (ASAR) and Sentinel-1 Differential Interferometric Synthetic Aperture Radar (DInSAR) imagery covering the time periods 2004–2009 and 2014–2016, respectively. The net reservoir water level, as measured by satellite radar altimetry, decreased approximately 60 m (∼13.5 km3) from 2004–2009, whereas, for 2014–2016, the net water level increased by approximately 51 m (∼11.2 km3). The individual Small BAseline Subset (SBAS) interferograms were heavily influenced by atmospheric effects that needed to be minimized prior to the time-series analysis. We tested several approaches including corrections based on global numerical weather model data, such as the European Centre for Medium-Range Weather Forecasts (ECMWF) operational forecast data, the ERA-5 reanalysis, and the ERA-Interim reanalysis, as well as phase-based methods, such as calculating a simple linear dependency on the elevation or the more sophisticated power-law approach. Our findings suggest that, for the high-mountain Toktogul area, the power-law correction performs the best. Envisat descending time series for the period of water recession reveal mean line-of-sight (LOS) uplift rates of 7.8 mm/yr on the northern shore of the Toktogul Reservoir close to the Toktogul city area. For the same area, Sentinel-1 ascending and descending time series consistently show a subsidence behaviour due to the replenishing of the water reservoir, which includes intra-annual LOS variations on the order of 30 mm. A decomposition of the LOS deformation rates of both Sentinel-1 orbits revealed mean vertical subsidence rates of 25 mm/yr for the common time period of March 2015–November 2016, which is in very good agreement with the results derived from elastic modelling based on the TEA12 Earth model.
1. Introduction
The water levels of large artificial water reservoirs constructed for hydroelectric power generation and irrigation are prone to significant changes over the course of a year. This periodic loading of the crust causes ground deformations of the surrounding area, alters pore pressure and changes stress on underlying faults and fractures, which may ultimately induce seismicity [1]. The amount of ground deformations of a reservoir’s surrounding can either be measured on individual points with levelling [2] or Global Navigation Satellite System (GNSS) measurements [3,4] or measured in a spatially continuous manner by means of Differential Synthetic Aperture Radar Interferometry (DInSAR). Thus far, in studies that are based on SAR data, either ERS-1/2 [5,6], Envisat Advanced Synthetic Aperture Radar (ASAR) [7] or a combination of those sensors [8,9] were used to quantify the regional deformation around a lake. Recently, ground deformations due to the water level changes in the Tehri Reservoir in the Himalaya region was investigated with ALOS PALSAR data [10].
Our aim in this study is to measure ground deformations induced by water level changes in the Toktogul Reservoir, which is located at N 41.8° E 72.9° in the northwest of Kyrgyzstan, Central Asia (Figure 1). This reservoir is fed by the Naryn River, which originates from glacial melt water of the Tien Shan mountain range. The lake is located at an elevation of approximately 870 m, and surrounding mountains reach elevations of 4300 m. It has existed since 1975, when the construction of the 214 m high and 293 m wide Toktogul Dam was completed [11,12]. At high water (Figure 2c), the reservoir has a length of 65 km, a width of 12 km, a surface area of 284 km2, and a maximum depth of 200 m [12]. As the water level decreases, the eastern elongated part, where the Naryn River enters the lake, goes dry (Figure 2b). Toktogul is the largest artificial water reservoir in the Syr Darya Basin, with a maximum capacity of 19.5 km3 [13]. Its main purposes are power generation for the Kyrgyz population in winter time and irrigation of agricultural areas located downstream in Uzbekistan and Kazakhstan in summer time [13,14]. These activities lead to a trans-boundary water policy conflict, which resulted in an exaggerated use of water in some years that could not be compensated by the incoming amount of water until the beginning of the following winter season (Figure 2).
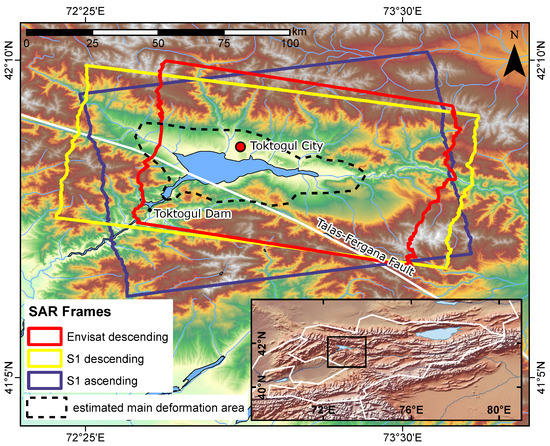
Figure 1.
Location of the Toktogul Reservoir, city and dam with the outlines of the cut SAR data frames that are used for the final analysis. The alignment of the Talas-Fergana Fault is based on vector data from the Kyrgyzstan Disaster Risk Data Platform [15]. The dashed outline denotes the estimated area of the main deformation. The inset shows the location of the area within Kyrgyzstan.
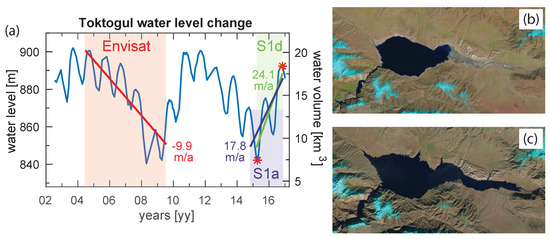
Figure 2.
(a) Toktogul water level change between 2002 and 2016 obtained from satellite radar altimetry. Red, purple and green highlighted periods correspond to Envisat and Sentinel-1 ascending (S1a) and Sentinel-1 descending (S1d) acquisition times, respectively. The corresponding regression lines denote the average water increase per year for each of the three SAR time series (note that differences between S1a and S1d are due to different covered time periods). The red asterisks correspond to the reservoir extents at low and high water levels, which are shown by Landsat-8 images from (b) 11.04.2015 and (c) 07.11.2016, respectively.
The southwestern edge of the reservoir coincides at a length of 20 km with the Talas-Fergana Fault, an area with moderate-to-high seismicity. Larger earthquakes of magnitude have been reported for the Chatkal Range in 1946, 65 km west of the Toktogul Reservoir [11], and of magnitude for the Suusamyr Valley in 1992, 70 km northeast of the Toktogul Reservoir [16]. No major events have been recorded in the direct lake area since the construction of the dam. Seismic activity is still constantly monitored at the power station with seismometers [17], but no ground-based geodetic observations are available to assess the deformation of the surrounding area.
Consequently, we measure the ground deformations of this particular region by interferometrically analysing a time series of Envisat ASAR data for the time period 2004–2009, in which the net water level decreased by approximately 60 m (∼13.5 km3), and a time series of Sentinel-1 data for the time period 2014–2016, in which the net water level increased by approximately 51 m (∼11.2 km3) (Figure 2). We expect that these large load changes on the ground lead to an uplift of the surrounding area in the case of water recession and to a subsidence response in the case of water replenishing.
Sentinel-1 is the latest generation of the European Space Agency’s (ESA) SAR missions and consists of two satellites, Sentinel-1A and Sentinel-1B, that were launched in April 2014 and April 2016, respectively. Together, these C-band-based SAR satellites are able to cover most regions of the world with the interferometric wide (IW) swath mode (swath width: 250 km; spatial resolution: 5 × 20 m in range and azimuth, respectively) from the same relative orbit every twelve days, whereas Europe and some selected areas are even monitored with a temporal resolution of six days. Compared to the Envisat ASAR C-band sensor, which only acquired data every 35 days with a swath width of 56–100 km (image mode single-look complex (IMS); spatial resolution: 8 × 4 m in range and azimuth, respectively), this mission is predestined for monitoring not only persistent linear deformations, but also intra-annual deformation changes on a large spatial scale.
Atmospheric effects in the SAR data caused by vertical stratification and turbulent water vapour variations play an important role in time-series investigations [6,18,19,20]. We therefore apply various correction approaches based on either global numerical weather models (in particular, the European Centre for Medium-Range Weather Forecasts (ECMWF) operational forecast analysis, the ERA-5 reanalysis and the ERA-Interim (ERA-I) reanalysis) or empirical models that rely on the dependency of the phase on the elevation of the terrain (in particular, the linear dependency and the power-law approach of Bekaert et al. [21]). The time series with the best working atmospheric correction approach is then used for a comparison to the reservoir’s water level variations that are extracted from satellite altimetry data. The measured ground deformation rates are further compared to the results obtained from elastic modelling of the surface deformations.
2. Materials and Methods
2.1. Lake Altimetry
At present, radar altimetry (RA) is widely used not only for monitoring global sea level changes, but increasingly also for measuring the water levels of rivers and lakes for hydrology applications [22,23,24]. Since the early 1990s, a series of RA missions has provided continuous measurements of water surface heights with 10- and 35-day repeat intervals. Novel processing technologies, such as retracking, allow the extraction of the water levels of smaller inland water bodies and reservoirs [23]. The accuracies of the derived water levels are slightly worse compared to open ocean applications but can still reach 5 cm. For hydrological applications, the water levels can be converted into volume changes using supplementary information such as hypsometry or lake extents extracted from remote sensing data.
The water level of the Toktogul Reservoir has been measured with RA since 1995—in particular, mostly every 35 days by the European ERS-2, Envisat and later by the Indo-French AltiKa missions. Some data are also available from the US-French Jason-1 and Jason-2 and the European CryoSat-2 missions. Using all available RA data, applying up-to-date environmental correction models and cross-checking for and applying inter-mission biases, a homogeneous time series of reservoir heights and reservoir volumes is constructed (Figure 2a). The internal accuracy is estimated from all high-rate measurements of one reservoir crossing (e.g., ∼50 measurements for AltiKa) and is mostly within the expected 5 cm root mean square error (RMSE) range with slightly higher values for the earlier missions.
In the case of the Toktogul Reservoir, sparse historical monthly volume information of the total volume is available for the full range of water levels from CA WATER Info [25] between 1984 and 2000, and some more recent information is made available by the reservoir operator [26]. This allows the construction of a polynomial transfer function (R2 = 0.9998), which can be used for converting all water height levels into reservoir volumes. These data can then be used to verify the accuracy of the RA-derived water heights, which is approximately ±0.3 m [24].
2.2. DInSAR Processing of Envisat ASAR and Sentinel-1 Data
We use Envisat ASAR IMS and Sentinel-1 IW SAR data to monitor deformations around the Toktogul Reservoir area. The Envisat data, only available in the descending orbit, were acquired between December 2003 and July 2009 and cover a time of decreasing annual water level, whereas Sentinel-1 ascending (S1a) and descending (S1d) acquisitions analysed for the time period of October 2014 until December 2016 correspond to an increasing annual water level. In the Envisat acquisition period, the highest water level measured with RA (referenced to the EIGEN-6C3 static gravity field [27]) was 900.5 m on 10 May 2004, and the lowest was 840.4 m on 22 April 2008. In the Sentinel-1 acquisition period, the lowest measured water level was 842.2 m on 24 April 2015, and the highest was 892.9 m on 29 October 2016 (Figure 2).
Data preprocessing is performed with the GAMMA software [28] as follows. First, for both sensors, single-look complex images are imported taking into account precise orbit ephemerides; in the case of Sentinel-1 data only, bursts covering the area of interest are concatenated. Second, images of each SAR time series are individually coregistered and cropped to the desired area of interest. Because Sentinel-1 data require a precise coregistration accuracy of a few thousands of a pixel in azimuth to prevent contamination with phase variations due to along-track differences in the Doppler centroids [29,30], we rely on the spectral diversity method for coregistration [31,32]. The outlines of the cropped SAR data frames are shown in Figure 1.
The single-look, coregistered SAR images are used to construct a network of interferograms by applying the Small BAseline Subset (SBAS) technique [33] implemented in StaMPS/MTI, the Stanford Method for Persistent Scatterers and Multi-Temporal InSAR [34]. The main objective of this approach is to generate interferograms from pixels that decorrelate only slightly over short time intervals. To identify such pixels, interferograms are built from SAR acquisitions that match the criteria of having small perpendicular, temporal and Doppler baselines, but with the restriction that all selected interferograms should be connected; thus, no isolated cluster is allowed in the network [35]. We constrain the Envisat network by a maximum spatial baseline of 500 m and a maximum temporal baseline of 2000 days, whereas, at the same time, the overall coherence between two interferograms should be at least 0.4. In the Sentinel-1 case, we use constraint values of 200 m, 365 days and 0.5. In the following, the selected interferograms are treated with topography removal and geocoding, for which we rely on the 1-arc resolution Shuttle Radar Topography Mission (SRTM) digital elevation model (DEM). The results are visually inspected, and decorrelated interferograms are discarded from the network. Unwrapping of the remaining interferograms is achieved by using a three-dimensional phase unwrapping approach [36]. Displacement values in line-of-sight (LOS) are subsequently retrieved by least-squares inversion of the unwrapped interferograms with respect to a reference area selected outside of the main deformation region (N 41.6930 E 73.1660, radius: 2 km).
By carefully investigating the residuals of the unwrapped phase of the SBAS interferograms and the inverted interferograms, we neglect scenes that introduce errors to the time series. The main error source is thus the snow coverage in winter time. After some problematic scenes are removed, we iteratively repeat the process of unwrapping, inverting and discarding until all remaining interferograms could be reliably unwrapped. A summary of the amounts of the used scenes and interferograms along with the corresponding SAR sensor specifications is presented in Table 1. The final network for all three SAR time series is shown in Figure 3.

Table 1.
SAR data specifications and summary of the amount of images used in the final networks. The covered time period that could be reliably unwrapped is as follows for the individual time series: Envisat: 24.10.2004–05.07.2009, Sentinel-1, descending (desc.): 23.03.2015–12.11.2016, ascending (asc.): 24.10.2014–18.11.2016.
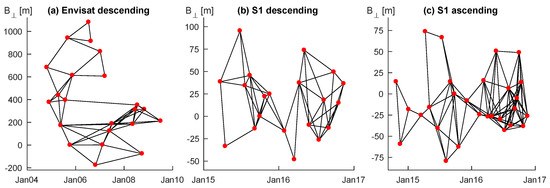
Figure 3.
Small BAseline Subset (SBAS) networks after offending interferograms are removed for (a) Envisat descending; (b) Sentinel-1 descending and (c) Sentinel-1 ascending time series. Red dots denote the time of the image acquisitions, and black lines show the interferograms.
All interferograms remaining in the network are further treated by removing (1) individual phase ramps; (2) the overall topography error; (3) estimated atmospheric influences; and (4) the phase oscillator drift (Envisat data only) [37]. From all these aspects, the most influential and simultaneously most challenging error aspect to remove is the effect of the atmosphere. Multiple approaches dealing with this issue are discussed in the following section.
2.3. Atmospheric Correction
Because the Toktogul Reservoir is located in a high-mountain area, atmospheric disturbances in the data are inevitable and must be corrected to avoid a misinterpretation as a loading signal. The success of atmospheric correction methods is highly dependent on the characteristics of the area of interest in terms of topography and its dominance either in stratified tropospheric delay or dynamical local weather and turbulence [38]. To reduce the impact of atmospheric artifacts in the Toktogul SAR data, we apply a range of tropospheric correction methods implemented in the MATLAB-based Toolbox for Reducing Atmospheric InSAR Noise (TRAIN, version 2beta) from Bekaert et al. [38].
The applied techniques can be divided into two main categories: (1) global numerical weather-model-based and (2) phase-based correction methods. In theory, weather-model-based approaches should be more effective because they should be able to compensate not only for vertical stratification, but also for turbulent water vapour variations in the lower troposphere. However, previous studies have shown that the success of the exact representation of stratification and turbulence is highly dependent on the area of interest [39] and that global models, such as ERA-I, also suffer from coarse temporal and spatial resolutions [40]. This disadvantage is now compensated for by newer available weather model data such as the ERA-5 reanalysis that are shipped with increased spatial and temporal resolutions. However, note that this type of data is not always easy to access and that it is currently only available for a limited range of time.
For comparison, we further apply phase-based corrections. These corrections have the advantage that the required external data are readily available but the disadvantage that they can only be used to treat vertical stratification, not turbulence mixtures. However, as Bekaert et al. [38] noted in his study, in regions where tropospheric delay is mainly correlated to topography, phase-based methods potentially outperform weather-based approaches.
We neglect spectrometer-related correction methods based on the Medium Resolution Imaging Spectrometer (MERIS) or the Moderate Resolution Imaging Spectroradiometer (MODIS) for the following reasons: MERIS data are available for Envisat data only and MODIS data are acquired between approximately 5:00 a.m. and 7:30 a.m. UTC. This differs by more than an hour from Sentinel-1 acquisition times (Table 1); thus, changes in atmospheric water vapour conditions may introduce more errors rather than correcting for turbulence. Furthermore, correction with spectrometer data requires daytime acquisitions under cloud-free conditions [41], which is often not the case in high-mountain areas.
Finally, we determine the best atmospheric correction by evaluating the RMSE values of deformation in time. To avoid an influence of loading-induced deformation on the analysis, we excluded for the RMSE calculation the area of main deformation (cf. Figure 1) from the overall atmosphere-corrected interferograms. For comparison, we also calculate the RMSE for unwrapped results that are only corrected for the DEM error and orbital plane but not for atmosphere. The derived RMSE values are an indicator of the best-performing atmosphere removal algorithm, but note that the absolute values of different SAR frames cannot be compared because the extents of the frames differ. The Sentinel-1 ascending image, for example, covers much more high-mountain areas compared to the Sentinel-1 descending images; thus, higher error values can be expected. Furthermore, the amount and location of the SBAS-derived points within the SAR frames also vary.
2.3.1. Tropospheric Delays from Numerical Weather Models
Temperature, relative humidity and pressure information from numerical weather models can be used to compute the hydrostatic and wet tropospheric delay [38,39,42]. For the Toktogul case, we apply three global models based on ECMWF data: first, the ECMWF operational forecast analysis (opECMWF); second, the ERA-5 global atmospheric reanalysis; and third, the ERA-I global atmospheric reanalysis. From these models, only the ERA-I solution is currently freely accessible at a reduced spatial resolution.
The opECMWF data are expected to be the most accurate of the three models because these data are used for routine short-term predictions. These data are distributed with a temporal resolution of 6 h, a spatial resolution of 0.1° and 25° pressure levels. Since July 2017, the new ERA-5 reanalysis has been available for the time period 2010–2016. Similar to opECMWF, ERA-5 comes with a high spatial resolution of 0.1° but has an increased temporal resolution of 1 h. Upper-air information is delivered at 37 pressure levels. The available ERA-5 data currently do not cover the Envisat acquisition time period. We therefore also consider the former ERA-I reanalysis that is available for the time period from 1979 to present. This reanalysis is also delivered with a temporal resolution of 6 h and contains 37 pressure levels, but it has a coarse spatial resolution of 0.75° [43].
To compare the influence of the temporal resolution, we apply two versions of the ERA-5 data: the hourly reanalysis and an artificially reduced version with a 6 h temporal resolution, similar to the ERA-I data. An overview of the model specifications is presented in Table 2.

Table 2.
Parameters of the applied numerical weather-model-based atmosphere corrections.
2.3.2. Phase-Based Tropospheric Delays
The Toktogul Reservoir is surrounded by high-mountain ranges, which influence the moisture content of the troposphere, which consequently has an impact on the phase delay of the radar signal. It is therefore straightforward to apply correction methods such as the power-law and linear tropospheric approaches that use the correlation of the phase signal with the topography.
The linear tropospheric correction assumes a uniform troposphere that is directly correlated to the elevation of the terrain. In principle, a linear relationship between phase delay and terrain height is estimated and subtracted from the entire interferogram. To prevent real tectonic signals from being taken into account during the linear dependency analysis, we exclude the estimated deformation area around the Toktogul Reservoir from the calculation (cf. Figure 1).
The power-law correction technique [21] is more sophisticated than the linear approach, as it considers a spatially varying troposphere within an interferogram. The method assumes a non-varying delay at the relative top of the troposphere and then applies a power-law function on the phase delay variations depending on elevation. It thus considers phase delays mainly due to hydrostatic and wet components of the refractivity. Delays due to the liquid component and the influence of the ionosphere on C-band SAR data are neglected because their influence is assumed to be small [21].
First approximations of the tropospheric delays that are used as coefficients for the power-law method can be calculated from balloon sounding data as distributed by the University of Wyoming [21]. We extract data for the Envisat and Sentinel-1 acquisition periods from the Taraz station (station no. 38341 at N 42.85° E 71.38°), which is located approximately 170 km northwest of Toktogul. We constrain the upper troposphere height to 10 km and extract a corresponding mean power-law decay coefficient of 1.51 ± 0.01 from the sounding data, which we use for all three InSAR time series.
The estimation of the spatially varying relation between topography and tropospheric phase is based on the assumption that the tropospheric signal is present in all wavelength scales. Tropospheric effects should thus be removed from the interferogram by band-filtering the signal, choosing a band for filtering that is insensitive to other signals such as turbulent troposphere, orbital errors and deformation. Furthermore, spatial variability of the phase delay is provided by dividing the area into multiple smaller windows, in which the coefficient describing the relation between topography and tropospheric phase is calculated locally [21,38].
In the Toktogul case, we have a pronounced topography around the reservoir, allowing us to set the window size to be comparatively small. Empirical tests show that, for the SAR time series, the following window sizes work best (window overlap: 50%): Sentinel-1, descending: 77 × 59 km; Sentinel-1, ascending: 68 × 78 km; and Envisat: 60 × 62 km. The relationship between topography and phase delay is computed for the following filtering band ranges: 2–4, 2–8, 2–16, 4–8, 4–16, 4–32, 8–16, 8–32, 8–64, 16–32, 16–64, 32–64, 32–128, and 64–128 km.
2.4. Deformation Decomposition of Sentinel-1 Data
Because Sentinel-1 data are available from two different orbits, it is possible to decompose the deformation into a vertical part and a horizontal part. However, because there are only two observations available, we cannot directly compute the 3D vector components. We thus neglect potential displacements in the north–south direction, for which LOS measurements are the least sensitive in any case due to the near polar orbit of the spacecraft.
The average S1d and S1a LOS displacement points are interpolated to 200 × 200 m grids, which are used as input for the deformation decomposition. Furthermore, we ensure that only results covering the same time period (March 2015–November 2016) are considered for the decomposition. The mean LOS displacements of the ascending () and descending () orbits are then used to discriminate between vertical and east-west displacements by solving the following equation [44,45]:
where and represent the incidence angles and and are the heading angles of Sentinel-1’s ascending and descending orbits, respectively.
2.5. Modelling of Elastic Surface Deformations
Considering surface deformations induced by short periodic mass variations, such as intra-annual water level changes, the purely elastic, instantaneous response of the Earth is an adequate approximation. In a spherical harmonic representation, the coefficients of the vertical and horizontal deformations and the geoid changes can be related linearly to the surface mass load through degree-dependent load Love numbers. Farrell [46] outlines the calculation of properly weighted sums of the load Love numbers for a given Earth model to form Green’s functions that provide the distance-dependent elastic response of the Earth model due to a unit point mass. Assigning the point mass response to any extended mass distribution by means of a convolution integral over the loaded region leads to the global displacement field. Because the convolution occurs in the spatial domain, the Green’s function approach is particularly useful if the spherical harmonic representation of the surface mass load is dominated by high-degree coefficients, such as in our case of the highly heterogeneous distribution of non-loaded and loaded regions around the Toktogul lake.
Rather than using one globally defined Green’s function for a customary idealization of the Earth by a model composed of spherically symmetric layers, we calculated geographically dependent local Green’s functions [47] that are valid especially for the crustal structure beneath the Toktogul region. For small-scale heterogeneous mass loads, the geological structure of the shallow crust becomes the most important; thus, we replaced the outermost 71 km of the 1D PREM Earth model [48] by the lateral variability given in the crustal model TEA12 provided by Tesauro et al. [49]. The deformation response depends mainly on the lithology of the upper and lower crystalline crustal layers (granite, mafic granite, diabase, diorite, and olivine), their thicknesses, and the varying thickness of the overlaying sediments. The changes in the crustal properties from PREM to TEA12 affect the near-field values of the local Green’s functions for distances to the load lower than 100 km.
To simulate elastic Earth surface deformations, the local Green’s function model was applied to the water storage variations composed from the Toktogul lake level changes as observed by satellite RA (Figure 2a), in combination with the changes of the lake surface area given by Landsat-8 images (Figure 2b,c). Finally, the trend in the modelled surface deformation was calculated for the same period as for the Sentinel-1 descending acquisition time S1d.
3. Results
A first general result of our study is that Sentinel-1 products are superior to Envisat results in the following aspects: (1) the wide swath of the Sentinel-1 sensor allows more freedom in cutting the scenes to the desired area of interest; hence, we capture the western region of the reservoir better with the Sentinel-1 time series than with the Envisat ones; (2) due to the higher temporal acquisition sampling, Sentinel-1 interferograms are affected less by decorrelation, which leads to a higher point density than in the Envisat time series. This again results in a better area coverage that can be taken into account for the deformation analysis; (3) since the orbital tube of Sentinel-1 is very narrow, the length of the spatial baseline between two images is a no critical rejection criterion, which ultimately leads again to a denser network of interferograms. In the following, we will provide more details regarding the improvement of the results due to different atmospheric corrections and then regarding the ground deformation correlated to water level changes. Furthermore, we provide a comparison of Sentinel-1-derived vertical ground deformation to elastic modelling results.
3.1. Atmospheric Corrections
First, we analyse the RMSE values of the individual power-law results, where we had applied different filter bands. It appears that, in the Toktogul case, small- to medium-scale bands generally perform better than longer ones (Table 3), but the results are not consistent among the three different SAR time series, which may again be explained by the different SAR frame extents. In the case of the Envisat descending time series, the lowest RMSE value of 8.0 mm is achieved with the 8–64 km filter band; in the case of S1d, the lowest RMSE value is 7.0 mm, derived by applying filter bands for a range of 4–32 km and 8–64 km; and, in the case of S1a, the lowest RMSE of 10.6 mm is found for filter bands of 2–8 km and 4-8 km range. In the following sections, whenever the results of the power-law correction method are mentioned, we are referring to the results from the best-performing filter band.

Table 3.
Root mean square errors for different power-law filtering bands. The best results are highlighted in bold. The area of main deformation (cf. Figure 1) is excluded from this estimation.
We now compare the RMSE values of the different correction techniques to determine the best atmospheric correction solution. The results show that, although phase-based methods are not able to represent turbulence mixtures, their correction performance is superior to the weather-model-based methods for all three SAR time series, which in all cases yield even higher RMSE values compared to the non-atmosphere-corrected time series (Table 4). This is also true for the ERA-5 1h solution with the highest temporal and spatial resolutions, which surprisingly does not lead to any improvement compared to the other numerical weather-based approaches.

Table 4.
Root mean square errors for different atmospheric correction techniques. ERA-5 data cover only the Sentinel-1 acquisition period and thus cannot be used for improving the Envisat time series. The best results are highlighted in bold. The area of main deformation (cf. Figure 1) is excluded from this estimation.
Among the phase-based corrections, the power-law method performs better than the linear one, although differences are small or (in the case of Envisat) even non-existent (Figure 4). This behaviour is expected because the power-law method is able to adapt to the variation of the vertical stratification and calculates individual corrections for windows smaller than the entire interferogram, whereas linear correction works on the entire image only. At the end, the best filter bands of the power-law technique improve the RMSE of Envisat by 9% from 8.8 mm to 8.0 mm, of S1d by 29% from 9.9 mm to 7.0 mm and of S1a by 16% from 12.6 mm to 10.6 mm.
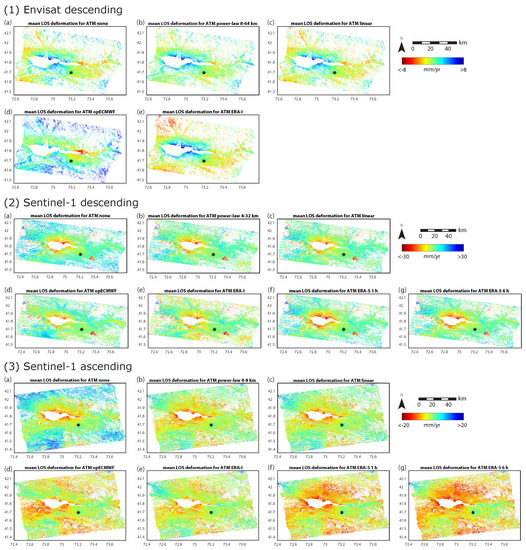
Figure 4.
Mean line-of-sight (LOS) deformation values for various atmospheric corrections of the (1) Envisat descending; (2) Sentinel-1 descending and (3) Sentinel-1 ascending time series. (a) no atmospheric correction applied; (b) best results of the power-law technique; (c) linear dependency on the topography; (d) correction with the operational weather model (opECMWF) analysis; (e) ERA-I weather model correction; (f) the ERA-5 1 h temporal resolution solution and (g) the ERA-5 6 h temporal resolution solution. The black asterisks show the location of the reference point.
Analysing the performance of different atmospheric correction methods in time (Figure 5) reveals that most variances appear in summer time and that winter acquisitions are much less affected. Furthermore, in the S1a time series, ground deformation variations due to different applied atmospheric correction approaches are significantly higher than in S1d or Envisat time series.
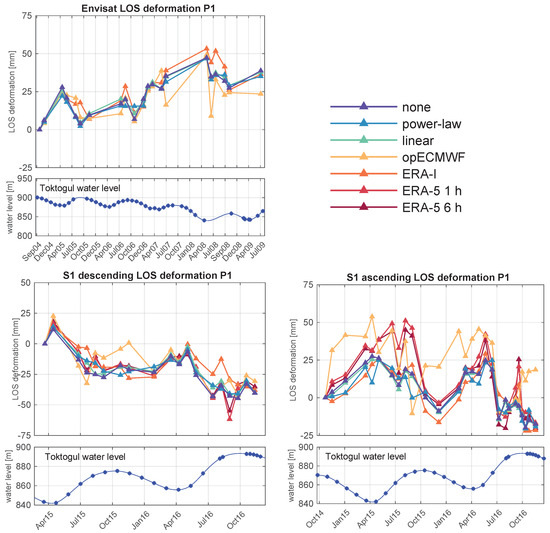
Figure 5.
Variances of the LOS deformation in time for all applied atmospheric corrections. The location of the exemplary point P1 is shown in Figure 6. For better visualization, deformation markers have been connected with lines, although this does not imply that we expect linear deformation in between.
3.2. Ground Deformation
The ground deformation pattern is discussed on the basis of the average Envisat, S1d and S1a power-law-corrected deformation maps (Figure 6—note that the red triangle area at the southeastern corner of the S1d time series shows an unwrapping artifact that we did not correct for because it is located far from the reservoir area and thus did not hamper our analysis). We additionally show the correlation of the water level data to the corresponding deformation data for four selected points (Figure 7). For these examples, the water level amplitudes are fitted to the power-law-corrected SAR time series to highlight the amount of their correlation. Note that we do not correct for any potential time lag between water level change and deformation during this fit and that differences between the overall ascending and descending Sentinel-1 LOS deformations are mainly due to the different time period coverages.
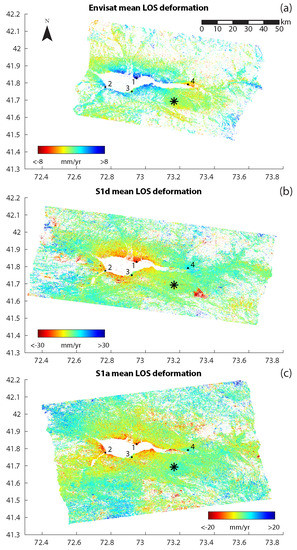
Figure 6.
Power-law-corrected mean LOS deformation maps for (a) Envisat; (b) S1d and (c) S1a SAR time series. Points 1-4 show the locations of the deformation time series shown in Figure 7, and the black asterisk denotes the reference point used in the time series. The red triangle area in the southeast corner of the S1d time series shows an unwrapping artifact that we did not correct for.
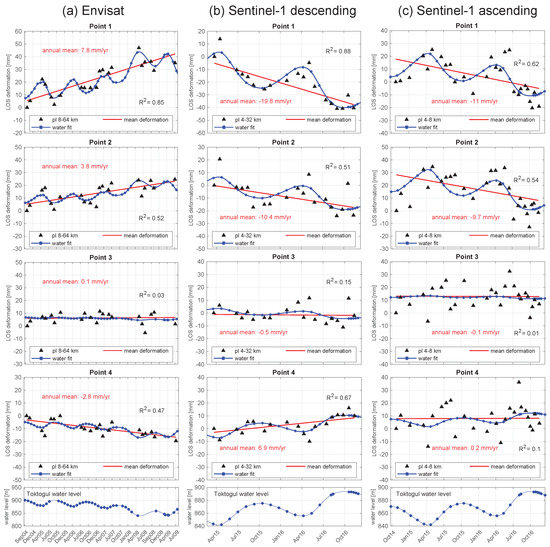
Figure 7.
(a) Envisat; (b) S1d and (c) S1a power-law-corrected LOS deformation in time (black triangles) for points 1-4 as in Figure 6. The red lines indicate the annual mean LOS deformation for the investigated time period. The blue lines in the bottom diagrams show the true Toktogul water level change, whereas the blue lines in the point figures represent the best fit of this water level to the shown deformation.
From the spatial perspective, all three mean deformation maps reveal a significant LOS deformation of the bedrock areas around the entire Toktogul Reservoir, whereas the strongest deformations are found north of the lake close to the Toktogul city area (point P1). In the time of water recession (Envisat time series), we observe for P1 LOS uplift rates of 7.8 mm/yr, which converts to 0.78 mm per one metre of water level loss. The reverse behaviour of subsidence is monitored for the time of water filling (Sentinel-1 time series). Here, the mean LOS values are on the order of −19.8 mm/yr (−0.82 mm per 1 m water level increase) and −11 mm/yr (−0.62 mm per 1 m water level increase) in the case of S1d and S1a, respectively. The intra-annual time series (Figure 7) for point P1 shows that the correlation between LOS deformation and water fit are higher for the Envisat (R2 = 0.85) and S1d (R2 = 0.88) time series compared to the S1a (R2 = 0.62) time series. From the Sentinel-1 data, it is clear that intra-annual LOS deformation changes appear simultaneously with the water level changes, which indicates an elastic response of the surface. At location P1, these intra-annual LOS deformation variations are on the order of 30 mm and more.
The same deformation process but with decreased rates and lower correlation rates are found west of the Talas-Fergana Fault (point P2). LOS values (and water level fit correlation rates) are on the order of 3.8 mm/yr (R2 = 0.52), −10.4 mm/yr (R2 = 0.51), and −9.7 mm/yr (R2 = 0.54) for Envisat, S1d and S1a, respectively, which convert to 0.38 mm, −0.43 mm and −0.54 mm per 1 m water level change.
Very intriguing are the results of a small area close to the reservoir (point P3) that do not show a distinct correlation to any water level changes. In all three SAR data time series, we find no significant deformation rates (LOS values are on the order of 0.1 mm/yr, −0.5 mm/yr and −0.1 mm/yr for Envisat, S1d and S1a, respectively), and intra-annual water level fit correlation rates (R2) are consistently below 0.2.
In the eastern region, at the entrance of the Naryn River (point P4), we observe contradictory but clearly intra-annual correlated deformation rates compared to points P1 and P2. Here, we find mean LOS subsidence rates of −2.8 mm/yr (−0.28 mm per 1 m water level change and R2 = 0.47) during the water recession phase captured by Envisat data and mean LOS uplift rates of 6.9 mm/yr (0.29 mm per 1 m water level change and R2 = 0.67) in the S1d time series that cover a water replenishing phase. Compared to S1d, S1a LOS deformation is less explicit and also only yields a low water level fit correlation value of R2 = 0.1.
The availability of ascending and descending data in the Sentinel-1 case allows a decomposition of the mean deformation data in the vertical and east–west directions (Figure 8) that can be compared to vertical deformation rates obtained from elastic modelling. For the purpose of decomposition, we truncated the ascending SAR time series to fit the time period of the descending SAR time series. Overall, the long-wave spatial pattern of the Sentinel-1-derived vertical deformation around the reservoir correlates very well with the trend in the vertical displacement for the same time interval as calculated by the elastic response of the Earth model due to water load changes (Figure 8a,c,d). In the case of the horizontal deformation, S1 measurements yield only noise but no definite deformation in one direction or the other (Figure 8b).
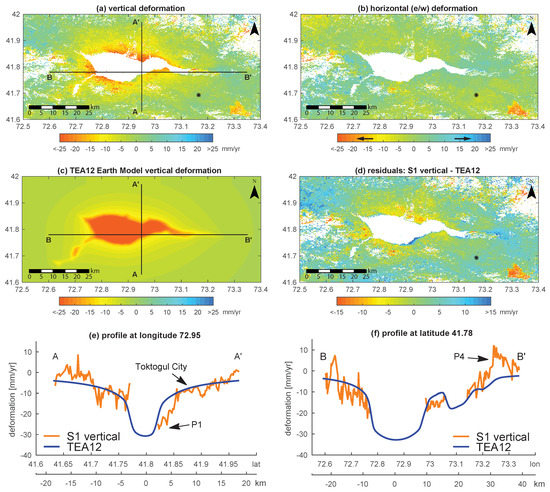
Figure 8.
(a) vertical and (b) horizontal (east/west) components of the decomposed Sentinel-1 ascending and descending LOS deformations for the time period March 2015–November 2016. Input data for the decomposition are the power-law-corrected mean LOS deformation maps; (c) vertical deformation from elastic modelling with the TEA12 Earth model; and (d) residuals from Sentinel-1 minus modelled vertical deformation. Negative values in the vertical case refer to subsidence, and blue values refer to uplift. In the horizontal case, positive values denote a motion towards the east, and negative values denote a motion towards the west. The black asterisk shows the location of the reference point. Measured and modelled vertical deformation rates for profiles and are given in (e, f), respectively.
Two perpendicular profiles further illustrate how well the measured and modelled data fit together and up to which distance the area is deforming. The 2 km closest to the reservoir are affected the most by subsidence rates of approximately −25 mm/yr (−1.07 mm per 1 m water level increase) (Figure 8e). The Toktogul city area is affected less by approximately −10 mm/yr (−0.41 mm per 1 m per 1 m water level increase). Non-affected areas are only found at a distance of approximately 15 km away from the reservoir shoreline. The comparison to modelled data also clearly outlines the anomaly of the measured uplift signal at point P4 (Figure 8f).
4. Discussion
Our study shows that DInSAR remote-sensing-derived displacements that were properly corrected for atmospheric effects can explain loading-induced ground deformations at the Toktogul Reservoir. The very good agreement of Sentinel-1 decomposed results to predictions of an elastic surface deformation model based on TEA12 proves that the derived LOS deformations can be mainly attributed to vertical displacements. In the following, we will discuss the artifacts remaining after atmospheric corrections and provide reasons for the observed variances of the ground deformations.
4.1. Atmospheric Corrections
It is often argued that the occurrence of atmospheric turbulences is random and thus cancel each other out when calculating the average LOS deformation [18,19,20]. However, we observe that artifacts remaining after the atmospheric correction that we mainly attribute to non-corrected turbulence do have an influence on the averaged LOS deformations in our case (Figure 4). Doin et al. [39] argue that the sign and amplitude of stratified tropospheric delay in high-mountain areas do not appear randomized. It is thus likely that non-corrected vertical stratification leaks into the results, leading to the observed differences and also to significant alterations in the LOS time series (Figure 5). These alterations appear mainly in the summer months, which can be related to increased water vapour content in the atmosphere compared to winter time. Furthermore, in summer, high evaporation rates originating from the lake surface also contribute to SAR signal delays.
The low performance of the weather-model-driven corrections may be explained by several reasons. First, the Toktogul Reservoir is located in a valley that is surrounded by high mountains, which leads to micro-climate artifacts that are not well captured by global numerical models. Second, within the region of Central Asia, in situ weather stations used to constrain the models are sparse; thus, the accuracy of the model predictions might not be comparable to a region such as Europe, where significantly more in situ data are available [50]. Third, especially in high-mountain areas, weather conditions are prone to rapid changes; hence, even a 1-h temporal resolution of a weather model might not be sufficient to represent the atmospheric conditions at the SAR acquisition time. Fourth, an increase in RMSE values after weather-model-based corrections was also found by Bekaert et al. [38], who attributed this to the incorrect estimation of the location of turbulence in the weather models.
4.2. Ground Deformation
The area with the highest deformation rates is north of the lake at P1, which is reasonable because it is located closest to the lake centre and its shoreline is rather flat (Figure 9a). Here, the two short time series of Sentinel-1 show a clear intra-annual correlation to the water level changes. Although the R2 is also high in the Envisat case, intra-annual variations are less obvious due to the much lower temporal sampling. The area in the west (P2), close to the Talas-Fergana Fault, is also prone to the same intra-annual deformation, but at lower rates. Here, the slopes of the high mountains are much steeper than at P1 and even reach the shoreline (Figure 9b).
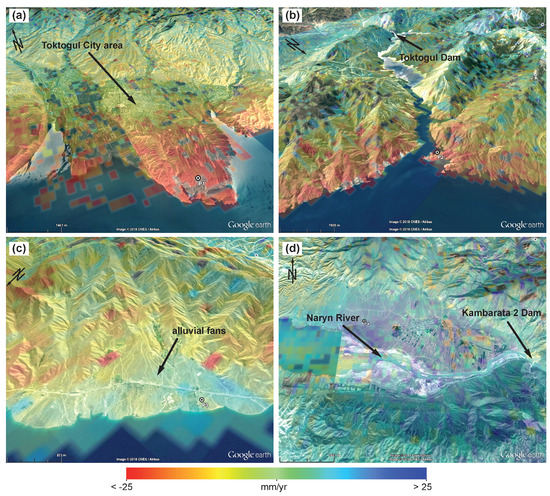
Figure 9.
Vertical deformation extracted from Sentinel-1 decomposition around (a) point P1 and the Toktogul city area; (b) point P2; (c) alluvial fans at point P3 and (d) the Naryn River entrance area at point P4. For the locations of the points (refer to Figure 6). Background imagery provided by Google ® Earth.
Anomalies in the overall deformation pattern are found at P3 and P4. As these are stringent in all time series, it is straightforward to assume that they are induced by local characteristics of the ground and not due to remaining atmospheric effects, artificial changes of landcover such as construction work or the influence of the Kambarata-2 hydropower plant, which is located east of the Naryn River entrance (Figure 9d) and only started operating in 2010 [51].
For P3, where no deformation could be measured, an overlay on DEM and optical remote sensing data reveals that this area is characterized by alluvial fans that are rather flat and consist of fluvial sediments (Figure 9c). The inverse deformation at P4 is also located in a rather flat and sedimentary area at the entrance of the Naryn River (Figure 9d). We believe that, in both areas, the height change in ground water level is the main source for the observed deformation pattern. At times of high reservoir water level, the ground water level in the sedimentary areas at P3 and P4 will also be higher compared to times at low reservoir water level. The increased amount of ground water and soil moisture prevents the SAR signal from penetrating as deep into the ground as in the case of dry material. This effect leads to a measured “uplift” signal at P4 in the Sentinel-1 time series, although the area is rather subsiding (cf. the model results in Figure 8c). However, because the area at P4 is very shallow and thus affected by only a small amount of load change, the reduced signal penetration into the ground is dominating. Conversely, we observe a “subsidence” signal in the Envisat time series because the ground water level is becoming lower here. In the case of P3, however, the area is located much more closely to the lake centre; thus, it is likely here that both effects, loading/unloading and radar penetration changes, are compensating each other, leading to the observed “non-deformation”. The hypothesis that the same process is affecting the deformation measurements at both locations is further underlined by the fact that residuals between measured and modelled deformations are on the same order at P3 and P4 (Figure 8d).
Another process that has the same contradictory effect is the compaction of the sediments at times of lower ground water levels and soil swelling at times of higher ground water levels. The related deformation might also contribute to the observed signals, but presumably at a much lower rate.
Compared to Envisat and S1d, a significantly lower correlation between LOS deformation and water level fit is found for the S1a time series. This result indicates that the atmospheric correction was rather poor for the S1a data. We relate this to increased lake evaporation rates that locally increase the moisture content in the low-level atmosphere since S1a data were acquired during local evening hours (UTC+6 h). In comparison, Envisat and S1d images were captured at noon and during morning hours, respectively. The relation to evaporation is further indicated by the fact that LOS deformation rates with the highest offsets from the water level fit can be found in summer time (Figure 7c). We view this mismatch of atmospheric correction also as the main driver for why we do not observe a clear uplift signal at P4 in the S1a time series. In principle, this can be overcome by an extension of the time series, although here it is not likely that the water level will increase much in the upcoming year because the reservoir is already at full capacity.
5. Conclusions
We have investigated the suitability of Sentinel-1 and Envisat SAR data for capturing surface loading effects due to water level changes in the Toktogul Reservoir. Since the study area is situated in a high-mountain terrain, the SAR acquisitions are severely affected by atmospheric noise that had to be removed prior to the deformation analysis. In our study, we have tested a global numerical weather model and phase-based removal approaches and found that, for the Toktogul area, the power-law method of Bekaert et al. [21] performed the best. However, the S1a evening acquisitions in summer time were significantly influenced by remaining atmospheric effects that we relate to non-corrected lake evaporation. We thus recommend for similar studies to either focus on morning or noon acquisitions or to make an effort to reduce the impact of such remaining effects.
Although only two years of Sentinel-1 data (2014–2016) were used, we found a strong correlation between the increase in the water level and the subsidence of the surrounding region. Areas north of the lake and within a range of 2 km to the shore were affected the most (25 mm/yr, which corresponds to a deformation rate of –1.07 mm per 1 m water level change), but measurable deformations occurred as far as 15 km away from the shore. Due to the dense acquisition interval, we were also able to retrieve intra-annual LOS deformation variations on the order of 30 mm. The analysis of intra-annual time series and water level change further revealed that ground deformations occurred simultaneously with water level changes, which indicated an elastic deformation response. We therefore estimated ground deformation rates with an elastic forward model that was based on the TEA12 Earth model. The results showed that the modelled ground deformation rates fit very well with our Sentinel-1 measured vertical deformations.
The SAR time series from Envisat was considerably longer (2004–2009). This time period was characterized by an overall release of the Toktogul Reservoir water; hence, we retrieved a corresponding inter-annual uplift deformation of the area. However, clearly correlated intra-annual changes were not extracted, which was related to the less temporal density of SAR acquisitions.
In terms of the Toktogul case study, our estimations of the dimension and spatial extent of deformation can contribute to seismic hazard prediction maps as presented by Abdrakhmatov et al. [52] or Bindi et al. [53]. The Talas-Fergana Fault to the southwest of the reservoir is a potential trigger for earthquakes. Such an event is especially dangerous if it induces a landslide as in the Suusamyr earthquake in 1992. If such a landslide collapses into the reservoir, it may induce a tsunami, which poses a severe threat to the dam [12].
We see several avenues for further research in the study area that would benefit from continuous intra-annual monitoring with Sentinel-1 data: (1) for areas such as the city of Toktogul, it is important to assess the potential consequences of the identified deformations and their implications on the stability of the buildings; (2) In combination with the observed Toktogul water level changes, the effects of varying water levels at the Kambarata 2 dam should be investigated. Focus should therefore be on the connections of the corresponding ground deformations to those of the Toktogul Reservoir; (3) Continuous SAR monitoring of the mountain slopes facing towards the lake can help in the early detection of instabilities such as slope failures that may eventually collapse into the lake [12]; and (4) via the elastic modelling, the deformations estimated from remote sensing in combination with the directly observed water mass loads allow constraining the specific Earth structure in the Toktogul region.
Acknowledgments
The Sentinel-1 and Envisat data used for this study are provided by the European Space Agency/Copernicus. The SRTM DEM data were derived from the Consortium for Spatial Information of the Consultative Group for International Agricultural Research (CGIAR–CSI). The Landsat data were obtained from the U.S. Geological Survey. We thank Deutscher Wetterdienst, Offenbach, Germany, and the European Centre for Medium Range Weather Forecast, Reading, U.K., for providing data from ECMWF’s operational forecast model, the ERA-5 reanalysis and the ERA-I reanalysis. This work was funded by the Initiative and Networking Fund of the Helmholtz Association in the framework of the Helmholtz Alliance “Remote Sensing and Earth System Dynamics” (EDA) and by the CAWa project (Contract No. AA7090002), funded by the German Federal Foreign Office. The study contributes to the “Advanced Earth System Modelling Capacity” (ESM) project of the Helmholtz Association of German Research Centres. We also appreciate the valuable comments and constructive suggestions of four anonymous reviewers, which greatly helped us to improve our manuscript.
Author Contributions
Mahdi Motagh and Julia Neelmeijer designed the study together. Julia Neelmeijer accomplished the InSAR and atmosphere correction processing, analysis and wrote the manuscript. Tilo Schöne processed the lake altimetry data and wrote the corresponding section of the manuscript. Robert Dill and Volker Klemann performed the modelling and provided the content for the related section. Mahdi Motagh contributed to the analysis, discussion and writing.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Simpson, D.W.; Leith, W.; Scholz, C. Two types of reservoir-induced seismicity. Bull. Seismol. Soc. Am. 1988, 78, 2025–2040. [Google Scholar]
- Kaufmann, G.; Amelung, F. Reservoir-induced deformation and continental rheology in vicinity of Lake Mead, Nevada. J. Geophys. Res.-Solid Earth 2000, 105, 16341–16358. [Google Scholar] [CrossRef]
- Bevis, M.; Kendrick, E.; Cser, A.; Smalley, R. Geodetic measurement of the local elastic response to the changing mass of water in Lago Laja, Chile. Phys. Earth Planet. Inter. 2004, 141, 71–78. [Google Scholar] [CrossRef]
- Wahr, J.; Khan, S.A.; van Dam, T.; Liu, L.; van Angelen, J.H.; van den Broeke, M.R.; Meertens, C.M. The use of GPS horizontals for loading studies, with applications to northern California and southeast Greenland. J. Geophys. Res.-Solid Earth 2013, 118, 1795–1806. [Google Scholar] [CrossRef]
- Cavalié, O.; Doin, M.P.; Lasserre, C.; Briole, P. Ground motion measurement in the Lake Mead area, Nevada, by differential synthetic aperture radar interferometry time series analysis: Probing the lithosphere rheological structure. J. Geophys. Res. 2007, 112, B03403. [Google Scholar] [CrossRef]
- Nof, R.N.; Ziv, A.; Doin, M.P.; Baer, G.; Fialko, Y.; Wdowinski, S.; Eyal, Y.; Bock, Y. Rising of the lowest place on Earth due to Dead Sea water-level drop: Evidence from SAR interferometry and GPS. J. Geophys. Res.-Solid Earth 2012, 117, B05412. [Google Scholar] [CrossRef]
- Zhao, W.; Amelung, F.; Doin, M.P.; Dixon, T.H.; Wdowinski, S.; Lin, G. InSAR observations of lake loading at Yangzhuoyong Lake, Tibet: Constraints on crustal elasticity. Earth Planet. Sci. Lett. 2016, 449, 240–245. [Google Scholar] [CrossRef]
- Furuya, M.; Wahr, J.M. Water level changes at an ice-dammed lake in west Greenland inferred from InSAR data. Geophys. Res. Lett. 2005, 32, L14501. [Google Scholar] [CrossRef]
- Doin, M.P.; Twardzik, C.; Ducret, G.; Lasserre, C.; Guillaso, S.; Jianbao, S. InSAR measurement of the deformation around Siling Co Lake: Inferences on the lower crust viscosity in central Tibet. J. Geophys. Res.-Solid Earth 2015, 120, 5290–5310. [Google Scholar] [CrossRef]
- Gahalaut, V.; Yadav, R.K.; Sreejith, K.M.; Gahalaut, K.; Bürgmann, R.; Agrawal, R.; Sati, S.; Kumar, A. InSAR and GPS measurements of crustal deformation due to seasonal loading of Tehri reservoir in Garhwal Himalaya, India. Geophys. J. Int. 2017, 209, 425–433. [Google Scholar] [CrossRef][Green Version]
- Simpson, D.W.; Hamburger, M.W.; Pavlov, V.D.; Nersesov, I.L. Tectonics and seismicity of the Toktogul Reservoir Region, Kirgizia, USSR. J. Geophys. Res. 1981, 86, 345–358. [Google Scholar] [CrossRef]
- Tibaldi, A.; Corazzato, C.; Rust, D.; Bonali, F.; Pasquarè Mariotto, F.; Korzhenkov, A.; Oppizzi, P.; Bonzanigo, L. Tectonic and gravity-induced deformation along the active Talas–Fergana Fault, Tien Shan, Kyrgyzstan. Tectonophysics 2015, 657, 38–62. [Google Scholar] [CrossRef]
- Savoskul, O.; Chevnina, E.; Perziger, F.; Vasilina, L.; Baburin, V.; Danshin, A.I.; Matyakubov, B.; Murakaev, R. Water, climate, food, and environment in the Syr Darya Basin. In Contribution to the Project ADAPT; Savoskul, O.S., Ed.; The Pennsylvania State University: State College, PA, USA, 2003. [Google Scholar]
- Keith, J.E.; McKinney, D.C. Options Analysis of the Operation of the Toktogul Reservoir. Available online: http://www.ce.utexas.edu/prof/mckinney/papers/aral/Issue7.html (accessed on 15 December 2017).
- Kyrgyzstan Disaster Risk Data Platform. Available online: http://geonode.mes.kg (accessed on 10 March 2017).
- Ghose, S.; Mellors, R.J.; Korjenkov, A.M.; Hamburger, M.W.; Pavlis, T.L.; Pavlis, G.L.; Omuraliev, M.; Mamyrov, E.; Muraliev, A.R. The MS = 7.3 1992 Suusamyr, Kyrgyzstan, Earthquake in the Tien Shan: 2. Aftershock Focal Mechanisms and Surface Deformation. Bull. Seismol. Soc. Am. 1997, 87, 23–38. [Google Scholar]
- Dovgan, V. Seismometric Monitoring of Toktogul Hydroelectric Power Station. In Proceedings of the IV International Conference “Problems of Cybernetics and Informatics” (PCI’2012), Baku, Azerbaijan, 12–14 September 2012; pp. 81–84. [Google Scholar]
- Zebker, H.A.; Rosen, P.A.; Hensley, S. Atmospheric effects in interferometric synthetic aperture radar surface deformation and topographic maps. J. Geophys. Res.-Solid Earth 1997, 102, 7547–7563. [Google Scholar] [CrossRef]
- Fialko, Y. Interseismic strain accumulation and the earthquake potential on the southern San Andreas fault system. Nature 2006, 441, 968–971. [Google Scholar] [CrossRef] [PubMed]
- Puysségur, B.; Michel, R.; Avouac, J.P. Tropospheric phase delay in interferometric synthetic aperture radar estimated from meteorological model and multispectral imagery. J. Geophys. Res. 2007, 112, B05419. [Google Scholar] [CrossRef]
- Bekaert, D.P.S.; Hooper, A.; Wright, T.J. A spatially variable power law tropospheric correction technique for InSAR data. J. Geophys. Res.-Solid Earth 2015, 120, 1345–1356. [Google Scholar] [CrossRef]
- Birkett, C.M. Radar altimetry: A new concept in monitoring lake level changes. Eos Trans. Am. Geophys. Union 1994, 75, 273–275. [Google Scholar] [CrossRef]
- Crétaux, J.F.; Abarca-del Río, R.; Bergé-Nguyen, M.; Arsen, A.; Drolon, V.; Clos, G.; Maisongrande, P. Lake Volume Monitoring from Space. Surv. Geophys. 2016, 37, 269–305. [Google Scholar] [CrossRef]
- Schöne, T.; Dusik, E.; Illigner, J.; Klein, I. Water in Central Asia: Reservoir Monitoring with Radar Altimetry Along the Naryn and Syr Darya Rivers. In Proceedings of the International Symposium on Earth and Environmental Sciences for Future Generations, Prague, Czech Republic, 22 June–2 July 2015; Springer: Cham, Switzerland, 2017; Volume 147, pp. 349–357. [Google Scholar]
- CA WATER Info. Available online: www.cawater-info.net (accessed on 31 January 2017).
- JSC “Electric Stations”. Available online: www.energo-es.kg (accessed on 31 January 2017).
- Förste, C.; Bruinsma, S.; Abrykosov, O.; Flechtner, F.; Dahle, C.; Neumayer, K.H.; Barthelmes, F.; König, R.; Marty, J.-C.; Lemoine, J.M.; et al. EIGEN-6C3—The newest high resolution global combined gravity field model based on the 4th release of the GOCE Direct Approach. In Proceedings of the 2013 IAG Scientific Assembly, 150th Anniversary of the IAG, Potsdam, Germany, 1–6 September 2013. [Google Scholar]
- Werner, C.L.; Wegmüller, U.; Strozzi, T.; Wiesmann, A. GAMMA SAR and Interferometric Processing Software. In Proceedings of the ERS-ENVISAT Symposium, Gothenburg, Sweden, 16–20 October 2000. [Google Scholar]
- Prats, P.; Marotti, L.; Wollstadt, S.; Scheiber, R. Investigations on TOPS interferometry with TerraSAR-X. In Proceedings of the 2010 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, Hawaii, 25–30 July 2010; pp. 2629–2632. [Google Scholar] [CrossRef]
- Prats-Iraola, P.; Scheiber, R.; Marotti, L.; Wollstadt, S.; Reigber, A. TOPS Interferometry With TerraSAR-X. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3179–3188. [Google Scholar] [CrossRef]
- Scheiber, R.; Moreira, A. Coregistration of interferometric SAR images using spectral diversity. IEEE Trans. Geosci. Remote Sens. 2000, 38, 2179–2191. [Google Scholar] [CrossRef]
- Wegmüller, U.; Werner, C.; Strozzi, T.; Wiesmann, A.; Frey, O.; Santoro, M. Sentinel-1 IWS mode support in the GAMMA software. Procedia Comput. Sci. 2016, 100, 431–436. [Google Scholar] [CrossRef]
- Berardino, P.; Fornaro, G.; Lanari, R.; Sansosti, E. A new algorithm for surface deformation monitoring based on small baseline differential SAR interferograms. IEEE T. Geosci. Remote 2002, 40, 2375–2383. [Google Scholar] [CrossRef]
- Hooper, A.J.; Bekaert, D.; Spaans, K.; Arıkan, M. Recent advances in SAR interferometry time series analysis for measuring crustal deformation. Tectonophysics 2012, 514–517, 1–13. [Google Scholar] [CrossRef]
- Hooper, A. A multi-temporal InSAR method incorporating both persistent scatterer and small baseline approaches. Geophys. Res. Lett. 2008, 35, L16302. [Google Scholar] [CrossRef]
- Hooper, A.J.; Zebker, H.A. Phase unwrapping in three dimensions with application to InSAR time series. J. Opt. Soc. Am. 2007, 24, 2737–2747. [Google Scholar] [CrossRef]
- Marinković, P.; Larsen, Y. On Resolving the Local Oscillator Drift Induced Phase Ramps in ASAR and ERS1/2 Interferometric Data—The Final Solution. In Proceedings of the Fringe 2015 workshop (ESA SP-731), Frascati, Italy, 23–27 March 2015. [Google Scholar]
- Bekaert, D.; Walters, R.; Wright, T.; Hooper, A.; Parker, D. Statistical comparison of InSAR tropospheric correction techniques. Remote Sens. Environ. 2015, 170, 40–47. [Google Scholar] [CrossRef]
- Doin, M.P.; Lasserre, C.; Peltzer, G.; Cavalié, O.; Doubre, C. Corrections of stratified tropospheric delays in SAR interferometry: Validation with global atmospheric models. J. Appl. Geophys. 2009, 69, 35–50. [Google Scholar] [CrossRef]
- Jolivet, R.; Agram, P.S.; Lin, N.Y.; Simons, M.; Doin, M.P.; Peltzer, G.; Li, Z. Improving InSAR geodesy using Global Atmospheric Models. J. Geophys. Res.-Solid Earth 2014, 119, 2324–2341. [Google Scholar] [CrossRef]
- Barnhart, W.D.; Lohman, R.B. Characterizing and estimating noise in InSAR and InSAR time series with MODIS. Geochem. Geophys. 2013, 14, 4121–4132. [Google Scholar] [CrossRef]
- Jolivet, R.; Grandin, R.; Lasserre, C.; Doin, M.P.; Peltzer, G. Systematic InSAR tropospheric phase delay corrections from global meteorological reanalysis data. Geophys. Res. Lett. 2011, 38, L17311. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: Configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Fialko, Y.; Simons, M.; Agnew, D. The complete (3-D) surface displacement field in the epicentral area of the 1999 M W 7.1 Hector Mine Earthquake, California, from space geodetic observations. Geophys. Res. Lett. 2001, 28, 3063–3066. [Google Scholar] [CrossRef]
- Motagh, M.; Shamshiri, R.; Haghshenas Haghighi, M.; Wetzel, H.U.; Akbari, B.; Nahavandchi, H.; Roessner, S.; Arabi, S. Quantifying groundwater exploitation induced subsidence in the Rafsanjan plain, southeastern Iran, using InSAR time-series and in situ measurements. Eng. Geol. 2017, 218, 134–151. [Google Scholar] [CrossRef]
- Farrell, W.E. Deformation of the Earth by surface loads. Rev. Geophys. 1972, 10, 761–797. [Google Scholar] [CrossRef]
- Dill, R.; Klemann, V.; Martinec, Z.; Tesauro, M. Applying local Green’s functions to study the influence of the crustal structure on hydrological loading displacements. J. Geodyn. 2015, 88, 14–22. [Google Scholar] [CrossRef]
- Dziewonski, A.M.; Anderson, D.L. Preliminary reference Earth model. Phys. Earth Planet. Inter. 1981, 25, 297–356. [Google Scholar] [CrossRef]
- Tesauro, M.; Audet, P.; Kaban, M.K.; Bürgmann, R.; Cloetingh, S. The effective elastic thickness of the continental lithosphere: Comparison between rheological and inverse approaches. Geochem. Geophys. Geosys. 2012, 13, Q09001. [Google Scholar] [CrossRef]
- Haiden, T.; Janousek, M.; Bauer, P.; Bidlot, J.; Dahoui, M.; Ferranti, L.; Prates, F.; Richardson, D.; Vitart, F. Evaluation of ECMWF forecasts, including 2014–2015 upgrades. In ECMWF Technical Memoranda; European Centre for Medium-Range Weather Forecasts: Reading, UK, 2015; Volume 765, pp. 1–51. [Google Scholar]
- Havenith, H.B.; Torgoev, I.; Torgoev, A.; Strom, A.; Xu, Y.; Fernandez-Steeger, T. The Kambarata 2 blast-fill dam, Kyrgyz Republic: Blast event, geophysical monitoring and dam structure modelling. Geoenviron. Disasters 2015, 2, 11. [Google Scholar] [CrossRef][Green Version]
- Abdrakhmatov, K.; Havenith, H.B.; Delvaux, D.; Jongmans, D.; Trefois, P. Probabilistic PGA and Arias Intensity maps of Kyrgyzstan (Central Asia). J. Seismol. 2003, 7, 203–220. [Google Scholar] [CrossRef]
- Bindi, D.; Abdrakhmatov, K.; Parolai, S.; Mucciarelli, M.; Grünthal, G.; Ischuk, A.; Mikhailova, N.; Zschau, J. Seismic hazard assessment in Central Asia: Outcomes from a site approach. Soil Dyn. Earthq. Eng. 2012, 37, 84–91. [Google Scholar] [CrossRef][Green Version]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).