Evaluating the Influence of Criteria to Attract Foreign Direct Investment (FDI) to Develop Supporting Industries in Vietnam by Utilizing Fuzzy Preference Relations

Abstract

In the early 2000s, Vietnam’s government concentrated on the promotion of supporting industries which can be seen as a “key” solution to sustaining economic growth, thereby improving the national welfare. However, Vietnam’s supporting industries still exhibit lower development and competitive weakness. The main reason for this condition is due to a lack of capital, technological innovation, and necessary management skills for development. Therefore, attracting foreign direct investment (FDI) for developing supporting industries offers the best strategy to realize this solution. However, attracting FDI to develop supporting industries represents a weakness which lies in both the quantity (total capital and projects) and quality of investment. So which factors are effective to attract FDI for developing supporting industries in Vietnam? This investigation establishes an analytical hierarchy framework available to the Vietnamese government and to policymakers in order to evaluate the influence of criteria needed to attract FDI for developing supporting industries based on eight main criteria. They include legal and institutional criteria, the market size of supporting industries, human resources, infrastructure facilities, technological development and innovation, domestic supply capacity, international cooperation and competition, and other criteria. This paper uses fuzzy preference relations (FPR) to evaluate the influence of criteria necessary to attract FDI for developing supporting industries, and these analytical results demonstrate that legal and institutional criteria, domestic supply capacity, human resources, technology development and innovation are all major considerations for attracting FDI.

1. Introduction

Vietnam has been late in developing its economy, which it started to reform in 1986 [1] and became emergent in the early 1990s [2]. The Vietnamese government decided, until 2020, to follow the process of industrialization and modernization to achieve success [3]. The government’s policy changed in 1991, and since then Vietnam has been pursuing an economic policy to join the global economy, such as the lifting of the United States (US) trade embargo in 1994, joining the ASEAN (Association of Southeast Asia Nations) in 1995 and the WTO (World Trade Organization) in 2007 [4]. Therefore, to successfully implement the process of industrialization and modernization, along with international economic integration, it is necessary to reduce dependence on imported goods and a burgeoning trade deficit [5]. Instead, Vietnam should actively pursue the supply of goods in the chain of production [6]. Competitive supporting industries may consistently contribute to the economic development and national welfare [7]. Such development causes a dynamic effect to occur that will promote technological innovation and human resources [8]. Moreover, the most important aspect for developing countries to improve economic self-sufficiency is to establish competitive supporting industries for foreign direct investment (FDI)-driven economic growth [9]. So, in the early 2000s, the Vietnamese government began to concentrate on promoting supporting industries which can be seen as a “key” solution towards economic sustainability for the development of the country, and thereby improve national welfare [5]. It is expressed in the decisions and policies that have been made [10,11,12,13,14].

Currently, the term “supporting industries” is using widely, especially in East Asia. It is interpreted differently in various fields of activity [15,16]. Supporting industries may be defined as a group of producers of manufactured inputs in which finished goods are produced through manufacturing processes consisting of both manufacturing inputs and assembly processes [5]. Supporting industries produce these inputs, more specifically, as intermediate and finished capital goods. The White Paper on Economic Cooperation of the Ministry of International Trade and Industry of Japan (MITI) defined supporting industries as the supply of raw materials, and those parts and capital goods used in assembly-type industries [17]. The United States (US) Department of Energy has defined supporting industries as those which supply materials and processes that are necessary to form and fabricate products before they are marketed to end-use industries [18]. In Vietnam, supporting industries are defined in accordance with Decision No. 12/2011/QĐ-TTg, promulgated by the Prime Minister: “The supporting industries are industries producing materials, spare parts, components, accessories or semi-finished products as means of the production of final products in production and assembly industries or of consumer products” [14]. The list of supporting industry products which are given priority for development are found under Decision No. 1483/QĐ-TTg by the Prime Minister, on 26 August 2011, including six industries: textile and apparel, leather and footwear, electronic and information industries, the manufacturing and assembly of automobiles, the mechanical industry, and supporting industry products for high-tech industries [13].

Vietnam’s supporting industries are still in the process of slowly developing. The situation of supporting industries in Vietnam is one of competitive weakness [9,19]. Due to the underdeveloped state of the local supporting industry in Vietnam, increased production costs, the risk of bigger trade deficits with foreign partners, lowered competitiveness of local products compared with regional peers, and imports of more expensive components and spare parts mostly purchased from Asian markets have greatly weakened Vietnam’s supporting industries [19,20]. The weakness of these industries is viewed to be one of the primary factors preventing industrial development and economic growth from taking place, as well as benefiting national welfare [5]. Some of the major factors leading to the weakness of supporting industries in Vietnam are a lack of capital, technological innovation, and the dearth of management skills for leading development [6]. While FDI is an important vehicle for the transfer of technology, contributing relatively more to growth than domestic investment [21,22], FDI significantly increases economic growth of recipient countries by bringing physical, advanced technological, and management expertise to bear [23,24,25]. Moreover, FDI is considered to increase domestic capital, to create employment and to raise incomes, to promote technology and to generate the transfer of skills through foreign technology and technical know-how, to boost host country economies, and investment, seen as the engine of economic growth in the long-term [26,27]. Therefore, attracting FDI for developing supporting industries is the best strategy to solve the problem of insufficient capitalization; however, attracting FDI for developing supporting industries in Vietnam is also a show of weakness, both in terms of quantity (total capital and projects) and quality [9]. As such, this study demonstrates which main factors are effective to attract FDI for developing supporting industries in Vietnam.

This study concentrates on identifying the main factors influencing the attraction of FDI for developing supporting industries in Vietnam and for evaluating them. This theoretical study involves personal interviews of involved policymakers, economists, foreign investors, and managers of six supporting industries, and practical considerations of the real situation of developing supporting industries hoping to attract FDI for developing supporting industries; the result indicates that there are eight main criteria influencing to attract FDI for developing supporting industry. These eight main criteria include the following: (1) the legal and institutional framework; (2) the market size of supporting industries; (3) domestic supply capacity; (4) technological development and innovation; (5) human resources; (6) infrastructure facilities; (7) international cooperation and competition; and (8) other criteria [28,29,30,31,32]. From those results, an analytical hierarchy framework to help Vietnam’s government and responsible policymakers to evaluate the influence of criteria to attract FDI to develop supporting industries based on the eight main criteria is established.

Accordingly, the analytic hierarchy process (AHP) method performs complicated pairwise comparison among the criteria [33], and it takes considerable time to obtain a convincing consistency index with an increasing number of criteria. In the fuzzy analytic hierarchy process (fuzzy AHP) method, establishing a pairwise comparison matrix requires n(n − 1)/2 judgments for a level with n criteria (alternatives). The number of comparisons increases as the number of criteria increases [33,34]. However, fuzzy preference relations was proposed method yields consistent decision rankings from only (n − 1) pairwise comparisons [35]. Therefore, the presented fuzzy preference relations method is an easy and practical way of making decisions. This study uses the fuzzy preference relations (FPR) [35,36,37,38,39] to calculate the criteria weights. This result will make clear the most important criteria.

2. Related Literature

2.1. The Role of Supporting Industries For Economic Growth

There are two questions that may arise: “What role can supporting industries play in promoting economic growth?” and “If a country has developed competitive supporting industries then would this country promote long-run economic development, or not?” This is the possible answer to those questions. The regular development of competitive supporting industries causes the dynamic effects in the promotion of technological innovation, thereby improving national welfare [8,40]”. Porter mentions that any globally competitive companies may benefit from domestic supporting industries, although it is unnecessary to become competitive in all supporting industries if there is specialization taking place in certain areas [41]. It is decidedly beneficial for developing countries to establish competitiveness standards among supporting industries for long-run economic growth to occur. Vietnam is considered a developing country at this time in the country’s relative growth, and the process of industrialization and modernization is still progressing on a post-war and post-colonial footing [2,42,43,44,45]. Therefore, the Vietnamese government is concentrating on promoting supporting industries. This is expressed through Vietnam supporting industry prospects under assessment by Japanese enterprises [46,47], and the decisions and policies under the aegis of Decision 34/2007/QD-BCN. This decision was promulgated on 31 July 2007 by the Minister of Industry and Trade: “Approving the planning of industrial development supports up to 2010 and vision to 2020” [11]. Further, other equally important decisions have been made to promote supporting industrial growth: Decision 12/2011/QD-TTg, on 24 February 2011, by the Prime Minister: “On development policies of some supporting industries” [14]; Decision 1843//QD-TTg, on 26 August 2011, by the Prime Minister: “On promulgating list of supporting industry products which are given priority for development” [13]; Decision 1556/QD-TTg, on 17 October 2012, by the Prime Minister: “Approval scheme, help developing small and medium enterprises in supporting industries field” [12]; and Decision 9028/QD-BCT, on 10 October 2014, by the Minister of Industry and Trade: “Approval master plan for developing supporting industries up to 2020, vision to 2030” [10]. However, the situation of Vietnam’s supporting industries is still materialized as slow development and competitive weakness. As a result, it is shown too minimally in the proportion of localization found in the amount of finished products. According to Vietnamese Governmental Reports [48] and General Statistics Office of Vietnam [49], the proportion of localization in the finished products of some supporting industries is as follows: 35.5% in mechanical industry; 32.5% in textile and apparel; 21.1% in leather and footwear; 16.8% in electronic and information industries; and 26.5% in manufacturing and the assembly of automobiles. Some of the major factors leading to the weakness of supporting industries in Vietnam are the lack of capital, insufficient technological innovation, and the dearth of management skills for development. So, the Vietnamese government should concentrate on developing supporting industries within Vietnam.

2.2. Attracting Foreign Direct Investment (FDI) for Developing Supporting Industries and Economic Growth to Occur

Developing countries can be improved national welfare by attracting FDI. It is FDI that supports economic growth, increases incomes, and promotes a greater rate of employment and technological transfer [27,50,51,52]. Assumedly, FDI could have beneficial spillover effects on the host countries, which may include the enhancement of job creation, knowledge transfer, and capital accumulation. Five main channels of technological diffusion are linked to FDI flows: Demonstration or imitation, exportation, competition, labor mobility, and backward and forward linkages with domestic firms [40,53]. Moreover, the customer base of supporting industries may include domestic assemblers, foreign assemblers located in the domestic market, and foreign assemblers in foreign countries. Foreign assemblers are often multi-national enterprises (MNEs) [40]. Research supports the theory that MNEs tend to have higher productivity than domestic firms if in the same sector and thereby contribute to GDP growth in developing countries [6,16]. Together, Dunning proposed the OLI, which stands for Location, Ownership, and Internalization, three potential sources of advantage that may underlie a firm’s decision to become a multinational. Wherein, location advantages focus on the question of where MNEs chooses to locate. They seek to avail of lower production costs in that locale [54]. Seemingly, developing countries expect that MNEs will be a positive impact on the productivity levels of domestic firms through a generation of positive externalities. FDI may generate positive externalities for the productivity growth of domestic suppliers through business relationships with MNEs (to be called “backward linkages” afterward) [40,51]. Moreover, the output and productivity of domestic supporting industries will be increased due to the additional demand and technology transfer that is caused by MNEs [16]. Furthermore, if increasing FDI causes positive externalities occurs for domestic suppliers and improves their productivity through backward linkages, national welfare in FDI host countries will also be improved [27,52].

In summary, developing countries will be improved national welfare by attracting FDI if their supporting industries will obtaining positive externalities that far exceed negative externalities present for domestic assemblers [5,40]. Finally, Porter stresses the importance of competitive supporting industries as a partner in any MNCs’ dynamic technology innovation, which serves as its obvious role as a recipient of technology transferred from the MNCs [41]. Therefore, it is important for developing countries strive to establish competitive supporting industries to achieve FDI-driven economic growth. In addition, domestic supporting industry is increasing their importance as a factor useful to attract FDI [8,9]. Additionally, in the reverse, FDI will promote developing supporting industries. From the real situation of developing supporting industries and attracting FDI to develop supporting industries, together with the results of the interviews with policymakers, economists, foreign investors and managers of six supporting industries, there are eight important factors for investment decision of foreign investors to invest into supporting industries in Vietnam. These factors have been identified to include the legal and institutional framework, the market size of supporting industries (i.e., total consumption of supporting industries products), human resources (i.e., quantity, salary, education, skill and moral), the infrastructure facilities (i.e., transport, power, information and communication), technological development and innovation, domestic supply capacity (i.e., total value and partition domestic supply, the quantity and size of supporting industries firms), international cooperation and competition, and other criteria (such as environment policy, culture, tax policy, land support, corruption, etc.).

3. Research Methodology

In this study, the proposed procedure utilizes the fuzzy preference relations (FPR) process to evaluate the influence of criteria useful to attract foreign direct investment (FDI) for developing supporting industries in Vietnam. It will give the brief descriptions of the FPR method.

Herrera-Viedma et al. [35] proposed the fuzzy preference relations, and in accordance with fuzzy preference relation [36,37,38,39].

3.1. Fuzzy Preference Relation

Expert preferences over a set of alternatives where X is denoted by a positive preference relation matrix $P\subset X\times X$ with membership function: ${\alpha }_p:X\times X\to [0,1]$, where ${\mathrm{p}}_{ij}=\alpha (x_i,x_j)$ indicates the ratio of the preference intensity of alternative x_i to that of x_j. Moreover, if p_ij = ${\displaystyle \sum _{i=1}^n{p}_{ij}}$ implies indifference between x_i and x_j (x_i ~ x_j), ${\text{p}}_{\text{ij}}=1$ indicates that x_i is absolutely preferred to x_j, ${\text{p}}_{\text{ij}}=0$ indicates x_j is absolutely preferred to x_i, and p_ij > $\frac{1}{2}$ indicates that x_i is preferred to $x_i$, $x_i>x_j$. Meanwhile, P is assumed to be an additive reciprocal, that is:

$$p_{ij}+p_{ji}=1 \forall i,j\in \left\{1,...,n\right\}$$

(1)

Proposition 3.1. Suppose that there is a set of alternatives, $X=\left\{x_1,...,x_n\right\}$, and is associated with it a reciprocal multiplicative preference relation $A=(a_{ij})$ with $a_{ij}\in \left[\frac{1}{9},9\right]$. Then, the corresponding reciprocal fuzzy preference relation, $P=(p_{\text{ij}})$ with, $p_{\text{ij}}\in [0,1]$, associated with A is given as follows:

$$p_{\text{ij}}=g(a_{\text{ij}})=\frac{1}{2}\cdot (1+{\log }_9{a}_{\text{ij}})$$

(2)

With this type of transformation function g, it can be related the research issues obtained for both kinds of preference relations.

3.2. On the Consistency of the Fuzzy Preference Relations

Proposition 3.2. Let $A=(a_{\text{ij}})$ be a consistent multiplicative preference relations, then the corresponding reciprocal fuzzy preference relations, $P=\text{g}(A)$, verifies the additive transitivity property.

Proof. For being $A=(a_{\text{ij}})$ consistent it has that $a_{\text{ij}}\cdot a_{jk}=a_{ik}\forall i,j,k$, or equivalently $a_{\text{ij}}\cdot a_{jk}\cdot a_{ki}=1$$\forall i,j,k$. Taking logarithms on both sides, it has

$${\log }_9{a}_{\text{ij}}+{\log }_9{a}_{jk}+{\log }_9{a}_{ki}=0 \forall i,j,k$$

(3)

Adding Equation (3) and dividing by Equation (2) on both sides then

$$\frac{1}{2}\cdot (1+{\log }_9{a}_{\text{ij}})+\frac{1}{2}\cdot (1+{\log }_9{a}_{jk})+\frac{1}{2}\cdot (1+{\log }_9{a}_{ki})=\frac{3}{2} \forall i,j,k.$$

(4)

The fuzzy preference relations $P=\text{g}(A)$, being $p_{\text{ij}}=\frac{1}{2}\cdot (1+{\log }_9{a}_{\text{ij}})$, verifies

$$p_{\text{ij}}+p_{jk}+p_{ik}=\frac{3}{2} \forall i,j,k$$

(5)

It follows that $P=\text{g}(A)$ verifies the additive transitivity property.

In such a way, in this paper, it considers the following definition of the consistent fuzzy preference relation:

Definition 3.1. A reciprocal fuzzy preference relation $P=(p_{\text{ij}})$ is consistent if

$$p_{\text{ij}}+p_{jk}+p_{ki}=\frac{3}{2} \forall i,j,k=1,...n.$$

(6)

In what follows, it will be using the term additive consistency to refer to consistency for fuzzy preference relations based on the additive transitivity property.

3.3. Additive Transitivity Consistency of the Fuzzy Preference Relations

Proposition 3.3-1. For a reciprocal fuzzy preference relation $P=(p_{\text{ij}})$, the following statements are equivalent:

$$p_{\text{ij}}+p_{jk}+p_{ki}=\frac{3}{2} \forall i,j,k$$

(7)

$$p_{\text{ij}}+p_{jk}+p_{ki}=\frac{3}{2} \forall i<j<k$$

(8)

Proposition 3.3-2. A fuzzy preference relation $P=(p_{\text{ij}})$ is consistent if and only if

$$p_{ij}+p_{jk}+p_{ik}=\frac{3}{2} \forall i\le j\le k.$$

(9)

Proposition 3.3-3. For a reciprocal additive fuzzy preference relation $P=(p_{\text{ij}})$, the following statements are equivalent:

$$p_{ij}+p_{jk}+p_{ki}=\frac{3}{2} \forall i<j<k$$

(10)

$$p_{i(i+1)}+p_{(i+1)(i+2)}+...p_{(j-1)j}+p_{ji}=\frac{j-i+1}{2} \forall i<j$$

(11)

4. Framework for Evaluating the Influence of Criteria to Attract Foreign Direct Investment (FDI) for Developing Supporting Industries in Vietnam under a Multi-Criteria Decision Making Process

4.1. Evaluated Criteria and Framework of the Evaluation Model

This study interviewed policymakers, economists, and foreign investors and managers of six supporting industries, together with the real situation of developing supporting industries and attracting FDI for developing supporting industries. It identified criteria and their attributes to be summarized as follows: $C_1$ the legal and institutional; $C_2$ the market size of supporting industries (total consumption of supporting industries product); $C_3$ domestic supply capacity (as total supply, quantity and size of supporting industries firms); $C_4$ the technological development and innovation; $C_5$ the human resources (i.e., quantity, salary, education, skill and moral); $C_6$ the infrastructure facilities (i.e., transport, power supply, information and communication,…); $C_7$ international cooperation and competition; $C_8$ the other criteria (culture, tax policy, land support, corruption, environment, etc.). An analytical hierarchy framework based on eight main criteria is established as the Figure 1.

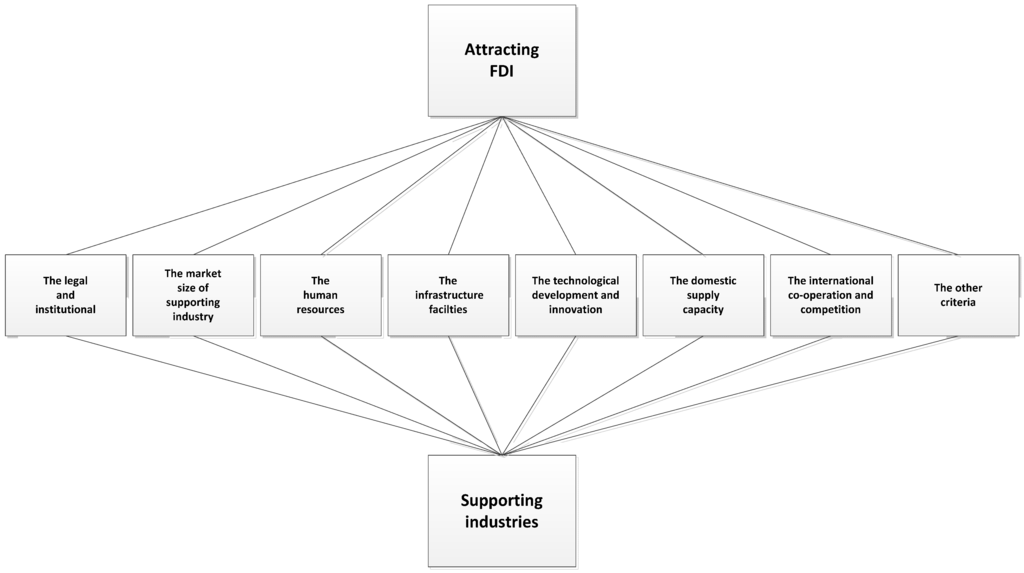
Figure 1. The analytical framework of this study.

Within the framework of attracting FDI for developing supporting industries, there are eight main criteria that influence the attraction of FDI.

4.2. Hierarchical Analytical Process to Evaluate the Influence of Criteria to Attract Foreign Direct Investment (FDI) for Developing Supporting Industries

4.2.1. Linguistic Variables

This paper compares pairs of criteria using expressions such as ‘‘Equally important (EQ)”, ‘‘Moderately important (MO)”, ‘‘Strongly important (ST)”, ‘‘Very strong importance (VS)”, and ‘‘Absolutely important (AB)”, using a five-level scale with values indicated by actual numbers (see Table 1).

Table 1. Linguistic terms for priority weights of influential factors.

Definition	Intensity of Importance
Equally important (EQ)	1
Moderately important (MO)	3
Strongly important (ST)	5
Very strong importance (VS)	7
Absolutely important (AB)	9
Intermediate values between two adjacent judgments	2, 4, 6, 8

4.2.2. Reciprocal Additive Consistent Fuzzy Preference Relations for Prioritizing the Evaluation Criteria

AHP separates a complex decision issue that creates elemental problems to produce a hierarchical model. Each of these preference relations is required the completion of all $\frac{n\cdot \left(n+1\right)}{2}$ judgments for a preference matrix containing n elements to be formed. To reduce the judgment times, this paper employs the reciprocal additive consistent fuzzy preference relations designed by Herrera-Viedma et al. [11], because it only requires $n-1$ judgments from a set of n elements.

The procedures of the reciprocal additive consistent fuzzy preference relations for prioritizing the assessment criteria are given below:

(1) This study establishes pairwise comparison matrices for all the criteria $\left(C_i,i=1,2,...,n\right)$ in the dimensions of the hierarchy system. The evaluators $\left(E_k,k=1,2,...,m\right)$ provide the more important of each of the pairs of considered criteria for a set of n-1 preference values $\left(a_{12},a_{23},...,a_{\left(n-1\right)n}\right)$, for

$$A^k=\begin{array}{c}\\ \begin{array}{c}{C}_1\\ C_2\\ ⋮\\ C_{n-1}\\ C_n\end{array}\end{array}\begin{array}{c}\begin{array}{ccccc}{C}_1& C_2& \cdots & C_{n-1}& C_n\end{array}\\ \left[\begin{array}{ccccc}1& a_{12}^k& \cdots & x& x\\ x& 1& a_{23}^k& x& x\\ ⋮& ⋮& \ddots & \ddots & ⋮\\ x& x& \cdots & 1& a_{(n-1)n}^k\\ x& x& \cdots & x& 1\end{array}\right]\end{array}$$

(12)

where $a_{\text{ij}}^k$ denotes the preference intensity toward considered criteria i and j are assessed by evaluator k, $a_{\text{ij}}=1$ indicates no difference between considered criteria i and j, $a_{\text{ij}}=3,5,7,9$ reveals that criteria i relatively important to criteria j, and $a_{\text{ij}}=\frac{1}{3},\frac{1}{5},\frac{1}{7},\frac{1}{9}$ indicates that considered criteria i is less important than criteria j. The sign ‘‘x” indicates the remaining $a_{\text{ij}}^k$, which can be done via inverse comparison.

(2) Transform the preference value $a_{\text{ij}}^k$ into $p_{\text{ij}}^k$ using an interval scale $\left[0,1\right]$, then derive the remaining $p_{\text{ij}}^k$ based on the reciprocal transitivity property, as follows:

$$p^k=\frac{1}{2}(1+{\log }_9{A}^k)=\begin{array}{c}\\ \begin{array}{c}{C}_1\\ C_2\\ ⋮\\ C_n\end{array}\end{array}\begin{array}{c}\begin{array}{cccc}{C}_1& C_2& \cdots & C_n\end{array}\\ \left[\begin{array}{cccc}0.5& p_{12}^k& x& x\\ x& 0.5& p_{23}^k& x\\ ⋮& ⋮& ⋮& ⋮\\ x& x& \cdots & 0.5\end{array}\right]\end{array}$$

(13)

where $p_{\text{ij}}=0.5$ indicates no difference between criteria i and j, $p_{\text{ij}}=1$ demonstrates that criteria i is absolutely important to criteria j, and $p_{\text{ij}}=0$ illustrates that the criteria is absolutely less important to criteria j. The remaining $p_{\text{ij}}^k$ can be calculated using Equations (1) and (11), but in an interval $\left[-a,1+a\right]$, and a transformed function is necessary to preserve the reciprocity and additive transitivity. The transformation function is, as follows:

$$f\left(p_{\text{ij}}^k\right)=\frac{p_{\text{ij}}^k+a}{1+2\cdot a}$$

(14)

where a denotes the absolute value of the minimum negative value or maximum positive value minus one in this preference matrix.

(3) Base on the opinions of evaluators will be obtained the aggregated weights of the criteria. Moreover, let $p_{\text{ij}}^k$ denote transforming the fuzzy preference value of evaluator k for assessing the criteria i and j. This paper uses the notation of the average value to integrate the judgment values of m evaluators, namely:

$$p_{\text{ij}}=\left(p_{\text{ij}}^1+p_{\text{ij}}^2+...+p_{\text{ij}}^m\right)/m$$

(15)

(4) Normalizing the aggregated fuzzy preference relation matrices $q_{\text{ij}}$ is used to indicate the normalized fuzzy preference values of each considered criteria, such as

$$q_{\text{ij}}=p_{\text{ij}}/{\displaystyle \sum _{i=1}^n{p}_{\text{ij}}}$$

(16)

(5) Using the ${\varpi }_i$ denoting the average priority weight of considered criteria, the priority of each criteria can be obtained, that is

$${\varpi }_i=\frac{1}{n}\cdot {\displaystyle \sum _{i=1}^n{q}_{\text{ij}}}$$

(17)

where n denotes the number of criteria considered.

5. Results

This study made use of six supporting industries in Vietnam as an example to demonstrate the framework. A total of 15 questionnaires were dispatched, and survey candidates included policymakers, economists, foreign investors and managers from six supporting industries.

Eight major evaluation criteria are useful to assess the problem of how FDI attracts developing supporting industries. The pairwise comparisons for these eight criteria are obtainable via interviews with the assessment representatives mentioned above.

The following examples will be clarify the computational process used to receive the priority weights utilizing a reciprocal additive consistent with the fuzzy preference relation approach:

(1) Based on interviews with 15 representatives regarding the importance of eight evaluation criteria, Table 2 lists the pairwise comparison matrices for a set of $n-1$ neighboring criteria $\left\{a_{12},a_{23},...,a_{78}\right\}$ into the corresponding number.

Table 2. The linguistic terms into corresponding numbers toward eight factors assessed by evaluators.

	E1	E2	E3	E4	E5	E6	E7	E8	E9	E10	E11	E12	E13	E14	E15
C1	7	9	9	6	8	9	9	7	9	5	8	5	8	6	5	C2
C2	1/3	1/5	1/6	1/2	1/4	1/7	1/5	1/5	1/5	1/3	1/5	1/2	1/6	1/2	1/3	C3
C3	5	5	4	1	3	7	2	5	4	2	3	6	4	1	3	C4
C4	1/4	1/3	1/4	1	1/3	1/4	1	1/3	1/2	1/3	1/3	1	1/2	1	1/2	C5
C5	3	3	3	2	3	4	1	3	2	2	5	1/2	2	2	3	C6
C6	5	8	6	4	6	8	6	6	7	4	8	5	6	4	5	C7
C7	1/3	2	1/2	3	2	4	3	1	1/2	3	1/2	4	3	1	1/2	C8

(2) The assessment of evaluator 1 (E1) can be served as an example and listed in Table 3. The linguistic terms, which can be transferred into corresponding numbers.

Table 3. Interval pairwise comparisons of the criteria.

E1	C1	C2	C3	C4	C5	C6	C7	C8
C1	1.0000	7.0000	x	x	x	x	x	x
C2	x	1.0000	0.3333	x	x	x	x	x
C3	x	x	1.0000	5.0000	x	x	x	x
C4	x	x	x	1.0000	0.2500	x	x	x
C5	x	x	x	x	1.0000	3.0000	x	x
C6	x	x	x	x	x	1.0000	5.0000	x
C7	x	x	x	x	x	x	1.0000	0.3333
C8	x	x	x	x	x	x	x	1.0000

x is a variable which can be calculated using Equations (1) and (11).

(3) Equation (2) was used to transform the elements (listed in Table 3) into an interval [0, 1], yielding the following values:

• $p_{12}=(1+{\log }_{9}7.0000)/2=0.9428$
• $p_{23}=(1+{\log }_{9}0.3333)/2=0.2500$
• $p_{34}=(1+{\log }_{9}5.0000)/2=0.8662$
• $p_{45}=(1+{\log }_{9}0.2500)/2=0.1845$
• $p_{56}=(1+{\log }_{9}3.0000)/2=0.7500$
• $p_{67}=(1+{\log }_{9}5.0000)/2=0.8662$
• $p_{78}=(1+{\log }_{9}0.3333)/2=0.2500$.

The remaining value then can be calculated using Equations (1) and (11) with $p_{21}$, $p_{31}$, $p_{81}$, $p_{82}$, and $p_{28}$ being used as examples:

• $p_{21}=1-p_{12}=1-0.9428=0.0572$
• $p_{31}=\frac{3-1+1}{2}-p_{12}-p_{13}=1.5-0.9428-0.2500=0.3072$
• $\begin{array}{l}{p}_{81}=\frac{8-1+1}{2}-p_{12}-p_{23}-p_{34}-p_{45}-p_{56}-p_{67}-p_{78}\\ =4-0.9428-0.2500-0.8662-0.1845-0.7500-0.8662-0.2500=-0.1098\end{array}$
• $\begin{array}{l}{p}_{82}=\frac{8-2+1}{2}-p_{23}-p_{34}-p_{45}-p_{56}-p_{67}-p_{78}\\ =3.5-0.2500-0.8662-0.1845-0.7500-0.8662-0.2500=0.3330\end{array}$
• $p_{28}=1-p_{82}=1-0.3330=0.6670$

The fuzzy preference relation matrix for eight evaluation criteria assessed by evaluator 1 is established in Table 4.

Table 4. Consistent fuzzy preference relation matrix of criteria E1.

E1	C1	C2	C3	C4	C5	C6	C7	C8
C1	0.5000	0.9428	0.6928	1.0590	0.7436	0.9936	1.3598	1.1098
C2	0.0572	0.5000	0.2500	0.6162	0.3008	0.5508	0.9170	0.6670
C3	0.3072	0.7500	0.5000	0.8662	0.5508	0.8008	1.1670	0.9170
C4	−0.0590	0.3838	0.1338	0.5000	0.1845	0.4345	0.8008	0.5508
C5	0.2564	0.6992	0.4492	0.8155	0.5000	0.7500	1.1162	0.8662
C6	0.0064	0.4492	0.1992	0.5655	0.2500	0.5000	0.8662	0.6162
C7	−0.3598	0.0830	−0.1670	0.1992	−0.1162	0.1338	0.5000	0.2500
C8	−0.1098	0.3330	0.0830	0.4492	0.1338	0.3838	0.7500	0.5000

Table 4 lists $p_{14}$, $p_{41}$, $p_{17}$, $p_{71}$, $p_{18}$, $p_{81}$, $p_{37}$, $p_{73}$, $p_{57}$, $p_{75}$ elements not in the interval [0,1]. Therefore, a linear transformation stated in Equation (14) will be employed to ensure the reciprocity and additive transitivity for the preference relation matrix. Table 5 lists the transformation matrix.

Table 5. The transformation matrix of criteria by linear solution.

E1	C1	C2	C3	C4	C5	C6	C7	C8
C1	0.5000	0.7575	0.6121	0.8251	0.6416	0.7870	1.0000	0.8546
C2	0.2425	0.5000	0.3546	0.5676	0.3841	0.5295	0.7425	0.5971
C3	0.3879	0.6454	0.5000	0.7130	0.5295	0.6749	0.8879	0.7425
C4	0.1749	0.4324	0.2870	0.5000	0.3165	0.4619	0.6749	0.5295
C5	0.3584	0.6159	0.4705	0.6835	0.5000	0.6454	0.8584	0.7130
C6	0.2130	0.4705	0.3251	0.5381	0.3546	0.5000	0.7130	0.5676
C7	0.0000	0.2575	0.1121	0.3251	0.1416	0.2870	0.5000	0.3546
C8	0.1454	0.4029	0.2575	0.4705	0.2870	0.4324	0.6454	0.5000

(4) Likewise, the above computational procedures have calculated the fuzzy preference relation matrices of the other 14 evaluators; therefore, using Equation (15), the aggregated pairwise comparison matrix of 15 evaluators will be derived, as listed in Table 6.

Table 6. Aggregated pairwise comparison matrices of 15 evaluators.

E	C1	C2	C3	C4	C5	C6	C7	C8
C1	0.5000	0.7433	0.5770	0.7157	0.6183	0.7221	0.9360	0.9655
C2	0.2567	0.5000	0.3337	0.4724	0.3750	0.4787	0.6927	0.7221
C3	0.4230	0.6663	0.5000	0.6387	0.5413	0.6450	0.8590	0.8884
C4	0.2843	0.5276	0.3613	0.5000	0.4026	0.5063	0.7203	0.7497
C5	0.3817	0.6250	0.4587	0.5974	0.5000	0.6038	0.8177	0.8472
C6	0.2779	0.5213	0.3550	0.4937	0.3962	0.5000	0.7140	0.7434
C7	0.0640	0.3073	0.1410	0.2797	0.1823	0.2860	0.5000	0.5294
C8	0.0345	0.2779	0.1116	0.2503	0.1528	0.2566	0.4706	0.5000
Total	2.2220	4.1686	2.8383	3.9479	3.1684	3.9984	5.7104	5.9458

(5) Equation (16) is applied to normalize the aggregated pairwise comparison matrix. Taking $q_{11}$ as an example:

$$q_{11}=0.5000/(0.5000+0.2567+0.4230+0.2843+0.3817+0.2779+0.0640+0.0345)=0.2250.$$

The priority weight of each evaluation criteria can then be obtained by Equation (17). The priority weight and rank of each influence assessed by 15 evaluators is listed in Table 7.

Table 7. Normalized matrix of priority weight and rank of influential factors.

E	C1	C2	C3	C4	C5	C6	C7	C8	Total	Weight	Ranking
C1	0.2250	0.1783	0.2033	0.1813	0.1951	0.1806	0.1639	0.1624	1.4900	0.1862	1
C2	0.1155	0.1199	0.1176	0.1197	0.1183	0.1197	0.1213	0.1215	0.9535	0.1192	6
C3	0.1904	0.1598	0.1762	0.1618	0.1708	0.1613	0.1504	0.1494	1.3201	0.1650	2
C4	0.1279	0.1266	0.1273	0.1266	0.1271	0.1266	0.1261	0.1261	1.0144	0.1268	4
C5	0.1718	0.1499	0.1616	0.1513	0.1578	0.1510	0.1432	0.1425	1.2292	0.1536	3
C6	0.1251	0.1250	0.1251	0.1250	0.1251	0.1250	0.1250	0.1250	1.0004	0.1251	5
C7	0.0288	0.0737	0.0497	0.0708	0.0575	0.0715	0.0876	0.0890	0.5287	0.0661	7
C8	0.0155	0.0667	0.0393	0.0634	0.0482	0.0642	0.0824	0.0841	0.4638	0.0580	8
Total	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	1.0000	8.0000	1.0000

The ranks of the evaluation criteria weights are thus substituted as:

C₁(0.1862) > C₃(0.1650) > C₅(0.1536) > C₄(0.1268) > C₆(0.1251) > C₂(0.1192) > C₈(0.0661) > C₇(0.0580).

The results show that the five main assessment attributes are legal and institutional framework (0.1862), domestic supply capacity (0.1650), human resources (0.1536), technological development and innovation (0.1268), and infrastructure facilities (0.1251). Meanwhile, the three least important attributes are market size of supporting industries (0.1192), international cooperation and competition (0.0661), and other criteria (0.0580).

6. Conclusions

This study surveyed approximately 15 policymakers, managers and economists to identify their assessment criteria discussed above. Based on the opinions derived from all survey respondents, this study finding were obtained:

The legal and institutional framework is the most important criteria for influencing the attraction of FDI for developing supporting industries, and which is considered by supporting industries to attract FDI. Vietnam has chosen to join AFTA (ASEAN Free Trade Area) and the WTO, which means that the Vietnamese government should concentrate on building special policies for the promotion of supporting industries involved with the change and improvement of the legal and institutional framework.

Domestic supply capacity, human resources, technological development and innovation, and infrastructure facilities have also received heavy-weight influence to attract FDI for the development of supporting industries. Notably, international co-operation and competition along with other criteria have not been taken seriously.

The fuzzy preference relations (FPR) method used to evaluate the influence of criteria to attract foreign direct investment (FDI) for developing supporting industries in Vietnam presented here is clearly applicable to the evaluation process. This paper proposed evaluation also reveals the concerns and preferences of all supporting industries and main industries. The results of this study provide a valuable reference for the Vietnamese government and policymakers to improve the legal and institutional framework, domestic supply capacity, human resources, technological development and innovation, and infrastructure facilities assistance, leading to the kind of environmental investment requisite to attracting FDI to develop supporting industries. Together, based on these results, we are continuing to survey on a large scale for future research to select a strategy for attracting FDI for supporting industries in Vietnam.