Enhancing Sustainability in Renewable Energy: Comparative Analysis of Optimization Algorithms for Accurate PV Parameter Estimation

Abstract

This study presents a comparative analysis of various optimization algorithms—Differential Evolution (DE), Particle Swarm Optimization (PSO), Arithmetic Optimization Algorithm (AOA), and Hippopotamus Optimization Algorithm (HOA)—for parameter identification in photovoltaic (PV) models. By utilizing RTC France solar cell data, we demonstrate that accurate parameter estimation is crucial for enhancing the efficiency of PV systems, ultimately supporting sustainable energy solutions. Our results indicate that DE achieves the lowest root mean square error (RMSE) of 0.0001 for the double-diode model (DDM), outperforming other methods in terms of accuracy and convergence speed. Both the HOA and PSO also show competitive RMSE values, underscoring their effectiveness in optimizing parameters for PV models. This research not only contributes to improved PV model precision but also aids in the broader effort to advance renewable energy technologies, thereby fostering a more sustainable future.

1. Introduction

The narrative of human advancements has been profoundly linked to the acquisition of energy throughout the written records of the world’s history. Energy is essential for the fulfillment of basic human needs. It is indispensable for social and financial advancement and prosperity, as well as for human health, survival, mobility, and communication [1]. Energy has been instrumental in the direction of human achievements, from the Great Pyramids of Ancient Pharaoh-ruled Egypt, which are considered the pinnacle of human intelligence and brainpower, to the industrial revolutions that have had a significant impact on hundreds of nations. Energy has been the silent architect of the world’s events throughout it all [2]. The capacity of humans to exploit and employ natural energy resources has significantly influenced these occasions, milestones, and accomplishments. Energy can be classified as either renewable or nonrenewable, based on its source and the extent to which it can be replenished progressively. Considering the global shift towards sustainable energy sources, optimizing photovoltaic (PV) systems is essential for reducing dependence on fossil fuels and lowering carbon emissions. Accurate PV modeling significantly enhances energy efficiency, directly contributing to sustainable development and climate change mitigation efforts. By improving parameter estimation in PV systems, this research plays a pivotal role in advancing the transition to renewable and environmentally friendly energy solutions, ultimately supporting a more sustainable future for all. Renewable energy sources (RESs) are classified as such because of their renewable nature and their consistent energy production without depletion. Solar, wind, bio, geothermal, hydro, and ocean energy comprise this category. These resources are widely utilized across various sectors, including transportation, residential heating, power generation, and industrial applications [1]. Solar energy is the ultimate renewable source within this framework, as it utilizes solar radiation to generate electrical energy. Photovoltaic (PV) systems can either retain the electrical energy they generate through the absorption of solar radiation in a battery or directly utilize it to power devices [3]. PV self-powered applications are viable because the Earth’s surface receives abundant solar radiation. As a result, solar energy has been extensively utilized in various applications, such as electricity generation, solar thermal systems, and photobiological processes. Its widespread availability makes it a crucial renewable energy source. The cost of PV generation is decreasing at an accelerated rate because of ongoing technological advancements [4]. Photovoltaic or PV technology can change one form of energy into another, including directly changing electromagnetic radiation from the sun into another form of energy, including electrical energy. The conversion takes place inside a photovoltaic (PV) module (solar cell), which consists of many solar cells that are interconnected with one another. These devices are popularly called by the name “photovoltaic electricity generators”. Moreover, the principal photovoltaic industry is implicated in the manufacturing of modules and cells that have dimensions and forms that are specified [5]. For the temperature regulation and cooling of photovoltaic systems, there are three separate types of models that are being used. They are single-diode (SD) models, double-diode (DD) models, and three-diode (TD) models [6]. PV is also being used for electricity generation purposes. Currently, these models are the essential representation of the solar photovoltaic cell. This research focuses on the three types of PV models, which are known as single-diode (SD), double-diode (DD), and triple-diode (TD) models. The aim is to improve the efficiency and longevity of any type of technological configuration of photovoltaic (PV) systems by understanding these aspects and adjusting to them [7]. Because of this, optimal mathematical modeling and reliable modeling methodologies for simulating or characterizing the behavior of photovoltaic cells (or modules) are of utmost importance. Scientists use algorithms to improve the speed and accuracy of numeric models that simulate how photovoltaic (PV) systems work. These models simulate the working of PV systems. Various techniques are applied for model calibration, annotation optimization, design optimization, uncertainty assessment, and much more. Additional applications include design optimization. Thanks to the advancements in computer technology, an increase in use of the metaheuristics has been seen during the last few decades. To solve optimization problems experienced in the real world, many types of metaheuristic algorithms have been developed and used, starting with the Genetic Algorithm (GA). Meta-heuristic algorithms’ capability to improve the accuracy of calculations, alleviate pressure on computational resources, and generate quality solutions to complex optimization issues are already established. Meta-heuristic optimization algorithms have gained significant attention for improving the accuracy and efficiency of photovoltaic (PV) system modeling. These algorithms are inspired by various natural, biological, and social phenomena, leading to diverse approaches in solving complex optimization problems. Researchers have categorized these algorithms into four main types: biology-based, physics-based, sociology-based, and mathematics-based approaches [8]. Biology-inspired algorithms, such as Differential Evolution (DE) and the Genetic Algorithm (GA), have been widely applied to PV modeling and parameter estimation [9]. The illustration of these algorithms can be found in Figure 1 [10]. To enhance convergence speed and solution quality, hybrid methods like Artificial Bee Swarm Optimization (ABSO) and the Adaptive Genetic Algorithm (AGA) have been introduced [9]. Sociology-based optimization techniques, including Harmony Search and Teaching Learning-Based Optimization (TLBO), have been employed for the classification of PV system parameters. These methods have shown promising results in refining the properties of the single-diode model (SDM) and the double-diode model (DDM) [9]. Physics-based algorithms, such as Simulated Annealing (SA) and Particle Swarm Optimization (PSO), are commonly used to optimize PV models by improving parameter estimation accuracy [10]. These methods have demonstrated effectiveness in handling the complex optimization challenges associated with solar energy systems. Several advanced optimization strategies, including Turbulent Flow Optimization (TFO), the Tree Growth-Based Optimizer, and the Harris Hawks Optimizer (HHO), have also been applied to PV parameter estimation. These approaches have significantly improved the precision and efficiency of solar cell modeling [11]. Comparative studies indicate that Differential Evolution (DE) consistently outperforms other algorithms in accuracy, achieving superior results in PV model optimization [12]. The goal of this study is to examine the effectiveness of different optimization algorithms in photovoltaic (PV) system modeling, based on the original and modified versions. To do this, we introduce a modification to PV parameter estimation and implement change iterations for resumption. A change in math is added into the optimization of solar (PV) systems to do this. The contributions of this paper are summarized as follows:

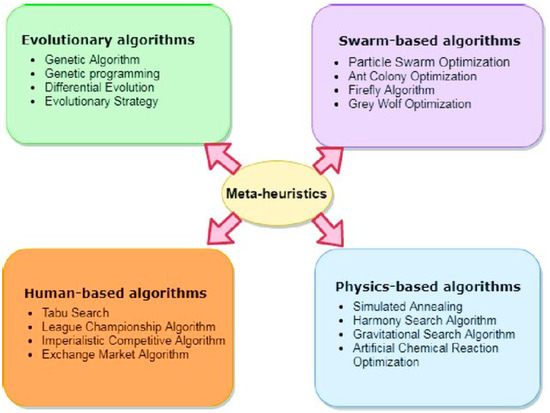
Figure 1. Different categories of meta-heuristic algorithms.

• Introducing advanced optimization algorithms, such as the Hippopotamus Optimization Algorithm (HOA), Arithmetic Optimization Algorithm (AOA), Genetic Algorithm (GA), Differential Evolution (DE), Particle Swarm Optimization (PSO), and Grey Wolf Optimizer (GWO), to identify unknown parameters in SDM, DDM, and TDM models.
• Evaluating the effectiveness of these algorithms in parameter identification for photovoltaic models through rigorous experimental testing.
• Comparing the performance of the employed algorithms against one another to assess their convergence speed, accuracy in minimizing the RMSE, and the ability to avoid local optima through various exploration-enhancing strategies. Differential Evolution (DE) employs mutation and crossover operations to maintain population diversity and escape local minima. Particle Swarm Optimization (PSO) utilizes inertia weight and velocity updates to balance exploration and exploitation, reducing the risk of premature convergence. The Hippopotamus Optimization Algorithm (HOA) integrates adaptive randomization and dynamic parameter tuning to enhance global search capabilities. Additionally, hybrid methods, such as combining DE with PSO, leverage the strengths of both techniques to further minimize stagnation in local optima. These strategies collectively improve the robustness of optimization algorithms in accurately estimating photovoltaic model parameters.
• Providing a comprehensive analysis based on experimental results to demonstrate the 111 strengths and weaknesses of each optimization technique.
• Highlighting the superior performance of specific algorithms, such as DE and the HOA, which yielded the most accurate results for parameter identification across the tested models.

The following is the order in which the remaining sections are presented: In the section under “Section: Definition of PV Models”, the topic of modeling of PV models is discussed. An explanation of the problem formulation can be found in Section 4. Section 5 is where the discussion of the simulation and the results takes place. In Section 6, the conclusions that have been drawn from this examination are offered.

2. Related Work

In recent years, meta-heuristic algorithms have been implemented to address the high processing time and accuracy challenges encountered in a variety of engineering applications. In recent years, numerous meta-heuristic algorithms have been proposed. Meta-heuristic algorithms have been effectively implemented to address optimization challenges in a variety of scientific disciplines, as numerous fields necessitate optimization. In general, a variety of meta-heuristic algorithms have been implemented to estimate the parameters of PV models.

A meta-heuristic optimization algorithm, the Honey Badger Algorithm (HBA), was introduced by [13] in 2022. This algorithm is inspired by the foraging behavior of honey badgers in nature. It surpasses reputable algorithms in terms of the quality of the solutions, the speed of convergence, and the balance between exploration and exploitation. Additionally, the HBA has undergone modifications, including dynamic search strategies and controlled randomization. These modifications enable it to become more proficient in the resolution of optimization issues, particularly in photovoltaic (PV) systems. It is also crucial to acknowledge that these modifications enhance overall efficacy, parameter calibration, and system configuration, thereby fostering the development of renewable energy technologies.

There is a study that was carried out in 2023 by [14] utilized the algorithm known as the Dandelion Optimizer (DO) and the Newton–Raphson approach in the PV algorithm to enhance the working capability of the PV algorithm. Since these algorithms are primarily of biological origin, it is important to note that, in the case of meta-heuristics, the DO algorithm is the main focus of this research. The extraction of PV parameters for optimization will impact the efficiency of the DO algorithm. Thus, the DO algorithm can be tweaked for enhancing its efficiency. In addition, the Newton–Raphson method is reputed for its efficiency in numerical analysis and optimization techniques. Thus, the improved DO algorithm adopts this technique which enhances its accuracy and efficiency in selecting the best PV parameters. The enhanced search capability and convergence speed have improved due to the modifications applied in enhancing the DO algorithm. Consequently, because of the adoption of this technique, the improved DO algorithm shows improved accuracy and effectiveness in the selection of the best PV parameters. This is because it has been modified.

In 2023, a study was conducted to investigate ways for enhancing the performance of photovoltaic arrays, as these will operate under shaded conditions. The DLCI, a meta-heuristic algorithm, is executed through the collective intelligence of some dynamic leaders. Different studies that have been worked upon for testing meta-heuristics for MPPT purpose are the GWO, WOA, MFO, ABC, and PSO algorithms, which are useful for diverse industrial and environmental optimization problems. The algorithms used in this study is nature-based or biology-inspired algorithms. The DLCI framework is modified, changed, and integrated to enhance the efficiency of optimization to reconfigure the PV array. The DLCI is always aiming to reconfigure a photovoltaic system with the global optimum. Adding the best characteristics of different nature-inspired algorithms, it overcomes the drawbacks of individual sub-optimizers. In the optimization process, the DLCI algorithm enhances global search and local search. As a result, the PV system’s performance is enhanced, allowing it to maximize its power output. The DLCI approach, grounded in collective intelligence, offers enhanced adaptability in varying environmental scenarios, especially under partial shading conditions. This is achieved by using several algorithms for minimizing the power losses and mismatch due to the shading effect. The DLCI scheme is among the key techniques for improving the performance of photovoltaic (PV) systems under extreme circumstances of partial shading. Simply stated, it enhances the lifespan, performance, and adaptability of a PV array reconfiguration.

A journal article [15] investigated improving the effectiveness of maximum power point tracking in an outdoor photovoltaic system in the year 2023. The results indicate that this issue could be dealt with via an enhanced variant of the Particle Swarm Optimization (PSO) method. This variant of the PSO setup adds a dynamic alteration factor to the basic PSO setup. In this study, we analyzed different algorithms, including the improved PSO algorithm. In this paper, the Grey Wolf algorithm was explored to improve the MPPT parameters. These methods have ample optimization benefits for tracking under a wide variety of environmental conditions. This work aims to improve the degraded PSO algorithm used in the Solar system for Maximum Power Point Tracking (MPPT) in outdoor Solar systems. The output power was maintained constantly due to the improvements, the tracking speed was remarkable, and the improved system performance.

With the use of hybrid Particle Swarm Optimization (PSO) techniques, this paper seeks to improve the basic PSO algorithm, with the help of additional optimization strategies. This is accomplished by utilizing hybrid PSO methods. PSO parameters and processes can more effectively cope with problems found in parameter estimation in PV systems due to this realist adjustment. The optimization process’s accuracy can be improved by using specific methods, which may employ the use of several target functions or diode models. In order to make sure that the outcomes are usable, practical, and plausible in real-world situations, some people may adopt various search processes and techniques. These people may also add new constraints to their search activities. A variety of optimization techniques are used by researchers to improve the parameter estimation capabilities of the photovoltaic (PV) system. Therefore, the process of optimizing the efficiency of photovoltaic (PV) cells can take a more accurate turn. Nagadurga’s 2023 developed method [16] was reviewed for its various meta-heuristic optimization methods to achieve maximum power point tracking in photovoltaic technology at the global level. Researchers have explored various algorithms, including Particle Swarm Optimization (PSO), Genetic Algorithm (GA), Ant Colony Optimization (ACO), Teaching Learning-Based Optimization (TLBO), Firefly Algorithm (FA), and Chimp Optimization Algorithm. All of them were either inspired by biology or nature itself. Researchers worked on these algorithms to enhance the power output of solar systems that were subjected to environments of partial shading. As a result, upgrades consist of changing search algorithms, periodic updates of parameters, and the addition of heuristics for balancing exploitational and explorational search abilities. These methods can be customized specifically to overcome the specific constraints imposed because of partial shading. Through this study, we aim towards enhancing the efficiency and effectiveness of monitoring solar photovoltaic (PV) systems all over the world at maximum power points.

Conversely, some studies utilized the original algorithms without alterations. For instance, the 2022 study “Golden Jackal Optimization” in [17] introduced a novel meta-heuristic algorithm inspired by the foraging behavior of golden jackals. This mathematical model addressed complex engineering design challenges through the algorithm’s searching, enclosing, and pouncing phases. The algorithm’s effectiveness was assessed using benchmark functions, comparing it with traditional optimization methods and other advanced meta-heuristic approaches. This research focused on the Golden Jackal Optimization algorithm and its application in addressing engineering design challenges within photovoltaic (PV) systems. The study did not address the modifications to the algorithm in photovoltaic systems. The algorithm’s effectiveness in tackling complex problems related to unidentified search spaces in various engineering fields was emphasized. In addition, a study conducted in 2022 revealed that the Transit Search (TS) algorithm, which is founded on the principles of physics, is superior to other optimization strategies. The fact that it had the lowest average error out of all the 73 problems that were examined is evidence of this. In addition, the TS algorithm achieves a computational complexity that is deemed acceptable when it is used to solve twenty limited problems with 200,000 iterations for each solution. In light of the fact that optimization problems are both diverse and difficult, the research highlights the importance of employing a number of different optimization methodologies. The TS algorithm is one of the meta-heuristic approaches that has been investigated as a result of this particular circumstance. In comparison to well-established algorithms, the study exhibited impressive performance across a variety of benchmark problems, which elucidates the potential of the method to effectively address complex optimization tasks.

In the year 2021, the method of optimization known as the Rat Swarm Optimizer (RSO) algorithm was investigated by [18]. This algorithm is influenced by the collective behavior that is observed in natural settings. Within the framework of optimizing photovoltaic (PV) systems, the RSO method was evaluated in comparison to a number of different optimization techniques. Particle Swarm Optimization (PSO), Genetic Algorithm (GA), and Differential Evolution (DE) are the algorithms that are included in this category. The purpose of this research was to evaluate the effectiveness of these algorithms in increasing the amount of electricity that photovoltaic (PV) systems produce under a variety of different scenarios. By successfully exploring the search space and delivering results that are comparable to those attained by other algorithms, the RSO algorithm demonstrated its efficiency in optimizing photovoltaic (PV) systems. The RSO algorithm is classified as coming from the biological field. It is not made clear in the study whether or not any adjustments were made to the Rat Swarm Optimizer (RSO) algorithm. The optimization of solar systems in their original, unaltered state was accomplished with the help of the RSO algorithm. In the context of optimizing photovoltaic (PV) systems, the primary purpose of this study is to investigate the functionality of the RSO, as well as a variety of optimization techniques.

The scholars of [19] put forward the Marine Predator Algorithm (MPA), in the year 2024, to propose PI controllers for grid-connected solar systems during Low Voltage Ride Through (LVRT). This paper intends to demonstrate the versatility and applicability of MPA-based controllers in a variety of scenarios, especially those which apply classical optimization techniques, such as the Grey Wolf Optimizer (GWO) and Particle Swarm Optimization (PSO). The MPAs technique outperforms the other methods for the parameters of DC-link voltage and active power. For example, it attains superior convergence rates. Furthermore, the overshoot is reduced by 14% to 40%. In addition, the settling time is faster and varies from 0.76 to 0.95 s. The PI controller of the PV system improved performance without any modification via algorithms. Thus, all approaches were executed in their original form.

The following Table 1 summarizes many of the optimization algorithms that are used for PV parameter extraction.

Table 1. Summary of studies on PV systems of modified algorithms.

Reference	Year	Algorithm	Results
[18]	2021	RSO	Enhancement of optimization
[17]	2022	Golden Jackal	Innovative and inventive algorithm
[13]	2022	HBA	Enhanced optimization
[20]	2022	Hybrid PSO	Refinement of parameter estimation
[21]	2022	TS	More promising optimization performance
[14]	2023	DO	Enhanced parameter identification
[16]	2023	PSO, GA, ACO, TLBO, FA, and Chimp Optimization Algorithm	Global and varied MPPT enhancement
[22]	2023	DLCI	Improvement of PV array reconfiguration
[15]	2023	Boosted MPPT	PSO functionality

3. Definition of PV Models

The single-diode model (SDM), double-diode model (DDM), and three-diode model (TDM) are widely used in PV modeling due to their ability to accurately represent the electrical characteristics of photovoltaic cells [23]. The choice of the appropriate model depends on the trade-off between computational complexity and accuracy required for a specific application. The SDM is preferred for general-purpose applications due to its simplicity and computational efficiency, although it may not accurately capture recombination losses in the solar cell. The DDM provides a more accurate representation of PV behavior, particularly under varying environmental conditions, by incorporating an additional diode to model recombination effects. Meanwhile, the TDM further enhances accuracy by introducing a third diode, making it suitable for highly detailed simulations in research applications, but it comes with increased computational requirements. This study evaluates these models to determine their effectiveness in PV parameter estimation and their suitability for different optimization techniques.

3.1. Single-Diode Model

An explanation of the equivalent circuit that is applicable to the SDM may be found in Figure 2. For the purpose of determining the current output of this model, the following equation is utilized:

$$I=I_{pv} - I_{D1} - I_{sh}$$

(1)

$$I=I_{pv}-I_{o1}\left[e^{{\displaystyle \frac{q\left(V+I{R}_s\right)}{n_{1}K{T}_c}}}-1\right]-{\displaystyle \frac{V+I{R}_s}{R_p}}$$

(2)

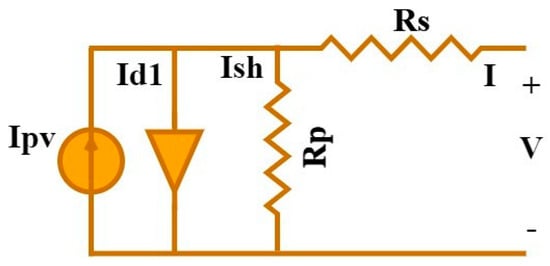
Figure 2. Equivalent circuit for single-diode models.

The single-diode model (SDM) is related to the capital I, which is the generation of the current. The current caused by light is called ${ I}_{pv}$ and the leakage currents are called $I_{sh}$. The dark saturation bumps are called $I_{D1}$. New models are also applied. The symbols R_p and R_s represent the shunt and series resistances, respectively. Also, n₁ indicates the ideality factor of the diode, kis denotes Boltzmann’s constant, q is the charge of the electron, and T_c is the absolute temperature of the working cell. The equation shows that the parameters subjected to estimation in the SDM are I_pv, $I_{D1}$, n₁, R_s, and R_p.

3.2. Double-Diode Model

An illustration of the electrical design for the DDM can be found in Figure 3. This schematic incorporates two diodes in order to improve the output quality. Within the context of this paradigm, the current output is determined by the following equations:

$$I=I_{pv}-I_{D1}-I_{D2}-I_{sh}$$

(3)

$$I=I_{pv}-I_{o1}\left[e^{{\displaystyle \frac{q\left(V+I{R}_s\right)}{n_{1}K{T}_c}}}-1\right]-I_{o2}\left[e^{{\displaystyle \frac{q\left(V+I{R}_s\right)}{n_{2}K{T}_c}}}-1\right]-{\displaystyle \frac{V+I{R}_s}{R_p}}$$

(4)

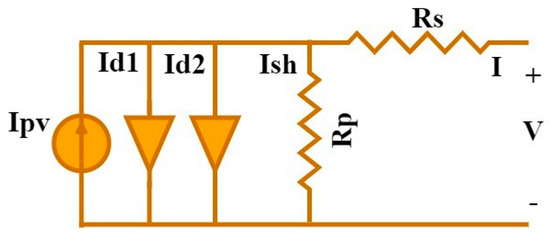
Figure 3. Equivalent circuit for double-diode model.

In the above expression, I_D2 is the dark saturation current of the second diode and n₂ is the ideality factor of the second diode. The parameters that must be estimated are I_pv, I_o1, n₁, R_s, R_p, I_o2, and n₂.

3.3. Three-Diode Model

An alternate method for the design of photovoltaic modules is presented by the three-diode model (TDM), which is illustrated in Figure 4. This model makes use of three diodes. Through the utilization of Equation (5), the current output of this model is determined.

$$I=I_{pv}-I_{D1}-I_{D2}-I_{D3}-I_{sh}$$

(5)

$$I=I_{pv}-I_{o1}\left[e^{{\displaystyle \frac{q\left(V+I{R}_s\right)}{n_{1}K{T}_c}}}-1\right]-I_{o2}\left[e^{{\displaystyle \frac{q\left(V+I{R}_s\right)}{n_{2}K{T}_c}}}-1\right]-I_{o3}\left[e^{{\displaystyle \frac{q\left(V+I{R}_s\right)}{n_{3}K{T}_c}}}-1\right]-{\displaystyle \frac{V+I{R}_s}{R_p}}$$

(6)

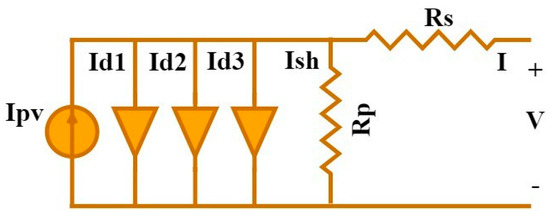
Figure 4. Equivalent circuit for three-diode models.

In this expression, I_D3 is the dark saturation current of the third diode and n₃ is the ideality factor of the third diode. The TDM requires the estimation of nine parameters, namely: I_pv, I_o1, n₁, R_s, R_p, I_o2, n₂, I_o3, and n₃.

4. Problem Formulation

The performance of photovoltaic (PV) models is assessed based on objective functions to minimize the value of the RMSE. The RMSE assesses how different the actual (experimentally) observed current is from the simulated current taken from the estimated parameters (Table 2). Equations (7) and (8) convey the RMSE mathematically.

Objective functions are used to reduce the mean square error in order to assess the viability of photovoltaic (PV) models. The RMSE measures how much the current that is measured in an experiment differs from the one that was simulated using the estimated parameters. The RMSE is defined mathematically by Equations (7) and (8).

$$I=I_{pv}-I_{D1}-I_{D2}-I_{D3}-I_{sh}$$

(7)

$$I=I_{pv}-I_{o1}\left[e^{{\displaystyle \frac{q\left(V+I{R}_s\right)}{n_{1}K{T}_c}}}-1\right]-I_{o2}\left[e^{{\displaystyle \frac{q\left(V+I{R}_s\right)}{n_{2}K{T}_c}}}-1\right]-I_{o3}\left[e^{{\displaystyle \frac{q\left(V+I{R}_s\right)}{n_{3}K{T}_c}}}-1\right]-{\displaystyle \frac{V+I{R}_s}{R_p}}$$

(8)

Here, I_exp is the experimentally observed current, N denotes the total number of data points, and X represents the vector of the decision variables associated with each PV model. The decision variable vectors are defined for the following models:

• Single-Diode Model (SDM):

  $$X=\left\{I_{pv},I_{o1},n_1,R_s,R_p\right\}$$
• Double-Diode Model (DDM):

  $$X=\left\{I_{pv},I_{o1},n_1,R_s,R_p,I_{o2},n_2\right\}$$
• Three-Diode Model (TDM):

  $$X=\left\{I_{pv},I_{o1},n_1,R_s,R_p,I_{o2},n_2,I_{o3},n_3\right\}$$

This paper focuses on optimizing these parameters using advanced meta-heuristic algorithms, particularly the Differential Evolution (DE) algorithm. DE’s performance is compared with several state-of-the-art optimization techniques, including the Hippopotamus Optimization Algorithm (HOA) [24], Genetic Algorithm (GA) [25], Particle Swarm Optimization (PSO) [26], Arithmetic Optimization Algorithm (AOA) [27], and Grey Wolf Optimizer (GWO) [28].

Table 2. The limits of the estimated parameters [29].

Parameters	Lower Bound	Upper Bound
Ipv	0	1
Io1, Io2 and Io3 (µA)	0	1
Rs, Rs1	0	0.5
Rp	0	100
n1, n2 and n3	1	2

Table 2. The limits of the estimated parameters [29].

Parameters	Lower Bound	Upper Bound
Ipv	0	1
Io1, Io2 and Io3 (µA)	0	1
Rs, Rs1	0	0.5
Rp	0	100
n1, n2 and n3	1	2

For this work, parameter bounds are derived from the RTC France solar cell dataset, a widely accepted benchmark in PV optimization studies. The comparative performance of these algorithms is evaluated based on RMSE minimization, convergence speed, and parameter accuracy. Accuracy is assessed using the Root Mean Square Error (RMSE), which measures the deviation between the experimentally observed and predicted values. Differential Evolution (DE) achieves superior accuracy by maintaining a diverse population and leveraging mutation and crossover strategies to refine solutions iteratively. Similarly, PSO fine-tunes its solutions through velocity updates and swarm intelligence, while the HOA applies adaptive search techniques to enhance precision and prevent parameter stagnation. Additionally, the experimental results are analyzed to highlight the robustness and precision of each method, with particular emphasis on the superior performance of DE in modeling PV systems. The objective is to enhance the accuracy of PV model parameter estimation, contributing to the efficient design and simulation of renewable energy systems.

5. Results and Simulation

This section presents a set of experiments to show the applicability of the proposed optimization algorithms, such as the Hippopotamus Optimization Algorithm (HOA), Arithmetic Optimization Algorithm (AOA), Genetic Algorithm (GA), Differential Evolution (DE), Particle Swarm Optimization (PSO), and Grey Wolf Optimizer (GWO), in identifying parameters of the three well-known PV models, namely, the single-diode model (SDM), double-diode model (DDM), and three-diode model (TDM). The photovoltaic models utilize the RTC France solar cell, with results for each model summarized in Table 3, Table 4 and Table 5. The aforementioned algorithms are employed to estimate the unknown parameters in these photovoltaic models. Each algorithm is implemented with a population size of 30 and it iterated for 100 generations, thereby establishing a standardized experimental framework. Comparative investigations are conducted to validate the accuracy and performance of these methods, benchmarking the algorithms against each other. The experiments utilize Google Co-lab, employing Python version 3.13.1 along with pertinent libraries for optimization and numerical computation. Every algorithm is subjected to 31 independent trials for robustness and impartiality in benchmarking. The research study is executed using the GPU-enabled cloud platform in Google Co-lab. All algorithms are computed in Python, specifically using libraries like NumPy version 2.2.3, SciPy version 1.15.2, and Matplotlib version 3.10.1. This method allows for a systematic evaluation of the algorithms’ capability of reducing the RMSE and identifying optimal parameters for the photovoltaic models. It provides information regarding the convergence rate, accuracy, and computing cost.

Table 3. Comparison of algorithms based on RTC France cell and SDM.

Algorithm	Iph (A)	Isd (A)	Rs (Ω)	Rp (Ω)	Non-Ideality	Isc (A)	Voc (V)	Imp (A)	Vmp (V)	Pmp (W)	Fill Factor	RMSE
HOA	0.9482	5.36 × 10−7	0	48.4515	1.4821	0.9482	0.5479	0.9999	0.4303	0.4303	0.8281	0.1307
GA	0.7859	4.07 × 10−7	0.0034	47.1925	1.4445	0.7859	0.5373	0.9999	0.4303	0.4303	1.0189	0.1918
DE	1	9.27 × 10−7	0.0101	100	1.4919	1	0.5326	0.9999	0.4303	0.4303	0.8078	0.0005
PSO	1	1.00 × 10−6	0.01	100	1.5	1	0.5326	0.9999	0.4303	0.4303	0.8079	1.31 × 10−7
AOA	0.5921	1.77 × 10−7	0.0494	93.7213	1.4458	0.5921	0.5581	0.9999	0.4303	0.4303	1.3019	0.6242
GWO	0.9116	6.26 × 10−9	0.0002	26.3633	1.1503	0.9116	0.5557	0.9999	0.4303	0.4303	0.8494	0.2068

Table 4. Comparison of algorithms based on RTC France cell and DDM.

Algorithm	Iph (A)	Io1 (A)	Io2 (A)	n1	n2	Rs (Ω)	Rp (Ω)	Isc (A)	Voc (V)	Imp (A)	Vmp (V)	Pmp (W)	RMSE
HOA	0.9609	3.38 × 10−7	5.37 × 10−8	1.4131	2.1633	0.0061	50.2621	0.9609	0.5396	0.9999	0.4303	0.4303	0.0614
GA	0.9432	4.79 × 10−7	4.77 × 10−9	1.7552	1.7805	0.0573	10.2567	0.9432	0.6537	0.9999	0.4303	0.4303	0.6005
DE	1	9.88 × 10−7	3.42 × 10−8	1.4985	2.3283	0.0100	92.4936	1	0.5325	0.9999	0.4303	0.4303	0.0001
PSO	1	1.00 × 10−6	1.00 × 10−7	1.5027	1.6508	0.0099	99.9692	1	0.5335	0.9999	0.4303	0.4303	0.0004
AOA	0.7207	2.63 × 10−7	8.89 × 10−8	1.6043	2.4334	0.0650	17.3512	0.7207	0.6112	0.9999	0.4303	0.4303	0.5537
GWO	0.9623	8.14 × 10−8	5.06 × 10−8	1.3012	2.7782	0.0039	36.6844	0.9623	0.5446	0.9999	0.4303	0.4303	0.1093

Table 5. Comparison of algorithms based on RTC France cell and three-diode model (TDM).

Algorithm	Iph (A)	Io1 (A)	Io2 (A)	Io3 (A)	n1	n2	n3	Rs (Ω)	Rp (Ω)	Isc (A)	Voc (V)	Imp (A)	Vmp (V)	RMSE
HOA	1	1.00 × 10−6	6.54 × 10−9	3.70 × 10−9	1.5124	1.5093	1.7913	0.0075	22.4997	1	0.5370	0.9999	0.4303	0.0261
GA	0.6782	8.44 × 10−7	8.57 × 10−8	9.65 × 10−9	1.8978	2.9386	1.3710	0.0578	56.6795	0.6782	0.6632	0.9999	0.4303	0.5807
DE	1	9.65 × 10−7	7.47 × 10−8	1.00 × 10−8	1.4958	3	3	0.0101	83.4497	1	0.5325	0.9999	0.4303	0.0005
PSO	1	1.00 × 10−6	1.00 × 10−7	0	1.5480	3	3	0	3.9267	1	0.5496	0.9999	0.4303	0.1046
AOA	0.6284	4.18 × 10−8	9.06 × 10−8	6.80 × 10−9	1.5836	2.3878	2.6047	0.1340	57.8373	0.6284	0.6725	0.9999	0.4303	0.6326
GWO	0.9999	6.10 × 10−10	5.35 × 10−10	3.43 × 10−10	1.5225	1	1.1682	0.0072	2.3600	0.9999	0.8302	0.9999	0.4303	0.1100

5.1. Experiments with Single-Diode Model

Table 3 displays the parameter values yielding the highest accuracy and Root Mean Square error (RMSE) results. Each optimization algorithm was run 30 times on the single-diode model (SDM) with RTC France solar cell data, and the experimental results are comprehensively provided. Among all the algorithms that have been tested, the Differential Evolution (DE) algorithm is able to provide the best RMSE at 0.00054. The performance of the DE algorithm can also be seen as quite consistent, as the deviations in the results are minimum. Even though DE is the most accurate of the options, other algorithms also give competitive results for some metrics, like PSO and the HOA with RMSEs of 1.31 × 10⁻⁷ and 0.13066, respectively. These algorithms also perform very well in terms of fill factor and convergence reliability. On the other hand, the Arithmetic Optimization Algorithm (AOA) and Grey Wolf Optimizer (GWO) demonstrate larger RMSE values of 0.6242 and 0.2068, respectively, suggesting less precise parameter estimation and greater variation.

Additionally, Figure 5c illustrates the minimum fitness values (RMSE) obtained during the trials for the two-diode model, providing further insight into the algorithms’ comparative performances. DE, again, achieves the smallest RMSE of 0.0001, underscoring its ability to minimize fitness values effectively and consistently. The convergence trends observed in Figure 5a confirm that DE not only stabilizes rapidly but also maintains superior accuracy throughout iterations. Other algorithms, such as PSO and the HOA, exhibit competitive yet more variable convergence patterns, while the AOA and GWO show irregular trends with significantly higher RMSE values. The convergence curve for the SDM (Figure 5a) illustrates how DE stabilizes and minimizes the RMSE over iterations, achieving optimal performance within 100 iterations. Figure 5b,d showcase the P-V and I-V characteristics derived from DE under standard illumination conditions, ensuring accurate representation of the photovoltaic cell’s performance. The I-V characteristics are generated by varying the terminal voltage (V) while measuring the output current (I), which helps in analyzing the electrical behavior of the PV model under different conditions. These characteristics are essential for evaluating the efficiency of parameter estimation techniques, as they determine key performance metrics, such as open-circuit voltage (Voc), short-circuit current (Isc), and maximum power point (MPP). The derived curves illustrate how DE accurately captures these electrical properties, making it a reliable optimization technique for PV parameter identification. These characteristics highlight the close alignment of the predicted and experimental results, confirming the effectiveness of the DE algorithm in optimizing PV model parameters. These visual comparisons, alongside the trials’ fitness data, reinforce DE’s exceptional performance in both the SDM and two-diode models, showcasing its reliability and precision for parameter identification in photovoltaic systems.

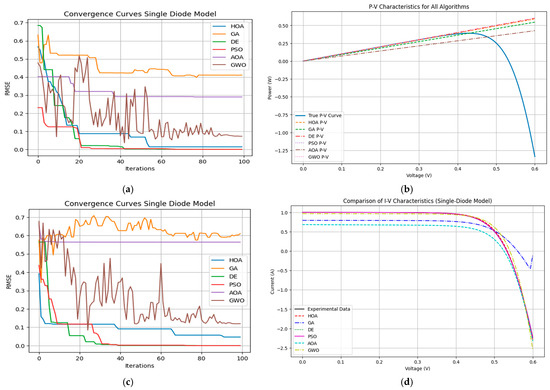
Figure 5. Comparison between algorithms based on SDM. (a) Convergence curve, (b) P-V characteristics, (c) trials’ minimum fitness value, and (d) I-V characteristics.

5.2. Experiments with Double-Diode Model

The recalculated RMSE values for the best and worst results are presented in Table 4, which were generated after running each optimization algorithm for 30 independent trials on the DDM-based RTC France solar cell. These iterations were conducted to ensure statistical reliability and minimize the impact of random variations in the optimization process. The Differential Evolution (DE) algorithm regularly delivers the most precise root mean square error (RMSE) of 0.000148, greatly surpassing other algorithms. This is the case among the algorithms that were tested. By demonstrating its usefulness in adjusting the DDM settings with a high degree of precision, DE has demonstrated its exceptional performance. The findings of other algorithms, such as the Hippopotamus Optimization Algorithm (HOA) and Particle Swarm Optimization (PSO), are also competitive. These methods achieve RMSE values of 0.000354 and 0.0614, respectively. Nevertheless, when compared to DE, these algorithms exhibit a slightly lower level of prediction accuracy. Techniques, such as the Arithmetic Optimization Algorithm (AOA) and the Grey Wolf Optimizer (GWO), on the other hand, produce RMSE values that are higher, with values of 0.5537 and 0.1093, respectively. This indicates that there is a greater degree of variability in parameter estimation. The convergence trajectory that is presented in Figure 6a demonstrates that DE is capable of effectively stabilizing and minimizing the RMSE, and it can achieve convergence within around one hundred iterations. Because DE does not converge as quickly as some other algorithms, its reliability in optimizing the DDM model is strengthened by the fact that it strikes a compromise between convergence stability and correctness. A visual representation of the P-V and I-V curves that were created by DE is presented in Figure 6b,d. The figures match very closely with the actual results. The trends of best fitness values for all the algorithms are illustrated in Figure 6c. As seen, DE is consistently able to outperform all others. Based on these plots, DE’s competency to accurately predict the behavior of the PV module is illustrated, reinstating DE as the best performing method for DDM parameter identification. The robustness of DE for modelling and optimizing solar systems is guaranteed by the presence of accuracy, stability, and consistency in DE.

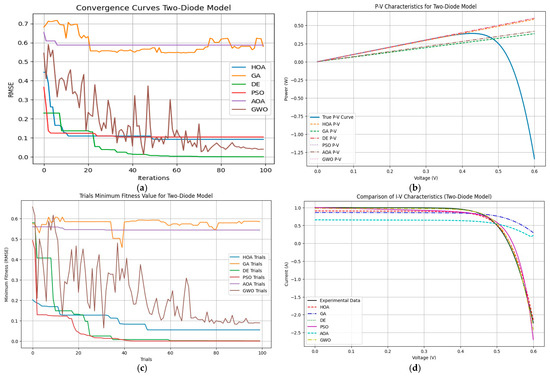
Figure 6. Comparison between algorithms based on DDM. (a) Convergence curve, (b) P-V characteristics, (c) trials’ minimum fitness value, and (d) I-V characteristics.

5.3. Experiments with Triple-Diode Model

This section uses a DE algorithm to find the TDM model’s optimal parameters for the RTC France solar cell to ascertain its performance. The experimental results obtained using DE and other optimization algorithms are given in Table 5. Of all the algorithms tested, DE showed remarkable performance after generating the lowest RMSE, which is 0.000542, and hence, it is the most accurate and reliable algorithm in this case. The convergence paths of the algorithms are shown in Figure 7a and the DE converges towards the optimal solution with higher accuracy and stability, as compared to the other tested algorithms. The convergence curve shows that DE attains the best RMSE value in about 80 iterations, indicating it achieves the right balance between efficiency and accuracy. Other algorithms like PSO and the HOA also perform competitively with RMSEs of 0.1046 and 0.0261, respectively. Nonetheless, these methods have comparatively more variance in convergence than DE. In contrast, the AOA and GWO algorithms show higher RMSE values of 0.6326 and 0.1099. Therefore, they exhibit less accuracy in estimating model parameters. Figure 7b,d show the P-V and I-V characteristics using DE-optimized parameters. These curves fit the experimental data remarkably well, which shows that DE can accurately predict the photovoltaic behavior of the RTC France cell. Apart from that, Figure 7c shows the trial run minimum fitness values, which further confirm the essential optimality of DE. The combination of DE’s superior accuracy, stability, and correlation with the experimental data reveals its efficiency as a reliable optimization algorithm for complex photovoltaic diode models. The reliability of DE with various parameters proves its usefulness in the optimization and modeling of photovoltaic systems.

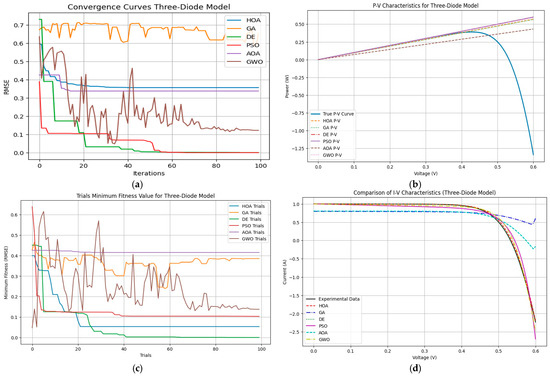
Figure 7. Comparison between algorithms based on TDM. (a) Convergence curve, (b) P-V characteristics, (c) trials’ minimum fitness value, and (d) I-V characteristics.

5.4. An Analysis That Evaluates Statistical Performance and Stability as a Comparison Analysis

Sections V-a, V-b, and V-c compare the three photovoltaic (PV) models: the single-diode model (SDM), double-diode model (DDM), and triple diode model (TDM). Within the context of these PV models, the effectiveness of various approaches utilizing algorithms such as the Hippopotamus Optimizer Algorithm (HOA), Genetic Algorithm (GA), Differential Evolution (DE), Particle Swarm Optimization (PSO), Arithmetic Optimization Algorithm (AOA), and Grey Wolf Optimizer (GWO) is assessed. The analysis evaluates the efficacy of each algorithm, using metrics such as the Root Mean Square Error (RMSE), fill factor, and convergence behavior. Concurrently, the standard deviation (SD) is utilized to assess the system’s dependability. When it comes to accuracy and reliability, the DE results are the best, providing the lowest RMSE for all models of PV. The HOA and PSO also show good accuracy and convergence, so they can also be used as alternatives for optimization problems. The GWO may have obtained mediocre scores, but its performance is better than the AOA. Also, the GWO and AOA have higher RMSE values. But they do contribute significantly to parameter diversity.

The convergence curve shows the iteration numbers that resulted in the smallest RMSEs, which are satisfactory for the HOA, DE, and PSO. Even though the AOA has a larger fill factor, its RMSE values indicate a trade-off between optimization goals and accuracy. By contrast, DE achieves the highest precision of all models.

The optimal RMSE values for the SDM, DDM, and TDM, as determined by the DE algorithm, are 0.000546723, 0.000148844, and 0.000542472, respectively. Additionally, the HOA demonstrates notable performance in achieving consistent parameter estimation across all models. Figure 5b,d, Figure 6b,d, and Figure 7b,d illustrate the absolute error between the power and current for each model, contrasting simulated results with empirical outcomes. These results prove that the DE, HOA, and PSO algorithms are more efficient and perform better than other methods. This study proves that DE is the most effective and reliable technique for the optimization of parameters in PV models. The HOA and PSO are also close contestants, with solid performances and convergence rates.

6. Conclusions

This research paper provided a comprehensive overview of state-of-the-art optimization algorithms for photovoltaic (PV) parameter estimation in different PV models, including single-diode model (SDM), double-diode model (DDM), and three-diode model (TDM). Using solar cell series data from RTC France, the algorithms were compared interms of accuracy, speed of convergence, and robustness. According to the results of the study, for the single-diode model (SDM), the best algorithm that performed was the DE algorithm. Its RMSE value was 0.0005. The PSO algorithm followed up, with an RMSE of 0.0001 and, lastly, the HOA with 0.1307. The DE algorithm proved best in fill factor and consistency, producing reliable and accurate results. The DE algorithm achieved the lowest RMSE value of 0.0001 in the double-diode model, making it the most accurate as well. The HOA’s RMSE was 0.0614, while PSO’s RMSE was 0.0004. The AOA and GWO both presented higher RMSE values and had a good trade-off between the convergence rate and accuracy. For the three-diode model (TDM), DE maintained its dominance, with an RMSE of 0.00054, followed by PSO with 0.1046 and the HOA with 0.0261. The analysis highlighted that DE consistently achieved superior results across all tested models, providing high accuracy and robust convergence behavior. The comparative analysis demonstrated that DE outperformed other algorithms across all three models, achieving the lowest RMSE and highest reliability. The visual alignment of I-V and P-V characteristics predicted by DE with experimental data validated its robustness. While the HOA and PSO also showed competitive performance, DE’s balance of computational efficiency and precision made it the most reliable choice for PV parameter optimization. These findings underscore the potential of advanced optimization algorithms to enhance the efficiency, accuracy, and operational lifespan of PV systems, contributing significantly to the adoption of renewable energy technologies. By enhancing the accuracy and reliability of PV systems, this research contributes to the broader goals of sustainable energy development. Future work should explore hybrid models and real-time implementations to further optimize PV performance under dynamic environmental conditions.