Exploring the Complex Relationships Between Influential Factors of Urban Land Development Patterns and Urban Thermal Environment: A Study on Downtown Shanghai

Abstract

The rapid urbanization process has exacerbated the urban heat island (UHI) effect in megacities like Shanghai. Urban green infrastructure (UGI) plays a crucial role in mitigating the UHI effect; however, its cooling capacity is subject to various urban land development patterns. This study examined 39 typical locations in downtown Shanghai to measure how urban land development patterns affect the UGI’s cooling capacity. Using a data-driven framework, we identified 12 key influencing factors and explored 4 interactions for building three regression models: multiple linear regression (MLR), partial least squares regression (PLSR), and support vector regression (SVR). For each of these models, we considered two variations: a basic model neglecting interactions and an enhanced model including interactions. Results showed that all enhanced models outperformed their basic counterparts. On average, the enhanced models increased their predictive power by 14.59% for training data and 32.15% for testing data. Additionally, among the three enhanced models, the SVR-enhanced models show the best performance, followed by the PLSR-enhanced models. Their mean predictive power increased by 8.33−37.43% for training data and 31.77−43.558% for testing data vs. the MLR-enhanced models. Overall, our findings revealed that impervious surfaces contribute positively to urban warming, while UGI acts as a negative contributor. Moreover, we highlighted how urban land development metrics, particularly the UGI’s percentage and spatial arrangements in relation to adjacent buildings, significantly affect the thermal environment. The findings can offer valuable insights for urban planners and decision-makers involved in managing UGI and developing strategies for UHI mitigation and urban climate adaptation.

1. Introduction

Since the era of the Industrial Revolution, global urbanization has accelerated the rapid expansion of urbanized and urbanizing areas. Until now, there has been cumulative evidence showing that rapid urbanization has profoundly altered the urban ecosystem, causing unprecedented environmental challenges to the sustainability of human society. Among these environmental challenges, the urban heat island (UHI) effect should be one of the key issues of particular concern. In big cities, factors such as dense populations, dominant impervious surfaces, increased energy consumption, and a deficiency of green spaces exacerbate the UHI effect during warm and hot seasons [1,2,3,4,5]. This intensification results in pronounced environmental pollution, increased energy consumption, heightened carbon emissions, and increased health risks [6,7,8,9,10]. Moreover, the synergistic urbanization and global warming exacerbate the adverse consequences of the UHI effect, as evidenced by numerous case studies reported in Asian, European, African, and American countries [11,12,13,14].

China has been one of the fastest-urbanizing countries over the past three decades, with an urbanization rate 2.14% higher than the global average and an annual urban growth rate of 7.9% [15,16]. This trend is expected to continue for the next 50 years or even longer, positioning China as the world’s leading engine of urban growth [17]. However, this rapid urbanization also emphasizes the country’s vulnerability to climate change. In this sense, Shanghai, as a representative megacity at risk from climate change, has seen a steady increase in the UHI effect since the 1980s. The number of hot summer days in the downtown area has significantly surpassed that of the suburban and exurban regions [18]. The degradation of the urban thermal environment negatively affects the quality of living for residents and restricts their outdoor activities. This issue is also closely related to urban energy consumption, environmental pollution, climate adaptability, and the sustainability of the urban ecosystem [19,20]. Therefore, both qualitatively and quantitatively investigating the urban thermal environment, particularly its underlying causes and driving factors, is vital for effective decision-making regarding UHI mitigation [21].

Urban green infrastructure (UGI), also referred to as ecological infrastructure, encompasses a wide range of landscape elements within city boundaries. These include urban parks and green spaces, as well as natural or semi-natural landscapes such as vegetation, lakes, and streams that are influenced by human activities. UGI’s cooling effects primarily depend on three aspects: transpiration from vegetation, shading provided by tree canopies, and the evaporation from water bodies [22,23]. Empirical studies have demonstrated that well-designed UGI patches can reduce ambient temperatures by up to 3.71 °C during summer months. Furthermore, the UGI’s cooling capacity increases significantly with patch size. As reported, UGI patches size over 5 hectares may produce a maximum cooling distance exceeding 200 m [24]. Compared with active cooling systems relying on fossil fuels, UGI offers nature-based cooling with advantages such as zero energy consumption, low maintenance costs, and near-zero carbon emissions. Therefore, UGI has become a vital component of ecological infrastructure for adapting to climate change and a cost-effective strategy for developing climate-resilient cities.

Currently, UGI planning and design often require a balance between esthetic appeal, functional utility, and ecological benefits. The cooling performance of such green spaces is largely influenced by two sets of factors: (1) the intrinsic biophysical attributes of the green space itself—such as vegetation type and patch size—and (2) its spatial configuration within the urban fabric. At a fine scale, the morphological characteristics of green patches (e.g., edge shape, internal structure) may interact in complex ways with adjacent buildings and roadways. For instance, street orientation may affect the duration of solar exposure on green areas, building height may alter local airflow patterns, and dense building shadows may reduce the evapotranspirative cooling capacity of vegetation [25]. The effectiveness of UGI in cooling urban areas is influenced by various spatial features. In densely populated megacities, however, the large-scale expansion of UGI often faces challenges due to population pressures, economic development needs, and policy constraints. Therefore, it is nearly impossible to fully address the UHI effect solely through the widespread development of UGI. To effectively adapt to climate change and mitigate the impacts of UHI while safeguarding public health, strategies must be based on scientific evaluation systems. These systems should quantify key indicators, such as building density and the morphology of green patches, to assess their specific effects on cooling performance.

Existing studies have primarily focused on the individual impacts of regional climatic conditions, human activities, and green infrastructure characteristics on the UGI’s cooling effect [26,27]. The importance of factors influencing the cooling effect of UGI has primarily been quantified using a range of statistical techniques, including the standardized coefficient approach in linear regression [28], the Geodetector for analyzing variable interactions [29], the random forest algorithm that accounts for nonlinear effects [30], and the variance decomposition method for assessing intergroup variable importance [31]. Nevertheless, each of these methods has inherent limitations. The standardized coefficient approach and random forest cannot adequately address multicollinearity, the Geodetector is less effective in handling continuous variables, and variance decomposition fails to incorporate variable interactions. As a result, mechanism interpretation has often been partial. For instance, Ziter et al. identified 40% vegetation cover as a peak cooling threshold [28], while Kong et al. observed that a 10% increase in vegetation cover leads to a 0.83 °C reduction in land surface temperature (LST) [32].

The methodological limitations mentioned above have created a knowledge gap in understanding how urban land development patterns influence the UGI’s cooling effects. This gap limits the assessment of UGI’s cooling potential, presenting a theoretical barrier to optimizing the spatial arrangement of UGI and surrounding landscapes in urban planning. To tackle this issue, this study focuses on Shanghai, a representative megacity in China that is experiencing an intensified UHI effect due to rapid urban growth [33]. To address this issue, this study focuses on Shanghai, a representative megacity in China that is experiencing an exacerbated UHI effect due to rapid urban growth. This study aims to test and compare several popular regression models for quantitatively examining the complex relationships between influential factors of urban land development patterns and the urban thermal environment indicated by LST. The authors seek to provide practical guidance for reinforcing the UHI’s cooling effect and mitigating the UHI effect.

2. Materials and Methods

2.1. Study Area

The geographical extent of Shanghai falls within latitudes 31°32′ N–31°27′ N and longitudes 120°52′ E–121°45′ E. It is situated on the eastern edge of the alluvial plain of the Yangtze River Delta (Figure 1). It borders the East China Sea to the east, faces Hangzhou Bay to the south, and adjoins Jiangsu and Zhejiang provinces to the west. As China’s economic capital, it yields approximately 5% of China’s GDP within its jurisdiction, accounting for 0.06% of China’s national territory [34]. The average elevation is around 4 m, with the terrain gently sloping from the northwest to the southeast [35]. Shanghai has a typical northern subtropical monsoon climate, with an annual mean temperature of approximately 15 °C. The average temperature in summer reaches 28 °C, while in winter it drops to around 4 °C. Based on local temperature records from 1981 to 2024, the average daily temperatures in July 2024 ranged from 27 °C to 36 °C, with extreme highs reaching 40 °C. In August, the average temperatures ranged from 27 °C to 37 °C, with the highest recorded extreme reaching 41 °C [36]. Consequently, downtown Shanghai usually suffers from the scorched summer days during these two months. Spatially, there exists a distinct pattern of summertime UHI effect between the urban core and urban fringe. To illustrate this varied spatial pattern of the UHI effect, we studied a total of 39 representative sample sites. These sites encompass a range of urban environments, including commercial facilities, residential communities, parks, universities, and colleges within the traditional urban core. Additionally, we examined commercial establishments, residential areas, industrial parks, and suburban parks located in the recently urbanized areas at the urban fringe. This variety represents the connection between different land development patterns and the corresponding levels of UHI intensity [33].

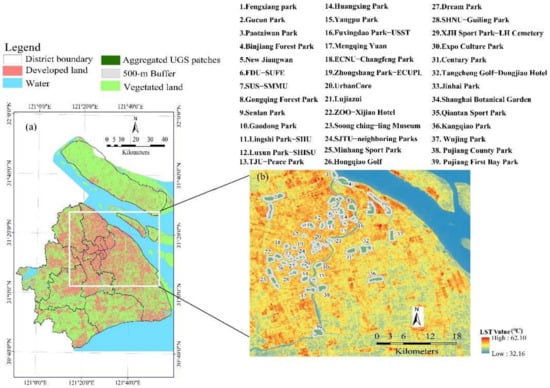
Figure 1. Location of study area showing the location of thirty-nine sites. (a) Land use in Metropolitan Shanghai. (b) Location of thirty-nine sites affected by the surface urban heat island, as indicated by the summertime mean annual land surface temperature (LST) in 2013—2022 [33]. Among these sites, 4, 7, 12, 17, 18, and 36 are classified as slightly urbanized areas on the urban periphery, while sites 8, 13, 30, and 33 are identified as slightly to moderately urbanized areas. Sites 23, 24, 27, 29, and 37 represent moderately urbanized areas, and the remaining sites are categorized as highly urbanized areas.

2.2. Data Sources

This study uses a multi-source dataset comprising satellite remote sensing imagery and supplementary data collected between 2013 and 2022. The primary data source is the Landsat-8 OLI/TIRS imagery. Supplementary interpretation datasets include Sentinel-2 imagery, the commercial Digital Thematic Maps of Shanghai Beijing Digital Space Technology Co., Ltd., Beijing, China, (2015), field-surveyed building indicators within Shanghai, publicly accessible online data (used to assist in identifying green space and building distributions), commercial platforms such as LocalSpace Viewer^©, Tianditu^©, and the free platform Baidu Map^© and their respective street-view services, as well as ground-truthing data collected by the research team.

These datasets can be referred to a recent publication [33]. Based on this work, we added three new sites and collected new data to explore how the urban land use features influence the UGS’s cooling effect from a new approach. Details are provided in Table 1.

Table 1. Description of datasets used in this study.

Dataset	Acquisition Date	Description
Thermally enhanced LST products	29 August 2013 3 August 2015 24 August 2017 16 August 2020 14 August 2022	Five thermally enhanced LST products retrieved from cloud-free Landsat-8 TIRS data (Level 1T, path/row: 118/38) were used as the indicator of urban thermal environment. Following a generalized radiative transfer equation [37], the initial LST retrieval was performed using Landsat-8’s band 10 data. Considering that the original 30 m-resolution LST data lacked the capacity to capture fine-scale thermal responses of different land use types, the thermally enhanced LSTs were used as the alternatives. A tedious procedure was applied to generate the thermally sharpened LSTs. A key point of this process is to randomly extract the at-sensor brightness temperature (BT) data from Landsat-8’s band 10 data. Within each scene of Landsat-8’s band 10 image, a cluster of random points (from 50,000 to 4.90 million) with 20 m intervals were generated and used to extract the BT values. Subsequently, an ordinary kriging method was employed to generate the multiple-resolution interpolated BT maps, which were further validated by 20 m land use maps. Thirdly, surface emissivity values were manually corrected by specific land use types. The 20 m thermally sharpened LSTs were generated using generalized radiative transfer equation. Finally, all the sharpened LSTs were resampled to 30 m and overlapped with raw LST at 30-m. Then a pixel-to-pixel comparison was performed to determine the least root mean square error (RMSE) between the thermally sharpened LSTs and raw LSTs. The validated thermally enhanced LSTs have a resolution of 20 m with acceptable RMSE (ranging from 0.2 to 0.4 °C). Details of generating these thermally enhanced LSTs can be referred to Zhang et al., 2024 [33].
Land Use Map of downtown Shanghai (2013)	-	This dataset contains 12 land use types. It was originally generated from high-resolution QuickBird imagery, using an object-oriented classification method. The land use classification was validated through field measurements. The overall classification accuracy reached 91.1% [38].
Digital Thematic Map of Shanghai	-	This dataset contains vector layers of land use and subcategories (e.g., buildings, green spaces, rivers, streams, transport lines, warehouses, and ports), sourced from both commercial and publicly accessible datasets. The commercial data were purchased from Beijing Digital Space TechnologyTM Co., Ltd., China. (2015). The open-access openstreet map (OSM) data was downloaded from https://www.openstreetmap.org/ (accessed on 7 September 2024) and used as a supplement.
Field Survey Data	-	Validated land use data were obtained from our research team’s seasonal and semi-annual field surveys for land use (2013–2022).
Satellite Map (91 Weitu)	-	A commercial integrated vector and aerial imagery system operated by Beijing Qianfan Vision TechnologyTM Co., Ltd., China
Google Maps	-	An open-access satellite imagery platform operated by Google LLCTM (accessed on 7 September 2024).
Mapworld (Tianditu)	-	An integrated vector and aerial imagery system operated by the National Geographic Information Public Service Platform of China.
PCL Data Repository	-	An open-access scientific data repository operated by the Pengcheng Lab© (https://data-starcloud.pcl.ac.cn/zh, (accessed on 7 September 2024)).

2.3. Methods

2.3.1. Calculation of 12 Explanatory Variables Representing Urban Land Development Patterns

Urban land development patterns refer to the spatial configuration and utilization of land resources under anthropogenic influence, encompassing multidimensional characteristics such as land use structure, development intensity, functional layout, and ecological effects. As China’s largest economic hub, Shanghai contributes approximately 5% of the national gross domestic product (GDP) while occupying less than 0.1% of the country’s total land area. By 2024, its permanent resident population reached 24.80 million [39], of which 80% of the population resides within an area of 4000 km². This area makes up the domain of downtown Shanghai, including the urban core, the newly urbanized area, and the urban periphery. In this study area, over 75% of the land is classified as developed land, including residential, commercial, and industrial uses [40].

Based on a data-driven analytical framework, this study selected 12 dual-dimensional landscape metrics to quantify the spatial heterogeneity of land development patterns in central Shanghai. These include six hardscape indicators and six softscape indicators. The first dimension comprises six hardscape variables that reflect urban development intensity: the proportion of building area (Building), the proportion of other impervious surfaces (OtherIS), mean building height (MBH), mean building distance (MBD), road density (RD), and floor area ratio (FAR). The second dimension includes six softscape variables that characterize the fragmentation of urban green infrastructure (UGI): proportion of UGI area (UGI), patch density (PD), landscape shape index (LSI), clumpiness index (CLUMPY), largest patch index (LPI), and connectivity index (COHESION).

Detailed definitions and calculation methods of each metric are provided in Table 2.

Table 2. Key Indicators Representing Urban Land Development Patterns impact LST in this study.

Dimension	Indicator (Abbreviation)	Definition
Hardscape Indicators	Building	Building percentage. It denotes the proportion (%) of land area occupied by buildings within the study area, including residential, office, hospital, school, commercial, and industrial facilities.
	OtherIS	Percentage of other impervious surfaces. It denotes the proportion (%) of land area covered by non-building impervious surfaces, such as paved roads, playgrounds, parking lots, bridges, and composting facilities.
	MBH	Mean Building Height. It is the arithmetic mean height (in meters) of all buildings within the study area.
	MBD	Mean Building Distance. It denotes the mean spacing (in meters) between adjacent buildings within clusters, calculated along specified directions.
	RD	Road Density. It denotes the total length of roads per unit area (km/km2), calculated as: $$RoadDensity={\displaystyle \frac{Total Road Lengt\mathrm{h}}{A}},$$ where Total Road Length is the total road length in meters, and A is the plot area in hectares.
	FAR	Floor Area Ratio. It is a unitless index denoting the ratio of total building floor area to the land area, reflecting built-up density. It is calculated as: $\mathrm{F}\mathrm{A}\mathrm{R}={\displaystyle \frac{\sum _{i=1}^n(c\times F)}{A}}$, where F is the building footprint (ha), c is the number of floors, and A is the plot area (ha).
Softscape Indicators	UGI	Urban Green Infrastructure Ratio. It denotes the proportion (%) of the study area covered by green and blue spaces, including trees, shrubs, grasslands, and water bodies (in m2). This index is actually the class-level metric named as PLAND−percentage of UGI within a specific landscape.
	PD	Patch Density. It denotes number of UGI patches per unit area (patches/ha), which is calculated as: $$\mathrm{P}\mathrm{D}={\displaystyle \frac{{\mathrm{N}}_i}{{\mathrm{A}}_i}}$$ where N is the number of patches, and Ai is the area of the study unit (ha).
	LSI	Landscape Shape Index. It is a dimensionless and unitless index reflecting the complexity of UGI patch shapes, which is calculated as: $$\mathrm{L}\mathrm{S}\mathrm{I}={\displaystyle \frac{0.25\mathrm{P}}{\sqrt{{\mathrm{A}}_i}}}$$ where P is the total patch perimeter (m), and Ai is the area of the study unit (ha).
	CLUMPY	Clumpiness Index. It is a unitless index quantifying the degree of spatial aggregation of UGI patches, which is calculated as: $$\mathrm{G}\mathrm{i}\mathrm{v}\mathrm{e}\mathrm{n}{\mathrm{G}}_{\mathrm{i}}=\left({\displaystyle \frac{{\mathrm{g}}_{\mathrm{i}\mathrm{i}}}{\sum _{\mathsf{\kappa }=1}^{\mathrm{m}}{\mathrm{g}}_{2,\mathsf{\kappa }}}}\right)$$ $$=\left[\begin{array}{c}{\displaystyle \frac{{\mathrm{G}}_{\mathrm{i}}-{\mathrm{P}}_{\mathrm{i}}}{1-{\mathrm{P}}_{\mathrm{i}}}}\mathrm{f}\mathrm{o}\mathrm{r}{\mathrm{G}}_{\mathrm{i}}\ge {\mathrm{P}}_{\mathrm{i}}\\ \mathrm{g}\\ {\displaystyle \frac{{\mathrm{G}}_{\mathrm{i}}-{\mathrm{P}}_{\mathrm{i}}}{1-{\mathrm{P}}_{\mathrm{i}}}}\mathrm{f}\mathrm{o}\mathrm{r}{\mathrm{G}}_{\mathrm{i}}<{\mathrm{P}}_{\mathrm{i}};{\mathrm{P}}_{\mathrm{i}}\ge 5\\ {\displaystyle \frac{{\mathrm{P}}_{\mathrm{i}}-{\mathrm{G}}_{\mathrm{i}}}{-{\mathrm{P}}_{\mathrm{i}}}}\mathrm{f}\mathrm{o}\mathrm{r}{\mathrm{G}}_{\mathrm{i}}<{\mathrm{P}}_{\mathrm{i}};{\mathrm{P}}_{\mathrm{i}}<5_{\mathrm{i}}\end{array}\right]$$ where gii is the number of like-adjacencies among pixels of class i, gik represents adjacencies between classes i and k, and Pi is the percentage of landscape occupied by class i (PLAND).
	LPI	Largest Patch Index. It is a unitless index denoting the percentage of total landscape area occupied by the largest single UGI patch. It is calculated as: $$\mathrm{L}\mathrm{P}\mathrm{I}={\displaystyle \frac{Max\left(a_i\right)}{{\mathrm{A}}_i}}\times 100$$ where Max(ai) is the area of the largest patch (m2), and Ai is the total area of the study unit (ha).
	COHESION	Connectivity Index. It is a unitless index reflecting the spatial connectedness of green patches. It is calculated as: $$\mathrm{C}\mathrm{o}\mathrm{h}\mathrm{e}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n}={\displaystyle \frac{1-\frac{\sum _{\mathrm{j}=\mathrm{i}}^{\mathrm{n}}{\mathrm{p}}_{\mathrm{i}\mathrm{j}}}{\sum _{\mathrm{j}=1}^{\mathrm{n}}{\mathrm{p}}_{\mathrm{i}\mathrm{j}}\sqrt{{\mathrm{a}}_{\mathrm{i}\mathrm{j}}}}}{\left(1-\frac{1}{\sqrt{\mathrm{A}}}\right)}}\times 100$$ where pij and aij are the perimeter and area (in pixels) of patch ij, and A is the total area of the study unit (ha).

Note: For detailed computational procedures, please refer to the FRAGSTATS v4.2 User Manual [41].

2.3.2. Regression Modeling

In this study, twelve indicators characterizing urban land development patterns were used as the independent variables. Meanwhile, the mean LST during five summer dates in 2013–2022 was used as the dependent variable. In this section, we adopted three widely used regression models to quantify the complex relationships between the independent and dependent variables as follows:

(1) Multiple Linear Regression (MLR)

Multiple Linear Regression (MLR) is a popular regression method based on the principle of Ordinary Least Squares (OLS). This method is widely applied for examining causal relationships between one dependent variable and multiple independent variables. It is primarily used for factor selection and statistical prediction. A specific type of multiple linear regression, referred to as complete regression, includes all potential independent variables in the model simultaneously to create a comprehensive regression equation. This approach enables a comprehensive evaluation of the potential impact of each variable on the dependent variable.

To test whether introducing the interactions between the independent variables will influence the model performance, we designed two variations for the MLR models. They contain a basic model neglecting interactions and an enhanced model including interactions. The basic model is expressed as follows:

$$LST=a+\underset{i=1}{\overset{n}{â}}{b}_i{x}_i+Î\mu$$

(1)

In Equation (5), within the modeling framework, $a$ denotes the intercept term, and $n$ represents the number of predictors included in the model, constrained to 1 ≤ $n$ ≤ 12. The coefficients b_i are the partial regression coefficients associated with the predictors x_i, comprising six hardscape indicators (Building, OtherIS, RD, FAR, MBH, MBD) and six softscape indicators (UGI, LSI, PD, LPI, CLUMPY, COHESION).

The enhanced model is formulated as follows:

$$LST=a+\underset{i=1}{\overset{12}{â}}{b}_i{x}_i+f(x_1Ã-x_2Ã-\dots Ã-x_i)+Î\mu$$

(2)

In Equation (6), f$\left(x_1Ã-x_2Ã-\dots Ã-x_i\right)$ represents the interaction terms among the predictors, which can be flexibly configured based on the research objectives. The term ε represents the random error. This term accounts for the portion of variability that cannot be explained by the model, reflecting the discrepancy between observed values and model predictions. Herein, based on Spearman’s rank correlation result, we found a statistically significant correlation between the independent variables (see Appendix A Table A2). We further assumed four interactions that may have finite physical associations with the variance of the LSTs. These interactions are: Interaction1 represents UGI × CLUMPY × LPI × COHESION; Interaction2 denotes UGI × PD × LSI; Interaction3 refers to Building × Road Density × FAR × MBH; and Interaction4 represents Building × RD × FAR × MBH × UGI. Please note that these interactions were adopted by the PLSR- and SVR-enhanced models.

The model selection process adheres to rigorous criteria—not all candidate models are included. To ensure the stability of the results and the accuracy of predictions, we only retained models that produce reliable outcomes and exhibit low prediction bias. Additionally, in the final model, we considered only those combinations of predictors that were physically meaningful or statistically significant in explaining the variance of the response variable.

(2) Partial Least Squares Regression (PLSR)

Partial least squares regression (PLSR) is a statistical modeling technique well-suited for addressing multicollinearity between dependent and independent variables. The basic and enhanced forms of the PLSR model have the same structure as the MLR models. However, unlike the MLR models, PLSR models do not require fixed predictor variables and is tolerant of measurement errors, thus demonstrating significant robustness in uncertainty quantification [42,43]. It has been widely applied in fields such as chemistry [44], environmental science [45], and finance [46], and is particularly effective when dealing with high-dimensional data or small sample sizes. In the PLSR modeling, three to ten components were evaluated to select the competing models with better predictive power. After numerous attempting, five components yielding both higher R² on the training and testing sets were adopted for further modeling.

(3) Support Vector Regression (SVR)

Support vector regression (SVR) is a non-parametric regression technique based on the principles of the support vector machine (SVM) algorithm. The core idea is to project the training dataset from a lower-dimensional space into a high-dimensional feature space via a kernel function, as with f(x) = w^Tx + b. This function achieves to effectively separate different groups of input data in a linearized manner. It seeks that the deviation between the predicted and actual values does not exceed a predefined threshold ε. Meanwhile, the weight vector w remains as small as possible, ensuring a smooth model [47]. SVR achieves this by incorporating an ε-insensitive loss function, which imposes no penalty for prediction errors within the ε margin but applies linear penalties for errors exceeding this threshold [48]. Compared to the MLR models, the SVR models typically perform better in modeling complex relationships between high-dimensional data. This method has been widely applied in ecological, environmental, geographical, and meteorological research [49,50].

In this study, all statistical analyses were conducted using the basic functions of R version 4.5 (R Core Team, 2024) [51] and a variety of specialized libraries. For example, library(pls) [52] was used to perform the PLSR analysis. In addition, library(e1071) was used to perform the SVR modeling [53].

2.3.3. Assessment of Regression Model Performance

An overall assessment of the performance of three regression models was conducted through the following steps. First, the data used for modeling was divided into a training set and a testing set. The training set consisted of 80% of the randomly selected data, which was utilized for model development. The testing set comprised the remaining 20%, which was employed to validate the predictive performance of the trained models. Second, to address the potential multicollinearity problem that may affect MLR models, we calculated the variance inflation factor (VIF), the coefficient of determination (R²), and the root mean square error (RMSE) for assessing model performance on the training and testing sets. In contrast, for PLSR and SVR models, which do not account for multicollinearity, the VIF is not applicable. Therefore, we used only R² and RMSE to evaluate the model performance for these two datasets. The VIF is calculated using the following formula:

$${VIF}_j={\displaystyle \frac{1}{1−R_j^2}}$$

(3)

In Equation (1), R_j denotes the coefficient of determination obtained by regressing the j variable on all other explanatory variables. The VIF is used to assess the degree of multicollinearity among the independent variables. A VIF value exceeding 10 indicates the presence of severe multicollinearity, necessitating a dimensional reduction in the variables [54].

The coefficient of determination, R², reflects the proportion of variance in the dependent variable that is explained by the model. A value closer to 1 suggests a higher goodness of fit. It is calculated using the following equation:

$${\mathit{SS}}_T={\mathit{SS}}_R+{\mathit{SS}}_E$$

(4)

$$R^2=1−{\displaystyle \frac{{\mathit{SS}}_E }{{\mathit{SS}}_T}}={\displaystyle \frac{{\mathit{SS}}_R }{{\mathit{SS}}_T}}={\displaystyle \frac{b^2{\mathit{L}}_{\mathit{xx}}}{L_y}}$$

(5)

The RMSE is also an important metric for evaluating model performance. It quantifies the average deviation between predicted values and observed values, providing a direct measure of the model’s predictive accuracy. A lower RMSE value indicates a stronger generalization capability of the model. The formula for RMSE is as follows:

$$RMSE=\sqrt{\underset{i=1}{\overset{n}{â}}{\displaystyle \frac{{(y_i−\widehat{y_i})}^2}{n}}}$$

(6)

In Equation (4), n represents the sample size, $y_i$ denotes the actual value of the i-th observation, and $\widehat{y_i}$ is the predicted value for the i-th observation.

3. Results

3.1. Overall Linkage Between Different Land Development Patterns and LST

Figure 2 shows the clusters of 39 sampling sites that represent various land development patterns. By examining the relationships between the observations and the influential factors related to these patterns, we identified six categories of sites. Table 3 outlines the overall connections between different land development patterns and LST. Generally, it can be observed that sites with low to medium development pressure have relatively lower LSTs compared to those with high to very high development pressure, which tend to exhibit higher LSTs.

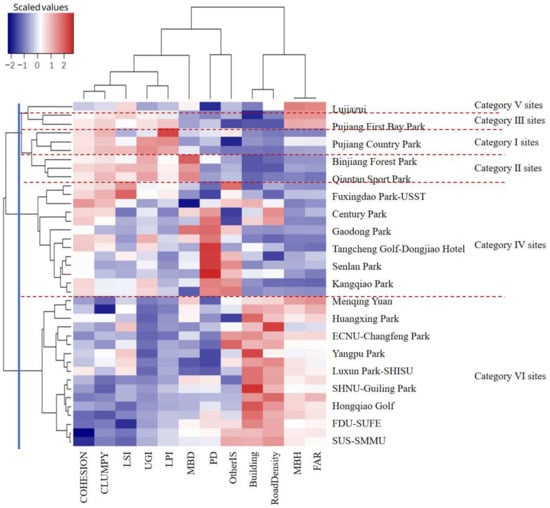
Figure 2. Heatmap depicting the clusters of 39 sampling sites that represent different land development patterns. Note: The vertical blue line in this figure divides the observations into six categories, which are further separated by the red dashed lines. Due to space constraints, this figure only displays 20 sites; however, all sites are included in the analysis.

Table 3. Overall linkage between different land development patterns and LST.

Category Site	General Description	Mean LST (°C)
I	This category is under low development pressure. The sites are characterized by relatively minor built-up land, such as lower Building, FAR, and MBH, but higher MBD and spatial connectivity and aggregation traits of the UGI, such as LPI, medium PLAND and CLUMPY.	42.183 ± 3.633 a
II	This category is under low to medium development pressure. The sites show lower Building and M BD, higher FAR and MBH, medium OtherIS, and lower RD. Meanwhile, they have higher spatial connectivity and aggregation traits of the UGI.	42.910 ± 2.351 a,b
III	This category is under medium development pressure. The sites show relatively lower traits of Building, FAR, MBH, MBD, OtherIS, and RD. Meanwhile, they have higher spatial connectivity and aggregation traits of the UGI.	45.551 ± 2.899 c
IV	This category is under medium to high development pressure. The sites exhibit medium Building, lower FAR, lower MBH, lower MBD, medium OtherIS, and medium RD. They are associated with higher PD, medium PLAND, COHESION, and LSI, with lower LPI and CLUMPY.	46.656 ± 3.086 d
V	This category is under very high development pressure, characterized by higher Building, higher FAR, higher MBH, lower MBD, medium OtherIS, and higher RD. In contrast, the UGI traits are characterized by lower LPI, PLAND, CLUMPY, PD, with medium COHESION and LSI.	49.681 ± 4.296 e
VI	This category is under very high development pressure, characterized by higher Building, medium FAR, medium MBH, lower MBD, medium OtherIS, and higher RD. In contrast, the UGI traits are characterized by lower LPI, PLAND, and CLUMPY, with medium PD, COHESION, and LSI.	49.902 ± 4.612 e,f

Note: The last column labeled with different letters denote statistical significance at p = 0.05 level.

3.2. Results of Basic Regression Models

Table 4 shows the overall performance of three basic regression models on both the training and testing sets.

Table 4. R² and RMSE of the Three Basic Models on Training and Testing Sets.

Basic Regression	Training		Test
	R2	RMSE	R2	RMSE
SVR	0.963 ** [0.932, 0.971]	0.606 [0.198, 0.976]	0.559 * [0.479, 0.581]	3.029 [1.123, 3.904]
PLSR	0.614 * [0.427, 0.772]	1.515 [0.559, 1.946]	0.479 * [0.430, 0.564]	3.321 [1.518, 4.292]
MLR	0.601 * [0.601, 0.602]	1.862 [0.670, 2.347]	0.363 * [0.362, 0.363]	3.067 [1.132, 3.939]

Note: Bold numbers represent the arithmetic mean of each statistic across the five summer dates from 2013 to 2022. The values in brackets indicate the minimum and maximum, respectively. The subscripts of ** and * denote statistically significant at p = 0.01 and p = 0.05, respectively.

On average, the MLR models achieved an R² of 0.601 and an RMSE of 1.862 on the training sets. This indicates that the model explains approximately 60.1% of the variance in the dependent variable and has an average prediction error of about 1.862 units on the training sets. However, on the testing sets, the R² dropped to 0.363, and the RMSE increased to 3.067, suggesting a decline in predictive performance and poor generalization capability.

The PLSR model yielded an R² of 0.614 on the training sets, slightly higher than that of the MLR models, with a lower RMSE of 1.515. On the testing sets, the R² was 0.479, outperforming the complete regression model, while the RMSE was 3.321, slightly higher than that of the complete regression. Overall, the PLSR model performed marginally better than the complete regression model on both training and testing datasets, likely due to its advantage in handling multicollinearity among predictors.

The SVR model achieved an R² of 0.963 and an RMSE of 0.606 on the training sets, demonstrating a substantially better fit compared to the other two basic regression models. However, on the testing sets, the R² decreased to 0.559 and the RMSE rose to 3.029, indicating potential overfitting. While the SVR model excelled on the training data, its generalization to unseen data was relatively limited.

In summary, across all three regression models, the models consistently exhibited significantly better performance on the training datasets than on the testing datasets.

3.3. Results of Enhanced Model Construction

Table 5 shows the overall performance of three enhanced regression models on both the training and testing sets.

Table 5. R² and RMSE of the Three Enhanced Models on Training and Testing sets.

Enhanced Regression	Training Set		Testing Sets
	R2	RMSE	R2	RMSE
SVR	0.973 ** [0.971, 0.979]	0.537 [0.198, 0.690]	0.705 * [0.583, 0.797]	3.257 [3.053, 3.612]
PLSR	0.767 ** [0.645, 0.823]	1.337 [0.494, 1.716]	0.647 * [0.543, 0.823]	3.092 [1.046, 3.843]
MLR	0.708 * [0.707, 0.708]	1.102 [0.406, 1.415]	0.491 * [0.488, 0.492]	3.361 [2.759, 3.648]

Note: Bold numbers represent the arithmetic mean of each statistic across the five summer dates from 2013 to 2022. The values in brackets indicate the minimum and maximum, respectively. The subscripts of ** and * denote statistically significant at p = 0.01 and p = 0.05, respectively.

As shown in Table 5, the MLR-enhanced model achieved a coefficient of determination R² of 0.708 on the training set, representing a significant improvement compared to its basic model (R² =0.601). Although this model’s RMSE on both training and testing sets was partially better than those of the PLSR and SVR models, all independent variables in this enhanced model exhibited VIFs greater than 10, indicating serious multicollinearity issues. Particularly, some perplexing results similar to those found in the basic model (Table 4) persisted, and the overall performance remained inferior compared to the other two enhanced models. In contrast, the PLSR-enhanced model showed a higher R² of 0.767 and a lower RMSE of 1.337, demonstrating comparatively better overall performance. The SVR-enhanced model explained 97.3% of the variance of the LSTs on the training sets with the lowest RMSE. Although the averaged RMSE of the enhanced SVR models on the testing sets was slightly higher than that of the enhanced PLSR models, their R² values were superior. This indicates that the enhanced SVR models demonstrated the strongest statistical explanatory power.

Specifically, the R² for the MLR models on the training sets increased from 0.601 in the basic models to 0.708, while the RMSE decreased from 1.862 to 1.102. On the testing sets, the R² rose from 0.363 to 0.491, and the RMSE dropped from 3.067 to 2.15. These results suggest that incorporating interaction effects improved the fitting and generalization performance of the MLR models on both the training and testing sets. The PLSR-enhanced models achieved an average R² of 0.767 on the training sets, outperforming the basic models (R² = 0.614). Accordingly, the average RMSE also decreased from 1.515 in basic models to 1.337 in enhanced models. On the testing sets, the average R² improved from 0.479 to 0.647. Meanwhile, the average RMSE slightly decreased from 3.321 to 3.092. These results indicate that the inclusion of interaction terms enhanced the performance of the PLSR model compared to its basic counterpart on both the training and testing datasets. In contrast, the SVR-enhanced model achieved an average R² of 0.973 on the training set, which is marginally higher than that of the basic models (R² = 0.963). Consequently, the average RMSE for the enhanced models decreased from 0.606 to 0.537 compared to the basic models. However, on the testing dataset, R² improved from 0.559 to 0.705, while RMSE increased from 3.029 to 3.257. This suggests that while the inclusion of interaction effects improved the fit of the SVR model on the training data, it slightly reduced its generalization ability on the testing set.

Overall, the three enhanced models outperformed their corresponding basic models, with the SVR-enhanced models showing the best comprehensive performance, followed by the PLSR-enhanced models. In contrast, the MLR-enhanced models.

4. Discussion

4.1. Analysis of Multicollinearity in the MLR Model

Numerous studies on the relationship between urban land use and thermal environmental responses have shown that higher proportions of impervious surface area, road density, and building coverage are typically associated with more pronounced urban warming effects [55,56,57]. In contrast, greater coverage of urban green infrastructure (UGI), higher values of metrics such as largest patch index, connectivity, and aggregation, are generally conducive to mitigating urban heat intensification [31,58,59]. Moreover, more complex landscape shapes and higher patch densities of UGI have been found to aggravate urban warming.

However, in the results of the Basic Regression model based on complete regression without considering interaction effects (Table 6), the partial regression coefficient for floor area ratio (FAR) is −4.583, and that for road density (RD) is −0.157, suggesting a negative relationship between these variables and urban warming. Conversely, the partial regression coefficients for the landscape shape index (LSI) and aggregation index (CLUMPY) are 35.879 and 0.342, respectively—implying a positive correlation between these metrics and urban temperature rise.

Table 6. Results of the Basic MLR Models Without Considering Interaction Effects.

Term	Variable	Coefficient	Variance Inflation Factor (VIF)
	Constant	56.164 [44.562, 61.391]	−
Hardscape Indicators	Building	24.977 ** [9.215, 32.067]	87.589 [87.589,87.59]
	OtherIS	9.659 ** [3.576, 12.37]	19.111 [19.111, 19.11]
	MBH	1.823 [0.671, 2.342]	169.914 [169.91, 169.915]
	FAR	−4.583 * [−5.888, −1.686]	197.472 [197.472, 197.47]
	MBD	0.022 [0.008, 0.028]	2.936 [2.935, 2.94]
	RD	−0.157 ** [−0.202, −0.058]	10.023 [10.024, 10.02]
Softscape Indicators	UGI	−4.828 * [−6.248, −1.755]	118.372 [118.373, 118.37]
	PD	0.224 * [0.083, 0.287]	4.107 [4.106, 4.11]
	LSI	35.879 ** [13.23, 46.068]	11.282 [11.282, 11.28]
	CLUMPY	0.342 * [0.13, 0.437]	34.176 [34.175, 34.18]
	LPI	0.078 [0.028, 0.1]	11.106 [11.105, 11.11]
	COHESION	−0.499 ** [−0.64, −0.184]	14.412 [14.413, 14.41]

Note: Bold numbers represent the arithmetic mean of each statistic across the five summer dates from 2013 to 2022. The values in brackets indicate the minimum and maximum, respectively. The subscripts of ** and * denote statistically significant at p = 0.01 and p = 0.05, respectively.

These observed relationships between the independent and dependent variables, as reported in Table 6, clearly deviate from established physical or biophysical understandings. In fact, 10 out of the 12 predictor variables in this model have VIFs exceeding 10.

This strongly indicates the presence of severe multicollinearity among the predictor variables. Such multicollinearity can obscure or distort the individual contribution of a given predictor to the LST, as its effect may be masked by stronger correlations between the LST and other variables. Consequently, the resulting partial regression coefficients may appear counterintuitive or inconsistent with theoretical expectations.

Therefore, the performance of the basic model based on complete regression is evidently inferior to that of the other two basic regression models.

4.2. Analysis of the Pathways Through Which the 12 Main Effects Influence LST

Table 7 presents the partial regression coefficients of the basic PLSR models. Given the substantial variation in measurement units (e.g., percentages, meters, square meters) among the 12 indicators, the raw (unstandardized) partial regression coefficients cannot directly reflect the relative strength of each predictor’s influence on the response variable, LST. To facilitate meaningful comparisons, all coefficients were standardized (see Column 4 of Table 7), and the model results were interpreted based on the standardized coefficients.

Table 7. Partial Regression Coefficients of Each Indicator in the Basic PLSR Models.

Term	Variable	Coefficient	Standardized Coefficient
	Constant	53.490 [43.544, 57.1977]	−
Hardscape Indicators	Building	2.204 [0.811, 2.829]	0.115 [0.114, 0.115]
	OtherIS	3.351 [1.233, 4.303]	0.076 [0.074, 0.079]
	MBH	−0.004 [−0.005, −0.001]	−0.009 [−0.011, −0.007]
	FAR	−0.007 [−0.009, −0.003]	−0.007 [−0.007, −0.007]
	MBD	−0.017 [−0.022, −0.006]	−0.075 [−0.077, −0.071]
	RD	0.0436 [0.016, 0.056]	0.093 [0.089, 0.099]
Softscape Indicators	UGI	−2.555 [−3.281, −0.94]	−0.148 [−0.17, −0.13]
	PD	−0.011 [−0.014, −0.004]	−0.025 [−0.026, −0.024]
	LSI	−1.783 [−2.289, −0.656]	−0.043 [−0.045, −0.042]
	CLUMPY	−0.284 [−0.365, −0.104]	−0.092 [−0.093, −0.091]
	LPI	−0.017 [−0.021, −0.006]	−0.092 [−0.093, −0.089]
	COHESION	−0.055 [−0.07, −0.02]	−0.090 [−0.092, −0.089]

Note: Bold numbers represent the arithmetic mean of each statistic across the five summer dates from 2013 to 2022. The values in brackets indicate the minimum and maximum, respectively.

A comparison of the standardized and unstandardized coefficients reveals that among the hardscape indicators, three variables—building coverage (Building: 2.204 → 0.115), other impervious surface area (OtherIS: 3.351 → 0.076), and road density (RD: 0.0436 → 0.093)—all exert a positive contribution to increased LST. Holding other variables constant, a one-standard-deviation increase in Building, OtherIS, and RD corresponds to increases of 0.115, 0.076, and 0.093 standard deviations in LST, respectively. Notably, the relative importance ranking of these indicators changes after standardization: while OtherIS exhibited the strongest effect in unstandardized form (3.351 > 2.204), after standardization Building surpasses OtherIS in importance (0.115 > 0.076). This result highlights how differences in measurement scale can distort coefficient estimates, while also emphasizing the dominant role of artificial surface spatial agglomeration in exacerbating urban thermal environments [60,61].

In contrast, the other three hardscape indicators—mean building height (MBH: −0.004), floor area ratio (FAR: −0.007), and mean building distance (MBD: −0.017)—have negative standardized coefficients close to zero, indicating relatively weak cooling effects compared to the stronger warming effects of Building, OtherIS, and RD. This may relate to the shading effects of built structures or improved airflow pathways, suggesting that appropriate adjustments to urban form and layout may help mitigate urban heat accumulation [62,63].

Softscape indicators exhibit similar discrepancies due to unit differences. For instance, the landscape shape index (LSI) shows a standardized coefficient of −0.043 (from an unstandardized −1.783), and CLUMPY’s coefficient changes from −0.284 to −0.092. Of particular note is the consistent dominance of UGI, whose coefficient remains the highest before and after standardization (−2.555 → −0.148), confirming its strong cooling effect and highlighting its irreplaceable role in regulating urban thermal conditions. This finding aligns with ecological theories on cooling via evapotranspiration and the low albedo of vegetated surfaces, further validating UGI’s critical role in urban climate regulation [64,65,66].

After removing the influence of differing measurement scales, the remaining five softscape indicators form two distinct clusters in terms of relative importance. Patch density (PD: −0.025) and LSI (−0.043) display similar, relatively low standardized effects, whereas CLUMPY (−0.092), largest patch index (LPI: −0.092), and COHESION (−0.090) demonstrate consistently stronger negative associations with LST. These results indicate that while all natural landscape elements contribute to mitigating urban heat island effects, their impact intensities vary substantially. This suggests that urban planning should not only prioritize increasing the proportion of UGI, but also emphasize enhancing the spatial connectivity and aggregation of green infrastructure [67,68,69].

4.3. Further Analysis of the Mechanism Behind Thermal Environment Anomalies at the Interaction Effect Scale

The results of the enhanced PLSR model incorporating interaction effects (Table 8) are consistent with those of the basic model (Table 7) [70,71]. However, by introducing interaction terms, this model further quantifies the relative contributions of both main effects and interaction effects of the explanatory variables to LST. The results show that the standardized partial regression coefficients of Interaction1 and Interaction2 are −0.094 and −0.061, respectively, both significantly negatively correlated with LST. This may be attributed to the fact that both interaction terms include the urban green infrastructure (UGI) variable. The interaction between UGI and other landscape pattern indicators or impervious surfaces exerts varying effects on urban warming, reflecting the integrated impact of green space on the urban thermal environment under different spatial structures.

Table 8. Partial Regression Coefficients of Each Indicator in the Enhanced PLSR Models.

Term	Variable	Coefficient	Standardized Coefficient
	Constant	53.490 [43.544, 57.1977]	−
Hardscape Indicators (Main Effect)	Building	2.204 [0.811, 2.829]	0.115 [0.114, 0.115]
	OtherIS	3.351 [1.233, 4.303]	0.076 [0.074, 0.079]
	MBH	−0.004 [−0.005, −0.001]	−0.009 [−0.011, −0.007]
	FAR	−0.007 [−0.009, −0.003]	−0.007 [−0.007, −0.007]
	MBD	−0.017 [−0.022, −0.006]	−0.075 [−0.077, −0.071]
	RD	0.0436 [0.016, 0.056]	0.093 [0.089, 0.099]
Softscape Indicators (Main Effect)	UGI	−2.555 [−3.281, −0.94]	−0.148 [−0.17, −0.13]
	PD	−0.011 [−0.014, −0.004]	−0.025 [−0.026, −0.024]
	LSI	−1.783 [−2.289, −0.656]	−0.043 [−0.045, −0.042]
	CLUMPY	−0.284 [−0.365, −0.104]	−0.092 [−0.093, −0.091]
	LPI	−0.017 [−0.021, −0.006]	−0.092 [−0.093, −0.089]
	COHESION	−0.055 [−0.070, −0.020]	−0.090 [−0.092, −0.089]
Interaction Effect	Interaction1	−0.132 [−0.170, −0.049]	−0.094 [−0.096, −0.091]
	Interaction2	0 [0, 0] ※	−0.061 [−0.062, −0.06]
	Interaction3	0 [0, 0] ※	0.011 [0.010, 0.013]
	Interaction4	−0.035 [−0.045, −0.013]	−0.096 [−0.098, −0.095]

Note: In this table, bold numbers indicate the mean values across the five summer dates from different years. The values in parentheses represent the minimum and maximum, respectively. This table includes four interaction terms: Interaction1 represents UGI × CLUMPY × LPI × COHESION; Interaction2 denotes UGI × PD × LSI; Interaction3 refers to Building × Road Density × FAR × MBH; and Interaction4 represents Building × RD × FAR × MBH × UGI. Particularly, for Interaction2 and Interaction3, the symbol ‘^※’ indicates that the unstandardized coefficients of Interaction2 and Interaction3 are extremely small, approaching zero.

For example, Interaction 1 illustrates the synergies between UGI’s area proportion, largest patch index (LPI), aggregation index (CLUMPY), and connectivity (COHESION). It shows that as the interaction traits of UGI increase, so does its cooling effect in mitigating the UHI effect. This cooling effect results from a combination of UGI’s evapotranspiration cooling, shading effects, and the forms of ecological ventilation corridors [72]. Similarly, Interaction2, which captures the interaction between UGI and patch density (PD) as well as landscape shape index (LSI), may indicate that green infrastructure has a stronger regulatory impact on urban thermal environments when characterized by moderate patch density and more complex shapes [32].

A clear contrast can be observed when comparing Interaction3, which excludes UGI, with Interaction4, which includes UGI. The standardized coefficient of Interaction3 is 0.011 and weakly positively correlated with LST, suggesting that interactions among purely hardscape variables—such as combinations of building-related indicators and road density—tend to exacerbate the urban heat island effect [73]. In contrast, Interaction4 yields a coefficient of −0.096, indicating a notable cooling effect and further reinforcing UGI’s critical role in modulating the thermal impacts of land use.

The mechanisms underlying this contrast can be explained by urban microclimate principles [74]. In scenarios represented by Interaction3—particularly in densely developed areas lacking green infrastructure, where building concentration, high road density, high floor area ratio, and tall average building height are prevalent—the combination of low surface albedo, high heat retention, and insufficient ecological cooling can lead to thermal accumulation [75,76]. However, when urban development is spatially coupled with UGI, as represented by Interaction4, the cooling effects of green patches can reduce the temperature of surrounding impervious surfaces through energy exchange processes, thereby achieving a positive regulatory effect on the thermal environment [77].

Figure 3 presents the quantitative results of the SVR-enhanced model, illustrating the contribution levels of 12 main effects and 4 interaction effects to LST. Among them, the top five contributing land development pattern indicators are: UGI (80.632), Interaction3 (Building × RD × FAR × MBH) (76.583), Building (73.836), Interaction1 (UGI × CLUMPY × LPI × COHESION) (70.018), and RD (65.202).

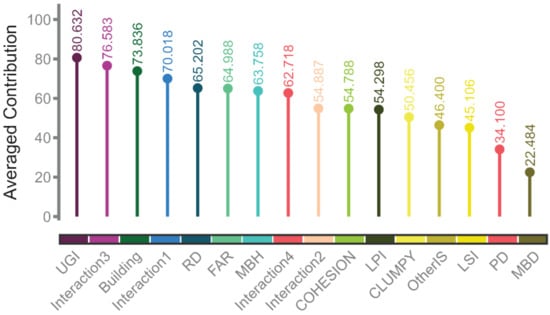
Figure 3. Average Contribution of Land Development Pattern Indicators in the SVR-Enhanced Model.

Further analysis indicates that among the top five indicators, the main hardscape variables—Building and RD—account for 40% of the contributions, and Interaction3, which involves only hardscape elements, ranks second. This suggests that impervious surfaces such as buildings and roads are core drivers of abnormal urban heat intensification and thus should be prioritized for intervention in urban heat island (UHI) mitigation strategies [78,79]. Notably, UGI ranks first in average contribution, underscoring that, beyond optimizing the spatial configuration of built-up areas, strengthening UGI development is a critical pathway to alleviating UHI effects [80].

Moreover, Interaction1, which captures the interaction between UGI and key landscape pattern metrics (CLUMPY, LPI, and COHESION), ranks fourth. Its high contribution validates that developing green space systems characterized by strong connectivity, high aggregation, and prominent patch features can significantly improve the thermal environment. This provides a concrete and actionable direction for landscape-based UHI mitigation [81].

However, as noted in earlier discussions, while the SVR-enhanced model effectively quantifies the average strength of each variable’s influence on LST, it cannot determine the direction (positive or negative) of those relationships. This limitation highlights the inadequacy of relying on a single model to fully unravel the complex mechanisms through which urban land development patterns impact the thermal environment [82]. In light of this, the study further compares the quantitative results from the SVR-enhanced model with those of the PLSR-enhanced model, as detailed below.

The PLSR-enhanced model, as illustrated in Figure 4, clearly demonstrates both positive and negative correlations between each indicator and LST through standardized partial regression coefficients. Among these indicators, UGI shows the strongest negative correlation with LST at −0.101, followed closely by Interaction4 at −0.096 and Interaction1 at −0.094. These negative correlations suggest that UGI and its related interactions—particularly Interaction1, which integrates UGI with CLUMPY, LPI, and COHESION—have significant cooling effects. Conversely, the indicators with positive correlations with the LST, such as Building (0.083), RD (0.0694), and OtherIS (0.0542), indicate that these hardscape elements are the main contributors to increasing urban warming. This result is consistent with the SVR model’s assessment of average importance, where Building and RD rank third and fifth, respectively.

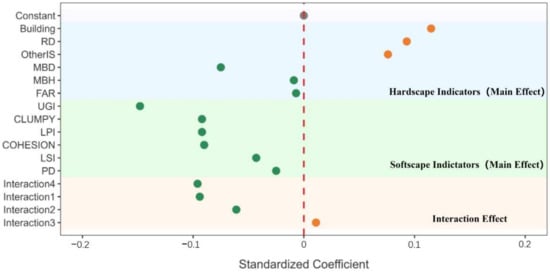
Figure 4. PLSR Enhanced Model’s Standardized Partial Regression Coefficients for Urban Land Development Pattern Indicators.Note:In this figure, the green dots represent positive values, and the orange dots represent negative values.

Although the analyses presented in Table 4 and Table 5 indicate that the enhanced SVR models outperform the enhanced PLSR models in terms of explanatory power (R² = 0.971) and prediction accuracy (RMSE = 0.537) compared to the PLSR model (R² = 0.767, RMSE = 1.337), both models provide critical insights from different analytical perspectives. The SVR-enhanced model excels at capturing the intensity of interactions among factors in complex nonlinear relationships, allowing us to identify which combinations of variables carry greater weight in their overall influence. In contrast, the enhanced PLSR models, with their strength in linear interpretation, clarify whether a given factor contributes to temperature increases or reductions. The SVR models, therefore, serve as a powerful tool for quantitatively deciphering nonlinear interactions, while the PLSR model supports qualitative judgment through its clarity in indicating directional influence.

Therefore, in exploring the nonlinear relationships between land development patterns and the thermal environment in megacities, the SVR- and PLSR-enhanced models each offer irreplaceable strengths. Their combined use enables a comprehensive and in-depth understanding of the complex influence mechanisms from both quantitative and qualitative, as well as nonlinear and linear perspectives. This integrated modeling strategy provides a robust theoretical foundation and clear direction for formulating scientifically sound and effective urban heat mitigation policies, ultimately supporting the development of a more livable urban thermal environment.

4.4. Implications to Practice in Land Use Management and UHI Mitigation

This study addressed the influential factors of urban land development patterns and their roles in negatively or positively contributing to the urban thermal environment. Our findings generally align with those of similar research [61,83,84]. However, our work strengthened the insightful analysis of the interactive effects among these influential factors, which make up a high-dimensional dataset used in this study. We quantitatively assessed the relative importance of both the main and interaction effects of the models on the thermal environment. We found that, alongside the main effect of these influential factors, the interactions among them play a significant role in UHI mitigation.

During the past three decades, downtown Shanghai has rapidly expanded its spatial domain at the loss of semi-natural landscapes, e.g., arable land and small water bodies at the urban fringe.

Recent urban land development has focused on creating large UGI patches within downtown Shanghai. However, a deficiency of ecological land, including green spaces and water bodies, remains a significant concern in unbalanced land development patterns and the UHI effect. Considering the drastic competition pressure of land development and very high economic costs, simply increasing the availability of ecological land by reducing construction areas presents significant challenges. Thus, substantially improving the UGI’s spatial connectivity and aggregation, particularly at the city core with dense buildings and high road density, should be given more priority. Based on our findings, we recommend the following actionable takeaways: (1) increasing the UGI’s share within the urban landscape; (2) improving the UGI’s spatial configuration, e.g., increasing LPI, CLUMPY, and COHESION and strengthening Interaction1−UGI × CLUMPY × LPI × COHESION; and (3) optimizing the spatial arrangement of the UGI and adjacent buildings, e.g., strengthening Interaction4−Building × RD × FAR × MBH × UGI.

To achieve these goals, we propose that recent urban renewal planning initiatives focus on enhancing the spatial connectivity of UGI without fundamentally altering the established urban spatial form and land structure. This task can be accomplished through strategies such as vertical greening, the establishment of small parks, the creation of blue-green spaces, and the implementation of green corridors. These methods aim to mitigate the fragmented characteristics of UGI within urban environments. For medium- and long-term urban renewal strategies, a comprehensive adjustment of land use patterns is imperative. This initiative entails the relocation of numerous densely developed, low-rise residential areas, which should be reconstructed as medium- to high-density buildings. By increasing the floor area ratio and modifying building spacing, it becomes possible to enhance the UGI’s area proportion and improve the effectiveness of urban ventilation corridors. Furthermore, the planning of ecological transportation corridors, characterized by tree-lined avenues, should be prioritized to foster a more favorable microclimate throughout the urban landscape. This approach can be replicated in neighboring cities within the Yangtze River basin and other cities located at a similar latitude, which have a similar local climate system.

4.5. Limitations and Future Prospects

This study has several apparent limitations. First, we primarily relied on the 30 m Landsat-8 LST datasets to represent the overall urban thermal environment. However, these LST datasets only capture daytime thermal infrared signals from the instantaneous field of view (IFOV). Thus, our results fail to capture diurnal cycles and lack the precision needed for characterizing detailed 3-D thermal profiles at the street level. Second, due to the lack of stereoscopic instruments for precise mapping, we only used the UGI’s two-dimensional traits to explore the UGI’s role in regulating the thermal environment. Therefore, we ignored the influence of the tree canopy’s vertical traits on the fine-scale thermal environment. Third, the model selection is limited to MLR, PLSR, and SVR. We did not employ other machine learning methods, such as random forests, extreme gradient boost, and deep-learning methods that utilize neural networks. Additionally, our modeling framework neglects the spatial and non-stationary models, such as the geographically weighted regression or geographically weighted random forests regression. These models may demonstrate superior performance in handling high-dimensional datasets with more competing predictive accuracy.

To tackle these challenges, we argue that future research should incorporate a UAV-thermal platform, Internet-of-Things-based thermal sensors, and thermally enhanced LST products derived from Landsat-8 TIRS data [33]. This integration will enable the production of within-daily LST series data. Additionally, it is essential to combine precise 3D data of vegetation traits and building geometry obtained from UAV-LiDAR platforms, along with information on tree or shrub shading and building shadows. These approaches will deepen our understanding of how vegetation and building spatial configurations contribute to physical cooling. By employing the proposed modeling framework, we can effectively examine the intricate relationships between urban land development patterns and the urban thermal environment at a fine scale. Additionally, future research should expand to more sampling sites to collect adequate data for validation with the numerical simulation outputs. This will ensure that the findings from out-of-sample inferences are more scientifically robust.

5. Conclusions

Taking downtown Shanghai as a case, this study quantitatively examines the complex relationships between influential factors of urban land development patterns and urban thermal environment indicated by the LSTs. We adopted MLR, PLSR, and SVR models, including their basic and enhanced models, to examine the abovementioned complex relationships. We then compared their model performance to determine which models had better interpretative power. The conclusions were summarized as follows.

(1) According to thermal physical traits, impervious surfaces and UGI are two contrasting contributors to variations in the urban thermal environment. Overall, metrics like Building, OtherIS, and road density (RD) are the main contributors to increasing the LSTs. They account for about 40% of the variance of the LSTs. Meanwhile, UGI is the strongest cooling factor. Its effectiveness in cooling increases when UGI exists in large, connected, and aggregated patches. In contrast, its fragmented patches are less effective.

(2) UGI cooling relies on composition, configuration, and spatial arrangement rather than its area proportion within the landscape. The basic and enhanced PLSR and SVR models outperformed the basic and enhanced MLR models in quantifying the relative importance of influential factors of urban land development patterns in the variance of the LSTs. In particular, when considering four interaction terms, both enhanced PLSR and SVR models remarkably increased their mean predictive power. These findings verified the importance of the interaction terms. Noteworthily, for urban settings with high floor area ratio and high road density but lacking adjacent UGI (Interaction-3), it was inclined to produce excess heat and thus increase the LSTs. Conversely, similar urban designs paired with spatially aggregated and contiguous UGI patches (Interaction-4) can lead to neutral or even reduced LST anomalies.

(3) Limitations such as a 30 m resolution for LST data, the lack of 3-D canopy data, and the focus on a single metropolitan area suggest the need for future research utilizing UAV-LiDAR technology, numerical simulation, and validation across multiple cities. Nevertheless, the SVR-PLSR models may serve as a useful approach to quickly assess urban land development patterns and related thermal health risks under different UGI conditions. This approach enables planners to move beyond merely increasing the planar metrics of UGI to implementing optimal configurations, settings, and combinations. It can help densely populated megacities adapt to a warmer future.