Abstract
As global temperatures continue to rise, surpassing the +2.5 °C threshold under current emissions scenarios, the urgency for sustainable, effective carbon management strategies has intensified. Geological carbon storage (GCS) has been explored as a potential mitigation tool; however, its large-scale feasibility remains highly uncertain due to concerns over storage permanence, leakage risks, and economic viability. This study proposes three advanced deep learning models—DeepDropNet, GateSeqNet, and RecurChainNet—to predict the Residual Trapping Index (RTI) and Solubility Trapping Index (STI) with enhanced accuracy and computational efficiency. Using a dataset of over 2000 high-fidelity simulation records, the models capture complex nonlinear relationships between key reservoir properties. Results indicate that GateSeqNet achieved the highest predictive accuracy, with an R2 of 0.95 for RTI and 0.93 for STI, outperforming both DeepDropNet and RecurChainNet. Ablation tests reveal that excluding post injection and injection rate significantly reduced model performance, decreasing R2 by up to 90% in RTI predictions. The proposed models provide a computationally efficient alternative to traditional numerical simulations, which makes them viable for real-time CO2 sequestration assessment. This work advances AI-driven carbon sequestration strategies, offering robust tools for optimizing long-term CO2 storage performance in geological formations and for achieving global sustainability goals.
1. Introduction
The primary driver of climate change is the increasing concentration of carbon dioxide (CO2) in the atmosphere. To address this global challenge, international agreements, such as those under the United Nations Framework Convention on Climate Change, aim to limit global temperature rise to approximately 1.5 °C by reducing CO2 emissions significantly. The ecological stakes of this challenge are profound, as rising CO2 levels contribute to ocean acidification, extreme weather events, and biodiversity loss, threatening ecosystems and human livelihoods [1,2]. Geological carbon storage (GCS) offers a critical strategy to mitigate these impacts by permanently sequestering CO2 in subsurface reservoirs, thereby reducing atmospheric concentrations and stabilizing climate systems. GCS is also considered a powerful measure for mitigating anthropogenic CO2 emissions [3] and the effectiveness of various potential GCS sites (e.g., saline aquifers) is evaluated through four trapping mechanisms: structural, residual, solubility, and mineral. Among these, residual (immobilized CO2 in pore spaces) and solubility (dissolute CO2 in formation fluids) mechanisms are regarded as the most reliable and secure methods for long-term and sustainable carbon capture and storage initiatives [4]. These mechanisms are less dependent on structural barriers and offer greater assurance in minimizing leakage risks and enhancing storage performance [5]. However, the accelerating climate crisis now points toward +2.5 °C trajectories [1], exposing the inadequacy of conventional carbon storage narratives. While GCS is deployed industrially, its ecological viability is constrained by leakage risks [6] and thermodynamic limits that cap potential impact at <5% of annual emissions [7]. This work therefore examines GCS trapping efficiency not as a climate solution but as a case study in the geological barriers facing techno-fix approaches, revealing fundamental physical constraints that challenge scalability.
While advanced reservoir simulators, initially developed for modeling petroleum storage, play a critical role in simulating GCS processes, substantial challenges tied to extensive data and computational requirements are posed. Also, numerical models that evaluate these mechanisms are both time-consuming and computation-costly [8,9,10], which highlight the imperative for robust algorithms capable of modeling subsurface CO2 repositories on a large scale. However, to minimize interpretation uncertainties, such simulations demand densely populated grids and extensive subsurface data—including geological, geophysical, and petrophysical details [11]—which are both costly and time-intensive to acquire. Additionally, high-resolution simulations necessitate elaborate numerical computations that spans from days to months. This computational burden renders it impractical to swiftly evaluate multiple storage sites or execute thorough sensitivity analyses, underscoring the necessity for more efficient methodologies to assess GCS feasibility and enhance storage performance.
Various machine learning models, such as ensemble learning techniques (including random forest and gradient boosting), have proven effective in improving model robustness and reducing variance [12,13]. These methods integrate multiple weak learners to enhance model generalization and have been extensively applied in assessing GCS and demonstrated generalization [14,15,16,17,18], while deep learning (DL) models, which are particularly advantageous for processing large-scale complex datasets and can mitigate the overfitting risks associated with traditional machine learning techniques, have been successfully utilized in investigating CO2 sequestration recently [19,20,21,22]. In particular, deep neural networks (DNNs), gated recurrent units (GRUs), and recurrent neural networks (RNNs) outperform in capturing nonlinear temporal dependencies from sequential data. DNNs are adept at modeling complex, nonlinear relationships in high-dimensional datasets, making them particularly effective for CO2 sequestration analysis. Their multi-layer architecture enables the extraction of intricate features, allowing for improved pattern recognition in heterogeneous reservoir conditions [23]. A GRU is highly effective in handling sequential data by efficiently managing long-term dependencies over extended sequences. Its ability to selectively retain and discard information makes it particularly suited for CO2 trapping predictions. RNN’s recurrent connections retain historical information, theoretically facilitating the capture of temporal dependencies in reservoir conditions, which is critical for tracking CO2 migration and trapping over time [24]. However, classical RNN architectures are prone to vanishing gradients, limiting their ability to effectively model long-term dynamics—particularly relevant for capturing extended residual trapping processes. These limitations, alongside broader gaps in prior work, highlight two key gaps: (1) no model has explicitly optimized for STI/RTI prediction, with most focusing on general storage capacity; (2) existing recurrent models lack gating mechanisms to balance short-term solubility and long-term residual trapping dynamics. Our DeepDropNet (with dropout regularization) and GateSeqNet (with GRU gating) address these by enhancing generalization in heterogeneous data and, in the case, of GateSeqNet, leveraging gating mechanisms to manage temporal dependencies across trapping mechanisms—overcoming the limitations of classical RNNs in tracking CO2 dynamics over time.
Thus, this study developed three advanced DL models to predict CO2 residual trapping index (RTI) and solubility trapping index (STI) in saline aquifers: the dropout-regularized DNN (hereafter referred to as DeepDropNet) serves as a baseline for capturing static nonlinear relationships in reservoir properties, critical for heterogeneous formations; the GRU-based sequential network (hereafter referred to as GateSeqNet) is included for its gating mechanisms, which address vanishing gradients in sequential data—essential for modeling temporal dynamics of solubility trapping; and the RNN with chained structure (hereafter referred to as RecurChainNet) is intentionally chosen despite its known limitations with long-term dependencies. By comparing it to GateSeqNet, we explicitly demonstrate how gating mechanisms improve performance in capturing residual trapping over extended periods, a key insight for CO2 storage applications.
By leveraging diverse reservoir characteristics derived from multiple real-field datasets, this study seeks to create reliable and efficient prediction models, as well as to provide valuable tools for rapid assessment of CO2 sequestration sites, ultimately contributing to global efforts to achieve net-zero emissions. While global climate targets continue to be missed, over 35 nations have now established carbon capture and storage as part of their legally binding Nationally Determined Contributions [25]. The bottleneck has shifted from policy commitment to implementation—particularly in verifying storage security at scale. This work directly addresses that gap by enabling rapid, low-cost assessment of trapping efficiency, a requirement for both national programs like Norway’s Longship project and corporate initiatives under mechanisms like the EU Emissions Trading System.
2. Dataset
Davoodi et al. [26,27] compiled 2000+ simulation records related to CO2 residual and solubility trapping, derived from synthetic models and actual field data. The dataset, according to sensitivity analysis, covers a wide range of influential reservoir variables from different synthetic models and actual fields worldwide—post injection (PI), porosity (), permeability (K), thickness (H), salinity (), depth (D), and injection rate (IR), as well as the RTI and STI, which are defined as follows:
For model training and evaluation, the dataset was split into training (80%) and testing (20%) sets using a fixed random seed to ensure reproducibility. All features and targets were normalized to a range of [0, 1] via min–max scaling. The training data was shuffled, while the test data remained unshuffled to maintain evaluation integrity. Table 1 lists those variables’ descriptive statistics, and their extensive ranges indicate a comprehensive representation of subsurface reservoir characteristics, as well as enhancing the utility of creating adaptable predictive DL models assessing CO2 residual and solubility trapping across diverse potential saline aquifers. Also, the dataset has no missing values for the included variables, facilitating running DL models straightforwardly without preprocessing.

Table 1.
Descriptive statistics for the key variables of CO2 reservoir sites. Units of each variable are shown in [].
3. Methods
Table 2 presents a comparative overview of the configured hyperparameters of the three models. These settings highlight various model architectures and training parameters, and the differences in layer complexity, dropout rates, and activation functions underscore the distinct approaches to learning representations and handling overfitting across these models. While these models are not state-of-the-art across all machine learning domains, they are structurally diverse and widely used in scientific and environmental modeling, providing a robust comparative baseline.

Table 2.
Tuned hyperparameters of the three models.
3.1. DeepDropNet
DeepDropNet comprises a class of artificial neural networks with multiple hidden layers between the input and output layers (Figure 1), within which each neuron implements nonlinear transformations, thereby allowing the network to capture underlying complex and nonlinear relationships within the input. The DeepDropNet employed in this predictive task was composed of linear fully connected layers, the ReLU (Rectified Linear Unit) activation, as well as the dropout that was employed as a regularization technique by selectively deactivating neurons to prevent overfitting and generated a random mask for each neuron in a given layer from a Bernoulli distribution:
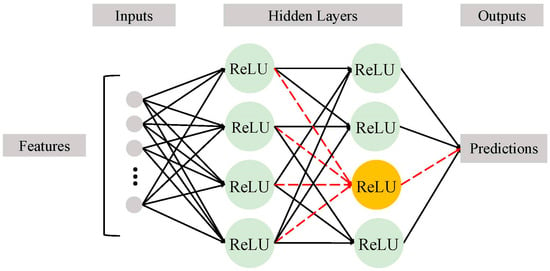
Figure 1.
Architecture of the DeepDropNet. The yellow circle highlights a dropout neuron, along with the red dashed lines.
Depending on the probability , the mask took a value of either 0 or 1 to determine whether a neuron was dropped or retained. Once the mask was applied, the output from layer was element-wise multiplied by the mask , resulting in the post-dropout output :
where outputs from dropped neurons were set to zero, while others were preserved.
Subsequently, a linear transformation was implemented on the masked output:
in which was adjusted by the weight matrix and the bias term . This formed a new linear combination for the next layer , which then underwent a nonlinear transformation by activation function to generate output :
Through these steps, dropout not only enhanced the network’s generalization but also strengthened each hidden unit’s robustness and reduced complex dependency among neurons.
3.2. GateSeqNet
As a variant of RNN, GateSeqNet is designed to address the typical vanishing gradient issue in traditional RNNs by introducing gating mechanisms (Figure 2) that regulate information flow within the unit and make GateSeqNet highly adept at capturing long-term dependencies. The primary components of a GateSeqNet are the update gate and the reset gate , which determine the degree to which both the previous hidden state and the current input should influence the current state , i.e., how much of the past information to be maintained or discarded:
where is the sigmoid activation function; is the weight matrix; is the candidate hidden state derived from the composite operation between and modulated through ; and is hyperbolic tangent function mapping variables to [−1, 1].

Figure 2.
Architecture of the GateSeqNet. and are element-wise operation of multiplication and addition, respectively.
3.3. RecurChainNet
RecurChainNet specializes in processing orderly sequential data due to its connections forming chain-like cycles (Figure 3), which enables RecurChainNet to maintain a memory of prior inputs and to make them particularly suited for tasks understanding context and temporal dynamics.
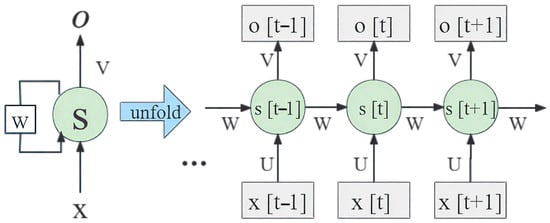
Figure 3.
Architecture of the RecurChainNet. The blue arrow demotes the unfolding operation that expands the recurrent connections through time to create a copied sequence of the network. Note that all replicas share the same weights and biases, ensuring consistent learning and memory utilization across the sequence.
RecurChainNet calculates the hidden state , as well as subsequent output , via activation function , weight matrices (, , and ), and bias terms ( and ) as follows:
of which is updated recursively at each time step by integrating current input with previous state , allowing them to capture dependencies that unfold over time. However, RecurChainNet is prone to issues like vanishing/exploding gradients, particularly evident when dealing with long sequences. These challenges can complicate training and affect the network’s ability to learn long-distance dependencies effectively.
3.4. Evaluation Metrics
Four statistical metrics—MSE (mean squared error), MAE (mean absolute error), determination coefficient (R2), and MAPE (mean absolute percentage error)—collectively offered a comprehensive assessment of the three models’ accuracy and reliability in forecasting outcomes:
among which and are the simulation and estimation of the target index (RTI or STI) from the th record, respectively; and denotes the index mean of all simulation records. These metrics ensured that model’s effectiveness in practical scenarios is thoroughly understood and quantified.
The four selected metrics are chosen for their complementary roles in evaluating regression performance for continuous targets (RTI and STI): MSE and MAE quantify absolute errors, with MSE emphasizing larger deviations to identify outliers critical for storage risk assessment. R2 directly indicates the proportion of variance explained, essential for assessing how well models capture complex relationships between reservoir properties and trapping indices. An R2 of 0.95 indicates that 95% of the variation in residual trapping across diverse reservoirs is explained by the model—near-complete alignment with simulated data. This high value signifies that the model can reliably distinguish between high-efficiency and low-efficiency storage scenarios, a critical capability for prioritizing sites with minimal leakage risk. Conversely, lower R2 values imply the model fails to capture 40% of real-world variability, introducing uncertainty in practical decision-making. MAPE enables scale-independent comparison via percentage errors, useful for interpreting results across diverse RTI/STI magnitudes.
Root-mean-square deviation (RMSD) is redundant as it is the square root of MSE. The chi-square (χ2) test, suited for categorical data, is inappropriate here due to the continuous nature of RTI/STI, which would lose precision if binned.
4. Results
4.1. Ablation Test
Figure 4 displays the evaluation metrics of predicting RTI and STI for the three neural networks as a function of hidden layers number. This ablation test offers insights about components’ contribution to model dynamics. For the DeepDropNet, RTI and STI predictions both show a significant variation in MAPE, indicating a sensitive adjustment in model performance responded to network depth. The R2 values are relatively stable, which demonstrates the consistent proportion of variance explained by the model. Notably, DeepDropNet exhibits stable MSE and MAE across varying hidden layer counts, particularly for STI predictions. This stability arises from its hierarchical feature learning and dropout regularization. The multilayer architecture captures both simple linear relationships (e.g., salinity-STI correlations) and complex nonlinear interactions (e.g., synergies between permeability and injection rate) through progressive feature abstraction. Meanwhile, the 0.3 dropout rate mitigates overfitting to noisy or idiosyncratic patterns, ensuring robust generalization even as network complexity increases. Together, these mechanisms enable DeepDropNet to maintain relative error consistency across diverse input complexities.

Figure 4.
Performance metrics variation of predicting RTI (top) and STI (bottom) from the DeepDropNet (DDN, left), RecurChainNet (RCN, middle), and GateSeqNet (GSN, right), with respect to the number of hidden layers.
The GateSeqNet panels reveal a decrease in R2 as the hidden layers number increases, particularly notable in the RTI predictions. This reduction with additional layers highlights potential architectural mismatch where the model’s increased complexity is not justified by the data’s structure, leading to poorer generalization on unseen data. This trend also suggests diminishing returns on additional complexity, i.e., beyond a certain point, more layers do not contribute to—or may even reduce—the model’s effectiveness in capturing predictive relationships. Noteworthily, both MSE and MAE see a slight rise while the MAPE has a pronounced one, especially in terms of predicting RTI, which denotes challenges in model scaling and efficiency when handling more complex architectures.
In the RecurChainNet configurations, the noticeable increase (decrease) in MAPE (R2) implies potential challenges with training stability, possibly because of the RecurChainNet’s vulnerability to issues like vanishing gradients. This inconsistency could highlight the model’s limitations in capturing more complex dependencies inherent in the data over longer sequences.
4.2. Model Performance
A comparative analysis of the loss value evolution across training epochs of the three networks (Figure 5) exhibits distinct behaviors when predicting RTI. The RecurChainNet shows a significant spike in loss at an early stage, which could indicate a sensitivity to initial conditions and/or instability in gradient updates tied to a high learning rate [28]. After this spike, the loss gradually stabilizes but remains higher compared to the other models, suggesting that the RecurChainNet may struggle with capturing the complexity of the RTI dataset or may require further tuning of hyperparameters. The GateSeqNet and DeepDropNet, in contrast, display a more consistent and smooth decline in loss. The GateSeqNet, in particular, shows the lowest loss among the three models, which may be attributed to better management of the vanishing gradient problem typically affecting RecurChainNet. A similar trend is observed when focusing on STI. The RecurChainNet again exhibits more volatile loss values throughout the training process, reinforcing the challenges it faces with this type of data. Both the GateSeqNet and DeepDropNet show significantly lower losses, with the GateSeqNet marginally outperforming the DeepDropNet.
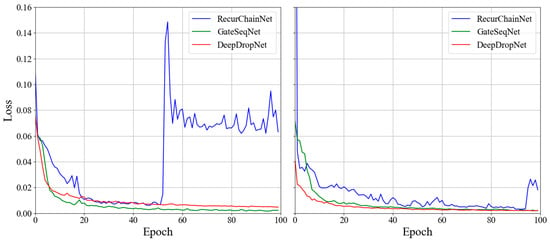
Figure 5.
Loss values evolution of RTI (left) and STI (right) across training epochs for the three neural networks: DeepDropNet (DDN), GateSeqNet (GSN), and RecurChainNet (RCN).
The computational efficiency, measuring inference time per sample (averaged over 1000 runs on a GeForce RTX 4070 GPU) and training duration is also evaluated: GateSeqNet showed 0.8 ms/sample with 4 min of training, DeepDropNet achieved 0.5 ms/sample with 3 min of training, and RecurChainNet had 1.2 ms/sample with 5 min of training. DeepDropNet exhibited the fastest inference, while GateSeqNet balanced accuracy and efficiency—both making them suitable for real-time applications—whereas RecurChainNet’s higher latency, combined with lower accuracy, reinforces its limited practical value for large-scale assessments.
Figure 6 and Figure 7 depict the estimation versus simulation for RTI and STI, as well as multiple evaluation metrics under optimal parameter settings. DeepDropNet exhibits a tight clustering of data points around the 1:1 line for both RTI and STI, signifying a high level of precision in capturing complex data relationships. Meanwhile, GateSeqNet also aligns closely with the ideal prediction, especially for STI predictions, underscoring its robustness in handling sequences. In contrast, RecurChainNet displays more scatter from the red line, especially in RTI predictions, reflecting the model’s challenges with learning long-term dependencies. On the other hand, both DeepDropNet and GateSeqNet achieved lower MSE (<0.2) and MAE (<0.4) but higher R2 values (>0.9). Conversely, RecurChainNet showed higher MSE (>0.6) and MAE (>0.6) in handling RTI sequences. Notably, higher MAPE (>0.8) occurred when predicting STI via DeepDropNet, which could reflect the model’s potential compounding errors in prediction across different scales of data.
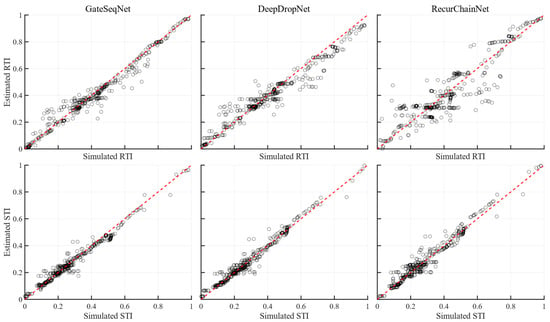
Figure 6.
Scatter plots of estimation versus simulation of RTI (top) and STI (bottom) from the three neural networks: GateSeqNet (left column), DeepDropNet (middle column), RecurChainNet (right column). The red dashed line indicates perfect alignment.

Figure 7.
Performance metrics of predicting RTI (left) and STI (right) of the three neural networks under optimal parameters.
Notably, the performance metrics are presented as point estimates derived from the test set, without error bars. This is standard for aggregated regression results in model comparisons, but it is worth noting that they represent mean values across all test samples, and individual predictions may exhibit variability. Future work could incorporate bootstrapped confidence intervals to quantify uncertainty in model performance.
4.3. Input Correlation and Sensitivity
The correlation coefficient bar chart (Figure 8) compares the strength and direction of relationships between input variables and the prediction targets (RTI and STI). The observed magnitudes differences reveal the various importance of input variables depending on the temporal scale of target prediction [29]. Specifically, certain variables (PI, , and K) that fluctuate rapidly exhibit strong positive correlations with STI while showing weaker or negative correlations with RTI. For instance, the marginal negative correlation between IR and RTI has a coefficient magnitude <0.1, indicating statistical negligibility. This pattern likely arises from two factors: (1) higher injection rates may reduce residual trapping efficiency by increasing fluid velocity, limiting CO2 immobilization in pore spaces; (2) confounding with PI duration, where short PI combined with high IR suppresses residual trapping. This aligns with the broader trend of variable-specific impacts on RTI vs. STI and reinforces the need to consider combined variable effects, as highlighted in the sensitivity analysis (Figure 9).

Figure 8.
Correlation coefficients of input variables with respect to RTI and STI.
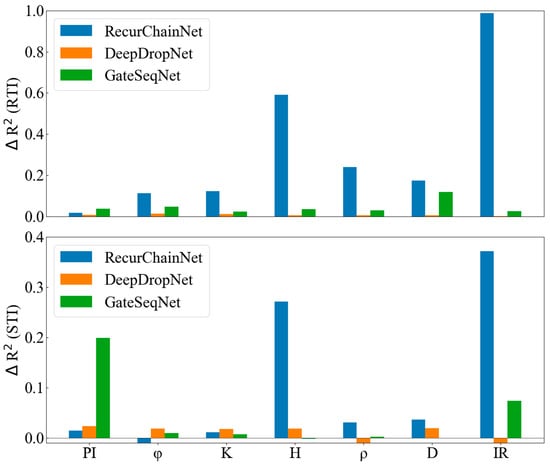
Figure 9.
Impact of excluding one input variable on determination coefficient for the three neural networks predicting RTI (top) and STI (bottom). ΔR2 was calculated as the coefficient under optimal settings minus that after eliminating one input variable.
Figure 9 assesses each variable’s contribution to the overall predictive power of the models. For interpretability, significance thresholds based on industry standards for regression models in geological studies [24] are defined as follows:
- ■
- Large impact: ΔR2 > 0.1 (notable performance decline when the variable is excluded, indicating critical importance).
- ■
- Moderate impact: 0.05 < ΔR2 ≤ 0.1 (substantial but manageable decline).
- ■
- Negligible impact: ΔR2 ≤ 0.05 (minimal change, suggesting the variable is non-critical or redundant).
For RTI predictions, the RecurChainNet shows the most sensitivity to the removal of individual input variables, as indicated by the significant ΔR2 values (exceeding the large impact threshold) across multiple variables (H, IR, etc.). This sensitivity aligns with RecurChainNet’s vulnerability to vanishing gradients and reliance on sequential dependencies, which can make the model particularly susceptible to changes in input data structure. The large shifts in ΔR2 also demonstrate that certain inputs play a critical role in guiding the model through its prediction of RTI, underscoring the need for careful variable selection to maintain model robustness. In contrast, GateSeqNet and DeepDropNet exhibit relatively stable performance with smaller ΔR2 values (mostly within the negligible or moderate impact ranges).
For STI predictions, the general pattern persists—RecurChainNet remains highly sensitive to variable exclusion (with ΔR2 values often exceeding 0.1), while GateSeqNet and DeepDropNet demonstrate greater resilience. For GateSeqNet, the notable shifts in ΔR2 (surpassing the large impact threshold) denote worse prediction after excluding PI and IR, suggesting that PI and IR are integral for its pattern learning capabilities and maintaining robustness. In contrast, both RecurChainNet and DeepDropNet display negative ΔR2 values, indicating improved performance when and IR that might introduce noise or redundancy were excluded, respectively.
5. Discussion
The GateSeqNet consistently demonstrated superior performance across both indices, achieving the lowest loss values and highest R2 scores. This strength is attributed to its advanced gating mechanisms that efficiently manage information flow and mitigate common issues like vanishing gradients, ensuring reliable outputs even when certain variables are excluded. These mechanisms allow GateSeqNet to retain important information over longer sequences without being overwhelmed by less relevant data, making it particularly adept at capturing long-term dependencies in the data [30]. The consistency in performance across both indices implies that GateSeqNet is well-suited for tasks requiring the modeling of complex dependencies and retaining information over extended sequences, which is crucial for accurately predicting trapping indices in geological reservoirs. These findings intersect critically with ecological economics frameworks: the 0.93 R2 accuracy of GateSeqNet predictions reveals not technical triumph, but rather the deterministic physical limits of solubility trapping under real-world reservoir conditions. When contextualized with latest climate models [31] and GCS lifecycle analyses [7], the results suggest GCS can only marginally alter—not prevent—catastrophic warming trajectories. This aligns with emerging paradigms that prioritize demand reduction over storage fantasies [2].
The DeepDropNet maintained a steady decrease in loss, reflecting its capability in learning hierarchical representations of data through layered architecture [32,33]. Its proficiency in capturing complex data patterns stems from inherent depth, which allows for effective modeling of nonlinear interactions [34] and less reliant on individual features to reduce the impact of excluding one variable [35]. However, its simpler structure relative to recurrent models like GateSeqNet suggests that it may benefit from further optimization to reach the same level of efficiency in tasks requiring intricate sequential data handling.
In contrast, the RecurChainNet showed notable limitations, particularly in handling longer sequences and maintaining stability over numerous epochs of training. Its inaccuracy in predicting RTI and STI, as evidenced by higher MSE and MAE values, emphasizes its inadequacies in modeling dependencies within the data. This aligns with the known challenges of RecurChainNet, such as vanishing gradients and difficulties in processing long sequences, which complicate training and reduce its effectiveness in capturing long-term dependencies.
The disparity in model performance highlights the importance of temporal modeling capabilities, particularly for handling short-term indices like STI. The contrasting relationships between input variables and RTI/STI, as revealed by the sensitivity analysis, suggest that certain features (e.g., porosity and permeability) significantly affecting short-term solubility trapping compared to long-term residual trapping. This underscores the need for a differentiated approach to feature engineering and variable selection, depending on the specific task and the temporal scale of the target prediction.
The urgency of these computational tools becomes clear when examining real-world constraints: current storage site assessments require 1–3 years and cost tens of millions of dollars per project [36]. Our models could reduce this to weeks while maintaining accuracy—a critical step for nations struggling to meet their Paris Agreement commitments through practical and sustainable carbon management. While political will remains imperfect, the technical capacity to validate storage security at climate-relevant scales no longer needs to be a limiting factor. From an ecological perspective, our models contribute to climate change mitigation by enabling rapid and accurate assessment of CO2 storage sites, a prerequisite for scaling up GCS to meet global emissions reduction targets. These models hold direct relevance for operational GCS projects: At In Salah (Algeria), where residual trapping in sandstone aquifers is critical for long-term storage security, GateSeqNet could optimize injection rates to enhance RTI, reducing leakage risks in heterogeneous formations. For Gorgon (Australia), a high-salinity reservoir, the models’ ability to predict STI under various salinity could inform solubility trapping strategies, supporting the project’s 10 Mt CO2/year storage target. In Porthos (the Netherlands), rapid assessment of trapping efficiency via DeepDropNet could streamline site characterization, aiding the project’s goal of storing 3.6 Mt CO2/year by 2026. By enabling cost-effective, real-time evaluation of trapping dynamics, these tools address key challenges in scaling such projects—from reservoir heterogeneity to regulatory compliance.
By reducing the time and cost of site assessments, our deep learning tools also address a key barrier to GCS deployment, supporting ecosystem preservation through stabilized climate conditions [3]. For instance, effective GCS can mitigate the ecological damage caused by rising CO2 levels, such as coral reef degradation and forest dieback, which are exacerbated by warming beyond 1.5 °C [1]. While GCS alone cannot fully address climate change, its role in reducing atmospheric CO2 complements other strategies, such as renewable energy adoption and reforestation, to protect biodiversity and ecosystem services. Moreover, our data underscores the models’ potential to accelerate sustainable development goals (SDG): GateSeqNet’s ability to optimize residual trapping aligns with SDG 13 by enhancing long-term storage security. Similarly, DeepDropNet’s efficiency in heterogeneous reservoirs supports SDG 9 by enabling cost-effective GCS infrastructure in diverse geological settings.
6. Conclusions
This study demonstrates the effectiveness of three deep learning models—DeepDropNet, GateSeqNet, and RecurChainNet—in predicting CO2 residual and solubility trapping indices in geological reservoirs. The GateSeqNet consistently outperformed others, particularly in managing long-term dependencies and maintaining stability through its gating mechanisms, which allowed for superior performance in both RTI and STI predictions. DeepDropNet was effective but less robust for sequential tasks, while RecurChainNet struggled with long sequences and data complexity due to vanishing gradients and input sensitivity.
Ablation and sensitivity analyses highlighted critical inputs like PI and IR: GateSeqNet’s STI predictions suffered when these were excluded, while RecurChainNet/DeepDropNet improved with certain input removals (indicating data redundancy/noise), emphasizing targeted feature selection. Ultimately, the study advances deep learning for GCS by offering efficient tools to assess sequestration potential, supporting climate change mitigation through scalable and sustainable carbon storage solutions.
While the results are promising, there are some limitations to this study. The dataset, while comprehensive, is simulation-derived and may not fully reflect real reservoir complexities. Mineral trapping—long-term and geochemically complex—is excluded due to insufficient consistent, public modeling data. Another important limitation is the black-box nature of the proposed models, which obscures the specific reservoir properties or mechanisms driving predictions. While DeepDropNet and GateSeqNet achieve high accuracy, they do not explicitly reveal how variables like porosity or injection rate influence RTI/STI.
Future work will validate models with field data from real GCS sites, use ensemble learning (e.g., boosting/stacking) to boost accuracy/robustness, and optimize models—especially RecurChainNet—to better handle long sequences and complex data. By integrating interpretable DL tools (e.g., SHAP) to quantify feature importance at the pixel and global scales, as well as physics-based constraints (e.g., Darcy’s law for fluid flow) into the loss function of deep learning models, could also enhance their predictive accuracy and interpretability, which will improve trust in model outputs for regulatory and operational decision-making in environmental applications.
Author Contributions
Y.C.: conceptualization, methodology, data curation, investigation, formal analysis, writing—review and editing, supervision, resources, funding acquisition. Z.L.: software, investigation, formal analysis, visualization, writing—original draft. M.C.: resources. J.L.: validation. Y.S.: resources, writing—review and editing, supervision, funding acquisition. All authors have read and agreed to the published version of the manuscript.
Funding
This research was jointly supported by the National Natural Science Foundation of China (No. 42301428), the Open Fund of State Key Laboratory of Remote Sensing and Digital Earth (No. OFSLRSS202306), the National Science Fund for Excellent Young Scholars (No. 62322514), the Anhui Science Fund for Distinguished Young Scholars (No. 2308085J25), and the National Key Research and Development Program of China (No. 2023YFC3709502).
Data Availability Statement
Data are contained within the article.
Acknowledgments
The authors appreciate four reviewers’ valuable comments which improved the paper’s quality.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- IPCC. Climate Change 2023 Synthesis Report; IPCC: Geneva, Switzerland, 2023. [Google Scholar] [CrossRef]
- Rockström, J.; Gupta, J.; Qin, D.; Lade, S.J.; Abrams, J.F.; Andersen, L.S.; Armstrong McKay, D.I.; Bai, X.; Bala, G.; Bunn, S.E.; et al. Safe and Just Earth System Boundaries. Nature 2023, 619, 102–111. [Google Scholar] [CrossRef]
- Nocito, F.; Dibenedetto, A. Atmospheric CO2 Mitigation Technologies: Carbon Capture Utilization and Storage. Curr. Opin. Green Sustain. Chem. 2020, 21, 34–43. [Google Scholar] [CrossRef]
- Khudaida, K.J.; Das, D.B. A Numerical Analysis of the Effects of Supercritical CO2 Injection on CO2 Storage Capacities of Geological Formations. Clean Technol. 2020, 2, 333–364. [Google Scholar] [CrossRef]
- Bradshaw, J.; Bachu, S.; Bonijoly, D.; Burruss, R.; Holloway, S.; Christensen, N.P.; Mathiassen, O.M. CO2 Storage Capacity Estimation: Issues and Development of Standards. Int. J. Greenh. Gas Control 2007, 1, 62–68. [Google Scholar] [CrossRef]
- Amano, C.; Zhao, Z.; Sintes, E.; Reinthaler, T.; Stefanschitz, J.; Kisadur, M.; Utsumi, M.; Herndl, G.J. Limited Carbon Cycling Due to High-Pressure Effects on the Deep-Sea Microbiome. Nat. Geosci. 2022, 15, 1041–1047. [Google Scholar] [CrossRef] [PubMed]
- Anderson, K.; Peters, G. The Trouble with Negative Emissions. Science 2016, 354, 182–183. [Google Scholar] [CrossRef]
- Akai, T.; Alhammadi, A.M.; Blunt, M.J.; Bijeljic, B. Modeling Oil Recovery in Mixed-Wet Rocks: Pore-Scale Comparison Between Experiment and Simulation. Transp. Porous Med. 2019, 127, 393–414. [Google Scholar] [CrossRef]
- Chen, B.; Pawar, R.J. Characterization of CO2 Storage and Enhanced Oil Recovery in Residual Oil Zones. Energy 2019, 183, 291–304. [Google Scholar] [CrossRef]
- Vo Thanh, H.; Sugai, Y.; Sasaki, K. Impact of a New Geological Modelling Method on the Enhancement of the CO2 Storage Assessment of E Sequence of Nam Vang Field, Offshore Vietnam. Energy Sources Part A Recovery Util. Environ. Eff. 2020, 42, 1499–1512. [Google Scholar] [CrossRef]
- Hou, G.; Naguib, H.M.; Chen, S.; Yao, H.; Lu, B.; Chen, J. Mechanisms and Optimal Reaction Parameters of Accelerated Carbonization of Calcium Silicate. J. Chin. Ceram. Soc. 2019, 47, 1175–1180. [Google Scholar]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Baghban, A.; Bahadori, A.; Mohammadi, A.H.; Behbahaninia, A. Prediction of CO2 Loading Capacities of Aqueous Solutions of Absorbents Using Different Computational Schemes. Int. J. Greenh. Gas Control 2017, 57, 143–161. [Google Scholar] [CrossRef]
- Jeon, P.R.; Lee, C.-H. Artificial Neural Network Modelling for Solubility of Carbon Dioxide in Various Aqueous Solutions from Pure Water to Brine. J. CO2 Util. 2021, 47, 101500. [Google Scholar] [CrossRef]
- Jeong, H.; Sun, A.Y.; Lee, J.; Min, B. A Learning-Based Data-Driven Forecast Approach for Predicting Future Reservoir Performance. Adv. Water Resour. 2018, 118, 95–109. [Google Scholar] [CrossRef]
- Vo Thanh, H.; Sugai, Y.; Nguele, R.; Sasaki, K. Integrated Workflow in 3D Geological Model Construction for Evaluation of CO2 Storage Capacity of a Fractured Basement Reservoir in Cuu Long Basin, Vietnam. Int. J. Greenh. Gas Control 2019, 90, 102826. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, H.; Chang, H.; Pan, Z.; Luo, X. Machine Learning Predictive Framework for CO2 Thermodynamic Properties in Solution. J. CO2 Util. 2018, 26, 152–159. [Google Scholar] [CrossRef]
- Khanal, A.; Shahriar, M.F. Physics-Based Proxy Modeling of CO2 Sequestration in Deep Saline Aquifers. Energies 2022, 15, 4350. [Google Scholar] [CrossRef]
- Kim, J.; Song, Y.; Shinn, Y.; Kwon, Y.; Jung, W.; Sung, W. A Study of CO2 Storage Integrity with Rate Allocation in Multi-Layered Aquifer. Geosci. J. 2019, 23, 823–832. [Google Scholar] [CrossRef]
- Song, Y.; Sung, W.; Jang, Y.; Jung, W. Application of an Artificial Neural Network in Predicting the Effectiveness of Trapping Mechanisms on CO2 Sequestration in Saline Aquifers. Int. J. Greenh. Gas Control 2020, 98, 103042. [Google Scholar] [CrossRef]
- Zhong, Z.; Sun, A.Y.; Yang, Q.; Ouyang, Q. A Deep Learning Approach to Anomaly Detection in Geological Carbon Sequestration Sites Using Pressure Measurements. J. Hydrol. 2019, 573, 885–894. [Google Scholar] [CrossRef]
- Tang, M.; Ju, X.; Durlofsky, L.J. Deep-Learning-Based Coupled Flow-Geomechanics Surrogate Model for CO2 Sequestration. Int. J. Greenh. Gas Control 2022, 118, 103692. [Google Scholar] [CrossRef]
- Vo-Thanh, H.; Amar, M.N.; Lee, K.-K. Robust Machine Learning Models of Carbon Dioxide Trapping Indexes at Geological Storage Sites. Fuel 2022, 316, 123391. [Google Scholar] [CrossRef]
- Canle, C. Global Status of CCS 2023; Global CCS Institute: Melbourne, Australia, 2023. [Google Scholar]
- Davoodi, S.; Thanh, H.V.; Wood, D.A.; Mehrad, M.; Rukavishnikov, V.S.; Dai, Z. Machine-Learning Predictions of Solubility and Residual Trapping Indexes of Carbon Dioxide from Global Geological Storage Sites. Expert Syst. Appl. 2023, 222, 119796. [Google Scholar] [CrossRef]
- Davoodi, S.; Thanh, H.V.; Wood, D.A.; Mehrad, M.; Rukavishnikov, V.S. Combined Machine-Learning and Optimization Models for Predicting Carbon Dioxide Trapping Indexes in Deep Geological Formations. Appl. Soft Comput. 2023, 143, 110408. [Google Scholar] [CrossRef]
- Pascanu, R.; Mikolov, T.; Bengio, Y. On the Difficulty of Training Recurrent Neural Networks. In Proceedings of the 30th International Conference on Machine Learning, Atlanta, GA, USA, 17–19 June 2013; pp. 1310–1318. [Google Scholar]
- Leung, K.K.; Rooke, C.; Smith, J.; Zuberi, S.; Volkovs, M. Temporal Dependencies in Feature Importance for Time Series Predictions. arXiv 2021, arXiv:2107.14317. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical Evaluation of Gated Recurrent Neural Networks on Sequence Modeling. arXiv 2014, arXiv:1412.3555. [Google Scholar] [CrossRef]
- Iyer, G.; Ou, Y.; Edmonds, J.; Fawcett, A.A.; Hultman, N.; McFarland, J.; Fuhrman, J.; Waldhoff, S.; McJeon, H. Ratcheting of Climate Pledges Needed to Limit Peak Global Warming. Nat. Clim. Change 2022, 12, 1129–1135. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; ISBN 978-0-262-03561-3. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition; The Computer Vision Foundation: New York, NY, USA, 2016; pp. 770–778. [Google Scholar]
- LeCun, Y.; Bengio, Y.; Hinton, G. Deep Learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef]
- Li, W.; Law, K.L.E. Deep Learning Models for Time Series Forecasting: A Review. IEEE Access 2024, 12, 92306–92327. [Google Scholar] [CrossRef]
- International Energy Agency Carbon Capture. Utilisation and Storage: The Opportunity in Southeast Asia; OECD Publishing: Paris, France, 2021; ISBN 92-64-96016-3. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).