Abstract
Efficiently quantifying stand density is crucial in sustainably managing mid-rotation loblolly pine (Pinus taeda L.) plantations. While various stand density measures, including basal area (BA), stand density index (SDI), relative spacing (RS), and live crown length ratio (CR), are used, ambiguity persists among these measures: are they each biologically sound and are they on par with each other in terms of density management? These topics were investigated by examining the relationships between measures and stand age, between measures and tree growth, and between measures using data from numerous long-term permanent plots established in loblolly pine plantations in east Texas. A strong trend of increasing density with age was found for all the measures. The trend followed an asymptotic trajectory when density was expressed as BA, SDI, or RS, adhering to biological expectations, but the trend showed a gradual decrease for CR. Strong and biologically sound relationships between DBH periodic annual increment () and BA or SDI were observed, suggesting that both measures match true DBH growth. However, linearly decreased with decreasing RS and with decreasing CR in a smooth curve, biasing from the biological expectation. Strong relationships existed between the measures, suggesting that these seemingly disparate measures are not independent of each other. Site index affected all investigated relationships in a manner of having higher densities at a given age or a greater at a given density for higher site index sites regardless of measures. The effects of initial planting density on the relationships were mostly negligible, having no practical significance, with few exceptions (the relationships of SDI–age, RS–age, and CR–RS). Among the measures evaluated, our results advocate for the use of to regulate mid-rotation loblolly pine plantation density such as determining the approximate biological timing for thinning in the Western Gulf region due to its biological soundness, ease of measurement, and feasibility of incorporating effects of site quality and planting density.
1. Introduction
Loblolly Pine (Pinus taeda L.) is the most important commercial species in the southern United States (US) including the Western Gulf region (WG). To maximize the plantation productivity of the species and economic return, regulating mid-rotation stand density is a routine practice. Stand density can be defined as “the degree of crowding within the stocked areas, using various spacing ratios based on crown length or diameter, tree height or diameter, and spacing” [1]. Given the broad definition, various density measures have been developed, with some focusing on tree growth status and others on site occupancy [2].
The most common density measures involve combining stand average tree size and the number of trees per unit area, such as basal area per hectare () and stand density index (SDI). Both measures have been incorporated into loblolly pine density-management diagrams [3,4,5]. Another density measure used is relative spacing (RS), which relates average intertree spacing to the average height of dominant trees, thus incorporating the number of trees and the site quality [6,7]. Crown length ratio (CR, the ratio of crown length to total tree height), an indicator of tree crown status and vigor, has also been used to quantify stand density indirectly for forest management [8]. With numerous measures being available, selecting the suitable one(s) for a specific management objective, such as determining “when to thin”, is a conundrum. Do these measures/criteria lead to similar judgments in density for a given stand? Are there any measures that outperform others? The topic is complex in that the degree of crowding and site utilization of a stand are dynamic in nature.
An ideal density measure should closely link stand density with stand development (i.e., stand age and tree growth) [9]. While the temporal trends of , SDI, RS, and CR with stand aging have been reported for loblolly pine in the southeastern (SE) United States (US) [7], such information is lacking for the WG populations. Basic principles of density–growth relationships were outlined for loblolly pine [10] and further empirically explored [11,12]. These studies similarly targeted the SE populations as well as focusing on volume growth and yield at the stand level. Loblolly pine log price varies greatly with log size, and, thus, producing larger diameter trees often is a priority. Therefore, knowing the relationship between density and growth at the tree level [1], which often conflicts with the relationships at the stand level, is important; this information, however, remains lacking in the existing literature. Overall, our knowledge of the efficiency of using the measures to describe stand density remains incomplete for loblolly pine, especially at the tree level and for the WG populations.
Relationships and consistencies between the measures provide additional valuable information to guide pine plantation density management. While the , SDI and RS of a stand relate to each other mathematically since they all account for the number of trees and tree growth, their biological explanations are not the same, e.g., and RS, respectively, focus on the relationships of the number of trees with tree DBH and height, while SDI is based on the rule of self-thinning. Thus, the relationships between these measures can be complex and should be examined using suitable data, which, however, has rarely been done. Between and SDI, while a double logarithm linear trend is expected theoretically [13], empirical data differently supported a linear relationship [14]. A strong, non-linear relationship between and RS was also reported [11]. Even though CR data cannot be transformed to other measures easily, CR was found to have a strong nonlinear relationship with RS [8]. Often, stand density is used to plan commercial thinning for pine plantations, e.g., to determine biological thin time. Currently, in the WG, when a loblolly pine stand approaches 25 m2 , 500 (45% of the maximum) SDI [3], 0.20 to 0.25 RS, or 35% CR, it is the biological time to thin. Do these measures lead to a similar time to thin for a given stand? The results from the few published studies on this topic are varied, with some studies supporting consistencies [8,12,15] but others finding inconsistencies between the measures [14]. Operationally, foresters may employ simple criteria such as using a combination of stand age and market criteria that thin loblolly pine stands around the age of 15 years since by that age virtually all trees have reached a merchantable size (e.g., 15 cm in DBH and 12 m in height). Given the wide use of these measures in pine density management, in particular, in determining thin time, understanding the relationships between measures and their relevance to the operational criteria would greatly help foresters in understanding stand development post-thinning.
The most important determinants influencing plantation productivity and density are site quality and initial planting density [2]. If the previously discussed relationships are predictable, are they affected by factors such as initial planting density and site quality? Some authors have recommended measures such as SDI since it is believed to be independent of factors such as stand age and site quality [3]. Even so, between two sites with the same number of trees, the higher quality sites (larger DBH) are expected to have larger SDI (see equation below). Others support the notion that the density of a stand partly depends on site quality and initial planting density [7,12]. Thus, it is essential that the measures used to quantify density are accurate and meaningful in describing the effects of site quality and planting density.
Analyses of density-related relationships can be conducted using data collected either from comparative thinning experiments or from long-term permanent plots [16]. For the latter, the relationships are strictly considered valid only when the permanent plots are undisturbed. For loblolly pine, with a tradition of repeated thinning, undisturbed, long-term plots are rare. The East Texas Pine Plantation Research Project (ETPPRP) installed numerous plots in loblolly pine plantations. These plots have not been intervened with since plot installation and were repeatedly measured on a 3-year cycle, thus providing a unique dataset for investigating the relationships. The objective was to evaluate the efficacy of common stand density measures (, SDI, RS, and CR) in describing loblolly pine stand density. This was accomplished by examining their relationships with stand age and tree growth and their interrelationships by using the long-term ETPPRP data. Our findings addressed two key research questions: (1) whether various measures align in identifying stand density development, and (2) do certain measures demonstrate superior performance in guiding key management activities? Given the wide use of these measures in determining biological thin time, a third question of whether the biological thin times by these measures match each other and agree with the operational thin time was also investigated. Our study offers significant insights for guiding one of the pivotal silvicultural practices—mid-rotation density management—in loblolly pine plantations.
2. Data and Methods
Between 1982 and 1984, the ETPPRP installed 185 plots (30.48 m × 30.48 m per plot or approximately 0.1 ha) in extensively managed loblolly pine plantations across east Texas [17]. To best represent the growing conditions unique to the region, all plots were in 22 contiguous counties across East Texas, generally between 30 and 35° north latitude and 93 and 95° west longitude. Surrounding each plot, two-row trees were kept as buffer trees. Plots (including the buffer rows) were shielded from routine plantation operations, ensuring no silvicultural interventions were conducted post-installation.
Trees were tagged and measured at plot installation and re-measured on a 3-year interval. DBH, total height (H), and stem height to live crown (bole height; nearest 1.0 ft) were measured and tree crown class (e.g., dominant, codominant, and others), insect and disease infection, and tree defect were recorded. Tree DBH was measured to the nearest 0.1 inches using a caliper, tree H and bole height were measured to the nearest 1.0 feet using a height pool or clinometer, and tree crown class was visually estimated. Tree CR was calculated as the ratio of crown length to H. Plantation age was determined as the time between the measurement date and the plantation establishment date derived from stand records. Original values in imperial English units were converted to metric values prior to analysis. Growth modeling typically requires at least three repeated measures (cycles) per plot, thus plots that were measured for only 1 or 2 cycles (in total 14 plots) were excluded. Data were cleaned and outliers were removed to remove potential measurement errors. After cleaning, the data from 171 plots (123,913 observations) were used. At plot establishment, plantations averaged 10 years old, with the youngest being 2 years old. The initial planting trees averaged 1749 trees ha−1, ranging from 897 to 3367 trees ha−1. At a base age of 25 years, the site index (SI) ranged from 9 to 28 m, which was calculated following Coble and Lee [18]. Most plots were measured for about 8 cycles, with the longest ones being measured for 12 cycles (10 plots). For the last measurement, the plots averaged 26 years old, ranging from 12 to 45 years. Table 1 lists detailed summary statistics.

Table 1.
Summary statistics of the ETPPRP plot data.
The average height of dominant/codominant trees (HD), tree DBH, and CR were calculated by plot and cycle. The number of trees and basal area were summarized by plot and cycle (referred to as and , respectively), which then were used to calculate quadratic mean diameter () as:
and were further expanded to a per hectare basis (in trees per ha and in m2 per ha). SDI (in trees per ha) [2] and RS were calculated as follows:
The periodic (3 year) annual increment of DBH (in cm ) was calculated as:
where and were plot average DBH at the beginning and end of the 3 year cycle.
Relationships of density–age, density–, and between-density measures were, respectively, modeled. For each relationship, multiple models, i.e., linear and nonlinear functions including Chapman–Richards, power, logistic, Weibull, exponential, expolinear, Farazdaghi [19,20,21], and others [8,11,12] were fitted and the best fit based on the coefficient of determination (R2) and the root mean square error (RMSE) was selected. R2 and RMSE were calculated as follows:
where and are the error sum of squares and the total sum of squares, respectively. and are the ith observed and predicted values, respectively, and n is the total number of observations. To facilitate comparison, RMSE was also expressed as a percentage of its overall average. Note that “bi” is used to refer to model parameters (See Table 2). The use of the same “bi” in models throughout the paper does not represent the mathematical equivalence unless clearly specified. For example, while b0 and b1 are used in different equations, they do not imply the same biological interpretation.

Table 2.
Selected models, model parameter estimates (standard errors), effects of high-quality sites or densely planted sites on model parameters, and the model performance.
Effects of initial planting density, expressed as the number of trees planted per hectare (IPT; obtained from the established reports), and site quality, expressed as SI, were incorporated into the selected model. For simplicity, IPT was classified into two groups and expressed using a dummy variable, M:
The threshold value of 1500 trees/ha was selected since loblolly pine plantations have been established using a density of 1500 trees or less in the past 20 years. The abbreviations “D” and “N” were used to distinguish sites initially planted at a high density and a normal density, respectively. SI was simply added to the model as a covariate.
Our modeling involved a few steps: a model including all fixed factors (full model) was developed, followed by selecting reasonable random covariance structures (e.g., plot to plot variation, data correlation to account for data relatedness, and weights to account for heterogeneity) under the full model, and removing insignificant fixed factors. Taking a power function (RS = b0 × ) which was selected to model the RS– relationship as an example (Table 2). b0 and b1 are model parameters, with b0 being a scaling factor and b1 representing the percentage change in RS resulting from a 1% increase in . IPT and SI were incorporated into the model via, respectively, expressing b0 and b1 as follows:
where b00 and b10 are the fixed-effect parameters for the reference sites of N and SI = 0 m, b02 and b12 are the differences of the D sites with the N sites, and b01 and b11 represent the changes in b00 and b10 with increasing SI. Under the full model, we found that a random plot-to-plot variation in b0 and a power variance function structure were suitable based on log-likelihood tests. Supplementary Table S1 provides details for the selected random structures by model. After selecting the random structures, the significance of b01, b11, b02, and b12 (hypothesis: estimate differs significantly from zero) was tested using the partial F-test at an = 0.05, unless otherwise specified. The insignificant variables were removed one by one, until all parameters were significant, which was reported as the final model (Table 2). Supplementary Table S2 provides the parameter estimates for adjusting significant SI and dense effects by model. The model performance was evaluated using R2 and RMSE and also the relationships between observed and predicted values, which are included in Supplementary Figure S1. Model assumptions (e.g., normality, equal variance, and independence) were visually checked using residual plots and were adjusted using weight functions and autoregression order 1 when required (S1). Package R was used for data analysis [22]. To show the effects of SI and density, predictions for sites with an SI of 18.282 (=60 ft) and 24.384 m (=80 ft) (SI18 and SI24, representing poor and good sites, respectively) paired with normal (N) and dense (D) densities by respective models were presented.
b0 = b00 + b01 × SI + b02 × M
b1 = b10 + b11 × SI + b12 × M
3. Results
3.1. Density—Age Relationships
The Chapman–Richards function modeled the age relationship well (Table 2; R2 = 0.93, RMSE = 5.0 m2 ha−1 (21.7%)). Starting at age 8, which marked the initiating crown closure of most loblolly pine plots in this study, initially increased rapidly with stand aging, gradually approached a maximum asymptote, and leveled off as the stands further grew older (Figure 1a). This relationship varied significantly with SI and IPT, yet the former had more influence than the latter. Both asymptote (b0) and rate (b1) increased with SI, leading to a larger at any given age and sooner approach to the asymptote for the higher SI sites. The D sites had a larger b1 than the N sites, resulting in a larger , but this difference reduced gradually with stand aging and eventually disappeared. At age 15, varied greatly from 21 (N + SI18 sites) to 33 m2 (D + SI24 sites). Similarly, the Chapman–Richards function was the best fit for the SDI–age relationship (Table 2; Figure 1b). Sites with higher SI or higher IPT greatly increased both asymptote (b0) and rate (b1), making the differences in SDI practically significant between SI18 and SI24 at a given IPT or between D and N sites at a given SI. At age 15, the SDI value ranged from 490 (N + SI18) to 750 (D + SI24). For both the –age and SDI–age relationships, SI and IPT did not affect the model parameter b2, the instantaneous rate of growth in the inflection point.
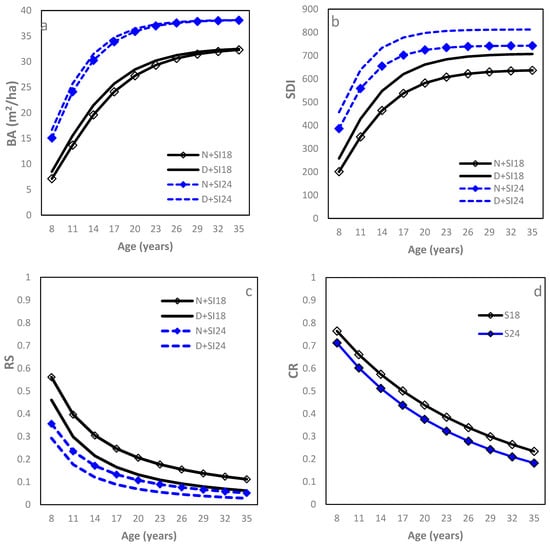
Figure 1.
Relationships between stand density measures and stand age of loblolly pine plantations planted at sites of two different SI (18 m and 24 m at age 25) and at an initial density of 1500 trees per hectare (D) or 1500 trees per hectare (N): (a) basal area per ha (BA); (b) stand density index (SDI); (c) relative spacing (RS); and (d) crown length ratio (CR).
The RS–age relationship was well fit using a power function (Table 2; R2 = 0.92, RMSE = 0.12 (28.50%)). Between ages 8 and 35 years, RS dropped rapidly with increasing stand age until about age 15, approached a low asymptote thereafter, and then remained relatively constant, forming an inverse “J” curve (Figure 1c). Sites with higher SI had a smaller b1 (decreasing faster) while D sites, in addition to a smaller b1, had a larger b0 than L sites. Therefore, sites with higher SI consistently had smaller RS and so were N sites compared to D sites. At age 15, the corresponding RS values were 0.11, 0.16, 0.20, and 0.28 for D + SI24, N + SI24, D + SI18, and N + SI18 sites, respectively.
A modified Chapman–Richards model fitted the CR–age relationship well (Table 2; R2 = 0.91 and RMSE = 0.08 (16.32%)). Starting at age 8, CR displayed a gradual and constant decline as age increased (Figure 1d). SI significantly affected model parameter b1, with the value being larger for sites of higher SI, while IPT did not show significant effects on either model parameter. Consequently, trees growing at higher SI sites had lower CR at any given age. At age 15, the CR were 0.55 and 0.49 for SI18 and SI24, respectively.
3.2. PAID–Density Relationships
The – relationship followed the Farazdaghi function (Table 2; R2 = 0.89, RMSE = 0.23 cm year−1 (28.05%)). Starting from the onset of crown closure ( = 10 m2), the decreased quickly with increasing to around 20 m2 and thereafter gradually approached a minimum asymptote (Figure 2a). Both b0 and b1 decreased significantly with increasing SI, resulting in larger for higher SI sites, although this difference decreased with increasing . Between D and L sites, no significant difference was found for each model parameter. At a of 25 m2, the was 0.50 for SI18 sites but increased to over 0.80 cm year−1 for the SI24 sites. Similarly, the Farazdaghi function fitted the –SDI relationship well (Table 2; R2 = 0.89, RMSE = 0.27 (32.92%)). SI negatively affected b0 and b2 and D sites had a smaller b2 than N sites (Table 2), leading to greater at higher SI sites and also in D sites compared to N sites. Even so, the actual difference in between D and N sites was small regardless of the SDI level, having no practical significance. The difference in between SI24 and SI18 was large when SDI was low (e.g., =300) but decreased quickly with increasing SDI (Figure 2b). At an of 500, the was above 0.71 for SI18 sites but increased to over 1.20 cm year−1 for the SI24 sites.
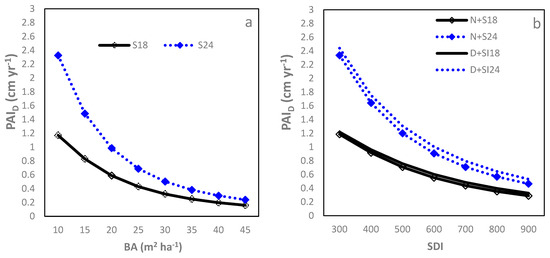
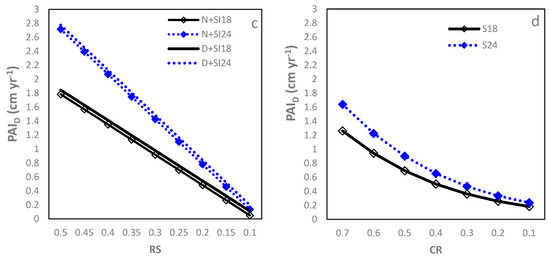
Figure 2.
Relationship between stand density measures and period annual increment in DBH () of loblolly pine plantations planted at sites of two different SI (18 m and 24 m) and at an initial density of 1500 trees per hectare (D) or 1500 trees per hectare (N): (a) basal area per ha (BA); (b) stand density index (SDI); (c) relative spacing (RS); and (d) crown length ratio (CR).
The –RS relationship was negatively linear, although the accuracy was relatively poor (Table 2; R2 = 0.66, RMSE = 0.32 cm year−1 (36.58%)). Increasing SI significantly reduced intercept (b0) but enhanced slope (b1) estimates while the D sites had a significantly larger b0 than the N sites. The differences between SI18 and SI24 sites were small when the RS was low, but increased quickly with increasing RS. An RS of 0.2 corresponded to a of 0.48, 0.54, 0.78, and 0.84 cm yr−1 for the N + SI18, D + SI18, N + SI24 and D + SI24, respectively (Figure 2c).
The expolinear growth function modeled the CR relationship well (Table 2; R2 = 0.94, RMSE=0.23 cm year−1 (28.05%)). With CR decreasing from 0.70 (around age 8) to 0.20 (around age 30), the gradually decreased in a nonlinear pattern (Figure 2d). Increasing SI significantly increased b0 only while IPT did not show a significant impact on model parameters. Therefore, at a given CR, the sites with higher SI had larger , but this advantage decreased quickly with reducing CR. At a CR of 0.4, the was 0.50 for SI18 sites and 0.65 cm year−1 for SI24 sites.
3.3. Between-Measures Relationships
Stand density index showed a strong, positive linear relationship with (Table 2; R2 = 0.95, RMSE = 0.08 (=4.88%)). Both SI and IPT significantly affected the intercept (b0, which increased with increasing SI or was greater for D sites than N sites). SI negatively affected the slope (b1) (Figure 3a), and, therefore, SDI increased slower with increasing at higher SI sites. Sites with greater SI had larger SDI at a given, as did the D sites compared to the L sites, although the differences were negligible from a practical viewpoint. At a of 25 m2, the corresponding SDI ranged from 551 to 593. Given the strong linear relationship of SDI–, the relationships of SDI with CR and RS are not presented here.
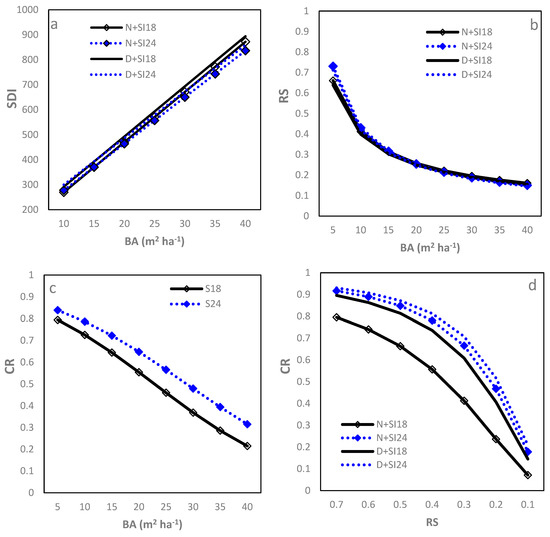
Figure 3.
Relationships between stand density measures of loblolly pine plantations planted at sites of two different SIs (18 m and 24 m) and at an initial density of 1500 trees per hectare (D) or 1500 trees per hectare (N): (a) between stand density index (SDI) and basal area per ha (BA); (b) relative spacing (RS) and BA; (c) crown ratio (CR) and BA; and (d) CR and RS.
The power function fitted the RS– relationship well (Table 2; R2 = 0.94, RMSE = 0.05 (18.52%)). RS decreased rapidly when increased from 5 to 15 m2 and then decreased gradually with further increasing to 40 m2 (Figure 3b). SI and IPT were found only to affect model b0, which increased with increasing SI and was smaller for D sites than N sites, leading to slightly smaller RS for sites with higher IPT and greater SI. Regardless of statistical significance, the practical influence of changing SI or planting density was negligible. At a of 25 m2, the RS was similar, being around 0.21 for the combinations of IPT and SI.
The logistic function fitted the CR– relationship best (Table 2; R2 = 0.93, RMSE = 0.09 (18.00%)). When increased from 5 to 40 m2, CR decreased in an approximately linear pattern (Figure 3c). The model parameters varied significantly with SI in that higher SI sites had larger b0 but smaller b1, leading to greater CR at any given for higher SI sites. No significant differences in both parameters were found between D and N sites (Figure 3c). At a of 25 m2, the CR were 0.46 and 0.57 for the SI18 and SI24 sites, respectively.
The Zhao et al. (2012) [8] model best fit the CR–RS relationship (Table 2; R2 = 0.93, RMSE = 0.08 (16.00%)). CR decreased slowly when RS changed from 0.70 to around 0.50, thereafter decreasing quickly to 0.15 at RS = 0.10. Both SI and IPT affected b0 significantly in that b0 decreased with increasing SI and planting density, leading to a substantially smaller CR for D + SI18 than the other combinations (Figure 3d). It could also be seen that the differences between the combinations were small when RS was either low (e.g., RS = 0.1) or high (e.g., RS = 0.7; Figure 3d). When RS = 0.2, the CR ranged from 0.41 to 0.52 other than N + SI18, which had 0.24.
4. Discussion
This modeling was performed to compare density measures commonly used for managing mid-rotation pine stand density, rather than to develop models for prediction or projection. While , SDI, and RS are not calculated using the same equations, they similarly account for the number of trees, tree size, and, indirectly, stand age via DBH ( and SDI) or height (RS) growth. CR, differently, is an indicator of tree vigor and links closely to tree growth, and thus is an indirect stand density measure. Therefore, each of these metrics is a different format of a general framework of stand density, which is inherently dynamic. While the data covered a wide age range from 2 to 45 years (Table 1), in terms of practical usefulness for mid-rotation density management, only the following period is relevant: from the onset of competition (e.g., around age 8 or 25% maximum SDI) to the onset of self-thinning (e.g., 30–35 m2 [23], 45% of maximum SDI [3], or 0.20–0.25 RS [24]). We focus on this period in the following discussion.
An important criterion for evaluating the measures is how strongly they adhere to basic expectations of stand aging or tree growth. The ecological and biological expectations during the period from crown closure to the onset of density-dependent mortality for the plantations under study would be very little mortality [25], which is accompanied by an increase in DBH growth at a decreasing rate, reaching an asymptote around an age of 18 years, and relatively constant height growth [26]. The diverging temporal trends in tree number and growth suggest that stand density development likely follows asymptotic trajectories during this period. Such a development trajectory of density was confirmed when density was measured by , SDI, or RS, with each asymptotically approaching maximum ( and SDI) or minimum (RS) values as stand ages in this study (Figure 1) and also in the SE US [6,7,8,11,27,28]. The maximum or minimum asymptotes in this study are comparable to those observed in the SE US plantations established in the 1980s [29] but were lower than those for intensively managed loblolly pine plantations [23]. CR similarly decreased with increasing age, yet in a more gradual, constant pattern with no obvious inflection points nor asymptote appearing, weakening its use as an indicator of density. A similar trend for CR–age to this study was reported for loblolly pine in the SE US [8,30].
For loblolly pine, tree declines quickly with crown closure but stabilizes after the onset of self-thinning [26]. The observed trends of –density adhered to the expectation when density was expressed as or SDI but biased away when density was measured by RS or CR (Figure 2). The moderately linear relationship between and RS in this study agrees with the findings in the SE US loblolly pine plantations [12]. While the simple linear relationship is feasible for use, the biological relationship between DBH growth and density might be more complicated than a simple linear relationship, suggesting the weakness of using RS as a measure of density or indicator of tree DBH growth. Note that RS is closely related to height growth, which often is minimally affected by stand density, a disadvantage for using RS as an indicator of stand density. Furthermore, due to the errors associated with height measurements, RS may introduce bias in estimating stand density values. The use of CR implies the assumption that reduced tree vigor will never recover adequately to regain significant growth rates when CR falls below a given level, such as 0.33 [27], but our results suggest a gradual decrease in with reducing CR, without showing clear infection or sudden decline, suggesting uncertainty in the validity of that assumption.
If the measures truly reflect stand density, it should be possible to empirically identify between-measure relationships. Toward this, our results were promising in that strong relationships existed among the measures, yet in different formats (Figure 3). In supporting [14], the data from this study suggest a strong linear relationship between SDI and BA and SDI exhibited a similar relationship with both age and PAID, as shown in Figure 2. This finding further supports the linear relationship between these two variables. The consistent trend highlights how as one increases, the other tends to follow suit, reinforcing the interconnectedness of these metrics in the context of forest management. SDI was calculated using a “b” value of 1.605, although some studies suggest that a value of 1.505 may be more appropriate for loblolly pine in the Western Gulf region [13]. However, changing the “b” value to 1.505 did not affect the SDI-related relationships observed in this study. The relationship between and RS was found in a reverse J shape, which is parallel to that reported by [11]. While CR cannot be easily converted to or RS by a simple transformation since they indicate density differently, CR showed an approximately linear relationship with and a decreasing concave curve with RS. Similar relationships between CR and SDI [14] and between CR and RS [8] to those of this study were reported in loblolly pine elsewhere. Based on the relationships observed in this study, a loblolly pine plantation with a of 25 m2 corresponded with an SDI from 557 to 590, an RS of around 0.21, and a CR from 0.46 to 0.57, depending on SI. When the plantations reached an average CR of 0.40, the values of RS ranged from 0.12 to 0.21 [8], which are roughly comparable to the corresponding values of RS in this study, ranging from 0.15 to 0.25.
Sites with higher site index values can support more trees and enhance tree growth, thus, SI is expected to affect the above relationships. While some have argued that the temporal trajectory of SDI or RS for loblolly pine remains constant regardless of site quality [2,3], empirical results based on loblolly pine plantations outside the WG [6,28] and in this study supported the expectation. Furthermore, this study confirmed that the practical impact of SI might be stand-stage dependent. Shortly before crown closure, or at the early stage of crown closure, sites with higher SI had higher densities by all the measures and greater tree growth rates. As inter-tree competition intensified with stand aging, stand density increased but tree growth rate decreased, yet at greater rates at higher SI sites. This study focused on the SI impacts for plantations that are 35 years old or younger. As such, any long-term SI impacts should be interpreted with caution, as they may not fully represent the dynamics and outcomes of older plantations. When density reached a high level (i.e., = 45 m2, SDI = 900, CR = 0.1 or RS = 0.1), SI effects on became practically insignificant. SI affected the between-measure relationships in more complex formats (Figure 3). While SI impacts were statistically significant on all the between-measure relationships, its practical significance on the relationships of RS– and SDI–were negligible. The effects of SI on the CR–RS relationship varied with IPT and RS levels. The difference in CR at a given RS could be substantial between N sites and D sites if the sites were of poor quality (SI18) and also when RS was >0.20. In supporting our results, Zhao et al. [8] found that the CR–RS relationship varied with SI and the SI effect was RS level dependent. The SI effect was substantial when RS > 0.20 but became negligible when RS approached 0.20. Note that in this study, site quality was simply expressed as SI, without considering other effects that may alter responses, including soil and climate conditions and genetics. Incorporating SI effects into stand density development is essential for making informed decisions regarding stand management to maximize productivity and ensure sustainable forest management.
Pine plantation density development is a dynamic process that is influenced by factors such as IPT. After planting, stands with higher IPT have more trees competing for resources, leading to faster canopy closure and higher densities (i.e., larger ), which, in turn, results in the earlier onset of self-thinning and slower basal area growth of individual trees. Nonetheless, these effects of IPT on the relationships investigated were not evident, with the effects being either marginal or having no practical significance, yet with few exceptions. The absence of clear effects of IPT could be due to a variety of factors, although inspective. First, the spacing at planting influences more on early stand development. Second, the effects of IPT might be underestimated since IPT was simply grouped into two categories. Finally, the data were collected from sites across east Texas, so the substantial variation in site conditions might mask the effects of IPT. The exceptions were the temporal trends of SDI and RS, with D sites having higher density by either measure. Trees in closer spacing generally grow height more quickly compared to trees in wider spacing, where diameter growth may be favored, leading to smaller RS and larger SDI. Indeed, our results also found that the denser sites had a larger , although its practical significance was insignificant, in particular after competition occurred. IPH also affected the CR–RS relationship, and the effects of IPT and SI on it were additive, as shown by the particularly low CR at the given RS for N + SI18 (Figure 3d). Observationally, the significant IPT effects on the SDI–age (Figure 1b) and CR–RS (Figure 3d) relationships became more evident when the stands entered the self-thinning stage. In parallel to our findings, significant effects of planting density on the CR–RS relationship were found in the SE loblolly pine plantations [8]. In this study, the observed effect of IPT on the –SDI relationship was even contradictory to the theoretical prediction. Typically, trees at N sites would have a greater than those at D sites at a given SDI. Nonetheless, our results supported a reverse pattern, even if the difference was negligible (Figure 2b). Overall, our understanding of the relationships between tree growth and IPT is still limited. Further research or a reevaluation of the data may be needed to better understand the role of IPT in stand density development.
One of the important uses of density in managing loblolly pine plantations is to plan mid-rotation thinning such as determining biological thinning time. Are the biological times by the measures on par with each other? By the current criteria for triggering a thin (reaching 25 m2 , 500 SDI, 0.20 to 0.25 RS, or 35% CR), the time judged by agreed with that by RS, but was later than that by SDI and earlier than that by CR. Results in such comparisons for loblolly pine populations outside the WG varied. In a study in the SE US, an RS of 0.20 corresponded to a of 20~30 m2 [11], supporting our results. A CR of 0.40 corresponded to an SDI of 710 in loblolly pine populations in the WG [14], which agrees with this study (SDI = 765) but corresponded approximately only to 555 in an SE population [15]. It is also of great interest to compare the biological thin times by these measures with the regional operational criterion, which often is determined by market and stand age, e.g., the first thin occurs around age 15 years. The results are promising in that the ranges at age 15 of (21 to 32 m2) and RS (0.15 to 0.26), depending mainly on SI, cover the respective criterion values, suggesting that the operational criterion concurs approximately with the biological thin times by these measures. However, the biological criterion of SDI (500) was located at the low end of the range (490 to 750) at age 15, and that of CR (0.35) was outside the range from 0.48 to 0.55, suggesting the disparity between these measures and the operational criterion. Factors other than SI and IPT such as physiographic region also influenced thin time [6]. At age 15 and for SE loblolly pine populations, the reached 35 m2, ranging from 32 m2 of 741 trees ha−1 to 40 m2 of 3706 trees ha−1, and the SDI was 800, ranging from 650 to 1000 [7], with both exceeding the respective values of this study. Even higher SDI (>1000 at age 15) was reported for the fertilized sites in the Atlantic coastal plain [28]. At age 11, the CR averaged 0.26 (at a density of 4445 trees ha−1) to 0.34 (at a density of 1111 trees ha−1) based on Poudel et al. [30], much lower than those observed in this study (CR = 0.63). Likely, the commercial thinning of loblolly pine should be practiced later in the WG than in the SE US.
For loblolly pine, producing more high-valued timber products such as sawtimber via density management is of utmost importance. Thus, maintaining a reasonable is an appropriate strategy [15]. If the goal is to maximize , without considering the market requirements, this study suggests thinning be scheduled as soon as the onset of crown closure begins. For loblolly pine in the WG, triggering a thin is justified when dominant/codominant tree DBH at mid-rotation grows 0.50 cm year−1 [31]. Our results show that thinning loblolly pine stands by the current biological criteria would result in 0.50 cm year−1 or more even at poor sites such as those with an SI of 18 m by all the measures other than by CR, which had a rate of 0.42 cm year−1. Determining the timing of thinning by SDI would achieve a higher , which, however, is a result of the thinning age by SDI being younger than those by other measures for a given stand.
The relationships of stand density with stand age and growth at stand level have been reported in other ecosystems [16,32,33]. With no surprise, their reported stand-level trends are not often consistent with the tree-level relationships observed in this study. Comparisons among stand density measures including number of trees, BA, and SDI have been made [12,34,35]; many of them appeared to be practically equivalent, showing little appreciable difference from their simpler counterparts in the way they represent density. Zeide [36] criticized BA and SDI as a density indicator for their lack of accounting for gaps caused by serious self-thinning, which, however, is unlikely to occur in mid-rotation loblolly pine plantations. This study compared the measures by biological expectations and based on individual tree growth. One finding from the study is that outperforms others in describing loblolly pine stand density since (1) has strong relationships with stand age and tree DBH growth, with both patterns being in line with biological expectations; (2) other density measures can be precisely predicted from ; (3) is easily understood, easily measured, and normally available for most managed plantations; and (4) has great flexibility in incorporating site index into decision-making. Moreover, the current commonly used criteria by results in acceptable growth in This study was based on data collected from loblolly pine plantations that were established in the 1980s and extensively managed. Southern pine silviculture has improved substantially in the past 20 years, including planting advanced genetics, applying fertilization, and competition control, among other treatments [37]. Relatively strong markets for larger diameter trees have led to planting low initial densities (<1500 trees ha−1, similar to the normal density sites in this study) in some areas. The resulting changes in stand survival and tree growth from these activities are expected to affect the models’ parameter estimates but are unlikely to change the trends found in this study. Ideally, these relationships should be investigated using data collected from intensively managed loblolly pine plantations. Before that information becomes available, however, the results of N + SI80 sites in this study can be treated as an interim guide for intensively managed loblolly pine plantations.
In conclusion, the strong density–age and density–growth relationships observed in this study by the density measures examined here signify their potential to link stand density with stand development. These seemingly disparate measures are not independent of one another. However, not all the measures are equally effective in regulating mid-rotation density; in particular, determining the biological time to thin. Among the four stand density measures, our results suggest the use of for this purpose since it is biologically sound, easily applicable, and flexible in facilitating the effects of site index and planting density. Our results suggest that the current criterion of CR may trigger thins too late, so more study is needed to understand if the criterion applies to WG loblolly pine plantations. Clearly, in addition to biological factors, other factors such as local wood markets can greatly influence the age of the first thinning. Although can provide a range of years for determining thinning schedules, a combination of with other factors might provide a better solution to determine the biological timing of the thinning of loblolly pine plantations.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/su16219452/s1, Table S1: Selected random structures of the final model by relationship. Table S2: Estimated model parameters for adjusting site index (SI) and dense density (M=D). Figure S1: Relationships between predicted vs. observed response variables by model (See Table 2).
Author Contributions
Conceptualization, Y.W.; methodology, Y.W. and X.L.; formal analysis, Y.W.; writing, Y.W.; writing—review and editing, D.C., J.G. and C.D.; data curation: D.C., J.G. and Y.W.; funding acquisition, Y.W. All authors have read and agreed to the published version of the manuscript.
Funding
The study was financially supported by ETPPRP and the McIntire-Stennis program.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The datasets presented in this article are not readily available because the data belong to a cooperative program, ETPPRP, and are not allowed to be shared by non-members.
Acknowledgments
We thank Caddo Sustainable Timberlands, Rayonier, Resource Management Service, Stephen F. Austin State University, and the McIntire-Stennis program for their support of this research as well as the ETPPRP student workers who helped collect data.
Conflicts of Interest
Author Dean Coble was employed by the company BTG Timberland Investment Group. The remaining authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
References
- Nyland, R.D.; Kenefic, L.S.; Bohn, K.K.; Stout, S.L. Silviculture: Concepts and Applications, 3rd ed.; Waveland Press Inc.: Long Grove, IL, USA, 2016. [Google Scholar]
- Burkhart, H.E.; Avery, T.E.; Bullock, B.P. Forest Measurements, 6th ed.; Waveland Press Inc.: Long Grove, IL, USA, 2019. [Google Scholar]
- Dean, T.J.; Baldwin, V.R., Jr. Using a Density-Management Diagram to Develop Thinning Schedules for Loblolly Pine Plantations; US For. Serv. Res. Pap. SO-275; US Forest Service: New Orleans, LA, USA, 1993; 7p.
- Williams, R.A. Stand density management diagram for loblolly pine plantations in North Louisiana. South. J. Appl. For. 1994, 18, 40–45. [Google Scholar] [CrossRef]
- Doruska, P.F.; Nolen, W.R., Jr. Use of stand density index to schedule thinnings in loblolly pine plantations: A spreadsheet approach. South. J. Appl. For. 1999, 23, 21–29. [Google Scholar] [CrossRef]
- Zhao, D.; Kane, M.; Borders, B. Development and applications of the relative spacing model for loblolly pine plantations. For. Ecol. Manag. 2010, 259, 1922–1929. [Google Scholar] [CrossRef]
- Zhao, D.H.; Kane, M. Differences in growth dynamics of loblolly and slash pine plantations in the southeastern United States. For. Ecol. Manag. 2012, 281, 84–92. [Google Scholar] [CrossRef]
- Zhao, D.; Kane, M.; Borders, B. Crown ratio and relative spacing relationships for loblolly pine plantations. Open J. For. 2012, 2, 110–115. [Google Scholar] [CrossRef]
- Zeide, B. Stand density and canopy gaps. In Proceedings of the 12th Biennial Southern Silvicultural Research Conference Cooperative; Gen. Tech. Rep. SRS–71; Connor, K.F., Ed.; U.S. Department of Agriculture, Forest Service, Southern Research Station: Asheville, NC, USA, 2004; 594p. [Google Scholar]
- Zeide, B. Thinning and growth: A full turnaround. J. For. 2001, 99, 20–25. [Google Scholar] [CrossRef]
- Yang, S.I.; Burkhart, H.E. Application of height- and diameter-Based relative spacing for estimation of stand basal area. For. Sci. 2018, 64, 28–32. [Google Scholar] [CrossRef]
- Allen, M.G., II; Burkhart, H.E. Growth-density relationships in loblolly pine plantations. For. Sci. 2019, 65, 250–264. [Google Scholar] [CrossRef]
- Williams, R.A. Stand density index for loblolly pine plantations in North Louisiana. South. J. Appl. For. 1996, 20, 110–113. [Google Scholar] [CrossRef]
- Dean, T.J. Using live-crown ratio to control wood quality: An example of quantitative silviculture. In Proceedings of the Tenth Biennial Southern Silvicultural Research Conference; Haywood, J.D., Ed.; US Forest Service, Southern Research Station: Asheville, NC, USA, 1999; pp. 511–514. [Google Scholar]
- Long, J.N. A practical approach to density management. For. Chron. 1985, 61, 23–27. [Google Scholar] [CrossRef]
- Allen, M.G., II; Brunner, A.; Antón-Fernández, C.; Astrup, R. The relationship between volume increment and stand density in Norway spruce plantations. Forestry 2021, 94, 151–165. [Google Scholar] [CrossRef]
- Lenhart, J.D.; Hunt, E.V., Jr.; Blackard, J.A. Establishment of permanent growth and yield plots in loblolly and slash pine plantations, pp. In Proceedings of the Third Biennial South Silvicultural Research Conference, 7–8 November 1984; Shoulders, E., Ed.; U.S. Department of Agriculture, Forest Service, Southern Forest Experiment Station: New Orleans, LA, USA, 1985; pp. 436–437. [Google Scholar]
- Coble, D.W.; Lee, Y.L. Use of a Generalized Sigmoid Growth Function to Predict Site Index for Unmanaged Loblolly and Slash Pine Plantations in East Texas; Gen. Tech. Rep. SRS-92; Connor, K.F., Ed.; U.S. Department of Agriculture, Forest Service, Southern Research Station: New Orleans, LA, USA, 2006; pp. 291–295.
- Weiskittel, A.R.; Hann, D.W.; Kershaw, J.A.; Vanclay, J.K. Forest Growth and Yield Modeling; John Wiley & Sons.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Burkhart, H.E.; Tomé, M. Modeling Forest Trees and Stands; Springer: Dordrecht, The Netherlands, 2012. [Google Scholar]
- Panik, M.J. Growth Curve Modelling: Theory and Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004; 437p. [Google Scholar]
- Pinheiro, J.C.; Bates, D.M. Mixed-Effects Models in S and S-PLUS; Springer: New York, NY, USA, 2000. [Google Scholar]
- Jokela, E.J.; Dougherty, P.M.; Martin, T.A. Production dynamics of intensively managed loblolly pine stands in the southern United States: A synthesis of seven long-term experiments. For. Ecol. Manag. 2004, 192, 117–130. [Google Scholar] [CrossRef]
- Henderson, J.E.; Roberts, S.D.; Grebner, D.L.; Munn, I.A. A graphical comparison of loblolly pine growth-and-yield models. South J. Appl. For. 2013, 37, 169–176. [Google Scholar] [CrossRef]
- Creighton, J. Growth of Loblolly Pine Planted at Low Densities; Virginia Department of Forestry: Chesapeake, VA, USA, 2017; Volume 135, 8p.
- Weng, Y.H.; Grogan, J.; Cheema, B.; Tao, J.; Lou, X.; Burkhart, H.E. Model-based growth comparisons between loblolly and slash pine and between silvicultural intensities in East Texas. Forests 2021, 12, 1611. [Google Scholar] [CrossRef]
- Demers, C.; Long, A.; Nowak, J. Thinning Southern Pines—A Key to Greater Returns; Florida Cooperative Extension Service; Institute of Food and Agricultural Science, University of Florida: Gainesville, FL, USA, 2005. [Google Scholar]
- Walker, T.D.; Bullock, B.P.; Smith, B.C.; McKeand, S.E. Modeling self-thinning patterns in loblolly pine with provenance and family effects. For. Sci. 2020, 66, 712–725. [Google Scholar] [CrossRef]
- Harold, E.; Burkhart, H.E.; Yang, S.I. A retrospective comparison of carrying capacity of two generations of loblolly pine plantations. For. Ecol. Manag. 2022, 504, 119834. [Google Scholar]
- Poudel, K.P.; Avery, S.C.; Granger, J.J. Live crown ratio models for loblolly pine (Pinus taeda) with beta regression. Forests 2021, 12, 140. [Google Scholar] [CrossRef]
- Texas A&M Forest Service. Timber Management: Thinning Pine Stands. Available online: https://tfsweb.tamu.edu/uploadedFiles/TFSMain/Manage_Forest_and_Land/Landowner_Assistance/Stewardship(1)/Thinning_Pine_Stands.pdf (accessed on 15 August 2023).
- Pretzsch, H. Stand density and growth of Norway spruce (Picea abies (L.) Karst.) and European beech (Fagus sylvatica L.): Evidence from long-term experimental plots. Eur. J. For. Res. 2005, 124, 193–205. [Google Scholar] [CrossRef]
- Brunner, A. Stand volume growth varies with age, site index, and stand density—Comments on Stokland. For. Ecol. Manag. 2021, 495, 119329. [Google Scholar] [CrossRef]
- Curtis, R.O. Stand Density Measures: An Interpretation. For. Sci. 1970, 16, 403–414. [Google Scholar]
- West, P.W. Comparison of stand density measures in even-aged regrowth eucalypt forest of southern Tasmania. Can. J. For. Res. 1982, 13, 22–31. [Google Scholar] [CrossRef]
- Zeide, B. How to measure stand density. Trees 2005, 19, 1–14. [Google Scholar] [CrossRef]
- Fox, T.R.; Jokela, E.J.; Allen, H.L. The development of pine plantation silviculture in the southern United States. J. For. 2007, 105, 337–347. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).