Sustainable Development of a Direct Methanol Fuel Cell Using the Enhanced LSHADE Algorithm and Newton Raphson Method

Abstract

This paper presents a mathematical model for stacks of direct methanol fuel cells (DMFCs) using an optimised method. In order to reduce the sum of squared errors (SSE) in calculating the polarisation profile, the suggested technique makes use of simulated experimental data. Given that DMFC is one of the viable fuel cell choices, developing an appropriate model is essential for cost reduction. However, resolving this issue has proven difficult due to its complex and highly nonlinear character, particularly when adjusting the DMFC model to various operating temperatures. By combining the algorithm and the objective function, the current work introduces a novel method called LSHADE (ELSHADE) for determining the parameters of the DMFC model. This technique seeks to accurately identify DMFCs’ characteristics. The ELSHADE method consists of two stages, the first of which is controlled by a reliable mutation process and the latter by a chaotic approach. The study also recommends an improved Newton–Raphson (INR) approach to deal with the chaotic nature of the I-V curve equation. The findings show that, when used on actual experimental data, the ELSHADE-INR technique outperforms existing algorithms in a variety of statistical metrics for accurately identifying global solutions.

1. Introduction

1.1. Motivation

Lately, there has been growing interest in the potential of substituting traditional power generation systems with fuel cells. To achieve an optimal design and performance, it is crucial to develop accurate system models. This requires a deep understanding of electrochemistry, materials, manufacturing, heat, and mass transfer. These elements are essential for creating a model that aligns with the fuel cell’s goals of cost-effectiveness, high performance, and stability. Polymer electrolyte membrane (PEM) fuel cells come in two main types: direct methanol fuel cells (DMFCs) and hydrogen fuel cells, both utilising PEM for proton transport. According to [1], DMFCs channel a methanol and water mixture (usually 0.5–2 M) to an anode, where an internal catalyst reforms it. DMFCs outperform hydrogen fuel cells due to their ease of fuel distribution and storage, reduced need for humidification, and simpler design. They are particularly well-suited for portable electronics since they do not require additional equipment. Despite these attractive advantages, DMFCs face significant technological challenges, such as the weak electro activity of methanol oxidation at the anode and the substantial volume of unwanted methanol passing through the PEM from the anode to the cathode. In line with this description, methanol crossover occurs when methanol permeates the membrane from the anode compartment to the cathode compartment and reacts there.

1.2. State-of-the-Art Approaches

Extensive research, both theoretical and experimental, has been conducted on methanol crossover in DMFCs. Table 1 shows the comparison of research performed by various researchers to date.

Table 1. Comparison of research.

Author/ Reference	Year	Type of Work	Results
Muhammad Aizaz Ud Din et al. [2]	2023	Theoretical	This manuscript provides a review on prospective future developments for the selection of a suitable methanol-tolerant catalyst for the oxygen reduction reaction in the design of high-performance, practical direct methanol fuel cells.
Gowthami Palanisamy et al. [3]	2023	Theoretical	This manuscript provides a review of the advances and utilisation of cost-effective cellulose materials (microcrystalline cellulose, nanocrystalline cellulose, cellulose whiskers, cellulose nanofibers, and cellulose acetate) as PEMs for DMFCs.
Tianyu Xia et al. [4]	2023	Experimental	This manuscript provides a proposed strategy to improve the catalytic performance of Pt-based nanocatalysts by constructing novel interfacial relationships in mixed dimensions to alleviate the imbalance between catalytic activity and catalytic stability caused by size effects.
Carmelo Lo Vechio et al. [5]	2023	Experimental	This manuscript provides insight into the large-scale application of ADMFC with commercial PGM-free materials.
Hakan Burhan et al. [6]	2023	Experimental	This manuscript provides an observation that PtCo nanoparticles with carbon hybrid support structures are more advantageous than single support structures due to the synergistic effect between carbon support structures and providing a larger surface area.
Bin Wang et al. [7]	2023	Experimental	In this manuscript, the properties of ABMCBs with various additive loadings were investigated as proton exchange membranes (PEMs). The results showed that higher water absorption and lower swelling were obtained simultaneously with increasing additive loading, which is very beneficial in the use of PEMs.

1.3. Contribution

Compared to PEMFC and SOFC fuel cells, there are relatively few publications on DMFC modelling in the literature. Researchers have found it challenging to solve the Butler–Volmer equation in most of these studies and thus have made assumptions and approximations to simplify the complexity of the equation in their publications. The use of underlying assumptions and approximations, however, can affect the accuracy of models for replicating experimental data for DMFC stack current density curves and stack voltage (J-V). Earlier works on parameter extraction primarily used the Newton–Raphson optimisation method [8,9], which has limitations such as high sensitivity to initial values, difficulty in distinguishing between multiple solutions, and convexity. In order to enhance the convergence capabilities of the LSHADE algorithm and increase population diversity, author has improved the LSHADE algorithm using chaotic maps. The Newton–Raphson algorithm has proven to be a great algorithm for solving complex mathematical models. As the complexity increase, the Newton–Raphson algorithms tends to oscillate around a local minima. To avoid this, the mentioned algorithm was improved to achieve the minimum error outcome, hence achieving accurate values for unknown parameters.

Despite their demonstrated superiority over other optimisation strategies, metaheuristic methods have not been implemented in parameter extraction from DMFC stack models. In addition to optimising solar cells, PEMFCs [10], SOFC fuel cells, and other systems, these approaches have also been successful in optimising other systems. The main contributions of this paper are as follows:

• The novel hybrid algorithm is designed for the extraction of the DMFC model’s unknown parameters.
• The DMFC model’s parameters are extracted to their maximum potential using a unique ELSHADE method.
• In order to validate the effectiveness of the proposed strategy, real experimental data are collected in various climatic conditions, and these data are compared with other established strategies.
• In order to evaluate the effectiveness and consistency of the proposed algorithm, the computation time of the fuel cell model is determined.
• Convergence curves and results at various operating temperatures are generated to assess the proposed algorithm’s consistency and robustness.
• Non-parametric statistical tests such as the Friedman ranking test and Wilcoxon rank sum test are used to determine the significance of the DMFC parameter estimates.

The rest of the paper has these sections: Section 2 explains the mathematical modelling of a direct methanol fuel cell. Section 3 briefly describes the materials and methods, parameters extraction, and optimisation algorithms implemented in the paper. Section 4 depicts the results and discussion of the optimisation data. The paper ends with a conclusion presented in Section 5.

2. Mathematical Formulation of DMFCs

A fuel cell is a device that continuously converts chemical energy into electrical energy and heat. It does not store energy like a battery but instead operates continuously by supplying fuel and oxidants. Unlike engines, fuel cells do not emit greenhouse gases as a result of their output. Therefore, they are considered an environmentally friendly alternative. A schematic of the DMFC stack is presented in Figure 1, and this study focuses on mathematically modelling the stack. A metaheuristic algorithm called ELSHADE is used to extract unknown parameters in the model. As shown in Equation (1), DMFC cell voltage is expressed as:

$$v_{cell}=p_{act}-p_{con}-p_{rev}-p_{ohm}$$

(1)

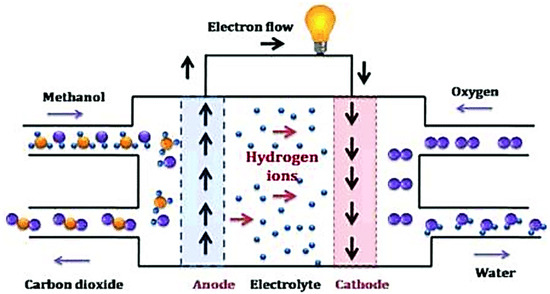
Figure 1. DMFC schematic [11].

The voltage within the cell is shown by $v_{cell}$, the concentration of the voltage is represented by $p_{con}$, the activation voltage is represented by $p_{act}$, the reversible voltage is represented by $p_{rev}$, and the ohmic voltage is represented by $p_{ohm}$.

The electrochemical equation for a direct methanol fuel cell (DMFC) can be represented by the following Equations (2)–(4):

$$\mathrm{Anode}: C{H}_{3}OH+H_{2}O\to 6H^{+}+6e^{-}+C{O}_2$$

(2)

$$\mathrm{Cathode}: \frac{3}{2}{O}_2+6H^{+}+6e^{-}\to 3H_{2}O$$

(3)

$$\mathrm{Overall} \mathrm{reaction}: C{H}_{3}OH+\frac{3}{2}{O}_2\to 2H_{2}O+C{O}_2+Heat$$

(4)

These equations represent the chemical reactions that occur at the anode and cathode of a DMFC. At the anode, methanol and water are oxidised to form carbon dioxide, protons (H⁺), and electrons (e⁻). At the cathode, oxygen is reduced to form water. The overall reaction combines the anode and cathode reactions to show that the oxidation of methanol with oxygen produces carbon dioxide, water, and energy in the form of electricity.

2.1. Activation Loss Voltage Expression

The activation voltage is determined by Equation (5), which is the required overvoltage to activate electrodes. The Butler–Volmer equation is employed to calculate the current density, $j_{max}$.

$$j_{max}=j_{eid}\left[e^{\left(\frac{\alpha nf}{rt}{p}_{act}\right)}-e^{-\left(\frac{\left(1-\alpha \right)nf}{rt}{p}_{act}\right)}\right]$$

(5)

The exchange current density is denoted as $j_{eid}$, and the value of α is between 0 and 1. Analytical solutions cannot be found for Equation (5) regarding activation voltage. To address this, the voltage $p_{act}$ in the first exponential of the equation is substituted with $p_{con}$, $p_{rev}$, $p_{ohm}$, and $v_{cell}$, leading to the following Equation (6):

$$j_{max}=j_{eid}\left[e^{\left(\frac{\alpha nf}{rt}\left(p_{con}-p_{ohm}-p_{rev}-v_{cell}\right)\right)}-e^{-\left(\frac{\left(1-\alpha \right)nf}{rt}{p}_{act}\right)}\right]$$

(6)

Equation (7) can be used to represent the expression for the updated activation voltage:

$$p_{act}=\frac{rt\left[\log \left(j_{max}+j_{eid}{e}^{\left(\frac{\alpha nf}{rt}\left(p_{con}-p_{ohm}-p_{rev}-v_{cell}\right)\right)}\right)-\log \left(j_{eid}\right)\right]}{\alpha nf}$$

(7)

2.2. Ohmic Loss Voltage Expression

The voltage loss attributed to resistance encountered by ions, electrons, and other substances during transport across a membrane is known as “ohmic loss voltage”. Equation (8) below depicts the ohmic voltage [6]:

$$p_{ohm}=r{j}_{cd}$$

(8)

The current density $j_{cd}$ and internal resistance r are the variables used to express the ohmic voltage in Equation (8).

2.3. Concentration Loss Voltage Expression

The voltage drop caused by mass transfer is referred to as concentration over potential. Using Fick’s law, the over potential due to concentration can be represented by Equation (9):

$$p_{con}=-\frac{rt}{\beta nf}\ln \left(1-\frac{j_{max}}{j_{limit}}\right)$$

(9)

Equation (10) provides a brief representation of $j_{max}$, which is used in Equation (9).

$$j_{max}=\frac{p_{rev}-v_{cell}-r{j}_{cd}}{r_{con}+r_{act}}$$

(10)

The parameter β, an empirical coefficient, and $j_{limit}$, the limiting current density, are denoted in Equation (10).

2.4. Reversible Loss Voltage Expression

Equation (11) depicts the reversible voltage that arises from the energetic activity involved in the formation and breaking of bonds at the electrode level, which is represented by the Nernst equation [12]:

$$p_{rev}=e_o+\frac{rt}{nf}\left[\log \left(c_{C{H}_{3}OH}\right)+\frac{3}{2}\log \left(p_{o_2}\right)\right]-\frac{rt}{nf}\left[2\log \left(p_{H_{2}O}\right)+\frac{3}{2}\log \left(p_{c_{2}o}\right)\right]$$

(11)

The equation for the reaction between methanol and oxygen can be represented by the potential $e_o$. The partial pressure of methanol present at the anode is denoted by $p_{C{H}_{3}OH}$. The partial pressure of water at the cathode is represented by $p_{H_{2}O}$, which equals 1 when liquid water is produced. The partial pressure of oxygen at the cathode is denoted by $p_{c_{2}o}$. The partial pressure of carbon dioxide is represented by $p_{c_{2}o}$. The universal gas constant is R (8.314 J/molK), Faraday’s constant is denoted by F (94,485 c/mol), and the number of electrons is represented by n. It is generally not possible to directly measure the pressures of CO₂ and H₂O experimentally. As a result, the term $-\frac{rt}{nf}\left[2\log \left(p_{H_{2}O}\right)+\frac{3}{2}\log \left(p_{c_{2}o}\right)\right]$ is assigned a value of C₁, which must be determined empirically. With this modification, the reversible voltage equation can be expressed as shown in Equation (12):

$$p_{rev}=e_o+\frac{rt}{nf}\left[\log \left(c_{C{H}_{3}OH}\right)+\frac{3}{2}\log \left(p_{o_2}\right)\right]+C_1$$

(12)

The variable “t” represents the temperature of the cell in Kelvin (K).

2.5. Fuel Cell Voltage Expression

Building on earlier theoretical work, the voltage of the fuel cell (V_cell) can be expressed using Equation (13) below:

$$v_{cell}=p_{act}-p_{con}-p_{rev}-p_{ohm}$$

(13a)

With

$$p_{act}=\frac{rt\left[\log \left(j_{max}+j_{eid}{e}^{\left(\frac{\alpha nf}{rt}\left(p_{con}-p_{ohm}-p_{rev}-v_{cell}\right)\right)}\right)-\log \left(j_{eid}\right)\right]}{\alpha nf}$$

(13b)

$$p_{ohm}=r{j}_{cd}$$

(13c)

$$p_{con}=-\frac{rt}{\beta nf}\ln \left(1-\frac{j_{max}}{j_{limit}}\right)$$

(13d)

$$p_{rev}=e_o+\frac{rt}{nf}\left[\log \left(c_{C{H}_{3}OH}\right)+\frac{3}{2}\log \left(p_{o_2}\right)\right]+C_1$$

(13e)

Equations (13a)–(13e) provide a set of expressions for the seven unknown parameters y in the form y = [$e_o$,$\alpha$,$r$,$j_{eid}$,$C_1$,$\beta$, r_eq].

2.6. Problem Formulation

In this study, the ELSHADE algorithm is introduced as an enhanced approach to parameter estimation for DMFCs. The algorithm uses optimisation techniques to predict the output voltage for a given current density input. The predicted output voltage is evaluated against the experimental values using SSE (sum of squared errors) as the metric. The objective function for SSE is given by Equation (14):

$$\mathrm{SSE}=MIN\left(F={{\displaystyle \sum }}_{i=1}^N{\left(V_{actual}-V_i\right)}^2\right)$$

(14)

Equations (15)–(21) present the constraints that apply to the DMFC.

$${\mathrm{e}}_{\mathrm{omin}}\le {\mathrm{e}}_{\mathrm{n}}\le {\mathrm{e}}_{\mathrm{omax}}$$

(15)

$${\beta }_{\min }\le \beta \le {\beta }_{\max }$$

(16)

$${\alpha }_{\min }\le \alpha \le {\alpha }_{\max }$$

(17)

$$r_{\min }\le r\le r_{\max }$$

(18)

$${j_{eid}}_{\min }\le j_{eid}\le {j_{eid}}_{\max }$$

(19)

$${\mathrm{req}}_{\min }\le \mathrm{req}\le {\mathrm{req}}_{\max }$$

(20)

$${C_1}_{\min }\le C_1\le {C_1}_{\max }$$

(21)

The experimental output voltage is denoted by $V_{actual},$ while $V_i$ represents the predicted output voltage obtained using different optimisation algorithms. With N representing the number of data points, the primary aim of this study is to minimise the SSE value to achieve improved performance, accuracy, and precision when estimating the DMFC parameters.

3. Materials and Methods

The DE approach was first proposed by Storn and Price [13]. SHADE secured third place in the IEEE CEC2013 competition, while LSHADE emerged as the winner in the CEC2014 competition [14]. This approach has been highly effective in tackling real-world optimisation problems [15]. In the basic DE algorithm, the mutation factor (G), crossover rate (DS), and population size (Q) are critical control factors that must be adjusted [16]. The population size Q consists of individual vectors (OQ), each of which has a decision variable (E). Therefore, j = 1, 2, ……, O_Q and k = 1, 2, ……, E. The maximum number of generations (H_Max) is used as a stopping criterion. Similar to other stochastic population-based search techniques, LSHADE utilises mutation, external archive, parameter adaption, crossover, and selection processes to determine optimal values for the optimisation problem. The LSHADE method can be divided into the following steps:

The first step, initialisation, involves generating an initial population by selecting random values for the decision variables within their feasible boundaries. Equation (22) represents the initialisation of the k-th decision variable’s j-th component [17]:

$$Y_{j,k}^{\left(0\right)}=Y_{min,k}+ran{d}_{j,k}\ast \left(Y_{max,k}-Y_{min,k}\right)$$

(22)

A value of $ran{d}_{j,k}$ is randomly selected from the range [0, 1], where “0” represents the population’s initial state. The next step involves mutation, which creates a random vector for each generation.

In the second step of the process, referred to as mutation, a mutant vector, denoted as $W_j^{\left(H\right)}$, is generated from each generation of the population using the “current-to-p-best/1” approach [14]. This mutant vector can be expressed mathematically as shown in Equation (23).

$$W_j^H=Y_j^H+G_j^H\left(Y_{pbest}^H-Y_j^H\right)+G_j^H\left(Y_{S_1^j}^H-Y_{S_2^j}^H\right)$$

(23)

From the OQ, two distinct vectors, namely $S_1^j$ and $S_2^j$, are randomly selected. The $Y_{pbest}^H$ refers to the highest-ranking vector from the set of Np*l(l € [0, 1]), where “l” denotes a control parameter that is expected to be small to promote more greedy behaviour. Additionally, $G_j^H$ represents the mutation scale parameters, which may be varied between generations.

The third step of LSHADE involves the use of an external archive to increase the diversity of the parent vectors, $Y_j^H$. When utilising the archive, $Y_j^H$ is selected from both the population and the archive Q u B. It is worth noting that Q and B are intended to be of the same size. If the size of the archive exceeds the limit of |B|, then certain items are removed to make room for new entries.

In order to create the offspring vector $V_j^H$, the adaptation of the mutation scale $G^H$ and crossover rate ${\mathrm{DS}}_j^H$ parameters is linked to the individual vector $Y_j^H$. The adaptation of these two parameters can be achieved through the use of Equations (24) and (25). This constitutes Step 4 of the process.

$$G_j^H=ran{d}_j \left(N_G, 0.1\right)$$

(24)

$$D{Q}_j^H=ran{d}_j \left(N_{DQ}, 0.1\right)$$

(25)

The values $ran{d}_j \left(N_G, 0.1\right)$ and $ran{d}_j \left(N_{DQ}, 0.1\right)$ are obtained from the Cauchy and normal distributions, respectively. It is important to note that the $G_j^H$ and $D{Q}_j^H$ values must lie within the range of [0, 1]. In cases where $G_j^H$ exceeds 1, it will be truncated, while if it is less than 0, Equation (14) will be iterated until a valid value is obtained. At the beginning of the analysis, N_G and N_DQ are both initialised to 0.5, as described in reference [15].

Assuming the offspring vector successfully competes with the parent vector at generation H, the current $G_j^H$ and $D{Q}_j^H$ values are considered to be effective and are consequently saved in T_G and T_DQ, respectively. Furthermore, at the conclusion of the generation, the contents of N_G and N_DQ memories are modified utilising the weighted Lehmer mean and weighted arithmetic mean, respectively, as exhibited in Equations (26) and (27) of reference [15].

$$N_{G,l}^H=\{\begin{array}{c}mea{n}_{XM} \left(T_G\right) if \left(T_G\right) \ne \varnothing \\ N_{G,l}^H, otherwise\end{array}$$

(26)

$$N_{DQ,l}^H=\{\begin{array}{c}mea{n}_{XB} \left(T_G\right) if \left(T_{DQ}\right) \ne \varnothing \\ N_{DQ,l}^H, otherwise\end{array}$$

(27)

The memory location to be updated is determined based on the index “l” which has a memory capacity of (I) where (I ≥ l ≥ 1). Whenever a new element is loaded into memory, the value of “l” is first set to 1 and then incremented. If the value of “l” exceeds the value of I, it is reset to 1. In case the individuals in generation H fail to produce an offspring vector, the memory update process will not take place.

In Step 5, the offspring vector $V_{j,k}^H$ is created by combining the components of the mutant vector $W_{j,k}^H$ with the target (parent) vector $Y_j^H$ using a binomial strategy. This process is represented in Equation (28).

$$V_{j,k}^H=\{\begin{array}{c}{W}_{j,k}^H if k=k_{rand} OR ran{d}_{j,k}\left[0,1\right]\le D{Q}_j^H\\ Y_j^H, otherwise\end{array}$$

(28)

The variable $k_{rand}$ is a random number chosen from the range of [1, E], and $D{Q}_j^H$ represents a value within the range of [0, 1].

In Step 6, a selection process takes place in which the parent and offspring vectors are compared, and the best fitting vector is selected for the subsequent generation. This process is represented by Equation (29).

$$Y_j^H=\{\begin{array}{c}{V}_{j,k}^H if g \left(V_j^H\right)\le g\left(Y_j^H\right)\\ Y_j^H, otherwise\end{array}$$

(29)

Step 7 involves the implementation of linear population size reduction in LSHADE, which improves its performance. In this process, the population size is dynamically decreased for every generation using Equation (30) [14].

$$O_q=round\left[\left(\frac{O_{q,min}-O_{q,ini}}{H_{max}}\right)\ast OGF+O_{q,ini}\right]$$

(30)

The population’s minimum number, denoted by $O_{q,min}$, is assumed to be 4, while $O_{q,ini}$ represents the initial size of the population. OGF stands for the number of fitness function evaluations, and $H_{max}$ refers to the maximum number of fitness function evaluations allowed for the population.

3.1. Improved Newton–Raphson Method

Traditional methods such as the NR and Lambert W function techniques are capable of handling nonlinear equations. However, these methods often converge quickly but not globally, leading to unfavourable outcomes. Moreover, their performance in classical form may deviate from the true and accurate root values. Therefore, it is essential to identify global solutions in a concise manner and within a few iterations. To address these concerns, the INR approach is proposed, which effectively improves the efficiency of identifying good initial condition values.

3.2. The Proposed Enhanced Algorithm

To enhance the convergence capabilities of the LSHADE algorithm and increase population diversity, it is split into two halves. The first half uses the “current-to-pbest/1” technique, as shown in Equation (13). In contrast, the second half utilises the guided-chaotic approach, represented by Equation (31) [18].

$$W_j^H=Y_{j,k}^H+ran{d}_1·\left(Y_{best,k}^H-Y_{j,k}^H\right)-P·ran{d}_2·\left(Y_{worst,k}^H-Y_{j,k}^H\right)$$

(31)

Equation (32) provides the expression for the chaotic perturbation, denoted as P.

$$y_{OGF}=4·Y_{OGF}·\left(1-Y_{OGF}\right)$$

where

$$P=y_{OGF+1}$$

(32)

Chaos possesses an advantage due to the presence of pseudo-random patterns in the cycles [19]. This chaotic distribution is employed to explore new search regions, resulting in a shift in the direction of the search from local to global [20].

4. Experiment and Results

To validate the proposed algorithm, a set of newly adopted metaheuristic algorithms including grey wolf optimiser (GWO) [21], LSHADE-W [22], LSHADE-NR [22], atom search optimisation (ASO) [23], and sine-cosine algorithm (SCA) [24] are utilised. The technical and operational data of the tested stack’s surface area of plate A is 25 cm². The cathode side oxygen pressure is 1.35 bar, and the reservoir side oxygen pressure is 1.5 bar. The flow rate of oxygen is 200 mL/min, and the flow rate of methanol is 1.94 mL/min. The temperature during the experiment was 80 degrees Celsius [25]. Table 2 shows the upper and lower boundaries of the control variables of the DMFC stack. The optimisation problem is resolved to estimate the values of the control variables ($e_o$, $\alpha$, $r$, $j_{eid}$, $C_1$, $\beta$, r_eq), which will be employed to develop an accurate model of the DMFC stack.

Table 2. DMFC lower and upper boundaries.

Parameters	Lower Boundaries	Upper Boundaries
$e_o$ (V)	0.83	1.23
$\alpha$	0	1
$r$	0	3
$j_{eid}$	0	0.3
$C_1$	−4.8	−0.5
$\beta$	0	2
req	0	50

4.1. Parameter Extraction

All programs were written in MATLAB 2020a and executed 30 times to evaluate the performance and efficiency of the proposed ELSHADE algorithm for estimating DMFC parameters in comparison to other algorithms such as GWO, LSHADE-W, LSHADE-NR, SCA, and ASO. Table 3 shows the parameters of the algorithm. Table 4 presents the DMFC parameter estimation results at STC (standard temperature condition) with SSE and computation time, while Figure 2 illustrates the scatter plot of the sum of the square error, standard deviation, and computation time at STC. Based on the scatter plot, it is observed that the proposed algorithm outperforms the other metaheuristic algorithms. The statistical findings of the DMFC are presented in Table 5. Additionally, Figure 3 shows the convergence curve at STC of DMFC, which indicates that the proposed algorithm has better performance than the other compared algorithms.

Table 3. Algorithm parameters.

Algorithm	Parameters	Values
SCA	Search agents	50
	Maximum iteration	1000
	a	2
	r1	a-t * ((a)/Max_iteration) (decreases linearly from a to 0)
	r2	(2 * pi) * rand
	r3	2 * rand
	r4	rand
ASO	Search agents	50
	Maximum iteration	1000
	Population of atoms (Atom_pop)	rand(Atom_Num,Dim). * (Up-Low) + Low
	Velocity of atoms (Atom_V)	rand(Atom_Num,Dim). * (Up-Low) + Low
GWO	Search agents	50
	Maximum iteration	1000
	Random Vector r1, r2	0, 1
	Coefficient Vector v	0 to 2
LSHADE-W	Search agents	50
	Maximum iteration	1000
	H	6
	$N^{init}$	$\mathrm{D} * r^{Nmin}$
	$N^{min}$	4
	$r^{Nmin}$	18
LSHADE-NR	Search agents	50
	Maximum iteration	1000
	H	6
	$N^{init}$	$\mathrm{D} * r^{Nmin}$
	$N^{min}$	4
	$r^{Nmin}$	18
	NR function
LSHADE-INR	Search agents	50
	Maximum iteration	1000
	H	6
	$N^{init}$	$\mathrm{D} * r^{Nmin}$
	$N^{min}$	4
	$r^{Nmin}$	18
	Lambert W function
	NR function

Table 4. DMFC parameter estimation.

Parameters/ Algorithms	SCA	ASO	GWO	LSHADE-W	LSHADE-NR	Proposed Algorithm (ELSHADE-INR)
$e_o$ (V)	0.8854	0.8475	1.2252	1.2292	0.8569	0.8499
$\alpha$	0.4231	0.4587	0.5507	0.2598	0.3587	0.8879
$r$	2.7859	1.0142	1.8523	1.3245	1.8200	1.4502
$j_{eid}$	0.1452	0.1847	0.2419	0.1295	0.1942	0.1076
$C_1$	−0.8559	−0.1124	−0.8235	−0.1124	−0.9614	−0.5418
$\beta$	0.1863	0.5347	0.2785	1.2503	0.1475	2.5048
req	21.617	12.870	25.755	21.117	32.159	17.852
SSE	1.16 * 10−03	1.11 * 10−04	2.08 * 10−04	1.03 * 10−04	1.35 * 10−04	1.13 * 10−05
Computation Time (s)	2.809	1.544	1.798	1.599	1.511	1.100

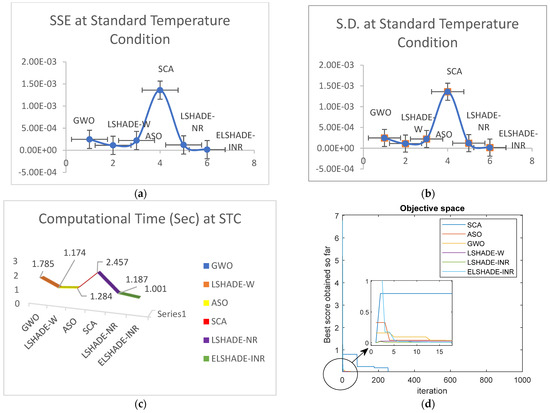
Figure 2. (a) Sum of square error, (b) standard deviation, (c) computational time, and (d) convergence curve at STC.

Table 5. DMFC Statistical Results.

Parameters/ Algorithms	SCA	ASO	GWO	LSHADE-W	LSHADE-NR	Proposed Algorithm (ELSHADE-INR)
Minimum	1.16 * 10−03	1.11 * 10−04	2.08 * 10−04	1.03 * 10−04	1.35 * 10−04	1.13 * 10−05
Maximum	2.06 * 10−03	2.20 * 10−04	3.85 * 10−04	2.00 * 10−04	2.07 * 10−04	1.55 * 10−05
Average	1.49 * 10−03	1.54 * 10−04	2.62 * 10−04	1.37 * 10−04	1.70 * 10−04	1.34 * 10−05
Standard Deviation (S.D)	3.91 * 10−04	4.15 * 10−05	7.36 * 10−05	3.70 * 10−05	2.70 * 10−05	1.74 * 10−06

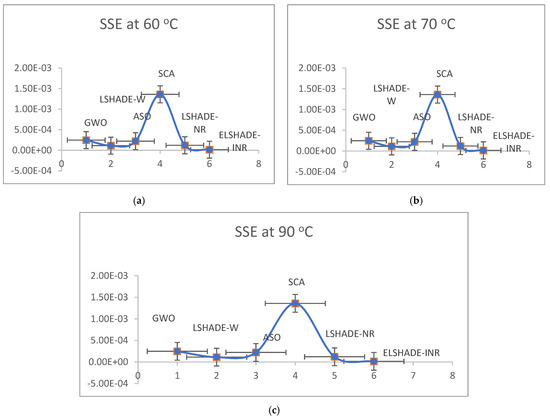
Figure 3. (a) Sum of square error at 60 °C, (b) 70 °C, and (c) 90 °C.

4.2. Convergence Analysis

Table 6 shows the parameter estimation of the DMFC at various operating temperatures (60, 70, and 90 °C), where SSE and computation time are calculated and presented. It is evident from this table that the proposed algorithm outperforms the compared algorithms in terms of both SSE and computation time. Figure 3 illustrates the SSE at different operating temperatures, confirming that the proposed algorithm is superior to the other algorithms. Additionally, Figure 4 depicts the computation time at various operating temperatures, which also demonstrates that the proposed algorithm is significantly more efficient than the other algorithms.

Table 6. Parameter estimation of DMFC at different operating temperatures.

Temperature (°C)	Parameters/Algorithms	SCA	ASO	GWO	LSHADE-W	LSHADE-NR	Proposed Algorithm (ELSHADE-INR)
60	$e_o$ (V)	0.8985	0.8785	0.8825	0.8874	0.8841	0.8501
	$\alpha$	0.1840	0.3623	0.2888	0.2376	0.2201	0.3103
	$r$	1.0152	1.2214	2.2853	2.9785	2.6786	2.0726
	$j_{eid}$	0.1076	0.1667	0.2552	0.1795	0.1841	0.1271
	$C_1$	−0.9614	−0.9618	−0.4041	−0.9660	−0.4711	−0.8377
	$\beta$	0.1063	0.0348	0.0287	0.0357	0.0287	0.0321
	req	21.171	14.457	20.061	11.957	16.835	21.523
	SSE	1.05 * 10−03	1.24 * 10−04	2.35 * 10−04	1.02 * 10−04	1.10 * 10−04	1.09 * 10−05
	Computation Time (s)	2.847	1.199	2.012	1.192	1.187	1.120
70	$e_o$ (V)	0.8254	0.8914	0.8795	1.18521	0.8695	0.8532
	$\alpha$	0.5011	0.4785	0.7991	0.5262	0.4203	0.5243
	$r$	1.4520	2.0598	2.6330	1.7230	2.7150	1.1961
	$j_{eid}$	0.1295	0.2453	0.1846	0.1198	0.1147	0.1559
	$C_1$	−0.8235	−0.2398	−0.1511	−0.9261	−0.7847	−0.9892
	$\beta$	0.0475	0.0125	0.3012	0.2085	0.5292	0.7713
	req	25.788	13.129	26.639	28.449	21.803	29.352
	SSE	1.36 * 10−03	2.21 * 10−04	2.47 * 10−04	1.12 * 10−04	1.21 * 10−04	1.50 * 10−05
	Computation Time (s)	2.598	2.147	2.195	1.258	1.267	1.110
90	$e_o$ (V)	0.8789	0.8758	0.8126	0. 8452	0.8012	0.8791
	$\alpha$	0.4211	0.7072	0.8982	0.9823	0.3454	0.1092
	$r$	1.8000	1.7850	1.5221	2.2335	1.5072	1.3422
	$j_{eid}$	0.1942	0.2853	0.1384	0.1574	0.2792	0.1564
	$C_1$	−0.1154	−0.8235	−0.1451	−0.1660	−0.1371	−0.1361
	$\beta$	0.2631	0.0792	0.1652	0.1752	0.2354	0.7041
	req	21.117	13.496	24.134	27.414	12.552	24.342
	SSE	2.26 * 10−03	2.61 * 10−04	4.64 * 10−04	1.85 * 10−04	2.04 * 10−04	1.95 * 10−05
	Computation Time (s)	2.457	1.284	1.785	1.174	1.187	1.001

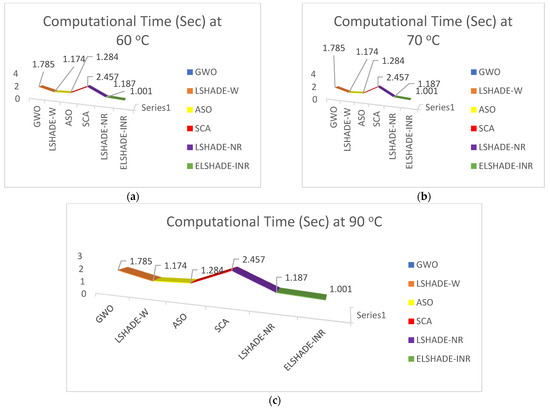
Figure 4. (a) Computational time at 60 °C, (b) 70 °C, and (c) 90 °C.

4.3. Non-Parametric Test

The statistical analysis results of the DMFC parameter estimation using the Friedman ranking test [26,27,28,29,30,31] are presented in Table 7. Based on the Friedman ranking, the performance of six different algorithms was evaluated to estimate the parameters of the DMFC. The proposed algorithm (ELSHADE-INR) achieved the highest rank, followed by LSHADE-NR and LSHADE-W at the second and third position, respectively. The GWO, ASO, and SCA algorithms achieved the fourth, fifth, and sixth ranks, respectively. The results clearly indicate that the proposed algorithm is more efficient, accurate, precise, and robust, performing significantly better than various other meta-heuristic algorithms. Additionally, the Wilcoxon rank sum test is applied to the samples, which is a secure and reliable non-parametric method for combined statistical analysis when samples are independent and dynamic programming is prominent. It is an easy but secure and reliable method for combined statistical analysis when samples are independent. Table 8 lists the calculated p-values and justifies that the performances of LSHADE-INR are significant at a significance level of 95%.

Table 7. Friedman ranking test.

Algorithm	LSHADE-INR	LSHADE-NR	LSHADE-W	GWO	ASO	SCA
Proposed Algorithm	1	2	3	4	5	6

Table 8. Wilcoxon Rank Sum Test.

Algorithm	LSHADE-INR	LSHADE-NR	LSHADE-W	GWO	ASO	SCA
Proposed Algorithm	3.4015 * 10−13	3.3092 * 10−13	3.3157 * 10−13	3.5841 * 10−13	3.1240 * 10−13	2.3587 * 10−13

5. Conclusions

In this paper, a new algorithm called ELSHADE-INR was introduced to obtain the optimal solution for the optimisation problem of DMFC parameter estimation. The key findings based on the results were as follows:

• A novel algorithm, ELSHADE-INR, was proposed.
• DMFC parameter estimation was performed using the proposed ELSHADE-INR algorithm at standard temperature conditions, and the obtained SSE and computational time values were compared with various other meta-heuristic algorithms. The results demonstrate that the proposed hybrid algorithm performs better and is more accurate.
• Convergence graphs and different operating temperature curves were obtained, which clearly show that the proposed algorithm has a faster convergence rate when compared to other meta-heuristic algorithms.
• A complete statistical analysis was conducted using the Friedman ranking test and Wilcoxon rank sum test to demonstrate the efficiency, performance, and robustness of the proposed algorithm. The ELSHADE-INR algorithm secured the first rank, indicating that it is the superior algorithm.

6. Future Scope

The proposed algorithm has effectively proven its competency in solving complex mathematical problems. It can be used for effectively estimating the unknown parameters of various renewable sources, for example, a solar three-diode model, economic load dispatch, and thermal scheduling.