A New Hybrid White Shark and Whale Optimization Approach for Estimating the Li-Ion Battery Model Parameters

Abstract

Constructing a reliable equivalent circuit of Li-Ion batteries using real operating conditions by estimating optimal parameters is mandatory for many engineering applications, as it controls the energy management of the battery in a hybrid system. However, model parameters can vary according to the electrochemical nature of the battery, so improving the accuracy of the battery model parameters is essential to obtain reliable and accurate equivalent circuits. Therefore, this paper proposes a new efficient hybrid optimization approach for determining the proper parameters of Li-ion battery Shepherd model equivalent circuits. The proposed algorithm comprises a white shark optimizer (WSO) and the whale optimization approach (WOA) for modifying the stochastic behavior of the WSO while searching for food sources. Minimizing the root mean square error between the estimated and measured battery voltages is the objective function considered in this work. The hybrid variant of the WSO (HWSO) was examined with two different types of batteries. Moreover, the proposed HWSO was validated versus a set of recent meta-heuristic approaches including the sea horse optimizer (SHO), artificial gorilla troops optimizer (GTO), coyote optimization algorithm (COA), and the basic version of the WSO. Furthermore, statistical analyses, mean convergence, and fitting curves were conducted for the comparisons. The proposed HWSO succeeded in achieving the least fitness values of 2.6172 × 10⁻⁴ and 5.6118 × 10⁻⁵ with standard deviations of 9.3861 × 10⁻⁵ and 3.2854 × 10⁻⁴ for battery 1 and battery 2, respectively. On the other hand, the worst fitness values were 6.5230 × 10⁻² and 6.6197 × 10⁻⁵ via SHO and WSO for both considered batteries. The proposed HWSO results prove the efficiency of the proposed approach in providing highly accurate battery model parameters with high consistency and a unique convergence curve compared to the other methods.

1. Introduction

Recently, energy storage systems (ESSs) have played an essential part in enabling the presence of various renewable energy sources (RESs) such as solar energy, wind, and fuel in the electric power grids. Integration of such systems to the grid makes it more flexible and reliable as they enhance the system management via acting as backup to unstable RESs. One of the most popular ESSs is the electrochemical battery. Constructing a reliable model for the battery represents a challenge due to the nonlinear nature of its operation. Identifying the most accurate model for the battery is still an abundant area of research. The parameters of the battery model can be identified with the aid of experimental data. Many works have been conducted in estimating the optimal parameters of the battery model.

Ferahtia et al. [1] identified the optimal parameters of lithium-ion batteries using an artificial ecosystem optimizer (AEO), the authors used the Shepherd model, and comparison in terms of convergence speed, efficiency, and identification accuracy was presented with other algorithms. The considered target was the root mean square error (RMSE) between the experimental and estimated battery data. In [2], the authors built a reduced model of a lithium polymer battery using state-space representation. Furthermore, the parameters of a constructed circuit were identified using three steps. In the first one, the battery state of charge (SOC) was estimated using nonlinear characteristics including the current and initial SOC. Then, the battery open circuit voltage was calculated based on the evaluated SOC in the first step, and the equilibrium algorithm (EA) was applied in the third step to identify the battery’s optimal parameters. Kim et al. [3] determined the parameters of a battery equivalent circuit via a Bayesian neural network with the aid of experimental data of battery voltage and current. A Li-ion battery equivalent circuit was formulated using a gradient-based algorithm employed to determine the equilibrium and dynamical parameters of the battery [4]. A complete review of different estimation methodologies employed in constructing battery equivalent circuits was presented in [5]. The authors categorized the battery model into mathematical, physical, and circuit-based models. A Wiener structure-based approach was introduced by Naseri et al. [6] to strengthen the battery classic equivalent circuit model via considering the nonlinearities of Li-ion batteries. Moreover, an extended-kernel iterative recursive least square approach was used for estimating the Wiener model parameters. In [7], the parameters of an electrochemical model of a Li-ion battery operated at different conditions were estimated using a particle swarm optimizer (PSO). The four parameters evaluated were the diffusion coefficients at anode and cathode as well as the intercalation and de-intercalation reaction rates at anode and cathode. The authors in [8] presented an estimation methodology to evaluate the parameters of a battery, SOC, and open circuit voltage. A hybrid Li-ion battery-supercapacitor energy storage system used in electric vehicles was modeled through identifying its parameters via experimental tests [9]. In [10], a Li-ion battery was modeled as a fractional-order equivalent circuit with its parameters estimated using a mixed swarm cooperative PSO with the aid of experimental data. A model of a Li-ion polymer battery was constructed using Simscape and Simulink/Matlab software, and its parameters were identified using an optimization toolbox in the used software [11]. Moreover, sum squared error (SSE) between the measured and calculated data was considered the fitness function to be minimized. In [12], a lead-acid battery equivalent circuit was built and the optimal parameters were identified experimentally. Additionally, the constructed model was validated via Matlab/Simulink. The authors in [13] used a resistance–capacitance equivalent circuit to simulate the dynamic behavior of a Li-polymer battery; additionally, the nonlinear relationship between the battery SOC and open circuit voltage was described using piecewise linear approximation with a variable coefficient. Moreover, the circuit parameters were evaluated using the moving window method to mitigate the least square error between the experimental and simulated data. In [14], an adaptive identification approach to find the battery circuit parameters was presented and the dynamics of the battery were simulated using a second-order equivalent circuit. The extended Kalman filter was used to identify the parameters in slow dynamics, while the recursive least square approach was used for fast dynamics. Different equivalent circuits of Li-ion batteries and several identification methods were reviewed in [15]; the authors classified the models into one-time constant, two-time constants, internal resistance, Thevenin, and others. Houssein et al. [16] presented a modified Coot algorithm (mCoot) to evaluate the optimal parameters of a Li-ion battery equivalent circuit and minimize the RMSE between the measured and estimated data. Du et al. [17] presented an on-line method of battery circuit parameter identification based on the Cramer–Rao lower bound; the authors validated the constructed model via comparing the obtained outputs with experimental data. The authors in [18] compared nine optimization algorithms employed to evaluate the optimal parameters of nine different battery models. The coevolutionary PSO-based methodology was used to evaluate the optimal parameters of a battery equivalent circuit with the aid of a parameter identification window in [19]. El-Sehiemy et al. [20] used the enhanced sunflower optimizer (ESFO) to identify the optimal parameters and SOC of a lithium-ion battery; a reduced state-space representation model was used to describe the operation of the battery. Single and multi-objective problems have been formulated considering either battery voltage or battery SOC or both as the targets. A Cuckoo search-based approach was employed to solve a multi-objective problem aimed at evaluating the optimal parameters of a Li-ion battery electrochemical model in [21]. The battery current and voltage were fed to the approach while the voltage error and the electrodes’ capacity error were the targets to be minimized. In [22], three different parameter identification methods were evaluated in constructing a battery Thevenin equivalent circuit. The methods were the PSO, extended Kalman filter, and recursive least square approach. Furthermore, the battery SOC was estimated via the model with identified parameters either at static or dynamic operations. Liu et al. [23] studied the electrochemical–thermal model of a Li-ion battery and sensitivity of parameter identification methods. Additionally, different design optimization methods under various operating conditions were analyzed. The battery surface and ambient temperatures were considered in an improved equivalent circuit of a Li-ion battery presented in [24]. A second-order RC equivalent circuit was considered, and its parameters were identified using an exponential function fitting method. Moreover, the battery SOC was estimated using the extended Kalman filter algorithm. Chun et al. [25] selected a deep learning algorithm of a convolutional neural network to evaluate the optimal parameters of a Li-ion battery equivalent circuit. In [26], a first-order equivalent circuit model of a Li-ion battery was experimentally constructed and its parameters were identified using the Cramer–Rao lower bound. A second-order RC model of a li-ion battery was established using the recursive least square approach in [27]. Shi et al. [28] estimated the Li-ion battery SOC using an adaptive extended Kalman filter, while the recursive least square approach with a forgetting factor was employed to estimate the optimal parameters of the battery equivalent circuit. Duan et al. [29] used the first-order RC model with parameters identified via the least square method of an extended Kalman filter to simulate the battery equivalent circuit. Moreover, a multi-time scale prediction model of an adaptive unscented Kalman filter was introduced to estimate the battery SOC. A methodology combining a neural network and a genetic algorithm (GA) was used to estimate the optimal parameters of a Li-ion battery circuit in [30]. A modified Thevenin model of a Li-ion battery was established and the model parameters were identified via a differential evolution algorithm in [31]. The parameter identification problem of a lead-acid battery Shepherd model was solved using a bald eagle search (BES) algorithm, such that the RMSE between the estimated and measured voltages was minimized in [32]. Some remarks of reported approaches employed in estimating the parameters of a battery equivalent circuit are given in Table 1. There are some shortcomings of the reported methods, which can be clarified as follows:

Table 1. Remarks of some reported works employed for constructing the battery circuit model.

Author	Year	Target	Method	Meta-heuristic	Battery Model	Limitations
Ferahtia et al. [1]	2021	RMSE	Artificial ecosystem optimizer	√	Shepherd model	The algorithm is easy to trap in local optima
Shaheen et al. [2]	2021	RMSE	Equilibrium algorithm	√	nRC-model	The algorithm has premature and slow convergence
Kim et al. [3]	2019	RMSE	Bayesian neural network	×	Pseudo-two-dimensional	Excessive data are required to train the neural network
Park et al. [4]	2018	Least square error	Gradient-based algorithm	√	Doyle fuller Newman model	The approach can go in the wrong direction because of frequent updates
Naseri et al. [6]	2021	MSE	Extended-kernel iterative recursive least square approach	×	Second-order RC	The least square approach has less desirable optimality characteristics
Rahman et al. [7]	2016	Sum square error	Particle swarm optimizer	√	Reduced partial differential	PSO has low convergence rate and easy to fall in local optima
Kwak et al. [8]	2019		Least square approach	×	First-order RC	The least square approach has less desirable optimality characteristics
Hu et al. [10]	2018	RMSE	Mixed swarm cooperative PSO	√	Fractional order	The presented approach required excessive computational efforts
Miniguano et al. [11]	2019	Sum square error	Matlab optimization toolbox	×	Five models	Nonlinear least square has less desirable optimality characteristics
Rahimi-Eichi et al. [13]	2013	Least square error	Least square approach	×	First-order RC	The least square approach has less desirable optimality characteristics
Dai et al. [14]	2016	RMSE	Extended Kalman filtering and recursive least square	×	Second-order RC	The least square approach has less desirable optimality characteristics
Houssein et al. [16]	2022	RMSE	Modified Coot algorithm	√	Shepherd model	The modified algorithm required large computational time
Du et al. [17]	2021	Absolute error	Cramer–Rao lower bound	×	Thevenin circuit	The algorithm is suitable for simple scenarios
Yu et al. [19]	2017	Sum absolute error	Co-evolutionary PSO	√	Third-order RC	The algorithm is complex, and the model hysteresis voltage is ignored
El-Sehiemy et al. [20]	2020	Sum square error	Enhanced sunflower optimizer	√	First-order RC	The modified algorithm required large computational time
Li et al. [21]	2022	Voltage error and electrodes’ capacity error	Cuckoo search	√	Pseudo-two-dimensional	Cuckoo search has slow speed and low convergence accuracy
Zhang et al. [22]	2021	Absolute error	PSO, extended Kalman filter, and recursive least square	√	Thevenin circuit	PSO has low convergence rate and easy to fall in local optima. Further, the least square approach has less desirable optimality characteristics.
Liu et al. [23]	2020	RMSE	Parameter sensitivity division approach	×	Pseudo-two-dimensional	The optimization approach is unclear
Huo et al. [24]	2020	Mean absolute error and RMSE	Exponential function fitting method	×	Second-order RC	The presented model ignored the temperature effects
Chun et al. [25]	2019	Least error	Convolutional neural network	×	Pseudo-two-dimensional	Excessive data are required to train the neural network
Song et al. [26]	2018		Cramer–Rao lower bound	×	First-order RC	The algorithm is suitable for simple scenarios
Ren et al. [27]	2020	Sum square error	Recursive least square approach	×	Second-order RC	The method is very sensitive to start values assigned by the user
Shi et al. [28]	2022	Mean absolute error and RMSE			Thevenin circuit
Duan et al. [29]	2020	RMSE	Adaptive double Kalman filter approach	×	First-order RC	The authors ignored the battery charge and discharge rates in the handled problem
Kim et al. [30]	2022	Least square error	Neural network and genetic algorithm	√	Pseudo-two-dimensional	Excessive data are required to train the neural network.
Shuai et al. [31]	2020	Absolute relative error	Differential evolution algorithm	√	Thevenin circuit	Differential evolution has slow convergence rate
Rezk et al. [32]	2022	RMSE	Bald eagle search algorithm	√	Shepherd model	The algorithm lacks adequate search efficiency and traps in local optima

• Some of the reported meta-heuristic optimization approaches suffer from premature and slow convergence rates; this defect causes trapping in local optima;
• Large computational times and efforts are other defects included in some other reported approaches in addition to excessive data that are required for training the neural network-based technique;
• Many researchers used algorithms that had less desirable optimal characteristics, while others ignored some important parameters such as battery temperature and hysteresis voltage.

These limitations are considered in this work via introducing an efficient, robust, and reliable hybrid approach comprising the white shark optimizer (WSO) and the whale optimization approach (WOA) to modify the stochastic behavior of the original WSO while searching for food sources.

The contributions of this work are given as:

• Proposing an efficient hybrid variant of the white shark optimizer for identifying the model parameters of two different Li-ion batteries with the Shepherd model;
• Using the spiral updating position strategy inspired by the whale optimization algorithm for enhancing the exploitation stage of the basic WSO;
• The proposed HWSO is validated versus SHO, GTO, COA, and WSO;
• Sets of statistical analyses, mean convergence, and fitting curves are conducted for the comparisons;
• The competence of the proposed HWSO is proved via the fetched results;
• Table 2 shows a comparison between the proposed approach and other methods in terms of complexity, required data, convergence rate, and trapping in local optima. The comparison clarifies the preference of the proposed methodology over the others;
  Table 2. Comparison between the proposed HWSO and others.

  Ref.	Required Data	Complexity	Convergence Rate	Trap in Local Optima?
  [1]	Few	Low	Fast	√
  [2]	Moderate	High	Slow	√
  [3]	Large	Moderate	Fast	×
  [4]	Moderate	High	NA	√
  [6]	Few	Low	Slow	NA
  [7]	Moderate	Low	Slow	√
  [8]	Few	High	Slow	√
  [10]	Few	High	Fast	×
  [11]	Moderate	Low	Slow	√
  [13]	Large	Moderate	Slow	√
  [14]	Large	High	Fast	NA
  [16]	Few	High	Fast	×
  [19]	Moderate	High	Fast	√
  [20]	Moderate	High	NA	NA
  [21]	Large	Moderate	Slow	√
  [25]	Large	Moderate	Slow	NA
  [27]	Large	High	Fast	√
  [28]	Large	High	Fast	√
  [30]	Large	High	Slow	√
  [31]	Large	Moderate	Slow	√
  [32]	Few	Large	Fast	√
  This work	Few	Low	Fast	×

• The rest of this paper is organized as follows: Section 2 handles the model of a Li-ion battery, Section 3 explains the main aspects of the WSO, Section 4 introduces the proposed hybrid WSO-based methodology, Section 5 shows the fetched results and discussions, and conclusions are given in Section 6.

2. The Li-Ion Battery Model

In this work, the considered battery is a Li-ion type with the Shepherd model given in [33], this model is selected as it needs little data from the datasheet given by the manufacturer and the discharge curve of the battery. The used model can easily reflect the characteristics of macro-level batteries for both voltage and current, which represents an important level of simulation. The equivalent circuit of the Shepherd model is given in Figure 1; it comprises a controlled voltage source and internal resistance. The value of the controlled voltage source depends on two formulas of battery charge and discharge modes. The terminal voltage of the battery can be expressed as follows [34]:

$$V_b=E_0-K\left(\frac{Q}{Q-it}\right)i-R·i+A·e^{-B·it},$$

(1)

where $E_0$ denotes the battery open circuit voltage at full capacity, $K$ is the polarization coefficient, $Q$ denotes the capacity of the battery, $it$ is the removed actual charge ($it=\int idt$), $i$ is the current of the battery, $R$ is the battery’s internal resistance, $A$ is the amplitude of the exponential zone, and $B$ represents the inverse time constant of the exponential zone. The modified Shepherd model given in [33] used polarization resistance effect and polarization voltage term in the discharge model as follows:

$$V_b=E_0-K\left(\frac{Q}{Q-it}\right)i^{*}-K\left(\frac{Q}{Q-it}\right)it-R·i+A·e^{-B·it},$$

(2)

where $i^{*}$ denotes the filtered current.

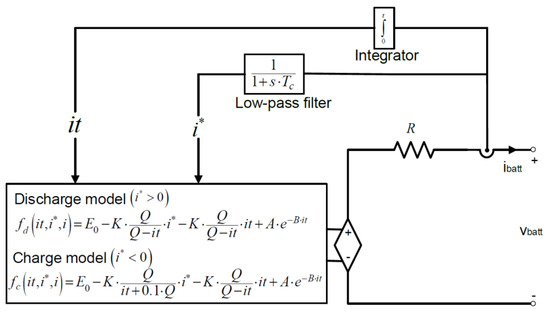
Figure 1. Li-ion battery model.

In the charging mode, the battery voltage can be written as [33]:

$$V_b=E_0-K\left(\frac{Q}{it-0.1·Q}\right)i^{*}-K\left(\frac{Q}{Q-it}\right)it-R·i+A·e^{-B·it}.$$

(3)

Additionally, the battery SOC of the battery can be calculated as follows [33]:

$$SOC\left(t\right)={SOC}_0-\frac{1}{Q}\int idt,$$

(4)

where ${SOC}_0$ represents the initial state of charge. Figure 2 shows the typical discharge characteristic of a Li-ion battery; Vfull, Vexp, and Vnom are the battery voltages at maximum capacity, at capacity during the end of the exponential zone, and at normal operation capacity, respectively.

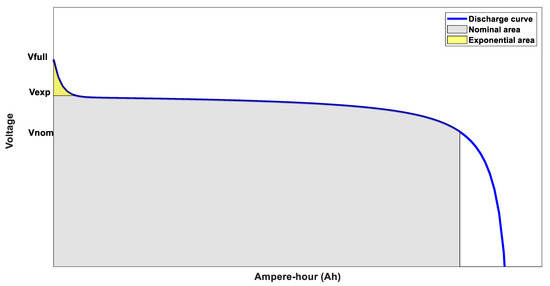
Figure 2. Typical discharge characteristic of a Li-ion battery.

In the manufacturer datasheet, there are some missing data, but they can be determined with the aid of a meta-heuristic approach and experimental data. In this work, the parameter identification process is simulated as an optimization problem with a fitness function of minimizing the RMSE between the estimated and measured battery voltages as follows:

$$Minimize J\left(k\right)=\sqrt{\frac{1}{n}\sum _{k=1}^n{\left(V_{be}\left(k\right)-V_{bm}\left(k\right)\right)}^2},$$

(5)

where $n$ is the number of data points, $V_{be}\left(k\right)$ denotes the battery’s estimated voltage at instant $k$, and $V_{bm}\left(k\right)$ represents the battery’s measured voltage at instant $k$. Seven parameters to be identified are $E_0$, $R$, $Q$, $K$, $A$, $B$, and τ.

The search space is identified via the following constraints [1]:

$$\begin{gathered} E_0^{min}\le E_0<E_0^{max} \\ {R}^{min}\le R<R^{max} \\ {Q}^{min}\le Q<Q^{max} \\ {A}^{min}\le A<A^{max} \\ {B}^{min}\le B<B^{max} \\ {\tau }^{min}\le \tau <{\tau }^{max}, \end{gathered}$$

(6)

where $min$ and $max$ denote the minimum and maximum limits, respectively.

3. White Shark Optimizer (WSO)

One of the most recent meta-heuristic approaches is the white shark optimizer (WSO), which has been proposed by Braik et al. [35]. The authors drew their inspiration for the algorithm from great white sharks’ dynamic behaviors, which include outstanding hearing senses and smell during navigating and foraging. The white sharks are highly adapted and magnificent hunters that have armed strong muscles and hunt dolphins, small whales, shellfish, seabirds, and seals, which represent their prey. The hunting strategy followed by great white sharks in catching their prey starts by rushing their prey via surprise tactics whereupon massive fatal strikes are generated.

Devouring the prey (food source) requires three behaviors, which are: the movement towards the prey using the waves’ hesitations produced via the prey’s movement, random search for food sources in the ocean depths, and locating nearby prey. These steps help the great white sharks in updating their positions to reach the best solutions. The WSO can be modeled via initializing a population matrix of initial solutions. I initial population matrix has a size of N × d, where N denotes the population size while d is the problem dimension, as follows [35]:

$$w=\left[\begin{array}{cccc}{w}_1^1& w_2^1& \dots & w_d^1\\ w_1^2& w_2^2& \dots & w_d^2\\ ⋮& ⋮& ⋮& ⋮\\ w_1^n& w_2^n& \dots & w_d^n\end{array}\right],$$

(7)

where $w_j^i$ represents the ith white shark location in the jth dimension. It can be calculated based on the lower (${lb}_j$) and upper (${ub}_j$) bounds of the search space in the jth dimension as [35]:

$$w_j^i={lb}_j+rand\times \left({ub}_j-{lb}_j\right),$$

(8)

where $rand$ is a random number within a range [0, 1]. The initial fitness values are calculated for the initial solutions given in Equation (7) and then an updating process is placed in case the new position is better than the previous one. When the great white shark observes the prey location via its wave hesitancy, it moves toward its prey in undulating movements with a velocity given as [35]:

$$v_{k+1}^i=\mu \left(v_k^i+p_1\left[w_{{gbest}_k}-w_k^i\right]\times c_1+p_2\left[w_{best}^{v_k^i}-w_k^i\right]\times c_2\right),$$

(9)

where $v_{k+1}^i$ and $v_k^i$ are the updated and current velocities of the ith white shark in iterations $k+1$ and $k$, respectively; $w_{{gbest}_k}$ denotes the global best location during the kth iteration; $w_k^i$ is the position of the ith white shark in iteration $k$; $c_1$ and $c_2$ are random numbers within a range [0, 1]; $w_{best}^{v_k^i}$ represents the ith best known location to the swarm during iteration $k$; and $v_k^i$ is the index vector number i for the great white sharks obtaining the best location, and it can be defined as follows [35]:

$$v=\left[n\times rand\left(1,n\right)\right]+1.$$

(10)

The parameters $p_1$ and $p_2$ are the great white sharks’ forces that control the $w_{{gbest}_k}$ and $w_{best}^{v_k^i}$ effects on $w_k^i$; they can be computed as follows [35]:

$$p_1=p_{max}+\left(p_{max}-p_{min}\right)\times e^{-{\left(\frac{4k}{K}\right)}^2},$$

(11)

$$p_2=p_{min}+\left(p_{max}-p_{min}\right)\times e^{-{\left(\frac{4k}{K}\right)}^2},$$

(12)

where $p_{min}$ and $p_{max}$ are the initial and inferior velocities to obtain better motion for the great white sharks, $p_{min}=0.5$ and $p_{max}=1.5$, and $K$ denotes the maximum iteration. The term $\mu$ in Equation (9) is the correction factor; it is used to analyze the convergence rate of the WSO via the following expression [35]:

$$\mu =\frac{2}{\left|2-t-\sqrt{t^2-4t}\right|},$$

(13)

where $t$ is the acceleration factor of the algorithm.

As stated before, the great white sharks spend most of time looking for valuable prey. Consequently, their positions change as they move toward their prey either by hearing the waves generated via prey movements or by smelling their prey’s scents. In this situation, the great white sharks move to random positions searching for the prey, this can be modeled as follows [35]:

$$w_{k+1}^i=\left\{\begin{array}{c}{w}_k^i•\neg \oplus w_o+ub•a+lb•b\hspace{1em}\hspace{1em}\hspace{1em}if rand<mv\\ \hspace{1em}{w}_k^i+\frac{v_k^i}{f}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}if rand\ge mv\end{array}\right.,$$

(14)

where $\neg$ is the operator of negation, $a$ and $b$ are binary vectors defined by Equations (15) and (16), $w_o$ represents logical vector computed via Equation (17), $f$ is the frequency of great white shark wavy motions and it can be calculated based on Equation (18) [35]:

$$a=sgn\left(w_k^i-ub\right)>0$$

(15)

$$b=sgn\left(w_k^i-lb\right)<0$$

(16)

$$w_o=\oplus \left(a,b\right)$$

(17)

$$f=f_{min}+\frac{f_{max}-f_{min}}{f_{max}+f_{min}},$$

(18)

where $f_{max}$ and $f_{min}$ are the maximum and minimum undulating frequencies of the great white shark’s undulating motions, respectively. The parameter $mv$ denotes the great white shark’s movement force; it is increased via the iterative process as follows [35]:

$$mv=\frac{1}{a_0+e^{\left(\frac{0.5K-5}{a_1}\right)}},$$

(19)

where $a_0$ and $a_1$ are two parameters used to manage the exploration/exploitation behaviors. The term $mv$ helps in accelerating the search speed and then strengthens the features of the exploration and exploitation behaviors of the WSO. This merit encouraged the author to apply such an algorithm in solving the handled problem. The motion towards the best great white shark that converges to the prey can be simulated as follows [35]:

$${\acute{w}}_{k+1}^i=w_{{gbest}_k}+r_1{\overrightarrow{D}}_w\times sgn\left(r_2-0.5\right)\hspace{1em}\hspace{1em}if r_3<S_s,$$

(20)

where ${\acute{w}}_{k+1}^i$ represents the ith great white shark new position with regard to its prey; the term $sgn\left(r_2-0.5\right)$ is responsible for changing the search direction as it gives either 1 or −1; $r_1$, $r_2$, and $r_3$ are random numbers within a range [0, 1]; and ${\overrightarrow{D}}_w$ represents the distance between the white shark and its prey as follows [35]:

$${\overrightarrow{D}}_w=\left|rand\times \left(w_{{gbest}_k}-w_k^i\right)\right|.$$

(21)

The parameter $S_s$ in Equation (20) is employed to describe the strength of the great white shark’s visual and olfactory senses when following its prey closely; it can be calculated as follows [35]:

$$S_s=\left|1-e^{\frac{-a_{2}k}{K}}\right|,$$

(22)

where $a_2$ is a parameter used to control the exploration/exploitation behaviors. A flowchart of the WSO is shown in Figure 3.

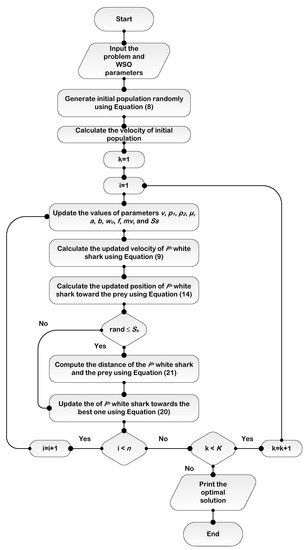
Figure 3. WSO flowchart.

4. The Proposed Hybrid WSO-Based Methodology

In the basic version of the WSO, the great white sharks follow one strategy while moving towards its prey location, which may cause the algorithm to be blinded to other optimal points around this location. Accordingly, another approach based on a spiral-shaped path has been integrated with the WSO in this work to enhance the exploitation behavior of the basic WSO. The implementation of the spiral-shaped path was inspired by whales’ behavior when swimming to prey locations, as reported in the whale optimization algorithm (WOA). The following relationship models the spiral path between the great white shark and its prey location:

$$W_{t+1}^i=\overrightarrow{D}·e^{hl}·cos\left(2 \pi l\right)+W_t^{*}$$

(23)

$$\overrightarrow{D}=\left|\overrightarrow{W^{*}}-\overrightarrow{W}\right|,$$

(24)

where $\overrightarrow{D}$ is the distance between the prey and the great white shark, $h$ is a constant for defining the shape of the logarithmic spiral, and $l$ is a random number in a range [−1, 1]. Using the spiral equation, the great white shark’s motion towards its prey, as in Equation (20), can be modified to be as follows:

$$w_{k+1}^i=\left\{\begin{array}{c}{w}_{{gbest}_k}+r_1{\overrightarrow{D}}_w\times sgn\left(r_2-0.5\right)\hspace{1em}\hspace{1em}\hspace{1em}if r_3<S_s\\ \overrightarrow{D}·e^{bl}·cos(2 \pi l)+w_t^{*}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}if r_3<S_s\end{array}\right..$$

(25)

The following pseudo code (see Algorithm 1) summarizes the main structure of the proposed HWSO when implemented for the battery model parameter estimation and optimization problem. In the first step, the lower and upper boundaries of the model parameters are assigned for generating the initial random set of solutions. Then, the corresponding initial objective function values in Equation (5) are calculated. Throughout the iteration numbers, the initial solution set is updated based on the main structure of the HWSO. Finally, the best determined parameters have been displayed after the termination criteria have been met.

Algorithm 1 A pseudo code summarizing the main structure of the proposed HWSO

1: Set the lower and upper limits of the battery model parameters 2: Determine the HWSO population size (n) and maximum number of iterations (K) 3: Generate the initial solutions (battery model parameters) set of WSO 4: Calculate the initial objective function of Equation (5) corresponding to the initial solutions 5: while (k < K) do 6:   Update the HWSO parameters using Equations (10)–(19) 7:   for i = 1 to n do 8:   Calculate the velocity using Equation (9). 9:   end for 10:  Ior i = 1 to n do 11:   if rand < $mv$ then 12:    Update the white shark’s location using Equation (14) first line 13:   else 14:    Update the white shark’s location using Equation (14) second line 15:   end if 16:  end for 17:  for i = 1 to n do 18:    if rand ≤ $S_s$ then 19:     Calculate the distance between the white shark the prey using Equation (19) 20:     Update the white shark location using Equation (25) first line 21:    else 22:     Update the white shark location using Equation (25) second line 23:    end if 24:   end for 25:   Evaluate and update the new battery model parameters 26:   k = k + 1 27: end while 28: Display the optimal battery model parameters obtained so far

5. Numerical Results and Discussions

The efficiency of the proposed HWSO in determining highly accurate battery model parameters was investigated using two sets of data for two different rates of lithium-ion batteries: The considered batteries’ nominal voltages (V) were 24 and 220, and the rated capacity (Ah) are 30 and 120, respectively. Furthermore, the battery model was simulated at an initial SOC of 100%, and the temperature effect was ignored in this work. The simulation time was selected as 10,000 s. The real data of both considered batteries are given in Table 3.

Table 3. Actual parameters of the considered batteries.

	${\mathit{E}}_0$ (V)	$\mathit{R}$ (Ω)	$\mathit{Q}$ (Ah)	K	$\mathit{A}$ (V)	$\mathit{B}$ (Ah−1)	$\mathit{\tau }$ (s)
Battery 1	26.0246	0.08	30	0.0045161	2.0154	2.0354	30
Battery 2	238.559	0.01833	120	0.01374	18.475	0.509	20

The HWSO was executed for 10 independent runs with a population size and iteration numbers of 25 and 150, respectively. Additionally, the simulated model of the battery was implemented for 3 s. For providing a comprehensive investigation of the HWO performance, it was compared with a set of recent optimizers including the sea horse optimizer (SHO), artificial gorilla troops optimizer (GTO), coyote optimization algorithm (COA), and the basic version of the WSO. All the algorithms were performed in the same settings for unbiased comparisons and statistical analyses were conducted. The mean convergence curves fetched by the proposed HWSO, basic WSO, and the other comparable techniques are depicted in Figure 4 in cases of determining the model parameters of batteries 1 and 2. The curves show that the proposed HWSO can escape from local solutions and converge to minimal objective function values versus the SHO and COA that are trapped to the objective function’s local values. Moreover, the proposed HWSO performances reveal remarkable behavior compared to the GTO and WSO as the spiral-motion path helps the algorithm discover better optimal values of the objective function. However, the convergence curves of the GTO and WSO illustrate the convergence of the algorithms after the first 130 iterations without updating that divulges their lacks in the efficient balancing between the exploration and exploitation cores.

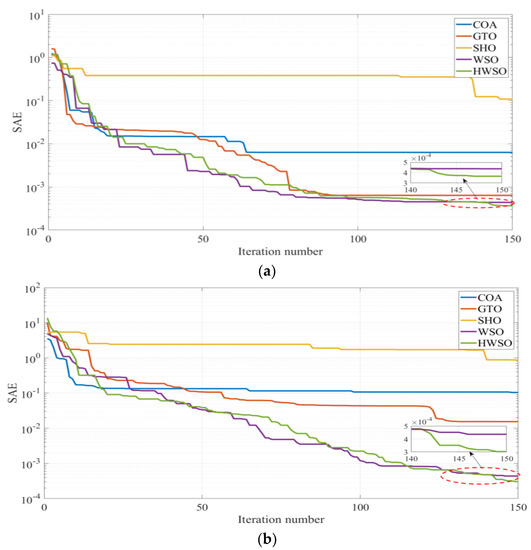
Figure 4. The mean convergence curves obtained with the HWSO, WSO, and other comparable techniques in the cases of (a) battery 1 and (b) battery 2.

The identified parameters of the battery model for the two studied types of batteries are reported in Table 4 and Table 5. It is worth noting that the estimated parameters with HWSO of Table 4 and Table 5 minimally deviate from the actual parameters in Table 3 of the two batteries studied. For evaluating the performance of the HWO statistically, Table 4 and Table 5 present the best, worst, mean, and standard deviation (SD) of the objective function. As per the reported data in the Tables, the proposed HWSO shows its superiority in achieving the least objective function values, 2.6172 × 10⁻⁴ and 5.6118 × 10⁻⁵, with high consistency compared to the other algorithms. Meanwhile, the SHO and COA performance affirm their disability in handling the battery modeling optimization problem. The WSO and GTO occupy the second and third ranks after the HWSO by reaching for objective functions of (2.9707 × 10⁻⁴, 5.8478 × 10⁻⁴) and (6.6197 × 10⁻⁵, 6.0177 × 10⁻⁴) regarding the two types of batteries, respectively. On the other hand, the work given in [1] achieved an objective function of 0.00900 with a standard deviation of 0.004595. For the second battery, the proposed algorithm outperformed the methodology given in [1]. Furthermore, the SD values prove the significant impact of integrating the spiral-motion path in enhancing the exploitation core of the optimizer; accordingly it realizes the optimal objective function value at each separate run.

Table 4. The identified parameters of the battery model and objective function values in the case of battery 1 using HWSO, WSO, and other comparable algorithms.

Model Parameters/Algorithm
Battery 1	COA	GTO	SHO	WSO	HWSO
$E_0$ (V)	26.110	26.107	26.236	26.155	26.213
$R$ (Ω)	0.0829	0.0824	0.0790	0.0800	0.0827
$Q$ (Ah)	29.579	29.941	29.500	29.754	29.977
$K$	0.0050	0.0049	0.0044	0.0055	0.0055
$A$ (V)	2.1373	2.1397	2	2.0846	2.0337
$B$ (Ah−1)	2.1090	2.1129	2	2.0720	2.0557
$\tau$ (s)	29.830	29.874	29.800	29.941	29.838
Best obj	3.6683 × 10−3	5.8478 × 10−4	6.5230 × 10−2	2.9707 × 10−4	2.6172 × 10−4
Worst	7.6792 × 10−3	6.8215 × 10−4	1.7342 × 10−1	6.0980 × 10−4	4.7305 × 10−4
Mean	6.6620 × 10−3	6.2419 × 10−4	1.2503 × 10−1	4.3774 × 10−4	3.9241 × 10−4
SD	1.9959 × 10−3	4.7959 × 10−5	5.6641 × 10−2	1.4213 × 10−4	9.3861 × 10−5
Computational time (s)	3912.605	4663.27	2567.456	919.074	1744.59

Table 5. The identified parameters of the battery model and objective function values in the case of battery 2 using HWSO, WSO, and other comparable algorithms.

Model Parameters/Algorithm
Battery 2	SSA [1]	COA	GTO	SHO	WSO	HWSO
$E_0$ (V)	238.556	238.009	238.859	238.890	238.682	238.568
$R$ (Ω)	19.1245	0.01548	0.01449	0.01278	0.01730	0.01918
$Q$ (Ah)	120.708	120.147	122.460	118	121.666	121.637
$K$	0.01374	0.01218	0.01293	0.01000	0.01250	0.01352
$A$ (V)	18.7152	18.9502	18.0755	18	18.3235	18.4857
$B$ (Ah−1)	0.50969	0.52409	0.53904	0.50000	0.52951	0.51050
$\tau$ (s)	19.9555	18.2464	19.7351	18	18.9890	19.5263
Best obj	0.00900	5.1578 × 10−2	6.0177 × 10−4	3.4100 × 10−1	6.6197 × 10−5	5.6118 × 10−4
Worst	0.019864	1.8692 × 10−1	7.2259 × 10−2	2.1958	9.7378 × 10−4	6.6383 × 10−4
Mean	0.009998	1.0384 × 10−1	1.8926 × 10−2	8.7029 × 10−1	5.1000 × 10−4	3.7127 × 10−4
SD	0.004595	5.9825 × 10−2	3.5557 × 10−2	8.8994 × 10−1	3.9079 × 10−4	3.2854 × 10−4

Additionally, the computational time is measured and tabulated in Table 4. the proposed HWSO consumed 1744.59 s, and thus it does not come in the first rank; however, the most important issue is achieving the least fitness value. On the other hand, the slowest approach is the GTO as it consumed 4663.27 s. To comprehensively evaluate the algorithms’ results, the notched boxplot based on an ANOVA test is plotted in Figure 5 to illustrate the variance in the objective function values over the set of independent runs. Moreover, the ANOVA tables are presented in Table 6 and Table 7 for the two batteries. The boxplots of Figure 5 provide evidence of the consistency of the HWSO as the variance between the objective function values throughout a set of independent runs is minimal in contrast to the SHO that shows a high difference between the minim, maximum, and median values (red mark in the middle of the box) of the objective function as illustrated for its boxplot. Moreover, the data of the ANOVA tables affirm the existence of a significant difference between the algorithms.

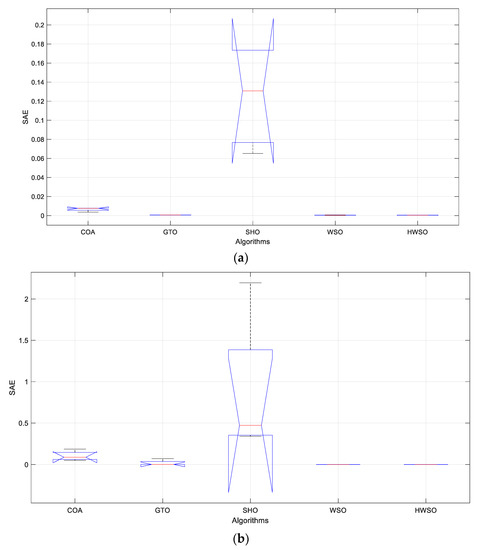
Figure 5. Boxplots of the objective function values obtained with the HWSO, WSO, and the other comparable techniques in the cases of (a) battery 1 and (b) battery 2 throughout the set of independent runs.

Table 6. ANOVA table in the case of battery 1.

Source	SS	df	MS	F	Prob > F
Column	0.04853	4	0.01213	18.89	1.01157 × 10−5
Error	0.00964	15	0.00064
Total	0.05817	19

Table 7. ANOVA table in the case of battery 2.

Source	SS	df	MS	F	Prob > F
Column	2.28387	4	0.57097	3.58	0.0305
Error	2.39051	15	0.15937
Total	4.67438	19

For testing the accuracy and efficiency of the identified parameters in representing the batteries’ behavior, the simulated model was implemented over a time horizon longer than that used in the optimization stage. The considered time of the simulation was 10,000 s. The fitted curves based on the identified parameters by HWSO and other techniques for the two batteries are depicted in Figure 6. The curves illustrate the high accuracy in the fitting while using the identified parameters of the HWSO that affirm its superiority in providing the highest quality solutions.

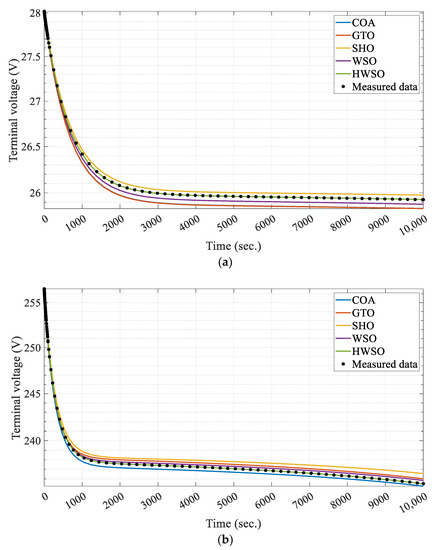
Figure 6. The fitted curves using the identified parameters by the HWSO, WSO, and the other comparable techniques in the cases of (a) battery 1 and (b) battery 2.

In order to validate the proposed HWSO, the current pattern shown in Figure 7 is applied on both considered batteries. The actual data given in Table 3 were used to collect the measured data. The measured and estimated SOC and terminal voltage via the proposed approach of battery 1 are shown in Figure 8; the results clarify that both data are closely matched. Furthermore, the measured and estimated data for battery 2 are given in Figure 9, and both curves converge. The obtained curves confirmed the preference of the proposed HWSO in constructing a reliable circuit of a Li-ion battery under a variable current pattern.

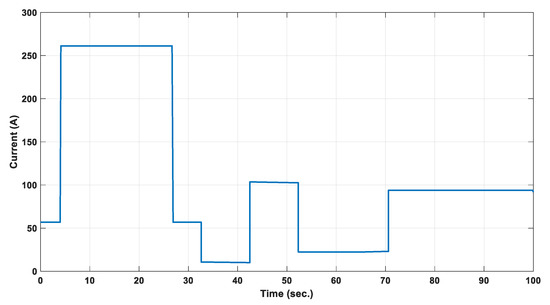
Figure 7. Battery current pattern.

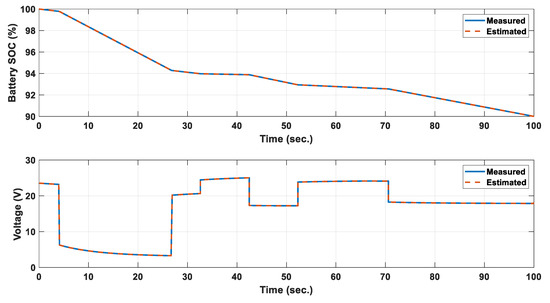
Figure 8. Measured and estimated SOC and terminal voltage of battery 1.

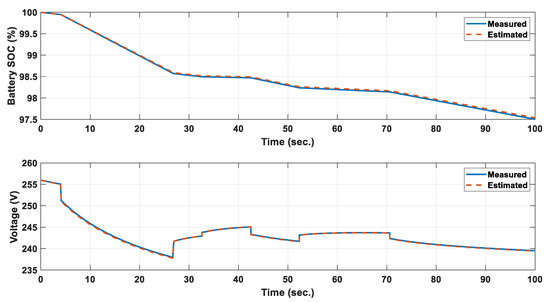
Figure 9. Measured and estimated SOC and terminal voltage of battery 2.

The obtained results affirmed the superiority of the proposed HWSO in constructing a reliable model of different Li-ion batteries.

6. Conclusions

This work aimed at solving the problem of the parameter identification of a Li-ion battery equivalent circuit with the aid of practical data. The goal was to obtain a model of the battery that simulates reality. This was achieved via proposing a new hybrid meta-heuristic approach comprising a white shark optimizer (WSO) and the whale optimization approach (WOA) for solving the problem of battery parameter estimation. The WSO stochastic behavior when searching for food was enhanced by incorporating the WOA. The importance of the proposed method lies in the fact that it overcame many of the problems encountered in previous methods, the most important of which being that of trapping in local optima. The Shepherd model of a Li-ion battery was constructed in Simulink/Matlab and the proposed HWSO was employed to determine the unknown parameters. The process was formulated as an optimization problem with an objective function to be mitigated of root mean square error between the measured and estimated voltages. Two types of Li-ion batteries with different capacities were analyzed and solved with the proposed HWSO. Furthermore, the approach was assessed by conducting excessive comparison with other optimizers, including the sea horse optimizer (SHO), artificial gorilla troops optimizer (GTO), coyote optimization algorithm (COA), and the basic version of the WSO. Moreover, statistical analyses, mean convergence, and fitting curves were conducted to assess the proposed HWSO. The fetched results revealed that the proposed approach outperformed all others with fitness values of 2.6172 × 10⁻⁴ and 5.6118e × 10⁻⁵ with standard deviations of 9.3861 × 10⁻⁵ and 3.2854 × 10⁻⁴ for battery 1 and battery 2, respectively, while the SHO and WSO were the worst optimizers with RMSE values of 6.5230 × 10⁻² and 6.6197 × 10⁻⁵, respectively. Moreover, the proposed HWSO outperformed the previous reported SSA approach that achieved an objective function of 0.00900 with a standard deviation of 0.004595. Furthermore, the statistical analyses confirmed the consistency of the HWSO, while the data of the ANOVA tables affirmed a significant difference between the comparable algorithms. The results proved the efficiency of the HWSO in establishing a highly accurate equivalent circuit for the Li-ion battery by identifying its optimal parameters. Future work will focus on applying the proposed method to construct equivalent circuits for several different batteries under different operating conditions. In addition, the battery charge and discharge rates will be considered in future works.