Abstract
With the rapid increase in new energy penetration, the uncertainty of the power system increases sharply. We can smooth out fluctuations and promote the more grid-friendly integration of new energy by combining it with energy storage. This paper proposes an evaluation method for assessing the value of a combined power plant system of new energy and energy storage using robust scheduling rules. Firstly, the k-means clustering algorithm is improved by using the elbow method in order to generate typical scenarios that can be used for the operation optimization of the combined power plant system of new energy and energy storage. Then, a two-stage robust optimization model of the combined power plant system of new energy and energy storage with a min–max–min structure is constructed according to the uncertainty of new energy. In this model, the operation constraints and coordinated control of wind–solar–thermal–storage units are considered. By constructing the uncertainty set of the new energy output, the overall operating cost of the system is minimized and uncertainty adjustment parameters are introduced to flexibly adjust the conservatism of the scheduling rules. Furthermore, based on the column and constraint generation algorithm and strong duality theory, the original problem can be decomposed into a master problem and subproblems with mixed integer linear characteristics for an alternating solution, so as to obtain the optimal solution of the original problem, and finally obtain the robust scheduling rule with the lowest operating cost under the worst scenario. Finally, based on the wind and solar power output curves and the output of each unit under the robust scheduling rules, combined with the value estimation method of the combined power plant system of new energy and energy storage, the value of the combined power plant system of new energy and energy storage is evaluated. Through the establishment of models and example analysis, it is proven that raising the quantity of the grid-connected power generated with new energy will cause an increase in the volatility of the power system; it will also bring considerable benefits to new energy plants, and the energy storage can improve the stability of the system. The above can provide references for the subsequent energy storage configuration in the planning of a combined power plant system of new energy and energy storage.
1. Introduction
Under the goal of “carbon peak, carbon neutral”, the use of new energy to reduce the proportion of traditional fossil energy and reduce the scale of carbon emissions is predominant in today’s energy development. Wind and solar energy are both forms of new energy, but both have instability and discontinuity, meaning that it is difficult to output stable power, and thus large-scale grid connection will have a non-negligible impact on the grid; therefore, the problem with new energy consumption is highlighted. Energy storage is a major way to reduce grid fluctuations caused by renewable energy generation, and it will play a unique role in the new power system. In order to promote the rapid development of new energy storage, in July 2021, the National Development and Reform Commission and the Energy Bureau jointly issued the “Accelerate the promotion of new energy storage development guiding opinions” [1], which put forward a sound combined power plant system of a new energy and energy storage project incentive mechanism. In order to support the construction or sharing mode implementation of new energy storage and new energy generation projects, a dynamic assessment of the system value and technology level, including competitive allocation, project approval (for the record), grid timing, system scheduling and operation arrangements, guaranteeing the number of hours of utilization, power auxiliary service compensation assessments, etc., to provide appropriate tilt, should be performed.
On the one hand, the joint operation of new energy units and energy storage provides an effective strategy to promote the system to consume new energy [2,3,4,5]. Jing et al. developed a mathematical model to optimize a hybrid solar–wind energy system with storage for a remote island with the genetic algorithm (GA) [5]. Liu et al. presented a capacity configuration optimization model that takes into account the demand response of domestic appliances in wind/solar/pumped storage and island microgrids and uses a particle swarm optimization (PSO) algorithm to obtain the optimal sizing of all the major pieces of equipment [6]. Li et al. proposed an optimal capacity configuration method for the grid-connected wind–photovoltaic–pumped–storage joint operation system and solved the model using the fast and elitist non-dominated sorting genetic algorithm-Ⅱ (NSGA-Ⅱ) [7]. The above studies evaluated the economic performance of the combined wind–optical–storage system and solved the optimal capacity allocation scheme of the system.
However, all of these studies only considered the system economics and did not study the reliability. Ma et al. took the lowest initial investment cost and contact line fluctuation as the optimization objectives and used dynamic planning methods to optimally allocate the energy storage capacity, while guaranteeing the system stability and economy [8]. Nguyen et al. investigated the optimal capacity allocation of the system under a zero-load shortage rate and evaluated the energy cost of the system [9].
On the other hand, the generation power of new energy, such as wind and solar, has an inherent uncertainty characterized by intermittency and stochasticity, which makes it difficult to predict accurately. Considering the uncertain schedulability of the new energy sources’ output power, achieving the economic and reliable operation of the power grid has become a hot research topic. Planning methods considering uncertainty comprise stochastic planning, scenario planning, and robust optimization [10,11]. Robust optimization has received increasing attention because the exact probability distribution of uncertainties is not required, and only their fluctuation ranges need to be counted [12]. Cho et al. considered the economic dispatch problem under the scenario of the maximum cost of the microgrid and distribution network interaction, constructed a min–max robust optimization model, and transformed it into a single-layer optimization problem for the solution using the scenario generation method [13]. Wang et al. built a two-stage robust model with a min–max–min structure, which considers standby scheduling and the economic dispatch mode under multiple scenarios of wind power [14]. However, the robust models in the above literature are unable to flexibly adjust the conservatism of the scheduling scheme. Chen et al. proposed a distributional uncertainty model where the probability distribution of load power can vary around a given reference distribution [15]. In addition, the fluctuation of the real-time electricity price is taken into account in the model, and regulation parameters are introduced in the objective function to control the robustness of the optimization scheme.
Meanwhile, the optimal scheduling of power systems considering the uncertainty of renewable energy operation has also been extensively studied by scholars [16,17,18]. A multi-timescale optimal scheduling model based on the wind power uncertainty and demand response was proposed to address the uncertainty of wind power integration, and during real-time scheduling, the deviation remaining after intraday scheduling is corrected [19]. Lu et al. proposed a multi-agent deep reinforcement learning (MADRL)-based algorithm with the strategic goal of achieving the real-time optimal scheduling of ADS, in which the uncertainty of renewable generations (RDGs), loads, and electricity prices is considered. While there has been significant research on the optimal operation of renewable energy systems, there is still a gap in proposing a stochastic-based optimization model that takes into account the uncertainties of both renewable energy resources and electricity prices simultaneously [20]. Emrani-Rahaghi et al. aimed to address this gap by introducing a probabilistic scenario-based model that considers both the uncertainties of renewable energy sources and electricity prices [21]. Integrating the energy storage system (ESS) optimally is the best solution so far. Al Ahmad derived and generalized a probabilistic distribution in order to consider the uncertainties of wind generators [22]. Moreover, a mixed integer non-linear optimization problem was constructed comprising three objective functions to be minimized simultaneously. The objectives comprised the total operation and planning cost of ESSs, the average voltage deviation, and average power losses. Lei et al. proposed an optimal operation strategy of hydro-unit level coordinated peak shaving and economic operation in a hydro–wind–PV hybrid system under uncertain conditions of wind and PV power [23]. This article described the uncertainty of wind and PV power using Latin hypercube sampling and scenario reduction methods, and a two-layer optimization model that considers wind and PV uncertainty is then established. Han et al. proposed a bi-level scheduling model to maximize the net revenue of the LSE from optimal DR bidding and energy storage system (ESS) scheduling by considering the impacts of the uncertainty of the demand response, and an online learning method was adopted to improve aggregation reliability [24]. Li et al. proposed a near-zero carbon emission power plant (NZCEP), integrating gas turbines, wind turbines, power-to-gas, and a carbon capture, utilization, and storage system, and a two-stage data-driven set-based robust optimization (DSRO) model, including a day-ahead dispatching phase and a real-time adjustment phase, was applied to ensure the consumption of renewable energy resources and to develop the optimal operating strategy for NZCEP participation under the electricity-carbon market [25].
Although the above studies have examined the joint operation of new energy and storage and the optimal scheduling of the power system taking into account the uncertainty of the new energy sources, there are no studies on the valuation of the system of “new energy + storage” power plants. By pricing the system’s capacity, which utilities can use in the capacity market based on the amount of that capacity they supply to the grid, one can gain a clearer understanding of the significance and economic advantages of the system. In order to better utilize the system’s potential advantages, provide relevant stakeholders a basis for decision-making, and advance sustainable energy, assessing the capacity value of a NESPS system can provide crucial information for the development of its economic planning and financial structure. It can also reveal the value of the NESPS system in terms of its reliability, flexibility, and economics. This will serve as a foundation for decision-making by pertinent stakeholders and support the growth of sustainable energy sources, as well as the modernization and transformation of the power system.
Therefore, this paper first determines the number of clusters of the k-means algorithm based on historical data using the elbow method, so as to obtain typical scenarios. Secondly, it proposes a robust scheduling rule for the uncertainty of wind power, and then, it improves the operation model of the combined power plant system of new energy and energy storage constructed with the objective of minimizing the comprehensive operation cost. The optimization model is improved, and the column and constraint generation algorithm and strong dyadic theory are used to transform the original problem into the main problem and sub-problems with mixed-integer linear forms. Finally, based on the robust scheduling scheme obtained from the solution, the system value of the combined power plant system of new energy and energy storage is evaluated by changing the energy storage capacity and the amount of new energy allowed to be fed into the system, which can be used as a reference for the subsequent configuration of energy storage capacity in the combined power plant system of new energy and energy storage.
The purpose of this study is to expand existing research in the following ways. In the introduction, we outline the main objectives of the study by introducing the background of the study, through a comprehensive review of the sustainable development literature, analyze the shortcomings of the existing research, and discuss the latest developments and trends in more depth. Section 2, using the uncertainty scenario reduction method, replaces the initial number of scenarios with scenarios built from several scenarios to simulate the scenarios encountered in the optimized operation of the new energy and energy storage combined power plant systems. In Section 3 and Section 4, we use robust optimization methods to solve the random properties of the scene output, and for the uncertainty of the new energy output, we build a two-stage robust optimization model to obtain the least costly robust scheduling rules in the harshest scenarios. In Section 5, for the two-stage robust optimization model described above, the column constraint generation algorithm is used to improve the optimization, effectively reducing the number of iterations and solving time. In Section 6, an annual wind/photovoltaic integrated scene set is selected to analyze the typical reduction scenarios and test the effectiveness of the improved algorithm and model. Section 7 summarizes the results of this study and illustrates its significance and importance.
2. Scenario Generation and Reduction Method
This section addresses the problems encountered in optimizing the operation of the combined power plant system of new energy and energy storage. It is necessary to improve the computational efficiency based on ensuring the accuracy of the original time sequence of the new energy. The advantages of scene reduction are reflected in the more complex scenarios that can be generalized by fewer typical scenarios, and the complexity of the computation is improved by reducing the number of similar scenarios in scenario generation by means of mathematical algorithms and other tools. In studying the new power system scheduling planning in line with the “dual carbon” target, as the length of time in the scheduling interval grows, this results in an exponential increase in the total number of generated scenarios, with multiple consecutive point-in-time scenarios producing “dimension disasters”. With the uncertainty scenario reduction method, the initial number of scene sets is replaced by a set built from a few scenarios. It is possible that the reduced scenes can achieve the purpose of maximally restoring the initial scenes in terms of probability.
2.1. K-Means Clustering Algorithm Based on the Elbow Method
The typical scenarios obtained from the combined power plant system of new energy and energy storage can better describe the probability distribution characteristics of the initial data because of the large number of clusters, but at the same time, if the number of clusters is too large, this can result in an increase in the complexity of the calculation of the subsequent model. For the purpose of improving computational efficiency, it is necessary to use the method based on the initial data characteristics to find the optimal number of clusters, and the elbow method has the characteristics of a simple procedure, and correcting the general k-means algorithm cannot determine the optimal number of shortcomings of the number of clusters, and therefore, this becomes the mainstream algorithm for determining the number of clusters.
The specific principle of the elbow method [26] is to define the clustering error (SE) with the help of the ratio of the average distance within clusters (nSE) and the average distance between clusters (wSE) in the following form:
where is the i-th cluster, represents the elements in , refers to the mean value of the elements in , and is the number of elements in .
When the number of initial elements increases, the degree of division of each sample will also become more detailed, and all the clusters will reach a more ideal degree of aggregation, which will lead to a decrease in the nSE; as the number of initial elements increases to a certain degree, the wSE is also smaller, but the SE is not necessarily small, so it is concluded that only when the nSE takes a smaller value, while the wSE takes a larger value, will it lead to a smaller value of the clustering distance. In the case where the number of clusters k is smaller than the actual number of clusters, increasing the value of k and reducing value of wSE will result in a larger drop in the value of nSE, which in turn will cause a large drop in the value of SE. In the case where the value of k is taken to be the actual number of clusters, increasing the value of k and slowing the reduction in nSE will result in only a slight change in the value of wSE, which ultimately results in the slowing of the drop in SE, and the overall curve takes on an elbow shape, and the value of k represented by the elbow is the true clustering number.
The k-means clustering algorithm based on the elbow method [27] searches for the most suitable cluster number in the search range of cluster numbers with the help of the elbow method, and the main steps are summarized as follows:
- Sept 1: Set the number of clusters as k and take any one of all of the initial scenes as the cluster center K1.
- Sept 2: Compare the distance between other scenes and the clustering center K1, and take the scene with the largest distance from K1 as the new clustering center K2; then, compare the distance between other scenes outside the two clustering centers and the two clustering centers, and take the scene with the largest distance as the new clustering center K3, and repeat the above steps to finally obtain k initial clustering centers.
- Sept 3: Redetermine the cluster centers of all clusters by comparing the distances between the scenes outside the cluster centers and all the cluster centers, and classify these scenes to the cluster center with the smallest distance from each other.
- Sept 4: Use the sum of the squares of the distances between all the scenes and the clustering center, according to which the scene is classified as the clustering error H. When there is a situation where the value of the clustering error H subtracted from the clustering center of two iterations is smaller than a certain convergence accuracy, the iteration ends and the clustering center of the last iteration is obtained—otherwise, repeat step 3.
2.2. Typical New Energy Scenario Generation and Reduction Method
The typical scenario reduction method involves generating typical scenarios that can be used for the scheduling optimization of a combined power plant system of new energy and energy storage by analyzing and processing new energy data in a combined power plant system of new energy and energy storage. For example, for the typical scenario of PV output in a combined power plant system of new energy and energy storage, the typical scenario reduction method reduces and recreates the scenarios with the help of the basic unit of clustering with the unit of days. If the total number of the original PV output scenarios is M, each day’s PV data are regarded as scenario m (m = 1, 2, … M), and each scenario m contains the PV output data of T time points, it is possible to use an M × T scenario to describe the output scene. Therefore, the entire PV output scene can be described with the help of an M × T order matrix. Based on the clustering algorithm, all the initial scene data are compared and analyzed, the initial M scene data are merged and finally reduced to obtain K scenes, a K × T order matrix is used to describe the typical PV scenes, and there are Nk initial scenes in the kth typical scene. With the help of the typical scene reduction method, the aim of reducing the number of scenes is achieved, and the timing of the typical initial data is not changed at the same time due to the fact that the timing of the data at T time points within the scene is not changed.
A finite number of discrete scenarios are used to represent the operating states of the wind and light power at T time points in the future, and each scenario corresponds to a time series of operating states, i.e.,
where is a certain prediction scenario; is the set of all prediction scenarios; wT(s) denotes the superimposed power value of wind and PV in the t-th time period under scenario ; and are the wind and PV power in the t-th time period under scenario , respectively; and is the value of the flexibility time scale.
Based on the wind and PV power at time t under a certain prediction scenario, the clustered wind-scenery combination scenario is reduced to a wind and PV treatment scenario based on the principle of linear proportional sharing, i.e.,
where and are the wind and PV power values at time t under the decomposed scenario s.
3. Robust Scheduling Rules
Robust optimization methods [26,27] are used to address the stochastic nature of the scenery output, i.e., an ensemble is used to portray the uncertainty. The specific mathematical meaning of is to denote the degree of fluctuation in the wind power output at moment t. This degree of fluctuation is based on the predicted value of the wind power output, which floats up and down within a given deviation interval.
where and denote the predicted values of PV output and load power in section t, respectively; denotes the predicted aggregated power value of the combined wind and PV outputs at moment t; and is the fluctuation value of the wind and solar outputs introduced by considering the uncertainty [28].
The uncertainty power constraints are expressed as follows:
where is the regulation capacity of the system flexibility unit at moment t, .
The uncertainty parameter constraints are expressed as follows:
where is the permissible fluctuation ratio of the scenery output at moment t.
For the solution of the uncertainty interval , the optimal robust scheduling interval is obtained from the following equation.
where and are the values of the left and right endpoints of the uncertainty interval, which are expressed as the minimum and maximum permissible fluctuation deviation of the wind power output, respectively; and the upward and downward flexibility adjustable power is provided by the conventional generating units, energy storage, and demand response, respectively.
4. Robust Optimal Scheduling Model for a Combined Power Plant System of New Energy and Energy Storage
This section addresses the uncertainty of new energy output. Using the box-type uncertainty set model to portray the new energy power uncertainty, considering the power generation characteristics of wind, light, fire, and energy storage units, to minimize the overall operating costs of the system, a two-stage robust optimization model of min–max–min structure is established. Robust scheduling rules with the lowest operating costs for the harshest scenarios are available. The model takes into account the operating constraints and coordination control of each unit in the system and introduces uncertainty adjustment parameters, which can adjust the conservatism of the scheduling scheme flexibly. Based on the column constraint generation algorithm and strong dual theory, the original problem can be solved alternately by decomposing it into the main problem and the sub-problem with the linear feature of a mixed integer.
4.1. Optimization Objectives
Considering the power generation characteristics of wind–optical–thermal–storage units and the system operation constraints, the operating objective of the system is to minimize the comprehensive operating cost, which mainly includes the operating cost of the thermal power system and the operating cost of the power station’s energy storage, among which the operating cost of the thermal power system consists of the cost of the thermal power unit’s coal consumption and the cost of pollutant emission, and the cost of the power station’s energy storage mainly consists of the cost of the charging/discharging of the energy storage.
where is the comprehensive operating cost, is the system thermal power operating cost, and is the charging and discharging cost of energy storage.
The system thermal power running cost is calculated as follows:
where is the cost of coal consumption and is the cost of pollutant emissions.
- (1)
- Coal consumption cost
The coal consumption cost of thermal power unit i at moment t is expressed as a quadratic function of the output:
where is the active output of thermal power unit i at moment t, and , , , are the fuel coefficients of thermal power unit i.
- (2)
- Pollutant emission cost
The cost of energy storage charging and discharging is calculated using Equation (17):
where is the discounted unit charge/discharge cost; and denote the storage charging/discharging power at time t, respectively; and η is the charge/discharge efficiency of the storage.
4.2. Constraints
The model constraints include constraints on the operating characteristics of the units, such as thermal power and energy storage, as well as constraint limitations on system operation, as follows:
- (1)
- Thermal power unit constraints
Thermal power units in the operation process are mainly subject to the unit power and climbing slippage rate and other constraints. The thermal power unit operation power constraints and climbing constraints are as follows:
where RU and RD are the upper and lower limits of the climbing slope of the thermal power unit, respectively; is the active power output of thermal power unit i at the moment of t − 1.
- (2)
- Energy storage constraints
The constraints to be satisfied by energy storage during the operation mainly include energy storage charging and discharging power constraints, energy storage charging and discharging quantity balance constraints, residual capacity constraints of energy storage in each time period, and energy storage charge state constraints.
The energy storage charging and discharging power constraints are as follows:
where is the maximum allowable charge/discharge power of the energy storage. denotes the charge/discharge state of the energy storage, where a value of 1 means discharge and a value of 0 means charge.
The energy storage charging and discharging capacity balance constraint is as follows:
The energy storage charging and discharging quantity balance constraint ensures that the capacity of the energy storage is equal at the beginning and end moments of the scheduling, which is conducive to the cyclic scheduling of the energy storage, and NT is the scheduling period, which takes the value of 24 h.
The residual capacity constraint of the energy storage in each time period is as follows:
where is the capacity of energy storage at the initial moment of scheduling, and and are the maximum/minimum residual capacities of energy storage allowed in the scheduling process. The main purpose of this constraint is to prevent the overcharging/overdischarging of the energy storage and to extend the service life of the energy storage [29].
The energy storage charge state constraint is as follows:
where is the time step, taken as 1 h; is the initial power of the energy storage; and are the upper and lower limits of the charge state of the energy storage, respectively; and is the efficiency of energy storage charging and discharging.
- (3)
- System operation constraints
The system operation constraint is mainly the system power balance constraint:
where and , respectively, are the uncertain variables of PV and wind power in the t-th time period.
4.3. Improved System Optimization Model Based on Robust Scheduling Rules
The objective of the robust optimization model of the system, improved based on robust scheduling rules, is to find the economically optimal scheduling scheme when the uncertain variable u changes towards the worst-case scenario within the uncertainty set U. The equivalent robust optimization model is as follows:
where the minimization in the outer layer is the first stage problem with the optimization variable x, and the maximum minimization in the inner layer is the second stage problem with the optimization variables u and y, where the minimization problem is equivalent to the objective function shown in Equation (26), which denotes the minimization of the operating cost:
The expressions for x and y are shown in Equations (27) and (28).
where denotes the feasible domain of the optimized variable y given a set of with the following expression:
where denote the dyadic variables corresponding to each constraint in the minimization problem of the second stage.
For each given set of uncertain variables u, Equation (25) reduces to a deterministic optimization model, and the purpose of the max structure in the second-stage optimization problem of the two-stage robust model is to find the worst-case scenario that results in the largest operating cost.
5. Solution Algorithm Based on C&CG
For the above two-stage robust optimization model, the column constraint generation (C&CG) algorithm is used to solve the model [30]. Similar to the Benders decomposition algorithm, the C&CG algorithm also obtains the optimal solution of the original problem by decomposing the original problem into a master problem and sub-problems and solving them alternately. The difference between the two is that the C&CG algorithm continuously introduces variables and constraints related to the subproblems during the process of solving the main problem, which can obtain a more compact lower bound on the value of the original objective function, thus effectively reducing the number of iterations.
The decomposition of Equation (25) yields a master problem in the form of the following:
where k is the current number of iterations, is the solution of the subproblem after the lth iteration, and is the value of uncertain variable in the worst scenario obtained after the l-th iteration.
The form of the subproblem after decomposition is as follows:
According to the strong dual theory, it can be transformed into max form and merged with the outer max problem to obtain the following dual problem:
There exists a bilinear term in Equation (32), and the corresponding to the optimal solution of this dual problem is a pole of the uncertainty set U; that is to say, when Equation (32) is taken to its maximum value, the value of the uncertain variable u should be the boundary of the fluctuation interval. In addition, in the “new energy + storage” power plant system, when the wind power and photovoltaic outputs are taken as the minimum value of the interval, the operating cost of the system is higher, which is more in line with the definition of the “worst-case” scenario. By introducing auxiliary variables and relevant constraints to linearize it, the sub-problem can be obtained in the form of the following:
where and denote the introduced continuous auxiliary variable and the upper bound of the dyadic variable, respectively, which can be taken as a sufficiently large positive real number.
After the above derivation and transformation, the two-stage robust model is finally decoupled into the main problem Equation (30) and sub-problem Equation (33) with a mixed-integer linear form, which can then be solved using the C&CG algorithm, and the flow is shown in Figure 1.
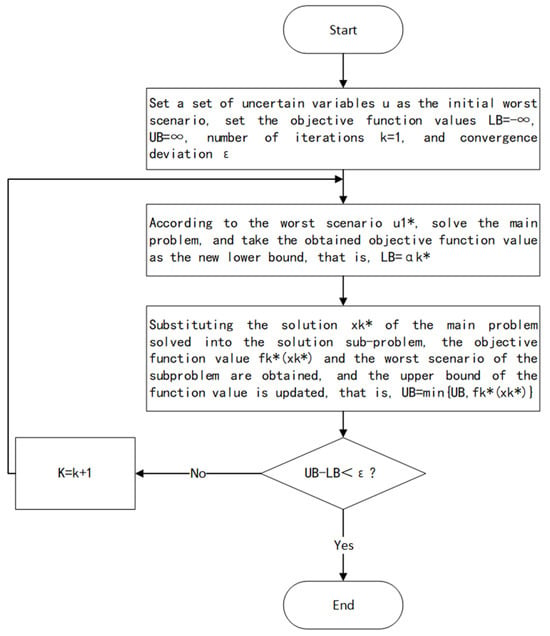
Figure 1.
Flow chart of the C&CG method to solve the two-stage robust optimization model, the * represents the optimal solution in the current iteration process.
6. Results & Discussions
6.1. Example Description
This paper analyzes a regional power grid in China as an example, which contains conventional thermal power units, wind turbines, photovoltaic units, energy storage units, etc. The installed capacities of the three conventional thermal power units are 1200 MW, 1600 MW, and 1600 MW, respectively, and the maximum outputs of the thermal power units are their respective configured capacities, with the minimum outputs being 0 and the maximum ramp rates being 600 MW/h, 800 MW/h, and 800 MW/h, respectively. The installed capacity of the wind turbine is 2000 MW, and the installed capacity of the photovoltaic unit is 140 MW; the configured capacity of the energy storage is 2000 MWh, the maximum and minimum charge states allowed during the scheduling process are 0.9 and 0.1, respectively, the maximum charging or discharging power is 400 MW, and the charging and discharging efficiency is 0.96. The program is coded on the MATLAB 2022a platform, the Gurobi called with the YALMIP toolkit is utilized as the solver.
A new energy-rich province in the northwest region of China was used as an example of typical scene generation. The research data for the year’s wind power and photovoltaic output of the original scene data were obtained, with a total of 365 time-series scenes throughout the year. We applied the k-means clustering algorithm described in the previous section to the comprehensive dataset for the scene reduction analysis to build a typical reduction scene and used the elbow method to determine the number of clusters and the clustering error as the number of clusters changed, as shown in Figure 2. It can be seen in the figure that when the number of clusters is less than three, the clustering error decreases more, and when the number of clusters is greater than three, the clustering error decreases at a significantly slower rate. According to the principle of the elbow method, the optimal number of clusters of the sample data is three, that is, producing three scenes.
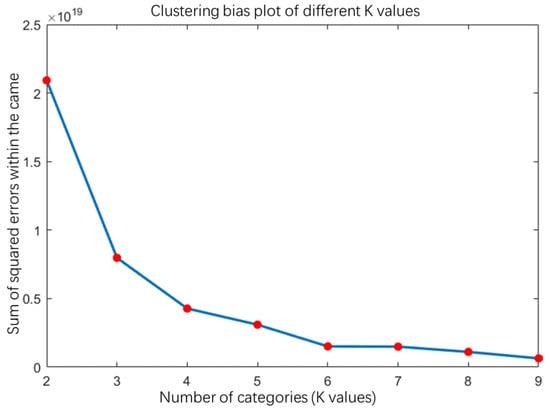
Figure 2.
Variation in the clustering error.
A set of data under typical daily scenarios of wind power and photovoltaic power is selected, as shown in Figure 3 and Figure 4, to simulate and validate the robust optimization model.
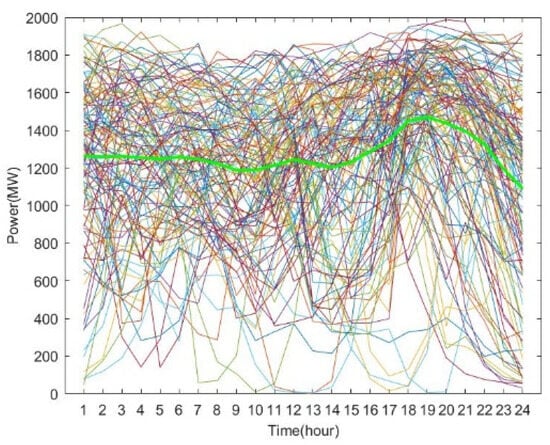
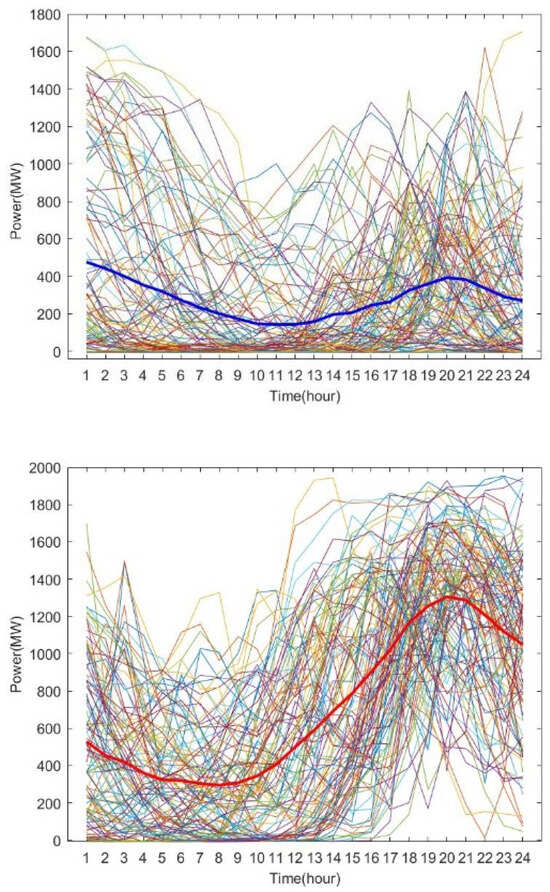
Figure 3.
Typical wind power scenarios after clustering.
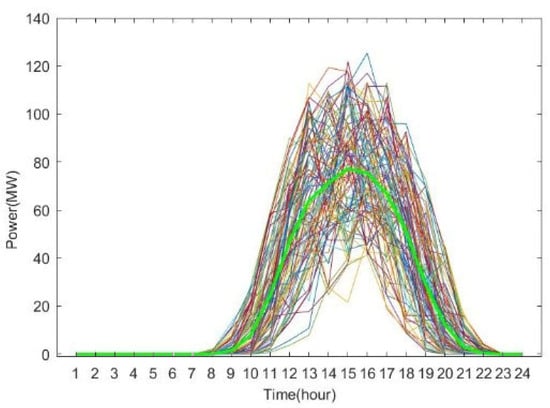
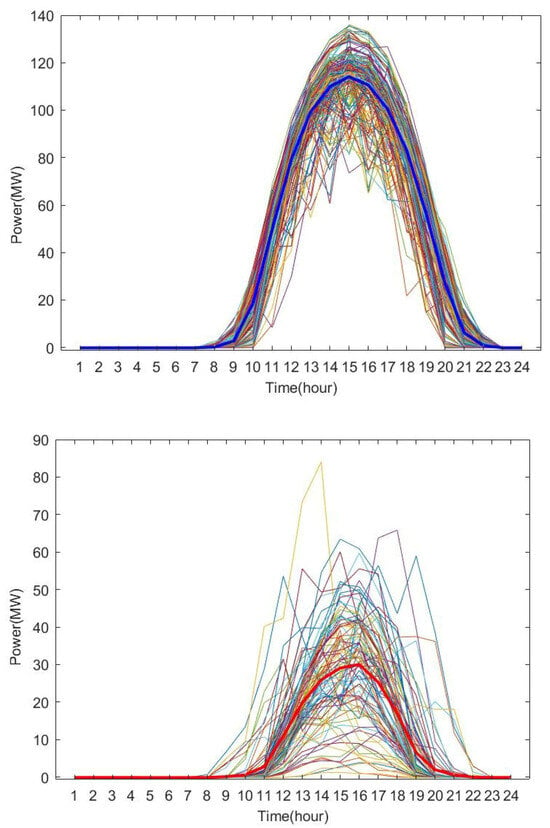
Figure 4.
Typical output scenarios of PV after clustering.
An analysis of Figure 3 and Figure 4 reveals that after clustering, the scenarios of wind power output and photovoltaic output can be divided into three categories: high, medium, and low. The proposed k-means clustering algorithm based on the elbow method in this paper effectively handles the uncertainties of wind power and photovoltaic output while controlling the number of scenarios as much as possible. In the robust optimization model, under the condition of acceptable computational complexity, the impact of the uncertainties in renewable energy output on the capacity value of the combined power plant system of new energy and energy storage can be adequately considered.
6.2. Robust Scheduling Scheme
The wind power uncertainty regulation parameter is set to 12, and the PV uncertainty regulation parameter is set to 9, which means that during the optimization process, the wind power output will be at the minimum of the prediction interval in 12 periods, the PV power output will be at the minimum of the prediction interval in 9 periods, and the rest of the periods will be equal to the predicted value. Based on the proposed robust scheduling rules, the maximum permissible fluctuation of wind and PV outputs in the “new energy + storage” power plant is 20% of the predicted value, and the predicted/actual wind and PV output curves are shown in Figure 5 and Figure 6, respectively. Figure 7 shows the convergence curve of the upper and lower bounds of the objective function in the iterative process of the column-constraint-generation algorithm, which shows that the algorithm is fast and has good convergence.
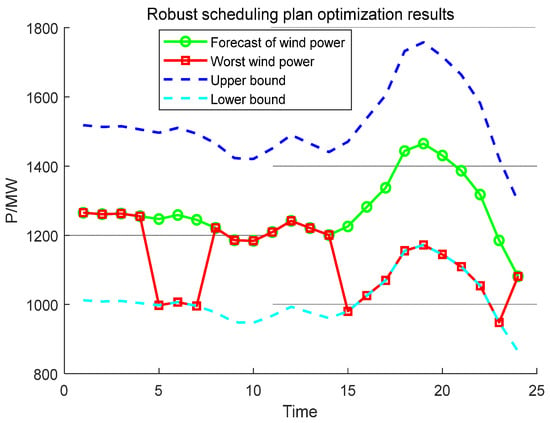
Figure 5.
Forecast/actual wind power output curve.
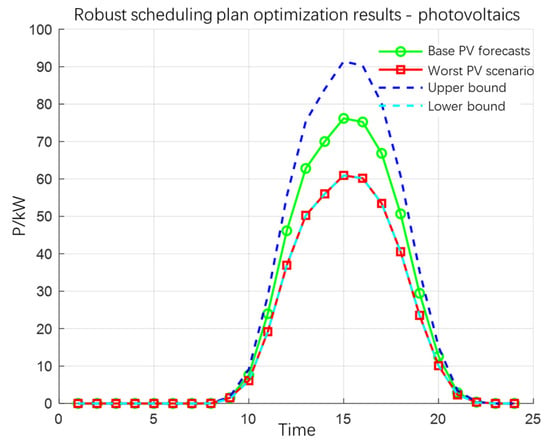
Figure 6.
Predicted/actual PV output curve.
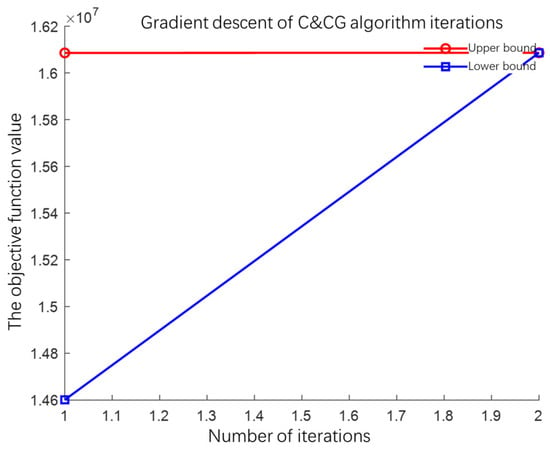
Figure 7.
Convergence curves of the UB and LB in the iterative process of the C&CG algorithm.
The final scheduling optimization results for each unit under the robust scheduling rule are shown in Figure 7. Among them, for the charging and discharging power of energy storage, the negative half-axis in the figure indicates that the energy storage is in a charging state, and the positive half-axis indicates that the energy storage is in a discharging state, which demonstrates that the energy storage unit is charged during the period with a low price of electricity and discharged during the period of the peak load or the peak price of electricity, so as to play the role of shaving peaks and filling valleys and balancing the power generation and consumption.
6.3. System Value Assessment
By changing the configuration of the storage capacity, from 0% and gradually increasing to 40%, we obtain the power station revenue and energy storage cost curve, as shown in Figure 8, where the new energy feed-in power × new energy feed-in tariff = power station revenue. In the allocation of storage, the power station revenue is reduced as the allocation of the storage capacity increases, and it increases when the allocation of the storage capacity reaches a certain level. Robust scenarios of wind power consumption tend to be saturated, and the power station revenue increase is no longer obvious, while the cost of energy storage planning with the increase in storage capacity monotonically increases. The two lines intersect at one point, and after the intersection point, the cost of energy storage planning will exceed the power station revenue, and the economic benefit enhancement brought about by energy storage planning will disappear. Therefore, in Figure 8, the intersection of the two lines will be recorded as the optimal allocation capacity of energy storage; at this time, the allocated storage capacity of about 25%, and the power plant revenue is 16.25 million yuan.
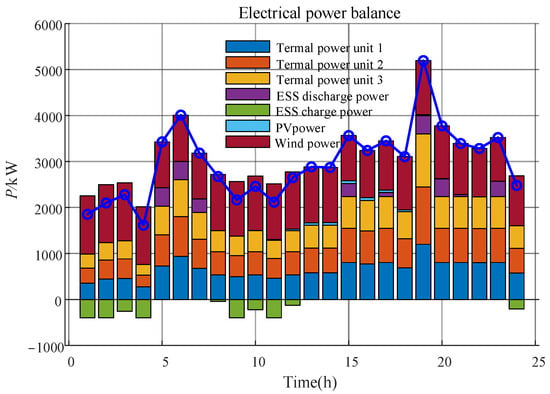
Figure 8.
The operation of each unit under the robust scheduling rule.
In order to study the impact of grid-allowed new energy feed-in power on the revenue of new energy power plants and to compare it with the impact of the distribution storage capacity on the revenue of power plants at the same time, in this paper, the amount of new energy allowed to be fed into the grid from 55% to 80% is varied, i.e., the value of x obtained in Section 2 is varied. And at the same time, the distribution and storage capacity in increments from 0% to 30% is also varied. Then, the combinatorial schemes corresponding to these ratios are solved based on the robust modeling. Finally, calculating the power plant revenue under the scenario corresponding to the rationing combination based on the power plant revenue equation proposed above, the evolution curve is obtained as shown in Figure 9.
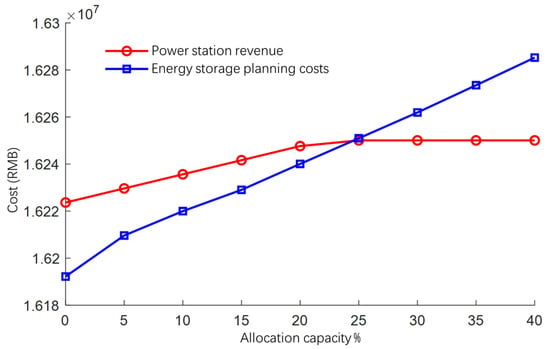
Figure 9.
Curve of power plant revenue and energy storage costs under different distribution and storage capacities.
From Figure 10, it can be clearly seen that as the proportion of the allowed new energy on-grid power increases, i.e., the x obtained in Section 2 increases, the volatility of the new energy increases, and the total output in the new energy robust scenario is increased, which is still within the range of the grid’s consumption. And the result is that the revenue of the power plant is increased with the proportion of the allowed new energy on-grid power. This level of growth can reach nearly 60 million RMB/(5%). In contrast, the increase in allocated storage capacity is weakly correlated with plant revenue growth, at about 0.5 million RMB/(5%). This is due to the flexible power regulation of thermal power units to the extent that the system itself has enough capacity for new energy consumption.
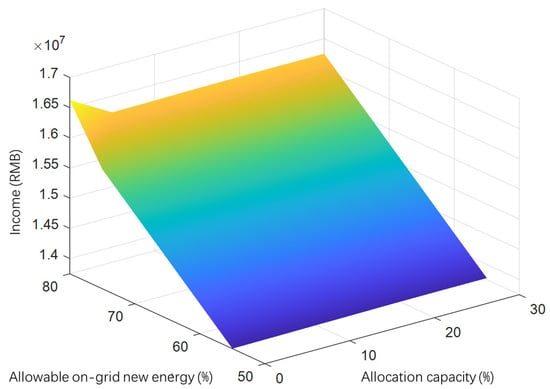
Figure 10.
Power plant revenue evolution curve.
Above all, although raising the amount of permitted feed-in power will cause an increase in the volatility of new energy grid-connected output and increase the possibility of wind and light abandonment, it will also bring considerable benefits to new energy power plants. And the main role of energy storage is not to improve the output yield of new energy power plants, but to improve the stability of the system.
7. Conclusions
In view of the volatility of the power system caused by the high proportion of new energy sources, such as wind power and photovoltaic power, this paper takes the combined power plant system of new energy and energy storage as an example and establishes an optimal system dispatch model based on the robust scheduling rule, which takes into account the uncertainty of the new energy output and adopts the columns and constraints generation algorithm (C&CG) to obtain a robust scheduling scheme. The value of the combined power plant system of new energy and energy storage is evaluated.
Through the example analysis in Section 6 and value assessment, it can be concluded that the proposed model takes into account the uncertainty of new energy output based on the robust scheduling rules after representing the new energy output as an uncertainty set, and the “worst-case” scenario of the combined power plant system of new energy and energy storage can be obtained by solving the two-stage robust optimization model. By solving the two-stage robust optimization model, we can obtain the robust scheduling scheme that minimizes the operating cost of the combined power plant system of new energy and energy storage under the “worst-case” scenario, and the scheduling scheme is more in line with the actual operation of the system. The combined power plant system of new energy and energy storage optimizes the output of conventional units after joining the system, effectively increasing the value gain of system operation and meeting the requirements for building a new type of power system under the “dual carbon” goal. New energy and energy storage can each grow their value gains as efficiently as 60 million RMB/(5%) and 0.5 million RMB/(5%). Then, although raising the amount of permitted feed-in power will cause an increase in the volatility of new energy grid-connected output and increase the possibility of wind and light abandonment, it will also bring considerable benefits to new energy power plants. And the main role of energy storage is not to improve the output yield of new energy power plants, but to improve the stability of the system.
Author Contributions
Conceptualization, W.S.; Methodology, S.W. and W.S.; Software, S.W.; Validation, W.S.; Data curation, S.W.; Writing—original draft, S.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data supporting reported results are available from the corresponding author upon reasonable request.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Central People’s Government of the People’s Republic of China. Guiding Opinions on Promoting Energy Storage Technology and Industrial Development. [EB/OL]. [2017-09-22]. Available online: http://www.gov.cn/xinwen/2017-10/12/content_5231304.htm (accessed on 1 September 2023).
- Yang, T.; Han, Z.; Shi, Z.; Man, L.; Ji, X.; Lou, S. Research on Coordinated Optimal Allocation Method of Composite Energy Storage in Energy Internet System. Electr. Meas. Instrum. 2021, 58, 8–13. [Google Scholar]
- Hou, L.; Ma, T.; Cai, Y.; Li, N.; Jia, Y.; Jin, T.; Pan, C. Research on Planning and Operation Optimization Model of Isolated Multi-energy Complementary System. Electr. Meas. Instrum. 2022, 59, 108–116. [Google Scholar]
- Javed, M.S.; Song, A.; Ma, T. Techno-economic Assessment of a Stand-alone Hybrid Solar-wind-battery System for a Remote Island Using Genetic Algorithm. Energy 2019, 176, 704–717. [Google Scholar] [CrossRef]
- Jing, Z.; Hu, R.; Yuan, J.; Zhu, J.; Wu, Q. Optimal Configuration of Island Microgrid with Wind/Solar/Pumped Storage and Load Response. Power Syst. Autom. 2017, 41, 65–72. [Google Scholar]
- Liu, Z.; Chen, X.; Zou, S.; Pan, Y.; Li, J. Capacity Optimization Allocation Method of Wind-Solar-Pumped Storage System Considering Carbon Emissions. Power Syst. Autom. 2021, 45, 9–18. [Google Scholar]
- Li, J.; Guo, B.; Niu, M.; Xiu, X.; Tian, L. Optimal Allocation Strategy of Energy Storage Capacity of Wind-Solar Storage System. Trans. China Electrotech. Soc. 2018, 33, 1189–1196. [Google Scholar]
- Ma, T.; Yang, H.; Lu, L.; Peng, J. Optimal design of an autonomous solar-wind-pumped storage power supply system. Appl. Energy 2015, 160, 728–736. [Google Scholar] [CrossRef]
- Nguyen, D.T.; Le, L.B. Risk-constrained profit maximization for microgrid aggregators with demand response. IEEE Trans. Smart Grid 2015, 6, 135–146. [Google Scholar] [CrossRef]
- Huang, J.; Wang, T.; Lin, X.; Li, Z.; Xiong, H.; Zhang, C. Robust Optimal Dispatch of Regional Integrated Energy System for Wind Power Consumption. Electr. Meas. Instrum. 2021, 58, 110–117. [Google Scholar]
- Zhu, G.; Lin, J.; Luo, Z.; Dai, S.; Qin, L.; Liu, C. Review of the Application of Robust Optimization in Power System Power Generation Planning. Proc. CSEE 2017, 37, 5881–5892. [Google Scholar]
- Wang, R.; Wang, P.; Xiao, G. A robust optimization approach for energy generation scheduling in microgrids. Energy Convers. Manag. 2015, 106, 597–607. [Google Scholar] [CrossRef]
- Cho, Y.; Ishizaki, T.; Ramdani, N.; Imura, J.I. Box-based temporal decomposition of multi-period economic dispatch for two-stage robust unit commitment. IEEE Trans. Power Syst. 2019, 34, 3109–3118. [Google Scholar] [CrossRef]
- Wang, X.; Liu, J.; Liu, Y.; Xu, L.; Ma, T.; Xu, W. Typical Load Curve Morphological Clustering Algorithm Using Adaptive Segmentation Aggregation Approximation. Power Syst. Autom. 2019, 43, 110–121. [Google Scholar]
- Chen, H.; Wang, Y.; Xuan, P.; Liang, Z.; Hua, D. Robust Economic Dispatch Method of Microgrid System with High Permeability Wind Power. Control. Theory Appl. 2017, 34, 1104–1111. [Google Scholar]
- Xie, D.; Hang, Z.; Zheng, F.; Pang, R.; Wan, Y.; Yuan, S.; Zhang, Z. Comparative Analysis of Reserve Configuration of Power System with Storage Considering the Uncertainty of New Energy. In Proceedings of the 2021 IEEE 5th Conference on Energy Internet and Energy System Integration (EI2), Taiyuan, China, 22–24 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 2490–2495. [Google Scholar]
- Liu, H.; Jiang, J.; Zhan, S.; Yang, X.; Yu, D.; Yan, G. Study on energy management model of integrated new energy-storage-charging system considering the influence of uncertainties. Fuel 2023, 331, 125784. [Google Scholar] [CrossRef]
- Huang, S.; Lu, H.; Chen, M.; Zhao, W. Integrated energy system scheduling considering the correlation of uncertainties. Energy 2023, 283, 129011. [Google Scholar] [CrossRef]
- Xu, H.; Chang, Y.; Zhao, Y.; Wang, F. A new multi-timescale optimal scheduling model considering wind power uncertainty and demand response. Int. J. Electr. Power Energy Syst. 2023, 147, 108832. [Google Scholar] [CrossRef]
- Lu, Y.; Xiang, Y.; Huang, Y.; Yu, B.; Weng, L.; Liu, J. Deep reinforcement learning based optimal scheduling of active distribution system considering distributed generation, energy storage and flexible load. Energy 2023, 271, 127087. [Google Scholar] [CrossRef]
- Emrani-Rahaghi, P.; Hashemi-Dezaki, H. Optimal scenario-based operation and scheduling of residential energy hubs including plug-in hybrid electric vehicle and heat storage system considering the uncertainties of electricity price and renewable distributed generations. J. Energy Storage 2021, 33, 102038. [Google Scholar] [CrossRef]
- ALAhmad, A.K. Voltage regulation and power loss mitigation by optimal allocation of energy storage systems in distribution systems considering wind power uncertainty. J. Energy Storage 2023, 59, 106467. [Google Scholar] [CrossRef]
- Lei, K.; Chang, J.; Wang, X.; Guo, A.; Wang, Y.; Ren, C. Peak shaving and short-term economic operation of hydro-wind-PV hybrid system considering the uncertainty of wind and PV power. Renew. Energy 2023, 215, 118903. [Google Scholar] [CrossRef]
- Han, R.; Hu, Q.; Cui, H.; Chen, T.; Quan, X.; Wu, Z. An optimal bidding and scheduling method for load service entities considering demand response uncertainty. Appl. Energy 2022, 328, 120167. [Google Scholar] [CrossRef]
- Li, Y.; Sun, Y.; Liu, J.; Liu, C.; Zhang, F. A data driven robust optimization model for scheduling near-zero carbon emission power plant considering the wind power output uncertainties and electricity-carbon market. Energy 2023, 279, 128053. [Google Scholar] [CrossRef]
- Liang, Z.; Chen, H.; Lei, J.; Zhang, C.; Zhao, W. Wind-Fire-Water-Gas-Nuclear-Pumped Storage Multi-Source Collaborative Rotation Backup Optimization Considering Wind Power Uncertainty. Power Grid Technol. 2018, 42, 2111–2119. [Google Scholar]
- Liang, Z.; Chen, H.; Wang, Y.; Zhang, C.; Zheng, X.; Wan, C. Robust Economic Dispatch of Microgrid including Electric Vehicle. Power Grid Technol. 2017, 41, 2647–2658. [Google Scholar]
- Wang, C.; Jiao, B.; Guo, L.; Tian, Z.; Niu, J.; Li, S. Robust scheduling of building energy system under uncertainty. Appl. Energy 2016, 167, 366–376. [Google Scholar] [CrossRef]
- Guo, L.; Liu, W.; Li, X.; Liu, Y.; Jiao, B.; Wang, W.; Wang, C.; Li, F. Energy management system for stand-alone wind-powered-desalination microgrid. IEEE Trans. Smart Grid 2016, 7, 1079–1087. [Google Scholar] [CrossRef]
- Luna, A.C.; Diaz, N.L.; Graells, M.; Vasquez, J.C.; Guerrero, J.M. Mixed-integer-linear-programming based energy management system for hybrid PV-wind-battery microgrids: Modeling, design and experimental verification. IEEE Trans. Power Electron. 2017, 32, 2769–2783. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).