Cooperative Reference Velocity Regulation Control for Virtual Coupling Systems of Heavy-Haul Trains

Abstract

Virtual coupling systems are important for improving the safety and efficiency of heavy-haul trains by coordinating the velocities of heavy-haul trains. However, the set point change of reference velocity leads to unsafe train operation. To address this issue, in this paper, a cooperative reference velocity regulation control method is proposed for virtual coupling systems of heavy-haul trains, which can smoothly adjust the train velocity during the operation process. Firstly, the heavy-haul trains are characterized by a cyber-physical model, where the physical layer models the longitudinal dynamics of the trains, while the cyber layer represents the communication topology of the trains using graph theory. Secondly, a cooperative control law is designed to achieve velocity consensus and maintain a safe distance between adjacent trains. The set point modulation method is utilized to smoothly adjust the reference velocity of heavy-haul trains, suppressing velocity fluctuations of heavy-haul trains. The proposed approach is validated through extensive simulations under acceleration and deceleration conditions. Simulation results verify that the proposed method can significantly reduce the velocity fluctuations during the operation of virtual coupling systems when compared with the classical cooperative control method.

1. Introduction

Virtual coupling systems have emerged as a promising technology to improve the transportation efficiency and capacity of heavy-haul trains [1]. Cooperative control has been extensively used in virtual coupling systems to coordinate the movements of multiple trains and maintain safe separation distances and avoid potential conflicts [2,3]. By coordinating train movements, cooperative control can allow trains to operate more closely together while maintaining safety, which can increase the overall capacity of the system. The priority of heavy-haul train operation is to guarantee that trains track the desired velocity and maintain safe inter-train distance [4].

Train-to-train communication plays a vital role in the virtual coupling systems of heavy-haul trains [5]. Several two-way communication technologies [6,7] have been proposed to enable train-to-train communication. The two-way communication technologies for heavy-haul trains include radio technology, LoRA technology and 5G technology [8]. With train-to-train communication systems, heavy-haul trains can exchange information about their position and velocity, which can be further utilized in the control law.

The emerging virtual coupling control technologies can be classified into four categories [9,10]: consensus-based control, model predictive control, sliding mode control and reinforcement learning control. Consensus-based control utilizes the state difference error between adjacent trains to ensure zero tracking error [11]. Model predictive control is used to find control actions that optimize one or more objectives based on the predictions of the system model [12]. Sliding mode control is a nonlinear discontinuous controller used to drive a system along a surface that satisfies certain system state requirements [13]. Reinforcement learning control is a model-free method that learns action values for specific states [14].

These control laws typically involve two terms: a velocity consensus term [15] and a distance separation term [16]. In the velocity consensus term, the train velocity is compared with the reference velocity and those of its neighbours to achieve velocity synchronization based on the consensus approach [17]. In the distance separation term, a potential function is typically designed where the minimum is chosen when the separation distance is equal to the desired distance, and then a gradient controller can be designed to guarantee the desired distance separation between neighbouring trains [18]. The artificial potential function can represent the deviation between the actual distance and the safe distance, which controls the tracking error to converge to a safe range rather than a constant value. Zhao et al. [19] made the distance between trains stay in a safe range based on artificial potential function. Based on the potential function and LaSalles invariance principle, a cooperative control strategy is designed to ensure a safe tracking operation [20].

In most cases, the tracking error of the closed-loop system is chosen as the velocity consensus term plus the distance separation term [21]. To improve the robustness of the closed-loop system, a compensator is typically required to guarantee the stability of the closed-loop system and suppress the tracking error to zero. Different compensators have been evaluated in the literature, including event-triggered compensators [22], sliding mode compensators [23], observer-driven compensators [24], optimal compensators [25], reinforcement learning compensators [26], PID compensators [27] and model predictive control (MPC) compensators [28,29]. These compensators can be utilized by considering the trade-off between complexity and accuracy in practical applications.

It is worth noting, however, that existing cooperative control methods typically lead to significant velocity fluctuations, which will result in safety risks during the operation process. From a system perspective, the velocity fluctuations are caused by the set-point jump when the train velocity changes from the initial velocity to the desired value [30]. For the second-order train model, we typically require the closed-loop system to operate in the under-damped mode, i.e., the damping ratio is chosen as 0.4–0.8, which will lead to the response fluctuation. When the system is over-damped, i.e., the damping ratio is larger than 1, the response fluctuation is avoided but the settling time is prolonged, which is not desirable in the virtual coupling system [31].

Set-point modulation has been considered as an effective approach to address the fluctuation problem, where the reference value of the closed-control system is adjusted according to the system output to suppress the the fluctuation [32]. Specifically, the set-point automatic adjustment based on regression prediction (cooperative reference velocity regulation) is a promising approach, where the output is predicted based on the regression model and further utilized in the reference adjustment [33]. cooperative reference velocity regulation has been widely used in the industrial applications, e.g., in [34], an energy management control strategy based on the regulation of the predicted reference value was proposed to ensure that the bus voltage can track the set value quickly and accurately.

Inspired by the aforementioned studies, this paper integrates the predictive reference regulation with the train cooperative control to improve the safety of the virtual coupling system. The virtual coupling system is designed according to the velocity consensus term and distance separation term. Then, the cooperative reference velocity regulation is integrated with the cooperative control system to suppress the fluctuation without changing the structure of the closed-loop system. Extensive simulation results are provided to verify that the proposed method can effectively suppress the velocity fluctuations when compared with the classical cooperative control method.

The contributions of this paper are three-fold:

(1) A cyber-physical model is proposed for the virtual coupling system of heavy-haul trains, and a cooperative control law is designed with the velocity consensus term and distance separation term.

(2) The cooperative reference velocity regulation is integrated with the cooperative control to suppress the fluctuation of the virtual coupling system without changing the structure of the closed-loop system.

(3) Extensive simulations are provided under the accelerating and decelerating modes to verify the effectiveness and superiority of the proposed cooperative reference regulation control method for virtual coupling systems.

The remainder of this paper is organized as follows. The cyber-physical model for multiple heavy-haul trains is shown in Section 2. In Section 3, we present the proposed cooperative predictive reference regulation control strategy. Section 4 discusses the results of our simulations conducted under various conditions. Finally, we summarize our work in Section 5.

2. Cyber-Physical Modelling

In this section, we establish physical and cyber layer models for heavy-haul trains to represent the operation of multiple trains. In the physical layer, we establish the longitudinal dynamic characteristics of the heavy-haul train, while in the cyber layer, we represent the communication topology among trains using graph theory. Figure 1 illustrates the cyber-physical model for multiple heavy-haul trains.

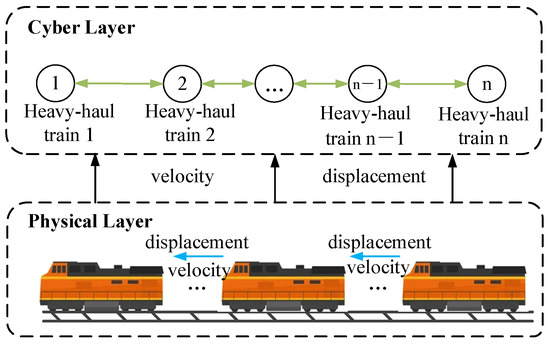
Figure 1. The diagram presents the cyber-physical model of the operation of multiple heavy-haul trains. The bidirectional communication between trains enables cooperative control, and a virtual train provides reference velocity and distance. This allows for safe and efficient train operation through coordination between trains.

2.1. Physical Modelling

The dynamic model for multiple heavy-haul trains is simplified by assuming that the trains are represented by a single mass point and the environmental conditions are not taken into account. Furthermore, only the longitudinal force is considered during the operation, resulting in a longitudinal dynamic model for the multiple heavy-haul trains. The traction of the heavy-haul train is produced by a power transmission device in the same direction as the driving direction, while the braking force is produced by the braking device in the opposite direction.

The longitudinal dynamic model for the heavy-haul trains can be expressed as follows:

$$\dot{x_i}\left(t\right)=v_i\left(t\right),$$

(1)

$$m_i\dot{v_i}\left(t\right)=u_i\left(t\right)-m_i{r}_i\left(t\right),$$

(2)

where $x_i\left(t\right)$, $u_i\left(t\right)$ and $v_i\left(t\right)$ are the position of the heavy-haul train, the traction force or the braking force and the velocity of train i, respectively. $m_i$ is the mass of the train i; $r_i\left(t\right)$ is the total resistance coefficient.

The total resistance coefficient $r_i\left(t\right)$ is composed of the mechanical resistance coefficient $r_i^m\left(t\right)$, air resistance coefficient $r_i^w\left(t\right)$ and an additional resistance coefficient ${r_i}^p\left(t\right)$. The equation for the total resistance coefficient is as follows:

$$r_i\left(t\right)=r_i^m\left(t\right)+r_i^w\left(t\right)+r_i^p\left(t\right).$$

(3)

The mechanical resistance coefficient $r_i^m\left(t\right)$ is

$$r_i^m\left(t\right)=c_i^{r_0}\left(t\right)+c_i^{r_1}\left(t\right)v_i,$$

(4)

where $c_i^{r_0}\left(t\right)$ and $c_i^{r_1}\left(t\right)$ are the experience coefficients of the heavy-haul train i.

The air resistance force coefficient $r_i^w\left(t\right)$ of the heavy-haul train i is

$$r_i^w\left(t\right)=c_i^{r_2}\left(t\right){v_i}^2,$$

(5)

where $c_i^{r_2}\left(t\right)$ is the air resistance coefficient.

The additional resistance coefficients $r_i^p\left(t\right)$ caused by environment factors are:

$$\begin{array}{c}{r}_i^p\left(t\right)=r_i^g\left(t\right)+r_i^c\left(t\right),\hfill \\ r_i^g\left(t\right)=gsin\left({\theta }_i\left(t\right)\right),\hfill \\ r_i^c\left(t\right)=0.004D_i\left(t\right),\hfill \end{array}$$

(6)

where $r_i^g\left(t\right)$ and $r_i^c\left(t\right)$ are the coefficients of grade resistance and curve resistance of the heavy-haul train i, respectively. The track grade is represented by ${\theta }_i\left(t\right)$ and the track curvature is represented by $D_i\left(t\right)$.

2.2. Cyber Modelling

Graph theory can be utilized to model the communication topology of multiple heavy-haul trains. A graph can be represented by a pair $\left\{\mathbf{V},\mathbf{E}\right\}$, where $\mathbf{V}=\{1,2,\dots ,n\}$ denotes a collection of sub-nodes, and $\mathbf{E}\subseteq \mathbf{V}\times \mathbf{V}$ represents a set of node-connected edges. The properties of the graph can be further simplified by utilizing three special matrices: the adjacency matrix, degree matrix and Laplace matrix.

The communication topology structure in the heavy-haul trains is represented by the matrix

$$\mathbf{A}=\left[a_{ij}\right]\in {\mathbf{R}}^{n\times n}$$

(7)

where $a_{ij}=1$ if velocity and displacement information can be exchanged between adjacent sub-nodes i and j, and $a_{ij}=0$ otherwise. The set of neighbouring trains for node i is defined as ${\mathbf{N}}_i=\left\{j|a_{ij}=1,j\in \mathbf{V}\right\}$.

We denote $d_i$ as the number of node i’s Neighbors, and then the adjacency matrix is defined as

$$\mathbf{D}=\mathrm{diag}{\left\{d_i\right\}}_n.$$

(8)

The Laplacian matrix of the interactive topology of trains can be expressed as

$$\mathbf{L}=\mathbf{D}-\mathbf{A}.$$

(9)

The Laplacian matrix represents the communication topology among trains. In this paper, we assume trains only communicate with physically adjacent Neighbors; thus, the Laplacian matrix for the velocity and position information is the same.

We can consider the existence of a reference velocity for the heavy-haul trains, which is represented as an abstract node denoted as 0.

The pinning matrix $\mathbf{G}$ is used to represent the interactions:

$$\mathbf{G}=\mathrm{diag}{\left\{g_i\right\}}_n,$$

(10)

where $g_i=1$ if node i can receive information from node 0 and $g_i=0$ otherwise.

To ensure the synchronization of multiple heavy-haul trains, there are two fundamental assumptions about the topology of the graph. Firstly, the graph must have at least one spanning tree, and the reference is pinned to at least one node. Secondly, the virtual node 0 is pinned to the root node of the spanning tree. With the help of the spanning tree, all nodes can track the reference.

3. Cooperative Predictive Reference Regulation Control

A cooperative predictive regulation control technique is proposed to achieve the control objectives mentioned above. The technique utilizes the set-point modulation theory to adjust the desired velocity of the train, which can improve the transient performance of the virtual coupling system.

3.1. Scheme of the Proposed Method

Figure 2 illustrates the closed-loop diagram of the virtual coupling system of a multiple-train system. The proposed strategy consists of three parts: a reference velocity regulator, a cooperative tracker and a compensator. The reference velocity regulator generates a modulated reference velocity for the closed-loop system. Each train measures its own velocity and position, and transmits the local information to its Neighbors. With modulated reference velocity, its own measurements and the transmitted neighboring information, each train generates its tracking error consisting of a consensus-based velocity tracker and potential function based distance separation tracker. The cooperative tracking error further goes to a compensator to stabilize the closed-loop system.

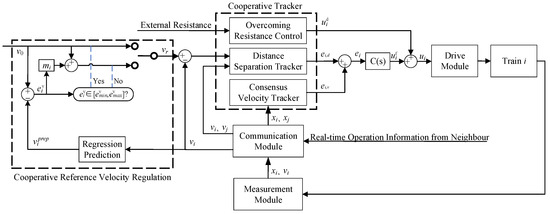
Figure 2. The closed-loop diagram of the multiple heavy-haul train system.

3.2. Cooperative Tracker

The cooperative tracker consists of a velocity tracker and a distance tracker, which will be introduced as follows.

3.2.1. Consensus-Based Velocity Tracker

Based on the previous research, several heavy-haul trains may be seen as a multi-agent system by treating each train as one agent. Every train in the system is capable of interaction and communication. The consensus algorithm often implements the state consistency for the multi-agent system. As a result, the cooperative consensus technique may be used to regulate heavy-haul trains so that they run at the same pace. Additionally, the cooperative consensus process just requires local contact to attain global consistency rather than gathering global knowledge. Therefore, each agent simply shares information with other agents that are nearby. The consensus-based velocity tracker is designed as

$$\underset{t\to \infty }{lim}{v}_r-v_i\left(t\right)=0,$$

(11)

$$\underset{t\to \infty }{lim}{v}_i\left(t\right)-v_j\left(t\right)=0,j\in N_i,$$

(12)

where $v_r$ is the reference velocity, and $v_j$ is the velocity of train j.

The design goal is to minimize the difference between adjacent train velocities, so that all train velocities can converge to the reference velocity $v_r$, as can be shown from Equations (11) and (12).

As a result, the chosen method should cause all heavy-haul trains’ velocities to tend toward the target velocity $v_r$, which is essential for the cooperation of multiple heavy-haul trains. The consensus control system is created in accordance with the cooperative control theory as follows:

$$e_{i,v}\left(t\right)=g_i\left[v_r-v_i\left(t\right)\right]+\sum _{j\in N_i}\left[v_j\left(t\right)-v_i\left(t\right)\right],$$

(13)

where $g_i$ is the pinning element. The first term guarantees the train’s velocity tracks the reference velocity and the second term ensures the velocity synchronization among neighbouring trains.

3.2.2. Distance Separation Tracker

The artificial potential function is introduced to control the relative distance of heavy-haul trains. Path planning and obstacle avoidance problems are typically addressed using real-time planning techniques like the artificial potential field theory. The mobile controlled plant can be viewed as a single particle on the two-dimensional surface. The goal of the control is to move while avoiding obstacles to a predefined location. An artificial potential field is made to reflect the environment the agent is located in. The goal point location has a low potential energy, while the obstacle places have large potential energies. The objective point is more desirable than the area with obstacles because the controlled plants are more likely to move to the site with lower potential energy. The controlled plant will eventually move toward the goal value, which is the area with the lowest potential energy.

An artificial potential field is generated and utilized to characterize the train’s safety. The potential energy of the artificial potential field increases with the difference between the real distance and the safety distance. Potential energy is reduced when the actual distance and the safety distance are equal. The goal of this technique is to set a specific safety spacing between heavy-haul trains. The artificial potential function $V\left(d_{ij}\right)$ is defined as follows:

$$V\left(d_{ij}\right)=\frac{1}{2}{(d_{ij}-d_r)}^2,$$

(14)

where the actual time between trains is $d_{ij}$, and $d_r$ is the desired distance. When two heavy-haul trains are close to one another, they must maintain a minimum safety distance of $d_r$. If train i is in front of train j and l is the length of the train, then $d_{ij}=x_i-x_j-l$.

This method creates an attractive force that pulls two trains closer together when the separation between them exceeds the safe distance. Instead, it generates a repulsive force that forces the trains apart. The distance separation tracker with potential field function is designed based on the separation between the front and back trains as follows:

$$e_{i,d}\left(t\right)=-\nabla V\left(d_{ij}\right)=d_r-d_{ij},i\in \left\{1,2,\cdots n\right\}.$$

(15)

3.3. Reference Velocity Regulation

In the classical cooperative control, the reference velocity is directly compared with the actual velocity to generate the tracking error. However, suppressing the velocity fluctuation and reducing the settling time are two contradictory objectives in the system design. In the following, we will propose a reference velocity regulation method to suppress the velocity fluctuations without prolonging the setting time.

The cooperative reference velocity regulation modifies the reference velocity $v_0$ of the train depending on the variance between the predictive velocity $v_i^{pred}$ of the train i and the reference velocity $v_0$. The cooperative reference velocity regulation consists of four phases, which will be discussed in detail later.

Step 1: The primary principle of cooperative reference velocity regulation is to modify the reference velocity $v_0$ according to the bias of the predictive velocity $v_i^{pred}$ at time $t+T_{pred}$. In this paper, a regression prediction algorithm is utilized to predict the coming error signal. Thus, predictive velocity $v_i^{pred}$ of train i is calculated firstly.

$$v_i^{pred}=v_i\left(t\right)+r{T}_{pred},i=1,2,\dots ,n,$$

(16)

where $v_i^{pred}$ is the predictive velocity of train i at time $t+T_{pred}$, $T_{pred}$ is the predicted horizon.

$$r=\frac{v_i\left(t\right)-v_i(t-T_{past})}{T_{past}},i=1,2,\dots ,n,$$

(17)

where r is the slope of velocity at time t of train i, $T_{past}$ is history velocity recording time.

Step 2: The predictive velocity $v_i^{pred}$ is then utilized to obtain the present error signal $e_i^v\left(t\right)$ of train i to reduce velocity fluctuations.

$$e_i^v\left(t\right)=v_i^{pred}-v_i\left(t\right),i=1,2,\dots ,n.$$

(18)

Step 3: The adjustment signal $m_i^r\left(t\right)$ of the train i is related to the predicted error signal and can be calculated by Equation (19).

$$m_i^r\left(t\right)=m^u\ast e_i^v\left(t\right).$$

(19)

The reference can be adjusted using $m_i^r\left(t\right)$, where $m_u$ is a scaling constant. Large $m_u$ lowers fluctuation while also slowing down the velocity of the system.

Step 4: In cooperative reference velocity regulation, each train’s reference velocity $v_r$ is adjusted through the following principle:

$$v_r=\left\{\begin{array}{cc}{v}_0,\hfill & e_{min}^v\le e_i^v\left(t\right)\le e_{max}^v\hfill \\ v_0+m_i^r\left(t\right),\hfill & otherwise\hfill \end{array}\right\},$$

(20)

where $v_0$ is the expected velocity during the high-velocity train operation, and the reference velocity $v_r$ is the velocity to the controller to generate the train force. The main principle of (20) is that the reference velocity is changed if the predicted error signal exceeds the acceptable range. The range is determined by $e_{min}^v$ and $e_{max}^v$. If the error signal is higher than $e_{max}^v$, the reference velocity will be set to cut down the settling time. When the error signal is lower than $e_{min}^v$, the reference velocity will be set to restrain the fluctuation.

With the set-point modification (17)∼(20), the reference velocity of the train can be controlled in real time according to the sensing operated velocity $v_i\left(t\right)$.

3.4. Closed-Loop Control System

With the velocity tracker and the distance separation tracker, the system-level tracking error is designed as

$$e_i=\alpha \ast e_{i,v}+\beta \ast e_{i,d},$$

(21)

where $\alpha$ and $\beta$ are the weights of the velocity tracking error and distance tracking error, respectively.

We define the vector forms of velocity tracking error ${\mathbf{E}}^{\mathbf{v}}$, distance tracking error ${\mathbf{E}}^d$, train velocity $\mathbf{V}$, reference velocity ${\mathbf{V}}_0$ and train position $\mathbf{P}$ as follows:

$$\begin{array}{c}{\mathbf{E}}^v={\left[\begin{array}{cccc}{e}_{1,v},& e_{2,v},& ···& e_{n,v}\end{array}\right]}^{\mathrm{T}}\hfill \\ {\mathbf{E}}^d={\left[\begin{array}{cccc}{e}_{1,d},& e_{2,d},& ···& e_{n,d}\end{array}\right]}^{\mathrm{T}}\hfill \\ \mathbf{V}={\left[\begin{array}{cccc}{v}_1,& v_2,& ···& v_n\end{array}\right]}^{\mathrm{T}}\hfill \\ {\mathbf{V}}_0={\left[\begin{array}{cccc}{v}_0,& v_0,& ···& v_0\end{array}\right]}^{\mathrm{T}}\hfill \\ \mathbf{d}={\left[\begin{array}{cccc}{d}_1,& d_2,& ···& d_n\end{array}\right]}^{\mathrm{T}}\hfill \end{array}$$

(22)

Then, the velocity tracking error vector is computed as

$${\mathbf{E}}^v=\mathbf{G}\left({\mathbf{V}}_0-\mathbf{V}\right)-\mathbf{L}\mathbf{V}.$$

(23)

For the Laplacian matrix $\mathbf{L}$, the row sums are always zero. Then, (23) can be further written as

$$\begin{array}{c}{\mathbf{E}}^v=\mathbf{G}\left({\mathbf{V}}_0-\mathbf{V}\right)-\mathbf{L}\mathbf{V}+\mathbf{L}{\mathbf{V}}_0\hfill \\ =\mathbf{G}\left({\mathbf{V}}_0-\mathbf{V}\right)+\mathbf{L}\left({\mathbf{V}}_0-\mathbf{V}\right)\hfill \\ =\left(\mathbf{G}+\mathbf{L}\right)\left({\mathbf{V}}_0-\mathbf{V}\right).\hfill \end{array}$$

(24)

In order to guarantee the velocity synchronization of trains in the virtual coupling system, it is required that the reference velocity pins to at least one train, and there is a directed spanning tree from the pinned train to the other ones. In this case, $\mathbf{G}+\mathbf{L}$ is invertible.

The control objective is to suppress the tracking error $e_i$ to zero. Then, a compensator is required to improve the robustness of the closed-loop system. Without loss of generality, a PID compensator is applied

$$C\left(s\right)=k_p+k_i/s.$$

(25)

Then, the feedback control law is designed as

$$u_i^f=C\left(s\right)e_i.$$

(26)

To compensate for the effects of basic resistance force, gravitational force, and curvature resistance force, a feedforward control input is designed as

$$u_i^d\left(t\right)=m_i(c_i^{r_0}+c_i^{r_1}{v}_i\left(t\right)+c_i^{r_2}{v}_i^2\left(t\right)+gsin{\theta }_i+0.004D_i).$$

(27)

The system-level control input includes the feedback control and feedforward control, which is represented as

$$u_i=u_i^f+u_i^d.$$

(28)

In (28), the system-level control input consists of the feedback control term and feedforward control term. The feedback term guarantees the velocity synchronization and desired distance separation. The feedforward term eliminates the distance and noise of the heavy-haul train.

4. Simulations

The simulation environment with three trains is built in Matlab/Simulink (version: 2022a) and comprehensive tests are run to verify the proposed high-train cooperative control technique. A desktop computer with a 12th Intel(R) Core(TM) i7-12700H CPU running at 2.30 GHz has the software loaded on it. The parameter configurations are provided first in this section. The performance metrics are explained next. Results of the experiment are presented at the end.

4.1. Parameter Setup

4.1.1. Physical Parameters

In our experiments, we consider three trains on the railway, with each having the same system parameters. The mass of each heavy-haul train is set to 240,000 kg, the length of the train is set to 160 m, the maximum power is 4000 kW, the desired velocity for all trains is 44 m/s and the maximum velocity is set to 65 m/s. The desired distance between trains is set to 200 m and the minimum safety distance is set to 120 m. The maximum acceleration and deceleration of the trains are set to 1 m/s${}^2$ and −1 m/s${}^2$, respectively. The constraints are implemented with a value limiter in the simulation.

The trains are assumed to run in a straight line, and each train is subject to the same resistance. The mechanical resistance coefficients are denoted by $c_0$ and $c_1$ and are set to 0.01176 N/kg and 0.00077616 N · s/ (m · kg), respectively. The additional resistance coefficient $c_2$ is set to 0.00016 N · s/(m${}^2·$ kg). The simulation time is set to 1000 s. The initial velocities of the three heavy-haul trains are 45 m/s, 25 m/s, and 30 m/s, and their initial positions are 420 m, 190 m, and 0 m, respectively.

4.1.2. Cyber Parameters

The parameters of the compensator are set as $k_p=7$ and $k_i=14$. The reference information is assumed available to all trains and the trains can communicate with each other. Then, the Laplacian and pinning matrix are represented as

$$\mathbf{L}=\left[\begin{array}{ccc}1& -1& 0\\ -1& 2& -1\\ 0& -1& 1\end{array}\right],$$

(29)

and the adjacency is set as

$$\mathbf{G}=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right].$$

(30)

4.2. Performance Metrics

The proposed method is evaluated using four performance metrics.

To evaluate the velocity tracking performance, the root-mean-square error of velocity (RMSEv) is used as a performance metric. The RMSEv can be calculated using the following equation:

$$\mathrm{RMSE}v=\frac{1}{n}\sum _{i=1}^n\left(\sqrt{\frac{1}{N}\sum _{k=1}^N{\left(v_i\left(k\right)-v_0\left(k\right)\right)}^2}\right),$$

(31)

where the number of trains is n and the tracking error between train i’s real velocity and its reference velocity at time k is $v_i\left(k\right)-v_0\left(k\right)$.

The consistency of relative displacement between trains is evaluated using the root-mean-square error of relative displacement (RMSE$\Delta x$). The RMSE$\Delta x$ is given by

$$\mathrm{RMSE}\Delta x=\frac{1}{n-1}\sum _{i=1}^{n-1}\left(\sqrt{\frac{1}{N}\sum _{k=1}^N{\left(\Delta x_{i,i+1}\left(k\right)-\Delta x_0\left(k\right)\right)}^2}\right),$$

(32)

where $\Delta x_{i,i+1}\left(k\right)$ is the distance between train i and train $i+1$, $\Delta x_0$ is the initial distance between trains.

RMSEv and RMSE$\Delta x$ represent the velocity tracking accuracy and distance tracking accuracy, respectively. A smaller $\mathrm{RMSE}v$ means the train velocity is more close to the reference velocity. Similarly, a smaller $\mathrm{RMSE}\Delta x$ means the distance between adjacent trains is more close to the desired distance. Maximum velocity fluctuation (MVF) and maximum relative distance fluctuation (MRDF) evaluate the fluctuation of velocity and relative displacement during the operation process. Smaller MVF and MRDF indicate a better transient performance during the operation process.

4.3. Simulation Condition

To test the efficacy of the proposed strategy, simulations are run under two scenarios of acceleration and deceleration operations. The proposed method and the traditional method are compared in the two scenarios. The proposed method is cooperative reference regulation control strategy from Section 3, which considers the reference value regulation. The traditional method is the cooperative control strategy without the reference value regulation.

4.3.1. Case 1: Acceleration Operation

In Case 1, the simulation considers the acceleration operating condition, where the reference velocity increases from 30 m/s to 44 m/s at 400 s. The simulation results for both the cooperative method and the proposed method are presented in Figure 3i,ii.

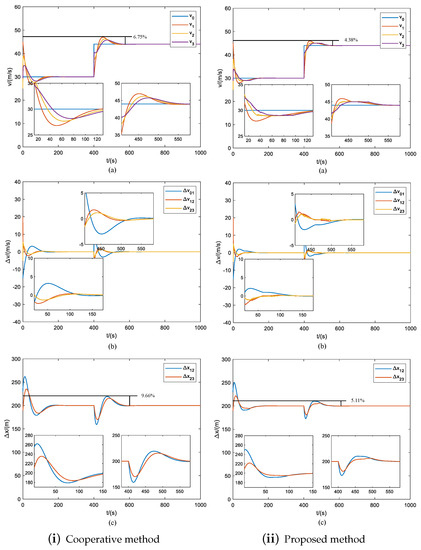
Figure 3. The cruise performance comparison of the cooperative method and proposed method in Case 1. The cooperative method is the cooperative control strategy without the reference value regulation shown in (i), and the proposed method is cooperative reference regulation control strategy shown in (ii). (a) Train velocity, (b) train velocity tracking error, (c) train relative displacement.

Figure 3(ia,iia) show that the settling time of both methods is almost the same, and both methods can converge the velocity to the reference value during the acceleration process. In addition, as seen in Figure 3(ib,iib), both methods can achieve consistent velocity for each train.

As seen in Figure 3(ic,iic), during the acceleration process, the traditional method shows fluctuations of 6.75% and 9.66% for velocity and relative displacement, respectively. The proposed method shows significantly reduced fluctuations of 4.38% and 5.11% for velocity and relative displacement, respectively.

Table 1 shows that all performance metrics corresponding to the proposed method are smaller than those corresponding to the traditional method, indicating better performance of the proposed method during the acceleration process.

Table 1. Comparison of two methods under acceleration operation.

	Metric	RMSEv	RMSE$\mathit{\Delta }\mathit{x}$	MVF	MRDF
Method
Cooperative		2.25	116.54	2.97	19.32
Proposed		2.06	40.73	1.93	10.22

4.3.2. Case 2: Deceleration Operation

In Case 2, the simulation is conducted under deceleration operating conditions, where the reference velocity decreases from 60 m/s to 44 m/s at 400 s. The simulation results of the cooperative method and the proposed method are presented in Figure 4i and Figure 4ii, respectively.

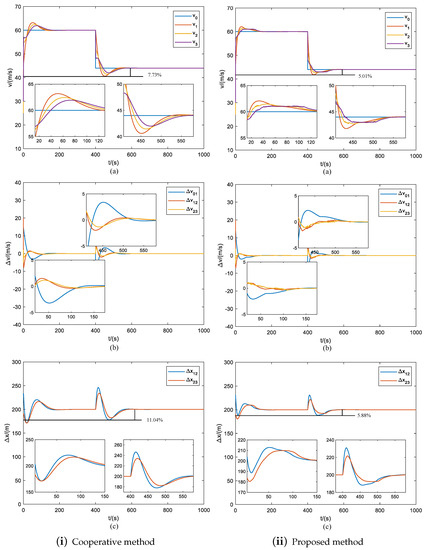
Figure 4. The cruise performance comparison of the cooperative method and proposed method in Case 2. The cooperative method is the cooperative control strategy without the reference value regulation shown in (i), and the proposed method is cooperative reference regulation control strategy shown in (ii). (a) Train velocity, (b) train velocity tracking error, (c) train relative displacement.

As seen in Figure 4(ia,iia), both the classical cooperative method and the proposed method exhibit some velocity fluctuation during the deceleration process, with the proposed method showing a slightly higher fluctuations of around 11.04% compared to the classical method’s 7.73%. Figure 4(ib,iib) illustrate good tracking and coordination capabilities for both methods during the deceleration process. Figure 4(ic,iic) show that the fluctuation of the proposed method is slightly higher than that of the classical method during the deceleration process, with the proposed method exhibiting an fluctuation of around 5.88%, while the classical method shows an fluctuation of around 5.01%.

As shown in Table 2, the proposed method also exhibits excellent performance in terms of fluctuation in the deceleration case. It should be noted that in the cruising process of heavy-haul trains, the distance between the trains is a crucial factor to consider. If the distance is too far, it may negatively affect the communication quality and operational efficiency, while if it is too close, there is a risk of collision. The proposed method can effectively reduce the fluctuation of the train velocity and relative displacement, ensuring efficient, stable and safe communication and operation of the train.

Table 2. Comparison of two methods under deceleration operation.

	Metric	RMSEv	RMSE$\mathit{\Delta }\mathit{x}$	MVF	MRDF
Method
Cooperative		2.54	90.11	3.40	22.08
Proposed		1.20	27.50	2.20	11.76

4.4. Simulation under Different Weights

To verify the tracking performance of the method under different velocity and distance tracking error weights, three sets of weight coefficients are set. The velocity and distance tracking error weights are set to 0.9 and 0.1; 0.5 and 0.5; 0.2 and 0.8, respectively.

In Figure 3ii, the weights of velocity and distance tracking error are set to 0.9 and 0.1 by default. In Figure 5i, the weights of velocity and distance tracking error are set to 0.5 and 0.5. In Figure 5ii, the weights of velocity and distance tracking error are set to 0.2 and 0.8. In Figure 5, the simulation is conducted under deceleration operating conditions, where the reference velocity decreases from 30 m/s to 44 m/s at 400 s.

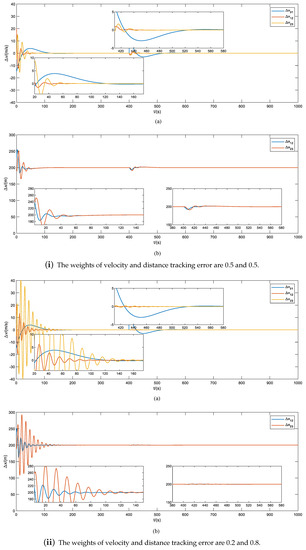
Figure 5. The cruise performance comparison of the proposed method under different weights. The weights of velocity and distance tracking error are set to 0.5 and 0.5 in (i), and the weights of velocity and distance tracking error are set to 0.2 and 0.8 in (ii). (a) Train velocity tracking error, (b) train relative displacement.

The simulation results show that Figure 3ii has smaller overshoot and less adjustment time than Figure 5i,ii. In Figure 5i, the train relative displacement is smaller, but the velocity tracking error has obvious fluctuations, which is not good for driving stability. In Figure 5ii, the velocity tracking error and train relative displacement have big overshoot, which is because the velocity weight is too small.

As shown in Table 3, the four metrics of the proposed method under three different weight settings are compared. The simulation results show that the setting of weights for velocity and distance error affects the performance of the method. And the larger weight of the velocity error, the better the method performance.

Table 3. Performance comparison of proposed method under different weights of velocity and distance.

	Metric	RMSEv	RMSE$\mathit{\Delta }\mathit{x}$	MVF	MRDF
Method
0.9 and 0.1		2.06	40.73	1.93	10.22
0.5 and 0.5		2.3	20.47	3.22	5.24
0.2 and 0.8		2.28	2.6	3.16	1.03

4.5. Simulation with Slope

In order to assess the effectiveness of the proposed method on slope conditions, a comparison was made between the tracking performance of the cooperative method and the proposed method. During the simulation, train 2 entered the slope area at 400 s, while train 1 had already passed the slope area and train 3 was not on the slope area. The simulation results of both methods are presented in Figure 6 and Figure 7, respectively.

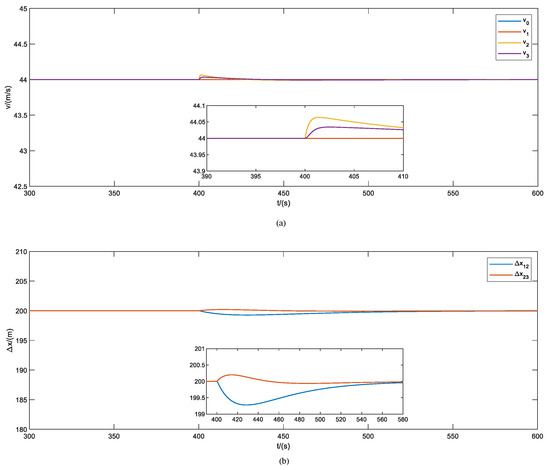
Figure 6. The cruise performance with slope of the cooperative method. (a) Train velocity tracking error, (b) train relative displacement.

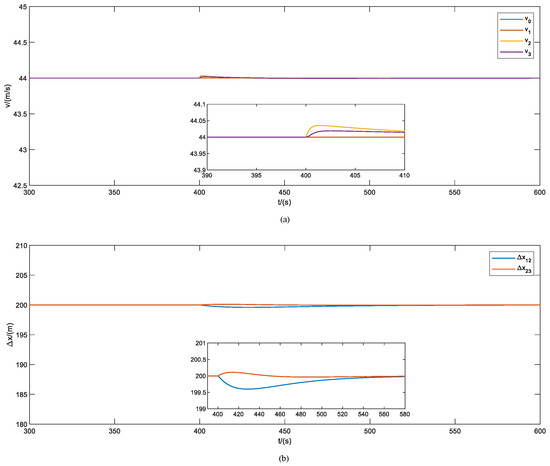
Figure 7. The cruise performance with slope of the proposed method. (a) Train velocity tracking error, (b) train relative displacement.

In Figure 6a and Figure 7a, the velocity fluctuation of the cooperative method and the proposed method under slope condition are shown. According to the simulation results, the proposed method exhibits lower velocity fluctuation compared to the cooperative method. This suggests that the proposed method is more effective in mitigating the impact of cooperative velocity tracking caused by the slope.

In Figure 6b and Figure 7b, the distance fluctuation of the cooperative method and the proposed method under slope condition are shown. According to the simulation results, the proposed method exhibits lower train relative displacement compared to the cooperative method. The proposed scheme can better overcome the influence of the cooperative distance tracking caused by the slope.

As shown in Table 4, the four metrics of two methods under slope conditions are compared. Based on the simulation results, it appears that the proposed method is more robust when it comes to changes in slope compared to the cooperative method.

Table 4. Performance comparison of two methods under slope conditions.

	Metric	RMSEv	RMSE$\mathit{\Delta }\mathit{x}$	MVF	MRDF
Method
Cooperative		0.09	1.21	0.07	0.72
Proposed		0.05	0.72	0.03	0.41

5. Conclusions

This paper proposes a cooperative predictive reference regulation control method for the virtual coupling system. The cyber-physical model of heavy-haul trains is built to characterize the longitudinal dynamic characteristics and their communication topologies. Secondly, a cooperative control law is designed to achieve velocity consensus and maintain a safe distance between adjacent trains. The cooperative reference velocity regulation is utilized to smoothly adjust the reference velocity of heavy-haul trains to suppress the fluctuations of the velocity and inter-train distance. Extensive simulation results verify that the proposed method can significantly reduce the velocity and distance fluctuations during the operation of virtual coupling systems when compared with the classical cooperative control method.