A New Hybrid Multi-Population GTO-BWO Approach for Parameter Estimation of Photovoltaic Cells and Modules

Abstract

Modeling the photovoltaic (PV) generating unit is one of the most important and crucial tasks when assessing the accurate performance of the PV system in power systems. The modeling of the PV system refers to the assigning of the optimal parameters of the PV’s equivalent circuit. Identifying these parameters is considered to be a complex optimization problem, especially with the deviation of the solar irradiance and the ambient temperature. In this regard, this paper proposes a novel hybrid multi-population gorilla troops optimizer and beluga whale optimization (HMGTO-BWO) model to evaluate the optimal parameters of the PV cell/panel; it is based on a multi-population strategy to improve its diversity and to avoid the stagnation of the conventional GTO. The BWO explorative and exploitative powers, which are based on synchronized motion and Lévy flight, are used. The suggested HGTO-BWO is implemented to minimize the root mean square error (RMSE) between the simulated and measured data for each cell/panel represented by a double diode model (DDM) and triple diode model (TDM). The proposed HGTO-BWO is investigated according to the standard and CEC-2019 benchmark functions, and the obtained results are compared with seven other optimization techniques in terms of statistical analysis, convergence characteristics, boxplots, and the Wilcoxon rank sum test. The minimum obtained RMSE values of the PVW 752 cell were 2.0886 × 10⁻⁴ and 1.527 × 10⁻⁴ for the DDM and TDM, respectively. Furthermore, the minimum fetched fitness value for the STM6-40/36 modules was 1.8032 × 10⁻³. The obtained results proved the effectiveness and preference of the suggested HGTO-BWO in estimating the parameters of the PV modules.

1. Introduction

Renewable energy sources (RESs) like wind and solar should be considered in order to mitigate the effects of climate change and rising temperatures, as well as to protect the planet from the pollution and destruction produced by traditional fossil energy [1]. The process of ecological transition involves identifying consumption and sustainable community models to reduce harmful emissions and to create reliance on power generation from renewable sources [2]. One of the aims of the sustainable development goals (SDGs), especially the seventh goal, is to obtain modern energy which is sustainable and highly reliable at the lowest cost [3]. There is a great deal of interest in RESs due to the enormous financial and environmental problems associated with traditional energy sources like fossil fuels. It is essential to transform the solar energy into different forms that may be utilized in daily life with the assistance of an appropriate device to exploit it [4,5]. Even though solar energy is abundant, its expansion is hampered by problems like fractional shadow, high construction cost, weather variation, and the need for costly storage. As a result, photovoltaic (PV) modeling is necessary to estimate the performance of a PV system before installation. Furthermore, the prediction of PV panel operating attributes is critical in solar PV system design, evaluation, simulation analysis, and control. Also, modeling aids in comprehending the functioning precept and attributes of the solar PV system under variable meteorological situations. The PV solar system is useful for capturing the solar energy and converting it into electrical power [5,6,7]; it has penetrated into many applications [5]. Moreover, the economic implications of the decreased lifetime and its causes are presented in [8]. One of the scientists’ priorities is to improve the efficiency and dependability of these technologies. Understanding the mechanisms of power absorption and conversion in solar cells, as well as correct modelling, can help in forecasting and designing them properly. One of the most critical challenges that researchers are facing is how to build a reliable model of the solar panel [9,10,11].

Changes in temperature and sun irradiance have significant impacts on the performance of PV systems [12]. Therefore, to maximize the performance of these systems, adequate mathematical models are required that precisely replicate the PV system behavior under several operational scenarios. Three of the most common PV system models, the single, double, and triple diode models (SDM, DDM, and TDM), are used [13,14].

The parameters of the SDM are simple to estimate as it only has five parameters, but its performance suffers from minimal irradiance scales and as a consequence of temperature changes. The DDM includes seven unknown parameters; it employs a second diode to achieve current reunification and to deal with other non-idealities [15]. However, the DDM suffers from some defects in recombining the current and other non-idealities. The final model is TDM, with nine ungiven parameters; it was introduced in [16]. Unfortunately, the nine parameters should be calculated as the manufacturers do not directly give them. To decrease the difference between the measured assessed power–voltage (P-V) and current–voltage (I-V) curves, the issue is converted into an optimization problem with a nonlinear objective function and a significant number of local minima.

Researchers are interested in employing metaheuristic algorithms to estimate the PV model parameters due to their notable success in handling various real-world optimization problems [5,6,7]. A hybrid seagull optimization algorithm architecture (HSOA) has been described for assessing the PV model parameters and developing a nonlinear control factor, which is dependent on the cosine function, to stabilize exploitation and exploration capabilities [1]. A springy whale optimization algorithm is described as an enhanced optimization technique to determine the parameters of PV cell/panel models [9]. Changes have been made to the way that the whales move in order to improve the algorithm performance. This helped the algorithm avoid the local solution, and the algorithm convergence speed was enhanced. In [13], an improved cuckoo search optimizer (ICSO) and a modified cuckoo search optimizer (MCSO) are implemented to solve the parameter evaluation issue of a PV system. Solar cell parameters have been evaluated through a genetic neural network (GNN) strategy [14]. The PV module characteristics have been identified with the aid of the tabu search optimizer (TSO) [15]; moreover, the lightning search algorithm, pattern search (PS), gravity search algorithm (GSA), genetic algorithm (GA), and PSO have been applied and compared to the presented approach [16].

In order to define the values of the ungiven parameters, the sooty tern optimization (STO) approach was developed for parameter evaluation of the PV cells/modules [17]. The hybrid particle swarm optimization (PSO) and rat search algorithm have been presented and combined as a hybrid approach for extracting the parameters of hybrid systems, including those of fuel cells and solar PVs [18]. The presented approach in that work reduced the likelihood of a local minimum and increased the algorithm accuracy. In [19], the animals migration optimizer (AMO) was introduced to construct the SDM of a PV system. The approach capacity for producing prompt, dependable, and consistent outcomes has been considered. In [20], a chaotic WOA for estimating the solar cell parameters was introduced; the key benefit of this method is that its parameters are automatically computed and adjusted using chaotic maps. In [21], a mathematical model for PV solar cells was created using the equilibrium optimizer (EO). The results using the EO have been compared with Harries hawk optimization (HHO), the teaching learn-based optimizer (TLBO), and PSO. In [22], the many approaches employed in constructing the SDM, DDM, and TDM of PV systems were reviewed and compared in terms of pros and cons.

The fractional-order Darwinian PSO methodology was used in [23] to enhance the conventional PSO method in evaluating the electrical parameters of PV cells/modules. To assign the solar cell parameters, the authors in [24] presented a hybrid honey badger algorithm and GTO [25]. These algorithms reduced the root mean square error (RMSE) between the simulated and measured results. In [26,27,28], a marine predatory animal (MPA) algorithm is described for computing the parameters of PV cells/panels in constant and varying weather situations. An improved stochastic fractal search algorithm has been used to solve the parameter appreciation of SDM solar cells and PV panels [29]. The authors in [30] presented the computational optimization method for extracting the parameters of solar cells/panels using an enhanced arithmetic optimization algorithm. In order to study the DDM-based circuit of a PV panel, practical tests to obtain the measured I-V and P-V characteristics have been conducted while considering various statistical analyses to determine the average, maximum, minimum, and standard deviations. A quick and efficient method for collecting the solar cell/panel parameters from the datasheet is provided in [31]. A niche PSO using a parallel computing technique was presented in [32] to identify the PV panel parameters. A multi-agent system (MAS) has been combined with CSO to estimate the parameters of various PV cells [33]. The circuits of SDM, DDM, and TDM for PV cells have been analyzed using the atomic orbital search to determine the ungiven parameters [34]. The tree seed algorithm has been used to calculate the parameters of the STM6-40/36 PV panel with different maximum fitness evaluations [35]. Moreover, a heterogeneous mechanism for the differential evolution algorithm (DE) [36], population diversity controlled DE [37], the artificial parameter-less optimization algorithm [38], random reselection PSO [39], the arithmetic operation algorithm based on the Newton–Raphson and Lambert W approaches [40], and adaptive slime mold [41] have been utilized to construct different equivalent circuits of PV cells/panels. A mayfly algorithm [42], northern goshawk optimization [43], and Newton–Raphson (NR) with an enhancement of a tuna swarm optimizer by a chaotic tent map [44] have been presented to evaluate the parameters of a TDM circuit. The parameters of a PV equivalent circuit were resolved by a chimp optimization algorithm with a robust niching approach [45], hybrid PSO with a gravitational search algorithm [46], chaos game optimization [47], an improved gradient-based optimizer based on sine cosine [48], DE enhanced by a chaotic map [49], and the predict output-based backpropagation neural network with EO [50]. Furthermore, the forensic-based investigation algorithm [51], the supply–demand optimizer [52], the enhanced hunger games search via the Laplacian Nelder–Mead approach [53], the Rao-1 optimization-based chaotic sequence [54], the arithmetic optimization algorithm-based guaranteed convergence and modified third-order NR [55], and the hybridized wind-driven optimization with fruit fly optimization [56] have been used to compute the parameters of various types of PV models.

Most of the reported studies have limitations, such as the falling into local optima, the requirement for numerous controlling parameters, and the complexity in implementation, in addition to the use of absolute algorithms without fundamental changes or modifications. The motivation of this study is to introduce a novel hybrid multi-population gorilla troops optimizer and beluga whale optimization (HGTO-BWO) to determine the PV cell/panel parameters such that all the gaps in the previous works are covered.

GTO is characterized by its ability to solve real-world problems with limited and unknown search space. On the other hand, the BWO has better stability, good convergence accuracy, stronger search ability, and a faster convergence rate. Therefore, hybridization between GTO and BWO results in a strong optimizer which is able to solve the handled problem with good efficiency. Table 1 provides a comparison of the recent work published in 2023 with regard to parameter estimations of PVs. The multi-population technique is applied to enhance the algorithm performance and avoid early convergence through dividing the entire population into many subgroups to preserve population variety. Different subgroups can be discovered throughout the whole search area and can reach the optimal solution efficiently by searching in different locations inside the search area at one time. Moreover, the optimization techniques can be easily and efficiently incorporated into multi-population methods [57,58]. The following are the major contributions of this article:

Table 1. A comparison of recent work published in 2023.

Ref.	Obj. Function	Model Type	Algorithm	Remark
[59]	RMSE	SDM, DDM and TDM	Hybrid chaotic NSO-PS	One type of PV is R.T.C used in all case studies; complexity and improved performance
[60]	RMSE	SDM and DDM	Growth optimizer	Ability to determine ungiven PV model parameters; low convergence
[61]	RMSE	SDM, DDM, and TDM	Chaos game optimization with least squares	Speed convergence and the RMSE values are similar to those of some other methods
[62]	Non-linear square with RMSE	SDM	GWO	Complexity in obj. function
[63]	RMSE	SDM, DDM, and TDM	Improved moth–flame algorithms	Low obj. function
Proposed	RMSE	SDM, DDM and TDM	HGTO-BWO	High performance and efficiency; avoids local optimum; fast convergence

• A novel approach of hybrid multi-population GTO-BWO is proposed in this work.
• The classical and CEC-C06 2019 benchmark functions are utilized to test and assess the proposed technique’s performance.
• The proposed HGTO-BWO is implemented to determine the ungiven parameters of TDM and DDM equivalent circuits of PV cells/panels.
• A comparison is made with TSA, the grey wolf optimizer (GWO), the whale optimization algorithm (WOA), the sine cosine algorithm (SCA), harmony search (HS), beluga whale optimization (BWO), and the artificial gorilla troops optimizer (GTO).
• The fetched results assure the effectiveness and validity of the suggested HGTO-BWO.

The rest of this article is as follows. Section 2 describes the mathematical model of solar PVs. Section 3 illustrates the problem expression, while the proposed hybrid multi-population GTO and BWO algorithm is presented in Section 4. The testing of the benchmark functions is presented in Section 5, and the application of the PV parameter estimation is given in Section 6. The conclusions are clarified in Section 7.

2. Modeling of Solar Photovoltaic (PV)

A solar PV cell is typically described through an electrical analogous circuit that includes current source, resistors, and a diode. Numerous PV cell modeling systems have evolved due to nonlinearity. The models of a PV cell are divided into three categories: single, double, and triple diode models. The prediction accuracy of the I-V curve is defined by the number of diodes in the model. Also, adding another diode, from one to three, enhances the model performance and precision at minimal irradiance levels. Similarly, the growth of modeling results in the development of the TDM. The model of the analogous circuit, its equations, and the specifications of the ungiven parameters are shown in Figure 1 and Figure 2. As the number of diodes grows, the number of model parameters to be evaluated grows and then the complexity of the problem is increased [64,65].

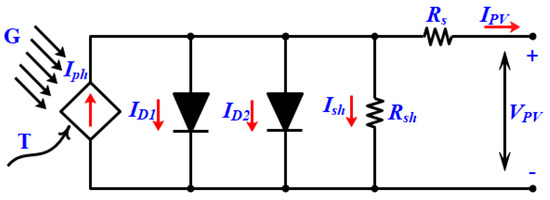
Figure 1. DDM equivalent circuit.

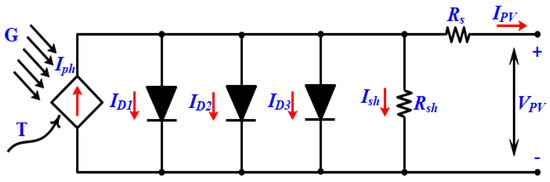
Figure 2. TDM equivalent circuit.

2.1. Double Diode Model (DDM)

The DDM uses dual diodes and dual resistors coupled in a series and shunted to the diode; this configuration is designed to compensate for the losses. The DDM of a solar cell is shown in Figure 1; with this concept, a second diode is added to reduce the transmission losses caused by the depletion layer carrier recombination and surface recombination, as specified by I_d2 [29,66]. The component of the current is represented by the current of the first diode I_d1.

The DDM can be formulated as follows:

$$I_{PV}=I_{ph}-I_{d1}-I_{d2}-I_{sh}$$

(1)

$$I_{PV}=I_{ph}-I_{d1}\left[exp\left[\frac{q\left[V_{PV}+R_s{I}_{PV}\right]}{A_{1}KT}\right]-1\right]-I_{d2}\left[exp\left[\frac{q\left[V_{PV}+R_s{I}_{PV}\right]}{A_{2}KT}\right]-1\right]-\left[\frac{V_{PV}+R_s{I}_{PV}}{R_{sh}}\right]$$

(2)

This model has seven parameters to be computed; they are provided as a vector, as given in Equation (3).

$$x=\left[A_1{A}_2{R}_s{R}_{sh}{I}_{d1}{I}_{d2}{I}_{ph}\right]$$

(3)

where $I_{d1}$, $I_{d2}$, and $I_{ph}$ are the reversal saturation currents of the diodes and photon current; $q$ is the electronic charge; $A_1$ and $A_2$ are the diodes’ ideality factors; $T$ denotes the temperature in Kelvin; $K$ refers to the Boltzmann constant; and $R_{sh}$ and $R_s$ are the shunt and series resistances.

2.2. Triple Diode Model (TDM)

Another model described in this work is the TDM; this model includes a current source, two resistors, and triple diodes, as shown in Figure 2. Dual diodes are considered in the model and are similar to those of the DDM, due to the reassembly and connection losses, while the third diode is due to the losses of the reassembly flow zones and boundaries [65,67].

The TDM can be expressed by following equations:

$$I_{PV}=I_{ph}-I_{d1}-I_{d2}-I_{d3}-I_{sh}$$

(4)

$$I_{PV}=I_{ph}-I_{d1}\left[exp\left[\frac{q\left[V_{PV}+R_s{I}_{PV}\right]}{A_{1}KT}\right]-1\right]-I_{d2}\left[exp\left[\frac{q\left[V_{PV}+R_s{I}_{PV}\right]}{A_{2}KT}\right]-1\right]-I_{d3}\left[exp\left[\frac{q\left[V_{PV}+R_s{I}_{PV}\right]}{A_{3}KT}\right]-1\right]-\left[\frac{V_{PV}+R_s{I}_{PV}}{R_{sh}}\right]$$

(5)

There are nine parameters to be evaluated in this model. The following vector can be used to represent them:

$$x=\left[A_1{A}_2{A}_3{R}_s{R}_{sh}{I}_{d1}{I}_{d2}{I}_{d3}{I}_{ph}\right]$$

(6)

2.3. PV Panel Model

The PV panel comprises numerous cells coupled in a series or parallel to produce greater voltage and current. Figure 3 illustrates the PV panel equivalent circuit.

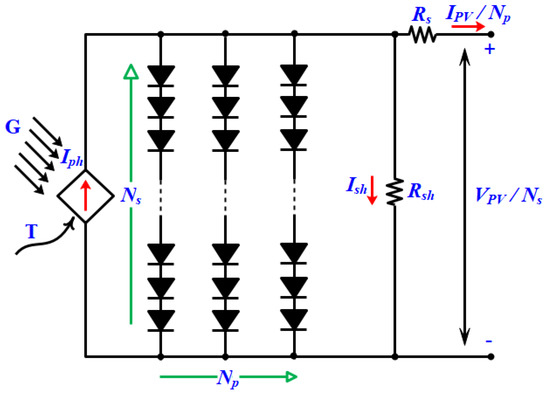
Figure 3. Solar PV module equivalent circuit.

The cells coupled in a series produce the same current. As a result, the panel output current can be written as given in Equation (7).

$$I_{PV}=I_{ph}\times N_p-I_{d1}\times N_p\left[exp\left[\frac{q\left[\raisebox{1ex}{$V_{PV}$}\!\left/ \!\raisebox{-1ex}{$N_s$}\right.+\raisebox{1ex}{$R_s$}\!\left/ \!\raisebox{-1ex}{$N_p$}\right.\times I_{PV}\right]}{A_{1}KT}\right]-1\right]-I_{d2}\times N_P\left[exp\left[\frac{q\left[\raisebox{1ex}{$V_{PV}$}\!\left/ \!\raisebox{-1ex}{$N_s$}\right.+\raisebox{1ex}{$R_s$}\!\left/ \!\raisebox{-1ex}{$N_p$}\right.I_{PV}\right]}{A_{2}KT}\right]-1\right]-\left[\frac{\raisebox{1ex}{$V_{PV}$}\!\left/ \!\raisebox{-1ex}{$N_s$}\right.+\raisebox{1ex}{$R_s$}\!\left/ \!\raisebox{-1ex}{$N_p$}\right.{\times I}_{PV}}{R_{sh}}\right]$$

(7)

where $N_s$ denotes the number of solar cells combined in a series, while $N_p$ denotes the number of cells connected in parallel [67,68]. Seven parameters should be calculated in the PV panel circuit; these are $A_1$, $A_2$, $R_s$, $R_{sh}$, $I_{d1}$, $I_{d2}$, and $I_{ph}$.

3. Problem Expression

In order to find the PV cell/panel equivalent circuit parameters, an optimization problem was formulated and solved to mitigate the RMSE between the measured current ($I_{\mathrm{M} }$) and the simulated one ($I_{\mathrm{S} }$). In the optimization formula, the unknown parameters are defined as design variables; the fitness value can be formulated as follows:

$$RMSE=\sqrt{\frac{1}{N_m}\sum _{i=1}^{N_m} f_{PV}(V_{PV},I_{PV},x{)}^2}=\sqrt{\frac{1}{N_m}\sum _{i=1}^{N_m} {\left(I_{\mathrm{M} }-I_{\mathrm{S} }\right)}^2}$$

(8)

where $N_m$ indicates the number of measured patterns, $f_{PV}$ refers to the PV model function, and $I_{\mathrm{M} }$ and $I_{\mathrm{S} }$ are the measured and simulated currents, respectively. The DDM objective function contains seven unknown parameters; it can be written as,

$$f_{DDM}\left(V_{PV},I_{PV},x\right)=I_{PV}-x_7+x_5\left(\mathit{exp}\left(\frac{q\left(V_{PV}+I_{PV}{x}_3\right)}{x_{1}KT}\right)-1\right)+x_6\left(\mathit{exp}\left(\frac{q\left(V_{PV}+{I_{PV}x}_3\right)}{x_{2}KT}\right)-1\right)+\frac{\left(V_{PV}+I_{PV}{x}_3\right)}{x_4}$$

(9)

where $x=\left[A_1{A}_2{R}_s{R}_{sh}{I}_{d1}{I}_{d2}{I}_{ph}\right]$.

On the other hand, the TDM objective function comprises nine unknown parameters, which can be expressed as,

$$f_{TDM}\left(V_{PV},I_{PV},x\right)=I_{PV}-x_9+x_6\left(\mathit{exp}\left(\frac{q\left(V_{PV}+I_{PV}{x}_4\right)}{x_{1}KT}\right)-1\right)+x_7\left(\mathit{exp}\left(\frac{q\left(V_{PV}+{I_{PV}x}_4\right)}{x_{2}KT}\right)-1\right)+x_8\left(\mathit{exp}\left(\frac{q\left(V_{PV}+{I_{PV}x}_4\right)}{x_{3}KT}\right)-1\right)+\frac{\left(V_{PV}+I_{PV}{x}_4\right)}{x_5}$$

(10)

where $x=\left[A_1{A}_2{A}_3{R}_s{R}_{sh}{I}_{d1}{I}_{d2}{I}_{d3}{I}_{ph}\right]$.

Finally, the TDM of the PV panel objective function can be written as,

$$f_{PV\_p}\left(V_{PV},I_{PV},x\right)=I_{PV}-x_7\ast N_p+x_5\ast N_p\left[exp\left[\frac{q\left[\raisebox{1ex}{$V_{PV}$}\!\left/ \!\raisebox{-1ex}{$N_s$}\right.+\raisebox{1ex}{$x_3$}\!\left/ \!\raisebox{-1ex}{$N_p$}\right.\ast I_{PV}\right]}{x_{1}KT}\right]-1\right]+x_6\ast N_P\left[exp\left[\frac{q\left[\raisebox{1ex}{$V_{PV}$}\!\left/ \!\raisebox{-1ex}{$N_s$}\right.+\raisebox{1ex}{$x_3$}\!\left/ \!\raisebox{-1ex}{$N_p$}\right.I_{PV}\right]}{x_{2}KT}\right]-1\right]+\left[\frac{\raisebox{1ex}{$V_{PV}$}\!\left/ \!\raisebox{-1ex}{$N_s$}\right.+\raisebox{1ex}{$x_3$}\!\left/ \!\raisebox{-1ex}{$N_p$}\right.{\ast I}_{PV}}{x_5}\right]$$

(11)

4. The Proposed Solution Methodology

This section describes and explains the main aspects of GTO, BWO, and the proposed HMGTO-BWO.

4.1. Gorilla Troops Optimizer (GTO)

The GTO is an efficient optimization algorithm that was inspired by the social life of gorillas, including their movements and lifestyles [69]. The leader in a gorilla group is known as a silverback and all the males and females follow it. The young male gorillas are known as blackbacks; they help the silverback and act as backup protection for the group. Two phases of exploitation and exploration form the GTO. Three operators are used in the exploration phases; the first operator is the migration to new locations, while the second operator is based on the movement of other gorillas; the third operator is dependent on the motion of the groups to known areas. In the GTO, the parameter $X$ refers to the gorilla position, and the $GX$ denotes the candidate gorilla locations, while the best solution position is represented as the silverback position. The exploitation phase is based on three motions of the gorillas, including their motion to a new unknown area, their motion to each other, and their movement to unknown locations. Mathematically, the exploration phase of the GTO can be described as follows:

$$GX(t+1)=\left\{\begin{array}{c}(UB-LB)\times r_1+LB, rand<p\\ \left(r_2-C\right)\times X_r\left(t\right)+L\times H, rand\ge 0.5\\ X\left(i\right)-L\times \left(L\times \left(X\left(t\right)-G{X}_r\left(t\right)\right)+r_3\times \left(X\left(t\right)-G{X}_r\left(t\right)\right)\right) rand<0.5\end{array}\right.$$

(12)

where $r_1$, $r_2$, and $r_3$ are random values in the range [0, 1]; $UB$ and $LB$ are the upper and lower limits of the variables; the $P$ operator is a generated random value; and $C$, $L$, and $H$ are operators that can be computed as follows:

$$C=F\times \left(1-\frac{t}{t_{\mathrm{m}\mathrm{a}\mathrm{x}}}\right)$$

(13)

$$F=\mathrm{c}\mathrm{o}\mathrm{s}\left(2\times r_4\right)+1$$

(14)

$$L=C\times l$$

(15)

$$H=Z\times X\left(t\right)$$

(16)

$$Z=[-C,C]$$

(17)

where $t_{\mathrm{m}\mathrm{a}\mathrm{x}}$ $and t$ are the maximum and current iterations, and $r_4$ is a random value in the range [0, 1]. The exploitation phase in this algorithm is based on the motion of the followers to the silverback gorilla. However, when the silverback dies or becomes ill, the male blackback gorillas become leaders; these gorillas fight to obtain the female gorillas. The exploitation phase mimics the motion of the males and females to the silverback. In addition to that, when the silverback dies or becomes old, the blackback gorilla males become leaders. Thus, the group may follow the silverback or the blackback gorilla males. The transition between the two movements can be adjusted using two operators, $C$ and $W$. In the case that $C\ge W$, the gorillas update their locations with respect to the silverback as follows:

$$GX(t+1)=M\times L\times \left(X\left(t\right)-X_{\mathrm{best} }\right)+X\left(t\right)$$

(18)

$$M={\left({\left|\frac{1}{N}\sum _{i=1}^N G{X}_i(t)\right|}^g\right)}^{\frac{1}{8}}$$

(19)

$$g=2^L$$

(20)

where $X_{\mathrm{best} }$ represents the silverback’s location. If $C<W$, the other gorillas follow the adult males; this may be described as follows:

$$GX\left(i\right)=X_{\mathrm{silverback} }-\left(X_{\mathrm{best} }\times Q-X\left(t\right)\times Q\right)\times A$$

(21)

$$Q=2\times r_5-1$$

(22)

$$A=\beta \times E$$

(23)

where $r_5$ represents a random value in the range [0, 1], $\beta$ denotes a predefined operator, and $E$ is a random value obtained from the normal distribution. The GTO’s pseudocode is depicted in Algorithm 1.

Algorithm 1 The Pseudocode of GTO

Start GTO $\mathbf{Input}: \mathrm{Set} \mathrm{the} \mathrm{parameters} \mathrm{of} \mathrm{the} \mathrm{GTO} (\mathrm{N}, t_{\mathrm{m}\mathrm{a}\mathrm{x}}$$, UB$$, LB$ $\mathbf{Output}: \mathrm{The} \mathrm{best} \mathrm{position} \mathrm{of} \mathrm{the} \mathrm{population} \left(X_{\mathrm{best} }\right)$ the corresponding fitness function.           Initialize the populations and calculate the objective functions and assign the best result. $\mathbf{While} \mathrm{t}<t_{\mathrm{m}\mathrm{a}\mathrm{x}}$ $\mathrm{Update} \mathrm{the} \mathrm{values} \mathrm{of} \mathrm{the} C$$, L$ using Equations (13) and (15).                       Update the positions of the gorillas according to (12).                       Compute the fitness function and assign the best solution. $\mathbf{If} C\ge W$                               Update the positions of the gorillas using Equation (18).                       Otherwise                               Update the positions of the gorillas using Equation (21).                       end                       Calculate the objective functions for the new locations and include them,                       if their values are better than the previous solutions       End while End GTO

4.2. Beluga Whale Optimization (BWO)

BWO is a new optimizer that was conceptualized from the motion, preying, and behavior of beluga whales (BWs) in the seas and oceans [70]. BWs are social creatures that share information and communicate together to search for food locations. Initially, the fitness function is expressed as follows:

$$F_X=\left[\begin{array}{c}f\left(x_{\mathrm{1,1}},x_{\mathrm{1,2}},\dots ,x_{1,d}\right)\\ f\left(x_{\mathrm{2,1}},x_{\mathrm{2,2}},\dots ,x_{2,d}\right)\\ ⋮\\ f\left(x_{n,1},x_{n,2},\dots ,x_{n,d}\right)\end{array}\right]$$

(24)

The swimming motion of the two BW pairs represents the exploration phase, which may be mathematically described as follows:

$$X_{i,j}^{t+1}=\left\{\begin{array}{ll}{X}_{i,p_j}^t+\left(X_{r,p_1}^t-X_{i,p_j}^t\right)\left(1+r_1\right)\mathrm{s}\mathrm{i}\mathrm{n}\left(2\pi r_2\right),& j= \mathrm{even} \\ X_{i,p_j}^t+\left(X_{r,p_1}^t-X_{i,p_j}^t\right)\left(1+r_1\right)\mathrm{c}\mathrm{o}\mathrm{s}\left(2\pi r_2\right),& j= \mathrm{odd} \end{array}\right.$$

(25)

where $X_{r,p_1}^t$ is a whale selected randomly from the generated BWs. The BWO exploitation phase is conceptualized from the hunting and preying process of BWs. They update their locations based on the best solution using the Levy flight strategy, as follows:

$$X_i^{\mathrm{t}+1}=r_3{X}_{\mathrm{best} }^t-r_4{X}_i^t+C_1\cdot L_F\cdot \left(X_r^t-X_i^t\right)$$

(26)

$$C_1=2r_4\left(1-t/t_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)$$

(27)

where $X_{\mathrm{best} }^t$ represents the best location, $X_r^t$ refers to a randomly selected BW, and $L_F$ is a Lévy flight function, which can be determined as follows:

$$L_F=0.05\times \frac{u\times \sigma }{|v{|}^{1/\beta }}$$

(28)

$$\sigma ={\left(\frac{\mathrm{s}\mathrm{i}\mathrm{n}(\pi \beta /2)\times \mathsf{\Gamma }(1+\beta )}{\beta \times \mathsf{\Gamma }\left(\right(1+\beta )/2)\times 2^{(\beta -1)/2}}\right)}^{1/\beta }$$

(29)

where $u$ and $v$ are random variables, and β is an adaptive variable used to enable the transition between the exploitation and the exploration phases; it can be calculated as,

$$B_f=B_0\left(1-t/2t_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)$$

(30)

where $B_0$ is a random value in the range [0, 1]. If $B_f>0.5$, the BWs update their locations in the exploration phase; otherwise, they update their locations in the exploitation manner. The final stage of the BWO is based on the whale fall of BWs when they have been attacked by the killer whales. The dead BWs are deposited on a deep seabed. This stage is represented as follows:

$$X_i^{t+1}=r_5{X}_i^t-r_6{X}_r^t+r_7{X}_{\mathrm{step} }$$

(31)

$$X_{\mathrm{step} }=\left(U_b-L_b\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(-C_{2}t/t_{\mathrm{m}\mathrm{a}\mathrm{x}}\right)$$

(32)

$$C_2=2W_f\times n$$

(33)

$$W_f=0.1-0.05t/t_{\mathrm{m}\mathrm{a}\mathrm{x}}$$

(34)

where $r_5$, $r_6$, and $r_7$ denote random variables in the range [0, 1]. The pseudocode of BWO is depicted in Algorithm 2.

Algorithm 2 The Pseudocode of the BWO

Start BWO $\mathbf{Input}: \mathrm{Set} \mathrm{the} \mathrm{parameters} \mathrm{of} \mathrm{the} \mathrm{BWO} (\mathrm{N}, t_{\mathrm{m}\mathrm{a}\mathrm{x}}$$, UB$$, LB).$ $\mathbf{Output}: \mathrm{The} \mathrm{best} \mathrm{position} \left(X_{\mathrm{best} }\right)$ of the populations and the corresponding fitness function. $\mathbf{While} \mathrm{t}<t_{\mathrm{m}\mathrm{a}\mathrm{x}}$                       Update the values of the using $C_1$$, B_f$, and $W_f$ using Equations (27), (30) and (34). $\mathbf{If} B_f>0.5$                                  // Exploration phase                                    Update the locations of the BWs using Equation (25).                       Otherwise                                  // Exploitation phase                                    Update the locations of the gorillas using Equation (26).                       end                                Compute the fitness functions for the new positions and select the best result. $\mathbf{If} B_f\ge W_f$                               // whale fall                                   Update the locations of the BWs using Equation (31).                       End                                Compute the fitness functions for the new positions and select the best result.     End while End BWO

4.3. The Proposed Hybrid Multi-Population GTO and BWO

The proposed HMGTO-BWO is introduced to solve complex and nonlinear optimization issues. The following steps describe the procedure of the proposed HMGTO-BWO:

Step 1: Define the parameters of the proposed HMGTO-BWO as well as the constraints of the problem.

Step 2: Generate a set of populations randomly.

Step 3: Divide the populations into three subpopulations (N₁, N₂, N₃), where N₁ = N₂ = N/3 and N₃ = N − (N1 + N2), where N, N₁, N₂, and N₃ are numbers of the population, the first subpopulation, the second subpopulation, and the third subpopulation, respectively.

Step 4: Update the populations in each subpopulation group based on the GTO, as illustrated in Section 4.1.

Step 5: Accept the new updated subpopulations if their values are better than those of the old populations.

Step 6: Combine the three subpopulations as one vector; it represents the initial populations of the BWO technique.

Step 7: Update the populations based on BWO, including the swimming motion, the Levy flight motion, and the fall of BWs.

Step 8: Repeat Step 3 to Step 7 until the stopping criterion is satisfied.

The step procedures of the suggested algorithm are depicted in Figure 4.

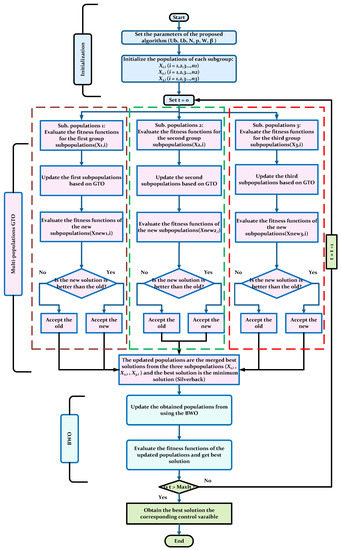
Figure 4. Flowchart of the proposed HMGTO-BWO.

The HGTO-BWO computational complexity is based on the initialization, fitness assessment, and updating of the silverbacks and BW, and it can be described as follows:

$$O\left(HGTO-BWO\right)={\left(Sub.Population1+Sub.Population2+Sub.Population3\right)}_{GTO}+BWO$$

(35)

$$\begin{gathered} O\left(HGTO-BWO\right)=\left[O\left(t_{max}\times \frac{1}{3}{N}_1\right)+O\left(t_{max}\times \frac{1}{3}{N}_1\times D\right)\times 2\right]+\left[O\left(t_{max}\times \frac{1}{3}{N}_2\right)+O\left(t_{max}\times \frac{1}{3}{N}_2\times D\right)\times 2\right] \\ +\left[O\left(t_{max}\times \frac{1}{3}{N}_3\right)+O\left(t_{max}\times \frac{1}{3}{N}_3\times D\right)\times 2\right]+O(N\times \left(1+1.1\times t_{max}\right)) \\ =O\left(\mathrm{N}\times \left(1+t_{max}+TD\right)\times 2+\left(1+1.1\times t_{max}\right)\right) \end{gathered}$$

(36)

where D is the dimension of the problem.

5. Testing of Benchmark Function

For a fair comparison between the suggested HGTO-BWO and the other algorithmic approaches, the maximum iterations number was set to 500; the population size was assigned to 30; and 30 runs were conducted for each considered optimizer. The proposed HGTO-BWO was investigated via the traditional benchmark functions and CEC 2019 functions. The fetched results were compared to TSA, GWO, WOA, SCA, HS, BWO, and GTO. The algorithms’ parameters are presented in Table A1 in Appendix A.

5.1. Traditional Benchmark Functions

The proposed HGTO-BWO was investigated via the solving of various traditional benchmark functions [71]; F1 to F13 have constant dimensions of 30, while the functions F14 to F23 have different dimensions. These functions are divided into the functions from F1 to F7, which are unimodal; F8 to F13, which are multi-modal; and F14 to F23, which are composites (See Supplementary Materials). Table 2 shows the statistical results of all the traditional benchmark functions; it includes the worst, average, best, standard deviation (std), and p-value. The values given in bold indicate the best solutions obtained by the proposed HGTO-BWO approach.

Table 2. Statistical analysis of traditional benchmark functions solved via the HGTO-BWO approach and other techniques.

Function No	Algorithm	Worst	Mean	Best	std	p-Value
F1	TSA	6.062× 10−21	8.593 × 10−22	1.829 × 10−24	1.367 × 10−21	1.21 × 10−12
	GWO	3.300 × 10−26	2.105 × 10−27	4.759 × 10−29	6.022 × 10−27	1.21 × 10−12
	WOA	6.553 × 10−70	2.364 × 10−71	2.778 × 10−83	1.197 × 10−70	1.21 × 10−12
	SCA	4.516 × 102	3.588 × 101	2.339 × 10−2	1.003 × 102	1.21 × 10−12
	HS	3.079 × 103	2.476 × 103	1.562 × 103	3.939 × 102	1.21 × 10−12
	BWO	1.925 × 10−257	1.272 × 10−258	1.274 × 10−272	0.00 × 100	1.21 × 10−12
	GTO	0.00 × 100	0.00 × 100	0.00 × 100	0.00 × 100	1.21 × 10−12
	HGTO-BWO	0.00 × 100	0.00 × 100	0.00 × 100	0.00 × 100	NAN
F2	TSA	4.979 × 10−13	1.128 × 10−13	1.047 × 10−14	1.206 × 10−13	3.02 × 10−11
	GWO	4.515 × 10−16	9.566 × 10−17	1.246 × 10−17	8.300 × 10−17	3.02 × 10−11
	WOA	1.156 × 10−48	7.100 × 10−50	1.076 × 10−56	2.454 × 10−49	3.02 × 10−11
	SCA	1.346 × 10−1	2.449 × 10−2	8.107 × 10−5	3.647 × 10−2	3.02 × 10−11
	HS	1.370 × 101	1.057 × 101	7.436 × 100	1.673 × 100	3.02 × 10−11
	BWO	1.849 × 10−129	6.467 × 10−131	1.310 × 10−137	3.37 × 10−130	3.02 × 10−11
	GTO	1.835 × 10−190	6.261 × 10−192	3.521 × 10−206	0.00 × 100	3.02 × 10−11
	HGTO-BWO	6.916 × 10−247	2.305 × 10−248	5.079 × 10−268	0.00 × 100	NAN
F3	TSA	2.826 × 10−3	3.329 × 10−4	1.572 × 10−8	7.279 × 10−4	1.21 × 10−12
	GWO	3.698 × 10−4	2.062 × 10−5	7.248 × 10−9	6.741 × 10−5	1.21 × 10−12
	WOA	7.244 × 104	3.723 × 104	2.987 × 103	1.716 × 104	1.21 × 10−12
	SCA	2.274 × 104	9.511 × 103	1.459 × 103	5.359 × 103	1.21 × 10−12
	HS	3.362 × 104	2.686 × 104	1.965 × 104	3.983 × 103	1.21 × 10−12
	BWO	1.555 × 10−242	1.060 × 10−243	2.864 × 10−257	0.00 × 100	1.21 × 10−12
	GTO	0.00 × 100	0.00 × 100	0.00 × 100	0.00 × 100	1.21 × 10−12
	HGTO-BWO	0.00 × 100	0.00 × 100	0.00 × 100	0.00 × 100	NAN
F4	TSA	7.663 × 10−1	2.588 × 10−1	1.258 × 10−2	2.234 × 10−1	3.02 × 10−11
	GWO	7.987 × 10−6	8.996 × 10−7	4.183 × 10−8	1.485 × 10−6	3.02 × 10−11
	WOA	9.425 × 101	5.178 × 101	7.053 × 10−2	3.113 × 101	3.02 × 10−11
	SCA	5.758 × 101	3.099 × 101	1.005 × 101	1.173 × 101	3.02 × 10−11
	HS	4.145 × 101	3.622 × 101	3.042 × 101	2.199 × 100	3.02 × 10−11
	BWO	3.880 × 10−126	3.095 × 10−127	2.571 × 10−133	7.804 × 10−127	3.02 × 10−11
	GTO	1.694 × 10−192	8.353 × 10−194	9.838 × 10−208	0.00 × 100	3.02 × 10−11
	HGTO-BWO	6.349 × 10−238	2.187 × 10−239	5.440 × 10−257	0.00 × 100	NAN
F5	TSA	2.889 × 101	2.838 × 101	2.609 × 101	7.737 × 10−1	2.37 × 10−12
	GWO	2.852 × 101	2.682 × 101	2.566 × 101	7.761 × 10−1	2.37 × 10−12
	WOA	2.877 × 101	2.794 × 101	2.728 × 101	5.032 × 10−1	2.37 × 10−12
	SCA	4.983 × 105	4.696 × 104	1.048 × 102	9.858 × 104	2.37 × 10−12
	HS	1.768 × 106	1.070 × 106	6.292 × 105	2.773 × 105	2.37 × 10−12
	BWO	8.153 × 10−6	1.346 × 10−6	1.618 × 10−9	2.176 × 10−6	2.37 × 10−12
	GTO	2.477 × 101	2.445 × 100	6.987 × 10−8	7.461 × 100	2.37 × 10−12
	HGTO-BWO	1.395 × 10−28	5.853 × 10−30	0.00 × 100	2.608 × 10−29	NAN
F6	TSA	4.820 × 100	3.817 × 100	2.590 × 100	6.004 × 10−1	1.212 × 10−12
	GWO	1.754 × 100	8.393 × 10−1	6.737 × 10−5	4.021 × 10−1	1.212 × 10−12
	WOA	9.864 × 10−1	3.725 × 10−1	1.355 × 10−1	1.979 × 10−1	1.212 × 10−12
	SCA	2.624 × 102	2.762 × 101	4.337 × 100	4.997 × 101	1.212 × 10−12
	HS	3.225 × 103	2.582 × 103	1.422 × 103	4.447 × 102	1.212 × 10−12
	BWO	2.490 × 10−13	1.879 × 10−14	1.153 × 10−17	4.703 × 10−14	1.212 × 10−12
	GTO	7.369 × 10−7	1.292 × 10−7	7.310 × 10−11	1.675 × 10−7	1.212 × 10−12
	HGTO-BWO	0.00 × 100	0.00 × 100	0.00 × 100	0.00 × 100	NAN
F7	TSA	2.022 × 10−2	9.471 × 10−3	1.816 × 10−3	4.734 × 10−3	3.02 × 10−11
	GWO	6.588 × 10−3	1.963 × 10−3	6.607 × 10−4	1.299 × 10−3	3.02 × 10−11
	WOA	1.522 × 10−2	3.099 × 10−3	5.474 × 10−5	3.995 × 10−3	3.16 × 10−10
	SCA	4.586 × 10−1	8.768 × 10−2	9.960 × 10−3	9.341 × 10−2	3.02 × 10−11
	HS	1.093 × 100	7.266 × 10−1	3.535 × 10−1	1.790 × 10−1	3.02 × 10−11
	BWO	4.232 × 10−4	1.563 × 10−4	3.893 × 10−7	1.160 × 10−4	1.70 × 10−2
	GTO	3.524 × 10−4	1.005 × 10−4	1.298 × 10−5	8.193 × 10−5	4.12 × 10−1
	HGTO-BWO	3.263 × 10−4	8.538 × 10−5	2.321 × 10−6	7.039 × 10−5	NAN
F8	TSA	−4.628 × 103	−5.706 × 103	−6.921 × 103	5.559 × 102	1.720 × 10−12
	GWO	−3.023 × 103	−6.026 × 103	−7.397 × 103	9.273 × 102	1.720 × 10−12
	WOA	−6.738 × 103	−1.051 × 104	−1.257 × 104	1.872 × 103	1.720 × 10−12
	SCA	−3.240 × 103	−3.726 × 103	−4.747 × 103	3.438 × 102	1.720 × 10−12
	HS	−1.130 × 104	−1.160 × 104	−1.196 × 104	1.851 × 102	1.720 × 10−12
	BWO	−1.257 × 104	−1.257 × 104	−1.257 × 104	1.548 × 10−8	4.562 × 10−11
	GTO	−1.257 × 104	−1.257 × 104	−1.257 × 104	1.868 × 10−5	4.562 × 10−11
	HGTO-BWO	−1.257 × 104	−1.257 × 104	−1.257 × 104	3.317 × 10−3	NAN
F9	TSA	2.745 × 102	1.924 × 102	1.364 × 102	3.806 × 101	1.212 × 10−12
	GWO	1.195 × 101	2.920 × 100	5.684 × 10−14	3.451 × 100	1.188 × 10−12
	WOA	5.684 × 10−14	1.895 × 10−15	0.00 × 100	1.038 × 10−14	3.337 × 10−1
	SCA	1.144 × 102	3.067 × 101	1.303 × 10−2	3.118 × 101	1.212 × 10−12
	HS	6.129 × 101	5.208 × 101	3.510 × 101	6.576 × 100	1.212 × 10−12
	BWO	0.00 × 100	0.00 × 100	0.00 × 100	0.00 × 100	NAN
	GTO	0.00 × 100	0.00 × 100	0.00 × 100	0.00 × 100	NAN
	HGTO-BWO	0.00 × 100	0.00 × 100	0.00 × 100	0.00 × 100	NAN
F10	TSA	1.926 × 101	1.676 × 100	1.077 × 10−12	3.633 × 100	1.212 × 10−12
	GWO	1.714 × 10−13	1.039 × 10−13	6.839 × 10−14	2.216 × 10−14	1.112 × 10−12
	WOA	7.994 × 10−15	4.796 × 10−15	8.882 × 10−16	2.529 × 10−15	1.233 × 10−9
	SCA	2.035 × 101	1.628 × 101	1.762 × 10−02	7.960 × 100	1.212 × 10−12
	HS	1.198 × 101	1.022 × 101	9.181 × 100	7.230 × 10−1	1.212 × 10−12
	BWO	8.882 × 10−16	8.882 × 10−16	8.882 × 10−16	0.00 × 100	NAN
	GTO	8.882 × 10−16	8.882 × 10−16	8.882 × 10−16	0.00 × 100	NAN
	HGTO-BWO	8.882 × 10−16	8.882 × 10−16	8.882 × 10−16	0.00 × 100	NAN
F11	TSA	7.086 × 10−2	1.139 × 10−2	0.00 × 100	1.437 × 10−2	3.453 × 10−7
	GWO	1.466 × 10−2	2.227 × 10−3	0.00 × 100	4.603 × 10−3	1.104 × 10−2
	WOA	1.334 × 10−1	8.450 × 10−3	0.00 × 100	3.220 × 10−2	1.608 × 10−1
	SCA	1.395 × 100	9.139 × 10−1	3.508 × 10−1	3.097 × 10−1	1.212 × 10−12
	HS	3.395 × 101	2.408 × 101	1.598 × 101	4.187 × 100	1.212 × 10−12
	BWO	0.00 × 100	0.00 × 100	0.00 × 100	0.00 × 100	NAN
	GTO	0.00 × 100	0.00 × 100	0.00 × 100	0.00 × 100	NAN
	HGTO-BWO	0.00 × 100	0.00 × 100	0.00 × 100	0.00 × 100	NAN
F12	TSA	1.763 × 1001	8.358 × 100	1.229 × 100	4.909 × 100	1.2 × 10−12
	GWO	8.906 × 10−2	4.194 × 10−2	1.302 × 10−2	1.904 × 10−2	1.2 × 10−12
	WOA	4.461 × 100	1.803 × 10−1	6.551 × 10−3	8.092 × 10−1	1.2 × 10−12
	SCA	7.264 × 106	2.860 × 105	6.013 × 10−1	1.328 × 106	1.2 × 10−12
	HS	2.270 × 105	5.098 × 104	1.847 × 103	5.045 × 104	1.2 × 10−12
	BWO	6.621 × 10−13	7.690 × 10−14	1.117 × 10−16	1.543 × 10−13	1.2 × 10−12
	GTO	1.505 × 10−7	3.881 × 10−8	3.088 × 10−10	4.298 × 10−8	1.2 × 10−12
	HGTO-BWO	1.571 × 10−32	1.571 × 10−32	1.571 × 10−32	5.567 × 10−48	NAN
F13	TSA	4.576 × 100	2.978 × 100	1.628 × 100	6.748 × 10−1	1.2 × 10−12
	GWO	1.141 × 100	6.990 × 10−1	1.132 × 10−1	2.570 × 10−1	1.2 × 10−12
	WOA	1.704 × 100	6.341 × 10−1	6.034 × 10−2	3.425 × 10−1	1.2 × 10−12
	SCA	2.870 × 106	2.229 × 105	2.964 × 100	6.961 × 105	1.2 × 10−12
	HS	2.840 × 106	1.215 × 106	3.453 × 105	5.884 × 105	1.2 × 10−12
	BWO	8.110 × 10−12	4.565 × 10−13	2.230 × 10−15	1.484 × 10−12	1.2 × 10−12
	GTO	6.478 × 10−2	4.357 × 10−3	8.216 × 10−12	1.414 × 10−2	1.2 × 10−12
	HGTO-BWO	1.35 × 10−32	1.35 × 10−32	1.35 × 10−32	5.567 × 10−48	NAN
F14	TSA	1.830 × 101	9.339 × 100	9.98 × 10−1	4.957 × 100	1.21 × 10−12
	GWO	1.267 × 101	4.948 × 100	9.98 × 10−1	4.243 × 100	1.21 × 10−12
	WOA	1.076 × 101	3.154 × 100	9.98 × 10−1	3.622 × 100	1.21 × 10−12
	SCA	1.076 × 101	2.114 × 100	9.98 × 10−1	2.498 × 100	1.21 × 10−12
	HS	9.980 × 10−1	9.980 × 10−1	9.98 × 10−1	1.873 × 10−7	1.21 × 10−12
	BWO	1.992 × 100	1.064 × 100	9.98 × 10−1	2.522 × 10−1	1.21 × 10−12
	GTO	9.980 × 10−1	9.980 × 10−1	9.98 × 10−1	5.831 × 10−17	1.61 × 10−01
	HGTO-BWO	9.980 × 10−1	9.980 × 10−1	9.98 × 10−1	0.00 × 100	NAN
F15	TSA	1.103 × 10−1	1.267 × 10−2	3.077 × 10−4	2.256 × 10−2	6.542 × 10−10
	GWO	2.036 × 10−2	6.373 × 10−3	3.075 × 10−4	9.316 × 10−3	1.651 × 10−9
	WOA	1.590 × 10−3	7.336 × 10−4	3.223 × 10−4	3.649 × 10−4	3.411 × 10−9
	SCA	1.624 × 10−3	1.029 × 10−3	5.172 × 10−4	3.986 × 10−4	9.499 × 10−10
	HS	1.562 × 10−2	2.036 × 10−3	6.734 × 10−4	2.721 × 10−3	4.490 × 10−10
	BWO	7.762 × 10−4	3.639 × 10−4	3.091 × 10−4	9.203 × 10−5	8.286 × 10−9
	GTO	1.223 × 10−3	3.991 × 10−4	3.075 × 10−4	2.794 × 10−4	7.665 × 10−1
	HGTO-BWO	1.223 × 10−3	3.685 × 10−4	3.075 × 10−4	2.323 × 10−4	NAN
F16	TSA	−1.000 × 100	−1.028 × 100	−1.032 × 100	9.652 × 10−3	6.319 × 10−12
	GWO	−1.032 × 100	−1.032 × 100	−1.032 × 100	3.067 × 10−8	6.319 × 10−12
	WOA	−1.032 × 100	−1.032 × 100	−1.032 × 100	2.284 × 10−9	6.319 × 10−12
	SCA	−1.031 × 100	−1.032 × 100	−1.032 × 100	3.080 × 10−5	6.319 × 10−12
	HS	−1.031 × 100	−1.032 × 100	−1.032 × 100	1.986 × 10−4	6.319 × 10−12
	BWO	−1.03 × 100	−1.031 × 100	−1.032 × 100	3.914 × 10−4	6.319 × 10−12
	GTO	−1.032 × 100	−1.032 × 100	−1.032 × 100	6.321 × 10−16	7.639 × 10−1
	HGTO-BWO	−1.032 × 100	−1.032 × 100	−1.032 × 100	6.388 × 10−16	NAN
F17	TSA	3.985 × 10−1	3.980 × 10−1	3.979 × 10−1	1.141 × 10−4	1.21 × 10−12
	GWO	3.988 × 10−1	3.979 × 10−1	3.979 × 10−1	1.706 × 10−4	1.21 × 10−12
	WOA	3.980 × 10−1	3.979 × 10−1	3.979 × 10−1	2.229 × 10−5	1.21 × 10−12
	SCA	4.262 × 10−1	4.010 × 10−1	3.979 × 10−1	6.015 × 10−3	1.21 × 10−12
	HS	3.997 × 10−1	3.981 × 10−1	3.979 × 10−1	4.448 × 10−4	1.21 × 10−12
	BWO	4.087 × 10−1	4.011 × 10−1	3.979 × 10−1	2.804 × 10−3	1.21 × 10−12
	GTO	3.979 × 10−1	3.979 × 10−1	3.979 × 10−1	0.00 × 100	NAN
	HGTO-BWO	3.979 × 10−1	3.979 × 10−1	3.979 × 10−1	0.00 × 100	NAN
F18	TSA	3.0 × 101	6.600 × 100	3.0 × 100	9.335 × 100	5.21 × 10−12
	GWO	3.0 × 100	3.0 × 100	3.0 × 100	3.081 × 10−5	5.21 × 10−12
	WOA	3.0 × 100	3.0 × 100	3.0 × 100	6.025 × 10−5	5.21 × 10−12
	SCA	3.0 × 100	3.0 × 100	3.0 × 100	1.173 × 10−4	5.21 × 10−12
	HS	3.006 × 100	3.001 × 100	3.0 × 100	1.271 × 10−3	5.21 × 10−12
	BWO	6.659 × 100	3.914 × 100	3.009 × 100	9.835 × 10−1	5.21 × 10−12
	GTO	3.0 × 100	3.0 × 100	3.0 × 100	9.257 × 10−16	3.146 × 10−02
	HGTO-BWO	3.0 × 100	3.0 × 100	3.0 × 100	1.414 × 10−15	NAN
F19	TSA	−3.862 × 100	−3.863 × 100	−3.86 × 100	1.091 × 10−4	7.57 × 10−12
	GWO	−3.855 × 100	−3.862 × 100	−3.86 × 100	2.427 × 10−3	7.57 × 10−12
	WOA	−3.834 × 100	−3.855 × 100	−3.86 × 100	7.989 × 10−3	7.57 × 10−12
	SCA	−3.843 × 100	−3.854 × 100	−3.862 × 100	3.439 × 10−3	7.57 × 10−12
	HS	−3.863 × 100	−3.863 × 100	−3.86 × 100	2.946 × 10−5	7.57 × 10−12
	BWO	−3.852 × 100	−3.858 × 100	−3.862 × 100	3.045 × 10−3	7.57 × 10−12
	GTO	−3.863 × 100	−3.863 × 100	−3.86 × 100	2.612 × 10−15	1.000
	HGTO-BWO	−3.863 × 100	−3.863 × 100	−3.86 × 100	2.612 × 10−15	NAN
F20	TSA	−2.840 × 100	−3.248 × 100	−3.321 × 100	1.106 × 10−1	2.646 × 10−7
	GWO	−3.103 × 100	−3.262 × 100	−3.322 × 100	7.766 × 10−2	2.646 × 10−7
	WOA	−3.055 × 100	−3.248 × 100	−3.322 × 100	9.266 × 10−2	6.828 × 10−7
	SCA	−1.454 × 100	−2.918 × 100	−3.220 × 100	3.302 × 10−1	2.319 × 10−11
	HS	−3.203 × 100	−3.302 × 100	−3.322 × 100	4.509 × 10−2	6.360 × 10−6
	BWO	−3.169 × 100	−3.267 × 100	−3.317 × 100	4.963 × 10−2	2.667 × 10−6
	GTO	−3.203 × 100	−3.298 × 100	−3.322 × 100	4.837 × 10−2	8.819 × 10−1
	HGTO-BWO	−3.203 × 100	−3.298 × 100	−3.322 × 100	4.837 × 10−2	NAN
F21	TSA	−2.603 × 100	−7.082 × 100	−1.012 × 101	3.387 × 100	1.406 × 10−11
	GWO	−2.682 × 100	−9.564 × 100	−1.015 × 101	1.828 × 100	1.406 × 10−11
	WOA	−2.585 × 100	−8.285 × 100	−1.015 × 101	2.950 × 100	1.406 × 10−11
	SCA	−4.973 × 10−1	−2.264 × 100	−5.364 × 100	1.829 × 100	1.406 × 10−11
	HS	−2.629 × 100	−5.921 × 100	−1.015 × 101	3.755 × 100	1.406 × 10−11
	BWO	−1.013 × 101	−1.015 × 101	−1.015 × 101	4.298 × 10−3	1.406 × 10−11
	GTO	−1.015 × 101	−1.015 × 101	−1.015 × 101	5.827 × 10−15	3.882 × 10−3
	HGTO-BWO	−1.015 × 101	−1.015 × 101	−1.015 × 101	6.506 × 10−15	NAN
F22	TSA	−1.826 × 100	−7.195 × 100	−1.034 × 101	3.555 × 100	6.387 × 10−12
	GWO	−5.088 × 100	−1.022 × 101	−1.04 × 101	9.702 × 10−1	6.387 × 10−12
	WOA	−1.836 × 100	−8.237 × 100	−1.04 × 101	3.179 × 100	6.387 × 10−12
	SCA	−9.062 × 10−1	−4.124 × 100	−7.417 × 100	1.629 × 100	6.387 × 10−12
	HS	−2.75 × 100	−5.982 × 100	−1.04 × 101	3.471 × 100	6.387 × 10−12
	BWO	−1.039 × 101	−1.04 × 101	−1.04 × 101	4.324 × 10−3	6.387 × 10−12
	GTO	−1.04 × 101	−1.04 × 101	−1.04 × 101	8.080 × 10−16	1.000
	HGTO-BWO	−1.04 × 101	−1.04 × 101	−1.04 × 101	8.080 × 10−16	NAN
F23	TSA	−1.671 × 100	−5.757 × 100	−1.041 × 101	3.745 × 100	7.574 × 10−12
	GWO	−2.422 × 100	−1.026 × 101	−1.054 × 101	1.481 × 100	7.574 × 10−12
	WOA	−1.672 × 100	−8.079 × 100	−1.054 × 101	3.345 × 100	7.574 × 10−12
	SCA	−9.436 × 10−1	−3.886 × 100	−5.962 × 100	1.374 × 100	7.574 × 10−12
	HS	−2.518 × 101	−6.977 × 100	−1.054 × 101	3.631 × 100	7.574 × 10−12
	BWO	−1.052 × 101	−1.053 × 101	−1.054 × 101	3.777 × 10−3	7.574 × 10−12
	GTO	−1.054 × 101	−1.054 × 101	−1.054 × 101	1.189 × 10−15	3.648 × 10−1
	HGTO-BWO	−1.054 × 101	−1.054 × 101	−1.054 × 101	2.356 × 10−15	NAN

5.2. CEC-C06 2019 Benchmark Functions

To verify the efficiency and validation of the suggested HGTO-BWO, it was tested and assessed with the modern functions of CEC-C06 2019 [72,73]. The CEC-C06 2019 benchmark function comprises 10 functions, where CEC01 to CEC03 have variable dimensions, while CEC04 to CEC10 have constant dimensions. The statistical analysis during the solving of CEC01 to CEC10 via the proposed HGTO-BWO and others was conducted, and the fetched results are tabulated in Table 3. The bold values given in Table 3 refer to the best results obtained through the proposed approach.

Table 3. Statistical analysis of CEC-C06 2019 benchmark functions solved via the proposed hybrid approach and others.

Function No	Algorithm	Worst	Mean	Best	Std	p-Value
CEC01	TSA	3.841 × 109	2.210 × 108	7.038 × 104	7.170 × 108	3.020 × 10−11
	GWO	4.821 × 109	3.646 × 108	4.506 × 104	9.087 × 108	3.020 × 10−11
	WOA	1.447 × 1011	2.554 × 1010	3.498 × 106	4.112 × 1010	3.020 × 10−11
	SCA	3.788 × 1010	8.327 × 109	2.425 × 107	8.725 × 109	3.020 × 10−11
	HS	9.231 × 1010	2.119 × 1010	3.137 × 109	1.969 × 1010	3.020 × 10−11
	BWO	8.286 × 104	6.219 × 104	4.906 × 104	8.071 × 103	3.020 × 10−11
	GTO	3.981 × 104	3.769 × 104	3.549 × 104	9.246 × 102	3.387 × 10−2
	HGTO-BWO	3.889 × 104	3.704 × 104	3.224 × 104	1.215 × 103	NAN
CEC02	TSA	1.956 × 101	1.840 × 101	1.735 × 101	7.225 × 10−1	1.061 × 10−11
	GWO	1.734 × 101	1.734 × 101	1.734 × 101	2.575 × 10−4	1.061 × 10−11
	WOA	1.747 × 101	1.735 × 101	1.734 × 101	2.329 × 10−2	1.061 × 10−11
	SCA	1.772 × 101	1.749 × 101	1.737 × 101	8.718 × 10−2	1.061 × 10−11
	HS	1.147 × 102	5.717 × 101	2.004 × 101	2.245 × 101	1.061 × 10−11
	BWO	1.780 × 101	1.755 × 101	1.744 × 101	8.285 × 10−2	1.061 × 10−11
	GTO	1.734 × 101	1.734 × 101	1.734 × 101	6.032 × 10−13	1.506 × 10−1
	HGTO-BWO	1.734 × 101	1.734 × 101	1.734 × 101	1.108 × 10−14	NAN
CEC03	TSA	1.271 × 101	1.27 × 101	1.27 × 101	1.298 × 10−3	1.720 × 10−12
	GWO	1.27 × 101	1.27 × 101	1.27 × 101	1.158 × 10−5	1.720 × 10−12
	WOA	1.27 × 101	1.27 × 101	1.27 × 101	2.173 × 10−6	1.720 × 10−12
	SCA	1.27 × 101	1.27 × 101	1.27 × 101	1.158 × 10−4	1.720 × 10−12
	HS	1.27 × 101	1.27 × 101	1.27 × 101	6.272 × 10−7	1.720 × 10−12
	BWO	1.27 × 101	1.27 × 101	1.27 × 101	1.160 × 10−4	1.720 × 10−12
	GTO	1.27 × 101	1.27 × 101	1.27 × 101	3.688 × 10−15	1.000
	HGTO-BWO	1.27 × 101	1.27 × 101	1.27 × 101	3.917 × 10−15	NAN
CEC04	TSA	9.665 × 103	4.501 × 103	1.712 × 102	2.214 × 103	3.020 × 10−11
	GWO	4.212 × 103	2.409 × 102	2.141 × 101	7.933 × 102	4.204 × 10−1
	WOA	6.893 × 102	3.777 × 102	1.490 × 102	1.541 × 102	3.020 × 10−11
	SCA	4.111 × 103	1.666 × 103	7.541 × 102	8.432 × 102	3.020 × 10−11
	HS	1.427 × 102	7.831 × 101	4.261 × 101	2.816 × 101	4.218 × 10−4
	BWO	1.211 × 104	7.614 × 103	2.383 × 103	2.226 × 103	3.020 × 10−11
	GTO	4.388 × 102	1.015 × 102	3.383 × 101	7.859 × 101	5.264 × 10−4
	HGTO-BWO	1.264 × 102	5.574 × 101	2.189 × 101	2.474 × 101	NAN
CEC05	TSA	4.893 × 100	3.033 × 100	1.560 × 100	8.286 × 10−1	4.504 × 10−11
	GWO	1.891 × 100	1.455 × 100	1.055 × 100	2.840 × 10−1	1.221 × 10−2
	WOA	2.786 × 100	1.862 × 100	1.287 × 100	3.340 × 10−1	4.616 × 10−10
	SCA	2.442 × 100	2.188 × 100	2.004 × 100	9.594 × 10−2	3.020 × 10−11
	HS	1.495 × 100	1.278 × 100	1.099 × 100	1.014 × 10−1	2.170 × 10−1
	BWO	4.149 × 100	3.617 × 100	2.867 × 100	3.177 × 10−1	3.020 × 10−11
	GTO	1.871 × 100	1.249 × 100	1.032 × 100	2.017 × 10−1	4.643 × 10−1
	HGTO-BWO	1.780 × 100	1.261 × 100	1.047 × 100	1.684 × 10−1	NAN
CEC06	TSA	1.184 × 101	1.106 × 101	9.047 × 100	6.621 × 10−1	3.020 × 10−11
	GWO	1.210 × 101	1.095 × 101	9.122 × 100	7.040 × 10−1	3.020 × 10−11
	WOA	1.141 × 101	9.831 × 100	7.546 × 100	9.329 × 10−1	4.504 × 10−11
	SCA	1.218 × 101	1.101 × 101	9.583 × 100	7.444 × 10−1	3.020 × 10−11
	HS	1.118 × 101	9.057 × 100	6.929 × 100	1.404 × 100	2.922 × 10−9
	BWO	1.200 × 101	1.090 × 101	9.780 × 100	5.720 × 10−1	3.020 × 10−11
	GTO	1.207 × 101	8.029 × 100	5.137 × 100	1.503 × 100	3.835 × 10−6
	HGTO-BWO	7.922 × 100	6.194 × 100	3.711 × 100	1.058 × 100	NAN
CEC07	TSA	1.035 × 103	5.909 × 102	1.111 × 102	2.431 × 102	1.010 × 10−8
	GWO	1.091 × 103	5.154 × 102	−1.534 × 101	3.448 × 102	4.639 × 10−5
	WOA	1.429 × 103	6.162 × 102	1.365 × 102	3.478 × 102	2.602 × 10−8
	SCA	1.140 × 103	7.929 × 102	4.640 × 102	1.563 × 102	3.020 × 10−11
	HS	7.648 × 102	2.673 × 102	−2.514 × 102	2.779 × 102	5.943 × 10−2
	BWO	1.183 × 103	8.537 × 102	5.020 × 102	1.761 × 102	3.020 × 10−11
	GTO	1.098 × 103	3.736 × 102	−1.016 × 102	2.990 × 102	1.680 × 10−3
	HGTO-BWO	4.571 × 102	1.388 × 102	−1.506 × 102	1.838 × 102	NAN
CEC08	TSA	7.051 × 100	6.333 × 100	5.427 × 100	4.589 × 10−1	9.063 × 10−8
	GWO	6.584 × 100	4.984 × 100	3.182 × 100	8.750 × 10−1	3.711 × 10−1
	WOA	7.060 × 100	5.965 × 100	4.795 × 100	5.548 × 10−1	1.493 × 10−4
	SCA	6.828 × 100	6.055 × 100	4.697 × 100	4.921 × 10−1	1.337 × 10−5
	HS	6.117 × 100	4.841 × 100	2.763 × 100	9.617 × 10−1	2.062 × 10−1
	BWO	6.843 × 100	6.311 × 100	5.657 × 100	2.931 × 10−1	2.922 × 10−9
	GTO	6.668 × 100	5.235 × 100	3.694 × 100	6.907 × 10−1	9.000 × 10−1
	HGTO-BWO	6.183 × 100	5.159 × 100	3.630 × 100	7.707 × 10−1	NAN
CEC09	TSA	1.579 × 103	2.795 × 102	3.468 × 100	4.309 × 102	3.020 × 10−11
	GWO	6.206 × 100	4.419 × 100	3.038 × 100	8.261 × 10−1	3.020 × 10−11
	WOA	2.169 × 101	5.703 × 100	3.495 × 100	3.128 × 100	3.020 × 10−11
	SCA	3.871 × 102	1.150 × 102	9.989 × 100	9.173 × 101	3.020 × 10−11
	HS	5.387 × 100	3.612 × 100	2.680 × 100	6.163 × 10−1	4.077 × 10−11
	BWO	1.964 × 103	1.230 × 103	6.707 × 102	3.098 × 102	3.020 × 10−11
	GTO	4.680 × 100	2.803 × 100	2.413 × 100	4.563 × 10−1	1.091 × 10−5
	HGTO-BWO	2.804 × 100	2.476 × 100	2.369 × 100	1.148 × 10−1	NAN
CEC10	TSA	2.065 × 101	2.047 × 101	2.022 × 101	1.108 × 10−1	3.338 × 10−11
	GWO	2.065 × 101	2.050 × 101	2.031 × 101	8.815 × 10−2	3.020 × 10−11
	WOA	2.052 × 101	2.028 × 101	2.007 × 101	1.117 × 10−1	2.371 × 10−10
	SCA	2.064 × 101	2.049 × 101	2.028 × 101	9.279 × 10−2	3.020 × 10−11
	HS	2.054 × 101	2.033 × 101	2.008 × 101	1.281 × 10−1	1.464 × 10−10
	BWO	2.061 × 101	2.044 × 101	2.020 × 101	1.031 × 10−1	3.338 × 10−11
	GTO	2.031 × 101	1.954 × 101	3.734 × 100	2.988 × 100	2.921 × 10−2
	HGTO-BWO	2.023 × 101	1.937 × 101	7.754 × 10−13	3.658 × 100	NAN

6. Application of HGTO-BWO: Parameter Estimation of PV Cell/Module

The proposed HGTO-BWO was applied to solve a vital problem regarding the identification of the optimal parameters of the PV cell/panel equivalent circuit with the aid of experimental data. The topic is very important as it is necessary to establish a reliable model of a PV system that simulates reality. This helps many researchers to conduct their work in the constructed circuit via the proposed methodology.

The parameters were computed in standard operating conditions for the PVM752 cell, STM6-40/36 panel, and PWP-201 module. Also, the double diode models for the KC200GT and MSX60 were constructed under various solar irradiances and temperatures. Table 4 shows the considered upper and lower limits of the design variables.

Table 4. The upper and lower limits of design variables for various PV cell/models.

Parameters	PVW 752		STM6-40/36		PWP-201		MSX60		KC200GT
	Lb	Ub	Lb	Ub	Lb	Ub	Lb	Ub	Lb	Ub
A1,2,3	1	2	1	60	1	50	1	2	1	2
Rs	0	0.8	0	0.36	0	2	0	2	0	2
Rsh	0	1000	0	1000	0	2000	0	500	0	500
Id1, Id2, Id3	0	1 × 10−6	0	50 × 10−6	0	50 × 10−6	0	10 × 10−6	0	10 × 10−6
Iph	0	0.5	0	2	0	2	0	8	0	16.4

6.1. Case 1: Constant Weather Conditions

6.1.1. PVW 752 Cell

The proposed HGTO-BWO was employed to determine the parameters of the DDM and TDM for a PVM752 GaAs thin film cell at 25 °C and 1000 W/m²; the electric characteristics of the PVM752 cell and the measured I-V data are presented in [74]. The convergence curves obtained by the considered optimizers for both models are shown in Figure 5. The RMSE value, statistical analysis, and optimal parameters of the DDM obtained through the proposed HGTO-BWO in comparison to the others are illustrated in Table 5. The least obtained RMSEs for the DDM and TDM were achieved by HGTO-BWO with values of 2.0886 × 10⁻⁴ and 1.527 × 10⁻⁴, respectively. On the other hand, the GTO approach ranked second, achieving fitness values of 4.6815 × 10⁻⁴ for the DDM and 2.278 × 10⁻⁴ for the TDM. The HS algorithm was the worst approach; it provided fitness values of 6.6870 × 10⁻¹ for the DDM and 3.738 for the TDM. Figure 6 shows the estimated and measured P-V and I-V curves of the DDM and TDM. It is notable that the estimated curves converge closely with the measured data; this means the PV cell/panel performed well and converged with the real one. The statistical parameters including best, worst, mean, and std are shown in Figure 7. The results shown in Table 5 verify the effectiveness of the suggested approach in extracting the parameters with the least fitness values compared to the other algorithms. The values given in bold indicate the best solutions obtained by the proposed HGTO-BWO approach.

Figure 5. Convergence curves for PVW 752: (a) DDM and (b) TDM.

Table 5. Optimal parameters of PVW752 PV cell DDM and TDM models.

Alg.	TSA	GWO [75]	WOA [76]	SCA	HS	BWO	GTO	HGTO-BWO
DDM
A1	1.7120	1.3103	1.7975	2.0000	1.9999	1.0000	1.9910	1.3954
A2	2.0000	2.0000	1.7975	2.0000	1.9998	1.0000	1.8486	1.8296
Rs	0.5153	0.5188	0.0000	0.0000	0.1255	0.0000	0.5764	0.6759
Rsh	1000.000	602.772	14.589	14.559	995.383	15.763	996.861	616.390
Id1	2.173 × 10−16	0.0 × 100	0.0 × 100	0.0 × 100	3.303 × 10−10	0.0 × 100	0.0 × 100	4.698 × 10−14
Id2	3.824 × 10−10	3.803 × 10−10	0.0 × 100	0.0 × 100	7.259 × 10−9	0.0 × 100	7.798 × 10−11	2.822 × 10−11
Iph	0.1002	0.1004	0.1138	0.1139	0.5000	0.1096	0.1000	0.1001
RMSE	7.1892 × 10−4	7.6797 × 10−4	2.5400 × 10−2	2.5400 × 10−2	6.6870 × 10−1	2.5504 × 10−2	4.6815 × 10−4	2.0886 × 10−4
Worst	2.5405 × 10−2	2.5416 × 10−2	8.3219 × 10−2	8.3219 × 10−2	1.8163 × 101	8.1095 × 10−2	2.5400 × 10−2	2.5400 × 10−2
Mean	3.3031 × 10−3	2.3763 × 10−2	3.8904 × 10−2	2.7333 × 10−2	6.1022 × 100	4.1477 × 10−2	2.2662 × 10−2	1.4662 × 10−2
std	4.7330 × 10−3	6.2492 × 10−3	2.4866 × 10−2	1.0555 × 10−2	4.4800 × 100	1.4131 × 10−2	6.5555 × 10−3	1.1001 × 10−2
p-value	7.9106 × 10−3	1.6060 × 10−9	2.1821 × 10−11	2.262 × 10−11	2.262 × 10−11	2.262 × 10−11	1.0147 × 10−3	NAN
TDM
A1	1.9293	1.6268	1.9620	1.0000	1.9987	1.0000	1.6157	1.9993
A2	2.0000	2.0000	1.9893	1.1864	1.9981	1.0000	1.0000	1.1530
A3	2.0000	1.9859	1.9977	1.1541	1.9995	1.0000	1.0050	1.9992
Rs	0.5356	0.5161	0.0000	0.0000	0.0027	0.0131	0.6605	0.7163
Rsh	853.5804	628.6429	94.9593	14.6251	996.7450	19.8767	608.0249	720.9139
Id1	2.471 × 10−11	0.0 × 100	2.422 × 10−10	0.0 × 100	6.784 × 10−9	0.0 × 100	3.779 × 10−12	1.708 × 10−10
Id2	3.088 × 10−10	3.559 × 10−10	0.0 × 100	0.0 × 100	1.092 × 10−9	0.0 × 100	0.0 × 100	1.371 × 10−16
Id3	2.362 × 10−11	2.097 × 10−11	0.0 × 100	0.0 × 100	2.872 × 10−8	0.0 × 100	0.0 × 100	2.894 × 10−20
Iph	0.1004	0.1003	0.0996	0.1137	0.4999	0.1015	0.1001	0.1000
RMSE	7.510 × 10−4	7.603 × 10−4	7.171 × 10−3	2.540 × 10−2	3.738 × 100	2.642 × 10−2	2.278 × 10−4	1.527 × 10−4
Worst	1.4277 × 10−2	1.7234 × 10−2	3.1417 × 10−1	3.1109 × 10−1	9.7810 × 10−3	1.4804 × 100	3.1880 × 10−3	2.4999 × 10−3
Mean	7.7371 × 10−3	5.9997 × 10−3	5.1015 × 10−2	1.5508 × 10−1	4.4487 × 10−3	4.6697 × 10−1	2.5146 × 10−3	1.9473 × 10−3
std	2.9796 × 10−3	2.7148 × 10−3	8.9905 × 10−2	1.4850 × 10−1	1.5576 × 10−3	3.2987 × 10−1	4.5441 × 10−4	1.4158 × 10−4
p-value	3.019 × 10−11	3.019 × 10−11	3.019 × 10−11	3.019 × 10−11	3.6897 × 10−11	3.019 × 10−11	3.2555 × 10−7	NAN

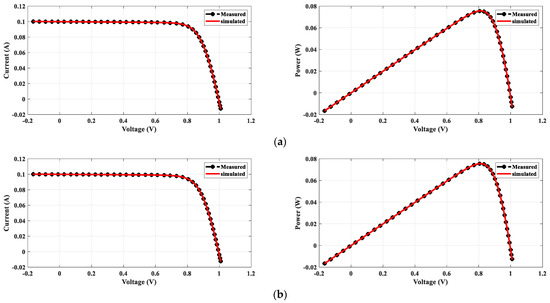
Figure 6. Measured and determined I-V and P-V curves for the PVM752 cell: (a) DDM and (b) TDM.

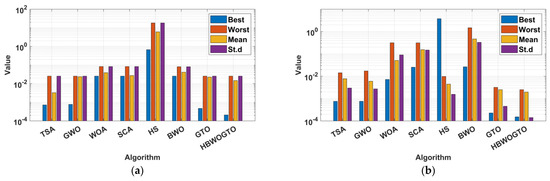
Figure 7. Bar chart of statistical analysis for the PVM752 cell: (a) DDM and (b) TDM.

6.1.2. PV Panel

The analyzed panels in this work were the Photowatt PWP-201 and STM6-40/36. The first one was investigated at 51 °C and 1000 W/m², while the PWP-201 module was investigated at 45 °C and 1000 W/m². The measured data for both considered panels are given in [54,77]. The fetched results for the DDMs of both panels are tabulated in Table 6. The proposed HGTO-BWO came in the first rank with the best RMSEs of 2.42508 × 10⁻³ for PWP-201 and 1.8032 × 10⁻³ for STM6-40/36, while the GTO approach was in the second rank with fitness values of 2.42511 × 10⁻³ and 1.88 × 10⁻³ for PWP-201 and STM6-40/36, respectively. The computed and measured P-V and I-V curves are shown in Figure 8. The obtained curves are completely consistent with the measured data, and this confirms the preference of the proposed method in obtaining an approved equivalent circuit that simulates reality. The mean ranking of the RMSE values is illustrated in Figure 9. It is confirmed that the proposed HGTO-BWO has the greatest rank among the applied algorithms, while Figure 10 illustrates the bar chart of the statistical analysis of the DDM. Moreover, the TDM optimal parameters and statistical analysis achieved by the proposed HGTO-BWO and the others are presented in Table 7. It is observed that the best fitness values were attained by the proposed HGTO-BWO with values of 2.2068 × 10⁻³ for PWP-201 and 1.7435 × 10⁻³ for STM6-40/36, while the worst fitness values were obtained via BWO with 1.5132 × 10⁻¹ and 2.4985 × 10⁻¹ for PWP-201 and STM6-40/36, respectively. Figure 11 depicts the measured and computed P-V and I-V curves of the TDM; the computed data converge with the measured ones; this validates the competence of the proposed HGTO-BWO. The mean ranking of the RMSE values and the statistical analysis for the TDM are presented in Figure 12 and Figure 13, respectively. The RMSE values in bold indicate the best solutions obtained by the proposed HGTO-BWO approach.

Table 6. The calculated parameters of DDM and statistical analysis for PWP-201 and STM6-40/36 panels.

Alg.	TSA	GWO [75]	WOA [76]	SCA	HS	BWO	GTO	HGTO-BWO
PWP201
A1	50.0000	50.0000	46.5652	50.0000	49.2825	1.0000	48.6368	48.6477
A2	48.3674	46.5502	49.9999	42.6562	49.5258	50.0000	1.0000	48.6330
Rs	1.1616	1.1824	1.1658	0.9700	1.1852	1.8645	1.2013	1.2012
Rsh	880.7826	1220.8951	1999.9965	904.1055	1420.8958	109.5641	977.9933	982.7504
Id1	4.343 × 10−6	4.180 × 10−6	0.0 × 100	4.661 × 10−6	3.556 × 10−6	0.0 × 100	3.477 × 10−6	2.886 × 10−6
Id2	3.688 × 10−7	2.946 × 10−7	4.923 × 10−6	0.0 × 100	5.916 × 10−7	3.483 × 10−6	0.0 × 100	5.988 × 10−7
Iph	1.0345	1.0303	1.0275	1.0158	1.0285	0.8628	1.0305	1.0305
RMSE	3.20292 × 10−3	2.56748 × 10−3	2.63181 × 10−3	2.42124 × 10−2	2.49283 × 10−3	2.34014 × 10−1	2.42511 × 10−3	2.42508 × 10−3
Worst	1.4277 × 10−2	1.7234 × 10−2	3.1417 × 10−1	3.1109 × 10−1	9.7810 × 10−3	1.4804 × 100	3.1880 × 10−3	2.4999 × 10−3
Mean	7.7371 × 10−3	5.9997 × 10−3	5.1015 × 10−2	1.5508 × 10−1	4.4487 × 10−3	4.6697 × 10−1	2.5146 × 10−3	1.9473 × 10−3
std	2.9796 × 10−3	2.7148 × 10−3	8.9905 × 10−2	1.4850 × 10−1	1.5576 × 10−3	3.2987 × 10−1	4.5441 × 10−4	1.4158 × 10−4
p-value	3.019 × 10−11	3.019 × 10−11	3.019 × 10−11	3.019 × 10−11	3.6897 × 10−11	3.019 × 10−11	3.2555 × 10−7	NAN
STM6-40/36
A1	55.8706	54.3091	59.9590	60.0000	57.9886	54.6034	59.9962	60.0000
A2	60.0000	55.3299	59.9590	26.9562	48.3514	54.8365	45.6821	43.5068
Rs	0.0902	0.1768	0.0190	0.0000	0.2181	0.0056	0.2450	0.2818
Rsh	929.6713	768.3818	999.3155	484.4850	649.1660	87.2447	611.4645	574.3640
Id1	1.121 × 10−6	1.564 × 10−6	5.814 × 10−6	5.764 × 10−6	1.966 × 10−6	7.834 × 10−7	2.858 × 10−6	2.855 × 10−6
Id2	3.006 × 10−6	3.692 × 10−9	0.000	0.000	1.356 × 10−7	7.834 × 10−7	5.815 × 10−8	2.551 × 10−8
Iph	1.6596	1.6584	1.6613	1.6695	1.6616	1.8222	1.6635	1.6643
RMSE	3.8737 × 10−3	3.2441 × 10−3	4.3087 × 10−3	7.5372 × 10−3	2.1464 × 10−3	7.7568 × 10−2	1.8800 × 10−3	1.8032 × 10−3
Worst	1.4277 × 10−2	1.7234 × 10−2	3.1417 × 10−1	3.1109 × 10−1	9.7810 × 10−3	1.4804 × 100	3.1880 × 10−3	2.4999 × 10−3
Mean	7.7371 × 10−3	5.9997 × 10−3	5.1015 × 10−2	1.5508 × 10−1	4.4487 × 10−3	4.6697 × 10−1	2.5146 × 10−3	1.9473 × 10−3
std	2.9796 × 10−3	2.7148 × 10−3	8.9905 × 10−2	1.4850 × 10−1	1.5576 × 10−3	3.2987 × 10−1	4.5441 × 10−4	1.4158 × 10−4
p-value	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.6897 × 10−11	3.0199 × 10−11	3.2555 × 10−7	NAN

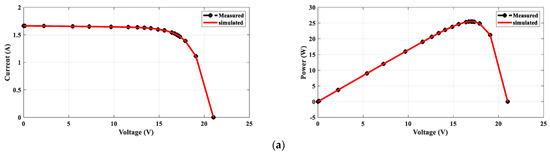
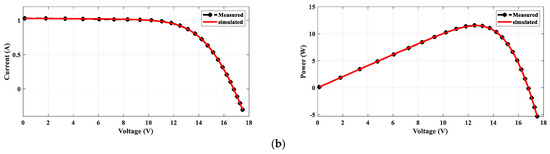
Figure 8. P-V and I-V curves for DDM: (a) STM6-40/36 and (b) PWP-201.

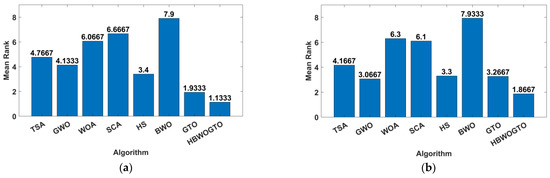
Figure 9. The mean ranking RMSE DDM of the Friedman test: (a) STM6-40/36 panels and (b) PWP-201.

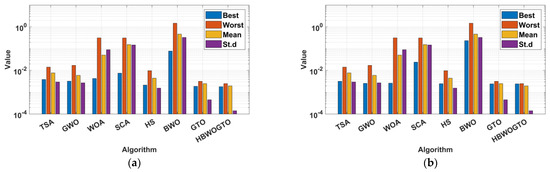
Figure 10. The statistical analysis for the DDM: (a) STM6-40/36 panels and (b) PWP-201.

Table 7. TDM optimal parameters and statistical analysis for PWP-201 and STM6-40/36 panels.

Alg.	TSA	GWO [75]	WOA [76]	SCA	HS	BWO	GTO	HGTO-BWO
PWP201
A1	50.0000	47.4470	50.0000	50.0000	49.3165	42.8772	49.9856	44.4743
A2	50.0000	49.7858	49.4766	6.9151	48.5919	1.0000	1.0000	14.9639
A3	49.2038	47.8414	9.1965	4.9402	48.4106	42.0707	48.6492	47.8405
Rs	1.1754	1.1860	1.1625	1.1260	1.1985	1.7161	1.2011	1.2922
Rsh	1434.1924	1248.8693	2000.0000	116.3588	1117.9430	171.5803	984.7595	1030.1916
Id1	4.635 × 10−8	5.765 × 10−7	4.924 × 10−6	4.681 × 10−6	8.715 × 10−7	0.0 × 100	0.0 × 100	4.465 × 10−9
Id2	3.161 × 10−6	3.603 × 10−6	0.0 × 100	0.0 × 100	2.462 × 10−6	0.0 × 100	0.0 × 100	4.699 × 10−20
Id3	1.405 × 10−6	0.0 × 100	0.0 × 100	0.0 × 100	2.458 × 10−7	3.997 × 10−7	3.488 × 10−6	2.730 × 10−6
Iph	1.0297	1.0291	1.0274	1.1189	1.0299	0.9035	1.0305	1.0297
RMSE	2.6051 × 10−3	2.4976 × 10−3	2.6738 × 10−3	2.7293 × 10−2	2.4956 × 10−3	1.5132 × 10−1	2.4251 × 10−3	2.2068 × 10−3
Worst	1.3165 × 10−1	7.2474 × 10−3	7.8391 × 10−1	7.8391 × 10−1	1.8873 × 10−2	7.8391 × 10−1	2.7425 × 10−1	2.7425 × 10−1
Mean	1.0840 × 10−2	3.4417 × 10−3	2.2133 × 10−1	2.4793 × 10−1	6.1577 × 10−3	4.6665 × 10−1	9.3345 × 10−2	2.9811 × 10−2
std	2.3150 × 10−2	1.1862 × 10−3	2.2042 × 10−1	1.7304 × 10−1	3.5373 × 10−3	1.6864 × 10−1	1.3011 × 10−1	8.2878 × 10−2
p-value	6.5238 × 10−7	3.8338 × 10−6	2.4324 × 10−9	4.1950 × 10−10	1.3848 × 10−6	5.4773 × 10−11	9.2129 × 10−3	NAN
STM6-40/36
A1	60.0000	18.8859	27.4319	60.0000	58.0623	50.3727	59.8760	59.8001
A2	60.0000	55.1060	59.9990	56.4263	57.8885	49.1217	45.3316	37.5844
A3	60.0000	56.1273	59.9990	60.0000	55.5272	49.1043	59.9974	59.9783
Rs	0.0003	0.1634	0.0123	0.0000	0.0883	0.0003	0.2649	0.3455
Rsh	933.7652	1000.00	861.6239	577.2329	901.7309	54.1090	570.3259	595.6377
Id1	1.215 × 10−6	0.0 × 100	0.0 × 100	0.0 × 100	2.489 × 10−6	3.932 × 10−8	1.808 × 10−13	3.100 × 10−6
Id2	2.828 × 10−6	1.365 × 10−6	5.857 × 10−6	0.0 × 100	7.033 × 10−7	3.932 × 10−8	5.465 × 10−8	1.456 × 10−9
Id3	1.804 × 10−6	7.092 × 10−7	0.0 × 100	5.828 × 10−6	3.482 × 10−7	3.932 × 10−8	2.653 × 10−6	8.272 × 10−9
Iph	1.6619	1.6569	1.6627	1.6656	1.6599	1.6349	1.6643	1.6643
RMSE	4.8420 × 10−3	3.4043 × 10−3	4.4379 × 10−3	6.1808 × 10−3	3.3162 × 10−3	2.4985 × 10−1	1.8235 × 10−3	1.7435 × 10−3
Worst	2.9048 × 10−2	2.0280 × 10−2	1.5378 × 100	1.5378 × 100	1.3253 × 10−2	1.3756 × 100	4.5153 × 10−3	3.2509 × 10−3
Mean	9.9667 × 10−3	6.9313 × 10−3	3.2435 × 10−1	2.3526 × 10−1	5.9740 × 10−3	4.4539 × 10−1	2.5938 × 10−3	2.0732 × 10−3
std	5.2223 × 10−3	3.9683 × 10−3	5.6249 × 10−1	2.8494 × 10−1	2.9328 × 10−3	2.5235 × 10−1	6.5633 × 10−4	3.0115 × 10−4
p-value	3.0199 × 10−11	3.019 × 10−11	2.9822 × 10−11	3.0199 × 10−11	3.019 × 10−11	3.0199 × 10−11	1.8575 × 10−3	NAN

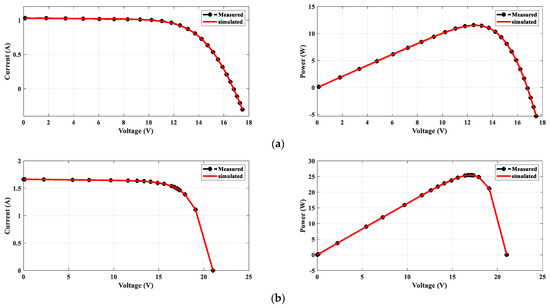
Figure 11. The I-V and P-V curves for TDM: (a) PWP-201 and (b) STM6-40/36.

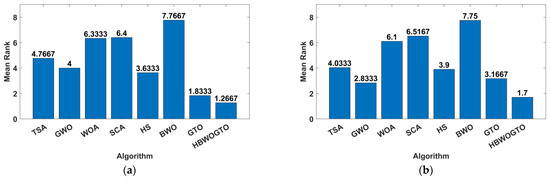
Figure 12. The mean ranking RMSE TDM of the Friedman test: (a) STM6-40/36 panels and (b) PWP-201.

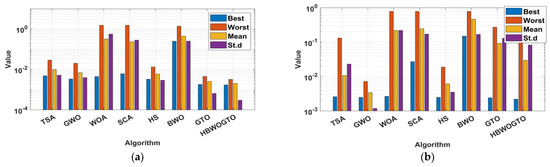
Figure 13. The statistical analysis for the TDM: (a) STM6-40/36 panels and (b) PWP-201.

6.2. Case 2: Variable Weather Conditions

The changes in temperature and solar radiation should be considered during the design of the PV system as they have great influence on the system’s efficiency [78]. The proposed HGTO-BWO constructed the DDM of MSX60 and KC200GT PV panels at various weather situations with the aid of the data given in [79]. Table 8 displays the statistical analysis of KC200GT in case A and B, where case A was conducted by operating the panel at 1000 W/m² and at the different temperatures of 25 °C, 50 °C, and 75 °C. In case B, the panel was operated at 25 °C and at the various irradiances of 1000 W/m², 800 W/m², 600 W/m², 400 W/m², and 200 W/m². The best RMSE values of 3.5092 × 10⁻³ and 1.6067 × 10⁻³ were obtained during operation at 25 °C and 50 °C via the proposed approach. Additionally, it achieved the minimum fitness values of 9.1596 × 10⁻⁴, 6.3910 × 10⁻⁴, 7.7891 × 10⁻⁴, and 2.3850 × 10⁻⁴ during operation at 800 W/m², 600 W/m², 400 W/m², and 200 W/m², respectively. Figure 14 illustrates the simulated and measured data of I-V and P-V curves. The statistical parameters of the approach during the establishment of the circuit of KC200GT at irradiances of 1000 W/m² and a temperature of 25 °C are illustrated in Figure 15 while the statistical analyses of MSX60 during various temperature and irradiances are displayed in Table 9. The proposed approach achieved the best RMSE values for MSX60 of 1.0765 × 10⁻⁴, 1.9324× 10⁻⁴, and 2.9790 × 10⁻⁵ at 1000 W/m² and temperatures of 25 °C, 50 °C, and 75 °C, respectively. Moreover, at 25 °C the fitness values were 1.1336 × 10⁻³ at 800 W/m²; 6.7775 × 10⁻⁴ at 600 W/m²; 2.4366 × 10⁻⁵ at 400 W/m²; and 5.9828 × 10⁻⁵ at 200 W/m². The estimated and measured curves are shown in Figure 16. Moreover, the bar chart of the statistical analysis for MSX60 at 1000 W/m² and 25 °C is given in Figure 17. The curves confirmed the efficiency and reliability of the suggested HGTO-BWO technique in establishing the PV panel equivalent circuit at different operating conditions.

Table 8. Statistical analysis of KC200GT obtained via the proposed approach and others.

Alg.	TSA	GWO [75]	WOA [76]	SCA	HS	BWO	GTO	HGTO-BWO
25 °C −1000 W/m2
Worst	2.9928 × 10−1	3.0217 × 10−1	4.8023 × 10−1	1.9379	1.1325 × 10−1	1.4025	4.8847 × 10−2	4.4998 × 10−2
Mean	1.2413 × 10−1	1.4665 × 10−1	2.0105 × 1001	5.6411 × 10−1	1.0267 × 10−1	8.1383 × 10−1	2.0235 × 10−2	1.7427 × 10−2
Best	7.4638 × 10−2	7.4290 × 10−2	5.6054 × 10−2	2.7115 × 10−1	8.4595 × 10−2	3.3635 × 10−1	4.3534 × 10−3	3.5092 × 10−3
std	5.0151 × 10−2	6.5383 × 10−2	1.0046 × 10−1	5.5487 × 10−1	5.7736 × 10−3	3.1312 × 10−1	1.2395 × 10−2	1.0633 × 10−2
p-value	3.019 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	4.3764 × 10−1	NAN
50 °C −1000 W/m2
Worst	3.6628 × 10−1	4.1794 × 10−1	5.4631 × 10−1	1.8390	7.5862 × 10−2	1.2964	9.7639 × 10−3	6.5681 × 10−3
Mean	8.4434 × 10−2	1.1236 × 10−1	1.7634 × 10−1	6.2204 × 10−1	5.7186 × 10−2	7.9166 × 10−1	5.5423 × 10−3	3.5076 × 10−3
Best	3.7404 × 10−2	2.3983 × 10−2	3.6157 × 10−2	2.3277 × 10−1	4.2992 × 10−2	2.7384 × 10−1	1.7663 × 10−3	1.6067 × 10−3
std	6.0767 × 10−2	1.2209 × 10−1	1.3871 × 10−1	4.9262 × 10−1	7.9771 × 10−3	2.3545 × 10−1	1.7398 × 10−3	1.2797 × 10−3
p-value	3.019 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	7.7387 × 10−6	NAN
75 °C −1000 W/m2
Worst	6.2182 × 10−1	1.0621 × 10−1	7.1242 × 10−1	1.7607	6.3285 × 10−2	1.5777	2.2913 × 10−2	1.6548 × 10−2
Mean	9.0915 × 10−2	4.9024 × 10−2	1.7288 × 10−1	5.6890 × 10−1	2.5581 × 10−2	7.3398 × 10−1	8.9380 × 10−3	7.5146 × 10−3
Best	1.6338 × 10−2	9.4445 × 10−3	1.1059 × 10−2	1.0406 × 10−1	7.6656 × 10−3	2.0249 × 10−1	6.6018 × 10−3	6.6031 × 10−3
std	1.3247 × 10−1	2.1144 × 10−2	2.2991 × 10−1	3.8031 × 10−1	1.5386 × 10−2	3.1381 × 10−1	3.3844 × 10−3	1.8398 × 10−3
p-value	3.3384 × 10−11	3.3384 × 10−11	3.3384 × 10−11	3.0199 × 10−11	1.4643 × 10−10	3.0199 × 10−11	1.0315 × 10−2	NAN
25 °C −800 W/m2
Worst	1.4449 × 10−1	2.2284 × 10−1	7.0500 × 10−1	1.4772	1.5979 × 10−1	1.1877	3.3746 × 10−2	3.2627 × 10−2
Mean	9.0134 × 10−2	1.0398 × 10−1	1.9967 × 10−1	2.5799 × 10−1	8.4035 × 10−2	6.0816 × 10−1	1.4743 × 10−2	1.1191 × 10−2
Best	3.5152 × 10−2	4.3232 × 10−2	6.5955 × 10−2	1.4555 × 10−1	6.0633 × 10−2	2.8132 × 10−1	1.2057 × 10−3	9.1596 × 10−4
std	2.6954 × 10−2	3.9288 × 10−2	1.5380 × 10−1	2.3535 × 10−1	1.8618 × 10−2	2.6438 × 10−1	9.0202 × 10−3	7.1797 × 10−3
p-value	3.019 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	8.2357 × 10−2	NAN
25 °C −600 W/m2
Worst	1.0078 × 10−1	1.0134 × 10−1	1.0689	1.0695	9.9952 × 10−2	1.1223	3.4077 × 10−2	2.8480 × 10−2
Mean	6.0087 × 10−2	6.2787 × 10−2	2.0351 × 10−1	2.7402 × 10−1	6.0285 × 10−2	4.7936 × 10−1	1.1981 × 10−2	7.9571 × 10−3
Best	2.5294 × 10−2	2.9938 × 10−2	6.4945 × 10−2	6.0119 × 10−2	4.9966 × 10−2	2.5931 × 10−1	1.2080 × 10−3	6.3910 × 10−4
std	1.6177 × 10−2	1.6123 × 10−2	1.8811 × 10−1	3.6424 × 10−1	1.1376 × 10−2	1.7777 × 10−1	7.7565 × 10−3	5.7342 × 10−3
p-value	3.3384 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	1.0315 × 10−2	NAN
25 °C −400 W/m2
Worst	9.3298 × 10−2	8.1703 × 10−2	2.4730 × 10−1	7.1507 × 10−1	1.2053 × 10−1	6.0211 × 10−1	2.3817 × 10−2	2.4774 × 10−2
Mean	5.3040 × 10−2	4.5807 × 10−2	1.0975 × 10−1	9.7278 × 10−2	4.4209 × 10−2	3.1765 × 10−1	9.7556 × 10−3	7.0046 × 10−3
Best	2.3846 × 10−2	1.2940 × 10−2	2.9330 × 10−2	3.0107 × 10−2	2.1731 × 10−2	1.1111 × 10−1	1.4399 × 10−3	7.7891 × 10−4
std	1.7438 × 10−2	1.8296 × 10−2	5.9500 × 10−2	1.1921 × 10−1	1.8535 × 10−2	1.2998 × 10−1	6.7435 × 10−3	5.4953 × 10−3
p-value	3.6897 × 10−11	6.0658 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.6897 × 10−11	3.0199 × 10−11	4.5146 × 10−2	NAN
25 °C −200 W/m2
Worst	4.7413 × 10−2	5.4922 × 10−2	3.4134 × 10−1	3.3976 × 10−1	6.1243 × 10−2	2.5166 × 1001	6.0751 × 10−3	9.9241 × 10−3
Mean	3.3437 × 10−2	3.3552 × 10−2	1.2126 × 10−1	5.6296 × 10−2	3.4866 × 10−2	1.2785 × 10−1	3.8762 × 10−3	2.6626 × 10−3
Best	8.0880 × 10−3	7.1727 × 10−3	4.4441 × 10−2	1.3225 × 10−2	1.3280 × 10−2	5.2239 × 10−2	3.8039 × 10−4	2.3850 × 10−4
std	1.1001 × 10−2	1.3676 × 10−2	9.2663 × 10−2	5.4823 × 10−2	1.0797 × 10−2	5.6607 × 10−2	1.6824 × 10−3	2.2870 × 10−3
p-value	4.5043 × 10−11	3.6897 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	1.9527 × 10−03	NAN

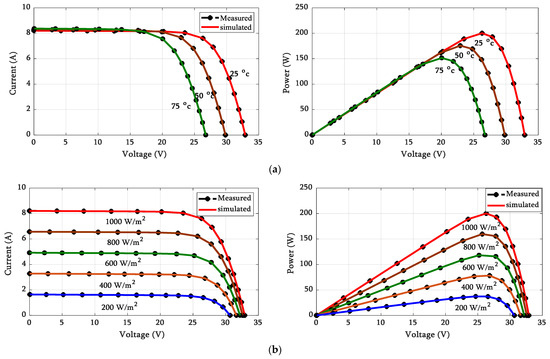
Figure 14. P-V and I-V curves of KC200GT: (a) constant irradiance of 1000 W/m² and (b) constant temperature of 25 °C.

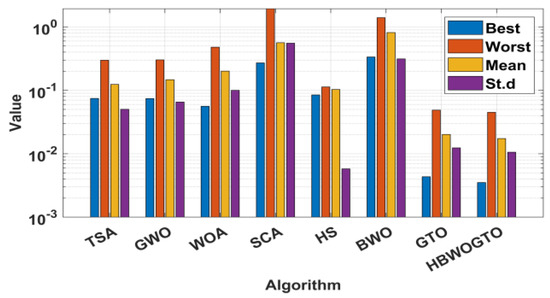
Figure 15. The statistical analysis for KC200Gt at 1000 W/m² and 25 °C.

Table 9. Statistical parameters of MSX60 panel obtained via the proposed approach and others.

Alg.	TSA	GWO [75]	WOA [76]	SCA	HS	BWO	GTO	HGTO-BWO
25 °C −1000 W/m2
Worst	6.5103 × 10−2	6.0081 × 10−2	7.6505 × 10−1	7.6471 × 10−1	4.8401 × 10−2	6.2681 × 10−1	2.1971 × 10−2	1.7942 × 10−2
Mean	4.4751 × 10−2	4.3733 × 10−2	1.3110 × 10−1	1.2951 × 10−1	3.8764 × 10−2	3.2185 × 10−1	1.0675 × 10−2	7.8333 × 10−3
Best	2.2794 × 10−2	2.5944 × 10−2	2.4565 × 10−2	4.6448 × 10−2	3.1247 × 10−2	6.6376 × 10−2	1.8986 × 10−3	1.0765 × 10−4
std	1.0134 × 10−2	8.8505 × 10−3	1.8165 × 10−1	1.7389 × 10−1	3.5080 × 10−3	1.5338 × 10−1	3.6012 × 10−3	3.2102 × 10−3
p-value	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	1.5846 × 10−4	NAN
50 °C −1000 W/m2
Worst	9.4706 × 10−2	1.0820 × 10−1	2.1100 × 10−1	7.7056 × 10−1	5.1888 × 10−2	6.8428 × 10−1	6.7625 × 10−3	5.6571 × 10−3
Mean	3.7155 × 10−2	4.3804 × 10−2	9.3860 × 10−2	1.4572 × 10−1	2.8151 × 10−2	3.5886 × 10−1	5.2558 × 10−3	1.9660 × 10−3
Best	1.8231 × 10−2	7.3825 × 10−3	1.8017 × 10−2	6.7026 × 10−2	2.3209 × 10−2	1.3748 × 10−1	2.3178 × 10−3	1.9324 × 10−4
std	2.0419 × 10−2	3.0053 × 10−2	5.3859 × 10−2	1.2205 × 10−1	5.3028 × 10−3	1.5568 × 10−1	1.4676 × 10−03	1.4357 × 10−3
p-value	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	8.4848 × 10−09	NAN
75 °C −1000 W/m2
Worst	1.6542 × 10−1	1.3157 × 10−1	2.5008 × 10−1	2.3490 × 10−1	3.6143 × 10−2	4.9704 × 10−1	5.2441 × 10−3	1.4355 × 10−3
Mean	3.0890 × 10−2	2.6953 × 10−2	8.4518 × 10−2	1.6671 × 10−1	1.2211 × 10−2	2.5469 × 10−1	1.0018 × 10−3	2.7448 × 10−4
Best	7.9526 × 10−3	5.4140 × 10−3	4.1026 × 10−3	3.1053 × 10−2	5.7215 × 10−3	7.9537 × 10−2	4.2011 × 10−5	2.9790 × 10−5
std	3.5408 × 10−2	3.1096 × 10−2	7.2347 × 10−2	5.0708 × 10−2	6.4175 × 10−3	1.0582 × 10−1	1.6193 × 10−3	2.6447 × 10−4
p-value	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.6322 × 10−1	NAN
25 °C −800 W/m2
Worst	5.2262 × 10−2	5.8604 × 10−2	6.1242 × 10−1	6.1262 × 10−1	4.0953 × 10−2	4.4466 × 10−1	1.2853 × 10−2	1.2248 × 10−2
Mean	3.5046 × 10−2	3.1685 × 10−2	1.0641 × 10−1	7.3537 × 10−2	2.9988 × 10−2	2.2502 × 10−1	8.6485 × 10−3	6.6717 × 10−3
Best	2.0629 × 10−2	1.0734 × 10−2	2.7649 × 10−2	3.4265 × 10−2	2.4251 × 10−2	6.6000 × 10−2	1.9350 × 10−3	1.1336 × 10−3
std	7.1751 × 10−3	9.9180 × 10−3	1.0964 × 10−1	1.0260 × 10−1	3.6823 × 10−3	9.9871 × 10−2	2.4842 × 10−3	2.6766 × 10−3
p-value	3.019 × 10−11	3.6897 × 10−11	3.019 × 10−11	3.019 × 10−11	3.019 × 10−11	3.019 × 10−11	2.2658 × 10−3	NAN
25 °C −600 W/m2
Worst	6.8702 × 10−2	5.1465 × 10−2	4.5790 × 10−1	4.5562 × 10−1	3.9280 × 10−2	3.7030 × 10−1	1.6311 × 10−2	1.3913 × 10−2
Mean	3.3254 × 10−2	2.8439 × 10−2	9.7793 × 10−2	6.3663 × 10−2	2.2989 × 10−2	1.9982 × 10−1	8.7540 × 10−3	5.6637 × 10−3
Best	9.8529 × 10−3	1.0988 × 10−2	1.5243 × 10−2	2.4905 × 10−2	1.3734 × 10−2	6.0603 × 10−2	1.0329 × 10−3	6.7775 × 10−4
std	1.3240 × 10−2	1.0653 × 10−2	1.0243 × 10−1	7.5057 × 10−2	7.5049 × 10−3	8.0178 × 10−2	3.4223 × 10−3	3.1345 × 10−3
p-value	6.0658 × 10−11	4.0772 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.6897 × 10−11	3.0199 × 10−11	1.4067 × 10−4	NAN
25 °C −400 W/m2
Worst	3.8949 × 10−2	4.4247 × 10−2	3.0055 × 10−1	2.9852 × 10−1	4.8025 × 10−2	1.8624 × 10−1	8.5444 × 10−3	8.5110 × 10−3
Mean	2.7298 × 10−2	2.7571 × 10−2	8.3476 × 10−2	6.4845 × 10−2	1.9225 × 10−2	1.0319 × 10−1	5.1743 × 10−3	3.1605 × 10−3
Best	1.1747 × 10−2	5.9229 × 10−3	2.0784 × 10−2	1.2556 × 10−2	6.7426 × 10−3	4.3302 × 10−2	8.5576 × 10−5	2.4366 × 10−5
std	7.4119 × 10−3	1.0414 × 10−2	5.8035 × 10−2	7.9820 × 10−2	8.3822 × 10−3	3.8071 × 10−2	2.2684 × 10−3	1.9135 × 10−3
p-value	3.019 × 10−11	4.0772 × 10−11	3.0199 × 10−11	3.0199 × 10−11	4.5043 × 10−11	3.0199 × 10−11	1.7836 × 10−4	NAN
25 °C −200 W/m2
Worst	2.9797 × 10−2	2.6406 × 10−2	7.1457 × 10−2	1.4110 × 10−1	3.2667 × 10−2	1.6797 × 10−1	7.5735 × 10−3	3.2257 × 10−3
Mean	1.6498 × 10−2	1.8636 × 10−2	3.4480 × 10−2	2.7961 × 10−2	1.7397 × 10−2	5.8459 × 10−2	1.7579 × 10−3	1.0399 × 10−3
Best	9.7357 × 10−3	1.0787 × 10−3	7.8442 × 10−3	6.3339 × 10−3	5.7370 × 10−3	2.6227 × 10−2	4.6560 × 10−4	5.9828 × 10−5
std	4.3918 × 10−3	6.1085 × 10−3	1.5446 × 10−2	2.2766 × 10−2	6.4824 × 10−3	2.5259 × 10−2	1.9112 × 10−3	7.0129 × 10−4
p-value	3.019 × 10−11	1.3289 × 10−10	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	3.0199 × 10−11	2.8378 × 10−1	NAN

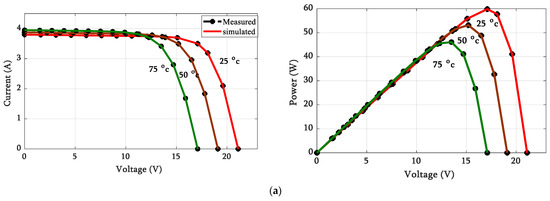
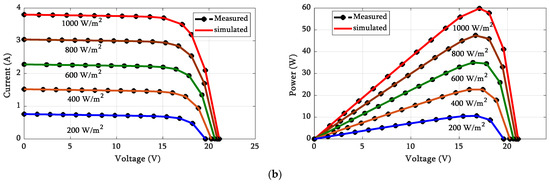
Figure 16. I-V and P-V curves of MSX60: (a) constant irradiance of 1000 W/m² and (b) constant temperature of 25 °C.

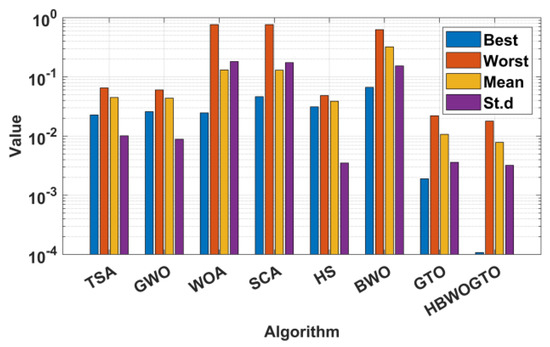
Figure 17. The statistical analysis for MSX60 at 1000 W/m² and 25 °C.

The fetched results demonstrated that the proposed HGTO-BWO is efficient in finding the optimal parameters of various models for the PV cell/panel as it outperformed the other regarded methodologies in all considered cases.

7. Conclusions

A new hybrid multi-population gorilla troops optimizer and beluga whale optimization (HGTO-BWO) was proposed to assign the PV cell/panel equivalent circuit by estimating its optimal parameters. In the proposed approach, a multi-population methodology was employed to improve the performance of the algorithm and to prevent it from falling into the local optima. The classical and CEC-C06 2019 benchmark functions were solved via the proposed approach to assess its performance. Two models, the double and triple diode models (DDM and TDM), were constructed for the PV cell/panel via minimizing the root mean square error (RMSE) between the simulated and measured currents. Various PV cells and panels operating in stable and variable weather situations were analyzed. Also, excessive comparison with TSA, SCA, GWO, WOA, HS, BWO, and GTO was conducted. The proposed approach findings can be summarized as follows:

• For the PVW 752 cell, the proposed HGTO-BWO achieved the best fitness values of 1.527 × 10⁻⁴ and 2.0886 × 10⁻⁴ for the TDM and DDM, respectively.
• The proposed approach achieved the lowest RMSEs of 2.42508 × 10⁻³ for the PWP-201 and 1.8032 × 10⁻³ for the STM6-40/36 DDM.
• The HGTO-BWO achieved the best fitness values of 2.2068 × 10⁻³ for the PWP-201 panel and 1.7435 × 10⁻³ for the STM6-40/36 TDM.
• For KC200GT, the minimum fitness values were 2.3850 × 10⁻⁴, 7.7891 × 10⁻⁴, 6.3910 × 10⁻⁴, and 9.1596 × 10⁻⁴ during operation at 200 W/m², 400 W/m², 600 W/m², and 800 W/m², respectively.
• For MSX60, the proposed methodology realized the best RMSE values of 1.0765 × 10⁻⁴, 1.9324 × 10⁻⁴, and 2.9790 × 10⁻⁵ at 25 °C, 50 °C, and 75 °C, respectively, while at 25 °C the fitness values were 1.1336 × 10⁻³ at 800 W/m², 6.7775 × 10⁻⁴ at 600 W/m², 2.4366 × 10⁻⁵ at 400 W/m², and 5.9828 × 10⁻⁵ at 200 W/m².

The results revealed that the proposed approach can be recommended as an efficient optimizer when constructing the PV unit equivalent circuit via identifying its parameters. The proposed method requires a great effort to implement and program, which is considered a major obstacle during implementation; in addition, a lot of time is needed. Therefore, simplifying this method and reducing the time required will be of interest to the authors of the future works. Moreover, the validation of the proposed methodology in estimating the parameters of the PV array when operated under different conditions will be considered in the next work.