Abstract
The valorisation of biomass by synthesising a multi-biomass corridor can be an optimistic pathway to solving the growing waste management problem. However, the supply chain problem usually involves a massive number of variables, including the connectivity of the sink source and the selection of a technology pathway. In this work, a “Decomposition Approach” was utilised, wherein a P-graph was incorporated with a conventional mathematical model to reduce the number of variables. Although this type of approach is well established with respect to solving biomass supply chain problems, no previous works have comprehensively considered the effect of the maximum allowable travel distance (MATD) on a supply chain model. A case study in Peninsular Malaysia involving oil palm, paddy, and coconut biomass was conducted using the proposed approach. Moreover, a multiple linear regression (MLR) tool for formulating the cost-correlated function based on the best technology pathway obtained from a P-Graph was incorporated. As a result, the net profit of the biomass corridor was estimated to be USD 0.87 billion, with 1.45 × 107 tonnes per year of biomass being sent to 39 processing hubs over a 20-year lifespan. Furthermore, a sensitivity analysis was also conducted to investigate the impact of several cost-related parameters on the net profit.
1. Introduction
It has been projected that there will be a significant increase in global energy consumption of approximately 50% between 2018 and 2050. This growth is primarily driven by non-Organisation for Economic Cooperation and Development (OECD) countries, particularly those in Asia [1,2]. This poses an urgent need to search for alternative energy sources that are renewable and sustainable. In the context of Malaysia, there are various types of renewable energy resources, namely, biomass, hydropower, and solar, that have a high potential to serve as an alternative source of power generation [3]. Recently, a great deal of research and development has focused on biomass, as it is a potentially valuable renewable energy resource [4]. Malaysia is one of the world’s leading agricultural countries; it mainly produces crops such as oil palms, paddy, coconuts, and rubber. After Indonesia, Malaysia is the next largest palm oil producer, accounting for 26% and 34% of the shares of global palm oil production and exportation, respectively [5]. In 2021, it was reported that 18.12 million tonnes of crude palm oil had been produced [6], which simultaneously resulted in the production of a substantial amount of palm oil biomass. In the palm oil industry, six different types of biomasses are produced, namely, empty fruit bunches (EFB), palm kernel shells (PKS), oil palm fronds (OPF), oil palm trunks (OPT), mesocarp fibre (MF), and palm oil mill effluent (POME) [7]. Due to the abundance of palm oil biomass, it is usually used as boiler fuel in palm oil mills to produce steam for electricity generation. Furthermore, the resulting wastes can be converted into pellets and organic compost. The biomass can also be transformed into higher-value products, such as bioethanol from EFB [8], activated carbon from PKS [9], and biogas from POME [10].
Paddy is also considered a major crop in Malaysia. It produces two types of biomasses, namely, paddy straw and rice husk [11]. In 2020, the total plantation area consisting of rice paddies across the whole country was estimated to be 644,854 ha, with an average yield of 4.01 tonnes of paddy per ha [12]. Paddy straw and rice husk are commonly combusted to generate energy, as both present HHV values ranging from 12.10 to 16.60 MJ/kg and 14.61 to 15.44 MJ/kg, respectively [13,14,15]. These lignocellulosic wastes can be utilised in applications in multiple sectors, including (but not limited to) as media for mushroom [16], ethanol, and biogas productions [17] and as adsorbents for the removal of pollutants from water [18]. Furthermore, based on statistics provided by the Department of Agriculture (DOA) [12], the total plantation area of coconut in Malaysia is 84,228 ha, yielding a production value of 0.57 million tonnes in 2021. Two of the major coconut biomasses are coconut shells and husks [19]. Coconut biomass can be transformed into electrical, thermal, or mechanical power via pyrolysis or gasification [20]. However, there is still minimal effort being exerted toward the utilisation of paddy and coconut biomass in Malaysia.
Hence, to foster the sustainable development in the renewable energy sector, it is imperative to establish a multi-biomass corridor that integrates underutilised biomass sources into the existing supply chain. The concept of a “biomass corridor” was first introduced by Ng et al. [21], defining it as an imaginary region that encompasses the facilities connecting biomass supply to product demand. In essence, the corridor encompasses a designated area with diverse, untapped biomass sources and processing hubs for the conversion of biomass into valuable products and the marketing of these products. Extending this concept to biomass supply chain management in Malaysia holds significant potential. However, designing an optimal structure for a biomass corridor poses a complex and challenging problem, involving activities such as biomass allocation, the application of technology, and transportation route design [22].
This challenge can be effectively addressed through the incorporation of process network synthesis (PNS) methodologies. PNS is an approach concerning the optimisation of material and energy flow systems. The goal of the approach is to identify the optimal configuration of processes and the corresponding network structure to achieve desired objectives, such as minimizing costs, maximizing resource utilization, and reducing environmental impacts [23]. To solve such complex combinatorial problems in a supply chain network, there are three major types of techniques that can be used, namely, mathematical modelling, multi-agent technology, and heuristic algorithms [24]. For the mathematical-modelling-based approach, the corresponding problem is structured in relation to linear programming (LP), mixed-integer programming (MIP), or mixed-integer linear programming (MILP). Numerous studies have been conducted to tackle the supply chain problem using traditional mathematical modelling due to its high capacity and affordability [25]. For instance, in one study, an automated targeting model (ATM) was modified for the supply chains of production and energy [26]. The results obtained showed that the utilisation of ATM is more advantageous than other common tools used in process integration due to its linearity. Another hybrid framework that comprises carbon emission pinch analysis and a superstructure-based optimisation technique was suggested by Leong et al. [27], with the corresponding study focusing on oil palm plantations in Selangor, Malaysia. The proposed framework optimised both CO2 emission minimisation targets and the bioenergy supply chain network simultaneously. In fact, the usage of such mathematical modelling approaches has been applied to solve other biomass supply chain problems (e.g., a coconut residue-based supply chain in Brazil [28] and a rice-straw-derived pellet supply chain in Japan [29]) as well.
Along these lines, the P-graph framework, which consists of both combinatorial and mathematical programming components, can be utilised for process network synthesis problems, e.g., azeotropic distillation [30], heat-integrated water regeneration networks [31], aquaponic farm design [32], ensuring negative emissions for polygeneration plants [33], and solving the biomass supply chain problem [34]. Friedler et al. [35] developed the P-graph to illustrate the structure of a process system using a unique bipartite graph, rendering it unlike other mathematical programming approaches. A P-graph can generate n-best solutions easily, while conventional mathematical modelling merely determines a single best solution. In a P-graph, there are nodes for the representation of materials and operating units as well as arcs for connection between an input and an output. Briefly, there are three important algorithms in a P-graph, namely, a maximal structure generator (MSG), a solution structure generator (SSG), and an accelerated branch-and-bound (ABB) algorithm. An MSG represents the model’s maximal structure, whereas an SSG comprises each solution structure. On the other hand, an ABB algorithm identifies the optimal structure.
Since the P-graph’s development in the 1990s, it has been applied extensively in the network synthesis of multiple sectors such as logistics and supply chains, technology and plant selections, and the planning and management of carbon capture and storage [36]. For example, a robust debottlenecking approach that incorporates a sustainability index into the P-graph framework had been developed for a given biomass supply chain [37]. The framework demonstrated exceptional ability in identifying the bottlenecks of the corresponding research problem effectively. Additionally, the P-graph method was used by Éles et al. [38] in the design of an energy system based on biomass in a rural area. In the results, it was observed that profits increased by about 31% with the developed MILP model, which includes different renewable resources, fermenters, and combined heat and power (CHP) plants. Although these studies have shown that the P-graph framework is capable of solving binary-intensive problems, the requirement for long computational times has limited its scalability, especially when one is dealing with large-scale problems that involve numerous entities. Therefore, to minimise the size of the problem, reduction approaches [39] must be introduced. Notably, How et al. [24] have developed a decomposition method that can systematically reduce the active variables required in a model by manually neglecting the infeasible options.
However, there are a few limitations in the previous works: (i) they have not comprehensively studied the effect of the maximum allowable travel distance (MATD) on the biomass supply chain model, which is expected to be one of the important parameters in designing the optimum biomass allocation, and (ii) they have merely addressed single-state problems, whose scalability to larger-scale problems (e.g., nation-wide problems) is still uncertain. Hence, this work aimed to address these limitations in order to further improve the corresponding model by applying a multi-regression tool to formulate the correlated cost function. In general, we aimed to allocate a set of biomass sources from Peninsular Malaysia to different sinks . In the processing hubs, biomass (r) is utilised as a renewable energy source in the production of heat, power, and value-added products (p) via different technologies (t). The products (p) such as biochar, py-oil, pellets, etc., are then sold to customers (k). Despite the effectiveness of the hybrid P-graph and mathematical programming approach (developed by How et al. [24]), its capability in solving a problem of a larger scale (i.e., previous research has only focussed on a single state) has yet to be tested.
To tackle these gaps, in this work, we aimed to extend the former P-graph-based hybrid to synthesize a biomass corridor across the entirety of Peninsular Malaysia, which contains a total of 11 states. The objectives of this work were as follows:
- Identify the optimal location in which to establish processing hubs (sinks) in Peninsular Malaysia;
- Evaluate the optimum allocation of various types of biomasses for valorisation;
- Evaluate the impact of the key parameters on the economic feasibility of the supply chain.
2. Methods
When multiple biomass sources across Peninsular Malaysia are considered, the result is a complex biomass supply chain problem. A decomposition algorithm was applied in this work, whereby the allocation and complex location were divided into smaller and simpler constituents [40]. As shown in Figure 1, there were 4 phases of this work. The first two phases concerned the identification of correlated cost functions by using the P-graph approach, while the last two phases concerned the optimisation of the model using a conventional mathematical model. The details of each phase are outlined in the following sections.
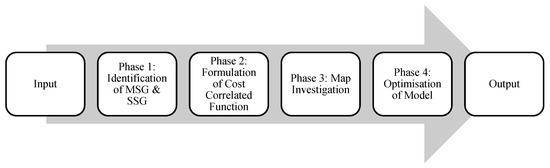
Figure 1.
Methodology for biomass supply chain network synthesis.
2.1. Phase I: Generation of MSG and SSG of Processing Hub
The combination of all viable process structures in a synthesis problem is known as maximal structure [41]. Prior to formulating the correlated cost function in Phase II, the P-graph framework proposed by Friedler et al. [41] was utilised to obtain the maximal structure of the processing hub. The information required by P-graph model comprises raw set (R), material set (M), product set (P), and operation unit (O). The cost-related variables, such as operating and capital costs, are pre-defined [42]. Figure 2 shows the maximal structure of a processing hub, where biomass (r) is turned into value-added products (p) via different technologies (t). Under certain pathways, intermediates (i) might be formed in between; therefore, another set of technologies (t′) is used to process them into the desired products (p). It should be noted that Figure 2 is just an illustrative example wherein there can be more than two technologies in between the raw material and final product.
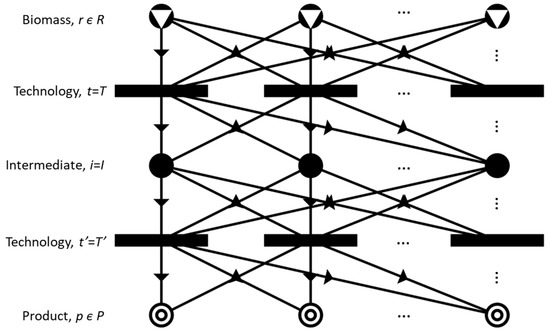
Figure 2.
Maximal structure in each processing hub.
2.2. Phase II: Formulation of Cost-Correlated Function
Since biomass sources are widely spread across Peninsular Malaysia, the supply chain model is generally complex and consists of a large number of “macro variables”. Moreover, a multi-biomass network must take a massive number of operational units, intermediates, and final products into account, resulting in many “micro variables”. It can be observed from Figure 3 that the term “macro variables” represents the flow variables between the supply chain entities and binary variables for hub selection, while the term “micro variables” refers to the internal flow variables between unit operations and binary variables for technology selection [24].
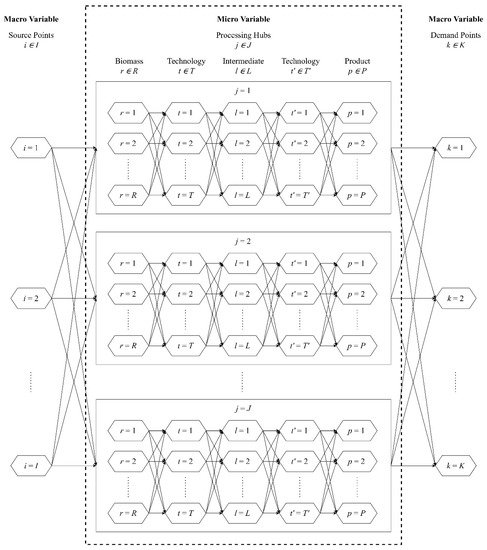
Figure 3.
Framework of superstructure for the biomass supply chain (modified with permission from How et al. [24]).
Additionally, to reduce the number of “micro variables”, the correlation between the amounts of raw material input to the hubs and gross profit is established by applying an ABB Algorithm in the P-graph framework. To obtain the n-best solutions, different amounts of raw materials are inputted into the model. There are different combinations of technology options in the processing hub for different solutions. Analysis of results is performed by establishing a correlation between the amount of raw materials input and maximal gross profit.
There are a few statistical models that can be used generally, namely, simple linear regression (SLR), multiple linear regression (MLR), and polynomial regression (PR). Three of these regression methods are designed to outline the correlation between a dependent variable and an independent variable(s). However, SLR is restricted to only a single independent variable that affects the dependent variable, which is not suitable in this case as this study involves various types of biomass feedstocks [43]. Moreover, the polynomial term in PR will alter the nature of the mathematical model such that is becomes a non-linear problem. This adds unnecessary complexity to the problem, and the optimality of the obtained solution is no longer guaranteed. On the other hand, MLR is an extension of SLR; it is a statistical method that involves several independent variables affecting the dependent variable [43]. The work performed by Thiangchanta and Chaichana [44] showed an example of utilising MLR to construct a mathematical model. In the same work, a heat load model was developed by the authors for an air-conditioned room. Ten independent thermodynamic parameters, including irradiation, temperature, and overall heat transfer, were considered to build the model. The heat load model was verified using a case study, and the error percentage was only 0.15%. Moreover, Rath et al. [45] built a prediction model to forecast the amount of new active cases of COVID-19 using MLR. The prediction model was constructed based on a case study in India, and it achieved a coefficient of determination (R2) value of 1. Moreover, Gowda et al. [46] developed a prediction model for diametrical deviations in machine components. The goal of the approach was to compensate for deviations due to thermal errors; hence, temperature(s) was employed as the independent variable(s). Several case studies were conducted, and the prediction model achieved an accuracy of 96.7%. Ottaviani and Marco [47] created an evaluation model to predict the total project cost required upon the completion of a project. This forecasting model was built by using 805 observed data from 29 completed real-life projects. The prediction model concluded that most of the projects would encounter cost overrun rather than be underbudgeted.
The amount of every biomass feedstock can serve as an independent variable that influences the maximal gross profit. Therefore, in this work, MLR model was utilised as the analytical tool to determine the correlation between the amount of raw materials input with maximal gross profit (i.e., the balanced cash flow between the revenue gained by selling the biomass-derived product and the cost associated with production). The Data Analysis tool in Microsoft Excel was used to carry out the MLR method [48]. The Data Analysis tool can be used after adding the ‘Analysis ToolPak’ application to the software through Excel Add-ins.
Gross profit (, USD) is a function of the amount of raw materials, and it was obtained using the MLR tool, as shown in Equation (1):
where denotes the amount of biomass r (ton), while refers to the respective cost constant for biomass r (USD/ton) obtained via the MLR model. Using this equation, the gross profit can be evaluated according to the number of feedstocks.
2.3. Phase III: Map Investigation
Map analysis was performed by conducting a site study of Peninsular Malaysia. Investigations of the locations of biomass sources and potential processing hubs were carried out in this phase to enable the synthesis of the supply chain model. There were three steps conducted in Phase III: regional division, elimination of infeasible area, and connectivity detachment. These steps were introduced to decrease the size of the model by removing the superfluous or infeasible “macro variables”.
2.3.1. Regional Division
It is necessary to selects sites for processing hubs in order to construct a supply chain model for a given case study. However, the area of a map to be investigated in a case study can be very large and complicated. Therefore, regional division was carried out by gridding the map to illustrate smaller zones. Each zone can be considered as a potential location at which to build a processing hub for the valorisation of biomasses. Figure 4a shows an example illustration of this step, where the grid lines divide the map area (Peninsular Malaysia) into smaller regions. The area enclosed by two pairs of adjacent horizontal and vertical grid lines constitutes a “zone”. An example of a “zone” is shown in Figure 4b. Similar step was carried out in the work performed by Lam et al. [49], where the study region was divided into a few supply and collections areas.
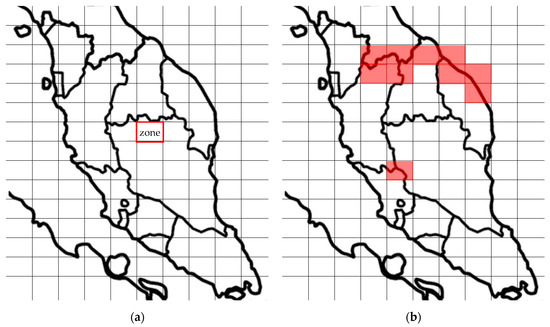
Figure 4.
Illustration of (a) regional division; (b) elimination of infeasible zones.
2.3.2. Elimination of Infeasible Zones
The zones that are unsuitable or not feasible for building a processing hub are known as “infeasible” zones. In particular, the “infeasible” zones include mountainous areas, reservoirs, reserve forests, lakes, residential areas, etc. Therefore, the “infeasible” zones can be removed from the model to reduce the burden on the solver, thus reducing the processing time of the solver. Figure 4b illustrates the infeasible zone elimination step, where the red shaded areas are the “infeasible” zones. Moreover, this step also eliminates the under-developed areas where there might not be consistent water or electricity supply.
2.3.3. Connectivity Detachment
Generally, in a supply chain problem, each source point i is connected to each possible processing hub j, while each processing hub j is connected to client k. The combinations of connectivity can produce a complex network with a large number of “macro variables”, leading to longer solving time. Since the efficiency of the model would be significantly reduced due to the large number of variables, the redundant “macro variables” were, therefore, removed [49]. Nevertheless, there is a limitation regarding the travelling distance in a real-world scenario, as the transportation costs of the raw material and product might exceed the profit generated. Hence, the maximum allowable travel distance (MATD, km) was considered for each biomass source. MATD can be calculated as the ratio of economic potential (EP, USD/ton) to the estimated transportation cost constant (, USD/ton/km), as presented in Equation (2). Figure 5 provides a depiction of connectivity detachment for various biomasses.
Figure 5.
Illustration of connectivity detachment.
2.4. Phase IV: Optimisation of Model
After the steps in Phase III have been applied, the remaining zones are the possible locations for constructing processing hubs. In Phase IV, a mathematical model is built to determine the optimal locations for processing hubs and an allocation pathway for biomass sources. The introduction of correlated cost function into the mathematical model can significantly reduce the number of variables. A description of the model’s formulation is outlined as follows:
Centralised hub j receives biomass r from source i to generate energy or to produce other valuable products. The amount of biomass r available in source i (, ton) must always be larger than the total amount of biomass transported from source i to processing hub j (, ton) at all times, as outlined in Equation (3):
A binary number is defined as a numerical value containing only two numbers, where 0 represents absence and 1 indicates presence. Therefore, binary variables are commonly used in mathematical programming to denote the selection of objects (i.e., equipment, processing hubs, etc.). In this case, the total amount of biomass received in processing hub j from source i (, ton/h) cannot exceed the hub’s capacity constraint (M, ton), while binary variable is introduced to denote the existence of a processing hub, as shown in Equation (4). It is worth mentioning that this is another key improvement on the former work [24], as the is now assigned based on the maximum hub capacity (a capacity constraint was not considered in the former work, which makes it less realistic). Accordingly, the value of binary variable is 1 if a processing hub is required; otherwise, the model will force the binary variable to be 0 to reduce investment costs.
The gross profit (, USD) can be calculated with the cost equation expressed previously, wherein it is a function of biomass amount, as presented in Equation (5):
The amount of final product p produced in processing hub j (, ton) can be evaluated by multiplying the amount of biomass received in processing hub j from source i (, ton) by the respective conversion factor for biomass r to be processed into final products p (, %) for all sources i, as shown in Equation (6). Furthermore, the total number of products p generated from processing hub j that were being sent to all customers k (, ton) cannot be more than the total amount of final product p produced in processing hub j (, ton), as outlined in Equation (7).
Moreover, transportation cost (, USD) is introduced into the system for the evaluation of economic performance. stems from the transportation cost of pre-processing, where biomass r is sent from source i to processing hub j (, USD), and post-processing, in which product k is sent from processing hub j to client p (, USD), as outlined in Equation (8). In particular, both of the transportation costs can be calculated via the multiplication of the material weights transported by the distance travelled (, km; , km) and the estimated transportation cost constant (, USD/ton/km), as shown in Equations (9) and (10), respectively. In reality, the route from one location to another is not a straight line. However, the exact distance is challenging to calculate, and a displacement equation is normally used to calculate the distance. Therefore, a reality factor (, km/km) of 1.2 is introduced into the displacement equation to account for the actual conditions of the road (e.g., crooked, bumpy, and/or curvy roads). Hence, the transportation distance between the source and destination, either to the processing hubs or the port (, km; , km), is determined by using displacement and reality factor, as shown in Equations (11) and (12):
where and represent the travelling distance between source i and processing hub j and between processing hub j and client k. , , , , , and are the x and y coordinates of source i, processing hub j, and client k respectively.
Moreover, the total capital cost of constructing processing hubs (, USD) can be calculated by implementing binary variable and the estimated investment cost for each hub (, USD), as presented in Equation (13). Furthermore, the annualised capital cost (, USD) can be determined via the application of capital recovery factor (CRF, %), as shown in Equation (14). Note that the CRF is computed using Equation (15):
where lifespan is denoted as (years), while the specified discounted rate is represented by (%). Note that readers can consider using other methods (e.g., the linear depreciation method) to annualise the capital cost depending on the nature of the problem. Lastly, the model was established to maximise the net profit (, USD), as shown in Equation (16).
The model proposed is an MILP problem. Hence, it can be solved using a conventional mathematical model; the global solver in Lingo x19.0 was used in this work.
3. Case Study
To achieve a sustainable future for renewable energy development in Malaysia, it is important to establish a multi-biomass network that integrates unused biomasses. In this case study, coconut husk, shell, rice husk, paddy straw, empty fruit bunches (EFB), and palm kernel shells (PKS) were chosen as biomass sources. The technology pathways used in this case study, together with the raw materials and products employed, are depicted in Figure 6. Furthermore, the construction of the superstructure of the process flow for each biomass was represented using a P-graph (see Figure 7), where the circular nodes refer to materials (biomass and products), while the horizontal nodes represent the operating units included in the case study (note that readers can refer to Friedler et al. [36] for more information on the user manual for the P-graph software). In addition, the unit prices of the materials (note that the logistic costs such as transportation costs are counted separately in Equation (8)) involved are compiled in Table 1.
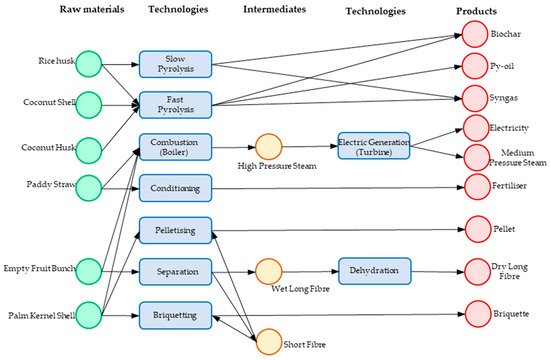
Figure 6.
Superstructure of the process flow of each biomass.
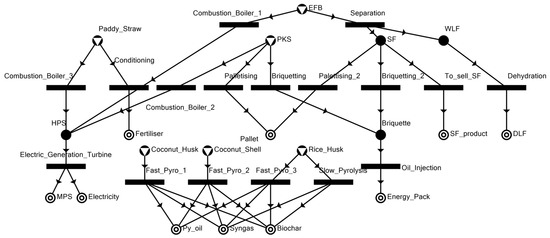
Figure 7.
Superstructure of the process flow of each biomass in P-Graph.

Table 1.
Material cost for biomass feedstocks, products, and utilities.
Generally, coconut biomass, namely, coconut shells and husks, can be further processed into biochar, py-oil, and syngas via fast pyrolysis. Similarly, rice husk with a high energy content can be used to produce py-oil, syngas, and biomass via fast and slow pyrolysis [52]. On the contrary, dried long fibre (DLF; the dried form of wet long fibre (WLF)), pellets, electricity, and briquettes are the value-added products and resources produced using EFB and PKS from oil palm biomass. Briefly, EFB was processed into DLF via processes such as drying, sieving, and bailing. In addition, high-pressure steam (HPS) was generated from the boiler-based combustion of paddy straw, EFB, and PKS. HPS was then used for electricity and medium-pressure steam (MPS) generation. An intermediate product, short fibre (SF), was generated and used to produce briquettes, for which an additive was incorporated to enhance calorific value. Similarly, PKS was converted into briquettes and pellets [24]. The coconut shells and husks were processed into three final products, namely, biochar, py-oil, and syngas, which can be used for energy generation [53]. Paddy straw was also used to produce fertiliser via conditioning. The respective conversion ratios, capital, and operating costs are listed in Table 2 (note that the linear conversion rate is expressed with the functional unit of the mass of the biomass input) and Table 3 (expressed in proportional forms, while maintenance costs are not considered explicitly in this work). It is worth noting that the technology pathways considered in this case study are based on the Malaysian context; this work, by no means, aims to cover all the potential technologies available on the market. Nevertheless, the proposed formulations can be easily adapted to other case studies that involve different sets of biomass and conversion technologies.

Table 2.
Conversion ratios for each technology.

Table 3.
Economic data for each technology (adapted with permission from Yeo et al. [50]).
In this work, Peninsular Malaysia was chosen as the study area due to its extensive biomass availability and its more developed modes of transportation. Figure 8 illustrates the oil palm and coconut biomass plantations and the paddy fields in the study area, with the respective crops’ availability values tabulated in Table A1 in the Appendix A [12,55]. Note that in this case study, the biomass yields were assumed to have the following values: 0.22 tons of EFB and 0.055 tons of PKS are produced per ton of oil palm fresh fruit bunches, respectively [56]; 0.7 tons of paddy straw [57] and 0.22 tons of rice husks [58] are generated per ton of rice grain harvested, respectively; and 0.35 tons of coconut husks and 0.12 tons of coconut shells are generated per ton of coconut harvested [59].
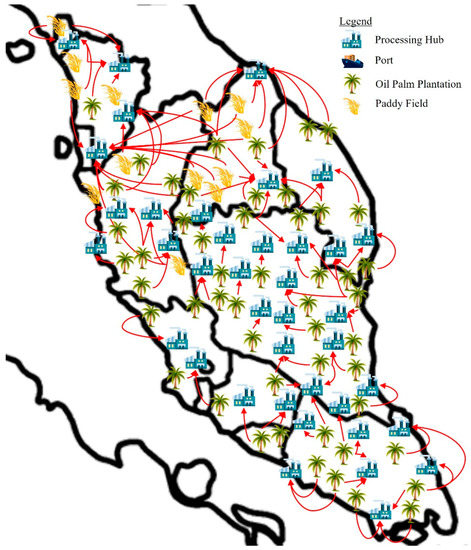
Figure 8.
Optimum processing hub location and biomass allocation design (note that the arrows refers to the optimal allocation of materials).
In Peninsular Malaysia, there are a total of 51 major oil palm plantation areas, each of them being over 20,000 ha, and they are distributed in Johor, Malacca, Pahang, Negeri Sembilan, Selangor, Perak, Kedah, Kelantan, and Terengganu. Moreover, there are four main plantation areas for coconuts, which can be found in Johor, Selangor, Perak, and Kelantan. The top three most productive paddy fields in 2020, which are located in Kedah, Kelantan, and Perak, were taken into consideration in this study [12]. The five main ports in Peninsular Malaysia are Johor Port, the Port of Tanjung Pelepas, Kuantan Port, Port Klang, and Penang Port. Regarding the development of the biomass corridor, it should be noted that the “demand points” refer to the exporting ports (except for MPS and electricity, which are assumed to be sold in the nearby area instead of being delivered to ports). Furthermore, the potential processing hubs have to be constructed at strategic locations, for which the major concerns are the availability of main roads and the distance between biomass sources and hubs. This is important for the minimisation of biomass transportation costs. Nevertheless, the utility and workforce supply network must be well established in these “potential” locations to build the hubs (see Table A2 in the Appendix A).
In the model, the processing hub’s capacity (M) was set to 5.00 × 105 tons, with an investment cost of approximately USD 1 million. On the other hand, the transportation cost constant () was obtained from an external logistic company, which was set to USD 0.1/ton/km. The remaining parameters involved in the model are shown in Table 4.

Table 4.
Parameters involved in the network.
4. Results and Discussions
A P-Graph was used to evaluate the optimal route for processing biomass. After this route was determined via the MSG and the SSG of the P-graph, the relevant biomass and products were utilised to construct a cost correlated function. Subsequently, the function was then incorporated into a mathematical model after an site investigation at Peninsular Malaysia.
4.1. Cost Correlated Function
Based on the results obtained using the P-Graph, the best pathways for processing rice husks and paddy straw are through fast pyrolysis and conditioning, respectively. Py-oil, biochar, and syngas were produced from the rapid pyrolysis of rice husks, while fertiliser was derived from paddy straw. On the other hand, pelletising and dehydration are the best pathways for EFB, in which pellets and DLF are produced, while the best pathway for PKS is through power generation to produce MPS and electricity. In this case, for the possible products, fertiliser, pellet, DLF, py-oil, biochar, and syngas were considered to be sent to the port for exportation, while MPS and electricity were considered to be sold to nearby plants or the grid. Subsequently, the formulated cost function for this case study could be obtained, as shown in Equation (17) (note that the coefficient constants in the cost function reflect the EP of the biomass):
where , and represent the quantities of EFB, PKS, rice husks, and paddy straw, respectively.
An optimisation model was formulated in LINGO x19.0 using the cost-correlated function obtained from the P-graph. Thus, the maximum profit gained, the number of hubs to establish, the respective strategic locations, and the optimal biomass allocation design could be obtained. As a result, it was determined that there were a total of 64 biomass sources being utilised. Coconut biomasses were not incorporated mainly because they have a negative EP, which indicates that they do not contribute any profits, even when utilised. This is because coconut biomasses have high raw material and technology costs of coconut biomasses but a relatively low product price when compared to oil palm and paddy biomasses. In particular, the cost of processing coconut biomasses is 38% higher than that of the revenue gained from selling coconut-derived products. Hence, based on the value of the EP of the biomasses, it can be concluded that paddy straw has the highest profit margin among the biomasses studied in this work.
4.2. Optimal Biomass Allocation Design
The optimal biomass allocation design is depicted in Figure 8, amounting to a total net profit of about USD 8.70 × 108. It can be seen that 39 out of the 47 potential processing hubs should be constructed to achieve maximum profits. If fewer hubs were established, the transportation costs would be expected to increase since some of the biomass will be transported to another hub that is further away from the source. If more hubs were constructed, despite the decrease in transportation costs, the savings is insufficient to cover the further increased investment costs of developing these hubs. For instance, if the number of hubs was set to 40 while all the other parameters were kept fixed, a total of USD 55,900 could be saved in terms of transportation costs. However, this amount cannot compensate for the investment cost required for the new hub (i.e., USD 1 million). The detailed amounts of biomass allocated to the respective processing hubs are shown in Table A3, Table A4, Table A5 and Table A6 in Appendix A.
As a result, there were a total of 5.86 × 106 tons of products (excluding MPS and electricity) being produced from all the processing hubs (see Figure 9), which were exported to the different ports (i.e., the customers in this case). The respective numbers of products transported to the port are presented in Figure 10.
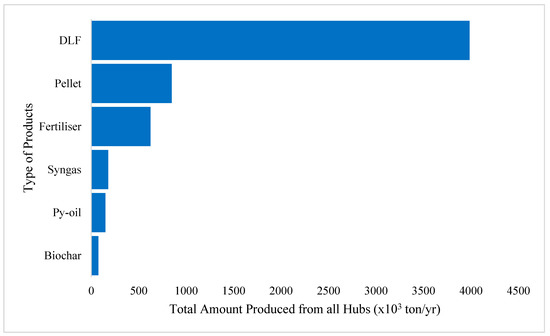
Figure 9.
Total amount of product produced from all processing hubs.
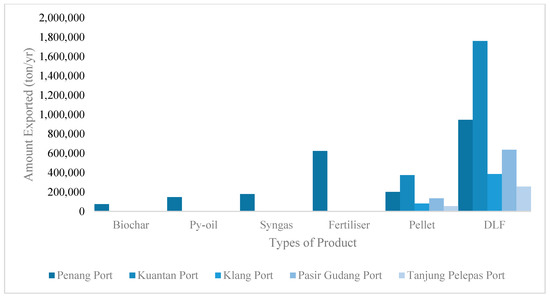
Figure 10.
Number of products exported to the respective ports.
By referring to Figure 9, it can be seen that DLF is used to produce the most products, while biochar is used to produce the fewest. This is collectively due to (i) a relatively decent unit price of DLF and (ii) the cheaper cost of EFB compared to the other biomasses. In addition, a higher wt% of EFB can be obtained from oil palm fresh fruit bunches compared to PKS. On the other hand, most of the pellets and DLF are exported to Kuantan Port due to the massive amount of oil palm plantations in Pahang state, as shown in Figure 10. The remaining products are mainly exported to Penang Port, as paddy plantations in Malaysia are mainly concentrated in the northern part of Peninsular Malaysia.
4.3. Sensitivity Analysis
In this section, a sensitivity analysis was performed to illustrate how one can determine the impact of several parameters on net profit . The selected parameters, including the maximum capacity of the processing hub , the transportation cost constant , the investment cost of the processing hub , and the unit price of the biomass, were varied. To ensure that the impact of each parameter was clearly captured, the one-parameter-at-a-time (OPAT) method was adopted (i.e., when one of the parameters varied, the remaining parameters were maintained at the same value, as depicted in the base case scenario). Table 5 shows an example of the variables in the sensitivity analysis of the maximum processing capacity of each hub. Figure 11, Figure 12, Figure 13 and Figure 14 illustrate the sensitivity analyses of the selected parameters, respectively.

Table 5.
Sensitivity analysis on the capacity of processing hub.
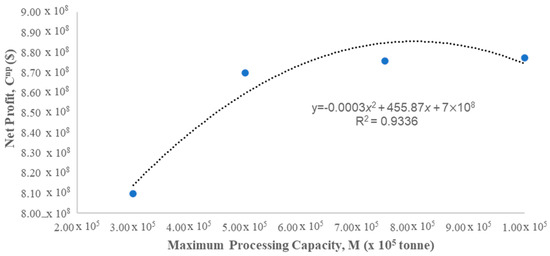
Figure 11.
Sensitivity analysis on capacity of processing hub, M.
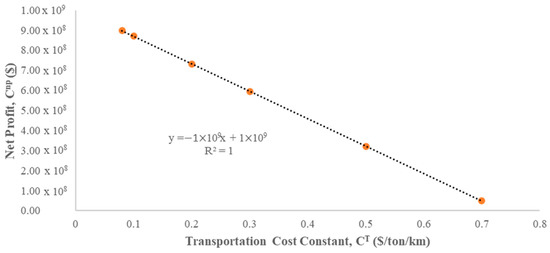
Figure 12.
Sensitivity analysis on capacity of transportation cost constant, .
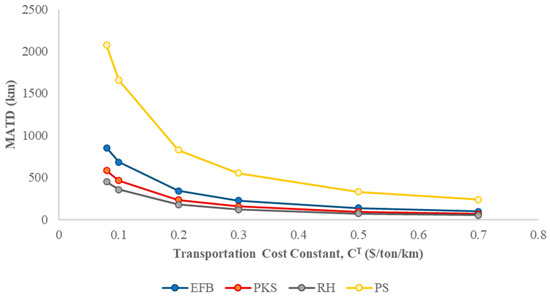
Figure 13.
MATD against transportation cost constant, .
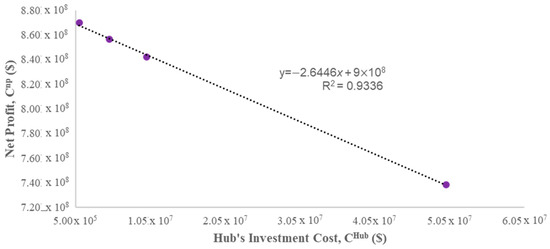
Figure 14.
Sensitivity analysis on hub investment costs, CHub.
By referring to Table 5 and Figure 11, it can be observed that the net profit increases when the maximum capacity of the processing hub increases. This is mainly because a greater extent of biomass allocation can be more cost-effective when the capacity constraint of a plant is increased (i.e., biomass can be sent to the nearby processing hub instead of being sent to other hubs due to capacity constraints). As a result, fewer processing hubs are required in the supply chain. This aligns with the concluding remarks provided in the study by Zhu et al. [60], revealing the positive impact of maximum capacity on the feasibility of a supply chain. Nevertheless, it should be noted that further increasing the capacity constraint from 1,000,000 tonnes/hub will not improve the overall profit any further (i.e., maintain a maximum value of USD 0.87 billion) given that the optimal number of hubs remains 38 after this point.
Based on Table 6 and Figure 12, the net profit decreases when the transportation cost constant increases, as a higher transportation cost constant indicates a higher transportation cost for both pre-processing and post-processing. The transportation cost constant is significantly correlated with the price of diesel. Hence, a higher transportation cost constant is imposed when the diesel price increases, and vice versa. Based on this result, it can be clearly seen that the optimal number of processing hubs has increased from 39 to 41 along with the transportation cost. More processing hubs were included to enable shorter total travel distances in order to combat the higher transportation cost constant [37]. Nevertheless, the number of hubs does not continuously elevate despite the fact that the cost constant increased 6.85-fold. This indicates that the cost savings in terms of transportation costs cannot compensate for the cost required for an additional processing hub [61]. Additionally, when the transportation cost constantly increases, the amount of biomass sent from the plantation areas to processing hubs decreases. This is because the value will affect the value of as shown in Equation (2); thus, some biomass sources were not selected because they were not feasible. Figure 13 displays the value for each type of biomass along with the value.

Table 6.
Sensitivity analysis variables of transportation cost constant.
By referring to Figure 13, it can be seen that as the value increases, the value for each biomass decreases. The changes in the value have the most significant impact on RH, as RH has the lowest EP among the four selected biomasses. When the value deviates, the optimal allocation of one biomass source to a hub will be affected. As a result, it is to be noted that the number of processing hubs being utilised will increase with the value, as shown in Table 7. This is simply due to two reasons: (i) the larger leads to a smaller , which reduces connection flexibility, and (ii) the becomes less dominant.

Table 7.
Sensitivity analysis variables of hub investment costs.
According to Table 7 and Figure 14, the net profit decreases when the investment cost of the hubs increases. However, it should be noted that the value of a hub’s investment cost used in this study is based on a rough assumption. Thus, a more accurate investment cost can be incorporated if a detailed economic analysis is conducted. In addition, when a hub’s investment cost increases, the number of hubs utilised decreases markedly. It was noticed that the amount of biomass processed remains constant despite the changes in the hub investment costs and the number of hubs being utilised. This is because in the base case scenario, the 39 hubs being utilised were not operating at their maximum capacities. Therefore, when the number of hubs decreases and the other parameters remain constant, the same amount of biomass can be delivered to another hub for processing.
In the conducted sensitivity analysis, the transportation cost constant was found to be the most significant parameter with respect to affecting the net profit. To further verify the results from the sensitivity analysis, the constraints used for the investigated parameters were monitored using dual price values (obtained from LINGO) to ensure that there were no constraints that were too strict. Dual price denotes the amount that an objective would improve by if the constant term of the constraint increased by one unit. Table 8 summarises the dual price value for the constant term of the capacity of a processing hub , the transportation cost constant and a processing hub’s investment cost in the base case scenario.

Table 8.
Dual price value.
Referring to Table 8, the transportation cost constant shows a dual price value of −0.318 × 1010, which can be interpreted as follows: an increase of one unit in the value will cause a decrease of USD 0.138 × 1010 in the net profit. The dual price values for the remaining two parameters can be interpreted in a similar manner. Therefore, the transportation cost constant is the most sensitive parameter, followed by a processing hub’s capacity and then the investment cost. However, the impact of the transportation cost constant could be minimised if the processing hub in question is located near the biomass sources. Thus, the processing hubs must be established at strategic locations near both biomass sources and a ports. Proper planning and careful consideration must be ensured before building a processing hub, as the price of diesel currently remains volatile. Moreover, other transportation modes such as railways and waterways can be considered to reflect real-life conditions. Nevertheless, it was found that a hub’s capacity and investment cost are interrelated. Therefore, sensitivity analyses can be performed to identify their relationship, where investment cost is expressed as a function of capacity in order to yield a more accurate result. To improve accuracy, a more detailed economic analysis to evaluate the investment costs can also be performed.
Lastly, as the downstream usage of biomass gains more popularity, the market price will increase due to the higher demand compared to that in the past. This would affect the economic attractiveness of the biomass conversion pathways. In other words, it is important for decision makers to understand the threshold limit of the price of biomass (i.e., the maximum biomass cost at which the pathway can still break even). Table 9 shows the respective threshold unit price of each biomass, including coconut husks and coconut shells, which were not recommended by the model. Based on the analysis, it can be gleaned that the coconut-biomass-based pyrolysis considered in this work can only be economically feasible if the unit prices of coconut husks and coconut shells were reduced by 65.5% and 84.13%, respectively. On the other hand, the other selected technologies would not be feasible if the unit prices of biomass were not controlled below the threshold limits (e.g., the rapid pyrolysis of rice husk will not be attractive if the rice husk price increases 2.4 fold compared to the unit cost stated in this case study). Such impacts align with the findings reported by Lo et al. [62], who commented that the acquisition price is one of the key factors that affect the overall feasibility of the biomass industry.

Table 9.
Threshold unit price to break even.
5. Conclusions
A hybrid method that incorporates both a P-graph and a mathematical modelling approach has been successfully applied to synthesise a multiple-biomass corridor for a large-scale problem in Peninsular Malaysia. The technologies available for processing empty fruit bunches, palm kernel shells, rice husks, paddy straw, coconut shells, and coconut husks were presented in this work, along with their associated conversion. Furthermore, the correlated cost function for oil palm and paddy biomass was developed using a P-graph. Subsequently, area fragmentation was carried out to determine the distance from each biomass source to each potential processing hub and the distance from the processing hubs to the ports. By adopting the proposed method, decision makers can obtain important insights into the feasibility of each biomass technology alongside strategies regarding the number and locations of processing hubs. In the base case scenario, 99.31% of the oil palm and paddy biomass available in Peninsular Malaysia was converted into valuable products, with an annual net profit of USD 0.87 billion. Additionally, a comprehensive sensitivity analysis was performed to investigate the impact of four parameters, namely, the capacity of a processing hub , the transportation cost constant , a processing hub’s investment cost , and the unit price of biomass, on the economic performance of the supply chain. This allows policymakers and process engineers to understand the bottlenecks of biomass conversion technologies and, therefore, attempt to tackle the problems effectively.
In terms of future extensions, to improve the robustness of the framework, sensitivity analysis on the degree of area fragmentation can be performed. Theoretically, more fragmentised zones will result in a solution that is closer to the actual global optimum but with the trade-off of greater computational time. Additionally, the model can be extended into stochastic programming to incorporate supply chain uncertainties, including (but not limited to) biomass availability, material unit costs, fuel prices, etc., so that one can understand the overall risk profile of the proposed supply chain [62]. With the aid of probabilistic data regarding each type of uncertainty, detailed plant design and a more comprehensive economic evaluation can be performed. To achieve this, collaborative research between process systems engineering and economic disciplines is highly recommended. With further regard to enhancing the model’s reliability, detailed transportation and logistics design can also be carried out to incorporate the additional costs required (e.g., considerations made for syngas transportation were not accounted for in the current work), the efficiency of the storage units, and time-sliced optimisation for effective scheduling into the current model. Moreover, it is worth considering the synergetic integration, or interaction between different entities or stakeholders competing for the same biomass resources using game theory approaches [63].
Author Contributions
Conceptualization, H.L.L.; methodology, J.C.A., Y.P.H. and H.Y.L.; software, Y.P.H. and H.Y.L.; validation, J.C.A.; formal analysis, J.C.A.; resources, Y.P.H.; data curation, H.Y.L.; writing—original draft preparation, H.L.L., J.C.A., Y.P.H. and H.Y.L.; writing—review and editing, A.C.M.L., H.L.L. and B.S.H.; visualization, A.C.M.L., J.C.A., Y.P.H. and H.Y.L.; supervision, H.L.L. and B.S.H.; project administration, H.L.L.; funding acquisition, B.S.H. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors would like to thank The University of Nottingham Malaysia for providing the opportunity to conduct this work.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Locations and availability of biomass sources.
Table A1.
Locations and availability of biomass sources.
| Source, i | Xi | Yi | Area (ha) | Availability (t/y) |
|---|---|---|---|---|
| i1 | 135.55 | 714.83 | 23,075.00 | 131,989.00 |
| i2 | 166.00 | 624.80 | 25,417.00 | 145,385.24 |
| i3 | 154.40 | 578.33 | 31,165.00 | 178,263.80 |
| i4 | 218.19 | 572.52 | 29,477.00 | 168,608.44 |
| i5 | 165.27 | 505.72 | 47,813.00 | 273,490.36 |
| i6 | 221.09 | 503.79 | 49,706.00 | 284,318.32 |
| i7 | 175.42 | 454.41 | 47,650.00 | 272,558.00 |
| i8 | 204.42 | 466.03 | 64,413.00 | 368,442.36 |
| i9 | 199.34 | 441.83 | 6649.00 | 25,801.44 |
| i10 | 221.82 | 415.69 | 47,650.00 | 272,558.00 |
| i11 | 339.97 | 766.14 | 5750.00 | 22,312.88 |
| i12 | 279.81 | 626.73 | 24,895.00 | 142,399.40 |
| i13 | 334.17 | 624.80 | 24,895.00 | 142,399.40 |
| i14 | 265.31 | 568.65 | 24,895.00 | 142,399.40 |
| i15 | 333.45 | 579.30 | 24,895.00 | 142,399.40 |
| i16 | 377.67 | 578.33 | 24,895.00 | 142,399.40 |
| i17 | 403.04 | 679.01 | 24,948.00 | 142,702.56 |
| i18 | 432.03 | 678.04 | 20,794.00 | 118,941.68 |
| i19 | 406.66 | 573.49 | 35,150.00 | 201,058.00 |
| i20 | 453.78 | 505.72 | 36,169.00 | 206,886.68 |
| i21 | 461.75 | 462.16 | 36,169.00 | 206,886.68 |
| i22 | 276.91 | 502.82 | 14,333.75 | 81,989.05 |
| i23 | 333.45 | 505.72 | 14,333.75 | 81,989.05 |
| i24 | 390.72 | 504.76 | 26,381.00 | 150,899.32 |
| i25 | 288.51 | 446.67 | 14,333.75 | 81,989.05 |
| i26 | 334.90 | 444.73 | 14,333.75 | 81,989.05 |
| i27 | 393.62 | 441.83 | 26,381.00 | 150,899.32 |
| i28 | 445.81 | 437.96 | 90,324.00 | 516,653.28 |
| i29 | 293.58 | 394.39 | 21,141.00 | 120,926.52 |
| i30 | 334.90 | 384.71 | 38,456.00 | 219,968.32 |
| i31 | 394.34 | 382.78 | 32,945.00 | 188,445.40 |
| i32 | 453.78 | 382.78 | 102,010.00 | 583,497.20 |
| i33 | 334.17 | 324.69 | 26,793.00 | 153,255.96 |
| i34 | 392.89 | 324.69 | 32,945.00 | 188,445.40 |
| i35 | 451.61 | 322.75 | 68,636.00 | 392,597.92 |
| i36 | 403.04 | 268.54 | 95,287.00 | 545,041.64 |
| i37 | 452.33 | 261.76 | 68,636.00 | 392,597.92 |
| i38 | 452.33 | 218.20 | 68,636.00 | 392,597.92 |
| i39 | 210.94 | 384.71 | 5047.00 | 19,584.88 |
| i40 | 220.37 | 345.02 | 28,150.00 | 161,018.00 |
| i41 | 263.14 | 379.87 | 23,255.00 | 133,018.60 |
| i42 | 239.21 | 261.76 | 27,110.00 | 155,069.20 |
| i43 | 293.58 | 216.26 | 29,049.00 | 166,160.28 |
| i44 | 376.22 | 260.80 | 73,493.00 | 420,379.96 |
| i45 | 372.59 | 205.61 | 29,262.00 | 167,378.64 |
| i46 | 351.57 | 170.76 | 54,131.00 | 309,629.32 |
| i47 | 406.66 | 194.97 | 108,043.00 | 618,005.96 |
| i48 | 508.15 | 156.24 | 62,814.00 | 359,296.08 |
| i49 | 466.10 | 141.72 | 181,738.00 | 1,039,541.36 |
| i50 | 396.51 | 116.55 | 46,639.00 | 266,775.08 |
| i51 | 437.11 | 90.41 | 58,695.00 | 335,735.40 |
| i52 | 457.41 | 90.41 | 8624.00 | 33,465.43 |
| i53 | 476.25 | 53.62 | 22,073.00 | 126,257.56 |
| i54 | 535.69 | 92.35 | 146,250.00 | 836,550.00 |
| i55 | 515.40 | 41.04 | 47,341.00 | 270,790.52 |
| i56 | 93.41 | 853.40 | 50,326.50 | 185,571.92 |
| i57 | 114.17 | 791.99 | 50,326.50 | 185,571.92 |
| i58 | 115.11 | 746.60 | 50,326.50 | 185,571.92 |
| i59 | 149.08 | 758.57 | 50,326.50 | 185,571.92 |
| i60 | 347.22 | 738.21 | 17,591.06 | 64,864.57 |
| i61 | 290.61 | 690.52 | 5552.06 | 20,472.44 |
| i62 | 334.01 | 695.09 | 9510.77 | 35,069.63 |
| i63 | 264.19 | 618.16 | 6692.85 | 24,678.95 |
| i64 | 318.92 | 622.93 | 6398.98 | 23,595.34 |
| i65 | 294.38 | 584.65 | 1211.45 | 4467.05 |
| i66 | 151.91 | 619.90 | 20,949.00 | 77,246.50 |
| i67 | 149.08 | 555.53 | 20,949.00 | 77,246.50 |
| i68 | 231.17 | 464.96 | 27,735.00 | 102,268.93 |

Table A2.
Locations of processing hubs.
Table A2.
Locations of processing hubs.
| Sink, j | Xj | Yj |
|---|---|---|
| j1 | 150.55 | 588.98 |
| j2 | 138.55 | 538.78 |
| j3 | 154.91 | 491.02 |
| j4 | 214.91 | 484.90 |
| j5 | 163.64 | 437.14 |
| j6 | 210.55 | 427.35 |
| j7 | 163.64 | 384.49 |
| j8 | 207.27 | 379.59 |
| j9 | 266.18 | 487.35 |
| j10 | 414.55 | 486.12 |
| j11 | 457.09 | 439.59 |
| j12 | 459.27 | 399.18 |
| j13 | 276.00 | 433.47 |
| j14 | 337.09 | 432.24 |
| j15 | 391.64 | 435.92 |
| j16 | 280.36 | 383.27 |
| j17 | 333.82 | 382.04 |
| j18 | 401.45 | 383.27 |
| j19 | 341.45 | 335.51 |
| j20 | 393.82 | 335.51 |
| j21 | 447.27 | 324.49 |
| j22 | 333.82 | 286.53 |
| j23 | 390.55 | 282.86 |
| j24 | 450.55 | 280.41 |
| j25 | 402.55 | 242.45 |
| j26 | 452.73 | 236.33 |
| j27 | 456.00 | 194.69 |
| j28 | 258.55 | 322.04 |
| j29 | 225.82 | 293.88 |
| j30 | 258.55 | 240.00 |
| j31 | 225.82 | 219.18 |
| j32 | 328.36 | 231.43 |
| j33 | 288.00 | 187.35 |
| j34 | 330.55 | 184.90 |
| j35 | 370.91 | 184.90 |
| j36 | 346.91 | 140.82 |
| j37 | 409.09 | 172.65 |
| j38 | 452.73 | 143.27 |
| j39 | 519.27 | 143.27 |
| j40 | 408.00 | 94.29 |
| j41 | 447.27 | 77.14 |
| j42 | 555.27 | 90.61 |
| j43 | 507.27 | 41.63 |
| j44 | 94.74 | 748.09 |
| j45 | 140.00 | 699.57 |
| j46 | 328.42 | 670.21 |
| j47 | 331.58 | 557.87 |

Table A3.
Amount of biomass allocated to processing hubs (j1 to j12).
Table A3.
Amount of biomass allocated to processing hubs (j1 to j12).
| i/j | j1 | j2 | j3 | j4 | j5 | j6 | j7 | j8 | j9 | j10 | j11 | j12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i2 | 145,385 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i3 | 170,451 | 7813 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i4 | 0 | 168,608 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i5 | 0 | 0 | 273,490 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i6 | 0 | 0 | 0 | 284,318 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i7 | 0 | 0 | 0 | 0 | 272,558 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i8 | 0 | 0 | 226,510 | 137,868 | 0 | 4064 | 0 | 0 | 0 | 0 | 0 | 0 |
| i9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i10 | 0 | 0 | 0 | 0 | 0 | 272,558 | 0 | 0 | 0 | 0 | 0 | 0 |
| i11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i12 | 106,917 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i14 | 0 | 113,920 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 142,214 | 0 | 0 |
| i20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 206,887 | 0 | 0 |
| i21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 206,887 | 0 |
| i22 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 81,989 | 0 | 0 | 0 |
| i23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i24 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 150,899 | 0 | 0 |
| i25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i26 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i27 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i28 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 293,113 | 120,209 |
| i29 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i30 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i31 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i32 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 379,791 |
| i33 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i34 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i35 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i37 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i38 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i39 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i40 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i41 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i42 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i43 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i44 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i45 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i46 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i47 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i48 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i49 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i50 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i51 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i52 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i53 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i54 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i55 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i56 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i57 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i58 | 0 | 44,376 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i59 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i60 | 0 | 15,511 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i61 | 0 | 4896 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i62 | 0 | 8386 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i63 | 0 | 24,679 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i64 | 0 | 5642 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i65 | 0 | 4467 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i66 | 77,247 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i67 | 0 | 77,247 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i68 | 0 | 24,456 | 0 | 77,813 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Sum | 500,000 | 500,000 | 500,000 | 500,000 | 272,558 | 276,622 | 0 | 0 | 81,989 | 500,000 | 500,000 | 500,000 |

Table A4.
Amount of biomass allocated to processing hubs (j13 to j23).
Table A4.
Amount of biomass allocated to processing hubs (j13 to j23).
| i/j | j13 | j14 | j15 | j16 | j17 | j18 | j19 | j20 | j21 | j22 | j23 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| i1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i22 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i23 | 0 | 0 | 65,591 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i24 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i25 | 81,989 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i26 | 0 | 81,989 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i27 | 0 | 0 | 150,899 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i28 | 0 | 0 | 103,331 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i29 | 0 | 0 | 0 | 120,927 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i30 | 0 | 0 | 0 | 0 | 219,968 | 0 | 0 | 0 | 0 | 0 | 0 |
| i31 | 0 | 0 | 0 | 0 | 0 | 188,445 | 0 | 0 | 0 | 0 | 0 |
| i32 | 0 | 0 | 0 | 0 | 0 | 96,304 | 0 | 0 | 107,402 | 0 | 0 |
| i33 | 0 | 0 | 0 | 0 | 0 | 0 | 153,256 | 0 | 0 | 0 | 0 |
| i34 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 188,445 | 0 | 0 | 0 |
| i35 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 392,598 | 0 | 0 |
| i36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 328,631 |
| i37 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i38 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i39 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i40 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i41 | 0 | 0 | 0 | 133,019 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i42 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i43 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i44 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 171,369 |
| i45 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i46 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i47 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i48 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i49 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i50 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i51 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i52 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i53 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i54 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i55 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i56 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i57 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i58 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i59 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i60 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i61 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i62 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i63 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i64 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i65 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i66 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i67 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i68 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Sum | 81,989 | 81,989 | 319,821 | 253,945 | 219,968 | 284,750 | 153,256 | 188,445 | 500,000 | 0 | 500,000 |

Table A5.
Amount of biomass allocated to processing hubs (j24 to j35).
Table A5.
Amount of biomass allocated to processing hubs (j24 to j35).
| i/j | j24 | j25 | j26 | j27 | j28 | j29 | j30 | j31 | j32 | j33 | j34 | j35 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i22 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i24 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i26 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i27 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i28 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i29 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i30 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i31 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i32 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i33 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i34 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i35 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i36 | 107,402 | 109,008 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i37 | 392,598 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i38 | 0 | 0 | 392,598 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i39 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i40 | 0 | 0 | 0 | 0 | 0 | 161,018 | 0 | 0 | 0 | 0 | 0 | 0 |
| i41 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i42 | 0 | 0 | 0 | 0 | 0 | 0 | 155,069 | 0 | 0 | 0 | 0 | 0 |
| i43 | 0 | 0 | 0 | 0 | 0 | 0 | 166,160 | 0 | 0 | 0 | 0 | 0 |
| i44 | 0 | 249,011 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i45 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 167,379 |
| i46 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 247,703 | 61,926 |
| i47 | 0 | 141,980 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i48 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i49 | 0 | 0 | 0 | 401,024 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i50 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i51 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i52 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i53 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i54 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i55 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i56 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i57 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i58 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i59 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i60 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i61 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i62 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i63 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i64 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i65 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i66 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i67 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i68 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Sum | 500,000 | 500,000 | 392,598 | 401,024 | 0 | 161,018 | 321,229 | 0 | 0 | 0 | 247,703 | 229,305 |

Table A6.
Amount of biomass allocated to processing hubs (j36 to j47).
Table A6.
Amount of biomass allocated to processing hubs (j36 to j47).
| i/j | j36 | j37 | j38 | j39 | j40 | j41 | j42 | j43 | j44 | j45 | j46 | j47 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| i1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 131,989 | 0 | 0 |
| i2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i3 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i5 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i6 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i7 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i8 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i9 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i10 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i11 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i12 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 28,480 | 7002 |
| i13 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 118,262 | 24,137 |
| i14 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 28,480 |
| i15 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 142,399 |
| i16 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 142,399 |
| i17 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 142,703 | 0 |
| i18 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 118,942 | 0 |
| i19 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 58,844 |
| i20 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i21 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i22 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i23 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 16,398 |
| i24 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i25 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i26 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i27 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i28 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i29 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i30 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i31 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i32 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i33 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i34 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i35 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i36 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i37 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i38 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i39 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i40 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i41 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i42 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i43 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i44 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i45 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i46 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i47 | 0 | 476,025 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i48 | 0 | 0 | 0 | 359,296 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i49 | 0 | 0 | 500,000 | 0 | 0 | 138,518 | 0 | 0 | 0 | 0 | 0 | 0 |
| i50 | 0 | 0 | 0 | 0 | 266,775 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i51 | 0 | 0 | 0 | 0 | 67,147 | 268,588 | 0 | 0 | 0 | 0 | 0 | 0 |
| i52 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i53 | 0 | 0 | 0 | 0 | 0 | 92,894 | 0 | 33,363 | 0 | 0 | 0 | 0 |
| i54 | 0 | 0 | 0 | 140,704 | 0 | 0 | 500,000 | 195,846 | 0 | 0 | 0 | 0 |
| i55 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 270,791 | 0 | 0 | 0 | 0 |
| i56 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 141,196 | 44,376 | 0 | 0 |
| i57 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 141,196 | 44,376 | 0 | 0 |
| i58 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 141,196 | 0 | 0 | 0 |
| i59 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 185,572 | 0 | 0 |
| i60 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 49,353 | 0 |
| i61 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 15,577 | 0 |
| i62 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 26,683 | 0 |
| i63 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i64 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 17,953 |
| i65 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i66 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i67 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| i68 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| Sum | 0 | 476,025 | 500,000 | 500,000 | 333,922 | 500,000 | 500,000 | 500,000 | 423,588 | 406,313 | 500,000 | 437,613 |
References
- EIA. EIA Projects Nearly 50% Increase in World Energy Usage by 2050, Led by Growth in Asia. 2019. Available online: https://www.eia.gov/todayinenergy/detail.php?id=41433 (accessed on 17 April 2022).
- Jin, C.; Lv, Z.; Li, Z.; Sun, K. Green finance, renewable energy and carbon neutrality in OECD countries. Renew. Energy 2023, 211, 279–284. [Google Scholar] [CrossRef]
- Raihan, A.; Tuspekova, A. Toward a sustainable environment: Nexus between economic growth, renewable energy use, forested area, and carbon emissions in Malaysia. Resour. Conserv. Recycl. Adv. 2022, 15, 200096. [Google Scholar] [CrossRef]
- Idris, M.N.M.; Hashim, H.; Leduc, S.; Yowargana, P.; Kraxner, F.; Woon, K.S. Deploying bioenergy for decarbonizing Malaysian energy sectors and alleviating renewable energy poverty. Energy 2021, 232, 120967. [Google Scholar] [CrossRef]
- MPOC. Malaysian Palm Oil Industry. 2021. Available online: https://mpoc.org.my/malaysian-palm-oil-industry/ (accessed on 17 April 2022).
- MPOB. Overview of the Malaysian Oil Palm Industry 2021. 2021. Available online: https://bepi.mpob.gov.my/images/overview/Overview2021.pdf (accessed on 17 April 2022).
- AIM. National Biomass Strategy 2020: New Wealth Creation for Malaysia’s Biomass Industry; AIM: Selangor, Malaysia, 2013. [Google Scholar]
- Derman, E.; Abdulla, R.; Marbawi, H.; Sabullah, M.K. Oil palm empty fruit bunches as a promising feedstock for bioethanol production in Malaysia. Renew. Energy 2018, 129, 285–298. [Google Scholar] [CrossRef]
- Rashidi, N.A.; Yusup, S. Production of palm kernel shell-based activated carbon by direct physical activation for carbon dioxide adsorption. Environ. Sci. Pollut. Res. 2018, 26, 33732–33746. [Google Scholar] [CrossRef]
- Chin, M.J.; Poh, P.E.; Tey, B.T.; Chan, E.S.; Chin, K.L. Biogas from palm oil mill effluent (POME): Opportunities and challenges from Malaysia’s perspective. Renew. Sustain. Energy Rev. 2013, 26, 717–726. [Google Scholar] [CrossRef]
- Grimm, A.M.; Dorsch, L.Y.; Kloess, G.H.; Enke, D.; Roppertz, A. Transition metal promoted combustion of rice husk and rice straw towards an energy optimized synthesis of biogenic silica. Biomass Bioenergy 2021, 155, 106282. [Google Scholar] [CrossRef]
- DOA. Plantation Statistics 2021. 2021. Available online: http://www.doa.gov.my/index/resources/aktiviti_sumber/sumber_awam/maklumat_pertanian/perangkaan_tanaman/booklet_statistik_tanaman_2021.pdf (accessed on 17 April 2022).
- Yerrayya, A.; Vishnu, A.K.S.; Shreyas, S.; Chakravarthy, S.R.; Vinu, R. Hydrothermal Liquefaction of Rice Straw Using Methanol as Co-Solvent. Energies 2020, 13, 2618. [Google Scholar] [CrossRef]
- Hu, Q.; Shao, J.; Yang, H.; Yao, D.; Wang, X.; Chen, H. Effects of binders on the properties of bio-char pellets. Appl. Energy 2015, 157, 508–516. [Google Scholar] [CrossRef]
- Kaniapan, S.; Pasupuleti, J.; Nesan, K.P.; Abubackar, H.N.; Umar, H.A.; Oladosu, T.L.; Bello, S.R.; Rene, E.R. A Review of the Sustainable Utilization of Rice Residues for Bioenergy Conversion Using Different Valorization Techniques, Their Challenges, and Techno-Economic Assessment. Int. J. Environ. Res. Public Health 2022, 19, 3427. [Google Scholar] [CrossRef] [PubMed]
- Kamthan, R.; Tiwari, I. Agricultural Wastes- Potential Substrates For Mushroom Cultivation. Eur. J. Exp. Biol. 2017, 7, 31. [Google Scholar] [CrossRef]
- Goodman, B.A. Utilization of waste straw and husks from rice production: A review. J. Bioresour. Bioprod. 2020, 5, 143–162. [Google Scholar] [CrossRef]
- Shamsollahi, Z.; Partovinia, A. Recent advances on pollutants removal by rice husk as a bio-based adsorbent: A critical review. J. Environ. Manag. 2019, 246, 314–323. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, R.K.; Sulaiman, S.A.; Yusup, S.; Dol, S.S.; Inayat, M.; Umar, H.A. Exploring the potential of coconut shell biomass for charcoal production. Ain Shams Eng. J. 2021, 13, 101499. [Google Scholar] [CrossRef]
- Curia, A.C.; Souza, A.R.D.; Zaro, J.R.; Barbieri, M.R.R.; Kappler, G.; Moraes, C.A.M. Waste Management and Application of Coconut Biomass and Fibre. In Vegetable Fiber Composites and their Technological Applications; Springer: Singapore, 2021; pp. 215–237. [Google Scholar] [CrossRef]
- Ng, W.P.Q.; Ng, R.T.L.; Lam, H.L.; Kamal, M.; Ng, E.H.; Ng, D.K.S. Biomass corridor synthesis for malaysia green energy supply chain. Chem. Eng. Trans. 2012, 29, 703–708. [Google Scholar] [CrossRef]
- Xu, X.; Liu, G.; Mola-Yudego, B. Barriers and opportunities for bioenergy expansion in Chinese rural areas. Energy Sustain. Dev. 2022, 70, 181–193. [Google Scholar] [CrossRef]
- Maier, S.; Narodoslawsky, M. Optimal Renewable Energy Systems for Smart Cities. Comput. Aided Chem. Eng. 2014, 33, 1849–1854. [Google Scholar]
- How, B.S.; Hong, B.H.; Lam, H.L.; Friedler, F. Synthesis of multiple biomass corridor via decomposition approach: A P-graph application. J. Clean. Prod. 2016, 130, 45–57. [Google Scholar] [CrossRef]
- Lee, Y.H.; Golinska-Dawson, P.; Wu, J.-Z. Mathematical Models for Supply Chain Management. Math. Probl. Eng. 2016, 2016, 1–4. [Google Scholar] [CrossRef]
- Foo, D.C.Y. Automated targeting model for aggregate planning in production and energy supply chains. Clean Technol. Environ. Policy 2015, 18, 1405–1414. [Google Scholar] [CrossRef]
- Leong, H.; Foo, D.C.; Ng, L.Y.; Andiappan, V. Hybrid approach for carbon-constrained planning of bioenergy supply chain network. Sustain. Prod. Consum. 2019, 18, 250–267. [Google Scholar] [CrossRef]
- Leitão, F.O.; Lacerda, M.S.; Thomé, K.M.; Rodrigues, E.C.C. The reverse logistics costs for the reuse of green coconut residues. Custos E Agronegocio 2021, 17, 156–187. [Google Scholar]
- Ishii, K.; Furuichi, T.; Fujiyama, A.; Watanabe, S. Logistics cost analysis of rice straw pellets for feasible production capacity and spatial scale in heat utilization systems: A case study in Nanporo town, Hokkaido, Japan. Biomass Bioenergy 2016, 94, 155–166. [Google Scholar] [CrossRef]
- Friedler, F.; Aviso, K.B.; Bertok, B.; Foo, D.C.; Tan, R.R. Prospects and challenges for chemical process synthesis with P-graph. Curr. Opin. Chem. Eng. 2019, 26, 58–64. [Google Scholar] [CrossRef]
- Chin, H.H.; Foo, D.C.; Lam, H.L. Simultaneous water and energy integration with isothermal and non-isothermal mixing—A P-graph approach. Resour. Conserv. Recycl. 2019, 149, 687–713. [Google Scholar] [CrossRef]
- Ondruška, V.; How, B.S.; Netolický, M.; Máša, V.; Teng, S.Y. Resource optimisation in aquaponics facility via process monitoring and graph-theoretical approach. Carbon Resour. Convers. 2022, 5, 255–270. [Google Scholar] [CrossRef]
- Pimentel, J.; Orosz, Á.; Aviso, K.B.; Tan, R.R.; Friedler, F. Conceptual Design of a Negative Emissions Polygeneration Plant for Multiperiod Operations Using P-Graph. Processes 2021, 9, 233. [Google Scholar] [CrossRef]
- Lo, S.L.Y.; Lim, C.H.; Benjamin, M.F.D.; Lam, H.L.; Sunarso, J.; How, B.S. Addressing supply uncertainties using multi-period stochastic economic evaluation: A graph-theoretic aided element targeting approach. Clean. Eng. Technol. 2022. [Google Scholar] [CrossRef]
- Friedler, F.; Tarján, K.; Huang, Y.; Fan, L. Graph-theoretic approach to process synthesis: Axioms and theorems. Chem. Eng. Sci. 1992, 47, 1973–1988. [Google Scholar] [CrossRef]
- Friedler, F.; Orosz, A.; Losada, J.P. P-Graphs for Process Systems Engineering: Mathematical Models and Algorithms, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2022. [Google Scholar]
- How, B.S.; Yeoh, T.T.; Tan, T.K.; Chong, K.H.; Ganga, D.; Lam, H.L. Debottlenecking of sustainability performance for integrated biomass supply chain: P-graph approach. J. Clean. Prod. 2018, 193, 720–733. [Google Scholar] [CrossRef]
- Les, A.; Heckl, I.; Cabezas, H. Modeling Renewable Energy Systems in Rural Areas with Flexible Operating Units. Chem. Eng. Trans. 2021, 88, 643–648. [Google Scholar] [CrossRef]
- Holló, C.; Imreh, B.; Imreh, C. Reduction techniques for the PNS problems: A novel technique and a review. Optim. Eng. 2008, 10, 351–361. [Google Scholar] [CrossRef]
- Tuncer, Y.; Tanik, M.M.; Allison, D.B. An overview of statistical decomposition techniques applied to complex systems. Comput. Stat. Data Anal. 2008, 52, 2292–2310. [Google Scholar] [CrossRef][Green Version]
- Friedler, F.; Tarjan, K.; Huang, Y.; Fan, L. Graph-theoretic approach to process synthesis: Polynomial algorithm for maximal structure generation. Comput. Chem. Eng. 1993, 17, 929–942. [Google Scholar] [CrossRef]
- Cao, J.; He, Y.-L.; Zhu, Q.-X. Maximal structure generation of superstructure for semantic triple generated by DEVS ontology in the process industry. Chemom. Intell. Lab. Syst. 2020, 205, 104119. [Google Scholar] [CrossRef]
- Cohen, J. Applied Multiple Regression/Correlation Analysis for the Behavioral Sciences, 3rd ed.; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 2003. [Google Scholar]
- Thiangchanta, S.; Chaichana, C. The multiple linear regression models of heat load for air-conditioned room. Energy Rep. 2020, 6, 972–977. [Google Scholar] [CrossRef]
- Rath, S.; Tripathy, A.; Tripathy, A.R. Prediction of new active cases of coronavirus disease (COVID-19) pandemic using multiple linear regression model. Diabetes Metab. Syndr. Clin. Res. Rev. 2020, 14, 1467–1474. [Google Scholar] [CrossRef]
- Gowda, C.R.; Dutta, R.; Pasha, A.T.; Ravi, L. Use of multiple linear regression to compensate for diametrical deviations in machined components due to thermal errors. Mater. Today Proc. 2021, 56, 2630–2639. [Google Scholar] [CrossRef]
- Ottaviani, F.M.; De Marco, A. Multiple Linear Regression Model for Improved Project Cost Forecasting. Procedia Comput. Sci. 2022, 196, 808–815. [Google Scholar] [CrossRef]
- Microsoft Load the Analysis ToolPak in Excel. 2022. Available online: https://support.microsoft.com/en-au/office/load-the-analysis-toolpak-in-excel-6a63e598-cd6d-42e3-9317-6b40ba1a66b4 (accessed on 6 June 2023).
- Lam, H.L.; Klemeš, J.J.; Kravanja, Z. Model-size reduction techniques for large-scale biomass production and supply networks. Energy 2011, 36, 4599–4608. [Google Scholar] [CrossRef]
- Yeo, S.Z.; How, B.S.; Ngan, S.L.; Ng, W.P.; Leong, W.D.; Lim, C.H.; Lam, H.L. An integrated approach to prioritise parameters for multi-objective optimisation: A case study of biomass network. J. Clean. Prod. 2020, 274, 123053. [Google Scholar] [CrossRef]
- Samsudin, M.H.; Hassan, M.A.; Idris, J.; Ramli, N.; Yusoff, M.Z.M.; Ibrahim, I.; Othman, M.R.; Ali, A.A.M.; Shirai, Y. A one-step self-sustained low temperature carbonization of coconut shell biomass produced a high specific surface area biochar-derived nano-adsorbent. Waste Manag. Res. J. 2019, 37, 551–555. [Google Scholar] [CrossRef] [PubMed]
- Tsai, W.; Lee, M.; Chang, Y. Fast pyrolysis of rice husk: Product yields and compositions. Bioresour. Technol. 2007, 98, 22–28. [Google Scholar] [CrossRef]
- Azeta, O.; Ayeni, A.O.; Agboola, O.; Elehinafe, F.B. A review on the sustainable energy generation from the pyrolysis of coconut biomass. Sci. Afr. 2021, 13, e00909. [Google Scholar] [CrossRef]
- Wang, Q.; Sarkar, J. Pyrolysis behaviors of waste coconut shell and husk biomasses. Int. J. Energy Prod. Manag. 2018, 3, 111. [Google Scholar] [CrossRef]
- MPOB. The Malaysian Oil Palm Industry Performance. 2021. Available online: https://prestasisawit.mpob.gov.my/en/plantations-planted (accessed on 19 April 2022).
- Booneimsri, P.; Kubaha, K.; Chullabodhi, C. Increasing power generation with enhanced cogeneration using waste energy in palm oil mills. Energy Sci. Eng. 2018, 6, 154–173. [Google Scholar] [CrossRef]
- International Rice Research Institute (IRRI). The value of sustainable rice straw management. 2018. Available online: https://www.irri.org/rice-straw-management#:~:text=Ratio%20of%20straw%20to%20paddy,per%20year%20produced%20in%20Asia (accessed on 1 June 2023).
- Yin, M.; Li, X.; Liu, Q.; Tang, F. Rice husk ash addition to acid red soil improves the soil property and cotton seedling growth. Sci. Rep. 2022, 12, 1–9. [Google Scholar] [CrossRef] [PubMed]
- DP CleanTech. Understanding Coconut as a Biomass Fuel. 2021. Available online: https://www.dpcleantech.com/medias/downloads/download/1520/521/22 (accessed on 1 June 2023).
- Zhu, A.; Han, Y.; Liu, H. Effects of adaptive cooperation among heterogeneous manufacturers on supply chain viability under fluctuating demand in post-COVID-19 era: An agent-based simulation. Int. J. Prod. Res. 2023, 1–27. [Google Scholar] [CrossRef]
- Zhou, J.; Xu, K.; Zhao, Y.; Zheng, H.; Dong, Z. Hub-and-Spoke Logistics Network Considering Pricing and Co-Opetition. Sustainability 2021, 13, 9979. [Google Scholar] [CrossRef]
- Lo, S.L.Y.; How, B.S.; Teng, S.Y.; Lam, H.L.; Lim, C.H.; Rhamdhani, M.A.; Sunarso, J. Stochastic techno-economic evaluation model for biomass supply chain: A biomass gasification case study with supply chain uncertainties. Renew. Sustain. Energy Rev. 2021, 152, 111644. [Google Scholar] [CrossRef]
- Marousi, A.; Charitopoulos, V.M. Game theoretic optimisation in process and energy systems engineering: A review. Front. Chem. Eng. 2023, 5, 1130568. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).