Abstract
This paper uses the Super SBM-DEA model and GML index method with undesirable output indicators to measure GTFP in 288 cities in China. Furthermore, we divide Chinese land into east, central, west, and northeast parts, and analyze their temporal and spatial evolution trends. It is shown that, firstly, China’s overall GTFP shows an upward fluctuating trend, in which green technical efficiency contributes more to the improvement of GTFP in Chinese cities, while green technological progress contributes less. Secondly, the urban GTFP in the eastern, central, western, and northeastern regions shows obvious differences, with the source of GTFP growth in the eastern region being mainly green technological progress, the source of growth in the central region being green efficiency improvement in the early stage and green technological progress in the later stage, while the source of growth in the western and northeastern regions is green efficiency improvement. Finally, combined with spatial distribution characteristic maps and kernel density estimation, GTFP shows spatial disequilibrium characteristics in China.
1. Introduction
The Chinese government has continuously stressed the need to transform the economic development mode from extensive development in the past to high-quality development with technological innovation and environmental protection as the core in recent years and put forward a series of green development goals accordingly. Among them, the improvement of Green Total Factor Productivity (GTFP) is the key to achieving the goal [1]. GTFP is the total factor productivity after taking environmental resources, energy resources, and ecological resources as rigid constraints of economic growth [2]. GTFP reveals the importance of ecological and environmental performance in the assessment of sustainable economic growth [3]. Urban GTFP represents the environmental and economic benefits of urban production activities comprehensively.
GTFP has an important role in green sustainable development [4]. GTFP highlights the environmental indicators in the economic growth process [5]. GTFP concerns resource use, resource waste, and environmental performance, which are included in the circular economy performance assessment [6,7]. GTFP is closely related to the quality of economic growth and the ability to reach the long-term sustainable development goals of a region [8]. Improving urban green total factor productivity is a necessary condition for building environmentally friendly and sustainable economic cities [9].
With the deepening of research, the current frontier method for GTFP measurement is the Data Envelopment Analysis (DEA) model [10]. Researchers have calculated the GTFP of different countries and industries using this method and obtained better results than the previous algorithm. In addition, it was found that the Global Malmquist–Luenberger (GML) productivity index method is better than the Malmquist–Luenberger, Global Malmquist, and Malmquist indices in terms of reflecting the dynamic change in GTFP efficiency value over a while [11]. Therefore, this paper applied the Super Efficiency Slacks-Based Measure (Super SBM) model to DEA with undesirable outputs, then combined it with the GML index method to calculate GTFP.
This paper selected 288 prefecture-level cities and cities above the level from 2006 to 2019 in China as study samples. This paper used the Super SBM with undesirable output and the GML index method to calculate urban GTFP, then analyzed the temporal and spatial variation of the GTFP. The main contributions of this paper are: (1) Improving the GTFP measurement method. The existing research usually used either the DEA model or the productivity index to calculate GTFP. This paper used the Super SBM-DEA model and GML index method to calculate GTFP. This method will measure the dynamic value of GTFP. (2) Adding the undesirable outputs of environmental pollution to the GTFP index system. Considering the existing research only selects one or more of the various environmental pollution indicators from air pollution indicators such as carbon dioxide, sulfur dioxide, and nitrogen to carry out empirical research and ignores water pollution, a more comprehensive environmental pollution indicator is constructed in this paper. (3) Adding environmental resources and energy resources as inputs to the GTFP index system. The current research on input indicators only includes labor and capital input and ignores environmental resource input, or only considers a single factor for resource input indicators but lacks constraints on multi-indicator environmental resources, this issue is also improved in this paper. (4) Discussing the temporal and spatial evolution of urban GTFP in prefecture-level cities and above in China. The existing research on GTFP is mainly concentrated at the macro level of country, region, and province, or the micro level of industry or industry, with less research on cities. In addition, the current studies on urban GTFP mainly focus on the discussion of its influencing factors and lack discussion of the specific reasons behind its temporal and spatial evolution and its sources of growth, which is also one of the main problems to be solved in this paper.
This paper is organized as follows. Section 2 is the literature review. Section 3 introduces the super-efficiency SBM model, the GML index model, the variables of the GTFP index system, and data sources. Section 4 analyzes the measurement results and discusses the temporal and spatial evolution of GTFP. Section 5 presents the research conclusions and our future research. The structure of this study is shown in Figure 1.
Figure 1.
Paper structure.
2. Literature Review
Productivity measures the effectiveness of various production input factors in economic production. GTFP measures the effectiveness of various production input factors in both economic and environmental production. Moreover, the input factors and output factors include not only economic variables, such as capital, labor, and GDP but also green variables. Green variables consist of energy consumption, ecology cost, environmental outputs, and environmental pollution [12]. An efficient GTFP means less input, more desirable outputs, and less undesirable outputs [13]. When the GTFP of a city achieves an efficient level, it indicates that this city may realize sustainable economic and environmental development. GTFP can be used to assess the sustainability performance of a certain industry [14,15]. GTFP also measures whether a region is headed toward sustainable development [16]. Therefore, urban GTFP can represent the sustainable development level of a city. This section will discuss the calculation methods of GTFP and review the application of GTFP.
2.1. Measurement of GTFP
At present, the common methods of calculating GTFP mainly include the Solow residual method, the distance function approach, and the DEA method [17]. The Solow residual method and distance function approach are relatively traditional methods for calculating GTFP. In the case of calculating GTFP, the Solow residual method adds environmental variables as input factors into the neoclassical economic growth model. Solow residual value method, which treats undesirable output as an input factor to deal with environmental constraint variables, violates the “material balance idea”, and the asymmetric treatment of desirable output and undesirable output cannot make a correct evaluation of economic performance and environmental performance [18]. The distance function approach is to calculate the shadow price of undesirable output through the distance function, constructs the productivity index with the distance function, and estimates GTFP by combining the parameter method. For example, in the early stage, Pittman (1983) [19] tried to include the undesirable output in TFP measurement and estimate GTFP by using the shadow price of pollutants from the data of producer emission reduction expenditure. However, since the distance function approach needs to make assumptions about the specific form of the production function, meanwhile, parameter estimation is required and the calculation steps are complicated, it is rarely used by scholars.
In the previous research process, the scholars did not clearly distinguish between the concepts of green efficiency and GTFP, so the main methods to measure GTFP were ecological footprint, carbon footprint, water footprint, and other commonly used methods to measure green efficiency. After 2014, The DEA models were gradually applied in calculating GTFP [20]. The DEA models became mainstream to measure GTFP until 2017 [21,22].
At present, DEA is the most commonly used method to calculate GTFP [23,24,25,26,27]. This method does not need to set an a priori production function but directly uses linear optimization to give the distance function and boundary production function for measurement after the observation data of sample points is obtained. The Charnes–Copper–Rhodes (CCR) model put forward by Charnes et al. (1978) [28] and the Banker–Charnes–Copper (BCC) model with variable returns to scale put forward by Banker et al. (1984) [29] based on CCR-DEA are the two earliest DEA models. Later, Andersen and Peterson (1993) [30] solved the problem that CCR and BCC could not be used to compare and evaluate the efficiency of multiple effective decision-making units by constructing the super-efficiency DEA model. Tone (2001) [31] successively proposed the non-radial and non-angler Slacks-Based Measure (SBM) DEA model. The SBM model solved the problem that previous DEA models could not deal with excess input and insufficient output, could not contain slack variables, and were affected by statistical data units. Then, Tone (2002) [32] derived the super-efficiency SBM model. The efficiency value calculated by the super-efficiency DEA model can be greater than 1. It is the mainstream tool in current research. Since GTFP calculation is not only based on the assumption of minimum input and maximum output, but also needs to consider the undesirable output such as pollutant emissions in the production process, Li et al. (2013) [33] proposed the Super-SBM model considering undesirable output, and calculated the environmental efficiency of some regions in China based on this. The Super-SBM model considering undesirable output is the current mainstream DEA method for calculating environmental efficiency. It is also the main method used in this paper to evaluate urban GTFP in China.
The results calculated by the DEA method are mainly static efficiency values. To investigate the dynamic changes in efficiency values, some scholars combine the DEA method with the productivity index method to explore the dynamic changes in efficiency values over a while. Oh (2010) [34] measured the TFP of OECD countries by using the Global Malmquist–Luenberger, Malmquist–Luenberger, Global Malmquist, and Malmquist indexes, respectively. It was found that the TFP value measured by the Global Malmquist and Malmquist index methods not considering undesirable output was significantly higher than the TFP measured by GML and ML considering undesirable output. It was also believed that the GML measurement process was the simplest and the measurement results were the most reliable. In research on industrial or regional GTFP, the DEA-Malmquist approach and DEA-ML approach were mostly used [35,36]. However, these two methods may not have feasible solutions. The GML index and its components are circularly cumulative. So, the GML index allows for a single measure of TFP changes and their decomposition, without the occurrence of no feasible solution. However, many studies that choose the DEA-GML approach failed to consider the undesirable output, which makes the calculated GTFP and its variation not the most reliable and optimal solution. Without undesirable output, the GTFP will be overestimated. Therefore, the Super SBM-GML index method is selected in this paper to not only solve the problem that the efficiency value of the SBM method cannot be greater than 1, but also solve the problem that other index methods may have no feasible solutions.
2.2. Application of GTFP
GTFP value can be used to monitor the effectiveness of environmental protection [37]. The increase in GTFP is regarded as an encouraging pointer toward improvement in the sustainable development of the regional economy. Ren and Ji (2021) [38] took the ascending GTFP in China’s coastal provinces to indicate the sustainability of the marine economy. Rusiawan et al. (2015) [39] applied GTFP to measure Indonesia’s sustainable development level.
In addition, GTFP is a reliable proxy indicator to study the sustainability of segmented industries. Zhong et al. (2023) [40] used the GTFP of the freshwater aquaculture industry to represent the extent of the harmony of the freshwater fishery economy and environment. Debbarma et al. (2022) [41] used GTFP to reflect India’s sustainable development level in the export industry under climate change. Meng and Zhao (2022) [42] considered the improvement of GTFP in the manufacturing industry to be a positive response to sustainable development and the climate crisis.
The spatiotemporal evolution trend of GTFP reflects the gap in green economy development among different regions. The industrial GTFP showed regional differences in China. Xiao et al. (2022) [43] found that the industrial GTFP in the northeast lagged far behind that in the eastern, western, and central regions. Li and Wang (2022) [44] used the GTFP of the logistics industry to evaluate whether the logistics industry had achieved low-carbon transformation and sustainable development. They found that the GTFP of the logistics industry in China showed temporal and spatial heterogeneity greatly. In addition, regional GTFP also exhibits regional differences in spatiotemporal evolution characteristics. Liu and Zhu (2022) [45] found that there were visible differences in the temporal-spatial evolution trend of GTFP among China’s coastal cities.
About green and sustainable development, some research paid attention to the firm level and micro level [46,47]. On the macro level, existing literature focused more on specific regions in China, such as urban agglomeration, specific provinces, or specific regions [48,49,50]. In the discussion of the spatial-temporal change in GTFP in these cities, more literature focuses on the results of GTFP changes and their influencing factors, and the lack of in-depth discussion on the changes [51,52]. In this paper, the results of GTFP in 288 Chinese cities from 2006 to 2019 are calculated by using the more frontier Super SBM-DEA model considering undesirable output and the GML index method. The temporal-spatial variation characteristics of GTFP also are discussed using the GML index decomposition and the characteristics maps of the spatial distribution and images of kernel density estimation, respectively.
3. Methodology
This section introduces the DEA model, GML productivity index model, data sources, and description of variables of our research.
3.1. Super SBM Model Considering the Undesirable Output
The nonparametric DEA model can effectively measure the efficiency of the decision-making unit (DMU). The CCR-DEA and BCC-DEA models are not suitable for measuring efficiency when the input and output may change in a non-proportional way, nor can they contain the undesirable output. The SBM model cannot be effectively refined in the optimal state, that is, the input-output relative efficiency value between DMU when the efficiency value is equal to 1; therefore, in this paper, the Super SBM model was selected to solve the above problems and measure the urban green efficiency considering undesirable output.
Suppose there are decision-making units (DMUs) in the production process, and each DMU is composed of three vectors: input (), desirable output (), and undesirable output (), where, , , are the quantity of input, desirable output, and undesirable output. They are defined as matrixes , and below:
where , , . The production possibility set is defined as shown in Formula (1):
where is the weight vector, represents that the actual input level is greater than the frontier input level, represents that the actual desirable output level is less than the frontier desirable output, represents that the actual undesirable output is greater than the frontier undesirable output level, and represents that it is assumed that the scale return of the production frontier is variable. Concerning the research of Li et al. (2013) [33], Li and Shi (2014) [53], and Chen (2019) [54] under the assumption of variable returns to scale, the following Super SBM model considering desirable output is constructed in this paper to measure the efficiency level of , as shown in Formula (2):
subject to:
where is the green efficiency value of the DMU, and are the average values of the input, desired output, and undesired output, respectively. When , the DMU is on the production frontier and is efficient, and a larger indicates that the DMU is more efficient. When , it indicates that the DMU is inefficient and needs further improvement in the number of inputs and outputs.
3.2. Global Malmquist–Leuenberger Productivity Index Model
GTFP also considers the relative relationship between actual production and production frontier as well as the change in production frontier boundary of each unit, so GTFP can be decomposed into efficiency change and technological progress level [55]. Therefore, we can get GTFP after measuring the static efficiency value with Super SBM and then measuring the dynamic change in efficiency value with the GML productivity index method. Compared with Malmquist, Luenberger, and ML indexes, GML is transitive and recyclable without the condition of no feasible solutions, so the DEA-GML index method is used in this paper to calculate urban GTFP in China.
By referring to the research of Oh (2010) [34], this paper first establishes the production possibility set at the moment based on Formula (1) production possibility set :
where t = 1,2 ⋯ T. Then build the set of global production possibility set:
Then, we build the contemporaneous directional distance functions (5) and the global directional distance functions (6):
where and denote the directional vectors of desired output and non-desired output, respectively. Then, we build the following GML Model with the assumption of variable returns to scale, as shown in Equation (7):
where is the GTFP at period. When , means the GTFP from period to has increased; when , it means the GTFP from period to is unchanged; when , it means the GTFP from period to has decreased. is the green technical efficiency () at period , which is equal to the value of at period. is the green technical efficiency change () from period to , and is the green technical progress level () from period to .
3.3. Method for Studying the Spatial Variation Trend of GTFP
To study the distribution pattern and variation of GTFP in different years, this paper uses Kernel Density Estimation (KDE) to estimate the spatial distribution of GTFP first. KDE is used to estimate the smoothed empirical probability density function and can be used in spatial analysis to describe the intensity of geographic event distribution over planar and mesh space. Therefore, we use the kernel density function of Gaussian distribution to estimate the urban GTFP and sub-regional urban GTFP in China for 2006, 2010, 2015, and 2019. The formula of the kernel density function is shown in Equation (8).
where is the number of cities, is the GTFP of the city, is the mean value, is the bandwidth and is the Gaussian kernel function. At a certain value, the larger the kurtosis of the KDE curve, the sharper the peak, indicating that there are more GTFP values at this level. When the kurtosis of the curve decreases, the width increases, indicating that the difference in GTFP among cities is decreasing. When the curve is skewed to the right and the right tail gradually lengthens, it indicates that the difference in GTFP between cities is increasing. When multiple peaks appear, it indicates that there is multipolar differentiation in the spatial distribution of GTFP.
Secondly, this paper presents the spatial distribution and agglomeration characteristics of GTFP by drawing spatial distribution characteristic maps in different years, to study the spatial variation patterns of GTFP. The spatial distribution feature map displays the spatial distribution position of GTFP values and shows whether GTFP in different cities and regions has spatial continuity. On the map, cities marked with similar colors or elements have GTFP at a similar level. Therefore, we use kernel density estimation diagrams and spatial distribution maps in different years to describe spatial distribution characteristics and the spatial variation of urban GTFP.
3.4. Variable Selection Specification
To calculate urban GTFP in China, the following indicators are selected as input variables, desirable output variables, and undesirable output indicators in this paper, concerning the research of Zhou et al. (2020) [56], Wang et al. (2022) [57], Meng and Qu (2022) [58]. The input indicators include capital, labor, and environmental resources. In this paper, the fixed assets investment is used to represent capital investment [59], and the number of urban employed persons at the end of the year is used to represent labor investment [60]. Furthermore, this paper selects natural and energy resources to represent the input of environmental resources. The urban built-up area is used to represent land resource investment [61], the total water supply is used to represent water resource investment, and the total social electricity consumption is used to represent energy investment. The desirable output indicators in this paper are the gross regional product () and the green land coverage area in urban built-up area, among them, is the proxy indicator of economic income and the green land coverage area in the urban built-up area is the proxy indicator of environmental income. Moreover, we add the bad outputs into the GTFP index system. The undesirable output indicators are indicators that have a negative impact on the urban environment, which include industrial sulfur dioxide emissions, industrial smoke and dust emissions, and industrial wastewater emissions.
The descriptive statistics of input-output variables used to measure urban GTFP in China are shown in Table 1. The standard deviation of all indicators is greater than the mean value, which indicates that the discrete degree of input-output index data is relatively large and the development gap between cities is relatively large.

Table 1.
Descriptive statistics of GTFP input-output variables in Chinese cities.
3.5. Data Sources
This paper studies 288 prefecture-level cities and cities directly under the central government in China, excluding Tibet, Hong Kong, Macau, and Taiwan due to the unavailability of data. To study the imbalance of regional GTFP changes in China, this paper divides China into four segments: eastern, central, western, and northeastern regions. Among them, the eastern region includes 84 prefecture-level cities in Jiangsu Province, Zhejiang Province, Hebei Province, Shandong Province, Guangdong Province, Hainan Province, and Fujian Province and three municipalities directly under the central government (Beijing, Tianjin, and Shanghai), for a total of 87 cities. The central region includes 80 prefecture-level cities in Anhui Province, Shanxi Province, Henan Province, Hubei Province, Hunan Province, and Jiangxi Province. The western region includes 83 prefecture-level cities in Sichuan Province, Guangxi Zhuang Autonomous Region, Guizhou Province, Yunnan Province, Shaanxi Province, Gansu Province, western Inner Mongolia Autonomous Region, Ningxia Hui Autonomous Region, Xinjiang Uygur Autonomous Region, Qinghai Province, and one municipality directly under the Central Government (Chongqing), a total of 84 cities. The northeast region includes 37 prefecture-level cities in Heilongjiang Province, Jilin Province, Liaoning Province, and the eastern part of the Inner Mongolia Autonomous Region. A total of 288 cross-sectional study subjects. It should be noted that individual prefecture-level cities such as Maanshan, Bijie, Tongren, Haidong, and Laiwu involve administrative division adjustments, and to maintain the smoothness of the data, they are uniformly treated according to the administrative division unit statistics in 2018.
We selected the period from 2006 to 2019 for the study. China’s “Eleventh Five-Year Plan” proposed that China should implement the basic national policy of resource conservation and environmental protection. It is proposed to build a national economic system with low investment, high production, low consumption, low emission and sustainable recycling, and a resource-saving and environment-friendly society. Therefore, this paper selects 2006, the starting year of the Eleventh Five-Year Plan, as the beginning of the period of the research sample, to 2019, the year of the most complete and latest data available.
The data were obtained from the 2006–2020 China City Statistical Yearbook [62], the 2006–2020 China Statistical Yearbook on Environment [63], the 2006–2020 China Statistical Yearbook [64], the 2006–2020 Statistical Yearbook of each prefecture-level city [65], and the 2005–2019 Statistical Bulletin on National Economic and Social Development [66]. The data access platforms are the CEI statistical database (https://ceidata.cei.cn/ (accessed on 1 January 2023)), the China Economic and Social Big Data Research Platform (https://data.cnki.net/ (accessed on 1 January 2023)), the China Statistical Information Network (http://www.tjcn.org/ (accessed on 1 January 2023)), and the Foresight Database (https://d.qianzhan.com/ (accessed on 1 January 2023)). This article used data from municipal districts, and for missing data, we fill in the processing with ARIMA linear interpolation.
4. Results
Based on the super-efficiency SBM-GML model considering undesirable output, this paper used the input-output data of 288 prefecture-level cities and above in China from 2005 to 2019 as well as MaxDEA 7.0 to calculate the GTFP index of Chinese cities from 2006 to 2019. It should be particularly noted that since the GTFP index of 2005–2006 includes 2006 in this paper, the urban GTFP value of 2006–2019 is calculated based on the data of 2005–2019. See Appendix A for the specific calculation results.
4.1. Time Trend of Green Total Factor Productivity in Chinese Cities
Table 2 shows the average value of GTFP and its decomposition index for Chinese cities in each study period. It can be seen from the calculation results that the average GTFP of Chinese cities in 2006–2019 was 1.0317, with an average increase of 3.17%. This shows that the green development level of Chinese cities is steadily improving, and the urban development model has changed from the traditional extensive growth of economic quantity to the intensive environment-friendly growth that takes into account the quality of economic growth. It can be seen from the index decomposition in Table 2 that the average value of technology change (TC) is 0.9986, with an average annual decrease in green technological progress of 0.32%, and the average value of green efficiency change (EC) is 1.0360, with an average annual increase in efficiency value of 3.60%. It can be seen that EC has a positive effect on the growth of GTFP, and the GTFP growth in Chinese cities mainly comes from the improvement of green efficiency.

Table 2.
Average annual GTFP and its decomposition in Chinese cities.
From the perspective of GTFP and its decomposition in each year, the GTFP value in 2006 was 0.9860, and GTFP in that year decreased by 1.40%, but the green efficiency value in 2006 was greater than 1, up by 0.48%. The GTFP in 2007 and 2008 increased by 3.44% and 2.62% respectively, which indicates that all cities have fully responded to the construction of ecological civilization proposed in the “Outline of the Eleventh Five-Year Plan”. In 2009, the GTFP value was 0.9814, and this year’s GTFP decreased by 1.86%, this may be because the economic losses caused by the financial crisis in 2008 spread to 2009. The GTFP value from 2010 to 2012 was greater than 1, and the GTFP increased by 1.97%, 7.29%, and 3.87% respectively. This is because, after the outbreak of the financial crisis in 2008, the Chinese government launched the “Four Trillion” plan to expand domestic demand and promote stable growth of the Chinese economy. After the four trillion-yuan investment, the urban GTFP in China is steadily rising. Although the “Four Trillion” plan has stimulated China’s economy in the short term and greatly increased the scale of China’s economy in the short term, it has also caused overcapacity, and its negative impact is reflected in the decline of the GTFP value in 2013, which decreased by 1.14% in 2013. After 2013, with the proposal of the concept of green development, the completion of the drafting of the Amendment to the Environmental Protection Law, as well as the promulgation of the “Twelfth Five-Year Plan” for the Prevention and Control of Air Pollution in Key Regions—China’s first comprehensive air pollution prevention and control plan, the GTFP value has been stable above 1.
To reflect the annual dynamic change process of the GTFP and its decomposition index of Chinese cities at and above the prefecture level from 2006 to 2019, this paper draws the change trend chart of the GTFP and its decomposition index of Chinese cities from 2006 to 2019, as shown in Figure 2. It can be seen from Figure 2 that the changing trend of GTFP is consistent with that of green efficiency EC, which shows that the changing trend of GTFP is largely affected by the change in green efficiency instead of technological progress. It indicates that China’s economic reform has indeed brought about significant efficiency improvement and produced an obvious “horizontal effect”. However, the input-output model of urban green development cannot be coordinated with technological progress, and technological progress cannot be integrated into the current urban green development model. China’s green economic reform has not produced an obvious “growth effect”, and Chinese cities cannot achieve sustained growth of GTFP in the long term.
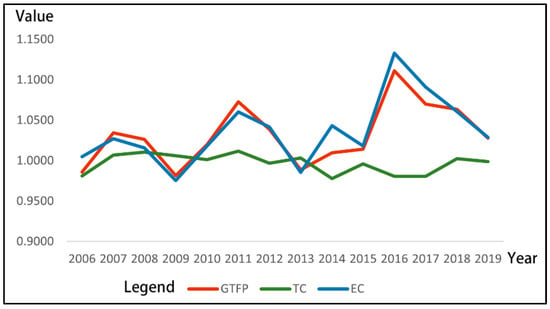
Figure 2.
Time trend of annual average GTFP and its decomposition in Chinese cities. Data sources: author’s calculation.
To further study the temporal and spatial evolution characteristics of GTFP in various regional cities in China from 2006 to 2019, this paper divides the samples of the study area into the east, the middle, the west, and the northeast for classification and statistical analysis, and the statistical results are shown in Table 3, Table 4, Table 5 and Table 6.

Table 3.
Annual average GTFP and its decomposition in eastern cities of China.

Table 4.
Annual average GTFP and its decomposition in central cities of China.

Table 5.
Annual average GTFP and its decomposition in western cities of China.

Table 6.
Annual average GTFP and its decomposition in northeastern cities of China.
It can be seen from Table 3 that the mean value of GTFP in eastern China is 1.0737, and the value of GTFP has increased from 1.0693 in 2006 to 1.0923 in 2019. The GTFP of the eastern region is greater than 1 in the study period, which indicates that the green development level of the eastern region is steadily rising. This is due to the first-mover advantage of the eastern region as a demonstration area for various green development policies. The green technology progress index in the eastern region increased from 1.0202 in 2006 to 1.0864 in 2019, while the green efficiency index decreased from 1.0482 to 1.0054. The TC value in the eastern region is the only one greater than 1 in the four regions, which indicates that only the improvement of GTFP in the eastern region depends on the progress of green technology. The decline of EC value in the eastern region is caused by the higher capital investment of the developed cities in the eastern coastal region compared to that in the central, western, and northeastern regions. However, due to the diminishing returns, to scale effect of capital and the late-developing advantage of capital, the growth rate of capital allocation efficiency in the backward areas in the central, western, and northeastern regions will exceed that in the eastern developed regions, so the green efficiency level in the eastern region will decline.
It can be seen from Table 4 that the GTFP of central cities has increased from 0.9756 in 2006 to 1.0378 in 2019, with an average of 1.0214, showing an “N” type change trend. The technological progress index of central cities has risen from 0.9161 in 2006 to 1.0144 in 2019, but the average is less than 1. The green efficiency change index in central cities dropped from 1.0650 in 2006 to 1.0231 in 2019, but the average value was greater than 1. From the perspective of all years, the GTFP improvement in central cities from 2006 to 2012 mainly depends on green efficiency improvement, but since 2013, the GTFP improvement mainly depends on green progress. It indicates that the central cities have thoroughly implemented the concept of green development, and the economic development model is no longer only dependent on the input of labor, capital, and energy, but begins to explore more green production technologies such as pollutant emission reduction, resource, and energy conservation, etc.
It can be seen from Table 5 that the GTFP of western cities increased from 0.9297 in 2006 to 0.9841, with an average of 1.0102. The technical progress index of western cities dropped from 0.9398 in 2006 to 0.9369 in 2019, and the technical efficiency index rose from 0.9893 in 2006 to 1.0504 in 2019. The growth rate of the change index of green technology efficiency in the western region is very high, which indicates that urban green development mainly depends on the increase in factor input. In contrast, the annual mean change in GTFP in western cities is similar to that in central cities, showing an “M” type change. After an increase of 1.32% in 2007, the GTFP has been less than 1. After briefly exceeding 1 in 2011 and 2012, it began to be less than 1 in 2013–2015. Then it was greater than 1 in 2016–2018, but it was less than 1 again in 2019. It indicates that the growth rate of GTFP in the western region cannot always be positive, and the fluctuation range is exceptionally large. This is because the western region, as a region with a large number of heavy industries, energy-intensive industries, and natural resources industries, has a low level of technological progress in the development and utilization of clean energy and clean technology, and sustainable growth cannot be achieved.
The GTFP of northeast cities increased from 0.9359 in 2006 to 0.9552 in 2019. The green progress index dropped from 0.9593 to 0.9458, with an average of 0.9770. The green efficiency change index rose from 0.9755 to 1.0099, with an average of 1.0274. It shows that the increase in GTFP in northeast China faces the same problem as that in west China, that is, it relies too much on resource allocation and ignores the progress of green technology. The average GTFP of northeast cities is 1.0036, with an average annual increase of 0.36%, which is far lower than that of the eastern, central, and western regions. The GTFP value in northeast China is less than 1 all year round, and only the GTFP value in 2011, 2014, 2015, 2016, and 2018 is greater than 1 over the past 14 years. This is because the traditional extensive, high pollution, and high emission industries cannot meet the needs of green development in northeast cities. The economic pillar industries of northeast cities have been developing in a high-carbon, high-energy consumption, and extensive manner for a long time. The industrial development ratio in northeast China is significant, the consumption of environmental resources is large, and the pollutant emission is large, which results in a long-term low GTFP index of northeast cities.
In general, the growth of urban GTFP in the eastern region is relatively large, the change in GTFP in the central and western regions is relatively similar, the growth of GTFP in the northeast region is relatively small, and there are great differences in the green development level between different regions in China. From the mean value of GTFP in eastern, central, western, and northeastern cities of China from 2006 to 2019, the GTFPs of the four regional cities are all greater than 1, which indicates that the GTFP of the four regions has an average upward trend in 14 years. Among them, the average annual growth rate of GTFP in cities in the eastern region is 7.37%, which is the fastest-growing region; the average annual growth rate of GTFP in the central region is 2.14%; the average annual growth rate of GTFP in the western region is 1.02%; and the average annual growth rate of GTFP in the northeast region is 0.36%. Moreover, the technological progress index of eastern cities is the only one greater than 1 in the four regions, which indicates that only the green technology in eastern cities has been innovated and developed, which may be caused by the “Matthew effect” of labor flow in various regions. From 2006 to 2019, the economic development of cities in the eastern region was faster, and the urban development was better than that of the central region, while the development of the central region was better than that of the western region and the northeast region; the economic prosperity also brought about the migration of talents. The talents moved from the northeast and the western region to the central or eastern region, and the top talents in the central region moved to the east, making the growth rate of urban talents in the northeast, the west, the central and the eastern regions increase in turn. In addition, compared with the eastern cities, the three regions of northeast, west, and central China have large gaps in the level of scientific research and education, the level of scientific research platform construction, and the conditions of scientific research equipment, which further widens the gap in the efficiency of labor allocation between them, and finally makes the technical progress index in the eastern region increase, while the technical progress index in other regions is decreasing. Another reason for the improvement of technological progress in the east is the large inflow of foreign capital. Compared with the cities in the other three regions, the eastern cities are more coastal in terms of geographical location. For example, Shanghai Port, Shenzhen Port, Guangzhou Port, Ningbo Zhoushan Port, Tianjin Port, and other large ports in China are located in the eastern region. Therefore, the degrees of opening up and foreign direct investment in the east are higher than those in other regions, and opening up helps advanced technologies and ideas to spread first in the east, so the progress of green technology in the east is significantly higher than that in the other three regions and is also the only region in China where green technology progress is rising among the four major sectors in China.
To more intuitively compare the time evolution differences of the average annual GTFP, TC, and EC in the nationwide, eastern, central, western, and northeastern regions from 2006 to 2009, line charts are drawn in this paper, as shown in Figure 3.
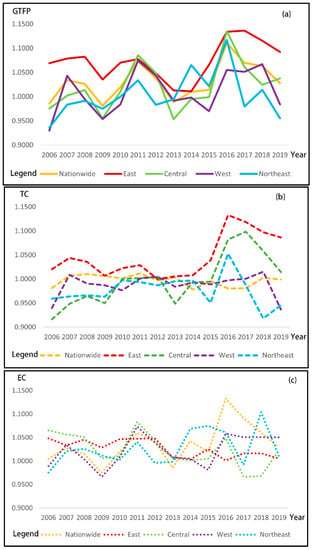
Figure 3.
Time trend of annual average GTFP, TC and EC in Chinese cities; (a) GTFP; (b) TC; (c) EC Data sources: author’s calculation.
It can be seen from Figure 3a that the changes in GTFP values in the eastern, central, western, and northeastern regions are quite different. Among them, the average annual value in the eastern region is higher than the average level of national GTFP, the central and western regions are the same as the national average level, and the GTFP values in most years in the northeast are lower than the national average level. The change in GTFP in eastern cities has always shown an upward trend and is higher than the national average GTFP. It indicates that the green economy level in northeast China is lower than that in other regions, and the construction of urban ecological civilization needs to be further improved. However, the GTFP level in the eastern region is improved due to the first-mover advantage brought by a series of policies to promote the implementation of green development in the eastern region.
From the above analysis, it can be found that on the time scale, the development of China’s urban GTFP shows an overall upward trend in fluctuation. From the perspective of growth contribution, from 2006 to 2011, the contribution of green technology efficiency improvement was higher than that of green technology progress. This indicates that before the concept of green development was put forward, the level of green technology progress in Chinese cities was relatively low, and it mainly affects the growth of GTFP by increasing the input of green resources. After 2012, the technological progress index rose, and green technological progress characterized by innovation began to affect the changes in China’s urban GTFP. From a regional perspective, the average GTFP value of eastern cities shows a steady upward trend, and the growth rate is significantly faster than the national average. This indicates that the eastern region, as the innovation area of China’s green technology and the leading demonstration area of China’s green economy, is the core driving force behind promoting urban GTFP in China. Moreover, the improvement of GTFP in the eastern region is mainly due to green technology progress, which indicates that the eastern cities have a high level of environmental governance, and green technology and clean energy have developed rapidly, which has promoted the continuous increase in the growth rate of green total factors in the region. The changing trend of GTFP in central and western cities is relatively similar in time, which is rising in fluctuation. The green technology progress index of the central and western cities is lower than that of the eastern regions, which is because the central and western cities are mainly undertaking the eastern industries and imitating the eastern high-tech industries in the process of urban green development. The GTFP value of northeast cities has always lagged behind the national average and is also far lower than the GTFP value of eastern, central, and western cities, with negative growth in most years. In addition, the green technology efficiency change index and green technology progress index in northeast China are at a low level. This is because the main industries in northeast China are industries with high energy consumption, high pollution, and low technical content, which results in the green development level of northeast China being far behind other regions. In future development, the central, western, and northeastern cities also need to continuously optimize and upgrade the industrial structure, develop and innovate green technologies, and put clean energy and clean technology into production.
4.2. Spatial Evolution Trend of Green Total Factor Productivity in Chinese Cities
We choose the starting year 2006 and ending year 2019 in this study as the time points for studying the spatial evolution trend of GTFP. To reflect significant spatial changes of GTFP over a period, we select a study time interval of 4 or 5 years between 2006 and 2019. Thus, 2010 and 2015 are chosen as the research time points at the same time.
This paper used Kernel Density Estimation to estimate GTFP in Chinese cities in 2006, 2010, 2015, and 2019 to study the distribution dynamics of GTFP in Chinese cities in different years. Based on Formula (8) in Section 3.3, Stata 16.0 software is used in this paper to generate the kernel density curves of the whole, eastern, central, western, and northeastern China, as shown in Figure 4a–e.
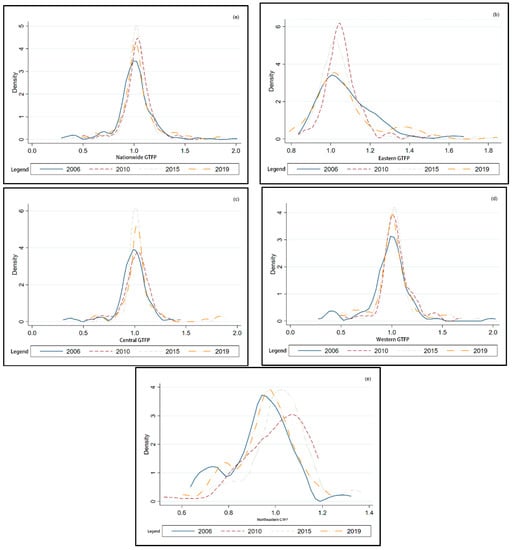
Figure 4.
Kernel Density Function Diagram of GTFP in Chinese cities; (a) Nationwide GTFP; (b) Eastern GTFP; (c) Central GTFP; (d) Western GTFP; (e) Northeastern GTFP.
The kernel density curve directly reflects the overall evolution characteristics of urban GTFP in China. It can be seen from Figure 4a that although the kernel density function of China’s overall GTFP in 2006, 2010, and 2019 did not have a strict single peak shape, the main peak was very prominent, which indicates that there was multipolar differentiation in urban GTFP in China. It can be seen from the tail shape that the tailing of the four years is obvious, which indicates that there is a relatively obvious regional difference in China’s GTFP level. In the kernel density curve in 2006, there was one obvious main peak and two secondary peaks, but the secondary peaks in the other three years were not prominent. Moreover, the peak in 2006–2019 showed a rise first and then a decline, but the peak in 2019 was still much higher than that in 2006, which indicates that the difference in China’s overall GTFP level was narrowing. From the position of the peaks in each year, the peaks in 2006 were concentrated on the left, and the peaks in 2010, 2015, and 2019 were relatively right, which indicates that the GTFP of most Chinese cities was low in 2006, but the GTFP values of all cities have increased since then. From the perspective of kurtosis, the kernel density curve of each year shows a trend of development from a broad peak to a sharp peak, which indicates that the difference in the GTFP level is gradually decreasing. From the perspective of location, the kernel density curve of China’s GTFP shifted slightly to the right from 2006 to 2015, and the kernel density curve shifted slightly to the left from 2015 to 2019, which indicates that the GTFP showed a trend of increasing first and then decreasing slightly. Moreover, the low-value area of GTFP fluctuated significantly in 2006, while the high-value area of GTFP fluctuated tremendously in 2019. Overall, the GTFP of Chinese cities in the whole study period showed a trend of development from low to high, and then back to some extent, with obvious differences in the GTFP level among cities, but the difference is gradually narrowing.
It can be seen from Figure 4b that the kernel density distribution curve of GTFP in the eastern region shifted to the right from 2006 to 2019, which indicates that the GTFP in the eastern region was generally upward. In 2019, there was an obvious double peak, with the main peak on the left and the secondary peak on the right. It shows that the overall urban GTFP in the east has the characteristics of polarization and spatial disequilibrium, and the agglomeration type has shown an obvious low-value agglomeration. Of course, the low-value agglomeration point of eastern cities is also above 1. The kurtosis of the main peak of the kernel density curve increased from 2006 to 2010. However, the kurtosis began to decline, and the image width gradually increased from 2010 to 2019. This shows that from 2006 to 2019, the gap of the GTFP index among cities in the eastern region showed a change feature of decreasing first and then increasing. From the tailing degree of the curve in the image, there is obvious right tailing in the four years, and it is more and more obvious. It indicates that the urban GTFP value in the high-value areas has increased from 2006 to 2019, and the proportion of high-value cities also increased. In general, the GTFP of cities in the eastern region has increased, but the differences between cities are large, showing the feature of first decreasing and then increasing.
It can be seen from Figure 4c that the kernel density distribution curve of GTFP in the central region shifted slightly to the right from 2006 to 2019, which indicates that the overall GTFP in the central region showed a slight upward trend. There are obvious single peaks in the four years, and there is no two-stage differentiation. However, the tailing phenomenon in 2019 is significantly more obvious than that in 2006, and the extensibility broadening of GTFP distribution has widened, which indicates that the gap between central cities is widening. In general, the GTFP change in the central region is small, but the difference between cities increases gradually.
It can be seen from Figure 4d that the kernel density distribution curve of GTFP in the western region shifted slightly to the right from 2006 to 2019, which indicates that the GTFP in the western region generally showed a slight increase. In 2006, there were two peaks, one high and one low, with the main peak on the right, which indicates that most areas of the western cities showed a high concentration of GTFP values. In 2010, there were also two peaks, one high and one low, but the main peak was on the left, which indicates that in 2010, the GTFP in the western region became a low-value concentration state. However, the gap between regions has widened. In 2015 and 2019, it gradually changed into a single peak, which indicates that the extreme numerical quantity has decreased. From the perspective of tailing, the tail of the kernel density curve in 2019 is shorter than that in 2006, which indicates that the difference in GTFP between cities in the west is narrowing. In general, the rise of GTFP in the western region is not obvious; the GTFP level is gradually converging, the polarization is gradually decreasing, and the difference between cities is also decreasing.
It can be seen from Figure 4e that the kernel density distribution curve of GTFP in northeast China shifted to the right from 2006 to 2015 and the left from 2015 to 2019, which indicates that the GTFP in northeast China showed a trend of rising first and then falling. In 2006, 2015, and 2019, the kernel density distribution curve of cities in northeast China showed a double-peak feature, with the main peak on the right and the secondary peak on the left, showing a two-level differentiation and a high-value agglomeration. From the tail characteristics, the kernel density curve in 2006, 2015, and 2019 did not have a significant tail, and there was a relatively significant tail in 2010. It shows that although there are urban differences in GTFP in northeast China, the differences tend to expand first and then decrease.
Further, to study the spatial distribution change characteristics of GTFP in Chinese cities, ArcGIS 10.2 software is used in this paper to draw the spatial feature map of GTFPs in 288 prefecture-level cities and above in China. Figure 5 shows the spatial distribution of China’s urban GTFP in 2006, 2010, 2015, and 2019. It can be seen from Figure 5 that the GTFP of Chinese cities presents a regional agglomeration distribution, and the GTFP value of cities in the eastern region is significantly higher than that of other regions. In 2006, the high value of GTFP was concentrated in the eastern coastal cities, municipalities directly under the central government, provincial capital cities, and some tourist cities, such as Sanya and Zhangjiajie. In 2010, the number of high-value cities was increasing, but the high value of GTFP was still mainly concentrated in cities in the eastern region and provincial capital cities, and the GTFP high-value cities in the central region have increased. The GTFP of surrounding cities is still at a low value. In 2015, the high value of GTFP was still concentrated in the eastern cities and other provincial capital cities or municipalities directly under the central government, and the provincial capital cities and the central cities of some urban agglomerations, such as Shanghai in the Yangtze River Delta urban agglomeration and Chongqing in the Chengdu-Chongqing urban agglomeration, began to have a relatively obvious radiation effect on the surrounding cities. The GTFP value of the surrounding cities of such cities was significantly higher than that of other cities. In 2019, the GTFP of Chinese cities is not only rising but also showing an obvious high and low distribution. Several neighboring cities presented similar GTFP levels, and the diffusion effect of provincial capital cities, municipalities directly under the central government, and central cities of urban agglomeration has also been further strengthened.
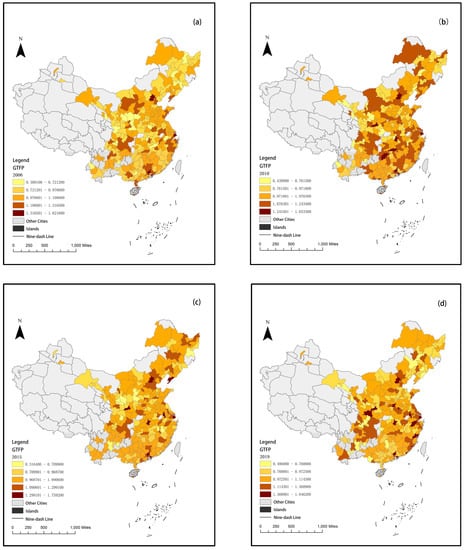
Figure 5.
Spatial distribution characteristics of GTFP in Chinese cities; (a) 2006; (b) 2010; (c) 2015; (d) 2019.
5. Conclusions and Future Research
5.1. Conclusions
This paper measured the urban GTFP of 288 prefecture-level and listed cities in China, and their change trends in time and space are analyzed. First of all, in this paper, the methods of measuring total factor productivity are classified and compared. The non-radial and non-angular super-efficiency SBM-GML index model considering undesirable output that can be used to calculate multi-input and multi-output and unit invariance are selected. The level of China’s urban GTFP from 2006 to 2019 is measured, the dynamic changes of GTFP in each year are calculated, and the sources of changes in GTFP are decomposed. After dividing China into regions according to the east, middle, west, and northeast regions, the differences in GTFPs in the four regions and the time evolution process of GTFPs in the national and regional cities are compared horizontally. Then, the changing trend of the spatial difference of GTFP is analyzed by drawing the kernel density function diagram of GTFP. The spatial distribution trend of China’s GTFP is analyzed by drawing the spatial distribution characteristic map of GTFP. Through the above analysis, the main conclusions of this paper are as follows:
- (1)
- The urban GTFP in China is growing. From 2006 to 2019, the average urban GTFP in China was high, with an average of 1.0317, which increased by 3.17% on average from 2006 to 2019. The annual average value of urban GTFP in China shows a trend of fluctuating growth; the GTFP value in 2007 and 2008 showed an upward trend, the GTFP value fell again in 2009, the GTFP in 2010–2012 was greater than 1, and the GTFP value after 2013 gradually increases stably. From a regional perspective, the urban GTFP in the east, middle, west, and northeast rose from 1.0693, 0.9756, 0.9297, and 0.9359 in 2006 to 1.0923, 1.0378, 0.9841, and 0.9552 in 2019, respectively. During the study period, the mean value of urban GTFP in the eastern region was the highest, followed by the central region, then the western region, and finally, the northeast region, which was 1.0737, 1.0214, 1.0102, and 1.0036, respectively. Among them, the average annual value of GTFP in the eastern cities grows steadily, the urban GTFP in the central and western regions has a relatively consistent change with the national GTFP, showing a cyclical fluctuation growth trend, and the average annual value of GTFP in the northeast region is low, which is below 1 in most years.
- (2)
- From the decomposition results of urban GTFP in China, green technology efficiency (EC) is the main source of contribution to the growth of urban GTFP in China, while green technology progress (TC) plays a weak role in promoting the growth of urban GTFP in China. EC changed from 1.0048 in 2006 to 1.0289 in 2019, with an average of 1.0360. TC changed from 0.9812 in 2006 to 0.9990 in 2019, with an average of 0.9968. The changing trend of EC is consistent with that of GTFP, while the change range of TC is small. Regionally, the east is the only region where the green technology progress index is rising, and also the only region with a TC value greater than 1. The TC and EC values in the east grow steadily. After 2013, the main source of the contribution of GTFP in the central region changed from EC to TC. The TC value in the western and northeastern regions is less than 1 in most years, and the main source of the increase in GTFP is EC.
- (3)
- Based on the spatial change trend of urban GTFP in China, there are significant differences in the GTFP of the eastern, central, western, and northeastern regions. According to the kernel density curve of GTFP, it can be seen that the differences in GTFP in cities across China are obvious, but the degree of differences is gradually decreasing. The GTFP in the eastern region has the characteristics of spatial disequilibrium of polarization and low-value aggregation. There are also obvious differences in GTFP in the central region, and the degree of differences is gradually increasing. The GTFP level in western cities shows the characteristics of first high-value clustering and then low-value clustering, and the degree of differences shows the change process of first increasing and then decreasing. The GTFP level in northeast China is characterized by two-stage differentiation, and the gap between cities is expanding first and then narrowing. It can be seen from the spatial distribution map of urban GTFP in China that the high value of GTFP is mainly distributed in the eastern coastal cities, provincial capitals, municipalities directly under the central government, and special economic zones.
5.2. Future Research
This paper measured the GTFP in Chinese cities, and analyzed and discussed their temporal and spatial evolution, regional differences, and spatial distribution characteristics. This paper has the following shortcomings, which need to be studied in the future.
Firstly, this paper lacks research on the factors influencing GTFP. In future research, we will focus on the effects of environmental regulation, technological innovation, fiscal policy, finance, economy, industrial structure, and urbanization level on GTFP.
Secondly, the GTFP measurement system constructed in this paper needs to be further optimized. We will refine the types of undesirable outputs in future research and focus on adding greenhouse gases related to carbon emissions to the measurement system.
Author Contributions
Conceptualization, R.Z.; methodology, R.Z.; software, R.Z.; validation, R.Z. and Y.Z.; formal analysis, Y.Z. and R.Z.; resources, R.Z.; data curation, R.Z.; writing—original draft preparation, R.Z. and Y.Z.; writing—review and editing, R.Z. and Y.Z.; visualization, R.Z. and Y.Z.; supervision, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Program of Gansu Province: Key R&D Program (Industrial Category), funder: Science and Technology Department of Gansu Province, funding number: 20YF3GA011.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Publicly available datasets were used in this study. All data come from China City Statistical Yearbook, China Statistical Yearbook on Environment, China Statistical Yearbook, Statistical Yearbook of each prefecture-level city, and Statistical Bulletin on National Economic and Social Development.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Measurement results of GTFP in Chinese cities.
Table A1.
Measurement results of GTFP in Chinese cities.
| City Name | 2006 | 2007 | 2008 | 2009 | 2010 | 2011 | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Beijing | 1.4775 | 1.4855 | 1.4475 | 1.4832 | 1.4392 | 1.4847 | 1.4035 | 1.4736 | 1.4242 | 1.4619 | 1.5090 | 1.4829 | 1.4568 | 1.4226 |
| Tianjing | 1.2695 | 1.2366 | 1.0488 | 1.0481 | 1.0115 | 1.0840 | 1.0642 | 1.0268 | 1.0778 | 1.1611 | 1.1285 | 1.0908 | 1.0820 | 1.2101 |
| Shijiazhuang | 1.0512 | 1.0198 | 1.1389 | 1.0630 | 1.0228 | 0.9908 | 0.9221 | 1.0272 | 1.0949 | 1.0226 | 1.2270 | 1.1642 | 0.9311 | 1.1375 |
| Tangshan | 0.9639 | 0.9637 | 1.0310 | 0.8017 | 1.0297 | 1.0747 | 0.9763 | 1.0125 | 0.9519 | 1.0435 | 0.9187 | 1.1474 | 1.0950 | 0.9881 |
| Handan | 1.0066 | 1.0689 | 1.0611 | 0.9033 | 1.0502 | 1.0588 | 1.0159 | 0.8268 | 0.9845 | 0.9494 | 1.1438 | 1.1846 | 0.9400 | 0.9498 |
| Zhangjiakou | 0.9374 | 0.9201 | 0.9882 | 0.8555 | 1.0397 | 1.0820 | 1.0441 | 0.9833 | 1.0063 | 1.0700 | 1.2472 | 1.0112 | 1.0491 | 1.0159 |
| Baoding | 1.0534 | 1.0577 | 1.0830 | 0.9643 | 1.0980 | 1.0034 | 0.8703 | 1.1079 | 0.9420 | 1.1076 | 1.1634 | 1.0973 | 1.0029 | 1.0544 |
| Cangzhou | 0.9207 | 0.9852 | 1.0567 | 0.9603 | 1.1369 | 0.8938 | 0.9766 | 1.0812 | 0.9928 | 1.1256 | 1.2265 | 1.0915 | 0.9088 | 0.9475 |
| Qinhuangdao | 0.9643 | 1.0280 | 1.0859 | 0.8628 | 1.0695 | 0.8609 | 0.9110 | 1.0801 | 0.9008 | 1.0971 | 1.1075 | 1.1218 | 1.0514 | 0.9991 |
| Xingtai | 1.0627 | 1.0336 | 1.0014 | 0.9514 | 1.0446 | 1.0655 | 1.0143 | 0.9551 | 1.0429 | 1.0646 | 1.0138 | 1.4186 | 1.1471 | 1.0197 |
| Langfang | 1.0002 | 0.9937 | 1.0222 | 0.9406 | 1.1281 | 0.9690 | 1.0033 | 0.9885 | 1.0783 | 1.1467 | 1.1427 | 1.1740 | 1.6424 | 1.0164 |
| Chengde | 1.0406 | 0.9601 | 1.2537 | 0.8848 | 1.0832 | 1.1494 | 1.2274 | 0.9096 | 0.9329 | 1.2022 | 1.0635 | 1.0532 | 1.6343 | 1.1756 |
| Hengshui | 1.0076 | 1.2424 | 1.0059 | 0.9136 | 1.0528 | 1.1248 | 1.0084 | 1.0567 | 0.9400 | 1.0082 | 1.2976 | 1.5966 | 1.0641 | 1.3108 |
| Shanghai | 1.6216 | 1.5076 | 1.5682 | 1.5663 | 1.5108 | 1.5272 | 1.6039 | 1.9739 | 1.7276 | 1.7592 | 1.7614 | 1.7309 | 1.8883 | 1.8462 |
| Nanjing | 1.3165 | 1.3899 | 1.4730 | 1.2897 | 1.2299 | 1.3206 | 1.2040 | 1.2471 | 1.3229 | 1.3670 | 1.3937 | 1.3763 | 1.3198 | 1.3797 |
| Wuxi | 1.0750 | 1.0690 | 1.0860 | 1.0972 | 1.0842 | 1.1440 | 1.0903 | 0.9844 | 0.9246 | 1.0367 | 1.1533 | 1.1615 | 1.1942 | 1.3566 |
| Xuzhou | 1.0925 | 1.1425 | 1.0796 | 1.0615 | 1.0066 | 1.0239 | 0.9145 | 0.9389 | 1.0696 | 1.0367 | 1.0781 | 1.1875 | 1.0355 | 1.0090 |
| Changzhou | 1.0408 | 1.0512 | 1.1232 | 1.0684 | 1.1220 | 1.0449 | 1.0838 | 0.9933 | 1.0262 | 1.0416 | 1.0866 | 1.0106 | 0.9682 | 1.0589 |
| Suzhou (Jiangsu Prov.) | 1.0915 | 1.0803 | 1.2294 | 1.0558 | 1.0846 | 1.0364 | 1.1124 | 1.1223 | 1.2005 | 1.2044 | 1.2983 | 1.2069 | 1.2086 | 1.3609 |
| Nantong | 1.0214 | 1.0872 | 1.0677 | 0.9373 | 1.0925 | 1.0741 | 1.1103 | 0.9523 | 1.0172 | 1.0861 | 1.1611 | 1.2236 | 1.2136 | 1.1343 |
| Lianyungang | 1.0496 | 1.0917 | 1.0339 | 1.0217 | 0.9999 | 0.9661 | 1.0289 | 1.0176 | 0.8059 | 1.1599 | 1.0960 | 1.0187 | 1.0241 | 1.0936 |
| Huaian | 0.9588 | 1.0267 | 0.9638 | 1.0220 | 1.0209 | 1.2168 | 1.0166 | 0.9721 | 1.0157 | 1.0413 | 1.1169 | 1.0246 | 1.0385 | 0.9703 |
| Yancheng | 0.9867 | 1.0168 | 1.0081 | 1.1321 | 1.0091 | 1.1374 | 1.0500 | 0.9573 | 0.9892 | 0.8959 | 1.1363 | 0.9911 | 1.0323 | 1.1531 |
| Yanzhou | 1.0792 | 1.0246 | 1.0046 | 1.0785 | 1.0784 | 1.1485 | 0.9883 | 0.9839 | 1.0419 | 1.0512 | 1.0424 | 1.0314 | 0.9989 | 1.0342 |
| Zhenjiang | 1.0332 | 1.0915 | 1.0444 | 1.0049 | 1.0132 | 0.9718 | 1.1253 | 0.9924 | 1.0177 | 1.0343 | 1.1430 | 1.3268 | 1.2177 | 1.2701 |
| Taizhou (Jiangsu Prov.) | 1.0221 | 1.0242 | 0.9784 | 1.0370 | 1.0591 | 1.1932 | 1.0684 | 0.8407 | 0.9841 | 1.1622 | 1.1290 | 1.0362 | 0.9308 | 0.9810 |
| Suqian | 0.9505 | 1.0234 | 1.0714 | 0.9964 | 0.9568 | 1.1195 | 0.9452 | 0.8617 | 1.0455 | 1.0707 | 1.1381 | 0.9993 | 0.9887 | 1.0298 |
| Hangzhou | 1.2335 | 1.2110 | 1.2219 | 1.2506 | 1.2434 | 1.2425 | 1.2147 | 1.1981 | 1.2809 | 1.2789 | 1.4029 | 1.4612 | 1.5173 | 1.5882 |
| Jiaxing | 1.1156 | 1.0308 | 1.0984 | 0.9823 | 1.0455 | 1.0889 | 1.0102 | 1.0193 | 1.0022 | 1.0652 | 1.3073 | 0.9380 | 1.1053 | 1.1435 |
| Huzhou | 0.9115 | 1.1513 | 1.0541 | 0.9379 | 1.1481 | 1.1233 | 0.9985 | 0.9891 | 1.0088 | 1.0144 | 1.1022 | 1.0471 | 1.0157 | 1.0278 |
| Zhoushan | 0.9728 | 1.2923 | 0.9982 | 0.9571 | 1.0736 | 1.1841 | 1.0122 | 0.9796 | 0.9523 | 1.0018 | 1.1400 | 1.0517 | 1.1087 | 0.9476 |
| Jinhua | 1.2149 | 1.0797 | 1.1367 | 0.9708 | 1.0146 | 1.0351 | 0.8590 | 1.0457 | 1.0550 | 0.9967 | 1.4034 | 0.9117 | 0.9869 | 1.0780 |
| Shaoxing | 1.0329 | 1.0668 | 1.0817 | 0.9203 | 1.0078 | 1.0394 | 1.0582 | 1.0253 | 0.8667 | 0.9915 | 1.1851 | 1.1837 | 1.3074 | 1.2699 |
| Wenzhou | 1.1307 | 1.1419 | 1.1454 | 1.0206 | 1.1053 | 1.0618 | 1.3204 | 1.0683 | 1.0260 | 0.9903 | 1.1095 | 1.2217 | 1.6396 | 0.9960 |
| Taizhou (Zhejiang Prov.) | 1.0947 | 1.0469 | 1.5295 | 0.9975 | 1.1408 | 0.8590 | 0.9679 | 1.0557 | 1.0371 | 0.9313 | 1.1830 | 1.2558 | 1.2014 | 1.1472 |
| Lishui | 1.1426 | 1.1327 | 1.0495 | 1.1109 | 1.0574 | 0.9818 | 1.0322 | 1.0351 | 1.0132 | 1.0047 | 1.0372 | 0.9611 | 1.0428 | 0.9627 |
| Quzhou | 0.9313 | 1.0895 | 1.0202 | 1.0347 | 1.0597 | 1.0320 | 1.0933 | 0.9842 | 0.9025 | 0.9222 | 1.0055 | 1.0496 | 1.1910 | 1.0547 |
| Ningbo | 1.1947 | 1.0489 | 1.0695 | 0.9849 | 1.0601 | 1.0622 | 0.9640 | 1.0631 | 0.9684 | 1.0449 | 1.1448 | 1.0387 | 1.0196 | 1.0172 |
| Fuzhou | 1.0328 | 0.9490 | 1.0497 | 1.0616 | 1.0431 | 0.9738 | 1.0108 | 1.0366 | 1.0369 | 0.9852 | 1.0742 | 0.9867 | 0.9832 | 1.0062 |
| Sanming | 0.9378 | 0.9355 | 1.0184 | 1.0549 | 1.1057 | 1.1757 | 1.0076 | 1.0349 | 1.0407 | 1.1318 | 1.1858 | 1.3395 | 1.1847 | 1.3410 |
| Nanping | 0.9766 | 0.9646 | 0.9390 | 1.0442 | 1.1834 | 1.1678 | 1.0851 | 1.0672 | 1.0220 | 0.9330 | 1.0325 | 1.0258 | 1.0754 | 1.0951 |
| Ningde | 1.0509 | 1.1437 | 0.9223 | 1.0429 | 1.0546 | 1.1519 | 1.0429 | 1.0171 | 1.0364 | 0.9786 | 1.1208 | 1.0037 | 1.0526 | 1.3895 |
| Putian | 1.0456 | 0.9047 | 1.1207 | 0.9291 | 1.0406 | 1.0069 | 0.9437 | 1.0578 | 0.9529 | 1.0219 | 1.1276 | 1.1211 | 1.0017 | 1.0782 |
| Quanzhou | 0.8831 | 0.9889 | 1.0261 | 1.0373 | 1.1299 | 0.8853 | 0.9490 | 1.0468 | 0.9783 | 1.0390 | 1.0850 | 1.0201 | 0.9059 | 1.1281 |
| Zhangzhou | 0.9467 | 0.9702 | 0.8925 | 0.9971 | 1.0289 | 1.0188 | 1.0473 | 0.9677 | 0.9767 | 1.0820 | 1.0242 | 1.0590 | 1.1645 | 1.1834 |
| Longyan | 0.9604 | 0.9049 | 1.0328 | 1.0427 | 1.0742 | 1.0468 | 1.0020 | 1.0128 | 1.0660 | 0.9312 | 1.1666 | 1.0888 | 0.9882 | 1.0368 |
| Xiamen | 1.0074 | 0.9417 | 1.1706 | 1.0887 | 0.9869 | 0.9961 | 1.0303 | 1.0155 | 0.9678 | 1.0325 | 1.1287 | 1.0420 | 1.1303 | 1.5375 |
| Qingdao | 1.1713 | 1.0647 | 1.0903 | 1.0279 | 1.0885 | 1.0441 | 1.0480 | 1.0302 | 0.9845 | 1.0763 | 1.2149 | 1.2141 | 1.3317 | 1.2221 |
| Ji`nan | 1.0546 | 0.9871 | 1.0289 | 1.0058 | 1.0242 | 1.0022 | 1.0385 | 1.0011 | 1.0326 | 1.0174 | 1.0370 | 1.0503 | 1.0311 | 1.0202 |
| Zibo | 0.9989 | 1.0557 | 1.0300 | 0.9808 | 0.9738 | 0.9469 | 1.0085 | 1.0352 | 0.9254 | 0.9808 | 1.0646 | 1.1905 | 1.0614 | 0.8933 |
| Zaozhuang | 1.0788 | 1.1123 | 1.0194 | 1.0462 | 1.0440 | 1.0525 | 1.0351 | 0.9811 | 1.0100 | 0.9947 | 1.1302 | 1.2166 | 0.9843 | 0.8932 |
| Yantai | 1.0792 | 1.1213 | 1.0692 | 1.0530 | 1.0597 | 1.0537 | 1.0417 | 0.9781 | 0.9936 | 0.9909 | 1.1585 | 0.9996 | 0.8735 | 1.1143 |
| Weifang | 1.0608 | 1.0150 | 0.9974 | 0.9957 | 0.9824 | 1.0191 | 0.9952 | 1.0052 | 0.9927 | 1.0535 | 1.0876 | 1.0872 | 0.9685 | 0.8631 |
| Ji’ning | 0.9938 | 0.9801 | 1.0348 | 0.9124 | 0.9552 | 1.0331 | 0.9364 | 0.9318 | 1.0198 | 0.9379 | 1.2360 | 1.0886 | 1.0063 | 1.0118 |
| Linyi | 1.0393 | 0.9918 | 1.0950 | 1.0359 | 0.8846 | 1.1557 | 0.8009 | 0.9138 | 0.8881 | 1.0763 | 1.0386 | 1.0194 | 1.0714 | 1.0221 |
| Tai’an | 1.0563 | 1.0600 | 1.0697 | 1.0368 | 1.0193 | 0.9696 | 1.0376 | 1.1284 | 0.9399 | 1.1037 | 1.1211 | 1.1156 | 0.9511 | 0.8995 |
| Liaocheng | 1.0282 | 0.9358 | 1.1266 | 1.0143 | 0.9620 | 0.9376 | 1.0375 | 0.9937 | 1.1529 | 1.0051 | 1.0266 | 1.0732 | 0.9592 | 0.9585 |
| Heze | 1.0517 | 1.1096 | 0.9982 | 0.9923 | 1.0887 | 1.0796 | 1.1385 | 0.8194 | 0.9169 | 0.9633 | 0.9923 | 1.2767 | 1.1474 | 0.9818 |
| Dezhou | 1.0409 | 1.0783 | 1.0810 | 0.9731 | 0.8808 | 0.9383 | 1.1010 | 1.0269 | 0.9887 | 1.0111 | 1.0507 | 1.1109 | 1.0160 | 0.8643 |
| Binzhou (Shandong Prov.) | 1.0747 | 1.0887 | 1.0701 | 1.0110 | 0.9998 | 1.0302 | 1.1008 | 1.1263 | 0.8093 | 0.8732 | 0.8007 | 1.3188 | 1.0174 | 1.0371 |
| Dongying | 1.0488 | 1.0459 | 1.1283 | 0.9505 | 1.0576 | 1.1647 | 0.9636 | 1.0318 | 0.9919 | 0.9823 | 1.0257 | 0.9845 | 1.0065 | 0.8416 |
| Weihai | 1.0855 | 1.1926 | 1.0895 | 1.0032 | 1.0009 | 0.8988 | 0.9274 | 0.9071 | 0.9040 | 0.9626 | 0.9951 | 1.4412 | 1.1442 | 1.0227 |
| Rizhao | 1.2045 | 0.9138 | 0.9153 | 0.9622 | 1.0787 | 0.9273 | 1.0388 | 0.9684 | 0.9457 | 1.0115 | 1.0303 | 1.0657 | 0.9868 | 0.8251 |
| Laiwu | 1.0025 | 1.1505 | 1.0004 | 0.8861 | 0.9090 | 0.9688 | 0.9502 | 0.9435 | 0.8908 | 0.8982 | 0.8654 | 0.9136 | 0.9677 | 1.0777 |
| Guangzhou | 1.5019 | 1.5396 | 1.6031 | 1.6298 | 1.6533 | 1.6168 | 1.5829 | 1.5714 | 1.5707 | 1.5456 | 1.4181 | 1.4839 | 1.4849 | 1.4897 |
| Shenzhen | 1.5350 | 1.5807 | 1.6026 | 1.7565 | 1.6086 | 1.6263 | 1.6166 | 1.6556 | 1.7091 | 1.6917 | 1.6752 | 1.6837 | 1.9100 | 1.6207 |
| Zhuhai | 0.9884 | 0.9240 | 1.0644 | 0.9848 | 1.0602 | 0.9841 | 0.9906 | 1.1186 | 0.9111 | 1.1087 | 0.8678 | 1.0503 | 1.0324 | 1.0952 |
| Shantou | 1.0149 | 0.9124 | 0.9183 | 1.0418 | 0.9580 | 0.9860 | 0.9230 | 1.0429 | 0.9596 | 1.0444 | 1.0401 | 1.0712 | 1.0265 | 1.3913 |
| Foshan | 1.1531 | 1.0374 | 0.9602 | 1.1733 | 1.1085 | 1.2387 | 0.8137 | 0.8998 | 1.0822 | 1.2144 | 1.7200 | 1.0040 | 0.9974 | 1.0353 |
| Shaoguan | 1.2545 | 1.0681 | 0.9445 | 1.0236 | 1.1828 | 0.9490 | 1.0320 | 0.9681 | 0.8301 | 1.1270 | 1.1514 | 1.0062 | 0.9780 | 0.9506 |
| Heyuan | 0.9334 | 0.9275 | 1.3417 | 0.9554 | 1.1433 | 1.0657 | 1.0318 | 1.0035 | 0.9860 | 0.9799 | 1.0717 | 1.0872 | 1.0077 | 1.0514 |
| Meizhou | 0.9961 | 0.8829 | 1.0458 | 1.2443 | 0.8358 | 1.0622 | 0.9358 | 0.9857 | 0.7275 | 0.9944 | 0.9908 | 0.9719 | 0.9634 | 0.9826 |
| Huizhou | 1.2126 | 0.9241 | 0.8944 | 1.2178 | 0.9539 | 1.0645 | 1.0098 | 1.0425 | 1.0308 | 1.0450 | 1.0435 | 1.0191 | 0.9885 | 0.9597 |
| Shanwei | 0.9112 | 0.8369 | 0.9803 | 1.0856 | 1.0821 | 0.9543 | 0.9309 | 0.9402 | 0.8793 | 1.0710 | 1.1746 | 1.0093 | 1.1551 | 1.0503 |
| Dongguan | 0.9539 | 0.9049 | 1.4156 | 0.7765 | 1.0906 | 1.0213 | 0.9768 | 1.0134 | 0.5104 | 1.1433 | 1.1008 | 1.0743 | 1.4340 | 1.0967 |
| Zhongshan | 1.0969 | 0.8577 | 1.2884 | 0.9767 | 1.0117 | 1.1208 | 1.2052 | 0.7885 | 0.9824 | 1.0455 | 1.0779 | 1.1092 | 1.0222 | 1.0207 |
| Jiangmen | 1.0499 | 0.9201 | 1.0614 | 0.9973 | 0.9705 | 1.0225 | 1.0046 | 0.9885 | 0.9533 | 0.9760 | 1.0429 | 1.1773 | 0.9235 | 1.0295 |
| Yangjiang | 0.9583 | 1.0567 | 1.0372 | 0.9172 | 1.1659 | 0.9655 | 1.0379 | 0.9654 | 0.9183 | 1.1441 | 1.3106 | 0.9627 | 1.2040 | 0.8754 |
| Zhanjiang | 1.1548 | 1.0332 | 1.0061 | 0.9197 | 1.0599 | 1.1202 | 0.9447 | 0.8819 | 0.9824 | 0.9979 | 0.9202 | 1.0311 | 0.9975 | 0.9141 |
| Maoming | 1.0366 | 1.2661 | 1.4890 | 0.9654 | 1.0205 | 1.0152 | 0.9738 | 0.7646 | 0.7294 | 0.9284 | 1.0759 | 1.1605 | 1.1813 | 1.0097 |
| Zhaoqing | 0.9154 | 2.6634 | 0.3633 | 0.9504 | 0.9936 | 1.0252 | 1.0290 | 0.9363 | 1.0993 | 0.9729 | 0.9945 | 1.1230 | 0.9800 | 0.9639 |
| Qingyuan | 1.1537 | 0.8019 | 1.0526 | 1.1120 | 0.9310 | 1.2266 | 1.1827 | 0.8267 | 0.7349 | 0.9819 | 1.0287 | 1.1882 | 0.9158 | 0.8882 |
| Chaozhou | 0.9262 | 1.0072 | 1.1232 | 0.9377 | 1.0448 | 1.1428 | 1.4342 | 0.4266 | 1.0934 | 0.9178 | 1.0657 | 1.0211 | 1.0970 | 0.9798 |
| Jieyang | 0.9518 | 1.2442 | 0.6818 | 0.8724 | 1.0001 | 1.0837 | 1.0363 | 0.4829 | 0.9236 | 0.9611 | 1.0853 | 1.4258 | 1.1583 | 0.9679 |
| Yunfu | 1.1033 | 0.8701 | 0.9047 | 1.1208 | 0.9570 | 1.1008 | 0.7431 | 0.9872 | 1.0420 | 1.0427 | 0.7691 | 1.0968 | 1.0934 | 1.0363 |
| Haikou | 1.1744 | 1.0090 | 0.9761 | 1.0267 | 1.1149 | 1.1610 | 1.1096 | 0.9218 | 1.1820 | 1.0227 | 1.1512 | 1.0672 | 1.1745 | 1.0268 |
| Sanya | 1.2278 | 0.9181 | 1.0520 | 0.9498 | 1.1819 | 0.9481 | 0.9956 | 1.2112 | 0.9465 | 1.2389 | 1.6109 | 0.9626 | 1.1342 | 1.0490 |
| Taiyuan | 1.0120 | 0.9395 | 1.0780 | 1.0378 | 0.9718 | 1.1551 | 0.9682 | 0.9700 | 1.0943 | 0.9406 | 1.0618 | 1.0904 | 1.0774 | 1.0709 |
| Datong | 1.0205 | 1.0235 | 0.9334 | 0.9317 | 0.9833 | 0.9955 | 0.9950 | 0.9509 | 1.0163 | 1.0693 | 1.4656 | 0.9661 | 1.0160 | 1.0078 |
| Yangquan | 0.9003 | 0.9713 | 1.1183 | 0.8975 | 0.8821 | 0.9608 | 0.9223 | 0.8950 | 1.0036 | 1.1488 | 0.9744 | 1.0906 | 1.0330 | 1.2407 |
| Changzhi | 1.0912 | 0.9899 | 1.0690 | 0.8461 | 1.0331 | 1.0673 | 0.9596 | 0.9462 | 0.9923 | 0.9687 | 1.1451 | 1.1692 | 1.1384 | 0.8472 |
| Jincheng | 1.0600 | 0.9045 | 1.0689 | 0.9758 | 1.1148 | 1.0420 | 1.0126 | 0.8978 | 1.0115 | 0.9892 | 0.9864 | 1.1678 | 1.2142 | 1.0390 |
| Shuozhou | 1.0215 | 0.9528 | 0.8169 | 0.9635 | 0.9020 | 1.0483 | 1.0703 | 0.9501 | 0.9790 | 0.8185 | 0.9239 | 0.9836 | 1.0542 | 0.9844 |
| Xinzhou | 1.1584 | 1.2893 | 0.9479 | 0.7671 | 1.1760 | 1.0986 | 1.0304 | 1.0169 | 0.9455 | 1.0801 | 0.9831 | 0.9936 | 0.9767 | 1.0149 |
| Jinzhong | 0.9672 | 1.0296 | 1.0442 | 1.0362 | 1.0253 | 1.1003 | 0.8535 | 0.9350 | 0.9937 | 1.0293 | 1.1684 | 1.0879 | 1.0023 | 1.0273 |
| Lvliang | 1.1282 | 0.9490 | 1.0801 | 0.9403 | 0.9219 | 1.0157 | 1.0127 | 0.6290 | 0.9400 | 0.6852 | 1.0533 | 1.0741 | 0.9377 | 0.9869 |
| Linfen | 0.4063 | 0.9594 | 0.9182 | 0.8564 | 1.1112 | 1.0012 | 1.0059 | 0.7965 | 0.4086 | 0.3744 | 1.0795 | 1.0723 | 1.0313 | 1.0288 |
| Yuncheng (Shanxi Prov.) | 1.0397 | 1.1814 | 1.0799 | 0.8576 | 0.9937 | 1.1758 | 0.9584 | 0.9925 | 1.0578 | 0.9499 | 1.1065 | 1.2619 | 1.0001 | 1.2095 |
| Xuancheng | 0.6862 | 1.5491 | 1.0675 | 1.0145 | 1.0922 | 0.6477 | 0.9836 | 0.7714 | 0.6714 | 0.9363 | 1.2736 | 0.9328 | 0.9746 | 0.9984 |
| Suzhou (Anhui Prov.) | 0.9879 | 1.0206 | 0.9289 | 0.8840 | 1.0263 | 0.8931 | 1.4066 | 0.7246 | 1.1213 | 1.0586 | 1.2008 | 1.0547 | 0.9218 | 0.9949 |
| Chuzhou (Anhui Prov.) | 1.1346 | 0.9197 | 0.9950 | 1.0786 | 1.0866 | 1.1708 | 1.0402 | 1.0400 | 0.9020 | 1.0422 | 1.1934 | 1.0176 | 0.8996 | 1.2589 |
| Chizhou | 1.1360 | 1.0617 | 1.0027 | 1.0152 | 1.0558 | 1.2313 | 1.0150 | 0.8868 | 0.9497 | 1.1856 | 1.2560 | 1.0410 | 1.0907 | 1.1329 |
| Fuyang | 1.1861 | 0.9612 | 1.0425 | 1.0174 | 0.9530 | 1.0062 | 0.9984 | 1.0001 | 0.9741 | 1.0613 | 1.1081 | 0.9882 | 1.0798 | 1.1859 |
| Lu’an | 0.8432 | 1.1653 | 1.0798 | 1.0654 | 0.9286 | 0.9681 | 0.9763 | 0.9924 | 1.1787 | 0.8905 | 1.3350 | 1.0089 | 0.7950 | 1.0611 |
| Hefei | 1.2585 | 1.1828 | 1.1515 | 1.1350 | 1.1279 | 1.2065 | 1.1647 | 1.1836 | 1.0701 | 1.1883 | 1.1204 | 1.0959 | 1.0609 | 1.1506 |
| Bengbu | 0.9427 | 0.9989 | 1.0234 | 0.8916 | 1.0218 | 1.0272 | 0.9672 | 0.9790 | 1.0282 | 1.0303 | 1.0797 | 1.0599 | 1.0370 | 1.0377 |
| Huainan | 1.0004 | 0.9834 | 1.0094 | 0.9690 | 0.7507 | 1.1129 | 1.0322 | 0.8843 | 1.0167 | 1.0426 | 1.1092 | 1.1665 | 1.0014 | 1.0509 |
| Tongling | 1.0415 | 0.8643 | 0.9677 | 1.0493 | 0.8165 | 1.4218 | 1.0859 | 0.8326 | 0.8885 | 1.1098 | 1.2559 | 0.9612 | 0.9131 | 0.8239 |
| Maanshan | 0.9825 | 0.9700 | 0.9814 | 0.9111 | 1.0632 | 1.0263 | 0.9881 | 1.1307 | 0.7572 | 1.0391 | 1.2895 | 1.0135 | 0.9701 | 1.0431 |
| Huaibei | 1.0225 | 1.1472 | 0.9168 | 0.8177 | 0.9554 | 1.1893 | 1.0089 | 0.9788 | 0.9905 | 1.0062 | 1.1811 | 1.1560 | 1.0390 | 0.9686 |
| Wuhu | 1.0836 | 0.9429 | 0.9231 | 0.9682 | 0.9886 | 1.1891 | 1.0349 | 0.8948 | 1.0154 | 0.9857 | 1.1185 | 1.0359 | 0.9891 | 1.0137 |
| Anqing | 1.0823 | 0.9044 | 0.9936 | 1.0317 | 1.0286 | 1.0191 | 1.1216 | 0.9067 | 1.0470 | 1.0320 | 1.1192 | 1.0511 | 0.9952 | 1.1645 |
| Huangshan | 1.0374 | 1.0414 | 1.0519 | 1.0225 | 0.9323 | 1.0584 | 1.0701 | 1.0473 | 1.0258 | 0.9945 | 1.0189 | 1.0336 | 0.9578 | 0.9667 |
| Bozhou | 0.8133 | 1.0221 | 1.0467 | 0.8442 | 0.8088 | 1.1043 | 1.2199 | 0.9687 | 0.8874 | 0.9712 | 1.2089 | 0.9645 | 1.1238 | 1.8171 |
| Nanchang | 1.1345 | 1.0739 | 1.0667 | 0.7277 | 0.9868 | 1.0393 | 1.0704 | 0.9301 | 1.0506 | 1.0063 | 1.0141 | 1.0848 | 1.1266 | 0.9661 |
| Jingdezhen | 1.0019 | 0.5267 | 0.8971 | 0.9535 | 0.5227 | 1.0089 | 1.0063 | 0.5587 | 0.9134 | 0.9777 | 0.9292 | 0.6068 | 0.5802 | 0.8730 |
| Pingxiang | 0.9371 | 0.8466 | 0.8669 | 0.9273 | 1.0763 | 1.1528 | 0.9891 | 0.9558 | 1.0364 | 1.0484 | 1.0827 | 1.2476 | 1.2073 | 1.0933 |
| Jiujiang | 0.3334 | 1.0075 | 1.0099 | 0.9395 | 1.1052 | 1.1339 | 0.9273 | 0.9743 | 0.9638 | 0.9656 | 1.2192 | 1.0425 | 1.0973 | 1.0397 |
| Xinyu | 1.0222 | 0.8768 | 0.8441 | 1.2045 | 1.0404 | 1.2367 | 1.0718 | 0.9593 | 0.8431 | 0.9655 | 1.1372 | 1.1718 | 0.9858 | 1.0231 |
| Yingtan | 0.9481 | 1.1679 | 0.9402 | 1.0677 | 1.0248 | 1.0873 | 1.2025 | 0.8734 | 0.9678 | 1.1016 | 1.2173 | 0.9605 | 1.0423 | 0.8772 |
| Ganzhou | 1.0375 | 1.2773 | 0.8382 | 1.1252 | 1.1572 | 0.9422 | 0.9719 | 0.9525 | 0.9301 | 0.9843 | 1.1078 | 1.3325 | 1.0498 | 1.0213 |
| Yichun | 0.9600 | 0.9152 | 0.9985 | 0.9560 | 1.0828 | 1.0460 | 1.0944 | 0.9721 | 1.0203 | 0.9437 | 1.0714 | 1.0525 | 1.1002 | 1.1217 |
| Shangrao | 1.0217 | 1.0154 | 1.1014 | 1.4446 | 1.1652 | 1.0823 | 1.6528 | 0.5985 | 1.0900 | 0.6732 | 0.9077 | 1.1790 | 1.0248 | 0.9233 |
| Ji’an | 1.0700 | 0.9637 | 0.8961 | 1.0093 | 1.0015 | 0.9903 | 1.2781 | 1.0239 | 0.8324 | 0.9557 | 1.1075 | 1.0023 | 0.9876 | 1.0530 |
| Fuzhou (Jiangxi Prov.) | 0.8689 | 0.8665 | 0.9150 | 1.0049 | 1.0015 | 1.1676 | 0.7815 | 1.0015 | 1.0550 | 0.9710 | 1.0613 | 1.0626 | 0.8689 | 0.9796 |
| Zhengzhou | 1.1080 | 1.0662 | 1.0893 | 1.0885 | 1.0290 | 1.1283 | 1.1616 | 1.0831 | 1.1841 | 1.1928 | 1.2140 | 1.1477 | 1.1680 | 1.2406 |
| Kaifeng | 0.9848 | 0.9727 | 0.9426 | 0.9858 | 0.9968 | 0.9458 | 1.0313 | 0.9329 | 0.9342 | 1.0276 | 1.3220 | 1.3546 | 1.1010 | 1.6949 |
| Luoyang | 0.9150 | 0.9201 | 0.9847 | 0.9191 | 0.9833 | 1.0819 | 1.0891 | 1.0095 | 1.1601 | 0.9908 | 1.2999 | 1.1188 | 1.0909 | 1.0226 |
| Pingdingshan | 0.8847 | 1.0691 | 1.1385 | 0.8621 | 1.0281 | 1.0100 | 0.9207 | 0.9406 | 1.0200 | 1.0165 | 1.3803 | 1.0949 | 1.0526 | 1.0838 |
| Anyang | 0.9444 | 0.9563 | 1.0523 | 0.9333 | 1.0013 | 1.1688 | 0.9274 | 1.0082 | 0.9730 | 1.1491 | 1.1809 | 1.0462 | 1.1077 | 0.9942 |
| Puyang | 1.0463 | 0.9247 | 1.0371 | 0.9042 | 0.8875 | 0.9714 | 0.8777 | 1.4004 | 0.9923 | 0.9828 | 1.2773 | 1.1592 | 1.0385 | 0.9198 |
| Xinxiang | 0.9711 | 0.9409 | 1.0268 | 1.0490 | 1.0907 | 1.1107 | 1.0343 | 0.9760 | 0.9295 | 0.9989 | 1.4813 | 1.0120 | 1.0270 | 1.0384 |
| Jiaozuo | 0.9362 | 0.9393 | 0.9826 | 0.9309 | 1.1504 | 1.1320 | 0.9559 | 0.9704 | 1.0656 | 1.0565 | 1.2622 | 1.0828 | 1.0556 | 1.0401 |
| Hebi | 0.8881 | 0.8331 | 0.9729 | 0.9146 | 1.0310 | 1.3241 | 1.0035 | 0.9851 | 0.9002 | 1.0366 | 1.2469 | 1.0899 | 1.1078 | 1.0127 |
| Xuchang | 0.9431 | 1.0150 | 0.9888 | 1.0303 | 0.9703 | 0.9719 | 1.0519 | 0.8892 | 1.0622 | 1.0127 | 1.0873 | 1.2128 | 0.9395 | 0.9433 |
| Luohe | 1.0621 | 0.9837 | 1.0056 | 0.9281 | 0.9540 | 1.0230 | 1.1466 | 1.0039 | 0.8308 | 0.4286 | 1.1946 | 0.8008 | 0.9998 | 0.9025 |
| Sanmenxia | 1.0500 | 1.2824 | 1.0604 | 1.0200 | 1.0805 | 1.0739 | 1.1270 | 1.0504 | 1.0394 | 0.9145 | 1.0265 | 1.1840 | 0.9586 | 1.0226 |
| Nanyang | 0.9434 | 1.0233 | 1.0076 | 0.9749 | 1.0379 | 0.9725 | 1.0081 | 0.9927 | 0.9106 | 1.1490 | 1.6421 | 1.0730 | 1.0973 | 1.0217 |
| Shangqiu | 0.9602 | 1.0782 | 1.0499 | 1.0192 | 1.1010 | 0.9924 | 1.0364 | 1.0093 | 1.0477 | 1.0039 | 1.2560 | 0.8826 | 0.9738 | 1.0871 |
| Xinyang | 0.8799 | 0.9935 | 1.3640 | 0.8924 | 1.0786 | 1.1323 | 1.3276 | 0.9196 | 0.9508 | 1.0697 | 1.0722 | 0.9301 | 1.0768 | 1.0291 |
| Zhoukou | 0.5779 | 0.8575 | 1.0221 | 0.9363 | 1.0257 | 0.9961 | 1.1498 | 0.9526 | 1.1155 | 0.9567 | 1.0839 | 0.9798 | 1.0083 | 1.1483 |
| Zhumadian | 1.0270 | 0.9457 | 1.0226 | 1.0119 | 1.0331 | 0.9798 | 0.9910 | 0.9568 | 0.9932 | 1.0194 | 1.0501 | 0.9945 | 0.9604 | 1.0363 |
| Wuhan | 1.2198 | 1.3980 | 1.3031 | 1.1792 | 1.3282 | 1.2733 | 1.2955 | 1.3321 | 1.3111 | 1.3483 | 1.3397 | 1.3904 | 1.4412 | 1.4032 |
| Huangshi | 0.9733 | 1.0007 | 1.0304 | 0.8449 | 0.8884 | 1.0709 | 1.1023 | 0.8803 | 0.9134 | 1.0103 | 1.0032 | 1.0468 | 1.0900 | 1.0012 |
| Shiyan | 0.9813 | 1.0054 | 1.0134 | 0.9890 | 0.6336 | 1.0092 | 1.0119 | 0.9740 | 0.9461 | 0.9887 | 1.1396 | 1.0672 | 1.1135 | 1.0399 |
| Jingzhou | 1.0112 | 1.0051 | 0.9689 | 0.9386 | 0.9758 | 1.1277 | 0.9448 | 1.0030 | 0.9708 | 0.9935 | 1.0029 | 1.1918 | 1.0373 | 1.0835 |
| Yichang | 1.0319 | 1.0298 | 1.0509 | 1.0096 | 0.9691 | 1.0726 | 1.1044 | 1.0950 | 0.9416 | 0.9477 | 1.0062 | 1.0091 | 0.9945 | 0.9986 |
| Xiangyang | 1.0060 | 1.0148 | 0.9434 | 1.1516 | 0.6879 | 1.3302 | 0.8531 | 1.0144 | 0.9822 | 1.1362 | 1.0648 | 1.1166 | 0.9998 | 0.9796 |
| Ezhou | 0.9529 | 0.9421 | 1.0662 | 0.8586 | 0.8974 | 1.1480 | 0.9580 | 0.9821 | 0.8890 | 0.9617 | 1.0295 | 1.1147 | 0.8653 | 1.0286 |
| Jingmen | 0.9449 | 0.9647 | 0.8985 | 0.8886 | 0.9218 | 0.9954 | 0.9963 | 1.0075 | 0.9902 | 1.0037 | 1.0931 | 1.0703 | 0.9678 | 0.9621 |
| Xiaogan | 0.6652 | 1.0023 | 0.9254 | 0.9372 | 0.6838 | 0.9843 | 1.0416 | 0.7904 | 0.9288 | 1.0504 | 1.1735 | 0.9671 | 0.9532 | 1.0498 |
| Huanggang | 0.9518 | 1.0286 | 1.1126 | 1.0377 | 1.1032 | 0.9984 | 0.8849 | 1.0039 | 1.0251 | 1.0265 | 1.2975 | 1.0264 | 0.8213 | 0.8970 |
| Xianning | 0.9321 | 0.8646 | 1.0088 | 0.9138 | 1.0539 | 1.4491 | 0.8575 | 0.8785 | 1.0713 | 1.0022 | 1.0346 | 1.0526 | 1.0114 | 1.0147 |
| Suizhou | 0.8302 | 0.8046 | 0.7906 | 0.5646 | 1.0154 | 1.0048 | 1.1018 | 0.9475 | 1.0375 | 1.0267 | 1.0896 | 0.7083 | 1.0735 | 0.6267 |
| Changshan | 1.1414 | 1.1333 | 1.2623 | 1.1414 | 1.2989 | 1.2194 | 1.1809 | 1.2001 | 1.2964 | 1.2966 | 1.3161 | 1.3058 | 1.3038 | 1.3483 |
| Zhuzhou | 1.0745 | 0.9842 | 0.9987 | 0.8370 | 1.0800 | 1.3700 | 1.0257 | 0.9445 | 1.0328 | 0.9938 | 1.0720 | 1.0405 | 1.0041 | 1.0391 |
| Xiangtan | 1.0196 | 0.9667 | 0.9838 | 0.8550 | 0.9465 | 1.2170 | 0.9873 | 0.9675 | 0.9041 | 1.0277 | 1.1185 | 1.1971 | 1.1334 | 1.0486 |
| Hengyang | 1.0119 | 1.0728 | 0.9849 | 0.8863 | 0.9153 | 0.8555 | 1.1590 | 0.9382 | 0.9755 | 0.9583 | 1.1051 | 1.0328 | 1.0087 | 1.0903 |
| Shaoyang | 0.9191 | 0.9518 | 1.2065 | 0.8755 | 1.3026 | 1.0297 | 1.0122 | 0.9380 | 1.0745 | 1.0103 | 1.0075 | 1.0563 | 1.0502 | 0.9444 |
| Yueyang | 1.0343 | 0.9112 | 0.9517 | 0.9023 | 1.0436 | 1.0461 | 1.0319 | 0.9405 | 1.0506 | 1.0570 | 1.0065 | 0.9870 | 1.0056 | 1.0417 |
| Changde | 0.8980 | 0.9537 | 0.9864 | 0.9945 | 1.1218 | 1.0396 | 0.8896 | 0.9520 | 0.9694 | 1.0045 | 1.0055 | 0.9535 | 0.9519 | 1.0265 |
| Zhangjiajie | 1.0511 | 1.0362 | 1.2086 | 0.7793 | 1.0146 | 1.0154 | 1.2220 | 0.8569 | 0.9981 | 1.0458 | 1.0877 | 0.9983 | 1.0057 | 0.6831 |
| Yiyang | 0.9143 | 0.9468 | 0.9610 | 0.9758 | 1.0180 | 1.1379 | 1.0055 | 0.9224 | 1.3648 | 0.8275 | 1.0308 | 0.9457 | 1.0482 | 1.0048 |
| Yongzhou | 0.8872 | 0.8553 | 0.9484 | 0.8762 | 1.1853 | 1.0428 | 1.2128 | 1.0078 | 1.0129 | 1.0700 | 1.0018 | 1.0026 | 1.0091 | 0.5685 |
| Binzhou (Shannxi Prov.) | 1.0632 | 0.9937 | 0.9360 | 0.8925 | 1.0721 | 1.0728 | 1.0589 | 1.0097 | 1.0047 | 1.0008 | 1.0039 | 0.9688 | 0.9380 | 0.9065 |
| Loudi | 1.1065 | 1.0450 | 1.1442 | 0.6791 | 1.1319 | 1.4629 | 0.9919 | 0.6065 | 1.2172 | 0.8868 | 1.0098 | 1.1614 | 0.9838 | 0.9149 |
| Huaihua | 0.9231 | 0.9990 | 0.9597 | 0.8488 | 1.1330 | 1.0506 | 1.1986 | 1.0083 | 0.9249 | 1.0225 | 1.0414 | 1.0480 | 1.0038 | 0.9878 |
| Ulanqab | 1.0214 | 1.0200 | 1.0149 | 1.0907 | 0.9179 | 0.9447 | 0.9427 | 0.9707 | 0.9487 | 0.9025 | 0.8944 | 0.9187 | 1.0580 | 0.9268 |
| Ordos | 1.1570 | 1.4055 | 1.7189 | 0.8186 | 1.2099 | 0.9997 | 1.1236 | 0.8983 | 0.9896 | 1.0261 | 1.0112 | 0.9961 | 1.0105 | 1.0548 |
| Bayan Nur | 0.8595 | 0.9505 | 1.0761 | 0.9149 | 1.1454 | 1.4615 | 0.6671 | 1.0811 | 1.0391 | 0.9887 | 1.1544 | 0.9110 | 1.1450 | 0.9960 |
| Hohhot | 1.1974 | 1.3981 | 1.0157 | 1.0525 | 0.9303 | 1.0255 | 1.2126 | 0.9579 | 0.8096 | 1.0214 | 1.0080 | 1.0381 | 1.1067 | 0.8903 |
| Baotou | 0.9526 | 1.0061 | 1.0312 | 1.0602 | 0.9707 | 0.9599 | 1.0867 | 0.9311 | 1.1185 | 1.0750 | 1.0519 | 0.9546 | 0.9971 | 0.9633 |
| Wuhai | 0.9523 | 0.9578 | 1.1063 | 0.8972 | 0.9125 | 0.9821 | 0.9469 | 0.9690 | 1.0275 | 0.9249 | 1.8616 | 0.9150 | 1.0650 | 1.0293 |
| Naning | 1.1216 | 1.0264 | 0.9600 | 0.9420 | 1.0158 | 0.9345 | 1.1068 | 1.0655 | 1.1647 | 0.8591 | 1.0757 | 1.0502 | 0.9678 | 0.9913 |
| Liuzhou | 1.1011 | 1.0226 | 1.0397 | 0.8978 | 0.9824 | 1.0844 | 1.0872 | 0.9466 | 0.9897 | 1.0490 | 1.0221 | 1.0439 | 1.1370 | 1.0052 |
| Guilin | 0.9601 | 0.8511 | 1.1113 | 1.0269 | 0.9893 | 1.0264 | 1.0156 | 1.0491 | 1.0074 | 1.0001 | 0.9799 | 0.9431 | 1.0419 | 0.9819 |
| Wuzhou | 0.9254 | 0.9779 | 0.9944 | 0.7966 | 1.0019 | 1.1692 | 1.1661 | 1.0722 | 1.1437 | 1.0109 | 1.0822 | 1.0152 | 0.9163 | 0.8682 |
| Beihai | 0.9406 | 1.8014 | 0.3221 | 0.9007 | 1.1000 | 1.1643 | 1.0021 | 1.1527 | 1.0309 | 0.9388 | 1.0397 | 1.0273 | 0.9737 | 1.0251 |
| Fangchenggang | 0.8599 | 0.9149 | 1.0286 | 0.8339 | 1.0951 | 1.0764 | 0.9597 | 1.1445 | 0.9802 | 0.9649 | 1.2241 | 1.1951 | 1.1306 | 1.1229 |
| Qinzhou | 0.9215 | 1.1936 | 0.7428 | 0.9056 | 1.0748 | 1.0703 | 1.2863 | 1.0426 | 0.9933 | 1.0723 | 1.0243 | 1.0514 | 1.0369 | 0.9656 |
| Guigang | 0.6121 | 0.9950 | 0.9663 | 0.9000 | 0.9987 | 1.2552 | 0.9573 | 1.0125 | 0.9923 | 0.9433 | 0.9168 | 0.8596 | 1.0318 | 0.9504 |
| Yulin | 0.9069 | 0.9479 | 1.1465 | 0.9356 | 1.0162 | 1.0037 | 1.0497 | 1.0004 | 0.9838 | 1.0114 | 1.0167 | 1.0975 | 0.8980 | 0.8465 |
| Hezhou | 0.7514 | 0.9655 | 0.9227 | 0.8555 | 1.0025 | 1.0855 | 1.0549 | 1.0632 | 0.8107 | 1.0056 | 0.9101 | 1.0098 | 1.1047 | 1.0868 |
| Baise | 0.8667 | 1.0861 | 0.9343 | 0.9341 | 1.1095 | 1.6421 | 0.6668 | 1.0102 | 1.1545 | 1.0685 | 1.0097 | 1.0557 | 0.8822 | 1.0267 |
| Hechi | 1.0169 | 1.0498 | 1.1078 | 0.9608 | 1.0334 | 1.0179 | 2.7083 | 0.4249 | 1.0829 | 1.0323 | 1.0297 | 0.9549 | 1.0826 | 1.0904 |
| Laibin | 0.9013 | 1.0340 | 0.8835 | 0.9918 | 0.9754 | 1.1546 | 1.0347 | 1.0496 | 1.1686 | 1.0482 | 1.0073 | 1.2637 | 0.9376 | 0.9630 |
| Chongzuo | 0.8488 | 0.9313 | 0.9276 | 0.8804 | 0.9841 | 1.1564 | 0.9803 | 1.1548 | 1.0854 | 1.0017 | 1.0078 | 0.9499 | 1.0039 | 0.4860 |
| Chongqing | 1.1221 | 1.1581 | 1.1277 | 1.0632 | 1.1841 | 1.2267 | 1.1787 | 1.0988 | 1.0825 | 1.2117 | 1.1893 | 1.2042 | 1.2106 | 1.2038 |
| Chengdu | 1.1916 | 1.1029 | 1.1551 | 1.0860 | 1.1668 | 1.2019 | 1.1440 | 1.0923 | 1.2164 | 1.2040 | 1.2550 | 1.2813 | 1.2007 | 1.2299 |
| Zigong | 1.0409 | 0.9749 | 0.9365 | 1.0409 | 1.0585 | 1.2003 | 1.0305 | 1.0732 | 1.0379 | 1.0502 | 1.0532 | 1.0185 | 1.0737 | 1.1674 |
| Panzhihua | 1.0459 | 1.0285 | 1.0280 | 0.8473 | 0.8812 | 0.9881 | 1.0027 | 1.0352 | 1.0180 | 1.0237 | 1.0302 | 1.0596 | 0.9574 | 0.9633 |
| Luzhou | 0.9133 | 1.0260 | 1.0575 | 0.9704 | 1.0320 | 1.1842 | 1.0892 | 0.9353 | 1.0128 | 1.0364 | 1.0565 | 1.1332 | 0.9314 | 1.0627 |
| Deyang | 0.9746 | 0.9778 | 1.0059 | 0.7007 | 1.1223 | 1.1366 | 1.0847 | 1.0698 | 0.9389 | 1.0699 | 1.1964 | 1.0384 | 1.0641 | 0.9458 |
| Mianyang | 1.0125 | 0.9872 | 0.8738 | 0.7891 | 1.1542 | 1.1629 | 1.1259 | 0.9586 | 1.0207 | 0.9900 | 1.1144 | 1.1144 | 1.1344 | 1.3374 |
| Guangyuan | 0.9559 | 1.7970 | 0.5316 | 0.7578 | 1.0420 | 1.2852 | 1.5997 | 1.0605 | 1.0753 | 0.9734 | 1.1107 | 1.1466 | 0.8399 | 1.0475 |
| Suining | 0.5546 | 1.1593 | 1.0278 | 0.7635 | 0.4399 | 1.2090 | 1.5766 | 0.5166 | 0.9453 | 0.9536 | 1.0074 | 0.9497 | 1.6895 | 0.5149 |
| Neijiang | 1.0194 | 1.1206 | 1.0326 | 1.0334 | 1.1034 | 1.2226 | 0.9738 | 1.0912 | 0.9955 | 0.8767 | 1.0280 | 1.3167 | 0.9352 | 1.0366 |
| Leshan | 0.9331 | 1.0139 | 1.0969 | 0.8420 | 0.9849 | 1.2091 | 1.0315 | 0.9841 | 0.9794 | 0.9859 | 1.0451 | 1.0929 | 1.1500 | 1.1477 |
| Nanchong | 1.1607 | 1.0505 | 0.9701 | 1.0218 | 1.0061 | 1.0316 | 1.0983 | 0.9858 | 1.0439 | 1.0524 | 0.9642 | 1.1042 | 1.6695 | 0.6638 |
| Yibin | 0.9360 | 1.1817 | 1.0326 | 0.9648 | 0.9701 | 1.2042 | 1.0401 | 0.9504 | 1.0193 | 1.0522 | 1.1061 | 1.3398 | 0.9477 | 1.1591 |
| Guang’an | 1.1685 | 0.8840 | 1.0357 | 1.0314 | 1.0197 | 1.1190 | 1.1079 | 0.7650 | 1.0926 | 1.0031 | 0.9203 | 1.3767 | 1.1395 | 0.9603 |
| Dazhou | 0.9761 | 1.2840 | 1.1370 | 0.9398 | 1.1589 | 1.0771 | 1.0106 | 1.0732 | 0.6747 | 1.0061 | 0.9606 | 0.9599 | 1.0903 | 1.2838 |
| Ziyang | 0.6438 | 1.0005 | 1.0370 | 0.9736 | 0.8848 | 1.6815 | 1.1014 | 0.9333 | 0.9672 | 0.8391 | 0.6327 | 0.9651 | 1.2930 | 0.6359 |
| Meishan | 0.9940 | 0.9743 | 1.0558 | 1.0234 | 0.9556 | 1.0862 | 1.0373 | 1.0672 | 1.1451 | 1.0507 | 0.9214 | 1.0043 | 1.0400 | 1.0129 |
| Bazhong | 0.8934 | 1.0391 | 0.7955 | 0.9618 | 1.1650 | 1.2033 | 1.0165 | 1.0102 | 0.9384 | 0.5512 | 0.4759 | 0.5732 | 0.9175 | 0.6113 |
| Ya’an | 0.9419 | 0.9867 | 0.9154 | 0.8904 | 0.6838 | 1.2789 | 0.9393 | 1.0788 | 0.7551 | 0.9949 | 1.1852 | 1.0462 | 1.0142 | 0.9898 |
| Guiyang | 1.0097 | 0.9553 | 1.1165 | 0.9648 | 1.0534 | 0.9722 | 0.8932 | 1.0509 | 0.9826 | 1.0189 | 1.0293 | 0.9452 | 0.9835 | 0.9882 |
| Liupanshui | 1.0317 | 1.1220 | 1.3217 | 1.0693 | 1.0651 | 1.0531 | 0.8017 | 0.9345 | 0.9635 | 0.9507 | 1.1381 | 0.9391 | 1.1864 | 0.8247 |
| Zunyi | 1.0618 | 1.0838 | 0.7758 | 0.9511 | 1.1102 | 0.9468 | 0.9091 | 1.0482 | 0.9910 | 1.0889 | 1.0819 | 1.0642 | 1.0577 | 1.1478 |
| Anshun | 0.6305 | 0.4917 | 1.0443 | 0.7200 | 0.6433 | 0.5750 | 0.9492 | 0.8937 | 0.8509 | 0.6198 | 1.4599 | 1.0013 | 1.2850 | 0.7290 |
| Bijie | 0.8173 | 1.4313 | 0.8763 | 1.0594 | 0.9942 | 1.4983 | 0.7769 | 1.2686 | 1.0648 | 0.9830 | 0.9860 | 1.1655 | 1.1644 | 1.1999 |
| Tongren | 1.0408 | 1.0360 | 1.0563 | 1.0635 | 1.0384 | 1.0639 | 0.8544 | 0.9281 | 1.1697 | 1.1808 | 1.0927 | 0.9844 | 1.1270 | 1.1438 |
| Kunming | 1.0616 | 1.2542 | 0.9713 | 0.9924 | 0.9172 | 1.1007 | 1.2102 | 0.9842 | 1.0758 | 1.0090 | 0.9445 | 1.0248 | 0.9891 | 1.1557 |
| Zhaotong | 1.1693 | 0.9633 | 1.0748 | 0.9541 | 1.0473 | 0.9867 | 1.0999 | 1.0478 | 1.0060 | 0.9795 | 1.1468 | 1.1025 | 0.9259 | 1.0529 |
| Qujing | 1.0353 | 1.1105 | 1.1199 | 1.1125 | 1.0596 | 1.0056 | 0.9206 | 0.8643 | 0.9881 | 0.6626 | 0.9815 | 1.1032 | 1.0378 | 0.5207 |
| Yuxi | 0.9472 | 1.0482 | 1.0353 | 0.9277 | 0.8912 | 1.1105 | 1.0730 | 0.7571 | 0.9943 | 0.9972 | 0.9241 | 1.0627 | 0.9731 | 0.6156 |
| Pu’er | 0.8589 | 0.9206 | 1.0308 | 0.9237 | 0.9354 | 0.7383 | 1.0945 | 1.0679 | 0.9869 | 1.0242 | 1.0685 | 1.0401 | 0.9974 | 1.2206 |
| Baoshan | 0.4361 | 0.8520 | 1.0020 | 0.5381 | 0.6352 | 0.9289 | 0.7222 | 0.9873 | 0.7368 | 0.8615 | 1.0321 | 1.6001 | 0.9626 | 1.0374 |
| Lijiang | 1.0390 | 1.0009 | 0.9810 | 0.8409 | 1.0349 | 0.7250 | 1.0698 | 1.0705 | 1.1567 | 1.0702 | 1.0379 | 1.1168 | 0.9582 | 0.9697 |
| Lincang | 1.0031 | 1.0356 | 0.9954 | 0.4469 | 1.0459 | 1.0505 | 0.9363 | 1.0489 | 0.5453 | 1.0640 | 0.9974 | 1.0251 | 1.0223 | 1.0498 |
| Xi’an | 1.2914 | 1.2651 | 1.3767 | 1.3101 | 1.3505 | 1.4304 | 1.4537 | 1.4131 | 1.4311 | 1.4207 | 1.4013 | 1.4597 | 1.4996 | 1.5156 |
| Tongchuan | 1.1694 | 0.9345 | 0.9985 | 1.0555 | 1.0718 | 1.0636 | 0.8764 | 1.0461 | 1.0102 | 0.9669 | 1.1219 | 1.0380 | 0.7982 | 0.9786 |
| Baoji | 0.8720 | 1.0555 | 0.8385 | 1.0478 | 1.1850 | 1.0952 | 1.0236 | 0.9101 | 0.8219 | 0.9403 | 1.1239 | 1.0884 | 1.0388 | 0.9798 |
| Xianyang | 1.0229 | 0.9624 | 1.0374 | 0.7805 | 1.0355 | 1.0448 | 1.1838 | 0.9253 | 1.0137 | 0.9547 | 1.3664 | 0.9238 | 1.0116 | 0.9503 |
| Weinan | 0.3980 | 1.0220 | 0.8164 | 1.0361 | 0.9823 | 0.9925 | 1.0600 | 1.0453 | 0.9666 | 0.9930 | 0.9708 | 1.2880 | 1.0486 | 0.9582 |
| Hanzhong | 0.8401 | 1.0691 | 1.0061 | 0.8863 | 0.9328 | 1.1238 | 0.9860 | 1.1470 | 0.9940 | 0.9565 | 0.9257 | 1.2404 | 1.5180 | 1.4382 |
| Ankang | 0.9852 | 0.8231 | 0.9527 | 1.0166 | 1.0647 | 1.0525 | 1.0203 | 0.9597 | 1.0361 | 1.0491 | 1.3997 | 0.8776 | 1.3040 | 1.0518 |
| Shangluo | 0.6877 | 0.9741 | 1.1225 | 1.0420 | 0.9631 | 1.0039 | 1.0184 | 1.0243 | 0.9812 | 1.0519 | 0.9857 | 0.9469 | 1.1861 | 0.9497 |
| Yan’an | 0.7089 | 1.0077 | 1.0603 | 0.8880 | 1.0276 | 1.1282 | 1.0780 | 1.0504 | 0.9659 | 0.8036 | 1.0923 | 1.0391 | 1.1044 | 0.8833 |
| Yulin | 1.0514 | 1.0502 | 0.8836 | 0.9340 | 1.1962 | 1.1122 | 1.6075 | 0.6770 | 0.8062 | 0.9923 | 1.1026 | 1.0035 | 1.0861 | 1.0115 |
| Lanzhou | 1.0676 | 1.0996 | 1.0948 | 1.1233 | 1.0586 | 0.9824 | 1.1335 | 1.1326 | 1.1135 | 1.0509 | 1.1152 | 1.1904 | 1.1879 | 1.1673 |
| Jiayuguan | 1.0752 | 1.1139 | 1.0956 | 0.9662 | 0.9893 | 1.0165 | 1.0614 | 0.9413 | 0.9616 | 0.8904 | 0.9013 | 1.2454 | 1.1268 | 0.9011 |
| Jinchang | 0.9435 | 1.2332 | 0.8565 | 1.0821 | 0.9519 | 0.9300 | 0.9026 | 1.2705 | 0.7750 | 1.0855 | 0.9024 | 0.8754 | 0.9824 | 1.0748 |
| Baiyin | 0.9316 | 1.0591 | 0.9978 | 0.9352 | 0.9870 | 1.1571 | 1.0311 | 1.1684 | 1.0248 | 1.0271 | 1.1759 | 1.0550 | 0.9538 | 0.9189 |
| Tianshui | 0.9090 | 0.8218 | 1.0005 | 1.0782 | 0.9450 | 1.0129 | 0.9886 | 1.0352 | 1.0403 | 1.1531 | 1.1044 | 1.0728 | 1.0080 | 0.9177 |
| Jiuquan | 1.0062 | 0.9623 | 1.0162 | 1.0354 | 0.9936 | 0.9256 | 0.9659 | 1.1151 | 0.8902 | 0.9444 | 1.3662 | 1.0114 | 0.9566 | 0.9553 |
| Zhangye | 0.9244 | 1.1146 | 1.1183 | 1.2836 | 0.7026 | 1.1015 | 0.8480 | 0.9982 | 1.0753 | 0.9236 | 0.9729 | 1.0999 | 0.8870 | 0.7469 |
| Wuwei | 1.0497 | 0.8970 | 1.0936 | 0.9523 | 0.9439 | 1.2318 | 0.9826 | 0.5385 | 1.0525 | 1.0385 | 1.0568 | 1.0269 | 1.0628 | 1.0048 |
| Dingxi | 0.8863 | 0.8607 | 0.9333 | 0.9364 | 0.9597 | 0.6506 | 1.0084 | 1.0004 | 0.4550 | 1.0637 | 1.0201 | 1.0654 | 1.0298 | 1.0292 |
| Longnan | 0.3161 | 0.8693 | 0.6234 | 0.9455 | 0.9375 | 1.0176 | 0.9950 | 0.7795 | 1.2280 | 0.8912 | 1.0698 | 1.1202 | 0.7340 | 1.0365 |
| Pingliang | 0.7486 | 0.9504 | 0.3573 | 0.4420 | 0.6372 | 1.0140 | 0.8382 | 1.0446 | 0.9925 | 0.6926 | 0.5586 | 0.9809 | 0.9215 | 0.6280 |
| Qingyang | 0.4201 | 1.0441 | 1.1238 | 0.4121 | 0.4892 | 1.0392 | 1.0566 | 0.5748 | 0.8128 | 0.3164 | 0.9545 | 0.8763 | 0.9852 | 0.9825 |
| Xining | 1.0901 | 0.9883 | 0.9702 | 0.8698 | 1.1386 | 0.9671 | 0.9647 | 0.9673 | 0.9874 | 1.0027 | 1.1513 | 1.0277 | 1.0610 | 0.9909 |
| Haidong | 0.3091 | 0.9642 | 1.0001 | 1.0689 | 0.7615 | 0.6931 | 0.6026 | 0.6984 | 1.0882 | 0.7605 | 0.7449 | 0.7941 | 0.7875 | 0.7279 |
| Yinchuan | 1.0688 | 1.1466 | 1.0065 | 1.1276 | 0.8299 | 0.8404 | 0.9878 | 0.9793 | 1.0718 | 1.1327 | 1.0027 | 0.6409 | 0.9792 | 0.9058 |
| Shizuishan | 0.9200 | 1.0659 | 1.0567 | 1.0208 | 0.5141 | 0.9982 | 0.9710 | 0.8915 | 0.9632 | 0.5336 | 1.0400 | 0.9054 | 1.2412 | 0.6062 |
| Wuzhong | 0.9821 | 0.6928 | 1.0076 | 1.0732 | 1.0831 | 1.2408 | 1.1764 | 0.9156 | 1.0329 | 0.9024 | 1.3221 | 1.0138 | 1.0618 | 1.0514 |
| Zhongwei | 0.9231 | 0.8431 | 1.0279 | 1.1680 | 0.9231 | 1.0266 | 1.1396 | 0.9142 | 1.0364 | 0.9041 | 0.9965 | 1.1459 | 1.1789 | 1.0614 |
| Guyuan | 1.0365 | 0.9745 | 0.7069 | 1.4038 | 1.0207 | 0.6858 | 0.4987 | 1.4837 | 1.0655 | 0.6465 | 1.0848 | 0.9386 | 1.2670 | 1.2698 |
| Urumqi | 0.9493 | 1.1763 | 0.9638 | 1.3964 | 1.0040 | 1.1221 | 0.7903 | 0.9976 | 1.0630 | 1.0799 | 0.9807 | 1.0178 | 1.0473 | 1.0241 |
| Kelamayi | 1.0166 | 0.9991 | 1.1352 | 0.9575 | 1.0214 | 0.8782 | 0.8774 | 0.9341 | 1.1168 | 0.9287 | 1.1442 | 1.1470 | 1.0922 | 1.0461 |
| Hulun Buir | 0.9905 | 0.9927 | 1.0101 | 0.7318 | 1.1004 | 1.4962 | 0.9602 | 0.6861 | 1.0418 | 1.0537 | 1.0629 | 0.9147 | 1.0049 | 1.0296 |
| Tongliao | 1.0611 | 1.0239 | 0.9718 | 1.0549 | 0.9946 | 1.0729 | 0.8928 | 1.0047 | 1.0000 | 0.9980 | 1.1215 | 0.8907 | 0.9667 | 0.7386 |
| Chifeng | 0.9543 | 1.0558 | 1.0422 | 1.1997 | 1.0724 | 0.9455 | 1.1462 | 0.9975 | 1.0067 | 1.0371 | 1.1836 | 1.0788 | 0.9940 | 1.0255 |
| Shenyang | 1.0786 | 1.0294 | 1.0350 | 1.0491 | 1.1824 | 1.0351 | 1.0106 | 0.9581 | 0.9626 | 1.2991 | 1.1987 | 1.1274 | 1.1481 | 1.2490 |
| Dalian | 1.2839 | 1.0037 | 1.0182 | 1.0121 | 1.1590 | 0.9525 | 1.0091 | 1.0039 | 0.9545 | 1.3666 | 1.1832 | 0.9076 | 1.0448 | 1.1007 |
| Anshan | 1.0199 | 0.8610 | 0.9534 | 0.9763 | 1.0866 | 0.8973 | 0.9296 | 0.9894 | 0.9299 | 0.9764 | 1.0111 | 1.0006 | 1.0659 | 0.8335 |
| Fushun | 1.0884 | 0.9790 | 0.8893 | 0.9163 | 1.1038 | 0.9587 | 0.9669 | 1.0516 | 0.9850 | 1.0339 | 1.0976 | 0.6673 | 1.0914 | 0.7600 |
| Benxi | 0.9900 | 1.0233 | 1.0001 | 0.9938 | 1.0612 | 0.8872 | 0.9406 | 1.0278 | 0.9259 | 1.0207 | 1.0048 | 1.0092 | 0.9563 | 0.9501 |
| Dandong | 0.8977 | 0.9760 | 0.8285 | 0.9535 | 1.0544 | 0.9710 | 0.8819 | 1.1066 | 0.9812 | 1.0091 | 1.0062 | 0.9558 | 0.7498 | 0.6033 |
| Jinzhou | 1.0029 | 1.0066 | 0.9786 | 0.9668 | 0.7395 | 1.0394 | 1.0075 | 1.1540 | 1.1661 | 0.8033 | 1.0064 | 1.0116 | 1.1056 | 0.9049 |
| Yingkou | 0.9811 | 0.8744 | 1.0720 | 0.9149 | 1.0324 | 1.2206 | 1.0871 | 0.9675 | 0.9408 | 1.0688 | 1.0438 | 1.0228 | 1.0737 | 1.0791 |
| Fuxin | 0.9582 | 0.9538 | 1.0008 | 0.9481 | 0.9477 | 0.7805 | 0.8424 | 1.0547 | 1.1028 | 1.1127 | 0.9598 | 0.7691 | 0.8547 | 0.9625 |
| Liaoyang | 0.9724 | 1.0168 | 1.0219 | 0.9255 | 1.0378 | 0.9036 | 0.9096 | 1.0763 | 1.0452 | 1.1246 | 1.0051 | 1.2366 | 1.1499 | 0.9195 |
| Tieling | 0.6917 | 0.9693 | 0.9558 | 1.3061 | 0.8621 | 1.1362 | 1.0636 | 1.1823 | 1.0089 | 0.9241 | 0.9625 | 1.0018 | 1.0064 | 1.0015 |
| Chaoyang | 0.8803 | 0.9098 | 1.0003 | 0.9903 | 1.0054 | 1.1631 | 0.9653 | 1.1008 | 1.0590 | 1.0906 | 1.0052 | 1.0045 | 0.9329 | 0.7848 |
| Panjin | 0.9968 | 0.9961 | 0.9953 | 0.9358 | 1.0484 | 1.0547 | 0.9876 | 0.8206 | 1.1070 | 1.0469 | 1.0422 | 1.2831 | 1.0325 | 1.0040 |
| Huludao | 0.9287 | 0.9310 | 0.9578 | 0.9407 | 0.8387 | 0.9890 | 1.1796 | 0.8217 | 0.9220 | 0.8445 | 0.9897 | 1.0819 | 0.8585 | 0.9725 |
| Changchun | 1.0622 | 0.9448 | 0.9835 | 0.9688 | 1.0504 | 1.0266 | 1.0233 | 1.0526 | 1.3157 | 1.1441 | 1.2121 | 1.0389 | 1.0963 | 1.1485 |
| Jilin | 0.9323 | 1.0728 | 1.0046 | 1.0781 | 1.0449 | 0.8934 | 1.1621 | 1.0052 | 1.1181 | 0.9712 | 1.1403 | 1.0426 | 1.1524 | 1.0523 |
| Siping | 0.8680 | 0.8731 | 0.7208 | 0.7465 | 1.1137 | 1.0323 | 1.0437 | 1.0411 | 0.9701 | 1.0382 | 1.7180 | 0.6513 | 1.2041 | 0.9463 |
| Liaoyuan | 0.7062 | 1.1750 | 0.9276 | 0.9958 | 0.9650 | 0.9889 | 0.9387 | 0.9430 | 0.8897 | 0.9495 | 1.3659 | 0.9138 | 0.9219 | 0.9052 |
| Tonghua | 0.7212 | 0.8690 | 1.0346 | 0.9715 | 1.1805 | 0.9319 | 1.0235 | 0.9569 | 1.0085 | 0.7578 | 1.3046 | 1.1207 | 0.9603 | 0.9396 |
| Baishan | 0.7811 | 0.8363 | 0.9508 | 1.1148 | 1.1414 | 1.1225 | 1.0459 | 0.9797 | 1.0015 | 0.9513 | 1.4367 | 0.9793 | 1.0843 | 1.0218 |
| Baicheng | 0.8001 | 0.9801 | 1.0342 | 1.0713 | 1.1002 | 0.9996 | 0.9304 | 1.0924 | 0.8785 | 1.1352 | 1.0146 | 0.7644 | 0.9843 | 1.1418 |
| Songyuan | 0.6768 | 0.9260 | 1.1693 | 0.9492 | 0.5234 | 0.8280 | 1.0146 | 0.9840 | 0.8834 | 1.1003 | 1.0057 | 0.8294 | 0.9763 | 0.7503 |
| Harbin | 0.9588 | 1.0276 | 1.0370 | 1.0678 | 0.9895 | 0.9551 | 0.9710 | 1.0403 | 1.0179 | 1.0464 | 1.0648 | 1.0803 | 1.0272 | 0.9046 |
| Qiqihar | 0.9454 | 1.0466 | 1.1443 | 0.9348 | 0.8313 | 0.9280 | 0.9353 | 0.8998 | 1.1728 | 0.9376 | 1.1204 | 0.9513 | 0.9796 | 0.9807 |
| Mudanjiang | 1.0774 | 0.9771 | 0.8358 | 0.8427 | 0.8915 | 1.3478 | 0.9761 | 1.0295 | 1.0769 | 0.7099 | 1.1922 | 1.3179 | 0.8921 | 0.7980 |
| Jiamusi | 0.9277 | 0.9895 | 1.0702 | 0.9702 | 1.1017 | 1.1235 | 0.9761 | 0.9055 | 1.1032 | 1.1735 | 1.4798 | 0.8038 | 1.0063 | 0.9487 |
| Jixi | 1.0513 | 1.3272 | 0.7153 | 0.9503 | 0.9244 | 1.0696 | 0.8884 | 0.9443 | 0.9428 | 0.8693 | 1.1609 | 0.9358 | 0.9996 | 1.0070 |
| Hegang | 0.8865 | 0.9754 | 0.9484 | 0.9574 | 0.9007 | 1.1874 | 0.9848 | 0.9553 | 0.9912 | 1.0819 | 0.9728 | 1.0153 | 1.0173 | 1.0510 |
| Shuangyashan | 0.8211 | 0.9711 | 1.0703 | 0.9725 | 0.8568 | 0.9687 | 0.9381 | 1.0252 | 1.0264 | 1.0480 | 0.9421 | 1.1098 | 1.1136 | 0.8310 |
| Qitaihe | 0.9437 | 0.9655 | 1.0024 | 1.0193 | 0.9153 | 1.5968 | 0.8355 | 0.8942 | 0.9787 | 0.9738 | 1.0035 | 1.0071 | 1.0029 | 0.9935 |
| Heihe | 1.0943 | 1.0133 | 1.0071 | 0.6908 | 1.1389 | 0.8828 | 0.9667 | 1.0384 | 1.0810 | 0.9791 | 1.1943 | 0.9135 | 1.0109 | 0.9840 |
| Yichun | 0.7115 | 0.8000 | 1.1221 | 1.0912 | 0.8626 | 0.9319 | 0.9657 | 1.0928 | 1.1291 | 1.1083 | 1.2880 | 1.0168 | 0.9726 | 1.1063 |
| Daqing | 0.9145 | 1.0352 | 1.1788 | 0.8654 | 1.1317 | 1.4037 | 0.8884 | 1.0279 | 1.7815 | 1.0070 | 0.8113 | 0.7986 | 1.0693 | 0.9255 |
| Suihua | 0.9700 | 0.9906 | 0.9909 | 1.0047 | 0.9971 | 0.5398 | 1.0854 | 0.8762 | 1.9102 | 1.0118 | 1.0146 | 0.9920 | 1.0151 | 0.9861 |
Data sources: author’s calculation.
References
- Yao, J.; Xu, P.; Huang, Z. Impact of urbanization on ecological efficiency in China: An empirical analysis based on provincial panel data. Ecol. Indic. 2021, 129, 107827. [Google Scholar] [CrossRef]
- Feng, G.; Serletis, A. Undesirable outputs and a primal Divisia productivity index based on the directional output distance function. J. Econom. 2014, 183, 135–146. [Google Scholar] [CrossRef]
- Feng, Y.; Zhong, S.; Li, Q.; Zhao, X.; Dong, X. Ecological well-being performance growth in China (1994–2014): From perspectives of industrial structure green adjustment and green total factor productivity. J. Clean. Prod. 2019, 236, 117556. [Google Scholar] [CrossRef]
- Cheng, Z.; Jin, W. Agglomeration economy and the growth of green total-factor productivity in Chinese Industry. Socio-Econ. Plan. Sci. 2022, 83, 101003. [Google Scholar] [CrossRef]
- Wang, M.; Pang, S.; Hmani, I.; Hmani, I.; Li, C.; He, Z. Towards sustainable development: How does technological innovation drive the increase in green total factor productivity? Sustain. Dev. 2021, 29, 217–227. [Google Scholar] [CrossRef]
- Sassanelli, C.; Rosa, P.; Rocca, R.; Terzi, S. Circular economy performance assessment methods: A systematic literature review. J. Clean. Prod. 2019, 229, 440–453. [Google Scholar] [CrossRef]
- Kristensen, H.S.; Mosgaard, M.A. A review of micro level indicators for a circular economy—Moving away from the three dimensions of sustainability? J. Clean. Prod. 2020, 243, 118531. [Google Scholar] [CrossRef]
- Khan, S.A.R.; Yu, Z.; Umar, M. A road map for environmental sustainability and green economic development: An empirical study. Environ. Sci. Pollut. Res. 2022, 29, 16082–16090. [Google Scholar] [CrossRef]
- Sun, Y.; Razzaq, A.; Kizys, R.; Bao, Q. High-speed rail and urban green productivity: The mediating role of climatic conditions in China. Technol. Forecast. Soc. 2022, 185, 122055. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhou, R.; Chen, N. An empirical study on coordinated development of energy consumption structure and green total factor productivity under spatial interaction. Econ. Res.-Ekon. Istraž. 2023, 36, 1226–1246. [Google Scholar] [CrossRef]
- Pastor, J.T.; Lovell, C.A.K. A Global Malmquist productivity index. Econ. Lett. 2005, 88, 266–271. [Google Scholar] [CrossRef]
- Wang, Z.; Jia, X. Analysis of energy consumption structure on CO2 emission and economic sustainable growth. Energy Rep. 2022, 8 (Suppl. S4), 1667–1679. [Google Scholar] [CrossRef]
- Xia, F.; Xu, J. Green total factor productivity: A re-examination of quality of growth for provinces in China. China Econ. Rev. 2020, 62, 101454. [Google Scholar] [CrossRef]
- Yang, J.; Li, L.; Liang, Y.; Wu, J.; Wang, Z.; Zhong, Q.; Liang, S. Sustainability performance of global chemical industry based on green total factor productivity. Sci. Total Environ. 2022, 830, 154787. [Google Scholar] [CrossRef] [PubMed]
- Feng, C.; Huang, J.; Wang, M. The sustainability of China’s metal industries: Features, challenges and future focuses. Resour. Policy 2019, 60, 215–224. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, G.; Skitmore, M.; Ballesteros-Pérez, P. A critical review of the current research mainstreams and the influencing factors of green total factor productivity. Environ. Sci. Pollut. Res. 2021, 28, 35392–35405. [Google Scholar] [CrossRef]
- Zhang, X.; Li, R.; Zhang, J. Understanding the green total factor productivity of manufacturing industry in China: Analysis based on the super-SBM model with undesirable outputs. Sustainability 2022, 14, 9310. [Google Scholar] [CrossRef]
- Hailu, A.; Veeman, T.S. Output scale, technical change, and productivity in the Canadian pulp and paper industry. Can. J. Forest Res. 2000, 30, 1041–1050. [Google Scholar] [CrossRef]
- Pittman, R.W. Multilateral productivity comparisons with undesirable outputs. Econ. J. 1983, 93, 883–891. [Google Scholar] [CrossRef]
- Chen, S.; Golley, J. ‘Green’ productivity growth in China’s industrial economy. Energy Econ. 2014, 44, 89–98. [Google Scholar] [CrossRef]
- Li, K.; Lin, B. Economic growth model, structural transformation, and green productivity in China. Appl. Energy 2017, 187, 489–500. [Google Scholar] [CrossRef]
- Zhu, X.; Chen, Y.; Feng, C. Green total factor productivity of China’s mining and quarrying industry: A global data envelopment analysis. Resour. Policy 2018, 57, 1–9. [Google Scholar] [CrossRef]
- Li, X.; Shi, P.; Han, Y.; Deng, A.; Liu, D. Measurement and Spatial Variation of Green Total Factor Productivity of the Tourism Industry in China. Int. J. Environ. Res. Public Health 2020, 17, 1159. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Chen, Y. Development of an SBM-ML model for the measurement of green total factor productivity: The case of pearl river delta urban agglomeration. Renew. Sustain. Energy Rev. 2021, 145, 111131. [Google Scholar] [CrossRef]
- Huang, X.; Feng, C.; Qin, J.; Wang, X.; Zhang, T. Measuring China’s agricultural green total factor productivity and its drivers during 1998–2019. Sci. Total Environ. 2022, 829, 154477. [Google Scholar] [CrossRef]
- Luo, Y.; Lu, Z.; Wu, C.; Mensah, C.N. Environmental Regulation Effect on Green Total Factor Productivity: Mediating Role of Foreign Direct Investment Quantity and Quality. Int. J. Environ. Res. Public Health 2023, 20, 3150. [Google Scholar] [CrossRef]
- Jiakui, C.; Abbas, J.; Najam, H.; Liu, J.; Abbas, J. Green technological innovation, green finance, and financial development and their role in green total factor productivity: Empirical insights from China. J. Clean. Prod. 2023, 382, 135131. [Google Scholar] [CrossRef]
- Charnes, A.; Cooper, W.W.; Rhodes, E. Measuring the efficiency of decision making units. Eur. J. Oper. Res. 1978, 2, 429–444. [Google Scholar] [CrossRef]
- Banker, R.D.; Cooper, A. Some Models for Estimating Technical and Scale Inefficiencies in Data Envelopment Analysis. Manag. Sci. 1984, 30, 1078–1092. [Google Scholar] [CrossRef]
- Andersen, P.; Petersen, N.C. A Procedure for Ranking Efficient Units in Data Envelopment Analysis. Manag. Sci. 1993, 39, 1261–1294. [Google Scholar] [CrossRef]
- Tone, K. A slacks-based measure of efficiency in data envelopment analysis. Eur. J. Oper. Res. 2001, 130, 498–509. [Google Scholar] [CrossRef]
- Tone, K. A Slacks-Based Measure of Super-Efficiency in Data Envelopment Analysis. Eur. J. Oper. Res. 2002, 143, 32–41. [Google Scholar] [CrossRef]
- Li, H.; Fang, K.; Yang, W.; Wang, D.; Hong, X. Regional environmental efficiency evaluation in China: Analysis based on the Super-SBM model with undesirable outputs. Math. Comp. Model. 2013, 58, 1018–1031. [Google Scholar] [CrossRef]
- Oh, D.H. A global Malmquist-Luenberger productivity index. J. Prod. Anal. 2010, 34, 183–197. [Google Scholar] [CrossRef]
- Cao, L.; Zhou, Z.; Wu, Y.; Huang, Y.; Cao, G. Is metabolism in all regions of China performing well?—Evidence from a new DEA-Malmquist productivity approach. Ecol. Indic. 2019, 106, 105487. [Google Scholar] [CrossRef]
- Xue, Y. Evaluation analysis on industrial green total factor productivity and energy transition policy in resource-based region. Energy Environ. 2022, 33, 419–434. [Google Scholar] [CrossRef]
- Zhang, H.; Dong, Y. Measurement and Spatial Correlations of Green Total Factor Productivities of Chinese Provinces. Sustainability 2022, 14, 5071. [Google Scholar] [CrossRef]
- Ren, W.; Ji, J. How do environmental regulation and technological innovation affect the sustainable development of marine economy: New evidence from China’s coastal provinces and cities. Mar. Policy 2021, 128, 104468. [Google Scholar] [CrossRef]
- Rusiawan, W.; Tjiptoherijanto, P.; Suganda, E.; Darmajanti, L. Assessment of Green Total Factor Productivity Impact on Sustainable Indonesia Productivity Growth. Procedia Environ. Sci. 2015, 28, 493–501. [Google Scholar] [CrossRef]
- Zhong, S.; Li, A.; Wu, J. Eco-efficiency of freshwater aquaculture in China: An assessment considering the undesirable output of pollutant emissions. Environ. Dev. Sustain. 2023, 25, 3555–3576. [Google Scholar] [CrossRef]
- Debbarma, J.; Choi, Y.; Yang, F.; Lee, H. Exports as a new paradigm to connect business and information technology for sustainable development. J. Innov. Knowl. 2022, 7, 100233. [Google Scholar] [CrossRef]
- Meng, F.; Zhao, Y. How does digital economy affect green total factor productivity at the industry level in China: From a perspective of global value chain. Environ. Sci. Pollut. Res. 2022, 29, 79497–79515. [Google Scholar] [CrossRef] [PubMed]
- Xiao, S.; Wang, S.; Zeng, F.; Huang, W.-C. Spatial Differences and Influencing Factors of Industrial Green Total Factor Productivity in Chinese Industries. Sustainability 2022, 14, 9229. [Google Scholar] [CrossRef]
- Li, M.; Wang, J. Spatial-temporal evolution and influencing factors of total factor productivity in China’s logistics industry under low-carbon constraints. Environ. Sci. Pollut. Res. 2022, 29, 883–900. [Google Scholar] [CrossRef]
- Liu, P.; Zhu, B. Temporal-spatial evolution of green total factor productivity in China’s coastal cities under carbon emission constraints. Sustain. Cities Soc. 2022, 87, 104231. [Google Scholar] [CrossRef]
- Sassanelli, C.; Terzi, S. Circular Economy and Sustainable Business Performance Management. Sustainability 2023, 15, 8619. [Google Scholar] [CrossRef]
- Vinante, C.; Sacco, P.; Orzes, G.; Borgianni, Y. Circular economy metrics: Literature review and company-level classification framework. J. Clean. Prod. 2021, 288, 125090. [Google Scholar] [CrossRef]
- Xiao, Q.; Wang, Y.; Liao, H.; Han, G.; Liu, Y. The Impact of Digital Inclusive Finance on Agricultural Green Total Factor Productivity: A Study Based on China’s Provinces. Sustainability 2023, 15, 1192. [Google Scholar] [CrossRef]
- Hou, S.; Song, L. Market Integration and Regional Green Total Factor Productivity: Evidence from China’s Province-Level Data. Sustainability 2021, 13, 472. [Google Scholar] [CrossRef]
- Feng, J.; Zhao, L.; Zhang, Y.; Sun, L.; Yu, X.; Yu, Y. Can climate change influence agricultural GTFP in arid and semi-arid regions of Northwest China? J. Arid. Land 2020, 12, 837–853. [Google Scholar] [CrossRef]
- Liang, Z.; Chiu, Y.-H.; Li, X.; Guo, Q.; Yun, Y. Study on the Effect of Environmental Regulation on the Green Total Factor Productivity of Logistics Industry from the Perspective of Low Carbon. Sustainability 2020, 12, 175. [Google Scholar] [CrossRef]
- Tang, M.; Cao, A.; Guo, L.; Li, H. Improving agricultural green total factor productivity in China: Do environmental governance and green low-carbon policies matter? Environ. Sci. Pollut. Res. 2023, 2, 52906–52922. [Google Scholar] [CrossRef]
- Li, H.; Shi, J. Energy efficiency analysis on Chinese industrial sectors: An improved Super-SBM model with undesirable outputs. J. Clean. Prod. 2014, 65, 97–107. [Google Scholar] [CrossRef]
- Chen, F.; Zhao, T.; Wang, J. The evaluation of energy—Environmental efficiency of China’s industrial sector: Based on Super-SBM model. Clean Technol. Environ. Policy 2019, 21, 1397–1414. [Google Scholar] [CrossRef]
- Newman, C.; Matthews, A. The productivity performance of Irish dairy farms 1984–2000: A multiple output distance function approach. J. Prod. Anal. 2006, 26, 191–205. [Google Scholar] [CrossRef]
- Zhou, L.; Zhou, C.; Che, L.; Wang, B. Spatio-temporal evolution and influencing factors of urban green development efficiency in China. J. Geogr. Sci. 2020, 30, 724–742. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, Y.; Liu, Z.; Liu, R.; Li, K. The impact and mechanisms of the Shanghai pilot free-trade zone on the green total factor productivity of the Yangtze River Delta Urban Agglomeration. Environ. Sci. Pollut. Res. 2022, 29, 40997–41011. [Google Scholar] [CrossRef] [PubMed]
- Meng, M.; Qu, D. Understanding the green energy efficiencies of provinces in China: A Super-SBM and GML analysis. Energy 2022, 239, 121912. [Google Scholar] [CrossRef]
- Zhang, B.; Yu, L.; Sun, C. How does urban environmental legislation guide the green transition of enterprises? Based on the perspective of enterprises’ green total factor productivity. Energy Econ. 2022, 110, 106032. [Google Scholar] [CrossRef]
- Yang, Z.; Wei, X. The measurement and influences of China’s urban total factor energy efficiency under environmental pollution: Based on the game cross-efficiency DEA. J. Clean. Prod. 2019, 209, 439–450. [Google Scholar] [CrossRef]
- Li, J.; Deng, J.; Wang, K.; Li, J.; Huang, T.; Lin, Y.; Yu, H. Spatiotemporal Patterns of Urbanization in a Developed Region of Eastern Coastal China. Sustainability 2014, 6, 4042–4058. [Google Scholar] [CrossRef]
- National Bureau of Statistics of China. China City Statistical Yearbook. 2020. Available online: https://ceidata.cei.cn/ (accessed on 1 January 2023).
- National Bureau of Statistics of China; Ministry of Environmental Protection of China. China Statistical Yearbook on Environment. 2020. Available online: https://d.qianzhan.com/ (accessed on 1 January 2023).
- National Bureau of Statistics of China. China Statistical Yearbook. 2020. Available online: https://data.cnki.net/ (accessed on 1 January 2023).
- Municipal Statistics Bureau. Municipal Statistical Yearbook. 2020. Available online: https://data.cnki.net/ (accessed on 1 January 2023).
- Investigation Team of Bureau of Statisitcs. The Statistical Bulletin on National Economic and Social Development. 2019. Available online: http://www.tjcn.org/ (accessed on 1 January 2023).
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).