Managing Resources Based on Influential Indicators for Sustainable Economic Development: A Case Study in Serbia

Abstract

The balance between resource consumption and the ability of natural systems to meet the needs of future generations emerges as a prerequisite of sustainability. Sustainability means aligning economic growth and development with the interest of the environment and social development. Decision-making is a significant responsibility in an environment and the business world because decisions affect the ecology and business performance. It is necessary to adopt new approaches in decision-making to find an appropriate method for assessing and setting priority goals. Various methods for multi-criteria decision-making have been developed, including the Analytic Hierarchy Process (AHP). The paper deals with the management of natural and human resources for the sustainable economic development of Serbia by selecting influential factors, relying on a multi-criteria decision-making framework. Appropriate methods have been applied: AHP and several fuzzy AHP (FAHP) approaches. These methods’ application enables the analysis of results from different aspects of expert opinion. Through a case study, this paper investigates the AHP method from several facets in which the identification of decision criteria is based on the perception of experts of different profiles. The findings of this research can be a guideline for decision-makers in resource management to enhance sustainable economic development. The case study confirms that the stability of the business environment and business sectors is the most influential indicator in all scenarios.

1. Introduction and Literature Review

The sustainable economic development of each state is conditioned primarily by natural (but also human) potentials, which are usually the backbone of the development of the region and the state [1]. Using these potentials while shaping them according to needs, people have survived and developed concerning economic and overall progress. At the same time, technical-technological development and especially the development of ICT has certainly improved everyday life and work without which it is impossible to imagine a modern way of functioning of people and economy, but it has also led to faster exploitation of the human environment, faster depletion of available natural resources [2]. Natural resources are a baseline for development and wealth creation. There is a possibility that the natural regeneration of resources can’t keep pace with industry progress. The enrichment of human potential can have a technological impact on increasing the contribution of natural resources to economic growth [3].

Serbia is a territorially small country, but it has quality natural and human resources. The best promotion of socially, environmentally, and economically sustainable growth is an issue that is increasingly at the center of interest [4]. In economic terms, Serbia has characterized by developed regions in the north and underdeveloped ones in the south. The basic premise of profitable and overall socio-economic development is balanced economic prosperity [5]. The management of natural and human resources and the implementation of sustainable development have imposed the need to pay more attention to profit-making aspects in the future [6,7]. Excessive exploitation of natural resources creates many interrelated problems that affect the health of ecosystems and social well-being in different regions.

The starting point is that further economic growth has based on resources’ smart exploitation [8,9]. The development of the Serbian economy in a sustainable direction can look only on achieving economic growth, primarily knowledge-based, information, people, education, and the quality of connections between people and institutions [10]. Sustainable economic development is needed based on the growth of a group of key economic indicators (GDP growth, employment, foreign trade, competitiveness and exports, investment, household standards) with a reduction in the solvent burden of external debt, as well as achieving lasting macroeconomic stability, the better quality of life, ecological condition and general well-being of society [11].

The population creates significant pressure on the capital, whose area is constantly expanding and prevents the balanced development of other cities and regions in the country. The challenges of Serbia’s spatial development are, among other things, a consequence of the late transition [12]. The key to the transition period was the privatization of state property with the return to a market-oriented economy. These have been mostly affected the economy due to reduced budget inflows, job losses, and shortages in the manufacturing sector. Some municipalities have already made progress in creating a stimulating business climate, and some have yet to work hard and intensively to realize their potential.

Lately, there has often been talking of a knowledge-based economy. The European Union, with Lisbon Strategy, and Serbia, with Sustainable Development Strategy, plan further economic development through an economy that bases economic prosperity 3 on education and knowledge [13].

The new phase of social processes is facing the public consciousness of citizens with the problem of determining the additional path of development, given that there is a need to review the accumulated experience and the appropriate transformation of the economic management system towards sustainable development. In a systematic approach to the sustainable development of the country as a whole, and especially the underdeveloped regions of Serbia, elements such as the state, society, people with their knowledge and skills, economy, ICT, ecology are precisely those elements that need to be included and viewed in a complex way [14]. Namely, these elements have been combined in the institutional sense known as a public-private partnership (PPP). It is necessary to develop new efficient decision-making models to improve the quality of social life. Through these models, one can create an economically sustainable development strategy, anticipate possible risk events, and minimize them in innovative PPP projects [15].

The naturally available wealth and human resources are the backbones of sustainable economic development [16]. Excessive exploitation of natural resources creates many interrelated problems that affect the health of ecosystems and social well-being in different regions.

The region’s sustainable economic development strategy includes the planned development achievements definition [17]. The region’s economy is an unfavorable economic structure with weak financial, natural, and technological resources and needs sustainable restructuring with an increase in gross domestic product, development of foreign trade, employment rate, investment, and competitiveness on the international market [18]. To use all the potential, serious work, strong leadership, and a clear vision have been necessary [19]. Strong leadership, setting investments as priorities for municipal activities, with focused work and energy can make a difference, as shown by the examples of some successful municipalities [20].

The strategic management in regional economic development should enable a timely and rational response of the region’s economy to all changes in the economic environs in which the region’s entities operate [21]. It is necessary to implement pre-planned steps such as analysis of the economic environment, the economic orientation of the district, formulation of the plan of economic development, implementation of the defined strategy, and implementation of strategic control [22].

The paper contains five sections. The introduction provides elementary remarks on the subject area in the framework of managing natural and human resources for the sustainable economic development of the region and literature review. The Section 2 provides the conceptual framework. The methodology, which consists of AHP, and fuzzy triangular AHP methods, is given in the Section 3. After them in this section, indicators are chosen within four different groups. Section 4 part presents the ranking results and comparison of the results of the given algorithms with the discussion. Concluding remarks and future research goals have been presented in the last Section 5.

2. Conceptual Framework

One of the basic concepts of the economics of natural resources and the environment is the concept of sustainable development. Despite the different interpretations that can be found in the literature, this concept today has a central place in considering the long-term perspective of the survival and progress of human race in aligning economic growth and development with the interests of environmental protection and social development.

The research process adopted in this paper is realized as Figure 1 shows.

Figure 1. Five steps in the research process.

The paper presents the factors that influence the managing natural and human resources for the economic development of Serbia through four groups (a framework for strengthening participation in the development, human social resources, economic potentials, and natural resources). Modeling a framework for supporting participation and managing resources in the sustainable economic development of Serbia is considered in this research from the aspect of crisp AHP and fuzzy approaches of method AHP to single out influential factors. Managers show interest in creating and implementing reliable modus for decision-making in the present and the future. Achieving sustainable development requires developing an appropriate strategy to achieve sustainable development by applying maintenance performance measurements [23]. The method Analytic Hierarchy Process (AHP) was introduced by Thomas L. Saati in 1980 [24,25]. It is a method for solving multi-criteria decision-making (MCDM) problems. After a comprehensive evaluation of several criteria, it points to the final choice of the best solution in the analyzed problem [26]. The AHP method is widely used, despite the need for consistency testing, primarily because of its flexibility and ease of use [27]. Many methods and applications of fuzzy AHP are expressed by numerous researchers [28,29]. In applying the Fuzzy Analytic Hierarchy Process (FAHP) method, we used Chang’s Extent analysis method (EAM) approach and the three-level optimism approach [30,31]. The results obtained by explained methods are compared with the results given by Interval AHP (IAHP) as in the paper [28].

More details about MCDM methods can be seen in the papers [32,33,34].

The goal is to single out influential factors obtained by methods application and compare the results. The task of the paper is to compare the extent to which these approaches can influence the decision choice of influencing factors. The methods used are given in Figure 2.

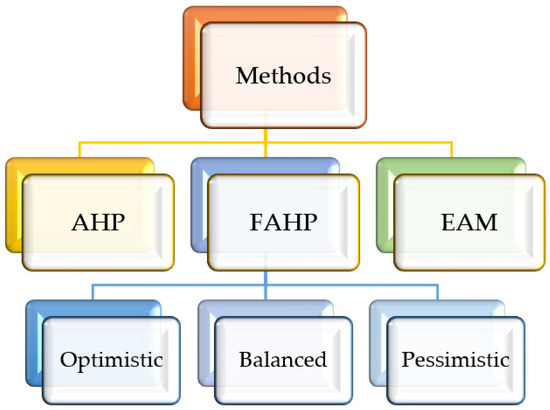
Figure 2. Schematic representation of methods.

3. Materials and Methods

AHP is a structured technique that enables the organization and analysis of complex decisions based on subjective assessment. Using multiple criteria for easy to understand and efficient dealing with qualitative and quantitative data are the main advantages of AHP.

Definition 1.

AHP is a multi-criteria decision-making technique to highlight the advantages among different criteria in the decision-making, compare decision-making alternatives for each criterion, and obtain the final ranking of decision alternatives. The outcome in AHP is deciding on the best of the decision alternatives.

The AHP method is realized through the following steps [35]:

(1)

Establishing a hierarchy by decomposing the problem of decision-making.

(2)

Creating comparison matrices by performing pairwise comparisons.

(3)

Calculation of weights and consistency of comparisons.

(4)

Aggregation of weights to obtain results and ranking of alternatives.

AHP has been used in various domains like business, industry, and engineering. Developing countries should use AHP for complex economic problems solutions from different development perspectives [36]. The essence of the AHP method is to pair the available options according to all evaluation criteria [37]. In the real world, data or information obtained from experts mainly includes uncertainty and ambiguity conditioned primarily by inaccuracies in human reasoning and decision-making environment uncertainty and incomplete details [38].

As a more powerful methodology for multi-criteria decision-making, the combined effect of fuzzy set theory and AHP is given by the FAHP. The FAHP method is applicable for solving the problem of multi-criteria analysis when accurately assessing (quantifying) the impact of indicators on the decision problem is not present. In addition, the introduction of the AHP or FAHP method allows minimizing subjective influences in decision- making.

3.1. Triangular Fuzzy Numbers and Fuzzy AHP Method

The fuzzy numbers are special fuzzy sets $F=\left\{\left(x,{\mu }_F\left(x\right)\right),x\in ℝ\right\},$ where ${\mu }_F:R\to \left[0,1\right]$ is a continuous function. The triangular fuzzy number (TFN), denoted with $\tilde{T}=\left(a,m,b\right),$ has membership function:

$${\mathsf{\mu }}_{\tilde{\mathrm{T}}}\left(x\right)=\{\begin{array}{c}\frac{x-a}{m-a}, x\in \left[a,m\right)\\ \frac{b-x}{b-m}, x\in \left[m,b\right]\\ 0, \mathrm{otherwise}.\end{array}$$

(1)

Definition 2.

For two triangular fuzzy numbers ${\tilde{T}}_1=\left(a_1,m_1,b_1\right)$ and ${\tilde{T}}_2=\left(a_2,m_2,b_2\right),$ and scalar $\lambda \in R$ arithmetic operations are:

• Addition:${\tilde{T}}_1\oplus {\tilde{T}}_2=\left(a_1+a_2,m_1+m_2,b_1+b_2\right),$
• Subtraction:${\tilde{T}}_1\ominus {\tilde{T}}_2=\left(a_1-b_2,m_1-m_2,b_1-a_2\right)$,
• Multiplication:${\tilde{T}}_1\odot {\tilde{T}}_2=\left(a_1·a_2,m_1·m_2,b_1·b_2\right),$
• Inverse:$T_1^{-1}={\left(a_1, m_1, b_1\right)}^{-1}=\left(1/b_1,1/m_1,1/a_1\right),$
• Division:${\tilde{T}}_1\oslash {\tilde{T}}_2={\tilde{T}}_1\odot T_2^{-1}=\left(a_1/b_2,m_1/m_2,b_1/a_2\right),$
• Scalar multiplication:$\lambda {\tilde{T}}_1=\left(\lambda a_1,\lambda m_1,\lambda b_1\right)$.

Denotations and meaning of the triangular fuzzy numbers (TFNs) are: $\tilde{1}=\left(1, 1, 3\right)$ is equal importance (both elements have the same impact); $\tilde{3}=\left(1, 3, 5\right)$ is moderate importance (one element has a slight advantage over the other); $\tilde{5}=\left(3, 5, 7\right)$ strong importance (strong advantage of one element over the other); $\tilde{7}=\left(5, 7, 9\right)$ very strong or demonstrated importance (very strong advantage of one element over the other); $\tilde{9}=\left(7, 9, 9\right)$ extreme importance (extreme (full) advantage of one element over the other). Intermediate values are $\tilde{2}=\left(1, 2, 3\right)$, $\tilde{4}=\left(3, 4, 5\right), \tilde{6}=\left(5, 6, 7\right) \mathrm{and} \tilde{8}=\left(7, 8, 9\right)$.

In recent decades, the fuzzy AHP method, based primarily on triangular fuzzy numbers, has proven suitable in a wide range of engineering, environment, industry, economy, etc. Since fuzzy weights are not as easy to calculate as crisp weights, most Fuzzy AHP applications use the extent analysis method proposed by Chang [30]. Like AHP, FAHP facilitates decompositions and comparisons in pairs, provides a hierarchical structure, and generates priority vectors while reducing in-consistencies. Also, fuzzy AHP can be used to solve different problems and different contexts.

The applied method consists of the following:

(1)

Establishing the main goal and the criteria and sub-criteria contributing to the overall goal; developing the problem hierarchy.

(2)

Obtaining the fuzzy comparison matrices. A pairwise comparison has been made using a fuzzified evaluation scale. Using triangular fuzzy numbers, we form a comparison matrix $\tilde{C}={\left({\tilde{c}}_{ij}\right)}_{n\times n}$ for a fuzzy comparison of criteria by pairs, where ${\tilde{c}}_{ij}$ is a fuzzy value that expresses the relative importance of one criterion to another. At the diagonal, the fuzzy values ${\tilde{c}}_{ii}$ express the relative importance of the criterion to itself. Because of that, we put that ${\tilde{c}}_{ii}=\left(1,1,1\right).$ The aggregation of different experts’ opinions is calculated by the averaging method. Based on the corresponding linguistic assessments of k experts $\left(a_i,m_i,b_i\right)$, aggregated crisp value has been obtained by $\frac{1}{k}\sum _{i=1}^k{m}_i$ rounding to the nearest integer. The corresponding fuzzy number value of the aggregate opinion is then obtained.

(3)

Examination of the comparison matrix $\tilde{C}$ consistency. We calculate the consistency index $CI$ and consistency ratio $CR$ for matrix $\tilde{C}={\left({\tilde{c}}_{ij}\right)}_{n\times n}$ by $CI=\frac{{\mathsf{\lambda }}_{max}-n}{n-1}$, $CR=\frac{CI}{RI}$, where ${\mathsf{\lambda }}_{max}$ represents the maximal eigenvalues, and RI is an accepted random index of a matrix $\tilde{C}$. The value $CR \le 0.10$ implies that we accept evaluated fuzzy elements of the matrix, while otherwise, we must remove the reasons for undesirably high estimations and repeat comparison in pairs until the degree of consistency belongs to desirable limits.

(4)

The fuzzy synthetic extents determination. The synthetic triangular fuzzy numbers have been calculated, according to Chang’s extent analysis method, by using triangular fuzzy numbers from the matrix $\tilde{C}={\left({\tilde{c}}_{ij}\right)}_{n\times n}$:

$${\tilde{\mathcal{S}}}_i={\sum }_{j=1}^n{\tilde{c}}_{ij}\odot {\left({\sum }_{i=1}^n{\sum }_{j=1}^n{\tilde{c}}_{ij}\right)}^{-1},i=\overline{1,n}.$$

(2)

First approach, Extent analysis method (EAM) [30]: The obtained synthetic triangular fuzzy numbers can be compared one with each other by calculating the degree of possibility that ${\tilde{T}}_1 \ge {\tilde{T}}_2$:

$$P\left({\tilde{T}}_1\ge {\tilde{T}}_2\right)=\underset{x\ge y}{\sup }\left[\min \left({\mu }_{{\tilde{T}}_1}\left(x\right),{\mu }_{{\tilde{T}}_2}\left(y\right)\right)\right].$$

(3)

This probability P has been approximated by the ordinate of the intersection point with abscise d (see Figure 3).

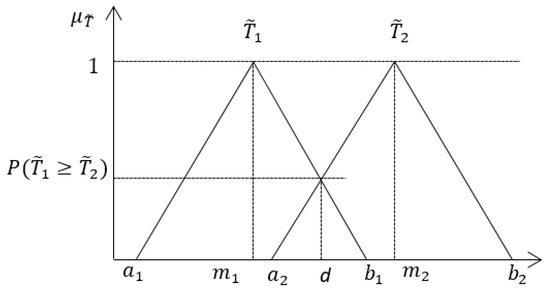
Figure 3. Intersection between membership functions ${\mu }_{{\tilde{T}}_1}$ and ${\mu }_{{\tilde{T}}_2}$.

By calculating ordinate of this intersection point, we obtain

$$P\left({\tilde{T}}_1\ge {\tilde{T}}_2\right)=\mathrm{hgt}\left({\tilde{T}}_1{{\displaystyle \cap }}^{ }{\tilde{T}}_2\right)=\{\begin{array}{c}1,\hspace{1em}\hspace{1em}\hspace{1em}if\hspace{1em}{m}_1 \ge m_2\\ 0,\hspace{1em}\hspace{1em}\hspace{1em}if\hspace{1em}{a}_2 \ge b_1\\ \frac{a_2-b_1}{\left(m_1-b_1\right)-\left(m_2-a_2\right)},\hspace{1em}otherwise. \end{array}$$

(4)

The degree of possibility that convex fuzzy number $\tilde{T}$ is greater than $k$ convex fuzzy numbers ${\tilde{T}}_i, i=\overline{1,k}$ is

$$P\left(\tilde{T}\ge {\tilde{T}}_1,{\tilde{T}}_2,\dots ,{\tilde{T}}_k\right)=\min P\left(\tilde{T}\ge {\tilde{T}}_i\right), \mathrm{for} i=\overline{1,k}.$$

(5)

Let $d^{\prime }\left(C_i\right)=\min P\left({\mathcal{S}}_i\ge {\mathcal{S}}_k\right),$ for $k=\overline{1,n}$, $k\ne i$. The weight vector is ${\mathcal{W}}^{\prime }={\left(d^{\prime }\left(C_1\right),d^{\prime }\left(C_2\right),\dots ,d^{\prime }\left(C_n\right)\right)}^T$, where $C_i$, $i=\overline{1,n}$ are $n$ elements. The normalized weight vector is a non-fuzzy number:

$$\mathcal{W}={\left(d\left(C_1\right),d\left(C_2\right),\dots ,d\left(C_n\right)\right)}^T,$$

(6)

which we can denote $\mathcal{W}={\left({\omega }_1,{\omega }_2,\dots ,{\omega }_n\right)}^T.$

Second approach: Based on total integral values calculated by [39],

$${\omega }_i^{\prime }\left({\tilde{S}}_i\right)=0.5\left(\nu b_i+m_i+\left(1-\nu \right)a_i\right),\hspace{1em}i=\overline{1,n},\hspace{1em}\nu \in \left[0,1\right],$$

(7)

We compare obtained TFNs: ${\tilde{S}}_i=\left(a_i, m_i,b_i\right)$. Real constant $\nu$ represents an optimism index, which explains the decision maker’s attitude toward the risk. The smaller values mean a higher degree of risk and a lower degree of optimism. In our research we have used values: $\nu$ = 0 (pessimistic viewpoints), $\nu$ = 0.5 (balanced viewpoints), and $\nu$ = 1 (optimistic viewpoints).

By normalization, we obtain the weight vector: $\mathcal{W}={\left({\omega }_1,{\omega }_2,\dots ,{\omega }_n\right)}^T$.

3.2. Considering Indicators for the Sustainable Economic Development

Factors influencing the implementation of the concept of natural and human resources management for the economic development of Serbia are expressed through four groups of criteria: a framework for strengthening participation in development, human resources, economic potential, natural resources, and are shown in Table 1.

Table 1. The overview of adopted indicators for the sustainable economic development.

S—Strengthening participation in the development [40]
S1—Economic development strategy based on knowledge and innovation [41,42]	S11—Development of a stimulating entrepreneurial environment [43] S12—Targeted investment attraction [44] S13—Development of potentials for the needs of the labor market
S2—Sustainable mobility and interactive city development [45,46]	S21—Increased accessibility of the city S22—Sustainable mobility of the central city zone [47] S23—Development of economic zones and logistics S24—Compliance of the traffic system with the needs of citizens S25—Increasing the share of pedestrians in cyclists as road users [48] S26—Improved safety conditions for all road users
S3—Improvement and development infrastructure services of citizens [49]	S31—Improving the quality of communal infrastructure S32—Creating a framework for high-quality utilities S33—Improving the level of information and communication with citizens
S4—Energy capital as a development opportunity [50]	S34—Increased efficiency coefficient of all PUCs individually S41—Improvement of energy infrastructure S42—Improving energy efficiency S43—Institutional environment for the development of energy systems and the provision of quality services [51]
S5—Improved social cohesion [52]	S44—Achieved in the billing system according to the energy consumed S51—Diversified, accessible, and quality social services S52—Improving the content of culture, sports, and tourism S53—Improving social development infrastructure S54—A single record system for users of social rights and services has been established S55- City Housing Strategy adopted S56—Implementation of investment plans in facilities and equipment of primary health care institutions
E—Economic potentials [53]
E1—Increasing competitiveness [54,55]	E11—Stability of business environment and business sector [56] E12—Global response to the COVID-19 pandemic [57]
E2—Suppression of the gray economy [58]	E21—Reducing the degree of the gray economy in GDP [59] E22—Reduction of the share of unregistered economic entities E23—Relative reduction of VAT
E3—Public-private partnership in support of local economic development and foreign direct investment (FDI) [60]	E31- Increase in efficiency and economy [61] E32- Reducing the pressure of public investment on the budget [62] E33- Increasing the level of foreign direct investment (FDI)
N—Natural resources [63]
N1—Use and protection of natural resources in planning [64]	N11—Implementation of the National Strategy on the Use and Protection of Natural Resources and Goods N12—Strategic environmental impact assessment of plans and programs N13—Environmental impact assessment of projects N14—Integrated prevention and control of environmental pollution
N2—Management of renewable natural resources and non-renewable natural resources [65]	N21—Reconciliation of the relationship between the degree of exhaustion of natural resources and their regeneration rate [66] N22—Design of available resources by quality, structure, amount, and capital investments N23—Direction of ecological aspects in the interest of the population of the local area
N3—Protection of resources and ecosystems through the principles of sustainable development [67]	N31—Creating ability of the environment to accept a certain amount of pollutants per unit of time and space so that there is no irreversible damage to the environment; N32—The impact of a product/service or system on the environment N33—Effective preservation of ecosystems and resources themselves [68] N34—Transparency-information of the wider local community
H—Human resources [69]
H1—Employment and labor market [70]	H11—Support for the development of local and inter-municipal employment policies H12—Increasing the impact of employment policy measures on the hard-to-employ H13—Suppression of the informal economy
H2—Improving the quality and accessibility of health services [71]	H21—Promoting the health and well-being of all citizens H22—Preventive care H23—Strengthening the operational capacity of the health system in line with EU standards data
H3—Education [72]	H31—Improving the quality and importance of secondary vocational education and adult education within the National Qualifications Framework H32—Ensuring access to and reaching higher levels of education for children at risk [73] H33—Education for all
H4—Social inclusion [74]	H41—Support for social inclusion through a more diverse offer of social services in the local community H42—Support for the transition from social assistance to work (“welfare-to-work”) through activation
H5—Technical assistance	H51—Announcement of new calls for cross-border cooperation programs H52—Finalization of the Operational Program Human Resources Development H53—Negotiations with individual bilateral donors, discussions on a new EU financial perspective [75]

4. Results and Discussion

In this section, the outlined algorithms have been applied. A group of experts in the area of economy, natural resources, and human resources rated the identification of decision criteria. Expert opinions are expressed based on the meaning and denotation of TFNs in Table 2. Expert assessments are aggregated based on the algorithm explanation in step (2). Experts agreed that some groups should retain a number of sub-criteria.

Table 2. Meaning and denotation of the TFNs.

Description TFNs	TFNs	Inverse TFNs	Denotation of TFNs	Denotation of Inverse TFNs
Equally important	$\tilde{1}=\left(1, 1, 3\right)$	$\tilde{1}-1$ = $\left(1/3, 1, 1\right)$	$\mathrm{E}$	$\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{E}$}\right.$
Equally to weakly important	$\tilde{2}=\left(1, 2, 3\right)$	$\tilde{2}-1$ = $\left(1/3, 1/2, 1\right)$	$\mathrm{EW}$	$\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{EW}$}\right.$
Weakly important	$\tilde{3}=\left(1, 3, 5\right)$	$\tilde{3}-1$ = $\left(1/5, 1/3, 1\right)$	$\mathrm{W}$	$\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{W}$}\right.$
Weakly to strong important	$\tilde{4}$ $=\left(3, 4, 5\right)$	$\tilde{4}-1$ = $\left(1/5, 1/4, 1/3\right)$	$\mathrm{WS}$	$\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{WS}$}\right.$
Strong important	$\tilde{5}$ $=\left(3, 5, 7\right)$	$\tilde{5}-1$ = $\left(1/7, 1/5, 1/3\right)$	$\mathrm{S}$	$\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{S}$}\right.$
Strong to very strongly important	$\tilde{6}$ $=\left(5, 6, 7\right)$	$\tilde{6}-1$ = $\left(1/7, 1/6, 1/5\right)$	$\mathrm{SV}$	$\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{SV}$}\right.$
Very strongly important	$\tilde{7}=\left(5, 7, 9\right)$	$\tilde{7}-1$ = $\left(1/9, 1/7, 1/5\right)$	$\mathrm{V}$	$\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{V}$}\right.$
Very strongly to absolutely important	$\tilde{8}$ $=\left(7, 8,9\right)$	$\tilde{8}-1$ = $\left(1/9, 1/8, 1/7\right)$	$\mathrm{VA}$	$\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{VA}$}\right.$
Absolutely important	$\tilde{9}$ $=\left(7, 9, 9\right)$	$\tilde{9}-1$ = $\left(1/9, 1/9, 1/7\right)$	$\mathrm{A}$	$\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$\mathrm{A}$}\right.$

Table 3 shows a matrix comparing the primary criteria, and Figure 4 shows the corresponding weights.

Table 3. Triangular fuzzy compare matrix of primary criteria.

	F	S	N	H
F	$\tilde{1}$	$\tilde{1}$	$\tilde{2}$	$\tilde{4}$
S	$\tilde{1}-1$	$\tilde{1}$	$\tilde{2}$	$\tilde{4}$
N	$\tilde{2}-1$	$\tilde{2}-1$	$\tilde{1}$	$\tilde{3}$
H	$\tilde{4}-1$	$\tilde{4}-1$	$\tilde{3}-1$	$\tilde{1}$

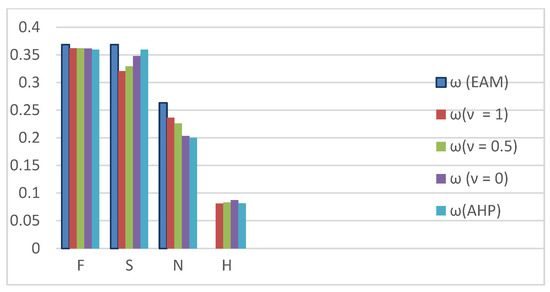
Figure 4. Corresponding weights for Chang’s approach, different degrees of optimism in FAHP and crisp AHP ($CI=0.006, CR=0.007)$.

Table A1, Table A2, Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9, Table A10, Table A11, Table A12, Table A13, Table A14, Table A15, Table A16, Table A17, Table A18, Table A19 and Table A20 with triangular fuzzy comparison matrices of sub-criteria and the corresponding weights for applied methods are in Appendix A.

The final rank of sub-sub-criteria, and their final weight for each sub-criterion, are in Table 4. The indicators are ranked according to the optimistic, balanced, and pessimistic views ($\nu =1, \nu =0.5, \nu =0$), the extent analysis method (EAM) on FAHP and AHP.

Table 4. Ranking of indicators with final weights by triangular fuzzy AHP method, AHP method and IAHP method $(I\omega$ is interval weight, p is probability).

	${\mathit{\omega }}_{\mathit{E}\mathit{A}\mathit{M}}$		${\mathit{\omega }}_{\mathit{\nu }=1}$		${\mathit{\omega }}_{\mathsf{\nu }=0.5}$		${\mathit{\omega }}_{\mathit{\nu }=0}$		$\mathit{I}\mathit{\omega }$	p		$\mathit{\omega }\left(\mathit{A}\mathit{H}\mathit{P}\right)$
E11	0.100666	E11	0.095156	E11	0.094012	E11	0.091420	S11	[8.63826,19.0926]	0.959395	E11	0.095807
E32	0.068298	E32	0.060143	S11	0.077816	S11	0.077491	S12	[4.75382,10.9277]	0.66159	S11	0.088968
S11	0.064537	N33	0.056326	E32	0.062224	E32	0.066205	E21	[4.70912,8.97667]	0.871921	E32	0.077548
N33	0.062361	E12	0.047578	N33	0.053412	E12	0.050789	N33	[3.92281,6.33196]	0.520358	N33	0.053058
E31	0.048790	S12	0.043947	E12	0.048828	S12	0.048970	S26	[3.17891,6.9234]	0.816068	S12	0.048961
N31	0.048423	N31	0.041460	S12	0.045329	N33	0.047105	S22	[2.92868,4.77265]	0.558448	E12	0.047903
S12	0.046103	N21	0.037358	N31	0.038585	E31	0.041838	S13	[2.07642,5.25352]	0.513292	E31	0.042676
E12	0.044741	E31	0.033894	E31	0.036246	E21	0.033955	S34	[2.80168,4.4438]	0.5	E21	0.035341
N21	0.041493	S11	0.032996	N21	0.035811	N31	0.032727	S33	[2.80168,4.4438]	0.747129	N31	0.032964
E21	0.039108	E21	0.028827	E21	0.030422	N21	0.032503	E11	[2.64639,3.76592]	0.550364	N21	0.032035
S33	0.030624	S13	0.025371	S13	0.025999	S13	0.027660	S43	[1.81144,4.34561]	0.5	S13	0.026944
S34	0.030624	S33	0.025188	S33	0.025013	S33	0.024555	S42	[1.81144,4.34561]	0.520348	S33	0.023801
E22	0.030367	S34	0.022304	S34	0.022765	E33	0.023632	E32	[2.69886,3.35506]	0.730681	S34	0.023801
N22	0.029641	E22	0.021219	E22	0.021977	S34	0.023616	H31	[1.88112,3.4493]	0.512562	E33	0.023486
E33	0.028319	N22	0.021053	N22	0.020861	E22	0.023591	N31	[2.17212,3.1189]	0.774858	E22	0.021957
S13	0.026760	S22	0.020602	E33	0.020789	N22	0.020540	S52	[1.64082,2.90676]	0.552408	H31	0.021409
S31	0.021887	E33	0.019567	S22	0.020150	H31	0.020205	S25	[1.73775,2.67714]	0.5	S22	0.018137
S22	0.021309	S26	0.019114	S26	0.018968	S22	0.018909	S21	[1.73775,2.67714]	0.662139	S26	0.018137
S26	0.021309	N32	0.018122	H31	0.018368	S26	0.018462	S31	[1.55898,2.51796]	0.739001	N22	0.017630
N11	0.018888	H31	0.017541	N32	0.016783	S42	0.014893	E22	[1.46285,2.14209]	0.646789	H11	0.013773
N12	0.018888	S31	0.016464	S31	0.015616	S43	0.014236	E31	[1.48524,1.92029]	0.675224	N32	0.013462
N23	0.017205	S42	0.014756	S42	0.014808	N32	0.014087	E12	[1.3232,1.88296]	0.73459	S42	0.013400
S21	0.016776	N11	0.014742	N11	0.014240	S31	0.013822	H11	[1.21722,1.7032]	0.513748	S43	0.013400
S25	0.016015	S21	0.013937	H11	0.013434	H11	0.013601	S51	[1.04206,1.85598]	0.588416	S31	0.013244
N13	0.013499	H11	0.013332	S43	0.013270	H41	0.013558	S41	[0.9555,1.78963]	0.577056	N11	0.011738
S42	0.013147	N12	0.013053	S21	0.013236	N11	0.013197	S24	[1.03337,1.58321]	0.618407	N12	0.011738
S43	0.013147	S43	0.012920	N12	0.012960	N12	0.012693	N22	[1.1401,1.34627]	0.5	H41	0.011126
N32	0.012876	H41	0.012639	H41	0.012918	N23	0.011602	N21	[1.1401,1.34627]	0.718915	S21	0.010174
S24	0.010677	S25	0.012449	S25	0.012054	S21	0.011464	H33	[0.71778,1.44861]	0.602178	S25	0.010174
S41	0.009492	N23	0.012154	N23	0.011965	S25	0.011017	N11	[0.759,1.25804]	0.540678	N23	0.009702
E23	0.008075	N13	0.009635	E23	0.009559	E23	0.010155	N34	[0.83114,1.1453]	0.5	E23	0.008967
S44	0.006231	N34	0.009309	N34	0.009049	S41	0.008886	N32	[0.83114,1.1453]	0.661054	S52	0.008699
S52	0.004730	E23	0.009275	N13	0.008890	H33	0.008564	H41	[0.70149,1.13498]	0.603941	N34	0.008393
S23	0.004462	S52	0.008171	S52	0.008215	N34	0.008375	S54	[0.61831,1.11409]	0.5	H33	0.008169
S51	0.003829	S24	0.008006	H33	0.008014	S52	0.008284	S53	[0.61831,1.11409]	0.661846	S41	0.007220
S53	0.002731	H33	0.007756	S41	0.007970	N13	0.007429	E33	[0.64874,0.92318]	0.56956	N13	0.006531
S54	0.002429	S41	0.007645	S24	0.007702	S24	0.006919	N12	[0.672,0.86174]	0.550236	S24	0.005896
S55	0.001546	H12	0.006962	H12	0.006820	H12	0.006396	S23	[0.5046,0.98125]	0.501867	E24	0.005590
S32	0.000000	S51	0.006134	S51	0.005987	E24	0.006037	S32	[0.52952,0.95455]	0.58258	H12	0.005585
S56	0.000000	S32	0.005652	S32	0.005756	S32	0.005944	S44	[0.33614,1.03286]	0.513851	S51	0.005525
E24	0.000000	H23	0.005442	H23	0.005474	S51	0.005637	E23	[0.49956,0.85014]	0.700636	S32	0.005401
N14	0.000000	S44	0.004830	E24	0.005154	H23	0.005448	H12	[0.49356,0.7153]	0.716183	H32	0.004676
N34	0.000000	E24	0.004764	S44	0.004904	S44	0.005098	S55	[0.37522,0.69381]	0.663563	H23	0.004669
H11	0.000000	S23	0.004646	S23	0.004527	H32	0.004968	H32	[0.28485,0.65808]	0.544825	S44	0.004167
H12	0.000000	S53	0.004210	S53	0.004165	S23	0.004209	H23	[0.40115,0.50832]	0.595829	S23	0.003729
H13	0.000000	H21	0.003982	H32	0.004122	S53	0.004051	N13	[0.40942,0.47951]	0.586548	S53	0.003278
H21	0.000000	S54	0.003780	S54	0.003825	S54	0.003912	E24	[0.32312,0.53]	0.558802	S54	0.003278
H22	0.000000	H32	0.003759	H21	0.003729	N14	0.003195	N23	[0.38003,0.44876]	0.840303	H51	0.002742
H23	0.000000	N14	0.003308	N14	0.003277	H21	0.003178	H51	[0.23827,0.44786]	0.89211	H21	0.002673
H31	0.000000	S55	0.002765	S55	0.002636	H42	0.003106	H21	[0.2296,0.29094]	0.898511	N14	0.002664
H32	0.000000	H51	0.002492	H51	0.002593	H51	0.002828	H13	[0.17111,0.26352]	0.500174	H13	0.002265
H33	0.000000	H13	0.002358	H42	0.002530	H13	0.002678	S56	[0.13099,0.30358]	0.794194	H42	0.002020
H41	0.000000	H42	0.002253	H13	0.002452	S55	0.002339	N14	[0.13746,0.19556]	0.778545	S55	0.001989
H42	0.000000	H22	0.001349	H22	0.001351	H22	0.001331	H42	[0.11091,0.17946]	0.999997	H22	0.001020
H51	0.000000	H52	0.001067	H52	0.001130	H52	0.001269	H22	[0.08761,0.11101]	0.615939	S56	0.000952
H52	0.000000	S56	0.000987	S56	0.001011	S56	0.001063	H52	[0.06855,0.11849]	1	H52	0.000903
H53	0.000000	H53	0.000268	H53	0.000298	H53	0.000360	H53	[0.02376,0.03902]		H53	0.00029

The final sequence of influencing factors (with weights) in managing natural and human resources for economic and regional development can be seen in Figure 5.

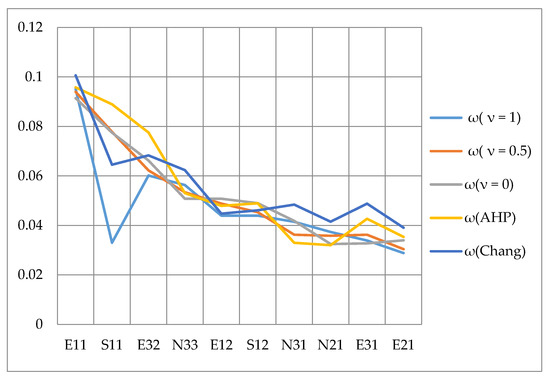
Figure 5. Graphical representation of final weights of influential indicators by AHP and FAHP with Chang approach and different degrees of optimism.

The results obtained by applying classical AHP and FAHP methods, whether they are different degrees of optimism or Chang’s approach, are favored as the most influential factor stability of the environment and business sector.

Based on the obtained final weights that represent the optimistic attitudes of decision-makers, the following are significant reductions in the pressure of public investment on the budget, efficient conservation of ecosystems and resources, and the global response to the COVID-19 pandemic. In the pessimistic scenario, the following indicators stand out: the development of a stimulating entrepreneurial environment, reducing the pressure of public investment on the budget, and global response to the COVID-19 pandemic. In the balanced scenario, the development of a stimulating entrepreneurial environment, reducing the pressure of public investments on the budget, efficient preservation of ecosystems and resources, as well as the global response to the COVID-19 pandemic are still important indicators.

Differences can be seen in the second factor of influence Chang’s approach and optimistic attitude favor reducing the pressure of public investment on the budget, and moderate and pessimistic attitudes, as well as the AHP method, emphasize the development of a stimulating entrepreneurial environment.

In both scenarios, the same group of indicators stands out by the dominant factor being the stability of the business environment and the business sector. However, the development of a stimulating entrepreneurial environment is not among the significant factors in the optimistic scenario, unlike the pessimistic one. On the other hand, efficient conservation of ecosystems and resources themselves resource-related environmental factors are not so significant in this scenario.

Although sustainable development has three dimensions: economic, environmental, and social, we have included in this study another dimension of the framework for strengthening participation in development to establish the extent to which indicators that stand out within this group affect economic growth and regional development. The optimistic scenario includes only one of these factors as the dominant ones, the targeted attraction of investments. The results obtained using the IAHP method favor precisely the indicators from this dimension because the estimates given using the interval method defined wider intervals that favored this group of factors. Thus, the most significant indicators by IAHP are the development of a stimulating entrepreneurial environment, targeted investment attraction, reducing the degree of the gray economy in GDP, effective preservation of ecosystems and resources themselves.

The measure chosen for the realization of comparative analysis of criterion weighting methods presented in this research is one of the most frequently used rank correlation coefficients used today to solve the problem of MCDM. Spearman’s correlation coefficient represents the measure of the strength and direction of the correlation between two ranked criteria [76]. This coefficient is given by (8)

$$S_c=-\frac{6{\sum }_{i=1}^n{\left(r_{x_i}-r_{y_i}\right)}^2}{n\left(n^2-1\right)},$$

(8)

where $r_{x_i}$ and $r_{y_i}$ are ranks of the element i in the compared rankings, $n$ is the number of elements in the ranking.

WS method rank correlation coefficient is new, and was introduced in [77]. The main goal of this coefficient is to choose indicators that are closer to the top of the considered ranking. It provides a typical ranking scenario where the first three places are the most significant and targets differences in the given ranks depending on what changes in positions are observed. This coefficient is used in many decision-making problems and coefficient is calculated as shown in (9)

$$WS=1-{\sum }_{i=1}^n\left(2^{-r_{x_i}}\frac{\left|r_{x_i}-r_{y_i}\right|}{\max \left\{\left|1-r_{x_i}\right|,\left|n-r_{x_i}\right|\right\}}\right).$$

(9)

A comparative analysis of the similarity of the methods is given in Table 5.

Table 5. Comparison similarity analysis of methods.

	FAHP $\mathit{\nu }=1$	FAHP $\mathit{\nu }=0.5$	FAHP $\mathit{\nu }=0$	FAHP Chang	AHP	IAHP
$\mathrm{FAHP} \nu =1$		$$\begin{gathered} Sc=0.997 \\ WS=0.964 \end{gathered}$$	$$\begin{gathered} Sc=0.988 \\ WS=0.964 \end{gathered}$$	$$\begin{gathered} Sc=0.877 \\ WS=0.991 \end{gathered}$$	$$\begin{gathered} Sc=0.989 \\ WS=0.964 \end{gathered}$$	$$\begin{gathered} Sc=0.836 \\ Ws=0.837 \end{gathered}$$
$\mathrm{FAHP} \nu =0.5$			$$\begin{gathered} Sc=0.995 \\ WS=0.997 \end{gathered}$$	$$\begin{gathered} Sc=0.871 \\ WS=0.991 \end{gathered}$$	$$\begin{gathered} Sc=0.995 \\ WS=0.999 \end{gathered}$$	$$\begin{gathered} Sc=0.845 \\ WS=0.877 \end{gathered}$$
$\mathrm{FAHP} \nu =0$				$$\begin{gathered} Sc=0.852 \\ WS=0.986 \end{gathered}$$	$$\begin{gathered} Sc=0.996 \\ WS=0.997 \end{gathered}$$	$$\begin{gathered} Sc=0.838 \\ WS=0.865 \end{gathered}$$
FAHP Chang					$$\begin{gathered} Sc=0.847 \\ WS=0.991 \end{gathered}$$	$$\begin{gathered} Sc=0.836 \\ WS=0.837 \end{gathered}$$
AHP						$$\begin{gathered} Sc=0.850 \\ WS=0.882 \end{gathered}$$

Figure 5 highlights the most influential indicators for AHP, fuzzy AHP with Chang’s (EAM) approach and the three-level optimism approach and Figure 6 shows the most influential factors singled out as measures by AHP and FAHP.

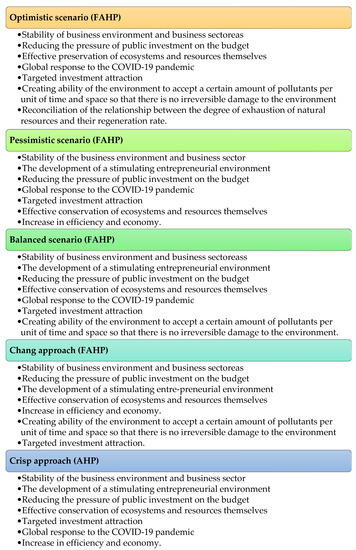
Figure 6. The most influential factors singled out as measures by AHP and FAHP.

5. Conclusions

Managing natural and human resources for economic and regional development is a global challenge that requires attention and importance in every society guided by the principles of sustainable development. Natural resources underpin economic activities in many ways. Issues about socially, environmentally, and economically sustainable promotion of growth in the best way have been increasingly at the heart of the interest. The strategy of economic development of the region includes defining a model for achieving the planned evolution of the state. Developing countries can apply a multi-criteria analysis in assessing and solving complex solvency problems from different perspectives. This paper examines the influential factors of sustainable economic development, taking into account the naturally available wealth also human resources as the backbone of the development of the region’s economy. The paper discusses indicators divided into four groups a framework for strengthening participation in development, human social resources, economic potential, and natural resources. In recent decades, the FAHP method, based primarily on triangular fuzzy numbers, was proven suitable in a wide range of fields of engineering, environment, industry, economy, etc. The approach in the indicators’ evaluation, given by unclear numbers, was significantly influenced the final results from the determination of influencing factors. Using methods, AHP and triangular fuzzy AHP, 57 different sub-criteria are ranked for identifying priorities in resource management and economic regional development. The triangular fuzzy of the AHP indicates the importance of the stability of the environment and the business sector for different degrees of optimism, namely the Chang approach and the classic AHP. The IAHP approach indicates the importance of stimulating entrepreneurial environment development. The analysis of the similarity of the results gives a generally satisfactory degree of similarity, although the second indicator already differs in some scenarios. The proposed model offers five scenarios, and it is up to the managers to decide on the most acceptable option. Such a proposal provides enough flexibility for the decision-maker. In future research, we intend to apply the spherical fuzzy analytic hierarchy process to find the best model to support IoT influence factors of entrepreneurship.