Conflict Resolution Model of Automated Vehicles Based on Multi-Vehicle Cooperative Optimization at Intersections

Abstract

The traditional conflict resolution algorithm is designed for automated vehicles based on the premise of the right of way, but there is an unclear road right of way at unsignalized intersections, which brings trouble to the decision making of automated vehicles. The objective of this work is to provide our system with evolving cooperative and non-cooperative decisions. We achieve this by integrating game theory into the decision making. When the system decides to drive cooperatively, the joint action is planned to optimize the overall revenue of multi-vehicles based on the cooperative game, considering the conflict relationship with its neighboring vehicles. When the system fails to perform cooperative driving or response timeout, the vehicle-mounted unit would take non-cooperative driving to optimize the trajectory considering only its individual benefit. The proposed model can provide our system with stability and robustness, which effectively solved the conflict resolution problem when the right of way was not clear at intersections. We have implemented some simulation experiments of cooperative and non-cooperative conflict resolution, the results show that the revenue among various interest groups is more balanced with a cooperative conflict resolution method. Compared with the non-collaborative driving decision, the conflict resolution time is shortened, and the average delay of each vehicle at intersections is reduced by 1~2 s, with an average reduction of approximately 5%. The research can provide a reference for collaborative driving of automated vehicles at unsignalized intersections.

1. Introduction

In recent years, many scholars have studied the conflict resolution of multi-vehicles at intersections. Aoude et al. [1] combined a support vector machine and Bayesian (SVM-BF) to identify driving intentions of vehicles approaching the intersection. By setting safety thresholds, the suspicious vehicles can be determined to avoid accidents. Wei J. et al. [2] proposed an algorithm that integrates driver intention prediction and cost function, so that driverless vehicles can interact better with other conflict vehicles. Xiong et al. [3,4] proposed a prediction method of driving intention of other vehicles based on the hidden Markov model (HMM). Then, the motion behavior of driverless vehicles was controlled by a hybrid state system to realize the conflict resolution at the freeway ramp. At the same time, Arda Kurt et al. [5] established the decision-making model of the driverless vehicle using the finite state machine (FSM) and probability model to realize the conflict resolution. However, the basic idea of these conflict resolution algorithms is the assumption that intersection priority as the prerequisite, the driverless vehicle mainly uses the slowdown or waiting of decision-making driving strategy at intersections. Although these models have realized a way to avoid conflicts, they are all a method of intelligent control of individual vehicles and limit the intersection traffic potential of driverless vehicles.

2. Related Work

At present, with the development of intelligent and connected vehicle technology, data interaction can be realized between automated vehicles and intelligent traffic facilities, so multi-vehicle collaborative control for autonomous driving has become a research hotspot [6,7]. Under the condition of vehicle-to-vehicle communication (V2V), the overall system conceptualization of autonomous driving is presented in Figure 1. Wang Pangwei et al. [8] designed a collision avoidance method of multi-vehicle collaborative response based on sliding mode control, and realized the purpose of collaborative collision avoidance by distributing the acceleration of the front and rear vehicles. L. EVIN [9] used the mixed integer linear programming model to coordinate the passage time of automated vehicles at conflict points, and optimized the optimal solution by means of the rolling time window. Fayazi [10] established an automatic driving intersection control model of automated vehicles based on mixed integer linear programming, and optimized the arrival time and driving speed at the intersection. However, the complexity of such model algorithms increases exponentially with the increase in variables, and the solution efficiency is not ideal.

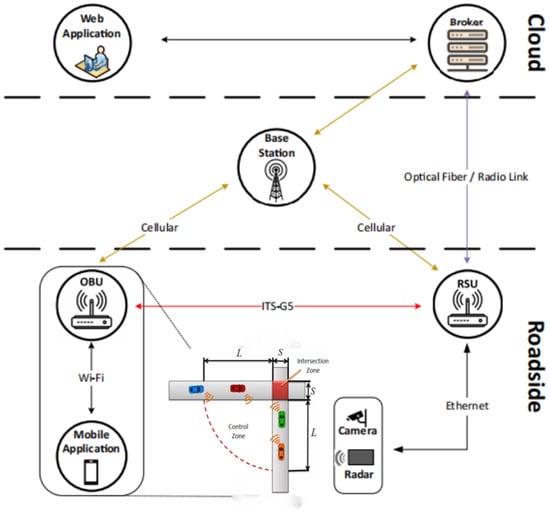
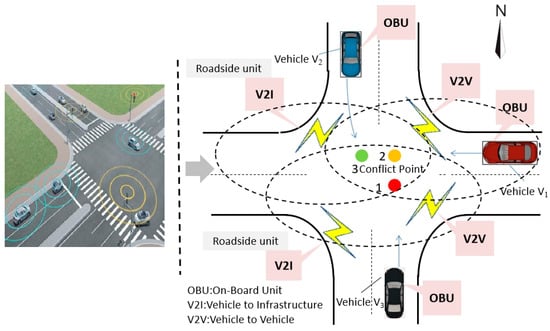
Figure 1. The overall system concept of autonomous driving based on network connection.

For such decision tasks, game theory can provide better judgment and identification of the evolution of uncertain situations. Hideyuki Kita et al. [11] used game theory to study the driver’s decision behavior at the highway ramp, the interaction of incoming vehicles and straight-crossing vehicles at the ramp was analyzed into a two-person non-zero cooperative game, and the model results were consistent with the decision behavior of drivers. Wang Meng et al. [12] proposed a prediction method of lane transformation and vehicle following control based on optimal control and dynamic game theory. Under the condition of vehicle-to-vehicle communication (V2V), Menendez-Romero C et al. [13] presented a novel method based on game theory that automatically adapts the driving behavior, integrating the merging intention of other vehicles. The ability to plan adequate courtesy behaviors improves public acceptance of autonomous systems and the comfort of the surrounding vehicles without considerably decreasing their own comfort. J. Nie et al. [14] proposed a decentralized cooperative lane-changing decision-making framework for connected automated vehicles, which showed the high potential of our proposed framework in traffic dynamics. YANG Z [15] used the cooperative game theory to propose a centralized coordination method for connected vehicles at unsignalized intersections, and an optimal strategy set was obtained by solving the constrained multi-objective optimization problem. However, there may be response timeout for the driving model, and the robustness of the model needs to be further improved.

The objective of this work is to provide our system with evolving cooperative and non-cooperative decisions. We achieve this by integrating game theory into the decision-making. When the system decides to drive cooperatively, the joint action is planned to optimize the overall revenue of multi-vehicles based on a cooperative game, considering the conflict relationship with its neighboring vehicles. When the system fails to perform cooperative driving or response timeout, the vehicle-mounted unit would take non-cooperative driving to optimize the trajectory considering only individual benefit. The proposed model can help automated vehicles cross intersections safely and more efficiently.

3. Method

3.1. Vehicle Conflict Analysis

When multiple vehicles are about to enter the conflict area at intersections, the parameter of post encroachment time (PET) is used to evaluate potential conflicts at intersections, which can be used as an important indicator to describe the possibilities among vehicles crossing the intersection with any angle.

The parameter $T_{\mathrm{pet}}$ is defined as the time difference between the front car leaving and the rear car entering the intersection area.

$$T_{\mathrm{pet}}=\{\begin{array}{c}{T}_{\mathrm{C}12}-T_{\mathrm{C}21}, T_{\mathrm{C}11}\le T_{\mathrm{C}21}\le T_{\mathrm{C}12}\\ T_{\mathrm{C}22}-T_{\mathrm{C}11}, T_{\mathrm{C}21}\le T_{\mathrm{C}11}\le T_{\mathrm{C}22}\end{array}$$

(1)

where $T_{C11}$ is the time when the vehicle C1 enters the encroachment zone; $T_{C12}$ is the time when the vehicle C1 leaves the encroachment zone; $T_{C21}$ is the time when the vehicle C2 enters the encroachment zone; $T_{C22}$ is the time when the vehicle C2 leaves the encroachment zone.

The intersection traffic conflicts are identified by comparing the value of $T_{\mathrm{pet}}$ and $T_{\mathrm{th}}$, and $T_{\mathrm{th}}$ is the threshold value of intersection conflict, which is 3 s, by referring to reference [11]. If there is $T_{\mathrm{pet}}>T_{\mathrm{th}}$ , the result of the system is “no conflict”. If there is $T_{\mathrm{pet}}\le T_{\mathrm{th}}$, the result of the system is “yes conflict”.

In this paper, we assume that all vehicles are equipped with vehicle to everything (V2X) communication systems and the communication effect is reliable, each vehicle will be able to V2V in real time and obtain accurate information of the surrounding vehicles’ movement within the communication range and there is no pedestrian and non-motor vehicle interference during the process of crossing the intersection [16,17,18].

3.2. Decision-Making Process

When the vehicles have entered the effective V2V communication range at intersections, the first step is to determine whether there is a potential conflict. If there is not potential conflict, the vehicle will be normal speed when crossing the intersection. If there is a potential conflict, the outputs of conflict resolution unit will be executed to avoid collision.

A collision resolution method based on multi-vehicle cooperative optimization is proposed, as shown in Figure 2. When the conflict resolution unit decides to drive cooperatively, the joint action is planned to optimize the overall revenue of multi-vehicle, and make all conflict vehicles run by a centralized control unit. When the system fails to perform cooperative driving or cooperative response timeout, the vehicle-mounted unit would take non-cooperative driving to ensure the stability and robustness of the system. When performing non-cooperative driving, the action is planned to minimize risk to the individual. Finally, all conflict vehicles’ states are updated in the communication range and the conflict vehicles in different driving directions would cross the intersection safely and efficiently.

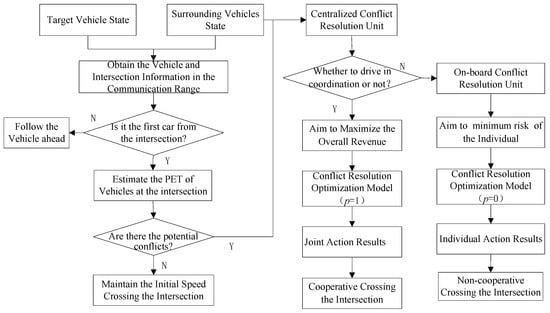
Figure 2. Conflict resolution method for intelligent connected vehicles (ICV) at unsignalized intersections.

3.3. Define Participants and Policies

The objective of this work is to provide our system with evolving cooperative and non-cooperative decisions. We achieve this by integrating game theory into the decision making. When the system decides to drive cooperatively, the joint action is planned to optimize the overall revenue of multi-vehicles based on a cooperative game, considering the motion information and the conflict relationship with its neighboring vehicles.

There are four elements of game behavior [19,20,21]:

The participants $C_i$ is the decision-making subject, the set of participants is $C$: $C=\left\{C_1, C_2, C_i\cdots , C_N\right\}$, where C_i is participant $i$.

The participants’ strategy set is $S$:

$S=\left\{S_1, S_2, S_i\cdots , S_N\right\}$, where the strategy refers to the behavior rules of participants under given information sets. The policies of each participant are formalized as $S_i:C_i\to a_i, i=1, 2, \cdots N,$ where $a_i$ represents the action taken by the participant $C_i$.

Income $U_i$ refers to the expected benefit level of the main body under a specific strategic combination. The utility of participants $C_i$ is not only related to their own strategies, but also to the strategies of other participants, it would be good if participants $C_i$ utility was $U_i=\left(s_1, s_2, s_i\cdots s_N\right)$, where $s_i$ is the main body i strategy, that is $s_i\in S_i$.

Nash Equilibrium. A game with N participants is described as $G=\left\{A, S, U\right\}$. If $S^{\ast }=\left(s_1^{\ast }, s_2^{\ast }, s_i^{\ast }\cdots s_N^{\ast }\right)$ is a Nash Equilibrium, the condition must be satisfied by

$$U_i(s_i^{*}, s_{-i}^{*})\ge U_i(s_i, s_{-i}^{*}) \forall s_i\in S_i$$

(2)

where $s_i^{*}$ represents the strategy chosen by the i participant; $s_{-i}^{*}$ represents the vector composed of the strategies of all participants except i; $U_i$ represents the utility level of the i participant; $S_i$ represents the strategy space of the i participant.

In this paper, the conflict vehicles at intersections are the participants, the variation of acceleration (acceleration, uniform speed and deceleration) is one of the conflict resolution strategies, the decision-making is made based on maximizing the expected utility of the involved participants. Our goal is to choose a joint action for the conflict vehicles so that the combined expected utility is maximized when cooperatively driving, the best strategy will be chosen by an optimization problem.

3.4. Profit Indicators Selection

Driving utility is not only related to the situation of vehicles, but also to the degree of conflict between vehicles. Therefore, safety profit, rapidity profit, and comfort profit are used to describe the overall driving utility [15,22,23].

(1) Security profit

Safety is the primary index to avoid collision. $\mathsf{\Delta }T$ denotes the time difference between the two vehicles arriving at the conflict point, when $\mathsf{\Delta }T$ is smaller, the possibility of conflict is greater and the security profit is smaller. The security profit $f_{safe}\left(\mathsf{\Delta }T\right)$ is adopted in Equation (3).

$$f_{safe}(\mathsf{\Delta }T)=\{\begin{array}{c}\infty , N<2\\ \frac{1}{\exp (-\mathsf{\Delta }T)}, N\ge 2\end{array}$$

(3)

where we assume that the time difference between any two vehicles arriving at the conflict point is $\mathsf{\Delta }{T}_{kj}$, and $\mathsf{\Delta }T=\max \left\{\mathsf{\Delta }{T}_{12}, \mathsf{\Delta }{T}_{kj}\cdots , \mathsf{\Delta }{T}_{(n-1)n}, N\ge 2\right\}$.

$$\begin{array}{l}\mathsf{\Delta }{T}_{kj}=|{\left\{{\left[v_k(t)/a_k(t)\right]}^2+2\left[L_k(t)/a_k(t)\right]\right\}}^{1/2}-v_k(t)/a_k(t)-\\ \hspace{1em}\hspace{1em}\hspace{1em}{\left\{{\left[v_j(t)/a_j(t)\right]}^2+2\left[L_j(t)/a_j\left(t\right)\right]\right\}}^{1/2}+v_j(t)/a_j(t)|\\ k\in N, j\ne k, j=1, 2\cdots N, t=1, 2, \cdots \end{array}$$

(4)

where: $t$ refers to the tth cycle and subscripts $k, j$ refer to vehicles $k$ and $j$; $a_k(t)$, $a_j(t)$, $v_k(t)$, $v_j(t)$ refer to the velocity and the acceleration of the target vehicle $k$ and the conflict vehicle $j$ at time $t$. $L_k(t)$, $L_j(t)$ refer to the distance between the two vehicles that are both approaching the conflict point.

(2) Rapidity profit

Rapidity profit refers to the premise that vehicles are expected to cross the intersection as quickly as possible. Therefore, it is reflected through the change of velocity in the model, the calculation of rapidity profit is as follows:

$$\begin{array}{l}{f}_{efficence}(\mathsf{\Delta }{v}_j^{})=v_j(t+1)-v_j(t)=a_j(t)\cdot \mathsf{\Delta }t\\ j\ne k, j=1, 2\cdots N, t=1, 2, \cdots \end{array}$$

(5)

where: $\mathsf{\Delta }{v}_j^{}$ refers to the velocity change of any vehicle $j$ in a period of time $\mathsf{\Delta }t$.

(3) Comfort profit

Since lane change is not involved in the process of vehicles crossing the intersection, the changes of longitudinal acceleration (expressed as $\left|\mathsf{\Delta }a\right|$) are employed as the index to describe the comfort profit. When the change of acceleration is smaller, the more comfortable the vehicle is and the higher the profit is. The comfort profit is as follows:

$$\begin{array}{l}{f}_{comfort}(\mathsf{\Delta }{a}_j^{})=\left|a_j(t)-a_j(t-1)\right|\\ j\ne k, j=1, 2\cdots N, t=1, 2, \cdots \end{array}$$

(6)

where: $\mathsf{\Delta }{a}_j^{}$ refers to the change of the vehicle $j$ acceleration from the $t-1$th cycle to the $t$th cycle, which includes all actions of the conflict resolution strategy set.

According to the above analysis, the profit function of the vehicle $j$ can be expressed as follows:

$$f(\cdot )=\alpha f_{safe}(\mathsf{\Delta }T)+\beta f_{efficence}(\mathsf{\Delta }{v}_j^{})+\gamma f_{comfort}(\mathsf{\Delta }{a}_j^{})$$

(7)

where: $\alpha$,$\beta$,$\gamma$ refer as the weights of security profit, rapidity profit, and comfort profit, in which $\alpha +\beta +\gamma =1$. $f(\cdot )$ represents as a normalized calculation and a zero-mean normalization method was adopted in this paper.

3.5. Model Objective Function

We assume that the acceleration set $(a_1, a_2, \cdots , a_n)$ of the conflict vehicles $j=1, 2, \cdots$$n$ is the joint action of multi-vehicles during the entire crossing process. Our goal is to choose a joint action for the conflict vehicles so that the overall driving utility is maximized with the cooperative game, thus the conflict resolution problem is modeled as a nonlinear optimization model with constraints as follows:

$$\begin{array}{l}\max F=f_k(a_1, a_2, \cdots , a_n)+p\cdot {\displaystyle \sum _{j=1}^{N-1}{f}_j(a_1, a_2, \cdots , a_n)}\\ s.t.\hspace{0.17em}\hspace{0.17em}{a}_{\min }\le a_k(t)\le a_{\max }, k\in N;\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{v}_{\min }\le v_k(t)\le v_{\max }, k\in N;\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{a}_{\min }\le a_j(t)\le a_{\max }, j\ne k, j=1, \cdots N;\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{v}_{\min }\le v_j(t)\le v_{\max }, j\ne k, j=1, \cdots N;\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{t}_0\le t\le t_d;\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{L}_k(t)-[v_k(t)t+\frac{1}{2}{a}_k(t)t^2]\cos {\phi }_k\ge 0\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{L}_j(t)-[v_j(t)t+\frac{1}{2}{a}_j(t)t^2]\sin {\phi }_j\ge 0\end{array}$$

(8)

where $(a_1, a_2, \cdots , a_n)$ refers to the joint action set of all the conflict vehicles; $f_k(a_1, a_2, \cdots , a_n)$ is the profit of the target vehicle; $f_j(a_1, a_2, \cdots , a_n)$ is the profit of the conflict vehicles $j$ calculated by the system when cooperative driving. $p$ refers to the cooperation coefficient between the conflict vehicles, its value is [0~1]; $p$ = 0 refers to a non-cooperative relationship between vehicles; $p$ = 1 refers to a cooperative relationship between vehicles; ${\alpha }_{\min }, {\alpha }_{\max }^{}$ are the acceleration limit for vehicle control, $v_{\min }, v_{\max }$ are the speed limit of vehicles driving at intersections. $t_0$, $t_d$ are the time for vehicles entering and leaving the conflict zone.

3.6. Model Solution

A genetic algorithm (GA) is used to solve the constrained nonlinear optimization Model (8). The optimal solution of each generation in the algorithm is saved by the fitness function. After several iterations, the “global” optimal solution $(a_1{}^{*}, a_2{}^{*}, \cdots , a_n{}^{*})$, the fitness function of genetic algorithm [7] can be expressed as

$$\max F=f_k(a_1, a_2, \cdots , a_n)+p\cdot {\displaystyle \sum _{j=1}^{N-1}{f}_j(a_1, a_2, \cdots , a_n)}$$

(9)

Hence, the best solution can be calculated using an optimization method in each cycle of the whole process. The solution is described as follows during the whole multi-vehicle crossing process.

Step1 Established genetic iterative number of total $\mathsf{\Gamma }$, population size $B$, optimization model of constraint satisfied Equation (2).

Step2 Randomly generated genetic individuals of group $B$ according to constraint conditions to form the initial population.

Step3 Updated the vehicle position and velocity, etc., according to vehicle motion model Model (8), and obtained the vehicle driving trajectory in the conflict area under each genetic individual (acceleration combination).

Step4 Used GA algorithm to solve the acceleration optimization solution under each genetic individual, respectively, and obtained the optimal reference driving trajectory of vehicles in the conflict area, and obtained the overall driving revenue at intersections according to Equation (6).

Step5 Evaluated and marked each genetic individual according to Equation (7).

Step6 Evaluated all genetic individual, if reached the iteration number of total $\mathsf{\Gamma }$, output the optimal individual and its optimal solution, and stopped the calculation, otherwise, went into Step7.

Step7 Selected regenerative individuals based on fitness function value, and cross-mutated them to generate the next generation of new individuals, so as to summarize the new generation of population and entered into the next iteration. The iteration calculation of each generation needed to meet the constraint conditions and returned to Step3.

Here, $G_{\Re }\left\{L_j(t+1), v_j(t+1)\right\}$ is the state of the vehicle $j$ calculated by the system according to Formula (10) in the tth cycle $k\in N$,$j\in M$.

$$\{\begin{array}{l}{L}_k(t+1)=L_k(t)-[v_k(t)t+\frac{1}{2}{a}_k(t)t^2]\cos {\varphi }_i, k\in N;\hfill \\ v_k(t+1)=v_k(t)-a_k(t)t, k\in N;\hfill \\ L_j(t+1)=L_j(t)-[v_j(t)t+\frac{1}{2}{a}_j(t)t^2]\cos {\varphi }_i, j\in \mathrm{M};\hfill \\ v_j(t+1)=v_j(t)-a_j(t)t, j\in \mathrm{M};\hfill \end{array}$$

(10)

where: $L_i(t+1)$, $L_j(t+1)$, $v_i(t+1)$, $v_j(t+1)$ refer to the position and velocity of vehicles $i$ and $j$ in the next step; ${\phi }_i, {\phi }_j$ refer to the heading angle of vehicles $i$ and $j$.

4. Results and Discussion

4.1. Simulation Scenarios

A simulation scenario for conflict resolution at unsignalized intersections was constructed as shown in Figure 3, it was assumed that the vehicle C1 traveled from south to north, the vehicle C2 traveled from east to west, the vehicle C3 traveled from north to east, this would form conflict points 1, 2, and 3, so two simulation experiments, such as two-vehicles conflict resolution and multi-vehicle conflict resolution, were set up in this paper.

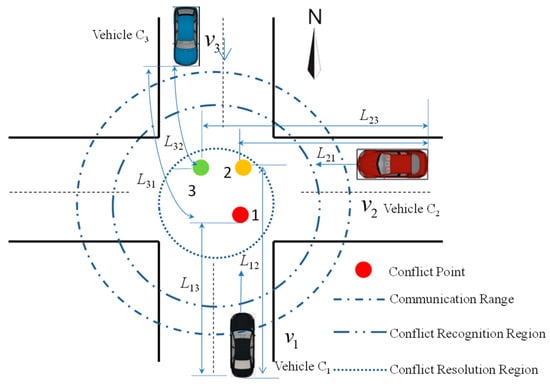
Figure 3. Experiment of collision resolution of vehicles at intersections.

In order to obtain the optimal set in the global scope as far as possible, numerical simulation experiments were carried out with MATLAB, the effectiveness of the optimal set was guaranteed in the population initialization, selection, crossover, and mutation of genetic algorithm, assuming that the population size was 50 individuals, the crossover probability was 0.8, the probability of variation was 0.05, the maximum algebra was 200 generations, and the step length was 0.5 s. The parameters of the simulation experiment were shown in Table 1 and Table 2.

Table 1. Parameter setting of two-vehicles conflict experiment.

Parameter	${\mathit{v}}_{\mathbf{max}}$ (m/s)	${\mathit{v}}_{\mathbf{min}}$ (m/s)	${\mathit{a}}_{\mathbf{max}}$ (m/s2)	${\mathit{a}}_{\mathbf{min}}$ (m/s2)	${\mathit{L}}_{\mathbf{12}}$ (m)	${\mathit{L}}_{\mathbf{21}}$ (m)	${\mathit{v}}_{\mathbf{1}}$ (m/s)	${\mathit{v}}_2$ (m/s)	$\mathit{\alpha }, \mathit{\beta }, \mathit{\gamma }$
Value	16.7	0	2	−2	140	125	13	10.5	0.4, 0.3, 0.3

Table 2. Parameter setting of multi-vehicle conflict experiment.

Parameter	${\mathit{L}}_{\mathbf{12}}$ (m)	${\mathit{L}}_{\mathbf{13}}$ (m)	${\mathit{v}}_{\mathbf{1}}$ (m/s)	${\mathit{L}}_{\mathbf{21}}$ (m)	${\mathit{L}}_{\mathbf{23}}$ (m)	${\mathit{v}}_{\mathbf{2}}$ (m/s)	${\mathit{L}}_{\mathbf{31}}$ (m)	${\mathit{L}}_{\mathbf{32}}$ (m)	${\mathit{v}}_{\mathbf{2}}$ (m/s)
Value	200	180	16.7	150	160	13.3	140	100	11.1

4.2. Results of Two-Vehicle Conflict

Take a two-vehicle conflict (conflict point 2 in Figure 3) as an example, there was a potential conflict ($T_{\mathrm{pet}}\le T_{\mathrm{th}}$). If the conflict resolution unit determined cooperative driving, it meant that the system executed the conflict resolution optimization algorithm to maximize the overall driving revenue, and the length of conflict resolution was 18 steps. The joint action of the two vehicles was shown in the Figure 4a. It can be seen that acceleration strategies of the vehicle C1 and C2 were constantly changing during the conflict resolution process. This is due to the best solution for every step being chosen by an optimization problem. If the system was in the case of non-cooperative driving, it was assumed that the conflicting vehicle C1 had the right of way, the conflict resolution algorithm was executed only to maximize individual revenue, and the length of conflict resolution was 22 steps. The action of the ego vehicle was shown in the Figure 4b. It can be seen that acceleration strategies of the vehicle C2 were very conservative.

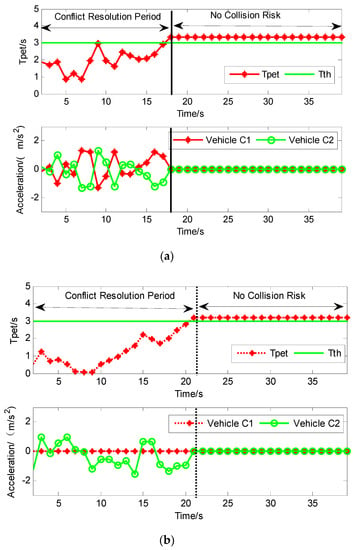
Figure 4. The conflict resolution result of vehicle C1 and vehicle C2 with cooperative and non-cooperative driving modes. Cooperative driving is that the joint action is planned to optimize the overall revenue of multi-vehicles and make all conflict vehicles run by a centralized control unit. When the system fails to perform cooperative driving or response timeout, the vehicle-mounted unit would take non-cooperative driving to ensure the stability and robustness of the system. (a) Cooperative driving; (b) Non-cooperative driving.

The speed and distance changes of the two vehicles in cooperative driving and non-cooperative driving were shown in Figure 5. It can be seen from Figure 5a that the conflict vehicle C1 increased its velocity and crossed the intersection conflict point at $T$ = 22 step earlier. The ego vehicle C2 reduced its velocity and crossed the intersection conflict point at $T$ = 30 step later. It made vehicles from different directions cross the intersection in sequence, which effectively solved the problem of right-of-way allocation and the conflict risk was avoided at intersections. It can be seen from Figure 5b that the conflict vehicle C1 continued to maintain its original velocity and crossed the intersection conflict point at $T$ = 25 step earlier. The ego vehicle C2 only took individual revenue as the goal and reduced its velocity crossing the intersection conflict point at = 31 step later.

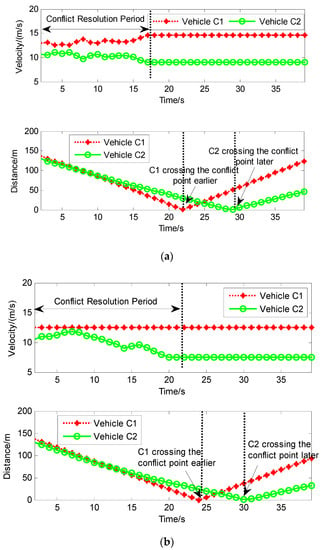
Figure 5. The speed and distance changes of two-vehicle conflict resolution with cooperative and non-cooperative driving modes. Cooperative driving is that the joint action is planned to optimize the overall revenue of multi-vehicles and make all conflict vehicles run by a centralized control unit. When the system fails to perform cooperative driving or response timeout, the vehicle-mounted unit would take non-cooperative driving to ensure the stability and robustness of the system. (a) Cooperative driving; (b) Non-cooperative driving.

4.3. Results of Multi-Vehicle Conflict

Take multi-vehicle conflicts as an example (such as conflict point 1 and conflict point 2), there were potential conflicts ($T_{\mathrm{pet}}\le T_{\mathrm{th}}$). When the conflict resolution unit determined cooperative driving, it meant that the system executed the conflict resolution optimization algorithm to maximize the overall driving revenue, and the length of conflict resolution was 38 steps. However, when the conflict resolution unit determined non-cooperative driving, the conflict resolution algorithm was executed only to maximize individual revenue, and the length of conflict resolution was 45 steps, as in Figure 6. It can be seen that cooperative driving makes all participants adjust their strategies, but non-collaborative driving avoids conflicts only by changing the behavior of one vehicle, which makes the multi-vehicle conflict resolution extremely inefficient.

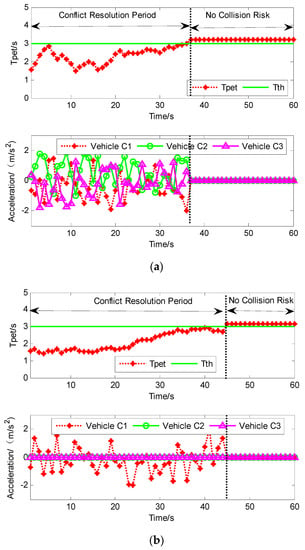
Figure 6. The conflict resolution result of vehicle C1, vehicle C2, and vehicle C3 with cooperative and non-cooperative driving modes. Cooperative driving is that the joint action is planned to optimize the overall revenue of multi-vehicles and make all conflict vehicles run by a centralized control unit. When the system fails to perform cooperative driving or response timeout, the vehicle-mounted unit would take non-cooperative driving to ensure the stability and robustness of the system. (a) Cooperative driving; (b) Non-cooperative driving.

The speed and distance changes of the multi-vehicle in cooperative driving and non-cooperative driving are shown in Figure 7. It can be seen from Figure 7a that the ego vehicle C2 increased its velocity and crossed the intersection conflict point at $T$ = 44 step earlier. For conflict vehicle C1, C3 reduced their velocity and crossed the intersection conflict point at $T$ = 50 step and $T$ = 60 step later. It made vehicles coming from different directions cross the intersection in sequence and the conflict risk was avoided. It can be seen from Figure 7b that for the conflict vehicle C2, C3 continued to maintain their original velocity and crossed the intersection conflict point at $T$ = 46 step and $T$ = 52 step earlier. The ego vehicle C1 reduced its velocity and crossed the intersection conflict point after all the conflicting vehicles were leaving.

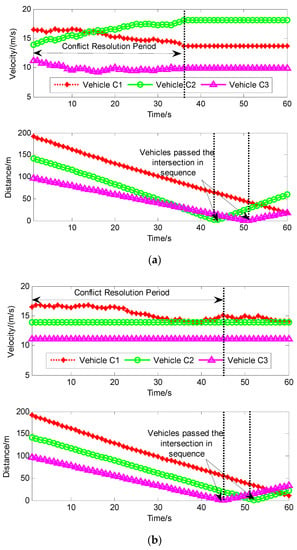
Figure 7. The speed and distance changes of multi-vehicle conflict resolution with cooperative and non-cooperative driving modes. Cooperative driving is that the joint action is planned to optimize the overall revenue of multi-vehicles and make all conflict vehicles run by a centralized control unit. When the system fails to perform cooperative driving or response timeout, the vehicle-mounted unit would take non-cooperative driving to ensure the stability and robustness of the system. (a) Cooperative driving; (b) Non-cooperative driving.

Many simulation experiments were carried out with cooperative and non-cooperative conflict resolution models, and several indicators were compared and analyzed, such as conflict resolution time, overall revenue, average velocity, average revenue, and undesirable acceleration. The results were shown in Table 3.

Table 3. Analysis of cooperative and non-cooperative conflict resolution models.

Conflict Resolution Strategy		Indicators
		Average Revenue		Average Velocity (m/s)	Unreasonable Acceleration (m/s2)	Conflict Resolution Duration	Overall Revenue
Two-vehicle conflict	Cooperative driving	Vehicle C1	0.0880	14.024	2	18	0.1529
		Vehicle C2	0.0649	10.035	1
	Non-cooperative driving	Vehicle C1	0.1279	9.060	1	22	0.1021
		Vehicle C2	−0.0258	12.250	0
Multi-vehicle conflict	Cooperative driving	Vehicle C1	0.1051	13.986	3	38	0.2332
		Vehicle C2	0.0846	16.972	1
		Vehicle C3	0.0435	9.039	2
	Non-cooperative driving	Vehicle C1	−0.0859	14.879	4	45	0.1650
		Vehicle C2	0.0971	12.989	0
		Vehicle C3	0.1538	11.267	0

It can be seen from Table 2 that the average revenue of vehicle C1 was 0.0880 and the average revenue of vehicle C2 was 0.0649 at the process of the two vehicles conflict resolution. It means that the performance of various stakeholders is balanced relatively, and the overall driving revenue is improved. Compared with the non-cooperative conflict resolution model, the time of conflict resolution is shortened by four steps, and the average delay per vehicle is reduced by 2 s at intersections, and the average reduction is approximately 5%. The performance of various stakeholders is balanced relatively at the process of the multi-vehicle conflict resolution. The time of conflict resolution is shortened by seven steps, and the average delay per vehicle is reduced by 3.5 s at intersections, and the average reduction is approximately 8%. Therefore, the conflict resolution model based on multi-vehicle cooperative optimization has certain significance for improving road traffic capacity. However, the collaborative driving optimization model has more undesirable acceleration times than the non-collaborative driving model, which reduces the vehicle driving comfort.

4.4. The Results Analysis with Compared Model

To further verify the efficiency of the proposed model, the decision-making model based on HMM [3,4] is compared with it. The results show the position and velocity changes of the two vehicles to the conflict point (Figure 8a,b).

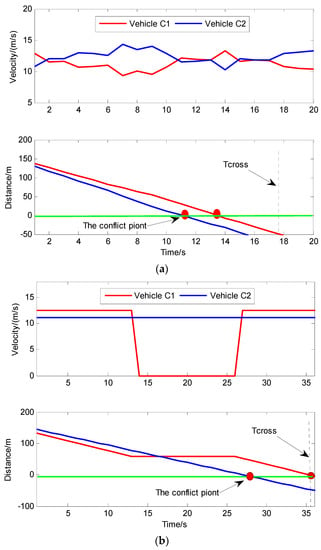
Figure 8. The results analysis of the model proposed in this paper and the compared model. (a) The model proposed in this paper; (b) The decision-making model based on HMM.

Figure 8 shows the change of the speed and distance of the vehicles at the intersection from the conflict point. The green line is the conflict point reference line. $T_{\mathrm{cross}}$ indicates the time of the conflict vehicles crossing the intersection. It can be seen from Figure 8 that the model proposed in this paper is not a one-time decision, and the strategy decision space is more detailed and dynamic, which optimizes the driving time. However, the decision-making model based on HMM requires the ego vehicle to decelerate and stop at the intersection until the conflict vehicle leaves the conflict point. Compared with the model based on HMM, it can decrease $T_{\mathrm{cross}}$ by 20%, which can obviously improve the traffic efficiency at urban unsignalized intersections.

5. Conclusions

When multiple automated vehicles shared the right of way at unsignalized intersections, this paper proposed a conflict resolution method based on multi-vehicle cooperative optimization, which optimized the velocity planning of automated vehicles in the event of conflict, and realized collaborative driving among multi-vehicles. The main contributions of this paper were as follows:

(1) The conflict resolution mainly met the requirement of no collision, and velocity planning was carried out by maximizing the overall driving revenues of various stakeholders. It made vehicles at different directions cross the intersections in sequence, which effectively solved the conflict resolution problem when the right of way was not clear at intersections.

(2) The conflict resolution unit contained two driving modes of cooperative and non-cooperative driving. If multiple vehicles failed to perform cooperative driving or respond to timeout, the system would take non-cooperative driving as output, in order to ensure the stability and robustness of the system.

(3) The simulation experiments of cooperative and non-cooperative conflict resolution were carried out, and the conflict resolution model in this paper would maximize the overall revenue, and the performance of various stakeholders was balanced relatively. Compared with the non-cooperative conflict resolution model, the time of conflict resolution was shortened, and the average delay per vehicle was reduced by 2~3 s at intersections, and the average reduction was approximately 5~8%, which improved the road capacity, so the validity and robustness of the model were verified. Therefore, the method in this paper will not only effectively solve the conflict resolution problem when the right of way is not clear at intersections, but also ensure the stability and robustness of conflict resolution.

We gain a better conflict resolution by including all possible outcomes to provide our system with stability and robustness, which effectively solved the conflict resolution problem when the right of way was not clear at intersections. It should be pointed out that the model in this paper is performed through a numerical simulation, where cooperative and non-cooperative driving are also implemented separately, and without in-depth study on the change frequency of state from the cooperative to the non-cooperative method verified. This problem can be regarded as the focus of future research and is of great significance in the promotion and application of intelligent and connected vehicles. Our further study is to design such a system, including this architecture, integrated hardware, and exchange frequency.