A Generalized Approach on Outage Performance Analysis of Dual-Hop Decode and Forward Relaying for 5G and beyond Scenarios

Abstract

This paper presents a generalized approach to the performance analysis of relay-aided communication systems for 5G-and-beyond scenarios. A dual-hop decoding and forwarding scheme is considered in the analysis. The relationship between the outage performance and cumulative distribution function (CDF) of the signal-to-noise ratio (SNR) is exploited to derive a universal expression of the outage probability that is valid for all fading scenarios, irrespective of their nature or complexity. Furthermore, an effort is made to parameterize the channel PDF in such a manner that reflects a practical fading scenario that is commonly encountered in current and future wireless communication systems. The analytical results obtained for various cases are validated through Monte-Carlo simulations.

1. Introduction

Dual-hop relaying is a special case of relay-aided communication technology in which information is transferred from the source to the destination via an intermediary relay station over two hops. Dual-hop relaying is commonly deployed in user cooperation diversity schemes. User cooperation diversity schemes help to improve communication system coverage, reliability, capacity, spectral efficiency, and power efficiency [1,2]. Dual-hop relaying is expected to become a popular solution for many 5G-and-beyond systems which require the provision of high data rates and reliable communication with good spectral and power efficiency. Dual-hop relaying is already being deployed in many popular wireless communication standards such as IEEE 802.16j/m and 3GPP LTE-Advanced [3] and is used in many communication systems such as wireless sensor networks (WSNs) and cellular communication systems. Dual-hop relaying technology was considered a key technology for 5G scenarios and beyond by the METIS project [4]. Therefore, analyses of its performance ought to be conducted, considering the channel characteristics that will be encountered in 5G systems and beyond. The propagation scenarios in 5G systems are diverse and include vehicular and machine-to-machine communication, communication in Internet of Things (IoT) systems, remote set-ups, and urban scenarios with high-density crowds. In addition to the propagation scenario, channel characteristics are also influenced by other factors such as transmission equipment (smart antennas), transmission frequency (mm-wave transmission), and the mobility of communicating devices. Since 5G channel characteristics are so diverse and peculiar, conventional statistical distributions such as the Rayleigh and Rican methods, etc., fail to accurately characterize most channel scenarios. There is, therefore, a need to study the performance of any technology that will be used in 5G systems and beyond using other more appropriate and versatile statistical distributions, the parameters of which can be modified to accurately represent a wide range of fading scenarios [4].

2. Related Works

Various channel models have been introduced in the literature to analyze the performance of relaying systems in 5G scenarios. These generalized fading models can be categorized into small-scale multipath scattering propagation models such as Rayleigh [5], Rican [6], Nakagami-m [7], Weibull [8], Nakagami-q [9], $\eta -\lambda -\mu$ [10], $\alpha -\lambda -\mu$ [11], $\kappa -\mu$ [12], $\alpha -\mu$, and $\eta -\mu$ fading; composite multipath shadowing line of sight (LOS) propagation (composite small- and large-scale fading) models such as generalized Gamma [13] and generalized K [14] fading; and composite multipath scattering and shadowing propagation models with LOS, such as the fluctuating two-ray (FTR) fading model [15,16].

To date, a number of studies have been performed on the performance analysis of relay-aided wireless communication systems [12,17,18,19,20,21,22,23]. The authors in [17] derived the expression of the outage probability for a dual-hop DF relaying over a Rayleigh-generalized gamma fading channel. In [18], a dual-hop system was analyzed in relation to mixed $\eta -\mu$ and gamma-gamma fading. The symbol error rate (SER) performance of an amplify-and-forward (AF) scheme in relation to asymmetric fading channels was examined in [19]. In [12], expressions were derived for the SER, outage probability, and outage capacity of a DF relaying over $\eta -\mu$ and $\kappa -\mu$ fading. Dixit and Sahu in [20] calculated the SER and outage of dual-hop DF relaying over Rice fading.

The performance of a single-branch single-relay AF relaying system over mixed Rayleigh–Nakagami-m fading was analyzed by Benmahmoud in [21]. Kapucu in [22] analyzed the performance of a dual-branch selection combining scheme over $\alpha -\kappa -\mu$ fading. The bit error rate (BER) expression for an M-ary phase-shift keying industrial cooperative relaying system was derived over generalized-K composite fading channels by Marjanovic et al. [23]. A summary of related works is presented in Table 1.

Table 1. Review of related works.

Ref.	Fading Channel	Coomunication System
[8]	Weibull	Dual-Hop	OP and Throughput
[9]	Hoyt	Generic	CDF
[10]	$\eta$-$\lambda$-$\mu$	Generic	PDF
[11]	$\alpha$- $\lambda$- $\mu$ and $\alpha$- $\eta$- $\mu$	Generic	PDF
[12]	Dual-Hop Mixed	DF relaying	SER, OP, and OC
[13]	Exp.-Gen. Gamma	Dual-Hop Underwater	OP, ABER, and EC
[14]	Gen.-K	DF	Secrecy Performance
[15]	FTR	mmWave	PDF, CDF and MGF
[16]	Rayleigh, Rician	SFBC-OFDM	BER
[17]	Rayleigh-Gen. Gamma	Dual-Hop DF	OP
[18]	$\eta$-$\mu$-gamma–gamma	dual hop	OP and EC
[19]	Asymmetric Fading	AF	SER
[20]	Rice Fading	DF Relay	BER and OP
[21]	Rayleigh–Nakagami-m	AF	OP and EC
[23]	Gene.-K Composite	Industrial	BER
Exp.	Exponential	Gen.	Generalized
OP	Outage Probability	OC	Outage Capacity
EC	Ergodic Capacity

2.1. Motivation

The performance analysis of most of the conventional relay-aided communication systems is performed based on the assumption that the fading channel between the source–relay and relay–destination links follows the same family as that of the fading PDFs, i.e., the channel PDF remains the same for the complete lifetime of the communication system. However, in 5G scenarios, this assumption is not always met as the fading conditions continue varying rapidly. Therefore, the performance of the system needs to be calculated repeatedly for all possible fixed and static fading scenarios. Therefore, a universal framework is required which can accommodate every fading scenario, and the computational resources can be saved by eliminating the need to derive the expressions repeatedly.

2.2. Contributions

The main contributions of this work are as follows:

• The development of a universal framework for the outage performance analysis of relay-aided communication systems for 5G-and-beyond scenarios;
• We formulate an outage probability expression that is valid for all fading scenarios, irrespective of the nature or complexity of the fading PDF; and
• The relationship between the outage performance and cumulative distribution function (CDF) of the signal-to-noise ratio (SNR) is exploited to derive the expression.
• Illustrations are presented regarding how to use the derived expression for the calculation of the outage probability.

To the best of the authors’ knowledge, no such framework is available in the literature to cater to all possible fading scenarios. The analytical results obtained for various cases are validated here by means of Monte-Carlo simulations. The rest of the paper is structured as follows: the system model is explained in Section 2 and the generalized outage probability expression is derived in Section 3. In Section 4 we illustrate the calculation of the outage probability for various test cases. The results and a discussion are presented in Section 5 and Section 6 we present the concluding remarks.

3. System Model

The system model consists of a source (S), a destination (D), and one relay (R). Communication between S and D is achieved with the aid of a relay node operating in half-duplex mode, which employs a DF-based algorithm. It is assumed that S, D, and R have a single antenna for transmission and reception. The power spectral density (PSD) of additive white Gaussian noise (AWGN) at the receiver is assumed to be $N_0$ with a mean of zero, $n\sim CN(0,N_0)$. The system model is shown in Figure 1.

Figure 1. System model of DF relaying system.

Let the instantaneous SNR between S-R and R-D be ${\gamma }_1$ and ${\gamma }_2$, respectively, defined as ${\gamma }_1=\frac{\parallel h_1{\parallel }^2{P}_1}{N_0}$ and ${\gamma }_2=\frac{\parallel h_2{\parallel }^2{P}_2}{N_0}$, where $h_1$ and $h_2$ are the channel coefficients between the source–relay and relay–destination links. $P_1$ and $P_2$ are the power transmitted by the source and the relay, respectively. Furthermore, let the PDF of ${\gamma }_1$ and ${\gamma }_2$ be $p_{{\gamma }_1}\left({\gamma }_1\right)$ and $p_{{\gamma }_2}\left({\gamma }_2\right)$, respectively. In order to support the unified approach of this study, it is assumed that the fading channel between S-R and R-D can belong to any family of PDFs. Furthermore, it is also assumed that $p_{{\gamma }_1}\left({\gamma }_1\right)$ and $p_{{\gamma }_2}\left({\gamma }_2\right)$ can acquire different fading envelopes. Furthermore, $p_{{\gamma }_1}\left({\gamma }_1\right)$ and $p_{{\gamma }_2}\left({\gamma }_2\right)$ are assumed to be independent, non-identical distributed (INID) varaibles.

4. Generalized Outage Probability Expression

The condition of an outage ensues when either ${\gamma }_1$ or ${\gamma }_2$, or both, fall below a certain specific threshold, ${\gamma }_{th}$. Therefore, the outage probability $p_{out}\left({\gamma }_{th}\right)$ for a dual-hop DF relay-based system can be calculated as [17]

$$p_{out}\left({\gamma }_{th}\right)=p({\gamma }_1\le {\gamma }_{th})\parallel p({\gamma }_2\le {\gamma }_{th})$$

(1)

After some mathematical manipulations, (1) can be simplified as

$$p_{out}\left({\gamma }_{th}\right)=p(min({\gamma }_1,{\gamma }_2)\le {\gamma }_{th})$$

(2)

Now, using the relation $(p\left({\gamma }_1\right)\le {\gamma }_{th})+(p\left({\gamma }_1\right)>{\gamma }_{th})=1$, $p_{out}\left({\gamma }_{th}\right)$ in (2) can be rewritten as

$$p_{out}\left({\gamma }_{th}\right)=1-p({\gamma }_1>{\gamma }_{th})p({\gamma }_2>{\gamma }_{th})$$

(3)

Representing $p({\gamma }_1>{\gamma }_{th})$ in the integral form leads to

$$p_{out}\left({\gamma }_{th}\right)=1-{\int }_{{\gamma }_{th}}^{\infty }{p}_{{\gamma }_1}\left({\gamma }_1\right)d{\gamma }_1{\int }_{{\gamma }_{th}}^{\infty }{p}_{{\gamma }_2}\left({\gamma }_2\right)d{\gamma }_2$$

(4)

Using the definition of the CDF of a random variable, (4) can be simplified as

$$p_{out}\left({\gamma }_{th}\right)=1-{\overline{P}}_{{\gamma }_1}\left({\gamma }_{th}\right){\overline{P}}_{{\gamma }_2}\left({\gamma }_{th}\right)$$

(5)

where ${\overline{P}}_{{\gamma }_1}\left({\gamma }_{th}\right)$ and ${\overline{P}}_{{\gamma }_2}\left({\gamma }_{th}\right)$ are the complementary cumulative distribution functions (CCDF) of $p_{{\gamma }_1}\left({\gamma }_1\right)$ and $p_{{\gamma }_2}\left({\gamma }_2\right)$ evaluated at ${\gamma }_{th}$. Using (5), the outage probability of a DF-aided relay communication system can be calculated for any fading scenario using the CDF of the SNR of the fading channel. In order to illustrate the calculation of the outage probability using (5), some cases involving different fading scenarios are explained in Section 4.

5. Calculation of Outage Probability Using (5)

In this section, the use of the derived outage probability expression (5) is demonstrated using various scenarios as follows.

Scenario 1: Let the fading envelopes of the two links take Rayleigh and generalized Gamma PDF values. The generalized Gamma distribution generalizes frequently used models for multipath, shadowing, and composite fading, containing Nakagami, Rayleigh, and Weibull distributions as special cases and a log-normal distribution as a limiting case [17].

The Rayleigh-generalized Gamma fading scenario models a scenario in which one link, represented by Rayleigh fading, is subjected to intense scattering with no line of sight of transmission and the other hop, represented by generalized Gamma fading, can experience either multipath fading, shadowing, or composite fading at any time. The Rayleigh fading model also applies to the propagation of reflected and refracted paths through the troposphere and ionosphere and to ship-to-ship radio links. Using the CDF expressions from Table 2 in (5), the outage probability for scenario 1 can be calculated as

$$p_{out}\left({\gamma }_{th}\right)=1-exp\left(\frac{-{\gamma }_{th}}{\overline{\gamma }}\right)\frac{\mathsf{\Gamma }\left(m,{\beta }^v{\gamma }_{th}^v\right)}{\mathsf{\Gamma }\left(m\right)}$$

(6)

Table 2. CDF expressions of some popular fading channels.

Sr. no.	Fading Channel	CDF Evaluated at and from ${\mathit{\gamma }}_{\mathbf{th}}$
Small-scale multipath scattering propagation models
1	Rayleigh [5]	$1-exp\left(\frac{-{\gamma }_{th}}{\overline{\gamma }}\right)$
2	$\eta -\lambda -\mu$ [10]	$\begin{array}{l}[1-{\left(\frac{2\sqrt{\eta (1+{\lambda }^2)}\widehat{b}}{{\widehat{r}}^2}\right)}^{2\mu }\frac{\sqrt{\pi }}{\gamma \left(u\right){\widehat{c}}^{2\mu }{\widehat{d}}^{\mu -0.5}}\\ {\sum }_{j=0}^{\infty }\frac{1}{j!\mathsf{\Gamma }(0.5+\mu +j)}\left(\frac{\widehat{d}}{2\widehat{c}}\right)\left(\mathsf{\Gamma }\left(2(\mu +j)\right)-\mathsf{\Gamma }\left(2(\mu +j),\frac{\widehat{c}{\gamma }_{th}}{\overline{\gamma }}\right)\right)]\end{array}$
3	$\alpha -\lambda -\mu$ [11]	$\begin{array}{l}\frac{\sqrt{\pi }{(1-{\lambda }^2)}^{\mu }}{2^{2\mu -1}\mathsf{\Gamma }\left(\mu \right)}{\sum }_{j=0}^{\infty }\frac{{\left(\frac{\lambda }{2}\right)}^{2j}}{j!\Gamma (j+\mu +0.5)}\\ \left(\mathsf{\Gamma }\left(2(\mu +j)\right)-\mathsf{\Gamma }(\mu +2j,\widehat{b}))\right),\widehat{b}=\frac{2\mu }{1-{\lambda }^2}{\gamma }_{th}^{\alpha }\end{array}$
4	Nakagami-m [7]	$1-\frac{\mathsf{\Gamma }\left(m,\frac{m}{\overline{\gamma }}{\gamma }_{th}\right)}{\mathsf{\Gamma }\left(m\right)}$
5	Weibull [8]	$1-exp\left(-\frac{{\gamma }_{th}}{\overline{\gamma }}\mathsf{\Gamma }{\left(1+\frac{2}{c}\right)}^{\frac{c}{2}}\right)$
6	Nakagami-q [9]	$\begin{array}{l}1-[Q\left(\alpha \left(q\right)\sqrt{\frac{{\gamma }_{th}}{4\overline{\gamma }}},\beta \left(q\right)\sqrt{\frac{{\gamma }_{th}}{4\overline{\gamma }}}\right)\\ -Q\left(\beta \left(q\right)\sqrt{\frac{{\gamma }_{th}}{4\overline{\gamma }}},\alpha \left(q\right)\sqrt{\frac{{\gamma }_{th}}{4\overline{\gamma }}}\right)]\end{array}$
Composite Multipath-Shadowing-LOS propagation (composite small- and large-scale fading)
7	Generalized Gamma [4]	$1-\frac{\mathsf{\Gamma }\left(m,{\beta }^v{\gamma }_{th}^v\right)}{\mathsf{\Gamma }\left(m\right)}$
8	Generalized K [14]	$\begin{array}{l}1-\left[\pi csc\left(\pi \alpha \right)\right(\frac{{\left(\Xi {\gamma }_{th}\right)}^m{}_1{F}_2(m;1-\alpha ;1+m;\Xi {\gamma }_{th})}{\mathsf{\Gamma }\left(k\right)\mathsf{\Gamma }1-\alpha \mathsf{\Gamma }(1+m)}\\ -\frac{{\left(\Xi {\gamma }_{th}\right)}^m{}_1{F}_2(k;1+\alpha ;1+k;\Xi {\gamma }_{th})}{\mathsf{\Gamma }\left(m\right)\mathsf{\Gamma }1+\alpha \mathsf{\Gamma }(1+k)}\left)\right]\end{array}$
Composite multipath scattering and shadowing propagation with an LOS component
9	FTR [15]	$\begin{array}{l}1-[\frac{1}{2^{m-1}}\frac{1+K}{\overline{\gamma }}{\left(\frac{m}{\sqrt{{(m+K)}^2-K^2{\mathsf{\Delta }}^2}}\right)}^m{\sum }_{q=0}^{\lfloor \frac{m-1}{2}\rfloor }{(-1)}^q{C}_q^{m-1}\\ {\left(\frac{m+K}{\sqrt{{(m+K)}^2-K^2{\mathsf{\Delta }}^2}}\right)}^{m-1-2q}{\gamma }_{th}{\varphi }_2^{\left(4\right)}(1+2q-m,m-q-0.5;-\frac{m(1+K)}{(m+K)\overline{\gamma }}{\gamma }_{th},\\ -\frac{m(1+K)}{(m+K(1+\mathsf{\Delta }))\overline{\gamma }}{\gamma }_{th},-\frac{m(1+K)}{(m+K(1-\mathsf{\Delta }))\overline{\gamma }}{\gamma }_{th},-\frac{1+K}{\overline{\gamma }}{\gamma }_{th}\left)\right]\end{array}$

Scenario 2: For this case, let the two links take Nakagami-m PDF and Weibull PDF respectively. Nakagami-m is a versatile generalized multipath fading distribution that is capable of modeling fading scenarios that are more severe than Rayleigh fading ($m<1$). Nakagami-m contains Rayleigh, One-sided Gaussian as special cases and AWGN as a limiting case [21] and it can be easily matched to equivalent Rice distribution [20]. Weibull fading has proven to produce a good fit to experimental data in multipath fading and contains Rayleigh fading as a special case. Weibull can also model fading scenarios worse than Rayleigh fading for $c<2$ [8]. This scenario models multipath fading in both links. Utilizing the expressions for CDF from Table 2 in (5), the outage probability for scenario 2 can be calculated as

$$p_{out}\left({\gamma }_{th}\right)=1-\frac{\mathsf{\Gamma }\left(m,\frac{m}{\overline{\gamma }}{\gamma }_{th}\right)}{\mathsf{\Gamma }\left(m\right)}exp\left(-\frac{{\gamma }_{th}}{\overline{\gamma }}\mathsf{\Gamma }{\left(1+\frac{2}{c}\right)}^{\frac{c}{2}}\right)$$

(7)

Scenario 3: In scenario 3, the links between S-R and R-D take the Weibull PDF and the Rayleigh PDF, respectively, representing a special case of both Rayleigh-generalized gamma fading and Nakagami-m-Weibull fading scenarios. This scenario is used to model multipath fading in both links, in which one link, represented by Rayleigh fading, is subjected to intense scattering with no line of sight of transmission and the other link, represented by Weibull fading, experiences fading that varies from worse to better than Rayleigh fading. Utilizing the CDF expressions from Table 2 in (5), the outage probability for scenario 3 can be calculated as

$$p_{out}\left({\gamma }_{th}\right)=1-exp\left(\frac{-{\gamma }_{th}}{\overline{\gamma }}\right)exp\left(-\frac{{\gamma }_{th}}{\overline{\gamma }}\mathsf{\Gamma }{\left(1+\frac{2}{c}\right)}^{\frac{c}{2}}\right)$$

(8)

Scenario 4: In scenario 4, the links take the Nakagami-m PDF and Nakagami-q PDF. Nakagami-q is a fading distribution which models short-term signal variations that span from one-sided Gaussian to Rayleigh fading. Such fading is usually observed on satellite links due to strong ionosphere scintillation. This scenario, therefore, models a system that experiences short-term signal variations in both links but one link is always subjected to signal variations that are worse than Rayleigh fading, as the case of satellite links suffering from ionosphere scintillation. Utilizing the CDF expressions from Table 2 in (5), the outage probability for scenario 4 can be calculated as

$$\begin{array}{cc}\hfill p_{out}\left({\gamma }_{th}\right)=1-\frac{\mathsf{\Gamma }\left(m,\frac{m}{\overline{\gamma }}{\gamma }_{th}\right)}{\mathsf{\Gamma }\left(m\right)}[& Q\left(\alpha \left(q\right)\sqrt{\frac{{\gamma }_{th}}{4\overline{\gamma }}},\beta \left(q\right)\sqrt{\frac{{\gamma }_{th}}{4\overline{\gamma }}}\right)\hfill \\ \hfill & -Q\left(\beta \left(q\right)\sqrt{\frac{{\gamma }_{th}}{4\overline{\gamma }}},\alpha \left(q\right)\sqrt{\frac{{\gamma }_{th}}{4\overline{\gamma }}}\right)]\hfill \end{array}$$

(9)

Scenario 5: In scenario 5, the links between S-R and R-D take the Rayleigh PDF and the $\eta -\lambda -\mu$ PDF. The $\eta -\lambda -\mu$ PDF is a generalized small-scale fading distribution which contains $\lambda -\mu$, $\eta -\mu$, Gamma, exponential, Hoyt, Nakagami-m, Rayleigh, and one-sided Gaussian fadingas special cases [10]. This scenario is used to model multipath fading in both links in which one link, represented by Rayleigh fading, is subjected to intense scattering with no line of sight of transmission and the other link, represented by $\eta -\lambda -\mu$, experiences a variety of multipath fading that varies from worse to better than Rayleigh fading. Utilizing the CDF expressions from Table 2 in (5), the outage probability for scenario 5 can be calculated as:

$$\begin{array}{cc}\hfill p_{out}\left({\gamma }_{th}\right)& =1-exp\left(\frac{-{\gamma }_{th}}{\overline{\gamma }}\right)[1-{\left(\frac{2\sqrt{\eta (1+{\lambda }^2)}\widehat{b}}{{\widehat{r}}^2}\right)}^{2\mu }\frac{\sqrt{\pi }}{\gamma \left(u\right){\widehat{c}}^{2\mu }{\widehat{d}}^{\mu -0.5}}\hfill \\ \hfill & \sum _{j=0}^{\infty }\frac{1}{j!\mathsf{\Gamma }(0.5+\mu +j)}\left(\frac{\widehat{d}}{2\widehat{c}}\right)\left(\mathsf{\Gamma }\left(2(\mu +j)\right)-\mathsf{\Gamma }\left(2(\mu +j),\frac{\widehat{c}{\gamma }_{th}}{\overline{\gamma }}\right)\right)]\hfill \end{array}$$

(10)

An important point to note here is that the derived expression can be used to calculate the outage performance of the system for any fading scenario. The only condition is that the CDF of SNR should be known.

6. Results and Discussions

In this section, the analytical results obtained from the derived outage probability expression (5) are presented and verified using simulation results. Results are provided for the fading scenarios discussed in Section 4. We observed in all plots that the analytical results were in accordance with the results obtained from the Monte-Carlo simulations.

6.1. Scenario 1: Rayleigh-Generalized Gamma Fading

The outage probability vs. SNR $\left(\overline{\gamma }\right)$ for scenario 1, Rayleigh-Generalized Gamma fading, for threshold SNR $\left({\gamma }_{th}\right)$ = 5 dB, 10 dB, and 20 dB is shown in Figure 2. The fading parameters were set at v = 1, m = 1, 2 in Figure 2a and v = 1, 2, m = 1 in Figure 2b. It can be observed in Figure 2a that m = 2 outperformed m = 1 in all cases, which was expected because of the increase in the fading parameter m at a constant value of v and $\left(\overline{\gamma }\right)$, leading to a reduction in fading severity and hence reducing the possibility of an outage. A similar trend can be observed in Figure 2b for v. It can be noted that increasing the threshold SNR while keeping other factors $m,v,\left(\overline{\gamma }\right)$ constant increased the outage probability of the system. This is because increasing $\left({\gamma }_{th}\right)$ means that more instantaneous SNR $\left(\overline{\gamma }\right)$ values will fall short of the threshold value, resulting in a higher probability of an outage. It can also be observed in Figure 2 that the curves of the outage performances for the same m and v but different $\left({\gamma }_{th}\right)$ parameters followed the same trends for a large range of SNR values. Furthermore, it can be observed that for a constant value of $\left({\gamma }_{th}\right)$ and channel parameters m & v, the outage performance improved with an increase in the average SNR value. For instance, at $\left({\gamma }_{th}\right)$ = 4 dB, v = 1, m = 1, the outage probability was 0.7958, 0.3949, and 0.05343 for average SNR values of 5 dB, 10 dB, and 20 dB, respectively.

Figure 2. Outage Probability under Rayleigh-Generalized gamma fading for (a) fading parameter m = 1, 2; ${\gamma }_{th}$ = 5 dB, 10 dB, 20 dB and (b) Fading parameter v = 1, 2; $\gamma$ = 5 dB, 10 dB, 20 dB.

6.2. Scenario 2: Nakagami-m-Weibull Fading

A plot of the outage probability vs. $\overline{\gamma }$ for scenario 2, Nakagami-m-Weibull fading, for $\left({\gamma }_{th}\right)$ = 1 dB and 10 dB, is shown in Figure 3. System performance was evaluated at each threshold value for Weibull parameters c = 0.1, 0.5 and 1.5, which represent fading scenarios worse than Rayleigh fading, and Nakagami parameter m = 1, which represents Rayleigh fading. It was observed that the general system’s behavior as the value of c and the threshold parameter $\left({\gamma }_{th}\right)$ varied was similar to that observed in Rayleigh-generalized gamma fading; thus, the performance improved with increased c values but worsened with increased $\left({\gamma }_{th}\right)$ values. For example, at c = 1.5 and an average SNR of 20 dB, an improvement of 85.4515% was observed in the outage performance when $\left({\gamma }_{th}\right)$ varied from 1 dB to 10 dB.

Figure 3. Outage probability vs. average SNR for Nakagami-m-Weibull fading.

By setting m = 1, a Rayleigh faded link was evaluated, and by setting $c<2$ on the other link, a worse-than-Rayleigh fading scenario was evaluated. It could therefore be observed that the performance of the system in this scenario, at $\left({\gamma }_{th}\right)$ = 10 dB was noticeably worse than the performance of the Rayleigh-generalized gamma fading for $m=v=1$. However, at c = 1.5, the performance of the system was very close to that of the Rayleigh–Rayleighfading scenario.

6.3. Scenario 3: Rayleigh–Weibull Fading

The outage probability vs. $\overline{\gamma }$ for scenario 3 (Rayleigh–Weibull fading) for $\left({\gamma }_{th}\right)$ = 1 dB, 2 dB, 3 dB, 5 dB, and 7 dB is shown in Figure 4. System performance was evaluated for Weibull parameter c = 1, which represents multipath fading worse than Rayleigh fading.

Figure 4. Outage probability vs. average SNR for Rayleigh-Weibull fading.

It was observed that the general system behavior as the threshold parameter $\left({\gamma }_{th}\right)$ varied was similar to that observed in Rayleigh-generalized Gamma fading and Nakagami-m-Weibull fading; thus, the performance worsened as $\left({\gamma }_{th}\right)$ increased. It was also observed that generally parallel behavior with different $\left({\gamma }_{th}\right)$ values but with the same c parameter was also exhibited in this scenario.In this scenario, one link was the Rayleigh-faded link and, by setting $c<2$, the other link was made worse than Rayleigh fading. We observed that the performance of the system in this scenario, at $\left({\gamma }_{th}\right)$ = 5 dB, was similar to that of the Rayleigh-generalized gamma fading for $m=v=1$, which was effectively the Rayleigh–Rayleigh fading scenario. We therefore observed that at lower values of $\left({\gamma }_{th}\right)$ fading in the system could be modeled as a Rayleigh–Rayleigh fading scenario.

6.4. Scenario 4: Nakagami-m—Nakagami-q Fading

In this scenario, unlike the previous scenarios, we studied the outage performance of the system with (a) various values of the fading parameter m, constant q = 0.5, $\overline{\gamma }$ = 10 dB and (b) m = 3, q = 0.1, 0.5, $\left({\gamma }_{th}\right)$ = 1 dB, 5 dB, 15 dB, as illustrated in Figure 5. The system was studied with the parameter m set at values of 0.5, 1.0, 1.5, 2.0, and 2.5, as shown in Figure 5a. By setting q < 1, one link always experienced worse-than-Rayleigh fading. In the other link, values of $m<1,m=1$ and $m>1$ indicated worse-than-Rayleigh, Rayleigh, and better-than-Rayleigh fading, respectively.

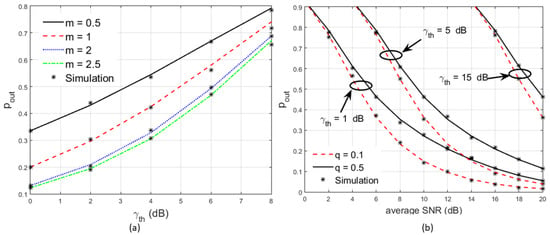
Figure 5. Outage Probability under Nakagami-mNakagami-q fading for (a) fading parameter m = 0.5, 1, 2, 2.5 and (b) Fading parameter q = 0.1, 0.5; ${\gamma }_{th}$ = 1 dB, 5 dB, 15 dB.

We observed that as m increased, the performance of the system improved, as was the case in the Rayleigh-generalized gamma scenario and other previous scenarios. However, at high values of $\left({\gamma }_{th}\right)>12$ dB, the outage performance equaled one for all cases. Furthermore, as shown in Figure 5b, the performance of the system was also affected by changes in the fading parameter q. For example, taking a fixed value of $\left({\gamma }_{th}\right)$ = 1 dB and an average SNR = 10 dB, the outage probability was calculated to be 0.2776 and 0.1409 for q = 0.5 and 1, respectively.

6.5. Scenario 5: Rayleigh—$\eta -\lambda -\mu$ Fading

The outage probability vs. $\overline{\gamma }$ for scenario 5, i.e., Rayleigh–$\eta -\lambda -\mu$ fading, for $\left({\gamma }_{th}\right)$ = 10 dB, is shown in Figure 6. The results are provided for the channel parameters $\eta$ = 0.5, 1, $\lambda$ = 0.5, 1, and $\mu$ = 0.5, 1. In this analysis, ${\delta }_x^2$, which is the average power of the in-phase component, was set at one. We observed that, out of these cases, the best outage performance was obtained at $\eta =\mu =0.5$ and $\lambda =1$. This shows that the more the propagation environment became non-homogeneous, the better the performance. We observed that increasing $\eta$ from 0.5 to 1 while keeping other parameters constant improved the performance of the system because as $\eta$ approached 1, the $\eta -\lambda -\mu$ fading approached the Rayleigh fading scenario.

Figure 6. Outage probability vs. average SNR for Rayleigh–$\eta -\lambda -\mu$ fading.

7. Conclusions

A universal expression of the outage probability has been derived for a dual-hop DF relay system. Analyses were carried out considering generalized fading scenarios, i.e., no restrictions were placed on the PDF of the SNR of the transmission link. This paper demonstrates a convenient way to analyze the outage behavior of a relay-aided system by utilizing the CDF of the per-hop SNR. Simulation results were used to verify the validity of the derived analytical expressions. Illustrations have been provided, choosing the PDF values of channels between S-R and R-D links to parameterize the commonly encountered practical fading scenarios faced by current and future wireless communication systems. The present work can be extended further in the future to include sophisticated system models such as multiple relay modes, complex forwarding schemes, and multiple antenna trans-receivers.