Experimental Study on Stiffness Degradation of Organic Matter-Disseminated Sand under Cyclic Loading

Abstract

Degradation of stiffness will occur in sand under cyclic loading. Organic matter-disseminated sand (OMDS) is a special sand in the northeast and western coastal region of Hainan Island. Through the stress-controlled dynamic triaxial test, the natural moisture content, vibration amplitude and consolidation ratio of OMDS under three types of cyclic loads (sine wave, triangular wave and rectangular wave) were studied. The results showed that the soil stiffness decreases with the increase in vibration times. The increase in natural moisture content and vibration amplitude, and the reduction in the consolidation ratio accelerate the softening of soil stiffness. Furthermore, based on the test results, an empirical formula was derived to reflect the rule of soil stiffness softening.

1. Introduction

With the construction of the Hainan free trade port, many structures are to be built in coastal areas. Organic matter-disseminated sand (OMDS) is a special sand in the northeast and western coastal region of Hainan Island, shown in Figure 1a. Figure 1b shows the scanning electron microscope photos of OMDS. It can be seen that the surface of the OMDS particles are obviously smoother, and there are fewer pores in the surface, which indicates that the organic matter has been immersed in pores and adsorbed to the surface of the sand particles, forming a film that wraps around the sand particles. The influence of waves, traffic and earthquakes on OMDS’s foundation should be of concern in engineering. In a wide range of studies, traffic loads could be approximately equivalent to triangular waves and sine waves, and wave loads could be equivalent to rectangular waves [1]. With the increase in dynamic cyclic load amplitude, the dynamic strain, porosity and pore pressure of soil increase, the internal structure of soil is reshaped as well, which induces the stiffness degradation of soil [2,3,4]. Under the cyclic load, the cumulative deformation of soil varies with vibration cycles [5,6], and due to the nonlinearity of soil, the stiffness acts in a complicated manner [7,8].

Figure 1. OMDS photos: (a) on-site photo; (b) SEM photo.

The characteristics of the long-term deformation and stiffness softening of soil under cyclic loading has been researched extensively by various countries’ scholars. Monismith et al. [9] proposed an exponential model for the relationship between the plastic strain of soft clay and vibration cycles. Introducing dynamic stress and static strength, Li and Selig [10,11] revised the Monismith function model and established a new function model. Idriss et al. [12] analyzed the relationship between the degradation index and vibration cycles, and established a functional relationship to describe the quantitative attenuation rule of soil cyclic stiffness. Yao et al. [13] modified the Idriss formula and redefined the softening index to describe the stiffness degradation of soft clay. Chai et al. [14] and Parr et al. [15] studied the dynamic characteristics of clay through dynamic triaxial tests, and obtained the double logarithmic relationship between dynamic strain and vibration cycles. Huurman [16] suggested that the stiffness degradation of sand was related to the cyclic stress ratio and vibration cycles. Yasuhara et al. [17] proposed a modified model function describing the relationship of the degradation index and vibration cycles based on the dynamic triaxial test of soil under cyclic loading. Tan et al. [18] analyzed the results of the cyclic triaxial test and cyclic simple shear test of cohesive soil with different plasticity indexes. Wang et al. [19] established a functional relationship between the degradation index and vibration cycles, and obtained the fracture toughness ratio of clay through the function. Huang et al. [20] introduced the dynamic deviatoric stress parameter into a functional model describing the relationship of the degradation index and vibration cycles. Cao et al. [21] established a stiffness degradation function for marine soft soil, and the relationship of the degradation index and vibration cycles was obtained by the function. Hong et al. [22] carried out a series of stress-path triaxial tests, with local strain measurements, to achieve path-dependent stiffness degradation curves of medium-dense Toyoura sand. Iraji et al. [23] modified the nonlinear Pastor–Zienkiewicz–Chan constitutive model to simulate the stiffness degradation of dense sands at dynamic loading. Mei et al. [24] analyzed the development laws between the axial permanent strain of coarse-grained soil and vibration cycles. Liu et al. [25] found that the softening index was exponentially related to cumulative pore pressure and cumulative strain.

In summary, it can be seen that the stiffness softening of clay, silt and sand under cyclic loading has been studied, while the dynamic properties of sand with organic matter are different from those of general sand. There are few reports on its stiffness degradation. In this study, the degradation laws of skeleton curves on OMDS samples were studied under three cyclic loadings with various natural moisture contents, consolidation ratios, confining pressures and vibration amplitudes.

2. Materials and Methods

2.1. Materials

The OMDS [26] was obtained from a site in Hainan Province, the upper layer soil to 1.2 m depth was cultivated soil, and the lower layer was OMDS, the sand used in this experimental study was extracted at depth ranging from 2 m to 5 m by thin-walled tube sampler. The coefficient of uniformity C_u was 2.07, the coefficient of curvature C_c was 1.25, the main physical parameters and particle grading curves are shown in Table 1 and Figure 2, respectively.

Table 1. Main physical parameters of OMDS.

Organic Content/%	Natural Moisture Content/%	Natural Density/g·cm−3	Minimum dry Density/g·cm−3	Maximum Dry Density/g·cm−3	Specific Gravity
5.32	12.23	1.617	1.570	1.723	2.62

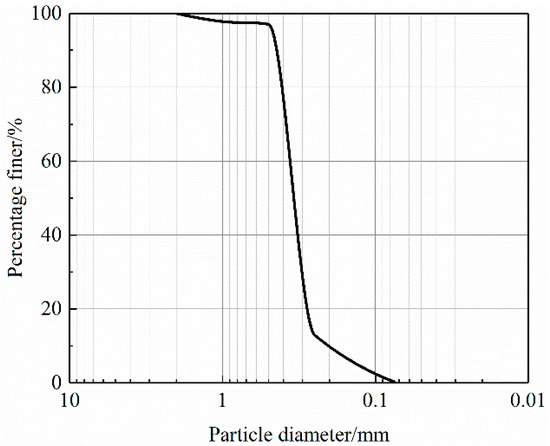
Figure 2. Grading curve of OMDS.

2.2. Sample Preparation

The OMDS samples were first air-dried and then passed through a sieve with opening size of 5 mm. Fully mixed with water and placed for 24 h, the sieved soil was cast into cylindrical molds which had 39.1 mm diameter and 80 mm height, as shown in Figure 3. First, the pumping saturation method was used for saturation, and then the back-pressure saturation was carried out by the dynamic triaxial instrument, until the sample saturation reached 95%. Lastly, the fully saturated samples were consolidated under the condition of isotropic consolidation.

Figure 3. Compacted OMDS samples: (a) compaction tool; (b) OMDS samples.

2.3. Scheme of Dynamic Triaxial Test

In this study, the dynamic responses of OMDS under multiple cyclic loading waves were studied, and the influence of vibration amplitude and vibration cycles was considered as well; therefore, DDS-70 dynamic triaxial test equipment shown in Figure 4 was adopted. The DDS-70 system can automatically generate sine waves, triangular waves and rectangular waves with various frequencies, the maximum frequency is 10 Hz. The confining pressure of the test was 100 kPa. Because the frequency had little influence on the sand sample [27], the test frequency was set 1.0, and the test process was undrained. The test scheme is shown in Table 2.

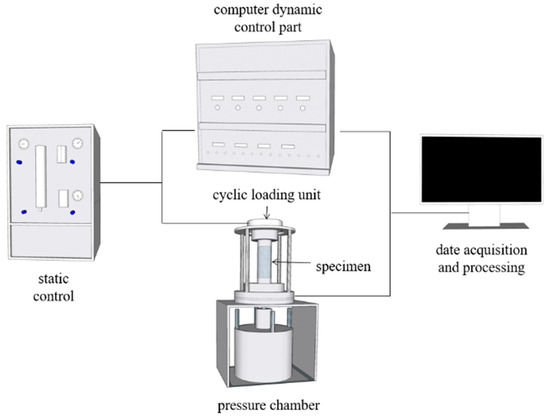
Figure 4. Schematic drawing of DDS-70.

Table 2. Scheme of dynamic triaxial test.

Sample	Consolidation Ratio	Natural Moisture Content/%	Wave Form	Vibrating Load/N
OMDS	1.0	10% 18% 24%	sine, triangular, rectangular sine, triangular, rectangular sine, triangular, rectangular	25, 70, 110, 150 25, 70, 110, 150 25, 70, 110, 150
	1.5	10% 18% 24%	sine, triangular, rectangular sine, triangular, rectangular sine, triangular, rectangular	25, 70, 110, 150 25, 70, 110, 150 25, 70, 110, 150
	2.0	10% 18% 24%	sine, triangular, rectangular sine, triangular, rectangular sine, triangular, rectangular	25, 70, 110, 150 25, 70, 110, 150 25, 70, 110, 150

3. Results

3.1. Skeleton Curve

The skeleton curve demonstrates the relationship between the dynamic shear stress (τ_d) and the dynamic shear strain (γ_d) [28,29], which could be expressed in terms of the dynamic axial stress (σ_d) and the dynamic axial strain (ε_d), as shown in Equations (1) and (2) [30,31].

$${\tau }_{\mathrm{d}}=0.5{\sigma }_{\mathrm{d}}$$

(1)

$${\gamma }_{\mathrm{d}}={\epsilon }_{\mathrm{d}}\left(1+\mu \right)$$

(2)

where τ_d is the dynamic shear stress; σ_d is the dynamic axial stress; γ_d is the dynamic shear strain; ε_d is the dynamic axial strain; and μ is the Poisson’s ratio. Since the lateral displacement of the samples were not measured in this study, it was not possible to experimentally determine the Poisson’s ratio value. Therefore, instead of using τ_d and γ_d, σ_d and ε_d were used to construct the skeleton curve.

Figure 5 shows the skeleton curves of ODMS samples with varying moisture contents and consolidation ratios, and under four confining pressure levels when the wave form was a sine wave. It can be seen that, with the increase in confining pressure, σ_d became larger at an identical ε_d. Moreover, a lower moisture content and larger consolidation ratio in general resulted in the increase in σ_d at an identical ε_d. The above variation law between dynamic stress and dynamic strain under various wave forms was basically the same.

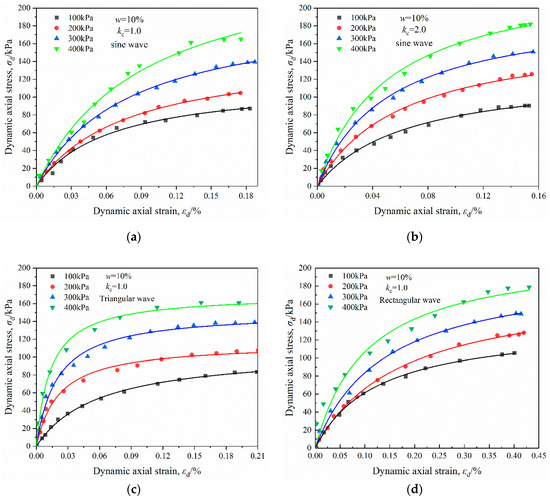
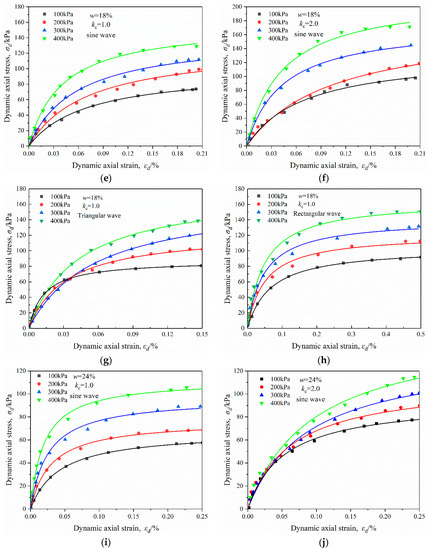
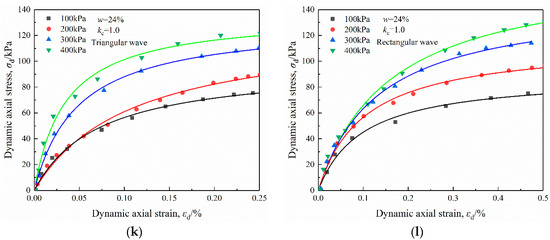
Figure 5. Skeleton curves of OMDS samples under dynamic triaxial test: (a) sine wave, 10% moisture content, 1.0 consolidation ratio; (b) sine wave, 10% moisture content, 2.0 consolidation ratio; (c) triangular wave, 10% moisture content, 1.0 consolidation ratio; (d) rectangular wave, 10% moisture content, 1.0 consolidation ratio; (e) sine wave, 18% moisture content, 1.0 consolidation ratio; (f) sine wave, 18% moisture content, 2.0 consolidation ratio; (g) triangular wave, 18% moisture content, 1.0 consolidation ratio; (h) rectangular wave, 18% moisture content, 1.0 consolidation ratio; (i) sine wave, 24% moisture content, 1.0 consolidation ratio; (j) sine wave, 24% moisture content, 2.0 consolidation ratio; (k) triangular wave, 24% moisture content, 1.0 consolidation ratio; (l) rectangular wave, 24% moisture content, 1.0 consolidation ratio.

3.2. Characteristics of Stiffness Degradation

Dynamic modulus is an important parameter of soil dynamic characteristics, which can reflect the stiffness characteristics under dynamic loads. Dynamic elastic modulus, E_d, is one dynamic modulus, which is defined as the ratio between σ_d and ε_d, plotted in Figure 6. It can be seen that, under conditions of the same moisture content and consolidation ratio, the various wave forms, E_d, became smaller at a given ε_d when the confining pressure was reducing.

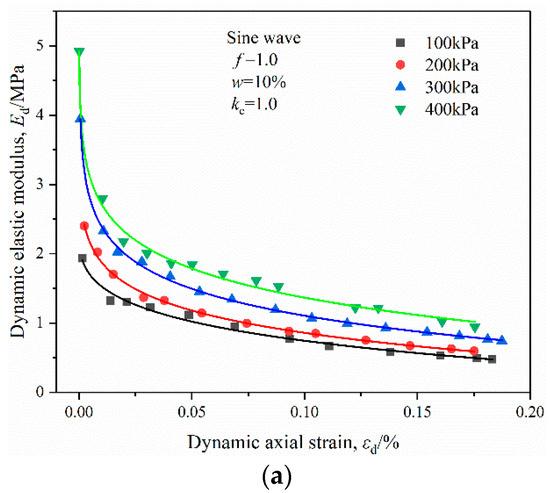
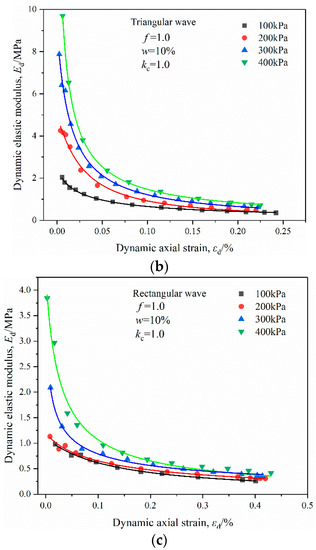
Figure 6. Variation in E_d and ε_d of OMDS samples under dynamic triaxial test: (a) sine wave; (b) triangular wave; (c) rectangular wave.

The degradation index, δ_d, can be used to quantify the attenuation of cyclic stiffness [8]. In the stress-controlled dynamic triaxial test, the ratio of the dynamic elastic modulus in the Nth cycle and the first cycle (i.e., the ratio of E_N:E₁) is the degradation index δ.

$${\delta }_{\mathrm{d}}=\frac{E_{\mathrm{N}}}{E_1}=\frac{{\sigma }_{\mathrm{d}}/{\left({\epsilon }_{\mathrm{d}}\right)}_{\mathrm{N}}}{{\sigma }_{\mathrm{d}}/{\left({\epsilon }_{\mathrm{d}}\right)}_1}=\frac{{\left({\epsilon }_{\mathrm{d}}\right)}_1}{{\left({\epsilon }_{\mathrm{d}}\right)}_{\mathrm{N}}}$$

(3)

where (ε_d)_N and (ε_d)₁ are the axial dynamic strain in the Nth and 1st cycle respectively, and σ_d is the dynamic axial stress.

3.2.1. Effects of Vibration Amplitude

Figure 7 shows the relationship of the degradation index and vibration cycles under various vibration amplitudes. It can be seen that the degradation index curve decreased sharply with the increase in vibration cycles under various cyclic loads, which indicates that the soil would be destroyed with fewer vibration cycles. Since the δ_d–N relationship is largely independent of the vibration amplitude, there was no critical stress for OMDS under cyclic loading, which was different from clay.

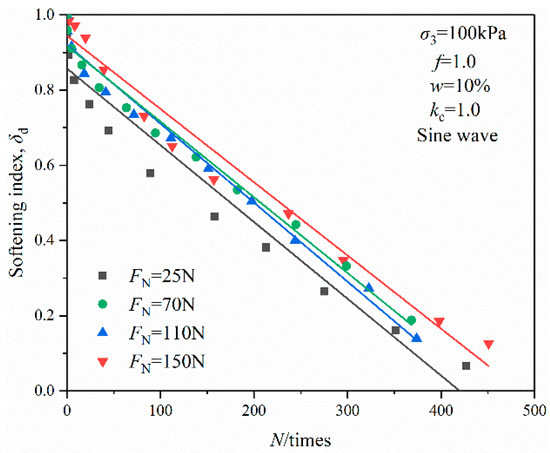
Figure 7. Relationship of degradation index and vibration cycles under various vibration amplitude.

3.2.2. Effects of Natural Moisture Content

Figure 8 shows the relationship of the degradation index and vibration cycles under various natural moisture contents. As observed, with the increase in vibration cycles, the degradation index curve tended to decrease rapidly in a nonlinear form, the variation range was smaller when the natural moisture content was smaller and the degradation degree was not obvious; when the natural moisture content reached 24%, the degradation index was larger than the other groups. This was consistent with the results reported by Zhong et al. [32] and was attributed to the fact that with the increase in moisture content, the water film surrounding the sand particles became thick, and the spacing between the sand particles increased. As a result, the interaction between the sand particles became weaker, which made the sand particles prone to dislocation deformation and the stiffness of OMDS prone to delegation. Figure 8 also shows that the curvatures of the degradation curves of various natural moisture contents were larger than those of vibration amplitude; the variation in natural moisture content had much influence on the degradation index.

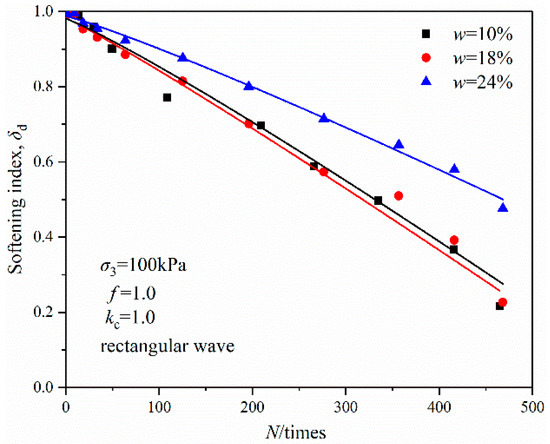
Figure 8. Relationship of degradation index and vibration cycles under various natural moisture contents.

3.2.3. Effects of Consolidation Ratio

Figure 9 shows the relationship of the degradation index and vibration cycles under various consolidation ratios. As observed, the degradation index curve decreased rapidly with the increase in vibration cycles. When the consolidation ratio k_c = 2.0, the variation rate of the degradation index curve was smaller than the other groups, which indicates that the pores’ volume of soil decreased after consolidation, and the pores’ water pressure also decreased in order to prevent the soil from instability or failure under vibration load. This was consistent with the results reported by Huang et al. [33] and was attributed to the fact that the larger the consolidation ratio, the greater the axial consolidation pressure, the higher the compaction degree of OMDS sample, the stronger the ability to resist elastic deformation, and the slower the stiffness degradation of OMDS. Figure 9 also shows that the curvature of the degradation index curve with different consolidation ratios was larger than that with different natural moisture contents, which shows a greater influence of the consolidation ratio on the degradation index.

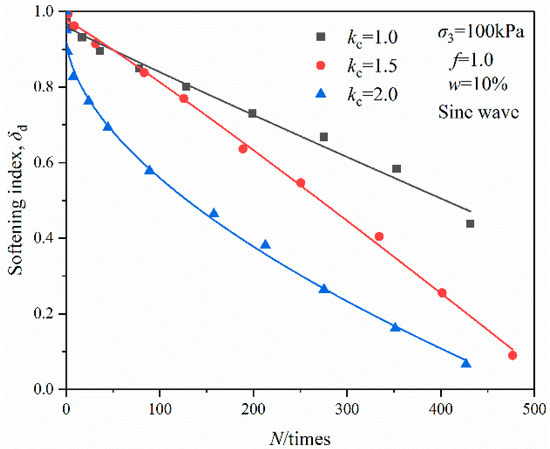
Figure 9. Relationship of degradation index and vibration cycles under various consolidation ratios.

3.2.4. Effects of Wave Form

Figure 10 shows the relationship of the degradation index and vibration cycles under various wave forms. As observed, the degradation index curves of OMDS showed nonlinear variation with the increase in vibration cycles under three kinds of wave loads. Under the same vibration cycles, the attenuation degree caused by the rectangular wave load was significantly greater than that by the sine wave and triangle wave. It was found that the soil was prone to degrade under the load of the rectangular wave. This was consistent with the results reported by Cao et al. [21] and was attributed to the fact that the work of the rectangular wave was much greater than that of the sine wave and triangle wave under the same vibration frequency, and the energy dissipation of soil was much greater as well.

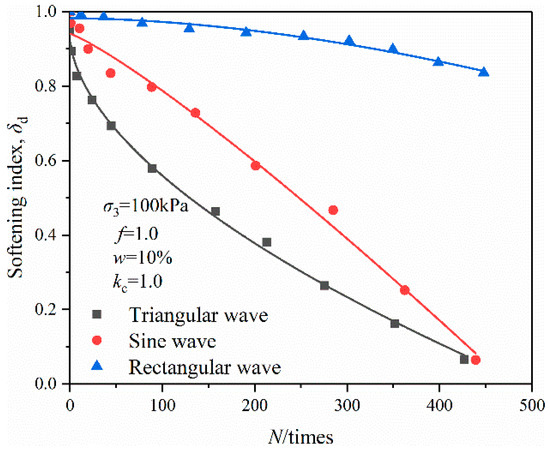
Figure 10. Relationship of degradation index and vibration cycles under various wave forms.

4. Degradation Model for OMDS

Based on the analysis of the test results and previous research, the functional relationship between the degradation index and vibration cycles of OMDS was established and is shown as

$${\delta }_{\mathit{d}}=1+m{N}^n$$

(4)

where m and n are test parameters, obtained by regression analysis; N and δ_d are the vibration cycles and degradation index, respectively.

In this paper, Equation (4) was used to calculate the relationship between the degradation index and vibration cycles of OMDS under various influence factors, and the results were compared with those of dynamic triaxial test (see Figure 11).

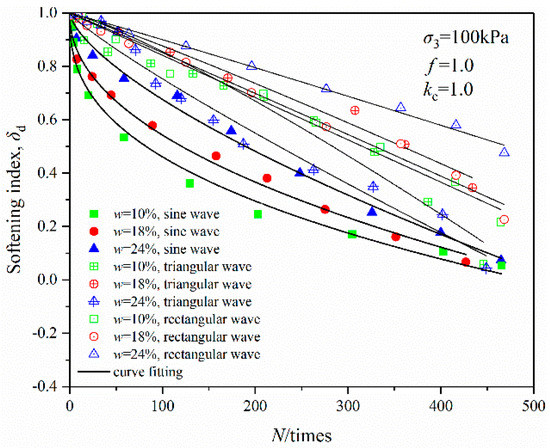
Figure 11. Fitting of degradation index under different cyclic loading wave forms.

The fitting results show that the application of Equation (4) can effectively simulate the softening curves of OMDS under cyclic loads with various amounts of moisture and wave forms such as the sine wave, triangular wave and rectangular wave, which can meet the needs of engineering construction (Table 3).

Table 3. Fitting parameters.

Wave Form	Moisture Content/%	Fitting Parameters
		m	n	R2
Sine wave	10 18 24	−0.01416 −0.05232 −0.09039	0.67934 0.47059 0.38753	0.87 0.90 0.89
Triangular wave	10 18 24	−0.00783 −0.00592 −0.00447	1.09822 1.19321 0.8703	0.79 0.82 0.85
Rectangular wave	10 18 24	−0.00837 −0.00134 −0.00157	1.03818 1.02179 1.00179	0.79 0.82 0.88

5. Discussion

Table 4 compares the degradation models constructed by several researchers, which were adopted to fit the degradation curve of OMDS with various moisture contents under sine wave cyclic loading, as shown in Figure 12 and Table 5.

Table 4. Degradation models.

Researcher	Degradation Model	Reference
Idriss et al.	${\delta }_{\mathrm{d}}=N^{-d}$	[12]
Yasuhara et al.	${\delta }_{\mathrm{d}}=1-d\lg N$	[17]
Yao et al.	${\delta }_{\mathrm{d}}={10}^{N^{-T}-1}$	[13]
This paper	${\delta }_{\mathrm{d}}=1+m{N}^n$	Present work

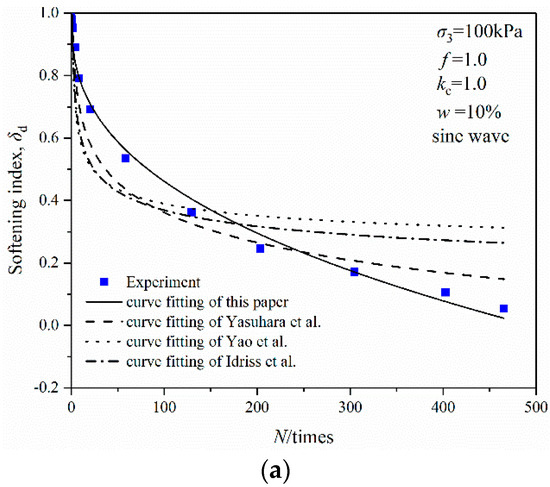
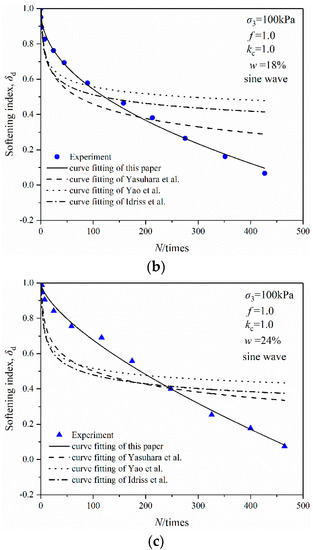
Figure 12. Comparison of degradation model: (a) w = 10%; (b) w = 18%; (c) w = 24%.

Table 5. Fitting effect of models based on the experimental data.

Sample	Wave Form	Moisture Content (%)	Residual Error Square Sum
			Idriss Model	Yasuhara Model	Yao Model	This Paper
OMDS	Sine wave	10	1.198	1.058	1.279	0.016
		18	1.472	1.239	1.617	0.007
		24	1.332	1.267	1.427	0.007

It can be seen that the stiffness degrades obviously in the initial stage of cyclic loading, and the performances of all four models are consistent. However, the stiffness degradation index of OMDS still decreases faster with the increase in vibration cycles. Then the degradation model of this paper can better represent this feature of OMDS under cyclic loading. The other three models show that the degradation index tends to stabilize as the vibration cycles increases, which is more suitable for the stiffness degradation characteristic of clay under cyclic loading.

6. Conclusions

The dynamic triaxial test of OMDS under different loads, consolidation ratios, natural moisture contents and wave forms was studied and analyzed, and the conclusions could be drawn as follows:

(1) Under cyclic loading, the soil stiffness decreases with the increase in vibration cycles. The increase in natural moisture content and vibration amplitude, and the reduction in the consolidation ratio accelerates the degradation of soil stiffness. The reason is that a higher moisture content results in the reduction in the interaction force between sand particles so that sand particles are prone to dislocation deformation; a lower consolidation ratio results in the decrease in sand compactness so that the ability to resist elastic deformation becomes weaker.

(2) The degradation index of stiffness decreases rapidly with the increase in vibration cycles, which indicates that the soil can be destroyed with fewer vibration cycles. The degradation index curves of the four load amplitudes are close to each other, which indicates that there is not a critical stress, which is different from cohesive soil. The variation amplitude of the degradation index curve is smaller when the moisture content is lower. The curvature of the degradation index curve with the same consolidation ratio is larger than that with different moisture contents. Among the different wave forms, the rectangular wave has the most obvious effect on the degradation index of OMDS.

(3) A degradation model for OMDS was established. Based on this model, the degradation index under various natural moisture contents and wave forms was fitted and analyzed. The degradation model of this paper can better represent the features of OMDS under cyclic loading.