Abstract
An analysis of the effect of vehicle loads on the fatigue life of local arch bridge suspenders in Southwest China was conducted by generating vehicle statistics, creating a fatigue vehicle model, and developing a fatigue life prediction method: First, the Midas model of an arch bridge was established, a random vehicle flow simulation was conducted in the Monte Carlo method, and the stress spectrum of the suspenders was calculated. Secondly, ANSYS software was used to estimate the fatigue life of the suspenders, and the accuracy of the proposed method was verified. Finally, the method was applied to the practical project of the Dafeng River Bridge in Southwest China. The results show that this method can predict the fatigue life of suspenders. It can be applied in the bridge health monitoring software system to realize real-time fatigue damage monitoring of the fatigue damage of suspenders, which could be used to predict the fatigue lives of bridges in Southwest China and provide references for the replacement of suspenders.
1. Introduction
As a key load-bearing component, suspenders play an important role in suspension bridges [1,2,3]. The working status of suspenders directly affects the safety of the whole bridge. Suspenders in the bridges are subject to repeated fatigue loads due to moving vehicles during the service period [4,5]. Then, fatigue damage produces and further causes the fatigue failure of the suspenders [6,7,8,9]. In practice, many suspenders even fractured when they experienced service life far below the expected service life, which seriously threatens the safety of bridges [10,11,12,13]. Therefore, predicting the fatigue life of suspenders under vehicle loads is the premise of ensuring the safety and reliability of bridges.
Researchers worldwide conducted a series of fatigue tests to predict suspenders fatigue life. Guo et al. [14] and Savrai et al. [15] conducted a series of various friction fatigue tests to study the fatigue characteristics and failure mechanism. Their study found that fatigue failure develops gradually from the surface, and the larger the friction amplitude, the shorter the service life. Roffey [16] and Iordachescu et al. [17] studied the fracture mechanism and conducted tensile and fatigue tests on the cable to reduce the steel wire fracture rate and lengthen the fatigue life span of the cable. They found that the tensile strength of the cable decreased. In addition, there were vertical propagation cracks in the cable whose depth reached as far as the radius of the cable. Feng et al. [18] ran cyclic loading fatigue damage tests on CFRP cables under different stresses and studied the evolution law and mechanism of fatigue damage of anchor cables. The stress affects the fatigue life of cables, and the cable damage first appears as longitudinal cracks and then gradually fractures. Wang et al. [19] and Chen et al. [20] carried out fatigue tests on high-strength steel wires under different stress levels, observing the crack propagation trend and shape, and combined with finite element software for modeling, they found that fatigue damage life can be evaluated according to fracture mechanics and numerical simulation.
Although the fatigue test cannot assess the fatigue damage of the suspenders caused by vehicle fatigue loads, many scholars have studied the effects of vehicle load on the fatigue life of suspenders from a theoretical and simulation perspective. Feng et al. [21] fatigue cycles were analyzed using finite element software, and stress and design life were taken into account when evaluating the life of suspenders made of different materials. It was found that the fatigue life of CFRP suspenders was faster than that of BFRP and steel. Jiang et al. [22,23] presented the fatigue analysis framework of stay cables under traffic loads, calculated the stress history of stay cables, determined the key stay cables according to the actual traffic data, and estimated the service life by establishing a fatigue model. It was found that fatigue greatly reduced the service life. Liu et al. [24] and Zhu et al. [25] used a multiscale probabilistic fatigue analysis method consisting of a finite element method and a vehicle load model to predict the remaining life of suspenders, and discovered that the remaining life of suspenders is lower than the design value. Li et al. [26] proposed to evaluate the cable damage state by the model of a vehicle-induced cable tension ratio, taking the ratio of vehicle-induced cable tension (tension ratio) as a variable and modeling the cable tension ratio model. According to the change of model-estimated parameters, the fatigue damage state of a cable under vehicle loads can be evaluated.
However, the above theory has not been applied to bridges in an actual service period, and the feasibility of actual projects cannot be verified. Therefore, theoretical application and actual projects have become the only way to study. Based on the future predicted transport load and multiscale finite element model, Sun et al. [27] proposed a multiscale fatigue damage calculation for long-span steel bridges. Combining their method with the actual long-span cable-stayed bridge, the researchers visualized fatigue damage accumulation and crack evolution of key components, and then calculated the damage accumulation to predict fatigue life. According to the traffic information on the real bridge, Fang et al. [28] established a probability model for vehicle parameters, simulated the dynamic response of the vehicle under the load with finite element software, predicted the fatigue life of the suspenders, and applied it to the Yangtze River Bridge project to obtain different suspenders’ lives and the most efficient replacement schedule. Li et al. [29] and Ni et al. [30] took Tsing Ma Bridge as an example combined with the health monitoring system, collected the traffic load on the bridge, estimated the life reliability index of suspenders, and provided decision making for the replacement and maintenance of suspenders. Based on an evaluation of the actual engineering health monitoring system and the dynamic strain data, Ye et al. [31] analyzed the stress spectrum under traffic load and evaluated the fatigue life of the bridge by identifying the main factors affecting the fatigue life.
Although the research results of the above vehicle loads on the fatigue life of suspenders are outstanding, Nowak et al. [32,33] found that the vehicle loads of bridges have obvious regional differences; that is, due to the obvious regional differences in the economic environment around the world, the vehicle loads vary significantly from place to place. Because of its many ports and economic development, the vehicle loads in Southwest China are different from those in other areas. Therefore, it is necessary to carry out vehicle statistics on typical sections in Southwest China, establish a standard fatigue vehicle model, and then predict the fatigue life of suspenders under vehicle loads in Southwest China.
2. Establishment of a Standard Fatigue Car Model
2.1. Vehicle Statistics
As a thoroughfare connecting Guangxi, Guizhou, Sichuan, and Hunan with Guangdong, Hong Kong, and Macao, the Third Xijiang Bridge is a vital link that connects various places. Many ports can be found nearby. Among them, the Longtou Port is the main inland port in China, an active hub of the regional comprehensive transportation system. It is also an important port for foreign trade in Southwest China. Therefore, in this study, vehicle statistics are made in the Third Xijiang Bridge, which is selected as a typical section in Southwest China.
The installation procedure of vehicle weighing system on the Third Xijiang Bridge cab be described as follows:
- Closure of lanes in a reasonable manner. The Xijiang Bridge has four lanes, and there are two lanes in the same direction. Therefore, in the same direction, the roadside lane is closed first, and the other lane is opened to traffic.
- Draw lines and cut grooves in the closed driveway.
- Cleaning and blow-drying the cut groove.
- Install the sensor in the groove, see Figure 1. The circuit leads to the roadside cabinet.
 Figure 1. Installation site photo.
Figure 1. Installation site photo. - Fill the groove with caulking glue, and it takes 3–8 h for the caulking glue to cure according to the weather conditions.
- Grind the joint sealant and the road surface.
As shown in Figure 2, the vehicle weighing system is installed and operational.

Figure 2.
Weighing system operation photo.
Based on data collected from the vehicle weighing system, information about vehicles in the past year was extracted, including vehicle axles, wheelbase, and vehicle weight. Because there are more than 5.5 million vehicles per year, 189 abnormal data with a vehicle weight of 0 can be ignored without affecting the results. Therefore, it is considered that in a typical road section, 15,075 vehicles pass through each day. Then they are classified according to wheelbase and vehicle weight. The specific classification method is as follows: First, the vehicle is classified by the number of axles, wheelbase Di, and weight W. Calculate the average and standard deviation of the wheelbase and weight after classification. Second, we combine vehicles with similar average weights and a wheelbase in the first classification, which reduces the number of categories and the calculation amount. The vehicle statistics are listed in Table 1.

Table 1.
Vehicle statistics.
On average, there are 13,905 two-axle vehicles per day, most of which are light. According to research on fatigue mechanism, the fatigue damage of suspenders under light load is very small, which can be ignored in the fatigue load spectrum [34]. Therefore, to simplify the data, vehicle weights under 30 kN (3 t) are excluded. All the weights of V1 are lower than 30 kN; they are all rejected. At the same time, the vehicles between V2 and V9, which are less than 30 kN, are excluded.
2.2. Establish a Standard Fatigue Car Model
Apart from the negligible V1 vehicle information, the remaining eight types of data are used as eight typical vehicle data sets. Based on the weighted average of the vehicle wheelbase, the equivalent axle load, and axle load distribution coefficient, eight typical fatigue vehicle models are established. The weighted average value of the vehicle wheelbase in a typical vehicle set is calculated as Equation (1), and the calculation results are shown in Table 2:
where Di is the i-th wheelbase of a typical fatigue car, Dij is the i-th wheelbase of the j-th vehicle in a typical vehicle assembly, and n is the total number of vehicles in a typical fatigue set.

Table 2.
The weighted average of the wheelbase in typical vehicle data.
A typical vehicle equivalent axle load refers to the axle loads of all vehicles in the typical vehicle data set converted into model vehicle axle loads. For the specific calculation formula in Equations (2) and (3), the results are shown in Table 3:
where Ai is the axle load of the i-th axle in a typical fatigue car model, fj is the frequency of the j-th vehicle in a typical vehicle assembly, Aij is the axle load of the i-th axle in the j-th vehicle in a typical vehicle assembly, and μi is the proportion of the axle load of the i-th axles to the weight of the whole car in a typical fatigue car mode.

Table 3.
Equivalent axle load A and axle load coefficient μ of typical vehicles.
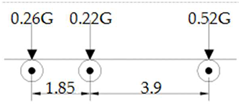
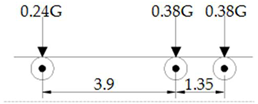
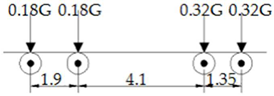
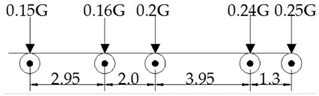
Establish eight typical fatigue car models that conform to this road section, as shown in Table 4.

Table 4.
Typical fatigue car mode.
However, the workload will still be huge when using models for analysis. To further simplify the workload, a standard fatigue car model which has the greatest impact on fatigue damage should be extracted from these eight typical models.
Table 4 shows that the most common vehicles that cause fatigue damage to suspenders on this road section are V6 and V9. The heaviest vehicle is the V9 model, with a weight of 404 kN, which may become the model with the greatest impact of fatigue damage. It is worth noting that V6, as the vehicle with the highest frequency, is second only to V9. It may also be the vehicle with the greatest impact of fatigue damage. Therefore, the V6 and V9 models are loaded to obtain the stress–time history curves. As shown in Figure 3 and Figure 4, the vehicle type with the most influence on fatigue damages is judged.

Figure 3.
V6 stress–time history curve.

Figure 4.
V9 stress–time history curve.
In the calculated cyclic stress amplitude σa, σa = (σmax − σmin)/2. V6 σa = 40.46 MPa, V9 σa = 47.77 MPa. From the calculation results, it can be seen that V9 is the vehicle that causes the maximum stress amplitude. Therefore, it is confirmed that V9 is used as the blueprint to establish the standard fatigue vehicle model. Model V9 is a six-axle car, and its wheelbase and axle weight distribution coefficient are known. To calculate the equivalent vehicle weight of V9, the axle weights of each axle are converted using fatigue damage equivalence. The calculation formula is Equation (4):
where W is the total mass of the standard fatigue car model; Wi is the equivalent mass of the i-th typical fatigue car, that is the sum of the above Ai; and fi is the i-th typical fatigue car frequency.
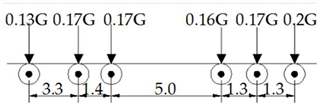
It is concluded that the equivalent vehicle weight in the daily average traffic volume data of the V9 model is 292.7 kN. The standard fatigue vehicle model is obtained according to the axle load distribution coefficient, as shown in Figure 5.

Figure 5.
Standard fatigue car model (length unit m, weight unit kN).
By following a similar processing method to the AASHTO code of the United States, the above-mentioned six-axis standard fatigue car model can be converted into a simplified standard fatigue car model. It is decided to combine the second and third shafts, as well as the fourth, fifth, and sixth shafts. The combined vehicle axis is located at the center of the coupling shaft. The simplified standard fatigue car model is shown in Figure 6.

Figure 6.
Simplified rear fatigue vehicle model (length unit m, weight unit kN).
3. Calculation Method of the Fatigue Life of Suspenders
The fatigue life calculation flow chart for suspenders is shown in Figure 7.

Figure 7.
Fatigue life calculation flow chart for suspenders.
Concrete Calculation Steps of the Fatigue Life of Suspenders
- Find or calculate the local standard fatigue car model.
- Traffic flow statistics on the bridge, which can be made by the health monitoring system.
- Establishment of the bridge MIDAS model.
- Simulation of random traffic flow based on the Monte Carlo method.
By studying the longitudinal spacing and lane distribution of vehicles, the traffic flow in the actual situation is simulated. To simplify the calculation, this paper simulates the random traffic flow in each lane within 1 h. This is to reflect the impact of the possible random traffic flow on the fatigue load spectrum of different suspender components in each lane.
The random traffic flow in 1 h mainly includes the total number of vehicles and the distance between vehicles. Based on the basic principle of the Monte Carlo method, the driving distance is taken as a random variable, and the variable is simulated to meet the normal distribution. Then, according to the principle of Monte Carlo random number extraction, the data of vehicle distance are simulated by MATLAB software. The simulated random number is tested to verify the simulation accuracy to form the random traffic flow information required for loading.
- 5.
- Calculation of suspenders’ stress spectrum.
First, in the MIDAS finite element model, a lane line with a step length of 1 m is established at the corresponding centerline of each lane. The stress influence line of each bridge suspender under the action of 1 kN is obtained after operation analysis. Then the stress influence line data of each suspender are transformed into a phasor. For example, in lane no. 1, the influence line for the i-th suspender becomes phasor Ai, and in lane no. 2, the influence line for the i-th suspender becomes phasor Bi, and so on.
After that, the random traffic flow information obtained above is sorted out to get the specific vehicle loading sequence. The stress spectrum of the suspender is calculated by matrix operation. The stress response caused by each vehicle is included in the matrix, and the distance between vehicles is taken as the step length. After superposition, the stress response matrix caused by all vehicles crossing the bridge within 1 h is obtained. MATLAB software can calculate data if they are large. The calculated result is multiplied by the impact coefficient (1 + μ), and the multiplied result plus the dead load stress of suspenders will finally get the stress spectrum of each suspender.
According to JTG D60-2004, General Code for Design of Highway Bridges and Culverts, the impact coefficient of reinforced concrete arch bridges is calculated as Equations (5) and (6):
where f is the fundamental frequency of the structure (Hz), μ is the impact coefficient, l is the calculated span of structure (m), E is the elastic modulus of the structural material (N/m2), Ic is the section moment of inertia of the midspan section of the structure (m4), and mc is the mass per unit length in the middle of the structure (kg/m).
The dead load stress of each suspender can be calculated by dividing the dead load value by the cross-sectional area of the suspender. The dead load value is measured by the bridge health monitoring system.
- 6.
- Calculation of the fatigue life of suspenders.
According to the linear cumulative damage theory [35], it is necessary to determine all the stress cycle amplitudes and their corresponding action times to predict the life of suspenders. Therefore, it is necessary to process the fatigue stress spectrum of the suspender. This information is then used to extract all the cyclic amplitudes by the rainflow method and count the action times of each cyclic amplitude.
According to the extracted stress amplitude and cycle times, the fatigue damage degree of suspenders can be calculated to predict the life of suspenders according to the S–N curve of materials [36].
- (a)
- The S–N curve of the material is modified by the mean stress [37].
Paulson et al. of the United States put forward the S–N fatigue curve of a grade 270 (equivalent to grade 1860 in China) steel strand with an average stress of 1050 MPa as Equation (7):
where σa is the stress amplitude, and N is the number of cycles.
Therefore, based on Equation (7), the mean stress is corrected. Because the suspenders may be corroded, Goodman, the stress line suitable for notched specimens, is selected for correction. The Goodman formula is as in Equation (8):
where σa′ is the ultimate fatigue stress amplitude, σar is the fatigue limit under symmetrical cycle, σb is the tensile strength, and σm is the mean value of stress.
In engineering, the stress corresponding to 107 cycles is considered the fatigue limit, so N = 107 cycles are brought into Equation (7) to obtain the ultimate fatigue stress amplitude σa′. Then, σa′ is brought into Equation (8) to obtain σar corresponding to an average stress of 1050 MPa. Thus, the ultimate fatigue amplitude is deduced as Equation (9).
The slope of the S–N curve of the material remains unchanged under different ultimate strengths. Therefore, the revised Equation (7) should be lgN = a − 3.5 lgσa and bring in N = 107, σa = σa′. The formula for obtaining a is as in Equation (10).
Therefore, the S–N fatigue curve after the mean stress correction is as in Equation (11).
- (b)
- Calculation of equivalent stress amplitude σae.
The single stress cyclic fatigue damage degree d can be calculated by Equation (12).
D = 1/N
The total fatigue damage degree D can be calculated by Equation (13).
D = Σd = Σ1/N
Order nσae3.5 = Σσa3.5, where n is the total number of cycles. The σae can be calculated by Equation (14).
- (c)
- Calculation of the fatigue life according to the fatigue damage degree.
Substitute the calculated equivalent stress amplitude σae into Equation (11) for σa to obtain the total number of cycles N corresponding to σae. The daily damage degree is equal to the number of calculation hours multiplied by the fatigue damage in 1 h (i.e., fatigue damage in 1 h under daytime traffic condition × 14 h + fatigue damage in 1 h under night traffic condition × 10 h).
Annual damage degree = the daily damage degree × 365.
The fatigue life of suspenders can be predicted as: 1/(annual damage degree).
4. Engineering Verification and Application
4.1. Brief Introduction of the Project
The Dafeng River Bridge (in Figure 8) is located in Gaotang Village, Qinzhou City, Guangxi, and crosses the Dafeng River at the bend of the river. The main span is a rigid frame tied steel box arch bridge, with a net span of 120.0 m, a net rise height of 27.0 m, a net rise/span ratio of 1:4.44, and a quadratic parabola for the arch axis. The bridge deck is horizontally divided into two independent and symmetrical bridges, left and right, each designed according to three lanes. Each bridge has a total of 14 suspenders, the spacing between suspenders is 8 m, and the suspenders are made of GJ15-27 whole bunch of extruded steel strand suspenders. Its standard value of tensile strength is fpk = 1860 MPa, the diameter of each steel strand is 15.20 mm, and the outer diameter of the suspenders is 126 mm. A cross-section view of the suspender is shown in Figure 9, and the Dafeng River Bridge structural layout is shown in Figure 10.

Figure 8.
Dafeng River Bridge.

Figure 9.
Cross-section view of the suspender of the Dafeng River Bridge.

Figure 10.
Dafeng River Bridge structural layout.
A health monitoring system is installed on the Dafeng River Bridge. The health monitoring system can receive and store the traffic flow video and pictures taken by the vehicle statistical camera device (as shown in Figure 8) installed on the Dafengjiang Bridge, and measure the traffic flow and other specific information on the Dafengjiang Bridge in real time.
4.2. Finite Element Verification
In order to verify the correctness of the proposed calculation method for the fatigue life of suspenders. A finite element method is used to calculate the life of the suspender of the Dafeng River Bridge. The results of finite element calculation are compared with those of the proposed method to carry out finite element verification.
Taking the no. 7 suspender of the Guangxi Dafeng River Bridge as an example, the ANSYS suspender model is established, which has a diameter of 126 mm and a length of 29.766 m. Its material characteristics are as follows: the density is 7850 kg/m3, Young’s modulus is 2.95 × 1011 Pa, Poisson’s ratio is 0.25, the tensile strength is fpk = 1860 MPa, and the inputted S–N curve is as in Figure 11. As shown in Figure 12, the grid is divided by sweeping. One end of the suspender is fixed and restrained, and the other end exerts a pressure of 207.422 MPa.

Figure 11.
Inputted S–N curve.

Figure 12.
Enlarged view of the suspender model and local grid.
The calculated life of the no. 7 suspender is shown in Figure 13. Under 207.422 MPa, the minimum life is 5.9374 × 106 cycles. When the stress value is 207.422 MPa in actual engineering, it occurs about once per hour, so the cycle is about 8760 times per year. Thus, the calculated fatigue life unit of the no. 7 suspender is changed from cycles to years as in Equation (15).

Figure 13.
The calculated life of the no. 7 suspender.
Similarly, the fatigue life of other suspenders is calculated, and the suspenders calculated by ANSYS are compared with the theoretical ones. The specific comparison is displayed in Table 5.

Table 5.
Comparison table between ANSYS and the theoretical calculation of suspenders’ life.
The above results show that the error between the suspender life calculated by ANSYS and that calculated by theory is less than 5%. Therefore, the method proposed in this paper is verified correctly.
4.3. Engineering Application
4.3.1. Traffic Flow Statistics
According to the health monitoring system installed on the Dafeng River Bridge, the traffic volume of the Dafeng River Bridge is counted. The bridge has six lanes and three lanes in one direction (the farthest distance from the suspender is lane no. 1, and lane nos. 2 and 3 are arranged successively close to the suspender). Lane no. 1 is mainly used by small cars (V1-type cars), and its contribution to the fatigue of the suspender can be neglected. Therefore, this paper mainly considers the traffic flow in lane nos. 2 and 3. According to the statistical vehicle information of the health monitoring system, the ratio of vehicles in lane nos. 2 and 3 is approximately 1:2. Considering the bridge comprehensively, 14 h during daytime (6:00–20:00) and 10 h at night (20:00–6:00) are defined. The traffic flow ratio between daytime and night is about 4:1. The hourly traffic flow of lane nos. 2 and 3 in different periods are listed in Table 6.

Table 6.
Fatigue traffic flow.
4.3.2. Establishment of the Bridge MIDAS Model
The finite element software MIDAS Civil is used to model the Dafeng River Bridge, and the main bridge is modeled as shown in Figure 14. Model suspenders and tie rods use strand 1860 in JTG-04(s), and the suspender section is equivalent to a circle with a diameter of 126 mm. The tie bar is composed of 31 steel strands, which are sheathed with HDPE. The outside diameter of the tie bar is 127 mm, and it is equivalent to a circle with a diameter of 127 mm.

Figure 14.
Full bridge finite element model diagram.
The whole bridge model has 1043 nodes and 1554 units, including 28 truss units, all of which are suspenders. There are a total of 180 plates, all of which are carriageway plates. The rest of the structure are all beam elements, totaling 1346 beam elements.
4.3.3. Simulation of Random Traffic Flow Based on Monte Carlo Method
Considering that trucks are the primary source of fatigue load and the Dafeng River Bridge is located in a high-speed section, this paper assumes that all vehicles run at 80 km/h. According to the traffic flow statistics above, the average vehicle distance between lane nos. 2 and 3 of the Dafeng River Bridge is determined as shown in Table 7.

Table 7.
Vehicle distance parameter simulation.
The simulated vehicle distance satisfies the normal distribution. The variance of vehicle distance is roughly defined, taking 40 and 20 for lane nos. 2 and 3 during the daytime and 120 and 60 at night, respectively. Using MATLAB software, according to the Monte Carlo random number extraction principle, the vehicle distance data are simulated.
The simulated random number is tested, and the results are listed in Table 8. It can be seen that four random groups of car distances are less than 2% error. Therefore, these data are used as car distances in random traffic flow data, and the car distance distribution is like a scatter plot, as shown in Figure 15.

Table 8.
Random data test of vehicle distance.

Figure 15.
Scatter diagram of the data distance of each group. (a) Scatter plot of the daytime lane no. 2 data group. (b) Scatter plot of the daytime lane no. 3 data group. (c) Scatter plot of the night lane no. 2 data group. (d) Scatter plot of the night lane no. 3 data group.
4.3.4. Simulated Traffic Load and Stress Spectrum Calculation of Suspenders
Lane nos. 2 and 3 have been identified as loading lanes. Therefore, in the MIDAS Civil finite element model, lane lines with a step length of 1 m are established at the centerlines of lane nos. 2 and 3. The stress influence lines of nos. 1–7 suspenders on the right side along the bridge direction under the action of 1 kN are obtained through operation analysis, as shown in Figure 16.


Figure 16.
Stress influence line of the suspender, (a) stress influence line of the no. 1 suspender, (b) stress influence line of the no. 2 suspender, (c) stress influence line of the no. 3 suspender, (d) stress influence line of the no. 4 suspender, (e) stress influence line of the no. 5 suspender, (f) stress influence line of the no. 6 suspender, (g) stress influence line of the no. 7 suspender.
As can be seen in Figure 16, because lane no. 3 is closer to the suspender than lane no. 2, the stress influence line is larger. The stress influence line data of each suspender are converted into a column phasor. Because the lane length is set to 120 m and the influence line step is 1 m, this vector is a 121 × 1 column vector, with lane no. 2 marked A1–A7 and lane No. 3 marked B1–B7.
The random traffic flow information obtained above is sorted out and recorded in sequence. The specific vehicle loading sequence is shown in Table 9 and Table 10.

Table 9.
Loading sequence of traffic on the bridge during daytime.

Table 10.
Loading sequence of traffic on the bridge at night.
The stress spectrum of the suspender is calculated by matrix operation, the stress response caused by each vehicle is included in the matrix, and the distance between vehicles is taken as the step length. After superposition, the stress response matrix caused by all vehicles crossing the bridge within 1 h is obtained. Because of the large data, MATLAB software is used to program and calculate. Then the data calculated by MATLAB are multiplied by the impact coefficient (1 + μ), and the dead load stress of the suspenders is added to get the stress spectrum of each suspender.
The basic frequency of the structure is calculated according to Equation (6) above, and the impact coefficient μ is obtained according to the above Equation (5). The specific calculation as Equation (16).
The dead load and dead load stress of suspenders are listed in Table 11:

Table 11.
Dead load and dead load stress of suspenders.
Taking the no. 7 suspender as an example, its stress spectrums are obtained by MATLAB, as shown in Figure 17 and Figure 18.

Figure 17.
Stress spectrum of the no. 7 suspender during daytime.

Figure 18.
Stress spectrum of the no. 7 suspender at night.
More vehicles pass during the daytime than at night, so the stress spectrum during the daytime is denser, which is consistent with the actual situation. So far, the fatigue stress spectrum of seven half-through arch bridge suspenders has been obtained.
4.3.5. Fatigue Life Calculation of Suspenders
The no. 7 suspender is chosen to elaborate the calculation of the fatigue life. The rain flow method is used to extract the stress amplitude of the no. 7 suspender during the daytime, and a total of 280 full-amplitude cycles are collected, as listed in Table 12.

Table 12.
Statistics of stress amplitude of the no. 7 suspender during the daytime.
The mean stress value is σm = 98.721 MPa, and the ultimate tensile stress of the steel wire of the suspender is σb = 1860 MPa.
The total fatigue loading cycles corresponding to σae are N = 1,158,594,655 cycles, and the number of actions is 280 cycles. Therefore, during the daytime, the hourly fatigue damage of the no. 7 suspender can be determined.
Likewise, the hourly fatigue damage of the no. 7 suspender at night and other suspenders can be obtained. The calculation results are obtained by repeating the former steps, which are listed in Table 13.

Table 13.
Fatigue life prediction of suspenders.
5. Conclusions
To calculate the suspenders’ fatigue life of arch bridges under vehicle loads in Southwest China, the vehicle statistics of typical sections in Southwest China are carried out, the standard fatigue vehicle model is established, and a method for calculating the suspenders’ fatigue life is proposed. This method uses the standard fatigue vehicle mode, bridge traffic flow, and MIDAS to simulate the random traffic flow. Then the stress spectrum of suspenders is obtained so that the fatigue life of each suspender is calculated. After that, the feasibility of this method is verified by finite element analysis and practical engineering. To sum up, the following conclusions are drawn:
- According to the traffic flow statistics of typical road sections, a standard fatigue vehicle model in Southwest China is established. Comparing our model with the standard fatigue vehicle in the Chinese General Code for Design JGD60-2015, we established that the model’s weight is lower. It is proved that even near the port, the number of heavy vehicles and their weight are not necessarily too high. There are differences in different regions, so it is inevitable to establish standard fatigue vehicles in Southwest China. Subsequently, this model can be used for vehicle fatigue simulation of similar road sections in Southwest China and other areas. It is not essential to obtain a large number of vehicle statistics and calculations again, thus improving the efficiency of further vehicle fatigue simulation.
- A set of calculation methods for the fatigue life of suspenders under the vehicle load is put forward. Compared with finite element calculation, this method has an error rate of less than 5% and can be effectively applied to practical projects, which proves its accuracy and feasibility. In the future, this method can be applied to the bridge health monitoring software system. According to the established standard fatigue vehicle model and the road traffic volume counted, the fatigue damage of bridge suspenders in Southwest China can be monitored in real time. Therefore, the fatigue life of bridges in Southwest China can be evaluated, which provides a reference for replacing suspenders.
- In practical engineering, the life of Dafeng River Bridge suspenders is calculated. It is found that the life of nos. 1–7 suspenders is on the rise. The life of the no. 1 suspender is the shortest, even less than one-third of that of the no. 7 suspender, mainly because the no. 1 suspender is short in length and close to the arch foot. Its stress amplitude is large under the action of vehicle load, so its fatigue damage is large and its fatigue life is low. Therefore, more attention should be paid to the health status of short suspenders near the arch foot in practical engineering.
Author Contributions
Conceptualization, Z.Z., H.W. and T.Y.; methodology, Z.Z., H.W. and L.W.; validation, Z.Z., H.W. and T.Y.; formal analysis, Z.Z., H.W., X.W. and T.Y.; investigation, Z.Z., H.W., T.Y. and L.W.; writing—original draft preparation, Z.Z. and H.W.; writing—review and editing, H.W. and T.Y.; project administration, H.W. X.W. and L.W.; funding acquisition, H.W. X.W. and L.W. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Science and Technology Base and Talent Special Project of Guangxi Province (grant number AD19245152), Key Research and Development Project of the Science and Technology Department of Guangxi Province (grant number: 2021AB22121), Science and Technology Base and Talent Project of Guangxi Science and Technology Department (grant number 2021AC19125), Nanning Excellent Young Scientist Program (grant numbers RC20180108 and RC20190206), Science and Technology Key R&D Project of Guangxi (grant number AB22035074), “Yongjiang Plan” of Nanning Leading Talents in Innovation and Entrepreneurship (grant number 2018-01-04), and National Key R&D Program of China (grant number 2021YFB2600604).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Feng, D.; Scarangello, T.; Feng, M.Q.; Ye, Q. Cable tension force estimate using novel noncontact vision-based sensor. Measurement 2017, 99, 44–52. [Google Scholar] [CrossRef]
- Deng, Y.; Zhang, M.; Feng, D.-M.; Li, A.-Q. Predicting fatigue damage of highway suspension bridge hangers using weigh-in-motion data and machine learning. Struct. Infrastruct. Eng. 2020, 17, 233–248. [Google Scholar] [CrossRef]
- Ye, H.; Duan, Z.; Tang, S.; Yang, Z.; Xu, X. Fatigue crack growth and interaction of bridge wire with multiple surface cracks. Eng. Fail. Anal. 2020, 116, 104739. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, X.; Wu, Z.; Zhu, Z. Fatigue behavior and failure mechanism of basalt FRP composites under long-term cyclic loads. Int. J. Fatigue 2016, 88, 58–67. [Google Scholar] [CrossRef]
- Pipinato, A.; Pellegrino, C.; Fregno, G.; Modena, C. Influence of fatigue on cable arrangement in cable-stayed bridges. Int. J. Steel Struct. 2012, 12, 107–123. [Google Scholar] [CrossRef]
- Fu, Z.; Ji, B.; Wang, Q.; Wang, Y. Cable force calculation using vibration frequency methods based on cable geometric pa-rameters. J. Perform. Constr. Facil. 2017, 31, 04017021. [Google Scholar] [CrossRef]
- Ji, B.; Chen, D.-H.; Ma, L.; Jiang, Z.-S.; Shi, G.-G.; Lv, L.; Xu, H.-J.; Zhang, X. Research on Stress Spectrum of Steel Decks in Suspension Bridge Considering Measured Traffic Flow. J. Perform. Constr. Facil. 2012, 26, 65–75. [Google Scholar] [CrossRef]
- Xu, X.; Huang, Q.; Ren, Y.; Zhao, D.-Y.; Zhang, D.-Y.; Sun, H.-B. Condition evaluation of suspension bridges for maintenance, repair and rehabilitation: A comprehensive framework. Struct. Infrastruct. Eng. 2019, 15, 555–567. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, T.; Huang, L.; Pan, Z. Fatigue life evaluation on short suspenders of long-span suspension bridge with central clamps. J. Bridge Eng. 2017, 22, 04017074. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, T.; Hebdon, M.H.; Zhang, Z. Corrosion Fatigue Analysis and Reliability Assessment of Short Suspenders in Suspension and Arch Bridges. J. Perform. Constr. Facil. 2018, 32, 04018060. [Google Scholar] [CrossRef]
- Li, S.; Xu, Y.; Zhu, S.; Guan, X.; Bao, Y. Probabilistic deterioration model of high-strength steel wires and its application to bridge cables. Struct. Infrastruct. Eng. 2014, 11, 1240–1249. [Google Scholar] [CrossRef]
- Sih, G.; Tang, X.; Li, Z.; Li, A.; Tang, K. Fatigue crack growth behavior of cables and steel wires for the cable-stayed portion of Runyang bridge: Disproportionate loosening and/or tightening of cables. Theor. Appl. Fract. Mech. 2008, 49, 1–25. [Google Scholar] [CrossRef]
- Liu, Y.; Xiao, X.; Lu, N.; Deng, Y. Fatigue Reliability Assessment of Orthotropic Bridge Decks under Stochastic Truck Loading. Shock Vib. 2016, 2016, 1–10. [Google Scholar] [CrossRef]
- Guo, T.; Liu, Z.; Correia, J.; de Jesus, A.M. Experimental study on fretting-fatigue of bridge cable wires. Int. J. Fatigue 2019, 131, 105321. [Google Scholar] [CrossRef]
- Savrai, R.; Osintseva, A. Effect of hardened surface layer obtained by frictional treatment on the contact endurance of the AISI 321 stainless steel under contact gigacycle fatigue tests. Mater. Sci. Eng. A 2020, 802, 140679. [Google Scholar] [CrossRef]
- Roffey, P. The fracture mechanisms of main cable wires from the forth road suspension. Eng. Fail. Anal. 2013, 31, 430–441. [Google Scholar] [CrossRef]
- Iordachescu, M.; Valiente, A.; De Abreu, M. Effect of environmentally assisted damage on fatigue resistance of tie-down cables after 30 years of service in a cable-stayed bridge. Eng. Fail. Anal. 2021, 126, 105455. [Google Scholar] [CrossRef]
- Feng, B.; Wang, X.; Wu, Z.; Yang, Y.; Pan, Z. Performance of anchorage assemblies for CFRP cables under fatigue loads. Structures 2020, 29, 947–953. [Google Scholar] [CrossRef]
- Wang, G.; Ma, Y.; Guo, Z.; Bian, H.; Wang, L.; Zhang, J. Fatigue life assessment of high-strength steel wires: Beach marks test and numerical investigation. Constr. Build. Mater. 2022, 323, 126534. [Google Scholar] [CrossRef]
- Chen, C.; Jie, Z.; Wang, K. Fatigue life evaluation of high-strength steel wires with multiple corrosion pits based on the TCD. J. Constr. Steel Res. 2021, 186, 106913. [Google Scholar] [CrossRef]
- Feng, B.; Wang, X.; Wu, Z. Fatigue life assessment of FRP cable for long-span cable-stayed bridge. Compos. Struct. 2018, 210, 159–166. [Google Scholar] [CrossRef]
- Jiang, C.; Wu, C.; Cai, C.; Jiang, X.; Xiong, W. Corrosion fatigue analysis of stay cables under combined loads of random traffic and wind. Eng. Struct. 2020, 206, 110153. [Google Scholar] [CrossRef]
- Jiang, C.; Wu, C.; Cai, C.; Xiong, W. Fatigue analysis of stay cables on the long-span bridges under combined action of traffic and wind. Eng. Struct. 2020, 207, 110212. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, T.; Chai, S. Probabilistic Fatigue Life Prediction of Bridge Cables Based on Multiscaling and Mesoscopic Fracture Mechanics. Appl. Sci. 2016, 6, 99. [Google Scholar] [CrossRef]
- Zhu, J.; Zhang, W. Probabilistic fatigue damage assessment of coastal slender bridges under coupled dynamic loads. Eng. Struct. 2018, 166, 274–285. [Google Scholar] [CrossRef]
- Li, S.; Wei, S.; Bao, Y.; Li, H. Condition assessment of cables by pattern recognition of vehicle-induced cable tension ratio. Eng. Struct. 2018, 155, 1–15. [Google Scholar] [CrossRef]
- Sun, B.; Xu, Y.-L.; Wang, F.-Y.; Li, Z.; Zhu, Q. Multi-scale fatigue damage prognosis for long-span steel bridges under vehicle loading. Struct. Infrastruct. Eng. 2019, 15, 524–538. [Google Scholar] [CrossRef]
- Fan, Z.; Ye, Q.; Xu, X.; Ren, Y.; Huang, Q.; Li, W. Fatigue reliability-based replacement strategy for bridge stay cables: A case study in China. Structures 2022, 39, 1176–1188. [Google Scholar] [CrossRef]
- Li, S.; Zhu, S.; Xu, Y.; Chen, Z.; Li, H. Long-term condition assessment of suspenders under traffic loads based on structural monitoring system: Application Tsing Ma Bridge. Structral Control. Health Monit. 2012, 19, 82–101. [Google Scholar] [CrossRef]
- Ni, Y.; Chen, R. Strain monitoring based bridge reliability assessment using parametric Bayesian mixture model. Eng. Struct. 2020, 226, 111406. [Google Scholar] [CrossRef]
- Ye, X.; Ni, Y.; Wong, K.; Ko, J. Statistical analysis of stress spectra for fatigue life assessment of steel bridges with structural health monitoring data. Eng. Struct. 2012, 45, 166–176. [Google Scholar] [CrossRef]
- Nowak, A.S. Live load model for highway bridges. Struct. Saf. 1993, 13, 53–66. [Google Scholar] [CrossRef]
- Nowak, A.S.; Nassif, H.; Defrain, L. Effect of truck loads on bridges. J. Transp. Eng. 1993, 119, 853–867. [Google Scholar] [CrossRef]
- Laman, J.A.; Nowak, A.S. Fatigue-load models for girder bridges. J. Struct. Eng. 1996, 122, 726–733. [Google Scholar] [CrossRef]
- Miner, M.A. Cumulative damage in fatigue. J. Appl. Mech. 1945, 12, A159–A164. [Google Scholar] [CrossRef]
- Lan, C.; Ren, D.; Xu, Y.; Li, N. Fatigue property assessment of parallel wire stay cableII: Fatigue life model for stay cable. China Civ. Eng. J. 2017, 50, 69–77. [Google Scholar]
- Lu, H. Study on Fatigue Damage and Safety Design Analysis of Suspender of Half-Through Arch Bridge. Master’s Thesis, Chongqing Jiaotong University, Chongqing, China, 2019. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).