Abstract
A dynamic game model based on multiple decision makers is developed to minimize pedestrian–vehicle conflicts at unsignalized crosswalks. The characteristics of pedestrians and drivers crossing the street are divided into traffic features, behavioral characteristics, and psychological factors, using data collected from a survey of pedestrian crossing behavior. Based on waiting delay and risk assessment, a utility model of pedestrian crossing choice behavior is presented, and a probability model for different phases of the waiting stage is developed by splitting the waiting process into three stages with pedestrian waiting duration. The payment function and the game model of pedestrian–vehicle conflict based on distinct previous decision makers are developed using game theory and “mixed strategy”, and they are resolved in equilibrium.
1. Introduction
In urban transportation systems, pedestrian crossing behavior often involves a significant risk of pedestrian–vehicle conflict, which requires specialized traffic facilities to protect pedestrians crossing the street. Currently, the existing infrastructures, such as street overpasses, underpasses, traffic signals, and pedestrian crossings, can separate pedestrians and vehicles in time and space to avoid conflicts, but most of the sections only take separate crosswalks as signs to guide pedestrians and remind vehicles to avoid under the present road conditions, not guaranteeing pedestrian crossing safety. Therefore, it is necessary to study the risk mechanism of pedestrian–vehicle conflict for unsignalized mid-block crosswalks.
Crossing pedestrians and vehicles have a conflict of traffic interests; both hope to pass first when they arrive at the crosswalk. In practice, when pedestrians and vehicles are on the crossing section without hard separation, one is bound to wait for the other to pass first, which then increases the risk of pedestrian–vehicle conflicts, and even traffic accidents. The existing studies are mostly based on the crossing characteristics of pedestrians and the decision-making behavior of drivers, with less consideration of the influence of different factors on the decision outcome, and a lack of quantitative research on the factors influencing the decision-making behavior.
Therefore, this research considers the influence of decision priorities on choice outcomes, combines game theory with decision behavior, explores the intrinsic connection between the interests of decision subjects and the existence of decision outcomes, introduces quantitative probability functions and payment utility values for decision makers’ choices, quantitatively analyzes the utility values generated by different choices, and investigates the mechanism of pedestrian–vehicle conflicts under pedestrian crossing behaviors, to reduce the probability of conflicts and minimize accident losses on the basis of reducing conflict risks and time delays.
2. Literature Review
At unsignalized control sections, there is a conflict between pedestrians and vehicles in which the main decision makers are pedestrians and drivers. Due to the lack of segregation facilities, pedestrian crossing behavior is influenced by a variety of factors. By analyzing the characteristics of crossing behavior, the safety of crossing behavior can be effectively improved and traffic accidents can be reduced [1].
The crossing pedestrian is an important component that contributes to the conflict phenomenon. The driver’s awareness of yielding and the pedestrian’s awareness of risk have a great impact on the safety of pedestrians crossing the street [2]. Nowadays, existing research separates the pedestrian from the crosswalk system and analyzes a particular characteristic of the pedestrian separately, concentrating on the study of the individual behavioral and psychological characteristics of the pedestrian. Duan and Long [3] constructed a decision model of pedestrians crossing an unsignalized street based on the logistic regression method to analyze the influence of different factors on pedestrian crossing decisions. In the phenomenon of pedestrian–vehicle conflict, pedestrian crossing speed is an important factor. Zheng et al. [4] construct bivariate logistic models for the interaction between pedestrians and vehicles at unsignalized crosswalks to investigate the effect of different factors on the severity of conflicts, which can be used to explain pedestrians’ crossing choices in different scenarios.
Zhang and Wang [5] explored the traffic psychology and traffic behavior of pedestrians crossing the street, as well as the effect of group behavior on the change of pace speed, while Wang et al. [6] showed that pedestrians decide their crossing speed and ways according to the position and speed of the approaching vehicle. In addition, pedestrian crossing behavior [7], factors influencing pedestrian crossing safety [8], the effect of crossing behavior on safety, and the phenomenon of phone use while crossing for pedestrians [9] are also studied in depth.
On the other hand, the study of driver characteristics mainly focuses on the driver’s decision-making behavior. When a moving vehicle encounters a pedestrian crossing in front of it, the driver makes a decision based on the actual situation and the pedestrian status, which is influenced by experience due to the different characteristics of drivers, even in the same scenario. Since “avoiding pedestrians” increases vehicle delays, some drivers tend to pass quickly when it is not necessary. Yu et al. [10] analyzed the delays caused by vehicles avoiding pedestrians, and the results showed that the delay is closely related to the volume of pedestrians. In addition, to overcome increased delays due to vehicle avoiding, Wang et al. [11] proposed a lane-splitting avoiding model based on the principles of pedestrian priority and efficiency to reduce vehicle delays, while not excessively increasing pedestrian delays. The personality and behavioral characteristics of drivers are also important factors in the generation of pedestrian–vehicle conflicts. Through big data [12] and scenario testing [13], it is found that drivers’ psychological burden increases when facing pedestrians crossing the street in a much greater way than in other cases, and the road hazard level can be classified in drivers’ heart rate to provide a theoretical basis for road safety control measures. Furthermore, Wang et al. [14] constructed intersection cellular automata models based on different driver personalities to analyze the effects of different combinations of proportions of driver characteristics on the average speed of the road.
Radhameri et al. [15] studied the yielding behavior of drivers on unsignalized roadways and evaluated the effect of different traffic signs on driver guidance, showing that the signs have a positive effect on vehicle yielding to pedestrians and can improve traffic safety in unsignalized streets. Lantieri et al. [16] analyzed driver attention and driving behavior to explore the safety effects of roadside LED lights on nighttime travel at unsignalized crosswalks, and showed that roadside lights are effective in increasing drivers’ probability of yielding and improving pedestrian detection distances. Tomas et al. [17] considered the actual road conditions of different scenarios and introduced road section speed as the upper speed limit to quantify the probability of drivers yielding on unsignalized road sections and to investigate the intrinsic connection between speed conditions and yielding probability.
As for pedestrian–vehicle conflict, the mathematical analysis method is used to establish the model of pedestrian–vehicle conflict, to grasp the significant characteristics of pedestrian–vehicle conflict in the unsignalized street. Noh et al. [18] constructed a potential risk analysis system for pedestrians at unsignalized crosswalks to uncover potential risk factors in pedestrian crossing scenarios, in order to detect safety behavior on unsignalized roadways. Yang et al. [19] explore the influence of road conditions and environmental conditions on accident severity, which can effectively identify the potential risk factors of traffic accidents. Ma et al. [20] developed a pedestrian–vehicle conflict probability estimation model based on the arrival volume and operational characteristics of pedestrians and vehicles, by estimating the probability of a decision subject appearing on a crosswalk. In addition, some scholars classified the causes and levels of pedestrian–vehicle conflict by sequence comparison [21], and constructed a new evaluation system for quantitative analysis of the severity of traffic accidents [22], and for correlation analysis among variables [23] to determine the factors affecting pedestrian–vehicle conflict levels.
Game theory considers the predicted and actual behaviors of individuals to obtain the optimization strategies of the game parties, which can be used to solve transportation problems. Wardrop [24] first combined problems in transportation with game theory to build the first and second principles of transportation network equilibrium, which laid the foundation of game theory in transportation research. Szeto [25] proposed two cooperative game concepts to determine the reliability of travel costs and showed that the classical game theoretic approach might overestimate the reliability of road network travel costs. Wei et al. [26] quantify the pedestrian–vehicle conflict and build a conflict game matrix between pedestrians and vehicles to establish a kinetic model of the evolution of pedestrian–vehicle conflict, to analyze the evolution direction and rate of pedestrian–vehicle encounters under different conditions. Chen et al. [27] proposed a game theory-based intelligent vehicle conflict decision model for avoiding traffic conflicts and saving time across unsignalized intersections.
As a result, most research focuses on the conflict subject, and there is sufficient research on pedestrian–vehicle crossing, crossing conflict, and behavioral characteristics, which form a more complete road traffic theory system, but conflict at unsignalized crossings has not yet been universally recognized in terms of theoretical system and practical application. There is a lack of research on the impact of the first decision on other subjects, the quantitative probability and payment utility of decision makers, and the combination of game theory and the problem of pedestrian–vehicle conflict in unsignalized streets.
In this paper, the behavioral characteristics of the participants are studied from the perspective of the decision sequence of traffic participants, to build an evaluation index system, and the utility payment division of pedestrian–vehicle conflict is made in terms of risk and delay. On this basis, a “hybrid strategy” is chosen according to the game of behavior between drivers and pedestrians, and a dynamic game model is established to analyze the mechanism of pedestrian–vehicle conflict and predict the decision-making behaviors of pedestrians and drivers under different situations, so as to obtain the optimal set of strategies, which can effectively alleviate the problem of pedestrian traffic safety, and is of great significance for solving urban traffic safety problems.
The remainder of this paper is organized as follows: in Section 3, the characteristics of the traffic participants in the unsignalized streets are analyzed by data collection and questionnaire survey; in Section 4, a dynamic game model between pedestrians and vehicles is constructed and solved based on different prior decision makers; and in Section 5, a summary concludes this paper.
3. Characteristic Analysis of Traffic Participants on Unsignalized Sections
In order to analyze the traffic characteristics of unsignalized crosswalks and the characteristics and influencing factors of crossing behavior, a field survey by video acquisition is needed to record pedestrian crossing behaviors. Three typical unsignalized sections with crosswalks were selected for survey in Mentougou District, Beijing, to exclude bias at single intersections and systematic errors. The road flow of the three sections met the research demand, and the sight distance conditions were favorable, leaving sufficient judgment time for drivers. No intersections were set on both sides of the road to attract vehicles, and the vehicle composition was mainly cars, excluding the interference of other factors. The survey time is chosen as that with high traffic volume, instead of the morning and evening peak hours, as it is considered that road congestion affects the survey data, since vehicle delay caused by congestion or waiting for pedestrians cannot be strictly distinguished. The survey was conducted from March 15 to March 22, 2019, with a daily data collection time of 120 min; the details of the survey are shown in Figure 1.
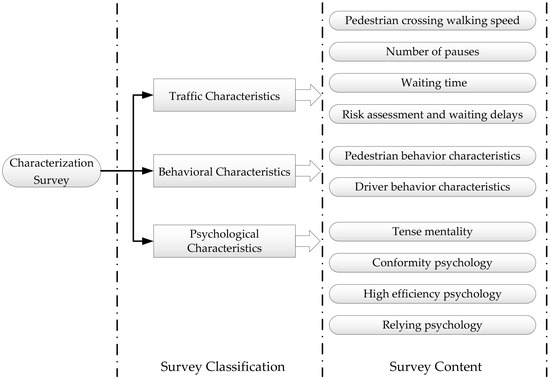
Figure 1.
Characterization Survey.
3.1. Traffic Characteristic Analysis
3.1.1. Pedestrian Crossing Walking Speed
The influence of walking speed was studied by individual pedestrian attributes. The average walking speed of the pedestrian group crossing the street is 1.25 m/s, with the peak concentrated at 1.1–1.3 m/s, which conforms to the normal distribution. In particular, age has the greatest influence on the average walking speed: where age increases, walking speed decreases. The overall walking speed of males was greater than that of females, and the higher the vehicle speed, the faster the pedestrian crosses the street. The percentage of pedestrian walking speed is shown in Figure 2.
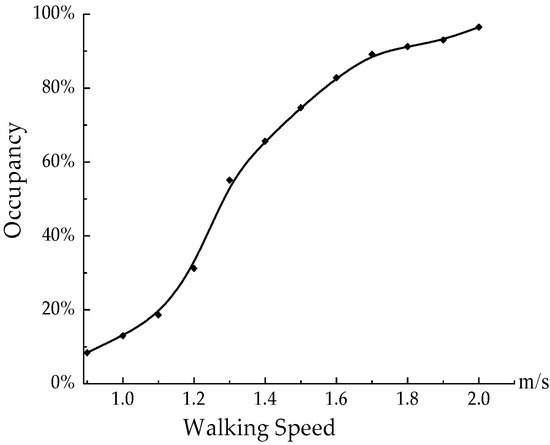
Figure 2.
Percentage at different walking speeds.
3.1.2. Characteristics of Pedestrians When Crossing the Street
Since the acceptance of safe crossing gaps varies, there are differences in pedestrians’ waiting time and number of pauses to cross the street. The active waiting time for crossing can reflect the traveler’s need for safe crossing gaps, while the passive waiting time can be used to study the effect of pedestrian psychological changes on behavioral decisions, which means a direct relationship between waiting time and pedestrians’ decision to cross with a risky rush.
As shown in Table 1, about 15% of pedestrians need to pause three times or more to cross the street, in order to reduce the risk of the crossing and ensure the safety gap of the crossing, of which 12.28% can directly cross the street, and 39.30% and 33.33% pause once and twice, respectively. The statistical results show that, although crosswalks are set up on the unsignalized road sections, the absence of clear distribution of road rights forces pedestrians to pause several times to cross the street smoothly. The waiting time shows the same trend as the number of pauses in the crossing, with 70.18% of the waiting times in the range of 10–30 s. In addition, the statistical results of the phenomenon of “rush” indicate that pedestrians become less aware of the safety risks associated with “rush” as the waiting time increases.

Table 1.
Pedestrian crossing features.
The judgment of pedestrians on crossing risk is immutable on a subjective basis, but when the waiting time exceeds a threshold value, the acceptable waiting time, pedestrians expand their acceptance of crossing risk and take actions such as rushing to cross because they believe the current delay loss exceeds the risk payoff.
3.1.3. Risk Assessment and Waiting Delay
Risk assessment results are an important basis for pedestrians to make crossing decisions, which include the distance from vehicles on the road to the crosswalk, pedestrians’ crossing pace, acceptable crossing gap and crossing mode, etc. The waiting delay affects the pedestrians’ judgment on the acceptable range of the above indicators, and a long waiting delay may even make the pedestrians cross, regardless of the risk.
As shown in Figure 3 and Figure 4, more than 80% of crossing pedestrians observe the location of vehicles at a distance of 10 m, while 14% of pedestrians observe at a distance of up to 30 m or more, which ensures that the pedestrian maintains a safe distance from straight ahead vehicles, to judge the passing conditions. When the vehicle is close, only 29.82% of pedestrians give crossing information and make signs to alert drivers when crossing the street, reducing the risk of crossing the street by informing drivers of their own choices.
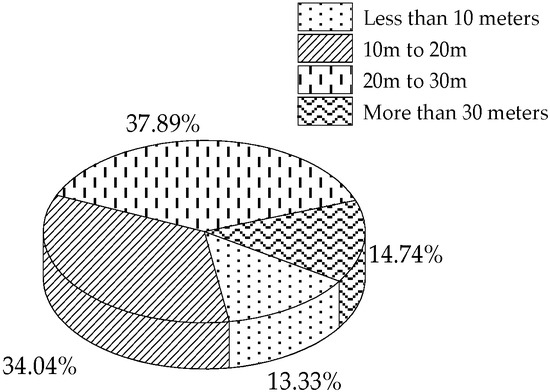
Figure 3.
Observation Distance.
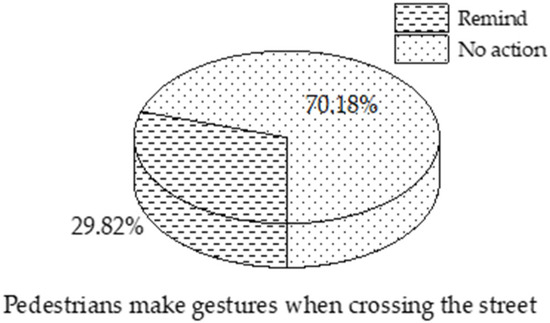
Figure 4.
Make a gesture before crossing the street.
The pedestrian safety crossing gap, a time interval for a pedestrian to safely cross the street, is judged by the speed of the arriving vehicle and the distance between vehicle and pedestrian. As shown in Figure 5, most pedestrians choose to cross the street only when the gap is greater than 5.25 s.
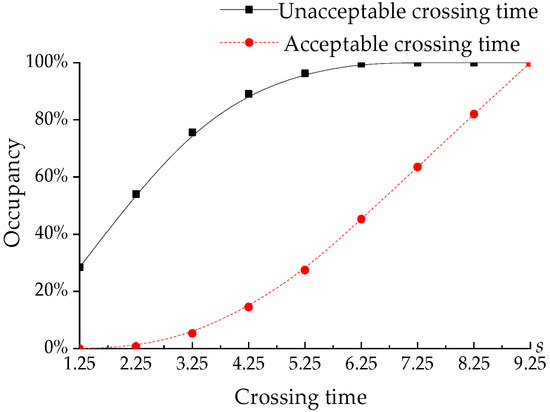
Figure 5.
Time gap for safe street crossing.
3.2. Behavioral Characteristic Analysis
3.2.1. Pedestrian Behavior Characteristics
Pedestrian crossing behavior characteristics mainly refer to the reaction characteristics of pedestrians when they judge whether to cross or encounter vehicles on unsignalized streets, which is jointly determined by the location of vehicles, waiting time, and the personality characteristics when pedestrians arrive at the crossing. The basic actions of pedestrian crossing include waiting, passing, avoiding, backing up, running, and moving sideways. The main decisions in crossing are “wait” and “cross.”
3.2.2. Driver Behavior Characteristics
When arriving at an unsignalized street, the driver takes actions such as “pass directly”, “slow down to avoid”, or “stop to avoid”, and use the warning horn depending on the vehicle speed, and the location and speed of pedestrians. The main decisions in crossing are “avoid” and “pass.”
3.3. Psychological Characteristic Analysis
When making crossing decisions at unsignalized crosswalk sections, pedestrians’ individual psychological state affects the decision a lot. Common psychological characteristics of pedestrians crossing the street include tense mentality, conformity psychology, efficiency psychology, and relying psychology.
At unsignalized intersections, there is a conflict between crossing pedestrians and vehicles, since pedestrians are not separated from vehicles in time and space. Pedestrians are often in a disadvantaged position compared to vehicles with fast and well-equipped safety equipment, and therefore pedestrians are nervous before crossing the street, which affects crossing decisions and judgments. Therefore, in this paper, we conducted a statistical analysis of pedestrians’ nervousness before crossing the street through a questionnaire. As shown in Table 2, about 70% of the pedestrians feel nervous when crossing the street and need to wait longer to seek a safe crossing gap. Nervousness increases pedestrians’ alertness and encourages them to walk faster. When encountering vehicles, pedestrians who crossed the street less frequently tended to “back off” to avoid risk or to reduce their nervousness, as shown in Table 2.

Table 2.
The impact of tension on pedestrians crossing the street.
As shown in Table 3, group crossing poses a psychological implication for pedestrians and drivers to improve the safety of pedestrian passing, but the crowd mentality reduces the times pedestrians observe the road and increases waiting delays with safety risks.

Table 3.
The impact of conformity psychology.
Due to the enhancement of enforcement of vehicle yielding to pedestrians at crosswalks, pedestrians feel a dependence on vehicle active yielding, which affects their judgment of acceptable gaps when crossing the street.
The high efficiency psychology causes pedestrians to cross the street by taking short cuts and accelerating, which contributes to the efficiency of pedestrian crossing and reduces delays, but affects drivers’ judgment of pedestrian trajectory, increasing the risk of crossing significantly.
Individual psychological differences in crossing decisions at unsignalized crosswalks can lead to different decision options. There are many factors that affect the psychological characteristics of individual pedestrians, such as age, gender, and personality differences, which have different effects on the key indicators of pedestrian crossing, such as anxious waiting psychology on the acceptable gap in crossing, risk estimation of pedestrian–vehicle conflict, and even their own crossing speed. Pedestrians also have some common psychological characteristics, including group psychology, dependency psychology, and efficiency optimization psychology, so it is important to study the externalization of the psychological characteristics in crossing behavior.
Currently, there is a prominent conflict where pedestrians cross on unsignalized roads, which seriously affects urban traffic safety, as the distribution of road rights is unclear. In order to protect pedestrians and other vulnerable groups, cities implement the policy of “yielding to pedestrians” to alleviate the pedestrian–vehicle conflict, which also raises a series of new problems. The original purpose of “Yield to Pedestrians” is to ensure the safety of pedestrians, but it only restrains drivers and raises their awareness of yielding through relevant measures; it does not restrict the behavior of pedestrians, which can easily give rise to other problems and cannot be effectively promoted. Therefore, it is necessary to study the mechanism of human–vehicle conflict on roads without signal control, to provide a new basis and new solutions to the crossing safety problem.
This chapter analyzes the psychological characteristics of pedestrians and drivers when conflicts exist, to construct the quantitative parameters and a decision–cost model based on the questionnaire.
4. Pedestrian–Vehicle Dynamic Game Model
4.1. Notation
To facilitate the presentation and analysis of pedestrian–vehicle conflict at unsignalized crosswalks based on Game Theory, all definitions and notations used throughout this work are described in Table 4.

Table 4.
Notation Definitions.
4.2. Utility Values of Pedestrian Crossing Decision Behavior
When crossing, pedestrians and vehicles do not pass safely at the same time, and there is a conflict between the utility values of both sides, which forms a game at unsignalized crosswalks. The payment utility values for the decision-making behavior are set based on risk assessment, delay, and whether the decision subject can safely cross the crosswalk, as shown in Table 5.

Table 5.
Strategy utility value table.
Since the game decision needs to be made according to the state of the pedestrian, three stages are distinguished to ensure the model’s complete description of the crossing behavior and to increase the differentiation of the stages. In addition, the critical range of the three stages is obtained by integrating the results of each index through different weight assignments based on the pedestrian crossing time, the crossing waiting time, and the proportion of pedestrian rush in different waiting times. The specific ranges are shown in Table 6.

Table 6.
Waiting time at different stages.
The first stage: pedestrians with short waiting times are emotionally stable and have a correct prediction of risk, and therefore can accept the loss of waiting delays and make rational decisions to avoid the risk of accidents.
The second stage: pedestrians who have waited for a period of time suffer from psychological fluctuations and anxiousness, resulting in a shift from risk avoidance to delay reduction, as well as a decrease in risk awareness and an increase in the probability of risky crossing.
The third stage: after a long wait or nearing the threshold of acceptable waiting, pedestrians tend to reduce delay losses and become more accepting of risk, risking crossing in most cases.
According to the characteristic analysis of pedestrian crossing, the range of waiting time at different stages is shown in Table 6.
When a vehicle meets a pedestrian at an intersection, the driver needs to make a decision based on the actual situation. If a single pedestrian is observed crossing the road, the driver may choose to “pass directly” to reduce delay, while if a pedestrian is observed crossing in a group, the driver’s risk of “go straight” becomes higher and the benefit decreases, prompting the driver to “slow down” or even “stop and wait”. Therefore, when a group of pedestrians crosses the street, the utility value of the decision needs to be adjusted according to the actual situation. A driver could slow down if the utility value of the safety risk is greater than the risk of delay, enabling pedestrians to cross the street safely.
The various types of utility values of behavioral strategies were initially quantified and divided into reasonable utilities under different stages, as shown in Table 7.

Table 7.
Value of utility payment table.
4.3. Pedestrian–Vehicle Dynamic Game Model and Solution
When crossing an unsignalized crosswalk, one first makes the decision, while the other observes the road situation and the former’s action to make a game decision, therefore a dynamic game model of pedestrian–vehicle conflict is constructed based on different decision makers.
4.3.1. Game Model of Pedestrian First Decision and Equilibrium Solution
Since the prior decision of pedestrians affects the decision of vehicles, the payment utilities are correlated with each other and can be obtained under different scenarios by calculating the initial utility value.
At the beginning of the decision, pedestrian A is divided into three different waiting stages with probabilities PR1, PR2 and PR3 (i.e., the initial phase of the pedestrian), and information on the stage’s probability distribution of pedestrian A is shared with vehicle B. Pedestrian A decides first to “cross” or “wait” according to the state of the pedestrian and road conditions, while vehicle B decides after receiving pedestrian A’s decision information to get the utility payment , as shown in Figure 6a.
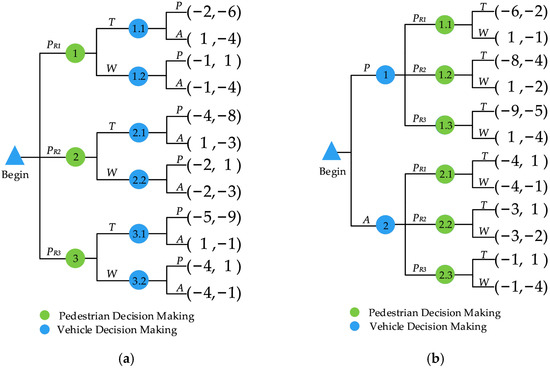
Figure 6.
General form of the unfolding game. (a) Pedestrian first decision. (b) Vehicle first decision.
The waiting stage probabilities obey a negative exponential distribution of with the probability distribution as follows:
Following the characterization in Section 3, the critical range of time for each waiting stage can be taken as:
At = 1/24, the specific probability values for the three waiting phases are given as follows:
Assuming that pedestrians choose “cross” first at all three stages, the two strategies of “pass” and “avoid” for vehicles are decided by the payment value. After the pedestrian first chooses to “cross”, the expected payment utility of the vehicle choosing to “pass” is:
If the “avoid” strategy of the vehicle brings the payment utility d > −17.34, then the vehicle chooses to “avoid”; otherwise, the two decision choices are not mutually optimal and no equilibrium solution exists. Therefore, it is important to raise the avoidance payment to increase the probability of drivers preferring the “avoid” strategy in real cases.
The game above is a pure strategy game, as the pedestrian and vehicle in the game model of pedestrian–vehicle conflict are completely opposed to each other. The pedestrian’s decision is affected by various factors, which cannot be used as the solution of the game model directly. Combining the actual situation, the “mixed strategy” [28] is proposed to enable all players to choose the strategy according to a certain probability.
The optimal probability distributions of the pedestrian and driver selection strategies are calculated by the mixed strategy, which can ensure the existence of stable solutions of Nash equilibrium and obtain reasonable Nash equilibrium solutions.
The expected utility function of game player i can be expressed as follows:
If for all gamers , there are
is a Nash equilibrium of mixed strategies.
The perfect Bayesian equilibrium solution steps for the pedestrian first decision game model under the mixed strategy are as follows:
Strategy hypothesis 1: As shown in Figure 6a, assume that pedestrians make random decisions at node 1 and choose the strategy “cross” at node 2 and node 3, while vehicles first observe pedestrians’ decisions and decide the strategy according to the payment utility value.
Hypothesis 2 on the probability of a random decision: Assume that the probabilities of pedestrians choosing the strategies “pass” and “wait” at node 1 are X and (1−X), while the probabilities of vehicles choosing the strategies “pass” and “avoid” after observing the pedestrians’ crossing decisions are Y and (1−Y), respectively.
The solution for X and Y: To obtain the equilibrium solution, pedestrians at node 1 choose the strategies “wait” and “cross” randomly, which means the payment utility of the two strategies is the same at node 1.
Solving the above equation results in Y = 0.67.
When pedestrians choose the strategy “cross”, the probability of vehicles choosing “avoid” at different stages can be calculated as follows:
Similarly, at node 2, the utility values of vehicles with different strategies chosen are definitely the same to obtain the equilibrium solution.
Solving the above equation gives the expression:
From Equation (10), it can be seen that the vehicle avoidance payment d is related to the pedestrian decision, in which the probability X of the pedestrian choosing to “cross” decreases as the vehicle avoidance payment d rises.
The probability of choosing various strategies in the pedestrian first decision model is shown in Table 8.

Table 8.
Strategy selection probability of the game model under mixed strategy.
In the pedestrian first decision game model with mixed strategies, the probability of choosing different strategies depends on the avoidance payment value of vehicles, which affects the probability of drivers choosing the “avoid” strategy and pedestrians choosing to “cross” or “wait.” Traffic management can improve the safety of pedestrians crossing the street by adjusting the vehicle payment value of “avoid” in accordance with realistic conditions.
4.3.2. Game Model of Vehicle First Decision and Equilibrium Solution
In reality, vehicles often form a new game by making decisions ahead of pedestrians to improve their own utility payment, so the game model of vehicle first decision is established, and the result is shown in Figure 6.
The game process is as follows: at the beginning of the game, the driver first decides to drive normally (or accelerate) or to slow down, and then the pedestrian chooses the waiting stage depending on the probability , obtaining the payment utility of both.
The expected utility of the vehicle choice strategy “pass” and “avoid” is given below:
The mixed strategy equilibrium solution is as follows:
and is given by the Equation (13):
Simplify:
The equilibrium solution of the mixed strategy game model for the driver’s first decision is explained as follows.
When the probability satisfies Equation (11), , the equilibrium game belongs to the mixed strategy game equilibrium, and the probability of vehicles choosing the “pass” and “avoid” is and , while the probability of pedestrians choosing the “wait” and “pass” are and , which satisfy Equation (14).
The equilibrium solution of the game model for vehicle first decision exhibits different results in three probabilities.
- (1)
- When the relationship of probability between pedestrians and vehicles satisfies , the strategy combination is (P, W), that is, the vehicle chooses to “pass” first and the pedestrian decides to “wait” after observing vehicles passing without slowing down, which ensure safe passage of vehicles with minimal risk to the pedestrian.
- (2)
- When , the strategy combination is (A, T), which means that the vehicle chooses to “avoid” first and then the pedestrian chooses to “cross”, so that the pedestrian can cross the street safely with lower risk.
- (3)
- When , the equilibrium is the game equilibrium of the vehicle’s first decision under the mixed strategy, and the equilibrium solution is the probability of strategy selection. The specific strategy combination is illustrated in Table 8.
As can be seen in Table 8, in the game model of the vehicle’s first decision, the equilibrium conditions and the probability of choosing a specific strategy are directly related to the waiting probability in the three stages. Strategy combinations of the higher risk (P, T) and longer delay (A, W) occur when the probability conditions are not satisfied.
In actual pedestrian crossing behavior, the optimal decision combination of pedestrians and vehicles is (polite, polite) when they are in a static game with complete information, while the optimal decision combination is (pass, polite) when they are in a dynamic game with one decision first.
Traffic management can improve the quality of drivers and pedestrians through road safety education, to increase active choices to avoid and modify the probability of the three waiting stages by warnings, prompts, inducements, and laws and regulations to achieve safe equilibrium in crossing behavior, and reduce risky conflicts and delay losses between vehicles and pedestrians. When the number of pedestrians on the roadside is not large, the driver can accelerate or sound the horn to notify the pedestrian, so that the pedestrian abandons the crossing and continues to wait, avoiding high-risk conflicts. Similarly, pedestrians can use crossing gestures to inform drivers and to urge vehicles to slow down in order to cross the street safely.
5. Conclusions and Prospects
Road traffic safety has been a hot topic that has attracted high attention, especially traffic accidents and pedestrian accidents. In urban unsignalized streets, pedestrians are guided to cross the street only by crosswalk signs, due to the lack of road infrastructure, which easily causes conflicts between pedestrians and vehicles. Therefore, it is of great practical significance to study the problem of pedestrian–vehicle conflicts on unsignalized streets, to improve safety and reduce the risk of pedestrians crossing the street. In order to further develop advanced models and technologies for safer and more sustainable transportation, this research establishes a dynamic game model based on multiple decision makers, which is developed to solve the problem of minimizing pedestrian–vehicle conflicts at unsignalized crosswalks. In this paper, the three types of characteristics of pedestrians and drivers are statistically analyzed to construct an evaluation system according to the influence of each index on the pedestrian crossing; then, the problem of pedestrian–vehicle conflict in unsignalized streets is studied from the perspective of game theory, to propose game models based on the first decision of pedestrians and vehicles with the “mixed strategy”, by establishing the probability function of three waiting stages according to the waiting time; finally, the equilibrium solutions of the two models are solved and analyzed for the actual significance and substance to improve the safety and efficiency of pedestrian crossing.
Therefore, the conclusions of the model can equalize the pedestrian crossing behavior safely, reduce the risk of conflict between vehicles and pedestrians, as well as delay loss, which can be used as a reference for traffic law makers and traffic management to regulate the traffic behavior of traffic participants, and provide a new idea to solve the conflict of unsignalized streets.
However, caution should be taken while directly referring to this conclusion, and several extensions may be considered in future work. First of all, the survey is limited in scope and the data results cannot fully reflect the actual situation, which should be investigated more comprehensively and more typically in the future. Second, the establishment of the game model assumes that all participants in the game are rational people and all decisions made are rational to maximize their own interests, which differs greatly from real situations, and an independent study can be conducted for individuals in the future to improve the research diversity. Finally, whether pedestrians or vehicles make a decision first, there is always one participant to respond based on the other’s decision, which in practice can be more misleading and biased.
Author Contributions
Conceptualization, X.S. and Y.W.; data curation, K.L. and Y.W.; funding acquisition, X.S. and H.L.; formal analysis, K.L. and S.M.; investigation, Y.W. and K.L.; methodology, X.S. and K.L.; project administration, X.S. and H.L.; Resources, H.L.; writing—original draft preparation, S.M. and Y.W.; writing—review and editing, X.S.; supervision, H.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Youth Project of Beijing Social Science Fund, grant number 20GLC048.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yang, Y.; He, K.; Wang, Y.P.; Yuan, Z.Z.; Yin, Y.H.; Guo, M.Z. Identification of dynamic traffic crash risk for cross-area freeways based on statistical and machine learning methods. Phys. A Stat. Mech. Appl. 2022, 595, 127083. [Google Scholar] [CrossRef]
- Fu, T.; Miranda, M.L.; Saunier, N. A novel framework to evaluate pedestrian safety at non-signalized locations. Accid. Anal. Prev. 2018, 111, 23–33. [Google Scholar] [CrossRef] [PubMed]
- Duan, J.D.; Long, K.J.; Li, L. Pedestrian behavior on un-signalized mid-block pedestrian crosswalk. Syst. Eng. 2013, 31, 116–121. [Google Scholar]
- Zheng, L.; Wen, C.; Guo, Y.; Laureshyn, A. Investigating consecutive conflicts of pedestrian crossing at unsignalized crosswalks using the bivariate logistic approach. Accid. Anal. Prev. 2021, 162, 106402. [Google Scholar] [CrossRef]
- Zhang, Q.G.; Wang, S.K. Pedestrian traffic psychology and traffic behavior analysis. J. Southeast Univ. 2019, 21, 142–144. [Google Scholar]
- Wang, Y.; Peng, Z.; Chen, Q. Simulated interactions of pedestrian crossings and motorized vehicles in residential areas. Phys. A Stat. Mech. Appl. 2018, 490, 1046–1060. [Google Scholar] [CrossRef]
- Wu, Z.C. Pedestrians’ crossing behaviors and safety at unmarked roadway in China. Accid. Anal. Prevent. 2011, 43, 1927–1936. [Google Scholar] [CrossRef]
- Zhuang, X.; Wu, C. The safety margin and perceived safety of pedestrians at unmarked roadway. Transp. Res. Part F Traffic Psychol. Behav. 2012, 15, 119–131. [Google Scholar] [CrossRef]
- Zhang, B.C.; Chen, F.; Wei, Y.Y. The effects of mobile phone on pedestrian crossing behavior and safety at uncontrolled mid-block crosswalks. J. Transp. Syst. Eng. Inf. Technol. 2018, 18, 136–141. [Google Scholar]
- Yu, X.C.; Chen, Y.L.; Shao, D. Traffic analysis at intersections that vehicles must yield the right-of-way to pedestrians: A case study in Shanghai. Urban Transp. China 2020, 18, 65–74. [Google Scholar] [CrossRef]
- Wang, H.; Liang, T.; Wang, J.B. Research on yielding mode of divided lanes for multi-lane road section with unsignalized crosswalks. J. Safe Sci. Technol. 2018, 14, 58–63. [Google Scholar]
- Liu, R.; Ma, X.Z.; Wu, B. Driving behavior statistical characteristics of the driver. J. Tongji Univ. 2019, 47, 832–841. [Google Scholar]
- Li, X.S.; Meng, F.S.; Zheng, X.L. Psychological characteristics of drivers in the stress scene based on heart rate variability. J. Shanghai Jiaotong Univ. 2018, 52, 163–168. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, D.; Chen, Z. Cellular automata model of multi-lane intersection considering driver characteristics. Highway 2020, 65, 263–267. [Google Scholar]
- Gómez, R.A.; Samuel, S.; Gerardino, L.R.; Romoser, M.R.; Collura, J.; Knodler, M.; Fisher, D.L. Do Advance Yield Markings Increase Safe Driver Behaviors at Unsignalized, Marked Midblock Crosswalks: Driving Simulator Study. Transp. Res. Rec. 2018, 2264, 27–33. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lantieri, C.; Costa, M.; Vignali, V.; Acerra, E.M.; Marchetti, P.; Simone, A. Flashing In-curb LEDs and Beacons at Unsignalized Crosswalks and Driver’s Visual Attention to Pedestrians During Nighttime. Ergonomics 2020, 64, 330–341. [Google Scholar] [CrossRef]
- Bertulis, T.; Dulaski, D.M. Driver Approach Speed and Its Impact on Driver Yielding to Pedestrian Behavior at Unsignalized Crosswalks. Transp. Res. Rec. 2014, 2464, 46–51. [Google Scholar] [CrossRef] [Green Version]
- Noh, B.; No, W.; Lee, J.; Lee, D. Vision-Based Potential Pedestrian Risk Analysis on Unsignalized Crosswalk Using Data Mining Techniques. Appl. Sci. 2020, 10, 1057. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Yuan, Z.; Chen, J.; Guo, M. Assessment of osculating value method based on entropy weight to transportation energy conservation and emission reduction. Environ. Eng. Manag. J. 2017, 16, 2413–2424. [Google Scholar] [CrossRef]
- Ma, Y.Y.; Wen, C.; Lu, S.Y. Pedestrian-vehicle conflict probability estimation at uncontrolled crosswalks. J. Chongqing Jiaotong Univ. 2020, 39, 15–22. [Google Scholar]
- Wu, W.J.; Chen, R.C.; Ma, F.W. Identify risks of pedestrian crossing based on sequence alignment method. J. Transp. Syst. Eng. Inf. Technol. 2018, 18, 101–107. [Google Scholar] [CrossRef]
- Yang, Y.; Wang, K.; Yuan, Z.; Liu, D. Predicting Freeway Traffic Crash Severity Using XGBoost-Bayesian Network Model with Consideration of Features Interaction. J. Adv. Transp. 2022, 2022, 4257865. [Google Scholar] [CrossRef]
- Peng, Y.; Jiang, P.; Sha, X.Y. Evaluation and impact analysis of pedestrian-vehicle conflict severity. J. Transp. Syst. Eng. Inf. Technol. 2019, 19, 175–181. [Google Scholar]
- Wardrop, J.G. Some theoretical aspects of road traffic research. Oper. Res. Soc. 1953, 4, 72–73. [Google Scholar] [CrossRef]
- Szeto, W.Y. Cooperative game approaches to measuring network reliability considering paradoxes. Transp. Res. Part C Emerg. Technol. 2011, 19, 229–241. [Google Scholar] [CrossRef] [Green Version]
- Wei, L.Y.; Cui, Y.F.; Li, D.Y. Evolution mechanism of conflict between pedestrian and vehicle based on evolutionary game theory. Acta Phys. Sin. 2018, 67, 37–49. [Google Scholar] [CrossRef]
- Chen, X.; Sun, Y.; Ou, Y.; Zheng, X.; Wang, Z.; Li, M. A Conflict Decision Model Based on Game Theory for Intelligent Vehicles at Urban Unsignalized Intersections. IEEE Access 2020, 8, 189546–189555. [Google Scholar] [CrossRef]
- Harsanyi, J.C. Games with randomly disturbed payoffs: A new rationale for mixed-strategy equilibrium points. Int. J. Game Theory 1973, 2, 1–23. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).