Abstract
This paper aims to estimate and decompose the spatial and temporal effect of a flood event occurring in the city of Laval in 1998 using a hedonic pricing model (HPM) based on a difference-in-differences (DID) estimator. The empirical investigation of the impact of flood as a natural disaster must take into account the fact that the negotiation process between buyers and sellers may well occur before the event. It is argued that the evaluation procedure needs to be adjusted to account for this reality because the estimation of the effects may otherwise be biased and isolate other effects. To test this hypothesis, the study focuses on transactions occurring between (1995 and 2001) and within designated floodplains to adequately isolate and decompose the impact of flood. The original database contains information on 252 single-family houses transactions. The results suggest that the estimation of the impact is time dependent, with a measured negative effect appearing several months after the flood, suggesting that the impact is hard to establish right after the event since transactions, and the final sale price, could have been fixed by negotiations well before the event. The statistical methodological framework of flood research should be adapted to account for the negotiation process occurring prior to the flood event to be able to correctly isolate the impact for the after event. The flooded area also needs to be precisely identified to be able to correctly estimate the flood impact on houses that have faced flood.
1. Introduction
Climate change has increased the occurrence of flood events [1,2]. Flood is the most costly [3] and most reoccurring natural hazard in Canada [4] with an average annual loss of 1–2 billion Canadian dollars [5]. Because of the increasingly associated monetary losses [6], flood mitigation is an important sustainable landscape policy issue. As natural disasters, the impact of floods is defined by the damage they cause to people or property [7]. The allocation for projects of flood relief/prevention depends on the accurate estimation of flood impact [8].
However, a floodplain is a popular settlement location because it also offers many positive amenities that attract people. Those amenities include the attractive view, the presence of transportation facilities, an adequate water supply and rich agricultural soil [9].
Thus, it is hard to exactly isolate the economic impact of flood events because of the two opposite effects in action [10,11]. For this reason, the estimation of the effect of flood through real estate property price remains a challenge [12].
In a meta-analysis of floodplain location price discount, Beltrán et al. [8] state that results are highly heterogenous (with a price discount range: −75.5% to +61% of a price premium). They underline the fact that it is difficult to guess a “best estimate” for a price discount percentage for being in a floodplain location.
The difficulty to adequately isolate the impact of flood might be related to methodological drawback in study designs. On the one hand, the use of information related to real estate goods located inside a floodplain (i.e., the use of floodplains as a proxy for inundated houses) may not be precise enough to identify the houses that have faced floods. As such, a flood plain depicts areas that are subjected to “a reasonable risk of being flooded” (i.e., demarks a floodplain area that has a probability that a flood event occurs in a certain land unit). These maps only depict a certain “event risk occurrence” [13] and do not necessarily return information for those houses that have face economic consequence of the event. In other words, using such a proxy to identify a price discount probably reflects the economic value of the perception of flood risk instead of the willingness to pay to avoid such an event.
On the other hand, a flood event may occur during a selling process, but after a negotiation process that fixes the final sale price. In Canada, the negotiation processes between sellers and buyers occur well before the transactions are officially recorded by selling contracts, a notarial procedure that usually takes place many weeks after [14]. Thus, taking the transaction date for the analysis, instead of the time when the good was launched on the market, does not necessarily identify the moment when the deal was sealed, which may have an important influence on the estimated impact. Therefore, the effect on property values could be measured well after the event.
Having those two methodological caveats in mind, the paper aims to investigate the impact of flood by varying the definition of the spatial and temporal delimitation. To do so, the analysis focuses on housing values for single-family houses located in proximity to the St. Lawrence river on the north shore of the island of Laval, a place that has experienced flood over the recent years [15]. In 1998, a major flood event occurred on the north shore of Laval, Canada: about 500 basements were flooded and about 50 households evacuated their houses. The analysis is conducted using data from 252 transactions of single-family houses that were collected from 1995 to 2001.
A hedonic pricing model (HPM) is used for the analysis by integrating a local difference-in-differences (DID) estimator, which adequately controls for possible spatial autocorrelation by limiting the geographical extent of the control area. The results indicate that the estimation of the impact is highly dependent on the definition of the spatial and temporal delimitation, putting emphasis on the importance of correctly addressing those concerns before estimating any statistical model.
The paper is divided into six main sections. The Section 1 presents the literature review where different empirical studies are presented, while the emphasis is put on the different methodological frameworks used to investigate the impact of floods on house prices. The Section 2 presents the methodology and the research strategy. The Section 3 is a presentation of the data that was used in the estimation of the models. The Section 4 is devoted to the presentation of the estimation results. The Section 5 presents the discussion, and the Section 6 concludes the paper.
2. Literature Review
The hedonic pricing model (HPM), as characterized by Rosen [16], has long been used to isolate the (marginal) contributions of amenities, both intrinsic and extrinsic, to residential property price. In the most general of terms, a residential property’s characteristics/attributes are related to the house price determination process. These attributes include intrinsic (i.e., internal) attributes of the residential unit (e.g., its lot size, its number of bedrooms, as well as the number of bathrooms, etc.) as well as its extrinsic (i.e., external) attributes (e.g., the proximity to a bus stop, the distance to the closest primary school or to a river, etc.).
As the quest to investigate the effect of flood on housing price varies, there rises an immanent uncertainty of the value of such an investigation. Intuitively, having recently faced floods is expected to have a negative effect on the value of damaged property. It is also expected to affect adjacent property price located in the same floodplain, since it indicates the possibility of facing future flood events, which might entail property damage. Flood mitigation measures taken to protect properties in flood prone areas are expected to have a positive or null effect on their value [17]. In the most basic of terms, economic theory proposes that, other things being equal, property price would suffer a reduction as a result of being located in a floodplain, since this natural disaster engenders economic costs.
Flood is considered as an extrinsic amenity, but the investigation of its impact depends on two contradictory forces at play. On the one hand, people are willing to pay for living close to the water (e.g., a river) because it is associated with a nice view and a certain lifestyle. As such, proximity to waterway is considered as a positive amenity. On the other hand, living close to the water has some drawbacks, such as the possibility that property gets flooded. The equilibrium between those two opposite effects depends on how the market perceives these competing forces, but also on the severity and the recurrence of floods. The perception is thus highly associated to people’s personal experience, such as living a flood event or remembering (forgetting) such an event.
While there is quite a volume of literature that analyzes the impact of flood on real estate price, most empirical studies use US or UK data. Most papers support the assumption that the risk of flood lowers house price. Luechinger and Raschky [18] report an average price discount for US houses in floodplains of 4–5%. Bélanger and Bourdeau-Brien [2] document a price discount on average of around 2% in the United Kingdom after putting into account the past episodes of flood. Bernstein et al. [19] report a growing and significant price discount for houses in proximity to sea.
Beltrán et al. [8], using a meta-analysis based on 37 published papers, reveal that price discount lies between −75.5% and +61%. This range is indicative of the state of uncertainty on the effect of floods on housing price which is shown in the varied results. In the case of a housing market that is efficient, property located in a floodplain should have a lower price than that of an equivalent property that is outside the floodplain.
Bélanger et al. [4] report that the existing literature shows “a large amount of disagreement about the level of flood risk” with a vast contrast of results. While there are papers that show no price discount at all [20], others report more than a 10% discount [21,22]. Such diverging results can be partially rationalized by several factors, including the fact flood is heterogeneous, varied by both geographical as well as hydrological factors. As a result, generalizations to other geographical locations are all but straightforward.
From an empirical point of view, Beltrán et al. [23] identify four main methodological approaches to investigate the impact of floods on real estate prices. The first group uses the standard HPM to compare the property price inside versus outside floodplain. The price differential is assumed to reflect the implicit price for flood risk on a housing market [21,22,24,25,26,27,28]. The second compares the price evolution before and after a flood event within a specific zone to investigate the impact of flood damage on the affected properties prices [29,30]. The third approach studies use difference-in-differences (DID) estimators to isolate the price differential within a floodplain location after a flood event occurs, as compared to another zone where no major event was observed [31,32,33,34]. Finally, the fourth uses an indirect estimation by looking at the effect of construction of flood defense and beach nourishment on property price [8,23,35,36,37].
From a methodological perspective, Beltrán et al. [21] highlight an inconsistency in the results of previous studies according to the definition of the flooding zone. Numerous studies analyzed the location effect for zones defined by being in a 500 or 100-year floodplain in coastal and inland locations. In such conditions, they suggest that results are inconsistent. This conclusion is supported by Aliyu et al. [37], who suggest that focusing on the event of flood itself rather than being inside a floodplain is more likely to depict significant impact on the value of property.
Finally, the literature also underlines the importance of the temporal dimension when analyzing the impact of floods on house prices. Atreya et al. [30,36] claim that the property price discount in response to a flood event disappears within four to nine years after the flood. Aliyu et al. [37] state that the empirical findings derived from their extensive review of the literature revealed that the concerns of the owners of residential property at risk of being flooded regarding the long-term loss of value of their property, are mostly unfounded. Discounts in price are observed in areas that are recently flooded but remain temporary. Montz [38] states that his research results show that flood devalues property in the short-term. However, as the time from the flood event increases, its effect decreases until it becomes insignificant. Pryce et al. [20] talk about amnesia and myopia to qualify such a phenomenon.
Thus, the literature clearly highlights the possible impact of the choice of delimiting the treatment/control zones to isolate the spatial impact of flood, but also the effect of time, since the impact can vary over time after the floods occur. This is what we propose to explore in this empirical investigation.
3. Methodology
The impact of flood on property price is often estimated relying on the classic hedonic function [26,31,39,40]. The hedonic model is conducted by regressing the sale price yit of a (complex) good i at a given period t, against all of its intrinsic attributes, denoted Xkit, and its extrinsic attributes, Zmit. Usually, the relationship is expressed using a semi-log form (where only the dependent variable is expressed using a log transformation) or in a log-log form (where the independent variables are also expressed using a log transformation (Equation (1)).
log(yit) = α0 + Ditαt + Xkitβk + Zmitθm + εit
On the left-hand side of the equation, log(yit), represents the sale price of housing unit i at time t in logarithmic form, which is stacked in a vector of dimension (NT × 1), where NT represents the total number of observations (NT = ). A log-linear functional form is utilized and is considered as one of the best and most used linear specifications of the hedonic pricing model [41,42,43,44]. On the right-hand side, Dit is a matrix of time dummy variables, of dimension (NT × (T–1)), indicating the moment when the transaction occurs, Xkit is a matrix of intrinsic amenities of goods and consists of a matrix of explanatory variables that has continuous descriptors (e.g., living area, age, etc.) as well as dichotomous variables (that indicate the presence versus the absence of housing attributes) and that is of dimension (NT × K), where K is the total number of intrinsic amenities, Zmit is a matrix of the extrinsic amenities of goods, of size (NT × M), where M is the total number of extrinsic amenities and εit is a vector of error terms, assumed to be independent and identically distributed (or iid) and of dimension (NT × 1).
The parameter α0 is a scalar representing the constant term, the vector αt, of dimension ((T–1) × 1), captures the nominal evolution of sale prices with time fixed effect to control for the differences in the sample composition in time periods [45], βk is a vector of parameters that measure the implicit price of each intrinsic characteristic and is of dimension (K × 1), and θm is a vector of parameters that measure the implicit price of each extrinsic characteristic and is of dimension (M × 1).
A difference-in-differences (DID) approach extend the hedonic pricing model by introducing two additional variables. First, a spatial variable, Ds, is used to identify a treatment area, i.e., a spatial delimitation where houses are more likely to be flooded, and a control area, i.e., where floods should not be observed. This variable is usually expressed through a dummy variable, taking a value of one if the houses are located in the treatment area, and zero otherwise. Second, a temporal variable, Dτ, is used to identify the moment of the flood event. This second variable takes a value of one if the transaction is observed after the event, and zero otherwise. Introducing these two new variables in the price equation (Equation (1)) makes it possible to obtain a hedonic pricing model that incorporates the DID estimator (Equation (2)):
where the parameter (scalar) δs controls for a common spatial fixed effect (treatment vs. control), the parameter (scalar) δτ isolates for a common temporal fixed effect (before vs. after), and the parameter (scalar) δsτ allows to isolate the impact of change on the treatment group after the event occurs. The parameter δsτ is the parameter of interest in this framework. It allows to capture the net effect of change caused by the flood event and is assumed to be homogenous.
log(yit) = α0 + Ditαt + Xkitβk + Zmitθm + Dsδs + Dτδτ + (Ds × Dτ)δsτ + εit,
This specification can be extended by decomposing the time dummy variable to consider the fact that the negotiation process within buyer and seller is not instantaneous (at least in Canada). The selling procedure first starts when the seller decides to put the house on the market (Figure 1). The buyer, who is looking for a new house, gathers information about the house by asking about the good and by visiting the house. If the buyer is interested in the house, a negotiation process starts between the seller and the buyer. The final result is twofold: (i) a deal is concluded (and the house is formally sold); or (ii) no deal occurs between the agents and there is no transaction (see Dubé and Legros [15]). If a deal occurs, then, the buyer and seller need to fix a date for the buyer to take possession. At this date (of a few days before or after), both the seller and the buyer make the transaction official by signing a notarial contract. This last action fixes the transaction date.
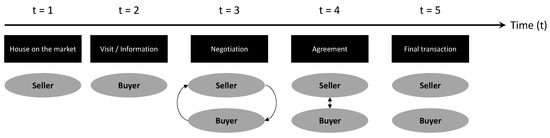
Figure 1.
Schematic representation of the chronology of a transaction. Adapted from Dubé and Legros (2016).
Thus, the final transaction date is not necessarily the better information to use when trying to isolate the before/after event impact. The deal can be concluded well before flood occurs, while the transaction date is recorded after the flood. There is a need to allow for such a possibility. It would be more accurate to divide the “after” dummy variable into, at least, two distinct parts. In such a case, the temporal dummy variable takes the form of a matrix of temporal dummies, Dζ, of dimension (NT × ζ), where ζ is the total number of “after” temporal periods and the vectors of coefficients, δζ and δsζ, are of dimension (ζ × 1) (Equation (3)).
where ◦ represents an Hadamard product matrix (a term-by-term multiplication), and the vector of parameters of interest, δsζ, allows to decompose the impact according to different effect within the chronology after the event. However, in such a decomposition, there is a perfect collinearity within the independent variables (i.e., between Dit and Dζ) if the temporal periods used are the same. This must be taken into account in the estimation process.
log(yit) = α0 + Ditαt + Xkitβk + Zmitθm + Dsδs + Dζδζ + (Ds◦Dζ)δsζ + εit
Of course, the models can be estimated using distinct definitions of a flood zone, Ds. The zones can be defined using: (i) administrative data that identify the usual floodplains area (based on the probability of facing floods within the next years); or (ii) the identification of the streets that have already been flooded over time. This decomposition culminated in a mean-effect model by zone (two models) and shows a mean year effect by zones (2 models). Those different avenues will be tested.
4. Data
The case study is based on Laval, a city located in the south west of the Canadian province of Quebec. It is considered as the largest of the Montreal suburbs and is located to its north. According to the Statistics Canada Census of 2016, the city of Laval has a land area of 247.23 square kilometers with a population of 422,993 and a total of private dwellings of 165,686. Laval city is an island that is separated from its surrounding territory by two rivers, according to Laval.ca. It is separated from the mainland by the river Des Milles Îles to the North. It is separated from Montreal Island by the river Des Prairies to the South. Laval occupies Îles Jésus and Îles Laval (Figure 2). Because of its specific geography, Laval island has been victim of many flood events and floods remain a main natural hazard in the territory.
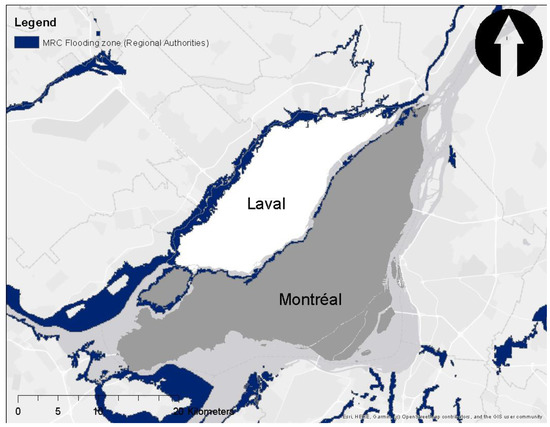
Figure 2.
Zone under study.
The analysis focuses on the effect of the 1998 flood event that evicted 3757 people from their houses in Quebec and Eastern Ontario as reported by the Montreal Gazette. The data used in this research is single-family transaction data. The data was purchased from the Greater Montreal Real Estate Board (GMREB). The data consists of a total number of 742 (NT) single-family house transactions spanning between 1995 and 2001 and located in Laval in the district of Fabreville (Figure 3).
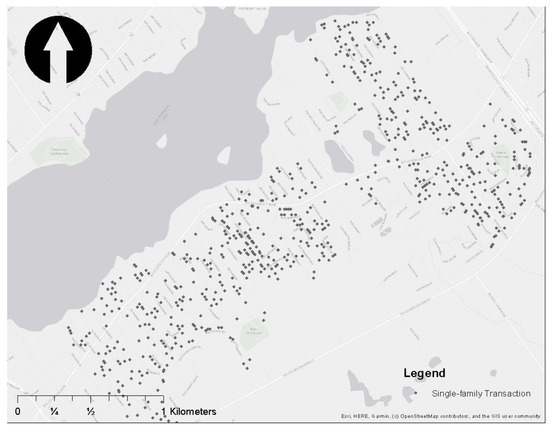
Figure 3.
Location of single-family house transactions, 1995–2001.
For each transaction, the database consists of information on the final sale price as well as the unit’s address, which enabled us to geocode the property to its location (i.e., coordinates) using GIS. It also includes intrinsic and extrinsic information on each property. With the exact location of each property, based on their X, Y coordinates, it was possible to calculate the distance of each property to the River using ArcMap software. A total of 14 independent variables were used in the analysis (Table 1). All characteristics of the neighborhoods are obtained from the 1996 Canadian census at the tract track level.

Table 1.
List of Variables in the Database.
Information on three distinct flooding zones were used to isolate the impact of flood on house price. Two zones were based on distinct flood plains published online by Données Québec. The first is the Grille de présence de zone inondable identifiée par les MRC [46]. This first grid is a spatial representation of flood zone mapping conducted by different regional county municipalities (or MRCs). The maps included in this grid were either integrated in the development and planning plan (schéma d’aménagement et de développement—or SAD) or in an interim control bylaw enacted in the MRC (règlement de contrôle intérimaire—or RCI). Since this grid is an amalgamation of data, it contains data from different years (as diverse as 1994, 1996, 2017, 2018, and 2019, etc.). The data also includes mapping of flood events of different severity that happen to be of different detail. The resulting database is quite large and not necessarily the most accurate to investigate the impact of floods (Figure 3). This definition of the MRC flood zone is larger than the usual 0–100 years flooding zone. It is used to define the “control” area and limit the spatial scope of the analysis, which also limits the possibility of omitting latent spatial information.
The second grid is the Base de données des zones inondables (BDZI) which is the database of the Ministère de l’environnement et de la lutte contre les changements climatiques [47] (MDDELCC). This grid is more precise than the former and is an amalgamation of flood zone mapping obtained from different partners. It includes information based on various sources, such as Programme de cartographie de la Convention Canada-Québec (1976–2001) and Programme de détermination des cotes de crues (1998–2004) (PDCC). The database does not include maps under development/review/litigation since they were not yet authorized by the direction de l’expertise hydrique (DEH). However, this second source resulted in a smaller adjacent flood plain that is used to identify a first “treatment” area (Figure 4). This zone is a good proxy for the 0–100 years flooding zone.
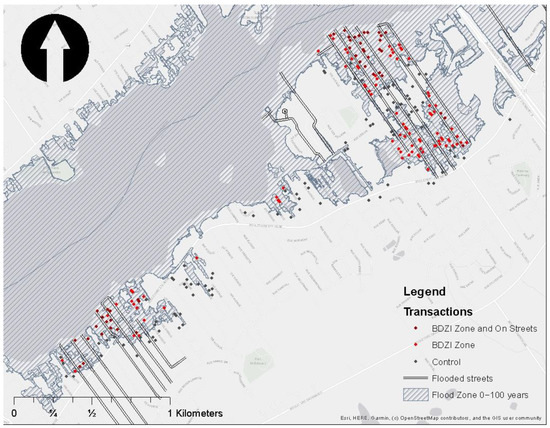
Figure 4.
Location of Transactions for Different Flooding Zones, Laval 1995–2001.
The third flooding area is defined using information on the flooded streets resulting from a more recent flood event that occurred in the same location in 2017 [48]. Since precise information on actual flooded streets (and consequently actual flooded houses) in 1998 is not available, this proxy was used to identify houses that were more likely to have experienced flood in 1998. The use of this proxy was possible because the flood event occurring in May 2017 had the same severity classification (i.e., was classified as an important event in severity) by a database of list of events provided by the Ministère de la securité publique (MSP). Though the 2017 flood published information is more recent, and thus is far from being accurate, one can argue that flood events usually re-occur in the same locations. The flooded streets were as following: (i) for the district of Sainte-Rose: Plateau Ouimet, Alfred, Elm, Touchette, Poplar, and Ste-Marguerite; and (ii) for the district of Fabreville: 2e Avenue, 3e Avenue, 4e Avenue, 7e Avenue, 8e Avenue, 9e Avenue, 10eAvenue, 39e Avenue, 40e Avenue, 41e Avenue, 42e Avenue, 44e Avenue, Bordeaux, 45e Avenue, Liverpool, Dion, Du Phare, du Chalutier, and Jean-Bart. This third data source is thus used as a second definition for the “treatment” area (Figure 4).
As a result, the effects of both floodplains were integrated as independent variables in the model. However, no specific information is available for houses that have been effectively hit. As such, the estimated impact does not necessarily reflect the real price discount on house price, but the perception of flood risk on house prices. The analysis is thus limited to identify the impact of flood perception on house price.
To make sure the effect is limited to houses that could have experienced flood, the transactions are limited to those located inside the identified larger flooding zone (MRC zone). This reduces the total sample size to 252 transactions (Table 2). The numbers of treatment and control transactions, depending on the way the treatment zone is defined, are relatively balanced (Table 3). In the first classification, we compared the BDZI zone (treatment) to the remaining of the MRC zone (control). In the second classification, we compared the transactions located on the street where houses have been flooded inside the BDZI zone (treatment) and the remaining of the MRC zone (control). For both treatment areas, the decomposition of the temporal period is based on two distinct specifications: (i) one for the year 1998 (where the transactions could have been concluded before the flood) and one for the remaining years; and (ii) one for each year (Figure 5).

Table 2.
Descriptive Statistics for House Transactions Depending on Location.

Table 3.
Descriptive Statistics for Treatment and Control Transactions.
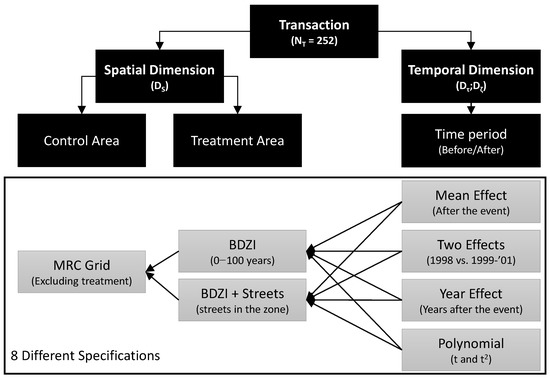
Figure 5.
The empirical estimation strategies illustratred.
5. Results
The basic specification appears to have a good overall prediction performance, with an R2 of 0.7254 for the sub-sample using only transactions within the MRC zone (Table 4). Most of the coefficients are significant and coherent with theoretical expectations. The coefficients that were estimated using the full sample or the sub-sample are comparable in magnitude, while the ones related to the smaller spatial delimitation appear to be less significant when using only the sub-sample. This is related to the fact that within a spatially limited neighborhood, amenities are relatively more homogenous, which reduces the possibility of having significant coefficients.

Table 4.
Estimation Results for the Basic Models.
Two distinct DID specifications based on different definition of the “treatment” and “control” zones were estimated for four different temporal specifications of the effects (Table 5 and Table 6—see Figure 5). The addition of the variables related to the DID estimator slightly raises the explanatory power of both models. The coefficients related to the cross-product of the dummy variables (Equations (2) and (3)) are used to calculate the impact of flood on house price after floods occurs. The impact of flood on housing price is estimated using the following formula: exp(δ) − 1 [49,50].

Table 5.
(A) Estimation Results for the DID Specification using the BDZI zone as Treatment. (B) Estimation of the impact by year.

Table 6.
(A) Estimation Results for the DID Specification using the BDZI and streets as Treatment. (B) Estimation of the impact by year.
In all cases, the Moran’s I index [51] calculated using a spatiotemporal weights matrix, limiting the spatial influence on other houses sold within one and a half month before and two and a half months after—[51,52,53], suggests that the residuals do not show any evidence of spatial autocorrelation at the 95% confidence interval. This suggests that the conclusions from the DID specification are adequate and does not require a SDID specification [54].
When using the BDZI zone as a treatment group (Table 5), the global mean effect is positive, δsτ = 0.0239, which suggests a positive prime of 2.42% on house values (Table 5B). The coefficient is not statistically significant, which implies that it can be conclude that the effect is not different from zero. However, this reality obscures the fact that many transactions occurring in 1998 after the flood event were mainly related to negotiations that occurred before the flood. As previously discussed, most of the transactions are usually closed in the first quarter of the year in Laval, while the buyers only take possession of the house in the beginning of the summer, i.e., between June and August. Thus, the measured positive premium may well be associated with deals that have been closed/sealed before the occurrence of flood.
When decomposing the effect into distinct years, the results clearly underline this pattern. The impact appears to be positive and significant in 1998 (after the flood occurs), with an estimated impact of about 20.1% (Table 5B—Column 2). This positive result suggests a price premium related to the proximity to the river before any flood event occurred since transactions had been concluded well before, while this premium is canceled out after the flood.
Regarding the third specification, the estimated coefficient is positive and significant for the mean effect, while the coefficients are negative and significant for the years 1999 to 2001. These results suggest a price premium of about 20.3% for 1998, while this premium fades about to 0 for the remaining years (Table 5B—Column 3). A formal statistical test for the significance of the combined effect (δsτ + δsτ = 0) suggests that the difference is not statistically significant.
Finally, the last specification using a polynomial continuous function return a prime pattern that is similar to the results obtained using a decomposition with a year time dummy (Table 5B—Column 4). The conclusions appear to be robust for all specifications and suggest that neglecting to account for the temporal dimension relates to the negotiation process and taking the transaction date to isolate the before/after impact may not be necessarily appropriate.
In all cases, the results suggest that if no flood had occurred in 1998, the sale price for houses located closer to the river would have been about 20% higher, which is about the premium measured during the first time period. However, after the occurrence of floods, this premium disappears, reflecting the negative impact of flood on risk perception. Floods have the effect of eliminating the positive location premium. Thus, the impact of floods appears to be a negative premium of about 20%.
The conclusion is similar when using the streets that have been really flooded during the 2017 event that are used to define the treatment area (Table 6). However, the negative mean effect measured during the whole time period suggests that this delimitation of the “treatment” area is probably closer to the real one. The mean impact of flood on house price, δsτ = −0.0426, suggests a negative risk prime of 4.2% on house values (Table 6B), but this premium is still not statistically significant.
The fact that the mean price premium when decomposing the impact by year is close to zero and not statistically significant also supports the point that the definition of the flooded streets appears to be a better proxy for the “treatment” zone. It is also reinforced by the fact that the mean global effect for floods is close from what Beltrán et al. [8] suggest as a rule of thumb, i.e., −4.6%.
When decomposing the effect by years following the flood, a negative, while not statistically significant premium is estimated for 1999 and 2000. The negative price premium is estimated to be between −5.7 and −9.9%, with a U-shape relation, showing that most of the impact concentrated within the first two years after the flood. Once again, the impact appears to be positive for the first year.
While the impacts are not statistically significant, they appear to be similar to the conclusion of Beltrán et al. [8], at least from a qualitative perspective. It should also be noted that the statistical analysis, and the significance, may well be affected here by the small number of observations within the “treatment” area. The sign of the coefficients nevertheless suggests that the perception of flood risk changes a year after the event, which suggests an adaptative process within the negotiation round between buyers and sellers. While the choice of the definition of the “treatment” zone does have an impact on the amplitude of the coefficients, it appears that the same conclusions are qualitatively reached.
6. Discussion
The overall positive impact of the 1998 Laval flood event in a simple specification DID model appears to be largely related to two methodological choices: (i) the delimitation of the “treatment” zone; and (ii) the adequate identification of the transaction, putting into account the negotiation process and the transactions occurring both before or after the flood. Thus, the estimated positive risk premium based on the 0–100 year flood plain might be related to the identification strategy where the perceived risk area is highly diverging from the real risk area. This mean effect is quickly canceled out when decomposing the effect over time.
The positive risk premium estimated is also biased by the fact that the timing of the transactions identified as before and after the event diverge. Some of the transactions did occur before the flood. In Canada, many transactions are usually signed in the first quarter of the year (i.e., before the 1998 flood which occurred in April), while the buyers take possession of the house around July 1st (i.e., after the flood hit). This temporal lag between the negotiation process and the final sale date is better captured by decomposing the premium within distinct time periods.
An analysis that aims to isolate the impact of flood on house prices instead of estimating a flood risk premium should simultaneously incorporate information about the houses that have been flooded and were not just located in a flooding zone, which represents a proxy of the real event. Moreover, the dates delimiting the before and after the flood event that are to be used for future analysis, should be based on the moment when the deal was signed, and not when the transaction was registered by authorities.
Based on the zone identifying houses that are likely to face flood within 0 to 100 years, the analysis suggests a negative risk premium, at least for 1999 and 2000. The negative risk premium after the year of the flood represents an important price discount that cancel the one estimated for 1998.
Both analyses suggest results suffer from the small samples available for investigating the relation based on a regression analysis. In such a situation, methodological works based on a matching analysis may be an adequate solution to estimate the net impact. A study by Dubé et al. [55] use such an approach and confirm the qualitative results presented here, but the approach based on a permutation test allows to retrieve significant (negative) impacts, even with a small sample size.
The analysis also reveals an interesting finding for future investigation and research: that the use of flood zones as the treatment group is problematic since they contain houses that were hit by flood and those that were not hit. Selecting houses that were hit by flood with precision as the treatment group is essential. This is proved by the fact that when the analysis was conducted over the whole sample size, i.e., over the flooding zone, the estimation results did not show any negative effect, which is counterintuitive. In other words, it is important, when conducting such an analysis, to adequately identify the treatment area, but also to restrict the spatial area to identify the control zone. The latter has already been underlined by Pilgram and West [56], who state that using a too large “control area” may bias the estimated premiums.
In the end, it appears that the empirical research based on the use of flood plains as the treatment group may fails to identify the willingness-to-pay (WTP) to avoid such negative externalities. An analysis based on flood plains does, in fact, reveal information on the mean flood risk premium. This risk premium is composed by the effect related to a mix of houses hit by the flood (which implies a possible negative effect) but also to other houses that have not been affected by the flood (which implies a positive effect). The mitigation of those opposite effects suggest that the risk premium may be seen as a lower bound of the WTP to avoid floods. It also explains why the literature depicts such heterogeneity of estimation.
Thus, while the statistical investigation is quite straightforward, it clearly appears that the choice of the two main parameters, i.e., the definition of zones and the identification of the time periods, has an important impact on the estimation results. The analysis underlines the importance of adequately defining the spatial dimension (i.e., the “treatment”/”control” areas), as well as the temporal dimension (i.e., identifying the transactions for which the negotiation process occurs both before or after the flood).
7. Conclusions
This paper attempts to test the methodological choices to investigate the impact of the 1998 flood occurring in the north of Laval (Canada) based on a revealed preferences approach using residential property price. The investigation is based on two different proxies to define the treatment zone likely to be hit by flood, since no information on houses that have been effectively hit is available. A particular attention is devoted to test for the impact of the delimitation of the before/after periods based on the negotiation process instead of the transaction date. The empirical investigation is based on information provided by single-family transactions between 1995 and 2001.
The statistical specifications are based on a difference-in-differences (DID) estimator using a generalized least squares (GLS). Since the impact of flood is geographically localized and does not yield to generalizations, this paper is an addition to flood history literature and shows how the spatial and the temporal delimitations are important methodological choices that can influence statistical estimations.
On the one hand, the analysis suggests that taking too-large definitions for the treatment zones may well result in an outcome that does not measure the willingness-to-pay (WTP) to avoid such negative externalities. Because not all the houses located inside the zone really faced flood, the analysis can introduce bias and may fail to adequately isolate what one really seeks to reach. In such a case, the statistical model can return a mean effect that results in a positive, even non-significant, effect. This drawback appears to be lessened when the treatment zone is defined by the streets where houses have been flooded. However, even such approach does not solve the entire problem.
On the other hand, limiting the before/after temporal dimension to the exact date of the event on the transaction date can bring additional bias, even more when the negotiation process, such as in the province of Québec, takes place months before the flood. To isolate the possible negative effect of floods, there is a need to focus on the moment when the deal between sellers and buyers occurs, instead of focusing on the date when the transactions are registered. Otherwise, it is not clear what is exactly measured. Moreover, the analysis could be better if information about the houses that has really been flooded is available.
After many tests, the results suggest a negative risk price premium that can vary between 5 and 10% for the case of Laval. This represents a reduction of about CAD 5000 to 8500. However, most of these conclusions need to be taken carefully since the small size of the sample available for the estimation introduces large variability, which yields many non-significant coefficients. Thus, while the qualitative analysis suggests that the specification of the zones and the timing of the transactions does have an important impact on the magnitude of the estimation process, the quantitative results are not robust.
In the end, the analysis suggests that there is a need to adequately isolate the houses that were flooded if one wishes to isolate the impact of a flood on house price. The recent availability of the LiDAR technology as well as the efforts that have been pushed forward to delimit more accurate flooded areas may help to get a better estimation in empirical research.
Author Contributions
Conceptualization, J.D. and M.A.; methodology, J.D.; software, M.A., J.D. and N.D.; validation, J.D. and N.D.; formal analysis, M.A. and J.D.; investigation, M.A.; resources, M.A., J.D. and N.D.; data curation, M.A.; writing—original draft preparation, M.A. and J.D.; writing—review and editing, J.D. and M.A.; visualization, J.D.; supervision, J.D.; project administration, J.D.; funding acquisition, J.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Marine Environmental Observation, Prediction and Response Network (MEOPAR).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used for the analysis could not be shared publicly.
Acknowledgments
The authors would like to thank Steve Plante.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Békés, G.; Horvath, A.; Sapi, Z. Flood Risk and Housing Prices: Evidence from Hungary; Discussion Paper; Institute of Economics, Centre for Economic and Regional Studies, Hungarian Academy of Science: Budapest, Hungary, 2016. [Google Scholar]
- Bélanger, P.; Bourdeau-Brien, M. The impact of flood risk on the price of residential properties: The case of England. Hous. Stud. 2018, 33, 876–901. [Google Scholar] [CrossRef]
- Sandink, D.; Kovacs, P.; Oulahen, G.; McGillivray, G. Making Flood Insurable for Canadian Homeowners; Discussion Paper; Institute for Catastrophic Loss Reduction and Swiss Reinsurance Company Ltd.: Toronto, ON, Canada, 2010; Available online: https://www.iclr.org/wp-content/uploads/PDFS/making-flood-insurable-for-canadian-homeowners.pdf (accessed on 8 February 2019).
- Bélanger, P.; Bourdeau-Brien, M.; Dumestre, M. The impact of flood zones on residential property prices: The case of Canada. J. Sustain. Real Estate 2018, 10, 135–162. [Google Scholar] [CrossRef]
- Jakob, M.; Church, M. The trouble with floods. Can. Water Resour. J. 2011, 36, 287–292. [Google Scholar] [CrossRef]
- Oubennaceur, K.; Chokmani, K.; Nastev, M.; Lhissou, R.; El Alem, A. Flood risk mapping for direct damage to residential buildings in Quebec, Canada. Int. J. Disaster Risk Reduct. 2019, 33, 44–54. [Google Scholar] [CrossRef]
- West, T.L. Flood Mitigation and Response: Comparing the Great Midwest Floods of 1993 and 2008. Masters’ Thesis, Naval Postgraduate School, Monterey, CA, USA, 2010. [Google Scholar]
- Beltrán, A.; Maddison, D.; Elliot, R.J.R. Is flood risk capitalized into property values? Ecol. Econ. 2018, 146, 668–685. [Google Scholar] [CrossRef]
- Eleuterio, J. Flood Risk Analysis: Impact of Uncertainty in Hazard Modelling Vulnerability Assessments on Damage Estimations. Ph.D. Thesis, University of Strasbourg, Strasbourg, France, 2012. [Google Scholar]
- Rossi-Hansberg, E.; Sarte, P.D. Economics of housing externalities. Int. Encycl. Hous. Home 2012, 2, 47–50. [Google Scholar]
- Verhoef, E.T.; Nijkamp, P. Externalities in the Urban Economy; Discussion Paper: 078/3; Tinbergen Institute: Rotterdam, The Netherlands, 2003. [Google Scholar]
- Hino, M.; Burke, M. Does Information about Climate Risk Affect Property Values? NBER Working Paper No. 26807; National Bureau of Economic Research: Cambridge, MA, USA, 2020; ISSN 08982937. [Google Scholar] [CrossRef]
- Square One Insurance Services, Canadian Flood Maps: Is Your Home in a Flood Zone? 2020. Available online: https://www.squareoneinsurance.com/resource-centres/home-personal-safety/canadian-flood-maps (accessed on 14 February 2019).
- Dubé, J.; Legros, D. A spatiotemporal solution for the simultaneous sale price and time-on-the-market problem. Real Estate Econ. 2016, 44, 846–877. [Google Scholar] [CrossRef]
- Dumestre, M. The Impact of Flood Risk on the Value of Residential Property: The Case of Quebec Province. Ph.D. Thesis, Université Laval, Québec, QC, Canada, 2017. [Google Scholar]
- Rosen, S. Hedonic prices and implicit markets: Product differentiation in pure competition. J. Political Econ. 1974, 82, 34–55. [Google Scholar] [CrossRef]
- Montz, B.E. The Impact of Hazard Area Disclosure on Property Values in Three New Zealand Communities; Natural Hazard Research Working Paper 76; Natural Hazards Research and Applications Information Center, University of Colorado: Boulder, CO, USA, 1992. [Google Scholar]
- Luechinger, S.; Raschky, P. Valuing Flood disasters using the life satisfaction approach. J. Public Econ. 2009, 93, 620–633. [Google Scholar] [CrossRef]
- Bernstein, A.; Gustafson, M.T.; Lewis, R. Disaster on the horizon: The price effect of sea level rise. J. Financ. Econ. 2019, 134, 253–272. [Google Scholar] [CrossRef]
- Pryce, G.; Chen, Y.; Galster, G. The impact of floods on house prices: An imperfect information approach with myopia and amnesia. Hous. Stud. 2011, 26, 259–279. [Google Scholar] [CrossRef]
- Donnelly, W.A. Hedonic price analysis of the effect of a floodplain on property values. J. Water Resour. Bull. 1989, 25, 581–586. [Google Scholar] [CrossRef]
- MacDonald, D.N.; White, H.; Taube, P.; Huth, W. Flood hazard pricing and insurance premium differentials: Evidence from the housing market. J. Risk Insur. 1990, 57, 654–663. [Google Scholar] [CrossRef]
- Beltrán, A.; Maddison, D.; Elliot, R. The impact of flooding on property prices: A repeat-sales approach. J. Environ. Econ. Manag. 2019, 95, 62–86. [Google Scholar] [CrossRef]
- Speyrer, J.F.; Ragas, W.R. Housing prices and flood risk: An examination using spline regression. J. Real Estate Financ. Econ. 1991, 4, 395–407. [Google Scholar] [CrossRef]
- Bin, O. A prediction comparison of housing sales prices by parametric versus semi-parametric regressions. J. Hous. Econ. 2004, 13, 68–84. [Google Scholar] [CrossRef]
- Bin, O.; Kruse, J.B. Real estate market response to coastal flood hazards. Nat. Hazards Rev. 2006, 7, 137–144. [Google Scholar] [CrossRef]
- Rambaldi, A.N.; Fletcher, C.S.; Collins, K.; McAllister, R.R. Housing shadow prices in an inundation-prone suburb. Urban Stud. 2013, 50, 1889–1905. [Google Scholar] [CrossRef]
- Meldrum, J.R. Floodplain price impacts by property type in boulder county, Colorado: Condominiums versus standalone properties. Environ. Resour. Econ. 2016, 64, 725–750. [Google Scholar] [CrossRef]
- Daniel, V.E.; Florax, R.J.; Rietveld, P. Flooding risk and housing values: An economic assessment of environmental hazard. Ecol. Econ. 2009, 69, 355–365. [Google Scholar] [CrossRef]
- Atreya, A.; Ferreira, S. Seeing is Believing? Evidence from property prices in inundated areas. Risk Anal. 2015, 35, 828–848. [Google Scholar] [CrossRef] [PubMed]
- Bin, O.; Polasky, S. Effects of Flood Hazards on Property Values: Evidence Before and After Hurricane Floyd. Land Econ. 2004, 80, 490–500. [Google Scholar] [CrossRef]
- Hallstrom, D.G.; Smith, V.K. Market responses to hurricanes. J. Environ. Econ. Manag. 2005, 50, 541–561. [Google Scholar] [CrossRef]
- Kousky, C. Learning from extreme events: Risk perceptions after the flood. Land Econ. 2010, 86, 395–422. [Google Scholar] [CrossRef]
- Atreya, A.; Ferreira, S.; Kriesel, W. Forgetting the Flood? An analysis of the Flood Risk Discount over Time. Land Econ. 2013, 89, 577–596. [Google Scholar] [CrossRef]
- Dundas, S. Benefits and ancillary costs of natural infrastructure: Evidence from the New Jersey coast. J. Environ. Econ. Manag. 2017, 85, 62–80. [Google Scholar] [CrossRef]
- McNamara, D.; Gopalakrishnan, S.; Smith, M.; Murray, A. Climate adaptation and policy-induced inflation of coastal property value. PLoS ONE 2015, 10, e0121278. [Google Scholar] [CrossRef]
- Aliyu, A.A.; Garkuwa, A.I.; Singhry, I.M.; Muhammad, M.S.; Baba, H.M. Impact of flooding on residential property values: A review and analysis of previous studies. In Proceedings of the Academic Conference of Nightingale Publications and Research International on Sustainable Development, Federal University of Technology, Minna, Education Resource Centre Conference Hall, Niger State, Nigeria, 31 March 2016; Volume 2. [Google Scholar]
- Montz, B.E. The effects of flooding on residential property values in three New Zealand communities. J. Disaster Stud. Manag. 1992, 16, 283–298. [Google Scholar] [CrossRef]
- Guttery, R.S.; Poe, S.L.; Sirmans, C.F. An empirical investigation of federal wetlands regulation and flood delineation: Implications for residential property owners. J. Real Estate Res. 2004, 26, 299–315. [Google Scholar] [CrossRef]
- Harrison, D.; Smersh, G.; Schwartz, A.L. Environmental Determinants of Housing Prices: The Impact of Flood Zone Status. J. Real Estate Res. 2001, 21, 1–20. [Google Scholar] [CrossRef]
- Cropper, M.L.; McConnel, K.; Deck, L.B. On the Choice of Functional Form for Hedonic Price Functions. Rev. Econ. Stat. 1988, 70, 668–675. [Google Scholar] [CrossRef]
- Rasmussen, D.; Zuehlke, T. On the choice of functional form for hedonic price functions. Appl. Econ. 1990, 22, 431–438. [Google Scholar] [CrossRef]
- Dubé, J.; Theriault, M.; Des Rosiers, F. Commuter rail accessibility and house values: The case of the Montreal South Shore, Canada, 1992–2009. Transp. Res. Part A Policy Pract. 2013, 54, 49–66. [Google Scholar] [CrossRef]
- Devaux, N.; Dubé, J.; Apparicio, P. Anticipation and post-construction impact of a metro extension on residential values: The case of Laval (Canada), 1995–2013. J. Transp. Geogr. 2017, 62, 8–19. [Google Scholar] [CrossRef]
- Wooldridge, M.J. Introductory Econometrics: A Modern Approach; South-Western, Cengage Learning: Mason, OH, USA, 2000. [Google Scholar]
- Données Québec, Le Carrefour Collaboratif en Données Ouvertes Québécoises. Grille de Présence de Zone Inondable Identifiée Par Les MRC. Available online: https://www.donneesquebec.ca/recherche/fr/dataset/grille-de-presence-de-zone-inondable-identifiee-par-les-mrc (accessed on 14 February 2019).
- Données Québec, Base de Données des Zones À Risque D’inondation (BDZI). Available online: https://www.donneesquebec.ca/recherche/fr/dataset/base-de-donnees-des-zones-inondables (accessed on 14 February 2019).
- Ville de Laval, Inondation à Laval–Bilan de la Situation: 11 mai 2017. Available online: https://www.laval.ca/Pages/Fr/Nouvelles/bilan-inondations-10-mai-2017.aspx (accessed on 20 February 2019).
- Dubé, J.; Legros, D.; Thériault, M.; Des Rosiers, F. Measuring and Interpreting Urban Externalities in Real-Estate Data: A Spatiotemporal Difference-in-Differences (STDID) Estimator. Buildings 2017, 7, 51. [Google Scholar] [CrossRef]
- Small, K.A.; Steimetz, S.S. Spatial hedonics and the willingness to pay for residential amenities. J. Reg. Sci. 2012, 52, 635–647. [Google Scholar] [CrossRef]
- Dubé, J.; Legros, D. Spatial Econometrics Using Microdata; ISTE Ltd, Wiley: London, UK, 2014. [Google Scholar]
- Dubé, J.; Legros, D. Spatial econometrics and the hedonic pricing model: What about the temporal dimension? J. Prop. Res. 2014, 31, 333–359. [Google Scholar] [CrossRef]
- Devaux, N.; Dubé, J. About the influence of time on spatial dependence: A meta-analysis using real estate hedonic pricing models. J. Real Estate Lit. 2016, 24, 31–66. [Google Scholar] [CrossRef]
- Dubé, J.; Thériault, M.; Des Rosiers, F. A spatial difference-in-differences estimator to evaluate the effect of change in public mass transit systems on house prices. Transp. Res. Part B 2014, 64, 24–40. [Google Scholar] [CrossRef]
- Dubé, J.; AbdelHalim, M.; Devaux, N. Evaluating the Impact of Floods on Housing Price Using a Spatial Matching Difference-in-Differences (SM-DID) Approach. Sustainability 2021, 13, 804. [Google Scholar] [CrossRef]
- Pilgram, C.A.; West, S.E. Fading premiums: The effect of light rail on residential property Sustainability alues in Minneapolis, Minnesota. Reg. Sci. Urban Econ. 2018, 69, 1–10. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).