Abstract
The extent to which the structural reform of the Peruvian electricity market in the 1990s has improved the technical efficiency levels of the distribution companies and whether some firm specific explanatory variables had influenced upon the efficiency was analysed for first time using a second stage Tobit model to study the influence of some firm specific explanatory variables on efficiency. Some authors have argued that the use of Tobit regression is inappropriate in the second stage of DEA and have suggested using other recently developed options. Due to this, it might be worth revisiting this issue and adding those other alternative models to check whether the conclusions obtained with the Tobit model could be upheld. The nine alternative models estimated allow us to confirm that the incentives generated by the reform process led to the firms becoming more efficient. Moreover, private management and the ratio of low voltage sales to medium voltage sales for each company positively affect efficiency, whereas investment per customer is negatively correlated to it.
1. Introduction
The situation prior to the 1993 reforms in the Peruvian electricity sector were characterised by centralised control of the distribution companies by the Ministry of Energy and Mines. These distribution companies, which were all state owned, had few investment prospects for modernizing or expanding new distribution grids and showed either negative or very low utilities, as well as high levels of technical and commercial losses (Electro Perú and Electro Lima, the two main state distribution companies, registered losses of US $301 and US $95 million in 1990, respectively [1]).
In 1992, the general opinion in the country was that the state had not properly fulfilled its role in the process of universal provision of energy, in ensuring energy supplies and in the reliability of the electrical system. In 1993, with the goal of overcoming these problems in the electricity sector, the enactment of an Electricity Concessions Law implemented the following. First, there was a process of vertically separating the industry, in order to divide the generating, transmission, dispatching and distribution into different economic entities. Second, was the privatization of the main assets of generation and distribution.
The underlying criterion for the 1993 reforms was the search for an improvement in the efficiency of the electricity distribution companies, combined with the realisation that the institutionalism associated with the state management had not provided efficient contracting of public utilities [2]. Other major problems were the absolute job security of the employees, the incapacity to have long term loans without political guarantees, directors being chosen based on wheeler dealing within the national and local governments, delays in tariff revisions associated with the political agendas of the national and local governments.
The regulatory framework in force since 1993 establishes that the regulation of distribution rates is carried out every four years, with a fixed cost of capital of 12% per year, in accordance with Peruvian law. The rates are based on the costs of an efficient model company. The regulator chooses in each regulatory process, an efficient company, then takes the main parameters of the network chosen as efficient and uses them to build a bottom-up (ideal) cost model for the rest of the companies that have this main features (density, etc.). In some rate review processes, the DEA approach has been used to define which company is efficient.
The evolution of the technical efficiency in the Peruvian electricity distribution companies, to evaluate whether reforms have enhanced the efficiency of those firms was studied by [3]. Moreover, other four efficiency explanatory variables were included in the analysis. In order to do that [3] rely on a dataset for fourteen distribution Peruvian companies during the period 1996 to 2006 and applied a Two-Stage Data Envelopment Analysis [4]. This method consists of estimating, in a second stage, a regression explaining the measurements of efficiency (θi) obtained via DEA in the first stage; this is achieved by means of a set of predetermined variables.
Some authors [5,6] have echoed the copious number of studies carried out following a two-stage Data Envelopment Analysis (studies using the two-stage DEA approach in the electricity distribution are reviewed in Section 3.2. The same methodology has also been used in other industries recently, such as [7] in banks and [8] in ports, to name but two). However, the proliferation of such studies has not been accompanied by a theoretical framework that permits to establish an appropiate estimate of the “true model”; this is due to the limitations of the strict empirical focus of the applied econometrics employed. In this sense, in the last fifteen years there has been an important conceptual development in the second stage methodology associated with measuring the technical efficiency using DEA. This conceptual development has been in the context of the academic debate between [5,6,9]. This explains the significant increase in the use of bootstrap techniques when carrying out inference on estimated models, be they linear models or Tobit, and also in the use of models that question the functional form associated with linear or Tobit models, as is the case of Fractional regression models (FRM).
In their paper [3] used a Tobit model in the second stage and their results suggests that there is a relationship between the restructuring of distribution sector and the enhancement of technical efficiency. Moreover, they found that investment per customer is negatively correlated with technical efficiency. Afterwards, [10] have argued that the use of Tobit regression (censored regression) is inappropriate in the second stage of DEA, and have suggested using other recently developed options which perform better. Consequently, it is worth revisiting [3] and adding those other alternative models to check whether their conclusions remain not only on the relationship between efficiency and reforms but also regarding the other efficiency drivers. This paper does it covering the same firms but a longer period (1996–2014). Summarizing the aim of the present paper is threefold: first, to discuss all approaches offered in the two-stage DEA literature; second, to compare and test the results gotten when applied all of them to our dataset, and third, to compare our results with those obtained by [3] to check whether their conclusions regarding the efficiency drivers could also be upheld by using the new models proposed by [10].
The paper is organized as follows. After an introduction, where we briefly summarize the reforms in Peru’s electricity distribution sector and present the aims of this paper, the second section briefly describes the data and presents the results obtained in the first stage. Afterwards, in section three, we undertake a brief and critical review of the literature on two-stage DEA from a methodological point of view, to identify what are the advantages and drawbacks of the different models employed. We also include a review of the empirical literature applying two-stage DEA to the distribution sector. Section four, presents, by firm, the specific explanatory variables which have been postulated as efficiency drivers in the second stage analysis, and the empirical results obtained from nine alternative models. Finally, section five presents the most relevant conclusions, possible policy implications, limitations and directions for future research.
2. First Stage Estimation: DEA Models, Data and Results
In regulated industries that use some form of cost comparison between companies, such as the electricity sector, the use of methodologies to measure the variation of efficiency and/or total factor productivity is frequent [11]. DEA has proven to be one of the most frequently chosen methods due to its acknowledged advantages, among them that do not impose restrictions on the production function or the cost function and thus results can be obtained with relatively small data sets ([12,13]).
As pointed out by [2,11], among others, the relationship between reforms in the electricity industry and efficiency is clear (some examples of recent studies related to the distribution of electricity and its regulatory processes could be found in Section 3.2). When it comes to measure the efficiency of electricity distribution companies the input-oriented DEA models are the chosen option ([11,14,15,16,17]) because the regulated company does not have control over the demand but over the inputs used for its production process. In other words, the demand for electric distribution services is a derived demand that is beyond the control of the firm and has to be met [11]. In order to make the comparison sensible we use the same input oriented DEA model than [3]:
s.t.
where λ is a vector describing the proportion of other firms used for constructing the efficient firm. X and Y are the efficient firm’ input and output vectors, and xh and yh are the inputs and outputs of the firm under evaluation. The efficiency of the evaluated firm is represented by θ. The constant returns to scale model (CRS) can be modified to assume variable returns to scale (VRS) by incorporating the convexity restriction; this is N1′ λ = 1, where N1 is one of a number of vectors.
Before conducting efficiency analyses, a variable selection process must be conducted with the appropriate care. To do so, several criteria are to be considered. Again, and in order to do the comparison sensible, we use a database which contains the same inputs and outputs variables than [3] but covers a longer time period (1996–2014). For the sake of brevity we only do a brief description of those variables and the criteria followed to select them.
The choice of variables was based on the availability of data, and on a review of the extant literature which showed that most papers follow [18] and consider four outputs: sales in MWh and number of customers, both variables for medium and Low voltage. Due to data restrictions, and following [15,19,20], two outputs were considered: sales in MWh and the numbers of customers. Regarding inputs, a distribution company requires work and a network infrastructure. Labour is related to the number of employees and the network infrastructure was measured through the net fixed assets due to other physical measures, such as the extension of the existing electricity grid, were not available for all years included in the dataset. Finally, the only undesirable factor incorporated in are the power losses in MWh because other variables, such as statistical information on interruptions and quality of the distribution networks has been available only since 2004. Table 1 shows the statistics for the variables selected which follow the general consensus found in the current literature (see [11] for a survey of the use of frontier studies in regulation of electricity distribution and Section 3.2).

Table 1.
Statistics of the Variables Used in the Model: 1996–2014.
Table 2 presents technical efficiency generated by DEA for two years, 1996 and 2014. The DEA results consider both CRS and VRS assumptions and show that there have been improvements in the period analysed and mainly in the case of the reformed firms which are those that at some point in the analysis period were managed by a private company.

Table 2.
Efficiency of the Electricity Distribution Firms: 1996–2014.
Moreover, the evolution of the technical efficiency under VRS for each year by firm are shown in Figure 1 and Figure 2. Figure 1 shows the firms that have been public throughout the period and Figure 2 shows those that at some point in the analysis period were managed by a private company (called “reformed”, as explained deeply in see Section 4. It should be noted that all firms which have been private during the whole period were always in the frontier (Edelnor, Luz del Sur and Edecañete) with the exception of Electro Sur Medio.
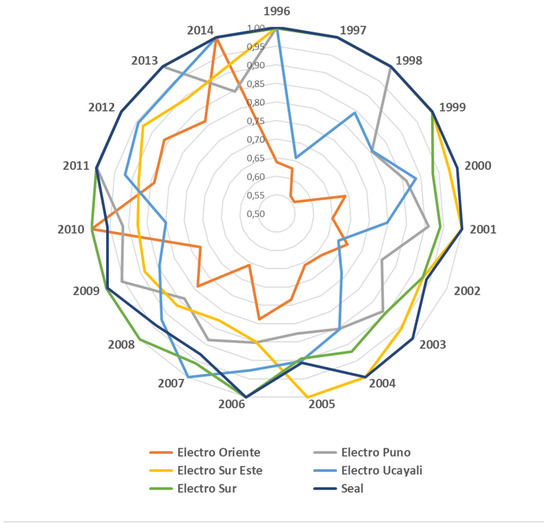
Figure 1.
Technical Efficiency (VRS) of public electricity distribution firms: 1996–2014.
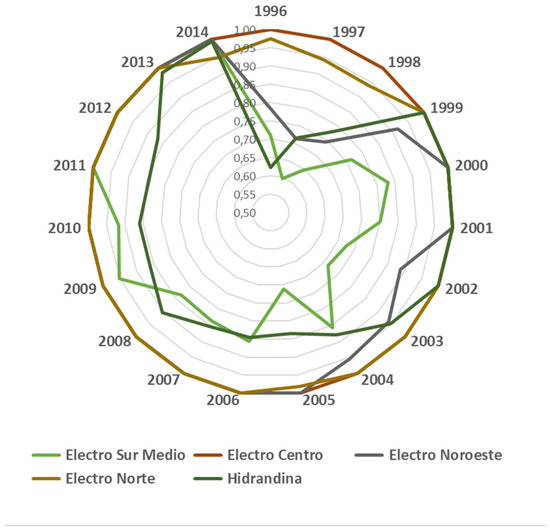
Figure 2.
Technical Efficiency (VRS) of reformed electricity distribution firms: 1996–2014.
The latter results confirm the ones obtained by [3], which leads to the conclusion that, the 1993 reforms seem to have had a positive effect on the distribution sector’s efficiency.
3. Two-Stage Data Envelopment Analysis
3.1. Brief and Critical Review of the Two-Stage DEA Literature
This section reviews the widespread two-stage DEA literature, where DEA efficiency estimates are regressed according to certain environmental variables in a second stage analysis. So , where is a normally distributed random variable with an average of zero and infinite variance.
The initial second stage models used a linear functional form and the ordinary least squares (OLS) method to estimate the parameters and to create individual and global statistical inference. Given that measuring efficiency by means of DEA in the first stage consists of values that are within the interval <0,1] that is, greater than zero and less than or equal to one, the use of OLS does not allow us to guarantee that any prediction will fall within the unitary interval [21]; the same is true of any marginal effect , which while being constant may fall outside the unitary interval [10].
To solve the aforementioned problem the empirical literature uses second-stage models that consider the discrete choice model with Tobit censoring instead of the OLS ([15]), so that:
The use of Tobit models in the second stage models assume that the data generating process censors the measured observed values of the efficiency at 0, when the true value of the unobserved efficiency , is less than or equal to zero; this is the same as the censors at one, when the true value of efficiency is greater or equal to one ([21]).
As [10] indicate, the Tobit model, which has been widely used, comes up against two serious problems. First, true unobserved efficiency has no values lower than zero nor greater than one; thus, the observed values estimated by DEA, between zero and one, are not the consequence of the censoring of the true efficiency, but the minimum and maximum values that result from a relative measurement associated with an efficient production frontier, whereby no relative value can surpass the frontier. Second, it is shown empirically that the measurements of DEA efficiency move away from the origin and tend to concentrate around one; thus, the mass of probability is concentrated to the right of the interval <0,1]. This contradicts the Tobit model’s approach which considers that in the interval [0,1].
On the other hand, Ref. [5] explain that the papers using both as Tobit and OLS models do not commence by describing the data generating process that underlie their models, so there are doubts over what they are actually estimating in these second stage models. Moreover, they set out that the DEA efficiency estimator is consistent, but that the asymptotic convergence rate is slow as it increases the sum of the number of inputs and outputs.
Moreover, Ref. [5] add that for the utilization of the DEA estimator, as a relative measurement of efficiency, the value of the DEA efficiency score of the DMU does not only depend on the inputs and outputs of the DMU itself, but on the inputs and outputs of the other DMUs that are taken into consideration; this sets out the existence of serial correlation in the dependent variables of the model , and additionally the correlation between the residual of the model and the predetermined variables . This brings into question the lack of skew and the efficiency of the Tobit and OLS models in a way that means it is not valid to carry out statistical inference on these models. Both authors set out to correct this by means of two algorithms that implement a bootstrap, one includes the correction of the skew together with the treatment of the serial correlation and the other only the problems related to the problems of serial correlation; in this way inference can be carried out correctly on the parameters on a truncated model.
In contrast to the issues raised by [5,9] criticize the use of the Tobit model in second stage models, since they find no theoretical justification for its use as a data generating process; this is in addition to questioning the fact that the DEA estimations are not censored variables. Moreover, Ref. [9] ran simulations to compare OLS with Tobit and found no significant differences in their predictions.
Refs. [9,21] all advocate the use of OLS in the second stage models; they do not accept the aforementioned serial correlation as relevant and have found similar predictive performances in the Tobit and OLS models. However, the said authors recognize that the use of discrete choice models ([22]) may represent an appropriate alternative, save for the complexity in the estimation and interpretation of the estimated parameters. These models have, by means of fractional regression models (FRM), been developed to estimate second stage models by [10].
One important advantage when using discrete choice models is that they themselves limit the results at the unitary interval as part of the data generating process, without the need to define the censoring of the data. To do so, it is only necessary to define that the conditioned mean of the DEA estimation is related by means of a particular functional form: logistics, probit, loglog or accumulated loglog. This is: , where:
Or alternative versions of these:
Whose graphics are shown in Figure 3.
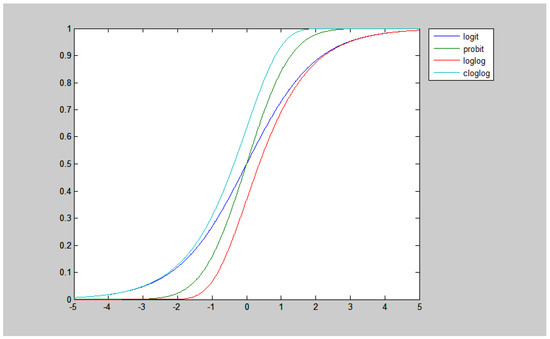
Figure 3.
Functions of Accumulated Density Used in FRM.
Since one of the most important discussions is related to the functional form of the second-stage equation, fractional models allow proposing a non-linear functional form that is reasonable as a way of representing the data generating process, so the extent that the true values of the DEA coefficient are limited by 0 and 1, and they are also concentrated around 1 rather than zero. Ref. [10] estimate these non-linear specifications, finding that the evidence for specification supports the non-linear specifications with respect to Tobit and OLS, especially the cloglog specification. However, there are the problems of skewing and efficiency associated with the problems of serial correlation with the dependent variables and the correlation between the residuals and the predetermined variables, as indicated by [5]; these make it necessary to carry out a bootstrap with each estimated model, so that valid inferences may be created.
The literature reviewed questions the use of the Tobit models, due to the data generating process of the true of efficiency not being censored, this applies to the higher and lower values that have not been analytically derived. Thus, Refs. [9,21], who are the authors that recommend estimation by means of OLS, confront both the problems of serial correlation and the correlation of the residuals and predetermined variables. However, they do not dispute that the main problem with OLS is that the predictions of the model may leave the positive unitary radius, and that the measurements of efficiency accumulate around the unitary values; this is a skew in the distribution of the data.
The nature of the measurement of parametric efficiency and of the DEA estimators make it clear that an unrestricted OLS model at the positive unitary circle is not conceptually consistent. Conversely, nor is it possible to establish that the measurements of efficiency and the DEA estimators reflect a process of data censorship, as the Tobit models set out. This being so, as [21] points out, fractional regression models (FRM) are considered to represent a better approach to the data generating process of the non-parametric measurements of efficiency, and they should be used to estimate second stage models.
3.2. Review of the Two-Stage DEA Power Distribution Literature
When it comes to select the regression model to be used in the second stage, Section 3.1 has shown that there is no consensus in the academic arena regarding what is the best option. For this reason, it is frequent to find empirical application using each different option.
Table 3 summarizes the empirical literature explaining the distribution companies’ efficiency thorough a two-stage DEA approach. Although we found several papers applying fractional models to explain efficiency levels in different sectors, such as Ref. [23] in airports; Ref. [24] in the agricultural sector; Ref. [25] in banks and Ref. [26] in the transport sector, to name a few; to the best of the authors knowledge, the present paper is the first one which applies fractional models to explain efficiency levels in the distribution sector.

Table 3.
DEA Second Stage Papers on the Distribution Sector.
As far as relates to the distribution by continent, Table 3 shows that most studies, seven out of twelve, has to do with a firm located in America: five in South America (Brazil: [27,28]; Colombia: [15]; Peru: [3]; present study) and only two in North America (USA: [29,30]). Moreover, three studies have to do with firms located in Europa (Norway: [31]; Turkey: [32]; United Kingdom: [33]); one is related to firms located in Asia (India: [34]) another related to firms placed in Oceania (Australia: [35]) and none related to firms located in Africa.
When it comes to the variables included in the first stage, almost all, ten out of twelve studies have used physical variables to measure the outputs. Moreover, all of them have used more than one output being the only exception [35]. The most popular option, five out of twelve, was to use three outputs [15,27,29,30,33] whereas four out of twelve used two outputs ([3,32,34]; present study) and two used more than three ([28,31]).
Table 3 shows that almost all studies use the output variables number of customer (10 out 12) in combination with energy sales ([3,15,29,30] and present study) or electricity delivered [27,31,32,33,34] with the only exception of [28]. With regards to the inputs variables included in the first stage, there are more variability and it is frequent to find not only physical but also monetary variables. It should be noted that the five studies that used only one input variable [27,28,29,30,31] chose a monetary variable which, usually, was total or operational expenditure. The most popular input physical variable was number of worker ([3,15,32,34] present study) which usually was combined with variables which represent stock of capital, such as transformer capacity [15,32,34], network length [15,32,34,35] or total assets ([3,34]; present study).
Finally, some papers have also included bad output such as Losses ([3,32,33]; present study) and duration of interruptions [32,33], both variables are associated with the quality in distribution networks. Therefore, we can conclude that the empirical literature measuring the efficiency level of the distribution firms differs slightly about the inputs and outputs employed in the first stage and our selection of variables to estimate technical efficiency in the first stage is quite standard.
Similarly, there are little differences in the DEA model selected in the first stage being the most noticeable the use of weight restrictions ([28,31]). Moreover, all studies reviewed chose an input orientation and calculate technical efficiency scores, usually under CRS, VRS assumptions, with the only exception of [33] where economic efficiency scores were also calculated.
However, when it comes to the second stage model selected, more variety could be found. The regression models chosen are linear models ([15,28,34]; present paper), fixed effect panel data ([29,30]; present paper), random effect panel data ([29,30,34]; present paper), tobit pooled [15,32,33] tobit with random effect ([3,15]; present paper); Simar and Wilson’s (2007) bootstrap truncated regression ([27]; present paper); Simar and Wilson’s (2007) double bootstrap truncated regression [35] and Fractional models (present paper). Therefore, from the methodology point of view, this paper contributes to the literature because it is the first one to use fractional models in the second stage.
Finally, the relationship between reforms in the electricity industry and efficiency is clear as pointed out by [2,11] and could be seen in some of the studies reviewed which are related to the distribution of electricity and the regulatory processes such as, for example, Refs. [27,28] in the case of Brazil and [3] and the present paper in the case of Peru, to name but two.
4. Two-Stage Data Envelopment Analysis (DEA): Results
4.1. Two-Stage Drivers
The estimated models that are subsequently presented take as their dependent variable the measurement of technical efficiency obtained via DEA (VRS) for Peruvian electricity distribution companies from 1996 to 2014. A series of variables that might explain the efficiency are considered as predetermined variables.
The first of those represents the business structure. To do so, we selected a variable that measures the proportion of low voltage sales with respect to those of medium voltage (LV/MV) for each company. This variable reveals the importance of the residential or industrial activity for the area that the distributor’s concession is responsible for. The preponderance of low voltage grids indicates that the business is residential in scale, and these grids have a lower unitary cost. In this sense, it can be expected that the relationship between this variable and efficiency is direct.
The second represents the investment in capital stock per customer (K/N), that in some way represents the density of the company’s grid, since the greater the capital stock per customer, then the less dense the grid is. This is due to the fact that a lower investment per customer is required in higher density urban areas as opposed to rural area where greater investment per customer is needed. Therefore, an inverse relationship between this variable and efficiency would be expected.
The third variable, the discrete variable named jungle, has to do with the fact that some distribution companies are placed in the Amazon jungle which it involves high costs of maintenance and operation due to the distances and the inaccessibility of the jungle. This requires transport using rivers and that the distribution company also owns the generating activity too (it should be noted that the data used here only corresponds to the electricity distribution units). This is typical in the distribution grids that are isolated from the interconnected national grid. If the company is located in the jungle, then the dummy variable takes the value one otherwise the dummy variable take the value zero.
The fourth variable is the mountain ranges, which has the value of one when the company is principally located in Andes. This reflects the difficulties with terrestrial transport rather than the geographical distances travelled in order to carry out maintenance and operations.
By means of the two discrete geographical variables, jungle and mountain, we have tried to represent, among others, such characteristics as the topography, altitude, rainfall and temperatures. Since there are principally rural areas, in both the jungle and the mountains, the grid density is low; this is especially so in the mountains, as the rural areas in the jungle are disconnected (by September 2015 there was 76% provision in the rural areas, whereas in 2010 the figure was 50%). The mountains rather than the geographical distances reflect the difficulties for land-based transport with regard to maintenance and operation. Both variables take a value of one when the company is located principally in the Andes or the Amazon Basin. It would be expected that these variables are inversely related to efficiency, since the geographical difficulties impose greater unit costs.
Finally, a qualitative variable to evaluate the reform of the industry was considered. When the reform process began the intention was to privatize all the firms but due to resistance from citizens in some places, certain distribution companies have remained state owned: Seal, Electro Puno, Electro Sur, Electro Sur Este, Electro Ucayali and Electro Oriente. Moreover, some companies were renationalized due to the concessionaires’ non compliance with the investment commitments: Hidrandina, Electro Norte, Electro Centro and Electro Noroeste. The reformed businesses, those that were privatized, take a value of one and those that were never privatized take a value of zero (the property variable was also tested; however, like the non-parametric Mann-Whitney test, it did not show a good result when compared to the reform variable.).
With regard to this research, a reformed company is one which at some time during the period of analysis was managed by a private company. For example, Electro Norte, Electro Centro, Electro Noroeste and Hidrandina are considered to be reformed as they were privatized for nearly two and a half years despite later returning to state ownership; during this period important changes in management were made.
Our main hypothesis is that the relationship between the reform variable and efficiency is positive, since the process of reforms allowed for significant improvements in the management of the former state companies. Previously, due to the political nature of managerial appointments within the Peruvian framework, these companies did not have the goal of profit maximization.
The descriptive statistics of the variables employed in the model analysed are summarized in Table 4. Huge variability can be seen within the data, and this means that an econometric estimation would be appropriate.

Table 4.
Second Stage Models of Variable Descriptive Statistics. 1996–2014.
Table 5 presents the simple correlations between the variables used, in particular the correlations between input variables and explanatory variables of efficiency; the latter are shaded in the Table 5. The vast majority of these values fall within the values that Banker and Natarajan (2008) do not take into account the validity of the parameters obtained by the second stage models ([9]; p. 56) using Montecarlo simulations, considering that the simple correlation values between −0.2 and +0.4 have no adverse impact on the estimated parameters of the second stage models that use OLS). However, the variable reform shows correlations that fall outside the suggested interval. For this reason it has been considered necessary to implement estimations of the parameters using a bootstrap in all models, with the objective of improving the estimators’ efficiency and consistency.

Table 5.
Matrix of Simple Correlations of Variables Used in the Model. 1996–2014.
4.2. Alternative Models and Results
In addition to the aforementioned correlation problem, there is the persistent conceptual problem associated with the unitary interval and the concentration of data around the value of one. Thus, the recommendation of [21] with regard to the use of the FRM models developed by [22] was followed, in order to estimate the second stage models; this is in accordance with [10].
Table 6 contains the results of the FRM models’ estimation, which we understand should be used in the second stage analysis; there are four specifications: logit, probit, loglog and cloglog, and we used the code (http://evunix.uevora.pt/~jsr/#Code accessed on 15 July 2015) developed by [10]. It has been observed that in all the models the variable reform shows a direct relationship with efficiency and with a high individual relevance; this validates the hypothesis of the reform’s positive effect upon the technical efficiency of the electricity distribution companies. Nevertheless, estimations of the four principal alternative models used in the literature with respect to second stages were also carried out, see Table 7. The objective was to evaluate the robustness of the previous results [3].

Table 6.
Second–Stage: Fractional Models.

Table 7.
Second-Stage: Alternatives to Fractional Models.
Thus, Table 7 shows the estimations made using OLS (pool data), the fixed and random effects (panel data) of the logarithmic model using a bootstrap in order to improve efficiency and infer adequately with regard to the model in its second stage, as suggested by [9]. Moreover, the Tobit model (xttobit en Stata) is shown and the truncated model with bootstrap by the #2 algorithm as developed by [5] based on the code implemented using Stata by [36].
As can be seen in Table 6 and Table 7 the sales ratio of low voltage versus the sales of medium voltage shows the expected positive sign in every model, and is statistically significant in all the FRM models; however, this is the case in only two of the alternatives. Ref. [3] also obtained the expected positive sign but the estimated parameter was not significant. However, a global significance test of this and other parameters, which were not significant individually, was accepted. The latter being evidence of multicollinearity problems, therefore [3] concluded that this variable must not be omitted.
The parameter estimated shows a direct correlation between the sales ratio of low voltage versus the sales of medium voltage and technical efficiency. Therefore, the estimated coefficient shows that the firms with a high share of residential customers are more efficient than firms with a high share of industrial and commercial customers. This result is expected and is related to the reduction in the fixed costs associated with the number of customers. It should be noted that in the case of Peru, large industrial and mining companies are supplied with electricity directly from generators and pay transmission and distribution tolls. Small and medium-sized companies are supplied by electricity distribution companies and mostly use medium-voltage distribution networks, while low-voltage networks meet residential demand and very small companies (especially services).
The capital stock per customer also shows the expected negative sign and is statistically significant in all the estimated models; see Table 6 and Table 7. That is to say, the greater the stock capital per customer resources then the lower the efficiency. This is explained by the higher investment per customer in rural areas or in urban districts with a low voltage network where economies of density are not possible. As stated in [3]: “This occurs especially in networks outside Lima, where there is electricity coverage to just over 50% of the families”.
The sign of the jungle variable is as expected, although it is only statistically significant with the OLS model, with exception in Simar-Wilson estimates whose sign is positive but statistically insignificant. However, the mountain variable shows the opposite of the expected sign, but is in no way statistically significant, and as such its coefficient cannot be rejected as being zero, with the exception of the Simar-Wilson estimation, where the sign is the expected one but it is not statistically significant al 95%. Therefore, and similarly to [3], our results indicate that the firms located in the jungle and mountains have not lower efficiencies than the others despite of the deployment problems in the Andean mountains and in the Amazon rainforest and, accordingly we have to conclude that these variables have no explanatory relevance in the efficiency of the Peruvian electricity distribution companies. However, due to the small number of companies that are in these circumstances, the results should be taken with caution and deserves further investigation.
Moreover, the sign of the trend variable in all the models is positive, which indicates that the measurement of technical efficiency grows with time. However, this variable is individually relevant in only three of the estimated models, and in the others is not elevated; see Table 7.
Table 6 and Table 7 show that with regard to the “reform” variable the estimated parameters have a positive sign for all the considered specifications, and in almost all the estimated models it is considered as a relevant variable. This shows that the distribution companies demonstrated greater technical efficiency after having been reformed, which is evidence of a positive correlation between reforms and the efficiency in Peruvian electricity distribution companies.
To summarize, after reviewing the two-stage Data Envelopment Analysis (DEA) literature in Section 3.1, we decided to estimate a total of nine models: four Fractional Regression Models (logit, probit, loglog y cloglog) and five alternatives (OLS, fixed and random effects of the logarithmic model using a bootstrap suggested by [9], Tobit model with a bootstrap and a truncated model with a bootstrap developed by [5]) and, as Table 6 and Table 7 have shown, all of them allow us to confirm that the incentives generated by the reform process led to the firms becoming more efficient. Moreover, when comparing our results with those in [3], with the exception of the Mountain variable, which has not been significant in any of the estimated models, the other variables maintained the same sign that was obtained by them. A lack of relevance is maintained for the Jungle and Mountain variables, but their ratio for sales of low and medium voltage and capital per customer improves slightly. The reform variable maintains the sign and the individual relevance.
This favourable empirical evidence for the reforms is not an evaluation of the positive aspects of the property regime itself or of some chance relationship, in the same sense as [2]. This is related to the differentiated characteristics in the institutional environment that private and public firms operate in Peru. Due to the framework of corporative government, private firms have the obligation to report their management activities to their minority shareholders, as suggested by [37] for Ukraine electricty distribution firms; Nonetheless, they do not face investment restrictions in contracting, consultancy or acquisition of services. However, the state distribution companies have to tolerate more and more administrative restrictions for investment objectives, complicated processes for acquiring inputs, subsequent audit processes from governmental offices and objectives related to profit maximization.
5. Conclusions
Two-Stage Data Envelopment Analysis DEA has been frequently used to identify the efficiency drivers in this sector. When it comes to analyse whether the sector reforms and/or the regulation changes have an influence on electricity market efficiency using DEA, a two stages process is needed, and as our review has shown it is key to analyse how the second stage is performed to get accurate estimates.
Recently, it has been argued that the use of Tobit regression (censored regression) is inappropriate for second stage DEA, and it has been suggested that other options which outperform the latter should be used. In this context, this paper has revisiting [3] by adding those other alternative models to check whether their conclusions could be upheld.
The present article covers a very important field in empirical literature related to efficiency issues. Its contributions are the following. First, this paper sheds light on the choice of a regression model for the second stage by presenting, discussing, and summarizing the arguments proposed by the different authors regarding all options available in the literature. Second, a survey of the empirical literature using a second stage DEA in the distribution sector has been performed which allows us to state that the present paper is the first to apply the different fractional models and also, it could be useful to other authors by present systematically the characteristics of the previous studies. Third, the estimation of all the second stage models identified in the empirical literature let us answer to the research question, i.e., the identification of the efficiency drivers in the Peruvian distribution sector after the reforms whatever of the model chosen in the second stage.
After reviewing the extensive two-stage Data Envelopment Analysis (DEA) literature, and following [21], we prefer the use of FRM models. However, we also carried out estimations of the principal alternative models using the second stage literature, with the goal of evaluating the robustness of the results.
The results of the nine alternative second stage models considered show that the results of [3] could be upheld and that the efficiencies of the analysed companies are directly related to the reforms of the sector that were initiated in the 1990s; also, they demonstrate that the proportion of low voltage versus medium voltage sales is inversely related to the investment per customer. The variables associated with the geographical difficulties do not appear to be relevant when explaining the inefficiencies in the distribution companies.
To conclude this research paper, the objective of the contrast between the reformed companies, and those that are not, is the empirical validation of the different environmental influences of the public and private institutionalism upon the efficiency of productivity in Peru. It is also the case that the aforementioned state institutionalism does not permit autonomy in the management of enterprises run on behalf of the Peruvian state. Therefore, policy measures should aim to correct this anomaly.
A limitation of this study should be considered. It would be interesting to check whether our results might be affected by using a higher number and/or different potential efficiency drivers not available in our data set. Among them could be measures of quality of the distribution networks such as, for example, interruptions (duration, frequency, etc.) or weather factors, such as, temperature variables and other whether conditions (rainfall, thunder, etc.). Therefore, future research should be focus on including these efficiency drivers. Moreover, another future extension of this work is to consider the use of the DEAS approach, as suggested by [38], to make inference of the estimated DEA score and their implications in the second stage models.
Last but not least, knowledge and accurate estimates of the distribution firms’ efficiency drivers are more and more crucial due to the potential utility of these measurements as support tools to regulators and governments, specially taking into account that the efficiency of the energy sector is becoming an important issue among growing concerns about global warming.
Author Contributions
Conceptualization, R.P.-R. and B.T.; methodology, R.P.-R. and B.T.; software, R.P.-R. and B.T.; validation, R.P.-R. and B.T.; formal analysis, R.P.-R. and B.T.; investigation, R.P.-R. and B.T.; resources, R.P.-R. and B.T.; data curation, R.P.-R. and B.T.; R.P.-R. and B.T. writing—original draft preparation, R.P.-R. and B.T.; writing—review and editing, R.P.-R. and B.T. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data used in this work can be found at https://www.osinergmin.gob.pe/seccion/institucional/regulacion-tarifaria/publicaciones/regulacion-tarifaria.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ariela, R.C. El Proceso de Privatizacines en el Perú Durante el Period 1991–2002; Serie de Gestión Pública; Instituto Latinoamericano de Planificación Económica y Social: Santiago, Chile, 2002. [Google Scholar]
- Zhang, Y.; Parker, D.; Kirkpatrick, C. Electricity sector reform in developing countries: An econometric assessment of the effects of privatization, competition and regulation. J. Regul. Econ. 2008, 33, 159–178. [Google Scholar] [CrossRef]
- Pérez-Reyes, R.; Tovar, B. Measuring efficiency and productivity change (PTF) in the Peruvian electricity distribution companies after reforms. Energy Policy 2009, 37, 2249–2261. [Google Scholar] [CrossRef]
- Coelli, T.; Prasada, D.S.; O’Donnell, C.; Battese, G. An Introduction to Efficiency and Productivity Analysis, 2nd ed.; Springer: New York, NY, USA, 2005. [Google Scholar]
- Simar, L.; Wilson, P.W. Estimation and inference in two stage semi-parametric models of production process. J. Econom. 2007, 136, 31–64. [Google Scholar] [CrossRef]
- Simar, L.; Wilson, P.W. Two-stage DEA: Caveat emptor. J. Product. Anal. 2011, 36, 205–218. [Google Scholar] [CrossRef]
- Da Silva, F.; Stasinakis, C.; Bardarova, V. Two-stage DEA-Truncated Regression: Application in banking efficiency and financial development. Expert Syst. Appl. 2018, 96, 284–301. [Google Scholar]
- Tovar, B.; Wall, A. Specialization, diversification, size and technical efficiency in ports: A empirical analysis using frontier techniques. Eur. J. Transp. Infrastruct. Res. 2017, 17, 279–303. [Google Scholar]
- Banker, R.D.; Natarajan, R. Evaluating contextual variables affecting productivity using data envelopment analysis. Oper. Res. 2008, 56, 48–58. [Google Scholar] [CrossRef]
- Ramalho, E.; Ramalho, J.S.; Henriques, P. Fractional regression models for second stage DEA efficiency analysis. J. Product. Anal. 2010, 34, 239–255. [Google Scholar] [CrossRef]
- Jamasb, T.; Pollitt, M. Benchmarking and regulation: International electricity experience. Util. Policy 2001, 9, 107–130. [Google Scholar] [CrossRef]
- Tovar, B.; Wall, A. Can ports increase traffic while reducing inputs? Technical efficiency of Spanish port authorities using a directional distance function approach. Transp. Res. Part A 2015, 71, 128–144. [Google Scholar]
- Ramos-Real, F.; Tovar, B. Revisiting electric utilities’ efficiency in the Southern African Power Pool, 1998–2009. J. Energy South Afr. 2020, 31, 1–13. [Google Scholar] [CrossRef]
- Thanassoulis, E. Comparative performance measurement in regulation: The case of English and Welsh Sewerage Services. J. Oper. Res. Soc. 2002, 53, 292–302. [Google Scholar] [CrossRef]
- Pombo, C.; Taborda, R. Performance and efficiency in Colombia’s power distribution system: Effects of the 1994 reforms. Energy Econ. 2006, 28, 339–369. [Google Scholar] [CrossRef]
- Ramos-Real, F.; Tovar, B.; Iootty, M.; de Almeida, E.F.; Pinto, H.Q. The evolution and main determinants of productivity in Brazilian electricity distribution 1998–2005: An empirical analysis. Energy Econ. 2009, 31, 298–305. [Google Scholar] [CrossRef]
- Tovar, B.; Ramos-Real, F.; de Almeida, E.F. Firm size and productivity. Evidence from the electricity distribution industry in Brazil. Energy Policy 2011, 39, 826–833. [Google Scholar]
- Hjalmarsson, L.; Veiderpass, A. Productivity in Swedish electricity retail distribution. Scand. J. Econ. 1992, 94, 193–205. [Google Scholar] [CrossRef]
- Neuberg, L. Two issues in the municipal ownership of electric power distribution systems. Bell J. Econ. 1977, 8, 303–323. [Google Scholar] [CrossRef]
- Hattori, T.; Jamasb, T.; Pollit, M.G. The Performance of UK and Japanese Electricity Distribution System 1985–1998: A Comparative Efficiency Analysis; DAE Working Paper WP 0212; Department of Applied Economics, University of Cambridge: Cambridge, UK, 2003. [Google Scholar]
- McDonald, J. Using least squares and tobit in second stage DEA efficiency analyses. Eur. J. Oper. Res. 2009, 197, 792–798. [Google Scholar] [CrossRef]
- Papke, L.E.; Wooldridge, J.M. Econometric methods for fractional response variables with an application to 401(k) plan participation rates. J. Appl. Econ. 1996, 11, 619–632. [Google Scholar] [CrossRef]
- Gutierrez, E.; Lozano, S. Efficiency assessment and output maximization possibilities of European small and medium sized airports. Res. Transp. Econ. 2016, 56, 3–14. [Google Scholar] [CrossRef]
- Raheli, H.; Rezaei, R.M.; Jadidi, M.R.; Mobtaker, H.G. A two-stage DEA model to evaluate sustainability and energy efficiency of tomato production. Inf. Process. Agric. 2017, 4, 342–350. [Google Scholar] [CrossRef]
- Martins, A. Efficiency determinants in Portuguese banking industry: An application through fractional regression models. Tour. Manag. Stud. 2018, 14, 63–71. [Google Scholar] [CrossRef]
- Neves, S.A.; Marquesa, A.C.; Moutinhoa, V. Two-stage DEA model to evaluate technical efficiency on deployment of battery electric vehicles in the EU countries. Transp. Res. Part D 2020, 86, 102489. [Google Scholar] [CrossRef]
- Leme, R.C.; Paiva, A.P.; Santos, P.E.S.; Balestrassi, P.P.; Galvão, L.D.L. Design of experiments applied to environmental variables analysis in electricity utilities efficiency: The Brazilian case. Energy Econ. 2014, 45, 111–119. [Google Scholar] [CrossRef]
- Da Silva, A.V.; Costa, M.A.; Lopes, A.L.M.; do Carmo, G.M. A close look at second stage data envelopment analysis using compound error models and the Tobit model. Socio-Econ. Plan. Sci. 2019, 65, 111–126. [Google Scholar] [CrossRef]
- Kwoka, J.E.; Pollitt, M.G. Do mergers improve efficiency? Evidence from restructuring the US electric power sector. Int. J. Ind. Organ. 2010, 28, 645–656. [Google Scholar]
- Kwoka, J.E.; Ozturk, S.; Sergici, S. Divestiture policy and operating efficiency in U. S. electric power distribution. J. Regul. Econ. 2010, 38, 86–109. [Google Scholar] [CrossRef][Green Version]
- Miguéis, V.; Camanho, A.; Bjørndal, E.; Bjørndal, M. Productivity change and innovation in Norwegian electricity distribution companies. J. Oper. Res. Soc. 2012, 63, 982–990. [Google Scholar] [CrossRef]
- Çelen, A. Efficiency and productivity (TFP) of the Turkish electricity distributioncompanies: An application of two-stage (DEA &Tobit) analysis. Energy Police 2013, 63, 300–310. [Google Scholar]
- Yu, W.; Jamasb, T.; Pollitt, M. Does weather explain cost and quality performance? An analysis of UK electricity distribution companies. Energy Police 2009, 37, 4177–4188. [Google Scholar]
- Bobde, S.; Tanaka, M. Efficiency evaluation of electricity distribution utilities in India: A two-stage DEA with bootstrap estimation. J. Oper. Res. Soc. 2018, 69. [Google Scholar] [CrossRef]
- Lee, B.L.; Wilson, C.; Simshauser, P.; Majiwa, E. Deregulation, efficiency and policy determination: An analysis of Australia’s electricity distribution sector. Energy Econ. 2021, 98, 105210. [Google Scholar] [CrossRef]
- Badunenko, O.; Tauchmann, H. Simar and Wilson Two-Stage Efficiency Analysis for Stata; FAU Discussion Papers in Economics, No. 08/2018; Friedrich-Alexander-Universität Erlangen-Nürnberg, Institute for Economics: Nürnberg, Germany, 2018. [Google Scholar]
- Berg, S.; Lin Ch Tsaplin, V. Regulation of State-Owned and Privatized Utilities: Ukraine Electricity Distribution Company Performance. J. Regul. Econ. 2005, 28, 259–287. [Google Scholar] [CrossRef]
- Ngo, T.; Tsui, K.W.H. Estimating the confidence intervals for DEA efficiency scores of Asia-Pacific airlines. Oper. Res. 2021. [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).