You are currently viewing a new version of our website. To view the old version click .
MDPIMDPI
Search all articles
Sustainability
Download PDF
  • Editor’s Choice
  • Article
  • Open Access

9 April 2019

Estimation of Gridded Population and GDP Scenarios with Spatially Explicit Statistical Downscaling

and
1
Department of Statistical Data Science, The Institute of Statistical Mathematics, 10-3 Midori-cho, Tachikawa, Tokyo 190-8562, Japan
2
Center for Global Environmental Research, National Institute for Environmental Studies, 16-2 Onogawa, Tsukuba, Ibaraki 305-8506, Japan
*
Author to whom correspondence should be addressed.
Sustainability2019, 11(7), 2106;https://doi.org/10.3390/su11072106
This article belongs to the Special Issue Land Cover Changes and Sustainable Urban Growth
Version Notes
Order Reprints

Abstract

This study downscales the population and gross domestic product (GDP) scenarios given under Shared Socioeconomic Pathways (SSPs) into 0.5-degree grids. Our downscale approach has the following features. (i) It explicitly considers spatial and socioeconomic interactions among cities, (ii) it utilizes auxiliary variables, including road network and land cover, (iii) it endogenously estimates the influence from each factor by a model ensemble approach, and (iv) it allows us to control urban shrinkage/dispersion depending on SSPs. It is confirmed that our downscaling results are consistent with scenario assumptions (e.g., concentration in SSP1 and dispersion in SSP3). Besides, while existing grid-level scenarios tend to have overly-smoothed population distributions in nonurban areas, ours does not suffer from the problem, and captures the difference in urban and nonurban areas in a more reasonable manner. Our gridded dataset, including population counts and gross productivities by 0.5 degree grids by 10 years, are available from http://www.cger.nies.go.jp/gcp/population-and-gdp.html.

1. Introduction

Socioeconomic scenarios are needed to project carbon dioxide (CO2) emissions, disaster risks, and other factors affecting sustainability from a long-term perspective. The Intergovernmental Panel on Climate Change (IPCC) published Shared Socioeconomic Pathways (SSPs) [1,2] that describe future socioeconomic conditions under various scenarios, including SSP1-3. SSP1 makes relatively good progress toward sustainability under an open and globalized world. SSP2 is a middle-of-the-road scenario assuming that the typical trends in the last decades will continue, and in SSP3, the world is closed and fragmented into regions, but it fails to achieve sustainability.
While the SSPs are devised in terms of country scenarios, finer scenarios (e.g., scenarios in terms of 0.5-degree grids) are required to analyze regional/city-level sustainability and resiliency. A number of studies have downscaled country-level socioeconomic scenarios into finer spatial units. Gaffin et al. (2004) [3] is an initial work which estimated the gridded population and GDP of the world. Unfortunately, based on [4], the authors’ approach has the following shortcomings: implausibly high growth rates, discontinuity of the projection algorithm before and after 2050, and assumption of independence between population and GDP. Studies [4,5] developed new algorithms to downscale population and GDP to address these limitations. Bengtsson et al. (2006) [6] estimated the gridded urban and nonurban population projection for 1990 to 2100. While the above-mentioned studies rely on trend extrapolation (e.g., GDP extrapolation assuming a constant growth rate), Hachadoorian et al. (2011) [7] compared the trend extrapolation methods with the cohort method, which is more sophisticated but requires population by age groups. The authors suggest that the trend extrapolation is more suitable for small area projections. Beyond simple extrapolation, Asadoorian (2007) [8] simulated future population distributions by imposing an assumption that population distribution in each country obeys a beta distribution. Nam and Reilly (2013) [9] downscaled populations by estimating city-size distributions using a rank-size rule-based approach. After global SSP scenarios were created by [1] in 2014, Jones and O’Neill (2013) [10] downscaled the population scenarios using a gravity model-based approach to consider urban and nonurban population changes that were consistent with the SSP narratives. Fujimori et al. (2017) [11] downscaled the SSP GDP scenarios to investigate their impact on climate modeling. Regionalized spatially fine scenarios have also been developed in the USA by [12,13,14], in Japan by [15], and in the Mediterranean costal area by [16].
Yet, these studies have several limitations. First, they do not consider interactions among cities. It is likely that spatial interactions, that is, interactions depending on geographical distance, are significant locally, while economic interactions are significant globally. These local and global interactions among cities must be considered in addition to spill over from cities to their neighbors.
Second, many of previous studies do not utilize auxiliary variables (e.g., land use, road network, location of airports), which seem useful for the consideration of urban form and functions, but rather, simply extrapolate past trends using a logistic growth model (e.g., [3]), share-of-growth model (e.g., [15]), gravity-type model (e.g., [5,10]), and so on. McKee et al.’s study of [13] is an exception, as it considers land use data, road network data, and so on. Nevertheless, their target area is limited to the USA. Also, they determine weights exogenously for each auxiliary variable. It is desirable to estimate the importance of each auxiliary variable endogenously.
The objective of this study is downscaling the country-level SSP1-3 scenarios into 0.5-degree grids while overcoming the two above limitations. Specifically, our downscale approach estimates the (i) intensity of interactions among cities and (ii) importance of auxiliary variables, from data. Although [10] already published gridded SSP population scenarios, they apply a simple approach ignoring auxiliary variables. Our study considering (i) and (ii) would be beneficial to develop more sophisticated gridded scenarios.

2. Downscale Approach

2.1. Overview

This study downscales the urban population, nonurban population, and gross domestic productivity (GDP) (Purchasing power parity (PPP), Billion USD in 2005 year rate) by country under SSP1-3 (Source: SSP Database [17]) into 0.5-degree grids. The urban and nonurban populations are obtained by dividing the SSP country population scenarios using share of urban populations projected by [18]. The target years are from 2010 to 2100 by five years.
We assume the following; (a) city population changes over time; (b) urban area expands or shrinks according to the city population change; and (c) city population, urban expansion/shrinkage, and other auxiliary variables determine gridded populations and gross productivities. Differences in SSPs are considered in steps (a) and (b) as we will explain later.
Under these assumptions, populations and GDPs are downscaled as summarized in Figure 1. Urban populations by country are downscaled into cities based on a city growth model, which considers (a). The estimated city populations are used to project (b) urban expansion/shrinkage. The city populations are further downscaled into 0.5-degree grids considering projected urban expansion and auxiliary variables summarized in Table 1. On the other hand, nonurban populations by country are downscaled into 0.5-degree grids considering projected urban expansion and the auxiliary variables. GDP is also downscaled considering urban expansion, the auxiliary variables, and downscaled urban and nonurban populations.
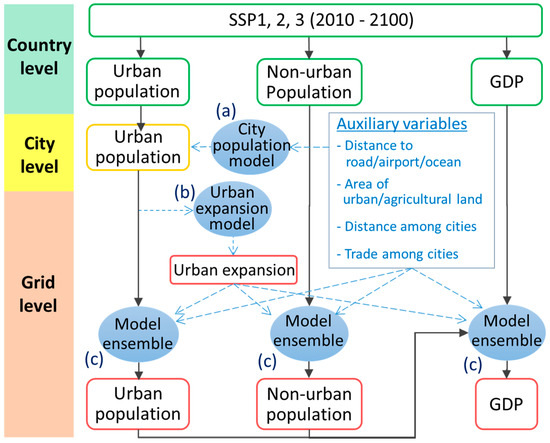
Figure 1. Procedure for population and gross domestic product (GDP) downscaling. Variables by countries, cities, and grids are coloured by green, yellow, and red, respectively. The black arrows represent the downscaling procedure while the blue arrows represent subprocessing to consider auxiliary variables. As this figure shows, urban population is downscaled from countries to cities to grids, while nonurban population is downscaled from countries to grids. GDP is downscaled from countries to grids by utilizing downscaled populations. (a), (b), and (c) in this figure correspond to (a), (b), and (c) described in Section 2.1.
Table 1. Auxiliary variables.
Hereafter, the city population model, the urban expansion/shrinkage model, and the downscaling model will be explained in Section 2.2 and Section 2.3, Section 2.4, and Section 2.5, respectively. For further details about these models, see Appendix A.

2.2. City Growth Model: Estimation with Current Data

This section estimates the impacts of local spatial interactions, global economic interactions, and auxiliary variables {Road dense, Airport dist, Ocean dist} on city population change between 1995 and 2000 (source: GRUMP Settlement Point dataset version 1; see Table 1) by fitting a city growth model. A distance-decay function is used to describe the spatial interactions, whereas the trade amount among cities, which is estimated from Trade amount (see Table 1), is used to describe the global economic interactions.
The results suggest that population increases rapidly in cities with dense road network and good access to airports. These results are intuitively consistent. Also, city growth in inland areas tends to be faster than that in coastal cities. This might be because coastal cities are already matured, and their populations are more stable than those of inland cities. It is estimated that both (local) spatial interaction and (global) economic interaction accelerate population increases (or mitigates population decrease). See Appendix A for further details about the city growth model and the estimation results.

2.3. Overview

Since SSP1-3 concerns globalization, business as usual (BAU), and fragmentation scenarios, respectively, different levels of socioeconomic interactions are assumed in each scenario. Specifically, we assume that the intensity of the economic interaction doubles by 2100 in comparison with 2000 in SSP1, stays constant in SSP2, and halves in SSP3. In each scenario, the intensity of the economic interaction between 2010 and 2100 is linearly interpolated. In other words, we assume a constant growth of the interaction network connectivity over the years. See Appendix A for further details.
Under these assumptions, city populations in 2005, 2010, … 2100 are estimated by sequentially applying the city growth model (see Section 2.2), which projects the 5-year-after populations.

2.4. Projection of Urban Area

Projected city populations are used to project urban expansion/shrinkage. The influence of projected city populations on urban area in 2000 is modeled by Equations (1) and (2):
U r b a n   a r e a g , 2000 = a + q g , 2000 ( r ) b + ε g , 2000
q g , 2000 ( r ) = ∑ c p c , 2000 exp ( − d c , g r )
where εg,2000 denotes disturbance. Urban areag,2000 is the urban area in the g-th grid in 2000 (see Table 1). qg,2000(r) represents the urbanization potential, where pc,2000 is the population in the c-th city in 2000, dc,g is the arc distance between the c-th city and the center of the g-th grid. a, b, and r are parameters. This model describes urbanization due to city population increase, and urban shrinkage due to city population decrease.
The a, b, and r parameters are estimated by maximizing the adjusted R2 of Equation (1). The estimate of r is 16.4, which implies that the distance at which 95% of the influence from city population change disappears is 49.2 (= 16.4 × 3) km. r = 16.4 is assumed for SSP2. On the other hand, r = 8.2 (= 0.5 × 16.4) is assumed for SSP1 to model compact urban growth, while r = 32.8 (= 2.0 × 16.4) is assumed in SSP3 to model dispersed growth. Figure 2 displays urbanization potentials estimated using Equation (2) in Europe in 2080. Because of the r values, potentials in SSP1 are the most compactly distributed while those in SSP3 are the most dispersed.
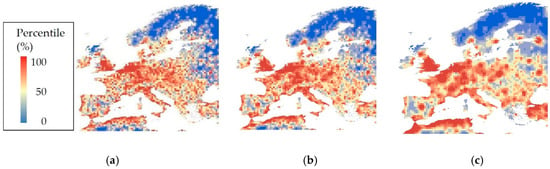
Figure 2. Projected urbanization potential in Europe in 2080. (a) SSP1, (b) SSP2, and (c) SSP3.
2000 is set as the base year, and urban areas in 2005, … 2100 are projected by substituting pc,2000 with p ^ c , 2005 ,… p ^ c , 2100 , which are city populations projected by the city growth model.
The expansion/shrinkage of agricultural areas is also modeled by a similar potential model (see Appendix A). Just like the urbanization projection, the model is used to project agricultural areas in 2005, 2010, … 2100 under the constraint that the sum of urban area and agricultural area must be equal or less than the area of each grid. Thus, each grid can have both urban and agricultural areas. In our downscaling, projected urban and agricultural areas are used as baseline variables, which will be explained in the next section.

2.5. Downscale Approach

Following Shiogama et al. (2011) [21], which suggest the robustness of an ensemble learning-based downscaling, sub-downscaling models are integrated by an ensemble learning technique. Each submodel distributes population or GDP in accordance with distribution weights, which are defined by (baseline variable) × (control variable). Baseline variables capture the difference in urban expansion/shrinkage assumed in each scenario whereas control variables capture the influence from auxiliary variables. These variables are given in Table 2.
Table 2. Baseline and control variables for the urban population, nonurban population, and GDP downscaling. Baseline variables are projected under each shared socioeconomic pathways (SSP). Control variables are constant across years.
Our urban population downscaling applies three baseline variables and four control variables. Thus, 12 submodels distribute urban populations proportionally to (baseline variable) × (control variable). Likewise, the nonurban population downscaling has 12 submodels, while the GDP downscaling has 16 submodels. In each case, downscaling is done by a weighted average of the submodels, where the weights are estimated by applying the gradient boosting (Freidman, 2002), which is an ensemble learning method.
Note that, while city population is projected by setting 2000 as the base year, the gradient-boosting-based downscaling is conducted for each year independently without setting any base year. A temporal smoothing is performed to the downscaling results to assure a gradual change of gridded estimates (see Appendix A). After all, distributions of populations and gross productivities in each country gradually change across years depending on the gradient boosting result, whereas total populations and GDPs in each country change following assumptions in SSPs by country.

3. Result

3.1. Parameter Estimation Result

As discussed, weights of each submodel, which equal the weights for each auxiliary variable, are estimated by the gradient boosting. The results suggest that urban potential explains 55% (SSP1), 54%, (SSP2), and 48% (SSP3) of urban population distributions and 69%, 68%, and 64% of nonurban populations. Regarding urban population downscaling, distance to the ocean has the biggest contribution (SSP1: 38%, SSP2: 47%, SSP3: 46%). Because many of megacities are near the ocean, the result is intuitively reasonable. Concerning nonurban population, distance to principal road has the largest contribution. It is suggested that nonurban population grows along principal roads. The contribution of principal roads is 48 % that is significant in SSP1. The percentage is calculated by aggregating shares of ag,t,k = (baseline variables) × (control variables) whose control variables equal Road (i.e., 48% = 3% + 3% + 41%; see Table A2). It might be because cities strongly interact in SSP1, and small cities emerge in between these cities. On the other hand, ocean is more important than principal road in SSP3.
Distribution of gross productivity, which is estimated by the GDP downscaling, depends on a wider variety of auxiliary variables than population distributions. In SSP1, (Urban pop × Constant) is estimated the most influential (18%), while (Urban pop × Airport dist) is the second most influential (14%). Based on the result, city growth and its interaction with airport encourage economic growth in SSP1. By contrast, (Urban potential × Road) and (Urban pot × Airport dist) have a strong impact in SSP3 with contributions of about 17%. The result is interpretable that dispersed urbanization in SSP3 yields dispersed economic growth along road network and nearby airports. In short, SSP1 and SSP3 result in compact and dispersed economic growth, respectively, and SSP2 lies in between them. See Table A2 in Appendix A for the full estimation results.

3.2. Downscaling Result

Figure 3 plots the estimated population distributions in 2080 under SSP1-3. Compared with SSP3, SSP1, and SSP2 show higher population density around megacities, including London, Paris, and New York (NY). By contrast, SSP3 has higher and dispersed population density in Africa and West-Middle Asia. Thus, the populations in SSP1 are concentrated while those in SSP3 are dispersed. The concentration and dispersed patterns are thought to be due to the spatial range parameter r that is set in Section 2.4 following scenario assumptions. It is verified that these parameters are useful to control urban expansion/shrinkage following scenario assumptions.
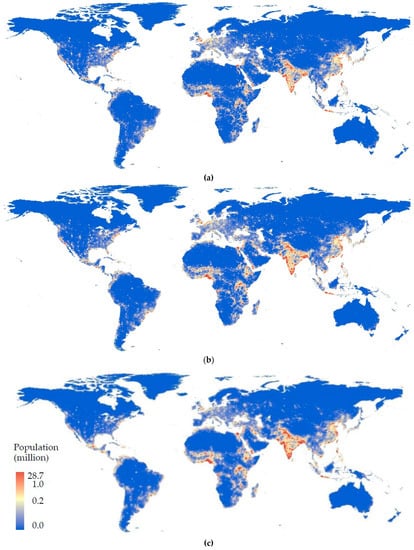
Figure 3. Downscaled population distributions in 2080. (a) SSP, (b) SSP2, and (c) SSP3.
Figure 4 displays the distributions of gross productivity in 2080. The results in SSP1 and SSP2 are relatively similar; both show considerable economic productivity around mega cities (e.g., London and NY). By contrast, economic productivity is small and dispersed in SSP3.
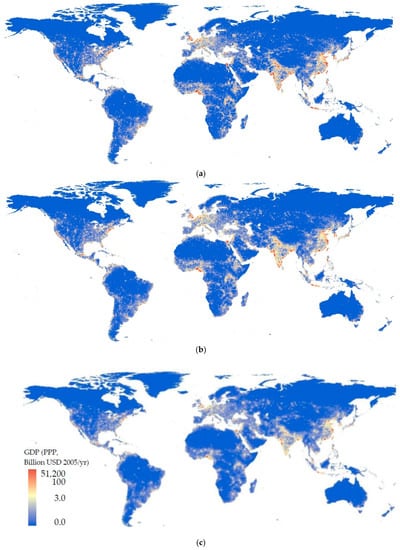
Figure 4. Downscaled gross productivities in 2080. (a) SSP1, (b) SSP2, and (c) SSP3.
To compare compactness/dispersion quantitatively, population densities in the grids, whose distances to the nearest city are between 0 and 10 km, 10 and 20 km, … 190 and 200 km are averaged respectively, and plotted in Figure 5 (left). For comparison, the evaluated values are standardized so that the sum becomes 1. This figure confirms that populations are concentrated in SSP1, moderate in SSP2, and dispersed in SSP3. The same is true for gridded gross productivities (see Figure 5 (right)). This figure also suggests that gross productivities are more concentrated in nearby cities than populations.
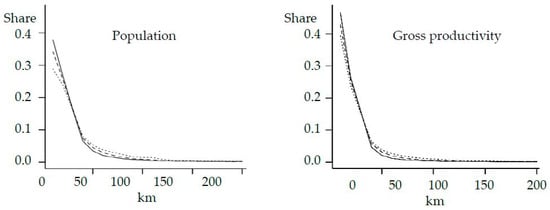
Figure 5. Average population densities/gross productivities in the grids, whose geometric centers are within 0–10 km, 10–20 km, … 190–200 km from the nearest city (GRUMP settlement point). Solid line: SSP1; Dashed line: SSP2; Dotted line: SSP3. For comparison, the evaluated values are standardized so that the sum becomes 1.
Figure 6 displays the results of the GDP downscaling in Europe and South-West Asia. In Europe, economic productivity around major cities (e.g., London and Paris) changes significantly depending on SSPs. In South-West Asia, compared with SSP1-2, SSP3 shows lower productivity in urban areas whereas higher productivity in nonurban areas. In other words, SSP3 results in dispersed economic growth. Considering such differences among SSPs would be important for analyzing future climate risks on socioeconomic activities.
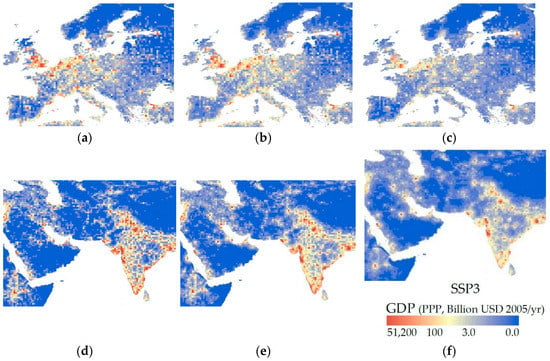
Figure 6. Downscaled gross productivities in 2080 (South and West Asia and Europe). Europe: (a), SSP1 (b), SSP2, and (c) SSP3. South-West Asia: (d) SSP1, (e) SSP2, and (f) SSP3.
Figure 7 compares our population estimates in 2080 in SSP2 with those of Jones and O’Neill (2015) [10]. Estimates of [10] tend to be overly smoothed (e.g., populations are uniformly distributed in desert areas in Saudi Arabia). It might be because the authors apply a gravity-based approach, which ignores auxiliary variables. In our results, such over smoothing is not conceivable. It is verified that consideration of auxiliary variables is also needed to avoid oversmoothing.
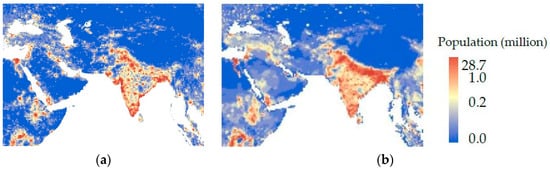
Figure 7. Comparison of estimated populations in South-West Asia in 2080 (SSP2). (a) our result, (b) Jones and O’Neill (2015) [10].
Finally, we evaluate the validity of our downscaling by comparing our population estimates using Gridded Population of the World in 2000 (GPW Version3; source: SEDAC), which is another gridded population database created by aggregating/proportionally distributing administrative data. Figure 8 compares our estimates and the GPW estimates in the (a) USA, (b) France, Spain, Portugal, and (c) Japan. This figure shows that our estimates are close to GPW. The R-squared values (R2) between these two estimates are (a) 0.89, (b) 0.82, (c) 0.82, respectively, while the R2 value across the world is 0.84. Figure 9 compares our estimates in 2010 with the population count estimates provided by History Database of the Global Environment (HYDE; [22]). The results again confirm that our estimates also have a similar tendency to the HYDE data. The local R2 values in countries (a), (b), and (c) are 0.84, 0.82, and 0.77, respectively, whereas the global R2 value equals 0.81. It is verified that our estimate, which replicates more than 80 percent of the variation in the GPW and HYDE estimates, is at least likely.
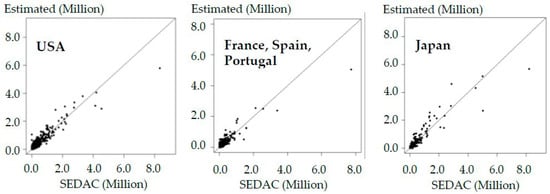
Figure 8. Comparison of our population estimates and the GPW estimates in 2000.
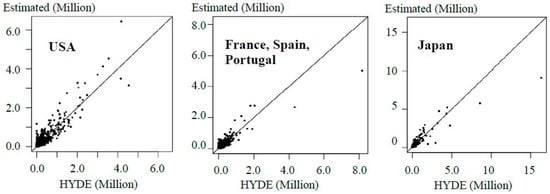
Figure 9. Comparison of our population estimates and the HYDE population counts in 2010.

4. Concluding Remarks

This study downscales SSP scenarios into 0.5-degree grids, using a model to consider spatial and economic interactions among cities and an ensemble learning technique to utilize multiple auxiliary variables accurately. The downscaling result suggests that SSP1, which refers to the sustainable scenario, yields a compact population distribution relative to SSP3, which denotes the fragmentation scenario. The results also show that GDP growth in major metropolitan areas changes significantly depending on the scenarios. These results are intuitively consistent. The consideration of such differences is critical to the estimation of grid level CO2 emissions, disaster risks, energy demand, and other variables determining future sustainability and resiliency.
Nonetheless, various other important issues require further study. First, spatially finer auxiliary data is needed to sophisticate our downscaling approach. For example, microscale urban data, such as industrial structure, detailed road network, and traffic volume, are required to describe urban phenomena such as industrial agglomeration, growth of transportation networks, and birth of new cities, which we could not consider. Since consideration of these factors can increase the uncertainty of downscaling, it is crucial to employ a robust estimation approach, such as ensemble learning (applied in this paper) or Bayesian estimation (as done by [23] for population projection).
Second, downscaling to finer grids is required. Although 0.5-degree grids are sufficient to evaluate socioeconomic activities in each region, these grids are not sufficient to quantify urban form, i.e., compact and disperse. Finer grids, such as 1-km grids, are required to analyze the impact of urban form on climate change mitigation and adaption. High-resolution auxiliary variables would be needed to achieve it.
Third, consideration of longer-term trend of urban expansion, population and economic growth is needed. Fortunately, historical data of gridded population, production, and so on, are now available at the HYDE database [22] Use of this database would especially be valuable to improve the accuracy of long-term projections.
Forth, it is important to discuss how to use our estimates for city-level economic policy-making. For example, our estimates, which reveal local emission intensity, are potentially useful to optimize carbon taxation, green bonding, and other mitigation policies for individual cities. Our estimates will also be useful to estimate local exposure to flood, heat, and other disasters; the estimated exposures will be useful to consider local adaptation policy, for example, through subsidy for encouraging people to move from high risk areas to safer areas. Related to policy-making, the project titled World Urban Database and Access Portal Tools (WUDAPT: http://www.wudapt.org/) is an interesting activity. The project aims to (i) collect data describing urban forms and functions (e.g., land cover, building structure, and building allocations), (ii) utilize the data to classify urban areas into 17 Local Climate Zones (LCZs) [24], and (iii) design universal policies for each of the LCZs toward improving climate resilience. While LCZs classify urban areas based on their influence on the ambient local climate and distributions of population and gross productivity are key factors determining CO2 emissions and amount of wasted heat. To combine our downscaled populations and GDPs with LCZs might be an interesting topic to devise appropriate policies.
Our downscaling results are available from “Global dataset of gridded population and GDP scenarios”, which is provided by the Global Carbon Project, National Institute of Environmental Studies (http://www.cger.nies.go.jp/gcp/population-and-gdp.html). This dataset summarizes population and GDP scenarios in 0.5 × 0.5 degree grids between 1980 and 2100 by 10 years. The gridded data between 2020 and 2100 are estimated by downscaling country-level SSP1-3 scenarios (SSP database: https://secure.iiasa.ac.at/web-apps/ene/SspDb/dsd?Action=htmlpage&page=about) as explained in this manuscript, whereas those in 1980–2010 are estimated by applying the same downscaling method to actual populations and GDPs by country (source: IMF data; http://www.imf.org/data).

Author Contributions

Methodology and Writing, D.M.; Administration, Y.Y.

Funding

This research was funded by the Global Climate Risk Management Strategies (S10) Project of the Ministry of the Environment, Japan.

Conflicts of Interest

The authors declare no conflict of interest.

Appendix A. Details of the Downscaling Approach

A.1. Projection of Urban Population and Urban Expansion

City Growth Model: Model

The 5-year population changes of 67,934 cities (source; SEDAC Settlement Point dataset; see Table 1 and Figure A1) are estimated using the following spatial econometric model.
Δ p t + 5 ( log ) = ( ρ g e o W g e o + ρ e 1 W e 1 + ρ e 2 W e 2 ) Δ p t ( log ) + α p t ( log ) + X t β + ε t E [ ε t ] = 0 ,   V a r [ ε t ] = σ 2 I
pc,t is the population of city c in year t. pt(log) and Δpt(log) are N × 1 vectors whose c-th elements are log(pc,t) and log(pc,t/pc,t-5), respectively. Xt is an N × K matrix of explanatory variables, εt is an N × 1 vector of disturbance with variance σ2, 0 is an N × 1 vector of zeros, I is an N × N identity matrix, α is a coefficient (scalar), and β is a K × 1 coefficient vector.
Sustainability 11 02106 g0a1
Figure A1. Populations in 67,934 cities (2000). Source: SEDAC.
Following the literature on spatial econometrics, Wgeo, We1, and We2 are given by row-standardizing (i.e., row sums are scaled to one) W0geo, W0e1, and W0e2, which describe connectivity among cities. W0geo is a spatial connectivity matrix whose (c, c’)-th element is exp(-dc,c’ /h), where dc,c’ is the arc distance between cities c and c’, and r is a range parameter. For instance, if h = 100 km, 95% of the spill over effects disappear within 300 km (=3 × 100 km; [25]). In other words, a large h implies global spill over from cities whereas a small h implies local spill over. W0e1 and W0e2 describe economic connectivity. Since we could not find any data on economic connectivity among cities, we approximated it with Equation (A2), which represents an estimate of trade amount between cities c and c’:
t ^ c , c ′ = p c P C p c ′ P C ′ T C , C ′
where PC is the population of the country, including the c-th city, and TC,C’ is the amount of trade between countries C and C’ (source: CoW data set; see Table 1). Equation (A2) simply distributes the amount of trade, TC,C’, in proportion to city populations. The (c, c’)-th element of W0e1 is given by t ^ c , c ′ if cities c and c’ are in different countries (i.e., C ≠ C’), and 0 otherwise. By contrast, the (c, c’)-th elements of W0e2 are given by t ^ c , c ′ if these cities are in the same country (i.e., C = C’), and 0 otherwise. Finally, We1 and We2 describe international and national economic connectivity, respectively.
If ρgeo is positive, population growth in a city increases the populations in its neighboring cities. When ρe1 and/or ρe2 is positive, population growth in a city increases the populations in foreign cities with strong economic connectivity. Intuitively speaking, ρgeo and ρe2 capture local interactions, and ρe1 captures global interactions.
In short, our city growth model projects 5-year-population-change considering attributes of the cities, local spatial interactions among neighboring cities, and global interactions among cities with strong economic connectivity.

City Growth Model: Estimation

We used the data of city populations (1990, 1995, and 2000) provided by GRUMP, and estimated Equation (A1) while assuming t = 1995. In other words, (population in 2005)/(population in 2000) is projected from (population in 2000)/(population in 1995). The spatial 2-step least squares (2SLS; [26]) is used for the estimation. Specifically, to estimate r in Wgeo, 2SLS is iterated while varying r values, and the optimal r value, which maximizes the adjusted R2, is identified.) The explanatory variables are road density (Road dens), distance to the nearest airport (Airport dist), and distance to the nearest ocean (Ocean dist; see Table 1), whose coefficients are denoted by βroad, βocean, and βairport, respectively.
Table A1 summarizes the estimated parameters. The table suggests that population increases rapidly in areas with dense road network and good access to airports, although the latter is statistically insignificant. These results are intuitively consistent. The positive sign of βocean suggests that city growth in inland areas is faster than that in coastal cities. This might be because coastal cities are already matured, and their populations are more stable than those of inland cities.
Regarding parameters describing interactions, βgeo has a statistically significant positive effect, whereas βe2 does not. Thus, geographic proximity is a significant factor determining local-scale city interactions. On the other hand, βe1, which quantifies global-scale interactions, is statistically significant. It is suggested that consideration of both local and global-scale interactions is important in city growth modeling.
The quasi-adjusted R2 for the population change in 5 years, Δpt+5, is 0.401, which is not very accurate. However, the value of R2 for the population after 5 years, pt+5, is 0.998. Since we focus on the latter, the accuracy of the model is sufficient.
While we used the 2SLS method, which is computationally efficient because of large samples, a Bayesian approach is also available to estimate the model Equation (A1) (see e.g., [27]). The Bayesian estimation, which explicitly considers uncertainty in model parameters, would be an important future task, to quantify uncertainty in our socioeconomic scenarios.
Table A1. Parameter estimates.
Table A1. Parameter estimates.
Estimatet-value
Intercept−6.19×10-4−8.12***
α1.87×10-38.98***
ρgeo9.56×10-1188.57***
ρe11.83×10-324.95***
ρe24.10×10-40.84
βroad1.21×10-33.46***
βocean2.10×10-42.19***
βairport−1.66×10-4−0.47
r209
Quasi-adjusted R2for Δpt+50.405
for pt+50.998
Note: *** Statistical significance at the 1 % level.

City Growth Model: Application for City Population Projections

Since SSP1-3 represents globalization, BAU, and fragmentation scenarios, respectively, different levels of international interactions are assumed in each scenario. Specifically, we assume that ρe1 doubles by 2100 in comparison with 2000 in SSP1, ρe1 is constant in SSP2, and ρe1 becomes half the value of 2000 by 2100 in SSP3. In each scenario, the values for ρe1 between 2000 and 2100 are linearly interpolated.
Using the ρe1 values, city populations in 2005, 2010, … 2100 are estimated by sequentially applying the city growth model, Equation (A1), which projects the 5-year-after populations.

Projection of Urban Potentials

Increase/decrease of city population encourages/discourages urbanization in the neighboring areas. Thus, this study evaluates urbanization potential using Equation (A2), which equals Equation (2) when t = 2000:
q g , t ( r ) = ∑ c p ^ c , t exp ( − d c , g r )
where p ^ c , t is the city population in year t, which is projected as explained just above, and dc,g is the arc distance between the c-th city and the center of the g-th grid. The potential qg,t(r) increases nearby cities with large population.
Although r is a range parameter just like h in W0geo, r represents the range of spill over around each city, whereas h (= 209 km; see Table A1) represents the range of spill over across cities. Thus, r must be smaller than h. Considering the consistency with the subsequent urban area projection in Section 2.4, r is given by a value maximizing the explanatory power of urban potential, qg,t(r’), on urban expansion. In other words, r is estimated by maximizing the adjusted R-squares (adj-R2) of the following model, Equation (2), which is estimated using the GRUMPS city population data in 2000. The estimated parameters in 2000 are r ^ = 16.4 , b ^ 0 = 21.89 , and b ^ q = 0.126 . r = 16.4 is assumed for SSP2. On the other hand, r = 8.2 (= 0.5 × 16.4) is assumed for SSP1 to model compact urban growth, while r = 32.8 (= 2.0 × 16.4) is assumed in SSP3 to model dispersed growth.

Projection of Urban Area

This section projects urban extent based on estimated urbanization potentials (see Figure 2). The 5-year change of urban area in each grid is projected by Equation (A4), which is derived from Equation (1):
Δ U r b a n   A r e a g , t + 5 = [ q g , t + 5 ( r ) − q g , t ( r ) ] b ^ q
We also project the expansion of nonurban residential areas due to the potentials. This study assumes that nonurban residential areas are proportional to Agri area (see Table 1), and the 5-year change is estimated by the following model:
Δ A g r i   A r e a g , t + 5 = [ q g , t + 5 A ( r A ) − q g , t A ( r A ) ] b ^ q A
The parameters in Equation (A4) for 2000 are estimated by the adjusted-R2 maximization of Equation (1) whose Urban Areag,2000 is replaced with Agri Areag,2000 (Equation (A5) is obtained from Equation (4) after the replacement). The estimated values are r ^ A = 12.1 and b ^ q A = 0.129 . While bqA = 0.129 is assumed across scenarios, rA values in SSP1-3 are given by 6.05, 12.1, and 24.2, respectively, just like r.
Urban areas and agricultural areas are projected by applying Equations (A4) and (A5) sequentially. In each sequence, if (Urban Areag,t+5 + Agri Areag,t+5) exceeds the area of the grid, Agri areag,t+5 is reduced. Urban Areag,2000 and Agri Areag,2000 are used as baseline areas. Thus, each grid can have both urban and agricultural areas.
The next section applies the estimated urban and nonurban areas as weights for proportional distribution. In the distribution, the range parameters, h, r, and rA control the share of populations and gross productivity nearby cities. For instance, if r is very small as in SSP1, most people and gross productivity are concentrated nearby cities. As such, the proportional distribution can describe both urban expansion and shrinkage depending on the range parameter values. Similarly, rA controls the nonurban population distribution. In case of SSP1, the small rA concentrates nonurban populations into grids with greater Agri Area with greater potentials. The populations are dispersed in SSP3 whose rA value is large.

A.2. Downscale Approach

We downscale the urban and nonurban populations and GDPs utilizing projected city populations, urbanization potentials, urban areas, and other auxiliary variables summarized in Table 1.
To date, numerous downscale methods have been proposed in quantitative geography, geostatistics, and other fields. The accurateness of the dasymetric mapping, which simply distributes populations in proportion to auxiliary variables, has been remarked upon in many comparative studies (e.g., [28,29]). We use Equation (A6), which modifies the dasymetric mapping model to consider differences in scenarios (Square root is used because distribution weights are defined by the product of two weight variables.):
f ( a g , t , k ) = a ˜ g , t s s p a g , t , k ∑ g ∈ C a ˜ g , t s s p a g , t , k Y C , t
where YC,t is population or GDP in country C including the g-th grid in year t. a ˜ g s s p is a baseline variable to control urban expansion/shrinkage assumed in each scenario. Urban areag,t, Agri areag,t, and UAgri areag,t (=Urban areag,t +Agri areag,t; see Table 2), which are projected under each SSP, are used to downscale urban population, nonurban population, and GDP, respectively.
ag,t,k is a control variable capturing influence from auxiliary variables, where k is the index of control variables. We are not sure which auxiliary variables are appropriate for ag,t,k. Hence, this study downscales population/gross productivity in g-th grid at year t, yg,t, using a weighted average of dasymetric mapping models, which is formulated as follows
y ^ g , t = ∑ k = 1 K ω k , t f ( a g , t , k )
where ωk,t measures the importance of the k-th submodel, f(ag,t,k). The following country level model is obtained by aggregating the grid-level model presented by Equation (A8).
Y C ( g ) , t = ∑ g ∈ C ( g ) ∑ k = 1 K ω k , t f ( a g , t , k )
ωk,t in the downscale model Equation (A7) is estimated by gradient boosting, which is an ensemble learning technique, for Equation (A8). As explained in Section 2.5, the gradient boosting takes a weighted ensemble mean of 12 submodels in the urban and nonurban population downscaling, while 16 submodels exist in the GDP downscaling. Meanwhile, our ensemble learning means averaging of the submodels based on the weights optimized by the gradient boosting.
Roughly speaking, the gradient boosting optimizes the weights, ωk,t: (i) the weights for the submodels are equally set by ωk,t = 1/K; (ii) residuals are evaluated using Equation (A8); (iii) samples (e.g., YC(g),t values) are weighted according to the size of the residuals; (iv) the ωk,t values are updated so that model accuracy is improved for samples with larger weights (i.e., larger residuals in step (ii)); and (v) steps (ii), (iii), and (iv) are iterated until convergence. The gradient boosting procedure is known to be robust even if the submodels are collinear.
The gradient boosting is performed for every target year. To assure the gradual change of the weights across years, the ωk,t value is replaced with ω - k , t = (ωk,t−1 + ωk,t + ωk,t+1)/3, which is their temporal moving average. Finally, the submodels in year t is averaged by the gradient boosting first, and the resulting models at time t−1, t, and t+1 are temporally averaged subsequently. Table A2 summarizes estimated ωk,t parameters in 2080. Section 3.1 discusses the parameter estimates.
Table A2. Estimated importance of auxiliary variables in 2080 (ag,k = baseline variables × control variables).
Table A2. Estimated importance of auxiliary variables in 2080 (ag,k = baseline variables × control variables).
Baseline VariablesUrban AreaUrban PopUrban Potential
Control Variables1RoadAirOcean1RoadAirOcean1RoadAirOcean
Urban PopulationSSP10.020.100.070.110.020.010.030.110.050.190.150.16
SSP20.090.050.050.100.020.020.030.110.030.130.120.26
SSP30.070.030.050.100.080.070.060.080.030.040.130.28
Baseline VariablesAgri AreaUrban PopUrban Potential
Control Variables1RoadAirOcean1RoadAirOcean1RoadAirOcean
Nonurban PopulationSSP10.030.040.070.030.020.030.030.060.080.410.130.07
SSP20.040.030.090.030.020.010.030.070.080.370.120.11
SSP30.070.020.100.040.010.010.030.090.050.170.190.23
Baseline VariablesUrban + Agri AreaUrban PopUrban PotentialSSP Pop
Control Variables1RoadAirOcean1RoadAirOcean1RoadAirOcean1RoadAirOcean
GDPSSP10.070.010.040.050.180.100.140.040.060.030.030.040.020.060.090.04
SSP20.100.020.030.050.140.090.080.030.080.080.050.060.080.030.070.03
SSP30.010.050.010.050.100.090.010.050.090.170.170.010.090.020.070.01

References

  1. O’Neill, B.C.; Kriegler, E.; Riahi, K.; Ebi, K.L.; Hallegatte, S.; Carter, T.R.; Mathur, R.; van Vuuren, D.P. A new scenario framework for climate change research: The concept of shared socioeconomic pathways. Clim. Chang. 2014, 122, 387–400. [Google Scholar] [CrossRef]
  2. O’Neill, B.C.; Kriegler, E.; Ebi, K.L.; Kemp-Benedict, E.; Riahi, K.; Rothman, D.S.; van Ruijven, B.J.; van Vuuren, D.P.; Birkmann, J.; Kok, K.; et al. The roads ahead: Narratives for shared socioeconomic pathways describing world futures in the 21st century. Glob. Environ. Chang. 2015, 42, 169–180. [Google Scholar] [CrossRef]
  3. Gaffin, S.R.; Rosenzweig, C.; Xing, X.; Yetman, G. Downscaling and geo-spatial gridding of socio-economic projections from the IPCC special report one missions scenarios (SRES). Glob. Environ. Chang. 2004, 14, 105–123. [Google Scholar] [CrossRef]
  4. Van Vuuren, D.P.; Lucas, P.L.; Hilderink, H. Downscaling drivers of global environmental change. Glob. Environ. Chang. 2007, 17, 114–130. [Google Scholar] [CrossRef]
  5. Grübler, A.; O’Neill, B.; Riahi, K.; Chirkov, V.; Goujon, A.; Kolp, P.; Prommer, I.; Scherbov, S.; Slentoe, E. Regional, national, and spatially explicit scenarios of demographic and economic change based on SRES. Technol. Forecast. Soc. 2007, 74, 980–1029. [Google Scholar] [CrossRef]
  6. Bengtsson, M.; Shen, Y.; Oki, T. A SRES-based gridded global population dataset for1990–2100. Popul. Environ. 2006, 28, 113–131. [Google Scholar] [CrossRef]
  7. Hachadoorian, L.; Gaffin, S.; Engelman, R. Projecting a gridded population of the world using ratio methods of trend extrapolation. In Human Population; Cincotta, R., Gorenflo, L., Eds.; Springer: New York, NY, USA, 2011; pp. 13–25. [Google Scholar]
  8. Asadoorian, M.O. Simulating the spatial distribution of population and emissions to 2100. Environ. Res. Econ. 2007, 39, 199–221. [Google Scholar] [CrossRef]
  9. Nam, K.-M.; Reilly, J.M. City size distribution as a function of socioeconomic conditions: An eclectic approach to downscaling global population. Urban Stud. 2013, 50, 208–225. [Google Scholar] [CrossRef]
  10. Jones, B.; O’Neill, B.C. Spatially explicit global population scenarios consistent with the Shared Socioeconomic Pathways. Environ. Res. Lett. 2015, 11, 084003. [Google Scholar] [CrossRef]
  11. Fujimori, S.; Abe, M.; Kinoshita, T.; Hasegawa, T.; Kawase, H.; Kushida, K.; Masui, T.; Oka, K.; Shiogama, H.; Takahashi, K.; et al. Downscaling global emissions and its implications derived from climate model experiments. PLoS ONE 2017, 12, e0169733. [Google Scholar] [CrossRef]
  12. Jones, B.; O’Neill, B.C. Historically grounded spatial population projections for the continental united states. Environ. Res. Lett. 2013, 8, 044021. [Google Scholar] [CrossRef]
  13. McKee, J.J.; Rose, A.N.; Bright, E.A.; Huynh, T.; Bhaduri, B.L. Locally adaptive, spatially explicit projection of US population for 2030 and 2050. Proc. Natl. Acad. Sci. USA 2015, 112, 1344–1349. [Google Scholar] [CrossRef]
  14. Fang, Y.; Jawitz, J.W. High-resolution reconstruction of the United States human population distribution, 1790 to 2010. Sci. Data 2018, 5, 180067. [Google Scholar] [CrossRef]
  15. Yamagata, Y.; Murakami, D.; Seya, H. A comparison of grid-level residential electricity demand scenarios in Japan for 2050. Appl. Energy 2015, 158, 255–262. [Google Scholar] [CrossRef]
  16. Reimann, L.; Merkens, J.L.; Vafeidis, A.T. Regionalized Shared Socioeconomic Pathways: Narratives and spatial population projections for the Mediterranean coastal zone. Reg. Environ. Chang. 2018, 18, 235–245. [Google Scholar] [CrossRef]
  17. SSP Database. International Institute for Applied Systems Analysis (IIASA). Available online: https://tntcat.iiasa.ac.at/SspDb/dsd?Action=htmlpage&page=about (accessed on 8 April 2019).
  18. Jiang, L.; O’Neill, B.C. Global urbanization projections for the Shared Socioeconomic Pathways. Glob. Environ. Chang. 2015, 42, 193–199. [Google Scholar] [CrossRef]
  19. Balk, D.L.; Deichmann, U.; Yetman, G.; Pozzi, F.; Hay, S.I.; Nelson, A. Determining global population distribution: Methods, applications and data. Adv. Parasitol. 2006, 62, 119–156. [Google Scholar]
  20. Schneider, A.; Friedl, M.A.; Potere, D. A new map of global urban extent from MODIS satellite data. Environ. Res. Lett. 2009, 4, 044003. [Google Scholar] [CrossRef]
  21. Shiogama, H.; Emori, S.; Hanasaki, N.; Abe, M.; Masutomi, Y.; Takahashi, K.; Nozawa, T. Observational constraints indicate risk of drying in the Amazon basin. Nat. Commun. 2011, 2, 253. [Google Scholar] [CrossRef]
  22. History Database of the Global Environment (HYDE). PBL Netherlands Environmental Assessment Agency. Available online: https://themasites.pbl.nl/tridion/en/themasites/hyde/ (accessed on 8 April 2019).
  23. Raftery, A.E.; Li, N.; Ševčíková, H.; Gerland, P.; Heilig, G.K. Bayesian probabilistic population projections for all countries. Proc. Natl. Acad. Sci. USA 2012, 109, 13915–13921. [Google Scholar] [CrossRef]
  24. Stewart, I.D.; Oke, T.R. Local Climate Zones for urban temperature studies. Bull. Am. Meteorol. Soc. 2012, 93, 1879–1900. [Google Scholar] [CrossRef]
  25. Cressie, N. Statistics for Spatial Data; Wiley: New York, NY, USA, 1993. [Google Scholar]
  26. Kelejian, H.H.; Prucha, I.R. 2SLS and OLS in a spatial autoregressive model with equal spatial weights. Reg. Sci. Urban Econ. 2002, 32, 691–707. [Google Scholar] [CrossRef]
  27. LeSage, J.; Pace, K.P. Introduction to Spatial Econometrics; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
  28. Fisher, P.F.; Langford, M. Modelling the errors in areal interpolation between zonal systems by Monte Carlo simulation. Environ. Plan. A 1995, 27, 211–224. [Google Scholar] [CrossRef]
  29. Hawley, K.; Moellering, H. A comparative analysis of areal interpolation methods. Cartogr. Geogr. Inf. Sci. 2005, 32, 411–423. [Google Scholar] [CrossRef]

Article Metrics

Citations

Article Access Statistics

Journal Statistics
Multiple requests from the same IP address are counted as one view.
Download PDF
Can Pay-As-You-Go, Digitally Enabled Business Models Support Sustainability Transformations in Developing Countries? Outstanding Questions and a Theoretical Basis for Future Research
Previous
Vulnerability Analysis of Urban Rail Transit Network within Multi-Modal Public Transport Networks
Next