Abstract
Green supplier selection, as a core part of green supply chain management, has attracted the attention of various researchers in the past decade. Plenty of green supplier selection methods based on multi-criteria group decision-making have been presented in previous literature. However, these approaches ignore the consensus level between the experts, and they rarely consider the priority level among the experts and the interdependent relationship between criteria. To handle these issues, an integrated framework of green supplier selection under the hesitant fuzzy linguistic (HFL) environment was established. In this framework, the preference information expressed by HFL was transformed into the hesitant 2-tuple linguistic (H2TL). Then, the consensus process was introduced into the green supplier selection process to increase the consensus level between experts. The H2TL prioritized operator and Choquet integral operator were respectively applied to construct the group decision matrix and derive the ranking order of green suppliers. Finally, we used a numerical example to demonstrate the validity and applicability of the presented framework and implemented a comparative analysis to highlight the features of the presented method.
1. Introduction
With the rapid development of economic globalization, humanity is facing some extremely serious problems, including resource shortage and environment pollution. In light of growing consumer awareness of environment protection and sustainable development, modern enterprise should focus on resource conservation and environmental sustainable development when they pursue economic interests and their own development. Green supply chain management (GSCM), which takes environment performance into account, is deemed a novel management mode for enterprise [1]. The main objective of implementing GSCM is to reduce the environmental pollution produced by activities related to the supply chain [2]. GSCM includes various activities, such as green product development, green purchasing, green production, green packaging, green warehousing, green marketing, green transportation, resource recycling, and green supplier selection. In these activities, green supplier selection can directly influence the competitiveness of a supply chain and the environmental performance of an enterprise [3], and it is a key part of GSCM [4]. Furthermore, efficient supply chain management can help enterprises to minimize supply chain and production risk, optimize inventory management, improve customer service levels, enhance competitive advantage, and increase profitability and customer satisfaction [5,6]. Therefore, to keep a strategically competitive advantage in the fiercely competitive global environment, it is significant for enterprises to select the most appropriate green supplier.
Green supplier selection is generally deemed a multi-criteria group decision-making (MCGDM) problem that includes many decision makers and evaluation criteria. In the literature, many green supplier selection methods based on MCGDM have been presented by a number of researchers [7,8,9,10,11,12]. In these approaches, the selection process of green supplier is usually implemented by several experts that come from different fields. However, there may exist a large deviation among the experts’ preference information for green supplier selection. Apparently, with the results derived by this preference information, it is difficult to guarantee that the finial decision scheme is accepted by the group of experts. However, this situation is ignored in the existing approaches to green supplier selection, that is, the consensus level among experts is not considered in the previous studies. The consensus reaching process aims at increasing the agreement level between experts [13] and is applied in group decision making before aggregating the evaluation information of experts. The consensus reaching process has been widely employed in different areas [14,15,16,17,18]. Therefore, it is necessary to introduce the consensus reaching process to the method of green supplier selection.
Green supplier selection, which involves various quantitative and qualitative criteria, is complex decision process [7,19]. To select a suitable green supplier, the selection process is commonly carried out by a group of experts with different backgrounds, experiences, expertise, and prestige, rather than an individual. In real decision making, members of the group of experts should be assigned to different priority levels. Nevertheless, the existing methods all assume that experts are of equal importance, which may lead to a biased result in the final decision. In order to handle this situation, the prioritized averaging (PA) operator was presented by Yager [20]. The prominent feature of the PA operator is its ability to reflect the priority levels among experts. Based on the advantage of the PA operator, it has been successfully applied to various problems [21,22,23,24]. In addition, the preference information provided by experts generally has aspects of uncertainty, vagueness, and hesitancy. To address this situation, Rodriguez et al. [25] originally presented the hesitant fuzzy linguistic term set to flexibly express an expert’s preference information. Many studies and applications concerning the hesitant fuzzy linguistic term set have been performed [25,26,27,28,29,30]. Accordingly, it is very interesting to apply the PA operator to aggregate the hesitant fuzzy linguistic preference of experts in the green supplier selection.
On the other hand, dependencies and interactions may exist among the evaluation criteria in green supplier selection. However, there are few approaches in previous literature that focus on this issue. Qin et al. [11] argued that the interaction among criteria should be taken into account in green supplier selection. To this end, Feyzioğlu and Büyüközkan [31] investigated the green supplier performance evaluation issue, taking into account the interdependent relationships among criteria. Nia et al. [32] presented a comprehensive green supplier selection method under a fuzzy environment, in which a Delphi method is used to determine the weight of criteria, and the Choquet integral is applied to obtain the best green supplier. However, these two methods have two drawbacks: (1) They fail to consider the consensus level between the experts; (2) They ignore the priority level between experts. Moreover, the Choquet integral has been widely utilized in many fields [33,34,35,36,37,38,39,40,41] due to its ability to depict the interdependent relationships among the criteria. Hence, selecting the best green supplier by combining the Choquet integral and other methods is meaningful work.
Based on the above discussion, the currently study aims at establishing a synthetical green supplier selection framework under the hesitant fuzzy linguistic environment to select the most appropriate green supplier, which considers both the priority levels among experts and the interdependent relationship between criteria simultaneously. The major contributions of our study are listed as follows. First, the consensus level between experts was improved by applying a consensus-reaching process before constructing the group decision matrix. Second, the priority level among experts was reflected by employing a priority aggregation operator to aggregate the individual preference. Furthermore, a comparative analysis with the existing methods was carried out to demonstrate the advantages of the presented framework. The remaining parts of this study are arranged in the following way. The related literature of green supplier selection, consensus reaching process, prioritized aggregation operator, and Choquet integral are reviewed in Section 2. Section 3 introduces the essential concepts of the hesitant fuzzy linguistic term set, 2-tuple linguistic variable and hesitant 2-tuple linguistic term set, and the definition of consensus measure. A synthetical framework for green supplier selection is presented in Section 4. In Section 5, a case study and a comparative analysis are carried out by applying the green supplier selection issue to an international automobile company. Finally, the conclusions of this article and suggestions for future studies are provided in Section 6.
2. State-of-the-Art Review
This section reviews related literature from four aspects, that is, green supplier selection, consensus reaching process, and application of the prioritized aggregation operator and the Choquet integral.
2.1. Methods for Green Supplier Selection
In light of green supplier selection being a typical multi-criteria decision-making (MCDM) issue, plenty of methods, particularly based on MCDM techniques, have been presented in the past decade. For instance, Handfield et al. [42] proposed a supplier selection approach based on an analytical hierarchy process in which evaluation criteria include environmental criteria. Büyüközkan [7] constructed a decision model for green supplier selection in which an axiomatic design is employed to obtain the best green supplier. Hashemi et al. [8] presented a synthetical green supplier selection approach by integrating an analytic network process and gray relational analysis (GRA). Ghorabaee et al. [9] established a new MCGDM method based on WASPAS (Weighted Aggregated Sum Product ASsessment) to evaluate green suppliers. Sari [10] constructed a new decision model based on an analytical hierarchy process, VIKOR (VIsekriterijumska Optimizacija I Kompromisno Resenje), and Monte Carlo simulation to the assessment for green supply chain management. Qin et al. [11] introduced the TODIM method into an interval type-2 fuzzy set and presented an MCGDM approach to handle green supplier selection. To evaluate the green performance of suppliers, Wang et al. [3] developed a comprehensive approach according to the cloud model and QUALIFLEX (QUALitative FLEXible multiple criteria) method. Yazdani et al. [43] presented a synthetical approach for green supplier selection by combining the decision-making trial and evaluation laboratory method, quality function deployment model, and complex proportional assessment. Liao et al. [12] put forward a hesitant fuzzy linguistic thermodynamic approach to deal with green supplier selection by combining cumulative prospect theory and PROMETHEE (Preference Ranking Organization METHod for Enrichment Evaluation) method. Banaeian et al. [44] applied the VIKOR, GRA, and TOPSIS (Technique for Order Preference by Similarity to an Ideal Solution) approaches to study a green supplier selection issue in the agri-food industry, and a comparison analysis between the three methods was carried out.
2.2. Consensus Reaching Process
The consensus reaching process is generally deemed an interactive and dynamic group negotiation process to enhance the consensus level among decision makers [13]. Therefore, the consensus reaching process for group decision-making has attracted the attention of various researchers. For example, Herrera et al. [45] presented the first soft consensus model in group decision-making with fuzzy linguistic preferences. Xu and Wu [46] established a discrete model to support the consensus reaching process in which a convergent algorithm was proposed to improve the consensus level between experts. To address the MCGDM problems with respect to group consensus requirements, Fu and Yang [47] presented a consensus model based on an evidential reasoning method. Dong et al. [48] constructed a consensus framework for group decision-making to handle non-cooperative behaviors between decision makers. Wu et al. [49] investigated a visual interaction consensus model in which a trust relationship is used to calculate the trust degree of experts, and a trust-based recommendation mechanism was designed to produce advice. In addition, the consensus reaching process also has been employed to solve different application problems. For example, Xu et al. [14] developed a dynamic consensus model for large-group emergency decision-making, in which an exit–delegation mechanism is utilized to handle clusters. Xu et al. [15] presented a consensus model with the hesitant fuzzy preference relations and applied it to water allocation management. Gong et al. [50], using a consensus decision model, investigated preferential voting problems related to abstention. To improve business process outsourcing, a framework based on a fuzzy linguistic consensus model was constructed by Ciasullo et al. [16]. Xu et al. [17] set up a two-stage consensus model and used it to deal with earthquake shelter selection.
2.3. Application of Prioritized Operator
Yager [51] explored prioritized MCDM problems, where a prioritization relationship exists among criteria. Next, in order to manage such MCDM problems, Yager [20] originally introduced a PA operator. To handle uncertainty and vagueness information, the PA operator has been extended to various environments by many scholars. For example, Yu and Xu [52] introduced the PA operator into the intuitionistic fuzzy context and devised an intuitionistic fuzzy PA operator. Wei [53] investigated PA operators under the hesitant fuzzy environment and proposed some hesitant fuzzy PA operators. Wu et al. [54] defined two simple neutrosophic PA operators and two effective cross-entropy measures of simple neutrosophic numbers. Moreover, the PA operator also has been used in several fields, such as that presented by Yu [21], wherein two triangular intuitionistic fuzzy prioritized operators were employed to handle a teaching quality evaluation. To cope with a water source management problem, Wang et al. [22] proposed a non-homogeneous group decision-making approach by applying the prioritized order-weighted averaging (OWA) operator. Ji et al. [55] developed a novel approach to select third-party logistics providers, for which the interdependent relationship and prioritization level among criteria are considered simultaneously. Ma et al. [23] investigated a medical treatment selection problem with different prioritization levels of decision makers by using the prioritized harmonic mean operators. Avilés-Ochoa et al. [24] defined a prioritized induced probabilistic ordered weighted averaging distance operator and used it to measure government transparency. Yu et al. [56] designed a mathematical model to explore hotel selection on websites, for which the weights of criteria are calculated according to the idea of the PA operator.
2.4. Application of Choquet Integral
Choquet [57] originally presented the concept of the Choquet integral in the environment of capacity theory. Next, Murofushi and Sugeno [58] defined the Choquet integral as a fuzzy integral function with regard to fuzzy measures, and the Choquet integral was successfully introduced by Grabisch [59] into the field of multi-criteria decision-making. To cope with the fuzzy information, the Choquet integral has been extended to several fuzzy environments. For instance, Tan and Chen [60] introduced the Choquet integral into an intuitionistic fuzzy environment and proposed an intuitionistic fuzzy Choquet integral operator. Yu et al. [61] explored the hesitant fuzzy aggregation operator based on the Choquet integral. Peng and Yang [62] investigated the Choquet integral operator under a Pythagorean fuzzy environment. In addition, the Choquet integral has also expanded to other fuzzy sets, such as the 2-tuple linguistic set [63], interval neutrosophic set [64], and hesitant 2-tuple linguistic set [65]. On the other hand, the prominent feature of the Choquet integral is its depiction of the interactions among input arguments. Inspired by this characteristic, the Choquet integral has been extensively used by many researchers to solve MCDM problems. For example, Wang et al. [66] utilized the Choquet integral to solve a two-sided matching decision-making problem for public–private partnership projects. For the site selection of a solar thermal power plant, Wu et al. [67] put forward a decision model based on the linguistic Choquet integral. Moradi et al. [68] employed game theory and the Choquet integral to establish a GIS-based MCDM model for earthquake vulnerability assessment. Ferrira et al. [69] constructed an evaluation framework for improving the decision-making virtuous cycle of ethical banking practices by applying the Choquet integral. Furthermore, the Choquet integral also has been applied to many areas, such as pattern recognition [33,34,35], selection of alternatives [36,37,38,39], and risk assessment [40,41].
3. Preliminary
In this section, the basic concepts of a hesitant fuzzy linguistic term set (HFLTS), 2-tuple linguistic variable and hesitant 2-tuple linguistic term set, and the definition of consensus measure are presented.
3.1. Hesitant Fuzzy Linguistic Term Set
Definition 1.
[25,26] Let be a discrete ordered linguistic term set and be a fixed set. An HFLTS, denoted by , is a finite subset of the consecutive linguistic terms of S. Then the mathematical expression of HFLTS is defined as follows
where is a collection of some linguistic terms in S and can be denoted as , where is the number of linguistic term in . For convenience, is designated as the hesitant fuzzy linguistic element (HFLE).
Definition 2.
[27] Let be an HFLE, the minimum and maximum linguistic term in is and , respectively. Let be an optimized parameter, then an added linguistic term can be defined as follows
Hence, we can add a linguistic term to HFLEs by employing different σ values. The optimized parameter σ is given by the decision maker, which is utilized to depict a decision maker’s risk preference.
3.2. The 2-Tuple Linguistic Variable
Definition 3.
[63] Let be a discrete ordered linguistic term set, and let be a crisp number representing the value of a symbolic aggregation. β, representing a 2-tuple linguistic variable, can be obtained by the following equivalent transformation function Δ
where round(·) is the common rounded function. On the contrary, a reverse equivalent transformation function can be employed to convert a 2-tuple linguistic variable into an equivalent crisp value β
3.3. The Hesitant 2-Tuple Linguistic Term Set
Definition 4.
[28,70] Let be a fixed set, be a discrete ordered linguistic term set, and be a 2-tuple linguistic variable on S, such that for any i > j. Then, a hesitant 2-tuple linguistic set is defined as
where is a collection of 2-tuple linguistic variables and can be defined as , where is the number of 2-tuple linguistic variables in . For convenience, is called to the hesitant 2-tuple linguistic element (H2TLE).
Definition 5.
[70] Let be an H2TLE, and is the number of 2-tuple linguistic variables in . The score function and variance function of can be respectively defined as follows
Definition 6.
[70] Let and be two H2TLEs on S, and and (i = 1, 2) are the score function and variance function, respectively. Then, the order relationships of and are defined as follows
- (1)
- If , then is superior , denoted by ;
- (2)
- If , then
- a.
- if , then is superior to , denoted by ;
- b.
- if , then is equal to , denoted by .
Definition 7.
Let and be two H2TLEs on S, where . Then, the distance between and can be defined as
3.4. Consensus Measure
Definition 8.
The consensus degree on elements (CDE) between experts and on the elements of alternatives with respect to criterion is defined as
Definition 9.
The consensus degree on alternatives (CDA) between experts and can be defined as
Definition 10.
The consensus degree on the individual evaluation matrix (CDI) of experts can be defined as
4. The Presented Green Supplier Selection Framework
In this section, we propose a new green supplier selection model under the hesitant fuzzy linguistic environment, which is based on the consensus reaching process, prioritized operator, and Choquet integral. In what follows, we depict the presented model for green supplier selection in four parts. In the first part, the desired criteria and alternatives of a company are determined, and hesitant fuzzy linguistic evaluation matrix is obtained. The second part presents the hesitant 2-tuple linguistic assessment matrix output based on the consensus reaching process. In the third part, the comprehensive hesitant 2-tuple linguistic evaluation matrix is constructed. In the fourth part, the comprehensive values of each alternative are calculated by employing the Choquet integral. The schematic diagram of the presented framework are shown in Figure 1.
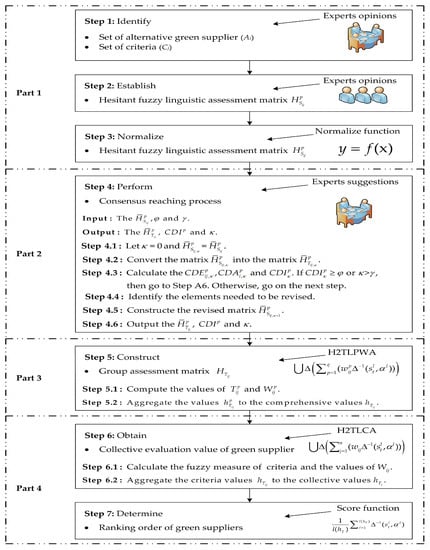
Figure 1.
The schematic diagram of the presented framework.
For the convenience of framework description, a detailed depiction of variables used in this study is provided in Table 1. The detailed steps of the presented framework are as follows:

Table 1.
The depiction of variables used in this study.
Step 1: Determine the set of alternatives and criteria.
A group of experts, denoted by , in which each expert has a different background and experience, is established first. Then, the collection of the alternatives and the criteria are identified by the group of experts, and they are denoted by and , respectively. In addition, hesitancy and ambiguity commonly exist in the expert’s judgment for green supplier selection problem. Therefore, the hesitant fuzzy linguistic is very suitable to express the expert’s preference.
Step 2: Establish the hesitant fuzzy linguistic evaluation matrix.
Assume that is a linguistic term set, which is utilized by experts to evaluate the alternative green suppliers with respect to each criterion. The hesitant fuzzy linguistic evaluation matrix provided by expert is denoted by
Step 3: Normalize the hesitant fuzzy linguistic evaluation matrix.
The criteria can be divided into two types, that is, benefit criteria and cost criteria. Hence, the cost criteria should be converted into benefit criteria according to Equation (14) [29], shown below. Then, the hesitant fuzzy linguistic assessment matrix is transformed into a normalized hesitant fuzzy linguistic assessment matrix: .
Step 4: Implement the consensus reaching process.
Let the individual normalized hesitant fuzzy linguistic assessment matrix , the consensus threshold , and the maximum number of iterations . Then the steps of consensus reaching process are described as follows.
Step 4.1: Let and .
Step 4.2: The normalized hesitant fuzzy linguistic assessment matrix is converted into a hesitant 2-tuple linguistic evaluation matrix, denoted by , according to Definition 3.
Step 4.3: Use Equations (11)–(13) to yield , , and , respectively. If for any or , then go to Step 4.6. Otherwise, go to the next step.
Step 4.4: Identify the elements that need to be revised based on the following equation:
Step 4.5: Construct the revised hesitant fuzzy linguistic assessment matrix.
Let be the revised hesitant fuzzy linguistic assessment matrix corresponding to . Then, can be generated by the following modification suggestions
where . Then, let , and go to Step 4.2.
Step 4.6: Let and . Obtain the revised individual hesitant 2-tuple linguistic assessment matrix , the consensus measure , and the number of iterations .
Step 5: Construct the group evaluation matrix.
In the process of green supplier selection, experts often have different priority levels because they come from different departments and have different backgrounds, experiences, expertise, and prestige. To reflect this feature in the information aggregation process, Yager [20] presented the prioritized aggregation operators. Inspired by the prominent characteristic of prioritized aggregation operators, Wang et al. [65] introduced the prioritized aggregation operators into the hesitant 2-tuple linguistic environment to propose a hesitant 2-tuple linguistic prioritized weighted averaging (H2TLPWA) operator. Therefore, the H2TLPWA operator is used to aggregate individual evaluation matrices to obtain a group evaluation matrix, denoted by .
Step 5.1: Compute the values of and according to the following equations.
Hence, we can obtain and as follows:
Step 5.2: Aggregate the individual evaluation values to comprehensive assessment values by using the H2TLPWA operator.
Then we yield the collective assessment matrix as follows:
Step 6: Obtain the collective evaluation value of each alternative.
Green supplier selection problems are related to multiple criteria, and in these criteria may exist some interactive or interdependent characteristics. To describe this situation, Choquet [57] proposed the Choquet integral model. The main advantage of the Choquet integral is its reflection of the interactive relationship among criteria. Based on the Choquet integral, Wang et al. [65] developed a hesitant 2-tuple linguistic Choquet averaging (H2TLCA) operator to deal with hesitant 2-tuple linguistic information. Consequently, the H2TLCA operator is employed to fuse the criterion values of green suppliers.
Step 6.1: Calculate the fuzzy measure of criteria and the value of in the following way.
Let C be a finite set, then . The -fuzzy measure satisfies the following conditions [71]:
Based on the boundary condition , the value of can be computed by the following equation [71]:
Then, we can obtain the criteria weight as follows.
Step 6.2: Aggregate the criteria values of each green supplier into collective values by the H2TLCA operator.
Step 7: Determine the ranking order of green suppliers.
The comprehensive score value of each green supplier can be calculated by Equation (8). Then, the priority of all green suppliers can be obtained by the descending order of .
5. An Illustrative Example
With the rapid development of economic globalization, an international automobile company is facing increasing competition pressure. To increase core competitiveness, GSCM has attracted the attention of many international automobile companies, because it can save production cost and protect the environment. Green supplier selection plays a core role in green supply chain management, which can directly influence the company’s core competitiveness and environmental protection level. In this section, therefore, we apply the presented model to solve a green supplier selection problem for an international automobile company.
5.1. Comparative Analysis
The detailed implementation steps of the illustrative example can be found in Appendix A.
There are some other MCDM approaches that have been presented to solve hesitant fuzzy linguistic MCDM problems. For example, the hesitant fuzzy linguistic TOPSIS (HFL-TOPSIS) method was proposed by Beg and Rashi [72], and the hesitant fuzzy linguistic VIKOR (HFL-VIKOR) method was developed by Liao et al. [73]. The detailed steps of the HFL-TOPSIS and HFL-VIKOR approaches are described in Appendix B and Appendix C, respectively. Here, we use these two methods to solve the illustrative example, and carry out a comparison analysis with the proposed framework.
5.1.1. Solve the Example Using the HFL-TOPSIS Method
Step 2: The positive idea solution and negative idea solution are obtained based on Equations (A3) and (A4).
Step 3: The distance between the comprehensive decision matrix and the positive idea solution and negative idea solution are computed.
Step 4: The relative closeness of each green supplier to the positive idea solution are calculated by Equation (A7).
Therefore, the ranking order of all green suppliers is obtained by descending order of the relative closeness, that is, .
5.1.2. Solve the Example Using the HFL-VIKOR Method
Step 1: The collective decision matrix is constructed by Equation (A8).
Step 2: For benefit criteria and cost criteria , the positive idea solution and negative idea solution can be calculated by Equations (A9) and (A10).
Step 3: The group utility and individual regret values are calculated based on Equations (A11) and (A12).
Step 4: The compromise measure for each supplier is obtained by Equation (A13).
Step 5: According to the increasing compromise measure, the priority order of green suppliers is determined as follows: . In addition, the qualifications and are satisfied at the same time. Consequently, green supplier is the only compromise solution.
5.2. Result Discussion
Based on the obtained results of the two comparative approaches, we can see that the best and worst green suppliers determined by the two comparative approaches and the presented method are respectively the same. That is, the best green supplier is , and the worst is . This reveals the validity of the presented method in this article. However, the ranking orders obtained by the presented method and the two comparative approaches are slightly different. The main reasons leading to this difference are the features of the two comparative approaches. Both the HFL-TOPSIS and HFL-VIKOR approaches fail to reflect the interdependency of criteria. In contrast, the H2TLCA operator employed in the presented method can better characterize the interdependency of criteria. In addition, the two comparative approaches utilized Equations (A1), (A2) and (A8) to establish the group decision-making matrix, and ignored the consensus level and priority level among experts. In this paper, nevertheless, the consensus reaching process and H2TLPWA operator are respectively used to increase the consensus level among experts and reflect the priority level among experts. Consequently, the ranking order of the green suppliers determined by the presented method is more accurate and reasonable.
Compared with the HFL-TOPSIS and HFL-VIKOR approaches, the prominent advantages of the presented method in this article can be summarized as follows:
- In the proposed framework, hesitant fuzzy linguistic information is transformed into hesitant 2-tuple linguistic information to avoid the loss of information, which makes the ranking result more accurate and reasonable.
- The presented method can improve the consensus level among experts by introducing the consensus reaching process into the green supplier selection problem. Therefore, the decision results obtained by this method can be well accepted by the organization or company.
- The priority order relationship between experts can be considered by using the H2TLPWA operator to construct the group decision matrix, which increases the application capacity of the presented method.
- By employing the H2TLCA operator to aggregate the criteria values of each green supplier, the interdependency of criteria are reflected, which makes this method closer to the real situation.
6. Conclusions
It is highly significant for a company to maintain competitive power in the globalized market by selecting the most suitable green supplier. Therefore, the green supplier selection problem, considering the consensus level among experts, the priority order relationship among experts, and the interdependency of criteria, is presented in this article. We established a hybrid green supplier selection framework by combining the consensus reaching process, H2TLPWA operator, and H2TLCA operator. In this framework, the consensus reaching process was used to enhance the consensus level among experts. Then, the H2TLPWA operator was applied to aggregate the individual evaluation to a group decision matrix, which reflects the priority order relationship between experts. To consider the interdependence of criteria, the comprehensive assessment value of each green supplier was obtained by the H2TLCA operator. Finally, the effectiveness and practicability of the presented model was validated by an illustrative example of green supplier selection, and a comparative analysis was conducted to demonstrate the advantages of the presented framework. The green supplier selection framework presented in this paper has some advantages, but there are several drawbacks that merit addressing in the future. In the real situation, the experts express the bounded rationality behavior under an uncertainty environment. Consequently, the bounded rationality behavior of experts should be incorporated into the presented model in further research. In addition, the other MCDM approaches, such as MULTIMOORA (MOORA plus Full Multiplicative Form), MABAC (Multi-Attributive Border Approximation area Comparison), and WASPAS (Weighted Aggregated Sum Product Assessment), can be extended to the presented model to solve green supplier selection problems.
Author Contributions
J.Z. and Y.L. conceived and designed the research, and checked and revised this paper. J.Z. collected and analyzed the data, and wrote the paper. The final manuscript has been read and approved by all authors.
Funding
This research was funded by National Natural Science Foundation of China [No. 71371156] and Doctoral Innovation Fund Program of Southwest Jiaotong University [No. D-CX201729].
Acknowledgments
The authors are very grateful to the reviewers and editor for the careful and constructive comments which are very helpful in improving the quality of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| HFLE | Hesitant Fuzzy Linguistic Element |
| HFLTS | Hesitant Fuzzy Linguistic Term Set |
| HFL-TOPSIS | Hesitant Fuzzy Linguistic TOPSIS |
| HFL-VIKOR | Hesitant Fuzzy Linguistic VIKOR |
| H2TLE | Hesitant 2-Tuple Linguistic Element |
| H2TLCA | Hesitant Fuzzy Linguistic Choquet Averaging |
| H2TLPWA | Hesitant Fuzzy Linguistic Prioritized Weighted Averaging |
| GRA | Grey Relational Analysis |
| GSCM | Green Supply Chain Management |
| MABAC | Multi-Attributive Border Approximation area Comparison |
| MCDM | Multi-Criteria Decision Making |
| MCGDM | Multi-Criteria Group Decision-Making |
| MOOR | Multi-Objective Optimization by Ratio Analysis |
| MULTIMOORA | MOORA plus Full Multipliative |
| OWA | Order Weighted Averaging |
| PA | Prioritized Averaging |
| PROMETHEE | Preference Ranking Organization METHod for Enrichment Evaluation |
| QUALIFLEX | Qualitative Flexible multiple criteria method |
| TODIM | an acronym in Portuguese of interactive and multiple attribute decision-making |
| TOPSIS | Technique for Order Preference by Similarity to an Ideal Solution |
| WASPAS | Weighted Aggregated Sum Product ASsessment |
| VIKORA | VIsekriterijumska Optimizacija I Kopromisno Resenje |
Appendix A
In what follows, the steps of the green supplier selection problem, solved by employing the presented approach, are described in detail.
Step 1: The collection of green suppliers and criteria are defined.
To choose the most suitable green supplier, a group of experts is formed, and it includes three experts who come from different departments in an international automobile company. Through preliminary screening, the group of experts identifies four potential green suppliers, , for further assessment. Four criteria to be taken into account in this green supplier selection process are: environment management systems , price , quality , and service level .
Step 2: The hesitant fuzzy linguistic evaluation matrices are provided by the group of experts.
Linguistic term set is used by experts to assess each green supplier with regard to each criterion. The assessment results provided by experts are shown in Table A1.

Table A1.
Hesitant fuzzy linguistic evaluation matrices.
Table A1.
Hesitant fuzzy linguistic evaluation matrices.
| Expert | Alternatives | ||||
|---|---|---|---|---|---|
Step 3: Normalize the hesitant fuzzy linguistic evaluation matrices.
In these criteria, criteria , , and are benefit criteria, while criterion is a cost criterion. Therefore, the evaluation value of criterion should be normalized according to Equation (13).
Step 4: Perform the consensus reaching process.
The consensus threshold and the maximum number of iterations are designated as and by the group of experts, respectively, before implementing the consensus reaching process. Then, the consensus reaching process is performed.
Step 4.1: Let and .
Step 4.2: Covert the hesitant fuzzy linguistic evaluation matrices into hesitant 2-tuple linguistic assessment matrices . The obtained results are shown in Table A2.

Table A2.
Hesitant 2-tuple linguistic assessment matrices
Table A2.
Hesitant 2-tuple linguistic assessment matrices
| Expert | Alternatives | ||||
|---|---|---|---|---|---|
From the results, we can see that . Then, go on the next step.
Step 4.5: According to Equation (17), the modification suggestions are generated. Then, let , and go to Step 4.2.
First iteration.
Step 4.2: Transform the hesitant fuzzy linguistic evaluation matrices into hesitant 2-tuple linguistic assessment matrices .
Based on the above results, we know that . Then, go to the next step.
Step 4.4: The elements that need to be modified are obtained based on Equations (14)–(16), that is, .
Step 4.5: According to Equation (17), the modification suggestions are generated. Then, let , and go to Step 4.2.
Second iteration.
Step 4.2: Transform the hesitant fuzzy linguistic evaluation matrices into hesitant 2-tuple linguistic assessment matrices .
According to the results, we know that for any p. Then, go to Step 4.6.
Step 4.6: Output the revised individual hesitant 2-tuple linguistic evaluation matrices , the consensus measure , and the number of iterations .
Step 5: Construct the group evaluation matrix.
Step 5.2: The group evaluation matrix is obtained by Equation (21), and the results are shown in Table A3.

Table A3.
Group evaluation matrix.
Table A3.
Group evaluation matrix.
Step 6: Obtain the collective evaluation value of each green supplier.
Step 6.1: Calculate the fuzzy measures of criteria and the value of . We suppose that , , , and . Then, is obtained based on Equation (23). According to the three axioms of the fuzzy measure [71], the fuzzy measures of criteria set are obtained, that is, , , , , , , , , , , . Further, the matrix is obtained based on Equation (24).
Step 6.2: The comprehensive evaluation value of each green supplier is aggregated by Equation (25).
Step 7: Determine the ranking order of green suppliers. According to Equation (8), the comprehensive score values of green suppliers are obtained, that is, , , , . Then, we obtain the priority order of green suppliers, which is .
Appendix B
In the following, the HFL-TOPSIS method [72] is described in detail.
Step 1: Establish the hesitant fuzzy linguistic group decision matrix by aggregating the individual evaluation matrix , where , and the and is calculated by the following equations:
Step 2: Determine the positive idea solution and negative idea solution by the following equations
where and are set of benefit criteria and cost criteria, respectively.
Step 3: Calculate the distance between the group decision matrix and the positive idea solution and negative idea solution.
Step 4: The relative closeness (RC) of each alternative is computed as follows:
where and .
Therefore, the priority of alternatives can be obtained by descending order of relative closeness.
Appendix C
In what follows, the HFL-VIKOR method [73] is depicted in detail.
Step 1: Construct the hesitant fuzzy linguistic group decision matrix as follows:
Step 2: Establish the positive idea solution and negative idea solution by the following equations
where and are sets of benefit criteria and cost criteria, respectively.
Step 3: The group utility and individual regrate values for alternative are determined by the following equations:
where and are the Euclidean distances between the two hesitant fuzzy linguistic term sets computed by Equation (7) in [74].
Step 4: The compromise measure for is calculated as follows:
where , , , and , and is the weight of the maximum group utility. Without loss of generality, .
Step 5: Rank alternatives by ascending order of , , and . The best alternative should satisfy the following two qualifications at the same time.
: , where and are the alternatives located in the first and second positions in the ranking list, respectively.
: should also be the first position ranked by and .
If the qualification is not satisfied, the maximum value of M is calculated as follows:
where M is the number of compromise solutions.
If the qualification is not satisfied, the compromise solutions are the alternatives and .
References
- Vachon, S. Green supply chain practices and the selection of environmental technologies. Int. J. Prod. Res. 2007, 45, 4357–4379. [Google Scholar] [CrossRef]
- Beamon, B.M. Designing the green supply chain. Logist. Inf. Manag. 1999, 12, 332–342. [Google Scholar] [CrossRef]
- Wang, K.Q.; Liu, H.C.; Liu, L.; Huang, J. Green supplier evaluation and selection using cloud model theory and the QUALIFLEX method. Sustainability 2017, 9, 688. [Google Scholar] [CrossRef]
- Blome, C.; Hollos, D.; Paulraj, A. Green procurement and green supplier development: Antecedents and effects on supplier performance. Int. J. Prod. Res. 2014, 52, 32–49. [Google Scholar] [CrossRef]
- Boran, F.E.; Genc, S.; Kurt, M.; Akay, D. A multi-criteria intuitionistic fuzzy group decision making for supplier selection with TOPSIS method. Expert Syst. Appl. 2009, 36, 11363–11368. [Google Scholar] [CrossRef]
- Chang, B.; Chang, C.W.; Wu, C.H. Fuzzy DEMATEL method for developing supplier selection criteria. Expert Syst. Appl. 2011, 38, 1850–1858. [Google Scholar] [CrossRef]
- Büyüközkan, G. An integrated fuzzy multi-criteria group decision-making approach for green supplier evaluation. Int. J. Prod. Res. 2012, 50, 2892–2909. [Google Scholar] [CrossRef]
- Hashemi, S.H.; Karimi, A.; Tavana, M. An integrated green supplier selection approach with analytic network process and improved Grey relational analysis. Int. J. Prod. Econ. 2015, 159, 178–191. [Google Scholar] [CrossRef]
- Ghorabaee, M.K.; Zavadskas, E.K.; Amiri, M.; Esmaeili, A. Multi-criteria evaluation of green suppliers using an extended WASPAS method with interval type-2 fuzzy sets. J. Clean. Prod. 2016, 137, 213–229. [Google Scholar] [CrossRef]
- Sari, K. A novel multi-criteria decision framework for evaluating green supply chain management practices. Comput. Ind. Eng. 2017, 105, 338–347. [Google Scholar] [CrossRef]
- Qin, J.; Liu, X.; Pedrycz, W. An extended TODIM multi-criteria group decision making method for green supplier selection in interval type-2 fuzzy environment. Eur. J. Oper. Res. 2017, 258, 626–638. [Google Scholar] [CrossRef]
- Liao, H.; Wu, D.; Huang, Y.; Ren, P.; Xu, Z.; Verma, M. Green logistic provider selection with a hesitant fuzzy linguistic thermodynamic method integrating cumulative prospect theory and PROMETHEE. Sustainability 2018, 10, 1291. [Google Scholar] [CrossRef]
- Cabrerizo, F.J.; Moreno, J.M.; Pérez, I.J.; Herrera-Viedma, E. Analyzing consensus approaches in fuzzy group decision making: Advantages and drawbacks. Soft Comput. 2010, 14, 451–463. [Google Scholar] [CrossRef]
- Xu, X.; Zhong, X.; Chen, X.; Zhou, Y. A dynamical consensus method based on exit–delegation mechanism for large group emergency decision making. Knowl. Based Syst. 2015, 86, 237–249. [Google Scholar] [CrossRef]
- Xu, Y.; Cabrerizo, F.J.; Herrera-Viedma, E. A consensus model for hesitant fuzzy preference relations and its application in water allocation management. Appl. Soft Comput. 2017, 58, 265–284. [Google Scholar] [CrossRef]
- Ciasullo, M.V.; Fenza, G.; Loia, V.; Orciuoli, F.; Troisi, O.; Herrera-Viedma, E. Business process outsourcing enhanced by fuzzy linguistic consensus model. Appl. Soft Comput. 2018, 64, 436–444. [Google Scholar] [CrossRef]
- Xu, Y.; Wen, X.; Zhang, W. A two-stage consensus method for large-scale multi-attribute group decision making with an application to earthquake shelter selection. Comput. Ind. Eng. 2018, 116, 113–129. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, R.; Li, Y. Failure mode and effects analysis considering consensus and preferences interdependence. Algorithm 2018, 11, 34. [Google Scholar] [CrossRef]
- Büyüközkan, G.; Cifci, G. A novel hybrid MCDM approach based on fuzzy DEMATEL, fuzzy ANP and fuzzy TOPSIS to evaluate green suppliers. Expert Syst. Appl. 2012, 39, 3000–3011. [Google Scholar] [CrossRef]
- Yager, R.R. Prioritized aggregation operators. Int. J. Approx. Reason. 2008, 48, 263–274. [Google Scholar] [CrossRef]
- Yu, D. Prioritized information fusion method for triangular intuitionistic fuzzy set and its application to teaching quality evaluation. Int. J. Intell. Syst. 2013, 28, 411–435. [Google Scholar] [CrossRef]
- Wang, H.; Xu, Y.; Merigó, J.M. Prioritized aggregation for non-homogeneous group decision making in water resource management. Econ. Comput. Econ. Cybern. Stud. Res. 2014, 48, 247–258. [Google Scholar]
- Ma, Y.X.; Wang, J.Q.; Wang, J.; Wu, X.H. An interval neutrosophic linguistic multi-criteria group decision-making method and its application in selecting medical treatment options. Neural Comput. Appl. 2017, 28, 2745–2765. [Google Scholar] [CrossRef]
- Avilés-Ochoa, E.; León-Castro, E.; Perez-Arellano, L.A.; Merigó, J.M. Government transparency measurement through prioritized distance operators. J. Intell. Fuzzy Syst. 2018, 34, 2783–2794. [Google Scholar] [CrossRef]
- Rodriguez, R.M.; Martinez, L.; Herrera, F. Hesitant fuzzy linguistic term sets for decision making. IEEE Trans. Fuzzy Syst. 2012, 20, 109–119. [Google Scholar] [CrossRef]
- Liao, H.; Xu, Z.; Zeng, X.J. Qualitative decision making with correlation coefficients of hesitant fuzzy linguistic term sets. Knowl. Based Syst. 2015, 76, 127–138. [Google Scholar] [CrossRef]
- Zhu, B.; Xu, Z. Consistency measures for hesitant fuzzy linguistic preference relations. IEEE Trans. Fuzzy Syst. 2014, 22, 35–45. [Google Scholar] [CrossRef]
- Rodriguez, R.M.; Martinez, L.; Herrera, F. A linguistic 2-tuple multicriteria decision making model dealing with hesitant linguistic information. In Proceedings of the 2015 IEEE International Conference on Fuzzy Systems, Istanbul, Turkey, 2–5 August 2015; pp. 1–7. [Google Scholar]
- Wei, C.; Ren, Z.; Rodriguez, R.M. A hesitant fuzzy linguistic TODIM method based on a score function. Int. J. Comput. Int. Syst. 2015, 8, 701–712. [Google Scholar] [CrossRef]
- Zhu, J.; Li, Y. Hesitant fuzzy linguistic aggregation operators based on the Hamacher t-norm and t-conorm. Symmetry 2018, 10, 189. [Google Scholar] [CrossRef]
- Feyzioğlu, O.; Büyüközkan, G. Evaluation of green suppliers considering decision criteria dependencies. In Multple Criteria Decision Making for Sustianable Energy and Transporation System; Springer: Berlin/Heidelberg, Germany, 2010; pp. 145–154. [Google Scholar]
- Nia, A.S.; Olfat, L.; Esaeili, A.; Rostamzadeh, R.; Antuchevičienė, J. Using fuzzy Choquet Integral operator for supplier selection with environmental considerations. J. Bus. Econ. Manag. 2016, 17, 503–526. [Google Scholar]
- Ng, T.F.; Pham, T.D.; Jia, X. Feature interaction in subspace clustering using the Choquet integral. Patern Recognit. 2012, 45, 2645–2660. [Google Scholar] [CrossRef]
- Kaczmarek, P.; Kiersztyn, A.; Pedrycz, W. Generalized Choquet integral for face recognition. Int. J. Fuzzy Syst. 2018, 20, 1047–1055. [Google Scholar] [CrossRef]
- Pacheco, A.G.C.; Krohling, R.A. Aggregation of neural classifiers using Choquet integral with respect to a fuzzy measure. Neurocomputing 2018, 292, 151–164. [Google Scholar] [CrossRef]
- Demirel, D.; Demirel, N.C.; Kahraman, C. Multi-criteria warehouse location selection using Choquet integral. Expert Syst. Appl. 2010, 37, 3943–3952. [Google Scholar] [CrossRef]
- Wen, X.; Yan, M.; Xian, J.; Yue, R.; Peng, A. Supplier selection in supplier chain management using Choquet integral-based linguistic operators under fuzzy heterogeneous environment. Fuzzy Optim. Decis. Mak. 2016, 15, 307–330. [Google Scholar] [CrossRef]
- Demirel, N.C.; Demirel, T.; Deveci, M.; Vardar, G. Location selection for underground natural gas storage using Choquet integral. J. Nat. Sci. Eng. 2017, 45, 368–379. [Google Scholar] [CrossRef]
- Büyüközkan, G.; Feyzioğlu, O.; Göçer, F. Selection of sustainable urban transportation alternatives using an integrated intuitionistic fuzzy Choquet integral approach. Transp. Res. D 2018, 58, 186–207. [Google Scholar] [CrossRef]
- Büyüközkan, G.; Da, R. Choquet integral based aggregation approach to software development risk assessment. Inf. Sci. 2010, 180, 441–451. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, R.; Li, G.; Li, Y. Failure risk assessment of subway vehicle door system considering expert preference correlation and psychological behavior. Comput. Integr. Manuf. Syst. 2018, 24, 689–702. (In Chinese) [Google Scholar]
- Handfield, R.; Waltonb, S.V.; Melnyk, S.A. Applying environmental criteria to supplier assessment: A study in the application of the Analytical Hierarchy Process. Eur. J. Oper. Res. 2002, 16, 70–87. [Google Scholar] [CrossRef]
- Yazdani, M.; Chatterjee, P.; Zavadskas, E.K.; Zolfani, S.H. Integrated QFD-MCDM framework for green supplier selection. J. Clean. Prod. 2017, 142, 3728–3740. [Google Scholar] [CrossRef]
- Banaeian, N.; Mobli, H.; Fahimnia, B.; Nielsen, I.E. Green supplier selection using fuzzy group decision making methods: A case study from the agri-food industry. Comput. Oper. Res. 2018, 89, 337–347. [Google Scholar] [CrossRef]
- Herrera, F.; Herrera-Videma, E.; Verdegay, J.L. A model of consensus in group decision making under linguistic assessment. Fuzzy Set Syst. 1996, 78, 73–87. [Google Scholar] [CrossRef]
- Xu, J.; Wu, Z. A discrete consensus support model for multiple attribute group decision making. Knowl. Based Syst. 2011, 24, 1196–1202. [Google Scholar] [CrossRef]
- Fu, C.; Yang, S. An evidential reasoning based consensus model for multiple attribute group decision analysis problems with interval-valued group consensus requirements. Eur. J. Oper. Res. 2012, 223, 167–176. [Google Scholar] [CrossRef]
- Dong, Y.; Zhang, H.; Herrera-Viedma, E. Integrating experts’ weights generated dynamically into the consensus reaching process and its applications in managing non-cooperative behaviors. Decis. Support Syst. 2016, 84, 1–15. [Google Scholar] [CrossRef]
- Wu, J.; Chiclana, F.; Fujita, H.; Herrea-Viedma, E. A visual interaction consensus model for social network group decision making with trust propagation. Knowl. Based Syst. 2017, 122, 39–50. [Google Scholar] [CrossRef]
- Gong, Z.; Zhang, N.; Li, K.W.; Martínez, L.; Zhao, W. Consensus decision models for preferential voting with abstentions. Comput. Ind. Eng. 2018, 115, 670–682. [Google Scholar] [CrossRef]
- Yager, R.R. Modeling prioritized multicriteria decision making. IEEE Trans. Syst. Man Cybern. B 2004, 34, 2396–2404. [Google Scholar] [CrossRef]
- Yu, X.; Xu, Z. Prioritized intuitionistic fuzzy aggregation operators. Inf. Fusion 2013, 14, 108–116. [Google Scholar] [CrossRef]
- Wei, G. Hesitant fuzzy prioritized operators and their application to multiple attribute decision making. Knowl. Based Syst. 2012, 31, 176–182. [Google Scholar] [CrossRef]
- Wu, X.H.; Wang, J.Q.; Peng, J.J.; Chen, X.H. Cross-Entropy and prioritized aggregation operator with simplified neutrosophic sets and their application in multi-criteria decision-making problems. Int. J. Fuzzy Syst. 2016, 18, 1104–1116. [Google Scholar] [CrossRef]
- Ji, P.; Wang, J.Q.; Zhang, H.Y. Frank prioritized Bonferroni mean operator with single-valued neutrosophic sets and its application in selecting third-party logistics providers. Neural Comput. Appl. 2016, 20, 1–15. [Google Scholar] [CrossRef]
- Yu, S.M.; Wang, J.; Wang, J.Q.; Li, L. A multi-criteria decision-making model for hotel selection with linguistic distribution assessments. Appl. Soft Comput. 2018, 67, 741–755. [Google Scholar] [CrossRef]
- Choquet, G. Theory of capacities. Ann. Inst. Fourier 1953, 5, 131–295. [Google Scholar] [CrossRef]
- Murofushi, T.; Sugeno, M. An interpretation of fuzzy measures and the Choquet integral as an integral with respect to a fuzzy measure. Fuzzy Set Syst. 1989, 29, 201–227. [Google Scholar] [CrossRef]
- Grabisch, M. Fuzzy integral in multicriteria decision making. Fuzzy Set Syst. 1995, 69, 279–298. [Google Scholar] [CrossRef]
- Tan, C.; Chen, X. Intuitionistic fuzzy Choquet integral operator for multi-criteria decision making. Expert Syst. Appl. 2010, 37, 149–157. [Google Scholar] [CrossRef]
- Yu, D.; Wu, Y.; Zhou, W. Multi-criteria decision making aased on Choquet integral under hesitant fuzzy environment. J. Comput. Inf. Syst. 2011, 7, 4506–4513. [Google Scholar]
- Peng, X.; Yang, Y. Pythagorean fuzzy Choquet integral based MABAC method for multiple attribute group decision making. Int. J. Intell. Syst. 2016, 31, 989–1020. [Google Scholar] [CrossRef]
- Yang, W.; Chen, Z. New aggregation operators based on the Choquet integral and 2-tuple linguistic information. Expert Syst. Appl. 2012, 39, 2662–2668. [Google Scholar] [CrossRef]
- Sun, H.X.; Yang, H.X.; Wu, J.Z.; Ouyang, Y. Interval neutrosophic numbers Choquet integral operator for multi-criteria decision making. J. Intell. Fuzzy Syst. 2015, 28, 2443–2455. [Google Scholar] [CrossRef]
- Wang, L.; Wang, Y.; Liu, X. Prioritized aggregation operators and correlated aggregation operators for hesitant 2-tuple linguistic variables. Symmetry 2018, 10, 39. [Google Scholar] [CrossRef]
- Wang, P.; Shen, J.; Zhan, B. A new method for two-sided matching decision making of PPP projects based on intuitionistic fuzzy choquet integral. J. Intell. Fuzzy Syst. 2016, 31, 2221–2230. [Google Scholar] [CrossRef]
- Wu, Y.; Geng, S.; Zhang, H.; Gao, M. Decision framework of solar thermal power plant site selection based on linguistic Choquet operator. Appl. Energy 2014, 136, 303–311. [Google Scholar] [CrossRef]
- Moradi, M.; Delavar, M.R.; Moshiri, B. A GIS-based multi-criteria analysis model for earthquake vulnerability assessment using Choquet integral and game theory. Nat. Hazards 2017, 87, 1–13. [Google Scholar] [CrossRef]
- Ferreira, J.J.M.; Jalali, M.S.; Ferreira, F.A.F. Enhancing the decision-making virtuous cycle of ethical banking practices using the Choquet integral. J. Bus. Res. 2018, 88, 492–497. [Google Scholar] [CrossRef]
- Wei, C.; Liao, H. A multigranularity linguistic group decision-making method based on hesitant 2-tuple sets. Int. J. Intell. Syst. 2016, 31, 612–634. [Google Scholar] [CrossRef]
- Sugeno, M. Theory of Fuzzy Integrals and Its Applications. Ph.D. Thesis, Tokyo Institute of Technology, Tokyo, Japan, 1974. [Google Scholar]
- Beg, I.; Rashid, T. TOPSIS for Hesitant Fuzzy Linguistic Term Sets. Int. J. Intell. Syst. 2013, 28, 1162–1171. [Google Scholar] [CrossRef]
- Liao, H.; Xu, Z.; Zeng, X.J. Hesitant fuzzy linguistic VIKOR method and its application in qualitative multiple criteria decision making. IEEE Trans. Fuzzy Syst. 2015, 23, 1343–1355. [Google Scholar] [CrossRef]
- Liao, H.; Xu, Z.; Zeng, X.J. Distance and similarity measures for hesitant fuzzy linguistic term sets and their application in multicriteri decision making. Inf. Sci. 2014, 271, 125–142. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).