Exploring the Decisive Risks of Green Development Projects by Adopting Social Network Analysis under Stakeholder Theory

Abstract

The Belt and Road initiatives related to green development projects are being increasingly considered globally. However, such projects face several risks resulting from stakeholder diversity. Although previous studies attempted to identify the risks caused by stakeholders, they found it difficult to provide a precise boundary to separate the risks attributable to a single stakeholder. This study adopts social network analysis to explore the decisive risks attributed to each stakeholder by considering a project’s stage. The results reveal that contractors take on the most risk and, thus, require real-time monitoring. Furthermore, all stakeholders need to collaborate with one another during the implementation stage of a project to mitigate the occurrence of risk. This study makes three contributions: it (1) provides a theoretical basis for enhancing the understanding of stakeholder theory; (2) offers specific guidelines for monitoring risks; and (3) enables stakeholders to understand their duties in controlling risks. Detailed discussions are provided in the remainder of the manuscript.

1. Introduction

Belt and Road initiatives are increasing in popularity throughout the world. Thus, developing countries want China to provide technology to improve their infrastructure, such as the Karot hydropower station project in Pakistan. Moreover, the Northeast of China was a famous old industrial area that generated lots of equipment for infrastructure development. However, infrastructure development requires more green development projects to achieve sustainability. Although these projects not only generate economic growth but also promote sustainable development [1], an appropriate approach to assess the risks and uncertainties associated with such projects is lacking. These risks and uncertainties are commonly caused by stakeholders, a concept that has been omitted in previous studies. Moreover, stakeholders might cause the decision maker to make an incorrect resource utilization decision related to green development.

Stakeholder theory was developed by Mitchell et al. [2] to manage and categorize stakeholders’ saliency in terms of the related absence of power, legitimacy, and persistence and to address how managers handle stakeholders’ claim priorities. Thus, studies have attempted to determine the relationships among stakeholders to prevent the occurrence of risks during project implementation. Yang et al. [3] integrated decisive risk management processes using a social network method to investigate the correlations among stakeholders. Yang and Zou [4] adopted a stakeholder risk analysis to assess the interactions among green development projects. Zhao et al. [5] applied a fuzzy synthetic analysis to develop a risk evaluation model to provide on-time, efficient, and reliable evaluations. Hwang et al. [6] conducted a comprehensive literature review and engaged in structured interviews to identify and evaluate the risk factors in green development projects and compare their critical risks with those in traditional projects and to propose mitigation measures that can address these risk factors. To clearly distinguish the risk factors among stakeholders, this study adopts five main groups, including owner, contractor, designer, supervisor and government, to facilitate further discussion.

Moreover, green development projects have increased rapidly over the past two decades. However, efforts to link risk assessments with the stakeholders in these projects remain limited. The current risk assessments of green development projects remain insufficient because they are not extensive enough to reflect real problems, and assessment tools require a combination of qualitative and quantitative data to allow engagement in deeper discussions [7]. In addition, the interactions among stakeholders are often neglected in previous studies [3]. Although several studies have attempted to develop a risk assessment framework for green development projects, methods to prevent occurrences of risk from stakeholders’ point of view are lacking [8]. In addition, the interactions among stakeholders are not yet well discussed [9].

Yang et al. [3] applied stakeholder-associated risk networks to compare the differences between Chinese and Australian green development projects. Yang et al. [10] utilized a non-dominated sorting genetic algorithm to explore a multi-objective optimization design for green development. To assess the risks regarding stakeholders, the algorithm relies on a multidimensional approach [11]. Previous studies often used quantitative data to assess a project’s performance and the potential risks; however, they failed to consider qualitative data that reflect the real situation. Accordingly, this study attempts to fill this gap by applying SNA to explore the critical risks among stakeholders.

To prevent such an occurrence, in this study, stakeholder theory in association with social network analysis (SNA) is proposed as a strategy to address these issues and mitigate risks and uncertainties. SNA is a conceptual network representation that enables stakeholder relationships to be arranged using nodes and links (edges in graph theory) based on specific types of social interactions [12]. Moreover, risks exist within the interrelations in reality. To consider these interrelations, SNA provides an efficient way to assess the complexity of a green development project [4]. Most of the current risk assessment approaches are based on the identification of risk factors. However, such assessments do not consider the interrelations among stakeholders during a project and lack intuitive and quantitative methods to analyze the correlations among stakeholders [13].

Therefore, the objective of this study is to explore the critical risks of green development projects by considering stakeholders’ interrelations through the adoption of SNA. This study makes three contributions. First, the findings provide a theoretical basis for enhancing the understanding of stakeholder theory in project-oriented cases. Second, the proposed method distills problems into a focal point, which offers a precise guideline for Belt and Road firms with respect to green development. Third, the precise guideline allows firms to improve their performance with limited resources. The remainder of this study is structured as follows: Section 2 provides a detailed discussion of the method and the proposed analytical procedures. The empirical results are discussed in Section 3. Theoretical and managerial implications are presented in Section 4. The final section provides the conclusions, research limitations, and directions for future studies.

2. Materials and Method

This section introduces the questionnaire formulation, data integration using SNA, and proposed analytical procedures.

2.1. Questionnaire

Five stakeholders were selected to investigate the risks related to the proposed measures: the owner, contractor, designer, supervisor, and government. Furthermore, there are fifty-four risks arranged under these five stakeholders (as shown in Table 1). To provide an extensive and comparable scale for the respondents, the questionnaire adopts a seven-point assessment scale. A lower number represents a weaker influence on a green development project’s risk. The assessments rely on the professional knowledge and work experience of the respondents in a related industry.

Table 1. Proposed measures.

Stakeholders	Risks
Owner	C1	Issues of project funding
	C2	Owner’s requirements
	C3	Owner’s green development investment was underestimated
	C4	Unreasonable schedule requirements
	C5	Inaccurate location of the project
	C6	Owner is inefficient
	C7	Owner makes unreasonable interventions during the process
	C8	Conflicts with owner’s requirements
	C9	Insufficient consideration across project requirements
	C10	Insufficient communication to coordinate participants in the project
	C11	Operations are unable to meet the regulations and achieve green certification
	C12	Evaluation results are unable to reach the level of green certification
	C13	Vague responsibilities
	C14	Certification risk causes incomplete declaration of materials
	C15	Project contract defects and changes result in claims
	C16	Lack of property management experience causes operational damage
	C17	Project demand and market share are overforecast
	C18	Project is unstable and lacks scientific maintenance
	C19	Lack of green development insurance products
Contractor	C20	Poor management ability
	C21	Failing to reach the green certification goal and causing claims
	C22	Underestimating the cost of the project and increasing the quoted price
	C23	Lack of experience managing technical personnel
	C24	Insufficient experience adopting new materials, technologies, and equipment
	C25	Insufficient knowledge of green development projects
	C26	Insufficient understanding of requirements, causing default
	C27	Poor feasibility of the construction method
	C28	Unstable performance of new materials and equipment
	C29	Turnover rate is too high
	C30	Unclear responsibilities among the subcontractors
	C31	Insufficient documentation of green materials
	C32	Lack of coordination with the designer
	C33	Increased construction difficulty generates security risk
	C34	Project requirements cause overdue risk
	C35	Scarce green materials drive up green product prices
	C36	Additional requirements for a trial operation
	C37	Lack of insurance for staff and equipment
	C38	Shortage of insurance for staff and equipment
	C39	Warranty risk
	C40	Lack of project insurance
Designer	C41	Design flaws
	C42	Design changes
	C43	Insufficient design integration experience for the project
	C44	Eco-design innovation risk
	C45	Insufficient innovation in construction and design
	C46	Inaccurate cost estimation
	C47	Insufficient on-site investigation results in a design that does not match real conditions
	C48	Lack of lifecycle assessment in the design
Supervisor	C49	Lack of experience in green development project supervision
	C50	Inadequate understanding of green development projects
	C51	Insufficient data collection and monitoring
	C52	Nonstandard supervision behavior
Government	C53	Overly expensive examination and approval procedures
	C54	Government intervenes unreasonably
	C55	Incomplete laws and regulations
	C56	Lack of relevant special clause to encourage a green development project
	C57	Policy changes

2.2. Data Integration with SNA

2.2.1. Network Density

Network density is defined as the ratio of the actual number of connections to the maximum number of theoretical correlations and is calculated as follows:

When the network is an indirect network:

$$DE=2p/q\left(q-1\right)$$

(1)

When the network is a directed network:

$$DE=p/q\left(q-1\right)$$

(2)

where $p$ indicates the actual correlation numbers, and $q$ represents the actors or vertexes. When the network density is greater, the influence of the network on the attitude and behavior of the actors is greater. A network that is closely linked not only provides social resources but also significantly constrains the development of the actors [14]. Higher density has greater effects on behaviors. In addition, assessing the degree of density helps identify regular internal patterns and decisive risks.

2.2.2. Degree Distribution

A vertex’s degree represents the number of edges that are connected to vertex $i$. The average of the degrees in a network can be written as $⟨DE⟩$. In a directed network, the degrees of vertexes can be categorized into out-degree and in-degree vertexes. The out-degree of vertex $i$ is the quantity of arcs that start from vertex $i$ that point to other vertexes. The in-degree of vertex $i$ is the number of arcs that start from other vertexes and end at vertex $i$. The point degree is defined as the number of lines that the vertexes contain and is represented as follows:

$$D{E}_i={\sum }_j{l}_{ij}+{\sum }_j{l}_{ji},$$

(3)

The average degree can be defined as follows:

$$⟨DE⟩=\frac{1}{q}{\displaystyle \sum }_{i}D{E}_{ij}=\frac{1}{q}{\displaystyle \sum }_{ij}{l}_{ij}$$

(4)

The maximum degree can be defined as follows:

$$D{E}_{\max }=\max D{E}_i$$

(5)

A degree distribution describes the number of points within the network. For a random network, the degree distribution refers to the probability distribution of the vertex degree in the graph. If using the frequency instead of the probability, the degree distribution can be classified as the in-degree and the out-degree frequency distribution. These distributions reveal the correlations among the risks, which provide the basis to explore the decisive risks.

2.2.3. Centrality Analysis of Network—Centrality and Centralization

Centrality refers to the measure of the degree to which each vertex is at the center of the network in a quantitative manner. Centrality mainly shows the degree centrality and the extent of the centralization. Centrality theory states that the center point has the maximum degree of vertexes in the network. Therefore, the center degree can be computed as follows:

$$C_{DE}\left(x\right)=DE\left(x\right)/\left(q-1\right)$$

(6)

where DE(x) denotes the degree of $x$, $q$ denotes the total number of nodes in the network, and $q-1$ denotes the maximum number of possible neighbors.

After determining the degree centrality of the network, each vertex is arrayed to determine the influence of the network. The extent of the center $C_{DE}^g$ can be calculated as follows:

$$C_{DE}^g=\frac{{{\displaystyle \sum }}_{XϵN}(C_{DE}^{*}-C_{DE}\left(x\right))}{\left(q-1\right)\max \left(C_{DE}^{*}-C_{DE}\left(x\right)\right)}$$

(7)

where $q$ represents the network to which the vertexes belong, and $C_{DE}^{*}=\max C_{DE}\left(x\right)$ represents the center value of the node that has largest degree of centrality. When $C_{DE}^g$ is smaller, the extent of network centralization will be weaker, and the difference in the vertexes in the network will be smaller. Conversely, more decentralization has more network centralization [14]. This approach can be used to determine the central point that affects the target network and offers a basis to purify the decisive risks.

2.2.4. Quantitative Analysis of Network Cohesion—K-Core

The majority of studies of complex networks only focus on macroscopic statistical analysis. However, it is difficult to ensure that the sample size is sufficient due to the contingency of the data and time limitations. Topological description theory combines macro statistical analysis with structural description theory to explain some phenomena more scientifically. K-core analysis is an efficient graphical method for analyzing a phenomenon as, in a sense, a type of node. Generally, the calculation of the vertex degree can only reveal the local connections of a single vertex, but it cannot explain the degree of condensation and dispersion of all the vertexes with higher degrees along the entire network. The K-core presents the maximum set of subnetworks that are not less than the value of K [14]. Based on the value of K, the network can be simplified into a cohesive group to reflect the internal standard.

2.2.5. Network Dependency Analysis—Island

An island is a subnetwork defined by multiple values or lines of attachment. An island possesses the largest subnetwork if it meets the following condition: the various vertexes in the subnetwork are directly or indirectly connected, and the internal connection value is greater than the outer vertex of the subnetwork. Once the top line adhesive value on the vertex is taken as the altitude of the vertex, the island is similar to a local peak network. Following this analogy, the similarities and differences between the islands and the surrounding structures can be shown, further reflecting the structure and laws of the network [14]. Moreover, an island can present the subordination of each risk to screen out the critical risks. Thus, the decisive risks possess the features of higher degrees of density (obtained from Section 2.2.2) and centrality (generated from Section 2.2.3) and an island (gathered from Section 2.2.4 and Section 2.2.5).

2.3. Proposed Analytical Procedures

• Identify the boundary of the network; this step requires analyzing the reliability of the questionnaire through a significance test and a correlation analysis. Next, the risk correlations in the green development project based on the proposed measures are identified.
• From the SNA, stakeholders are arranged by risk correlation in the green development project, which then provides a visualization of the risk correlations.
• The correlations among the risks can be expressed by the lines between the points in the social network, which are presented as edges. A direct edge is called an arc. Therefore, the risk factors and the risk correlations can be described by a social network diagram. Based on the risk correlations, Pajek software is used to draw a non-weighted directed diagram with 54 vertexes.
• Using SPSS22 statistical software and Pajek software, the network parameters of the risk correlations are calculated.
• K-core is a quantitative analysis of the network’s cohesion and seeks the risk correlation. The island represents a network dependency analysis of the project’s risk network. The controllable decisive risks that affect the global risk correlation are then identified. From the perspective of the correlation among the risks and based on the relevant parameters of the calculation, the key controllable risks in the green development project are extracted, and risk management strategies are proposed.

3. Empirical Results

This section provides the background of the case and the analytical results to support deeper discussion.

3.1. Case Background

Northeast China plays an important role in China’s military and political positioning (as shown in Figure 1). This area connects three countries, Russia, Mongolia and North Korea, with Bi-Hai Bay. Therein, crude oil is delivered from Daqing, China to Tayshet and Nakhcidka, Russia, and another oil pipeline is under construction to Irkutsk, Russia. In addition, the Chinese government will increase the number of entry points from two to four to promote business activities in the area. The present value of Northeast China is clear given the nuclear issue with North Korea.

Figure 1. Northeast region of China.

Green projects in China are being aggressively pursued. Preliminary achievements have been made in the fields of policy making, evaluation, and technology, which have led to several demonstration projects in various areas. However, the green projects are still in their initial stages, and the majority of small green development projects are mainly concentrated in coastal and economically developed areas. Many difficulties and obstacles exist to promoting green development in Northeast China (shown in Figure 1). Thus, this study adopts this area as its main case for exploring the decisive risks when encouraging green development by considering that stakeholders guide green development firms in making accurate decisions to mitigate risks and uncertainties.

3.2. Analytical Results

1.

The period under investigation is between 1 July 2016, and 26 January 2017, and the invited respondents include academic and technical personnel from Jilin, Heilongjiang, and Liaoning provinces, as indicated in Figure 1. In the pilot study, 94 respondents were invited to join the assessment, and 91 responded. Of these 91, only 85 questionnaires were valid, for a validated return rate of 90%. Based on the results of the pilot study, non-significant items were deleted from the initial questionnaire to enhance its reliability and validity. In the following stage, 400 revised questionnaires were distributed, and 312 were returned, with 285 valid respondents (71.25% validated return rate). The questionnaire adopted a random distribution but screened out the area, concentrating only on respondents from Jilin, Heilongjiang, and Liaoning provinces, by using IP selection.

2.

Moreover, owner, contractor, designer, supervisor and government are considered the main groups of green development projects. Therefore, this study distributed the questionnaire based on these five groups as categorized in previous studies. Table 2 shows the detailed information of the respondents. Then, the seven sub-items of the working unit are merged into the five main groups of owner, contractor, designer, supervisor and government to focus the discussion.

Table 2. Respondent Information.

Items		Frequencies	Percentage
Age	25 and under	39	12.26%
	26–35 years old	134	42.14%
	36–45 years old	66	20.75%
	46–55 years old	76	23.9%
	56 years old and above	3	0.94%
Working Experience	5 years and below	34	10.69%
	6–10 years	80	25.16%
	11–15 years	139	47.31%
	16–20 years	22	6.92%
	more than 20 years	43	13.52%
Working Unit	University	61	19.18%
	Government Department	31	9.75%
	Tender office	6	1.89%
	Construction unit	30	9.43%
	Design Unit	49	15.41%
	Construction unit	41	12.89%
	Consultant (including supervision)	5	1.57%
	Other	95	29.87%
Number of Green Development Projects	0–1	31	9.75%
	2–5	111	34.91%
	6–10	155	48.74%
	11–20	13	4.09%
	21 or more	8	2.52%

3.

Subsequently, Statistical Product and Service Solutions 22 was employed to calculate the overall Cronbach’s alpha coefficient of 0.989, which is greater than 0.9. This result shows that the entire questionnaire possesses good reliability. The Cronbach’s alpha coefficients for each subsection are shown in Table 3.

Table 3. Cronbach’s alpha coefficients for all stakeholders.

Stakeholders	Cronbach’s Alpha
Overall Scale	0.989
The risk consideration of the owner	0.969
The risk consideration of the contractor	0.977
The risk consideration of the designer	0.957
The risk consideration of the supervisor	0.921
The risk consideration of the government	0.932

4.

Spearman correlation coefficients present the correlations among the 57 risks related to green development projects (as shown in Appendix A). All values reach a significance level of 0.01, except for the items with values of 1.000. This correlation table establishes six levels to classify the relationships: $\left|r_{ij}\right|=0$ means that two factors have no relationship; $0.3\le \left|r_{ij}\right|<0.5$ represents a lower relationship; $0.5\le \left|r_{ij}\right|<0.8$ represents a medium relationship; $0.8\le \left|r_{ij}\right|<1$ represents a higher relationship; and $\left|r_{ij}\right|=1$ indicates a complete relationship.

5.

The lines of the vertexes in the social network indicate the correlations among the risk factors and are called edges. The transformation of the risk correlations can indicate the weight of the edges. Figure 2 shows the nondirected weighted diagram with 57 vertexes and 1462 edges by applying Pajek software.

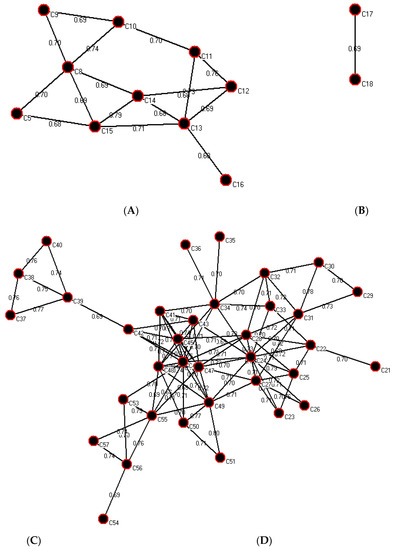Figure 2. Island map of the 43-core risk correlation network.

6.

Adopting Equation (1) to compute the density of the network, $DE=\frac{2P}{q\left(q-1\right)}=0.916$. Subsequently, the average degree of the risk correlation of the network is obtained using Equations (3)–(5); the results show that $⟨DE⟩=49.193$ and $k_{max}=55$. Furthermore, by employing Pajek software, the degree and frequency for each node in the risk network can be calculated, as shown in Table 4.

Table 4. Frequency distribution of risks.

Degree	Frequency	Frequency (%)	Accumulating Frequency	Accumulating Frequency (%)	Risks
14	1	1.7544	1	1.7544	C2
19	1	1.7544	2	3.5088	C1
36	2	3.5088	4	7.0175	C6, C7
38	1	1.7544	5	8.7719	C3
39	1	1.7544	6	10.5263	C52
43	1	1.7544	7	12.2807	C44
45	2	3.5088	9	15.7895	C50, C56
46	1	1.7544	10	17.5439	C51
48	5	8.7719	15	26.3158	C5, C8, C12, C19, C57
49	3	5.2632	18	31.5789	C11, C53, C54
50	4	7.0175	22	38.5965	C14, C29, C40, C55
51	4	7.0175	26	45.614	C35, C37, C47, C49
52	11	19.2982	37	64.9123	C4, C10, C13, C16, C17, C18, C30, C36, C38, C39, C43
53	4	7.0175	41	71.9298	C9, C20, C23, C26
54	12	21.0526	53	92.9825	C15, C21, C24, C25, C27, C31, C32, C34, C42, C45, C46, C48
55	4	7.0175	57	100.0000	C22, C28, C33, C41
Subtotal	57	100.0000

7.

Equations (6) and (7) are utilized to generate the extent of the centralization, as $C_{DE}^g=\frac{{{\displaystyle \sum }}_{XϵN}(C_{DE}^{*}-C_{DE}\left(x\right))}{\left(q-1\right)\max \left(C_{DE}^{*}-C_{DE}\left(x\right)\right)}=\frac{5.53}{\left(56\times 0.71\right)}\approx 0.139$. Then, adopting K-core enables an exploration of the undirected network risk, which extracts a 43-core network with 50 vertexes. This 43-core network can be isolated into four islands, as shown in Table 5. The four islands are presented in Figure 2 to clarify the correlations among the networks. Then, the networks can be used to identify the controllable key risks with higher degree values, higher degrees of centrality, and island values within the control process of a single stakeholder, as shown in Figure 3.

Table 5. Island information for the 43-core risk network.

Island Label	Island Value (Altitude)	Number of Vertexes	Vertex Label
A	0.675	10	C5, C8, C9, C10, C11, C12, C13, C14, C15, C16
B	0.689	2	C17, C18
C	0.758	4	C37, C38, C39, C40
D	0.698	30	C21, C22, C23, C24, C25, C26, C27, C28, C29, C30, C31, C32, C33, C34, C35, C36, C41, C42, C43, C44, C45, C46, C47, C48, C49, C50, C51, C53, C55, C56, C57

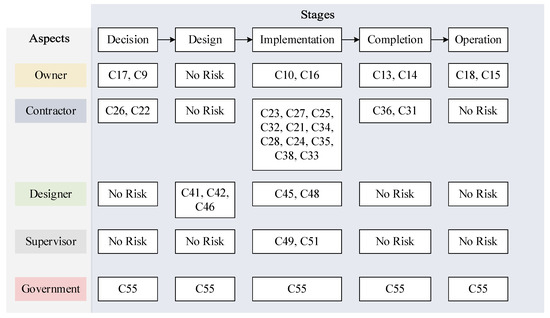Figure 3. Decisive risks of stakeholders in different stages.

4. Implications

Previous studies failed to precisely clarify the risks of green development projects under single stakeholders at different stages. However, the analytical results of this study show that each stakeholder has its own risk control point in the different project stages. In the decision stage, the owner, contractor, and government undertake the risk. The owner must comprehensively consider the project requirements (C9) and prevent overforecasting the project’s demand and market share (C17). Potential risks exist for the contractor in underestimating project costs, increasing the quoted price (C22), and having an insufficient understanding of the project requirements, which can cause default (C26). Then, the government has the responsibility of creating extensive laws and regulations (C55) to guarantee that green development projects have legal protection.

In the design stage, only the designer and the government have risk control points. During this stage, risks might occur through design flaws (C41), design changes (C42), and inaccurate estimations of costs (C46). The government retains the same risk as in the decision stage. Moreover, all stakeholders suffer from potential risks in the implementation stage. Insufficient communication and coordination among the participants in the project (C10) and a lack of property management experience can cause operational damage (C16), which are the potential risks of the owner. Failing to achieve the green certification goal, thereby causing claims (C21), a lack of experience managing technical personnel (C23), insufficient experience adopting new materials, technologies, and equipment (C24), insufficient knowledge of green development projects (C25), poor feasibility of the construction method (C27), unstable performance of new materials and equipment (C28), lack of coordination with the designer (C32), increased construction difficulty that generates security risk (C33), project requirements that cause overdue risks (C34), scarcity of green materials that greatly increases the price of green products (C35), and a shortage of insurance for staff and equipment (C38) are the potential risks for the contractor. The designer must be concerned about insufficient innovation in construction and design (C45) and lack of a life cycle assessment in the design (C48). The supervisor risks having a lack of experience in green development project supervision (C49) and insufficient data collection and monitoring (C51). The government has the same risk as in the decision stage. As presented, the contractor has the most responsibility to prevent risks from occurring because there are eleven control points that need to be considered.

In the completion stage, the designer and the supervisor have no potential risks to control. Nevertheless, the owner’s risks are vague responsibilities and certification risks that cause incomplete declaration of the materials. The contractor’s risks include insufficient documentation of green materials (C31) and additional requirements for the trial operation (C36). The government has the same risks as those stated in the decision stage. Finally, the owner and the government are the only two risk undertakers in the operations stage. Project contract defects and changes that result in claims (C15) and the project experiencing instability and a lack of scientific maintenance (C18) are the risks for the owner. The government has the same risk as in the decision stage.

In considering all the stages when discussing the pressures of risk absorption, the contractor faces the most pressure, with fifteen risks during an entire green development project. For this reason, the contractor is the key stakeholder who must engage in on-site monitoring of the project. In addition, the contractor must address the needs of the staff for the project, including insurance, safety, working conditions, and compensation, among others. The stakeholder who faces the second most pressure is the owner, who must address at least two risks in all stages except for the design stage. The results also reveal that if the government does not develop complete laws and regulations to ensure that the project runs smoothly, the entire project will suffer from risks regardless of the stage. Thus, the government is an important stakeholder in mitigating the occurrence of risk in a green development project.

Moreover, there are several policy insights are recommended for preventing the risks occurrence of green development project as shown in the following Table 6.

Table 6. The Policy for Preventing the Risks among Stakeholders.

Stakeholders	Stages	Policy for Preventing the Risks
Owner	Decision	Owner needs to make transparent communications with designers, supervisors and contractors for ensuring the project can process fluently.
	Implementation	Owner musts concentrate on the management of contract divides the duties in guaranteeing the implementation following the plans.
	Completion	Promoting the knowledge of certifications for green development project avoids the dispute over completion.
	Operation	Owner shall enhance the operation maintenance for sticking with the project goals.
Contractor	Decision	Contractor shall fully understand each complex procedure of project and give the trainings to technical persons before project started.
	Implementation	Contractor needs to participate the government training courses aggressively for accumulating the knowledge and experiences in terms of green development project. In addition, it requires having well communications and coordination with designer.
	Completion	Contractor must make the cost following with the pilot investigations and forecasting effectively and ensures the quotations with reasonable price.
Designer	Decision	Designer shall prevent the changes of original design. Thus, it requires making double check with owner, contractor and supervisor to eliminate the change suddenly. If the designer takes the innovation design into the project, it requires making feasibility study and demonstration adequately.
	Implementation	During the implementation stage, designer needs to participate the entire project period for guaranteeing the construction fulfil the concept of design.
Supervisor	Implementation	While the implementation stage, supervisor is required patriating the training course for reinforcing the knowledge of green development project. Subsequently, all the reported documentations are required finishing by the supervisor.
Government	All the stages	Government needs to accelerate the related policy establishment in terms of green development project, standardize the local criteria and clarify the rights and duties.

5. Conclusions

Belt and Road initiatives in terms of green development projects are attracting increased attention throughout the world. An increasing number of countries want to participate in these initiatives and obtain the co-benefits of sustainability. However, several risks remain for stakeholders when launching such projects. Although previous studies adopted stakeholder theory to discuss project-oriented cases, addressing the risks undertaken from a single stakeholder point of view is insufficient. Thus, this study proposes the employment of SNA to explore the decisive risks for each stakeholder. SNA enables the interrelations among the risks to be considered by structuring a correlation network and providing a visual analysis that then uses K-core to screen out unnecessary risks. This process can enable stakeholders to focus on their particular risk control points to guarantee project success.

The contribution of this study can be divided into three parts: (1) providing evidence to support the theoretical basis for enhancing the understanding of the application of theory; (2) offering specific guidelines for green development firms to monitor their projects and prevent the occurrence of risk; and (3) showing that each stakeholder can fulfill its duty by controlling its risks; (4) recommending the related policies for stakeholders in different stage. Furthermore, the project manager can establish a buffer zone based on the results, which provide clear boundaries for making claims once a risk is realized. This study uses stakeholder theory to address the risks involved in green development projects and offers an effective and reliable measure to simplify a complex problem.

The analytical results reveal that stakeholders need to check the control points for potential risks in different project stages. The contractor plays a critical role in mitigating the risks in all stages, given that fifteen risks are present during the decision, implementation, completion, and operation stages. The owner has the second most risks, with eight. Although the government has only one risk throughout an entire project, establishing comprehensive laws and regulations is fundamental to avoiding risk. The supervisor is a low-risk undertaker in a green development project. Furthermore, the key part of a green development project is the implementation stage, which requires that all stakeholders collaborate to mitigate the risk. Subsequently, the operation stage of a green development project has a lower level of risk that the owner and government must consider.

There are several limitations to this study. Although this study attempts to consider the possible risks involved in a green development project, it still not sufficiently comprehensive to reflect actual situations. Thus, future studies should include as many additional potential risks as possible. In addition, a questionnaire is employed in this study, but it lacks an assessment of quantitative data. Integrating qualitative and quantitative data to assess risks should occur in a future study. The sample selected was only from Northeast China, making generalization of the results of this study difficult. To overcome this weakness, all regions in China should be considered in future studies. The proposed analytical procedure can be applied to different cases to provide comparisons among different countries. Finally, future studies could propose hybrid methods to improve the current results based on SNA.