Integrating Elliptic Curve Cryptography with the Modbus TCP SCADA Communication Protocol

Abstract

SCADA systems monitor critical industrial, energy and other physical infrastructures in order to detect malfunctions, issue alerts and, in many cases, propose or even take remedial actions. However, due to their attachment to the Internet, SCADA systems are, today, vulnerable to attacks such as, among several others, interception of data traffic, malicious modifications of settings and control operations data, malicious modification of measurements and infrastructure data and Denial-of-Service attacks. Our research focuses on strengthening SCADA systems with cryptographic methods and protection mechanisms with emphasis on data and messaging encryption and device identification and authentication. The limited availability of computing power and memory in sensors and embedded devices deployed in SCADA systems make render cryptographic methods with higher resource requirements, such as the use of conventional public key cryptography such as RSA, unsuitable. We, thus, propose Elliptic Curve Cryptography as an alternative cryptographic mechanism, where smaller key sizes are required, with lower resource requirements for cryptographic operations. Accordingly, our approach integrates Modbus, a commonly used SCADA communication protocol, with Elliptic Curve Cryptography. We have, also, developed an experimental set-up in order to demonstrate the performance of our approach and draw conclusions regarding its effectiveness in real SCADA installations.

1. Introduction

Supervisory Control and Data Acquisition or SCADA systems are industrial, automated, supervision infrastructures based on information technologies which are embedded in industrial installations as well as production lines to ascertain continuous correct operation, enforce quality control and raise alarms in case of malfunctions or efforts of malicious interference.

In general, interconnected SCADA system components are installed in critical parts of industrial infrastructures, such as electricity grids, power generation stations, and nuclear power reactors, in order to detect malfunctions and raise alerts for remedial actions. Most importantly, for increased versatility and real time alerting capabilities as well as remote control purposes, during the last decades SCADA systems are installed so as to be connected to the Internet and the Internet of Things (IoT). This versatility, however, comes at the cost of exposing SCADA systems and supervised infrastructures to all the cybersecurity threats that beset the Internet. Thus, today, SCADA systems are vulnerable to attacks such as, among several others, interception of data traffic, malicious modifications of settings and control operations data, malicious modification of measurements and infrastructure data and Denial-of-Service attacks.

Numerous SCADA system failures have been recorded because of a targeted attack or a non-targeted (i.e., incidental) malware infection [1]. Except for accidental SCADA system infections by viruses their target was simple computers, there are also cases of targeted attacks with software made specifically for SCADA. Such attacks are more recent and are mainly aimed at impacting the physical world while, in parallel, they may also target industrial espionage. The first such attack is in 2009, targeting several companies (Shell, BP, Exxon). The virus that attacks these systems is Night Dragon, which belongs to the category Remote Access Trojans [2]. His purpose was data theft and espionage through e-mail theft. Then we have one of the most notorious targeted SCADA attacks which attracted the attention of the security and safety research communities and organizations and sparked the alert in SCADA system security. This attack was launched in 2010 by a virus named Stuxnet and was aimed at an enriched uranium nuclear facility in Iran. The purpose of Stuxnet was to intercept and modify data that was read from or written to PLCs (Programmable Logic Controller- the heart of SCADA systems). In addition, Stuxnet aimed at impairing the nuclear facility and cause devastating damage and, even, human life losses. The result was the destruction of, almost, 1/5 of the nuclear centrifuges.

After this incident, the interest in securing SCADA systems, and not only the supervised (by SCADA) physical establishment, increased considerably. In the years that followed, more malware nodules resembling Stuxnet appeared (e.g., Flame and Duqu) [3], some of which even using portions of Stuxnet’s code. After the incidents discussed above (and several others) as well as the high cyberattack costs for the targeted organization, the SCADA research community is engaged in strengthening SCADA systems with cryptographic methods and cryptographic protection mechanisms with emphasis on data and messaging encrypted protection and device identification and authentication. However, the limited computation capabilities of many SCADA sensors and embedded devices as well as the Internet/IoT connectivity, SCADA systems are vulnerable to numerous attacks [4].

Modbus is a data communications protocol for use with its PLCs (Programmable Logic Controllers) and has become as a standard communication protocol. It is commonly used and widespread of connecting industrial devices, such as IoTs and applications. It supports communication among multiple devices connected to a network. Modbus places few restrictions on the format of the data to be transmitted and the data use character via communication lines. However, it does not itself support security of both the data and the commands it manages from interception, and apparently does not support cryptography [5].

In order to address the weaknesses discussed above, our work provides the following contributions:

• The deployment of the Modbus protocol in SCADA, although is particularly common, has not been studied extensively from the point of view of data and application security as well as IoT/sensor device identification and authentication. In particular, the customary Modbus protocol does not provide end-to-end encryption facilities. Such facilities are provided by our libraries as we demonstrate in what follows.
• Our approach targets one of the most critical aspects of today’s physical infrastructures which are interconnected on the Internet for remote surveillance based on SCADA/Modbus-like systems: Cyber Physical Security (CPS). Our work enables secure information exchange based on confidentiality, integrity and authentication of involved information exchanges in installations such as smart grids, energy transmission lines, natural gas processing stations, nuclear plants etc. Our approach targets, especially, the attached IoT/sensor devices which are, frequently, the weakest links in a SCADA/Modbus deployment and, thus, the most attractive targets of cybercriminals.
• The IoT devices that area usually deployed in SCADA/Modbus installations are, usually, inexpensive and open hardware in order to facilitate massive deployment and easy application development. However, this leads to some inherent weaknesses with respect to computational power, which may limit their ability to handle conventional crypto algorithms due to the large parameter sizes they require. Elliptic curves are particularly useful in this respect since they require much smaller key sizes than conventional cryptosystems for achieving similar security levels. In other words, they require less memory and computation power from IoT/sensor devices than conventional cryptosystems do. The major reason behind the increased security of Elliptic Curve based cryptosystems, in comparison with conventional ones, is that the discrete logarithm problem for elliptic curves appears to have exponential expected time complexity, in contrast to general groups (e.g., multiplicative) which have a discrete logarithm problem of subexponential time complexity. This characteristic of elliptic curves leads to cryptosystems which possess similar security levels with conventional ones but with much smaller key sizes, as we explain in Section 3.
• Our approach creates a new set of Modbus libraries which can replace, readily, all Modbus installation existing today since they do not interfere with the client/server application level (see Section 4 as well as the associated discussion therein). Moreover, our approach extends the Modbus protocols to IIoT (Industrial IoT) devices in general. We demonstrate this extension with an experimental setup on an IIoT device which can be incorporated in any SCADA/Modbus installation (see Section 5).

In summary, our contribution is a fully compatible, “plug-in”, Modbus extension fully compatible with existing installations which, also, incorporates IIoT/sensor device security as part of the Modbus extension, owning to the flexibility and small computational requirements of Elliptic Curve Cryptography. Our work also provides a fully working proof of concept of the extended library in an experimental set-up incorporating both server and IIoT devices.

In this paper we describe a fully developed secure SCADA environment based on extensive cryptographic extension of the Modbus libraries. The parts of the mechanism are key generation and distribution, message encryption and decryption. Our implementation is based on two C language libraries, which were extensively modified so as to incorporate security mechanisms, the libmodbus [6] and the ECCLIB [7] libraries.

The Libmodbus library provides an implementation of the Modbus/TCP protocol in C and the ECCLIB provides the necessary functionality to implement cryptographic protocols based on Elliptic Curve Cryptography of ECCLIB. The ECCLIB is a library in C++ that obtain algebraic operations and a rich variety of cryptographic protocols for Elliptic Curve Cryptography in fields of the form $F_p$, where $p$ is an odd prime based on the Complex Multiplication method.

In our work, Libmodbus and ECCLIB were modified and combined in such way in order to enhance Modbus/TCP protocol leading to a modified version of it, focusing on the security of the data exchanged among the devices and the supervisory servers. The mechanisms we implemented include key generation, key exchange/sharing, message authentication, data integrity check, and encryption/decryption of data.

The key generation and key exchange protocols we implemented using Elliptic Curve Cryptography functionality. The encryption/decryption keys created by the SCADA devices are stored in their local memory and are consider “alive” only for the duration of the current communication session. These keys are used in encryption/decryption of the exchanged messages, in establishing the integrity of the messages and in the authentication process of the involved entities.

The modified library was compiled for the Android operating system, to implement the server side in Android. The client side can be installed on any computer. The communication between the entities of client and server implements an example of the successful establishment of sessions using Elliptic Curve Cryptography, based on secure sessions of Modbus wireless communication between a portable device acting as a supervisor station and a monitoring and control workstation. Our first performance measurements are, also, very promising and show the feasibility of embedding Elliptic Curve Cryptography into SCADA systems, giving a significant approach to an area that had not been studied.

Our approach has two goals. The first was to embed a key generation and exchange mechanism in Modbus, while keeping the basic Modbus functionality unchanged. The second was to assess the result of the new Modbus considering its performance in comparison with the original Modbus implementation. In other words, our approach aims at exploring the feasibility of integrating encryption functionality in industrial SCADA protocols as well as the interoperability of this integration with existing SCADA installations based on Modbus.

2. Related Work

There is a significant number of research papers and standards focusing on SCADA security, vulnerabilities, and ways to protect the infrastructures that deploy SCADA. When it comes to protecting SCADA systems themselves from attacks, there are many studies that suggest the use of cryptographic techniques.

There are several standards published, both, by specialized US agencies, such as NSA and NIST, as well as private organizations that propose several SCADA security methods, including cryptography. Many of those studies are, mostly, focused on the integration of authentication and cryptographic protocols, as a means of protecting industrial systems’ Internet traffic [8]. In [9], the authors deploy and assess both symmetric and asymmetric cryptography as a means to protect Modbus and IEC 6087 traffic.

In a previous paper, [10], the authors deploy the already existing mechanisms for integrity in SCADA systems to develop a new, low latency, cryptographic protocol. They also make use of block ciphers for the encryption of the SCADA Internet traffic. The authors of [11] add an additional field to the standard Modbus packet and use both RSA (Rivest-Shamir-Adleman) public-key cryptosystem and AES (Advanced Encryption Standard) to generate keys and encrypt Internet traffic. Another work, discussed in [12], proposed the possible use of Elliptic Curves for Lowpan sensor networks, and particularly their integration into the TLS (Transport Layer Security) protocol. Our concrete approach for this functionality is to use the Elliptic Curve based Diffie Hellman key exchange protocol to generate and exchange shared communication keys, thus providing an alternative to the RSA and AES cryptosystems used in the previous papers.

Extensive research has also been conducted for the identification of the vulnerabilities and the specialized attack vectors of SCADA systems. An attack taxonomy given in [13] categorized the SCADA attacks according to the type (Serial/TCP) of Modbus. In [14], a study was published on the security concerns about IP-based SCADA networks. In [15] a study can be found on the vulnerabilities of SCADA systems and potential security strengthening approaches. The authors also carried out experiments on SCADA/DNP3 testbeds and presented their results with respect to SCADA systems’ robustness against cyberattacks.

There have been some recent efforts to incorporate encryption capabilities in the Modbus protocol [16] by the Modbus Organization. This approach relies on TLS to support the encryption, thus requiring the setup of a PKI (Public Key Infrastructure) which may impose several other functional dependencies on third party libraries. Another similar approach to securing SCADA communications has been published [17], which uses ECC (Elliptic Curves Cryptography) to secure Modbus communications. Our approach is different from this since it evaluates the computational load, in terms of additional execution time required, in specific resource limited devices, a Linux PC and an Android IIoT device. Although, an Android device may not be a traditional SCADA device, it has already been proposed and implemented [17,18] and it may gain more popularity in the future, with the growing needs for easier industrial control and remote monitoring.

Authentication functionality is, also, necessary for the authentication of each IoT device as well the data the devices exchange. However, it is often neglected over the confidentiality functionality. In our approach, the IoT devices participating in the communication can exchange encrypted messages among themselves and the SCADA infrastructure after having been authenticated first.

In summary, to the best of our knowledge, our approach comprises one of the first studies in embedding Elliptic Curve Cryptography functionality in Modbus as a pillar to SCADA systems. Moreover, this enhancement of Modbus comes at a full compatibility with existing Modbus deployments since the client/server interface layers have not been changed. To our knowledge, only one approach in this context, i.e., Elliptic Curve Cryptography and Modbus, exists in [19] that only focuses on the man-in-the-middle attack in SCADA systems when they allow participants which do not authenticate themselves as well as the communication keys they use.

3. Elliptic Curve Cryptography

The use of elliptic curves in cryptography was introduced independently by Neal Koblitz [20] and Victor Miller [21] in 1986–1987. Elliptic Curve based cryptography has a number of merits over conventional cryptography which we discuss, briefly, below.

Elliptic curves, in general, offer greater flexibility in the definition of a suitable underlying group structure for cryptographic use. For instance, for a specific prime$p$ there is only one multiplicative/additive group over $p$. As we will explain, however, although elliptic curves are, also, defined over the elements of $F_p$, they also incorporate two more parameters that may be varied and, thus, give rise to numerous different additive groups for the same underlying field $F_p$ for the specific prime $p$.

Moreover, most attacks on elliptic curve cryptosystems rely on solving the Elliptic Curve Discrete Logarithm Problem or ECDLP. As of today, no subexponential algorithm is known for this problem, while subexponential algorithms exist for the underlying problems of other, conventional, cryptosystems such as ElGamal.

Formally, an elliptic curve is defined as follows ([22]):

Definition 1 (Elliptic Curve).

Let F be a field with operations “+” (“addition”) and “$\ast$” (“multiplication”) and characteristic (denoted by char($F$)) other than 2 and 3. The characteristic of a field$F$with the multiplication operation denoted by “$\ast$”, is the least natural number$n$(if there exists such a number at all) such that$nr=0$for every$r$in$F$. Also let$a$and$b$be two members of$F$such that$4a^3+27b^2\ne 0$in$F$. The condition$4a^3+27b^2\ne 0$guarantees that the equation$y^2=x^3+ax+b$does not have multiple roots in the field$F$.

Then the elliptic curve of the equation $y^2=x^3+ax+b$over the field F, denoted by E(F), is the set of pairs (x, y) of elements of F that make the equation hold along with a special point denoted by “$°$” called the point at infinity. The expression $-16\left(4a^3+27b^2\right)$ is called the discriminant of $E\left(F\right)$ and it is denoted by $\Delta \left(E\left(F\right)\right)$.

The point at infinity “$°$” may be thought of as a point infinitely away from the 0 point on the y-axis, where all lines parallel to this axis “intersect”. It can be shown that the points defined over an elliptic curve form an additive group.

The definition for the Elliptic Curve Discrete Logarithm Problem (ECDLP) is as follows:

Definition 2 (Elliptic Curve Discrete Logarithm Problem-ECDLP).

Let$E$be an elliptic curve over a finite field$F_q$, P a point on$E(F_q)$of order$n$and$Q$a point on$E(F_q)$such that$Q=tP$, with$0\le \left|t\right|<n-1$. The ECDLP consists in determining the value of$t$.

The ECDLP is computationally hard, and the security of EC-based cryptography relies on this hardness property. More precisely, what makes the groups defined on elliptic curves exceptional, cryptographically, compared to groups used in conventional cryptography is that the best-known algorithms for solving the ECDLP require exponential (in the key size) expected time complexity. It, thus, appears that there is no apparent characteristics of general elliptic curve groups that can be exploited in order to reduce this time complexity to subexponential.

In some more detail, we will now compare the key sizes, for equivalent security levels, of an EC-based cryptosystem depending on $E\left(F_q\right)$, i.e., the additive group formed by a suitably chosen elliptic curve over a finite field $F_q$, and a conventional cryptosystem relying on the multiplicative group of the finite field $F_p$, for primes $p$ and $q$ ($p$ and $q$ may be equal, but not necessarily). The key for this comparison is the difficulty of solving the discrete logarithm problem in each of these two cryptosystems (see [23,24,25,26,27,28,29]). Our discussion below follows the excellent exposition given in [23].

Let $n=\left[{\log }_{2}q\right]$ be the size of the underlying field $F_q$of the elliptic curve $E\left(F_q\right)$ and $N=\left[{\log }_{2}p\right]$ the size of $F_p$. Note that according to Hasse’s Theorem (see, e.g., [23]) the actual number of elements of $E\left(F_q\right)$ ranges from $q+1-2\sqrt{q}$ up to $q+1+2\sqrt{q}$ and, thus, for our purposes, this number can be approximated by $n=\left[{\log }_{2}q\right]$, with respect to order of magnitude.

We, now, define the following function, where $c$ is a positive real constant and the “log” without a subscript denotes natural logarithms (base $e$) that are, customarily, denoted by “ln”:

$$L\left(p,v,c\right)=e^{c{\left(\log p\right)}^v{\left(\mathrm{loglog} p\right)}^{1-v}},$$

(1)

The behavior of this function depends, heavily, on the values of$v$. When $v=0$, this function is reduced to the following:

$$L\left(p,0,c\right)=e^{c\mathrm{loglog} p}={\left(\log p\right)}^c,$$

(2)

which is polynomial in the size of $p$.

When $v=1$, then the function becomes exponential in the size of $p$:

$$L\left(p,1,c\right)=e^{c\log p}=p^c,$$

(3)

Finally, for $v$ in the open interval (0,1), the function lies between the polynomial and the exponential extremes, and it is called sub-exponential.

It can then be shown that the discrete logarithm problem in $F_p$ can be solved in time proportional to [23,24,25,26,27,28,29]

$$L\left(p,\frac{1}{3},c_0\right)=e^{c_0{(\log p)}^{\frac{1}{3}}{(\mathrm{loglog} p)}^{\frac{2}{3}}},$$

(4)

where the value of the constant c₀ is approximately 1.92. If by C_CONV($N$) denotes the complexity of solving the discrete logarithm problem in a cryptosystem based on $F_p$ with $n=\left[{\log }_{2}q\right]$, then the following holds:

$$C_{conv}\left(N\right)=e^{c_0{N}^{\frac{1}{3}}{(\log N)}^{\frac{2}{3}}},$$

(5)

which is sub-exponential in the size of the field $F_p$. However, if by C_EC($n$) denotes the complexity of solving the discrete logarithm problem on $E\left(F_q\right)$, with $n=\left[{\log }_{2}q\right]$, the best-known algorithms to date can solve it in time proportional to

$$C_{EC}\left(n\right)=2^{\frac{n}{2}}=\sqrt{q},$$

(6)

which is exponential in the size of the field $E\left(F_q\right)$.

We proceed by setting C_CONV($N$) = C_EC($n$), so as to equate the security level for both cryptosystems and then solve for $N$ in order to deduce the key size in bits (i.e., $N$) required by a conventional cryptosystem to attain security levels equivalent to an Elliptic Curve based cryptosystem with key size n. In other words, we use this equation to see for a given value of key size $n$ of an Elliptic Curve cryptosystem, which key size $N$ corresponds for a conventional cryptosystem that attains equivalent security levels. After solving this equation for $N$, we derive the following (see [23] for an expression without the involved constants):

$$N=\frac{1}{4}\frac{n^3}{LambertW{(\frac{1}{2}\sqrt{ln2}\sqrt{\frac{n^3}{b^3{c}^3}})}^2{b}^3{c}^3},$$

(7)

with $b$ approximately equal to 4.91 and $c$ approximately equal to 1.92 (please [24] for a derivation of these values).

The plot of (7) in Figure 1, shows, visually, a comparison of key sizes of equivalent security EC-based (with key size $n$) and conventional cryptosystems (with key size $N$).

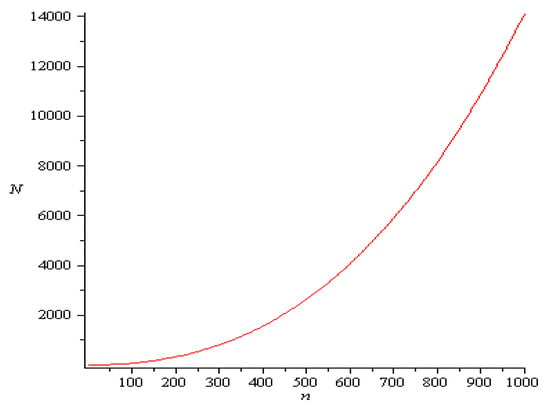
Figure 1. Comparison of key sizes for attaining equivalent security level for EC-based (key size $n$) and conventional cryptosystems (key size $N$).

Equation (7), in essence, reflects the well-founded by theoretical and applied research results, that the discrete logarithm problem defined for the additive groups of elliptic curves is, computationally, harder than the discrete logarithm problem for the multiplicative groups $Z_q^{\ast }$, where $q$ is a prime, deployed by conventional cryptosystems [15].

4. Architecture and Implementation

As stated in the introduction, for our implementation we used an open-source Modbus library. We chose Modbus because it is one of the most common protocols used in industrial networks and is supported by a variety of devices in those networks. Modbus is an application-layer protocol and has a client/server architecture. It enforces communication between devices connected on different types of communication channels. For example, a few devices might be connected using serial buses to the network and others may have TCP connections to connect to the network. The TCP version of the protocol enables Modbus devices to be accessed through the Internet using the reserved 502 port.

Modbus uses several function codes for its services. Each function code can result in a different action by a PLC or an actuator. It supports request/reply communication during which the client sends a request to the server and the server send a reply with a data or a confirmation.

To modify the library, the first consideration was the level of the library where our new security mechanisms would be placed. It was deemed appropriate that the mechanisms should be placed on a relatively low level. This served the purpose of keeping the same functionality on the higher level of Modbus functions, thus achieving interoperability with existing installations (our Modbus variant is a “plug-in” replacement of the initial Modbus variant).

Thus, the general architecture of a SCADA application based on the modified Modbus architecture is shown in Figure 2.

Figure 2. Modified Modbus Architecture.

The shaded parts are the ones which we have modified: the lighter shaded part represents the modifications related to the handshake protocols so as to deploy the incorporated security mechanisms while the darker shaded part represents the implemented security mechanisms. We should emphasize that we have not altered the upper layers, i.e., The application and the core function layers, so that our modified libraries can be incorporated directly, as a “plug-in”, in existing Modbus implementations without and changes in the way that applications interact with the libraries.

The operations that were added to the Modbus protocol are the following: key generation, key distribution, message encryption and message decryption. Key generation and key distribution were implemented as separate functions of the Modbus protocol as opposed to encryption and decryption, which were included in the send and receive functions. The encryption used in the Modbus

In our implementation, we encrypt the whole Modbus ADU. The size of the ADU is typically 260 bytes. When a request/response is, at first, created, it is stored in a uint8 array, however, to process it, it has to be converted to a multiple precision integer. The resulting number must be encrypted using the ECCLIB. To make that possible, we increased the size of the field on which the elliptic curve is defined. Consequently, larger messages could be processed by the library.

The implementation of the entire mechanism was based on ECCLIB, a C library for Elliptic Curve Cryptography. A dependency graph is provided in Figure 3, to give a more detailed explanation of the structure. Again, the shaded parts are the ones which we have modified.

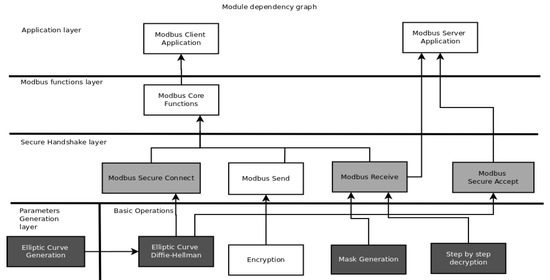
Figure 3. The proposed library and its place within the Modbus protocol.

The colored functions were either implemented or modified. The encryption function (appearing in the bottom layer) is not colored since it is used, unchanged, as implemented in the original ECCLIB.

A brief description of the library’s functionality and operations is provided below. We describe the additional operations that are taking place in a typical Modbus transaction. All operations, except the initial phase of parameter generation, are executed at the initiation of every new Modbus session [4,6,7,9,10,11,12,14].

4.1. Parameter Generation

We assume that the elliptic curve parameters are created and deployed before any communication takes place. These parameters are the base point of the curve and the order of the curve. This is a prerequisite for the implementation of our key distribution algorithm. The parameters are stored locally in each device and before initiating communication, each device uses them to generate its own keys.

For the rest of the operations, a time sequence diagram is provided in Figure 4.

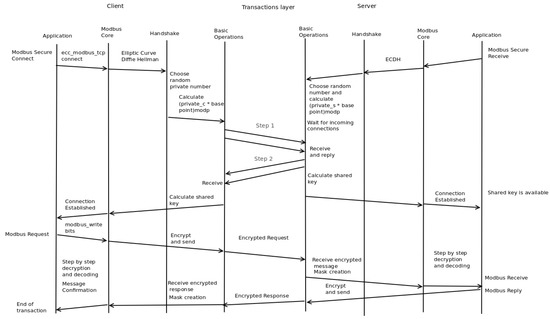
Figure 4. Time-sequence diagram for the library operations.

4.2. Key Generation/Distribution

For the generation of the shared key the Elliptic Curve Diffie Hellman algorithm was implemented. The exchange takes place during the initial connection between two devices. In SCADA systems the communication is usually initiated by the client/master, thus these devices are the ones to begin the exchange. Let us assume that we have Device 1 and Device 2 which wish to establish as secure communication channel. Based on the ECDH algorithm, Device 1 and Device 2 choose random private numbers d1 and d2, correspondingly. Subsequently, a key is computed by each device who multiply the private random number d (d1 or d2) with the public base point G of the elliptic curve. The resulting K1 = d1*G and K2 = d2*G keys are also points on the Elliptic Curve and, thus, they consist of two parts or Cartesian coordinates. However, in our implementation only one coordinate is used for the generation of the shared key. Therefore, only the first coordinate is exchanged.

The keys are multiple precision integers based on the GNU Multiple Precision Arithmetic Library (https://gmplib.org/). To be received correctly, the keys are converted to a character array. Afterwards the device exchanges keys with another device over an insecure channel based on the Elliptic Curve Diffie-Hellman key exchange protocol. The keys could be intercepted at this point; however, the eavesdropper can only obtain the values K1, K2 which are exchanged over the channel. To find the value of d, the eavesdropper would have to solve the Elliptic Curve Discrete Logarithm Problem (ECDLP) which is is hard, computationally (the best-known algorithms require exponential time). After the exchange of the values, the devices compute the shared key by multiplying S = d1*K2 and S = d2*K1. These values are equal since d1*K2 = d1*(d2*G) and d2*K1 = d2*(d1*G). As we stated above, an eavesdropper can know only the K1, K2 values and, thus, it is not computationally feasible to find out the shared key. For implementation purposes, the value S, which is received as a character string is, again, converted to a multiple precision integer based on the GNU library.

Finally, each device stores the computed shared key in the temporary session structure which contains all the information of the Modbus session. The structure has been modified to include a GNU large integer array. The stored key is valid only for the duration of a single Modbus communication session. The key is recomputed each time a new communication section is required [30,31,32,33].

4.3. Encrypted Communication

After the keys have been established the encrypted communication can be initiated. The library we have used for our implementation contains the complete Modbus functionality implemented as a set of C functions. Modbus was first developed as a serial protocol and to this day the serial version is, still, used. Libmodbus provides both serial and TCP modes of operation for the Modbus protocol suite. Our implementation is a part of the Modbus TCP backend. The TCP backend “send” function includes, now, the full encryption functionality (point-to-point encryption). However, the decryption functionality was implemented on a higher level in the “receive” Modbus function, due to the way Modbus handles the received messages.

In some more detail, the backend “send” function encrypts each message using the key that is stored in the appropriate Modbus data structure of the device. The encrypted message is a character array and, thus, it does not need any type conversions. The Modbus “receive” function has been modified, however, more extensively. For a Modbus request to be processed correctly, it has to be received according to a specific sequence of steps. At first, the function’s return code is received and checked to determine how many bytes remain in the request. Based on the value of this code, the recipient knows how many more data items remain to be decrypted in the “receive” Modbus function. Thus, the remaining bytes are read and processed accordingly. This Modbus functionality must be preserved in the modified version of the protocol. Consequently, the decryption process should also be performed in the same sequence of steps followed by the “receive” function. As we deploy the one-time pad algorithm, the messages are decrypted using an XOR mask comprised of the shared key.

The encryption/decryption functionalities embedded in the Modbus send/receive functions, respectively, were implemented with the corresponding cryptograpahic functions of the ECCLIB, based on two separate functions. The first function is responsible for the generation of the XOR mask which is then stored to be used for the decryption process. The mask length was set to the largest possible value. This was an essential decision since Modbus messages can vary in size and the encryption/decryption process should be able to handle all possible message sizes. The second function is responsible for executing the one-time pad algorithm in the corresponding parts of the message and the mask.

4.4. Android Implementation

To demonstrate the use and functionalities of the proposed library on a mobile device, which can be part of a SCADA network as an IIoT device, the modified Elliptic Curve based Modbus library was fully compiled for the Android operational system. Our extensions on the Modbus library require the ECCLIB and GMP libraries. The ECCLIB was compiled from C source code, but we used the precompiled GMP version for the Android Operating System [34]. Using the compiled libraries, a simple Modbus server was developed running on the resource limited Android device. The final generated library was named libsmodbus.so.

For the main server application, which uses libsmodbus.so, “gen-libs” was used as a foundation. A simple C file provided the functionality of a Modbus server. The file contained a JNI function, that could be called from the Main Activity of the application. Finally, the Main Activity consists of a main view, generated when the application is created and the JNI function, which is called when the application starts running.

In our implementation, we encrypt the whole Modbus ADU. The size of the ADU is typically 260 bytes. When a request/response is, at first, created, it is stored in a uint8 array, however, to process it, it has to be converted to a multiple precision integer. The resulting number must be encrypted using the ECCLIB. To make this possible, we increased the size of the field on which the elliptic curve is defined. Consequently, larger messages can be processed by the library.

5. Experiments, Results and Discussion

5.1. Experimental Set-Up

Many SCADA systems often contain different types of computers, with varying computational and storage capabilities. To simulate this diverse type of environment, we tested the secure Modbus communication functionalities using a regular PC as a client and an Android device as a server. Both devices’ specifications are shown in Table 1:

Table 1. Server and Client characteristics.

	Server	Client
CPU	Qualcomm Snapdragon 820	Intel Core i7
CPU Speed	2.2 GHz	2 GHz
Memory	4.0 GB	7.8 GB
Disk Capacity	23 GB	44.8 GB
OS	Android 7.0	Kali GNU 64 bit

The evaluation environment includes the Arduino Industrial 101 IIoT device, which is an evaluation platform for the Arduino 101 LGA module. This evaluation platform is based on the ATmega32u4. Arduino supports a Linux distribution based on OpenWRT called LininoOS. The board has integrated WiFi (IEEE 802.11b/g/n functions up to 150 Mbps 1 × 1 2.4 GHz), 3 GPIOs (of which 2 can be used as PWM outputs), 4 analog inputs, 1 USB, 1 Ethernet signal on Pins and a built-in DC/DC converter. If the board is connected to a computer through a micro USB cable, it can be programmed in the usual way of programming the microcontroller using the Arduino IDE. The complete features of the board (see Figure 5) are shown in Table 2 (see [35]):

Figure 5. Arduino Industrial Board.

Table 2. Features of the board.

Feature	Model/Value of Feature
Microcontroller	ATmega32u4
Flash Memory	32 KB
SRAM	2.5 KB
EEPROM	1 KB
Clock Speed	16 MHz
CPU	Atheros AR9331
WiFi	IEEE 802.11b/g/n
RAM	64 MB DDR2
Flash Memory	16 MB
Input Voltage	5 V
Digital I/O Pins	20 (7 exported on header)
PWM Output	7 (2 exported on header)
Consumption	130 mA
PCB Size	42 × 51 mm
GPIO	3 Exported on headers
DogOLED Support	1 Exported on headers
Weight	0.012 Kg
Product Code	A000126

Consequently, it was necessary to compile the libraries for the Android operating system. Considering that the libraries were all written in C, it was essential to use the Android Native Development Kit to compile them. Along with the Modbus library the ECCLIB and the GMP library were also compiled, as shared libraries. They were included in the application, which implemented the functionality of a Modbus server.

With respect to the supported operations, the Modbus/TCP protocol can be used to perform the main read and write commands, which are issued from the Client/Master. In our implementation the tested operations were the following: single bit read/write, multiple bits read/write, single register read/write and multiple registers read/write. All the operations were tested using the server, running on the Android device and the client, running on the Linux PC. Each test consisted of a single session between the client and the server.

The modified version of the protocol performs the key exchange during the initial connection between the devices. Consequently, for each different session, the server and the client need to agree upon a different shared key. Thus, each different session requires an additional key establishment operation during the connection.

We assumed that the elliptic curve parameters are chosen once, during the setup phase, and every session key is derived from these parameters. This is a realistic approach since the parameters, despite being the same, are nevertheless combined (based on appropriate elliptic curve protocols) with a random value which is generated before the establishment of each new session. More precisely, this “obscure” operation consists in the product of a random value with the point of the elliptic curve that are multiplied together and transmitted. Consequently, an eavesdropper will not be able to extract the random value from the product with the point, as this would require the solution the (computationally hard) ECDLP problem.

As stated before, for our experiments we used a desktop computer, acting as the client, and an Android device acting as the server. Both devices were connected to a central access point, the client through an Ethernet wired connection and the server through a wireless connection.

5.2. Results

The main objective of our work was to examine the feasibility and performance of incorporating security mechanisms based on elliptic curves into the Modbus protocol. In order to assess feasibility and performance, three factors have to be considered: the storage requirements for the modified Modbus library modules, the overhead that the EC layer adds to the standard Modbus communication overhead and the requirements in run-time memory and CPU speed.

We, first, consider the storage requirements of the library modules. As stated before, for our experiments, an Android device was used, acting as a server. The libraries were ported to this device, as described in Section 4. The end Android application was packaged as an apk file of size 3.2 MB. After the apk file was installed in the device, the application required 12.06 MB of storage: 5.49 MB of code and 6.57 MB of data. These requirements are easily manageable by several IoT and IIoT devices.

The client application, which was used to connect to this Android device performing a small number of requests, required a storage size of 12.1 KB. The compiled shared libraries used during the execution of the program and their respective sizes are reported in Table 3.

Table 3. Sizes of compiled libraries.

Library Name	Size (in Kilobytes)
libecc-lib.so	293.7
libgmp.so	512.5
libmodbus.so	68.8

Considering, now, the overhead that the mechanism adds to the standard Modbus communication protocols, we had to determine how many additional bytes were sent over the communication channel, how frequently they were sent and what was the additional delay, as compared to the standard Modbus protocol, due to these additional bytes.

The main modification in the communication protocol of Modbus was the additional information exchange that takes place during the connection. What happens in the modified version is that before any Modbus packet exchange, the devices connect and during the connection they establish a shared key. The algorithm used for the establishment is Diffie-Hellman’s, thus each device sends the values it calculated using a private number and the curve base point. Consequently, the additional bytes that the protocol sends are dependent on the size of the underlying finite field of the used Elliptic Curve. In ECCLIB, which was used for the implementation, the size of the finite field is determined by the parameter “bitlength”. This parameter is critical for the security of the implementation, and this is the key size for the cryptographic EC-based primitives.

To calculate the average duration of the key exchange process, the time required to generate a shared key in 20 consecutive sessions was measured for each pair of devices. We use 4 pairs and repeat the communication between pairs for 1000 times during each run of the experiment. After the connection to the same network of each pair of devices, 20 consecutive sessions were performed, and the time required for each one to successfully generate a key was measured.

We used different field sizes, to generate the corresponding curves and use them to create keys of various sizes. For each different size, we considered the size of the information exchanged during the connection phase. The results are presented in Table 4.

Table 4. EC-based vs. conventional crypto key sizes and resulting overhead.

Equivalent EC Key/Conventional Cryptography Key Sizes	Overhead (Bytes) for Storing Numbers for the EC Key Size
175/1044	22
192/1293	24
224/1853	29

It is important to note that the overhead times given above are incurred each time a connection is established but only once when the connection is initiated. After the communication starts, the shared key is created and from this point on, every Modbus message is encrypted using only this key, with no additional information exchange being necessary. During each session, the client can send any number of encrypted messages to the server. Thus, the small overhead imposed by our modification on the standard Modbus library depends only on the number of new session establishments between a client and a server and not on the duration of their subsequent interaction.

As for the additional execution time induced by the modified key exchange algorithm, it was measured as a function of the key size, for every Modbus function affected by our modifications. To calculate the average execution time of Elliptic Curve Diffie Hellman for each key size, we measured the time needed for the key establishment, for 100 consecutive sessions. The result for each key size was the average value of these measurements. The results are shown in Table 5 and Figure 6.

Table 5. ECDH times in relation to key size.

Key Size (Bytes)	ECDH Time (s)
22	0.004486
24	0.004715
28	0.008835
48	0.009598
64	0.010705
128	0.010904

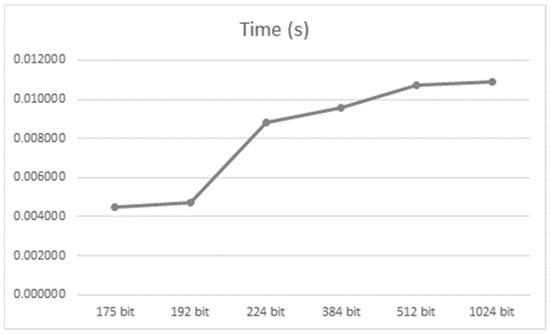
Figure 6. Execution times for corresponding key lengths.

We observe that the performance degrades as the size of the finite field is increased. However, the degradation is not significant. Considering that a size of 192 bits (24 bytes) is, usually, adequate in several practical cases, this choice could offer the best solution in terms of performance and security.

In addition, the execution times of the encryption and decryption functions were measured. We present the time measurements in Figure 7 and Figure 8. Our goal was to observe the delay that the encryption and decryption operations added to a specific Modbus function and assess the impact of our modifications on the communication efficiency between client and server. The function that was tested was the “modbus_write_bit” function (for a detailed description of the function, see the Modbus library documentation available at [36]).

Figure 7. Execution times for encryption.

Figure 8. Execution times for decryption.

It is apparent that for both functions, i.e., encryption and decryption, the performance is not very sensitive to the size of the finite field. The cause of this similarity in the execution times is that both encryption and decryption use the one-time pad with bitwise XOR to produce the ciphertext and plaintext, respectively. XOR, as a bit-wise operation, is very fast to compute on the hardware level almost independently of the size of the operands (unless they are very large, requiring repeating the operation several times sequentially). Consequently, selecting the finite field size is of concern only in relation with the other requirements (mainly overhead and performance) for the key establishment phase.

To provide a more accurate, comparative, assessment of the new version of the library, the execution time for all Modbus functions was measured for, both, the original Modbus library, and the secure version. The results are shown in Figure 9.

Figure 9. Comparison of Modbus and Modbus with encryption.

It is evident that the overhead induced by our library on the original Modbus is very small and can be tolerated in exchange of the important security benefits offered by EC-based cryptography.

6. Conclusions

Nowadays, critical infrastructures, such as electricity grids or industrial installations handling dangerous materials, become increasingly targeted by cyberattacks as they have been interconnected to remote monitoring communication infrastructures due to the need for 24/7 remote monitoring and control. Thus, customary SCADA systems have been enhanced to include outwards communication functionality, most often over the Internet. To protect communication various cryptographic protocols have been incorporated in the standard Modbus protocol suite.

However, because of the limited computational and storage capabilities of the customarily used SCADA sensors and embedded devices, SCADA systems are vulnerable to numerous attacks since the crypto key sizes that can ensure a sufficient level of security are primitively large for SCADA devices. Elliptic Curve based cryptography can offer the same security levels with the conventional crypto algorithms deployed in various Modbus implementations using much smaller keys. Based on this fact, in this paper we presented a portable modified version of a commonly deployed SCADA protocol, the Modbus TCP protocol, using Elliptic Curve cryptography library modules in a way that does not interfere with Modbus functionality. The experimental evaluation of the library showed that it imposes almost no overhead on Modbus making it an attractive solution for upgrading Modbus into the EC based crypto domain gaining the corresponding benefits in security.

Our future work plans include the implementation the of ECDH (Elliptic-curve Diffie-Hellman) and the ECDSA (Elliptic Curve Digital Signature Algorithm) protocols as well as the comparison of ECC, ECDH and ECDSA for resource limited devices used in SCADA systems in order to determine the most efficient approaches with respect to calculation times. Finally, an equally important future work goal is the case study of how to counteract an attacker who could steal and use the private key for Elliptic Curve cryptosystems for malicious actions, assuming the role of an authenticated entity among the devices supporting a SCADA architecture.