Abstract
The inherent predictability of inter-annual variation in forest productivity remains unknown. Available field-based data sources for understanding this variability differ in their spatial resolution, temporal resolution, and typical units of measure. Nearly all other tree and forest characteristics are in practice derived from measurements of diameter at breast height (DBH). Therefore, diameter increment reconstructed annually from tree-ring data can be used to estimate annual growth increments of wood volume, but the accuracy and precision of these estimates requires assessment. Annual growth estimates for n = 170 trees sampled for whole stem analysis from five tree species (jack pine, lodgepole pine, black spruce, white spruce, and trembling aspen) in Western Canada were compared against increments derived from breast height measurements only. Inter-annual variability of breast height and whole tree growth increments was highly correlated for most trees. Relative errors varied by species, diameter class, and the equation used to estimate volume (regional vs. national). A simple example of the possible effect of this error when propagated to the stand level is provided.
1. Introduction
Changes in climate and other environmental conditions can cause annual forest growth to deviate from its long-term historic average, with significant impacts on large-scale estimates of carbon stock changes and forest dynamics. Both spatial and inter-annual variability of tree growth and forest productivity are fundamental for the assessment of future forest management options as well as the annual reporting of forest carbon balances, but the inherent predictability of this inter-annual variation remains unknown [1]. Available data for understanding inter-annual variation differ in their temporal resolution, spatial coverage, and typical units of measure [2,3]. For example, eddy covariance sites provide data on ecosystem carbon fluxes with high temporal resolution. These data can be used to assess site-specific factors affecting inter-annual variation in fluxes, but the measurements are limited to a few sites over a limited number of recent years. Larger amounts of data may be obtained from forest inventory plots, where data such as the diameter, height, vital status, and species of trees are periodically recorded. Allometric relationships can be used to convert measured tree characteristics into stock and stock change estimates for various tree- and stand-level metrics such as wood volume or biomass. This approach provides large-scale estimates on changes resulting from both growth and mortality, allowing the assessment of long-term trends over landscapes [4]. However, the temporal resolution of these data is limited, typically only 5 to 10 years, so they may not provide the annual scale data required for analyzing tree response to annual climate fluctuations. Recent studies have noted the potential utility of tree ring data in terrestrial carbon cycle research [5], as it can lengthen the available time series of annually resolved estimates of ecosystem production or growth increment [3,6,7,8]. In these applications, ring width measurements are instead used to generate various tree or forest level estimates of annual growth increment. This is possible because past diameter at breast height (DBH), the most basic measurement of trees from which nearly all other tree and forest characteristics are derived, can be reconstructed annually from ring-width measurements. Therefore, tree-ring data could potentially form the basis for assessing stand-level changes in forest productivity, as well as in the development and evaluation of data products and ecosystem models [3,9,10].
An issue remains in that relatively little effort has been put into evaluating the accuracy of estimates derived from breast height, relative to actual whole tree growth increments [11,12,13]. For example, stem growth at breast height can over- or underestimate whole-tree annual increments under warm and dry climate [13,14,15]. Presently, the best available method for obtaining annual growth increment data is full stem analysis [16,17,18], which involves felling and sectioning the main stem at regular intervals. Annual wood volume and height increments can be calculated from ring-widths measured and cross-dated on these sections. Stem analysis is labour-intensive, so large-scale application for obtaining annual growth increment data is likely cost-prohibitive. However, it can provide a useful estimate of true annual growth increment, against which alternatives derived from data at breast height only, which is more widely available, can be compared. In this paper, we evaluate annual growth increment estimates of wood volume (m3) derived from past diameters reconstructed from breast height ring widths compared to the same estimates obtained from full stem analysis data, when both estimates are available for the same tree. We did this using data from five species common in the Western Canadian boreal forest: lodgepole pine (Pinus contorta Dougl. var. latifolia Engelm.) jack pine (Pinus banksiana Lamb.), black spruce (Picea mariana (Mill.) B.S.P.), white spruce (Picea glauca (Moench) Voss.), and trembling aspen (Poplus tremuloides Michx.). The purpose of this evaluation is to determine the potential error associated with measures of volume growth increment, derived from tree ring measurements at breast height only, in terms of the actual value of the growth increment, as well as its pattern of inter-annual variation. We also apply our estimates of error to an example stand where tree-ring data have previously been used to estimate inter-annual variation in growth [2,3], to estimate the potential stand level magnitude of this error.
2. Materials and Methods
2.1. Stem Analysis Data Collection and Measurement
Full stem analysis data were obtained from 173 trees sampled at various points in time from 1994 to 2010 in the Western Canadian boreal forest. Samples were collected in four jurisdictions: Alberta, Saskatchewan, Manitoba, and the Northwest Territories, and for five species, lodgepole pine (n = 30) jack pine (n = 15), black spruce (n = 68), white spruce (n = 28), and trembling aspen (n = 31). The characteristics of the sample trees (at time of sampling) are further detailed in Table 1. These stem analysis data were acquired from several projects. Some were collected during the 1994 field campaign of the Boreal Ecosystem-Atmosphere Study (BOREAS) campaign from locations near Prince Albert, Saskatchewan, and Thompson, Manitoba. Sites, stands, soils, and the detailed stem analysis data and procedures are described elsewhere [19,20].

Table 1.
Summary of characteristics of trees sampled for stem analysis in this study.
Briefly, tree height and DBH were measured on each sample tree prior to felling. Disks were cut at heights of 0.3 m, 1.0 m, 1.3 m, 2.0 m, and at 1 m intervals to the top of the stem. Fresh diameters were measured in the field for each disk. In the lab, each disk was dried in a 70 °C oven for three days, after which diameters and bark thickness were re-measured. For each disk, two radii were selected, 180° apart and avoiding compression wood. These radii were then sampled, X-rayed, and analyzed for ring width using DendroScan [21]. Additional samples were collected in 2005 and 2006 as a part of a study validating tree biomass models in the Canadian province of Alberta. The field methods were similar to those for the BOREAS project, with the exception that disks were sampled at slightly different heights: 0.3 m, 1.3 m, 2.8 m, and then at intervals of 2.5 m to the top of the stem. Disks were dried as for the BOREAS data. However, rather than processing for X-ray analysis with DendroScan, the samples were sanded with progressively finer sandpaper, scanned at 1600 dpi, and ring widths were then measured using CDendro (Cybis Elektronik & Data, Stockholm, Sweden). An additional 21 stem analyses were conducted during the summer of 2010 as part of a study validating tree biomass models for the Liard Valley, NWT, Canada. The disks on these trees were collected at heights of 0.3 m, 1.3 m, 5.0 m, and every 4.0 m to the top of the stem, and processed in the lab in the same way as the 2005–2006 samples. For all samples, ring widths were cross-dated between all the disks in each tree to ensure correct ring dating, and corrected by proportion to the mean fresh outside bark diameter of each disk.
2.2. Stem Analysis Growth Estimates
The ring-width measurements for each disk section for each tree were input into a spreadsheet program that calculated annual estimates of tree height (m) and stem volume (m3). Historical tree height (m) was interpolated assuming equal annual height growth within a log section, and assuming that each disk cuts through the middle of a growth cycle, and was referred to as stem analysis height (HTs). Volume was calculated from ring width measurements on each of the disk sections and summed for the entire tree for each year, and referred to as stem analysis volume (Vs). The volume for each log section was calculated using Smalian’s formula, V = (L(Ab + At)/2), for the top section from the volume of a paraboloid, V = (LAb)/2, and for the stump section from the volume of a cylinder V = LAb, where V is the volume of the section (cm3), L is the length of the section (cm), Ab is the cross-sectional area of the base of the section (cm2), and At is the cross-sectional area of the top of the section (cm2). Note that, while the stem analysis-based measurements were taken as the true standard against which alternatives derived from the breast height sample were compared, they are not themselves without uncertainty. For example, estimates derived from stem analysis will differ depending on the method used to interpolate height between cross sections [18], which standard model is used to determine log volume [22,23], the number of cross-cuts sampled, and the number of radii measured along each sample [12], and because trees are not perfectly round in cross section [24,25].
2.3. Model-Based Growth Estimates
The breast height (1.3 m) sample taken from each tree was used as a reconstructed estimate of the past breast height diameter (DBH) of each tree, from which we then calculated annual increments of wood volume for comparison to the estimates derived from stem analysis. We describe the methods used for each of these in the following sections, and an additional summary is provided in Table 2.

Table 2.
Summary of the volume and height estimation methodologies used in the comparisons.
2.3.1. Height Estimation
Height was estimated from DBH using regional height–diameter equations, which use the Chapman-Richards function:
where H is the tree height (m), Dob is the outside bark diameter (DBH, cm), and a, b, and c are the parameters obtained from published sources for Alberta ([31], Table S1) and Manitoba ([29], Table S1). Trees in Saskatchewan and the Northwest Territories also used the Alberta parameters, as regional parameters were not available for these jurisdictions. We calculated two height increment series from the annually reconstructed DBH, (1) a raw height series (HTr), which used the height estimate directly from Equation (1), as well as (2) a corrected height series (HTc), where a ratio between the final predicted height from the raw height series and the measured tree height was used as a correction factor and applied to the raw height series to scale past predicted heights so that the final height in the corrected series was equal to the measured height at the time the tree was sampled.
2.3.2. Volume Estimation
Estimates of volume increment were obtained from the reconstructed DBH, both alone and in combination with height estimated using Equation (1), both in raw (HTr) and corrected form (HTc). We first used a national scale taper equation that uses DBH only as a predictor (VNd) [26]:
where d is the diameter at different cross-section heights (h), indices i, j, k, and m respectively refer to province, plot, tree, and cross section, β0, β1, and β2 are fixed-effect parameters, and δi, δij, and δijk are random effects associated with the province, plot, and tree, respectively [26]. We also tested two methods that use both DBH and H as predictors. The first was also a national level taper equation (VNdh) [26]:
where d is the diameter at different cross-section heights (h), indices i, j, k, and m respectively refer to province, plot, tree, and cross section, β2 is a fixed-effect parameter, and δi, δij, and δijk, are random effects associated with the province, plot, and tree, respectively [26] (Table S2). The second was a different taper equation (VRdh) [27], for which regional parameter estimates were generally available [28,29,30]:
where d is the inside bark diameter at height i along the stem (cm), DBH is the diameter at breast height (cm) of the tree outside bark, H is the total height (m), and Xi is , where hi is the cross-section height i, p is the relative height of the inflection point, typically assumed to be 0.25, and zi is the relative height (hi/H) [27]. Parameters a0, a1, a2, b1, b2, b3, b4, and b5 were obtained from published sources Saskatchewan [28], Manitoba [29], and Alberta [30] (Table S3). Regional parameters were not available for the Northwest Territories; therefore, for trees in that jurisdiction, the Alberta parameters were used. Estimates of volume for each of the methods tested were obtained by numerical integration, and the volume increment from the difference in volume between subsequent years.
2.4. Comparison of Estimates
For volume increment, we conducted five comparisons, representing combinations of different volume equations (VNd, VNdh, and VRdh) and height estimation options (HTr (VNdhr or VRDhr) or HTc (VNdhc or VRdhc)), which were in each case assessed against stem analysis volume (Vs), which was considered true. Details on these comparisons are provided in Table 2. Differences were assessed using relative error,
where is the estimated growth metric (height or volume) determined from the reconstructed DBH only, and is the same metric determined from the stem analysis for the ith year. For analysis, we grouped relative errors by species and 5 cm DBH class, and used the distribution of errors in each class as an indicator of the magnitude and potential significance of differences relative to the estimates derived from stem analysis. When the value zero (indicating no difference between the breast height and whole tree-derived volume increment) was below the 2.5th percentile of all differences in a class, we considered the estimates to be biased high. When zero was between the 2.5th and 25th percentiles, we considered them borderline high, between the 25th and 75th percentiles unbiased, between the 75th and 97.5th percentiles borderline low, and greater than the 97.5th percentile, low.
2.5. Inter-Annual Variation
An additional aim was to determine if annual increment values derived from stem analysis and their alternative were statistically in phase. To do this, we compared a first-differenced time series of each comparison variable and assessed the value of the cross correlation at lag zero, as well as determined the fraction of cases in which the cross correlation peaked at lag zero, relative to shifting the comparison time series forwards or backwards by up to five years.
2.6. Stand-Level Example Application
Errors at the tree-level were also propagated to the stand level for an example fixed area plot in Saskatchewan, Canada, for which samples for dendrochronological analysis were collected at breast height from all live and dead (standing and fallen) trees present at the time of sampling, and that has previously been used in assessments of mortality, competition dynamics, and ecosystem production [2,3]. The observed distribution of error for the regional volume model for jack pine using DBH and HTc as input was propagated using n = 1000 Monte Carlo simulations, under a simple assumption of an independence of errors among trees and size classes.
3. Results
3.1. Comparison of Estimates
Relative errors varied by species, diameter class, the equation used to estimate volume (regional vs. national), and whether or not the equation used only DBH or both DBH and HT as predictors (Figure 1). Estimates derived from breast height only were only biased high or low in relatively few species, diameter class, and volume equation categories (n = 13/175, 7%). Most (52%) showed no bias, and the rest (41%) were borderline high or low (Figure 1). The average range of errors across classes was ±50%, with some small differences among species. In general, the widest distribution of errors for any species or diameter class was for small trees (<10 cm DBH), and in particular for the national model that used only DBH as a predictor. For models that used both DBH and HT, the use of HTc rather than HTr, or a regional rather than a national model had only a marginal influence on the distribution of relative errors in any species or diameter class. The number of annual increment observations available for comparison by species and diameter class is provided in Table S4.
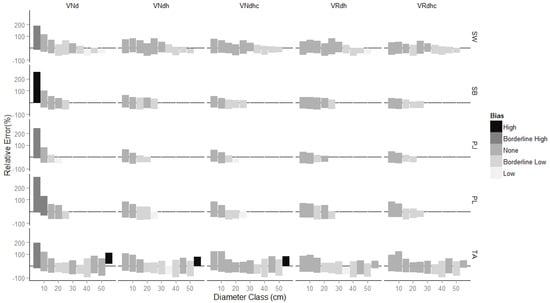
Figure 1.
Relative error in estimation of volume increment from DBH reconstructed from tree-ring data, in comparison to volume increment derived from whole stem analysis for the same trees. Errors are plotted by species (rows) and 5 cm DBH class. The bars represent the range of the 2.5th and 97.5th percentiles of the relative errors in each class. Bars are plotted in different shades as a function of the percentile location of zero with the distribution of errors in a diameter class, and interpreted as described in the text. The columns represent different potential methods for estimating volume increment, national equations using DBH only (VNd), national equations using DBH and raw HT (VNdh), national equations using DBH and corrected height (VNdhc), regional equations using DBH and raw HT (VRdh), and regional equations using DBH and corrected height (VRdhc).
3.2. Inter-Annual Variation
For the assessment of the cross-correlation of inter annual variability between breast height and stem analysis-derived growth metrics, we show results for HTr only, as results for HTc are virtually identical. For volume increment, the cross correlation was maximized at lag zero for 94% of cases for estimates derived from DBH only using the national volume model (median 0.83 and 95% were between 0.20 and 0.99), and for 99% of samples for estimates derived from both DBH and HT for the national (median 0.92, 95% between 0.56 and 0.99), and regional models (median 0.93, 95% between 0.63 and 0.99).
3.3. Example Application
Results for the propagation of errors to a stand level example are provided in Figure 2. This particular example used a regional volume for jack pine in Saskatchewan and corrected estimate of height increment. Estimates of volume increment derived from breast height were within the propagated error range for ages less than 30 years. For ages greater than 30 years, the ranges fell below the point estimate derived from the breast height sample, indicating that it was biased to a high degree relative to whole tree increments. It is likely that many trees passed from a size class where the error distribution was unbiased (VRdhc for PJ, Figure 1), to one where the bias was borderline low. Relative to the median of the error simulations, the range of values typically spanned ±5%.
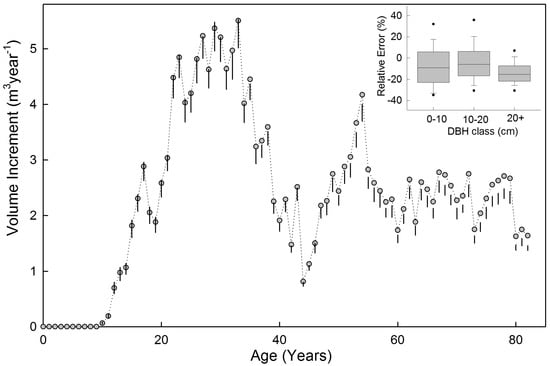
Figure 2.
Time series of above ground volume increment (m3·ha−1·year−1) with stand age for a 900 m2 fixed area jack pine plot in Saskatchewan, Canada, for which all live and dead trees present in the stand at age 82 were sampled at breast height for ring width measurement. The line plot represents volume increment derived from these measurements using a regional volume model using corrected height as input. Error bars represent the 2.5th and 97.5th percentiles of stand level estimates of volume increment, derived from diameter class-based relative errors (inset graph) derived from the observed difference in breast height and whole tree-derived growth increment for this species and volume estimation method.
4. Discussion
In this paper, we evaluated annual growth increment estimates of wood volume (m3) derived from past DBH reconstructed from ring widths and compared these to estimates obtained from full stem analysis data, when both estimates are available for the same tree. This was done using data from n = 170 trees for five species common in the Western Canadian boreal forest: lodgepole pine, jack pine, black spruce, white spruce, and trembling aspen. The main results were that relative errors varied by species, diameter class, and the equation used to estimate volume and that the direction of inter-annual variability for whole tree and breast height estimates of volume increment were highly correlated for nearly all trees. In general, when estimates of volume increment are derived from models that use both DBH and HT as predictors, the total range of values spanned by the relative errors is narrower, relative to volume increment derived from a model using DBH only. The range of observed relative errors for national models was similar to that of regional models, at least for the species tested here. When tree-level errors were propagated to estimates of error for volume increment at the stand level, the overall range of errors was narrower, typically ±5% for our example jack pine stand, at least for our simple procedure that assumed the observed errors were independent. The overall range of errors is less than what is currently assumed to be the uncertainty of growth increments applied by Canada’s National Forest Carbon Monitoring, Accounting, and Reporting system to estimate the carbon balance of Canada’s managed forest [32], but it should be kept in mind that additional error would arise from model and measurement errors that were not accounted for, and at young ages from trees that have died and subsequently decayed such that they could not be detected when the stand was sampled [33]. In this analysis, breast height estimates were consistently high relative to whole tree estimates after age 30–40, but this is likely a result specific to this particular combination of tree species and volume estimation method.
Few other studies have attempted to compare the relative accuracy of different methods of measuring the annual incremental growth of trees. Similar to our analysis, standardized ring-width growth series at breast height and standardized whole-tree growth series of volume increment were highly correlated for high-elevation red spruce (Picea rubens) forests [11]. For European beech (Fagus sylvatica), the breast-height growth series were also highly correlated to whole-tree volume or biomass-increment series [13], but the breast-height series showed higher sensitivity to weather variation. An analysis of the relative accuracy of various full stem analysis sampling protocols for measuring volume increment found that it was possible to increase precision by increasing the density of sections sampled along the stem, and by measuring more radii at each sample [12]. Our results are essentially in line with these previous findings, in that we found that the direction of inter-annual variation in volume increment derived from breast height only was highly correlated with whole tree increment obtained by stem analysis. Our observation that using models with a height predictor generally improved the estimation of volume increment is interesting because this occurs even though total height estimates derived from stem analysis are calculated as the mean height increment between cross-cut segments. Interpolation between cross-cut segments means that stem analysis samples do not actually measure the inter-annual variability of height growth. There is no method presently available for retrospectively obtaining this information, except for some species that consistently grow a single annual whorl of branches. Ground-based measurements of height cannot resolve annual height increments for tall, slow growing trees [2,34], though height growth can be prospectively monitored with some accuracy by tree climbing [35].
Although it likely would have been of interest, we could not conduct a comparison for biomass increment because stem analysis does not provide a direct estimate of biomass that could be considered true. We could have compared estimates generated using reconstructed DBH only with estimates generated using DBH and HT, as alternative models that could have been applied do exist [36,37]. However, this analysis would have been a model inter-comparison exercise that compares the relative difference between estimates of biomass increment using DBH and HT relative to the use of DBH only, not an accuracy assessment directly. The estimation of biomass from tree level allometric equations remains challenging, and the current state of work in this area shows that changes in allometric equations can result in large variations in estimated biomass [38].
Some further challenges need to be considered when inferring above-ground forest increment from radial tree growth. Stand structure and density along with necessary biometric and metadata would be useful to upscale tree biomass estimates to the site level [39,40] and to efficiently select sample trees for estimating climate relationships in an unbiased manner [41]. An alternative, such as was used in our example application where tree level errors were propagated to the stand level, is to sample all live and dead trees in fixed area plots to reconstruct the growth of the whole stand [2,3], a method that has shown promise if the aim is to successfully detect climate and global change-related trends from tree-ring data [42], but remains challenged by the inability to sample trees that have died in the past and subsequently decayed [33]. In addition, replacing the relatively basic equations used in this study with more sophisticated methods that are sensitive to the effect of stand conditions on height–diameter relationships [43], tree volume [44,45], or biomass [46] should also improve the estimates of annual growth increment that could be obtained at both the tree and forest levels, for species where such models are available.
5. Conclusions
The ability to estimate annual growth increment over a long time period at a large spatial scale from field-based data would be a tremendous asset. Such data can be obtained by tree-ring analysis, which is increasingly being used in forestry applications to address questions around the effect of forestry practices, climate, insect outbreaks, global change, and other disturbances in commercially viable, closed-canopy forests as well as a wide range of unmanaged forest and woodland types. Traditionally, tree-ring data have been collected from old trees at climate-sensitive sites for reconstructing past climatic variation, and expressed in unitless ring-width indices. Therefore, observed causes and trends may not be applicable to more productive and managed forests. We have shown that translating these instead into tree- and forest-level estimates of annual growth increment in units that are of greater interest in forestry applications can provide reasonable estimates relative to alternative data on whole tree growth obtained by stem analysis.
Supplementary Materials
The following are available online at www.mdpi.com/1999-4907/7/12/303/s1, Table S1: Height–diameter model parameters [1,2], Table S2: National taper model parameters [3], Table S3: Regional taper model parameters [1,4,5,6], Table S4: Number of annual increment observations available for comparison by species and diameter class. Values in the diameter class column represent the largest diameter of tree in that class.
Acknowledgments
The authors would like to thank Shongming Huang and Yonghe Wang for comments on a previous version of the manuscript, and Thierry Varem-Sanders for extensive assistance with sample processing and data analysis. Funding for this study was provided in part by Canadian Forest Service and program of the Federal Panel on Energy Research and Development (PERD).
Author Contributions
Juha Metsaranta and Jagtar Bhatti both have contributed substantially to idea, data collection, data analysis and finally the manuscript writing.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Luo, Y.; Keenan, T.F.; Smith, M. Predictability of the terrestrial carbon cycle. Glob. Chang. Biol. 2015, 21, 1737–1751. [Google Scholar] [CrossRef] [PubMed]
- Metsaranta, J.M.; Lieffers, V.J. Using dendrochronology to obtain annual data for modelling stand development: A supplement to permanent sample plots. Forestry 2009, 82, 163–173. [Google Scholar] [CrossRef]
- Metsaranta, J.M.; Kurz, W.A. Inter-annual variability of ecosystem production in boreal jack pine forests (1975–2004) estimated from tree-ring data using CBM-CFS3. Ecol. Mod. 2012, 224, 111–123. [Google Scholar] [CrossRef]
- Hember, R.A.; Kurz, W.A.; Metsaranta, J.M.; Black, T.A.; Coops, N.C.; Guy, R.D. Accelerated regrowth of temperate-maritime forests due to environmental change. Glob. Chang. Biol. 2012, 18, 2026–2040. [Google Scholar] [CrossRef]
- Babst, F.; Alexander, M.R.; Szejner, P.; Bouriaud, O.; Klesse, S.; Roden, J.; Ciais, P.; Poulter, B.; Frank, D.; Moore, D.J.P.; et al. A tree-ring perspective on the terrestrial carbon cycle. Oecologia 2014, 176, 307–322. [Google Scholar] [CrossRef] [PubMed]
- Graumlich, L.J.; Brubaker, L.B.; Grier, C.C. Long-term trends in forest net primary productivity: Cascade Mountains, Washington. Ecology 1989, 70, 405–410. [Google Scholar] [CrossRef]
- Babst, F.; Bouriaud, O.; Alexander, R.; Trouet, V.; Frank, D. Toward consistent measurement of carbon accumulation: A multi-site assessment of biomass and basal area increment across Europe. Dendrochronologia 2014, 32, 153–161. [Google Scholar] [CrossRef]
- Fang, O.; Wang, Y.; Shao, X. The effect of climate on the net primary production (NPP) of Pinus koraiensis in the Changbai Mountains over the past 50 years. Trees 2016, 30, 281–294. [Google Scholar] [CrossRef]
- Bunn, A.G.; Hughes, M.K.; Kirdyanov, A.V.; Losleben, M.; Shishov, V.V.; Berner, L.T.; Oltchev, A.; Vaganov, E.A. Comparing forest measurements from tree rings and a space based index of vegetation activity in Siberia. Environ. Res. Lett. 2013, 8, 035034. [Google Scholar] [CrossRef]
- Babst, F.; Bouriaud, O.; Papale, D.; Gielen, B.; Jansenns, I.A.; Nikinmaa, E.; Ibrom, A.; Wu, J.; Bernhofer, C.; Köstner, B.; et al. Above-ground woody carbon sequestration measured from tree rings is coherent with net ecosystem productivity at five eddy-covariance sites. New Phytol. 2014, 201, 1289–1303. [Google Scholar] [CrossRef] [PubMed]
- LeBlanc, D.C. Relationship between breast-height and whole-stem growth indices for red spruce on Whiteface Mountain, New York. Can. J. For. Res. 1990, 20, 1399–1407. [Google Scholar] [CrossRef]
- Newton, P.F. A stem analysis computational algorithm for estimating volume growth and its empirical evaluation under various sampling strategies. Comput. Electron. Agric. 2004, 44, 21–31. [Google Scholar] [CrossRef]
- Bouriaud, O.; Breda, N.; Dupouey, J.-L.; Granier, A. Is ring width a reliable proxy for stem-biomass increment? A case study in European beech. Can. J. For. Res. 2005, 35, 2920–2933. [Google Scholar] [CrossRef]
- Chhin, S.; Hogg, E.H.; Lieffers, V.J.; Huang, S. Growth–climate relationships vary with height along the stem in lodgepole pine. Tree Phys. 2010, 30, 335–345. [Google Scholar] [CrossRef] [PubMed]
- Van der Maaten-Theunissen, M.; Bouriaud, O. Climate-growth relationships at different stem heights in silver fir and Norway spruce. Can. J. For. Res. 2012, 42, 958–969. [Google Scholar] [CrossRef]
- Duff, G.H.; Nolan, N.J. Growth and morphogenesis in the Canadian forest species: I. The controls of cambial and apical activity in Pinus resinosa. Can. J. Bot. 1957, 31, 471–513. [Google Scholar] [CrossRef]
- Shea, S.R.; Armson, K.A. Stem analysis of jack pine (Pinus banksiana Lamb.): Techniques and concepts. Can. J. For. Res. 1972, 2, 392–406. [Google Scholar] [CrossRef]
- Dyer, M.E.; Bailey, R.L. A test of six methods for estimating true height from stem analysis data. For. Sci. 1987, 33, 3–13. [Google Scholar]
- Halliwell, D.H.; Apps, M.J. BOReal Ecosystem-Atmosphere Study (BOREAS) Biometry and Auxiliary Sites: Overstory and Understory Data; Natural Resources Canada, Canadian Forest Service, Northern Forestry Centre: Edmonton, AB, Canada, 1997.
- Varem-Sanders, T.M.L.; Cambpell, I.D. BOReal Ecosystem-Atmosphere Study (BOREAS) Biometry and Auxiliary Sites: X-ray Densitometry of Tree Allometry Samples; Natural Resources Canada, Canadian Forest Service, Northern Forestry Centre: Edmonton, AB, Canada, 1998.
- Varem-Sanders, T.M.L.; Cambell, I.D. DendroScan: A Tree-Ring Width and Density Measurement System; UBC Press: Vancouver, BC, Canada, 1996. [Google Scholar]
- Martin, A.J. Testing volume equation accuracy with water displacement techniques. For. Sci. 1984, 30, 41–50. [Google Scholar]
- Figueiredo-Filho, A.; Schaaf, L.B. Comparison between predicted volumes estimated by taper equations and true volumes obtained by the water displacement technique (xylometer). Can. J. For. Res. 1999, 29, 451–461. [Google Scholar] [CrossRef]
- Biging, G.S.; Wensel, L.C. The effect of eccentricity on the estimation of basal area and basal area increment of coniferous trees. For. Sci. 1988, 34, 621–633. [Google Scholar]
- Bakker, J.D. A new, proportional method for reconstructing historical tree diameters. Can. J. For. Res. 2005, 35, 2515–2520. [Google Scholar] [CrossRef]
- Ung, C.H.; Guo, X.J.; Fortin, M. Canadian national taper models. For. Chron. 2014, 89, 211–224. [Google Scholar] [CrossRef]
- Kozak, A. A variable-exponent taper equation. Can. J. For. Res. 1988, 18, 1362–1368. [Google Scholar] [CrossRef]
- Gál, J.; Bella, I.E. New Stem Taper Functions for 12 Saskatchewan Timber Species; Information Report NOR-X-338; Natural Resources Canada, Canadian Forest Service, Northern Forestry Centre: Edmonton, AB, Canada, 1994.
- Klos, R. Ecologically Based Taper Equations for Major Tree Species in Manitoba. Master’s Thesis, Lakehead University, Thunder Bay, ON, Canada, 2004. [Google Scholar]
- Huang, S. Ecologically Based Individual Tree Volume Estimation for Major Alberta Tree Species Report #1 Individual Tree Volume Estimation Procedures for Alberta: Methods of Formulation and Statistical Foundations; Alberta Sustainable Resource Development, Public Lands and Forests Division: Edmonton, AB, Canada, 1994.
- Huang, S. Ecologically Based Individual Tree Volume Estimation for Major Alberta Tree Species Report #2 Ecologically Based Individual Tree Height-Diameter Models for Major Alberta Tree Species; Alberta Sustainable Resource Development, Public Lands and Forests Division: Edmonton, AB, Canada, 1994.
- Metsaranta, J.M.; Shaw, C.H.; Kurz, W.A.; Boisvenue, C.; Morken, S. Uncertainty of inventory-based estimates of the carbon dynamics of Canada’s managed forest (1990–2014). Can. J. For. Res. 2016. in review. [Google Scholar]
- Metsaranta, J.M.; Lieffers, V.J.; Wein, R.W. Dendrochronological reconstruction of jack pine snag and downed log dynamics in Saskatchewan and Manitoba, Canada. For. Ecol. Manag. 2008, 255, 1262–1270. [Google Scholar] [CrossRef]
- Hasenauer, H.; Monserud, R.A. Biased predictions for tree height increment models developed from smoothed ‘data’. Ecol. Mod. 1997, 98, 13–22. [Google Scholar] [CrossRef]
- Sumida, A.; Miyaura, T.; Torii, H. Relationships of tree height and diameter at breast height revisited: Analysis of stem growth using 20-year data of an even-aged Chamaecyparis obtuse stand. Tree Phys. 2013, 33, 106–118. [Google Scholar] [CrossRef] [PubMed]
- Lambert, M.C.; Ung, C.H.; Raulier, F. Canadian national tree aboveground biomass equations. Can. J. For. Res. 2005, 35, 1996–2018. [Google Scholar] [CrossRef]
- Ung, C.H.; Bernier, P.; Guo, X.J. Canadian national biomass equations: New parameter estimates that include British Columbia data. Can. J. For. Res. 2008, 38, 1123–1132. [Google Scholar] [CrossRef]
- Weiskittel, A.R.; MacFarlane, D.W.; Radtke, P.J.; Affleck, D.L.R.; Temesgen, H.; Woodall, C.W.; Westfall, J.A.; Coulston, J.W. A call to improve methods for estimating tree biomass for regional and national assessments. J. For. 2015, 113, 414–424. [Google Scholar] [CrossRef]
- Garcia, O. Sampling for tree-ring analysis. In Presented at Integrating Forest Information Over Space and Time, Canberra, Australia, 13–17 January 1992; pp. 110–128.
- Osawa, A.; Abaimov, A.P.; Kajimoto, T. Feasibility of estimating total stem volume and aboveground biomass from measurement on the largest trees in even-aged pure stands. Can. J. For. Res. 2001, 31, 2042–2048. [Google Scholar] [CrossRef]
- Mérian, P.; Bert, D.; Lebourgeois, F. An approach for quantifying and correcting sample size-related bias in population estimates of climate-tree growth relationships. For. Sci. 2013, 59, 444–452. [Google Scholar] [CrossRef]
- Nehrbass-Ahles, C.; Babst, F.; Klesse, S.; Nöttzli, M.; Bouriaud, O.; Neukom, R.; Dobbertin, M.; Frank, D. The influence of sampling design on tree-ring based quantification of forest growth. Glob. Chang. Biol. 2014, 20, 2867–2885. [Google Scholar] [CrossRef] [PubMed]
- Sharma, M.; Zhang, S.Y. Height-diameter models using stand characteristics for Pinus banksiana and Picea mariana. Scand. J. For. Res. 2004, 19, 442–451. [Google Scholar] [CrossRef]
- Sharma, M.; Zhang, S.Y. Variable-exponent taper equations for jack pine, black spruce and balsam fir in eastern Canada. For. Ecol. Manag. 2004, 198, 39–53. [Google Scholar] [CrossRef]
- Sharma, M.; Parton, J. Modelling stand density effects on taper for jack pine and black spruce plantations using dimensional analysis. For. Sci. 2009, 55, 268–282. [Google Scholar]
- Almedag, I.S.; Stiell, W.M. Spacing and Age Effects on Biomass Production in Red Pine Plantations. For. Chron. 1982, 58, 220–224. [Google Scholar] [CrossRef]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).