Heterogeneous Genetic Learning and Comprehensive Learning Strategy Particle Swarm Optimizer

Abstract

In canonical PSO, maintaining an appropriate balance between exploration and exploitation is vital for optimizing particle behavior. However, this balance can be difficult to achieve in some complex scenarios. To tackle this issue, this study proposes an innovative PSO variant, named the heterogeneous genetic learning and comprehensive learning strategy PSO (HGCLPSO). The HGCLPSO incorporates the genetic learning strategy (GLS) and comprehensive learning strategy (CLS) to form heterogeneous sub-populations, effectively balancing the exploration and exploitation capabilities. Furthermore, a potentially excellent gene activation (PEGA) mechanism is designed to update the archived position of gbest (Abest) by learning some excellence gene of individual particles to further enhance the GLS sub-population exploitation ability. A repulsive mechanism is incorporated into the CLS sub-population to prevent premature convergence and preserve diversity. Additionally, a local search operator based on the BFGS Quasi-Newton method is utilized to fine-tune the best solution during the later stages of evolution. To evaluate the performance of HGCLPSO, it is benchmarked against eight renowned PSO variants and six additional evolutionary algorithms using the CEC2014 and CEC2017 test suites as well as a real-world WSN coverage engineering problem. Experimental outcomes show that HGCLPSO obtains the optimal average rank in the majority of test problems, which verifies its robustness and competitiveness as an optimization tool for addressing continuous optimization tasks.

1. Introduction

In the field of computational intelligence, a multitude of swarm intelligence optimization algorithms have been proposed or evolved, such as genetic algorithms (GA) [1], particle swarm optimization (PSO) [2], Snow ablation optimizer [3], Starfish optimization algorithm (SFOA), [4] and others. These methods have increasingly become the go-to solutions for complex problems that traditional optimization algorithms struggle to address. Among them, the PSO algorithm has attracted widespread interest in many fields such as image encryption [5], multi-AGV path planning [6], UWB base station deployment optimization [7], satellite navigation [8,9], and resource allocation [10] due to its simplicity, few parameter requirements, fast convergence and strong optimization ability.

In the original PSO algorithm, each individual converges or concentrates on the personal history best position (pbest) and global best position (gbest) within the population, which can lead to a loss of diversity and premature convergence. As a result, its performance tends to degrade when faced with optimization problems that feature many local optima or are non-separable [11]. To address this, various PSO variations have been developed with the aim of striking the right balance between global exploration and local exploitation in different aspects of the problem, as well as enhance convergence speed in an effort to find global optimum solutions for diverse challenges. These variants can generally be classified into four main types: firstly, population neighborhood topology and multi-swarm tactics; secondly, parameter control techniques; thirdly, novel learning strategies; and lastly, hybrid PSO methods that integrate with other algorithms. However, a conflict often arises between uni-modal and multi-modal problems. For example, the former benefit from reduced population diversity, which aids in exploitation, while the latter require greater population diversity to help the algorithm move away from local optima and facilitate global exploration. A concise summary of these four categories is presented as follows.

The first category of PSO variants involves the introduction of new topological structures in the neighborhood and multi-swarm strategies to manage exploration and exploitation through different information-sharing mechanisms among particles, thus mitigating premature convergence. In FIPS [12], each individual updates its position by considering the pbest of all its neighbors, meaning that every particle is influenced by all individuals in the population. Nasir [13] developed a DNLPSO algorithm where a particle selects an exemplar from the best positions of its neighbors, allowing its velocity to be influenced by both historical and neighbor-based information. Qu recently proposed the LIPS algorithm to address multi-modal problems, utilizing local best information from nearby particles (based on Euclidean distance) to guide the search for the global optimum [14]. Liang [15] introduced the DMS-PSO algorithm in 2006 that divides the population into smaller swarms with a continuously evolving neighborhood structure. To tackle large-scale optimization problems, the CCPSO2 [16] algorithm splits the decision variables into smaller multi-swarms.

The second category focuses on adaptive parameter control techniques. In HPSO-TVAC, individual velocity updates use time-varying acceleration coefficients c1 and c2. In the FST-PSO method [17], a novel fuzzy logic (FL) approach independently calculates the inertia weight, cognitive/social component, and velocity limits for each particle, eliminating the need for predefined parameter settings. APSO employs evolutionary state estimation to categorize the population’s state into exploration, exploitation, convergence, and escape phases, and adjusts the inertia weights and acceleration coefficients based on these states [18]. Additionally, APSO-VI [19] dynamically adjusts the inertia weight based on the average absolute velocity, using feedback control to align with a specified nonlinear ideal velocity.

The third category of PSO variants introduces a novel learning approach to enhance search efficiency. This approach, known as the generalized “learning PSO” paradigm, integrates learning operators or specific mechanisms into the traditional PSO algorithm, allowing particles to acquire learning abilities to improve the universality and robustness. The CLPSO algorithm can be a typical representative of this category [20], where each particle updates its decision variables by learning from multiple previous pbest positions. This strategy can increase the population search effectiveness. OLPSO employs orthogonal experimental design (OED) to merge the pbest and gbest positions, creating a learning exemplar for each particle [21]. This orthogonal approach helps guide the search more effectively, improving overall performance. GOPSO utilizes Cauchy mutation and generalized opposition-based learning techniques [22]. Additionally, SL-PSO [23] incorporates social learning strategies, where particles learn from the demonstrators (better-performing particles within the swarm).

GL-PSO [24] divides operation into two stages. Genetic algorithm operators—crossover, mutation, and selection—are employed in the first stage to generate promising learning examples. The second stage updates the swarm’s position and velocity using the standard PSO algorithm. Another approach, Dimensional Learning PSO (DLPSO), introduced by Xu [25], enhances learning by allowing each particle’s pbest to learn from the corresponding dimension of the gbest. This results in a learning example that combines the best information from both the individual and global experiences. However, no single PSO algorithm with a single learning method has proven universally effective across all problem types. The Hybrid Collaborative Learning PSO (HCLPSO) [26] addresses this by dividing the population into two sub-populations: one focused on exploration, updating velocities using the Comprehensive Learning Strategy (CLS), and the other focused on exploitation, using a global version of the CLS for velocity updates. TSLPSO combines dimensional learning strategies (DLS) and CLS to achieve a relative balance between exploration and exploitation capabilities [25]. HCLDMS-PSO [27] further divides the population into two subgroups: one using CLS with gbest for exploitation, and the other employing the DMS-PSO algorithm to enhance exploration. In Self-Learning PSO (SLPSO) [28], each individual can deceptively switch between four different learning strategies, including learning from its own pbest, a randomly chosen nearby position, another particle’s pbest, and the gbest position. Numerous other learning mechanisms are also being actively researched, expanding the potential of PSO [29,30,31,32].

The fourth category are hybrid PSO with other algorithms to enhance its performance on complex problems. Each method integrated into a hybrid PSO brings its own strengths. For example, Xin [33] explored several hybrid combinations of Differential Evolution (DE) and PSO. Kran and Gündüz [34] developed a hybrid PSO and Artificial Bee Colony (ABC) algorithm. In those hybrid algorithms, the information is exchanged between the particle swarm and other individuals to improve search capabilities. In addition, various specific search operators have been integrated into PSO, such as mutation operators [25], two differential mutations [35], chaos-based initialization with robust update strategies [36], and aging mechanisms [37]. These auxiliary techniques aim to increase the diversity of the population and accelerate convergence.

Previous studies have highlighted issues with PSO, such as “oscillation” and the “two steps forward, one step back” phenomenon. These problems can be mitigated, and search efficiency enhanced, by using PSO variants with unique learning techniques [20,21,23,24,25,28]. However, for both uni-modal and multi-modal problems, it is difficult for a single learning strategy to achieve a balance between exploration and exploitation capability. In response, we propose a Heterogeneous Genetic Learning and Comprehensive Learning Strategy PSO (HGCLPSO), which combines the GLS and CLS to efficiently identify and preserve promising solutions. This approach is inspired by algorithms such as HCLPSO, HCLDMS-PSO, TSLPSO, and HCLDMS-PSO. The whole population is compartmentalized into two sections to guide the particle search. The GLS sub-population uses a global topology to generate learning examples, optimizing exploitation, while the CLS sub-population learns from the pbest of multiple particles across different dimensions, enhancing exploration. However, the GLS sub-population may suffer from a lack of exploitation capacity due to misleading information or insufficient convergence if the ideal solution is not found. To address this, we introduce a new Potential Excellent Gene Activation (PEGA) mechanism, which improves the exploitation ability of the GLS sub-population by updating the archived position of gbest (Abest) with high-quality genes from individual particles. Additionally, a repulsive mechanism is incorporated into the CLS sub-population, causing particles to generate repulsive responses based on their distance from the global optimal solution (Abest), preventing premature convergence and maintaining diversity. Lastly, a local search operator utilizing the BFGS Quasi-Newton method is employed in the latter phases of evolution to enhance the optimal solution.

The performance of HGCLPSO is initially measured using 30D and 50D CEC2014 test suite problems, and it is compared to eight advanced PSO variants. Next, the 30D CEC2017 test suite is utilized to further assess HGCLPSO, comparing it against six non- PSO meta heuristics and five advanced PSO variants. The algorithm’s effectiveness is then tested on a real-world coverage control problem in wireless sensor networks (WSNs). The experimental results demonstrate that HGCLPSO achieves the best average rank across most test problems, confirming it as a robust and competitive optimization tool for continuous optimization problems.

2. Related Work

2.1. Canonical PSO

In canonical PSO, each particle represents a potential solution with its own position and velocity. Initially, all particles are randomly assigned across the search space. Subsequently, each particle is guided toward pbest and gbest positions by the following equation:

$$v_{\mathrm{i}}^d(t+1)=\omega \ast v_{\mathrm{i}}^d(t)+c_1\ast r_1\ast [\mathrm{p}\mathrm{b}\mathrm{e}\mathrm{s}{\mathrm{t}}_{\mathrm{i}}^d(t)-x_{\mathrm{i}}^d(t)]+c_2\ast r_2\ast [{\mathrm{g}\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}^d(t)-x_{\mathrm{i}}^d(t)]$$

(1)

$$x_{\mathrm{i}}^d(t+1)=x_{\mathrm{i}}^d(t)+v_{\mathrm{i}}^d(t+1)$$

(2)

where $d=1,2,...,D$ are the dimensions of the optimization problem. The ith particle position and velocity are $x_i^d(t)$ and $v_i^d(t)$ ($i=1,2,...,N$), respectively. $\omega$ is the inertia weight parameter, $c_1$ and $c_2$ are the acceleration coefficients, and $r_1$ and $r_2$ are two random numbers generated within the range of [0, 1]. In addition, $pbes{t}_i^d$ and ${gbest}^d$ are the pbest and gbest position for the ith particle in the dth dimension. The particle velocity update consists of three distinct components. The first component, inertia, retains the particle’s previous speed, reflecting its “memory”. The second component, known as “cognition", represents the particle’s own knowledge. The third component, “socialization", involves the exchange of information and collaboration between particles.

2.2. GL-PSO

The Genetic Learning PSO (GL-PSO) [24] employs a two-layer cascading structure to generate high-quality learning exemplars. In the first layer, GA operators—crossover, mutation, and selection [1]—are applied to produce promising learning examples. The second layer updates the particle velocity according to Equation (3):

$$v_{\mathrm{i}}^d(t+1)=\omega \ast v_{\mathrm{i}}^d(t)+c_1\ast r_1\ast [e_i^d(t)-x_{\mathrm{i}}^d(t)]$$

(3)

where $e_i^d(t)$ is constructed to replace two exemplars $pbes{t}_i^d$ and ${gbest}^d$ to guide the evolution direction of particle i. The pseudo code for generating a promising exemplar for the ith particle is presented in Algorithm 1. In summary, each particle undergoes GA operators based on the historical data of particles in each generation. As a result, the generated learning exemplars are not only of high quality but also exhibit good diversity. Numerous numerical experiments have shown that this approach enhances search capability and efficiency of PSO.

Algorithm 1. Pseudo code for breeding a GLS exemplar ${\mathrm{e}}_i^d(t)$
1:	For i = 1 to N do
2:	/* Exemplar update: Crossover */
3:	For d = 1 to D do
4:	Randomly select a particle $k\in \left\{1,2,\dots ,N\right\}$
5:	If $f(P_i)<f(P_k)$then
6:	$e_i^d=r_d\cdot pbes{t}_i^d+(1-r_d)\cdot gbes{t}^d$
7:	else
8:	$e_i^d=pbes{t}_k^d$
9:	End if
10:	End for
11:	/* Exemplar update: Mutation */
12:	For d = 1 to D do
13:	If rand(0,1) < pm then
14:	$e_i^d=rand(l{b}^d,u{b}^d)$;
15:	End if
16:	End for
17:	/* Exemplar update: Selection */
18:	Evaluate $f(e_i)$
19:	If $f(e_i)<f(E_i)$then
20:	$E_i=e_i$;
21:	End if
22:	If $f(E_i)$ stagnated for $s_g$ generations then
23:	Select local optimal $E_j$ by $0.2\ast N$ tournament selection
24:	End if
25:	End for

2.3. CLPSO

In CLPSO [20], all particles update their velocity by considering both their pbest position and the pbest of other particles across different dimensions according to Equation (4):

$$v_{\mathrm{i}}^d(t+1)=\omega \ast v_{\mathrm{i}}^d(t)+c_1\ast r_1\ast [\mathrm{p}\mathrm{b}\mathrm{e}\mathrm{s}{\mathrm{t}}_{\mathrm{f}\mathrm{i}(\mathrm{d})}^d(t)-x_{\mathrm{i}}^d(t)]$$

(4)

where $f_i(d)=[f_i(1),f_i(2),\cdots f_i(D)]$ determines which particle’s pbest is to be followed in the dth dimension. Each individual has a distinct learning probability value, denoted as Pc, which is computed using Equation (5):

$$P{c}_i=a+b*{\displaystyle \frac{(\exp (10(i-1)/(N-1))-1)}{(\exp (10)-1)}}$$

(5)

where $a=0.05$, and $b=0.45$. A tournament selection method is employed to select the guiding particle. The specific or detailed implementation process can be referred to in the original literature. Accordingly, the learning example $pbes{t}_{\mathrm{f}\mathrm{i}(\mathrm{d})}^d$ is a new position that channels the particles in the search space into a new orientation. The refresh gap m is defined as the number of evaluations that must pass in order to prevent the function evaluations from being squandered in the wrong direction. A fresh $pbes{t}_{\mathrm{f}\mathrm{i}(\mathrm{d})}^d$ will be generated until the particle stops improving if the subsequent moves in generation m are not improved. In this manner, the flying direction of the particle is updated using the most accurate historical data available for all particles. This guarantees that the population diversity can be preserved by the CLPSO algorithm and a premature convergence can be avoided. The test shows that while the CLPSO is less effective at handling uni-modal problems, it has clear advantages for solving multi-modal challenges.

3. The Proposed HGCLPSO Method

In GL-PSO, the learning exemplar is created using both the particle’s pbest and gbest in a global topology, similarly to a global version of PSO. While this mechanism enables a high convergence rate, it can also lead to a rapid loss of particle diversity, reducing the algorithm’s exploration capability. Experimental results indicate that GL-PSO performs less effectively on complex multi-modal functions compared to uni-modal and simpler multi-modal functions [24], highlighting GLS’s strong exploitation ability. In contrast, CLPSO adjusts individual velocity by considering the pbest position of all other particles, which allows each dimension of a particle to draw knowledge from various sources. Therefore, CLS enhances population diversity and strengthens global exploration, which helps a particle escape a local optimum by learning from others, thus avoiding premature convergence. By combining the strengths of GLS and CLS, it is possible to effectively balance exploration and exploitation capabilities.

(1)

GLS sub-population and CLS sub-population hybrid

We suggest employing GLS and CLS to form heterogeneous sub-populations, which in turn boost the canonical PSO algorithm search capacity within the search space. The first sub-population is allocated to the GLS with the population size of N1 responsible for exploitation in the search range and the second sub-population is assigned to the CLS with the remaining population size N2 (i.e., N-N1) for exploration, respectively. In this way, it is worth noting here that the learning exemplar $pbes{t}_{\mathrm{f}\mathrm{i}(\mathrm{d})}^d$ constructed by CLS sub-population particles is learning from different dimensions of the whole population of individuals, not just the CLS sub-population range.

(2)

Potentially excellent gene activation mechanism (PEGA)

In the GLS sub-population, if the gbest has not yet converged to the optimal solution, particles in the GLS sub-population may maintain good diversity but lack sufficient exploitation, which negatively impacts the balance of search capabilities in the proposed HGCLPSO algorithm. In canonical PSO, the gbest is updated or replaced by the pbest information from all dimensions. This can result in valuable information being lost. There are two opposing factors that affect the gbest position: One is that improvements in certain dimensions of gbest can enhance the fitness of the overall best individual. On the other hand, while the overall fitness may improve, some dimensions of the gbest position may worsen, leading to the “two steps forward, one step back” phenomenon.

To address or mitigate this issue, we introduce the Potentially Excellent Gene Activation (PEGA) mechanism, which monitors the pbest position to help accelerate the improvement of the gbest position, specifically the archived gbest position (Abest). The Abest position is initially the same as the gbest position in the first generation. As a particle’s pbest improves over time, a counter, success_count, is incremented. When success_count exceeds a threshold value S, the pbest position may contain useful information in certain dimensions, even if its overall fitness is low. In such cases, the gbest position should incorporate potentially valuable information from the corresponding dimensions of the pbest. However, identifying which dimensions or combinations of dimensions from the improved pbest are beneficial for the Abest position is challenging. To address this, we define a learning probability (PL) for each dimension of Abest, based on a Sigmoid function, to determine how much information should be transferred from the pbest particle, as follows:

$$P{L}^d={\displaystyle \frac{1}{1+\exp (-\frac{1}{5}(d-\frac{D}{2}))}}$$

(6)

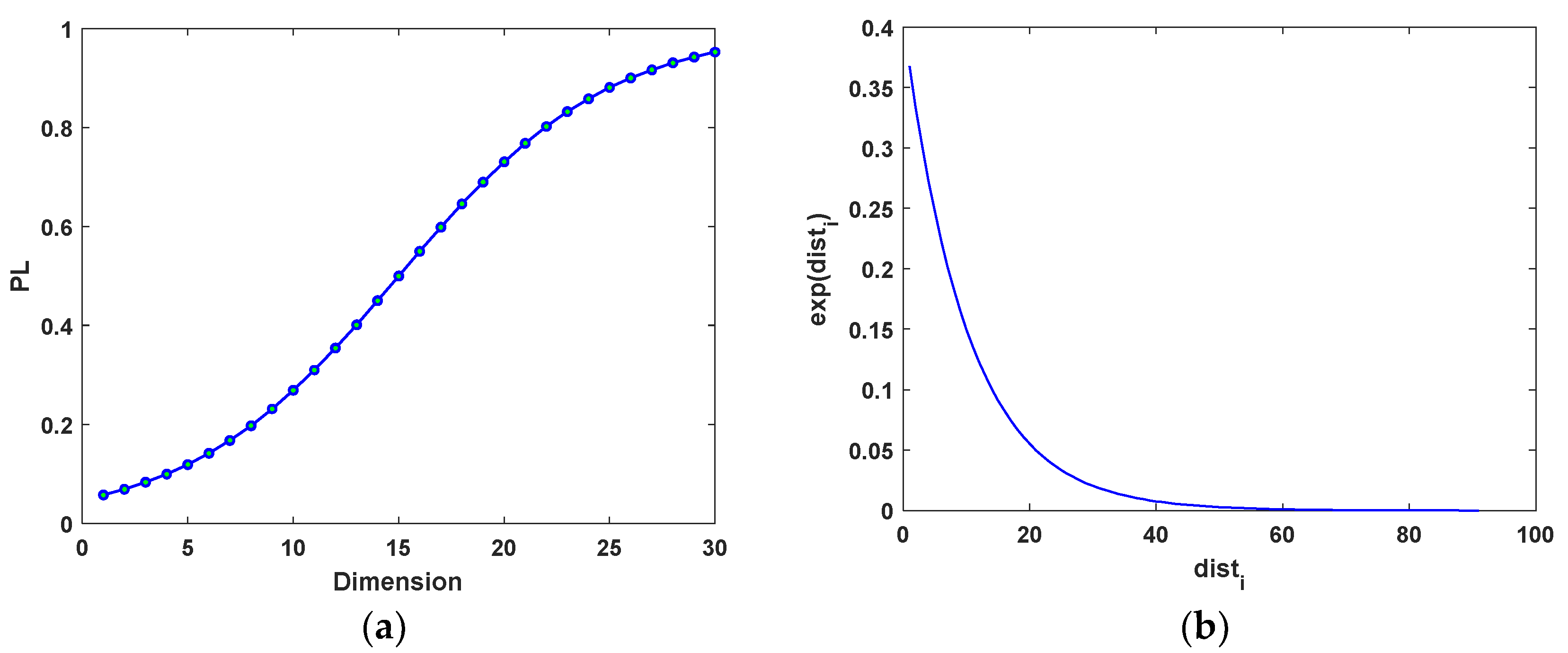
where $P{L}^d,d=1,2,\cdots ,D$ distribute between 0.0 and 1.0 for the dth dimension of all particles. For 30D problems, the PL values for different dimensions are shown in Figure 1a. For a certain dimension d, if a random number is less than PL, the ${Abest}^d$ is replaced by ${pbest}^d$, and the new Abest position fitness $fit(Abest)$ is evaluated. If the new Abest position performs better than the previous one, it replaces the old one; otherwise, the update is skipped. Algorithm 2 outlines the process for updating the Abest position. Introducing the learning probability has two key advantages: first, it helps HGCLPSO save computational resources, and second, it reduces the likelihood of incorporating potentially irrelevant information from the pbest position.

Algorithm 2. Pseudo code for updated Abest position
1:	For i = 1 to N do
2:	If success_count(i) > S then
3:	For d = 1 to D do
4:	If rand < PLd then
5:	temp = Abest;
6:	If tempd = = pbestd then
7:	continue
8:	End if
9:	tempd = pbestd
10:	If fit(temp) < fit(Abest) then
11:	Abestd = tempd
12:	End if
13:	End if
14:	End for
15:	End if
16:	End for

After generating the Abest position, the formula for breeding a GLS exemplar ${\mathrm{e}}_i^d$ in Algorithm 1, line 6 will be replaced as follows:

$$e_i^d=r_d\cdot pbes{t}_i^d+(1-r_d)\cdot Abes{t}^d$$

(7)

(3)

Repulsive mechanism

Although the CLS sub-population can maintain high population diversity, with the development of evolution, its particles will gradually learn from the excellent genes in the GLS sub-population and gradually lose diversity. However, when solving complex problems with many local optimums, the population may locate a pseudo optimal area and spread misinformation. Then, the CLS sub-population particles are easily attracted to the same region. To prevent premature convergence in the CLS sub-population and avoid clustering, we introduce a repulsive mechanism [38]. If a particle in the CLS sub-population becomes too close to the current optimal position (Abest), its position and velocity are adjusted using Equations (8) and (9). Meanwhile, the GLS sub-population continues its operation unaffected by this mechanism.

$$\begin{array}{l}{x}_{\mathrm{i}}^d=x_{\mathrm{i}}^d\pm r^d\cdot (U^d-L^d)\cdot \exp (-dis{t}_i)\\ dis{t}_i=\sqrt{{\displaystyle {\sum }_{d=1}^D{(Abes{t}^d-x_{\mathrm{i}}^d)}^2}}\end{array}$$

(8)

$$v_{\mathrm{i}}^d=L^d+r^d\cdot (U^d-L^d)$$

(9)

where $r^d$ is a random number that is uniformly distributed within the interval [0, 1], while $U^d$ and $L^d$ represent the upper and lower limits of the search space, respectively. It is worth noting that the second part in Equation (8) is an exponential decay function related to the distance $dis{t}_i$. According to the repulsive force curve shown in Figure 1b, if a particle in the CLS sub-population is closer to Abest, it will be repulsed by greater repulsive force to explore further regions of the search range, while a particle far from Abest is hardly affected. Since this repulsive mechanism has a strong destructive effect on the evolution of the CLS sub-population, it is operated every R generations to stimulate the CLS sub-population to retain high diversity.

(4)

BFGS Quasi-Newton local search

Since exploitation is key to improving solution accuracy, we incorporate the widely used BFGS Quasi-Newton method [39,40] in HGCLPSO as a local search operator. Only Abest is chosen to conduct the local-searching procedure at the later evolutionary stage of the HGCLPSO. In all tests, the Quasi-Newton technique receives no gradient information; hence, we assign [0.05 * MaxFEs] evaluations to refine Abest based on the BFGS Quasi-Newton method. In this study, the BFGS Quasi-Newton local-searching operator is realized using the function “fminunc” in Matlab R2021a.

Incorporating all the aforementioned features, the pseudo code for HGCLPSO is provided in Algorithm 3. Seeing in Supplementary Materials, the MATLAB source code for HGCLPSO can be accessed at https://github.com/wangshengliang2018/HGCLPSO (accessed on 2 September 2022).

Algorithm 3. Pseudo code for the proposed HGCLPSO algorithm
1:	Set population size parameter N, N1, N2; Set learning probability parameter PL;
2:	Set GLS and CLS parameter;
3:	Initialize particle position Xi and velocity Vi (1 ≤ i ≤ N);
4:	Evaluate Xi and record the fitness fit(Xi), fes = N;
5:	Initialize the pbesti = Xi and the pbest fitness value fit(pbesti) = fit(Xi);
6:	Initialize the gbest = [pbesti |min(fit(pbesti)),1 ≤ I ≤ N]; Abest = gbest;
7:	Initialize the GLS exemplar by Algorithm 1 with Equation (7) for the first sub-population;
8:	Initialize the CLS exemplar for the second sub-population;
9:	While (iter <= max_iteration) and (fes <= 0.95*MaxFEs)
10:	fit(last_pbest) = fit(pbest);
11:	For i = 1:N1
12:	Update the GLS sub-population Xi and Vi according to Equations (3) and (2);
13:	End for
14:	If mod(iter, R) == 0 then
15:	For i = N1 + 1:N
16:	Update the CLS sub-population Xi and Vi according to Equations (8) and (9);
17:	End for
18:	Else
19:	For i = N1 + 1:N
20:	Update the CLS sub-population Xi and Vi according to Equations (4) and (2);
21:	End for
22:	End if
23:	For i = 1:N
24:	Evaluate all Xi fitness;
25:	Update the pbesti and gbest;
26:	If fit(gbest) < fit(Abest) then
27:	Abest = gbest;
28:	End if
29:	If  fit(pbesti) < fit(last_pbesti) then
30:	success_count(i) = success_count(i) + 1;
31:	Else
32:	success_count(i) = 0;
33:	End if
34:	Update Abest position by Algorithm 2;
35:	End for
36:	Update the GLS exemplar by Algorithm 1 with Equation (7);
37:	Update the CLS exemplar;
38:	End While
39:	Assign 0.05∗MaxFEs for Abest to carry out the BFGS Quasi-newton local search operator.

Population diversity is a key indicator for assessing both exploitation and exploration abilities. We analyze the diversity of the GLS sub-population, the CLS sub-population, and the overall population throughout the evolution process. The formulas for calculating the diversity measure are given in Equations (10) and (11):

$$Diversity={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N\sqrt{{\displaystyle \sum _{d=1}^D{(X_i^d(t)-\overline{X^d})}^2}}}$$

(10)

$$\overline{X^d}={\displaystyle \frac{1}{N}}{\displaystyle \sum _{i=1}^N{X}_i^d(t)}$$

(11)

where N represents the population size, and $\overline{X^d}$ refers to the average position of the dth dimension across the entire population. Small population diversity suggests that the population is being exploited within a constrained area since the particles condense close to the population center. High population diversity suggests that a larger area is being explored and that the population’s particles are spread out from its core.

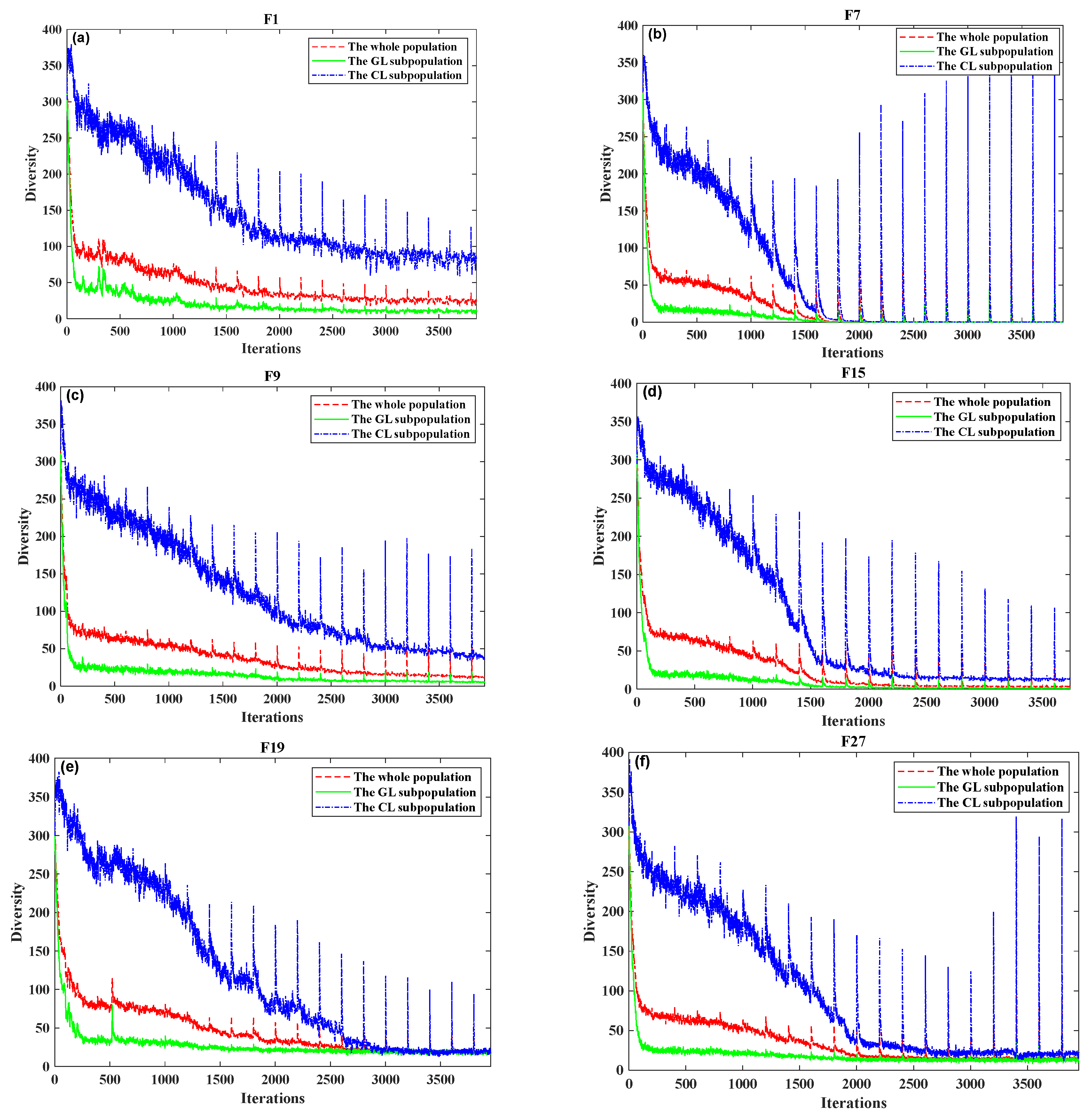
Figure 2 displays the diversity measure value curves of F1, F7, F9, F15, F19, and F27 in the CEC2014 test suite function [41]. According to Figure 2, the CLS sub-population often has higher diversity than the GLS sub-population, while the whole population diversity falls between the two. Since there are no data from gbest to serve as a central guiding direction, it is not surprising that the CLS subgroup maintains the maximum diversity. Additionally, the presence of the repulsive mechanism is clearly established to have caused a rise in the diversity of CLS sub-populations or mutation. In the early stages of evolution, the CLS population members are relatively distant from the gbest individuals, resulting in a weak repulsive force. As the evolution progresses, the CLS population moves closer to the ideal individuals, generating a stronger repulsion that helps prevent premature convergence. The global topological structure and PEGA updating mechanism for the GLS example generate the smallest diversity and the fastest convergence in the GLS sub-population, respectively. Due to the collaborative effort of the GLS and CLS sub-populations in balancing exploitation and exploration, the overall population diversity remains moderate. The role design of the GLS and CLS sub-populations fulfills our expectations, as demonstrated by the experimental results comparing diversity measures.

4. Experimental Results and Analysis

In Section 4.1, we modify the key parameters of the HGCLPSO algorithm using the CEC2014 test suite, focusing on uni-modal and simple multi-modal functions (F1~F16). Section 4.2 compares the performance of HGCLPSO with eight advanced PSO variants using the CEC2014 test suite to evaluate its robustness against shift and rotation functions. In Section 4.3, we compare HGCLPSO with other state-of-the-art evolutionary algorithms (EAs) on the CEC2017 test suite [42]. Section 4.4 applies HGCLPSO and other EAs to solve the coverage problem in WSNs. The CEC2014 test suite contains 30 test functions, and the problem definitions and code are available for download from the GitHub repository (https://github.com/P-N-Suganthan/CEC2014) (accessed on 2 September 2022). The CEC2017 test suite (https://github.com/P-N-Suganthan/CEC2017-BoundContrained) (accessed on 2 September 2022) consists of 29 test functions. In this suite, F2 is excluded due to its instability, especially in higher dimensions.

The evaluation criteria involve calculating the mean error and standard deviation for each algorithm, then ranking their performance. The final ranking for each algorithm is determined by averaging its individual ranks. In Section 4.2 and Section 4.3, we apply the widely used non-parametric Wilcoxon rank sum test [43] at a 0.05 significance level to statistically assess the significance of the differences between the results of the algorithms compared, strengthening the validity of the experimental findings. The symbols “+”, “=”, and “−” respectively indicate that the performance of the HGCLPSO algorithm is significantly better than, without significant difference, and worse than the compared algorithms. In addition, we also performed the Friedman test to determine whether the algorithm results were statistically significant, further supporting the experimental conclusions. All algorithms are implemented in MATLAB R2021a and executed on a laptop with an Intel Core i5 11400 CPU (2.60 GHz) and 8 GB RAM, running Microsoft Windows 10.

4.1. HGCLPSO Algorithm Parameter Tuning

There exist two parameters, i.e., two sub-population sizes (N1 and N2) and threshold value parameter S in the Abest update process, which need to be tuned in the proposed HGCLPSO algorithm. Our preliminary experiments indicate that setting the parameter S to 3 leads to excessive use of computational resources, which negatively impacts the population’s evolution. On the other hand, when S is set greater than 5, the update probability of Abest significantly decreases, hindering the GLS sub-population’s exploitation ability. However, when S is set to 4, these issues are well-balanced. Therefore, we will not discuss the tuning of this parameter further. We just use the CEC2014 benchmark function to test and compare the influence of two different sub-population sizes (N1 and N2) on the parameters. The runtime, population size, dimensions, and MaxFEs are set to 31, 40, 30, and 300,000, respectively. The final ranking is determined by calculating the average rank across 16 benchmark functions.

When N1 equals zero, the proposed HGCLPSO algorithm degenerates into the canonical CLPSO algorithm with the repulsive mechanism and BFGS Quasi-Newton local search. When N1 equals N, the proposed HGCLPSO algorithm will become the GL-PSO algorithm with the Abest update mechanism and BFGS Quasi-Newton local search. So, the above two cases are not included in our discussion of parameter adjustment. We assign the value of N1 from 0.1*N to 0.9*N with an interval of 0.1*N, for a total of nine cases for the final ranking statistical analysis.

Table 1. Calibration of two sub-population sizes (N1 and N2) in the HGCLPSO algorithm.

Functions	Criteria	0.1*N+ 0.9*N	0.2*N+ 0.8*N	0.3*N+ 0.7*N	0.4*N+ 0.6*N	0.5*N+ 0.5*N	0.6*N+ 0.4*N	0.7*N+ 0.3*N	0.8*N+ 0.2*N	0.9*N+ 0.1*N
F1	mean	4.83 × 10−02	6.76 × 10−03	1.05 × 10−02	1.65 × 10−02	3.79 × 10−02	2.76 × 10−01	1.13 × 10−01	8.32 × 10−02	7.06 × 10−02
	std	1.06 × 10−01	1.06 × 10−02	2.88 × 10−02	3.31 × 10−02	1.17 × 10−01	4.58 × 10−01	2.85 × 10−01	1.89 × 10−01	1.83 × 10−01
	rank	5	1	2	3	4	9	8	7	6
F2	mean	4.66 × 10+01	8.01 × 10+00	3.72 × 10+01	1.03 × 10+02	3.25 × 10+00	3.14 × 10+01	1.71 × 10+01	2.79 × 10−01	2.02 × 10+00
	std	8.34 × 10+01	1.88 × 10+01	8.14 × 10+01	1.81 × 10+02	8.89 × 10+00	5.93 × 10+01	3.61 × 10+01	4.38 × 10−01	2.82 × 10+00
	rank	8	4	7	9	3	6	5	1	2
F3	mean	1.85 × 10+00	4.88 × 10−01	1.35 × 10+00	1.95 × 10+00	3.28 × 10+00	2.08 × 10−01	1.45 × 10+00	3.83 × 10−02	3.20 × 10−01
	std	3.92 × 10+00	1.48 × 10+00	3.23 × 10+00	3.59 × 10+00	4.57 × 10+00	6.22 × 10−01	3.34 × 10+00	7.23 × 10−02	9.07 × 10−01
	rank	7	4	5	8	9	2	6	1	3
F4	mean	3.62 × 10−01	0.00 × 10+00	0.00 × 10+00	0.00 × 10+00	3.62 × 10−01	7.25 × 10−01	2.50 × 10−09	3.50 × 10−09	1.32 × 10−09
	std	1.20 × 10+00	0.00 × 10+00	0.00 × 10+00	0.00 × 10+00	1.20 × 10+00	1.61 × 10+00	8.28 × 10−09	8.64 × 10−09	4.38 × 10−09
	rank	6	1	1	1	5	7	3	4	2
F5	mean	2.00 × 10+01	2.00 × 10+01	2.00 × 10+01	2.00 × 10+01	2.00 × 10+01	2.00 × 10+01	2.00 × 10+01	2.00 × 10+01	2.00 × 10+01
	std	3.32 × 10−06	3.93 × 10−05	1.52 × 10−04	1.10 × 10−05	3.32 × 10−05	4.89 × 10−05	1.52 × 10−05	6.25 × 10−05	2.66 × 10−05
	rank	9	3	1	8	5	4	7	2	6
F6	mean	1.56 × 10+01	1.46 × 10+01	1.48 × 10+01	1.37 × 10+01	1.38 × 10+01	1.27 × 10+01	1.37 × 10+01	1.11 × 10+01	1.12 × 10+01
	std	2.54 × 10+00	2.33 × 10+00	2.21 × 10+00	4.55 × 10+00	2.98 × 10+00	4.61 × 10+00	4.67 × 10+00	4.05 × 10+00	3.40 × 10+00
	rank	9	7	8	4	6	3	5	1	2
F7	mean	7.00 × 10+00	3.81 × 10+00	2.37 × 10−01	4.03 × 10−02	7.39 × 10−03	4.93 × 10−03	7.38 × 10−03	8.51 × 10−03	5.82 × 10−03
	std	1.08 × 10+01	8.64 × 10+00	7.58 × 10−01	1.14 × 10−01	6.87 × 10−03	6.61 × 10−03	8.60 × 10−03	1.04 × 10−02	9.02 × 10−03
	rank	9	8	7	6	4	1	3	5	2
F8	mean	6.24 × 10+00	2.80 × 10+00	1.45 × 10+00	1.27 × 10+00	3.62 × 10−01	0.00 × 10+00	0.00 × 10+00	0.00 × 10+00	0.00 × 10+00
	std	5.52 × 10+00	5.15 × 10+00	2.76 × 10+00	2.82 × 10+00	1.20 × 10+00	0.00 × 10+00	0.00 × 10+00	0.00 × 10+00	0.00 × 10+00
	rank	6	5	4	3	2	1	1	1	1
F9	mean	4.66 × 10+01	5.07 × 10+01	6.38 × 10+01	5.46 × 10+01	6.01 × 10+01	5.68 × 10+01	5.69 × 10+01	6.30 × 10+01	5.10 × 10+01
	std	1.13 × 10+01	1.04 × 10+01	1.22 × 10+01	1.53 × 10+01	9.01 × 10+00	1.51 × 10+01	1.70 × 10+01	2.78 × 10+01	2.02 × 10+01
	rank	1	2	9	4	7	5	6	8	3
F10	mean	1.45 × 10+02	2.24 × 10+02	1.97 × 10+02	1.79 × 10+02	2.24 × 10+02	1.91 × 10+02	9.86 × 10+01	1.38 × 10+02	5.32 × 10+01
	std	1.73 × 10+02	1.55 × 10+02	1.67 × 10+02	1.51 × 10+02	1.55 × 10+02	1.59 × 10+02	1.46 × 10+02	1.65 × 10+02	1.21 × 10+02
	rank	4	9	7	5	8	6	2	3	1
F11	mean	2.62 × 10+03	2.23 × 10+03	2.66 × 10+03	2.48 × 10+03	2.43 × 10+03	2.52 × 10+03	2.46 × 10+03	2.33 × 10+03	2.99 × 10+03
	std	6.11 × 10+02	5.40 × 10+02	3.90 × 10+02	5.83 × 10+02	5.99 × 10+02	1.01 × 10+03	5.26 × 10+02	5.26 × 10+02	9.51 × 10+02
	rank	7	1	8	5	3	6	4	2	9
F12	mean	2.42 × 10−01	2.33 × 10−01	1.65 × 10−01	1.59 × 10−01	1.40 × 10−01	1.39 × 10−01	1.62 × 10−01	1.52 × 10−01	2.11 × 10−01
	std	6.58 × 10−02	8.16 × 10−02	1.06 × 10−01	6.09 × 10−02	6.27 × 10−02	7.31 × 10−02	7.32 × 10−02	8.68 × 10−02	1.20 × 10−01
	rank	9	8	6	4	2	1	5	3	7
F13	mean	2.96 × 10−01	3.04 × 10−01	3.21 × 10−01	3.16 × 10−01	3.19 × 10−01	3.60 × 10−01	3.41 × 10−01	3.23 × 10−01	3.42 × 10−01
	std	7.03 × 10−02	6.94 × 10−02	6.96 × 10−02	4.27 × 10−02	6.10 × 10−02	6.49 × 10−02	7.35 × 10−02	8.27 × 10−02	5.94 × 10−02
	rank	1	2	5	3	4	9	7	6	8
F14	mean	2.32 × 10−01	2.38 × 10−01	2.17 × 10−01	2.61 × 10−01	2.44 × 10−01	2.53 × 10−01	2.80 × 10−01	2.79 × 10−01	2.87 × 10−01
	std	3.43 × 10−02	3.83 × 10−02	3.73 × 10−02	3.89 × 10−02	3.27 × 10−02	5.62 × 10−02	5.24 × 10−02	4.76 × 10−02	6.47 × 10−02
	rank	2	3	1	6	4	5	8	7	9
F15	mean	1.83 × 10+01	1.54 × 10+01	2.92 × 10+01	2.71 × 10+01	1.07 × 10+01	9.74 × 10+00	1.63 × 10+01	1.61 × 10+01	3.89 × 10+01
	std	3.45 × 10+01	2.76 × 10+01	7.57 × 10+01	5.15 × 10+01	1.49 × 10+01	8.35 × 10+00	3.17 × 10+01	1.91 × 10+01	6.34 × 10+01
	rank	6	3	8	7	2	1	5	4	9
F16	mean	1.02 × 10+01	1.05 × 10+01	1.01 × 10+01	1.04 × 10+01	1.03 × 10+01	1.04 × 10+01	1.02 × 10+01	1.02 × 10+01	1.03 × 10+01
	std	6.74 × 10−01	8.60 × 10−01	8.41 × 10−01	5.41 × 10−01	8.60 × 10−01	6.64 × 10−01	6.48 × 10−01	8.33 × 10−01	9.51 × 10−01
	rank	2	9	1	8	5	7	3	4	6
Average rank		5.69	4.38	5.00	5.25	4.56	4.56	4.88	3.69	4.75
Final rank		8	2	6	7	3	3	5	1	4
Best/2nd Best/Worst		2/2/4	3/2/2	4/1/1	1/0/1	0/3/1	4/1/2	1/1/0	4/2/0	2/4/3

presents the results of tuning the sizes of two sub-populations (N1 and N2). Based on the final rankings, the combination of N1 = 0.8*N and N2 = 0.2*N yielded the best average rank for F1–F16 compared to other configurations. Thus, the sub-population sizes N1 = 0.8*N and N2 = 0.2*N, along with the threshold parameter S = 4, are selected in subsequent experiments. While this configuration may not be optimal for every minimization problem, it generally enables HGCLPSO to achieve satisfactory solutions across various functions.

4.2. Experimental Results and Analysis of CEC2014 Test Suite

In this section, we compare HGCLPSO with eight other state-of-the-art PSO variants to validate its effectiveness on the CEC2014 test suite. These variants include CLPSO [20], OLPSO [21], SL-PSO [23], HCLPSO [26], GL-PSO [24], EPSO [44], TSLPSO [25], and HCLDMS-PSO [27]. Detailed parameter settings are provided in

Table 2. Parameter settings of the nine PSO variants.

Algorithm	Parameter Setting	Year	Ref.
CLPSO	$w$ = 0.9~0.2, c = 1.49445, Pc = 0.05~0.5, m = 5	2006	[20]
OLPSO	w = 0.9~0.4, c = 2.0, G = 5	2011	[21]
SL-PSO	$\mathit{N}=\mathit{M}+⌊\mathit{D}/10⌋$, M = 100, $\beta =0.01$, $\alpha =0.5$	2015	[23]
HCLPSO	$w$ = 0.99~0.29, c1 = 2.5~0.5, c2 = 0.5~2.5, K: 3~1.5	2015	[26]
GL-PSO	w = 0.7298, c = 1.49618, pm = 0.01, sg = 7	2016	[24]
EPSO	Reference the original paper	2017	[44]
TSLPSO	w1 = w2 = 0.9~0.4, c1 = c2 = 1.49445, c3 = 0.5~2.5	2019	[25]
HCLDMS-PSO	w = 0.99~0.29, w2 = 0.99~0.29, c1 = 2.5~0.5, c2 = 0.5~2.5, pm = 0.1	2020	[27]
HGCLPSO	w1 = 0.7298, w2 = 0.9~0.4, c1 = 1.49618, c2 = 3~1.5, PL, S = 4, R = 200	-	-

. CLPSO and GL-PSO are discussed in Section 2.2 and Section 2.3, respectively. OLPSO leverages an orthogonal learning strategy to generate learning exemplars for particle updates. SL-PSO integrates a dimension-dependent parameter management strategy with social learning for updating positions and velocities. HCLPSO employs a comprehensive learning strategy and divides the population into two subgroups to perform exploration and exploitation functions, respectively. EPSO combines five PSO strategies—such as inertia weight PSO and CLPSO-gbest—through a self-adaptive mechanism. TSLPSO uses DLS and CLS techniques to manage exploration and exploitation. Meanwhile, HCLDMS-PSO separates the population into CL and DMS subgroups, with the CL subgroup focused on exploitation using CLS and the DMS subgroup on exploration using DMS-PSO.

4.2.1. Results for 30 Dimensional Problems

The unified parameters for all 30 CEC2014 test problems are as follows: population size = 40, problem dimension = 30, number of runs = 31, and MaxFEs = 300,000. The experimental outcomes are listed in

Table 3. Comparison of experimental results for nine PSO variants on 30D CEC2014 test functions.

Functions	Criteria	HGCLPSO	HCLDMS-PSO	TSLPSO	ESPO	GL-PSO	HCLPSO	SL-PSO	OLPSO	CLPSO
F1	mean	9.49 × 10−02	2.77 × 10+06	3.74 × 10+06	3.10 × 10+06	1.09 × 10+07	3.83 × 10+06	3.83 × 10+05	1.58 × 10+07	9.24 × 10+06
	std	3.37 × 10−01	2.96 × 10+06	2.68 × 10+06	2.37 × 10+06	1.32 × 10+07	3.47 × 10+06	2.96 × 10+05	8.90 × 10+06	2.77 × 10+06
	rank	1	3	5	4	8	6	2	9	7
F2	mean	6.80 × 10+00	3.67 × 10+02	2.05 × 10+01	9.62 × 10+01	2.56 × 10+00	1.05 × 10+01	1.32 × 10+04	4.80 × 10+05	3.00 × 10+00
	std	2.00 × 10+01	4.75 × 10+02	4.35 × 10+01	1.18 × 10+02	4.83 × 10+00	1.54 × 10+01	1.09 × 10+04	3.56 × 10+05	3.98 × 10+00
	rank	3	7	5	6	1	4	8	9	2
F3	mean	8.63 × 10−01	4.13 × 10+02	8.47 × 10+01	9.26 × 10+01	3.03 × 10+02	2.14 × 10+02	7.78 × 10+03	6.05 × 10+03	4.03 × 10+02
	std	2.38 × 10+00	6.00 × 10+02	2.61 × 10+02	9.59 × 10+01	1.34 × 10+03	2.79 × 10+02	5.67 × 10+03	4.83 × 10+03	3.95 × 10+02
	rank	1	7	2	3	5	4	9	8	6
F4	mean	5.14 × 10−01	1.44 × 10+02	7.75 × 10+01	1.11 × 10+02	1.51 × 10+02	1.23 × 10+02	2.55 × 10+01	1.68 × 10+02	7.40 × 10+01
	std	1.36 × 10+00	2.40 × 10+01	3.64 × 10+01	4.00 × 10+01	4.05 × 10+01	3.51 × 10+01	2.84 × 10+01	2.53 × 10+01	2.48 × 10+01
	rank	1	7	4	5	8	6	2	9	3
F5	mean	2.00 × 10+01	2.02 × 10+01	2.01 × 10+01	2.07 × 10+01	2.00 × 10+01	2.03 × 10+01	2.09 × 10+01	2.07 × 10+01	2.04 × 10+01
	std	1.02 × 10−05	5.85 × 10−02	5.77 × 10−02	8.10 × 10−02	2.61 × 10−02	4.13 × 10−02	6.15 × 10−02	7.18 × 10−02	4.84 × 10−02
	rank	1	4	3	7	2	5	9	8	6
F6	mean	9.59 × 10+00	2.96 × 10+00	6.88 × 10+00	6.12 × 10+00	8.39 × 10+00	7.78 × 10+00	7.93 × 10−01	8.22 × 10+00	1.27 × 10+01
	std	3.64 × 10+00	2.12 × 10+00	2.30 × 10+00	2.05 × 10+00	3.36 × 10+00	2.57 × 10+00	8.01 × 10−01	3.21 × 10+00	1.85 × 10+00
	rank	8	2	4	3	7	5	1	6	9
F7	mean	2.96 × 10−03	1.60 × 10−03	3.08 × 10−05	4.77 × 10−03	3.50 × 10−03	1.20 × 10−03	3.18 × 10−04	6.57 × 10−01	8.51 × 10−05
	std	1.27 × 10−02	2.99 × 10−03	6.07 × 10−05	6.20 × 10−03	7.49 × 10−03	2.00 × 10−03	1.77 × 10−03	1.83 × 10−01	9.18 × 10−05
	rank	6	5	1	8	7	4	3	9	2
F8	mean	9.90 × 10−14	2.25 × 10+01	2.35 × 10−13	3.43 × 10+00	2.49 × 10-13	2.27 × 10−12	1.74 × 10+01	2.92 × 10+00	1.17 × 10−13
	std	7.03 × 10−14	4.75 × 10+00	6.52 × 10−14	2.71 × 10+00	5.66 × 10-13	7.83 × 10−12	4.17 × 10+00	1.61 × 10+00	2.04 × 10−14
	rank	1	9	3	7	4	5	8	6	2
F9	mean	5.15 × 10+01	2.67 × 10+01	4.79 × 10+01	5.25 × 10+01	5.30 × 10+01	4.50 × 10+01	2.42 × 10+01	7.50 × 10+01	5.19 × 10+01
	std	1.52 × 10+01	5.97 × 10+00	8.01 × 10+00	1.26 × 10+01	1.86 × 10+01	9.77 × 10+00	2.22 × 10+01	2.89 × 10+01	6.47 × 10+00
	rank	5	2	4	7	8	3	1	9	6
F10	mean	8.11 × 10−01	7.86 × 10+02	6.49 × 10+00	1.40 × 10+02	5.16 × 10−01	4.97 × 10+00	3.21 × 10+02	1.46 × 10+02	1.44 × 10+00
	std	2.02 × 10+00	2.86 × 10+02	4.74 × 10+00	1.20 × 10+02	8.53 × 10−01	1.70 × 10+00	1.74 × 10+02	1.19 × 10+02	8.99 × 10−01
	rank	2	9	5	6	1	4	8	7	3
F11	mean	2.42 × 10+03	2.09 × 10+03	1.94 × 10+03	2.63 × 10+03	2.63 × 10+03	2.04 × 10+03	8.41 × 10+02	3.23 × 10+03	2.19 × 10+03
	std	5.13 × 10+02	4.61 × 10+02	5.19 × 10+02	8.01 × 10+02	6.60 × 10+02	3.69 × 10+02	4.37 × 10+02	7.92 × 10+02	2.95 × 10+02
	rank	6	4	2	7	8	3	1	9	5
F12	mean	1.22 × 10−01	3.24 × 10−01	1.74 × 10−01	8.79 × 10−01	1.25 × 10−01	3.23 × 10−01	2.16 × 10+00	1.20 × 10+00	3.25 × 10−01
	std	5.41 × 10−02	1.14 × 10−01	5.86 × 10−02	1.18 × 10−01	5.00 × 10−02	7.52 × 10−02	7.74 × 10−01	1.73 × 10−01	5.83 × 10−02
	rank	1	5	3	7	2	4	9	8	6
F13	mean	2.55 × 10−01	1.72 × 10−01	2.22 × 10−01	3.35 × 10−01	3.98 × 10−01	2.26 × 10−01	1.82 × 10−01	3.88 × 10−01	2.97 × 10−01
	std	6.88 × 10−02	3.86 × 10−02	6.40 × 10−02	6.45 × 10−02	1.21 × 10−01	6.56 × 10−02	3.49 × 10−02	7.25 × 10−02	4.40 × 10−02
	rank	5	1	3	7	9	4	2	8	6
F14	mean	2.39 × 10−01	2.41 × 10−01	2.23 × 10−01	2.72 × 10−01	3.42 × 10−01	2.28 × 10−01	4.02 × 10−01	2.83 × 10−01	2.35 × 10−01
	std	4.59 × 10−02	3.47 × 10−02	3.22 × 10−02	3.17 × 10−02	4.62 × 10−02	3.92 × 10−02	8.20 × 10−02	3.83 × 10−02	2.36 × 10−02
	rank	4	5	1	6	8	2	9	7	3
F15	mean	4.83 × 10+00	4.16 × 10+00	4.62 × 10+00	1.07 × 10+01	5.01 × 10+00	5.11 × 10+00	5.56 × 10+00	1.80 × 10+01	7.39 × 10+00
	std	1.39 × 10+00	8.56 × 10−01	1.41 × 10+00	3.69 × 10+00	1.52 × 10+00	1.54 × 10+00	4.48 × 10+00	1.91 × 10+00	1.07 × 10+00
	rank	3	1	2	8	4	5	6	9	7
F16	mean	1.02 × 10+01	9.06 × 10+00	9.90 × 10+00	1.11 × 10+01	9.97 × 10+00	9.87 × 10+00	1.20 × 10+01	1.18 × 10+01	1.01 × 10+01
	std	6.94 × 10−01	7.71 × 10−01	6.10 × 10−01	4.34 × 10−01	7.63 × 10−01	4.80 × 10−01	3.45 × 10−01	4.74 × 10−01	2.94 × 10−01
	rank	6	1	3	7	4	2	9	8	5
F17	mean	1.61 × 10+03	3.55 × 10+05	3.60 × 10+05	4.36 × 10+05	4.82 × 10+05	3.08 × 10+05	1.12 × 10+05	1.05 × 10+06	7.43 × 10+05
	std	3.57 × 10+03	1.64 × 10+05	3.37 × 10+05	2.93 × 10+05	9.50 × 10+05	1.97 × 10+05	7.20 × 10+04	5.32 × 10+05	3.76 × 10+05
	rank	1	4	5	6	7	3	2	9	8
F18	mean	1.31 × 10+02	3.03 × 10+03	3.21 × 10+02	1.14 × 10+03	5.01 × 10+03	3.73 × 10+02	1.30 × 10+03	8.92 × 10+04	1.05 × 10+02
	std	5.53 × 10+01	1.97 × 10+03	2.33 × 10+02	1.26 × 10+03	4.88 × 10+03	3.88 × 10+02	2.07 × 10+03	2.85 × 10+05	3.93 × 10+01
	rank	2	7	3	5	8	4	6	9	1
F19	mean	6.77 × 10+00	5.64 × 10+00	6.24 × 10+00	6.36 × 10+00	1.74 × 10+01	5.69 × 10+00	6.85 × 10+00	9.79 × 10+00	8.36 × 10+00
	std	2.79 × 10+00	1.42 × 10+00	1.63 × 10+00	1.24 × 10+00	2.51 × 10+01	1.45 × 10+00	1.25 × 10+00	4.85 × 10+00	1.54 × 10+00
	rank	5	1	3	4	9	2	6	8	7
F20	mean	2.09 × 10+02	4.91 × 10+02	6.37 × 10+02	5.18 × 10+02	7.00 × 10+03	4.12 × 10+02	1.77 × 10+04	9.81 × 10+03	2.28 × 10+03
	std	4.01 × 10+02	4.08 × 10+02	9.01 × 10+02	1.98 × 10+02	1.54 × 10+04	2.19 × 10+02	8.83 × 10+03	9.32 × 10+03	1.64 × 10+03
	rank	1	3	5	4	7	2	9	8	6
F21	mean	6.35 × 10+02	4.22 × 10+04	3.31 × 10+04	5.49 × 10+04	8.99 × 10+04	5.40 × 10+04	5.73 × 10+04	2.84 × 10+05	6.22 × 10+04
	std	4.21 × 10+02	3.51 × 10+04	2.43 × 10+04	4.28 × 10+04	3.66 × 10+05	4.77 × 10+04	4.26 × 10+04	3.08 × 10+05	3.40 × 10+04
	rank	1	3	2	5	8	4	6	9	7
F22	mean	1.58 × 10+02	1.43 × 10+02	1.30 × 10+02	1.77 × 10+02	4.25 × 10+02	1.06 × 10+02	1.67 × 10+02	2.88 × 10+02	1.50 × 10+02
	std	1.17 × 10+02	8.53 × 10+01	8.84 × 10+01	1.16 × 10+02	1.94 × 10+02	9.88 × 10+01	1.41 × 10+02	1.58 × 10+02	8.62 × 10+01
	rank	5	3	2	7	9	1	6	8	4
F23	mean	3.14 × 10+02	3.16 × 10+02	3.15 × 10+02	3.15 × 10+02	3.16 × 10+02	3.16 × 10+02	3.15 × 10+02	3.17 × 10+02	3.15 × 10+02
	std	1.83 × 10−09	1.52 × 10−01	4.11 × 10−02	3.99 × 10−02	2.98 × 10−01	1.32 × 10−01	1.22 × 10−12	3.83 × 10−01	2.30 × 10−02
	rank	1	8	3	5	6	7	2	9	4
F24	mean	2.26 × 10+02	2.26 × 10+02	2.25 × 10+02	2.26 × 10+02	2.32 × 10+02	2.26 × 10+02	2.30 × 10+02	2.30 × 10+02	2.22 × 10+02
	std	1.63 × 10+00	1.62 × 10+00	2.35 × 10+00	1.48 × 10+00	5.32 × 10+00	4.71 × 10+00	5.80 × 10+00	2.31 × 10+00	9.71 × 10+00
	rank	6	5	2	4	9	3	8	7	1
F25	mean	2.01 × 10+02	2.06 × 10+02	2.07 × 10+02	2.07 × 10+02	2.11 × 10+02	2.07 × 10+02	2.06 × 10+02	2.10 × 10+02	2.09 × 10+02
	std	3.69 × 10+00	1.27 × 10+00	1.13 × 10+00	1.24 × 10+00	3.10 × 10+00	1.21 × 10+00	1.76 × 10+00	2.23 × 10+00	9.39 × 10−01
	rank	1	3	4	6	9	5	2	8	7
F26	mean	1.00 × 10+02	1.00 × 10+02	1.00 × 10+02	1.00 × 10+02	1.07 × 10+02	1.00 × 10+02	1.10 × 10+02	1.04 × 10+02	1.00 × 10+02
	std	7.26 × 10−02	3.15 × 10−02	5.43 × 10−02	6.16 × 10−02	2.49 × 10+01	5.52 × 10−02	3.00 × 10+01	1.80 × 10+01	6.51 × 10−02
	rank	3	1	4	6	8	2	9	7	5
F27	mean	4.48 × 10+02	3.80 × 10+02	4.06 × 10+02	4.04 × 10+02	5.16 × 10+02	4.07 × 10+02	3.56 × 10+02	4.96 × 10+02	4.13 × 10+02
	std	4.74 × 10+01	3.49 × 10+01	4.10 × 10+00	2.22 × 10+00	9.03 × 10+01	4.07 × 10+00	4.46 × 10+01	9.50 × 10+01	4.61 × 10+00
	rank	7	2	4	3	9	5	1	8	6
F28	mean	9.23 × 10+02	9.18 × 10+02	9.23 × 10+02	9.28 × 10+02	1.02 × 10+03	9.50 × 10+02	9.05 × 10+02	1.20 × 10+03	1.01 × 10+03
	std	1.19 × 10+02	3.21 × 10+01	4.80 × 10+01	5.90 × 10+01	1.79 × 10+02	4.12 × 10+01	6.06 × 10+01	1.38 × 10+02	4.88 × 10+01
	rank	3	2	4	5	8	6	1	9	7
F29	mean	1.28 × 10+03	1.33 × 10+03	1.11 × 10+03	1.36 × 10+03	1.50 × 10+03	1.07 × 10+03	1.80 × 10+03	2.97 × 10+06	9.22 × 10+02
	std	3.06 × 10+02	2.23 × 10+02	1.48 × 10+02	2.11 × 10+02	4.47 × 10+02	1.17 × 10+02	5.00 × 10+02	9.21 × 10+06	1.08 × 10+02
	rank	4	5	3	6	7	2	8	9	1
F30	mean	1.30 × 10+03	4.40 × 10+03	2.72 × 10+03	3.15 × 10+03	1.31 × 10+04	3.24 × 10+03	3.26 × 10+03	7.21 × 10+03	3.71 × 10+03
	std	9.99 × 10+02	1.59 × 10+03	6.89 × 10+02	1.01 × 10+03	9.25 × 10+03	1.05 × 10+03	9.66 × 10+02	4.38 × 10+03	8.10 × 10+02
	rank	1	7	2	3	9	4	5	8	6
Average rank		3.17	4.20	3.20	5.57	6.63	3.87	5.27	8.17	4.93
Final rank		1	4	2	7	8	3	6	9	5
Best/2nd Best/Worst		12/2/0	5/4/2	2/7/0	0/0/0	2/2/7	1/6/0	5/6/7	0/0/13	3/3/1

, with the best rank results highlighted in bold. Additionally,

Table 4. Wilcoxon rank sum test results for 30D CEC2014 test suite problems.

Functions	Pairwise Comparison HGCLPSO Versus
	HCLDMS-PSO	TSLPSO	EPSO	GL-PSO	HCLPSO	SL-PSO	OLPSO	CLPSO
F1	+	+	+	+	+	+	+	+
F2	+	+	+	=	+	+	+	+
F3	+	+	+	+	+	+	+	+
F4	+	+	+	+	+	+	+	+
F5	+	+	+	=	+	+	+	+
F6	−	−	−	=	−	−	=	+
F7	=	=	=	=	=	=	+	=
F8	+	+	+	=	+	+	+	=
F9	−	=	=	=	=	−	+	=
F10	+	+	+	=	+	+	+	+
F11	−	−	=	=	−	−	+	=
F12	+	+	+	=	+	+	+	+
F13	−	=	+	+	=	−	+	+
F14	=	=	+	+	=	+	+	=
F15	=	=	+	=	=	−	+	+
F16	−	=	+	=	−	+	+	=
F17	+	+	+	+	+	+	+	+
F18	+	+	+	+	+	+	+	=
F19	=	=	=	=	=	=	+	+
F20	+	+	+	+	+	+	+	+
F21	+	+	+	+	+	+	+	+
F22	=	−	+	+	−	=	+	=
F23	+	+	+	+	+	+	+	+
F24	=	=	=	+	=	+	+	−
F25	+	+	+	+	+	+	+	+
F26	−	−	=	=	−	−	=	=
F27	−	−	−	+	−	−	+	−
F28	=	=	=	+	+	−	+	+
F29	=	−	=	=	−	+	+	−
F30	+	+	+	+	+	+	+	+
+/=/−	15/8/7	15/9/6	20/8/2	16/14/0	16/7/7	19/3/8	28/2/0	18/9/3

presents the statistical results of the Wilcoxon rank sum test, while

Table 5. Ranks obtained through Friedman test for 30D CEC2014 test suite problems.

Algorithm	HGCLPSO	HCLDMS-PSO	TSLPSO	EPSO	GL-PSO	HCLPSO	SL-PSO	OLPSO	CLPSO
Average rank	3.62	4.56	3.89	5.44	5.39	4.44	4.81	7.68	5.17
Final rank	1	4	2	8	7	3	5	9	6
p-value	2.30461 × 10−13

displays the Friedman test rankings for all the algorithms when applied to 30-dimensional problems.

For F1–F3, HGCLPSO outperforms others on functions F1 and F3. GL-PSO, however, provides the best solution on F2. Notably, HGCLPSO ranks third on F2, demonstrating that it benefits from the strong exploitation capabilities of GL-PSO, contributing to its excellent performance on uni-modal problems. In the case of F4–F16, HGCLPSO ranks first on F4, F5, F8, and F12, and second on F10. SL-PSO performs best on multi-modal functions F6, F9, and F11. HCLDMS-PSO leads on F13, F15, and F16, while TSLPSO excels on F7 and F14. GL-PSO ranks highest on F10. For hybrid and composition functions F17–F30, HGCLPSO delivers the best results on F17, F20, and F21, as well as on F23, F25, and F30—totaling six out of 14 test functions. CLPSO performs best on F18, F24, and F29. HCLDMS-PSO achieves the best solution on F19 and F26, while SL-PSO excels on F27 and F28. HCLPSO outperforms others on F22. Overall, HGCLPSO demonstrates the strongest performance, mainly due to the exploration capabilities of its CLS sub-population. The final row of Table 3 summarizes the number of (Best/2nd Best/Worst) rankings for each algorithm. In total, HGCLPSO delivers the best performance on 12 out of 30 benchmark problems, achieving the highest overall ranking, while TSLPSO ranks second among the compared PSO algorithms.

Table 4 demonstrate that HGCLPSO outperforms the other eight PSO variants on most of the 30D CEC2014 test problems. Notably, it achieves significantly better solutions on F1, F3, F4, F17, F20, F21, F25, and F30, surpassing all other algorithms in these cases. Additionally, the Friedman test results in the last row of Table 5 reveal a p-value of 2.30461 × 10⁻¹³, indicating that there are statistically significant differences between the nine algorithms. The average rank of HGCLPSO across all 30D CEC2014 benchmark functions is 3.62, confirming that it is the top-performing PSO variant in the comparison.

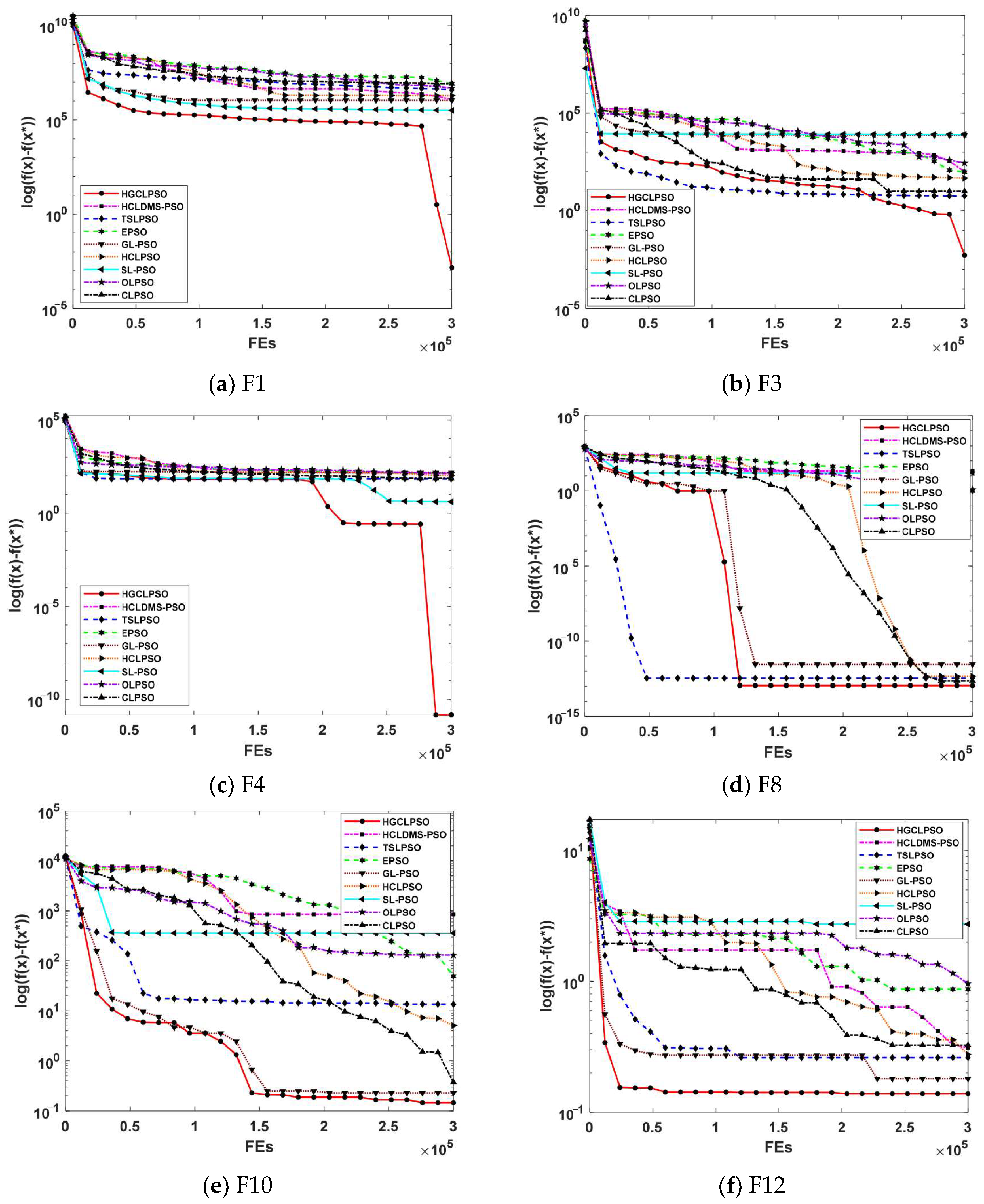
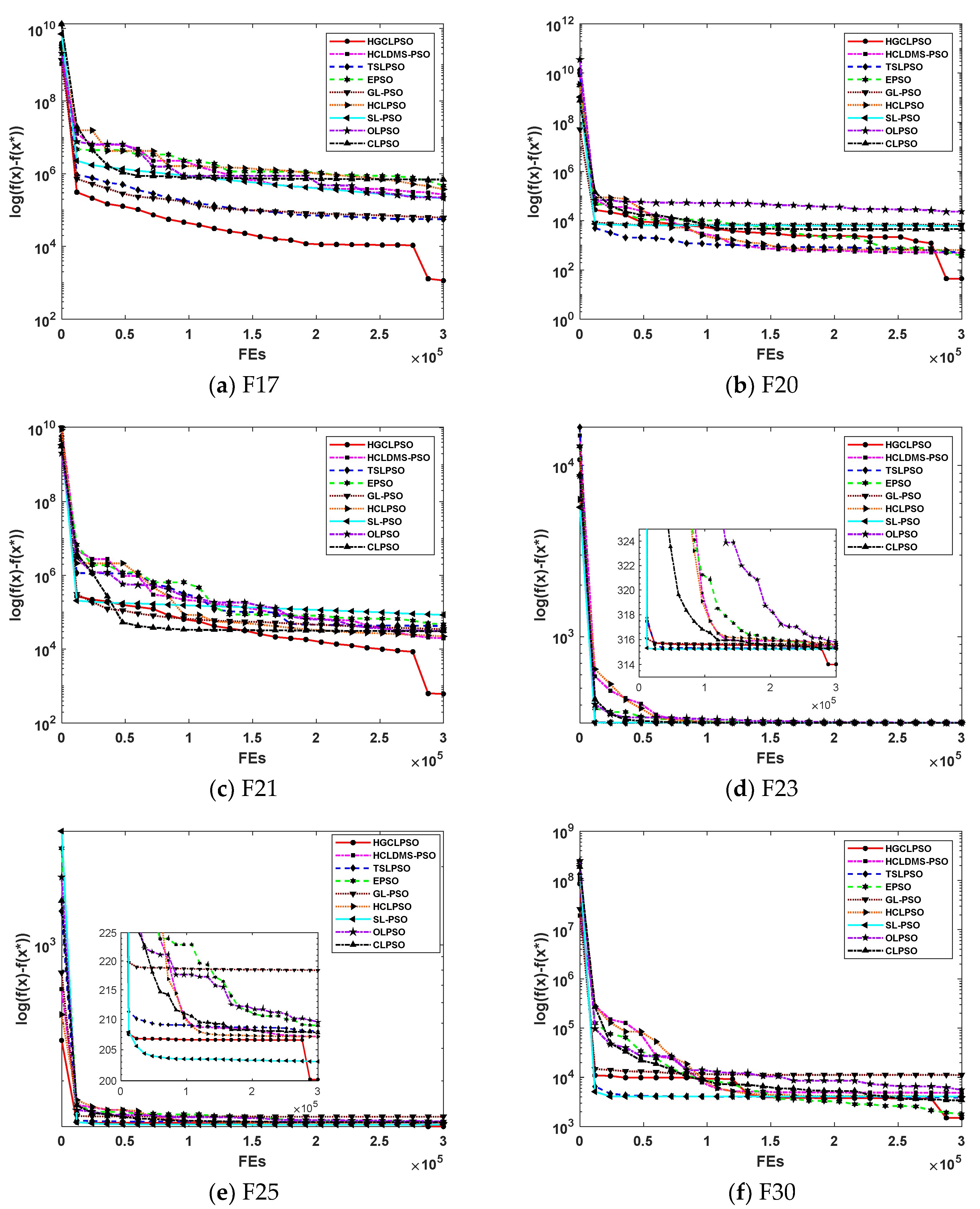
To analyze the convergence performance, convergence graphs based on 31 runs for the 30D problems are presented. Figure 3 and Figure 4 show the convergence curve of the nine PSO variants for 12 CEC2014 benchmark functions, i.e., F1, F3, F4, F8, F10, F12, F17, F20, F21, F23, F25, and F30. It is evident from the graphs that HGCLPSO demonstrates a faster convergence rate compared to the other eight PSO variants in the early stages of evolution, particularly on F1, F10, F17, F21, and F25. While algorithms like TSLPSO, SL-PSO, and GL-PSO also show rapid convergence on functions such as F3, F4, F10, F12, F20, F23, and F30, HGCLPSO leverages its local search capabilities in the later stages to achieve better overall solutions. In summary, the convergence analysis confirms that HGCLPSO not only converges quickly but also consistently delivers superior performance across most 30D benchmark problems.

4.2.2. Results for 50 Dimensional Problems

For the 50D CEC2014 test suite functions, the parameters are set as follows: population size = 40, number of runs = 51, and MaxFEs = 500,000. The experimental results are summarized in

Table 6. Comparison of experimental results for nine PSO variants on 50D CEC2014 test functions.

Functions	Criteria	HGCLPSO	HCLDMS-PSO	TSLPSO	EPSO	GL-PSO	HCLPSO	SL-PSO	OLPSO	CLPSO
F1	mean	2.76 × 10−01	5.97 × 10+06	5.17 × 10+06	1.01 × 10+07	1.14 × 10+07	8.06 × 10+06	7.75 × 10+05	1.13 × 10+08	1.86 × 10+07
	std	1.09 × 10+00	3.69 × 10+06	4.11 × 10+06	8.42 × 10+06	9.11 × 10+06	7.69 × 10+06	2.83 × 10+05	3.27 × 10+07	5.13 × 10+06
	rank	1	4	3	6	7	5	2	9	8
F2	mean	3.72 × 10+01	1.35 × 10+03	7.57 × 10+02	1.54 × 10+04	6.30 × 10+03	3.19 × 10+02	9.10 × 10+03	7.29 × 10+08	2.14 × 10+01
	std	1.32 × 10+02	1.34 × 10+03	2.64 × 10+03	2.30 × 10+04	6.68 × 10+03	2.72 × 10+02	8.63 × 10+03	2.58 × 10+08	1.99 × 10+01
	rank	2	5	4	8	6	3	7	9	1
F3	mean	1.11 × 10−01	2.29 × 10+03	3.34 × 10+02	1.54 × 10+03	2.23 × 10+03	2.16 × 10+03	1.92 × 10+04	1.00 × 10+05	3.47 × 10+03
	std	2.03 × 10−01	1.18 × 10+03	4.00 × 10+02	8.31 × 10+02	3.19 × 10+03	1.48 × 10+03	8.08 × 10+03	2.32 × 10+04	1.48 × 10+03
	rank	1	6	2	3	5	4	8	9	7
F4	mean	2.35 × 10−01	1.35 × 10+02	1.02 × 10+02	1.35 × 10+02	1.89 × 10+02	1.31 × 10+02	9.24 × 10+01	3.79 × 10+02	1.26 × 10+02
	std	9.47 × 10−01	2.84 × 10+01	1.83 × 10+01	2.18 × 10+01	4.77 × 10+01	1.56 × 10+01	6.28 × 10+00	5.63 × 10+01	1.57 × 10+01
	rank	1	7	3	6	8	5	2	9	4
F5	mean	2.00 × 10+01	2.04 × 10+01	2.01 × 10+01	2.08 × 10+01	2.00 × 10+01	2.04 × 10+01	2.11 × 10+01	2.12 × 10+01	2.05 × 10+01
	std	4.56 × 10−06	8.07 × 10−02	7.66 × 10−02	5.15 × 10−02	6.61 × 10−02	5.48 × 10−02	3.00 × 10−02	4.61 × 10−02	3.49 × 10−02
	rank	1	4	3	7	2	5	8	9	6
F6	mean	2.34 × 10+01	1.20 × 10+01	1.71 × 10+01	1.92 × 10+01	2.29 × 10+01	2.36 × 10+01	1.57 × 10+00	3.40 × 10+01	3.01 × 10+01
	std	4.98 × 10+00	3.76 × 10+00	4.35 × 10+00	4.35 × 10+00	5.75 × 10+00	4.25 × 10+00	1.42 × 10+00	3.22 × 10+00	1.92 × 10+00
	rank	6	2	3	4	5	7	1	9	8
F7	mean	4.52 × 10−03	5.05 × 10−03	4.96 × 10−04	3.76 × 10−03	5.84 × 10−03	5.87 × 10−03	1.21 × 10−03	7.27 × 10+00	3.20 × 10−03
	std	9.54 × 10−03	6.74 × 10−03	8.15 × 10−04	6.53 × 10−03	6.77 × 10−03	8.67 × 10−03	2.85 × 10−03	2.18 × 10+00	2.54 × 10−03
	rank	5	6	1	4	7	8	2	9	3
F8	mean	2.03 × 10−13	5.36 × 10+01	3.81 × 10−13	1.16 × 10+01	3.39 × 10−13	1.95 × 10−02	3.56 × 10+01	9.06 × 10+01	2.27 × 10−13
	std	2.75 × 10−13	9.14 × 10+00	7.48 × 10−14	5.24 × 10+00	9.49 × 10−13	1.39 × 10−01	8.32 × 10+00	1.54 × 10+01	2.27 × 10−14
	rank	1	8	4	6	3	5	7	9	2
F9	mean	1.15 × 10+02	5.71 × 10+01	1.05 × 10+02	1.15 × 10+02	1.06 × 10+02	1.13 × 10+02	1.78 × 10+02	3.76 × 10+02	1.21 × 10+02
	std	2.91 × 10+01	1.06 × 10+01	1.96 × 10+01	2.24 × 10+01	1.84 × 10+01	1.55 × 10+01	9.14 × 10+01	2.61 × 10+01	1.51 × 10+01
	rank	6	1	2	5	3	4	8	9	7
F10	mean	6.36 × 10−01	1.96 × 10+03	2.53 × 10+01	2.50 × 10+02	3.90 × 10−01	5.44 × 10+00	1.10 × 10+03	2.45 × 10+03	2.98 × 10+00
	std	8.06 × 10−01	4.58 × 10+02	4.77 × 10+01	2.16 × 10+02	3.51 × 10−01	1.33 × 10+00	4.49 × 10+02	5.74 × 10+02	1.00 × 10+00
	rank	2	8	5	6	1	4	7	9	3
F11	mean	4.93 × 10+03	4.80 × 10+03	4.81 × 10+03	4.99 × 10+03	4.96 × 10+03	4.17 × 10+03	2.04 × 10+03	1.18 × 10+04	4.62 × 10+03
	std	7.22 × 10+02	6.66 × 10+02	8.11 × 10+02	1.24 × 10+03	7.57 × 10+02	5.16 × 10+02	7.03 × 10+02	6.15 × 10+02	3.32 × 10+02
	rank	6	4	5	8	7	2	1	9	3
F12	mean	1.64 × 10−01	4.65 × 10−01	2.00 × 10−01	8.90 × 10−01	1.72 × 10−01	3.23 × 10−01	3.26 × 10+00	3.25 × 10+00	3.74 × 10−01
	std	5.24 × 10−02	1.49 × 10−01	6.04 × 10−02	1.11 × 10−01	8.60 × 10−02	6.90 × 10−02	4.21 × 10−01	3.54 × 10−01	4.64 × 10−02
	rank	1	6	3	7	2	4	9	8	5
F13	mean	3.52 × 10−01	2.28 × 10−01	3.32 × 10−01	4.82 × 10−01	4.56 × 10−01	3.44 × 10−01	2.92 × 10−01	8.54 × 10−01	3.74 × 10−01
	std	8.00 × 10−02	3.83 × 10−02	6.62 × 10−02	8.34 × 10−02	8.37 × 10−02	6.11 × 10−02	4.67 × 10−02	1.01 × 10−01	4.58 × 10−02
	rank	5	1	3	8	7	4	2	9	6
F14	mean	3.25 × 10−01	3.26 × 10−01	2.84 × 10−01	3.32 × 10−01	5.16 × 10−01	3.11 × 10−01	4.05 × 10−01	1.95 × 10+00	3.16 × 10−01
	std	1.63 × 10−01	1.86 × 10−01	3.75 × 10−02	3.64 × 10−02	2.25 × 10−01	3.65 × 10−02	1.36 × 10−01	1.07 × 10+00	1.98 × 10−02
	rank	4	5	1	6	8	2	7	9	3
F15	mean	1.46 × 10+01	9.62 × 10+00	8.99 × 10+00	2.08 × 10+01	1.41 × 10+01	1.20 × 10+01	2.84 × 10+01	1.14 × 10+02	1.78 × 10+01
	std	4.24 × 10+00	2.06 × 10+00	1.86 × 10+00	8.85 × 10+00	4.63 × 10+00	3.32 × 10+00	1.60 × 10+00	4.16 × 10+01	2.18 × 10+00
	rank	5	2	1	7	4	3	8	9	6
F16	mean	1.81 × 10+01	1.85 × 10+01	1.84 × 10+01	2.01 × 10+01	1.82 × 10+01	1.83 × 10+01	2.19 × 10+01	2.22 × 10+01	1.87 × 10+01
	std	8.86 × 10−01	7.27 × 10−01	7.20 × 10−01	6.18 × 10−01	9.31 × 10−01	6.97 × 10−01	2.89 × 10−01	3.02 × 10−01	4.30 × 10−01
	rank	1	5	4	7	2	3	8	9	6
F17	mean	1.88 × 10+03	5.51 × 10+05	1.43 × 10+06	9.88 × 10+05	2.28 × 10+06	7.43 × 10+05	9.63 × 10+04	7.19 × 10+06	3.00 × 10+06
	std	6.47 × 10+02	3.50 × 10+05	1.05 × 10+06	6.62 × 10+05	3.05 × 10+06	7.18 × 10+05	5.05 × 10+04	2.90 × 10+06	1.12 × 10+06
	rank	1	3	6	5	7	4	2	9	8
F18	mean	5.10 × 10+02	5.57 × 10+02	2.50 × 10+02	4.13 × 10+02	1.05 × 10+03	1.56 × 10+02	1.56 × 10+03	1.75 × 10+06	1.46 × 10+02
	std	8.15 × 10+02	5.97 × 10+02	1.53 × 10+02	2.09 × 10+02	1.15 × 10+03	5.35 × 10+01	1.40 × 10+03	1.51 × 10+06	3.98 × 10+01
	rank	5	6	3	4	7	2	8	9	1
F19	mean	4.74 × 10+01	4.87 × 10+01	1.76 × 10+01	2.50 × 10+01	5.51 × 10+01	3.56 × 10+01	1.92 × 10+01	7.57 × 10+01	1.90 × 10+01
	std	1.97 × 10+01	1.89 × 10+01	4.58 × 10+00	1.51 × 10+01	2.04 × 10+01	1.85 × 10+01	7.23 × 10+00	1.74 × 10+01	2.98 × 10+00
	rank	6	7	1	4	8	5	3	9	2
F20	mean	1.81 × 10+02	9.34 × 10+02	1.08 × 10+03	1.32 × 10+03	7.53 × 10+03	1.74 × 10+03	2.50 × 10+04	4.31 × 10+04	1.01 × 10+04
	std	3.91 × 10+02	5.20 × 10+02	1.11 × 10+03	6.22 × 10+02	6.02 × 10+03	1.44 × 10+03	1.10 × 10+04	1.83 × 10+04	4.25 × 10+03
	rank	1	2	3	4	6	5	8	9	7
F21	mean	1.36 × 10+03	3.54 × 10+05	6.35 × 10+05	5.07 × 10+05	7.43 × 10+05	4.41 × 10+05	1.15 × 10+05	4.15 × 10+06	1.68 × 10+06
	std	7.02 × 10+02	2.02 × 10+05	6.12 × 10+05	3.81 × 10+05	1.37 × 10+06	4.98 × 10+05	6.01 × 10+04	2.13 × 10+06	5.23 × 10+05
	rank	1	3	6	5	7	4	2	9	8
F22	mean	6.07 × 10+02	3.07 × 10+02	5.44 × 10+02	6.65 × 10+02	1.04 × 10+03	6.22 × 10+02	3.09 × 10+02	1.06 × 10+03	6.02 × 10+02
	std	2.69 × 10+02	1.32 × 10+02	1.71 × 10+02	2.11 × 10+02	3.33 × 10+02	1.51 × 10+02	2.00 × 10+02	2.97 × 10+02	1.55 × 10+02
	rank	5	1	3	7	8	6	2	9	4
F23	mean	3.37 × 10+02	3.47 × 10+02	3.44 × 10+02	3.45 × 10+02	3.46 × 10+02	3.45 × 10+02	3.44 × 10+02	3.60 × 10+02	3.44 × 10+02
	std	6.61 × 10−09	6.93 × 10−01	1.15 × 10−01	1.97 × 10−01	9.77 × 10−01	2.54 × 10−01	4.20 × 10−13	3.01 × 10+00	8.45 × 10−02
	rank	1	8	3	6	7	5	2	9	4
F24	mean	2.67 × 10+02	2.67 × 10+02	2.63 × 10+02	2.63 × 10+02	2.71 × 10+02	2.66 × 10+02	2.74 × 10+02	3.01 × 10+02	2.63 × 10+02
	std	3.89 × 10+00	4.85 × 10+00	4.30 × 10+00	3.73 × 10+00	6.30 × 10+00	3.44 × 10+00	3.20 × 10+00	4.09 × 10+00	3.23 × 10+00
	rank	5	6	1	3	7	4	8	9	2
F25	mean	2.00 × 10+02	2.15 × 10+02	2.15 × 10+02	2.17 × 10+02	2.24 × 10+02	2.17 × 10+02	2.11 × 10+02	2.34 × 10+02	2.17 × 10+02
	std	1.56 × 10−02	2.43 × 10+00	2.14 × 10+00	3.29 × 10+00	4.05 × 10+00	2.06 × 10+00	2.88 × 10+00	6.18 × 10+00	1.43 × 10+00
	rank	1	4	3	7	8	5	2	9	6
F26	mean	1.00 × 10+02	1.00 × 10+02	1.00 × 10+02	1.00 × 10+02	1.40 × 10+02	1.00 × 10+02	1.55 × 10+02	1.45 × 10+02	1.00 × 10+02
	std	4.37 × 10−01	6.34 × 10−02	7.68 × 10−02	7.47 × 10−02	4.96 × 10+01	6.21 × 10−02	5.00 × 10+01	8.71 × 10+01	6.09 × 10−02
	rank	2	1	3	6	7	4	9	8	5
F27	mean	7.31 × 10+02	5.18 × 10+02	6.66 × 10+02	7.26 × 10+02	9.22 × 10+02	7.88 × 10+02	4.48 × 10+02	1.14 × 10+03	6.78 × 10+02
	std	9.45 × 10+01	5.66 × 10+01	1.91 × 10+02	2.09 × 10+02	1.03 × 10+02	1.90 × 10+02	5.99 × 10+01	6.49 × 10+01	2.55 × 10+02
	rank	6	2	3	5	8	7	1	9	4
F28	mean	1.53 × 10+03	1.34 × 10+03	1.44 × 10+03	1.52 × 10+03	1.89 × 10+03	1.55 × 10+03	1.35 × 10+03	2.48 × 10+03	1.81 × 10+03
	std	2.00 × 10+02	7.52 × 10+01	1.16 × 10+02	1.62 × 10+02	4.48 × 10+02	1.03 × 10+02	1.68 × 10+02	1.61 × 10+02	1.12 × 10+02
	rank	5	1	3	4	8	6	2	9	7
F29	mean	1.81 × 10+03	2.56 × 10+03	1.87 × 10+03	2.47 × 10+03	7.66 × 10+06	1.72 × 10+03	2.45 × 10+03	1.81 × 10+07	1.43 × 10+03
	std	3.19 × 10+02	1.07 × 10+03	3.14 × 10+02	7.96 × 10+02	2.66 × 10+07	2.69 × 10+02	4.48 × 10+02	4.52 × 10+07	1.60 × 10+02
	rank	3	7	4	6	8	2	5	9	1
F30	mean	4.74 × 10+03	1.66 × 10+04	1.35 × 10+04	2.10 × 10+04	3.93 × 10+04	1.83 × 10+04	1.19 × 10+04	5.00 × 10+04	1.48 × 10+04
	std	2.26 × 10+03	1.95 × 10+03	2.37 × 10+03	4.13 × 10+03	1.69 × 10+04	3.04 × 10+03	1.85 × 10+03	1.37 × 10+04	1.61 × 10+03
	rank	1	5	3	7	8	6	2	9	4
Average rank		3.03	4.33	3.07	5.70	6.03	4.43	4.77	8.93	4.70
Final rank		1	3	2	7	8	4	6	9	5
Best/2nd Best/Worst		13/3/0	5/4/0	5/2/0	0/0/0	1/3/0	0/4/0	3/11/2	0/0/28	3/3/0

,

Table 7. Wilcoxon rank sum test results with a significance level of $\alpha =0.05$ for 50D CEC2014 test suite problems.

Functions	Pairwise Comparison HGCLPSO Versus
	HCLDMS-PSO	TSLPSO	EPSO	GL-PSO	HCLPSO	SL-PSO	OLPSO	CLPSO
F1	+	+	+	+	+	+	+	+
F2	+	+	+	+	+	+	+	+
F3	+	+	+	+	+	+	+	+
F4	+	+	+	+	+	+	+	+
F5	+	+	+	=	+	+	+	+
F6	−	−	−	=	=	−	+	+
F7	=	−	=	=	=	−	+	=
F8	+	+	+	=	+	+	+	+
F9	−	=	=	=	=	+	+	=
F10	+	+	+	=	+	+	+	+
F11	=	=	=	=	−	−	+	−
F12	+	+	+	=	+	+	+	+
F13	−	−	+	+	−	−	+	−
F14	=	−	=	+	=	+	+	=
F15	−	−	+	=	−	+	+	+
F16	+	=	+	=	=	+	+	+
F17	+	+	+	+	+	+	+	+
F18	=	−	=	=	−	+	+	−
F19	=	−	−	=	−	−	+	−
F20	+	+	+	+	+	+	+	+
F21	+	+	+	+	+	+	+	+
F22	−	=	=	+	=	−	+	=
F23	+	+	+	+	+	+	+	+
F24	=	=	=	+	=	+	+	=
F25	+	+	+	+	+	+	+	+
F26	=	=	=	+	=	+	+	=
F27	−	−	=	+	=	−	+	−
F28	−	−	=	+	=	−	+	+
F29	+	=	+	+	=	+	+	−
F30	+	+	+	+	+	+	+	+
+/=/−	16/7/7	14/7/9	18/10/2	18/12/0	14/11/5	22/0/8	30/0/0	18/6/6

and

Table 8. Ranks obtained through Friedman test for 50D CEC2014 test suite problems.

Algorithm	HGCLPSO	HCLDMS-PSO	TSLPSO	EPSO	GL-PSO	HCLPSO	SL-PSO	OLPSO	CLPSO
Average rank	3.37	4.36	3.61	5.38	5.41	4.47	4.67	8.83	4.90
Final rank	1	3	2	7	8	4	5	9	6
p-value	3.4904 × 10−17

. Since the convergence behavior is similar to that observed for the 30D problems, the corresponding convergence graphs are not included in this section.

For F1–F16, HGCLPSO outperforms the others on F1 and F3, and achieves the best results on F4, F5, F8, F12, and F16, totaling seven out of 16 test functions. CLPSO performs best on the uni-modal function F2, with HGCLPSO ranking second. TSLPSO excels on functions F7, F14, and F15. HCLDMS-PSO delivers the best solutions for F9 and F13. SL-PSO performs best on F6 and F11, while GL-PSO excels on F10. For the hybrid and composition functions F17–F30, HGCLPSO shows excellent performance on F17, F20, F21, F23, F25, and F30, achieving the best results in six out of 14 test problems. HCLDMS-PSO leads on F22, F26, and F28. TSLPSO performs best on F19 and F24, while CLPSO is the top performer on F18 and F29. SL-PSO achieves the best results on F27. As indicated by the average ranks in Table 6, HGCLPSO achieves the optimal average rank of 3.03, while TSLPSO ranks second with an average of 3.07. This outcome mirrors the 30D test problem results, where both algorithms are influenced by HGCLPSO’s performance on specific functions like F6, F9, F11, F19, and F27.

Table 7 reveals that HGCLPSO significantly outperforms the eight other PSO variants on most of the 50D CEC2014 test functions. Additionally, Table 8 presents the Friedman test rankings for all nine algorithms applied to the 50D problems. The p-value of 3.4904 × 10⁻¹⁷, reported in the last row of Table 8, strongly suggests that there are substantial differences between the nine algorithms. Among them, HGCLPSO ranks the highest with an average rank of 3.37, indicating its superior performance.

4.2.3. Results for Computational Time

Table 9. Comparison of mean computation time(s) for CEC2014 test suite problems.

Algorithm	HGCLPSO	HCLDMS-PSO	TSLPSO	EPSO	GL-PSO	HCLPSO	SL-PSO	OLPSO	CLPSO
30D problems	3.87	5.43	4.35	5.73	3.71	4.64	3.52	3.04	4.76
50D problems	9.11	13.29	9.84	12.65	9.02	10.48	8.34	7.19	10.84

presents the mean computation time of nine PSO algorithms. The computation time (in seconds) for each run was recorded for 30D and 50D CEC2014 problems. Among the compared algorithms, OLPSO requires the least computation time, followed by SL-PSO, which takes a slightly longer time. The computation times of the HGCLPSO and GL-PSO algorithms are nearly identical. The use of the CL strategy enhances the search performance of CLPSO, HCLPSO, and TSLPSO, but results in higher computational costs. EPSO and HCLDMS-PSO, which combine various PSO strategies to leverage their complementary strengths, also incur greater computational costs. Overall, HGCLPSO strikes a balance between competitive performance and computational efficiency, delivering excellent results without excessive time consumption.

4.3. Experimental Results and Analysis of CEC2017 Test Suite

In this section, the performance of HGCLPSO is also evaluated using 30D CEC2017 test suite problems [42], using the same parameter settings: MaxFEs set to 300,000, a population size of 40, and each algorithm is run independently 31 times. This comparison aims to show that HGCLPSO remains competitive when contrasted with several state-of-the-art EAs. In addition to HCLDMS-PSO, TSLPSO, GL-PSO, HCLPSO, and CLPSO discussed in Section 4.2, other advanced EAs are also included in the comparison, as follows:

• moth flame optimization (MFO) [45]
• whale optimization algorithm (WOA) [46]
• Artificial Bee Colony Algorithm (ABC) [47]
• butterfly optimization algorithm (BOA) [48]
• bat algorithm (BA) [49]
• grey wolf optimizer (GWO) [50]

The parameter settings for all PSO variants remain consistent with those used in the previous experiments, and the other EAs are based on the configurations from their original references. The mean errors and standard deviations are presented in

Table 10. The mean errors and standard deviation results obtained on 30D CEC2017 test suite problems.

Functions

F1

F3

F4

F5

F6

F7

Metrics

mean

std

mean

std

mean

std

mean

std

mean

std

mean

std

HGCLPSO

1.37 × 10+01

4.02 × 10+01

2.01 × 10−06

5.85 × 10−06

1.93 × 10+00

2.03 × 10+00

5.85 × 10+01

1.52 × 10+01

1.36 × 10−04

5.01 × 10−04

9.79 × 10+01

1.69 × 10+01

HCLDMS-PSO

8.78 × 10+02

1.19 × 10+03

4.41 × 10+01

4.62 × 10+01

1.03 × 10+02

7.74 × 10+00

2.63 × 10+01

6.24 × 10+00

1.74 × 10−02

1.44 × 10−02

3.45 × 10+01

1.15 × 10+01

TSLPSO

3.03 × 10+01

3.54 × 10+01

6.55 × 10+01

1.92 × 10+02

7.44 × 10+01

1.50 × 10+01

4.32 × 10+01

1.05 × 10+01

9.01 × 10−09

5.02 × 10−08

8.41 × 10+01

1.07 × 10+01

GLPSO

3.75 × 10+03

4.92 × 10+03

4.33 × 10+00

2.37 × 10+01

1.52 × 10+01

2.68 × 10+01

6.47 × 10+01

2.06 × 10+01

1.27 × 10−03

2.48 × 10−03

9.35 × 10+01

1.54 × 10+01

HCLPSO

1.33 × 10+02

2.90 × 10+02

3.73 × 10−04

5.99 × 10−04

4.82 × 10+01

2.94 × 10+01

5.02 × 10+01

9.75 × 10+00

3.41 × 10−13

9.74 × 10−14

8.44 × 10+01

9.21 × 10+00

CLPSO

2.04 × 10+01

4.09 × 10+01

2.49 × 10+04

7.84 × 10+03

6.08 × 10+01

2.19 × 10+01

4.77 × 10+01

6.86 × 10+00

3.41 × 10−11

2.18 × 10−11

8.41 × 10+01

8.73 × 10+00

ABC

2.63 × 10+02

3.25 × 10+02

1.27 × 10+05

2.62 × 10+04

3.91 × 10+01

3.03 × 10+01

9.69 × 10+01

1.41 × 10+01

1.83 × 10−14

4.25 × 10−14

1.11 × 10+02

1.14 × 10+01

MFO

1.16 × 10+10

6.72 × 10+09

8.34 × 10+04

5.93 × 10+04

8.35 × 10+02

7.38 × 10+02

1.80 × 10+02

4.47 × 10+01

3.53 × 10+01

1.05 × 10+01

4.41 × 10+02

1.86 × 10+02

WOA

2.31 × 10+06

1.75 × 10+06

1.63 × 10+05

6.60 × 10+04

1.43 × 10+02

4.02 × 10+01

2.91 × 10+02

5.50 × 10+01

7.02 × 10+01

1.16 × 10+01

5.22 × 10+02

7.94 × 10+01

BOA

4.39 × 10+10

6.18 × 10+09

7.07 × 10+04

9.62 × 10+03

6.45 × 10+03

2.70 × 10+03

3.46 × 10+02

3.00 × 10+01

7.01 × 10+01

1.01 × 10+01

5.64 × 10+02

5.07 × 10+01

GWO

1.43 × 10+09

1.19 × 10+09

3.66 × 10+04

1.10 × 10+04

1.72 × 10+02

7.70 × 10+01

1.05 × 10+02

4.12 × 10+01

6.62 × 10+00

3.75 × 10+00

1.45 × 10+02

4.67 × 10+01

BA

8.76 × 10+10

1.72 × 10+10

2.72 × 10+05

9.36 × 10+04

2.84 × 10+04

8.27 × 10+03

5.58 × 10+02

6.76 × 10+01

1.24 × 10+02

1.51 × 10+01

1.65 × 10+03

2.51 × 10+02

Functions

F8

F9

F10

F11

F12

F13

Metrics

mean

std

mean

std

mean

std

mean

std

mean

std

mean

std

HGCLPSO

5.96 × 10+01

1.14 × 10+01

9.99 × 10+01

1.46 × 10+02

2.96 × 10+03

5.04 × 10+02

5.00 × 10+01

2.10 × 10+01

8.73 × 10+02

3.72 × 10+02

3.06 × 10+02

3.72 × 10+02

HCLDMS-PSO

2.89 × 10+01

7.10 × 10+00

7.56 × 10−02

1.26 × 10−01

2.22 × 10+03

5.36 × 10+02

4.81 × 10+01

3.17 × 10+01

1.10 × 10+05

1.70 × 10+05

3.28 × 10+03

4.00 × 10+03

TSLPSO

5.08 × 10+01

8.79 × 10+00

2.35 × 10+01

2.73 × 10+01

2.33 × 10+03

5.55 × 10+02

4.35 × 10+01

2.23 × 10+01

1.37 × 10+05

2.31 × 10+05

8.47 × 10+02

5.08 × 10+02

GLPSO

5.53 × 10+01

1.54 × 10+01

4.29 × 10+01

5.84 × 10+01

2.80 × 10+03

6.32 × 10+02

6.43 × 10+01

3.50 × 10+01

1.89 × 10+04

7.96 × 10+03

1.26 × 10+04

1.23 × 10+04

HCLPSO

5.38 × 10+01

8.22 × 10+00

2.98 × 10+01

3.39 × 10+01

2.14 × 10+03

2.82 × 10+02

4.71 × 10+01

3.19 × 10+01

2.73 × 10+04

1.25 × 10+04

6.47 × 10+02

7.23 × 10+02

CLPSO

5.34 × 10+01

6.91 × 10+00

7.66 × 10+01

3.60 × 10+01

2.14 × 10+03

2.84 × 10+02

8.17 × 10+01

2.10 × 10+01

4.64 × 10+05

2.66 × 10+05

3.33 × 10+02

2.57 × 10+02

ABC

1.04 × 10+02

1.89 × 10+01

1.11 × 10+03

5.27 × 10+02

2.36 × 10+03

3.19 × 10+02

3.03 × 10+02

2.43 × 10+02

4.44 × 10+05

3.22 × 10+05

4.62 × 10+03

5.36 × 10+03

MFO

2.00 × 10+02

3.83 × 10+01

5.88 × 10+03

1.94 × 10+03

4.32 × 10+03

7.91 × 10+02

2.85 × 10+03

3.80 × 10+03

1.86 × 10+08

3.40 × 10+08

8.34 × 10+07

3.03 × 10+08

WOA

2.13 × 10+02

4.40 × 10+01

6.07 × 10+03

1.72 × 10+03

5.37 × 10+03

9.47 × 10+02

3.91 × 10+02

9.72 × 10+01

3.42 × 10+07

2.62 × 10+07

1.45 × 10+05

8.41 × 10+04

BOA

3.01 × 10+02

1.99 × 10+01

7.68 × 10+03

9.56 × 10+02

7.66 × 10+03

2.35 × 10+02

4.00 × 10+03

1.35 × 10+03

6.03 × 10+09

2.19 × 10+09

2.52 × 10+09

2.32 × 10+09

GWO

8.58 × 10+01

2.77 × 10+01

7.90 × 10+02

5.74 × 10+02

2.93 × 10+03

5.80 × 10+02

4.59 × 10+02

4.28 × 10+02

4.10 × 10+07

6.26 × 10+07

8.21 × 10+06

3.18 × 10+07

BA

4.87 × 10+02

6.30 × 10+01

2.41 × 10+04

7.29 × 10+03

8.86 × 10+03

5.45 × 10+02

4.00 × 10+04

2.09 × 10+04

1.85 × 10+10

4.33 × 10+09

1.59 × 10+10

7.21 × 10+09

Functions

F14

F15

F16

F17

F18

F19

Metrics

mean

std

mean

std

mean

std

mean

std

mean

std

mean

std

HGCLPSO

2.98 × 10+02

5.15 × 10+02

1.15 × 10+02

8.10 × 10+01

5.23 × 10+02

1.87 × 10+02

1.41 × 10+02

7.60 × 10+01

9.20 × 10+01

6.26 × 10+01

1.12 × 10+02

5.64 × 10+01

HCLDMS-PSO

3.84 × 10+03

3.85 × 10+03

1.15 × 10+04

7.15 × 10+03

2.72 × 10+02

1.88 × 10+02

8.34 × 10+01

3.53 × 10+01

8.57 × 10+04

5.34 × 10+04

1.45 × 10+04

1.33 × 10+04

TSLPSO

1.10 × 10+04

7.85 × 10+03

3.35 × 10+02

4.21 × 10+02

3.91 × 10+02

1.54 × 10+02

8.80 × 10+01

4.30 × 10+01

1.18 × 10+05

6.97 × 10+04

2.77 × 10+02

3.72 × 10+02

GLPSO

7.15 × 10+03

6.92 × 10+03

5.58 × 10+03

5.05 × 10+03

9.79 × 10+02

2.76 × 10+02

2.95 × 10+02

1.60 × 10+02

1.10 × 10+05

6.31 × 10+04

7.31 × 10+03

7.40 × 10+03

HCLPSO

7.94 × 10+03

6.90 × 10+03

3.23 × 10+02

3.74 × 10+02

5.78 × 10+02

1.59 × 10+02

1.62 × 10+02

9.48 × 10+01

1.07 × 10+05

7.10 × 10+04

2.05 × 10+02

3.74 × 10+02

CLPSO

2.57 × 10+04

1.98 × 10+04

1.32 × 10+02

7.68 × 10+01

5.27 × 10+02

1.57 × 10+02

1.61 × 10+02

6.67 × 10+01

1.62 × 10+05

8.99 × 10+04

6.70 × 10+01

5.23 × 10+01

ABC

1.12 × 10+05

8.61 × 10+04

8.96 × 10+02

6.87 × 10+02

6.94 × 10+02

2.05 × 10+02

3.06 × 10+02

1.00 × 10+02

2.07 × 10+05

1.11 × 10+05

1.67 × 10+03

2.15 × 10+03

MFO

1.34 × 10+05

3.18 × 10+05

3.77 × 10+04

2.47 × 10+04

1.55 × 10+03

3.26 × 10+02

8.20 × 10+02

2.44 × 10+02

1.97 × 10+06

4.20 × 10+06

1.33 × 10+07

3.64 × 10+07

WOA

8.01 × 10+05

9.48 × 10+05

8.12 × 10+04

7.55 × 10+04

1.87 × 10+03

3.64 × 10+02

7.56 × 10+02

2.76 × 10+02

2.08 × 10+06

2.15 × 10+06

2.89 × 10+06

2.11 × 10+06

BOA

1.05 × 10+06

1.00 × 10+06

9.61 × 10+07

1.00 × 10+08

2.47 × 10+03

3.53 × 10+02

9.48 × 10+02

1.77 × 10+02

9.49 × 10+06

8.76 × 10+06

1.47 × 10+08

1.61 × 10+08

GWO

2.80 × 10+05

4.07 × 10+05

5.25 × 10+05

9.48 × 10+05

7.70 × 10+02

2.49 × 10+02

2.83 × 10+02

1.74 × 10+02

1.16 × 10+06

1.62 × 10+06

5.61 × 10+05

1.48 × 10+06

BA

2.96 × 10+07

2.83 × 10+07

2.83 × 10+09

1.84 × 10+09

6.57 × 10+03

2.13 × 10+03

1.23 × 10+04

1.96 × 10+04

3.10 × 10+08

2.57 × 10+08

4.40 × 10+09

2.49 × 10+09

Functions

F20

F21

F22

F23

F24

F25

Metrics

mean

std

mean

std

mean

std

mean

std

mean

std

mean

std

HGCLPSO

2.04 × 10+02

6.46 × 10+01

2.67 × 10+02

1.94 × 10+01

4.80 × 10+02

1.02 × 10+03

4.06 × 10+02

1.25 × 10+01

5.00 × 10+02

2.38 × 10+01

3.81 × 10+02

3.29 × 10+00

HCLDMS-PSO

8.69 × 10+01

5.03 × 10+01

2.28 × 10+02

6.67 × 10+00

1.81 × 10+02

4.51 × 10+02

3.80 × 10+02

7.09 × 10+00

4.45 × 10+02

7.18 × 10+00

3.90 × 10+02

2.73 × 10+00

TSLPSO

1.22 × 10+02

7.21 × 10+01

2.55 × 10+02

1.20 × 10+01

3.61 × 10+02

7.03 × 10+02

3.95 × 10+02

8.95 × 10+00

4.58 × 10+02

6.83 × 10+01

3.88 × 10+02

9.78 × 10−01

GLPSO

4.32 × 10+02

1.54 × 10+02

2.65 × 10+02

2.00 × 10+01

8.08 × 10+02

1.48 × 10+03

4.22 × 10+02

2.05 × 10+01

4.94 × 10+02

2.68 × 10+01

3.90 × 10+02

9.55 × 10+00

HCLPSO

2.29 × 10+02

8.90 × 10+01

2.42 × 10+02

4.69 × 10+01

1.88 × 10+02

4.90 × 10+02

4.07 × 10+02

1.08 × 10+01

4.93 × 10+02

2.14 × 10+01

3.87 × 10+02

1.35 × 10+00

CLPSO

1.89 × 10+02

6.10 × 10+01

2.36 × 10+02

4.57 × 10+01

1.28 × 10+02

4.63 × 10+01

4.03 × 10+02

9.74 × 10+00

4.59 × 10+02

1.11 × 10+02

3.87 × 10+02

8.79 × 10−01

ABC

3.05 × 10+02

1.01 × 10+02

2.98 × 10+02

5.05 × 10+01

1.56 × 10+03

1.45 × 10+03

4.31 × 10+02

3.06 × 10+01

5.39 × 10+02

1.95 × 10+02

3.84 × 10+02

1.20 × 10+00

MFO

7.12 × 10+02

2.27 × 10+02

3.80 × 10+02

4.41 × 10+01

4.27 × 10+03

1.38 × 10+03

5.33 × 10+02

3.10 × 10+01

5.72 × 10+02

3.41 × 10+01

9.22 × 10+02

5.70 × 10+02

WOA

7.59 × 10+02

1.86 × 10+02

4.71 × 10+02

5.97 × 10+01

3.85 × 10+03

2.43 × 10+03

7.43 × 10+02

9.54 × 10+01

7.78 × 10+02

8.07 × 10+01

4.50 × 10+02

3.01 × 10+01

BOA

8.74 × 10+02

1.30 × 10+02

4.56 × 10+02

8.94 × 10+01

2.60 × 10+03

1.06 × 10+03

8.01 × 10+02

8.90 × 10+01

9.20 × 10+02

1.19 × 10+02

1.62 × 10+03

4.15 × 10+02

GWO

3.76 × 10+02

1.36 × 10+02

2.84 × 10+02

1.59 × 10+01

2.29 × 10+03

1.48 × 10+03

4.55 × 10+02

5.14 × 10+01

5.27 × 10+02

4.96 × 10+01

4.73 × 10+02

2.73 × 10+01

BA

1.57 × 10+03

1.66 × 10+02

7.56 × 10+02

8.05 × 10+01

9.11 × 10+03

7.53 × 10+02

1.62 × 10+03

2.10 × 10+02

1.88 × 10+03

2.51 × 10+02

7.13 × 10+03

2.25 × 10+03

Functions

F26

F27

F28

F29

F30

Metrics

mean

std

mean

std

mean

std

mean

std

mean

std

HGCLPSO

1.10 × 10+03

7.38 × 10+02

5.00 × 10+02

2.24 × 10+01

3.30 × 10+02

5.81 × 10+01

5.68 × 10+02

1.02 × 10+02

3.41 × 10+03

7.29 × 10+02

HCLDMS-PSO

1.26 × 10+03

1.09 × 10+02

5.18 × 10+02

5.78 × 10+00

4.25 × 10+02

2.56 × 10+01

4.95 × 10+02

4.04 × 10+01

8.80 × 10+03

3.20 × 10+03

TSLPSO

7.77 × 10+02

6.20 × 10+02

5.16 × 10+02

6.19 × 10+00

3.96 × 10+02

4.10 × 10+01

5.35 × 10+02

7.00 × 10+01

5.91 × 10+03

2.00 × 10+03

GLPSO

1.68 × 10+03

6.19 × 10+02

5.32 × 10+02

9.73 × 10+00

3.34 × 10+02

5.59 × 10+01

7.26 × 10+02

1.81 × 10+02

4.62 × 10+03

1.56 × 10+03

HCLPSO

5.24 × 10+02

5.29 × 10+02

5.16 × 10+02

6.52 × 10+00

3.48 × 10+02

5.44 × 10+01

5.83 × 10+02

7.36 × 10+01

5.17 × 10+03

2.16 × 10+03

CLPSO

6.63 × 10+02

4.19 × 10+02

5.13 × 10+02

5.53 × 10+00

4.28 × 10+02

1.21 × 10+01

5.65 × 10+02

7.02 × 10+01

6.64 × 10+03

1.95 × 10+03

ABC

7.82 × 10+02

8.96 × 10+02

5.15 × 10+02

5.00 × 10+00

3.94 × 10+02

1.50 × 10+01

6.57 × 10+02

1.00 × 10+02

5.57 × 10+03

1.54 × 10+03

MFO

3.26 × 10+03

5.44 × 10+02

5.58 × 10+02

2.42 × 10+01

1.28 × 10+03

8.45 × 10+02

1.31 × 10+03

2.79 × 10+02

6.40 × 10+05

7.56 × 10+05

WOA

4.92 × 10+03

1.09 × 10+03

6.74 × 10+02

1.04 × 10+02

4.91 × 10+02

2.97 × 10+01

1.82 × 10+03

3.86 × 10+02

9.68 × 10+06

8.21 × 10+06

BOA

5.76 × 10+03

1.14 × 10+03

7.47 × 10+02

9.18 × 10+01

2.68 × 10+03

7.12 × 10+02

2.31 × 10+03

4.15 × 10+02

2.28 × 10+08

1.41 × 10+08

GWO

2.03 × 10+03

3.58 × 10+02

5.39 × 10+02

1.75 × 10+01

6.02 × 10+02

7.33 × 10+01

8.96 × 10+02

1.99 × 10+02

5.59 × 10+06

4.93 × 10+06

BA

1.18 × 10+04

2.23 × 10+03

2.65 × 10+03

4.72 × 10+02

7.77 × 10+03

2.25 × 10+03

1.14 × 10+04

8.02 × 10+03

2.50 × 10+09

1.23 × 10+09

, while the ranks of mean performance and the Wilcoxon rank sum test results are shown in

Table 11. Rank of mean performance and Wilcoxon rank sum test between HGCLPSO and other EAs on 30D CEC2017 test suite.

Functions	HGCLPSO	HCLDMS-PSO	TSLPSO	GL-PSO	HCLPSO	CLPSO	ABC	MFO	WOA	BOA	GWO	BA
F1	1	6(+)	3(+)	7(+)	4(+)	2(+)	5(+)	10(+)	8(+)	11(+)	9(+)	12(+)
F3	1	4(+)	5(+)	3(=)	2(+)	6(+)	10(+)	9(+)	11(+)	8(+)	7(+)	12(+)
F4	1	7(+)	6(+)	2(+)	4(+)	5(+)	3(+)	10(+)	8(+)	11(+)	9(+)	12(+)
F5	5	1(−)	2(−)	6(=)	4(−)	3(−)	7(+)	9(+)	10(+)	11(+)	8(+)	12(+)
F6	5	7(+)	4(−)	6(+)	2(−)	3(=)	1(−)	9(+)	11(+)	10(+)	8(+)	12(+)
F7	6	1(−)	3(−)	5(=)	4(−)	2(−)	7(+)	9(+)	10(+)	11(+)	8(+)	12(+)
F8	6	1(−)	2(−)	5(=)	4(=)	3(−)	8(+)	9(+)	10(+)	11(+)	7(+)	12(+)
F9	6	1(−)	2(−)	4(−)	3(−)	5(=)	8(+)	9(+)	10(+)	11(+)	7(+)	12(+)
F10	8	3(−)	4(−)	6(=)	1(−)	2(−)	5(−)	9(+)	10(+)	11(+)	7(=)	12(+)
F11	4	3(=)	1(=)	5(=)	2(=)	6(+)	7(+)	10(+)	8(+)	11(+)	9(+)	12(+)
F12	1	4(+)	5(+)	2(+)	3(+)	7(+)	6(+)	10(+)	8(+)	11(+)	9(+)	12(+)
F13	1	5(+)	4(+)	7(+)	3(+)	2(+)	6(+)	10(+)	8(+)	11(+)	9(+)	12(+)
F14	1	2(+)	5(+)	3(+)	4(+)	6(+)	7(+)	8(+)	10(+)	11(+)	9(+)	12(+)
F15	1	7(+)	4(+)	6(+)	3(+)	2(=)	5(+)	8(+)	9(+)	11(+)	10(+)	12(+)
F16	3	1(−)	2(−)	8(+)	5(=)	4(=)	6(+)	9(+)	10(+)	11(+)	7(+)	12(+)
F17	3	1(−)	2(−)	7(+)	5(=)	4(=)	8(+)	10(+)	9(+)	11(+)	6(+)	12(+)
F18	1	2(+)	5(+)	4(+)	3(+)	6(+)	7(+)	9(+)	10(+)	11(+)	8(+)	12(+)
F19	2	7(+)	4(=)	6(+)	3(=)	1(−)	5(+)	10(+)	9(+)	11(+)	8(+)	12(+)
F20	4	1(−)	2(−)	8(+)	5(=)	3(=)	6(+)	9(+)	10(+)	11(+)	7(+)	12(+)
F21	6	1(−)	4(−)	5(=)	3(−)	2(−)	8(+)	9(+)	11(+)	10(+)	7(+)	12(+)
F22	5	2(=)	4(=)	6(−)	3(=)	1(+)	7(+)	11(+)	10(+)	9(+)	8(+)	12(+)
F23	4	1(−)	2(−)	6(+)	5(=)	3(=)	7(+)	9(+)	10(+)	11(+)	8(+)	12(+)
F24	6	1(−)	2(−)	5(=)	4(=)	3(=)	8(+)	9(+)	10(+)	11(+)	7(+)	12(+)
F25	1	6(+)	5(+)	7(+)	3(+)	4(+)	2(+)	10(+)	8(+)	11(+)	9(+)	12(+)
F26	5	6(=)	3(=)	7(+)	1(−)	2(=)	4(=)	9(+)	10(+)	11(+)	8(+)	12(+)
F27	1	6(+)	5(+)	7(+)	4(+)	2(=)	3(+)	9(+)	10(+)	11(+)	8(+)	12(+)
F28	1	6(+)	5(+)	2(−)	3(+)	7(+)	4(+)	10(+)	8(+)	11(+)	9(+)	12(+)
F29	4	1(−)	2(=)	7(+)	5(=)	3(=)	6(+)	9(+)	10(+)	11(+)	8(+)	12(+)
F30	1	7(+)	5(+)	2(+)	3(+)	6(+)	4(+)	8(+)	10(+)	11(+)	9(+)	12(+)
Average rank	3.24	3.48	3.52	5.31	3.38	3.62	5.86	9.28	9.52	10.76	8.03	12.00
Final rank	1	3	4	6	2	5	7	9	10	11	8	12
+/=/−		14/3/12	12/5/12	18/8/3	12/10/7	12/11/6	26/1/2	29/0/0	29/0/0	29/0/0	28/1/0	29/0/0

.

From the results in Table 10 and Table 11, HGCLPSO performs best on 12 out of 29 test functions (F1, F3, F4, F12–F15, F18, F25, F27, F28, F30), ranking first. HCLDMS-PSO excels on functions F5, F7–F9, F16, F17, F20, F21, F23, F24, and F29. HCLPSO achieves the best rank results on F10 and F26. CLPSO provides the best solution for F19 and F22. TSLPSO performs best on F11, while ABC ranks first on F6. Based on the average ranks, HCLDMS-PSO takes the top spot, followed by HCLPSO in second and HCLDMS-PSO in third. Table 11 clearly shows that HGCLPSO is superior to most other evolutionary algorithms, with its performance being nearly on par with HCLDMS-PSO, TSLPSO, and HCLPSO. However, HGCLPSO outperforms algorithms like GL-PSO and CLPSO on most test functions. Notably, HGCLPSO also surpasses several well-known EAs, including ABC, MFO, WOA, BOA, GWO, and BA.

Table 12. Ranks obtained through Friedman test for 30D CEC2017 test suite problems.

Algorithm	HGCLPSO	HCLDMS-PSO	TSLPSO	GL-PSO	HCLPSO	CLPSO	ABC	MFO	WOA	BOA	GWO	BA
Average rank	3.25	3.71	3.64	4.87	3.66	4.27	5.69	9.04	9.57	10.59	7.74	11.99
Final rank	1	4	2	6	3	5	7	9	10	11	8	12
p-value	3.98 × 10−49

shows that HGCLPSO differs significantly from all other PSO variants and six other EAs on the CEC2017 test suite, with a Friedman test p-value of 3.98E-49 and average rank of 3.25.

4.4. HGCLPSO Performance on the WSNs Coverage Problem

HGCLPSO is further evaluated using the WSNs coverage control problem, a widely recognized real-world optimization challenge [51]. WSNs are integral to various applications such as target tracking, disaster warning, and wearable technology. These networks are typically large and dense, with significant overlap in their coverage areas. Random deployment of sensor nodes often fails to ensure complete coverage, leading to coverage gaps within the WSNs. Therefore, coverage control plays a crucial role in optimizing WSN architecture and minimizing energy consumption.

Suppose $N$ sensor nodes are deployed randomly in a two-dimensional target monitoring area, which can be viewed as a node set $G=\left\{n_1,n_2,n_3,\cdots ,n_N\right\}$, where $n_i$ denotes node $i$. The coordinate of node $i$ is $n_i(x_i,y_i)$, and its sensing radius is $r_i$. If point $P(x_p,y_p)$ is within the sensing radius of node $n_i$, we assume that it is covered by node $n_i$. The sensing rate $p(n_i,P)$ for pixel $P$ covered by $n_i$ is as follows:

$$p(n_i,P)=\left\{\begin{array}{l}\begin{array}{ll}1,& d(n_i,P)\le r_i\end{array}\\ \begin{array}{ll}0,& d(n_i,P)>r_i\end{array}\end{array}\right.$$

(12)

The distance between pixel $P$ and node $n_i$ is $d(n_i,P)=\sqrt{{(x_i-x_p)}^2+{(y_i-y_p)}^2}$. Because pixel $P$ can be covered by several nodes at the same time, we consider whether pixel $P$ is covered by node set $G$:

$$p(G,P)=1-{\displaystyle \prod _{n_i\in N}\left[1-p(n_i,P)\right](i=1,2,3,\cdots ,N)}$$

(13)

Finally, the coverage rate of the target area is formulated as follows:

$$MaximumF(x)={\displaystyle \frac{{\displaystyle \sum _{P\in j\times k}p(G,P)}}{j\times k}}$$

(14)

where $j$ and $k$ denote the length and width of the target area. Swarm intelligence is an effective approach for optimizing node deployment and enhancing network performance. This experiment uses a 30D WSNs coverage control problem with the sensor node $N$ set to 15. The sensing radius $r_i$ is 15 m, while the target region is $100\times 100$ m² in size. For this experiment, all 15 EA algorithms from Section 4.2 and Section 4.3 were used. MaxFEs, run times, and population size were all set to 40, 30, and 300,000, respectively.

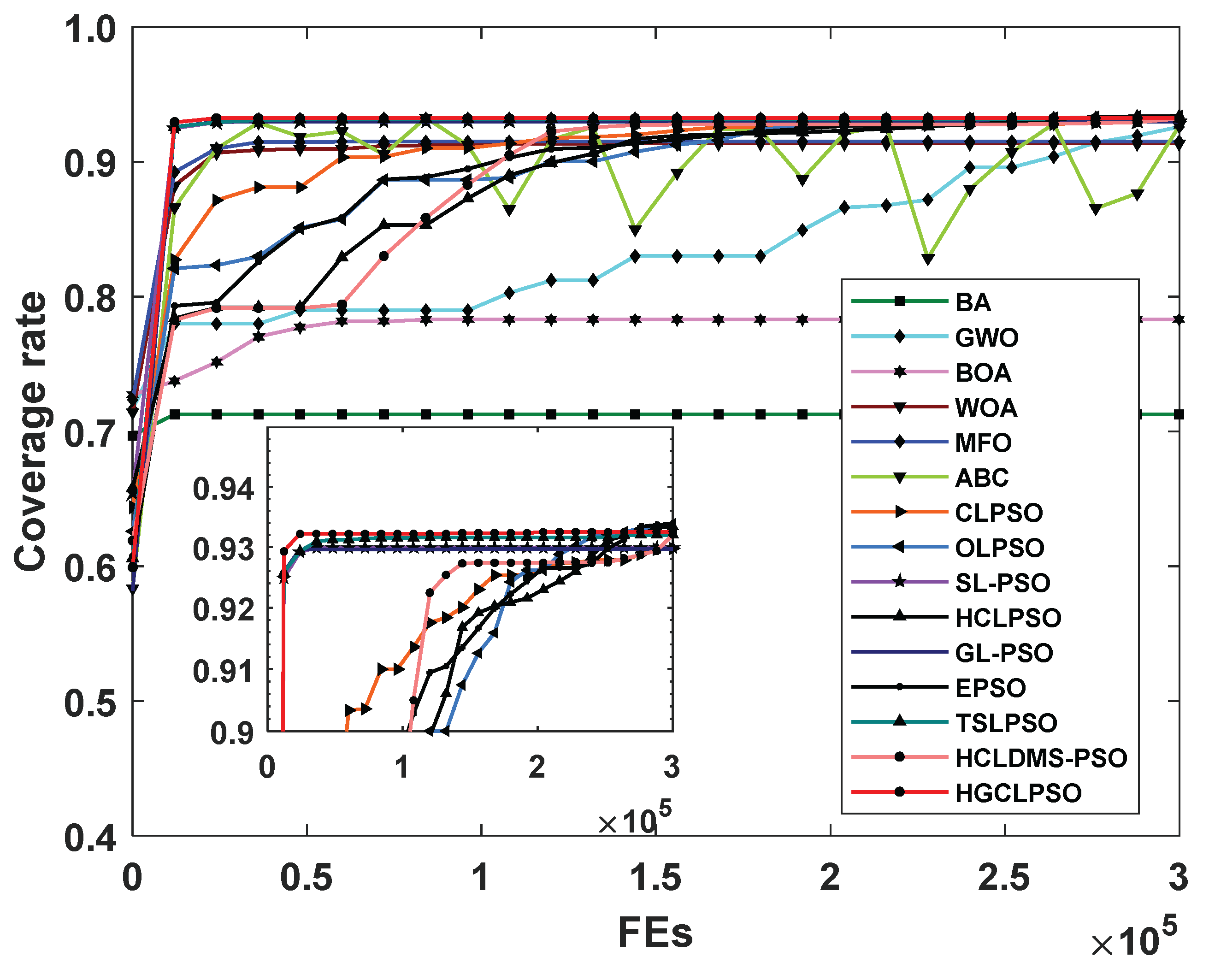
As shown in

Table 13. Comparison of performance on 30D WSNs coverage problem.

Algorithm	HGCLPSO	HCLDMS-PSO	TSLPSO	EPSO	GL-PSO	HCLPSO	SL-PSO	OLPSO
mean	0.9351	0.9322	0.9306	0.9334	0.9327	0.9327	0.9325	0.9316
std	8.99 × 10−04	1.25 × 10−04	0.0030	0.0013	0.0021	0.0025	0.0021	0.0011
rank	1	7	9	2	4	5	6	8
Algorithm	CLPSO	ABC	MFO	WOA	BOA	GWO	BA
mean	0.9305	0.9332	0.9200	0.9042	0.7811	0.9266	0.7446
std	6.80 × 10−04	0.0021	0.0093	0.0093	0.0053	0.0048	0.0424
rank	10	3	12	13	14	11	15

, HGCLPSO achieves the highest mean coverage rate of 0.9351. It outperforms EPSO and ABC, which rank second and third, respectively. Additionally, HGCLPSO surpasses six other EAs and seven PSO variants. The method demonstrates a notably fast convergence in the early stages, as evidenced by the coverage rate convergence curve in Figure 5. Overall, HGCLPSO is not only effective for a wide range of benchmark functions but also well-suited to address real-world engineering problems.

4.5. Discussion

The above experimental results demonstrate the effectiveness of the HGCLPSO algorithm in tackling a range of problems from the CEC2014 and CEC2017 test suites, as well as a real-world engineering challenge. It excels in terms of convergence accuracy, speed, and reliability. The learning approaches used by algorithms such as CLPSO, OLPSO, SL-PSO, and GL-PSO, which rely on a single learning strategy, are insufficient for addressing more complex problems. In contrast, HGCLPSO employs both GLS and CLS to construct exploitation and exploration sub-populations, respectively. Similarly to HCLPSO, TSLPSO, and HCLDMS-PSO, HGCLPSO uses different learning strategies to generate these sub-populations. A novel PEGA mechanism is introduced to enhance exploitation, and a repulsive mechanism is incorporated to prevent premature convergence of the CLS sub-population. Additionally, a local search operator is applied in the later stages of evolution to help HGCLPSO avoid local optima. Thanks to these strategies, HGCLPSO demonstrates strong optimization performance on most problems, achieving the best results on 12 and 13 functions out of the 30D and 50D CEC2014 test suite problems, respectively. However, the HGCLPSO algorithm does not perform as well on certain functions, such as F6, F7, F22, and F27, which affects its overall ranking. In the CEC2017 test suite, HGCLPSO shows sub-optimal performance on F7, F8, F9, F10, F21, and F24. This behavior can be explained by the “no free lunch” theorem [52], which states that no single algorithm can outperform all others across every type of problem.

The ranks from each function, along with two statistical tests, indicate that HGCLPSO, as well as three two-sub-population PSO variants utilizing the CL strategy (HCLPSO, TSLPSO, and HCLDMS-PSO), generally outperform the other PSO variants. By leveraging the enhanced exploration ability of the CL strategy, these PSO variants construct exploitation sub-populations through different mechanisms. This combination creates an effective paradigm to balance exploration and exploitation capacity, helping particles explore new areas, increase their chances of escaping local optima, and avoid premature convergence. Furthermore, in HGCLPSO, GL and CL exemplars guide particle searches, replacing the conventional pbest and gbest. This single-guided learning mechanism helps avoid the “oscillation” problem often seen with dual guidance in traditional PSOs. In GL-PSO, there is no guarantee that the learning exemplars will remain effective across all dimensions. If exemplars degrade in certain dimensions, particles learning from them may hinder the algorithm’s efficiency, leading to the “two steps forward, one step back” issue. To address this, the proposed PEGA mechanism helps preserve the valuable information in particles, ensuring that the exemplars do not degrade and mitigating this phenomenon.

5. Conclusions

In this paper, we introduce a novel PSO variant, HGCLPSO, which utilizes GLS and CLS to create two distinct sub-populations, effectively balancing exploration and exploitation—a long-standing core challenge in the field of swarm intelligence optimization. To enhance the exploitation capability of the GLS sub-population, we propose a Potentially Excellent Gene Activation (PEGA) mechanism. This mechanism updates the Abest position by learning from high-performing genes of individual particles, ensuring the discovery of better global solutions and filling the gap in targeted gene-driven optimization for PSO variants. Additionally, to prevent premature convergence in the CLS sub-population and preserve diversity, we incorporate a repulsive mechanism that increases the repulsive force when individuals are too close to the optimal position. Finally, in the later stages of evolution, a BFGS quasi-Newton local search operator is applied to the Abest to help avoid local optima, which strengthens the reliability of optimization results for complex problems.

We compare HGCLPSO with eight state-of-the-art PSO variants using the CEC2014 test suite, evaluating solution accuracy, convergence speed, statistical significance, and computational time. The results show that HGCLPSO achieves competitive accuracy while maintaining fast convergence. Additional experiments on the CEC2017 test suite and real-world engineering problems further demonstrate the superiority of HGCLPSO over several other PSO variants and EAs, highlighting its potential to provide more efficient and robust optimization tools for both academic research and industrial applications. The research significance of HGCLPSO lies in two key aspects: first, it enriches the theoretical framework of PSO variants by integrating multi-strategy collaboration and adaptive mechanism design, offering new insights for the development of swarm intelligence algorithms; second, it addresses critical limitations of existing algorithms in balancing exploration and exploitation, as well as maintaining diversity, which promotes the advancement of optimization technology for complex problems.

Future research will focus on developing new mechanisms or exploring alternative strategies to better balance exploitation and exploration capabilities, particularly for high-dimensional and multi-objective optimization problems. Additionally, in our ongoing studies, we plan to apply HGCLPSO to more complex real-world engineering challenges, such as renewable energy system optimization and intelligent manufacturing process scheduling, to expand its application scope and maximize its practical impact.