Abstract
Diesel engines power much of the heavy-duty equipment used in underground mines, where exhaust emissions pose acute environmental and occupational health challenges. However, predicting the amount of air required to dilute these emissions is difficult because exhaust mass flow and pollutant concentrations vary nonlinearly with multiple operating parameters. We apply deep learning to predict the total exhaust mass flow and carbon monoxide (CO) concentration of a six-cylinder gas–diesel (dual-fuel) turbocharged KAMAZ 910.12-450 engine under controlled operating conditions. We trained artificial neural networks on the preprocessed experimental dataset to capture nonlinear relationships between engine inputs and exhaust responses. Model interpretation with Shapley additive explanations (SHAP) identifies torque, speed, and boost pressure as dominant drivers of exhaust mass flow, and catalyst pressure, EGR rate, and boost pressure as primary contributors to CO concentration. In addition, symbolic regression yields an interpretable analytical expression for exhaust mass flow, facilitating interpretation and potential integration into control. The results indicate that deep learning enables accurate and interpretable prediction of key exhaust parameters in dual-fuel engines, supporting emission assessment and mitigation strategies relevant to underground mining operations. These findings support future integration with ventilation models and real-time monitoring frameworks.
1. Introduction
Diesel engines remain the backbone power source for heavy mobile equipment and underground mining fleets due to their high-power density, reliability, and ease of service. At the same time, controlling diesel exhaust pollutants in mines is critical for health and safety. The International Agency for Research on Cancer classifies diesel engine exhaust as carcinogenic to humans (Group 1) [1]. In the landmark Diesel Exhaust in Miners Study (DEMS), elevated long-term exposure to diesel aerosols was linked to increased lung cancer risk [2,3]. Although methodological debates (e.g., the healthy worker effect) arose [4,5], recent analyses continue to confirm a positive dose–response between diesel exposure and lung cancer when exposure assessments are rigorously accounted for [6]. These findings underscore the importance of limiting diesel emissions in confined occupational settings.
Underground mine environments, with constrained airflow, extensive tunnel networks, and multiple co-located emission sources, pose additional challenges for emission control. Ventilation guidelines from NIOSH detail the major diesel exhaust contaminants (gases and particulates) and recommend strategies to improve airflow distribution at working faces [7]. Strict limits exist for toxic gases like carbon monoxide (CO)—for example, NIOSH’s recommended exposure limit is 35 ppm (time-weighted average) with a 200 ppm ceiling [8]. Ventilation airflow quantity in mines is commonly scaled to engine power using regulatory or best-practice unit airflow factors on the order of 0.05–0.09 m3·s−1 per kW [9,10]. In Ontario, Canada, regulations explicitly require at least 0.06 m3·s−1 per kW for diesel equipment in underground mines [10]. Modern mine ventilation design increasingly leverages calibrated network models and CFD simulations to optimize air delivery [11,12], alongside demand-based ventilation control, in order to reduce energy consumption while maintaining contaminant dilution [13]. Even so, ventilation capacity is ultimately finite, making real-time emission reduction at the source a priority.
In Russian practice, historically, an empirical design norm was adopted that directly links the required fresh air quantity to installed diesel power in workings. Analyses focused on underground diesel operation show that the long-used 5 m3·min−1 per 1 hp norm can be conservative for modern engines with efficient aftertreatment and improved fuel quality. CFD-based justification indicates that values near ~3.6 m3·min−1 per 1 hp ensure adequate dilution for representative locomotives without exceeding maximum allowable concentrations [14,15]. Complementary measures—such as diesel fuel blends with vegetal (bio-) components—demonstrated >20% reductions in CO, CO2, and NOx in full-scale tests, further easing ventilation constraints [16]. Russian studies also emphasize how equipment configuration influences dilution effectiveness: exhaust pipe location and jet characteristics materially affect gas dispersion, allowing recommended ratios of ventilation-air to exhaust-gas flow to be derived for different designs [17]. With respect to hygienic limits in Russia, ventilation design, monitoring points, and compliance are tied to strict maximum allowable concentrations (e.g., for CO on the order of tens of ppm), and integrated toxicity assessments sometimes use CO-equivalent to compare mixed-pollutant loads against the CO threshold—tools that support planning and operational decisions under multiple constraints [18]. Taken together, the current Russian literature argues for balancing normative air-quantity methods with model-based optimization and targeted source control.
One promising pathway to lower exhaust emissions is dual-fuel operation using cleaner fuels such as natural gas (NG) or hydrogen in combination with diesel. Dual-fuel (also known as gas–diesel) combustion retains many advantages of compression ignition while displacing a portion of diesel with NG or hydrogen. Reviews have reported significant reductions in diesel particulate matter (DPM) and NOx emissions under dual-fuel operation. However, challenges have been noted, including ignition delays that tend to increase with high NG substitution, and engine performance becomes more sensitive to operating conditions [19]. At partial engine loads, several studies have observed increased CO emissions in dual-fuel modes, likely due to incomplete oxidation in cooler, lean combustion zones [20]. Moreover, “methane slip”—the release of unburned methane in NG–diesel engines—emerges as a major greenhouse gas concern [21,22,23]. Mitigating these issues places a premium on accurate, real-time estimation and control of combustion parameters (air–fuel mixture, EGR rates, ignition timing) in scenarios where ventilation and dilution capacity are limited.
A recent brief review by Semin and Kormshchikov shows accelerating adoption of AI in mine ventilation—covering monitoring, gas and equipment dynamics, and control—and outlines key gaps in scaling and loss modeling [24].
Data-driven modeling has rapidly advanced to serve as a virtual sensing and control aids for engine emissions and airflow. Machine learning (ML) models can accurately estimate engine-out emissions and mass flow rates in both laboratory and on-road settings [25,26,27,28,29]. For example, neural network models have been used to estimate diesel-engine mass airflow under semi-transient operating conditions, improving the speed of control calibrations [25]. Similarly, hybrid approaches combining physical insight with ML have been applied to develop virtual sensors for exhaust gas recirculation (EGR) flow [26]. Emphasis for field deployment is on creating lightweight and transferable models that remain robust against variability in operating conditions [27,28,29]. In Russia, related ML work has predominantly targeted methane (as the principal explosion-hazard gas) and general ventilation risks. A recurrent neural network (LSTM) trained on multivariate time series from coal-mine operations achieved ~67–70% accuracy in predicting methane concentration, demonstrating the feasibility of real-time gas-content forecasting under incomplete information [30]. Additional studies used RNNs to forecast air pollutant concentrations from monitoring data and described methodologies for deploying neural network technologies at coal enterprises, including real-time methane prediction and ventilation optimization (e.g., adaptive ventilation-on-demand tied to machine presence and predicted exhaust volumes) [31,32]. Although published Russian examples focused specifically on CO from diesel machines are still limited, the demonstrated architectures and data pipelines are directly transferable to CO prediction, where emissions depend nonlinearly on load, speed, fuel composition, aftertreatment efficiency, and local ventilation regime [30,31,32].
Equally important is the interpretability of these black-box models. In complex powertrain applications, understanding why a model predicts a certain emission level builds trust and aids in engineering insight. Post hoc explanation tools such as SHAP (Shapley Additive Explanations) provide additive feature attributions and are increasingly used in engine ML studies [33]. For instance, SHAP can rank the influence of inputs (like speed, load, EGR fraction) on a predicted emission, thus aligning model behavior with engineering intuition. Beyond feature importance, symbolic regression is gaining traction as a means to extract transparent, analytic formulas from data. Recent developments (e.g., the AI Feynman algorithm) have shown that symbolic regression can rediscover physics-consistent laws from data [34,35]. This approach has been applied to emissions modeling in energy systems, yielding compact formulae that approximate the behavior of more complex models [36]. By bridging machine learning and mechanistic understanding, such techniques enhance the explainability and acceptance of data-driven models in safety-critical domains.
In recent years, deep learning methods have achieved state-of-the-art predictive performance for internal combustion engine emissions and DPM formation. For practical applications, researchers have also begun integrating deep learning into engine control and adaptation frameworks. Norouzi et al. developed an LSTM-based nonlinear model predictive control for diesel engines, demonstrating simultaneous reduction in NOx emissions and fuel consumption via real-time optimization [37]. Shin et al. employed a transfer-learning approach to predict transient diesel emissions (NOx, DPM, total hydrocarbons) across different operating regimes, showing that a model trained on one set of conditions can be efficiently re-trained (with minimal new data) to predict emissions in a new domain with high accuracy [38]. On the modeling side, deep neural networks and hybrid architectures have delivered remarkably high accuracy in emission-prediction tasks. For example, Yu et al. introduced a deep kernel learning approach that outperformed conventional machine learning models and high-dimensional model representation techniques in capturing diesel engine emissions dynamics [39]. Recurrent neural network architectures (including LSTM, GRU, and bidirectional RNN) have attained coefficients of determination R2 > 0.93 for gaseous emissions (NOx, CO, CO2) and DPM across diesel and gasoline-engine studies [40,41]. In comparative studies, GRU networks sometimes surpassed LSTMs in predicting CO and NOx, whereas LSTMs performed better for CO2 predictions [40]. Deep convolutional networks have likewise proven effective: Estrada et al. reported CO2 estimation errors below 2.5% using a deep learning-based engine model, while also achieving inference speeds about 8–10× faster than real time for simulation and control tasks [42]. Similarly, Soltanalizadeh et al. showed that a deep regression learning approach can accurately predict engine performance and emissions, significantly improving on traditional empirical models [43]. These examples illustrate the potential of deep learning to serve as high-fidelity virtual emission sensors and surrogates for engine behavior, provided that their predictions remain reliable across a wide range of conditions.
To further improve the reliability and transparency of emission models, recent research has turned to physics-informed and hybrid “gray-box” approaches. In gasoline direct injection engines, adding physical constraints to ML models has yielded notable gains—for instance, Jayaprakash et al. developed a physics-aware ensemble model for DPM prediction that achieved a 29% higher R2 and 21% lower RMSE than a purely black-box model [44]. Physics-Informed Neural Networks (PINNs) are another emerging tool. Nath et al. applied PINNs to diesel engine mean value models to predict gas flow dynamics while simultaneously identifying unknown parameters, ensuring that the learned model respects underlying physical laws [45]. Operator learning frameworks have also been explored for real-time engine predictions. Kumar et al. introduced a DeepONet-based neural operator that maps engine control inputs (e.g., speed, fuel injection, EGR, VGT positions) to multiple output states of a diesel engine; their model can predict intake/exhaust manifold pressures and other states in real time, with a maximum reported error around 6.5% [46]. In the realm of hybrid modeling, Hu et al. combined a zero-dimensional physical engine simulation with a CNN–GRU network to capture combustion dynamics, allowing the model to reproduce cylinder pressure and heat release traces with low error [47]. For next-generation low-carbon engines, gray-box models have shown particular promise: Shahpouri et al. developed a hybrid time series model for transient NOx emissions in a hydrogen–diesel dual-fuel engine, which incorporated a 1D physics-based component into an ML model. The gray-box model achieved slightly higher accuracy (R2 > 0.97) than a comparable black-box model (R2 > 0.96) on transient cycles, although at the cost of greater computational load [48]. This trade-off between fidelity and speed highlights the ongoing need to balance physical interpretability with the real-time performance requirements of engine control and onboard diagnostics.
Building on the above advances, the present study follows an explainable data-driven paradigm for emission prediction on a six-cylinder turbocharged gas–diesel engine (KAMAZ 910.12-450) relevant to underground mining applications. We leverage a dataset of 45,984 steady-state operating points spanning wide ranges of speed, load, EGR, and fueling. Input features include engine torque, speed, boost (charge-air) pressure, an EGR-related parameter, diesel and methane fuel flow rates, and catalyst outlet pressure and temperature. Low-variance inputs were removed, and multicollinearity was analyzed to refine the feature set. We train machine learning models (including neural networks) to predict two key outputs: the total exhaust mass flow rate and the concentration of CO in the exhaust.
2. Materials and Methods
2.1. Feature Definition and Selection (Database), Training and Test Set Formation
Experimental data were collected on a 6-cylinder inline gas–diesel (dual-fuel) KAMAZ 910.12-450 engine with turbocharging. The dataset was obtained from multiple engine test campaigns carried out over five days and was merged into a single time-synchronized array for model training.
The resulting array is a time-series dataset of physical quantities (37 columns and 72,212 rows). The overall dataset structure is presented in Table 1.

Table 1.
Dataset structure.
Data preprocessing was performed, which included imputing missing values, filtering physically irrelevant quantities, removing low-variance features, and selecting a set of features with low mutual correlation. After removing rows with missing or physically irrelevant values, the gaps were imputed using a k-nearest neighbors algorithm with 500 neighbors and Euclidean distance. As a result, the dataset size was reduced from 72,212 to 54,162 rows, ensuring data consistency and integrity for subsequent model training and analysis.
We removed low-variance features from the dataset. These included ambient/barometric pressure, oil temperature, intake humidity, coolant temperature, and intake pressure and temperature.
One challenge in machine learning is the presence of strongly correlated features in the dataset. On the one hand, if two features are highly interrelated, the information they convey is duplicated; therefore, to enable more accurate training, one of the features should be removed. On the other hand, when the phenomenon under study is a complex, interdependent system, a change in one parameter may lead to a change in another.
To analyze the features, pairwise Pearson correlation coefficients were computed and a correlation matrix was constructed, as shown in Figure 1.
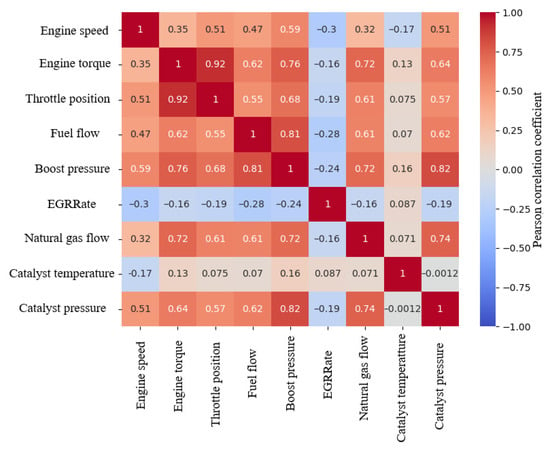
Figure 1.
Feature correlation matrix.
Analysis of the correlation matrix showed that only the throttle position is strongly correlated with torque. Boost pressure, pre-catalyst pressure, and fuel flow also exhibit strong correlations; however, as shown, these parameters had high importance and were therefore not excluded from consideration.
After pre-processing, the dataset contained 45,984 synchronized measurements of total exhaust mass flow and gas concentrations across various operating regimes.
For the exhaust emission analysis, a key set of parameters was considered: engine torque, engine speed, boost pressure, the exhaust gas recirculation (EGR) parameter, liquid fuel flow, methane flow, and catalyst pressure and temperature.
In machine learning, splitting the original data into training and test sets is a critical step. In this study, the source dataset was split in the standard 80/20 ratio. To verify the robustness of the results, several experiments were performed with different random splits of the data. In all cases, the 80/20 ratio was preserved, and the average performance metrics remained stable, confirming the adequacy of the chosen approach.
Analysis of the feature distributions (such as engine speed, torque, and boost pressure) showed that they are non-uniform and sparse (Figure 2). Consequently, traditional regression and interpolation methods may be ineffective due to complex nonlinear relationships and data sparsity.
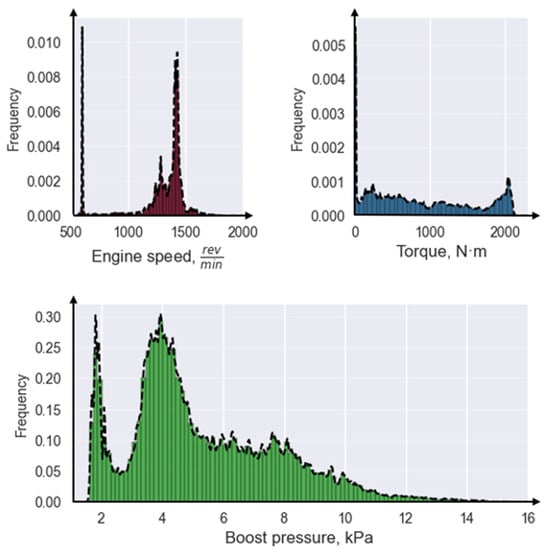
Figure 2.
Distributions of gas–diesel engine operating parameters.
In this work, a two-stage approach to model training is proposed. The first stage consisted of using an artificial neural network for initial training and for modeling complex nonlinear dependencies. The second stage consisted in generating a uniform grid of synthetic data, followed by constructing a symbolic regression model to determine an analytical dependence between the target variable and the features. This combined method preserves machine-learning accuracy while maintaining interpretability.
2.2. ANN Structure and Training Algorithm
In this work, to solve the problem of predicting the exhaust gas concentration and the total exhaust mass flow rate, we used a fully connected feed-forward artificial neural network that approximates the relationship by means of a vector function:
where is the -th feature of the dataset, and is the target variable (exhaust gas flow rate and CO concentration).
The graph representation of a fully connected artificial neural network (ANN) is shown in Figure 3.
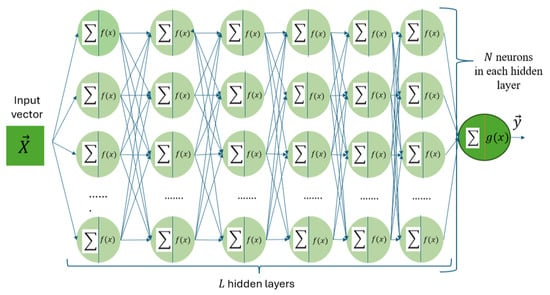
Figure 3.
Overall ANN architecture for the task.
An ANN consists of L + 2 layers of neurons, where L is the number of hidden layers. The input layer receives the function arguments (features), and the output layer generates the result of the neural network. ANNs consist of layers of interconnected neurons; each layer may contain an arbitrary number of neurons, independent of the other layers. Formally, the analytical representation of a neuron is as follows:
where is the value output by the -th neuron of layer ; and are the weight coefficients and the bias of the -th neuron of layer ; is the input feature vector from the previous layer; and is the activation function of layer .
The activation function is a nonlinear function that determines which neurons are activated and how information propagates between the layers of a neural network. In principle, any nonlinear function may be used; however, its choice affects the speed and efficiency of training an ANN. Nonlinearity enables the network to learn complex high-dimensional dependencies and represent them in a lower-dimensional space. This enables the model to generalize effectively and to solve complex tasks. The choice of activation function depends on the network architecture and the problem being addressed. For output layers, the choice is dictated by the task type (classification vs. regression).
All hidden layers of the ANN share the same functional form of the transfer (activation) function. The class of activation functions used in the computations is given by the analytical expressions listed in Table 2.

Table 2.
Types of activation functions.
Normalization of the dataset is a step performed prior to model training that helps eliminate differences in attribute scales and accelerates ANN convergence. This process is implemented using the following transformation:
where denote the minimum and maximum values of the corresponding input and output variables.
The normalization process is aimed at eliminating differences in feature scales, which accelerates convergence and improves the stability and efficiency of ANN training.
Model training was performed using the Adam modification of the backpropagation algorithm. This optimization method is an extension of stochastic gradient descent (SGD) with adaptive estimates of the moments of the gradient.
Analytically, the ANN weights are updated according to the following equations:
where and are the model weights at iterations and , respectively; is the gradient of the loss function L with respect to , and are the first and second bias-corrected moments and is the learning rate.
Quantitatively, the degree of mismatch is characterized by the loss function L, which was taken to be binary cross-entropy:
where is the current ANN prediction for the input vector .
At each training step, mini-batch training was used to estimate the gradient of the loss function. Accordingly, the gradient of the loss function is computed over a sample comprising multiple mini-batches:
where B is the mini-batch size.
Mini-batch training helps improve convergence and the computational efficiency of ANN training. Mini-batches provide less noisy gradient estimates, which makes training more stable. Compared with full-batch training, mini-batches allow more frequent weight updates, accelerating convergence, especially on large datasets.
In deep neural networks, proper weight initialization plays a key role in the training process. If the weights are too large or too small, vanishing or exploding gradients may occur. To avoid these issues, Xavier initialization was used.
Xavier initialization is designed to keep the variance of the inputs and outputs of each layer approximately the same during both forward and backward propagation in the ANN. This keeps gradients at a stable magnitude across all layers. The network weights are drawn from a normal distribution with zero mean and some variance (the specific value is not specified in the source). The mathematical form of the Xavier initialization is as follows:
where is the number of neurons in the input layer, and is the number of neurons in the ANN’s output layer.
Many factors affect the performance of an ANN, but the network architecture has a substantial impact. To select the optimal architecture, we investigated how the number of neurons in a hidden layer, the number of hidden layers, and the choice of activation function for the hidden-layer neurons influence accuracy for two models that predict the total exhaust mass flow and the CO concentration.
3. Results
3.1. Selecting the Optimal ANN for Total Exhaust Mass Flow
We consider how ANN accuracy depends on the number of neurons in the hidden layers. A standard rule for selecting the number of artificial neurons in a layer is as follows:
where is the number of input parameters; this gives . In [49], it is proposed to choose the number of neurons according to the following equation:
which gives 13 neurons. Figure 4 shows that the standard formula underestimates the required number of neurons, whereas the formula of [49] overestimates it (is excessive).
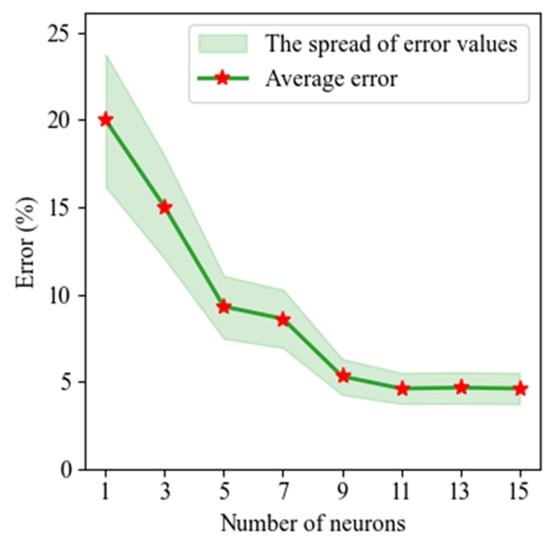
Figure 4.
Error for total exhaust mass flow as a function of the number of neurons in a single-layer ANN.
As shown in Figure 4, the prediction error for the total exhaust mass flow on the test data decreases up to N = 10, after which it decreases much more slowly, which becomes disproportionate to the growth in ANN complexity, i.e., the number of trainable weight and bias parameters. Having chosen, based on the data presented in Figure 4, N = 10 as the optimal number of neurons per layer, we then investigated ANN accuracy as a function of the number of hidden layers. The results are shown in Figure 5.
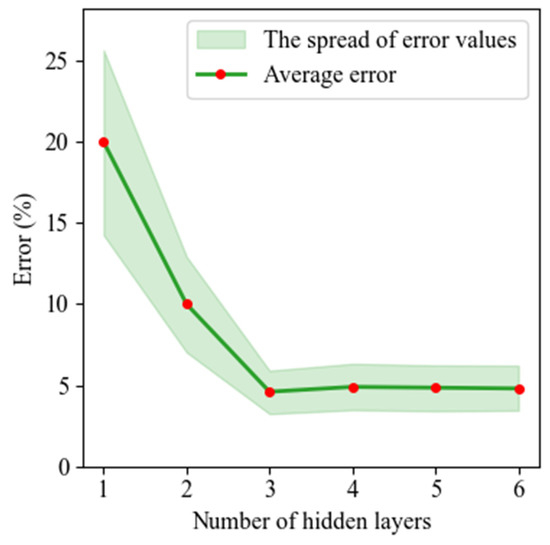
Figure 5.
Error for total exhaust mass flow as a function of the number of hidden layers.
A single-layer network yields a large error on the test data (about 20% with a spread of 7%, which indicates that the ANN is undertrained). As shown in Figure 5, the number of hidden layers increases, the error and the model’s variance decrease up to L = 3. Further increasing the number of layers in the model and hence its complexity does not lead to a reduction in error.
In the exhaust mass flow prediction model, the number of hidden layers was limited to L = 3. The next goal in optimizing the ANN architecture for the task was to determine the activation function for the hidden layers.
Based on the parametric studies performed, the baseline ANN structure was chosen as a network with L = 3 hidden layers and N = 10 neurons per layer. We then examined the effect of the hidden-layer activation function type (Figure 6) on the total exhaust mass flow. An unexpected result was that the error function, erf(x), with the same ANN structure, yielded an order-of-magnitude lower training error than other activation functions specifically designed for ANNs.

Figure 6.
Error for total exhaust mass flow as a function of the activation function.
To assess the contribution of each feature to the model’s predictive accuracy, we used the SHAP method [50], an interpretability tool for machine learning models. The method is based on Shapley value theory from game theory, originally devised to allocate payoffs to players according to their contribution to the overall outcome. SHAP computes each feature’s contribution to a model prediction as the average marginal contribution of that feature across all possible coalitions of the remaining features.
Analysis of feature importance (Figure 7) showed that only three gas–diesel engine parameters have a significant effect on the intake air flow: torque, engine speed, and boost pressure.
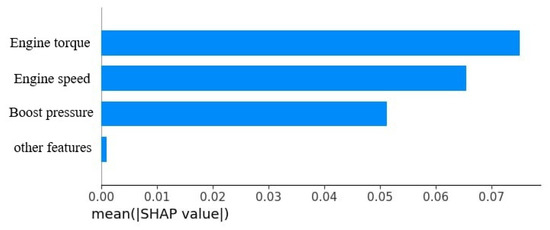
Figure 7.
Analysis of feature importance in the ANN for predicting total exhaust mass flow.
Based on this analysis, an optimal ANN architecture was proposed for predicting the total exhaust mass flow (Figure 8).
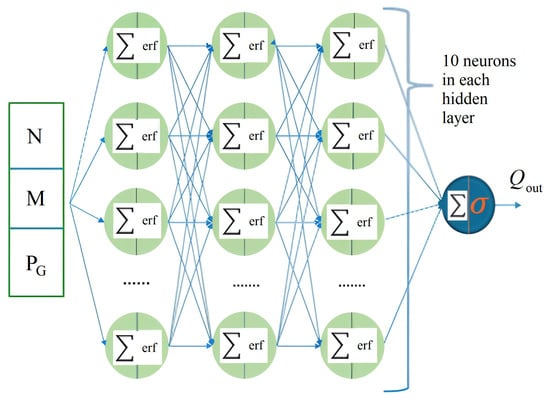
Figure 8.
Optimal ANN model for predicting the total exhaust mass flow of a gas–diesel engine.
Validation on the test data shows good generalization capability of the deep learning models (Figure 9). An important fact is that the model contains significantly fewer weights and biases than the size of the training set, which indicates the presence of a relationship between the input features and the target variable.
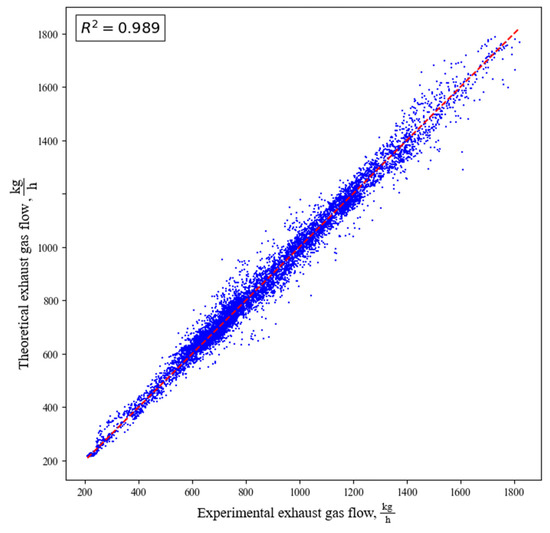
Figure 9.
Validation curve for total exhaust mass flow.
3.2. Determination of the Optimal ANN Model for Predicting CO in a Gas–Diesel Engine
To determine the optimal ANN configuration, a study was conducted on how the number of neurons affects the prediction error of CO concentration. It was found that the minimum error occurs at N = 80 neurons in the hidden layer (Figure 10).
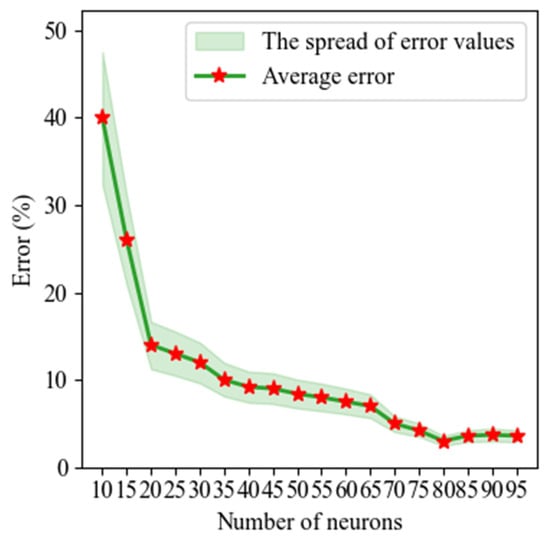
Figure 10.
Error for CO as a function of the number of neurons in a single-layer ANN.
Based on the data presented in Figure 10, N = 80 was selected as the optimal number of neurons per layer, after which the ANN’s accuracy was studied as a function of the number of hidden layers. The next step showed that the ANN achieves the best accuracy at L = 6 hidden layers (Figure 11).
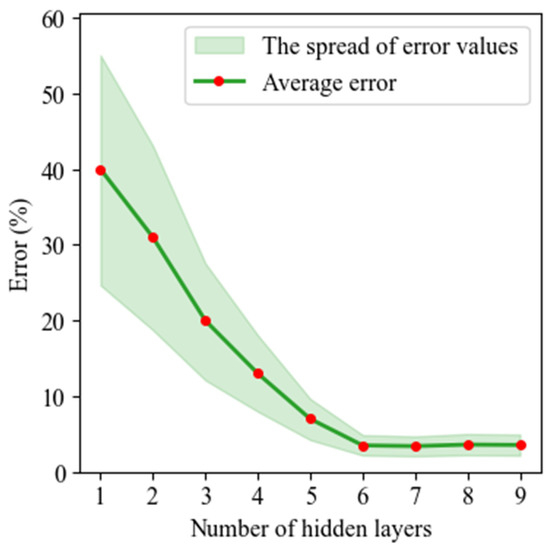
Figure 11.
Error for CO concentration as a function of the number of hidden layers.
Following the parametric studies, the baseline ANN architecture was chosen as a network with L = 6 hidden layers and a hidden-layer width of N = 80. The subsequent objective in optimizing the ANN architecture for the task was to determine the activation function for the hidden layers.
As shown in Figure 12, for the same ANN architecture, the activation function erf(x) yields the lowest error on the test dataset. In our view, the superior performance of the error function (erf) arises from its smooth analytical derivative, which stabilizes backpropagation and improves training efficiency. Its relevance to CO modeling is also physically grounded: diffusion and mass transfer processes in combustion can be expressed through erf integrals, enabling the network to better approximate the nonlinear mechanisms driving CO formation.
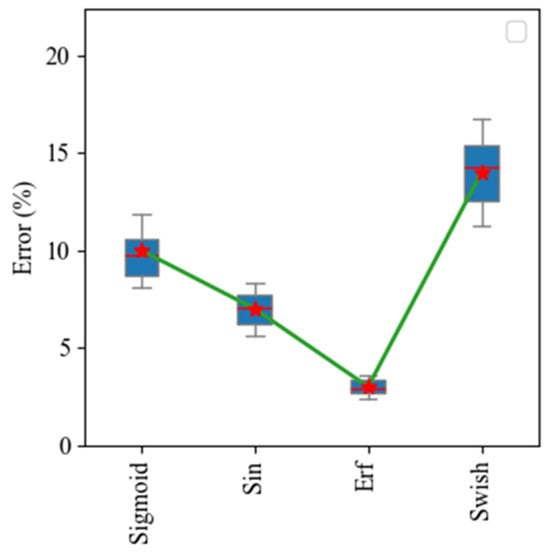
Figure 12.
Error for CO concentration as a function of the ANN activation function.
After the training process was completed, the input data of the test dataset were used to verify the ANN; the results are shown in Figure 13. The ANN verification curves for CO (Figure 13) demonstrate a high degree of agreement between the network’s predictions and the test values that were not used for training.
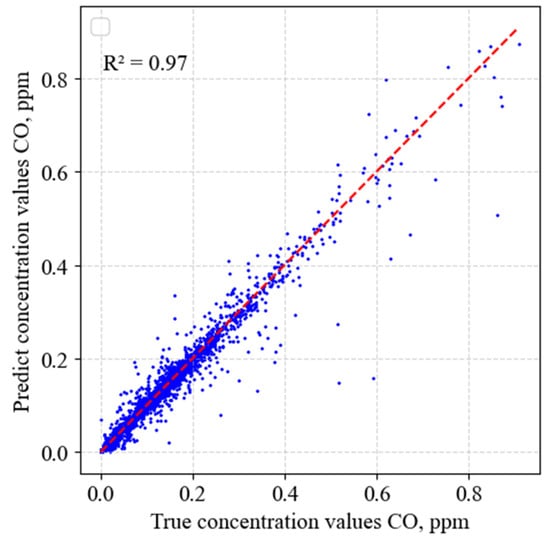
Figure 13.
Verification curve for CO concentration.
As shown in Figure 14, three features exert a dominant influence on the CO concentration: catalyst pressure, the exhaust gas recirculation (EGR) parameter, and boost pressure.
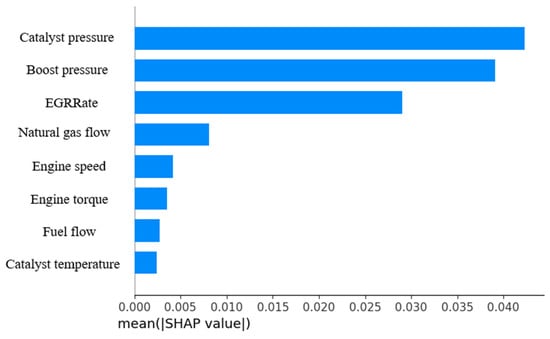
Figure 14.
Analysis of feature importance in the ANN for predicting CO.
The effect of increasing boost pressure on CO concentration in the exhaust of an internal combustion engine is an important aspect when analyzing the performance of the boosting system and environmental indicators. Under normal operating conditions, raising boost pressure tends to reduce the carbon monoxide content in the exhaust gases. This is explained by improved combustion conditions of the fuel–air mixture due to an increased air supply, which leads to more complete oxidation of hydrocarbons and the conversion of CO to CO2.
With higher boost pressure, more oxygen is delivered to the cylinders, optimizing the combustion process and reducing the likelihood of over-rich zones, which are a primary source of CO. An additional factor in lowering the CO concentration is the rise in the combustion chamber temperature, which promotes the thermal decomposition of intermediate combustion products and their subsequent oxidation.
The principal mechanism by which EGR affects combustion is the replacement of part of the fresh charge with inert exhaust gases, which reduces peak temperatures in the combustion chamber. This temperature reduction would, in theory, favor an increase in CO emissions because conditions for complete oxidation of the fuel deteriorate. In practice, however, more complex relationships are observed. With an optimally tuned EGR system, a moderate decrease in carbon monoxide concentration is observed in the exhaust gases. This effect is achieved by improving the homogeneity of the fuel–air mixture and reducing local over-rich zones.
It is noteworthy that, according to the SHAP analysis, engine speed and engine torque exhibit relatively low mean importance values compared with catalyst pressure, turbine pressure, and EGRRate. We attribute this to two main factors. First, the presence of turbocharging, exhaust gas recirculation, and catalytic after-treatment systems in the studied engine partly dilutes the classical relationship between torque/speed and CO concentration. Second, the chosen ranges of the investigated parameters result in greater variability for pressure- and EGR-related features, which increases their relative importance in the model.
3.3. Using the Trained ANN to Determine the Analytical Dependence of the Exhaust Mass Flow of a Gas–Diesel Engine
The trained ANN emulates the behavior of the exhaust mass flow as a function of the operating parameters of the gas–diesel engine. Figure 15 presents exhaust mass flow model distribution maps at various boost-pressure values. Each map is constructed from 50,000 ANN predictions for different values of engine speed and torque.
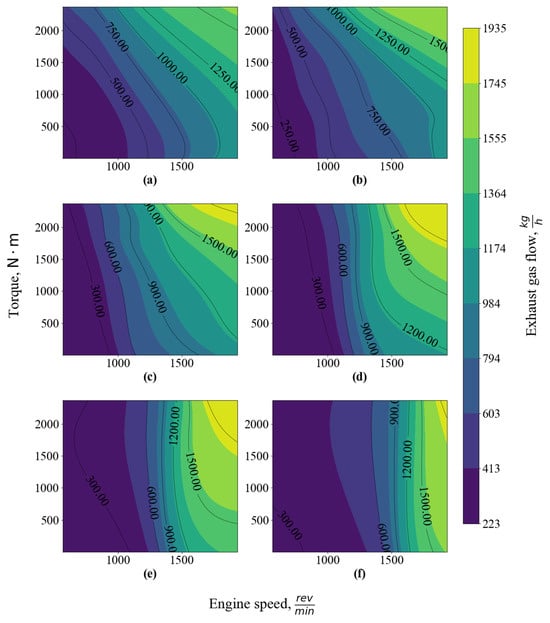
Figure 15.
Distribution of exhaust mass flow at various boost pressures: (a) P = 1.6 kPa; (b) P = 4.7 kPa; (c) P = 7.9 kPa; (d) P = 11 kPa; (e) P = 14.1 kPa; and (f) P = 17.3 kPa.
Figure 15 shows that the minimum exhaust mass flow is observed at idle. As torque and engine speed increase, the exhaust mass flow increases. Increasing boost pressure expands the region of low exhaust mass flow, while at the same time increasing the exhaust mass flow at high torque and speed values of the gas–diesel engine.
The influence of torque is due to the fact that as it rises, the demand for air to ensure efficient combustion also grows, since greater crankshaft output requires more intensive combustion of the fuel–air mixture. The engine control system adjusts fuel delivery in accordance with the incoming air flow; therefore, as torque increases, the air flow (and thus the exhaust mass flow) automatically increases to maintain an optimal air–fuel ratio.
Engine speed directly affects the intake air flow, where an increase in crankshaft rotational frequency and the number of working cycles per unit time rises, leads to a more intensive induction through the intake system. At high speeds, air flow inertia can limit cylinder filling, but in turbocharged engines, this effect is offset by forced induction. In addition, as speed increases, exhaust gas velocity rises, which accelerates the turbine and, consequently, increases boost pressure.
Boost pressure plays a key role in regulating air flow because the turbocharger forces additional air into the intake manifold, increasing the mass of oxygen in the cylinders. As engine load rises, the control system adjusts boost to provide the necessary amount of air for burning the increased fuel charge.
Thus, these three parameters are interrelated and determine the exhaust mass flow: torque sets the air demand, engine speed affects the rate at which air is supplied, and boost pressure provides additional pressurization when needed. The engine management system balances these factors to ensure optimal operating conditions and maximize the combustion efficiency of the fuel–air mixture.
3.4. Determination of the Analytical Dependence of a Gas–Diesel Engine’s Exhaust Mass Flow on Operating Parameters
To determine the analytical dependence of the exhaust mass flow on the operating parameters of a gas–diesel engine, the method of symbolic regression was used. This approach makes it possible to automatically find mathematical expressions that best describe the experimental data without specifying the model structure a priori.
The essence of the method is to identify, within the space of mathematical expressions, a model that optimally matches the data in terms of the balance between accuracy and simplicity. Unlike ordinary regression, which restricts the model structure in advance to a single analytical form, symbolic regression can determine both the form and the parameters of the most suitable mathematical models by exploring an unbounded hypothesis space. This makes it possible to uncover complex nonlinear relationships in the data.
One implementation option for symbolic regression is to use evolutionary search. The population (a set of analytical solutions) evolves by assembling partial mathematical expressions. As building blocks, constants, elementary functions, variables, and mathematical operators are used.
As binary operators, standard mathematical operations were employed: +, −, ∗ and / (using a larger set of complex operators—exponentiation, minimum, and maximum—did not improve the predictive power of the formula but did worsen its mathematical complexity). The evolutionary algorithm used standard operators acting on the population: point mutations to modify individual nodes of expressions with probability 5%, mutations to replace subtrees of solutions (5%), and two-point crossover to exchange subtrees between individuals (80%).
The algorithm was initialized with 50 parallel populations, each containing 1000 solution trees with a complexity degree not exceeding 20. 10,000 optimization iterations were performed to determine the optimal analytical dependence. The optimality of the resulting formula was determined by the Pareto front of expression complexity and error on the test dataset.
The analytical dependence found by the algorithm is given by the following parametric equation:
where –the exhaust mass flow (kg/h), —the fuel flow (kg/h), –the natural-gas flow (kg/h), –the engine torque (N·m), –the engine speed (rpm) and –the boost (turbocharger) pressure (kPa). The numerical coefficients of the analytical dependence are given in Table 3.

Table 3.
Parameters of the analytical dependence.
Figure 16 shows the verification of the analytical dependence for total exhaust mass flow. The closeness of the curves confirms that the formula adequately predicts the total exhaust mass flow. The determination coefficient was R2 = 0.98. The maximum model error does not exceed 7% and is observed under peak load conditions.
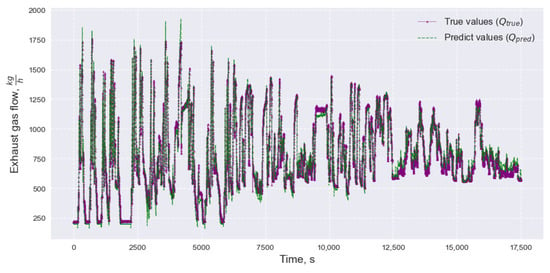
Figure 16.
Verification of the analytical dependence for total exhaust mass flow.
3.5. Using the ANN to Predict CO Concentration
The trained ANN emulates the behavior of CO concentration as a function of the operating parameters of the gas–diesel engine. A map of CO concentration in the (speed–boost pressure) plane is shown in Figure 17. It can be seen that, at any engine speed, a slight increase in boost pressure sharply reduces the carbon monoxide concentration and then reaches a plateau as boost continues to rise. The main reason for this behavior is the additional air forced into the cylinders, which promotes more complete fuel combustion.
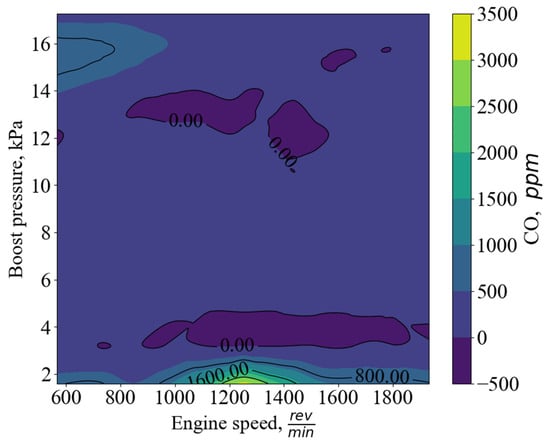
Figure 17.
Distribution of CO concentration over engine speed and boost pressure.
A map of CO concentration in the (engine speed–EGR) plane is shown in Figure 18. At high EGRRate values, the CO concentration is minimal regardless of engine speed. At low exhaust gas recirculation values, the CO concentration reaches about 800 ppm at both low and high speeds. A peak in CO emission is observed in the 1000–1400 rpm range.
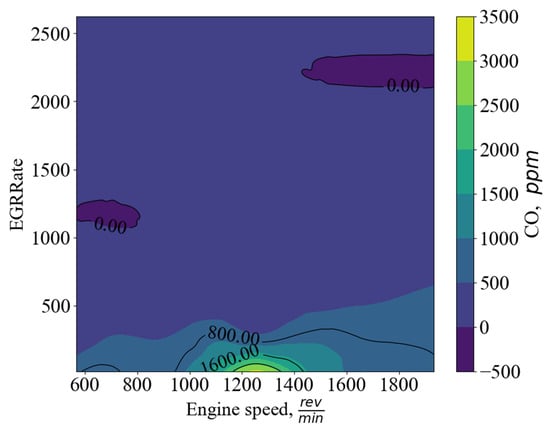
Figure 18.
Distribution of CO concentration over engine speed and EGR.
According to Figure 19, it follows that the most intensive formation of CO occurs at moderate engine speeds in the 1000–1400 rpm range. The variation in carbon monoxide (CO) concentration is closely related to the conditions under which the chemical reactions proceed, especially the combustion processes.
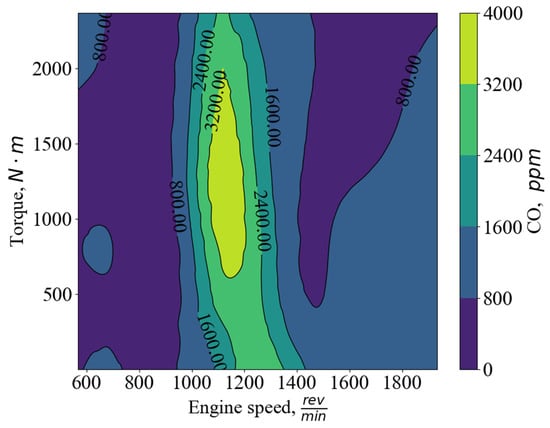
Figure 19.
Distribution of CO concentration over engine speed and torque.
The primary cause of changes in CO concentration is incomplete fuel combustion. At an ideal fuel–air ratio and a certain temperature, the fuel oxidizes completely, producing predominantly carbon dioxide. However, if oxygen is insufficient or the temperature is too low, the reaction stops at an intermediate stage, leading to the formation of carbon monoxide.
4. Discussion
The results confirm that ANN-based models can effectively capture nonlinear dependencies between engine operating conditions and emissions. For exhaust mass flow, the three most significant input factors are engine torque, speed, and boost pressure, while for CO emissions, catalyst pressure and EGR rate (along with boost/turbo pressure) dominate the predictions. These findings align with engineering expectations: torque and speed directly determine the airflow (and thus exhaust flow) through fuel–air intake, and CO emissions are strongly influenced by aftertreatment efficiency (catalyst pressure indicates restrictions and performance) and the combustion quality (affected by EGR and boost).
An important outcome is that the symbolic regression approach provided interpretable mathematical expressions, effectively bridging data-driven and analytical modeling. The derived formula for exhaust mass flow (though complex) offers insight into how torque, speed, and boost interact to influence flow. The form of the formula suggests diminishing returns (through exponents and saturation terms) at high torque and speed, which matches physical intuition (e.g., flow cannot increase indefinitely linearly due to constraints like choking or efficiency losses). Such an interpretable model can be valuable for engineers to quickly estimate exhaust requirements or to incorporate into larger system simulations (like mine ventilation models) without embedding a full neural network.
These findings align with prior research and provide a pathway to integrating AI tools into combustion and emission control strategies. By having both a high-accuracy ANN and a simplified formula, one can use the ANN for precise control and monitoring and use the formula for analysis or real-time simulation, where simplicity and transparency are required.
One point to discuss is computational load. The chosen ANN models are relatively small (especially the exhaust flow model with a 3 × 10 architecture), so they run in microseconds on modern microcontrollers, making them feasible for onboard use. The CO model is larger (6 × 80), but even that can be executed in a few milliseconds, which is fast enough for real-time control in an engine ECU given typical cycle times (on the order of 10 ms or more). During development, we verified that the models could be distilled or pruned if needed to reduce complexity further with minimal loss of accuracy.
Another aspect is explainability and trust. The SHAP analysis results (not all detailed above) provided a ranking of feature importance for different operating regimes. For example, at high loads, torque and boost had extremely high SHAP values for exhaust flow (which is intuitive, as they essentially set the airflow), whereas at low loads and varying EGR, the catalyst pressure indicator can momentarily influence flow readings (due to its correlation with exhaust back-pressure). For CO, SHAP confirmed that in regions where EGR is used, the EGR rate heavily drives CO (higher EGR often raises CO due to oxygen dilution), and where EGR is zero, other factors like turbo pressure and equivalence ratio (reflected indirectly through torque and fuel flows) matter more. Such a nuanced understanding increases confidence that the ANN is not extrapolating in bizarre ways; rather, it aligns with known combustion behavior.
Future work could extend this study by incorporating transient operation (the current models are for steady-state points). Techniques like LSTM-based sequence models or hybrid physical models could be applied to transient emission spikes. Another area is expanding the symbolic regression approach to CO emissions—though CO is much harder to capture with a simple formula, any partial analytical insight would be valuable.
5. Conclusions
Using a comprehensive experimental dataset from a six-cylinder gas–diesel (dual-fuel) KAMAZ 910.12-450 engine, we developed ANN models to predict two critical emission parameters: the total exhaust mass flow and the CO concentration. The results demonstrate that deep learning enables both high predictive accuracy and interpretability, allowing the extraction of human-understandable rules from trained models. The proposed methodology integrates artificial neural networks (ANNs), SHAP-based feature attribution, and symbolic regression to produce robust, explainable models validated on independent test data. Key findings and outcomes include
- The optimal ANN architecture comprises three hidden layers with 10 neurons per layer and uses the error function (erf) activation. The model achieves R2 ≈ 0.989 on test data, capturing dependencies between torque, engine speed, and boost pressure. Symbolic regression produced a compact analytical formula that closely reproduces the ANN predictions, enabling fast engineering-grade airflow calculations.
- The optimal ANN consists of six hidden layers with 80 neurons per layer, also using erf activation, achieving R2 ≈ 0.97. Catalyst pressure, EGR rate, and boost pressure dominate the predictions, while torque and speed remain secondary. The higher variability in CO formation is correctly reflected by the model.
- SHAP-based analysis confirmed that torque, speed, and boost pressure primarily affect mass flow, whereas catalyst pressure, EGR rate, and boost pressure dominate CO predictions. The models reproduce known combustion trends, including the impact of oxygen availability and mixture dynamics.
- The derived analytical expression for mass flow predicts unseen test points within ~5% error, offering a lightweight surrogate suitable for real-time applications, ECU integration, and mine ventilation system simulations.
- The models generalize well across the entire operating envelope and extrapolate slightly beyond it, suggesting they captured underlying physical relationships rather than overfitting noise.
Overall, this study demonstrates that combining ANNs, SHAP-based explainability, and symbolic regression creates a powerful, interpretable framework for modeling emissions in dual-fuel internal combustion engines. The resulting models provide engineering-grade predictions suitable for ventilation network simulations, airflow compliance checks, and the development of advanced emission reduction strategies.
The main practical contribution of this study is providing guidance on calculating the required air volume for mine ventilation when using ICE vehicles. Previous calculation methods did not account for engine turbocharging and relied on the engine speed and the displacement volume as the main parameters. Our results highlight that turbocharging is a critical factor that fundamentally alters the classical relationship between exhaust flow rate and engine parameters (engine speed and displacement volume).
Future work will focus on extending the proposed methodology to include other pollutants such as NOx and DPM, as well as evaluating model performance under transient operating conditions relevant to underground mining applications.
Author Contributions
Conceptualization, I.P., M.S., E.G., L.L. and O.P.; methodology, I.P., M.S., E.G., L.L. and O.P.; software, D.K., A.I. and M.V.; validation, I.P., E.G., A.I. and M.V.; formal analysis, I.P., M.S., E.G., A.I. and M.V.; investigation, I.P., M.S., E.G., A.I. and M.V.; resources, E.G. and L.L.; data curation, E.G. and L.L.; writing—original draft preparation, M.S. and D.K.; writing—review and editing, I.P., M.S. and E.G.; visualization, M.V.; supervision, L.L. and O.P.; project administration, L.L. and O.P.; funding acquisition, I.P., M.S. and D.K. All authors have read and agreed to the published version of the manuscript.
Funding
The study was carried out with the financial support of the Ministry of Science and Higher Education of the Russian Federation within the state assignment (project nos. 122030100425–6 and 121111800053–1).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data presented in this study are available on request from the corresponding author.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AI | Artificial Intelligence |
| ANN | Artificial Neural Network |
| CNN | Convolutional Neural Network |
| CFD | Computational Fluid Dynamics |
| CO | Carbon Monoxide (a toxic exhaust gas) |
| CO2 | Carbon Dioxide |
| DPM | Dust Particulate Matter |
| EGR | Exhaust Gas Recirculation |
| GRU | Gated Recurrent Unit (a type of RNN cell) |
| LSTM | Long Short-Term Memory (a type of recurrent neural network) |
| ML | Machine Learning |
| NG | Natural Gas |
| NOx | Nitrogen Oxides (collective term for NO and NO2 emissions) |
| PINN | Physics-Informed Neural Network |
| RNN | Recurrent Neural Network |
| SHAP | Shapley Additive Explanations (an interpretability method) |
| THC | Total Hydrocarbons |
| NMHC | Non-Methane Hydrocarbons |
| VGT | Variable Geometry Turbocharger (or Turbine) |
References
- IARC. Diesel and Gasoline Engine Exhausts and Some Nitroarenes; IARC Monographs on the Identification of Carcinogenic Hazards to Humans; IARC: Lyon, France, 2013; Volume 105. [Google Scholar]
- Attfield, M.D.; Schleiff, P.L.; Lubin, J.H.; Blair, A.; Stewart, P.A.; Vermeulen, R.; Coble, J.B.; Silverman, D.T. The Diesel Exhaust in Miners Study: A Cohort Mortality Study with Emphasis on Lung Cancer. J. Natl. Cancer Inst. 2012, 104, 869–883. [Google Scholar] [CrossRef] [PubMed]
- McClellan, R.O. Re: The Diesel Exhaust in Miners Study: A Nested Case–Control Study of Lung Cancer and Diesel Exhaust, a Cohort Mortality Study with Emphasis on Lung Cancer, and the Problem with Diesel. J. Natl. Cancer Inst. 2012, 104, 1843–1845. [Google Scholar] [CrossRef] [PubMed]
- Möhner, M. The Hidden Impact of a Healthy-Worker Effect on the Results of the Diesel Exhaust in Miners Study. Eur. J. Epidemiol. 2016, 31, 803–804. [Google Scholar] [CrossRef]
- Chowdhury, R.; Shah, D.; Payal, A.R. Healthy Worker Effect Phenomenon: Revisited with Emphasis on Statistical Methods—A Review. Indian J. Occup. Environ. Med. 2017, 21, 2–8. [Google Scholar] [CrossRef]
- Romero Starke, K.; Bolm-Audorff, U.; Reissig, D.; Seidler, A. Dose-Response Relationship between Occupational Exposure to Diesel Engine Emissions and Lung Cancer Risk: A Systematic Review and Meta-Analysis. Int. J. Hyg. Environ. Health 2024, 256, 114299. [Google Scholar] [CrossRef]
- Bugarski, A.D.; Janisko, S.J.; Cauda, E.G. Diesel Aerosols and Gases in Underground Mines: Guide to Exposure Assessment and Control; U.S. Department of Health and Human Services, Centers for Disease Control and Prevention, National Institute for Occupational Safety and Health, Office of Mine Safety and Health Research: Pittsburgh, PA, USA; Spokane, WA, USA, 2011.
- NIOSH. Carbon Monoxide—NIOSH Pocket Guide to Chemical Hazards; CDC/NIOSH Online Resource, Updated 2024. Available online: https://www.cdc.gov/niosh/npg/npgd0105.html (accessed on 1 September 2025).
- Halim, A. Ventilation Requirements for Diesel Equipment in Underground Mines—Are We Using the Correct Values? Luleå University of Technology Report; Luleå University of Technology: Luleå, Sweden, 2017; pp. 1–29. [Google Scholar]
- Ontario Ministry of Labour. Ventilation Requirements for Diesel-Powered Equipment in Underground Mines; Government of Ontario Regulation, Updated 2023. Available online: https://www.ontario.ca/laws (accessed on 1 September 2025).
- Karagianni, M.; Benardos, A. Ventilation Design Modeling and Optimization for an Underground Bauxite Mine. Mater. Proc. 2021, 5, 29. [Google Scholar] [CrossRef]
- Yi, H.; Kim, M.; Lee, D.; Park, J. Applications of Computational Fluid Dynamics for Mine Ventilation. Energies 2022, 15, 8405. [Google Scholar] [CrossRef]
- Haney, R.A. Ventilation Requirements for Modern Diesel Engines. In Proceedings of the 14th U.S./North American Mine Ventilation Symposium, Salt Lake City, UT, USA, 17–20 June 2012; pp. 1–8. [Google Scholar]
- Korshunov, G.I.; Eremeeva, A.M.; Seregin, A.S. Justification of reduction in air requirement in ventilation of coal roadways with running diesel engines. Min. Inform. Anal. Bull. (MIAB) 2022, 3, 47–59. [Google Scholar] [CrossRef]
- Malykh, I.B.; Kornev, A.V.; Korshunov, G.I.; Seregin, A.S. To the question of ventilation of underground mine workings during operation of diesel-hydraulic locomotives. Min. Inform. Anal. Bull. (MIAB) 2022, 61, 140–156. [Google Scholar] [CrossRef]
- Korshunov, G.I.; Eremeeva, A.M.; Drebenstedt, C. Justification of the Use of a Vegetal Additive to Diesel Fuel as a Method of Protecting Underground Personnel of Coal Mines from the Impact of Harmful Emissions of Diesel-Hydraulic Locomotives. J. Min. Inst. 2021, 247, 39–47. [Google Scholar] [CrossRef]
- Gendler, S.G.; Seregin, A.S.; Belekhov, P.A. Study of the Influence of Operational and Design Characteristics of Diesel Equipment on Gas Contamination of Underground Mine Workings. Russ. Min. Ind. 2025, 4, 170–177. [Google Scholar] [CrossRef]
- Chmykhalova, S.V. Development of the Foundations of a Methodology for Accounting for Aerological Risks during the Operation of Transport Machines with Internal Combustion Engines. Min. Inform. Anal. Bull. (Sci. Tech. J.) 2021, 74–87. [Google Scholar]
- Wei, L.; Geng, P. A Review on Natural Gas/Diesel Dual-Fuel Combustion. Fuel Process. Technol. 2016, 142, 264–278. [Google Scholar] [CrossRef]
- Diané, A.; Yomi, G.W.; Zongo, S.; Daho, T.; Jeanmart, H. Characterization, at Partial Loads, of the Combustion and Emissions of a Dual-Fuel Engine Burning Diesel and a Lean Gas Surrogate. Energies 2023, 16, 5587. [Google Scholar] [CrossRef]
- Peng, W.; Yang, J.; Corbin, J.; Trivanovic, U.; Lobo, P.; Kirchen, P.; Rogak, S.; Gagné, S.; Miller, J.W.; Cocker, D. Comprehensive Analysis of the Air-Quality Impacts of Switching a Marine Vessel from Diesel Fuel to Natural Gas. Environ. Pollut. 2020, 266 Pt 3, 115404. [Google Scholar] [CrossRef]
- Kuittinen, N.; Heikkilä, M.; Lehtoranta, K. Review of Methane Slip from LNG Engines. Available online: https://tuhat.helsinki.fi/ws/portalfiles/portal/282364163/D1.1_Review_of_methane_slip_from_LNG_engines.pdf (accessed on 31 January 2023).
- Lehtoranta, K.; Vesala, H.; Flygare, N.; Kuittinen, N.; Apilainen, A.-R. Measuring Methane Slip from LNG Engines with Different Devices. J. Mar. Sci. Eng. 2025, 13, 890. [Google Scholar] [CrossRef]
- Semin, M.; Kormshchikov, D. Application of Artificial Intelligence in Mine Ventilation: A Brief Review. Front. Artif. Intell. 2024, 7, 1402555. [Google Scholar] [CrossRef]
- Savioli, T.; Pampanini, M.; Visani, G.; Esposito, L.; Rinaldini, C.A. Engine Mass Flow Estimation through Neural Network Modeling in Semi-Transient Conditions: A New Calibration Approach. Fluids 2024, 9, 239. [Google Scholar] [CrossRef]
- Tabaček, J. Exhaust Gas Recirculation and Air Flow Virtual Sensors for Internal Combustion Turbocharged Engines. Master’s Thesis, Brno University of Technology, Brno, Czechia, 2016. [Google Scholar]
- Falai, A.; Misul, D.A. Data-Driven Model for Real-Time Estimation of NOx in a Heavy-Duty Diesel Engine. Energies 2023, 16, 2125. [Google Scholar] [CrossRef]
- Park, J.J.; Lee, S.; Shin, S.; Kim, M.; Park, J. Development of a Light and Accurate NOx Prediction Model for Diesel Engines Using Machine Learning and XAI Methods. Int. J. Automot. Technol. 2023, 24, 559–571. [Google Scholar] [CrossRef]
- Shen, Q.; Wang, G.; Wang, Y.; Zeng, B.; Yu, X.; He, S. Prediction Model for Transient NOx Emission of Diesel Engine Based on CNN–LSTM Network. Energies 2023, 16, 5347. [Google Scholar] [CrossRef]
- Buzmakov, D.M.; Kashnikov, A.V. Forecasting Methane Concentration in the Working Area of a Coal Mine Using Recurrent Neural Networks (LSTM). Gornoe Ekho (Mining Echo) 2020, 4, 94–98. [Google Scholar] [CrossRef]
- Vegera, D.V.; Kudyashov, A.A.; Novikova, A.A. Prediction of Gas Concentrations Using a Recurrent Neural Network. Inzhenernyi Vestn. Dona (Eng. J. Don) 2024, 7, 56. [Google Scholar]
- Shedko, Y.N.; Kharchenko, K.V.; Zudenkova, S.A.; Moskvitina, E.I.; Babayan, L.K. Implementation of Neural-Network Technologies to Improve Efficiency and Safety of Production Processes at Coal Enterprises in Russia. Ugol 2024, 9, 115–122. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Lee, S.-I. A Unified Approach to Interpreting Model Predictions. Adv. Neural Inf. Process. Syst. 2017, 30, 4765–4774. [Google Scholar]
- Udrescu, S.-M.; Tegmark, M. AI Feynman: A Physics-Inspired Method for Symbolic Regression. Sci. Adv. 2020, 6, eaay2631. [Google Scholar] [CrossRef] [PubMed]
- Schmidt, M.; Lipson, H. Distilling Free-Form Natural Laws from Experimental Data. Science 2009, 324, 81–85. [Google Scholar] [CrossRef]
- Kochueva, O.; Nikolskii, K. Data Analysis and Symbolic Regression Models for Predicting CO and NOx Emissions from Gas Turbines. Computation 2021, 9, 139. [Google Scholar] [CrossRef]
- Norouzi, A.; Shahpouri, S.; Gordon, D.C.; Winkler, A.; Nuss, E.; Abel, D.; Andert, J.; Shahbakhti, M.; Koch, C.R. Deep learning based model predictive control for compression ignition engines. Control Eng. Pract. 2022, 127, 105299. [Google Scholar] [CrossRef]
- Shin, S.; Kim, M.; Park, J.; Lee, S.; Min, K. Task Transfer Learning for Prediction of Transient Nitrogen Oxides, Soot, and Total Hydrocarbon Emissions of a Diesel Engine. IEEE Access 2023, 11, 72462–72476. [Google Scholar] [CrossRef]
- Yu, C.; Seslija, M.; Brownbridge, G.P.E.; Mosbach, S.; Kraft, M.; Parsi, M.; Davis, M.; Page, V.J.; Bhave, A. Deep kernel learning approach to engine emissions modeling. Data-Centric Eng. 2020, 1, e4. [Google Scholar] [CrossRef]
- Uluocak, İ. Comparative Study of Emission Prediction Using Deep Learning Models. Çukurova Üniversitesi Mühendislik Fakültesi Derg. 2025, 40, 337–346. [Google Scholar] [CrossRef]
- Fu, C.; Cao, X.; Liang, L.; Su, T.; Guan, W.; Pan, M.; Zhang, Z.; Chen, H.; Zhou, X. Prediction of emission characteristics of diesel/n-hexanol/graphene oxide blended fuels based on fast outlier detection–sparrow search algorithm–bidirectional recurrent neural network. Process Saf. Environ. Prot. 2024, 187, 1076–1096. [Google Scholar] [CrossRef]
- Estrada, P.M.; de Lima, D.; Bauer, P.; Mammetti, M.; Bruno, J. Deep learning in the development of energy management strategies of hybrid electric vehicles: A hybrid modeling approach. Appl. Energy 2023, 329, 120231. [Google Scholar] [CrossRef]
- Soltanalizadeh, S.; Hairi Yazdi, M.R.; Esfahanian, V.; Nejat, M. Prediction of emission and performance of internal combustion engine via regression deep learning approach. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2024; ahead of print. [Google Scholar]
- Jayaprakash, B.; Wilmer, B.; Northrop, W.F. Initial development of a physics-aware machine learning framework for soot mass prediction in gasoline direct injection engines. SAE Int. J. Adv. Curr. Pract. Mobil. 2023, 6, 2005–2020. [Google Scholar] [CrossRef]
- Nath, K.K.; Meng, X.; Smith, D.J.; Karniadakis, G.E. Physics-informed neural networks for predicting gas flow dynamics and unknown parameters in diesel engines. Sci. Rep. 2023, 13, 13683. [Google Scholar] [CrossRef]
- Kumar, V.; Goswami, S.; Smith, D.J.; Karniadakis, G.E. Real-time prediction of gas flow dynamics in diesel engines using a deep neural operator framework. arXiv 2023, arXiv:2304.00567. [Google Scholar]
- Hu, D.; Wang, H.; Yang, C.; Wang, B.; Duan, B.; Wang, Y. Engine combustion modeling method based on hybrid drive. Heliyon 2023, 9, e21494. [Google Scholar] [CrossRef] [PubMed]
- Shahpouri, S.; Gordon, D.; Shahbakhti, M.; Koch, C.R. Transient NOx emission modeling of a hydrogen–diesel engine using hybrid machine learning methods. Int. J. Engine Res. 2024, 25, 2249–2266. [Google Scholar] [CrossRef]
- Kiani, M.K.D.; Ghobadian, B.; Tavakoli, T.; Nikbakht, A.M.; Najafi, G. Application of Artificial Neural Networks for the Prediction of Performance and Exhaust Emissions in SI Engine Using Ethanol–Gasoline Blends. Energy 2010, 35, 65–69. [Google Scholar] [CrossRef]
- Çay, Y.; Korkmaz, I.; Çiçek, A.; Kara, F. Prediction of Engine Performance and Exhaust Emissions for Gasoline and Methanol Using Artificial Neural Network. Energy 2013, 50, 177–186. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).