Optimal Design of One-Sided Exponential Adaptive EWMA Scheme Based on Median Run Length

Abstract

High-quality processes, characterized by low defect rates, typically exhibit an exponential distribution for time-between-events (TBE) data. To effectively monitor TBE data, one-sided exponential Adaptive Exponentially Weighted Moving Average (AEWMA) schemes are introduced. However, the run length (RL) distribution varies with the magnitude of the process mean shift, rendering the median run length (MRL) a more pertinent performance metric. This paper investigates the RL properties of one-sided exponential AEWMA schemes using a Markov chain method. An optimal design procedure based on MRL is developed to enhance the one-sided exponential AEWMA scheme. Comparative analyses reveal that the one-sided exponential AEWMA scheme provides better balanced protection against both minor and major shifts in the process mean compared to EWMA-type and Shewhart schemes. Finally, two practical case studies illustrate the application of AEWMA schemes in manufacturing.

1. Introduction

Quality control is essential for manufacturing and service industries to ensure product qualify and enhance operational efficiency [1]. Statistical process control (SPC) serves as a critical tool in ensuring product quality by monitoring and controlling the state of processes [2]. Among various SPC tools, monitoring schemes are extensively used to identify shifts in process parameters. Conventional monitoring schemes, like the Shewhart-type scheme, are efficient at detecting large shifts but are typically less sensitive to small or moderate shifts. To address this limitation, advanced memory-type monitoring schemes such as the Exponentially Weighted Moving Average (EWMA) [3] and the Cumulative Sum (CUSUM) [4] schemes, which incorporate historical information from previous observations, have been developed. The EWMA scheme is especially adept at identifying minor to moderate changes in process parameters, owing to its method of integrating historical data with a focus on more recent measurements. The EWMA statistic calculates a weighted average of previous data values, giving higher weight to the most recent observations. The effectiveness of the EWMA scheme largely depends on the selection of the smoothing parameter, $\lambda$, which is often fine-tuned for optimal detection of a particular magnitude of shift [5,6,7]. However, when the actual shift size differs from the expected one, the performance of the EWMA scheme can be significantly impacted.

To overcome this limitation, adaptive EWMA (AEWMA) schemes have been proposed. AEWMA schemes adjust the smoothing parameter dynamically based on the observed data, thereby providing better performance across a range of shift sizes. This adaptability makes AEWMA schemes more robust and versatile in various industrial settings. For example, Capizzi and Masarotto (see [8]) introduced the concept of adaptive EWMA schemes, demonstrating their enhanced capability to identify various magnitudes of shifts. Shu (see [9]) introduced an AEWMA scheme to surveil the shift in process variance, showing its effectiveness in various scenarios. Tang et al. (see [10]) developed a variable sampling interval (VSI) AEWMA scheme, which further improved the detection performance by adjusting the sampling intervals dynamically. Ugaz et al. (see [11]) presented an AEWMA-S² scheme with an adaptive smoothing parameter, aimed at overcoming the inefficiency of traditional schemes in detecting various shifts. Zaman et al. (see [12]) developed an AEWMA scheme based on the Hampel function, providing a robust approach to detect changes in the process location.

High-quality processes are distinguished by minimal defect rates, often measured in parts per million (ppm) or as low as parts per billion (ppb) [13]. These processes are prevalent in industries such as semiconductor manufacturing, healthcare, and earthquake monitoring [14]. Traditional monitoring schemes, which assume a normal distribution, are not well-suited for monitoring processes with strictly positive variables due to issues such as high false alarm rates and the appearance of negative lower control limits (LCL). These issues can lead to misleading assessments of process stability and performance [15]. To address these challenges, specialized monitoring schemes have been developed. One common approach is to employ time-between-events (TBE) monitoring schemes, which focus on the time intervals between consecutive events, such as defects or failures. TBE data are typically modeled using a skewed distribution, such as the exponential distribution [16,17], which is a natural fit for the inter-arrival times of a homogeneous Poisson process [18]. Gan (see [19,20]) proposed the one- and two-sided exponential EWMA schemes. Pehlivan and Testik (see [21]) investigated the robustness of the exponential EWMA scheme when the TBE data deviate from an exponential distribution. Hu et al. (see [22]) proposed an AEWMA scheme for monitoring the TBE based on the Gamma distribution. They found that the proposed scheme exhibited a superior average run length (ARL) compared to existing monitoring schemes across various shift sizes.

Most studies on exponential schemes focus on the ARL as the primary performance metric. However, the ARL alone can be misleading because the shape of run length (RL) distribution alters depending on the size of the shift. Notably, the RL distribution for the exponential EWMA scheme tends to be skewed, particularly under in-control conditions [23]. This skewness can affect the interpretation of the scheme’s performance, making it important to consider additional metrics or the entire distribution of RL when evaluating monitoring scheme effectiveness. In such cases, the median run length (MRL) offers a more insightful measure of scheme performance [24]. The optimization of monitoring schemes involves selecting the best parameters to achieve desired performance metrics. For traditional monitoring schemes, this often involves minimizing the ARL for a specific shift size. However, as discussed earlier, the ARL alone may not provide a complete picture of scheme performance, especially for skewed RL distributions. Therefore, optimizing monitoring schemes based on MRL has gained increasing attention in recent years. Maravelakis et al. (see [25]) studied the RL properties of run rules EWMA schemes by employing integral equations, providing a theoretical foundation for optimizing these schemes. Tang et al. (see [26]) proposed an optimal design procedure for the AEWMA scheme based on MRL, showing that the resulting schemes performed uniformly better than traditional EWMA schemes.

Motivated by the fact that AEWMA schemes can provide more balanced monitoring performance compared to traditional EWMA schemes [22], and that MRL is a more reasonable performance metric for exponential monitoring schemes [24], this paper aims to develop an optimized design for one-sided exponential AEWMA schemes using MRL as the performance metric. The RL properties are investigated using a Markov chain approach, in considering the two cases of upper-sided and lower-sided schemes. The optimal design procedures, in terms of MRL, are proposed for a range of mean parameter shift. The performance of the proposed schemes is assessed and compared to existing monitoring schemes using MRL.

The remainder of this paper is structured as follows: In Section 2, the proposed one-sided exponential AEWMA scheme is introduced. The Markov chain models are used to investigate the RL properties of the proposed schemes in Section 3. The optimal design procedures for the MRL-based one-sided exponential AEWMA schemes are presented in Section 4. In Section 5, the performance of the proposed schemes with existing ones is compared. Two practical case studies are shown in Section 6. Finally, the conclusion and the suggested directions for future study are given in Section 7.

2. Exponential Monitoring Schemes for TBE Data

2.1. Exponential Distribution

Suppose the t-th sample of TBE variable is $X_t(t=1,2,\cdots ,t)$. Each $X_t$ is independent and exponentially distributed, characterized by a mean of $\theta$, denoted as $exp\left(\theta \right)$. The probability density function (p.d.f.) and cumulative distribution function (c.d.f.) of the random variable $X_t$ are, respectively,

$$\begin{array}{ccc}\hfill f\left(x\right)=& {\displaystyle \frac{1}{\theta }}{e}^{-{\displaystyle \frac{x}{\theta }}},\hfill & \hfill x\ge 0,\end{array}$$

(1)

$$\begin{array}{ccc}\hfill F\left(x\right)=& 1-e^{-{\displaystyle \frac{x}{\theta }}},\hfill & \hfill x\ge 0.\end{array}$$

(2)

When the process is in-control, $\theta ={\theta }_0$. For convenience of study, the random variable $X_t$ is standardized using ${\theta }_0$ to obtain $Y_t$,

$$Y_t={\displaystyle \frac{X_t}{{\theta }_0}}={\displaystyle \frac{\theta }{{\theta }_0}}·{\displaystyle \frac{X_t}{\theta }}=c·S_t,$$

(3)

where $c=\theta /{\theta }_0$, $S_t=X_t/\theta$. According to [27], $S_t\sim exp\left(1\right)$, and its c.d.f. is given by:

$$F_S\left(s\right)=1-e^{-s},s\ge 0.$$

(4)

In this study, our primary objective is to detect any deviation in the parameter $\theta$ from its in-control value, denoted as ${\theta }_0$. When the process shifts out-of-control, an increase in ${\theta }_0$ is signaled by a coefficient $c>1$, whereas a decrease is indicated by $c<1$. It is assumed that ${\theta }_0$ is known a priori. However, if this parameter is unknown, it must be estimated using in-control samples gathered during Phase II of the process. Future studies should delve into the influence of parameter estimation on the efficacy and reliability of the monitoring schemes.

2.2. One-Sided Exponential EWMA Schemes for TBE Data

In the context of the exponential EWMA scheme, the implementation of two independent one-sided control charts is recommended, detailed below:

• To detect an increase in the process parameter $(c>1)$, the upper-sided exponential EWMA schemes monitoring statistic for the tth sample is

  $$Q_t^{+}=\max (B^{+},(1-{\lambda }^{+})Q_{t-1}^{+}+{\lambda }^{+}{Y}_t),t=1,2,\dots ,$$

  (5)

  where the smoothing parameter ${\lambda }^{+}\in (0,1]$ is a fixed value. The reflecting boundary $B^{+}$ and starting value $Q_0^{+}$ are suggested to be set to $0.5$ and 1, respectively [24].
• To detect a decrease in the process parameter $(c<1)$, the lower-sided exponential EWMA schemes monitoring statistic for the tth sample is

  $$Q_t^{-}=\min (B^{-},(1-{\lambda }^{-})Q_{t-1}^{-}+{\lambda }^{-}{Y}_t),t=1,2,\dots ,$$

  (6)

  where the smoothing parameter ${\lambda }^{-}\in (0,1]$ is a fixed value. The reflecting boundary $B^{-}$ and starting value $Q_0^{-}$ are suggested to be set $2.0$ and 1, respectively [24].

An out-of-control signal is alarmed when $Q_t^{+}>UC{L}^{+}(Q_t^{-}<LC{L}^{-})$, where $UC{L}^{+}\left(LC{L}^{-}\right)$ is the upper (lower) control limit of the scheme. When the smoothing parameter ${\lambda }^{+}\left({\lambda }^{-}\right)$ is larger, it indicates that the current sample is given more weight. In particular, when ${\lambda }^{+}\left({\lambda }^{-}\right)=1$, the scheme simplifies to a Shewhart-type scheme.

2.3. One-Sided Exponential AEWMA Schemes for TBE Data

For one-sided exponential EWMA schemes, using a small smoothing parameter ${\lambda }^{+}\left({\lambda }^{-}\right)$ can quickly detect small process shifts, whereas a larger ${\lambda }^{+}\left({\lambda }^{-}\right)$ is necessary for sudden large shifts to increase the weight of the current sample statistic and enhance the scheme’s detection capability for large shifts. According to Capizzi and Masarotto (see [8]), a fixed-parameter EWMA scheme cannot simultaneously ensure optimal performance for different sizes of process shifts. Therefore, the AEWMA scheme is recommended to monitor various shifts in the process by adapting the parameter as a function of the prediction error, thereby providing a more balanced detection performance. Similar to the one-sided exponential EWMA scheme, two separated one-sided exponential AEWMA schemes are suggested as follows:

• An upper-sided exponential AEWMA scheme is suggested to detect an increase in the process parameter $(c>1)$,

  $$\begin{array}{cc}\hfill A_t^{+}& =\max (B^{+},A_{t-1}^{+}+\varphi \left(e_t\right))\hfill \\ \hfill & =\max (B^{+},\omega \left(e_t\right)Y_t+(1-\omega \left(e_t\right))A_{t-1}^{+}),t=1,2,\dots ,\hfill \end{array}$$

  (7)

  where $A_t^{+}$ is the tth statistic (the starting value $A_0^{+}=1$), and $\omega \left(e_t\right)=\varphi \left(e_t\right)/e_t$ where $\varphi \left(e_t\right)$ is a score function. For simplicity, Huber’s score function is used, as suggested by Capizzi and Masarotto (see [8])

  $$\varphi \left(e\right)=\left\{\begin{array}{cc}e+(1-{\lambda }^{+})k\hfill & \mathrm{if}e<-k\hfill \\ {\lambda }^{+}e\hfill & \mathrm{if}\left|e\right|\le k\hfill \\ e-(1-{\lambda }^{+})k\hfill & \mathrm{if}e>k\hfill \end{array}\right.,$$

  (8)

  where the threshold parameter $k\ge 0$.
• A lower-sided exponential AEWMA scheme is suggested to detect a decrease in the process parameter ($0<c<1$),

  $$\begin{array}{cc}\hfill A_t^{-}& =\min (B^{-},A_{t-1}^{-}+\varphi \left(e_t\right))\hfill \\ \hfill & =\min (B^{-},\omega \left(e_t\right)Y_t+(1-\omega \left(e_t\right))A_{t-1}^{-}),t=1,2,\dots ,\hfill \end{array}$$

  (9)

  where $A_t^{-}$ is the tth statistic (the starting value $A_0^{-}=1$), and $\omega \left(e_t\right)=\varphi \left(e_t\right)/e_t$ where $\varphi \left(e_t\right)$ is a score function

  $$\varphi \left(e\right)=\left\{\begin{array}{cc}e+(1-{\lambda }^{-})k\hfill & \mathrm{if}e<-k\hfill \\ {\lambda }^{-}e\hfill & \mathrm{if}\left|e\right|\le k\hfill \\ e-(1-{\lambda }^{-})k\hfill & \mathrm{if}e>k\hfill \end{array}\right.,$$

  (10)

  where the threshold parameter $k\ge 0$.

As k approaches infinity ($\varphi \left(e\right)\approx \lambda e$), the AEWMA scheme reduces to the EWMA-type scheme. Conversely, as k approaches zero ($\varphi \left(e\right)\approx e$), the AEWMA scheme reduces to the Shewhart-type scheme.

3. RL Properties of the One-Sided Exponential AEWMA Schemes

3.1. A Markov Chain Method to RL Properties

The performance of a monitoring scheme is typically evaluated by RL measures, such as ARL, MRL, and standard deviation of RL (SDRL), etc. In general, evaluating the RL properties of EWMA-type schemes can be accomplished through three primary methods: integral equations [25], which provide exact solutions but can be mathematically complex; Markov chain methods [28,29,30], which offer a flexible and computationally efficient approach; and Monte Carlo simulations [31,32], which are useful for obtaining empirical results and handling more complex scenarios. In this paper, a Markov chain model is developed to assess the RL and MRL performance of the proposed one-sided exponential AEWMA schemes. Without loss of generality, the in-control region is divided into N subintervals, labeled as $i=1,2,\cdots ,N$. Each state of the Markov chain is defined by these subintervals, and the value of the corresponding one-sided exponential AEWMA statistic is approximated using the midpoint of each subinterval. The scheme statistic $A_t^{+}\left(A_t^{-}\right)$ is considered to be in transient-state i if it falls within the i-th subinterval. If $A_t^{+}\left(A_t^{-}\right)$ falls outside the control limits, it is considered to be in the absorbing-state, indicating that the process is out-of-control. Based on the above state space partition, a $(N+1)\times (N+1)$ one-step transition probability matrix $\mathbf{P}$ can be constructed as follows:

$$\begin{array}{c}\hfill \mathbf{P}=\left[\begin{array}{cc}\mathbf{Q}& (\mathbf{I}-\mathbf{Q})\mathbf{1}\\ {\mathbf{0}}^{⊺}& 1\end{array}\right],\end{array}$$

(11)

where $\mathbf{I}$ is an identity matrix, and $\mathbf{1}$ is a column vector of ones. The transient transition probability matrix $\mathbf{Q}={\left[p_{i,j}\right]}_{N\times N}$ contains the probabilities $p_{i,j}$ of transitioning from state i to state j.

For the upper-sided exponential AEWMA scheme, the in-control interval $[B^{+},UC{L}^{+})$ is divided into N subintervals, each subinterval $[H_i^{+}-{\Delta }^{+},H_i^{+}+{\Delta }^{+})$, $i=1,2,\cdots ,N$ with a width of $2{\Delta }^{+}={\displaystyle \frac{UC{L}^{+}-B^{+}}{N}}$, where $H_i^{+}$ represents the center value of the ith subinterval:

$$H_i^{+}=B^{+}+(2i-1){\Delta }^{+},i=1,2,\cdots ,N.$$

(12)

The transient transition probability matrix $\mathbf{Q}={\left[p_{i,j}\right]}_{N\times N}$ is given by:

$$p_{i,j}=\left\{\begin{array}{ccc}\mathrm{Pr}(A_t^{+}<H_j^{+}+{\Delta }^{+}|A_{t-1}^{+}=H_i^{+}),\hfill & & j=1,\hfill \\ \\ \mathrm{Pr}(H_j^{+}-{\Delta }^{+}\le A_t^{+}<H_j^{+}+{\Delta }^{+}|A_{t-1}^{+}=H_i^{+}),\hfill & & j=2,\dots ,N.\hfill \end{array}\right.$$

(13)

Substituting Equations (3) and (7) into Equation (13) yields

$$p_{i,j}=\left\{\begin{array}{ccc}\mathrm{Pr}\left(\varphi (c{S}_t-H_i^{+})<H_j^{+}-H_i^{+}+{\Delta }^{+}\right),\hfill & & j=1,\hfill \\ \\ \mathrm{Pr}\left(H_j^{+}-H_i^{+}-{\Delta }^{+}\le \varphi (c{S}_t-H_i^{+})<H_j^{+}-H_i^{+}+{\Delta }^{+}\right),\hfill & & j=2,\dots ,N.\hfill \end{array}\right.$$

(14)

From Equation (8), it is known that $\varphi \left(e\right)$ is invertible, and its inverse function is invertible ${\varphi }^{-1}\left(z\right)$ given by:

$${\varphi }^{-1}\left(z\right)=\left\{\begin{array}{cc}z-\left(1-\lambda \right)k\hfill & \mathrm{if}z<-\lambda k\hfill \\ z/\lambda \hfill & \mathrm{if}\left|z\right|\le \lambda k\hfill \\ z+\left(1-\lambda \right)k\hfill & \mathrm{if}z>\lambda k\hfill \end{array}\right.,$$

(15)

Substituting Equation (15) into Equation (14) yields:

$$p_{i,j}=\left\{\begin{array}{ccc}\mathrm{Pr}\left(S_t^{+}<{\displaystyle \frac{{\varphi }^{-1}(H_j^{+}-H_i^{+}+{\Delta }^{+})+H_i^{+}}{c}}\right),\hfill & & j=1,\hfill \\ \\ \mathrm{Pr}\left({\displaystyle \frac{{\varphi }^{-1}(H_j^{+}-H_i^{+}-{\Delta }^{+})+H_i^{+}}{c}}\le S_t^{+}<{\displaystyle \frac{{\varphi }^{-1}(H_j^{+}-H_i^{+}+{\Delta }^{+})+H_i^{+}}{c}}\right),\hfill & & j=2,\dots ,N.\hfill \end{array}\right.$$

(16)

Since $S_t^{+}\sim exp\left(1\right)$, its c.d.f. is given by Equation (4), and we have:

$$p_{i,j}=\left\{\begin{array}{ccc}{F}_s\left({\displaystyle \frac{{\varphi }^{-1}(H_j^{+}-H_i^{+}+{\Delta }^{+})+H_i^{+}}{c}}\right),\hfill & & j=1,\hfill \\ \\ F_s\left({\displaystyle \frac{{\varphi }^{-1}(H_j^{+}-H_i^{+}+{\Delta }^{+})+H_i^{+}}{c}}\right)-F_s\left({\displaystyle \frac{{\varphi }^{-1}(H_j^{+}-H_i^{+}-{\Delta }^{+})+H_i^{+}}{c}}\right),\hfill & & j=2,\dots ,N.\hfill \end{array}\right.$$

(17)

For the lower-sided exponential AEWMA scheme, the in-control interval $(LC{L}^{-},B^{+}]$ is divided into N subintervals, each subinterval $(H_i^{-}-{\Delta }^{-},H_i^{-}+{\Delta }^{-}]$ with a width of $2{\Delta }^{-}={\displaystyle \frac{B^{-}-LC{L}^{-}}{N}}$, where $H_i^{-}$ represents the center value of the ith subinterval:

$$H_i^{-}=B^{-}-(2i-1){\Delta }^{-},i=1,2,\cdots ,N.$$

(18)

Similarly, the transient transition probability matrix $\mathbf{Q}={\left[p_{i,j}\right]}_{N\times N}$ for the lower-sided exponential AEWMA scheme can be obtained, where

$$p_{i,j}=\left\{\begin{array}{ccc}\mathrm{Pr}(A_t^{-}>H_j^{-}-{\Delta }^{-}|A_{t-1}^{-}=H_i^{-}),\hfill & & j=1,\hfill \\ \\ \mathrm{Pr}(H_j^{-}-{\Delta }^{-}<A_t^{-}\le H_j^{-}+{\Delta }^{-}|A_{t-1}^{-}=H_i^{-}),\hfill & & j=2,\dots ,N.\hfill \end{array}\right.$$

(19)

Substituting Equations (3), (9) and (15) into Equation (19) and combining with Equation (4) yields:

$$p_{i,j}=\left\{\begin{array}{ccc}1-F_s\left({\displaystyle \frac{{\varphi }^{-1}(H_j^{-}-H_i^{-}-{\Delta }^{-})+H_i^{-}}{c}}\right),\hfill & & j=1,\hfill \\ \\ F_s\left({\displaystyle \frac{{\varphi }^{-1}(H_j^{-}-H_i^{-}+{\Delta }^{-})+H_i^{-}}{c}}\right)-F_s\left({\displaystyle \frac{{\varphi }^{-1}(H_j^{-}-H_i^{-}-{\Delta }^{-})+H_i^{-}}{c}}\right),\hfill & & j=2,\dots ,N.\hfill \end{array}\right.$$

(20)

Assume the initial probability vector for the process is $\mathbf{q}={(q_1,q_2,\cdots ,q_N)}^{⊺}$, where

$$\begin{array}{c}\hfill q_j=\left\{\begin{array}{c}1,A_0^{+}\in [H_i^{+}-{\Delta }^{+},H_i^{+}+{\Delta }^{+})\mathrm{or}{A}_0^{-}\in [H_i^{-}-{\Delta }^{-},H_i^{-}+{\Delta }^{-}),\hfill \\ 0,\mathrm{others}.\hfill \end{array}\right.\end{array}$$

(21)

As discussed in [33,34], the steps required for a Markov chain to reach the absorbing-state can be modeled as a Discrete Phase random variable, characterized by $(\mathbf{Q},\mathbf{q})$. The probability mass function (p.m.f.) $f_{RL}(\ell |\mathbf{Q},\mathbf{q})$ and the c.d.f. $F_{RL}(\ell |\mathbf{Q},\mathbf{q})$ of the RL distribution for the one-sided exponential AEWMA schemes are given by:

$$\begin{array}{ccc}\hfill f_{RL}(\ell |\mathbf{Q},\mathbf{q})& =& {\mathbf{q}}^{⊺}{\mathbf{Q}}^{\ell -1}\mathbf{1}-{\mathbf{q}}^{⊺}{\mathbf{Q}}^{\ell }\mathbf{1},\hfill \end{array}$$

(22)

$$\begin{array}{ccc}\hfill F_{RL}(\ell |\mathbf{Q},\mathbf{q})& =& 1-{\mathbf{q}}^{⊺}{\mathbf{Q}}^{\ell }\mathbf{1}.\hfill \end{array}$$

(23)

Finally, the ARL and MRL values of the proposed one-sided exponential AEWMA scheme can be computed as follows:

$$ARL={\mathbf{q}}^{⊺}{(\mathbf{I}-\mathbf{Q})}^{-1}\mathbf{1},$$

(24)

$$F_{RL}(MRL-1|\mathbf{Q},\mathbf{q})⩽0.5\mathrm{and}{F}_{RL}\left(MRL\right|\mathbf{Q},\mathbf{q})>0.5.$$

(25)

However, the Markov chain method can be computationally intensive due to the complexity involved in calculating the transient transition probability matrix $\mathbf{Q}$. To address this issue, it is recommended to set the number of states N in $\mathbf{Q}$ to 300. This adjustment significantly enhances computational speed while incurring only a minimal loss in precision. Empirical studies have demonstrated that an N value of 300 provides a good balance between accuracy and efficiency, making it suitable for practical applications [35,36]. Furthermore, when calculating the MRL, it is suggested to employ the bisection method to improve computational efficiency.

3.2. Interpretation Problems of ARL

The RL of the one-sided exponential AEWMA scheme is distributed skewly. Figure 1 shows the p.d.f. curves for the RL distribution of the lower-sided exponential AEWMA scheme, where $({\lambda }^{-},k,LC{L}^{-})=(0.051,1.168,0.768)$ meets the in-control ARL ($AR{L}_0$) of 370, and the process mean shift $c\in \{0.1,0.5,0.8,1\}$. From Figure 1, it is evident that the RL distributions of the lower-sided exponential AEWMA scheme are significantly skewed under both in-control and out-of-control conditions.

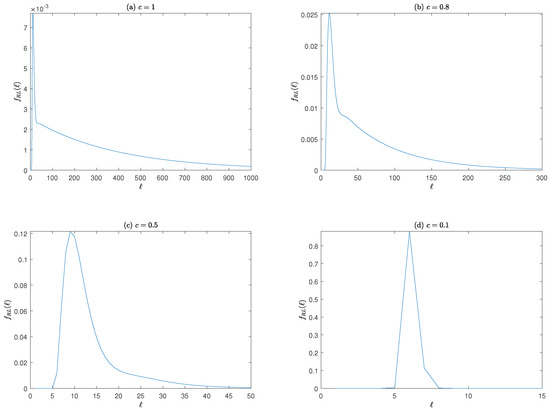
Figure 1. Several p.m.f. plots of the RL distribution of the lower-sided exponential AEWMA scheme when $({\lambda }^{-},k,LC{L}^{-})=(0.051,1.168,0.768)$, $c\in \{0.1,0.5,0.8,1\}$.

In the in-control state, the discrepancy between $AR{L}_0$ and the in-control MRL ($MR{L}_0$) is large. However, the difference between the out-of-control ARL ($AR{L}_1$) and out-of-control MRL ($MR{L}_1$) decreases as the process mean shift increases. This suggests that the shape of the RL distribution for the lower-sided exponential AEWMA scheme evolves with the magnitude of the process mean shift, becoming increasingly symmetric as the shift grows larger.

Therefore, in the design of the one-sided exponential AEWMA scheme, using ARL as the sole indicator of the monitoring scheme’s statistical performance lacks consideration of the bias in the RL distribution. The interpretation based on ARL differs for the two cases where the RL distribution is either symmetric or highly biased. Using MRL as the statistical performance indicator for the one-sided exponential AEWMA scheme is more intuitive and reasonable.

4. Design Procedures of the One-Sided Exponential AEWMA Scheme

4.1. The Joint Effect of Parameter $\lambda$ and k

To investigate the performance of the one-sided exponential AEWMA scheme, it is necessary to select the parameters $({\lambda }^{+},k,UC{L}^{+})$ or $({\lambda }^{-},k,LC{L}^{-})$. This paper will use the MRL as the performance metric to study the effects of parameters ${\lambda }^{+}\left({\lambda }^{-}\right)$ and k on the performance of the scheme. When $MR{L}_0=200$ and $c\in \{1.04,1.1,1.2,1.4\}$, Figure 2 provides the contour plot of $MR{L}_1$ values for the lower-sided exponential AEWMA scheme. From Figure 2, it can be observed that near the optimal parameter ${\lambda }^{-}$ value of the scheme, the $MR{L}_1$ value is also smaller. When monitoring smaller process mean shifts (e.g., $c=0.9$), the $MR{L}_1$ value tends to increase as k decreases; on the other hand, when monitoring larger process mean shifts (e.g., $c=0.01$), the $MR{L}_1$ value decreases as k decreases.

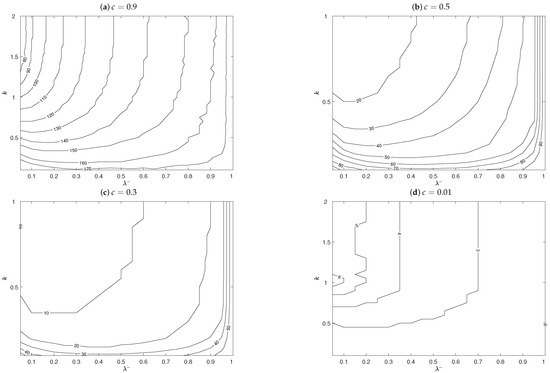
Figure 2. Contour plot of $MR{L}_1$ values for the lower-sided exponential AEWMA scheme when $MR{L}_0=200,c\in \{0.01,0.3,0.5,0.9\}$.

When $MR{L}_0=200$ and $c\in \{1.04,1.1,1.2,1.4\}$, Figure 3 provides the contour plot of $MR{L}_1$ values for the upper-sided exponential AEWMA scheme. Similarly, near the optimal parameter ${\lambda }^{+}$ value of the upper-sided exponential AEWMA scheme, the $MR{L}_1$ value of the scheme is also smaller, and the $MR{L}_1$ value generally increases as k decreases.

Figure 3. Contour plot of $MR{L}_1$ values for the upper-sided exponential AEWMA scheme when $MR{L}_0=200,c\in \{1.04,1.1,1.2,1.4\}$.

4.2. Optimal Design Procedures

Capizzi and Masarotto (see [8]) transformed the multi-objective optimization problem into a progressive optimization problem for two different shift sizes using a hierarchical and weighted approach, providing an optimization algorithm for the AEWMA scheme based on ARL. However, this algorithm is complex and computationally intensive. Shu (see [9]) introduced a sequential search method to determine the approximate optimal parameters for the AEWMA scheme, which is both simpler and requires less computational effort. In this study, we also employ this sequential search method for the one-sided exponential AEWMA scheme. The optimization design procedures are outlined as follows:

• Determine the required $MR{L}_0$, the small process mean shift $c_1$, and the large process mean shift $c_2$.
• For the given small shift $c_1$, under the constraint of $MR{L}_0$, determine the corresponding smoothing parameter ${\lambda }^{+}\left({\lambda }^{-}\right)$ for the optimal one-sided exponential AEWMA scheme.
• Select a small constant $\xi$ to constrain the performance loss that might result from introducing the threshold parameter k at the shift $c_1$.
• Set the smoothing parameter ${\lambda }^{+}\left({\lambda }^{-}\right)$ obtained in step 2 for the one-sided exponential AEWMA scheme.
• Given the constraint that the percentage increase in $MR{L}_1$ for the one-sided exponential AEWMA scheme monitoring the small shift $c_1$ is less than $\xi$, find the threshold parameter k and $UC{L}^{+}\left(LC{L}^{-}\right)$ that minimize the $MR{L}_1$ value for the large shift $c_2$.

The optimal design procedures, though computationally demanding, can be effectively employed in industrial production by pre-optimizing parameters for specified $MR{L}_0$, $c1$, and $c2$. This facilitates the pre-determination of optimal parameters, which can then be directly integrated into production monitoring systems. With these parameters in place, computational efficiency is greatly enhanced, ensuring the approach is well-suited for real-time monitoring in industries with critical timing constraints.

5. Comparisons of the Performance

This section employs MRL as the performance metric to evaluate and compare the effectiveness of one-sided exponential AEWMA, EWMA, and Shewhart schemes. Table 1 and Table 2 provide the optimized parameters and corresponding $MR{L}_1$ for lower-sided exponential monitoring schemes designed to monitor downward shifts, with $MR{L}_0$ set at $\{100,200,300,500\}$. For the lower-sided exponential AEWMA scheme, the parameters $({\lambda }^{-},k,LC{L}^{-})$ are optimized for the shift range $[c_2,c_1]$, where smaller process mean shifts $c_1\in \{0.6,0.8\}$ and larger shifts $c_2=0.01$. Similarly, the parameters $({\lambda }^{-},LC{L}^{-})$ for the lower-sided exponential EWMA scheme are optimized for the shift size $c_1$, while the parameter $LC{L}^{-}$ for the lower-sided exponential Shewhart scheme is constrained to achieve the desired $MR{L}_0$. For instance, in Table 2, when $MR{L}_0=300$, $c_1=0.6$, and $c_2=0.01$, the optimized parameters $({\lambda }^{-},k,LC{L}^{-})=(0.089,1.025,0.597)$ for the lower-sided exponential AEWMA scheme are derived using the optimization procedure outlined in Section 4.

Table 1. The optimal parameters and $MR{L}_1$ for the lower-sided exponential AEWMA, EWMA, Shewhart scheme when $c_1=0.8,c_2=0.01,MR{L}_0\in \{100,200,300,500\}$.

		${\mathit{MRL}}_0=100$			${\mathit{MRL}}_0=200$			${\mathit{MRL}}_0=300$			${\mathit{MRL}}_0=500$
		AEWMA	EWMA	Shewhart	AEWMA	EWMA	Shewhart	AEWMA	EWMA	Shewhart	AEWMA	EWMA	Shewhart
	${\mathit{\lambda }}^{-}$	0.060	0.060	-	0.051	0.051	-	0.052	0.052	-	0.051	0.051	-
	$\mathit{k}$	1.100	-	-	1.150	-	-	1.175	-	-	1.250	-	-
$\mathit{c}$	${\mathit{LCL}}^{-}$	0.778	0.736	0.0069	0.779	0.716	0.0035	0.754	0.688	0.0023	0.737	0.664	0.0014
1.00		100	100	100	200	200	200	300	300	300	500	500	500
0.80		29	29	80	43	43	160	55	54	240	73	70	400
0.75		22	23	75	31	34	150	38	41	225	49	51	375
0.70		17	20	70	22	28	140	27	33	210	34	40	350
0.65		14	17	65	17	23	130	20	27	195	24	32	325
0.60		11	14	60	14	20	120	16	23	180	19	27	300
0.55		10	13	55	12	17	110	14	19	165	16	23	275
0.50		9	11	50	11	15	100	12	17	150	14	20	250
0.45		8	10	45	10	14	90	11	15	135	12	17	225
0.40		7	9	40	9	12	80	10	14	120	11	16	200
0.35		7	9	35	8	11	70	9	12	105	10	14	175
0.30		6	8	30	7	10	60	8	11	90	9	13	150
0.25		6	7	25	7	9	50	8	10	75	9	12	125
0.20		6	7	20	6	9	40	7	10	60	8	11	100
0.15		5	6	15	6	8	30	7	9	45	8	10	75
0.10		5	6	10	6	8	20	6	8	30	7	9	50
0.05		5	6	5	5	7	10	6	8	15	7	9	25
0.03		5	6	3	5	7	6	6	8	9	7	9	15
0.01		4	5	1	5	7	2	6	8	3	6	8	5

Table 2. The optimal parameters and $MR{L}_1$ for the lower-sided exponential AEWMA, EWMA, Shewhart scheme when $c_1=0.6,c_2=0.01,MR{L}_0\in \{100,200,300,500\}$.

		${\mathit{MRL}}_0=100$			${\mathit{MRL}}_0=200$			${\mathit{MRL}}_0=300$			${\mathit{MRL}}_0=500$
		AEWMA	EWMA	Shewhart	AEWMA	EWMA	Shewhart	AEWMA	EWMA	Shewhart	AEWMA	EWMA	Shewhart
	${\mathit{\lambda }}^{-}$	0.101	0.101	-	0.100	0.100	-	0.089	0.089	-	0.079	0.079	-
	$\mathit{k}$	1.150	-	-	1.075	-	-	1.025	-	-	1.200	-	-
$\mathit{c}$	${\mathit{LCL}}^{-}$	0.655	0.629	0.0069	0.599	0.579	0.0035	0.597	0.580	0.0023	0.616	0.577	0.0014
1.00		100	100	100	200	200	200	300	300	300	500	500	500
0.60		13	14	60	18	19	120	22	22	180	23	26	300
0.55		11	12	55	15	16	110	18	19	165	18	22	275
0.50		10	11	50	13	14	100	15	16	150	15	18	250
0.45		9	10	45	11	12	90	13	14	135	13	16	225
0.40		8	9	40	10	11	80	11	12	120	12	14	200
0.35		7	8	35	9	10	70	10	11	105	11	13	175
0.30		7	7	30	8	9	60	9	10	90	10	11	150
0.25		6	7	25	7	8	50	8	9	75	9	10	125
0.20		6	6	20	7	7	40	8	8	60	8	10	100
0.15		5	6	15	6	7	30	7	8	45	8	9	75
0.10		5	5	10	6	6	20	7	7	30	7	8	50
0.05		5	5	5	6	6	10	6	7	15	7	8	25
0.03		5	5	3	6	6	6	6	7	9	7	7	15
0.01		4	5	1	5	6	2	6	6	3	6	7	5

The tables demonstrate that the lower-sided exponential AEWMA scheme consistently delivers robust performance across various shift sizes. For smaller mean shifts in the production process, the lower-sided exponential AEWMA scheme performs comparably to the EWMA scheme but significantly outperforms the Shewhart scheme. For example, in Table 1, when $MR{L}_0=200$, $c_1=0.8$, and $c_2=0.01$, if the current process mean shift $c=0.8$, the $MR{L}_1$ of the lower-sided exponential Shewhart scheme is 160, while the $MR{L}_1$ for the lower-sided exponential AEWMA and EWMA schemes are both 43. This indicates that both exponential EWMA-type schemes can detect process mean shifts much more rapidly than the Shewhart scheme. In contrast, for moderate shifts such as $c=0.65$, the $MR{L}_1$ of the lower-sided exponential AEWMA and EWMA schemes are 17 and 23, respectively, highlighting the AEWMA scheme’s superior effectiveness over the EWMA scheme. Only for substantial shifts ($c<0.05$) does the exponential Shewhart scheme marginally outperform the AEWMA and EWMA schemes in detecting downward shifts. The robustness of the AEWMA scheme is particularly notable, as it maintains consistent performance across a wide range of shift sizes. Unlike the Shewhart scheme, which performs better only for very large shifts, the AEWMA scheme exhibits superior sensitivity for both small and moderate shifts, making it a more dependable choice for practical applications. Additionally, Table 3 and Table 4 provide analogous comparisons for upper-sided exponential monitoring schemes, further emphasizing the AEWMA scheme’s robust performance in detecting upward shifts.

Table 3. The optimal parameters and $MR{L}_1$ for the upper-sided exponential AEWMA, EWMA, Shewhart scheme when $c_1=1.02,c_2=5,MR{L}_0\in \{100,200,300,500\}$.

		${\mathit{MRL}}_0=100$			${\mathit{MRL}}_0=200$			${\mathit{MRL}}_0=300$			${\mathit{MRL}}_0=500$
		AEWMA	EWMA	Shewhart	AEWMA	EWMA	Shewhart	AEWMA	EWMA	Shewhart	AEWMA	EWMA	Shewhart
	${\mathit{\lambda }}^{+}$	0.050	0.050	-	0.052	0.052	-	0.050	0.050	-	0.050	0.050	-
	$\mathit{k}$	1.336	-	-	1.432	-	-	1.452	-	-	1.497	-	-
$\mathit{c}$	${\mathit{h}}^{+}$	4.325	1.277	4.9651	4.975	1.369	5.6616	5.500	1.401	6.0681	6.100	1.454	6.5798
1.02		86	83	90	168	161	179	246	235	266	398	380	439
1.04		75	71	82	143	132	160	204	189	237	321	296	388
1.10		53	47	63	92	80	119	123	108	173	180	157	275
1.20		33	29	44	52	45	78	65	56	109	86	75	167
1.30		23	20	32	35	30	54	41	36	74	52	46	110
1.40		18	16	24	25	22	40	30	26	53	36	32	76
1.50		14	13	19	20	18	30	23	21	40	27	25	56
1.60		12	11	16	16	15	24	19	17	31	22	20	42
1.70		10	9	13	14	12	20	16	14	25	18	17	33
1.80		9	8	11	12	11	16	14	13	20	16	15	27
1.90		8	7	10	11	10	14	12	11	17	14	13	22
2.00		7	7	8	9	9	12	11	10	15	12	11	19
2.10		7	6	8	9	8	10	10	9	13	11	10	16
2.20		6	6	7	8	7	9	9	8	11	10	10	14
2.30		6	5	6	7	7	8	8	8	10	9	9	12
2.40		5	5	6	7	6	7	7	7	9	8	8	11
2.50		5	5	5	6	6	7	7	7	8	8	8	10
2.60		5	5	5	6	6	6	7	6	7	7	7	9
2.70		4	4	5	6	5	6	6	6	7	7	7	8
2.80		4	4	4	5	5	5	6	6	6	6	6	7
2.90		4	4	4	5	5	5	5	5	6	6	6	7
3.00		4	4	4	5	5	5	5	5	5	6	6	6

Table 4. The optimal parameters and $MR{L}_1$ for the upper-sided exponential AEWMA, EWMA, Shewhart scheme when $c_1=1.1,c_2=5,MR{L}_0\in \{100,200,300,500\}$.

		${\mathit{MRL}}_0=100$			${\mathit{MRL}}_0=200$			${\mathit{MRL}}_0=300$			${\mathit{MRL}}_0=500$
		AEWMA	EWMA	Shewhart	AEWMA	EWMA	Shewhart	AEWMA	EWMA	Shewhart	AEWMA	EWMA	Shewhart
	${\mathit{\lambda }}^{+}$	0.053	0.053	-	0.051	0.051	-	0.050	0.050	-	0.050	0.050	-
	$\mathit{k}$	1.303	-	-	1.379	-	-	1.414	-	-	1.467	-	-
$\mathit{c}$	${\mathit{h}}^{+}$	5.425	1.292	4.9651	5.925	1.363	5.6616	6.475	1.401	6.0681	7.000	1.454	6.5798
1.10		48	47	63	83	80	119	112	108	173	164	157	275
1.20		30	29	44	47	45	78	59	56	109	78	75	167
1.30		21	20	32	31	30	54	38	36	74	48	46	110
1.40		16	16	24	23	22	40	27	26	53	33	32	76
1.50		13	13	19	18	18	30	21	21	40	26	25	56
1.60		11	11	16	15	15	24	17	17	31	21	20	42
1.70		10	9	13	13	12	20	15	14	25	17	17	33
1.80		9	8	11	11	11	16	13	13	20	15	15	27
1.90		8	7	10	10	10	14	11	11	17	13	13	22
2.00		7	7	8	9	9	12	10	10	15	12	11	19
2.10		6	6	8	8	8	10	9	9	13	11	10	16
2.20		6	6	7	8	7	9	8	8	11	10	10	14
2.30		5	5	6	7	7	8	8	8	10	9	9	12
2.40		5	5	6	6	6	7	7	7	9	8	8	11
2.50		5	5	5	6	6	7	7	7	8	8	8	10
2.60		5	5	5	6	6	6	6	6	7	7	7	9
2.70		4	4	5	5	5	6	6	6	7	7	7	8
2.80		4	4	4	5	5	5	6	6	6	6	6	7
2.90		4	4	4	5	5	5	5	5	6	6	6	7
3.00		4	4	4	5	5	5	5	5	5	6	6	6

6. Two Illustrative Examples

To showcase the practical application of the monitoring scheme proposed in this paper, we employ two diverse datasets. The first dataset originates from OLED production, where precise monitoring is crucial for maintaining high-quality standards in advanced display technology [37]. The second dataset comprises data from mining accidents, highlighting the importance of effective monitoring in safety-critical environments to promptly detect anomalies and prevent potential disasters [38].

6.1. Example 1

Using the example from the study by Qu et al. (see [37]), consider a production process for OLED components to illustrate the application of the optimized lower-sided exponential AEWMA scheme based on MRL. The dataset consists of 30 intervals of failure times from accelerated life tests in the OLED production process. Assuming an exponential distribution but with unknown parameters, the bootstrap method was employed to estimate the process mean using the first 10 data points (see Table 5). The remaining 20 data points (see Table 6) were reserved for testing purposes.

Table 5. Phase I samples $Z_t$ (in minutes) of the intervals of failure times from accelerated life tests in the OLED production line.

t	${\mathit{Z}}_{\mathit{t}}$	t	${\mathit{Z}}_{\mathit{t}}$
1	1.07	6	1.26
2	0.54	7	0.48
3	0.54	8	1.78
4	0.72	9	1.26
5	2.53	10	2.27

Table 6. Phase II samples $X_t$ (in minutes) and corresponding monitoring statistics $A_t^{-}$, $A_{tL}^{-}$ and $Q_t^{-}$ of the optimal lower-sided exponential schemes for the OLED production process.

t	${\mathit{X}}_{\mathit{t}}$	${\mathit{A}}_{\mathit{t}}^{-}$	${\mathit{A}}_{\mathit{tL}}^{-}$	${\mathit{Q}}_{\mathit{t}}^{-}$	t	${\mathit{X}}_{\mathit{t}}$	${\mathit{A}}_{\mathit{t}}^{-}$	${\mathit{A}}_{\mathit{tL}}^{-}$	${\mathit{Q}}_{\mathit{t}}^{-}$
1	2.19	1.294	1.240	1.294	11	0.94	1.413	1.020	1.247
2	1.10	1.284	1.233	1.284	12	1.08	1.395	1.023	1.239
3	0.60	1.248	1.200	1.248	13	2.31	1.443	1.360	1.294
4	0.97	1.234	1.188	1.234	14	3.11	1.723	1.706	1.389
5	3.16	1.773	1.706	1.334	15	0.28	1.648	1.230	1.331
6	2.93	1.833	1.706	1.417	16	0.66	1.597	1.200	1.296
7	0.99	1.789	1.669	1.395	17	0.68	1.549	1.173	1.264
8	1.28	1.763	1.649	1.389	18	0.75	1.507	1.151	1.237
9	0.12	1.507	1.070	1.323	19	0.47	1.453	1.116	1.197
10	0.19	1.438	1.024	1.264	20	1.82	1.473	1.152	1.230

To achieve a robust estimation of the process mean, the initial 10 data points were used to compute the maximum likelihood estimate (MLE) of the process mean ${\widehat{\theta }}_0=1.245$. Subsequently, the bootstrap method [39,40] was utilized to generate multiple resamples from these 10 data points. For each resample, the MLE of ${\widehat{\theta }}_0$ was calculated, thereby constructing a distribution of estimates. Based on this distribution, the $95\%$ confidence interval for ${\widehat{\theta }}_0$ was determined as $[{\widehat{\theta }}_{0L},{\widehat{\theta }}_{0U}]=[0.853,1.706]$. This approach allowed for a more accurate and reliable estimation of the process mean while accounting for the variability inherent in the data.

The factory employs an optimal lower-sided exponential AEWMA scheme to monitor downward shifts in the process mean. Suppose the process mean shift to be monitored is within $[c_2,c_1]=[0.01,0.8]$, and the acceptable $MR{L}_0$ is 300. The parameters $({\lambda }^{-},k,LC{L}^{-})=(0.052,1.175,0.754)$ for the optimal lower-sided exponential AEWMA scheme can be obtained through the design steps in Section 4. Then, multiplying $B^{-}$, k, and $LC{L}^{-}$ by ${\widehat{\theta }}_0=1.245$ yields the reflection boundary ${B^{-}}^{\prime }$, threshold parameter $k^{\prime }$, and lower control limit $LC{L}^{\prime }$ for the optimal lower-sided exponential AEWMA scheme:

$$\begin{array}{cccccc}\hfill {B^{-}}^{\prime }& =\hfill & & 2\hfill & \hfill \times 1.245& =2.490,\hfill \\ \hfill k^{\prime }& =\hfill & & 1.175\hfill & \hfill \times 1.245& =1.463,\hfill \\ \hfill LC{L}^{\prime }& =\hfill & & 0.754\hfill & \hfill \times 1.245& =0.9387.\hfill \end{array}$$

The monitoring statistic $A_t^{-}$ for the optimal lower-sided exponential AEWMA scheme in the OLED production process can be calculated using Equation (9) (see Table 6).

To enhance the robustness of the monitoring scheme and address the uncertainty in estimating the process mean, the low bound of the bootstrap confidence interval, ${\widehat{\theta }}_{0L}=0.853$, was used to recalculate the adjusted parameters ${B_L^{-}}^{\prime }$, $k_L^{\prime }$, and $LC{L}_L^{\prime }$. These adjusted parameters offer a more cautious estimation of the control limits, ensuring that the monitoring scheme remains effective if the true process mean exceeds initial estimates. The recalculated parameters are as follows:

$$\begin{array}{cccccc}\hfill {B^{-}}_L^{\prime }& =\hfill & & 2\hfill & \hfill \times 0.853& =1.706,\hfill \\ \hfill k_L^{\prime }& =\hfill & & 1.175\hfill & \hfill \times 0.853& =1.002,\hfill \\ \hfill LC{L}_L^{\prime }& =\hfill & & 0.754\hfill & \hfill \times 0.853& =0.6432.\hfill \end{array}$$

The AEWMA statistic $A_{tL}^{-}$ is then calculated using Equation (9), with the updated parameters (refer to Table 6 for details).

Furthermore, to facilitate a comparative analysis with the existing EWMA-type and Shewhart-type schemes in practical applications, we consider the case where $c=0.8$ and $MR{L}_0=300$. The optimal parameters for the EWMA-type scheme were obtained from Table 1, which are $({\lambda }^{-},LC{L}^{-})=(0.052,0.688)$. Subsequently, $B^{-}$ and $LC{L}^{-}$ were multiplied by the scaling factor ${\widehat{\theta }}_0=1.245$, resulting in ${B^{-}}^{\prime }=2.490$ and $LC{L}^{\prime }=0.8566$. The corresponding optimal EWMA scheme statistic $Q_t^{-}$ can be computed using the Equation (6) (see Table 6).

For the Shewhart-type scheme, the control limit was set at $0.0023$ to satisfy $MR{L}_0=300$. After multiplying this value by the scaling factor ${\widehat{\theta }}_0=1.245$, the adjusted lower control limit $LC{L}^{\prime }$ is calculated as $LC{L}^{\prime }=0.0023\times 1.245=0.0029$.

Observations from the data indicate that until $t=4$, $A_t^{-}=Q_t^{-}$, suggesting that the prediction error is relatively small during this period, and the performance of the AEWMA scheme closely resembles that of the EWMA scheme. After $t=4$, the prediction error increases, leading to $A_t^{-}>Q_t^{-}$. This suggests that the AEWMA scheme may better accommodate larger shifts in the process mean after this point.

Figure 4, Figure 5, Figure 6 and Figure 7 illustrate the application of these schemes in the OLED production process monitoring, respectively. As shown in these figures, no alarm signals are generated across all three schemes, indicating that the process remains in-control throughout the monitoring period. As depicted in Figure 5, some sample statistics fall within the reflection boundaries ${B_L^{-}}^{\prime }$, suggesting that the probability of the system’s estimated parameters reaching ${\widehat{\theta }}_{0L}$ is relatively low.

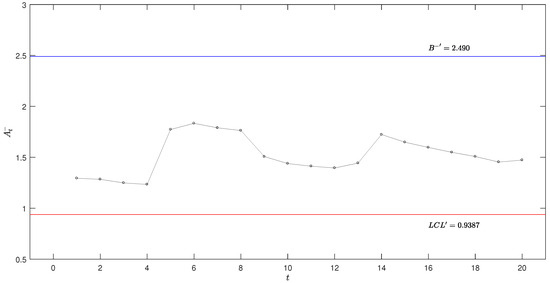
Figure 4. Optimal lower-sided exponential AEWMA scheme in the OLED production process.

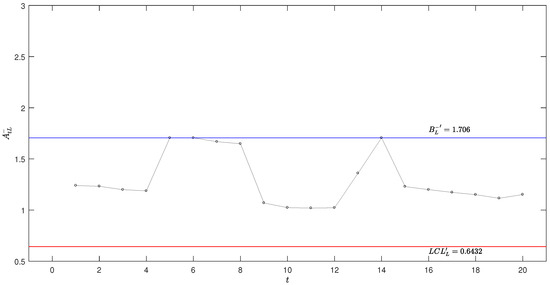
Figure 5. Adjusted optimal lower-sided exponential AEWMA scheme in the OLED production process.

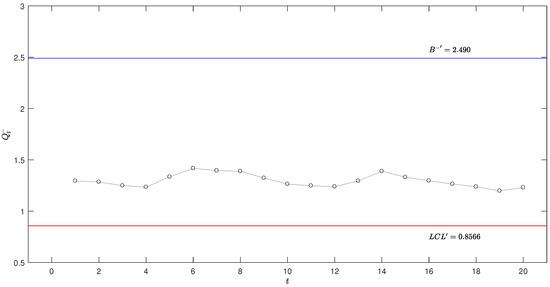
Figure 6. Optimal lower-sided exponential EWMA scheme in the OLED production process.

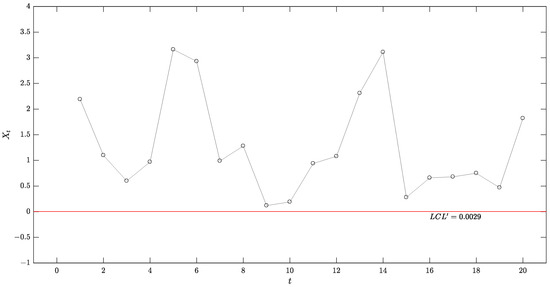
Figure 7. Lower-sided exponential Shewhart scheme in the OLED production process.

6.2. Example 2

The dataset introduced by Jarrett includes the time intervals between coal mine explosions occurring from 15 March 1851, to 22 March 1962, measured in days [38]. Assuming an exponential distribution with unknown parameters, the bootstrap method was used to estimate the process mean using the first 160 data points (see Table 7). The remaining 30 data points (see Table 8) were reserved for testing purposes. To obtain a robust estimate of the process mean, the initial 160 data points were employed to compute the MLE, yielding ${\widehat{\theta }}_0=182.3$. Subsequently, the bootstrap method generated multiple resamples from these data points. For each resample, the MLE of ${\widehat{\theta }}_0$ was recalculated, thereby forming a distribution of estimates. Based on this distribution, the $95\%$ confidence interval for ${\widehat{\theta }}_0$ was determined as $[{\widehat{\theta }}_{0L},{\widehat{\theta }}_{0U}]=[146,223.5]$.

Table 7. Phase I samples $Z_t$ (in days) of explosions in mines from 15 March 1851 to 22 March 1962.

t	${\mathit{Z}}_{\mathit{t}}$	t	${\mathit{Z}}_{\mathit{t}}$	t	${\mathit{Z}}_{\mathit{t}}$	t	${\mathit{Z}}_{\mathit{t}}$	t	${\mathit{Z}}_{\mathit{t}}$
1	157	33	36	65	45	97	55	129	354
2	123	34	110	66	6	98	93	130	307
3	2	35	276	67	208	99	59	131	275
4	124	36	16	68	29	100	315	132	78
5	12	37	88	69	112	101	59	133	17
6	4	38	225	70	43	102	61	134	1205
7	10	39	53	71	193	103	1	135	644
8	216	40	17	72	134	104	13	136	467
9	80	41	538	73	420	105	189	137	871
10	12	42	187	74	95	106	345	138	48
11	33	43	34	75	125	107	20	139	123
12	66	44	101	76	34	108	81	140	456
13	232	45	41	77	127	109	286	141	498
14	826	46	139	78	218	110	114	142	49
15	40	47	42	79	2	111	108	143	131
16	12	48	1	80	0	112	188	144	182
17	29	49	250	81	378	113	233	145	255
18	190	50	80	82	36	114	28	146	194
19	97	51	3	83	15	115	22	147	224
20	65	52	324	84	31	116	61	148	566
21	186	53	56	85	215	117	78	149	462
22	23	54	31	86	11	118	99	150	228
23	92	55	96	87	137	119	326	151	806
24	197	56	70	88	4	120	275	152	517
25	431	57	41	89	15	121	54	153	1643
26	16	58	93	90	72	122	217	154	54
27	154	59	24	91	96	123	113	155	326
28	95	60	91	92	124	124	32	156	1312
29	25	61	143	93	50	125	388	157	348
30	19	62	16	94	120	126	151	158	745
31	78	63	27	95	203	127	361	159	217
32	202	64	144	96	176	128	312	160	120

Table 8. Phase II samples $X_t$ (in days) and corresponding monitoring statistics $A_t^{+}$, $A_{tU}^{+}$ and $Q_t^{+}$ of the optimal upper-sided exponential schemes for the explosions in mines.

t	${\mathit{X}}_{\mathit{t}}$	${\mathit{A}}_{\mathit{t}}^{+}$	${\mathit{A}}_{\mathit{tU}}^{+}$	${\mathit{Q}}_{\mathit{t}}^{+}$	t	${\mathit{X}}_{\mathit{t}}$	${\mathit{A}}_{\mathit{t}}^{+}$	${\mathit{A}}_{\mathit{tU}}^{+}$	${\mathit{Q}}_{\mathit{t}}^{+}$
1	275	187.120	226.178	187.120	16	364	275.213	236.824	219.292
2	20	178.430	215.457	178.430	17	37	262.826	226.433	209.813
3	66	172.584	207.685	172.584	18	19	250.147	215.646	199.890
4	292	178.793	212.069	178.793	19	156	245.251	212.545	197.608
5	4	169.704	201.250	169.704	20	47	234.942	203.937	189.777
6	368	180.016	209.921	180.016	21	129	229.433	200.040	186.616
7	307	186.619	214.969	186.619	22	1630	1382.521	1326.591	261.672
8	336	194.387	221.263	194.387	23	29	276.479	332.409	249.573
9	19	185.266	210.745	185.266	24	217	273.386	326.408	247.879
10	329	192.741	216.894	192.741	25	7	254.479	309.799	235.354
11	330	199.878	222.776	199.878	26	18	242.182	294.625	224.051
12	312	205.708	227.415	205.708	27	1358	1110.521	1054.591	283.017
13	536	288.521	243.462	222.884	28	2366	2118.521	2062.591	391.332
14	145	281.058	238.342	218.834	29	952	1199.479	1255.409	420.486
15	75	270.343	229.848	211.354	30	632	879.479	935.409	431.485

To effectively monitor and promptly detect upward shifts in the process mean, an optimally designed upper-sided AEWMA scheme is implemented, utilizing MRL as the performance metric. This approach enhances the sensitivity of the monitoring scheme in identifying potential increases in event frequency, thereby facilitating timely intervention and improving safety monitoring in critical environments.

The current monitoring objective focuses on detecting shifts in the process mean within the range $[c_1,c_2]=[1.02,5]$, with an in-control MRL ($MR{L}_0$) of 200. Following the optimization procedure detailed in Section 4, the optimal parameters for the upper-sided monitoring scheme are determined to be $({\lambda }^{+},k,LC{L}^{+})=(0.052,1.432,4.975)$. For practical implementation, these parameters are scaled by ${\widehat{\theta }}_0$, yielding the adjusted parameters ${B^{+}}^{\prime }$, $k^{\prime }$, and $UC{L}^{\prime }$. Specifically, the adjusted parameters are computed as:

$$\begin{array}{cccccc}\hfill {B^{+}}^{\prime }& =\hfill & & 0.5\hfill & \hfill \times 182.3& =91.2,\hfill \\ \hfill k^{\prime }& =\hfill & & 1.432\hfill & \hfill \times 182.3& =261.054,\hfill \\ \hfill UC{L}^{\prime }& =\hfill & & 4.975\hfill & \hfill \times 182.3& =906.943.\hfill \end{array}$$

The optimal upper-sided AEWMA scheme statistic $A_t^{+}$ is calculated using Equation (7) (refer to Table 8 for details). To refine the monitoring scheme and account for the uncertainty in the estimation of the process mean, we consider the upper-bound of the bootstrap confidence interval, ${\widehat{\theta }}_{0U}=223.5$, to recalculate the adjusted parameters ${B_U^{+}}^{\prime }$, $k_U^{\prime }$, and $UC{L}_U^{\prime }$. These adjusted parameters provide a more conservative estimate of the control limits, ensuring the monitoring scheme’s effectiveness even under conditions where the true process mean might be higher than initially estimated. The recalculated parameters are as follows:

$$\begin{array}{cccccc}\hfill {B^{+}}_U^{\prime }& =\hfill & & 0.5\hfill & \hfill \times 223.5& =111.8,\hfill \\ \hfill k_U^{\prime }& =\hfill & & 1.432\hfill & \hfill \times 223.5& =320.052,\hfill \\ \hfill UC{L}_U^{\prime }& =\hfill & & 4.975\hfill & \hfill \times 223.5& =1111.913.\hfill \end{array}$$

The AEWMA statistic $A_{tU}^{+}$ is then calculated using Equation (7), with the updated parameters (refer to Table 8 for details).

As shown in the table, at $t=22$, $A_t^{+}$ reaches a value of $1382.521$, and $A_{tU}^{+}$ reaches a value of $1326.591$, both exceeding their respective control limit $UC{L}^{\prime }$ and $UC{L}_U^{\prime }$, as highlighted in bold. Additionally, it is noteworthy that at $t=27$, the AEWMA statistic $A_t^{+}$ exceeds its control limit $UC{L}^{\prime }$, signaling a potential out-of-control condition. In contrast, the adjusted AEWMA statistic $A_{tU}^{+}$ remains below its respective control limit $UC{L}_U^{\prime }$ at this time point. This discrepancy highlights the sensitivity of the AEWMA scheme to upward shifts in the process mean, while the adjusted scheme, which incorporates the upper bound of the bootstrap confidence interval, provides a more conservative estimate. This observation underscores the importance of considering parameter uncertainty in the design of monitoring schemes to ensure robust performance under varying conditions.

To promote a comparative analysis in practical applications, we also evaluate the setting where $c=1.02$ and $MR{L}_0=200$. For the EWMA-type scheme, the optimal parameters derived from Table 3, which are $({\lambda }^{+},UC{L}^{+})=(0.052,1.369)$. These parameters were then scaled by the factor ${\widehat{\theta }}_0=182.3$, resulting in ${B^{+}}^{\prime }=91.2$ and $UC{L}^{\prime }=249.569$. The corresponding optimal statistic for the EWMA scheme, $Q_t^{+}$, can be computed using Equation (5) (see Table 8). For the Shewhart-type scheme, the control limit was set at $5.6616$ to satisfy $MR{L}_0=200$. After scaling this value by ${\widehat{\theta }}_0=182.3$, the adjusted upper control limit $UC{L}^{\prime }$ is calculated as $UC{L}^{\prime }=5.6616\times 182.3=1032.110$.

According to the data presented in Table 8, at time points $t=22,27,28$, when $X_t$ undergoes a sudden increase, $A_t^{+}$ shows a more significant increment compared to $Q_t^{+}$. This observation indicates that, under such conditions, the monitoring performance of the AEWMA scheme aligns more closely with that of the Shewhart scheme.

Figure 8, Figure 9, Figure 10 and Figure 11 visually illustrates these monitoring schemes, clearly showing that at $t=22$, the schemes emit an out-of-control signal, suggesting a notable shift in the process mean. Furthermore, it can be observed that when $X_t$ (at $t=23$) experiences a sudden decrease, the EWMA-type scheme continues to emit an out-of-control signal. In contrast, the AEWMA and Shewhart schemes quickly adapt to the new data, returning to the in-control region and thereby reducing unnecessary alarms. This behavior underscores the importance of selecting a monitoring scheme that balances sensitivity to shifts with the ability to avoid false alarms, making the AEWMA scheme particularly suitable for scenarios requiring rapid detection of changes while minimizing false alerts.

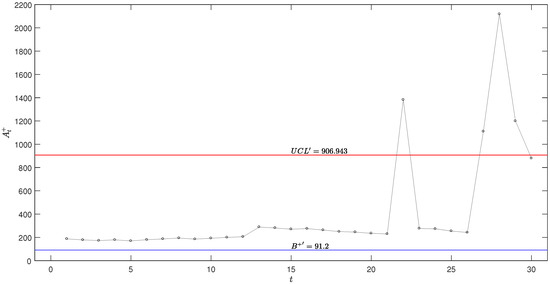
Figure 8. Optimal upper-sided exponential AEWMA scheme with ${\widehat{\theta }}_0$ for the coal mine explosions.

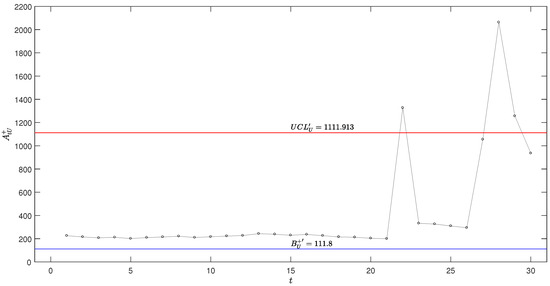
Figure 9. Adjusted optimal upper-sided exponential AEWMA scheme with ${\widehat{\theta }}_{0U}$ for the coal mine explosions.

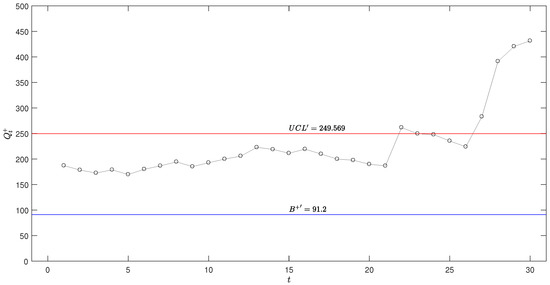
Figure 10. Optimal upper-sided exponential EWMA scheme with ${\widehat{\theta }}_0$ for the coal mine explosions.

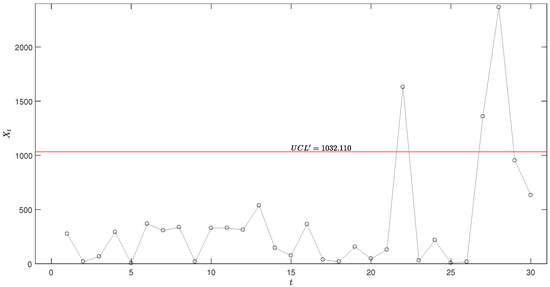
Figure 11. Upper-sided exponential Shewhart scheme with ${\widehat{\theta }}_0$ for the coal mine explosions.

7. Discussion

This paper addresses the limitation of the one-sided exponential AEWMA scheme in simultaneously monitoring different magnitudes of process shifts. Through an analysis of the RL distribution for both upper- and lower-sided schemes, we observed that the RL distribution is skewed. To mitigate this bias, we proposed using the MRL as a statistical performance indicator for the monitoring scheme.

An optimal design procedure based on MRL was developed to enhance the performance of the one-sided exponential AEWMA scheme. This procedure ensures more balanced and robust detection of both small and large shifts, thereby improving overall scheme sensitivity. Additionally, the performance of the one-sided exponential AEWMA scheme, one-sided exponential EWMA scheme, and one-sided exponential Shewhart scheme, all based on MRL, is compared. Finally, the proposed one-sided exponential AEWMA scheme based on MRL is illustrated through two case studies: monitoring failure intervals in OLED production and detecting increases in coal mine explosion frequencies.

In conclusion, the proposed one-sided exponential AEWMA scheme based on MRL provides a robust solution for monitoring process shifts of varying magnitudes, outperforming traditional monitoring schemes in many scenarios. Future research could extend this approach to other types of processes and distributions, focusing on the robustness of the AEWMA scheme across different distributions. Investigating its performance under non-exponential distributions and exploring its applicability in diverse industries would further validate its effectiveness and broaden its utility.