Multi-Objective Optimization Scheduling of a Wind–Solar Energy Storage Microgrid Based on an Improved OGGWO Algorithm

Abstract

To achieve the optimal solution between construction costs and carbon emissions in the multi-target optimization scheduling, this paper proposes a multi-objective optimization scheduling design for wind–solar energy storage microgrids based on an improved oppositional gradient grey wolf optimization (OGGWO) algorithm. First, two new features were added to the traditional grey wolf optimization (GWO) algorithm to solve the multi-target optimization scheduling of grid-connected microgrids, aiming to improve solution quality and convergence speed. Furthermore, Gaussian walk and Lévy flight are introduced to enhance the search capability of the proposed OGGWO algorithm. This method expands the search range while sacrificing only a small amount of search speed, contributing to obtaining the global optimal solution. Finally, the gradient direction is considered in the feature search process, allowing for a comprehensive understanding of the search space, which facilitates achieving the global optimum. Experimental results indicate that, compared to traditional methods, the proposed improved OGGWO algorithm can achieve standard deviations of 4.88 and 4.46 in two different scenarios, demonstrating significant effectiveness in reducing costs and pollution.

1. Introduction

With the global emphasis on sustainable development and environmental protection, the construction of new power systems dominated by new energy, and the large-scale development of energy sources such as wind and solar power, are receiving increasing attention. However, due to the randomness of power generation and output fluctuations, they face the problem of consumption in actual power grids. The wind–solar–hydrogen storage system, as an effective solution, has its optimized management crucial for ensuring stability and economy of energy supply. Microgrids can overcome the voltage and frequency instability caused by the volatility and randomness of renewable energy outputs, such as photovoltaics and wind power, through the coordinated control of energy storage output. However, as the scale of microgrids has increased significantly, efficiently utilizing renewable energy output has become critically important.

Microgrids can integrate multiple distributed energy resources (DERs), such as microturbines (MTs), wind turbines (WTs), batteries (BATs), fuel cells (FCs), photovoltaics (PVs), and other energy sources [1,2]. When constructing microgrid scheduling models, many variables are considered, so intelligent algorithms are mostly used for solving. Yingjun et al. [3] proposed a microgrid grid–connected optimization scheduling model based on mutation particle swarm algorithm, and simulated it to verify the feasibility and superiority of the optimized PSO algorithm applied to the microgrid optimization scheduling model in different time periods. Wu et al. [4] improved the Empire Competition Algorithm using Gaussian and Cauchy mutations, and solved the microgrid optimization scheduling model using the Gaussian Cauchy Empire Competition Algorithm. The correctness of the model and the superiority of the solution method were verified. Singh et al. [5] proposed a multi-strategy collaborative for bottle sea squirts (MSC-BSS), which considers both operation and environmental pollution simultaneously. With comprehensive cost as the objective function, constraints such as power balance, ramp rate, and extreme power of interconnection lines are set. Then, MSC-BSS is utilized to address the microgrid scheduling model. By comparing simulation results, the superiority of MSC-BSS over other algorithms and the rationality of optimizing microgrid systems are verified. Although intelligent algorithms have good solving accuracy, they are prone to getting stuck in local optima during the solving process, which can lead to the inability to fully utilize renewable energy.

The broad integration of new energy sources into the grid has raised the level of uncertainty in power dispatch, making the optimization of microgrid scheduling an important research focus. Qiao et al. [6] proposed a day ahead real-time collaborative scheduling method for wind power storage large-scale bases, which determines the start–stop plan and adjustable output range of thermal power units based on rough wind power prediction. In the real-time stage, scheduling strategies are generated according to quantile rules based on the current wind and solar output. He et al. [7] introduced an optimization strategy for the engagement of wind, thermal, and energy storage systems in frequency regulation utilizing robust model predictive control. Response models for wind, fire, and energy storage were established separately, and a double-layer robust optimization model was constructed to minimize the frequency regulation cost of the system under the maximum uncertainty of wind turbine output. Lin et al. [8] proposed a wind–fire storage collaborative frequency regulation control strategy based on multi-scale decomposition, which can effectively achieve the joint participation of wind–fire storage in frequency regulation. Thermal power units generate certain carbon emissions and have significant start-up, shutdown, and operating costs. The ability to regulate resources during power generation is limited, so it is crucial to consider a coordinated multi-target optimization scheduling strategy for wind, fire, and storage systems.

In dealing with the economic dispatch problem of smart microgrids, it is necessary to consider the practical problems in the power dispatch process of smart microgrid systems, so multi-target optimization of the joint system is often required. Teo et al. [9] used the NSGA II algorithm with operating costs and pollutant emissions as objective functions to achieve multi-target optimization operation of a grid-connected microgrid testing system. Teo et al. [10] proposed an adaptive genetic algorithm to optimize the operation of microgrids by considering power loss and voltage distribution as objective functions, and used multi-target optimization methods to solve the upper level optimization model of distribution network scheduling. Al-Tameemi et al. [11] introduced a multi-target PSO algorithm to solve the multi-target energy management issue in grid connected microgrids, with operating costs and pollutant emissions as objective functions. Simulation was conducted in a microgrid testing system composed of wind turbines, solar cells, batteries, internal combustion engines, and diesel generators. Zhang et al. [12] constructed a dual layer optimization configuration model for cloud energy storage driven by economic, low-carbon, and reliable multiple objectives, and implemented a model solution based on a second-generation nondominated genetic algorithm, verifying the effectiveness of the cloud energy storage mode in improving system investment and operation efficiency. However, in current research, the proposed multi-target optimization algorithms are not accurate enough in finding the optimal solution between reducing pollutant emissions and minimizing power generation costs, and their convergence speed is slow.

Mirjalili introduced GWO motivated by the predatory actions of grey wolves [13]. Usually, there are four wolf types: Alpha, then Beta, Delta, and lastly Omega [14,15]. In a wolf pack, the Alpha is the dominant leader and the primary decision-maker, while other pack members must follow Alpha’s orders and decisions. The second position is occupied by the Beta wolf, who acts as a mediator between the Alpha wolf and the rest of the wolves. It helps the alpha wolf and becomes the first choice of nominee for Alpha, in case the Alpha wolf dies or is too old for swarm management. In terms of rank, Omega is the lowest-ranked grey wolf [16,17], following other top-ranked grey wolves. Delta tends to manage Omega wolves, while also assisting Alpha and Beta wolves. As the number of iterations of the GWO algorithm increases, the diversity of the grey wolf population decreases, leading to a decrease in search ability and a tendency to fall into local optima rather than global optima. Opposition-based learning (OBL) is a powerful optimization tool, and the successful implementation of OBL involves evaluating the populations of opposite and current stations of the same generation in order to obtain better candidate solutions for a given problem [18].

In order to obtain the optimal value of multi-objective optimization scheduling in terms of carbon emission cost and time-dependent electricity tariffs, this paper proposes a multi-objective optimization scheduling design for wind–solar energy storage microgrids based on an improved oppositional gradient grey wolf optimization (OGGWO) algorithm. The main contributions are as follows:

(1) The OGGWO is introduced for multi-target optimization planning of grid-tied microgrids, enhancing solution quality and convergence speed. This algorithm incorporates instantaneous considerations of estimates and their equivalent oppositional estimates, leveraging the advantages of gradient features to provide output boundaries for thermal power units. Additionally, the combination of gradient features takes into account the gradient direction during the optimization scheduling process, facilitating an improved approximation of candidate solutions for objective cost and emissions.

(2) To improve the exploration capabilities of the introduced OGGWO algorithm, Gaussian random walk and Lévy flight strategies are incorporated, which increase the search range while sacrificing minimal search speed, aiding in obtaining a global optimal solution.

This paper is organized as follows. Section 2 introduces the microgrid optimization scheduling model used in this paper, an improved grey wolf optimization algorithm with opposite gradients, and the multi-objective optimization process of microgrids. In Section 3 is the example analysis, which proves the advantages of the proposed OGGWO algorithm in two different scenarios. The conclusion is made in Section 4.

2. Microgrid Optimization Scheduling Model

This section is divided into two parts: 2.1 Mathematical Model of Microgrid and 2.2 Grey Wolf Optimization Algorithm Based on Oppositional Gradient. The objective function equation in Section 2.1 is combined with the constraint equation to establish a mathematical model for microgrid optimization scheduling. The purpose of microgrid optimization scheduling is to minimize consumption costs and pollution emissions while satisfying power constraints. Then, the introduced OGGWO algorithm in Section 2.2 is used to find the optimal solution of the objective function equation when satisfying the constraint equation.

2.1. Mathematical Model of Microgrid

2.1.1. Objective Function

The task of multi-objective optimization for microgrids is to minimize economic costs and carbon emissions as much as possible while satisfying all constraints. The optimization and scheduling objective functions of microgrids are mainly divided into cost objective function and carbon emission objective function.

Cost objective function: The target function of power generation and the purchase cost objective function is shown as

$$\min f_1(X)={\displaystyle {\sum }_{i=1}^T\left\{\left.\begin{array}{c}{\displaystyle {\sum }_{i=1}^{Ng}\left[U_i(t)P_{Gi}(t)B_{Gi}(t)+S_{Gi}(t)\left|U_i(t)-U_i(t+1)\right|\right]-\left(P_{Grid}(t)B_{Grid}(t)\right)+}\\ {\displaystyle {\sum }_{j=1}^{Ns}\left[U_j(t)P_{si}(t)B_{sj}(t)+S_{sj}\left|U_j(t)-U_j(t+1)\right|\right]-\left(P_{Grid}(t)B_{Grid}(t)\right)}\end{array}\right\}\right.}$$

(1)

where T represents the total duration, N_g represents the generation of energy, N_s represents a storage unit, U_i(t) represents the state of the i-th generate unit at time t (on or off), P_Gi(t) represents the output capacity when the i-th storage device is turned on, and B_Gi(t) represents the energy cost of the i-th storage device at time t when it is turned on. The energy cost of the j-th storage device at time t when turned off is B_Sj(t), and S_Gi(t) and S_sj(t) represent the costs involved in the i-th storage device and j-th storage device during the startup or shutdown function, respectively. In addition, P_Grid(t) and B_Grid(t) represent the capacity and cost exchanged with the provided market, respectively.

Emission mitigation: The objective function for emission mitigation can be shown as

$$\min f2(X)={\displaystyle {\sum }_{t-1}^T\left\{\left.{\displaystyle {\sum }_{i=1}^{Ng}\left[U_i(t)P_{Gi}(t)E_{Gi}(t)\right]+{\displaystyle {\sum }_{j=1}^{Ns}\left[U_j(t)P_s(t)E_{sj}(t)\right]}}+\left(P_{Gridj}(t)E_{Gridj}(t)\right)\right\}\right.}$$

(2)

where E_Gi(t) represents the pollution level of the i-th generator unit, and the pollution level of the J storage unit is represented by E_tj(t). E_Gr(t) indicates the pollution level in the market at time t.

2.1.2. Restriction Condition

The main constraint on electricity is the limit of the power generated by the generator set, which can be divided into power equilibrium conditions, climbing speed limit, and inequality constraint.

Power Equilibrium Conditions: The constraint condition for power balance is to ensure dynamic balance between power production and consumption in microgrids

$${\displaystyle \sum _{k=1}^{Nk}{P}_{LK}}\left(t\right)={\displaystyle \sum _{i=1}^{Ng}\left[P_{Gi}\left(t\right)\right]}+{\displaystyle \sum _{j=1}^{Ns}\left[P_{sj}\left(t\right)\right]}+\left(P_{Grid}\left(t\right)\right)$$

(3)

where P_LK represents the K quantity at the load level, and N_k represents the total number of available load levels in the power grid.

Climbing Speed Limit: Climbing speed limit refers to the maximum rate at which a generator set or other component in the power system can change its output power per unit time

$$R_{down}^i\cdot \Delta t\le P{\left(h\right)}^i-P{\left(h-1\right)}^i\le R_{up}^i\cdot \Delta t$$

(4)

where $R_{down}^i$ represents the decrease in output power of ithDG, and $R_{up}^i$ indicates an increase in j^thDG output power. In addition, Δt represents the time step, measured in hours.

Inequality Constraint: All units discussed in this paper have upper and lower bounds on their power generation capability. The units include distributed generators, storage devices, and markets

$$\begin{array}{l}{P}_{Gi,\min }\left(t\right)\le P_{Gi}\left(t\right)\le P_{Gi,\max }\left(t\right)\\ P_{sj,\min }\left(t\right)\le P_{sj}\left(t\right)\le P_{sj,\max }\left(t\right)\\ P_{Grid,\min }\left(t\right)\le P_{Grid}\left(t\right)\le P_{Grid,\max }\left(t\right)\end{array}$$

(5)

where P_Gi,min(t) indicates the minimum output power in the open state; P_Gi,max(t) indicates the maximum output power in the open state; P_Sj,min(t) and P_Sj,max(t) represent the minimum and maximum output power in the closed state, respectively; and P_Grid,min(t) and P_Grid,max(t) represent the minimum and maximum values of the power exchanged between customs and the market, respectively.

The constraint on the charging and discharging rate of storage devices is shown as

$$\begin{array}{l}{SOC}_{tj}\left(t\right)={SOC}_{tj}\left(t-1\right)+P_{chg}/D_{chg}\left(t\right)\\ 0\le \left|P_{chg}/D_{chg}\left(t\right)\right|\le P_{CDSj,\max }\end{array}$$

(6)

where SOC_tj(t) represents the current charging amount of the storage unit at that time, SOC_tj(t−1) represents the amount of charge before the storage unit was charged, Pchg/Dechg(t) corresponds to the charging (discharging) amount at the th hour, and the maximum charging (discharging) rate is represented by PCD_tj,max.

2.2. Grey Wolf Optimization Algorithm Based on Oppositional Gradient

This paper adds two new features to the traditional GWO algorithm, forming a grey wolf optimizer based on opposing gradients. The first feature is the introduction of a new OBL based program in the OGGWO algorithm for updating the position formula of Omega Wolf, using gradient data to improve the development and exploration skills of the algorithm. The second feature is the introduction of Gaussian walk and Lévy flight (LF) in traditional GWO, allowing for random selection of Gaussian walk or Lévy flight to update the wolf’s position in each iteration. These random walks enhance the randomness of the improved OGGWO model and facilitate exploration. Gaussian walk generates a compact cluster with many small steps and executes an equal number of loops. These small steps are randomly selected, which can help the algorithm avoid local optima and enhance the search capability of the proposed OGGWO model [19]. In this case, OGGWO can randomly switch between Gaussian and LF walks [20]. The mathematical expressions for Gaussian walk and Lévy flight are shown in Equations (7) and (8)

$$X_i^{t+1}=X_i^t+N\left(0,\sigma \right)$$

(7)

$$X_i^{t+1}=X_i^t+Levy\left(\beta \right)$$

(8)

where $N\left(0,\sigma \right)$ represents a Gaussian distribution with a mean of 0 and a standard deviation of σ, Lévy (β) represents a Lévy distribution with a parameter of β, and $X_i^t$ represents the position of the i-th wolf.

Figure 1 illustrates the flowchart of the introduced grey wolf optimization algorithm based on adversarial gradient for multi-target optimization scheduling of wind and thermal storage microgrids.

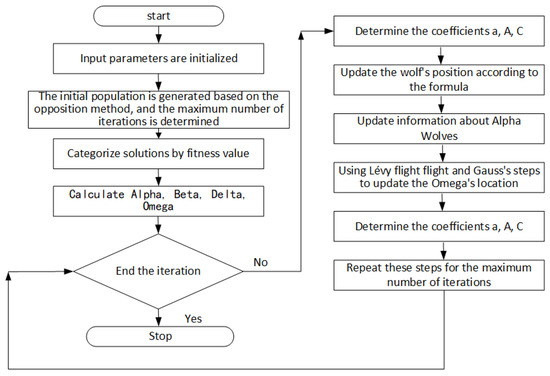
Figure 1. Flowchart of the grey wolf optimizer based on the opposing gradient.

The overall flowchart is as shown above, and the detailed steps are listed below:

Step 1: The position of grey wolves (search agents) is randomly initialized in the search space.

This step further fixes the number of iterations, followed by population size (number of wolves).

Step 2: For each search agent, the fitness value is determined as it denotes the distance between prey and the wolf.

Step 3: The opposite points are initialized and used to generate the opposite population so as to calculate the fitness values of every individual population.

Step 4: Sorting is executed for both current and opposite populations (pop and opop respectively), in line with their fitness values.

Step 5: The nP number of the fittest solution is selected out of a combination of current and the corresponding opposite population.

Step 6: Based on fitness values, three solutions are found such as best (a), second-best (b) and finally, the third best (d). These solutions correspond to Alpha, Beta, and Delta category wolves, respectively.

Step 7: Based on Equation (9), the position of the grey wolves is modified

$$X_W^i\left(t+1\right)=\gamma {\displaystyle \frac{\partial f^{Min}}{\partial X^i}}\le {\displaystyle \frac{\partial f}{\partial X_w^i}}\left(t\right)<\gamma {\displaystyle \frac{\partial f^{Max}}{\partial X^i}}for i=1,\cdots ,m and w=1,\cdots ,n$$

(9)

$$X_W^i\left(t\right)=rand\left(0,1\right){\lambda }^i\left(t\right)\left({\displaystyle \frac{\partial f}{\partial X_w^i}}\left(t\right)\right), \mathrm{Otherwise}, \mathrm{for} \mathrm{i}=1,\cdots ,\mathrm{m} \mathrm{and} \mathrm{w}=1,\cdots ,\mathrm{n}$$

(10)

In this equation, i corresponds to the index of decision variables in an optimization problem. On the contrary, n denotes the count of grey wolves.; ${\displaystyle \frac{\partial f^{Max}}{\partial X^i}}$ and ${\displaystyle \frac{\partial f^{Min}}{\partial X^i}}$ correspond to the maximum positive slope and minimum negative rate of change in every dimension at each step of the algorithm. Furthermore, γ represents a continuous parameter determined in the range [0, 1], rand(0, 1) represents a random number with an interval of (0, 1). As per the formulation given above,${\lambda }^i$ is updated using Equation (11) as given herewith

$${\lambda }^i\left(t\right)={\displaystyle \frac{0.1\left[U{b}^i-L{b}^i\right]}{max\left(\left|\frac{\partial f^{Min}}{\partial X^i}\right|,\left|\frac{\partial f^{Max}}{\partial X^i}\right|\right)}}$$

(11)

where L_b represents the lower bound and U_b represents the upper bound of the problem. This results in the following equation straightforwardly:

$$\left|{\lambda }^i\left(t\right){\displaystyle \frac{\partial f}{\partial X_w^i}}\left(t\right)\right|\ge 10\left(U{b}^i-L{b}^i\right)$$

(12)

The gradient of the problem in few optimization problems may remain unknown. This is attributed to the non-differentiability of objective function or discrete features possessed by decision variables. In order to overcome these issues, the following equation is presented:

$${\displaystyle \frac{\partial f}{\partial x}}={\displaystyle \frac{\left[f\right(t)-f(t-1\left)\right]}{\left[X\right(t)-X(t-1\left)\right]}}$$

(13)

Step 8: The fitness value is updated based on the modified position of grey wolves.

Step 9: Alpha, Beta, and Delta values are updated.

Step 10: The position of Omega wolves is updated using Equations (14) and (15) that employ Gaussian walk and Lévy flight

$$\begin{array}{c}{X}_{W,new}^i=X_W^i+KGaussian\left(\left|{\theta }_i\right|,\sigma \right)-\left(\xi \times {\theta }_i-{\xi }^{\prime }\times X_W^i\right),\\ for i=1,\cdots ,m and w=1,\cdots ,n\end{array}$$

(14)

$$\begin{array}{c}{X}_{W,new}^i=X_W^i+X_W^{i}Levy\left(\eta \right),\hfill \\ fori=1,\cdots ,mandw=1,\cdots ,n\hfill \end{array}$$

(15)

In the formula, the best solution is denoted by ${\theta }_i$ whereas $\left|\sigma \right|$ corresponds to the standard deviation of Gaussian distribution. The Gaussian parameter is changed by OGGWO as $\sigma =\left|K\times \left(x_i-BP\right)\right|$, while it also reduces the length of steps at the time of iterations by fixing = ${\displaystyle \frac{\log \left(l\right)}{l}}$. Here, l corresponds to the number of iterations. Further, $X_{W,new}^i$, now corresponds to the new position of the wolves, whereas $X_W^i$ denotes the current position. In addition to these, ${\xi }^{\prime }$ and $\xi$ denote random numbers in (0, 1]. Equation (16) denotes the calculation for Lévy flight

$$Lexy\left(x\right)={\displaystyle \frac{\left[0.01\times \sigma \times r_1\right]}{{\left|r_2\right|}^{\frac{1}{\beta }}}}$$

(16)

where the random numbers are denoted by r₁ and r₂ between (0, 1]; and β corresponds to constant, which is equal to 1.5. In Equation (14), σ is computed with the help of the following equation:

$$\sigma ={\left[\Gamma \left(1+\beta \right)\sin \left({\displaystyle \frac{\pi \beta }{2}}\right)/\left({\displaystyle \frac{\Gamma \left(1+\beta \right)}{2}}\beta \left[2^{{\displaystyle \frac{\left(\beta -1\right)}{2}}}\right]\right)\right]}^{1/\beta }$$

(17)

Step 11: The opposite population is created out of the current population using the jumping rate.

Step 12: The nP number of the fittest solution is selected after integrating the current and the opposite populations.

Step 13: Steps 3–7 are repeated until the maximum number of iterations is achieved.

Step 14: The best solution is achieved as the output.

As per the steps discussed above, the leading framework remains the same in both GGWO and OGGWO. However, significant changes are made in the latter. For example, OGGWO leverages a mix of original and gradient-based operators to update the position of wolves more than the conventional GWO operators. Further, a new function is also added in OGGWO to determine the gradient’s objective function at every point in the solution space [21]. In addition to the above, Gaussian walk and Lévy flight have been incorporated in OGGWO to increase randomness during the closure of every iteration. This phenomenon significantly increases both the exploration and exploitation capability, as long steps and short steps shift the particles in the solution space.

3. Example Analysis

In order to demonstrate the robustness and generalization ability of the proposed OGGWO algorithm, this paper conducted experiments in two different scenarios. Scenario 1 is the distributed energy operation with emission economic restrictions and Scenario 2 is the maximum operation of renewable energy.

3.1. Example Setup

(1) The starting parameters of the OGGWO algorithm are as follows: population number S = 30, maximum iteration count Gm = 1000, maximum limit Ub = 100 for each variable, and minimum limit Lb = −100 for each variable. The microgrid is composed of a diesel generator with a power change range of 18~60 kW, a wind turbine with an installed capacity of 90 kW, a photovoltaic array with an installed capacity of 85 kW, and an energy storage system with a rated capacity of 900 kWh and daily load. The value of P_LK is 230 KW. The initial values of $P_{Gi,\min }\left(t\right)$, $P_{Gi,\max }\left(t\right)$, $P_{sj,\min }\left(t\right)$, $P_{sj,\max }\left(t\right)$, $P_{Grid,\min }\left(t\right)$, and $P_{Grid,\max }\left(t\right)$ are 163 KW, 224 KW, 81 KW, 112 KW, 97 KW, and 156 KW, respectively.

(2) The microgrid model in this paper consists of wind turbines, photovoltaic power generation, internal combustion engines, fuel cells, and batteries. Their relevant operating parameters include the maximum and minimum limits of output capacity for each device, ramp rate constraints, equipment maintenance factors, installation costs, etc., as shown in Table 1. These data are sourced from the internal company database of a wind farm in Jiangxi Province, China.

Table 1. Relevant parameters of the power supply equipment.

Equipment Type	Power Upper Limit (KW)	Lower Limit of Power (KW)	Climbing Rate (KW/MIN)	Maintenance Coefficient (CNY/kW)	Capacity Factor (%)	Depreciation Period (year)	Installation Cost (CNY/kW)
WT	50	0	5	0.032	22.13	10	2.34
PV	30	0	10	0.006	29.34	20	6.61
MT	60	0	5	0.049	54.78	10	1.72
FC	40	0	5	0.029	33.62	10	4.23
BAT	30	−30	5	0.002	32.67	10	0.09

(3) Due to the fact that wind and light are clean energy sources, the pollutants generated are almost zero. Therefore, only the treatment costs of pollutants generated by internal combustion engines, fuel cells, and large power grids are considered. The pollutant emission coefficients and treatment costs of various pollutants are shown in Table 2.

Table 2. Pollution treatment cost and discharge coefficient.

Types of Pollutants	Pollutant Control Costs (CNY)	Pollutant Emission Coefficient (g/kwh)
		MT	FC	Grid
CO	10.18	0.047	0	0.079
CO2	0.28	715	484	889
NOX	13.209	0.27	0.017	1.511
SO2	67.136	0.038	0.0033	1.37

(4) This paper divides a day into three time periods, and the electricity prices for each period are calculated based on the usage time electricity pricing scheme: valley period 0:00–7:00 and 23:00–24:00; during regular hours, 7:00–10:00, 15:00–18:00, and 21:00–23:00; and during the peak hours of 10:00–15:00 and 18:00–21:00. The corresponding electricity buying and selling cost data are shown in Table 3.

Table 3. Usage-time electricity cost table.

Time Interval	Electricity Purchase (CNY/kWh)	Electricity Sales (CNY/kWh)
Valley period	0.52	0.39
Regular period	0.94	0.69
Peak period	1.32	1.06

(5) The output power of wind turbines and photovoltaic power generation introduced in this paper is taken from the typical daily power generation data in East China on December 29. The wind and solar energy output curves for Scenario 1 are shown in Figure 2a and the wind and solar energy output curves for Scenario 2 are shown in Figure 2b.

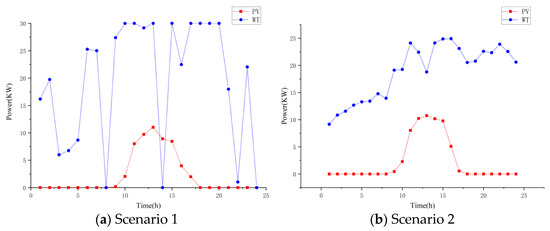
Figure 2. Wind and solar power output in two scenarios.

3.2. Simulation Analysis of Scenario 1

Scenario 1 involves the operation of all DGs and power grids under emission/economic restrictions as illustrated in [22]. Table 4 illustrates the optimal 24 h power generation plan to minimize costs and emission levels without evaluation criteria. From Table 4, it is evident that in the initial few hours of the day, the majority of the load demand is met by fuel cells existing within the power grid and utilities through common coupling points.

Table 4. Optimal power generation plan in Scenario 1.

Hour	MT (MW)	FC (MW)	PV (KW)	WT (MW)	BAT (CNY/kWh)	Grid (MW)
1	17.28	30.04	0	9.95	−30.12	37.88
2	19.65	27.28	0	11.51	−4.81	7.56
3	6.03	22.12	0	8.12	−20.16	44.14
4	6.86	30.11	0	12.55	−12.49	24.21
5	8.79	23.13	0	12.12	−19.89	43.38
6	25.39	0	0	13.67	−18.24	54.31
7	25.13	24.11	0	12.14	−25.68	48.73
8	0	30.06	0	13.48	2.45	44.32
9	27.48	27.14	0.28	15.26	−27.34	48.56
10	29.88	30.21	2.15	19.45	29.16	−14.53
11	30.06	29.62	8.14	24.37	26.29	−24.87
12	29.29	28.14	9.83	22.14	11.14	−11.94
13	30.00	29.97	11.14	19.33	−29.87	25.78
14	0	30.01	8.92	24.13	29.24	−6.24
15	30.00	30.07	8.55	24.99	27.35	−29.78
16	22.48	24.66	3.99	19.98	−20.23	45.12
17	30	30	1.98	23.47	−29.98	46.53
18	30	30	0	18.98	9.81	46.21
19	30	22.19	0	19.01	1.02	35.78
20	30	30	0	22.31	−0.59	22.28
21	17.99	19.79	0	12.99	6.94	35.29
22	1.02	28.93	0	21.08	27.98	5.99
23	22.05	0	9	13.09	−8.16	42.02
24	0	0	0	20.11	29.41	17.48

Moreover, the microgrid’s regulatory controller sequentially powers units and exports energy, boosting revenue during certain study periods while cutting net emissions. Conversely, the battery is recharged early each day, particularly taking advantage of lower-cost charging times. As the load curve peaks later in the day, the battery discharges. Incorporating renewable sources like solar and wind reduces pollution but raises operational expenses, making them economically impractical. Hence, it’s essential to cap the energy from these sources within set emission/economic limits. The BCS parameter refers to the temperature coefficient of the bypass diode under short-circuit conditions, which is the rate at which the performance of the bypass diode (such as forward voltage) changes with temperature when the photovoltaic panel is operating under short-circuit conditions.

In order to highlight the superiority of the proposed OGGWO algorithm in Scenario 1, this paper compared the simulation results with other classic optimization algorithms in Table 5. It can be seen that the standard deviation values of the cost and emission targets of the proposed OGGWO are 19.97 and 4.72, respectively, with a minimum cost of 1146.55, minimum emissions of 1262.74, and a BCS of 1223.83, which are the minimum values compared to other classical optimization algorithms.

Table 5. Comparison of the simulation results in Scenario 1.

Algorithm	Parameter	Cost (CNY)	Emissions (Kg)
EDNSGA-II [23]	Minimum cost	1164.01	1230.66
	Minimum emissions	1283.80	1175.99
	BCS	1243.40	1212.7
	standard deviation	22.71	5.08
NSGA-II [23]	Minimum cost	1295.70	1236.5
	Minimum emissions	173.77	1199.08
	BCS	1317.47	1216.54
	standard deviation	24.66	7.08
PSO	Minimum cost	1316.53	1241.29
	Minimum emissions	1378.31	1203.12
	BCS	1341.82	1220.07
	standard deviation	33.51	8.14
CSA	Minimum cost	1310.50	1239.86
	Minimum emissions	1373.45	1202.18
	BCS	1334.62	1219.14
	standard deviation	31.79	7.99
GWO	Minimum cost	1261.65	1234.08
	Minimum emissions	1337.12	1195.64
	BCS	1286.07	1214.31
	standard deviation	24.19	6.87
GGWO	Minimum cost	1153.99	1228.14
	Minimum emissions	1268.69	1173.67
	BCS	1230.25	1212.03
	standard deviation	21.22	4.88
OGGWO	Minimum cost	1146.55	1226.71
	Minimum emissions	1262.74	1172.48
	BCS	1223.83	1211.28
	standard deviation	19.97	4.72

Figure 3 displays the outcomes of the optimization algorithm’s analysis. The results indicate that the suggested optimization algorithm has yielded outstanding performance regarding cost and emission objectives for both the optimal and worst-case scenarios. Furthermore, it demonstrated a higher rate of convergence.

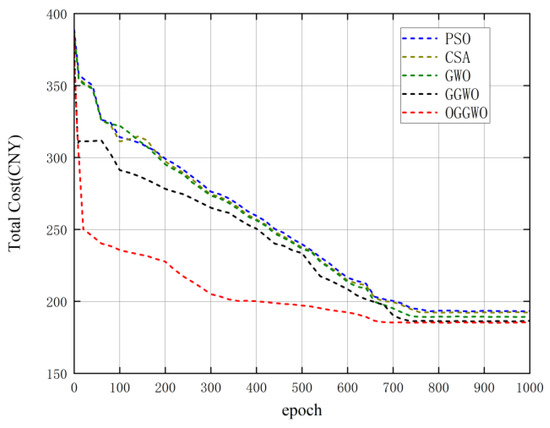
Figure 3. Cost convergence properties of Scenario 1.

To highlight the effectiveness of the introduced OGGWO algorithm, Figure 3 and Figure 4 map out the convergence patterns of OGGWO in comparison to other optimization techniques, aiming for the best possible solution and individual goals. The data indicate that the OGGWO approach hit the nadir for the cost objective after 705 cycles and then remained constant, while the GWO algorithm achieved convergence at 713 cycles. Furthermore, the algorithm detailed in this study reached its nadir at 734 cycles, as opposed to the 745 cycles required for the GWO algorithm to reach convergence.

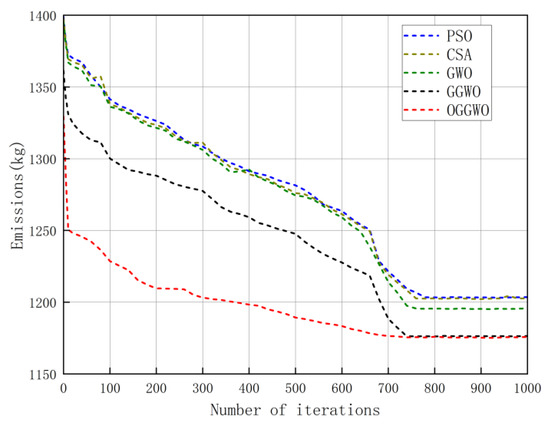
Figure 4. Emission aggregation characteristics of Scenario 1.

Figure 5 displays the Pareto fronts for the trade-off objectives achieved by different methods, facilitating comparison and the identification of optimal compromise solutions. The illustration suggests that the introduced algorithm is proficient in addressing nonlinear multi-objective optimization issues, as the Pareto optimal frontier of non-dominated solutions is evenly distributed. Consequently, the proposed algorithm expends less computational effort in diminishing emissions and operational expenses. The optimization outcomes robustly validate the algorithm’s capability to tackle equality and inequality concerns prevalent in energy management scenarios.

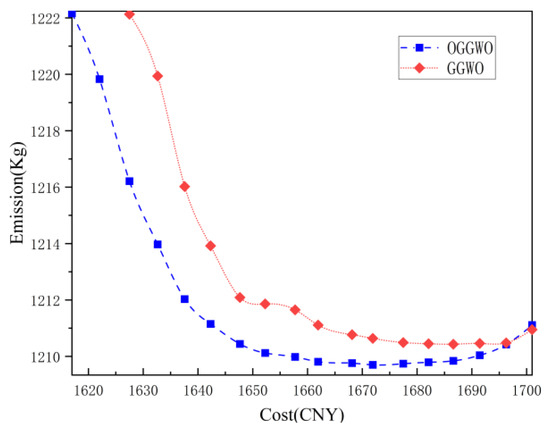
Figure 5. The emission cost balancing characteristics of Scenario 1.

The experimental results show that the cost deviation and emission deviation of the OGGWO algorithm proposed in this paper in Scenario 1 are CNY 21.22 and 4.88 kg, respectively. The minimum emission is 1172.48 kg and the minimum cost is CNY 1146.55, both of which are lower than other optimization algorithms.

3.3. Simulation Analysis of Scenario 2

In order to highlight the superiority of the OGGWO algorithm proposed in this paper in Scenario 2, the algorithm was compared with other classic optimization algorithms, and the results are shown in Table 6. Table 6 provides a comparative analysis of the statistical performance of OGGWO versus other optimization algorithms across individual objectives. When evaluating the outcomes of the GWO algorithm against the proposed OGGWO algorithm across different objectives, it becomes evident that the GWO algorithm exhibits certain deficiencies and variable performance levels.

Table 6. Comparison of the simulation results in Scenario 2.

Algorithm	Parameter	Cost (CNY)	Emissions (Kg)
EDNSGA-II [23]	Minimum cost	1491.69	1231.56
	Minimum emissions	1586.34	1162.4
	BCS	1573.12	1215.63
	standard deviation	42.15	1215.63
PSO	Minimum cost	1520.18	1205.29
	Minimum emissions	1589.91	1168.12
	BCS	1554.07	1184.89
	standard deviation	46.80	7.63
CSA	Minimum cost	1513.45	1203.14
	Minimum emissions	1573.71	1166.58
	BCS	1540.06	1183.28
	standard deviation	45.31	7.58
GWO	Minimum cost	1484.88	1200.23
	Minimum emissions	1551.88	1160.25
	BCS	1502.96	1179.27
	standard deviation	37.25	6.64
GGWO	Minimum cost	1464.54	1197.38
	Minimum emissions	1587.72	1158.03
	BCS	1490.75	1177.49
	standard deviation	34.67	4.63
OGGWO	Minimum cost	1457.80	1210.24
	Minimum emissions	1580.05	1156.79
	BCS	1473.14	1175.82
	standard deviation	33.34	4.46

Table 7 highlights the efficacy of the proposed algorithm in handling multi-objective optimization and the optimal distribution of power among units. The data in this table suggest that the deployment of high-performance units is crucial for simultaneously achieving economic and emission targets. From Table 7, it can be inferred that compared to other optimal solutions, the proposed algorithm appropriately handles multi-target optimization problems while also ensuring the minimum diversity of each objective and experiment. In contrast to the primary scenario, the overall operational expenses of the microgrid have risen in the secondary scenario. However, when compared to the earlier state, there has been a reduction in net emissions.

Table 7. Optimal power generation plan in Scenario 2.

Hour	MT (MW)	FC (MW)	PV (KW)	WT (MW)	BAT (CNY/kWh)	Grid (MW)
1	29.76	0	0	9.58	−27.26	50.23
2	16.11	15.71	0	10.26	−17.72	30.25
3	6.52	22.43	0	11.18	−19.12	37.13
4	23.24	3.36	0	12.75	−21.64	42.15
5	6.16	19.58	0	14.36	−28.64	57.34
6	25.78	3.26	0	14.24	−26.21	54.78
7	26.14	23.15	0	14.23	−23.76	43.12
8	7.75	24.78	0.36	12.61	−15.34	57.64
9	0	28.66	0.41	18.17	25.64	18.31
10	26.90	28.45	2.35	17.85	28.64	−13.88
11	27.31	27.94	9.16	23.33	28.36	−28.46
12	29.76	0	11.36	21.55	28.46	−5.13
13	0	21.14	11.86	19.72	−4.64	41.21
14	26.31	28.31	11.24	23.76	24.31	−30.13
15	0	0	9.25	23.34	18.63	36.01
16	26.54	28.45	5.11	23.72	−28.76	35.77
17	24.12	28.86	0.38	22.35	−27.63	52.11
18	11.25	20.12	0.27	21.64	17.44	33.46
19	29.36	28.32	0	21.72	−28.97	58.22
20	28.76	3.41	0	20.36	−6.24	55.14
21	26.58	27.48	0	20.75	−21.25	4122
22	27.77	0	0	21.43	27.14	3.42
23	19.56	19.36	9	22.34	−18.31	34.13
24	8.52	20.23	0	21.74	−21.47	38.13

Figure 6 and Figure 7 depict the convergence trends for operating costs and emissions of the OGGWO, GGWO, GWO, CSA, DE, and PSO algorithms. The figures reveal that the OGGWO algorithm exhibits consistent and rapid convergence in locating the optimal solution, suggesting the Pareto optimal frontiers for both OGGWO and GGWO algorithms. These illustrations suggest that the OGGWO algorithm is a viable option for addressing multi-objective energy management challenges, outperforming other optimization methods. Furthermore, the OGGWO algorithm presented in this study ensures an optimal spread of non-dominated solutions and is suitable for extensive standard testing systems.

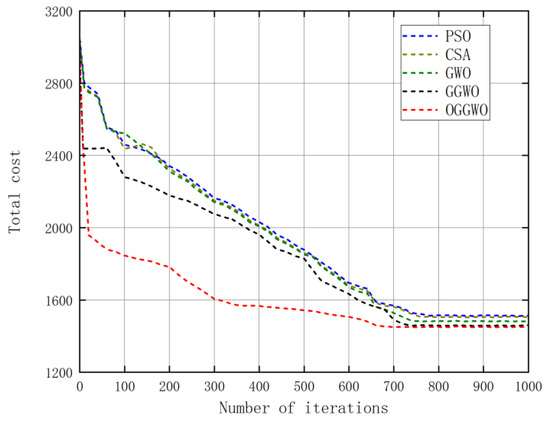
Figure 6. Cost convergence characteristics of Scenario 2.

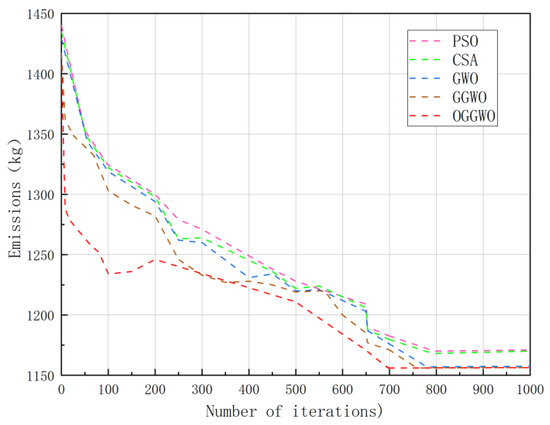
Figure 7. The mission convergence properties of Scenario 2.

The cost deviation and emission deviation of the OGGWO algorithm proposed in this paper in Scenario 2 are CNY 33.34 and 4.46 kg, respectively. The minimum emission is 1156.79 kg and the minimum cost is CNY 1457.80, both of which are lower than other optimization algorithms. This indicates that the OGGWO algorithm proposed in this paper obtains better results in Scenario 2, and as shown in Figure 8, the convergence speed of the OGGWO algorithm proposed in this paper is faster in Scenario 1.

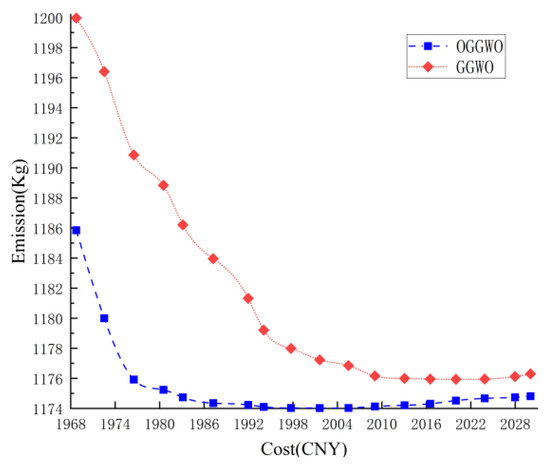
Figure 8. The emission cost balancing characteristics of Scenario 2.

4. Conclusions

This paper focuses on the optimal solution problem considering factors such as construction cost and carbon emissions, and proposes a grey wolf optimizer (OGGWO) based on adversarial gradient to solve the multi-objective optimization scheduling of grid-connected microgrids, which can improve the quality of solution and convergence speed. This algorithm includes instantaneous consideration of estimation and its equivalent inverse estimation, utilizing the advantages of gradient features to provide information about the output boundary of thermal power units. At the same time, the combination of gradient features considers the gradient direction in the optimization scheduling process to achieve enhanced approximation of target cost and emission candidate solutions. In order to enhance the exploration and development capabilities of the proposed OGGWO algorithm, Gaussian walk and Lévy flight techniques are introduced to increase the search range of the solution while sacrificing a small amount of search speed, which helps to obtain the global optimal solution. The cost deviation and emission deviation of the OGGWO algorithm proposed in this paper in Scenario 2 are CNY 33.34 and 4.46 kg, respectively. The minimum emission is 1156.79 kg and the minimum cost is CNY 1457.80, both of which are lower than other optimization algorithms. This indicates that the OGGWO algorithm proposed in this paper obtains better results in Scenario 2, and as shown in Figure 7, the convergence speed of the OGGWO algorithm proposed in this paper is faster in Scenario 1.

Although OGGWO has enhanced its exploration capabilities by introducing Gaussian walk and Lévy flight techniques, there is still room for further optimization of the application of these technologies. For example, it is possible to consider adaptively adjusting the probability distribution parameters of Gaussian walk and Lévy flight to better balance the relationship between global search and local search.