Abstract
Nonnegative matrix factorization can be used to automatically detect topics within a corpus in an unsupervised fashion. The technique amounts to an approximation of a nonnegative matrix as the product of two nonnegative matrices of lower rank. In certain applications it is desirable to extract topics and use them to predict quantitative outcomes. In this paper, we show Nonnegative Matrix Factorization can be combined with regression on a continuous response variable by minimizing a penalty function that adds a weighted regression error to a matrix factorization error. We show theoretically that as the weighting increases, the regression error in training decreases weakly. We test our method on synthetic data and real data coming from Rate My Professors reviews to predict an instructor’s rating from the text in their reviews. In practice, when used as a dimensionality reduction method (when the number of topics chosen in the model is fewer than the true number of topics), the method performs better than doing regression after topics are identified—both during training and testing—and it retrains interpretability.
1. Introduction
Nonnegative matrix factorization (NMF) is a highly versatile data science technique with far-reaching applications. It can identify thematic elements, i.e., groups of words that appear frequently together in a corpus, which together convey a common message [1]. More generally, it can be used to decompose an image into identifiable patterns [2] and as a general-purpose dimensionality reduction or preprocessing method before applying other machine learning methods, as has been done in studying various diseases [3,4]. Similar to singular value decomposition (SVD) [5], NMF provides a low rank factorization. In NMF, a nonnegative matrix representing a corpus (or other nonnegative dataset) is factored into a low rank approximation where the inner dimension, r, between W and H is such that and ; however, unlike SVD, there is an additional constraint that both W and H are nonnegative, i.e., and This nonnegativity enforces that the data in X are represented by a nonnegative combination of the dictionary atoms in the factorization, which lends itself to human interpretability. For example, in the foundational work [2], Lee and Seung show that NMF, when applied to facial images, decomposes the images into recognizable parts such as noses, eyes, and mouths.
When applied to a document-term matrix [6] X, where row i of X represents document i and column j represents the frequencies of word j across the documents, the classical NMF method amounts to
where, for , denotes the Frobenius norm of A with . Other variations on the penalty function exist, including the Kullback–Leibler divergence [7]. After computing W and H, we interpret row j of H as the jth topic, its components being the weight of each word in that topic, and row i of W as the topic-encoding of document i, i.e.,
Throughout this manuscript we make use of “colon notation” where “:“ means the full range of indices for a row/column, “a:b” indicates a consecutive range of indices from a to b, etc.
The rest of our paper is organized as follows: the general context to our work and our main contributions are stated in Section 2; in Section 3, we provide the formulation of our method, its algorithmic implementation, its theoretical properties, and their proofs; in Section 4, we provide a proof of concept through synthetic data; in Section 5, we test our method on a real dataset from Rate My Professors; and finally we conclude our work in Section 6.
2. Relation to Current Work and Contributions
When designing algorithms to handle multiple objectives simultaneously, a weighted penalty function that combines the multiple objectives is often used [8]. For example, with LASSO regression [9], one seeks a linear model that also does model selection by zeroing out parameters that are less significant. This can be done by minimizing a least squares error with a weighted penalty for the -norm of the parameters. Prior authors have combined NMF with a linear regression procedure to maximize the predictive power of a classifier [10,11,12]. This is accomplished through a penalty function that combines NMF with another objective function—a (semi) supervised approach. Semi-supervised NMF can also be applied to guide NMF to identify topics with desired keywords [13].
In this paper, we combine NMF with a linear regression model to predict the value of a continuous response variable. We consider synthetic data along with a real dataset that pairs written commentary with a real-valued observation. In particular, we use reviews from the Rate My Professors website [14,15] that include all student comments for a professor along with the mean rating in [1, 5]. Due to the averaging, the rating is effectively a continuous variable.
3. Model
We provide the framework for our proposed continuous semi-supervised nonnegative matrix factorization method (CSSNMF).
3.1. Formulation
We consider having a document-term matrix [6] for n documents with their associated word frequencies in the m columns—a “bag of words” where each document is represented only by the frequencies of its words. Each document has a corresponding value in so that we can associate with X the vector . Put another way: each document is represented as a row of X, call it , which stores the frequencies of each of the m words within the corpus; then, to each such x there is an observation (and over n documents, this generates ). We choose and as hyper-parameters where r denotes the number of topics and is weight put on the regression error.
In the real data that we look at, each row of X will represent the reviews written for one university instructor, with frequencies of the words in the columns. For each instructor in the dataset, the mean value of their respective student ratings will be a single component of Y. From a predictive standpoint, we would like to predict the mean rating of an instructor based only on the words in their review, i.e., take a vector of the word frequencies and make a prediction of their mean rating (the hat indicates a prediction). We want the prediction to be as close to the true mean rating as possible. The topic modelling aspect of this is that instead of using the full x vector of dimension m, we approximate x as a nonnegative linear combination of r topic vectors (interpretable vectors of word frequencies). We effectively compress x to a vector of dimension and we model the rating as a linear combination of the components of w.
Given , , and , we define a penalty function that combines topic modelling with a linear regression based on the topic representations. The intuition with the weighting is that as the weight increases, topic modelling is still done, but more and more emphasis is put on producing an accurate regression on Y. We define
and where is given by
The matrix with its column of 1s allows for an intercept: given a topic representation , we predict a value
When , we seek
When , we define
We also impose a normalization constraint, that
so that the topics have unit length in .
Remark 1
(Sum of Topic Representations). If is normalized so its rows sum to 1 then it is also the case that by noting that and summing over j.
When , has no effect upon and we first perform regular NMF over W and H and, as a final step, we choose to minimize the regression error. In other words, if , we do NMF first and then find the best given the already determined weights for each document. It seems intuitive, however, that the regression could be improved if and W both were being influenced by the regression to Y, which is what our method aims to do when . From a practical perspective, if , then the regression error becomes dominant and we may expect the topics as found in H to be less meaningful. In Section 3.2, we state some theoretical properties of our method as it is being trained.
Once and are known, we can make predictions for the response variable corresponding to a document. This amounts to finding the best nonnegative topic encoding for the document and using that encoding in the linear model—see Section 3.3.
Remark 2
(Uniqueness). Using our established notation, we remark that if and , then and , where , , and for any invertible with and both having all entries nonnegative. Thus, uniqueness of an optima, if it exists, can only be unique up to matrix multiplications.
3.2. Theoretical Results
We present two important behaviors of CSSNMF with regard to increasing and its effect upon predicting the response variable.
Proposition 1
Theorem 1
Remark 3.
Proposition 1 and Theorem 1 are based on obtaining a global minimum. In practice, we may only find a local minimum.
Proposition 1 and Theorem 1 are statements pertaining to training the model. Assuming we have the optimal solutions, Proposition 1 tells us that the regression error for is no worse than the regression error with and could, in fact, be better. Thus, the intuition that selecting topics while paying attention to the regression error is practical. Then Theorem 1 says that the regression error is weakly monotonically decreasing as increases. In practical application, we find the error strictly monotonically decreases.
Before proceeding to algorithmic procedures, we prove Proposition 1 and Theorem 1.
3.3. Algorithm
Our minimization approach is iterative and based on the alternating nonnegative least squares [16] approach. Due to the coupling of NMF and regression errors, other approaches such as multiplicative or additive updates [17] are less natural. Each iteration consists of: (1) holding H and fixed while optimizing each row of W separately (nonnegative least squares); (2) holding W and fixed while optimizing each column of H separately (nonnegative least squares); and finally (3) holding W and H fixed while optimizing over . The error is nondecreasing between iterations and from one optimization to the next. We now derive and justify this approach (Algorithm 1) in increasing complexity of cases.
| Algorithm 1: Overall CSSNMF algorithm. | |||||
| Input :A matrix , | |||||
| a vector , | |||||
| a positive integer , | |||||
| a scalar , | |||||
| a relative error tolerance , and | |||||
| a maximum number of iterations . | |||||
| Output:Minimizers of Equations (6)–(9): nonnegative matrix , | |||||
| nonnegative matrix , and | |||||
| vector | |||||
| 1 | |||||
| 2 | Elementwise, , , | ||||
| 3 | |||||
| 4 | while and do | ||||
| 5 | as per Algorithm 2 | ||||
| 6 | as per Algorithm 3 | ||||
| 7 | as per Algorithm 4 | ||||
| 8 | Normalize W, H, and as per Algorithm 5 | ||||
| 9 | |||||
| 10 | if then | ||||
| 11 | |||||
| 12 | end if | ||||
| 13 | |||||
| 14 | |||||
| 15 | end while | ||||
| 16 | return | ||||
| Algorithm 2: Updating W. |
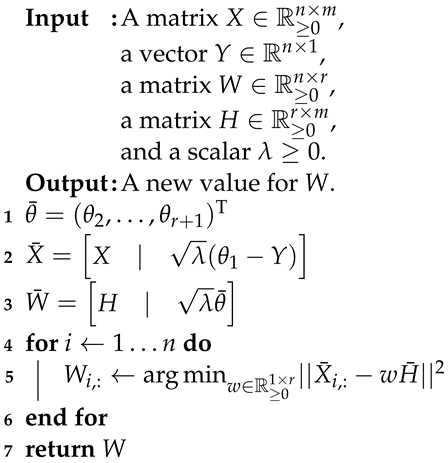 |
| Algorithm 3: Updating H. |
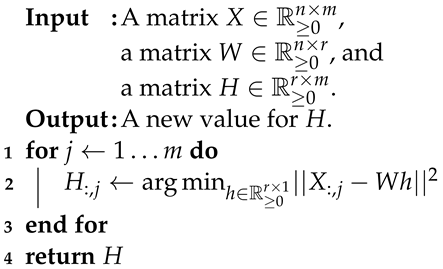 |
| Algorithm 4: Updating . | ||
| Input | :A vector , and | |
| a matrix | ||
| Output | :A new value for . | |
| 1 | ||
| 2 | ||
| 3 | return | |
| Algorithm 5: Normalization process. | ||
| Input | :A matrix , | |
| a matrix , and | ||
| a vector | ||
| Output | :New values for W, H, and . | |
| 1 | a vector of row sums of H. | |
| 2 | ||
| 3 | . | |
| 4 | . | |
| 5 | ||
| 6 | return W, H, and . | |
- W and H fixed.
If W and H are given and only can vary, then Equation (2) is minimized when is minimized. If has full rank or is overdetermined, this happens when the error, , is orthogonal to the column span of or that
When is underdetermined or has full rank, we require with minimized (for uniqueness) whereby
See Algorithm 4. Thus, when does not have full rank, the solution is where is the pseudoinverse of . See [18] for a discussion of pseudoinverses. In applications, we only expect to see overdetermined systems because the number of topics r should be less than the number of documents
- and fixed.
If W and are given and only H can change, then minimizing Equation (2) requires minimizing . We can expand this error term out in the columns of H:
Because columnwise the terms of the sum are independent, we can minimize each column of H separately to minimize the sum, i.e.,
as given in Algorithm 3.
- and fixed.
When H and are fixed, then Equation (2) can be written out as
where and . Defining matrices
we can rewrite Equation (15) as
which can be minimized through
This is precisely Algorithm 2.
For our optimizations and linear algebra, we used Numpy [19] and SciPy [20]. The nonnegative least squares routine employs an active set method to solve the least squares minimization problem with inequality constraints [21]. The active set method amounts to gradually building up the set of active constraints (those for which their not being enforced in the unconstrained problem would result in constraint violation or equality, i.e., a regression variable with a nonnegativity constraint being less than or equal to 0) and then optimizing over the passive set (all variables not in the active set) once identified with equality constraints on the active set [22]. This method can also be parallelized [23].
In addition to the steps outlined within these algorithms, we employed two additional modifications: (1) we defined , and any entries in H less than were replaced by (otherwise on some occasions, the W update step would fail); and (2) the minimizations at times yielded worse objective errors than already obtained and, when this happened, we did not update to the worse value.
As noted with other NMF routines, we might not reach a global minimizer [24]. In practice, the minimization should be run repeatedly with different random initializations to find a more ideal local minimum.
From an application standpoint, we wish to run the model on documents it has not been trained on. Algorithm 6 stipulates how a prediction takes place. We first find the best nonnegative decomposition of the document, a vector in , into the topic basis, projecting to dimensions. With the representation in topic-coordinates, we then use the linear model.
| Algorithm 6: Prediction process. | ||
| Input | :A matrix , | |
| a vector , | ||
| and a vector . | ||
| Output | :Model prediction for response variable, . | |
| 1 | Compute . | |
| 2 | Compute . | |
| 3 | return | |
An implementation of our algorithm can be found on our BitBucket repository, accessed on 21 February 2023.
4. Synthetic Datasets
In our synthetic data, we generate a matrix X that has nonnegative factors W and H, but we add noise. We also generate a response vector Y given as the matrix–vector product with noise. We investigate four items: (1) that the method does in fact work to decrease the objective function; (2) whether the regression errors decrease with increasing ; (3) the effects of overfitting; and (4) the model robustness to noise.
4.1. Generating Synthetic Data
Our synthetic data generation can be summarized as follows:
- We fix values of , , and
- We then define
- We pick such that each entry is . We likewise choose
- We set .
- We pick such that each element is
- We set
- We perturb X with noise and Y with noise .
- Any negative X-entries are set to 0.
We consider two different forms for and :
- Being elementwise and or
- Being elementwise and .
Note that in the synthetic data, the true number of topics is . In testing our synthetic data, we run Algorithm 1 where and . We use of the data for training and for testing.
4.2. Investigation
We confirm that the error in the objective function decreases with each iteration of Algorithm 1 in Figure 1—done with Gaussian noise.
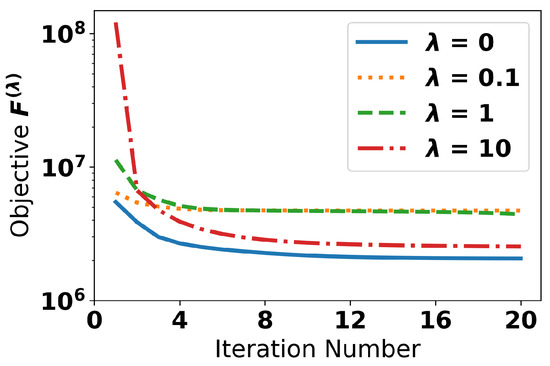
Figure 1.
Illustration of decreasing objective function at topics for }.
With the regression error being the mean squared prediction error, from Figure 2, we see the regression error in the training does tend to decrease with . (There are a few small exceptions, which we believe stem from randomizations leading to an assortment of different local optima.) The overall scale of the testing errors gets smaller as r goes from 1 to 4 and then stays steady or even gets slightly worse as r increases from 4. Indeed, is the “correct” synthetic value. Given the noise as either Gaussian or uniform, the variances of , , and , , serve as loose estimates for the best possible testing loss (the loss could very well be higher as noise is added to the matrix X as well). When the training errors are smaller than this estimate, it suggests overfitting.
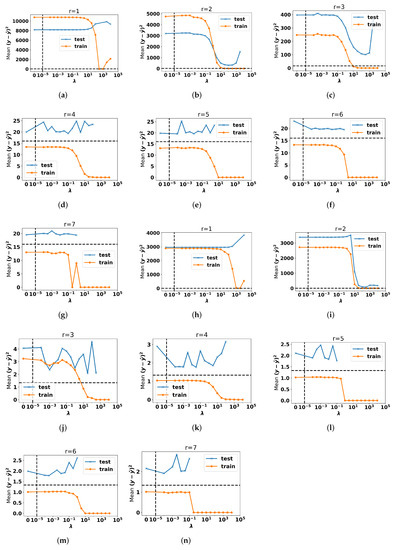
Figure 2.
Regression errors with varying regression weight with different numbers of topics r for Gaussian noise (a–g) and uniform noise (h–n). The values used are the set For each and r, fifty trials were run and the regression errors corresponding to the best overall objective function were recorded. Points with for which the regression error exceeds times the regression error at are not displayed. The dashed horizontal line is the estimated minimal mean regression error. The dashed vertical line is the transition point between a linear and logarithmic x-scale.
To study robustness with noise, we allow the level Gaussian noise to vary in the problem and evaluate the regression error on testing data. To ensure each noise level starts with the same ground truth, we start with unperturbed X and Y (as per Section 4.1 with ) and compute matrices and vectors with the same size as X and Y with elementwise entries. Then, for each level of noise under investigation, we scale these unit normal distributions by a noise level and examine the testing error as the varies with (rank below true rank), (correct rank), and (number of chosen topics above correct rank). Figure 3 illustrates the results. The noise is handled well with in that a higher does tend to improve the testing error; however, at higher noise levels , it seems suitable minima are harder to find when is large. With and , the testing does not benefit with increasing at any noise level.
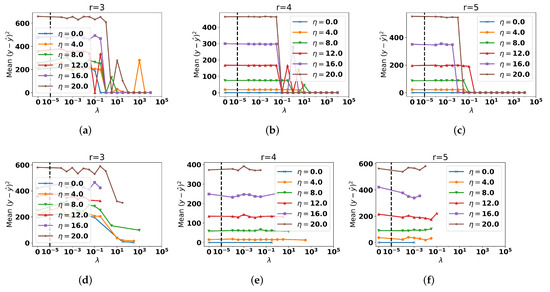
Figure 3.
Regression errors at various noise levels with varying regression weight . The true number of topics is . The top row, (a–c), depicts the training errors, and the bottom row, (d–f), depicts the testing errors. The first column, (a,d), is for a low rank approximation , the second column, (b,e), is for an approximation of correct rank , and the third column, (c,f), is for when the number of topics used is larger than the true number of topics. For each , , and r, fifty trials were run, and the regression errors corresponding to the best overall objective function were recorded. Points with for which the regression error exceeds times the regression error at are not displayed. The dashed vertical line is the transition point between a linear and logarithmic x-scale.
Taken together, we anticipate that CSSNMF will perform well provided the number of topics chosen does not exceed the true number of topics in the dataset (difficult to assess). We expect that the optimal predictions on unseen data should occur at a large enough that the testing errors have decreased and plateaued. In Figure 2, we see that for large , when overfitting is an issue, the testing performance is seldom better than where (classical NMF and then regression) and, in fact, is often much worse.
5. Rate My Professors Dataset
Here we study our method on real data [15] coming from Rate My Professors where for each instructor in the dataset, all corresponding student comments are combined to generate a written narrative and we have the instructor’s rating (mean of all responses).
5.1. Pre-Processing
The corpus was first processed via term frequency–inverse document frequency (TF-IDF) [25] with the TfidfVectorizer class in Python’s scikit learn package [26]. We used arguments min_df=0.01, max_df=0.15, stop_words=’english’, norm=‘l1’, lowercase=True. We found the ratings were not balanced: there were 57 on the interval [1, 2), 235 on the interval , 494 on the interval [3, 4), and 629 on the interval [4, 5]. To balance the dataset, we extracted only a random subset of 57 reviews in each interval (all ratings on were used). Overall, we obtained a corpus matrix X that was . The open right-end of the intervals ensures data are not duplicated.
5.2. Choice of Topic Number and Regression Weight
We did not know the true number of topics in the dataset and chose topics of , and 11, with . We present the results for 11 topics that gave the best results. See Figure 4. We note that, for large enough , the testing error outperforms the testing error for . The optimal point was at .
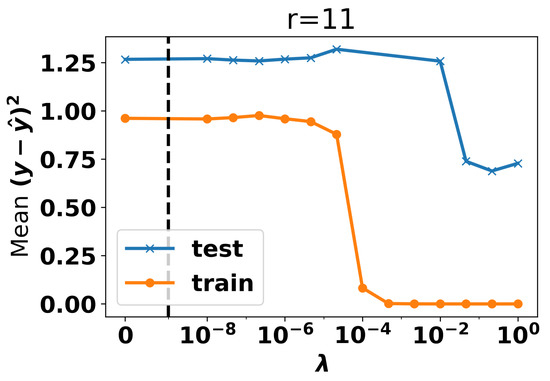
Figure 4.
Errors in training and validation on Rate My Professor dataset with topics. Points with for which the regression error exceeds times the regression error at are not displayed. The dashed vertical line is the transition point between a linear and logarithmic x-scale.
We comment that it is generally difficult to know precisely where the testing error will be minimized, only that, based on observations of the synthetic data, the testing error is often better than the case after the training error has dropped. We speculate that the level of noise in this dataset results in the testing errors not dropping below .
5.3. Prediction
We examine the rating prediction by plotting histograms of predicted ratings where the true ratings were in and —the closed intervals are used here. Figure 5 depicts these histograms along with the mean predicted rating and true rating. The predictions are often within range, and the mean predicted values are very close to the true means over each interval. We can also see the general predictive strength in the scatterplot of actual vs. predicted ratings in Figure 6.
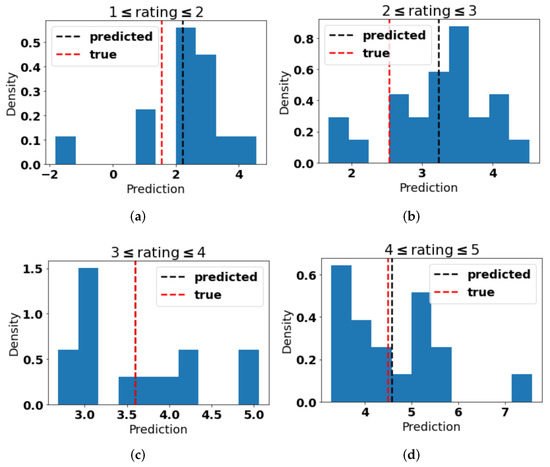
Figure 5.
Histograms of the predicted mean rating for various ranges of true ratings ([1, 2] in (a), [2, 3] in (b), [3, 4] in (c), and [4, 5] in (d)). The vertical dashed lines represent the mean values. The predicted and true means are as follows: and for ratings in [1, 2], and for ratings in [2, 3], and for ratings in [3, 4] (the lines are indistinguishable), and and for ratings in [4, 5].
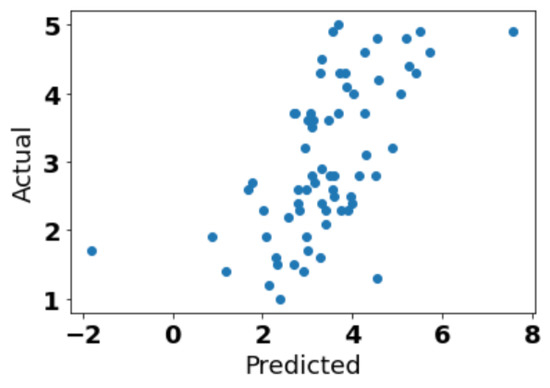
Figure 6.
Scatterplot of Rate My Professor ratings: actual mean rating vs. predicted mean rating.
These results suggest the model is able to identify topics and associated -weights so as to generate predictions that are consistent with true ratings. For example, in the case where ratings are in , we see the peak of the predictions is around 2, not exceeding 4, with some predictions as low as ; then, in the case of ratings in , the model peaks around and makes some predictions above 7. There is a clear capacity for the topics to shift the predictions.
5.4. Topics Identified
It is important that the method not only have predictive power, but also produce interpretable topics. We now look at the 11 topics with their associated -weights. We find
Note that suggests that for a set of reviews with no topics, the average rating would be around —this suggests it is the presence of positive/negative topics that raise/lower the rating.
In Figure 7 and Figure 8, we plot the words in the topics associated with positive and negative ratings. The topics are interpretable. For positive topics, we find Topic 10 (suggestive of extra credit), Topic 6 (suggestive of being inspiring), Topic 8 (suggestive of being approachable/brilliant), and Topic 11 (suggestive of being nice/enjoyable class) and words such as “recommend” in a couple of them. A few words seem out of place, such as “hate” in Topic 11, but that can be explained by some positive reviews having phrases such as “i hated chemistry in high school and after taking her class i don t [sic] hate chem as much.” Among the negative topics, we see Topic 4 (being horrible) and Topic 5 (being unfair).
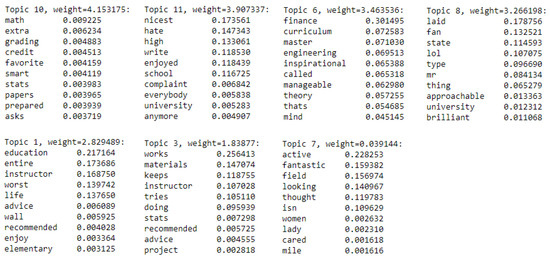
Figure 7.
Topics with positive -weights. The -weight is given as the topic weight. The strength of each word is given numerically beside each of the top 10 words.
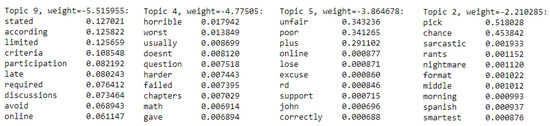
Figure 8.
Topics with negative weights. The weight is given as the topic weight. The strength of each word is given numerically beside each of the top 10 words.
As a whole, the topics are consistent with intuitive notions of what would be associated with higher or lower ratings. It is also interesting to look at the -topic weights quantitatively. For example, Topic 2 (mentioning rants and sarcasm) and Topic 4 (suggestive of being harder and failing students) contribute negatively to the score, but being a harder teacher seems to contribute more negatively to the rating than ranting. To elaborate more: because the row sums of the corpus matrix X and those of the topic matrix H sum to 1, we have that the sum of the topic weights for each document are approximately 1 as per Remark 1. All topics exist on the “same scale” within a document (roughly in ) and must roughly sum to 1; therefore, the sizes of the weights in for each topic can be ordered by their positive/negative contributions.
The fact that instructor difficulty has a negative effect on rating and the easiness has a positive effect has been found in another study [27] that looked at Rate My Professors data on instructor easiness and overall quality ratings. It is also interesting that many of the “dimensions” detected through our study, such as being approachable/nice (niceness), being hard/easy (difficulty), and being inspiring, were dimensions naturally identified by other scholars [28] who analyzed Rate My Professors data by hand through reading comments and classifying key phrases within the comments. In this latter study, however, each dimension could be positive or negative, depending on how it was used.
6. Conclusions and Future Work
We have developed CSSNMF as a means to combine NMF with regression on a continuous response variable. We accomplished this by minimizing an objective function that combines an NMF error with a weighted regression error. We have shown that the regression error in training is weakly decreasing with the regression error weight and that, in practical applications, the error strictly decreases. The topics identified can outperform the quantitative accuracy of topics formed through NMF alone while retaining a high degree of interpretability (as found with real data). The method is robust to noise and tends to perform best on new data when there is a dimensionality reduction, i.e., when the number of topics fit for is fewer than the true number of topics.
We expect that our methods can be applied to very large datasets as our algorithmic steps involve hierarchical alternating nonnegative least squares [16], which could even be handled in parallel [29] (with or without parallel nonnegative least squares), and a least squares problem (Equation (12)) with a small matrix to invert.
Although our analysis focused on the case of linear regression, incorporating nonlinearities would be of interest. We also noted the challenge in choosing the appropriate given only training data. A more theoretical understanding of when testing errors drop substantially could be explored, but this may be dataset-specific.
Author Contributions
Conceptualization, M.R.L. and D.N.; methodology, M.R.L.; software, M.R.L.; validation, M.R.L.; formal analysis, M.R.L.; investigation, X.D., F.L. and A.S.; data curation, M.R.L. and D.N.; writing—original draft preparation, M.R.L.; writing—review and editing, X.D., F.L., A.S. and D.N.; visualization, M.R.L.; supervision, M.R.L.; project administration, M.R.L. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
The data used have been cited and are publicly available. Our code is available at https://bitbucket.org/3k1m/cssnmf/src/master/, accessed on 21 February 2023.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chen, Y.; Zhang, H.; Liu, R.; Ye, Z.; Lin, J. Experimental explorations on short text topic mining between LDA and NMF based Schemes. Knowl.-Based Syst. 2019, 163, 1–13. [Google Scholar] [CrossRef]
- Lee, D.D.; Seung, H.S. Learning the parts of objects by non-negative matrix factorization. Nature 1999, 401, 788–791. [Google Scholar] [CrossRef] [PubMed]
- Lao, H.; Zhang, X. Regression and Classification of Alzheimer’s Disease Diagnosis Using NMF-TDNet Features From 3D Brain MR Image. IEEE J. Biomed. Health Inform. 2021, 26, 1103–1115. [Google Scholar] [CrossRef] [PubMed]
- Lai, Y.; Hayashida, M.; Akutsu, T. Survival analysis by penalized regression and matrix factorization. Sci. World J. 2013, 2013. [Google Scholar] [CrossRef]
- Stewart, G.W. On the early history of the singular value decomposition. SIAM Rev. 1993, 35, 551–566. [Google Scholar] [CrossRef]
- Shahnaz, F.; Berry, M.W.; Pauca, V.P.; Plemmons, R.J. Document clustering using nonnegative matrix factorization. Inf. Process. Manag. 2006, 42, 373–386. [Google Scholar] [CrossRef]
- Joyce, J.M. Kullback-leibler divergence. In International Encyclopedia of Statistical Science; Springer: Berlin/Heidelberg, Germany, 2011; pp. 720–722. [Google Scholar]
- Marler, R.T.; Arora, J.S. The weighted sum method for multi-objective optimization: New insights. Struct. Multidiscip. Optim. 2010, 41, 853–862. [Google Scholar] [CrossRef]
- Freijeiro-González, L.; Febrero-Bande, M.; González-Manteiga, W. A critical review of LASSO and its derivatives for variable selection under dependence among covariates. Int. Stat. Rev. 2022, 90, 118–145. [Google Scholar] [CrossRef]
- Austin, W.; Anderson, D.; Ghosh, J. Fully supervised non-negative matrix factorization for feature extraction. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 5772–5775. [Google Scholar]
- Zhu, W.; Yan, Y. Joint linear regression and nonnegative matrix factorization based on self-organized graph for image clustering and classification. IEEE Access 2018, 6, 38820–38834. [Google Scholar] [CrossRef]
- Haddock, J.; Kassab, L.; Li, S.; Kryshchenko, A.; Grotheer, R.; Sizikova, E.; Wang, C.; Merkh, T.; Madushani, R.; Ahn, M.; et al. Semi-supervised Nonnegative Matrix Factorization for Document Classification. In Proceedings of the 2021 55th Asilomar Conference on Signals, Systems, and Computers, Pacific Grove, CA, USA, 31 October–3 November 2021; pp. 1355–1360. [Google Scholar]
- Li, P.; Tseng, C.; Zheng, Y.; Chew, J.A.; Huang, L.; Jarman, B.; Needell, D. Guided Semi-Supervised Non-negative Matrix Factorization on Legal Documents. Algorithms 2022, 15, 136. [Google Scholar] [CrossRef]
- Rate My Professors. Available online: https://www.ratemyprofessors.com/ (accessed on 17 February 2023).
- He, J. Big Data Set from RateMyProfessor.com for Professors’ Teaching Evaluation. 2020. Available online: https://doi.org/10.17632/fvtfjyvw7d.2 (accessed on 21 February 2023).
- Kim, H.; Park, H. Nonnegative matrix factorization based on alternating nonnegativity constrained least squares and active set method. SIAM J. Matrix Anal. Appl. 2008, 30, 713–730. [Google Scholar] [CrossRef]
- Lee, D.; Seung, H.S. Algorithms for non-negative matrix factorization. Adv. Neural Inf. Process. Syst. 2000, 13. [Google Scholar]
- Klein, C.A.; Huang, C.H. Review of pseudoinverse control for use with kinematically redundant manipulators. IEEE Trans. Syst. Man Cybern. 1983, 2, 245–250. [Google Scholar] [CrossRef]
- Harris, C.R.; Millman, K.J.; van der Walt, S.J.; Gommers, R.; Virtanen, P.; Cournapeau, D.; Wieser, E.; Taylor, J.; Berg, S.; Smith, N.J.; et al. Array programming with NumPy. Nature 2020, 585, 357–362. [Google Scholar] [CrossRef]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for Scientific Computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef]
- scipy.optimize.nnls. Available online: https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.nnls.html (accessed on 17 February 2023).
- Bro, R.; De Jong, S. A fast non-negativity-constrained least squares algorithm. J. Chemom. J. Chemom. Soc. 1997, 11, 393–401. [Google Scholar] [CrossRef]
- Luo, Y.; Duraiswami, R. Efficient parallel nonnegative least squares on multicore architectures. SIAM J. Sci. Comput. 2011, 33, 2848–2863. [Google Scholar] [CrossRef]
- Berry, M.W.; Browne, M.; Langville, A.N.; Pauca, V.P.; Plemmons, R.J. Algorithms and applications for approximate nonnegative matrix factorization. Comput. Stat. Data Anal. 2007, 52, 155–173. [Google Scholar] [CrossRef]
- Joachims, T. A Probabilistic Analysis of the Rocchio Algorithm with TFIDF for Text Categorization. Technical Report, Carnegie-Mellon Univ Pittsburgh pa Dept of Computer Science. 1996. Available online: https://apps.dtic.mil/sti/citations/ADA307731 (accessed on 21 February 2023).
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Bleske-Rechek, A.; Fritsch, A. Student Consensus on RateMyProfessors Com. Pract. Assess. Res. Eval. 2011, 16, 18. [Google Scholar]
- Hartman, K.B.; Hunt, J.B. What ratemyprofessors. com reveals about how and why students evaluate their professors: A glimpse into the student mind-set. Mark. Educ. Rev. 2013, 23, 151–162. [Google Scholar]
- Moon, G.E.; Ellis, J.A.; Sukumaran-Rajam, A.; Parthasarathy, S.; Sadayappan, P. ALO-NMF: Accelerated locality-optimized non-negative matrix factorization. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining, Virtual, 6–10 July 2020; pp. 1758–1767. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).