Abstract
Automatic grouping (clustering) involves dividing a set of objects into subsets (groups) so that the objects from one subset are more similar to each other than to the objects from other subsets according to some criterion. Kohonen neural networks are a class of artificial neural networks, the main element of which is a layer of adaptive linear adders, operating on the principle of “winner takes all”. One of the advantages of Kohonen networks is their ability of online clustering. Greedy agglomerative procedures in clustering consistently improve the result in some neighborhood of a known solution, choosing as the next solution the option that provides the least increase in the objective function. Algorithms using the agglomerative greedy heuristics demonstrate precise and stable results for a k-means model. In our study, we propose a greedy agglomerative heuristic algorithm based on a Kohonen neural network with distance measure variations to cluster industrial products. Computational experiments demonstrate the comparative efficiency and accuracy of using the greedy agglomerative heuristic in the problem of grouping of industrial products into homogeneous production batches.
1. Introduction
The search for a clustering algorithm that has both high accuracy and stability of the result, and, at the same time, a high speed of operation, is one of the problems of cluster analysis. The clustering result depends on the initially selected number of subsets, as well as the selected measure of similarity (dissimilarity) [1]. One of the most famous automatic grouping models is the k-means model [2], which was proposed by Steinhaus [3]. The goal of the k-means problem is to find k points (centers, centroids) X1, …, Xk in an M-dimensional space, such that the sum of the squared distances from the known points (data vectors) A1, …, Am to the nearest of the required points reaches a minimum:
Optimization model (1) can be considered as a location problem, where the points Xj have to be placed in an optimal way. Location theory has been developing for a long time separately from cluster analysis while solving very close or completely identical problems. Weiszfeld proposed an iterative procedure for solving the Weber problem, one of the simplest location problems, based on an iterative weighted least squares method [4]. This algorithm determines a set of weights that are inversely proportional to the distances from the current estimate to the sample points and creates a new estimate that is the weighted average of the sample according to these weights. In specific situations, Weiszfeld’s algorithm is very slow and does not always converge.
Local search methods for solving location problems are used in Ref. [5]. The standard local descent algorithm starts with an initial solution S = {X1, …, Xk}, chosen randomly or with the help of some auxiliary algorithm. At each step of the local descent, there is a transition from the current solution to a neighboring solution with a smaller value of the objective function until the local optimum is reached. The key problem here is to find the set of neighboring solutions n(S). At each step of the local search, the neighborhood function n(S) specifies a set of possible search directions. Neighborhood functions can be very diverse, and the neighborhood relation is not always symmetrical. Local search algorithms are widely used to solve NP-hard discrete optimization problems. However, simple local descent does not allow the finding of the global optimum of the problem.
Local search methods were further developed in so-called metaheuristics, in particular in the search algorithm with variable neighborhoods (variable neighborhoods search, VNS). Its main idea is to systematically change the neighborhood function and the corresponding change in the landscape during the local search.
The k-means problem was algorithmically implemented by S. Lloyd [6]. For the observation vector X, the k-means algorithm is designed to determine k centers and assign data points (objects) to each center to form clusters Cj, j = 1… k while minimizing the difference between the objects within the cluster. In the k-means algorithm, it is necessary to initially predict the number of groups (clusters).
In addition, the result obtained depends on the initial choice of centers, which is one of the main disadvantages of the algorithm. The modern literature offers many approaches to setting the initial centroids for the k-means algorithm, which are basically various evolutionary and random search methods. One of the most popular methods is the k-means++ algorithm [7], where the first centroid is chosen randomly and further selection goes with a certain probability. Moreover, in Ref. [8], a similar method is developed based on finding areas with maximum density. In Ref. [9], the authors propose a brute-force approach to the initialization of the k-means algorithm. Kalczynski et al. in Ref. [10] introduce three algorithms (merging, construction and separation) to create starting solutions of the k-means problem. In Ref. [11], a heuristic-based algorithm to improve the initial seeding of the k-means clustering described is implemented, where a hybrid approach with a genetic algorithm and the differential evolution heuristic is used. Detailed overviews of the existing initialization approaches may be found in Refs. [12,13,14].
The Kohonen neural network [15] of the vector quantization type is an autoassociator closely related to k-means. This competitive network can be related to unsupervised learning. The Kohonen learning law is an algorithm that finds the centroid (called “codebook vector”) closest to each training case and moves the winning centroid closer to the training case. Another type of Kohonen network is the self-organizing map competitive network that provides a topological mapping from the input space to the clusters. Kohonen networks are used in many fields of interest, such as speech recognition [16,17], image compression [18,19], image segmentation [20], face recognition [21,22,23], classification of weather patterns [24], malware detection [25], seasonal sales planning [26], medical decision-making [27,28], e-learning recommendations [29], denial of service attack defense detection [30], groundwater quality assessment [31], exploration of the investment patterns [32] and others.
Greedy agglomerative heuristic procedures [33,34] are tools to improve a result in a certain neighborhood of the solution. An agglomerative procedure starts with some solution S containing an excessive number of centroids and sequentially removes them. The elements of the clusters, related to the removed centroids, are redistributed among the remaining clusters. The greedy strategies are used to decide which clusters are most similar to be merged together at each iteration of the agglomerative procedure. For subsequent iterations, the chosen method is that which gave the best increase in the objective function in the previous iterations. The practice of solving NP-hard problems shows the efficiency of the transition from randomized recombination procedures to the search for the best recombination method [35]. The authors in Ref. [36] proposed methods of greedy agglomerative heuristics based on the location theory models. Algorithms using these methods are often randomized, but the results are quite stable. The method of greedy agglomerative heuristics uses evolutionary algorithms as one of the ways to organize a global search.
To date, the vast majority of the algorithms developed for continuous location problems use the most common distance measures (Euclidean, Manhattan). However, taking into account the characteristics of the feature space of a specific practical problem, the choice of a distance measure can lead to an increase in the accuracy of clustering. For instance, Itakura–Saito distance was used to build the learning vector quantization algorithm. In Ref. [19], a method is proposed for using the Mahalanobis distance as the basis for grouping. The Mahalanobis distance was also used to cluster incoming data into neural nodes in a self-organizing incremental neural network [22]. Kohonen networks with graph-based augmented metrics are presented in Ref. [37]. In Ref. [38], a distance measure for a self-organizing map is defined based on data distribution, and it is calculated with the use of an energy function. A distance metric learning method is often applied. For instance, in Ref. [22], the Mahalanobis matrix is computed, which assures small distances between the nearest neighbor points from the same class and the separation of points belonging to different classes by a large margin. Metric learning for the SOM based on the adaptive subspaces is represented in Ref. [39]. Furukawa [40] offers a nonlinear metrics learning method. The authors in Ref. [41] use an ensemble approach to metric learning with objective function generalization. Yoneda and Furukawa [42] propose a co-training approach, which collapses the objective function, thereby avoiding undesirable local optima.
In our work, our aim is solving the problem of the automatic grouping of objects. As a base, we use different types of Kohonen networks and modify them with the greedy agglomerative heuristic and different types of distance measures. Then, we test our approach on the applied problem.
The rest of this paper is organized as follows. In the Section 2, we introduce the Kohonen neural network model and propose our new algorithm involving the greedy agglomerative heuristic procedure. In the Section 3, we describe the computational experiments with a practically important dataset. In the Section 4 and Section 5, we discuss the results and provide a short conclusion.
2. Kohonen Neural Networks for Clustering Problem
2.1. Distance Measures
In clustering problems, the key concept is the concept of distance metrics between objects. Metric is a function that determines the measure of the distance between objects in the metric space Rp. Metric space is a set of points with a distance function d(xi, yi). The distance of order p between two points is determined by the Minkowski function (lp–norm) [1,43,44]:
where x and y are vectors of parameter values, M is the vector dimension. The parameter p is determined by the researcher; it can be used to progressively increase or decrease the weight of the i-th variable. Special cases of the Minkowski function depend on the p value. For p = 2, the function calculates the Euclidean distance between two points (l2–norm):
The squared Euclidean distance is often used:
For p = 1, the function calculates the Manhattan distance, also called rectangular (l1–norm):
For p = ∞, the function calculates the Chebyshev distance, returning the largest value of the difference between the object parameters modulo:
In addition to the cases of the dependence of the distance function on the parameter p, there are other methods for calculating distances, for example, the Mahalanobis distance [45]. Mahalanobis distance can be defined as a measure of dissimilarity (difference) between vectors from the same probability distribution with the covariance matrix C:
If the covariance matrix is identity, then the distance becomes equal to Euclidean. The covariance matrix is defined as:
where μ is expected value. In most cases, the literature presents problems with Euclidean or Manhattan metrics.
In our study, we use five different types of distance measures to evaluate which one is preferable in our case.
2.2. Vector Quantization Networks and Self-Organizing Kohonen Maps
A Kohonen network [15,39] is a self-organized neural network that enables us to allocate groups (clusters) of input vectors that have some common features. The Kohonen network (or Kohonen layer) is a single-layer network, each neuron of which is connected to all components of the input vector. The input vector is a description of one of the objects to be clustered. The number of neurons coincides with the number of clusters K that the network should allocate. Linear weighted adders are used as neurons in the Kohonen network. Each j-th neuron is described by a vector of weights Wj = (w1j, w2j, …, wMj), where M is input vector dimension, j = 1…K. The input vector has the form Xi = (x1i, x2i, …, xMi), i = 1…N, where N is number of objects.
According to the methods of adjusting the input weights of the adders and the problems being solved, many varieties of Kohonen networks are distinguished [46]. The most famous of them are:
- Vector quantization networks (VQ), closely related to k-means method;
- Self-organizing Kohonen maps (SOM), which provide a “topological” mapping from the input space to the clusters. Neurons in SOMs are organized into a grid (usually two-dimensional);
- Learning vector quantization networks (LVQ), which include supervised learning and used for classification problems.
First two types of Kohonen networks refer to unsupervised learning, considered in this article.
Vector quantization consists of replacing a continuous distribution by a finite set of quantizers while minimizing a predefined distortion criterion and may be used to determine groups (clusters) of data sharing common properties [46]. Since vector quantization is a natural application for k-means, the centroids are also referred to as a “codes”, and the table mapping codes to centroid is often referred to as a “codebook”.
Competition mechanisms are used to train the network according to principle “winner takes all”, for instance, simple competitive learning (SCL) algorithm [47]. When the vector X is fed to the network input, the neuron wins, the weight vector of which is the least different from the input vector: . This problem with K key vectors Wj in the feature space of the observed data X in terms of vector quantization is defined as a minimization of encoding distortion, i.e., as minimization problem:
where V(j) consists of points Xi ∈ X closest to Wj.
The SCL algorithm is in fact the online version of the Lloyd’s algorithm. If all data points are known in advance, this algorithm works offline as a batch algorithm (batch vector quantization, BVQ). The k-means method is an intermediate version, where only one data point is randomly chosen, and only the winning centroid is updated as the mean value of its cluster [46]. Thus, we can say that Kohonen networks have an advantage over the k-means model in that they allow organizing the online clustering. Basic version of SCL algorithm is represented in Algorithm 1.
| Algorithm 1. Basic SCL algorithm |
| Required: Set of initial data vectors X1, …, XN, where N is the number of points; set the number of neurons K; η0 (η = η0), where η0 is the initial learning rate; set the step of changing the learning rate Δη; |
| 1. Set the weight of each neuron Wj () |
| 2. While η > 0: |
| 3. for do |
| 4. for do |
| 5. Find the closest neuron Wcl to Xi: |
| 6. Update the closest neuron: Wcl = Wcl + η⋅(Xi − Wcl) |
| 7. η = η − Δη |
Self-organizing Kohonen maps [15,39] produce a mapping from a multidimensional input space onto a lattice of neurons. The mapping is topology-preserving in that neighboring neurons respond to “similar” input patterns. SOMs are typically organized as one- or two- dimensional lattices for the purpose of visualization and dimensionality reduction. During training, the winner neuron and its topological neighbors are adapted to make their weight vectors more similar to the input pattern that caused the activation. SOM algorithm with time limit is represented in Algorithm 2.
Thus, the SCL algorithm is a particular case of the SOM algorithm, when the neighborhood is reduced to zero. The magnitude of the changes decreases with time and is smaller for neurons far away from the winning neuron. The learning rates and neighborhood functions can be applied in various ways. However, these functions should be decreasing [48].
| Algorithm 2. Basic SOM algorithm |
| Required: Set of initial data X1, …, XN, where N is the number of points; set the number of neurons K; η0 (η = η0), where η0 is the initial learning rate. |
| 1. Set the weight of each neuron Wj () |
| 2. t = 0 |
| 3. While maximum time is not exceeded: t ≤ Tmax: |
| 4. Randomly choose Xi from initial data X1, …, XN. |
| 5. Find the closest neuron Wcl to Xi: |
| 6. Update the closest neuron Wcl and its neighbors V(Wcl). |
| Here, V(Wcl) is the set of indexes in the neighborhood of Wcl, including Wcl: |
| For each p in V(Wcl): |
| Wp = Wp + η(t) · h(t,d (Wp,Wcl)) · (Xi − Wp), |
| where η(t) is learning rate, h(t,d (Wp,Wcl)) is neighborhood function. |
| 7. t = t + 1 |
| 8. End while |
Several methods can be used to initialize the neurons. The simplest one is when the initial values are chosen randomly. Another method is to initialize the weights by the average of the minimum and the maximum values of the elements of the vectors that have to be classified.
Moreover, there are different types of stopping rules that can be applied at step 2 of Algorithm 1 and step 3 of Algorithm 2. A fixed threshold for the error, time limit of fixed number of algorithm repeating can be used.
2.3. Proposed Algorithms
For our purposes, we take as a basis the Kohonen network. First, we use vector quantization type (Algorithm 3). The idea is to initialize the excess number of neurons and then gradually decrease their number. The algorithm processes data points one by one. After a certain step, the neuron is removed, the removal of which shows the smallest increase in the value of the objective function. The learning rate decreases after a certain number of steps SN.
| Algorithm 3. SCL-based algorithm with a greedy agglomerative heuristic (SCL-GREEDY) |
| Required: Set of initial data X1, …, XN, where N is the number of points; set the number of neurons K1; η0 (η = η0), where η0 is the initial learning rate; set the step of changing the learning rate Δη |
| 1. Increase the number of neurons k times K = K · K1 |
| 2. Set the weight of each neuron Wj () |
| 3. Determine the number of steps to calculate η: SN = trunc(N/K), jj = 1 |
| 4. While η > 0: |
| 5. For , do |
| 6. For , do |
| 7. Find the closest neuron Wcl to Xi: |
| 8. Update the closest neuron Wcl: Wcl = Wcl +η·(Xi − Wcl) |
| 9. For each neuron Wj, calculate sum of distances to the initial data |
| X1, …, Xi: |
| 10. IF i%(SN + 1) == 0, THEN Recalculate η: jj = jj + 1, η = η0/jj |
| 11. IF K <> K1, THEN remove neuron Wj with the maximum sum of distances |
| 12. η = η – Δη |
| 13. End while |
SOM-based algorithm with a greedy agglomerative heuristic is represented in Algorithm 4.
Batch versions of described algorithms are similar to their online versions except that the neuron weights are recalculated after passing through all sample points. We denote batch version of SCL algorithm as BVQ (as in Ref. [46]) and batch version of SOM algorithm as BSOM.
| Algorithm 4. SOM-based algorithm with a greedy agglomerative heuristic (SOM-GREEDY) |
| Required: Set of initial data X1, …, XN, where N is the number of points; set the number of neurons K1; η0 (η = η0), where η0 is the initial learning rate. |
| 1. Increase the number of neurons k times K = k · K1 |
| 2. Set the weight of each neuron Wj () |
| 3. t = 0 |
| 4. While maximum time is not exceeded: t ≤ Tmax: |
| 5. Randomly choose Xi from initial data X1, …, XN. |
| 6. Find the closest neuron Wcl to Xi: |
| 7. Update the closest neuron Wcl and its neighbors V(Wcl). |
| Here, V(Wcl) is the set of indexes in the neighborhood of Wcl, including Wcl: |
| For each p in V(Wcl): |
| Wp = Wp + η(t) · h(t,d (Wp,Wcl)) · (Xi − Wp), |
| where η(t) is learning rate, h(t,d (Wp,Wcl)) is neighborhood function. |
| 8. For each neuron Wj, calculate sum of distances to the initial data X1, …, Xi: |
| 9. IF K <> K1, THEN remove neuron Wj with the maximum sum of distances |
| 10. η = η − Δη |
| 11. t = t + 1 |
| 12. End while |
3. Computational Experiment and Analysis
For the experiment, we considered the sample consisting of four different homogeneous batches of electronic radio components [49]. The total number of devices in all batches is 446. We considered various combinations of batches: mixed lots from four, three and two batches. Four-batch mixed lot contains 62 parameters (features), three-batch mixed lot and two-batch mixed lot contain 41 parameters. The difficulty of the sample is that the number of parameters in it is large enough relative to the number of sample elements.
Each experiment is performed in online mode and in batch mode. We used different types of distance measures: Chebyshev distance (ChD), Euclidean distance (EuD), squared Euclidean distance (SEuD), Mahalanobis distance (MahD), Manhattan distance (ManD). The choice of the method for initializing the weight coefficients was also different: average, random and with preliminary clustering by the k-means algorithm. Each experiment was run 30 times.
Algorithms were implemented in Java. For the computational experiments, we used the following test system: AMD Ryzen 5-1600 6C/12T 3200MHz CPU, 16 CB RAM. Each experiment took an average of 1 min of computer time.
3.1. Experiments in Online Mode
In this section, we compare the results of the experiment performed with SCL and SCL-GREEDY methods. Experiment with initial number of neurons K1 coinciding with a given number of clusters is marked as SCL; experiments with the initial number of neurons exceeding the specified number of clusters by two (K = 2 × K1) and three (K = 3 × K1) times are marked as SCL-GREEDY(2) and SCL-GREEDY(3).
Computational experiments showed that the use of the greedy agglomerative heuristic in SCL algorithm, in most cases, improves the accuracy of batch separation. Moreover, clustering accuracy decreases with increasing number of homogeneous batches in a mixed lot (Figure 1).
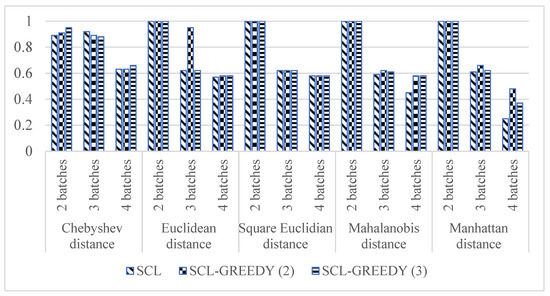
Figure 1.
Accuracy of device clustering for SCL, SCL-GREEDY(2) and SCL-GREEDY(3) algorithms.
With regard to the influence of the distance measure on the clustering accuracy, it can be noted that the Chebyshev distance has an advantage over the others except two-batch mixed lot. However, in the case of the Chebyshev distance, we were dealing with a large coefficient of variation and a span coefficient for 3 and 4 mixed lots.
Moreover, for various combinations of batches, the minimum (Min), maximum (Max), mean (Mean), standard deviation (σ), coefficient of variation (V) and the span factor (R) of the objective function are calculated (Table 1, Table 2, Table 3, Table 4 and Table 5, Figure 2).

Table 1.
Objective function value summarized after 30 attempts (Chebyshev distance).

Table 2.
Objective function value summarized after 30 attempts (Euclidean distance).

Table 3.
Objective function value summarized after 30 attempts (squared Euclidean distance).

Table 4.
Objective function value summarized after 30 attempts (Mahalanobis distance).

Table 5.
Objective function value summarized after 30 attempts (Manhattan distance).
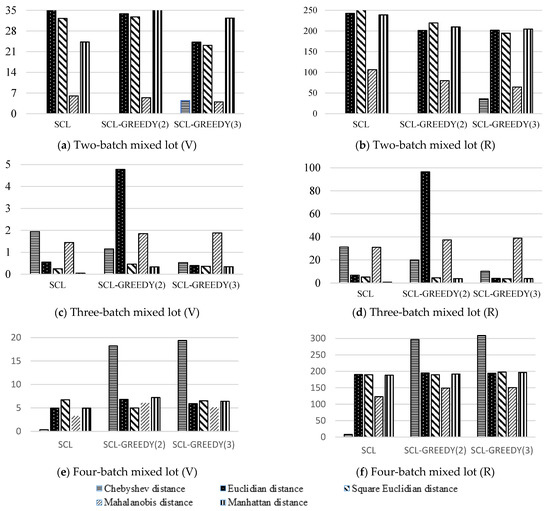
Figure 2.
(a) Coefficient of variation of the objective function value for two-batch mixed lot; (b) span factor of the objective function value for two-batch mixed lot; (c) coefficient of variation of the objective function value for three-batch mixed lot; (d) span factor of the objective function value for three-batch mixed lot; (e) coefficient of variation of the objective function value for four-batch mixed lot; (f) span factor of the objective function value for four-batch mixed lot.
Statistical significance of difference in the objective function values given by SCL algorithm and best of its greedy version were tested with Wilcoxon rank sum test. The best (minimal) mean values of objective function are given in bold if the precedence is statistically significant at p ≤ 0.05.
For Chebyshev distance, the best objective function value was achieved with SCL-GREEDY(3) algorithm for two and three batches in a mixed lot. For four batches, the difference between algorithms was insignificant. The coefficient of variation and span factor have minimal values with SCL algorithm for two-batch mixed lot and four-batch mixed lot. For three-batch mixed lot, the coefficient of variation and span factor show best result with SCL-GREEDY(3).
For Euclidean distance, the best objective function value was achieved with SCL-GREEDY(3) algorithm for two and four batches, and with SCL-GREEDY(2) for three batches. The coefficient of variation and span factor have minimal values with SCL-GREEDY(3) algorithm for almost all mixed lots. For the four-batch mixed lot, the coefficient of variation shows best result with SCL algorithm.
For squared Euclidean distance, for all mixed lots, SCL-GREEDY(3) gives the best value of objective function. Besides, SCL-GREEDY(3) algorithm gives minimal values of the coefficient of variation and span factor for the two-batch mixed lot and minimal value of the span factor for the three-batch mixed lot. SCL-GREEDY(2) algorithm gives minimal values of the coefficient of variation and span factor for the four-batch mixed lot. SCL algorithm for the three-batch mixed lot gives minimal value of the coefficient of variation.
For Mahalanobis distance, the difference between objective function values was insignificant for two-batch mixed lot. For three-batch and four-batch mixed lots, the minimal objective function value was achieved with SCL-GREEDY(3) algorithm. The coefficient of variation and span factor have minimal values with SCL-GREEDY(3) for the two-batch mixed lot. For the three-batch and four-batch mixed lots, the coefficient of variation and span factor show best result with SCL algorithm.
For Manhattan distance, the precedence of SCL-GREEDY(3) algorithm in objective function value was observed for all mixed lots. The coefficient of variation and span factor have minimal values with SCL algorithm for almost all mixed lots. For the two-batch mixed lot, the span factor shows best result with SCL-GREEDY(3) algorithm.
From Figure 2, it can be seen that the coefficient of variation is minimum with Chebyshev distance and Mahalanobis distance for mixed two-batch lot. For mixed three-batch lot, the coefficient of variation is minimum with square Euclidean distance and Manhattan distance. The worst (maximum) value it shows with Chebyshev distance for four-batch lot; other distances are similar to each other in this case.
The span factor shows the best result with Chebyshev distance and Mahalanobis distance for mixed two-batch lot. For mixed three-batch lot and four-batch lot, the span factor is the best with square Euclidean distance and Manhattan distance.
3.2. Experiments in Batch Mode
In this section, we compare the results of the experiment performed with modifications of BVQ and SOM algorithms. Experiment with initial number of neurons K1 coinciding with a given number of clusters is marked as BVQ and SOM; experiments with the initial number of neurons exceeding the specified number of clusters by two (K = 2 × K1) and three (K = 3 × K1) times are marked as BVQ-GREEDY(2), BVQ-GREEDY(3), SOM-GREEDY(2) and SOM-GREEDY(3). We used different methods for initializing the weight coefficients: by average, by random and with preliminary clustering by the k-means algorithm.
Experiments showed that, like in online mode, clustering accuracy decreases with increasing number of homogeneous batches in a mixed lot (Table 6, Table 7 and Table 8). Moreover, it can be seen that the use of the greedy agglomerative heuristic in batch mode improves the accuracy of batch separation for BVQ algorithm but degrades for SOM algorithm.

Table 6.
Accuracy of device clustering for BVQ, SOM, BVQ-GREEDY(2), BVQ-GREEDY(3), SOM-GREEDY(2) and SOM-GREEDY(3) algorithms (two-batch mixed lot).

Table 7.
Accuracy of device clustering for BVQ, SOM, BVQ-GREEDY(2), BVQ-GREEDY(3), SOM-GREEDY(2) and SOM-GREEDY(3) algorithms (three-batch mixed lot).

Table 8.
Accuracy of device clustering for BVQ, SOM, BVQ-GREEDY(2), BVQ-GREEDY(3), SOM-GREEDY(2) and SOM-GREEDY(3) algorithms (four-batch mixed lot).
From Table 6, it can be seen that, for two-batch mixed lot, all presented algorithms exceed k-means in accuracy. However, BVQ, SOM-GREEDY(2), SOM-GREEDY(3) algorithms showed worse results for random initialization with Mahalanobis distance.
From Table 7, it can be seen that, for three-batch mixed lot, all presented algorithms were approximately equal to k-means algorithm in accuracy except Chebyshev distance. For BVQ algorithm, its greedy version was more accurate, but, for SOM algorithm, its greedy version was better only for Chebyshev distance.
From Table 8, it can be seen that, for four-batch mixed lot, all presented algorithms were approximately equal to k-means algorithm in accuracy except Chebyshev distance. For BVQ algorithm, its greedy version was more accurate. For SOM algorithm, on the contrary, result was generally better than its greedy version.
Characteristics of objective function value for batch-type algorithms with various combinations of distance measure and initialization method are given in Table A1, Table A2, Table A3, Table A4, Table A5, Table A6, Table A7, Table A8, Table A9, Table A10, Table A11, Table A12, Table A13, Table A14 and Table A15 of Appendix A. Results were tested with Wilcoxon rank sum test. Statistically significant superiority in objective function value between BVQ algorithm and its greedy version, SOM algorithm and its greedy version at p ≤ 0.05 highlighted in bold.
It turned out that, in the vast majority of cases, minimal objective function value was demonstrated by SOM algorithm without influence of initialization method or distance measure. Minimal value of coefficient of variation and span factor were achieved with Euclidean, squared Euclidean and Manhattan distance and initialization by average.
From Figure 3, Figure 4 and Figure 5, it can be seen that initialization by k-means increases the coefficient of variation value for any type of mixed lot composition.
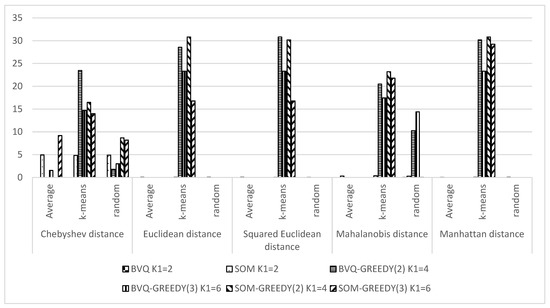
Figure 3.
Coefficient of variation of the objective function value for the two-batch mixed lot.
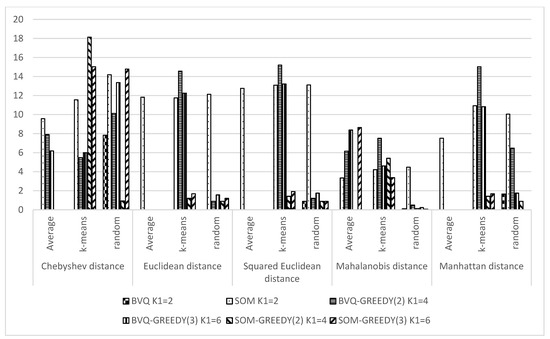
Figure 4.
Coefficient of variation of the objective function value for the three-batch mixed lot.
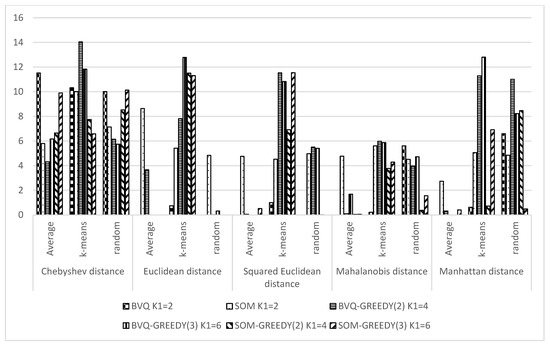
Figure 5.
Coefficient of variation of the objective function value for the four-batch mixed lot.
4. Discussion
It can be summarized that the use of the greedy agglomerative heuristic procedure with the simple competitive learning algorithm in online mode improves the objective function value in the majority of the cases. In the other cases, the difference between our new algorithms and the known algorithms is insignificant (see two exceptions in our computational experiments: the four batches with Chebyshev distance and two batches with Mahalanobis distance).
It can be noted that, in the vast majority of cases, the use of a triple number of neurons in the greedy agglomerative heuristic procedure provided a smaller value of the objective function than double.
Regarding the stability of the results (coefficient of variation and span factor values), none of the algorithms have demonstrated advantages over the others.
The minimal values of the objective function were achieved with the squared Euclidean distance measure for two batches and with the Euclidean distance measure for three batches and with the Chebyshev distance measure for four batches.
In almost all the cases, the clustering accuracy of the SCL-GREEDY version was the same as or better than the SCL algorithm. The only exception was the three-batch mixed lot with Chebyshev distance.
Concerning batch mode algorithms, the situation was different. The greedy version of the BVQ algorithm demonstrated a better objective function value than the BVQ in 42% of the cases and a worse objective function value than the BVQ in 37% of the cases. In 23% of the cases, the difference was statistically insignificant. The SOM algorithm was better than its greedy version in the vast majority of cases.
The accuracy of the clustering in batch mode is similar to the situation with the objective function. Applying a greedy heuristic to the BVQ algorithm improves the clustering accuracy. However, the greedy version of the SOM algorithm exhibits less clustering accuracy.
5. Conclusions
In our work, we proposed algorithms for products clustering based on a Kohonen network and self-organizing Kohonen maps using the greedy agglomerative heuristic procedure in online and batch modes. We performed experiments with different distance measures (Euclidean, squared Euclidean, Manhattan, Chebyshev, Mahalanobis), different ways of neuron weights initialization (average, random, k-means) and different numbers of extra neurons in the greedy heuristic procedure.
The studies have shown that the used distance measure, in most cases, does not significantly affect the clustering accuracy. The way of neuron weights initialization plays a role for the stability of the objective function: the coefficient of variation for any type of mixed lot composition was higher (worse) with k-means initialization.
In batch mode, in the vast majority of cases, the minimal objective function value was demonstrated by the SOM algorithm without the influence of the initialization method or distance measure.
The computational experiments showed that the use of the greedy agglomerative heuristic in online mode, in most cases, improves the accuracy of homogeneous batch separation. In batch mode, the greedy heuristic improves the accuracy for the vector quantization algorithm and, on the contrary, reduces the accuracy for self-organized maps.
The study of the batch mode and online mode of algorithms for clustering products using the greedy agglomerative heuristic procedure on a large number of homogeneous batches is an interesting area for further research.
Author Contributions
Conceptualization, G.S., L.K. and E.T.; methodology, G.S. and L.K.; software, G.S. and L.V.; validation, G.S., N.R. and E.T.; formal analysis, L.K.; investigation, L.V.; resources, L.V. and L.K.; data curation, L.K.; writing—original draft preparation, G.S. and E.T.; writing—review and editing, L.K., G.S., N.R. and E.T.; visualization, G.S.; supervision, L.K.; project administration, L.K.; funding acquisition, L.K. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the Ministry of Science and Higher Education of the Russian Federation, project no. FEFE-2020-0013.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Objective function value summarized after 30 attempts (Chebyshev distance, initialization by average).
Table A1.
Objective function value summarized after 30 attempts (Chebyshev distance, initialization by average).
| Parameter | BVQ | SOM | BVQ- GREEDY(2) | BVQ- GREEDY(3) | SOM- GREEDY(2) | SOM- GREEDY(3) |
|---|---|---|---|---|---|---|
| Two-batch mixed lot | ||||||
| K1 = 2 | K1 = 4 | K1 = 6 | K1 = 4 | K1 = 6 | ||
| Min | 207.903 | 194.919 | 204.323 | 204.113 | 205.657 | 206.582 |
| Max | 207.903 | 217.269 | 204.323 | 216.201 | 205.657 | 249.768 |
| Mean | 207.903 | 203.274 | 204.323 | 205.577 | 205.657 | 222.260 |
| σ | 0.000 | 10.011 | 0.000 | 3.144 | 0.000 | 20.395 |
| V | 0.000 | 4.925 | 0.000 | 1.529 | 0.000 | 9.176 |
| R | 0.000 | 22.351 | 0.000 | 12.088 | 0.000 | 43.187 |
| Three-batch mixed lot | ||||||
| K1 = 3 | K1 = 6 | K1 = 9 | K1 = 6 | K1 = 9 | ||
| Min | 342.987 | 252.824 | 294.450 | 303.473 | 258.930 | 254.905 |
| Max | 342.987 | 353.693 | 342.987 | 345.475 | 258.930 | 254.905 |
| Mean | 342.987 | 334.532 | 317.101 | 331.474 | 258.930 | 254.905 |
| σ | 0.000 | 32.018 | 25.064 | 20.495 | 0.000 | 0.000 |
| V | 0.000 | 9.571 | 7.904 | 6.183 | 0.000 | 0.000 |
| R | 0.000 | 100.869 | 48.537 | 42.001 | 0.000 | 0.000 |
| Four-batch mixed lot | ||||||
| K1 = 4 | K1 = 8 | K1 = 12 | K1 = 8 | K1 = 12 | ||
| Min | 553.715 | 493.863 | 493.936 | 493.368 | 553.548 | 559.033 |
| Max | 701.325 | 578.828 | 563.388 | 561.249 | 705.364 | 701.241 |
| Mean | 613.034 | 523.175 | 548.875 | 528.842 | 576.858 | 616.482 |
| σ | 70.632 | 30.295 | 23.659 | 32.589 | 38.347 | 61.034 |
| V | 11.522 | 5.791 | 4.311 | 6.162 | 6.647 | 9.900 |
| R | 147.610 | 84.965 | 69.452 | 67.881 | 151.816 | 142.208 |

Table A2.
Objective function value summarized after 30 attempts (Chebyshev distance, initialization by k-means).
Table A2.
Objective function value summarized after 30 attempts (Chebyshev distance, initialization by k-means).
| Parameter | BVQ | SOM | BVQ- GREEDY(2) | BVQ- GREEDY(3) | SOM- GREEDY(2) | SOM- GREEDY(3) |
|---|---|---|---|---|---|---|
| Two-batch mixed lot | ||||||
| K1 = 2 | K1 = 4 | K1 = 6 | K1 = 4 | K1 = 6 | ||
| Min | 207.903 | 195.429 | 204.323 | 204.113 | 205.657 | 216.201 |
| Max | 207.903 | 217.037 | 335.401 | 337.849 | 335.401 | 337.849 |
| Mean | 207.903 | 204.757 | 230.805 | 320.018 | 270.697 | 307.738 |
| σ | 0.000 | 9.869 | 54.136 | 47.057 | 44.573 | 43.024 |
| V | 0.000 | 4.820 | 23.455 | 14.705 | 16.466 | 13.981 |
| R | 0.000 | 21.608 | 131.079 | 133.737 | 129.744 | 121.648 |
| Three-batch mixed lot | ||||||
| K1 = 3 | K1 = 6 | K1 = 9 | K1 = 6 | K1 = 9 | ||
| Min | 258.930 | 252.467 | 294.450 | 303.473 | 258.930 | 254.905 |
| Max | 258.930 | 347.462 | 366.993 | 365.509 | 366.993 | 366.993 |
| Mean | 258.930 | 328.184 | 349.165 | 351.103 | 302.155 | 335.717 |
| σ | 0.000 | 37.900 | 19.111 | 21.056 | 54.798 | 50.449 |
| V | 0.000 | 11.548 | 5.473 | 5.997 | 18.136 | 15.027 |
| R | 0.000 | 94.995 | 72.543 | 62.036 | 108.063 | 112.088 |
| Four-batch mixed lot | ||||||
| K1 = 4 | K1 = 8 | K1 = 12 | K1 = 8 | K1 = 12 | ||
| Min | 554.632 | 495.630 | 493.396 | 566.491 | 555.149 | 692.980 |
| Max | 703.198 | 664.941 | 719.547 | 719.547 | 732.274 | 878.714 |
| Mean | 648.439 | 557.872 | 589.796 | 625.305 | 690.896 | 721.950 |
| σ | 66.907 | 55.821 | 82.804 | 73.941 | 53.478 | 47.524 |
| V | 10.318 | 10.006 | 14.039 | 11.825 | 7.740 | 6.583 |
| R | 148.566 | 169.311 | 226.151 | 153.056 | 177.125 | 185.735 |

Table A3.
Objective function value summarized after 30 attempts (Chebyshev distance, initialization by random).
Table A3.
Objective function value summarized after 30 attempts (Chebyshev distance, initialization by random).
| Para- meter | BVQ | SOM | BVQ- GREEDY(2) | BVQ- GREEDY(3) | SOM- GREEDY(2) | SOM- GREEDY(3) |
|---|---|---|---|---|---|---|
| Two-batch mixed lot | ||||||
| K1 = 2 | K1 = 4 | K1 = 6 | K1 = 4 | K1 = 6 | ||
| Min | 207.903 | 195.096 | 204.323 | 204.113 | 205.657 | 206.582 |
| Max | 207.903 | 218.493 | 214.846 | 216.201 | 251.462 | 249.768 |
| Mean | 207.903 | 206.037 | 205.904 | 209.754 | 225.213 | 230.583 |
| σ | 0.000 | 10.063 | 3.660 | 6.242 | 19.539 | 18.841 |
| V | 0.000 | 4.884 | 1.778 | 2.976 | 8.676 | 8.171 |
| R | 0.000 | 23.396 | 10.523 | 12.088 | 45.805 | 43.187 |
| Three-batch mixed lot | ||||||
| K1 = 3 | K1 = 6 | K1 = 9 | K1 = 6 | K1 = 9 | ||
| Min | 258.930 | 252.251 | 258.930 | 254.905 | 357.439 | 254.905 |
| Max | 366.993 | 347.509 | 366.993 | 364.023 | 366.993 | 364.023 |
| Mean | 357.453 | 315.496 | 348.951 | 336.351 | 365.296 | 333.542 |
| σ | 28.002 | 44.784 | 35.296 | 44.964 | 3.362 | 49.308 |
| V | 7.834 | 14.195 | 10.115 | 13.368 | 0.920 | 14.783 |
| R | 108.063 | 95.259 | 108.063 | 109.118 | 9.554 | 109.118 |
| Four-batch mixed lot | ||||||
| K1 = 4 | K1 = 8 | K1 = 12 | K1 = 8 | K1 = 12 | ||
| Min | 552.568 | 497.795 | 493.396 | 493.368 | 556.048 | 552.696 |
| Max | 698.601 | 620.549 | 561.092 | 561.078 | 705.538 | 702.573 |
| Mean | 601.527 | 533.155 | 531.922 | 513.349 | 583.717 | 614.007 |
| σ | 60.196 | 38.032 | 32.671 | 29.471 | 49.765 | 62.183 |
| V | 10.007 | 7.133 | 6.142 | 5.741 | 8.525 | 10.127 |
| R | 146.033 | 122.754 | 67.696 | 67.710 | 149.490 | 149.877 |

Table A4.
Objective function value summarized after 30 attempts (Euclidean distance, initialization by average).
Table A4.
Objective function value summarized after 30 attempts (Euclidean distance, initialization by average).
| Parameter | BVQ | SOM | BVQ- GREEDY(2) | BVQ- GREEDY(3) | SOM- GREEDY(2) | SOM- GREEDY(3) |
|---|---|---|---|---|---|---|
| Two-batch mixed lot | ||||||
| K1 = 2 | K1 = 4 | K1 = 6 | K1 = 4 | K1 = 6 | ||
| Min | 186.160 | 185.969 | 186.346 | 186.372 | 186.346 | 186.372 |
| Max | 186.160 | 186.207 | 186.346 | 186.372 | 186.346 | 186.372 |
| Mean | 186.160 | 186.087 | 186.346 | 186.372 | 186.346 | 186.372 |
| σ | 0.000 | 0.061 | 0.000 | 0.000 | 0.000 | 0.000 |
| V | 0.000 | 0.033 | 0.000 | 0.000 | 0.000 | 0.000 |
| R | 0.000 | 0.237 | 0.000 | 0.000 | 0.000 | 0.000 |
| Three-batch mixed lot | ||||||
| K1 = 3 | K1 = 6 | K1 = 9 | K1 = 6 | K1 = 9 | ||
| Min | 314.924 | 241.647 | 241.731 | 241.795 | 314.924 | 310.298 |
| Max | 314.924 | 315.304 | 241.731 | 241.795 | 314.924 | 310.298 |
| Mean | 314.924 | 258.499 | 241.731 | 241.795 | 314.924 | 310.298 |
| σ | 0.000 | 30.571 | 0.000 | 0.000 | 0.000 | 0.000 |
| V | 0.000 | 11.826 | 0.000 | 0.000 | 0.000 | 0.000 |
| R | 0.000 | 73.657 | 0.000 | 0.000 | 0.000 | 0.000 |
| Four-batch mixed lot | ||||||
| K1 = 4 | K1 = 8 | K1 = 12 | K1 = 8 | K1 = 12 | ||
| Min | 546.596 | 492.597 | 492.933 | 492.903 | 552.883 | 548.802 |
| Max | 546.596 | 655.370 | 549.751 | 492.903 | 552.883 | 548.804 |
| Mean | 546.596 | 521.356 | 541.720 | 492.903 | 552.883 | 548.803 |
| σ | 0.000 | 45.038 | 19.809 | 0.000 | 0.000 | 0.001 |
| V | 0.000 | 8.639 | 3.657 | 0.000 | 0.000 | 0.000 |
| R | 0.000 | 162.772 | 56.818 | 0.000 | 0.000 | 0.001 |

Table A5.
Objective function value summarized after 30 attempts (Euclidean distance, initialization by k-means).
Table A5.
Objective function value summarized after 30 attempts (Euclidean distance, initialization by k-means).
| Parameter | BVQ | SOM | BVQ- GREEDY(2) | BVQ- GREEDY(3) | SOM- GREEDY(2) | SOM- GREEDY(3) |
|---|---|---|---|---|---|---|
| Two-batch mixed lot | ||||||
| K1 = 2 | K1 = 4 | K1 = 6 | K1 = 4 | K1 = 6 | ||
| Min | 186.160 | 186.007 | 186.346 | 186.372 | 186.346 | 186.372 |
| Max | 186.160 | 186.235 | 335.401 | 337.849 | 335.401 | 337.849 |
| Mean | 186.160 | 186.105 | 216.157 | 297.455 | 236.031 | 317.652 |
| σ | 0.000 | 0.061 | 61.715 | 69.337 | 72.732 | 53.300 |
| V | 0.000 | 0.033 | 28.551 | 23.310 | 30.814 | 16.779 |
| R | 0.000 | 0.227 | 149.055 | 151.477 | 149.055 | 151.477 |
| Three-batch mixed lot | ||||||
| K1 = 3 | K1 = 6 | K1 = 9 | K1 = 6 | K1 = 9 | ||
| Min | 314.924 | 241.768 | 241.731 | 241.795 | 314.924 | 310.298 |
| Max | 314.924 | 312.783 | 325.737 | 325.737 | 325.737 | 323.263 |
| Mean | 314.924 | 258.406 | 264.133 | 300.787 | 316.366 | 318.737 |
| σ | 0.000 | 30.364 | 38.453 | 36.848 | 3.805 | 5.357 |
| V | 0.000 | 11.751 | 14.558 | 12.250 | 1.203 | 1.681 |
| R | 0.000 | 71.015 | 84.006 | 83.943 | 10.813 | 12.965 |
| Four-batch mixed lot | ||||||
| K1 = 4 | K1 = 8 | K1 = 12 | K1 = 8 | K1 = 12 | ||
| Min | 546.596 | 492.696 | 492.933 | 492.903 | 552.883 | 561.003 |
| Max | 559.778 | 554.321 | 711.945 | 704.490 | 711.945 | 711.945 |
| Mean | 548.117 | 523.082 | 565.934 | 613.940 | 599.916 | 647.609 |
| σ | 4.069 | 28.343 | 44.202 | 78.438 | 69.019 | 73.181 |
| V | 0.742 | 5.418 | 7.811 | 12.776 | 11.505 | 11.300 |
| R | 13.182 | 61.624 | 219.011 | 211.587 | 159.062 | 150.942 |

Table A6.
Objective function value summarized after 30 attempts (Euclidean distance, initialization by random).
Table A6.
Objective function value summarized after 30 attempts (Euclidean distance, initialization by random).
| Para- meter | BVQ | SOM | BVQ- GREEDY(2) | BVQ- GREEDY(3) | SOM- GREEDY(2) | SOM- GREEDY(3) |
|---|---|---|---|---|---|---|
| Two-batch mixed lot | ||||||
| K1 = 2 | K1 = 4 | K1 = 6 | K1 = 4 | K1 = 6 | ||
| Min | 186.160 | 185.954 | 186.346 | 186.372 | 186.346 | 186.372 |
| Max | 186.160 | 186.211 | 186.346 | 186.372 | 186.346 | 186.372 |
| Mean | 186.160 | 186.100 | 186.346 | 186.372 | 186.346 | 186.372 |
| σ | 0.000 | 0.062 | 0.000 | 0.000 | 0.000 | 0.000 |
| V | 0.000 | 0.033 | 0.000 | 0.000 | 0.000 | 0.000 |
| R | 0.000 | 0.258 | 0.000 | 0.000 | 0.000 | 0.000 |
| Three-batch mixed lot | ||||||
| K1 = 3 | K1 = 6 | K1 = 9 | K1 = 6 | K1 = 9 | ||
| Min | 314.924 | 241.634 | 314.924 | 310.298 | 314.924 | 310.298 |
| Max | 314.924 | 312.797 | 325.737 | 320.973 | 325.737 | 320.973 |
| Mean | 314.924 | 260.991 | 315.645 | 313.145 | 315.645 | 311.722 |
| σ | 0.000 | 31.661 | 2.792 | 4.886 | 2.792 | 3.756 |
| V | 0.000 | 12.131 | 0.885 | 1.560 | 0.885 | 1.205 |
| R | 0.000 | 71.163 | 10.813 | 10.675 | 10.813 | 10.675 |
| Four-batch mixed lot | ||||||
| K1 = 4 | K1 = 8 | K1 = 12 | K1 = 8 | K1 = 12 | ||
| Min | 703.485 | 492.661 | 711.930 | 699.061 | 711.945 | 707.793 |
| Max | 703.485 | 550.607 | 711.945 | 707.793 | 711.945 | 707.793 |
| Mean | 703.485 | 528.546 | 711.944 | 707.096 | 711.945 | 707.793 |
| σ | 0.000 | 25.546 | 0.004 | 2.242 | 0.000 | 0.000 |
| V | 0.000 | 4.833 | 0.001 | 0.317 | 0.000 | 0.000 |
| R | 0.000 | 57.946 | 0.015 | 8.732 | 0.000 | 0.000 |

Table A7.
Objective function value summarized after 30 attempts (squared Euclidean distance, initialization by average).
Table A7.
Objective function value summarized after 30 attempts (squared Euclidean distance, initialization by average).
| Parameter | BVQ | SOM | BVQ- GREEDY(2) | BVQ- GREEDY(3) | SOM- GREEDY(2) | SOM- GREEDY(3) |
|---|---|---|---|---|---|---|
| Two-batch mixed lot | ||||||
| K1 = 2 | K1 = 4 | K1 = 6 | K1 = 4 | K1 = 6 | ||
| Min | 186.160 | 185.962 | 186.346 | 186.372 | 186.346 | 186.372 |
| Max | 186.160 | 186.233 | 186.346 | 186.372 | 186.346 | 186.372 |
| Mean | 186.160 | 186.092 | 186.346 | 186.372 | 186.346 | 186.372 |
| σ | 0.000 | 0.070 | 0.000 | 0.000 | 0.000 | 0.000 |
| V | 0.000 | 0.038 | 0.000 | 0.000 | 0.000 | 0.000 |
| R | 0.000 | 0.271 | 0.000 | 0.000 | 0.000 | 0.000 |
| Three-batch mixed lot | ||||||
| K1 = 3 | K1 = 6 | K1 = 9 | K1 = 6 | K1 = 9 | ||
| Min | 314.924 | 241.673 | 241.731 | 241.795 | 314.924 | 310.298 |
| Max | 314.924 | 312.911 | 241.731 | 241.795 | 314.924 | 310.298 |
| Mean | 314.924 | 265.496 | 241.731 | 241.795 | 314.924 | 310.298 |
| σ | 0.000 | 33.876 | 0.000 | 0.000 | 0.000 | 0.000 |
| V | 0.000 | 12.759 | 0.000 | 0.000 | 0.000 | 0.000 |
| R | 0.000 | 71.238 | 0.000 | 0.000 | 0.000 | 0.000 |
| Four-batch mixed lot | ||||||
| K1 = 4 | K1 = 8 | K1 = 12 | K1 = 8 | K1 = 12 | ||
| Min | 546.596 | 492.541 | 549.130 | 492.903 | 552.883 | 548.802 |
| Max | 546.596 | 544.710 | 549.751 | 492.903 | 552.883 | 559.135 |
| Mean | 546.596 | 509.981 | 549.586 | 492.903 | 552.883 | 550.164 |
| σ | 0.000 | 24.249 | 0.284 | 0.000 | 0.000 | 2.840 |
| V | 0.000 | 4.755 | 0.052 | 0.000 | 0.000 | 0.516 |
| R | 0.000 | 52.169 | 0.621 | 0.000 | 0.000 | 10.333 |

Table A8.
Objective function value summarized after 30 attempts (squared Euclidean distance, initialization by k-means).
Table A8.
Objective function value summarized after 30 attempts (squared Euclidean distance, initialization by k-means).
| Parameter | BVQ | SOM | BVQ- GREEDY(2) | BVQ- GREEDY(3) | SOM- GREEDY(2) | SOM- GREEDY(3) |
|---|---|---|---|---|---|---|
| Two-batch mixed lot | ||||||
| K1 = 2 | K1 = 4 | K1 = 6 | K1 = 4 | K1 = 6 | ||
| Min | 186.160 | 186.010 | 186.346 | 186.372 | 186.346 | 186.372 |
| Max | 186.160 | 186.200 | 335.401 | 337.849 | 335.401 | 337.849 |
| Mean | 186.160 | 186.113 | 236.031 | 297.455 | 226.094 | 317.652 |
| σ | 0.000 | 0.050 | 72.732 | 69.337 | 68.228 | 53.300 |
| V | 0.000 | 0.027 | 30.814 | 23.310 | 30.177 | 16.779 |
| R | 0.000 | 0.189 | 149.055 | 151.477 | 149.055 | 151.477 |
| Three-batch mixed lot | ||||||
| K1 = 3 | K1 = 6 | K1 = 9 | K1 = 6 | K1 = 9 | ||
| Min | 314.924 | 241.634 | 241.731 | 241.795 | 314.924 | 310.298 |
| Max | 314.924 | 315.223 | 325.737 | 323.263 | 325.737 | 325.737 |
| Mean | 314.924 | 275.027 | 269.733 | 295.038 | 317.087 | 317.326 |
| σ | 0.000 | 35.995 | 40.991 | 38.981 | 4.477 | 6.079 |
| V | 0.000 | 13.088 | 15.197 | 13.212 | 1.412 | 1.916 |
| R | 0.000 | 73.589 | 84.006 | 81.468 | 10.813 | 15.439 |
| Four-batch mixed lot | ||||||
| K1 = 4 | K1 = 8 | K1 = 12 | K1 = 8 | K1 = 12 | ||
| Min | 546.596 | 492.561 | 492.933 | 560.904 | 552.883 | 560.904 |
| Max | 559.778 | 555.250 | 711.945 | 711.945 | 711.945 | 711.945 |
| Mean | 549.233 | 530.534 | 585.963 | 658.380 | 570.195 | 636.706 |
| σ | 5.458 | 24.015 | 67.564 | 71.294 | 39.403 | 73.474 |
| V | 0.994 | 4.527 | 11.530 | 10.829 | 6.911 | 11.540 |
| R | 13.182 | 62.688 | 219.011 | 151.041 | 159.062 | 151.041 |

Table A9.
Objective function value summarized after 30 attempts (squared Euclidean distance, initialization by random).
Table A9.
Objective function value summarized after 30 attempts (squared Euclidean distance, initialization by random).
| Para- meter | BVQ | SOM | BVQ- GREEDY(2) | BVQ- GREEDY(3) | SOM- GREEDY(2) | SOM- GREEDY(3) |
|---|---|---|---|---|---|---|
| Two-batch mixed lot | ||||||
| K1 = 2 | K1 = 4 | K1 = 6 | K1 = 4 | K1 = 6 | ||
| Min | 186.160 | 185.969 | 186.346 | 186.372 | 186.346 | 186.372 |
| Max | 186.160 | 186.183 | 186.346 | 186.372 | 186.346 | 186.372 |
| Mean | 186.160 | 186.088 | 186.346 | 186.372 | 186.346 | 186.372 |
| σ | 0.000 | 0.048 | 0.000 | 0.000 | 0.000 | 0.000 |
| V | 0.000 | 0.026 | 0.000 | 0.000 | 0.000 | 0.000 |
| R | 0.000 | 0.214 | 0.000 | 0.000 | 0.000 | 0.000 |
| Three-batch mixed lot | ||||||
| K1 = 3 | K1 = 6 | K1 = 9 | K1 = 6 | K1 = 9 | ||
| Min | 314.924 | 241.651 | 314.924 | 310.298 | 314.924 | 310.298 |
| Max | 325.737 | 315.550 | 325.737 | 320.973 | 325.737 | 320.973 |
| Mean | 315.645 | 272.613 | 316.366 | 315.280 | 315.645 | 311.010 |
| σ | 2.792 | 35.746 | 3.805 | 5.513 | 2.792 | 2.756 |
| V | 0.885 | 13.112 | 1.203 | 1.748 | 0.885 | 0.886 |
| R | 10.813 | 73.899 | 10.813 | 10.675 | 10.813 | 10.675 |
| Four-batch mixed lot | ||||||
| K1 = 4 | K1 = 8 | K1 = 12 | K1 = 8 | K1 = 12 | ||
| Min | 703.485 | 492.663 | 562.352 | 561.616 | 711.909 | 707.793 |
| Max | 703.485 | 550.840 | 711.945 | 707.793 | 711.945 | 707.793 |
| Mean | 703.485 | 523.502 | 701.972 | 697.952 | 711.942 | 707.793 |
| σ | 0.000 | 26.008 | 38.625 | 37.718 | 0.009 | 0.000 |
| V | 0.000 | 4.968 | 5.502 | 5.404 | 0.001 | 0.000 |
| R | 0.000 | 58.177 | 149.592 | 146.177 | 0.035 | 0.000 |

Table A10.
Objective function value summarized after 30 attempts (Mahalanobis distance, initialization by average).
Table A10.
Objective function value summarized after 30 attempts (Mahalanobis distance, initialization by average).
| Parameter | BVQ | SOM | BVQ- GREEDY(2) | BVQ- GREEDY(3) | SOM- GREEDY(2) | SOM- GREEDY(3) |
|---|---|---|---|---|---|---|
| Two-batch mixed lot | ||||||
| K1 = 2 | K1 = 4 | K1 = 6 | K1 = 4 | K1 = 6 | ||
| Min | 201.387 | 194.572 | 205.657 | 206.582 | 205.657 | 206.582 |
| Max | 201.387 | 197.145 | 205.657 | 206.582 | 205.657 | 206.582 |
| Mean | 201.387 | 195.929 | 205.657 | 206.582 | 205.657 | 206.582 |
| σ | 0.000 | 0.568 | 0.000 | 0.000 | 0.000 | 0.000 |
| V | 0.000 | 0.290 | 0.000 | 0.000 | 0.000 | 0.000 |
| R | 0.000 | 2.573 | 0.000 | 0.000 | 0.000 | 0.000 |
| Three-batch mixed lot | ||||||
| K1 = 3 | K1 = 6 | K1 = 9 | K1 = 6 | K1 = 9 | ||
| Min | 326.463 | 312.110 | 287.148 | 288.169 | 326.463 | 288.169 |
| Max | 326.463 | 361.353 | 348.315 | 350.407 | 326.463 | 350.407 |
| Mean | 326.463 | 342.690 | 295.317 | 332.825 | 326.463 | 325.676 |
| σ | 0.000 | 11.448 | 18.173 | 27.895 | 0.000 | 28.141 |
| V | 0.000 | 3.341 | 6.154 | 8.381 | 0.000 | 8.641 |
| R | 0.000 | 49.242 | 61.168 | 62.238 | 0.000 | 62.238 |
| Four-batch mixed lot | ||||||
| K1 = 4 | K1 = 8 | K1 = 12 | K1 = 8 | K1 = 12 | ||
| Min | 758.068 | 572.730 | 728.875 | 696.210 | 757.097 | 756.752 |
| Max | 758.068 | 663.835 | 730.771 | 722.998 | 757.734 | 757.838 |
| Mean | 758.068 | 619.269 | 730.508 | 709.527 | 757.375 | 757.390 |
| σ | 0.000 | 29.509 | 0.663 | 11.950 | 0.269 | 0.344 |
| V | 0.000 | 4.765 | 0.091 | 1.684 | 0.036 | 0.045 |
| R | 0.000 | 91.104 | 1.896 | 26.788 | 0.638 | 1.086 |

Table A11.
Objective function value summarized after 30 attempts (Mahalanobis distance, initialization by k-means).
Table A11.
Objective function value summarized after 30 attempts (Mahalanobis distance, initialization by k-means).
| Parameter | BVQ | SOM | BVQ- GREEDY(2) | BVQ- GREEDY(3) | SOM- GREEDY(2) | SOM- GREEDY(3) |
|---|---|---|---|---|---|---|
| Two-batch mixed lot | ||||||
| K1 = 2 | K1 = 4 | K1 = 6 | K1 = 4 | K1 = 6 | ||
| Min | 201.387 | 194.573 | 205.657 | 206.582 | 205.657 | 206.582 |
| Max | 201.387 | 197.148 | 335.401 | 337.849 | 335.401 | 337.849 |
| Mean | 201.387 | 195.931 | 222.956 | 311.596 | 231.606 | 294.093 |
| σ | 0.000 | 0.680 | 45.653 | 54.350 | 53.719 | 64.052 |
| V | 0.000 | 0.347 | 20.476 | 17.442 | 23.194 | 21.779 |
| R | 0.000 | 2.575 | 129.744 | 131.268 | 129.744 | 131.268 |
| Three-batch mixed lot | ||||||
| K1 = 3 | K1 = 6 | K1 = 9 | K1 = 6 | K1 = 9 | ||
| Min | 348.315 | 291.064 | 287.148 | 317.121 | 326.463 | 335.463 |
| Max | 348.315 | 361.323 | 366.993 | 366.993 | 366.993 | 365.509 |
| Mean | 348.315 | 340.856 | 347.631 | 353.627 | 337.082 | 358.806 |
| σ | 0.000 | 14.370 | 26.144 | 16.298 | 18.241 | 12.100 |
| V | 0.000 | 4.216 | 7.521 | 4.609 | 5.411 | 3.372 |
| R | 0.000 | 70.258 | 79.846 | 49.872 | 40.531 | 30.046 |
| Four-batch mixed lot | ||||||
| K1 = 4 | K1 = 8 | K1 = 12 | K1 = 8 | K1 = 12 | ||
| Min | 758.068 | 554.372 | 725.168 | 701.832 | 757.148 | 763.684 |
| Max | 764.357 | 677.513 | 852.818 | 892.642 | 845.107 | 836.489 |
| Mean | 758.487 | 613.179 | 765.066 | 741.820 | 773.655 | 800.642 |
| σ | 1.624 | 34.378 | 45.733 | 43.564 | 29.147 | 34.313 |
| V | 0.214 | 5.607 | 5.978 | 5.873 | 3.768 | 4.286 |
| R | 6.289 | 123.141 | 127.650 | 190.810 | 87.959 | 72.805 |

Table A12.
Objective function value summarized after 30 attempts (Mahalanobis distance, initialization by random).
Table A12.
Objective function value summarized after 30 attempts (Mahalanobis distance, initialization by random).
| Para- meter | BVQ | SOM | BVQ- GREEDY(2) | BVQ- GREEDY(3) | SOM- GREEDY(2) | SOM- GREEDY(3) |
|---|---|---|---|---|---|---|
| Two-batch mixed lot | ||||||
| K1 = 2 | K1 = 4 | K1 = 6 | K1 = 4 | K1 = 6 | ||
| Min | 331.089 | 194.303 | 205.657 | 206.582 | 335.258 | 337.849 |
| Max | 331.107 | 196.693 | 335.401 | 337.849 | 335.401 | 337.849 |
| Mean | 331.106 | 195.717 | 326.716 | 320.358 | 335.387 | 337.849 |
| σ | 0.005 | 0.503 | 33.490 | 46.116 | 0.038 | 0.000 |
| V | 0.001 | 0.257 | 10.251 | 14.395 | 0.011 | 0.000 |
| R | 0.018 | 2.390 | 129.744 | 131.268 | 0.143 | 0.000 |
| Three-batch mixed lot | ||||||
| K1 = 3 | K1 = 6 | K1 = 9 | K1 = 6 | K1 = 9 | ||
| Min | 443.219 | 305.398 | 437.281 | 437.742 | 440.640 | 438.611 |
| Max | 444.607 | 361.336 | 444.378 | 439.538 | 444.607 | 439.598 |
| Mean | 444.133 | 338.766 | 442.954 | 438.906 | 444.084 | 439.413 |
| σ | 0.479 | 15.177 | 2.163 | 0.540 | 1.011 | 0.275 |
| V | 0.108 | 4.480 | 0.488 | 0.123 | 0.228 | 0.063 |
| R | 1.388 | 55.937 | 7.097 | 1.795 | 3.967 | 0.987 |
| Four-batch mixed lot | ||||||
| K1 = 4 | K1 = 8 | K1 = 12 | K1 = 8 | K1 = 12 | ||
| Min | 764.357 | 564.890 | 764.433 | 771.053 | 839.280 | 838.055 |
| Max | 856.541 | 673.446 | 836.222 | 866.897 | 851.622 | 874.529 |
| Mean | 818.674 | 614.438 | 787.136 | 790.511 | 845.713 | 854.250 |
| σ | 45.914 | 27.721 | 31.284 | 37.296 | 3.154 | 13.329 |
| V | 5.608 | 4.512 | 3.974 | 4.718 | 0.373 | 1.560 |
| R | 92.185 | 108.556 | 71.789 | 95.844 | 12.342 | 36.475 |

Table A13.
Objective function value summarized after 30 attempts (Manhattan distance, initialization by average).
Table A13.
Objective function value summarized after 30 attempts (Manhattan distance, initialization by average).
| Parameter | BVQ | SOM | BVQ- GREEDY(2) | BVQ- GREEDY(3) | SOM- GREEDY(2) | SOM- GREEDY(3) |
|---|---|---|---|---|---|---|
| Two-batch mixed lot | ||||||
| K1 = 2 | K1 = 4 | K1 = 6 | K1 = 4 | K1 = 6 | ||
| Min | 186.160 | 185.971 | 186.346 | 186.372 | 186.346 | 186.372 |
| Max | 186.160 | 186.184 | 186.346 | 186.372 | 186.346 | 186.372 |
| Mean | 186.160 | 186.068 | 186.346 | 186.372 | 186.346 | 186.372 |
| σ | 0.000 | 0.053 | 0.000 | 0.000 | 0.000 | 0.000 |
| V | 0.000 | 0.028 | 0.000 | 0.000 | 0.000 | 0.000 |
| R | 0.000 | 0.214 | 0.000 | 0.000 | 0.000 | 0.000 |
| Three-batch mixed lot | ||||||
| K1 = 3 | K1 = 6 | K1 = 9 | K1 = 6 | K1 = 9 | ||
| Min | 314.924 | 241.918 | 241.887 | 241.991 | 314.924 | 310.298 |
| Max | 314.924 | 315.391 | 241.887 | 241.991 | 314.924 | 310.298 |
| Mean | 314.924 | 247.062 | 241.887 | 241.991 | 314.924 | 310.298 |
| σ | 0.000 | 18.565 | 0.000 | 0.000 | 0.000 | 0.000 |
| V | 0.000 | 7.514 | 0.000 | 0.000 | 0.000 | 0.000 |
| R | 0.000 | 73.473 | 0.000 | 0.000 | 0.000 | 0.000 |
| Four-batch mixed lot | ||||||
| K1 = 4 | K1 = 8 | K1 = 12 | K1 = 8 | K1 = 12 | ||
| Min | 690.643 | 493.142 | 551.927 | 493.236 | 703.810 | 692.768 |
| Max | 690.643 | 546.207 | 555.852 | 493.236 | 703.810 | 700.558 |
| Mean | 690.643 | 497.063 | 554.659 | 493.236 | 703.810 | 697.752 |
| σ | 0.000 | 13.597 | 1.765 | 0.000 | 0.000 | 2.854 |
| V | 0.000 | 2.735 | 0.318 | 0.000 | 0.000 | 0.409 |
| R | 0.000 | 53.065 | 3.925 | 0.000 | 0.000 | 7.790 |

Table A14.
Objective function value summarized after 30 attempts (Manhattan distance, initialization by k-means).
Table A14.
Objective function value summarized after 30 attempts (Manhattan distance, initialization by k-means).
| Parameter | BVQ | SOM | BVQ- GREEDY(2) | BVQ- GREEDY(3) | SOM- GREEDY(2) | SOM- GREEDY(3) |
|---|---|---|---|---|---|---|
| Two-batch mixed lot | ||||||
| K1 = 2 | K1 = 4 | K1 = 6 | K1 = 4 | K1 = 6 | ||
| Min | 186.160 | 185.934 | 186.346 | 186.372 | 186.346 | 186.372 |
| Max | 186.160 | 186.214 | 335.401 | 337.849 | 335.401 | 337.849 |
| Mean | 186.160 | 186.071 | 226.094 | 297.455 | 236.031 | 266.997 |
| σ | 0.000 | 0.064 | 68.228 | 69.337 | 72.732 | 78.067 |
| V | 0.000 | 0.035 | 30.177 | 23.310 | 30.814 | 29.239 |
| R | 0.000 | 0.281 | 149.055 | 151.477 | 149.055 | 151.477 |
| Three-batch mixed lot | ||||||
| K1 = 3 | K1 = 6 | K1 = 9 | K1 = 6 | K1 = 9 | ||
| Min | 314.924 | 241.851 | 241.887 | 241.991 | 314.924 | 310.298 |
| Max | 314.924 | 315.759 | 325.737 | 325.737 | 325.737 | 323.263 |
| Mean | 314.924 | 254.400 | 269.547 | 305.952 | 317.087 | 317.568 |
| σ | 0.000 | 27.821 | 40.504 | 33.132 | 4.477 | 5.352 |
| V | 0.000 | 10.936 | 15.027 | 10.829 | 1.412 | 1.685 |
| R | 0.000 | 73.908 | 83.850 | 83.746 | 10.813 | 12.965 |
| Four-batch mixed lot | ||||||
| K1 = 4 | K1 = 8 | K1 = 12 | K1 = 8 | K1 = 12 | ||
| Min | 690.643 | 493.044 | 551.927 | 493.236 | 695.985 | 696.331 |
| Max | 700.891 | 555.231 | 706.183 | 705.449 | 711.926 | 892.642 |
| Mean | 692.693 | 508.407 | 645.549 | 633.408 | 705.483 | 714.682 |
| σ | 4.243 | 25.699 | 72.850 | 81.067 | 5.039 | 49.382 |
| V | 0.613 | 5.055 | 11.285 | 12.799 | 0.714 | 6.910 |
| R | 10.247 | 62.187 | 154.257 | 212.213 | 15.941 | 196.311 |

Table A15.
Objective function value summarized after 30 attempts (Manhattan distance, initialization by random).
Table A15.
Objective function value summarized after 30 attempts (Manhattan distance, initialization by random).
| Para- meter | BVQ | SOM | BVQ- GREEDY(2) | BVQ- GREEDY(3) | SOM- GREEDY(2) | SOM- GREEDY(3) |
|---|---|---|---|---|---|---|
| Two-batch mixed lot | ||||||
| K1 = 2 | K1 = 4 | K1 = 6 | K1 = 4 | K1 = 6 | ||
| Min | 186.160 | 186.004 | 186.346 | 186.372 | 186.346 | 186.372 |
| Max | 186.160 | 186.259 | 186.346 | 186.372 | 186.346 | 186.372 |
| Mean | 186.160 | 186.098 | 186.346 | 186.372 | 186.346 | 186.372 |
| σ | 0.000 | 0.061 | 0.000 | 0.000 | 0.000 | 0.000 |
| V | 0.000 | 0.033 | 0.000 | 0.000 | 0.000 | 0.000 |
| R | 0.000 | 0.255 | 0.000 | 0.000 | 0.000 | 0.000 |
| Three-batch mixed lot | ||||||
| K1 = 3 | K1 = 6 | K1 = 9 | K1 = 6 | K1 = 9 | ||
| Min | 314.924 | 241.891 | 241.887 | 310.298 | 314.924 | 310.298 |
| Max | 325.737 | 315.597 | 325.737 | 320.973 | 325.737 | 310.298 |
| Mean | 318.529 | 251.905 | 312.939 | 315.280 | 315.645 | 310.298 |
| σ | 5.276 | 25.304 | 20.254 | 5.513 | 2.792 | 0.000 |
| V | 1.656 | 10.045 | 6.472 | 1.748 | 0.885 | 0.000 |
| R | 10.813 | 73.706 | 83.850 | 10.675 | 10.813 | 0.000 |
| Four-batch mixed lot | ||||||
| K1 = 4 | K1 = 8 | K1 = 12 | K1 = 8 | K1 = 12 | ||
| Min | 703.264 | 493.211 | 711.715 | 704.380 | 711.772 | 867.281 |
| Max | 885.950 | 549.237 | 891.441 | 882.936 | 891.058 | 884.912 |
| Mean | 715.546 | 510.358 | 779.266 | 730.258 | 850.182 | 882.353 |
| σ | 47.141 | 24.750 | 85.747 | 60.068 | 71.982 | 4.286 |
| V | 6.588 | 4.850 | 11.004 | 8.226 | 8.467 | 0.486 |
| R | 182.686 | 56.026 | 179.727 | 178.556 | 179.286 | 17.632 |
References
- Shirkhorshidi, A.S.; Aghabozorgi, S.; Wah, T. A comparison study on similarity and dissimilarity measures in clustering continuous data. PLoS ONE 2015, 10, e0144059. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Youguo, L.; Haiyan, W. A clustering method based on k-means algorithm. Phys. Procedia 2012, 25, 1104–1109. [Google Scholar]
- Steinhaus, H. Sur la divisiondes corps materiels en parties. Bull. Acad. Polon. Sci. 1956, 4, 801–804. [Google Scholar]
- Weiszfeld, E.; Plastria, F. On the point for which the sum of the distances to n given points is minimum. Ann. Oper. Res. 2009, 167, 7–41. [Google Scholar] [CrossRef]
- Nicholson, T. A sequential method for discrete optimization problems and its application to the assignment, traveling salesman and tree scheduling problems. J. Inst. Math. Appl. 1965, 13, 362–375. [Google Scholar]
- Lloyd, S.P. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef] [Green Version]
- Arthur, D.; Vassilvitskii, S. K-means++: The advantages of careful seeding. In Proceedings of the Eighteenth Annual ACM-SIAM Symposium on Discrete Algorithms, New Orleans, LA, USA, 7–9 January 2007; pp. 1027–1035. [Google Scholar]
- Bradley, P.S.; Fayyad, U.M. Refining initial points for k-means clustering. In Proceedings of the Fifteenth International Conference on Machine Learning (ICML 1998), Madison, WI, USA, 24–27 July 1998; Volume 98, pp. 91–99. [Google Scholar]
- Golasowski, M.; Martinovič, J.; Slaninová, K. Comparison of k-means clustering initialization approaches with brute-force initialization. In Advanced Computing and Systems for Security. Advances in Intelligent Systems and Computing; Springer: Singapore, 2017; Volume 567, pp. 103–114. [Google Scholar]
- Kalczynski, P.; Brimberg, J.; Drezner, Z. Less is more: Simple algorithms for the minimum sum of squares clustering problem. IMA J. Manag. Math. 2021, dpab031. [Google Scholar] [CrossRef]
- Mustafi, D.; Sahoo, G. A hybrid approach using genetic algorithm and the differential evolution heuristic for enhanced initialization of the k-means algorithm with applications in text clustering. Soft Comput. 2019, 23, 6361–6378. [Google Scholar] [CrossRef]
- Jain, A.K. Data clustering: 50 years beyond k-means. Pattern Recogn. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Ahmed, M.; Seraj, R.; Islam, S.M.S. The k-means algorithm: A comprehensive survey and performance evaluation. Electronics 2020, 9, 1295. [Google Scholar] [CrossRef]
- Celebi, M.E.; Kingravi, H.A.; Vela, P.A. A comparative study of efficient initialization methods for the k-means clustering algorithm. Expert Syst. Appl. 2013, 40, 200–210. [Google Scholar] [CrossRef] [Green Version]
- Kohonen, T. Self-Organizing Maps; Springer: Berlin/Heidelberg, Germany, 1995. [Google Scholar]
- Kohonen, T.; Somervuo, P. Self-organizing maps of symbol strings with application to speech recognition. In Proceedings of the Workshop on Self-Organizing Maps (WSOM’97), Espoo, Finland, 4–6 June 1997; pp. 2–7. [Google Scholar]
- Świetlicka, I.; Kuniszyk-Jóźkowiak, W.; Świetlicki, M. Artificial neural networks combined with the principal component analysis for non-fluent speech recognition. Sensors 2022, 22, 321. [Google Scholar] [CrossRef] [PubMed]
- Ettaouil, M.; Lazaar, M.; Ghanou, Y. Vector quantization by improved Kohonen algorithm. J. Comput. 2012, 4, 2151–9617. [Google Scholar]
- Younis, K.S.; Rogers, S.K.; DeSimio, M.P. Vector quantization based on dynamic adjustment of Mahalanobis distance. In Proceedings of the IEEE 1996 National Aerospace and Electronics Conference NAECON, Dayton, OH, USA, 20–23 May 1996; Volume 2, pp. 858–862. [Google Scholar] [CrossRef]
- Paul, S.; Gupta, M. Image segmentation by self-organizing map with Mahalanobis distance. Int. J. Emerg. Technol. Adv. Eng. 2013, 3, 2250–2459. [Google Scholar]
- Sun, Y.; Liu, H.; Sun, Q. Online learning on incremental distance metric for person re-identification. In Proceedings of the 2014 IEEE International Conference on Robotics and Biomimetics, Bali, Indonesia, 5 December 2014. [Google Scholar]
- Plonski, P.; Zaremba, K. Improving Performance of self-organising maps with distance metric learning method. In Proceedings of the International Conference on Artificial Intelligence and Soft Computing, Zakopane, Poland, 29 April 29–3 May 2012; Rutkowski, L., Korytkowski, M., Scherer, R., Tadeusiewicz, R., Zadeh, L.A., Zurada, J.M., Eds.; Springer: Berlin/Heidelberg, Germany, 2012; Volume 7267. [Google Scholar] [CrossRef] [Green Version]
- Saleh, A.; Naoyuki, T.; Rin-Ichiro, T. Face recognition under varying illumination using Mahalanobis self-organizing map. Artif. Life Robot. 2008, 13, 298–301. [Google Scholar] [CrossRef]
- Natita, W.; Wiboonsak, W.; Dusadee, S. Appropriate learning rate and neighborhood function of self-organizing map (SOM) for specific humidity pattern classification over Southern Thailand. Int. J. Modeling Optim. 2016, 6, 61–65. [Google Scholar] [CrossRef] [Green Version]
- Mahindru, A.; Sangal, A.L. SOMDROID: Android malware detection by artificial neural network trained using unsupervised learning. Evol. Intel. 2022, 15, 407–437. [Google Scholar] [CrossRef]
- Grinyak, V.M.; Yudin, P.V. Kohonen self-organizing map in seasonal sales planning. In SMART Automatics and Energy. Smart Innovation, Systems and Technologies; Solovev, D.B., Kyriakopoulos, G.L., Venelin, T., Eds.; Springer: Singapore, 2022; Volume 272. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, H.; Li, S.; Wang, L. Survival risk prediction of esophageal cancer based on the Kohonen network clustering algorithm and kernel extreme learning machine. Mathematics 2022, 10, 1367. [Google Scholar] [CrossRef]
- Kiseleva, E.I.; Astachova, I.F. Intelligent support for medical decision making. In Advances in Automation III. RusAutoCon 2021. Lecture Notes in Electrical Engineering; Radionov, A.A., Gasiyarov, V.R., Eds.; Springer: Cham, Switzerland, 2022; Volume 857. [Google Scholar] [CrossRef]
- Mawane, J.; Naji, A.; Ramdani, M. A cluster validity for optimal configuration of Kohonen maps in e-learning recommendation. Indones. J. Electr. Eng. Comput. Sci. 2022, 26, 482–492. [Google Scholar] [CrossRef]
- Huang, X. Application of computer data mining technology based on AKN algorithm in denial of service attack defense detection. Wirel. Commun. Mob. Comput. 2022, 2022, 4729526. [Google Scholar] [CrossRef]
- Amiri, V.; Nakagawa, K. Using a linear discriminant analysis (LDA)-based nomenclature system and self-organizing maps (SOM) for spatiotemporal assessment of groundwater quality in a coastal aquifer. J. Hydrol. 2021, 603, 127082. [Google Scholar] [CrossRef]
- Kovács, T.; Ko, A.; Asemi, A. Exploration of the investment patterns of potential retail banking customers using two-stage cluster analysis. J. Big Data 2021, 8, 141. [Google Scholar] [CrossRef]
- Kuehn, A.A.; Hamburger, M.J. A heuristic program for locating warehouses. Manag. Sci. 1963, 9, 643–666. [Google Scholar] [CrossRef]
- Alp, O.; Erkut, E.; Drezner, Z. An efficient genetic algorithm for the p-median problem. Ann. Oper. Res. 2003, 122, 21–42. [Google Scholar] [CrossRef]
- Agarwal, C.C.; Orlin, J.B.; Tai, R.P. Optimized crossover for the independent set problem. Oper. Res. 1997, 45, 226–234. [Google Scholar] [CrossRef] [Green Version]
- Kazakovtsev, L.A.; Antamoshkin, A.N. Genetic algorithm wish fast greedy heuristic for clustering and location problems. Informatica 2014, 38, 229–240. [Google Scholar]
- Andras, P.; Idowu, O. Kohonen networks with graph-based augmented metrics. In Proceedings of the Workshop on Self-Organizing Maps (WSOM 2005), Paris, France, 5–8 September 2005; pp. 179–186. [Google Scholar]
- Horio, K.; Koga, T.; Yamakawa, T. Self-organizing map with distance measure defined by data distribution. In Proceedings of the 2008 World Automation Congress, Waikoloa, HI, USA, 28 September–2 October 2008; pp. 1–6. [Google Scholar]
- Kohonen, T.; Kaski, S.; Lappalainen, H. Self-organized formation of various invariant-feature filters in the adaptive-subspace SOM. Neural Comput. 1997, 9, 1321–1344. [Google Scholar] [CrossRef]
- Furukawa, T. SOM of SOMs. Neural Netw. 2009, 22, 463–478. [Google Scholar] [CrossRef] [Green Version]
- Arnonkijpanich, B.; Hasenfuss, A.; Hammer, B. Local matrix adaptation in topographic neural maps. Neurocomputing 2011, 74, 522–539. [Google Scholar] [CrossRef] [Green Version]
- Yoneda, K.; Furukawa, T. Distance metric learning for the self-organizing map using a co-training approach. Int. J. Innov. Comput. Inf. Control 2018, 14, 2343–2351. [Google Scholar] [CrossRef]
- Alfeilat, H.; Hassanat, A.; Lasassmeh, O.; Tarawneh, A.; Alhasanat, M.; Salman, H.; Prasath, V. Effects of distance measure choice on K-Nearest Neighbor classifier performance: A review. Big Data 2019, 7, 221–248. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Weller-Fahy, D.J.; Borghetti, B.J.; Sodemann, A.A. A Survey of Distance and similarity measures used within network intrusion anomaly detection. IEEE Commun. Surv. Tutor. 2015, 17, 70–91. [Google Scholar] [CrossRef]
- McLachlan, G. Mahalanobis distance. Resonance 1999, 4, 20–26. [Google Scholar] [CrossRef]
- De Bodt, E.; Cottrell, M.; Letremy, P.; Verleysen, M. On the use of self-organizing maps to accelerate vector quantization. Neurocomputing 2004, 56, 187–203. [Google Scholar] [CrossRef] [Green Version]
- Haykin, S. Neural Networks and Learning Machines; Pearson Education: New York, NY, USA, 2009. [Google Scholar]
- Fausett, L. Fundamental of Neural Networks: Architectures, Algorithms, and Applications; Prentice Hall International: Hoboken, NJ, USA, 1994; pp. 169–175. [Google Scholar]
- Shkaberina, G.S.; Orlov, V.I.; Tovbis, E.M.; Kazakovtsev, L.A. On the optimization models for automatic grouping of industrial products by homogeneous production batches. In Mathematical Optimization Theory and Operations Research 2020, Communications in Computer and Information Science; Kochetov, Y., Bykadorov, I., Gruzdeva, T., Eds.; Springer: Cham, Switzerland, 2020; Volume 1275, pp. 421–436. [Google Scholar]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).