Modular Stability Analysis of a Nonlinear Stochastic Fractional Volterra IDE

Abstract

We define a new control function to approximate a stochastic fractional Volterra IDE using the concept of modular-stability.

1. Introduction

The stochastic fractional nonlinear Volterra-IDE is used in the science of engineering, management, economics and biophysics since many problems in these areas can be simulated by the stochastic fractional nonlinear Volterra-IDE. As a result, because of the important role these equations play in applied sciences, many researchers have investigated and presented numerical results for these equations. We refer the reader to methods such as the Galerkin method, shifted Legendre polynomials, and the collocation method based on radial basis functions (see [1,2]). In this paper, we study the existence of solutions for the stochastic fractional nonlinear Volterra-IDE:

$$\left\{\begin{array}{c}{}^H{\mathbb{D}}_{0+}^{\ell ,\kappa ;\aleph }\hslash (\varrho ,\theta )=f(\varrho ,\theta ,\hslash (\varrho ,\theta ))+{\int }_0^{\theta }k(\varrho ,\theta ,\vartheta ,\hslash (\varrho ,\theta ))d\vartheta ,\hfill \\ \\ {\mathcal{I}}_{0+}^{1-\lambda }\hslash (\varrho ,0)=\vartheta ,\hfill \end{array}\right.$$

(1)

with $\theta \in [0,M]$, where $f(\varrho ,\theta ,\hslash )$ is a continuous random operator (in short CRO) with respect to all the variables $\varrho$, $\theta$ and ℏ on ${\rm Y}\times [0,M]\times \mathbb{R}$, $k(\varrho ,\theta ,\vartheta ,\hslash )$ is a CRO with respect to $\varrho$, $\theta$, $\vartheta$ and ℏ on ${\rm Y}\times [0,M]\times \mathbb{R}\times \mathbb{R}$, $\vartheta$ is a fixed number, ${}^H{\mathbb{D}}_{0+}^{\ell ,\kappa ;\aleph }\hslash (.)$ is defined later in (2) where $\varrho \in {\rm Y}$, $0<\ell <1$, $0\le \kappa \le 1$ and ${\mathcal{I}}_{0+}^{1-\lambda }(.)$ is the ℵ-Riemann–Liouville stochastic fractional integral, where $0\le \lambda <1$, and ${\rm Y}$ is defined in the next section. We consider a new space called the modular space, which was first introduced in 1950 by Nakano [3]. Later, Musielak and Orlicz generalized it in [4], and we also refer the reader to [5] for more information. In this article, we use a fixed point technique, and it is of interest to note that this technique in modular spaces is a generalization of the technique in classical spaces and, to date, nonlinear and asymptotic contractions maps, as well as quasi-contraction mappings in modular spaces, have been studied in the literature. The description of our article is as follows:

We introduce a new space called a modular space and we examine the existence and uniqueness of solutions of stochastic fractional Volterra IDE in this new space. Furthermore, in this article, we consider the aggregation function and use special functions as inputs to the aggregation function to create a control function that for the solution of the equation has the best approximation. Finally, we present a practical example to illustrate our theory.

2. Preliminaries

Here, we let ${\Xi }_1=[0,M]$, with $M>0$, ${\Xi }_2=(0,\infty )$, ${\Xi }_3=(0,1]$, ${\Xi }_4=[0,\infty ]$ and ${\Xi }_5=[0,1]$ (note ${\Xi }_5^{\circ }=(0,1)$ denotes the interior of ${\Xi }_5$).

Definition 1.

Consider the linear space S and ν from $S\times {\Xi }_2$ to ${\Xi }_2$ such that

 (MI) 

${\nu }_{\tau }\left(\varpi \right)=0$ for any $\tau \in {\Xi }_2$ iff $\varpi =0$;

(MII) 

${\nu }_{\tau }\left(a\varpi \right)={\nu }_{\frac{\tau }{\left|a\right|}}\left(\varpi \right)$ for each $\varpi \in S$, $\tau \in {\Xi }_2$ and $a\in \mathbb{R}$ with $a\ne 0$;

(MIII) 

${\nu }_{\tau +\gamma }(\varpi +\Im )\le {\nu }_{\tau }\left(\varpi \right)+{\nu }_{\gamma }(\Im )$ for all $\varpi ,\Im \in S$ and $\tau ,\gamma \in {\Xi }_2$;

 (MIV) 

${\nu }_{.}\left(\varpi \right):{\Xi }_2\to {\Xi }_3$ is continuous.

Then, $(S,\nu )$ is called a modular normed-space (in short, MNS).

Let $(S,\nu )$ be an MNS. A sequence $\left\{{\varpi }_n\right\}\subset S$ is modular convergent to $\varpi \in S$ in MNS $(S,\nu )$, if for any $ϵ\in {\Xi }_5^{\circ }$ and $\tau \in {\Xi }_2$, there exists a positive integer $N_{ϵ,\tau }\in {\Xi }_2$ such that ${\nu }_{\tau }({\varpi }_n-\varpi )<ϵ$ when $n\ge N_{ϵ,\tau }$. A sequence $\left\{{\varpi }_n\right\}\subset S$ is modular Cauchy in MNS $(S,\nu )$, if for any $ϵ\in {\Xi }_5^{\circ }$ and $\tau \in {\Xi }_2$, there exists a positive integer $N_{ϵ,\tau }\in {\Xi }_2$ such that ${\nu }_{\tau }({\varpi }_n-{\varpi }_m)<ϵ$ whenever $n,m\ge N_{ϵ,\tau }$. An MNS in which every Cauchy sequence is convergent is said to be an MBS.

An example of a modular norm is

$$\begin{array}{c}\hfill {\nu }_{\tau }\left(\varpi \right)=\frac{\parallel \varpi \parallel }{g\left(\tau \right)},\end{array}$$

in which $g:{\Xi }_2\to {\Xi }_2$ is a nondecreasing function for all $\tau \in {\Xi }_2$ and $\varpi$ is a member of a normed linear space $(W,\parallel .\parallel )$.

Consider the probability measure space $({\rm Y},{\Xi }_2,\Xi )$, and let $\left(U,B_U\right)$ and $\left(S,B_S\right)$ be Borel measureable spaces, for MNS U and S. If $\{\varrho :\mathcal{F}(\varrho ,\varpi )\in B\}\in {\Xi }_2$ for every $\varpi$ in U and $B\in B_S$, we say $\mathcal{F}:{\rm Y}\times U\to S$ is a random operator.

To prove our main result, we use an alternative fixed point theorem (AFPT) (we refer the reader to [6,7]).

Definition 2

([8]). The gamma function is defined as

$$\begin{array}{c}\hfill \lambda \left(z\right)={\int }_0^{\infty }{e}^{-⅁}{⅁}^{z-1}d⅁,\end{array}$$

where $z\in \mathbb{C}$, $Re\left(z\right)>0$.

Consider $\ell \in \mathring{{\Xi }_5}$ and the integrable random operator f on ${\Xi }_1$ and the nondecreasing random operator $\aleph \in C^1({\rm Y}\times {\Xi }_1)$ with ${\aleph }^{\prime }(\varrho ,⅁)\ne 0$, for each $⅁\in {\Xi }_1$. The right-sided ℵ-Hilfer stochastic fractional derivative is defined by [9,10]

$$\begin{array}{c}\hfill {}^H{\mathbb{D}}_{0+}^{\ell ,s;\aleph }f(\varrho ,\theta )={\mathcal{I}}_{0+}^{s(1-\ell );\aleph }\left(\frac{1}{{\aleph }^{\prime }(\varrho ,\theta )}\frac{d}{d\theta }\right){\mathcal{I}}_{0+}^{(1-s)(1-\ell );\aleph }f(\varrho ,\theta ).\end{array}$$

(2)

In the following, we present the definitions that are needed to obtain the control function (for more details, see [11]).

Definition 3.

The complex exponential function is defined as

$$Exp\left(\theta \right)=\sum _{\varsigma =0}^{\infty }{\displaystyle \frac{{\theta }^{\varsigma }}{\Gamma (\varsigma +1)}},\theta \in C,$$

(3)

Definition 4.

The generalized exponential function, which is called Mittag–Leffler function, is defined as

$$E_t\left(\theta \right)=\sum _{\varsigma =0}^{\infty }{\displaystyle \frac{{\theta }^{\varsigma }}{\theta (1+t\varsigma )}}p\in C,R\left(p\right)>0,\theta \in C,$$

(4)

Definition 5.

The Gauss Hypergeometric series, which is called the Hypergeometric function, is defined as

$$E_t^{s_1,s_2}\left(\theta \right)={\displaystyle \frac{\Gamma \left(t\right)}{\Gamma \left(s_1\right)\Gamma \left(s_2\right)}}\sum _{\varsigma =0}^{\infty }{\displaystyle \frac{\Gamma (s_1+\varsigma )\Gamma (s_2+\varsigma )}{\Gamma (t+\varsigma )}}{\displaystyle \frac{{\theta }^{\varsigma }}{\varsigma !}},s_1,s_2,t\in C,R\left(s_1\right),R\left(s_2\right),R\left(t\right)>0.$$

(5)

We can rewrite the above series via the Mellin–Barnes integral as

$$E_t^{s_1,s_2}\left(\theta \right)={\displaystyle \frac{\Gamma \left(t\right)}{\Gamma \left(s_1\right)\Gamma \left(s_2\right)}}{\displaystyle \frac{1}{2\pi i}}\int {\displaystyle \frac{\Gamma \left(x\right)\Gamma (s_1-x)\Gamma (s_2-x)}{\Gamma (t-x)}}{(-\theta )}^{-x}dx.$$

(6)

Definition 6.

The Maitland function, which is called the Wright function, is defined as

$$E_t^{s_1}\left(\theta \right)=\sum _{\varsigma =0}^{\infty }{\displaystyle \frac{{\theta }^{\varsigma }}{\varsigma !\Gamma (s_1\varsigma +t)}},s_1\in (-1,\infty ),t,\theta \in C.$$

(7)

The generalized Wright function, which is called the Fox–Wright function, is defined as

$$E_{[(t_1,T_1),(t_2,T_2),\dots ,(t_{ı},T_{ı})]}^{[(s_1,S_1),(s_2,S_2),\dots ,(s_{\zeta },S_{\zeta })]}\left(\theta \right)=\sum _{\varsigma =0}^{\infty }{\displaystyle \frac{{\prod }_{j=1}^{\zeta }\Gamma (S_j\varsigma +s_j)}{{\prod }_{j=1}^{ı}\Gamma (T_j\varsigma +t_j)}}{\displaystyle \frac{{\theta }^{\varsigma }}{\varsigma !}}.$$

(8)

Definition 7.

For $0\le {\gamma }_1\le {\gamma }_2$, $1\le {\gamma }_3\le {\gamma }_4$, $\{x_{\ell },y_{\ell }\}\in \mathbb{C}$, $\{u_{\ell },v_{\ell }\}\in {\mathbb{R}}^{+}$, we define the following functions

• ${\psi }_1\left(f\right)={\prod }_{\ell =1}^{{\gamma }_1}\Gamma (y_{\ell }-v_{\ell }f),$
• ${\psi }_2\left(f\right)={\prod }_{\ell =1}^{{\gamma }_3}\Gamma (1-x_{\ell }+u_{\ell }f),$
• ${\psi }_3\left(f\right)={\prod }_{\ell ={\gamma }_3+1}^{{\gamma }_3}\Gamma (1-y_{\ell }+v_{\ell }f),$
• ${\psi }_4\left(f\right)={\prod }_{\ell ={\gamma }_1+1}^{{\gamma }_2}\Gamma (x_{\ell }-u_{\ell }f).$

In the above functions, ${\gamma }_1=0$ if and only if ${\psi }_2\left(f\right)=1$, ${\gamma }_3={\gamma }_4$ if and only if ${\psi }_3\left(z\right)=1$ and ${\gamma }_1={\gamma }_2$ if and only if ${\gamma }_4\left(f\right)=1$. According to the above functions, we consider ${\mathcal{H}}_{{\gamma }_2,{\gamma }_4}^{{\gamma }_3,{\gamma }_1}\left(f\right)=\frac{{\psi }_1\left(f\right){\psi }_2\left(f\right)}{{\psi }_3\left(f\right){\psi }_4\left(f\right)}$. The Mellin–Barnes integral (M-BI) representation of the H-Fox function (H-FF) is

$$\begin{array}{c}\hfill H_{{\gamma }_2,{\gamma }_4}^{{\gamma }_3,{\gamma }_1}\left(u\right)=\frac{1}{2\pi i}{\int }_{\mathcal{A}}{\mathcal{H}}_{{\gamma }_2,{\gamma }_4}^{{\gamma }_3,{\gamma }_1}\left(f\right)u^{f}df,\end{array}$$

(9)

where $u^f=exp\left\{f\right(log\left|u\right|+iargu\left)\right\}$ and $\mathcal{A}\in \mathbb{C}$ is a path. Furthermore, the symbol $H_{{\gamma }_2,{\gamma }_4}^{{\gamma }_3,{\gamma }_1}\left(u\right)=H_{{\gamma }_2,{\gamma }_4}^{{\gamma }_3,{\gamma }_1}\left[u|\begin{array}{cc}& {(x_{\ell },{ϵ}_{\ell })}_{\ell =1,\cdots ,{\gamma }_2}\hfill \\ & {(y_{\ell },{\rho }_{\ell })}_{\ell =1,\cdots ,{\gamma }_2}\hfill \end{array}\right]$ is considered for this integral.

Now we introduce the aggregation function because, in this paper, we use this function as a control function.

Definition 8.

For a natural and fixed number k and $\mathfrak{J}\in \mathbb{R}$, an aggregation function is a function ${\mathfrak{A}}^k:{\mathfrak{J}}^k\to \mathfrak{J}$, which is nondecreasing, that is, for all $j\in [1,\dots ,k]$

$$p_j\le q_j⟹{\mathfrak{A}}^k(p_1,\dots ,p_k)\le {\mathfrak{A}}^k(q_1,\dots ,q_k),$$

hold for the desired k-tuples $(p_1,\dots ,p_k)\in {\mathfrak{J}}^k,(q_1,\dots ,q_k)\in {\mathfrak{J}}^k.$

The natural k represents the arity of the aggregation function when no confusion arises, and the aggregation function can be given as $\mathfrak{A}$.

Now we consider some examples of aggregation functions. The arithmetic, the geometric, the projection, the order statistic, the minimum and maximum, the median are aggregation functions.

Example 1.

The arithmetic mean function $AM:{\mathbb{R}}^k⟶\mathbb{R}$ is defined by

$$AM\left(p\right)=\frac{1}{k}\sum _{j=1}^k{p}_j.$$

Example 2.

The geometric mean function $GM:{\mathbb{R}}^k⟶\mathbb{R}$ is defined by

$$GM\left(p\right)={\left(\prod _{j=1}^k{p}_j\right)}^{\frac{1}{k}}.$$

Example 3.

The projection function ${\mathcal{P}}_{\Im }:{\mathbb{R}}^k⟶\mathbb{R}$ for $\Im \in \left[k\right]$ and ℑth argument is defined by

$${\mathcal{P}}_{\Im }\left(p\right)=p_{\Im },$$

where $p_{(\Im )}$ is the ℑth lowest coordinate of p, i.e., $p_{\left(1\right)}\le \cdots \le p_{(\Im )}\le \cdots p_{\left(k\right)}$. Furthermore, the following functions show the $\mathcal{PF}$ in the first and last coordinates

$$\begin{array}{cc}\hfill {\mathcal{P}}_F\left(p\right)& ={\mathcal{P}}_1\left(p\right)=p_1,\hfill \\ \hfill {\mathcal{P}}_L\left(p\right)& ={\mathcal{P}}_k\left(p\right)=p_p.\hfill \end{array}$$

(10)

Example 4.

The order statistic function $O{S}_{\Im }:{\mathbb{R}}^k⟶\mathbb{R}$ with the ℑth argument and ℑth lowest coordinate is defined by

$$O{S}_{\Im }\left(p\right)=p_{(\Im )},$$

for any $\Im \in \left[k\right]$.

Example 5.

The minimum function and maximum function are defined as follows, respectively,

$$\begin{array}{cc}\hfill MIN\left(p\right)& =\underset{j=1}{\overset{k}{\bigwedge }}{p}_j,\hfill \\ \hfill MAX\left(p\right)& =\underset{j=1}{\overset{k}{\bigvee }}{p}_j.\hfill \end{array}$$

(11)

Example 6.

The median function is defined for odd and even values of $(p_1,\cdots ,p_{2\Im -1})$ and $(p_1,\cdots ,p_{2\Im })$, respectively,

$$\begin{array}{cc}\hfill & MED(p_1,\cdots ,p_{2\Im -1})=p_{(\Im )},\hfill \\ \hfill & MED(p_1,\cdots ,p_{2\Im })=\mathfrak{AM}(p_{(\Im )},p_{(\Im +1)})=\frac{p_{(\Im )}+p_{(\Im +1)}}{2}.\hfill \end{array}$$

(12)

According to the above functions, we consider the following set:

$$\begin{array}{c}\hfill \Delta =\left\{Exp\left({\displaystyle \frac{-\parallel \theta \parallel }{\tau }}\right),E_p\left({\displaystyle \frac{-\parallel \theta \parallel }{\tau }}\right),E_p^{m_1,m_2}\left({\displaystyle \frac{-\parallel \theta \parallel }{\tau }}\right),E_p^{m_1}\left({\displaystyle \frac{-\parallel \theta \parallel }{\tau }}\right),{\mathrm{H}}_{{\gamma }_2,{\gamma }_4}^{{\gamma }_3,{\gamma }_1}\left({\displaystyle \frac{-\parallel \theta \parallel }{\tau }}\right)\right\},\end{array}$$

and the necessary calculations were performed on the considered set, and the results are shown in the table below.

From the calculations in Table 1, we consider the minimum function as the control function and define it as follows

$${\phi }_{\tau }\left(\theta \right)=\bigwedge \left\{Exp\left({\displaystyle \frac{-\parallel \theta \parallel }{\tau }}\right),E_p\left({\displaystyle \frac{-\parallel \theta \parallel }{\tau }}\right),E_p^{m_1,m_2}\left({\displaystyle \frac{-\parallel \theta \parallel }{\tau }}\right),E_p^{m_1}\left({\displaystyle \frac{-\parallel \theta \parallel }{\tau }}\right),{\mathrm{H}}_{{\gamma }_2,{\gamma }_4}^{{\gamma }_3,{\gamma }_1}\left({\displaystyle \frac{-\parallel \theta \parallel }{\tau }}\right)\right\}.$$

In the following, after the table, in Figure 1, we provide a graphical representation of some aggregation functions.

Table 1. Calculation of aggregation function according to special functions for different values.

$\mathit{\theta }$	$\mathit{A}\mathit{M}(\Delta )$	$\mathit{G}\mathit{M}(\Delta )$	$\mathit{M}\mathit{A}\mathit{X}(\Delta )$	$\mathit{M}\mathit{I}\mathit{N}(\Delta )$	$\mathit{M}\mathit{E}\mathit{D}(\Delta )$
$0.2$	$0.8080213850$	$0.1309431397$	$1.124151808$	$0.00005753566833$	$1.105170918$
$0.3$	$0.8643139212$	$0.1490999010$	$1.548626550$	$0.00008260506014$	$1.161834243$
$0.4$	$0.9247680550$	$0.1663238147$	$1.668199962$	$0.0001071434790$	$1.221402758$
$0.5$	$0.9898018722$	$0.1835845210$	$1.794667420$	$0.0001318755004$	$1.284025417$
$0.6$	$1.059899323$	$0.2013893746$	$1.928408155$	$0.0001573709088$	$1.349858808$

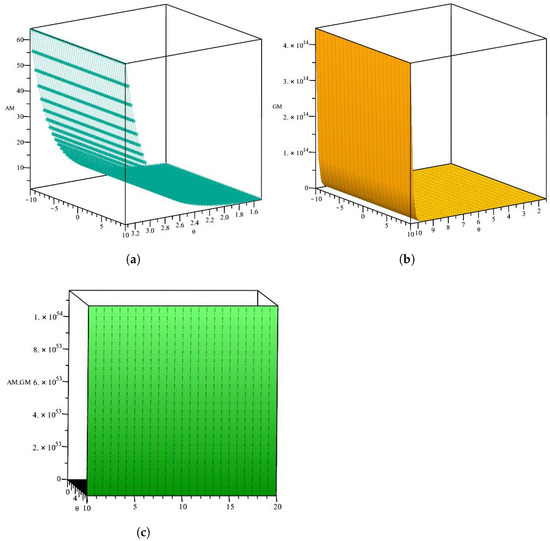
Figure 1. Graph of aggregate functions AM and GM for, $\tau =2$ and different values $\theta$. (a) The aggregation arithmetic mean function for $\theta \in (\frac{3}{2},\frac{10}{3})$. (b) The aggregation arithmetic mean function for $\theta \in (1.5,10.5)$. (c) The aggregation geometric mean function for $\theta \in (0,10)$.

Definition 9.

Consider the continuously differentiable random operator $\hslash (\varrho ,\theta )$ and let ${\phi }_{\tau }\left(\theta \right)$ be a modular control function satisfying

$$\begin{array}{c}\hfill {\nu }_{\tau }\left({}^H{\mathbb{D}}_{0+}^{\ell ,\kappa ;\aleph }\hslash (\varrho ,\theta )-f(\varrho ,\theta ,\hslash (\varrho ,\theta ))-{\int }_0^{\theta }k(\varrho ,\theta ,\vartheta ,\hslash (\varrho ,\theta ))d\vartheta \right)\le {\phi }_{\tau }\left(\theta \right),\end{array}$$

for each $\theta \in {\Xi }_1$, $\tau \in {\Xi }_2$ and $\varrho \in {\rm Y}$. If there exists a solution ${\hslash }_0(\varrho ,\theta )$ of the VIDE (1) and a fixed number $C>0$ with

$$\begin{array}{c}\hfill {\nu }_{\tau }\left(\hslash (\varrho ,\theta )-{\hslash }_0(\varrho ,\theta )\right)\le {\phi }_{\frac{\tau }{C}}\left(\theta \right),\end{array}$$

for all $\theta \in {\Xi }_1$, $\tau \in {\Xi }_2$ and $\varrho \in {\rm Y}$, in which C is autonomous of $\hslash (\varrho ,\theta )$ and ${\hslash }_0(\varrho ,\theta )$, then we say that (1) has Hyers–Ulam–Rassias stability.

3. Main Results

We assume the following:

Hypothesis 1 (H1).

Let $M,L_f,L_k>0$ be fixed numbers with $M\left(L_f+L_k\right)\in \mathring{{\Xi }_5}$ and let the CROs $f:{\rm Y}\times {\Xi }_1\times \mathbb{R}\to \mathbb{R}$ and $k:{\rm Y}\times {\Xi }_1\times {\Xi }_1\times \mathbb{R}\to \mathbb{R}$ satisfy

$$\begin{array}{c}\hfill {\nu }_{\tau }\left(f(\varrho ,\theta ,{\hslash }_1)-f(\varrho ,\theta ,{\hslash }_2)\right)\le {\nu }_{{\displaystyle \frac{\tau }{L_f}}}\left({\hslash }_1-{\hslash }_2\right),\end{array}$$

(13)

for all $\theta \in {\Xi }_1$, ${\hslash }_1,{\hslash }_2\in \mathbb{R}$, $\tau \in {\Xi }_2$ and $\varrho \in {\rm Y}$, and

$$\begin{array}{c}\hfill {\nu }_{\tau }\left(k(\varrho ,\theta ,\vartheta ,{\hslash }_1)-k(\varrho ,\theta ,\vartheta ,{\hslash }_2)\right)\le {\nu }_{\frac{\tau }{L_k}}\left({\hslash }_1-{\hslash }_2\right),\end{array}$$

(14)

for all $\theta ,\vartheta \in {\Xi }_1$, ${\hslash }_1,{\hslash }_2\in \mathbb{R}$, $\tau \in {\Xi }_2$ and $\varrho \in {\rm Y}$.

Theorem 1.

Assume $\left(H1\right)$, the nondecreasing random operator $\aleph \in C({\rm Y}\times {\Xi }_1)$ with ${\aleph }^{\prime }(\varrho ,\theta )\ne 0$ and the continuously differentiable random operator $\hslash :{\rm Y}\times {\Xi }_1\to \mathbb{R}$ satisfying

$$\begin{array}{c}\hfill {\nu }_{\tau }\left({}^H{\mathbb{D}}_{0+}^{\ell ,\kappa ;\aleph }\hslash (\varrho ,\theta )-f(\varrho ,\theta ,\hslash (\varrho ,\theta ))-{\int }_0^{\theta }k(\varrho ,\theta ,\vartheta ,\hslash (\varrho ,\vartheta ))d\vartheta \right)\le {\phi }_{\tau }\left(\theta \right),\end{array}$$

(15)

for all $\theta ,\vartheta \in {\Xi }_1$, $\hslash \in \mathbb{R}$, $\tau \in {\Xi }_2$ and $\varrho \in {\rm Y}$, where $\phi :{\Xi }_1\times {\Xi }_2\to {\Xi }_3$ is a continuous modular set with

$$\begin{array}{c}\hfill {\nu }_{\tau }\left(\frac{1}{\lambda (\ell )}{\int }_0^{\theta }{\aleph }^{\prime }(\varrho ,\varpi ){(\aleph (\varrho ,\theta )-\aleph (\varrho ,\varpi ))}^{\ell -1}\phi (\varpi ,\tau )d\varpi \right)\le {\phi }_{\frac{\tau }{M}}\left(\theta \right),\end{array}$$

(16)

for each $\theta \in {\Xi }_1$, $\tau \in {\Xi }_2$ and $\varrho \in {\rm Y}$. Then, we can find a unique CRO ${\hslash }_0:{\rm Y}\times {\Xi }_1\to \mathbb{R}$, such that

$$\begin{array}{cc}\hfill {\hslash }_0(\varrho ,\theta )& =\frac{{(\aleph (\varrho ,\theta )-\aleph (\varrho ,0))}^{\lambda -1}}{\Gamma \left(\lambda \right)}\vartheta \hfill \\ \hfill & +{\mathcal{I}}_{0+}^{\ell ;\aleph }f(\varrho ,\theta ,{\hslash }_0(\varrho ,\theta ))\hfill \\ \hfill & +{\mathcal{I}}_{0+}^{\ell ;\aleph }\left[{\int }_0^{\varpi }k(\varrho ,\theta ,\vartheta ,{\hslash }_0(\varrho ,\vartheta ))d\vartheta \right],\hfill \end{array}$$

(17)

with ${\mathcal{I}}_{0+}^{1-\lambda ;\aleph }\hslash (\varrho ,0)=\vartheta$, $0<\ell <1$, $0\le \kappa \le 1$ and

$$\begin{array}{c}\hfill {\nu }_{\tau }\left(\hslash (\varrho ,\theta )-{\hslash }_0(\varrho ,\theta )\right)\le {\phi }_{\frac{M\tau }{1-M\left(L_f+L_k\right)}}\left(\theta \right),\end{array}$$

(18)

for each $\theta \in {\Xi }_1$, $\tau \in {\Xi }_2$ and $\varrho \in {\rm Y}$.

Proof. 

For $\wp ,j\in U$, we set

$$\begin{array}{c}\hfill \partial (\wp ,j)=inf\left\{C\in {\Xi }_4:{\nu }_{\tau }\left(\wp (\varrho ,\theta )-j(\varrho ,\theta )\right)\le {\phi }_{\frac{\tau }{C}}\left(\theta \right)\right\},\end{array}$$

(19)

for each $\theta \in {\Xi }_1$, $\tau \in {\Xi }_2$ and $\varrho \in {\rm Y}$, where

$$\begin{array}{c}\hfill U=\left\{\wp :{\rm Y}\times {\Xi }_1\to \mathbb{R}\mathrm{is}\mathrm{CRO}\right\}.\end{array}$$

Let $\Omega :U\to U$ be given by

$$\begin{array}{cc}\hfill \Omega \wp (\varrho ,\theta )& =\frac{{(\aleph (\varrho ,\theta )-\aleph (\varrho ,0))}^{\lambda -1}}{\Gamma \left(\lambda \right)}\vartheta \hfill \\ \hfill & +{\mathcal{I}}_{0+}^{\ell ;\aleph }f(\varrho ,\theta ,\wp (\varrho ,\theta ))\hfill \\ \hfill & +{\mathcal{I}}_{0+}^{\ell ;\aleph }\left[{\int }_0^{\varpi }k(\varrho ,\theta ,\vartheta ,\wp (\varrho ,\vartheta ))d\vartheta \right],\hfill \end{array}$$

(20)

for all $\wp \in {\Xi }_1$, $\theta \in {\Xi }_1$ and $\varrho \in {\rm Y}$.

First we show $\Omega$ is strictly contractive on U. Let $\partial (\wp ,j)\le C_{\wp j}$ for any $\wp ,j\in U$, $C_{\wp j}\in {\Xi }_4$ be a fixed number, then from (19) we have

$$\begin{array}{c}\hfill {\nu }_{\tau }\left(\wp (\varrho ,\theta )-j(\varrho ,\theta )\right)\le {\phi }_{\frac{\tau }{C_{\wp j}}}\left(\theta \right),\end{array}$$

(21)

for each $\theta \in {\Xi }_1$, $\tau \in {\Xi }_2$ and $\varrho \in {\rm Y}$. From (13), (14), (16), (20) and (21), we have

$$\begin{array}{cc}\hfill & {\nu }_{\tau }\left(\Omega \wp (\varrho ,\theta )-\Omega j(\varrho ,\theta )\right)\hfill \\ \hfill & ={\nu }_{\tau }\left(\frac{1}{\Gamma (\ell )}{\int }_0^{\theta }{\aleph }^{\prime }(\varrho ,\varpi ){(\aleph (\varrho ,\theta )-\aleph (\varrho ,\varpi ))}^{\ell -1}{\nu }_{\tau }\right(f(\varrho ,\varpi ,\wp (\varrho ,\varpi ))-f(\varrho ,\varpi ,j(\varrho ,\varpi ))\hfill \\ \hfill & +{\int }_0^{\varpi }k(\varrho ,\theta ,\vartheta ,\wp (\varrho ,\vartheta ))-k(\varrho ,\theta ,\vartheta ,j(\varrho ,\vartheta ))d\vartheta \left)d\varpi \right)\hfill \\ \hfill & \le {\nu }_{\tau }(\frac{1}{\Gamma (\ell )}{\int }_0^{\theta }{\aleph }^{\prime }(\varrho ,\varpi ){(\aleph (\varrho ,\theta )-\aleph (\varrho ,\varpi ))}^{\ell -1}max\{{\nu }_{\tau }\left(f(\varrho ,\varpi ,\wp (\varrho ,\varpi \left)\right)-f(\varrho ,\varpi ,j(\varrho ,\varpi \left)\right)\right)\hfill \\ \hfill & ,{\nu }_{\tau }\left({\int }_0^{\varpi }k(\varrho ,\theta ,\vartheta ,\wp (\varrho ,\vartheta ))-k(\varrho ,\theta ,\vartheta ,j(\varrho ,\vartheta ))d\vartheta \right)\left\}d\varpi \right)\hfill \\ \hfill & \le {\nu }_{\tau }(\frac{1}{\Gamma (\ell )}{\int }_0^{\theta }{\aleph }^{\prime }(\varrho ,\varpi ){(\aleph (\varrho ,\theta )-\aleph (\varrho ,\varpi ))}^{\ell -1}max\{{\nu }_{\frac{\tau }{L_f}}\left(\wp (\varrho ,\varpi )-j(\varrho ,\varpi )\right)\hfill \\ \hfill & ,{\nu }_{\frac{\tau }{L_k}}\left(\wp (\varrho ,\varpi )-j(\varrho ,\varpi )\right)\left\}d\varpi \right)\hfill \\ \hfill & \le {\nu }_{\tau }\left(\frac{1}{\Gamma (\ell )}{\int }_0^{\theta }{\aleph }^{\prime }(\varrho ,\varpi ){(\aleph (\varrho ,\theta )-\aleph (\varrho ,\varpi ))}^{\ell -1}{\nu }_{\frac{\tau }{L_f+L_k}}\left(\wp (\varrho ,\varpi )-j(\varrho ,\varpi )\right)d\varpi \right)\hfill \\ \hfill & \le {\nu }_{\tau }\left(\frac{1}{\Gamma (\ell )}{\int }_0^{\theta }{\aleph }^{\prime }(\varrho ,\varpi ){(\aleph (\varrho ,\theta )-\aleph (\varrho ,\varpi ))}^{\ell -1}{\phi }_{\frac{\tau }{C_{\wp j}(L_f+L_k)}}\left(\varpi \right)d\varpi \right)\hfill \\ \hfill & \le {\phi }_{\frac{\tau }{M{C}_{\wp j}(L_f+L_k)}}\left(\theta \right),\hfill \\ \hfill \end{array}$$

(22)

and we conclude that

$$\begin{array}{c}\hfill \partial (\Omega \wp ,\Omega j)\le {\phi }_{\frac{\tau }{M{C}_{\wp j}(L_f+L_k)}}\left(\theta \right),\end{array}$$

for all $\theta \in {\Xi }_1$ and $\tau \in {\Xi }_2$. Hence, we deduce that $\partial (\Omega \wp ,\Omega j)\le \left[M\left(L_f+L_k\right)\right]\partial (\wp ,j)$ for any $\wp ,j\in U$, and recall $0<M\left(L_f+L_k\right)<1$.

Now (20), enables us to find $C\in {\Xi }_2$, with

$$\begin{array}{cc}\hfill & {\nu }_{\tau }\left(\Omega j_0(\varrho ,\theta )-j_0(\varrho ,\theta )\right)\hfill \\ \hfill & ={\nu }_{\tau }(\frac{{(\aleph (\varrho ,\theta )-\aleph (\varrho ,0))}^{\lambda -1}}{\Gamma \left(\lambda \right)}\vartheta +{\mathcal{I}}_{0+}^{\ell ;\aleph }f(\varrho ,\theta ,j_0(\varrho ,\theta ))\hfill \\ \hfill & +{\mathcal{I}}_{0+}^{\ell ;\aleph }\left[{\int }_0^{\varpi }f(\varrho ,\theta ,\vartheta ,j_0(\varrho ,\vartheta ))d\vartheta \right]-j_0(\varrho ,\theta ))\hfill \\ \hfill & \le {\phi }_{\frac{\tau }{C}}\left(\theta \right),\hfill \end{array}$$

for arbitrary $j_0\in U$, for all $\theta \in {\Xi }_1$, $\tau \in {\Xi }_2$ and $\varrho \in {\rm Y}$. The boundedness property of

$$f(\varrho ,\varpi ,j_0(\varrho ,\varpi )),k(\varrho ,\theta ,\vartheta ,j_0(\varrho ,\vartheta )),j_0(\varrho ,\theta )$$

and (19) imply that $\partial (\Omega j_0,j_0)<\infty$. From the AFPT, we can find a CRO ${\hslash }_0:{\rm Y}\times {\Xi }_1\to \mathbb{R}$ such that ${\Omega }^n{\hslash }_0\to {\hslash }_0$ in $(U,\partial )$ and $\Omega {\hslash }_0={\hslash }_0$.

Since j and ${\hslash }_0$ are bounded on ${\Xi }_1$ for each $j\in U$ and ${max}_{\theta \in {\Xi }_1}{\phi }_{\tau }\left(\theta \right)>0$, then we have a fixed number $C_{\wp j}\in {\Xi }_4$ with

$$\begin{array}{c}\hfill {\nu }_{\tau }\left(j_0(\varrho ,\theta )-j(\varrho ,\theta )\right)\le {\phi }_{\frac{\tau }{C_j}}\left(\theta \right),\end{array}$$

for any $\theta \in {\Xi }_1$, $\tau \in {\Xi }_2$ and $\varrho \in {\rm Y}$. Thus $\partial (j_0,j)<\infty$ for any $j\in U$.

Therefore, $U=\{j\in U:\partial (j_0,j)<\infty \}$. Furthermore, the AFPT and (17), imply the uniqueness of ${\hslash }_0$.

Using (15) and (Theorem 5 in [9]), we have

$$\begin{array}{cc}\hfill & {\nu }_{\tau }(\hslash (\varrho ,\theta )-\frac{{(\aleph (\varrho ,\theta )-\aleph (\varrho ,0))}^{\lambda -1}}{\Gamma \left(\lambda \right)}\vartheta \hfill \\ \hfill & -{\mathcal{I}}_{0+}^{\ell ;\aleph }f(\varrho ,\theta ,\hslash (\varrho ,\theta ))-{\mathcal{I}}_{0+}^{\ell ;\aleph }\left[{\int }_0^{\varpi }k(\varrho ,\theta ,\vartheta ,\hslash (\varrho ,\vartheta ))d\vartheta \right])\hfill \\ \hfill & \le \frac{1}{\Gamma (\ell )}{\int }_0^{\theta }{\aleph }^{\prime }(\varrho ,\varpi ){(\aleph (\varrho ,\theta )-\aleph (\varrho ,\varpi ))}^{\ell -1}{\phi }_{\tau }\left(\varpi \right)d\varpi .\hfill \end{array}$$

Then, from (16) and (20), we obtain

$$\begin{array}{cc}\hfill & {\nu }_{\tau }\left(\hslash (\varrho ,\theta )-\Omega \hslash (\varrho ,\theta )\right)\hfill \\ \hfill & \le \frac{1}{\Gamma (\ell )}{\int }_0^{\theta }{\aleph }^{\prime }(\varrho ,\varpi ){(\aleph (\varrho ,\theta )-\aleph (\varrho ,\varpi ))}^{\ell -1}{\phi }_{\tau }\left(\varpi \right)d\varpi \hfill \\ \hfill & \le {\phi }_{\frac{\tau }{M}}\left(\theta \right),\hfill \end{array}$$

for any $\theta \in {\Xi }_1$, $\tau \in {\Xi }_2$ and $\varrho \in {\rm Y}$, which implies

$$\begin{array}{c}\hfill \partial (\hslash ,\Omega \hslash )\le M.\end{array}$$

(23)

From the AFPT and (23), we deduce that

$$\begin{array}{c}\hfill \partial (\hslash ,{\hslash }_0)\le \frac{1}{1-M(L_f+L_k)}\partial (\Omega \hslash ,\hslash )\le \frac{M}{1-M(L_f+L_k)},\end{array}$$

which implies (18). □

Theorem 2.

Consider $\ell ,\kappa \in \mathring{{\Xi }_5}$ and the nondecreasing random operator $\aleph \in C^1({\rm Y}\times {\Xi }_1)$ with ${\aleph }^{\prime }(\varrho ,\theta )\ne 0$ for all $\theta \in {\Xi }_1$. Let $L_f,L_k\in {\Xi }_2$ be fixed numbers such that $\frac{\left(L_f+L_k\right)}{\Gamma (\ell +1)}\in \mathring{{\Xi }_5}$. Consider the CROs $f:{\rm Y}\times {\Xi }_1\times \mathbb{R}\to \mathbb{R}$ and $k:{\rm Y}\times {\Xi }_1\times {\Xi }_1\times \mathbb{R}\to \mathbb{R}$ satisfying (13) and (14), respectively. Let $\epsilon \in \mathring{{\Xi }_5}$, and consider the continuously differentiable random operator $\hslash :{\rm Y}\times {\Xi }_1\to \mathbb{R}$ such that

$$\begin{array}{c}\hfill {\nu }_{\tau }\left({}^H{\mathbb{D}}_{0+}^{\ell ,\kappa ;\aleph }\hslash (\varrho ,\theta )-f(\varrho ,\theta ,\hslash (\varrho ,\theta ))-{\int }_0^{\theta }k(\varrho ,\theta ,\vartheta ,\hslash (\varrho ,\vartheta ))d\vartheta \right)\le {\phi }_{\tau }\left(\epsilon \right),\end{array}$$

and

$${\nu }_{\tau }\left({(\aleph (\varrho ,\theta )-\aleph (\varrho ,0))}^{\ell }\right)\le {\nu }_{\tau }\left(\theta \right),$$

for all $\theta ,\vartheta \in {\Xi }_1$, $\hslash \in \mathbb{R}$, $\tau \in {\Xi }_2$ and $\varrho \in {\rm Y}$. Then, we can find a unique CRO ${\hslash }_0:{\rm Y}\times {\Xi }_1\to \mathbb{R}$ satisfying (17) and

$$\begin{array}{c}\hfill {\nu }_{\tau }\left(\hslash (\varrho ,\theta )-{\hslash }_0(\varrho ,\theta )\right)\le \frac{{(\aleph (\varrho ,T)-\aleph (\varrho ,0))}^{\ell }{\phi }_{\tau }\left(\epsilon \right)}{\Gamma (\ell +1)-{(\aleph (\varrho ,T)-\aleph (\varrho ,0))}^{\ell }\left[T\left(L_f+L_k\right)\right]},\end{array}$$

(24)

for all $\theta \in {\Xi }_1$, $\hslash \in \mathbb{R}$, $\tau \in {\Xi }_2$ and $\varrho \in {\rm Y}$.

Proof. 

Let $U=\left\{\wp :{\rm Y}\times {\Xi }_1\to \mathbb{R}\mathrm{is}\mathrm{CRO}\right\}$. Consider the complete ${\Xi }_4$-valued metric on U given by

$$\begin{array}{c}\hfill \partial (\wp ,j)=inf\left\{C\in {\Xi }_4:{\nu }_{\tau }\left(\wp (\varrho ,\theta )-j(\varrho ,\theta )\right)\le \left(\frac{\tau }{\tau +C}\right)\right\},\end{array}$$

(25)

for each $\theta \in {\Xi }_1$, $\tau \in {\Xi }_2$ and $\varrho \in {\rm Y}$ [10].

Consider $\Omega :U\to U$ in which

$$\begin{array}{cc}\hfill \Omega \wp (\varrho ,\theta )& =\frac{{(\aleph (\varrho ,\theta )-\aleph (\varrho ,0))}^{\lambda -1}}{\Gamma \left(\lambda \right)}\vartheta \hfill \\ \hfill & +{\mathcal{I}}_{0+}^{\ell ;\aleph }f(\varrho ,\theta ,\wp (\varrho ,\theta ))\hfill \\ \hfill & +{\mathcal{I}}_{0+}^{\ell ;\aleph }\left[{\int }_0^{\varpi }k(\varrho ,\theta ,\vartheta ,\wp (\varrho ,\vartheta ))d\vartheta \right],\hfill \end{array}$$

(26)

for all $\theta \in {\Xi }_1$ and $\varrho \in {\rm Y}$.

Let $\wp ,j\in U$ and consider a fixed number $C_{\wp j}\in {\Xi }_4$ such that $\partial (\wp ,j)\le C_{\wp j}$ and

$$\begin{array}{c}\hfill {\nu }_{\tau }\left(\wp (\varrho ,\theta )-j(\varrho ,\theta )\right)\ge \left(\frac{\tau }{\tau +C_{\wp j}}\right),\end{array}$$

(27)

for each $\theta \in {\Xi }_1$, $\tau \in {\Xi }_2$ and $\varrho \in {\rm Y}$. Using (13), (14), (26) and (27), we have

$$\begin{array}{cc}\hfill & {\nu }_{\tau }\left(\Omega \wp (\varrho ,\theta )-\Omega j(\varrho ,\theta )\right)\hfill \\ \hfill & ={\nu }_{\tau }\left(\frac{1}{\Gamma (\ell )}{\int }_0^{\theta }{\aleph }^{\prime }(\varrho ,\varpi ){(\aleph (\varrho ,\theta )-\aleph (\varrho ,\varpi ))}^{\ell -1}{\nu }_{\tau }\right(f(\varrho ,\varpi ,\wp (\varrho ,\varpi ))-f(\varrho ,\varpi ,j(\varrho ,\varpi ))\hfill \\ \hfill & +{\int }_0^{\varpi }k(\varrho ,\theta ,\vartheta ,\wp (\varrho ,\vartheta ))-k(\varrho ,\theta ,\vartheta ,j(\varrho ,\vartheta ))d\vartheta \left)d\varpi \right)\hfill \\ \hfill & \le {\nu }_{\tau }(\frac{1}{\Gamma (\ell )}{\int }_0^{\theta }{\aleph }^{\prime }(\varrho ,\varpi ){(\aleph (\varrho ,\theta )-\aleph (\varrho ,\varpi ))}^{\ell -1}max\{{\nu }_{\tau }\left(f(\varrho ,\varpi ,\wp (\varrho ,\varpi \left)\right)-f(\varrho ,\varpi ,j(\varrho ,\varpi \left)\right)\right)\hfill \\ \hfill & ,{\nu }_{\tau }\left({\int }_0^{\varpi }k(\varrho ,\theta ,\vartheta ,\wp (\varrho ,\vartheta ))-k(\varrho ,\theta ,\vartheta ,j(\varrho ,\vartheta ))d\vartheta \right)\left\}d\varpi \right)\hfill \\ \hfill & \le {\nu }_{\tau }(\frac{1}{\Gamma (\ell )}{\int }_0^{\theta }{\aleph }^{\prime }(\varrho ,\varpi ){(\aleph (\varrho ,\theta )-\aleph (\varrho ,\varpi ))}^{\ell -1}max\{{\nu }_{\frac{\tau }{L_f}}\left(\wp (\varrho ,\varpi )-j(\varrho ,\varpi )\right)\hfill \\ \hfill & ,{\nu }_{\frac{\tau }{L_k}}\left(\wp (\varrho ,\varpi )-j(\varrho ,\varpi )\right)\left\}d\varpi \right)\hfill \\ \hfill & \le {\nu }_{\tau }\left(\frac{1}{\Gamma (\ell )}{\int }_0^{\theta }{\aleph }^{\prime }(\varrho ,\varpi ){(\aleph (\varrho ,\theta )-\aleph (\varrho ,\varpi ))}^{\ell -1}{\nu }_{\frac{\tau }{L_f+L_k}}\left(\wp (\varrho ,\varpi )-j(\varrho ,\varpi )\right)d\varpi \right)\hfill \\ \hfill & \le {\nu }_{\tau }\left(\frac{1}{\Gamma (\ell )}{\int }_0^{\theta }{\aleph }^{\prime }(\varrho ,\varpi ){(\aleph (\varrho ,\theta )-\aleph (\varrho ,\varpi ))}^{\ell -1}\left(\frac{\tau \left(L_f+L_k\right)}{\tau +C_{\wp j}}\right)d\varpi \right)\hfill \\ \hfill & \le {\nu }_{\tau }\left({(\aleph (\varrho ,\theta )-\aleph (\varrho ,0))}^{\ell }\left(\frac{\tau \Gamma (\ell +1)\left(L_f+L_k\right)}{\Gamma (\ell +1)\left(\tau +C_{\wp j}\right)}\right)\right)\hfill \\ \hfill & \le {\nu }_{\tau }\left({(\aleph (\varrho ,\theta )-\aleph (\varrho ,0))}^{\ell },\frac{\tau }{\left(\frac{\tau \left(L_f+L_k\right)}{\Gamma (\ell +1)\left(\tau +C_{\wp j}\right)}\right)}\right)\hfill \\ \hfill & \le {\nu }_{\frac{\tau }{\left(\frac{\tau \left(L_f+L_k\right)}{\Gamma (\ell +1)\left(\tau +C_{\wp j}\right)}\right)}}\left(\theta \right),\hfill \end{array}$$

for each $\theta \in {\Xi }_1$, $\tau \in {\Xi }_2$ and $\varrho \in {\rm Y}$. Therefore

$$\begin{array}{c}\hfill \partial (\Omega \wp ,\Omega j)\le \left(\frac{\tau \left(L_f+L_k\right)}{\Gamma (\ell +1)\left(\tau +C_{\wp j}\right)}\right)\partial (\wp ,j),\end{array}$$

for each $\wp ,j\in U$ and $\varrho \in {\rm Y}$. Let $j_0\in U$. We can find a fixed number $C\in {\Xi }_2$ with

$$\begin{array}{cc}\hfill & {\nu }_{\tau }\left(\Omega j_0(\varrho ,\theta )-j_0(\varrho ,\theta )\right)\hfill \\ \hfill & ={\nu }_{\tau }(\frac{{(\aleph (\varrho ,\theta )-\aleph (\varrho ,0))}^{\lambda -1}}{\Gamma \left(\lambda \right)}\vartheta +{\mathcal{I}}_{0+}^{\ell ;\aleph }f(\varrho ,\theta ,j_0(\varrho ,\theta ))\hfill \\ \hfill & +{\mathcal{I}}_{0+}^{\ell ;\aleph }\left[{\int }_0^{\varpi }k(\varrho ,\theta ,\vartheta ,j_0(\varrho ,\vartheta ))d\vartheta \right]-j_0(\varrho ,\theta ))\hfill \\ \hfill & \le \frac{\tau }{\tau +C},\hfill \end{array}$$

for all $\theta \in {\Xi }_1$ and $\varrho \in {\rm Y}$.

The boundedness of

$$f(\varrho ,\varpi ,j_0(\varrho ,\varpi )),a,k(\varrho ,\theta ,\vartheta ,j_0(\varrho ,\vartheta )),j_0(\varrho ,\theta )$$

and (25), imply that $\partial (\Omega j_0,j_0)<\infty$.

By the AFPT, we can find a CRO ${\hslash }_0:{\rm Y}\times {\Xi }_1\to \mathbb{R}$ with ${\Omega }^n{j}_0\to {\hslash }_0$ in $(U,\partial )$ and $\Omega {\hslash }_0={\hslash }_0$, so ${\hslash }_0$ satisfies (17). By Theorem 1, we obtain $\{j\in U:\partial (j_0,j)<\infty \}=U$. Furthermore, the AFPT and (17) imply the uniqueness of ${\hslash }_0$.

Now, using (15) and (Theorem 5 in [9]), we have

$$\begin{array}{cc}\hfill & {\nu }_{\frac{\tau \Gamma (\ell +1)}{{(\aleph (\varrho ,T)-\aleph (\varrho ,0))}^{\ell }}}(\hslash (\varrho ,\theta )-\frac{{(\aleph (\varrho ,\theta )-\aleph (\varrho ,0))}^{\lambda -1}}{\Gamma \left(\lambda \right)}\vartheta -{\mathcal{I}}_{0+}^{\ell ;\aleph }f(\varrho ,\theta ,{\hslash }_0(\varrho ,\theta ))\hfill \\ \hfill & -{\mathcal{I}}_{0+}^{\ell ;\aleph }\left[{\int }_0^{\varpi }k(\varrho ,\theta ,\vartheta ,{\hslash }_0(\varrho ,\vartheta ))d\vartheta \right])\hfill \\ \hfill & \le {\phi }_{\tau }\left(\epsilon \right),\hfill \end{array}$$

for all $\theta \in {\Xi }_1$ and $\varrho \in {\rm Y}$, which implies

$$\begin{array}{c}\hfill \partial (\hslash ,\Omega \hslash )\le {\phi }_{\tau }\left(\epsilon \right)\frac{{(\aleph (\varrho ,T)-\aleph (\varrho ,0))}^{\ell }}{\Gamma (\ell +1)}.\end{array}$$

By the AFPT and (19), we deduce that

$$\begin{array}{c}\hfill \nu \frac{\tau \left(\Gamma (\ell +1)-{(\aleph (\varrho ,T)-\aleph (\varrho ,0))}^{\ell }[L_f+\frac{T}{2}{L}_k]\right)}{{(\aleph (\varrho ,T)-\aleph (\varrho ,0))}^{\ell }}\left(\hslash (\varrho ,\theta )-{\hslash }_0(\varrho ,\theta )\right)\le {\phi }_{\tau }\left(\epsilon \right),\end{array}$$

which implies (24) for all $\theta \in {\Xi }_1$. □

4. Example

Example 7.

We consider the stochastic fractional nonlinear Volterra-IDE:

$$\left\{\begin{array}{c}{}^H{\mathbb{D}}_{0+}^{\frac{1}{5},\frac{1}{10};\aleph }\hslash (\varrho ,\theta )=0.5({sin}^2(\hslash (\varrho ,\theta ))+{cos}^2(\hslash (\varrho ,\theta )))-0.02(\varrho +\theta )\hfill \\ +{\int }_0^{\theta }0.03({sin}^2(\hslash (\varrho ,\theta ))+{cos}^2(\hslash (\varrho ,\theta )))cos(\varrho +\theta +\vartheta )+4\vartheta d\vartheta ,\hfill \\ \\ {\mathcal{I}}_{0+}^{\frac{1}{2}}\hslash (\varrho ,0)=\vartheta \hfill \end{array}\right.$$

(28)

where $\ell =\frac{1}{5}$, $\kappa =\frac{1}{10}$, $\lambda =\frac{1}{2}$, $f(\varrho ,\theta ,\hslash (\varrho ,\theta ))=0.5({sin}^2(\hslash (\varrho ,\theta ))+{cos}^2(\hslash (\varrho ,\theta )))-0.02(\varrho +\theta )$, $k(\varrho ,\theta ,\vartheta ,\hslash (\varrho ,\theta ))=0.03({sin}^2(\hslash (\varrho ,\theta ))+{cos}^2(\hslash (\varrho ,\theta )))cos(\varrho +\theta +\vartheta )+4\vartheta$. Considering $L_f=0.5\sqrt{2}$, $L_k=0.03\sqrt{2}$ and $M=0.08$, for functions f and k, we have

$$\begin{array}{cc}\hfill & {\nu }_{\tau }(0.5({sin}^2\left({\hslash }_1(\varrho ,\theta )\right)+{cos}^2\left({\hslash }_1(\varrho ,\theta )\right))-0.02(\varrho +\theta )\hfill \\ \hfill & -0.5({sin}^2\left({\hslash }_2(\varrho ,\theta )\right)-{cos}^2\left({\hslash }_2(\varrho ,\theta )\right))+0.02(\varrho +\theta ))\hfill \\ \hfill & \le {\nu }_{{\displaystyle \frac{\tau }{0.5\sqrt{2}}}}\left({\hslash }_1-{\hslash }_2\right),\hfill \end{array}$$

(29)

for all $\theta \in {\Xi }_1$, ${\hslash }_1,{\hslash }_2\in \mathbb{R}$, $\tau \in {\Xi }_2$ and $\varrho \in {\rm Y}$, and

$$\begin{array}{cc}\hfill & {\nu }_{\tau }(0.03({sin}^2\left({\hslash }_1(\varrho ,\theta )\right)+{cos}^2\left({\hslash }_1(\varrho ,\theta )\right))cos(\varrho +\theta +\vartheta )\hfill \\ \hfill & -4\vartheta -0.03({sin}^2\left({\hslash }_2(\varrho ,\theta )\right)-{cos}^2\left({\hslash }_2(\varrho ,\theta )\right))cos(\varrho +\theta +\vartheta )+4\vartheta )\hfill \\ \hfill & \le {\nu }_{\frac{\tau }{0.03\sqrt{2}}}\left({\hslash }_1-{\hslash }_2\right),\hfill \end{array}$$

(30)

for all $\theta ,\vartheta \in {\Xi }_1$, ${\hslash }_1,{\hslash }_2\in \mathbb{R}$, $\tau \in {\Xi }_2$ and $\varrho \in {\rm Y}$.

According to the function $\aleph \in C({\rm Y}\times {\Xi }_1)$ with ${\aleph }^{\prime }(\varrho ,\theta )\ne 0$, if we have

$$\begin{array}{cc}\hfill & {\nu }_{\tau }{(}^H{\mathbb{D}}_{0+}^{\frac{1}{5},\frac{1}{10};\aleph }\hslash (\varrho ,\theta )=0.5({sin}^2(\hslash (\varrho ,\theta ))+{cos}^2(\hslash (\varrho ,\theta )))-0.02(\varrho +\theta )\hfill \\ \hfill & +{\int }_0^{\theta }0.03({sin}^2(\hslash (\varrho ,\theta ))+{cos}^2(\hslash (\varrho ,\theta )))cos(\varrho +\theta +\vartheta )+4\vartheta d\vartheta )\hfill \\ \hfill & \le {\phi }_{\tau }\left(\theta \right),\hfill \end{array}$$

(31)

for all $\theta ,\vartheta \in {\Xi }_1$, $\hslash \in \mathbb{R}$, $\tau \in {\Xi }_2$ and $\varrho \in {\rm Y}$, where $\phi :{\Xi }_1\times {\Xi }_2\to {\Xi }_3$ is a continuous modular set with

$$\begin{array}{c}\hfill {\nu }_{\tau }\left(\frac{1}{\lambda (\ell )}{\int }_0^{\theta }{\aleph }^{\prime }(\varrho ,\varpi ){(\aleph (\varrho ,\theta )-\aleph (\varrho ,\varpi ))}^{\frac{-4}{5}}\phi (\varpi ,\tau )d\varpi \right)\le {\phi }_{\frac{\tau }{0.08}}\left(\theta \right),\end{array}$$

(32)

for each $\theta \in {\Xi }_1$, $\tau \in {\Xi }_2$ and $\varrho \in {\rm Y}$, then, we can find a unique CRO ${\hslash }_0:{\rm Y}\times {\Xi }_1\to \mathbb{R}$, such that

$$\begin{array}{cc}\hfill {\hslash }_0(\varrho ,\theta )& =\frac{{(\aleph (\varrho ,\theta )-\aleph (\varrho ,0))}^{-\frac{1}{2}}}{\Gamma \left(\lambda \right)}\vartheta \hfill \\ \hfill & +{\mathcal{I}}_{0+}^{\frac{1}{5};\aleph }0.5({sin}^2\left({\hslash }_0(\varrho ,\theta )\right)+{cos}^2\left({\hslash }_0(\varrho ,\theta )\right))-0.02(\varrho +\theta )\hfill \\ \hfill & +{\mathcal{I}}_{0+}^{\frac{1}{5};\aleph }\left[{\int }_0^{\varpi }0.03({sin}^2\left({\hslash }_0(\varrho ,\theta )\right)+{cos}^2\left({\hslash }_0(\varrho ,\theta )\right))cos(\varrho +\theta +\vartheta )+4\vartheta d\vartheta \right],\hfill \end{array}$$

(33)

with ${\mathcal{I}}_{0+}^{\frac{1}{2};\aleph }\hslash (\varrho ,0)=\vartheta$, and

$$\begin{array}{c}\hfill {\nu }_{\tau }\left(\hslash (\varrho ,\theta )-{\hslash }_0(\varrho ,\theta )\right)\le {\phi }_{\frac{0.08\tau }{0.9400373450}}\left(\theta \right),\end{array}$$

(34)

where $M\left(L_f+L_k\right)=0.05996265503$, for each $\theta \in {\Xi }_1$, $\tau \in {\Xi }_2$ and $\varrho \in {\rm Y}$.

In the following, we have shown the exact solution of Equation (28) in Figure 2.

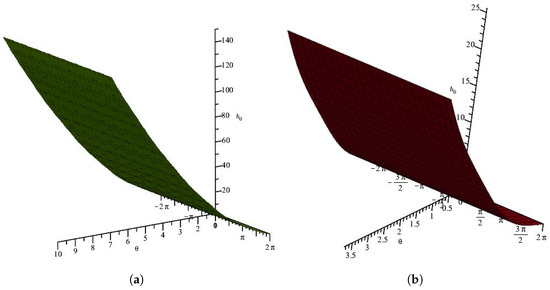
Figure 2. Graphic representation of the exact solution of Equation (28) for different values. (a) The exact solution of stochastic fractional nonlinear Volterra-IDE for $\theta \in (1,10)$. (b) The exact solution of stochastic fractional nonlinear Volterra-IDE $\theta \in (\frac{1}{10},\frac{15}{4})$.

5. Conclusions

In this paper, we have considered a nonlinear stochastic fractional Volterra integro-differential equation, and we have presented a modular stability result for it. We have investigated the stability in the considered space by introducing special functions and considering the aggregation function, and we have obtained the best approximation for the desired equation. An application of our results is also presented, and we have provided graphical representations for some important functions and solved examples. In future work, we hope to extend our results with a nonstandard finite difference scheme and spatio-temporal numerical modeling [2,12,13,14,15,16,17,18,19,20,21,22,23,24].