Abstract
Tandem repeats (TRs) are important components of eukaryotic genomes; they have both structural and functional roles: (i) they form essential chromosome structures such as centromeres and telomeres; (ii) they modify chromatin structure and affect transcription, resulting in altered gene expression and protein abundance. There are established links between variations in TRs and incompatibilities between species, evolutionary development, chromosome mis-segregation, aging, cancer outcomes and different diseases. Given the importance of TRs, it seemed essential to develop an efficient, sensitive and automated application for the identification of all kinds of TRs in various genomic sequences. Here, we present our new GRM application for identifying TRs, which is designed to overcome all the limitations of the currently existing algorithms. Our GRM algorithm provides a straightforward identification of TRs using the frequency domain but avoiding the mapping of the symbolic DNA sequence into numerical sequence, and using key string matching, but avoiding the statistical methods of locally optimizing individual key strings. Using the GRM application, we analyzed human, chimpanzee and mouse chromosome 19 genome sequences (RefSeqs), and showed that our application was very fast, efficient and simple, with a powerful graphical user interface. It can identify all types of TRs, from the smallest (2 bp) to the very large, as large as tens of kilobasepairs. It does not require any prior knowledge of sequence structure and does not require any user-defined parameters or thresholds. In this way, it ensures that a full spectrum of TRs can be detected in just one step. Furthermore, it is robust to all types of mutations in repeat copies and can identify TRs with various complexities in the sequence pattern. From this perspective, we can conclude that the GRM application is an efficient, sensitive and automated method for the identification of all kinds of TRs.
1. Introduction
Repetitive DNA is an important component of eukaryotic genomes, comprising more than 50% of the genome size in most species [1,2]. It is composed of a large number of different classes of repetitive DNA sequences, either dispersed or arranged in tandem [2,3,4]. Among tandem repetitive DNA, there are moderately repetitive DNAs, such as ribosomal RNA (rRNA) and protein-coding gene families or short tandem telomeric repeats, as well as highly repetitive non-coding microsatellite and satellite sequences [3].
Tandem repeats (TRs) have a propensity to mutate and become polymorphic by expansion or contraction in the number of repeat units. This may be due to slippage during DNA replication, unequal crossing-over during recombination, or the imprecise repair of double-strand DNA breaks [5,6,7]. Tandem repeats appear in two different structural forms: as the TRs of individual head-to-tail monomers, forming monomeric arrays, and as the TRs of nmer higher order repeats (HOR): copies consisting of TRs of n head-to-tail monomers. Divergence among HOR copies in a HOR array is small, below ~5%, while divergence among monomers within each HOR copy is sizably larger, 20–40% [8,9,10].
The significance of repetitive DNA in the genome is not completely understood, and it has been considered to have both structural and functional roles. Various TR arrays are generally found in heterochromatin and form essential chromosome structures such as centromeres and telomeres [11,12]. Tandem repeat DNAs are implicated in centromeric functions, such as segregation in mitosis and meiosis, essential during cell division, the pairing of homologous chromosomes, sister chromatid attachment and the formation of kinetochore structures. In addition, the most interesting potential role of TRs is gene regulation, related to a general concept that the regulatory system of genomes is encoded in networks of repetitive sequence relationships [13,14]. If present in upstream regulatory regions, TRs can modify the chromatin structure and affect transcription, resulting in altered gene expression and protein abundance [5,15,16,17,18,19,20]. In this sense, there are established links between TRs and phenotypes in a wide range of organisms, including humans [21]. For example, TR derepression is associated with cancer outcomes [22], chromosome mis-segregation and aneuploidy [23] and aging [24]. In addition, a variation in TR copy number has been associated with genetic incompatibilities between species [25], evolutionary development [26,27,28] and with different diseases, such as fragile-X mental retardation [29], Huntington’s disease [30], myotonic dystrophy [31], spinal and bulbar muscular atrophy [32] and Friedreich’s ataxia [33].
Given the importance of the known and potential biological roles of TRs and their usefulness in other biological studies, the identification and analysis of all types of TRs are currently of substantial interest. From this perspective, it seemed essential to us to develop an efficient and sensitive algorithm for the identification of all kinds of TRs in various genomic sequences.
A vast range of algorithms already exists for the direct or indirect detection of TRs in DNA sequence [34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49]. In general, all TR detection algorithms can be divided into two main categories: flexible statistical string-matching algorithms, and signal processing algorithms. Although these algorithms use a whole range of different methods and powerful analysis tools developed in traditional signal processing, all suffer from significant limitations. Some of the relevant observed problems that are analyzed and pointed out in Refs. [36,40,41,42,43,44,45,48,49,50,51] could be summarized as follows. Statistical string-matching algorithms have problems with: (i) repeats containing sizeable substitutions and/or insertions/deletions, (ii) repeats having very large repeat units (above 2 kb), (iii) several overlapping possible repeat structures, and (iv) excessive running time. Signal-processing algorithms have problems with (i) numerical artifacts, (ii) the poor resolution of spectral analyses and (iii) significant background noise that masks information. In general, because of the approximate, polymorphic and copy number variant nature of repeat units, the identification of TRs is a very complex problem, and different algorithms exhibit different degrees of robustness for various types of repeats [50]. Accordingly, in order to detect as many different types of polymorphic repeats as possible, some algorithms introduce an arbitrarily threshold, as well as user-defined parameters, which influence the results. In this way, depending on the choice of parameters/thresholds, the algorithms identify only one part of the TRs (for example, only small ones, or only approximately regular ones) and ignore the others. Therefore, it is clear that there still remains a high potential for improving the efficiency of different methods and algorithms for TR detection.
Here, we present our new GRM algorithm, and accompanying GRM application, which is designed to overcome all of the above-mentioned limitations: (i) it does not require any prior knowledge of the sequence structure (ii) it does not use any arbitrary or user-defined parameters/thresholds; (iii) it is robust to substitutions and insertions/deletions, as well as to the various complexities of the sequence pattern; (iv) it is applicable to all repeat units, from very small to very large, as large as tens of kilobasepairs; (v) it is very fast (detection of all the TRs in an average size (50 Mbps) chromosome takes less than a minute on a personal computer).
Our new GRM algorithm incorporates the main ideas presented in [50,52,53], with significant modifications and extensions to achieve the goal of the detection and extraction of all the TRs in one step. The main advantage of the new algorithm is that, unlike the previous one, it is fully automated and does not require any prior knowledge of the sequence, or any knowledge of GRM diagram analysis. The user of the GRM application simply loads the DNA sequence and gets a report of all the TRs in a given sequence, their positions, TR copy numbers, TR lengths and the TR sequences broken down into repetitive units.
Science is entering into a new era of genomics, with high-resolution maps based on long reads, where centromeric regions are accurately represented [54]. Now, in centromeric regions, canonical HOR units, many structural variant types with a high variation in relative frequency, have become accessible and prompted the development of new software programs to precisely find or characterize TR using DNA-sequencing data. Global Repeat Map is just such a novel software, which enables the precise identification of complex repeats [55,56]. Complete sequencing requires highly sophisticated software for its analysis.
The remainder of this paper is organized as follows. In Materials and Methods, we present a new GRM algorithm. In Results, we present the usage of the GRM application for the entire sequence of human, chimpanzee and mouse chromosome 19. Finally, in Discussion, we describe directions for future research and development and the possible improvements of the application.
2. Materials and Methods
2.1. Algorithm Outline
In the first step, we create a dimensional array, , of three-dimensional vectors
where is the length of the observed sequence, and is the length of the key string ( = 8). The first component of each vector in array contains the vector’s position in the sequence (), and the second component of each vector contains an integer value of the subsequence with the length of 8 bps whose first nucleotide is at the position , i.e., (Figure 1). The third component, , represents the fragment’s length in bps, and its value is calculated in the next step.

Figure 1.
Scheme of construction of N − k dimensional array of three-dimensional vectors in the first step of the GRM algorithm.
In the second step, we sort array on two levels; the criterion for the first sorting level is the second vector’s component, , and the criterion for the second sorting level is the first vector’s component, In this way, all vectors with end up at the beginning of the array (sorted by the first component , and all vectors with end up at the end of the array (also sorted by the first component . Note that, in the sorted array, the first component of the vector generally no longer corresponds to its position in the sequence, i.e., . Next, we subtract the first components of all adjacent vectors and write down the difference in the third component of minuend vector, i.e., . Because all adjacent vectors in the sorted array have identical second component, the difference written in actually represents the minimum distance between two identical key strings in a sequence, which is known as a fragment length. The exceptions are adjacent vectors in which the second component changes (for example, from to ), in which case we assign zero to the the third component of the minuend.
In the third step, we sort back array by the first component to get the initial array in which now each vector has its fragment length written in the third component. In this array, the position of each vector again corresponds to its first component, i.e., . Next, we divide resulting array in smaller subarrays of variable length where is integer between 100 and 2000. In the case of large , the resulting subarray can contain more different TRs and the most dominant TR could saturate the others. On the other hand, too small value of would result in excessive algorithm running time. We bypass this conundrum by starting each subarray with sufficiently small bp, calculate its GRM diagram, and increase as long as only peaks of one TR and its multiples are present in the GRM diagram. As the upper limit of this procedure, we took the length bp, because for a too large subarray, noise in the GRM diagram can mask new peaks, i.e., a new TR. In this way, we ensure that the algorithm detects all TRs without spending too much running time in the following steps.
In the fourth step, we use the GRM diagram of each subarray from last step. By identifying the prominent GRM peak (fragment lengths with higher frequency), we detect dominant subarray’s TR unit and its multiples. Next, we merge all adjacent subarrays, which have approximately same dominant TR units or their multiples, into larger subarrays, because they contain the same TRs and therefore should be considered, in the next step, as the same subarray.
In the last step, for each subarray, we identify most frequent vectors that have the same second component and the third component equal to the dominant fragment length. Using the second component of these vectors (now converted back in an 8 bp string) as a cutting string (or “computer enzyme”), we cut the sequence in each subarray into TRs’ basic units, analyze them and display results in the report (Figure 2a, Supplementary Tables S1–S3).
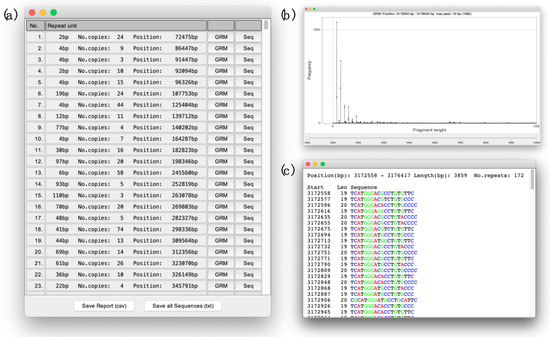
Figure 2.
(a) The report listing of all TRs in the observed sequence. (b) The GRM diagram of the subarray in which chosen TR (No. 251, Repeat unit 19 bp, Supplementary Table S1) was found. (c) The report with the repetitive sequence (No. 22, repeat unit 19 bp, Supplementary Table S1) displayed as a series of basic repetitive units (19 bp).
2.2. Application Usage and Output
The GRM graphical user interface application is freely available at http://genom.hazu.hr/tools.html, accessed on 1 November 2022. As we mentioned before, the application does not require any user-defined threshold or parameters. Input to the application consists simply of a sequence file in the fasta format (.fa) or any similar format with the header first line (the name and/or sequence description), followed by a body. The body should consist of a genomic sequence, which can be broken into lines (as in fasta file) or can also be in one line. The sequence should generally consist of four nucleotides, A, C, G, T and the symbol ‘N’ in possible places where the nucleotides have not yet been identified. All other symbols within the sequence that may appear as a typo or ambiguity between two or more nucleotides are converted during the load process into ‘N’s.
After the sequence-loading phase, the application autonomously goes through the steps described in the Algorithm outline and, as a result, delivers a report listing all the TRs in the observed sequence (Figure 2a). In the report, next to each identified TR, there is the button that displays the GRM diagram (Figure 2b) of the subarray in which TR was found and the button that displays the new report (Sequence report) with the repetitive sequence itself (Figure 2c). In the Sequence report, the sequence is displayed over copies of TR basic units obtained by a dominant key string obtained in the last step described in the Algorithm outline. In each Sequence report, each nucleotide is colored with its own color to make it easier for visual identification of deviations from the ideal TR copies, such as deletions, insertions or substitution of individual or group nucleotides. The exceptions are very long sequences of TRs that require a lot of time for coloring, and therefore they are displayed without colors. In addition, at the bottom of the main report (Figure 2a) there are two buttons, the button for exporting the entire main report, and the button for exporting all TR sequences in one file.
3. Results
As a case study, we analyzed three whole chromosome sequences: Homo sapiens chromosome 19, assembly GRCh38.p13 (NCBI Reference Sequence: NC_000019.10), Pan troglodytes chromosome 19 assembly Clint_PTRv2 (NCBI Reference Sequence: NC_036898.1) and Mus musculus chromosome 19, assembly GRCm39 (NCBI Reference Sequence: NC_000085.7) (Table 1).

Table 1.
Case study genome information for reference and representative genomes. Homo sapiens assembly GRCh38.p13, Pan troglodytes assembly Clint_PTRv2 and Mus musculus assembly GRCm39. Download sequences and annotation from GenBank (https://www.ncbi.nlm.nih.gov/genome/51, https://www.ncbi.nlm.nih.gov/genome/202, https://www.ncbi.nlm.nih.gov/genome/52, accessed on 1 November 2022).
Due to size, the GRM report of all the TRs and their sequences is given in Supplementary Data (for human chromosome 19 in Supplementary Table S1 and Supplementary Data S1, for chimpanzee chromosome 19 in Supplementary Table S2 and Supplementary Data S2 and for mouse chromosome 19 in Supplementary Table S3 and Supplementary Data S3). In the following text, we analyze the results for human chromosome 19 in more detail, and then we give a comparative analysis of the results for these three chromosomes.
3.1. Human Chromosome 19
Let us consider three characteristic TRs in human chromosome 19. We start with No. 251 from Supplementary Table S1, TRs with repeat unit 19 bp (172 copies, RefSeq NC_000019.10 position 3,172,558–3,176,417 bp). In the GRM diagram for the subsequence containing these TRs (Figure 3a), prominent peaks appear for fragment lengths of 19 bp and its multiples. The multiples of the 19 bp peak in the GRM diagram and the points at the higher fragment lengths in the Fragment diagram (Figure 3b) occur due to different mutations (insertions, deletions, substitutions) in the components (“key string”) of the vectors . Due to these mutations, “key string” does not have its identical pair at a TR length distance but finds it on multiples of these lengths (Figure 3b). In the case of completely regular TRs, we would have all points at y = 39 bp in the Fragment graph (Figure 3b), which would result in only one peak in the GRM diagram (Figure 3a). During step four (Algorithm outline), we identify all major peaks, where the largest one defines TR for the observed subarray, and other peaks help in the decision on possible merging with the adjacent subarrays. At higher peaks for the observed 19bp TRs there is a shift in one bp, which is the result of one nucleotide insertion in the basic repeat unit. By inspecting sequence No. 251 in Supplementary Data S1, we can confirm that 19 bp TR is repeated with lengths (19 bp, 19 bp, 20 bp, 19 bp, 20 bp, 20 bp, 19 bp, 19 bp, 19 bp, 19 bp, 20 bp, 19 bp, 19 bp, 20 bp, 19 bp, 20 bp, 19 bp, 19 bp, 20 bp, …).
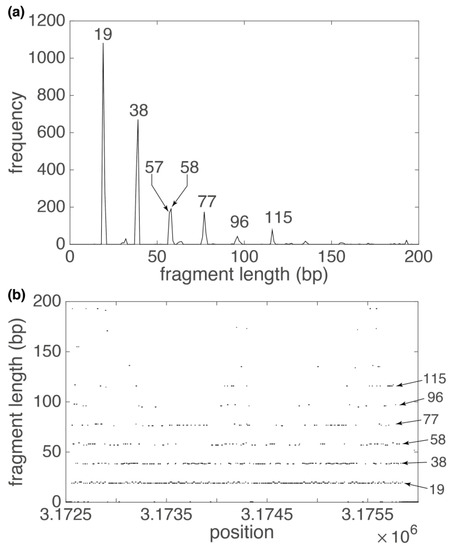
Figure 3.
GRM diagram (a) and Fragment diagram (b) for 19 bp TR subarray in human chromosome 19 (Supplementary Table S1, repeat No. 254). (a) Pronounced GRM peaks at correspond to basic repeat unit of 19 bp and its multiples. Deviations from perfect multiples of the basic unit occur due to insertions and deletions. (b) Each dot in the Fragment diagram corresponds to fragment length (component of vector at that position (component of vector . In the Fragment diagram, the density of the points decreases with increasing multiples of the basic repetitive unit, which corresponds to a decrease in the height of the peaks in corresponding GRM diagram.
The next example is No. 538, TRs with a basic repetitive unit of 7456 bp (three copies, RefSeq NC_000019.10 position 8,743,683–8,766,063 bp) from Supplementary Table S1. In the GRM diagram for THE subsequence containing these TRs (Figure 4a), there is only one prominent peak (fragment lengths of 7456 bp) due to the small number of copies of these TRs and due to the relatively small mutual deviation of the individual TR copies. All nucleotide substitutions in these copies are visible as small peaks in the GRM diagram (Figure 4a) and as dispersed dots in the Fragment diagram (Figure 4b). The inserts in Figure 4a,b show that, in addition to nucleotide substitutions, there are also nucleotide deletions and insertions in different parts of the TR copies, which are manifested as smaller peaks around the main 7456 bp peak in the GRM diagram, and as points around y = 7456 bp in the Fragment diagram.
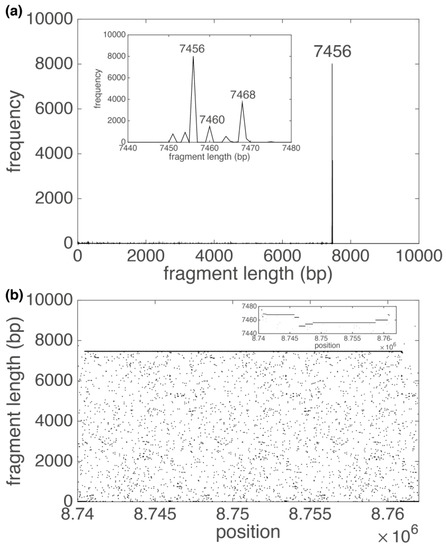
Figure 4.
GRM diagram (a) and Fragment diagram (b) for 7456 bp TR subarray in human chromosome 19 (Supplementary Table S1, repeat No. 538). (a) The pronounced GRM peak at 7456 bp corresponds to basic repeat unit of 7456 bp. Insert gives magnified presentation of weak peaks around 7456 bp, which are sizably screened by a 7456 bp peak. (b) Each dot in the Fragment diagram corresponds to the fragment length (component of vector at that position (component of vector . Insert gives magnified presentation of points around 7456 bp, which are consequence of nucleotide mutation in TR copies. In the Fragment diagram, most points are located around y = 7456 bp, which corresponds to 7456 bp peak in the GRM diagram. The other points in the Fragment diagram create a small noise, which is visible in the GRM diagram as tiny peaks.
The most interesting example is No. 1243, TRs with a repetitive unit 2896 bp (12 copies, RefSeq NC_000019.10 position 24,412,442–24,447,210 bp), from Supplementary Table S1. The GRM diagram (Figure 5a) and Fragment diagram (Figure 5b) reveal the basic monomer units of length 171 bp that are organized as TRs of 17 mer (17·171 bp ≈ 2896 bp) into higher order repeats (HOR), each consisting of 17 monomers. In general, for monomeric arrays, frequencies of peaks at ~(basic monomer length)·n bp gradually decrease with increasing n and a peak sizably above this background is an indication for HOR. In addition, due to the deletion and insertion of whole monomers in our 17 mer HOR copies, there are noticeable peaks at fragment lengths 2724 bp (~171·16 bp) and 3067 bp (~171·18 bp) (Figure 5a), respectively.
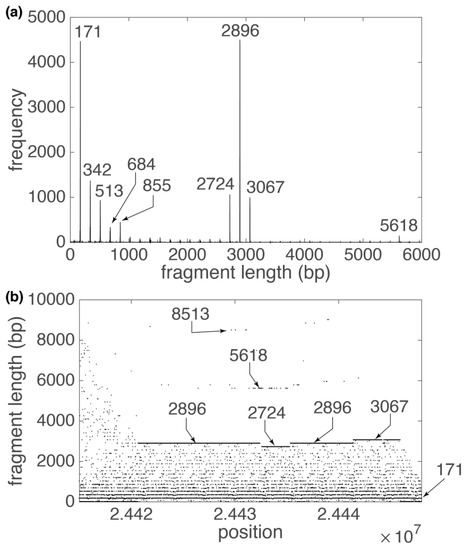
Figure 5.
GRM diagram (a) and Fragment diagram (b) for alpha satellite 2896 bp HOR subarray in human chromosome 19 (Supplementary Table S1, repeat No. 1243). (a) Pronounced GRM peaks that correspond to alpha satellite HORs are denoted. The pronounced GRM peak at 2896 bp is a signature of 17 mer HOR (2896: 171 ≈ 17). (b) Each dot in the Fragment diagram corresponds to fragment length (component of vector at that position (component of vector . In the Fragment diagram, most points are located around y = , which corresponds to multiples of alfa satellite lengths and peaks in GRM diagram. The highest concentration of points is at y = 2896 bp, which corresponds to 17 mer HOR length. There is also a smaller concentration of points at positions 5168 bp and 8513 bp, which are approximately multiples of 17 mer HOR length.
The 171 bp monomers are known as alpha satellite monomers [9] and they are the most abundant constituent of centromeres in human and other primate chromosomes. In particular, the centromeric region of human chromosomes contains alpha satellite DNA composed of diverged monomers, some sections without, and some with a higher order repeat structure (HORs) [57,58]. In pericentromeric regions, alpha satellite DNAs are surrounded by arrays of “classical” satellites (satDNA 1–4) [59,60]. The GRM application confirms these findings and shows that the centromere of the human chromosome 19 is composed of 17 mer HOR (2746 bp), which is surrounded by a series of ~171 bp TRs (Table 1, Supplementary Table S1 and Figure 6). In addition, as can be seen from Figure 6, some of the ~171 bp alpha satellite arrays from Table 1 are organized into HORs, but their highest peak in GRM diagram is a ~171 bp peak, so the GRM application classified them as ~171 bp TRs.
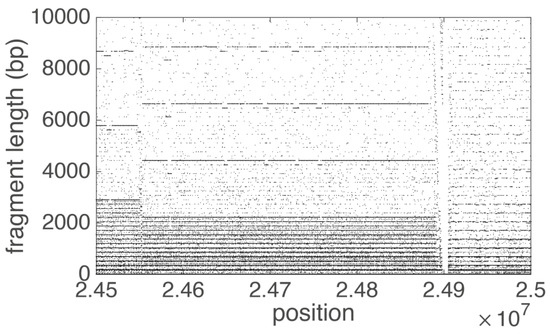
Figure 6.
Fragment diagram for part of centromeric region of human chromosome 19. Each dot in the Fragment diagram corresponds to the fragment length (component of vector ) at that position (component of vector . On the left side of the diagram the alpha satellite monomers are organized in 17 mer HOR (2896: 171 ≈ 17) structures, in the middle in 13 mer HOR (2216: 171 ≈ 13) structures and on the left in tandem monomeric arrays without any HOR structures.
3.2. Comparison of Human, Chimp and Mouse Chromosome 19 GRM Results
The GRM application found 3026 different arrays of TRs in human chromosome 19 (ReqSeq NC_000019.10), 2827 arrays of TRs in chimpanzee chromosome 19 (ReqSeq NC_036898.1) and 7316 arrays of TRs in mouse chromosome 19 (ReqSeq NC_000085.7). In total, in human chromosome 19 these TRs comprised 5,332,298 bp, in chimpanzee chromosome 19, 3,044,102 bp, and in mouse chromosome 19, 7,399,221 bp. Given that human, chimpanzee and mouse chromosome 19 have approximately the same number of nucleotides, it is obvious that the mouse genome has, on average, the most TR arrays.
However, the distribution of repetitive DNA in these three organisms is significantly different (Figure 7). While in mouse chromosome 19 the largest number of repeats come from short TRs, in chimpanzee and human chromosome 19 a large proportion comes from medium-long and long TRs. This is largely due to ~171 bp alpha satellite DNA, which completely builds the centromeric and pericentromeric regions of chimpanzee and human genomes [61]. In addition, as we have shown in example three, in the centromeric region of human chromosome 19, parts of these alpha satellite monomers are organized into different nmer HOR structures (Table 2, Figure 5 and Figure 6).
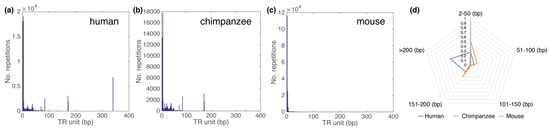
Figure 7.
Distribution of repetitive sequences over TR unit length in human (a), chimpanzee (b) and mouse (c) chromosome 19. (a–c) The range of the abscissa is limited to TRs of length 400 bp for better visibility. (d) Radar chart with the proportion of bases in TR, divided into five groups according to the length of the basic TR unit (0–50 bp, 51–100 bp, 101–150 bp, 151–200 bp and >200 bp). Human 340 bp TRs are in most cases alpha satellite 2 mer HORs with basic ~171 bp repetitive monomer.

Table 2.
TRs from human chromosome 19 centromeric region. The data are result of the GRM application and are part of the analysis given in Supplementary Table S1. Some of ~171 bp alpha satellite arrays in table are additionally organized in HORs as can be concluded from Figure 6 (left side of Fragment diagram).
On the other hand, although the chimpanzee’s centromeric region of chromosome 19 is also composed of ~171 bp alpha satellite monomers (TRs No. 1159–No. 1216 from Supplementary Table S2), it completely lacks organization into higher-order structures. Furthermore, mouse chromosome 19 has no alpha satellites at all, neither in the form of monomeric arrays, nor organized into HORs. In the mouse centromeric region, the GRM application finds only ~210 bp and ~384 bp TRs (Supplementary Table S3), which are organized in monomeric arrays without higher-order structures. These TRs are interesting examples of highly conserved, tandemly multiply repeated sequences in the centromeric and pericentromeric regions of the mouse genoma. Namely, it was found that there are two tandemly repeated sequences in the mouse genome, known as minor (MiSat) and major (MaSat) satellites, composed of 120-bp and 234-bp repeat units, respectively [62,63]. However, it was shown that there are two levels of subunits within the 234-bp repeat unit (4 7–11 bp basic subunits form 28 bp/30 bp secondary HOR subunits, 228 bp/30 bp secondary subunits form 58 bp tertiary subunits and 458 bp/60 bp subunits form 234 bp quartic HOR units [63]. The differences between the human, chimpanzee and mouse TRs are due to their different evolutionary development (or possible sequence methods used for covering gaps in centromere sequence assembly).
4. Discussion
In this study, we present our new GRM application based on the ideas of Key string and the GRM diagram that we introduced earlier in Refs. [50,64,65]. As a case study, using the GRM application, we analyze whole human, chimpanzee and mouse chromosome 19. In these chromosomes, we identify over 10,000 different arrays of TRs and HORs and analyze three characteristic examples from the human chromosome, which indicate substantial differences between DNA TR organization in the human, chimpanzee and mouse genome.
Let us comment on the comparison with other known computer tools for the identification and analyses of TRs [34,35,36,37,38,39,40,41,42,43,44,45,46,47,48,49]. Unlike all the listed algorithms, the GRM application can identify all types of TRs, from the smallest (2 bp TR arrays) to the very large, as large as tens of kilobasepairs. It is very important to emphasize that the GRM application, unlike most other TR algorithms, does not require any prior knowledge of sequence structure and does not require any user-defined parameters or thresholds. In this way, it ensures that the full spectrum of TRs can be detected in just one step and that results do not depend on any initial input. Furthermore, it is robust to all types of mutations in TR copies and, therefore, can identify TRs with various complexities in the sequence pattern. In addition, the GRM application offers additional GUI tools: (i) the GRM diagram, which can be used to analyze the internal structure of each TR and to discover possible HOR structures within it; and (ii) the Sequence report that displays TR sequences as a series of basic repetitive units with colored nucleotides. In this way, the Sequence report can be used for the visual and easy identification of all kinds of indels (insertions, deletions and substitutions). Furthermore, this representation of TRs over a series of individual copies can easily be used for the additional statistical analysis of the differences between them or to search for a consensus sequence. Finally, the GRM application is very fast, efficient and simple from a computational viewpoint, with powerful graphical user interface applications. It provides a fast scan of TRs in a whole chromosome sequence, taking 1–2 min computing time per average chromosome using MacBook with a 1.6 GHz Dual-Core Intel Core i5 processor.
Next, let us comment on the possible flaws of the GRM application. The weakest point of this algorithm is the part of the third step (Algorithm outline), in which we divide the resulting array into smaller subarrays of variable length. As we explain in the Algorithm outline, we started with a size of 100 bp for each subarray, calculated a GRM diagram, and increased the size of a subarray as long as only the peaks of one TR and its multiples were present. As the upper limit of this procedure, we took the length of 2000 bp. Detailed analysis indicated that, although the starting subarray was very small, it was still possible that there were two TRs within it, and that it expanded in the direction of increasing one. In that way, one of TRs remained saturated by the other. The precondition for this event is that the saturated TR is also saturated in the previous adjacent subarray, i.e., that the previous subarray starts with a dominant TR, which eventually saturates a smaller part of the second TR before the substring expansion stops. From those arguments, it is clear that the probability of this event is quite small, but it is still possible. Therefore, we started to develop a new deep learning (deep neural network) algorithm that would replace the third step procedure described in the Algorithm outline. This algorithm, based on the TR motifs from the Fragment diagram (Figure 3a, Figure 4a, Figure 5a and Figure 6), will recognize whether there are one, none or more TRs in a subarray. Based on the algorithm judgment, it will be decided whether to reduce or increase the starting subarray. This will also allow us to speed up the GRM application, because the third step will start with a wider subarray and will move in the direction of expansion or contraction.
Furthermore, there is a minor inconsistency in a way the GRM Report displays HOR structures (Figure 2a). Namely, in the case when basic monomers are organized into HOR structures, the GRM application sometimes lists the basic monomer and sometimes the HOR basic unit, depending on the highest peak in the GRM diagram. This issue can be resolved in the presented application by the user activating the GRM diagram GUI option next to each TR with the potential internal structure. We believe that the already mentioned deep learning algorithm could automatize this process.
5. Conclusions
This paper shows that the GRM application can identify all the TRs in an arbitrarily large genomic sequence of any organism. Therefore, the GRM application provides the opportunity to determine the complete TR annotation for different species. Complete TR annotations will enable the analysis of the TRs’ single-nucleotide variants and monomer copy-number variants within primates and other eukaryotic lineages and their interspecies comparison. In the case of centromeric TRs, these studies could reveal the mechanism of TR formation and their organization within centromeric regions, which will help us to understand their role in centromeric function, and in particular their role in the formation of functional kinetochore. In a general case, the study of interspecies TR differences will indicate the possible role of TRs in the gene regulatory network and consequently their impact on morphological and phenotypic difference, disease onset, genetic incompatibilities between species and evolutionary development.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/a15120458/s1, Supplementary Data S1: Sequence report for Homo sapiens chromosome 1 assembly GRCh38.p13 (NCBI Reference Sequence: NC_000022.11), Supplementary Data S2: Sequence report for Pan troglodytes chromosome 19 assembly Clint_PTRv2 (NCBI Reference Sequence: NC_000085.7), Supplementary Data S3: Sequence report for Mus musculus chromosome 19, assembly GRCm39 (NCBI Reference Sequence: NC_036898.1), Supplementary Table S1: GRM report for Homo sapiens chromosome 1 assembly GRCh38.p13 (NCBI Reference Sequence: NC_000022.11), Supplementary Table S2: GRM report for Pan troglodytes chromosome 19 assembly Clint_PTRv2 (NCBI Reference Sequence: NC_000085.7), Supplementary Table S3: GRM report for Mus musculus chromosome 19, assembly GRCm39 (NCBI Reference Sequence: NC_036898.1).
Author Contributions
Conceptualization, M.G. and V.P.; methodology, M.G.; software, M.G., I.V. and L.M.; validation, I.V. and L.M.; formal analysis, I.V. and L.M.; investigation, M.G. and V.P.; resources, M.G.; data curation, L.M.; writing—original draft preparation, M.G.; writing—review and editing, V.P. and I.V.; visualization, M.G.; supervision, V.P.; project administration, M.G.; funding acquisition, M.G. All authors have read and agreed to the published version of the manuscript.
Funding
This work was fully supported by Croatian Science Foundation under the project IP-2019-04-2757.
Data Availability Statement
The GRM graphical user interface application (JAR file) is freely available at http://genom.hazu.hr/tools.html, accessed on 1 November 2022. It can be run on any platform that has Java Runtime Environment (JRE) installed (freely available at https://www.oracle.com/java/technologies/javase-downloads.html, accessed on 1 November 2022). Reference genome sequences used to test the application are freely available at https://www.ncbi.nlm.nih.gov/genome, accessed on 1 November 2022.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; or in the decision to publish the results.
References
- Santos, V.; Da Silva, E.F.; Almeida, C. Genome size and identification of repetitive DNA sequences using low coverage sequencing in Hancornia speciosa Gomes (Apocynaceae: Gentianales). Genet. Mol. Biol. 2020, 43, e20190175. [Google Scholar] [CrossRef] [PubMed]
- Biscotti, M.A.; Olmo, E.; Heslop-Harrison, J.S. Repetitive DNA in eukaryotic genomes. Chromosome Res. 2015, 23, 415–420. [Google Scholar] [CrossRef] [PubMed]
- López-Flores, I.; Garrido-Ramos, M. The Repetitive DNA Content of Eukaryotic Genomes. Genome Dyn. 2012, 7, 1–28. [Google Scholar] [CrossRef] [PubMed]
- Belyayev, A.; Josefiová, J.; Jandová, M.; Kalendar, R.; Krak, K.; Mandák, B. Natural History of a Satellite DNA Family: From the Ancestral Genome Component to Species-Specific Sequences, Concerted and Non-Concerted Evolution. Int. J. Mol. Sci. 2019, 20, 1201. [Google Scholar] [CrossRef] [PubMed]
- A Bolton, K.; Ross, J.P.; Grice, D.M.; A Bowden, N.; Holliday, E.G.; A Avery-Kiejda, K.; Scott, R.J. STaRRRT: A table of short tandem repeats in regulatory regions of the human genome. BMC Genom. 2013, 14, 795. [Google Scholar] [CrossRef] [PubMed]
- Debrauwère, H.; Buard, J.; Tessier, J.; Aubert, D.; Vergnaud, G.; Nicolas, A. Meiotic instability of human minisatellite CEB1 in yeast requires DNA double-strand breaks. Nat. Genet. 1999, 23, 367–371. [Google Scholar] [CrossRef]
- Brinkmann, B.; Klintschar, M.; Neuhuber, F.; Hühne, J.; Rolf, B. Mutation Rate in Human Microsatellites: Influence of the Structure and Length of the Tandem Repeat. Am. J. Hum. Genet. 1998, 62, 1408–1415. [Google Scholar] [CrossRef] [PubMed]
- Sullivan, L.L.; Chew, K.; Sullivan, B.A. α satellite DNA variation and function of the human centromere. Nucleus 2017, 8, 331–339. [Google Scholar] [CrossRef]
- Warburton, P.E.; Willard, H.F. Genomic analysis of sequence variation in tandemly repeated DNA. Evidence for localized homogeneous sequence domains within arrays of alpha-satellite DNA. J. Mol. Biol. 1990, 216, 3–16. Available online: https://www.ncbi.nlm.nih.gov/pubmed/2122000 (accessed on 1 November 2022). [CrossRef]
- Willard, H.F.; Waye, J.S. Chromosome-specific subsets of human alpha satellite DNA: Analysis of sequence divergence within and between chromosomal subsets and evidence for an ancestral pentameric repeat. J. Mol. Evol. 1987, 25, 207–214. Available online: https://www.ncbi.nlm.nih.gov/pubmed/2822935 (accessed on 1 November 2022). [CrossRef]
- Garrido-Ramos, M.A. Satellite DNA: An Evolving Topic. Genes 2017, 8, 230. [Google Scholar] [CrossRef] [PubMed]
- Jagannathan, M.; Warsinger-Pepe, N.; Watase, G.J.; Yamashita, Y.M. Comparative Analysis of Satellite DNA in the Drosophila melanogaster Species Complex. G3 Genes|Genomes|Genet. 2017, 7, 693–704. [Google Scholar] [CrossRef] [PubMed]
- Britten, R.J.; Kohne, D.E. Repeated Sequences in DNA. Hundreds of thousands of copies of DNA sequences have been incorporated into the genomes of higher organisms. Science 1968, 161, 529–540. [Google Scholar] [CrossRef] [PubMed]
- Davidson, E.H.; Britten, R.J. Regulation of Gene Expression: Possible Role of Repetitive Sequences. Science 1979, 204, 1052–1059. [Google Scholar] [CrossRef] [PubMed]
- Sulovari, A.; Li, R.; Audano, P.A.; Porubsky, D.; Vollger, M.R.; Logsdon, G.A.; Warren, W.C.; Pollen, A.A.; Chaisson, M.J.P.; Eichler, E.E.; et al. Human-specific tandem repeat expansion and differential gene expression during primate evolution. Proc. Natl. Acad. Sci. USA 2019, 116, 23243–23253. [Google Scholar] [CrossRef] [PubMed]
- Usdin, K. The biological effects of simple tandem repeats: Lessons from the repeat expansion diseases. Genome Res. 2008, 18, 1011–1019. [Google Scholar] [CrossRef]
- Sawaya, S.; Bagshaw, A.; Buschiazzo, E.; Kumar, P.; Chowdhury, S.; Black, M.A.; Gemmell, N. Microsatellite Tandem Repeats Are Abundant in Human Promoters and Are Associated with Regulatory Elements. PLoS ONE 2013, 8, e54710. [Google Scholar] [CrossRef]
- Lemos, B.; Branco, A.T.; Hartl, D.L. Epigenetic effects of polymorphic Y chromosomes modulate chromatin components, immune response, and sexual conflict. Proc. Natl. Acad. Sci. USA 2010, 107, 15826–15831. [Google Scholar] [CrossRef]
- Feliciello, I.; Akrap, I.; Ugarković, D. Satellite DNA Modulates Gene Expression in the Beetle Tribolium castaneum after Heat Stress. PLoS Genet. 2015, 11, e1005466. [Google Scholar] [CrossRef]
- Joshi, S.S.; Meller, V.H. Satellite Repeats Identify X Chromatin for Dosage Compensation in Drosophila melanogaster Males. Curr. Biol. 2017, 27, 1393–1402.e2. [Google Scholar] [CrossRef]
- Lower, S.S.; McGurk, M.P.; Clark, A.G.; Barbash, D.A. Satellite DNA evolution: Old ideas, new approaches. Curr. Opin. Genet. Dev. 2018, 49, 70–78. [Google Scholar] [CrossRef] [PubMed]
- Bersani, F.; Lee, E.; Kharchenko, P.V.; Xu, A.W.; Liu, M.; Xega, K.; MacKenzie, O.C.; Brannigan, B.W.; Wittner, B.S.; Jung, H.; et al. Pericentromeric satellite repeat expansions through RNA-derived DNA intermediates in cancer. Proc. Natl. Acad. Sci. USA 2015, 112, 15148–15153. [Google Scholar] [CrossRef] [PubMed]
- Aldrup-MacDonald, M.E.; Kuo, M.E.; Sullivan, L.L.; Chew, K.; Sullivan, B.A. Genomic variation within alpha satellite DNA influences centromere location on human chromosomes with metastable epialleles. Genome Res. 2016, 26, 1301–1311. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Li, J.; Suzuki, K.; Qu, J.; Wang, P.; Zhou, J.; Liu, X.; Ren, R.; Xu, X.; Ocampo, A.; et al. A Werner syndrome stem cell model unveils heterochromatin alterations as a driver of human aging. Science 2015, 348, 1160–1163. [Google Scholar] [CrossRef]
- Ferree, P.M.; Barbash, D.A. Species-Specific Heterochromatin Prevents Mitotic Chromosome Segregation to Cause Hybrid Lethality in Drosophila. PLoS Biol. 2009, 7, e1000234. [Google Scholar] [CrossRef]
- Pennacchio, L.A.; Rubin, E.M. Genomic strategies to identify mammalian regulatory sequences. Nat. Rev. Genet. 2001, 2, 100–109. [Google Scholar] [CrossRef]
- Visel, A.; Akiyama, J.A.; Shoukry, M.; Afzal, V.; Rubin, E.M.; Pennacchio, L.A. Functional autonomy of distant-acting human enhancers. Genomics 2009, 93, 509–513. [Google Scholar] [CrossRef]
- Noonan, J.P.; McCallion, A.S. Genomics of Long-Range Regulatory Elements. Annu. Rev. Genom. Hum. Genet. 2010, 11, 1–23. [Google Scholar] [CrossRef]
- Verkerk, A.J.; Pieretti, M.; Sutcliffe, J.S.; Fu, Y.-H.; Kuhl, D.P.; Pizzuti, A.; Reiner, O.; Richards, S.; Victoria, M.F.; Zhang, F.; et al. Identification of a gene (FMR1) containing a CGG repeat coincident with a breakpoint cluster region exhibiting length variation in fragile X syndrome. Cell 1991, 65, 905–914. [Google Scholar] [CrossRef]
- MacDonald, M.E.; Ambrose, C.M.; Duyao, M.P.; Myers, R.H.; Lin, C.; Srinidhi, L.; Barnes, G.; Taylor, S.A.; James, M.; Groot, N.; et al. The Huntington’s Disease Collaborative Research Group: A novel gene containing a trinucleotide repeat that is expanded and unstable on Huntington’s disease chromosomes. Cell 1993, 72, 971–983. [Google Scholar] [CrossRef]
- Fu, Y.H.; Pizzuti, A.; Fenwick, R.G.; King, J.; Rajnarayan, S.; Dunne, P.W.; Dubel, J.; Nasser, G.A.; Ashizawa, T.; de Jong, P.; et al. An Unstable Triplet Repeat in a Gene Related to Myotonic Muscular Dystrophy. Science 1992, 255, 1256–1258. [Google Scholar] [CrossRef] [PubMed]
- La Spada, A.R.; Wilson, E.M.; Lubahn, D.B.; Harding, A.E.; Fischbeck, K.H. Androgen receptor gene mutations in X-linked spinal and bulbar muscular atrophy. Nature 1991, 352, 77–79. [Google Scholar] [CrossRef]
- Campuzano, V.; Montermini, L.; Moltò, M.D.; Pianese, L.; Cossée, M.; Cavalcanti, F.; Monros, E.; Rodius, F.; Duclos, F.; Monticelli, A.; et al. Friedreich’s Ataxia: Autosomal Recessive Disease Caused by an Intronic GAA Triplet Repeat Expansion. Science 1996, 271, 1423–1427. [Google Scholar] [CrossRef]
- Sevim, V.; Bashir, A.; Chin, C.-S.; Miga, K.H. Alpha-CENTAURI: Assessing novel centromeric repeat sequence variation with long read sequencing. Bioinformatics 2016, 32, 1921–1924. [Google Scholar] [CrossRef]
- Roy, A.; Raychaudhury, C.; Nandy, A. Novel techniques of graphical representation and analysis of DNA sequences—A review. J. Biosci. 1998, 23, 55–71. [Google Scholar] [CrossRef]
- Benson, G. Tandem repeats finder: A program to analyze DNA sequences. Nucleic Acids Res. 1999, 27, 573–580. [Google Scholar] [CrossRef] [PubMed]
- Chakravarthy, A.N.S.; Iasemidis, L.D.; Tsakalis, K. Autoregressive modeling and feature analysis of DNA sequences. EURASIP J. Adv. Signal Process. 2004, 1, 13–28. [Google Scholar] [CrossRef]
- Krishnan, A.; Tang, F. Exhaustive whole-genome tandem repeats search. Bioinformatics 2004, 20, 2702–2710. [Google Scholar] [CrossRef]
- Nandy, M.A.H.; Basak, S.C. Mathematical descriptors of DNA sequences: Development and applications. ARKIVOC 2006, 9, 211–238. [Google Scholar] [CrossRef]
- Leclercq, S.; Rivals, E.; Jarne, P. Detecting microsatellites within genomes: Significant variation among algorithms. BMC Bioinform. 2007, 8, 125. [Google Scholar] [CrossRef]
- Sharma, P.C.; Grover, A.; Kahl, G. Mining microsatellites in eukaryotic genomes. Trends Biotechnol. 2007, 25, 490–498. [Google Scholar] [CrossRef] [PubMed]
- Merkel, A.; Gemmell, N. Detecting short tandem repeats from genome data: Opening the software black box. Brief. Bioinform. 2008, 9, 355–366. [Google Scholar] [CrossRef] [PubMed]
- Richard, G.-F.; Kerrest, A.; Dujon, B. Comparative Genomics and Molecular Dynamics of DNA Repeats in Eukaryotes. Microbiol. Mol. Biol. Rev. 2008, 72, 686–727. [Google Scholar] [CrossRef] [PubMed]
- Saha, S.S.B.; Magbanua, Z.V.; Peterson, D.G. Computational approaches and tools used in identification of dispersed repetitive DNA sequences. Trop. Plant Biol. 2008, 1, 85–96. [Google Scholar] [CrossRef]
- Saha, S.; Bridges, S.; Magbanua, Z.V.; Peterson, D.G. Empirical comparison of ab initio repeat finding programs. Nucleic Acids Res. 2008, 36, 2284–2294. [Google Scholar] [CrossRef] [PubMed]
- Arniker, S.B.; Kwan, H. Graphical representation of DNA sequences. In Proceedings of the IEEE International Conference Electro/Information Technology, Windsor, ON, Canada, 7–9 June 2009; pp. 311–314. [Google Scholar] [CrossRef]
- Lorenzo-Ginori, J.V.; Rodríguez-Fuentes, A.; Abalo, R.G.; Rodríguez, R.S. Digital signal processing in the analysis of genomic sequences. Curr. Bioinform. 2009, 4, 28–40. [Google Scholar] [CrossRef]
- Zhou, H.; Du, L.; Yan, H. Detection of Tandem Repeats in DNA Sequences Based on Parametric Spectral Estimation. IEEE Trans. Inf. Technol. Biomed. 2008, 13, 747–755. [Google Scholar] [CrossRef]
- Parisi, V.; De Fonzo, V.; Aluffi-Pentini, F. STRING: Finding tandem repeats in DNA sequences. Bioinformatics 2003, 19, 1733–1738. [Google Scholar] [CrossRef]
- Glunčić, M.; Paar, V. Direct mapping of symbolic DNA sequence into frequency domain in global repeat map algorithm. Nucleic Acids Res. 2012, 41, e17. [Google Scholar] [CrossRef]
- Tørresen, O.K.; Star, B.; Mier, P.; A Andrade-Navarro, M.; Bateman, A.; Jarnot, P.; Gruca, A.; Grynberg, M.; Kajava, A.V.; Promponas, V.J.; et al. Tandem repeats lead to sequence assembly errors and impose multi-level challenges for genome and protein databases. Nucleic Acids Res. 2019, 47, 10994–11006. [Google Scholar] [CrossRef]
- Paar, V.; Glunčić, M.; Basar, I.; Rosandić, M.; Paar, P.; Cvitković, M. Large Tandem, Higher Order Repeats and Regularly Dispersed Repeat Units Contribute Substantially to Divergence Between Human and Chimpanzee Y Chromosomes. J. Mol. Evol. 2010, 72, 34–55. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Paar, V.; Glunčić, M.; Rosandić, M.; Basar, I.; Vlahović, I. Intragene Higher Order Repeats in Neuroblastoma BreakPoint Family Genes Distinguish Humans from Chimpanzees. Mol. Biol. Evol. 2011, 28, 1877–1892. [Google Scholar] [CrossRef] [PubMed]
- Miga, K.H.; Alexandrov, I.A. Variation and Evolution of Human Centromeres: A Field Guide and Perspective. Annu. Rev. Genet. 2021, 55, 583–602. [Google Scholar] [CrossRef]
- Altemose, N.; Logsdon, G.A.; Bzikadze, A.V.; Sidhwani, P.; Langley, S.A.; Caldas, G.V.; Hoyt, S.J.; Uralsky, L.; Ryabov, F.D.; Shew, C.J.; et al. Complete genomic and epigenetic maps of human centromeres. Science 2022, 376, eabl4178. [Google Scholar] [CrossRef]
- A Easterling, K.; Pitra, N.J.; Morcol, T.B.; Aquino, J.R.; Lopes, L.G.; Bussey, K.C.; Matthews, P.D.; Bass, H.W. Identification of tandem repeat families from long-read sequences of Humulus lupulus. PLoS ONE 2020, 15, e0233971. [Google Scholar] [CrossRef]
- Schueler, M.G.; Higgins, A.W.; Rudd, M.K.; Gustashaw, K.; Willard, H.F. Genomic and Genetic Definition of a Functional Human Centromere. Science 2001, 294, 109–115. [Google Scholar] [CrossRef] [PubMed]
- Rudd, M.K.; Willard, H.F. Analysis of the centromeric regions of the human genome assembly. Trends Genet. 2004, 20, 529–533. [Google Scholar] [CrossRef]
- Prosser, J.; Frommer, M.; Paul, C.; Vincent, P. Sequence relationships of three human satellite DNAs. J. Mol. Biol. 1986, 187, 145–155. [Google Scholar] [CrossRef]
- Moyzis, R.K.; Albright, K.L.; Bartholdi, M.F.; Cram, L.S.; Deaven, L.L.; Hildebrand, C.E.; Joste, N.E.; Longmire, J.L.; Meyne, J.; Schwarzacher-Robinson, T. Human chromosome-specific repetitive DNA sequences: Novel markers for genetic analysis. Chromosoma 1987, 95, 375–386. [Google Scholar] [CrossRef]
- Aldrup-MacDonald, M.E.; Sullivan, B.A. The Past, Present, and Future of Human Centromere Genomics. Genes 2014, 5, 33–50. [Google Scholar] [CrossRef]
- Guenatri, M.; Bailly, D.; Maison, C.; Almouzni, G. Mouse centric and pericentric satellite repeats form distinct functional heterochromatin. J. Cell Biol. 2004, 166, 493–505. [Google Scholar] [CrossRef] [PubMed]
- Komissarov, A.S.; Gavrilova, E.V.; Demin, S.J.; Ishov, A.M.; Podgornaya, O.I. Tandemly repeated DNA families in the mouse genome. BMC Genom. 2011, 12, 531. [Google Scholar] [CrossRef] [PubMed]
- Glunčić, M.; Vlahović, I.; Paar, V. Discovery of 33mer in chromosome 21—The largest alpha satellite higher order repeat unit among all human somatic chromosomes. Sci. Rep. 2019, 9, 12629. [Google Scholar] [CrossRef] [PubMed]
- Rosandic, M.; Paar, V.; Basar, I. Key-string segmentation algorithm and higher-order repeat 16mer (54 copies) in human alpha satellite DNA in chromosome 7. J. Theor. Biol. 2003, 221, 29–37. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).