Abstract
Quantum annealers, such as the device built by D-Wave Systems, Inc., offer a way to compute solutions of NP-hard problems that can be expressed in Ising or quadratic unconstrained binary optimization (QUBO) form. Although such solutions are typically of very high quality, problem instances are usually not solved to optimality due to imperfections of the current generations quantum annealers. In this contribution, we aim to understand some of the factors contributing to the hardness of a problem instance, and to use machine learning models to predict the accuracy of the D-Wave 2000Q annealer for solving specific problems. We focus on the maximum clique problem, a classic NP-hard problem with important applications in network analysis, bioinformatics, and computational chemistry. By training a machine learning classification model on basic problem characteristics such as the number of edges in the graph, or annealing parameters, such as the D-Wave’s chain strength, we are able to rank certain features in the order of their contribution to the solution hardness, and present a simple decision tree which allows to predict whether a problem will be solvable to optimality with the D-Wave 2000Q. We extend these results by training a machine learning regression model that predicts the clique size found by D-Wave.
Keywords:
D-Wave 2000Q; machine learning; maximum clique; prediction; quantum annealing; QUBO; regression 1. Introduction
Quantum annealing is an emerging technology with the potential to provide high quality solutions to NP-hard problems. In this work, we focus on the devices built by D-Wave Systems, Inc., specifically the D-Wave 2000Q annealer, designed to minimize functions of the following form,
where are unknown binary variables. The linear weights and the quadratic coupler weights are chosen by the user and define the problem under investigation. If , Equation (1) is called a quadratic unconstrained binary optimization (QUBO) problem, and if it is called an Ising model. Both QUBO and Ising model formulations are equivalent [1]. Many important NP-hard problems can be expressed as the minimization of a function of the form of Equation (1), see [2]. In the remainder of the article, we focus on the QUBO formulation.
The D-Wave 2000Q device aims to minimize a function of the form of Equation (1) via a process called quantum annealing. For this, Equation (1) is mapped to a physical system, consisting of hardware qubits which are situated on the D-Wave chip. Those are initialized in a superposition (enforced by a so-called transverse field), with no information about the problem (Equation (1)) at the start. During annealing, the system transitions from the initial superposition of all qubits to the actual problem Hamiltonian of Equation (1), where it is hoped that a slow transition gives the system enough time to arrange itself in an energy minimum along the path. After annealing, a solution of Equation (1) is read off from the hardware qubits. Although solutions returned by the D-Wave 2000Q annealer for minimization problems of the type of Equation (1) are typically of very high quality, they are not guaranteed to be optimal. In fact, there is no guarantee that the solutions returned by a D-Wave device keep any level of accuracy.
In this article, we aim to identify those types of QUBOs that are solvable on D-Wave 2000Q with given hardware parameters, without actually using the annealer. This could help decide on what resources (annealing time, number of reads) should be allocated to some problem of interest in advance.
We focus on the maximum clique (MC) problem, and explore two different types of classifications. First, we train a binary machine learning classification model on basic problem characteristics (such as density of the input graph) to discriminate between solvable and unsolvable instances of MC. The resulting model also allows us to rank the features used for training by importance. Classification is performed using the open source machine learning package scikit-learn in Python [3]. Second, we show that the decision problem of whether an MC instance will be solved optimally by D-Wave can be predicted with high accuracy by a simple decision tree on the same basic problem characteristics. Third, we train a machine learning regression model to predict the clique size returned by the annealer.
Let be a graph (referred to as original graph) consisting of a vertex set and edge set . A clique in G is any subgraph C of G that is complete, i.e., there is an edge between each pair of vertices of C. The MC problem asks us to find a clique of maximum size, called a maximum clique, which is an NP-hard problem with many applications. To solve an instance of MC on the D-Wave annealer, we proceed as follows:
- The task of finding a maximum clique has to be mapped to a formulation of the type of Equation (1). As shown in [1,4], the QUBO functionfor all , achieves a minimum if and only if the vertices for which form a maximum clique, where the two constants can be chosen as , [4]. It is noteworthy that any function of the type of Equation (1) can be represented as a graph P itself, which is used to embed the QUBO problem into the quantum processor. In this representation, each of the n variables becomes a vertex with vertex weight , and each edge between vertices i and j is assigned an edge weight . We call P the unembedded graph.
- To minimize Equation (1) on D-Wave, its corresponding unembedded graph has to be mapped onto the physical hardware qubits on the chip of the D-Wave 2000Q. Since the connectivity of the hardware qubits, called the Chimera graph (see Figure 1), is limited (in particular, all pairwise connections are not possible), a minor embedding of P onto the Chimera graph has to be computed. In a minor embedding, each vertex of P (referred to as a logical qubit) is mapped onto a connected set of hardware qubits, called a chain. Note that in Equation (1), all pairwise connections require the specification of a weight, and, as such, a coupler weight, called the chain strength, is also required for each pair of connected chain qubits. If chosen appropriately, the chain strength ensures that hardware qubits representing the same logical qubit take the same value after annealing is complete. The minor embedding of P onto the Chimera graph is a subgraph of the Chimera graph and, thus, a new graph . We call the embedded graph. Roughly speaking, the closer the topology of P resembles the one of the Chimera graph, the easier it will be to embed it onto the D-Wave 2000Q hardware, and the larger the embeded problems P can be.
 Figure 1. The hardware graph H of D-Wave 2000Q is a array of unit cells, wherein each unit cell is a bipartite graph. The depicted graph is the hardware connectivity graph of the D-Wave 2000Q machine at Los Alamos National Laboratory, showing a few of its qubits disabled due to hardware errors. The particular connectivity structure of the hardware graph is referred to as a Chimera graph.
Figure 1. The hardware graph H of D-Wave 2000Q is a array of unit cells, wherein each unit cell is a bipartite graph. The depicted graph is the hardware connectivity graph of the D-Wave 2000Q machine at Los Alamos National Laboratory, showing a few of its qubits disabled due to hardware errors. The particular connectivity structure of the hardware graph is referred to as a Chimera graph. - After annealing, it is not guaranteed that chained qubits on the Chimera graph take the same value, even though they represent the same logical qubit. This phenomenon is called a broken chain. To obtain an interpretable solution of logical qubits, definite values have to be assigned to each logical qubit occurring in Equation (1). Although there is no unique way to accomplish this task, D-Wave offers several default methods to unembed chains. Those include majority vote or minimize energy. Majority vote sets the value of a chained qubit to the value (zero or one) taken most often among the hardware qubits which represent the logical qubit. In case of a draw, an unbiased coin flip is used. The minimize energy option determines the final value of all logical qubits via a post-processing step using some form of gradient descent. We employ majority vote in the remainder of the article.
Applying machine learning to predict features of a quantum device is a timely area of research. Existing work mostly focuses on gate quantum computing. For instance, machine learning is employed to help tune the behavior of quantum systems, such as computing the overlap of two quantum states [5], quantum circuit optimization [6,7], or readout of states with higher assignment fidelities under noise conditions [8]. Other works address parameter tuning of variational quantum algorithms [9] or the quantum approximate optimization algorithm (QAOA) algorithm of [10], see [11]. The closest to our approach is [12], wherein the authors use machine learning techniques to identify graph problems that are easy to solve using QAOA. However, they use the quantum gate model and their specific objective is a bit different—to decide whether QAOA or the classical Goemans-Williamson algorithm will perform better on instances of the maximum cut problem. In contrast, we compare the quality of the solution found with the quantum algorithm against an optimal solution, and our optimization problem is the maximum clique problem.
Somewhat related, in [13,14] the authors use a differential evolution optimizer to tune three parameters of D-Wave 2000Q, namely spin reversal, anneal offsets, and chain weights. However, machine learning methods are not used, and the objective is to optimize parameters, rather than predict performance.
Finally, some authors have addressed the difficulty of solving NP-hard problems to optimality by trying to develop classical approximation algorithms for them or proving the difficulty of their prediction. For the MC problem, it has been shown in [15] that for every positive , no polynomial-time algorithm exists that approximately computes the maximum clique size to within a factor of , unless P = NP, which indicates the MC problem is hard to solve even approximately. There have also been results establishing the fixed-parameter intractability of the MC problem [16]. The difference between those results and our work is that we do not try to determine the difficulty of any particular instance of the MC clique problem per se, but how difficult that problem is for the D-Wave 2000Q quantum annealer. Moreover, some of our results also take into account some tunable hardware parameters used for the annealer, in addition to the input graph parameters. No similar results currently exist in the literature.
This article is structured as follows. Section 2 introduces the machine learning methodology we employ to predict the behavior of D-Wave 2000Q. Experimental results are given in Section 3, where we consider the classification problem of predicting whether D-Wave 2000Q can solve a particular MC instance, the computation of a simple decision tree allowing us to classify problem instances manually, and the prediction of the clique size returned by the annealer using a machine learning regression model. The article concludes with a discussion in Section 4.
2. Methods
We aim to predict both if an instance of MC is solvable by D-Wave 2000Q to optimality, as well as the size of the clique which will be found by the annealer.
We first generate a set of 47000 Erdős-Rényi random graphs. For each graph, we first choose its number of vertices uniformly at random in , and its density p uniformly at random in . We then insert any of the pairwise edges after an independent coin flip with probability p. Using these 47000 Erdős-Rényi random graphs, we generate a dataset of 47000 MC instances by applying the QUBO formulation of Equation (1). We use of those 47000 MC instances for training, the remaining are used for validation. The upper bound of 65 vertices is determined by the largest size of a complete graph embeddable on D-Wave’s Chimera architecture. We specifically do not use any graphs with zero degree nodes.
Next, we compute an embedding E of a complete 65 node graph onto the Chimera architecture with the help of the minorminer module of the D-Wave Ocean API [17]. Since any graph with at most 65 nodes is a subgraph of the complete 65 node graph, we can re-use the embedding E to map any problem instance of up to 65 vertices onto the D-Wave 2000Q annealer. Different embeddings typically use different hardware qubits, and map logical qubits to chains of different lengths, both of which can alter the performance of the D-Wave 2000Q. In order to be able to compare and interpret results across different graphs, we thus keep the embedding fixed in all experiments. Moreover, the D-Wave API provides a tool to compute the chain strengths for an embedding, called uniform torque compensation [18]. We always compute all chain strengths using this feature. For each graph on which MC is to be solved, we request 1000 anneals from D-Wave 2000Q after embedding. The best D-Wave result (i.e., the largest clique found) among those 1000 anneals is saved for each graph after unembedding with the majority vote option (see Section 1).
2.1. Classification
Our task is to relate graph features to a given binary indicator from D-Wave expressing if an instance could be solved by the annealer to optimality. Several avenues exist to accomplish this task, for instance via (penalized) linear regression or logistic regression, or via more sophisticated machine learning models. The following highlights some of the challenges.
First, in order to have a well-defined decision problem for finding maximum cliques, we require a ground truth determined with a classical method. We define an instance of MC to be solvable by the D-Wave 2000Q if the clique determined by D-Wave has size equal to the maximum clique size found with the function graph_clique_number of the NetworkX package in Python [19,20], which is an exact solver. In this case, the class label was set to 1 (solvable), and 0 otherwise.
Second, a couple of choices have to be made, both regarding the machine learning model for regression, as well as the set of graph features selected for prediction. We decided to use a decision tree classifier for two main reasons: The classifier achieved good performance in the classification task we consider and, most importantly, it allows us to obtain an interpretable output in the form of a decision tree. The decision tree highlights in what order or importance the features contribute to solvability on the D-Wave 2000Q, and by tuning the decision tree for simplicity, it allows one to (manually) determine with high probability in advance if an instance is likely solvable.
Third, an assortment of graph-related features has to be selected to serve as inputs to the machine learning model. Those features are selected to cover a wide variety of potential metrics impacting solvability, however the list below is neither exhaustive nor rigorously proven. The following features went into the machine learning model threefold (unless noted otherwise), precisely for the original input graph G, its unembedded graph P of the MC problem, and its embedded graph on the Chimera architecture (see Section 1):
- the graph density (Graph_Density);
- the minimal, maximal, and average degree of any vertex (Graph_Min_Degree,Graph_Max_Degree, and Graph_Mean_Degree);
- the number of triangles in the input and unembedded graphs (Graph_Num_Triangles);
- the number of nodes and edges (Graph_Num_Nodes and Graph_Num_Edges);
- the five largest eigenvalues of the adjacency matrix (Graph_Largest_Eigenvalue,Graph_2nd_Largest_Eigenvalue, etc., up to Graph_5th_Largest_Eigenvalue), and the spectral gap (the difference between the moduli of the two largest eigenvalues) of the adjacency matrix (Graph_Spectral_Gap). For brevity of notation, we refer with “eigenvalue of a graph” to the eigenvalue of its adjacency matrix.
Additionally, for the embedded graph on the Chimera architecture, we included the following features into the model:
- the minimal, maximal, and average chain length occurring in the embedding(Min_Chain_Length, Max_Chain_Length, and Avg_Chain_Length);
- the chain strength computed with D-Wave’s uniform torque compensation feature (Chain_Strength), see [18], using either a fixed UTC prefactor (Section 3.1) or a randomly selected one in (Section 3.2);
- the annealing time (in microseconds), which was selected uniformly at random in (Annealing_Time).
In total, there were 46 features that were included as inputs to the machine learning model.
Using those features of the training MC instances and their maximum clique result computed by the D-Wave 2000Q annealer, we train a machine learning classifier implemented in the sklearn.tree.DecisionTreeClassifier() class provided in scikit-learn [3]. After performing a grid search across the following parameters, we selected max_depth=5, random_state=0, and min_impurity_decrease=0.005. All other parameters were kept at their default values. To weigh solvable MC instances by D-Wave more heavily than unsolvable ones, the option class_weight=’balanced’ was employed. The option of balanced class weightings was chosen as only about of the test problems are solvable. Therefore, a model that classifies all instances as unsolvable will still be 87–89% accurate. By setting class_weight=’balanced’, we assign a weight to the solvable problems that is inversely proportional to how often they appear in the dataset, thus penalizing incorrectly classified solvable problems by a factor of about .
During training, we noticed that the decision tree machine learning model appears to have trouble with problems that return a clique size of zero. This was due to a suboptimal QUBO formulation we used for MC, and the problem disappeared when using the formulation of [1,4]. However, similar issues might occur with other problems, highlighting that the present approach might be most suitable for problem classes that can be solved sufficiently well on D-Wave. Additionally, it is challenging to tune the decision tree in such a way as to obtain good performance and interpretable results simultaneously. Applying the decision tree classifier using default parameters usually results in very large trees having many redundant branches, which are poorly interpretable. However, this issue can be alleviated by increasing the Gini impurity (parameter min_impurity_decrease) while simultaneously decreasing the maximal depth of the tree (parameter max_depth).
2.2. Regression
In contrast to predicting solvability alone, we also attempt to predict the actual clique size found by the D-Wave 2000Q device from graph and annealer features alone. Therefore, in this section, our aim is not the prediction of a binary decision (solvable, not solvable), but predicting an integer response (precisely, an integer within the range of possible clique sizes ). For this task, no ground truth (via a classical solver) is needed.
As in the previous section, several regression models are suitable for this task. We chose to predict the clique size returned by D-Wave 2000Q with gradient boosting, a popular machine learning regression model. Whereas random forests build deep independent trees, gradient boosting works by constructing an ensemble of dependent shallow trees, each one improving on the previous one. Although shallow trees by themselves are usually only weak predictive models, combining (or “boosting”) them in an ensemble allows for powerful machine learning models. We employed the GradientBoostingRegressor() class [21] in scikit-learn [3]. Similarly to the classification setting, we performed a grid search across selected parameters, and set n_estimators=200, and random_state=0. All other parameters were kept at their default values.
The graph and annealer features included in the model are the same as the ones outlined in the previous section. One caveat is worth mentioning. It is not always true that the set of vertices (given by the bitstring indicating the clique vertices with a 1) returned by the D-Wave 2000Q annealer actually forms a clique. Therefore, to train the model, we verify first if the result returned by D-Wave 2000Q is a clique. If it is, we use the clique size in the regression, otherwise we use a value of zero.
3. Experimental Results
This section presents our results when training the machine learning models described in Section 2 on random MC instances. As outlined in Section 2, the embedding of a complete 65 vertex graph onto D-Wave’s Chimera architecture was fixed for all experiments to enable transferability and interpretability of our results across different MC instances.
We first consider a fixed annealing time and a fixed UTC prefactor parameter (Section 3.1), and then generalize the results to random annealing times and random UTC prefactors (Section 3.2). For both cases, the classification and regression problems are considered.
3.1. Fixed Annealing Time and Fixed UTC Prefactor
In this section, the annealing time was held fixed at 100 microseconds, and the UTC prefactor of D-Wave’s uniform torque compensation feature for computing the chain strength was empirically fixed at , which yielded good approximate cliques with D-Wave.
3.1.1. Classification
We start by looking at the classification problem. After fitting a decision tree classifier with scikit-learn, we obtain the tree displayed in Figure 2.
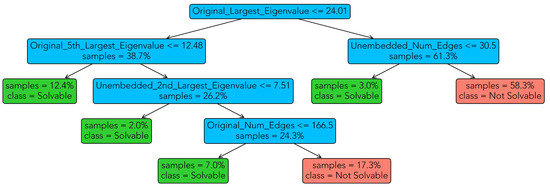
Figure 2.
Decision tree for classification of MC instances into solvable and unsolvable, using the features outlined in Section 2. Setting of fixed annealing time and fixed UTC prefactor. Left branches denote true bifurcations, right branches denote false bifurcations. Green leaves are solvable cases, red leaves are unsolvable cases, and inner nodes are colored in blue.
Several observations regarding Figure 2 are noteworthy. First, the tree is sufficiently simple to allow for a manual classification of MC instances into solvable and unsolvable ones by D-Wave 2000Q. The most decisive feature turns out to be the largest eigenvalue of the adjacency matrix of the input graph. If it is larger than the threshold given in Figure 2, the number of edges in the unembedded problem graph seems to be a good predictor of solvability. This is sensible, since less connections in the unembedded problem tend to facilitate embedding and solving on D-Wave. However, further work is needed to understand how to the 5’th largest eigenvalue of the adjacency matrix of the input graph comes into play. Here, a smaller 5’th largest eigenvalue tends to facilitate solvability. Finally, the second largest eigenvalue of the unbedded problem graph (as before, smaller eigenvalues tend to facilitate solvability) and, moreover, the number of edges in the input graph (smaller instances tend to be more likely to be solvable than larger ones) tend to be good predictors of solvability—a finding which seems straightforward.
Although the importance of the 5’th largest eigenvalue (of the adjacency matrix of the input graph) is a surprising result, the predictive power of the largest and second largest eigenvalues is sensible, since those are well known to predict a variety of structural properties of a graph, see [22,23]: for instance, the largest eigenvalue is related to the largest degree of a graph. In two follow-up experiments, removing only the 5’th largest eigenvalue from the set of predictors turned out to decrease performance marginally (the accuracy decreases by 0.37%, and the recall decreases by 0.51%). Removing all eigenvalues apart from the largest one seems to decrease performance more substantially (the accuracy drops by 2.9%, but the recall goes up by 0.83%).
One may wonder whether the nodes of the decision tree labeled as “Solvable” correspond to subclasses of graphs for which MC can be solved exactly in polynomial time or are easier in any other way, but there is no published work to support such hypothesis. In fact, we are aware of no research that links properties of the 5’th largest eigenvalue with any other non-trivial graph property.
An evaluation of the decision tree of Figure 2 on the unseen validation data yields the confusion matrix given in Table 1. We observe that our machine learning model is able to accurately classify solvable instances with a probability of around , and unsolvable ones with a probability of around .

Table 1.
Confusion matrix for evaluating the decision tree (Figure 2) on the test dataset. Setting of fixed annealing time and fixed UTC prefactor.
3.1.2. Regression
Next, we consider the prediction of the clique size that the D-Wave 2000Q annealer will find on certain MC instances, as a function of the features outlined in Section 2. All results in this section were obtained with the gradient boosting regressor of scikit-learn.
Figure 3 shows both the predicted D-Wave clique size versus the one actually found by the annealer (left plot), as well as the permutation importance ranking of the features returned by the gradient boosting algorithm (right plot). Permutation importance ranking is a means to compute the importance of each feature [24]. It works by measuring the increase in the prediction error of the model after we permuted the feature’s values, which breaks the relationship between the feature and the true outcome (since breaking the relationship between a feature and the outcome makes classification easier).
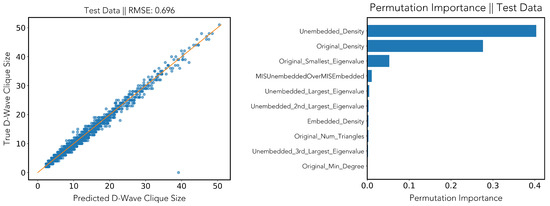
Figure 3.
Regression via gradient boosting. (Left): predicted D-Wave clique size vs. true D-Wave clique size. (Right): permutation importance ranking. Setting of fixed annealing time and fixed UTC prefactor.
We observe that, indeed, the model allows for a relatively accurate forecast of the found clique size, with a root mean square error of which is quite low considering the predicted values lay in the range of up to 50. The most important features seem to be the density of the unembedded graph, the density of the original input graph, and the smallest eigenvalue of its adjacency matrix.
3.2. Random Annealing Time and Random UTC Prefactor
To see if the aforementioned results generalize, we repeated the same experiment with a random annealing time (sampled uniformly at random within the interval of microseconds), and a random UTC prefactor (sampled uniformly at random within the interval ). The dataset used for classification contained 49,000 samples and was generated as outlined in Section 2. We again consider both classification and regression. Note that in contrast to Section 3.1, where only graph features were used to train the machine learning models, in this section we have two additional parameters in our model (annealing time and UTC prefactor), which are related to the quantum annealing algorithm.
3.2.1. Classification
Figure 4 shows the decision tree we obtain on the test dataset after fitting a decision tree classifier with scikit-learn. It is similar to the one of Section 3.1 in that it is suitably simple to allow one to classify MC instances manually. However, the importance of the features has changed: The number of edges, though previously also included in the tree of Figure 2, is now the first decision point. Instances with a large number of edges are likely not solvable by D-Wave, whereas most cases belonging to the left branch (number of edges at most 220) are solvable. Similarly to Section 3.1, the 5’th largest eigenvalue of the adjacency matrix of the input graph is an important feature. New in this scenario is the importance of the chain strength for the classification, whereby small chain strengths used to embed a problem are favorable for solvability.
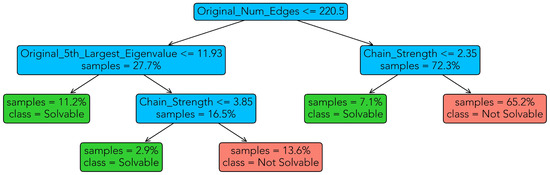
Figure 4.
Decision tree for classification of MC instances into solvable and unsolvable, using the features outlined in Section 2. Setting of random annealing time and random UTC prefactor. Left branches denote true bifurcations, right branches denote false bifurcations. Green leaves are solvable cases, red leaves are unsolvable cases, and inner nodes are colored in blue.
On the validation dataset, the decision tree of Figure 4 shows a similar performance to the one of the previous section. Results are summarized in Table 2 and show that our classifier is able to classify solvable instances correctly with an accuracy of around , and unsolvable ones with an accuracy of around .

Table 2.
Confusion matrix for evaluating the decision tree (Figure 4) on the test dataset. Setting of random annealing time and random UTC prefactor.
3.2.2. Regression
Finally, we repeat the machine learning regression with the help of the gradient boosting regressor of scikit-learn. Figure 5 shows the results of this experiment.
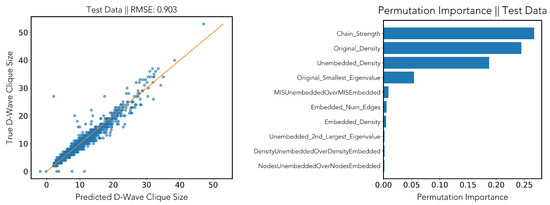
Figure 5.
Regression via gradient boosting. (Left): predicted D-Wave clique size vs. true D-Wave clique size. (Right): permutation importance ranking. Setting of random annealing time and random UTC prefactor.
On the test dataset, we are able to very accurately predict the clique size which D-Wave 2000Q will find, achieving a low root mean square error of (Figure 5, left). The most important features for regression seem to be chain strength, the density of the original input graph, and the density of the unembedded graph. The smallest eigenvalue of the adjacency matrix of the original input graph seems to play a minor role.
4. Discussion
In this contribution, we aim to understand some of the factors contributing to the hardness of a problem instance sent to the D-Wave 2000Q annealer. We focus on the MC problem, and train several machine learning models on several thousand randomly generated input problems with the aim to learn features to (a) predict if D-Wave 2000Q will be able to solve an instance of MC to optimality, and (b) predict the size of the clique that the D-Wave 2000Q device will find.
We show that indeed, for specific problem of predicting the clique size, a relatively small number of features of the input problem, its QUBO formulation and its embedding onto the D-Wave Chimera architecture seems to suffice to predict solubility with high precision. Those features can be summarized in a simple decision tree, which even allows one to manually classify MC instances. A regression analysis demonstrated that the clique size the D-Wave 2000Q will find can, likewise, be predicted with a low root mean square error.
This article leaves scope for a variety of avenues for future work. For instance, it is unknown how these results generalize to other NP-hard problems, how well prediction will work on future D-Wave machines (or even other quantum annealers), and it remains to be investigated if the presented results can be improved by fitting more sophisticated machine learning models.
Author Contributions
Methodology, A.B. and E.P.; software, A.B. and E.P.; writing—original draft, G.H.; writing—review & editing, H.N.D.; funding acquisition, H.N.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work has been supported by the US Department of Energy through the Los Alamos National Laboratory. Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy (Contract No.~89233218CNA000001) and by the Laboratory Directed Research and Development program of Los Alamos National Laboratory under project numbers 20190065DR and 20180267ER. The work of Hristo Djidjev has been also partially supported by the Grant No. BG05M2OP001-1.001-0003, financed by the Science and Education for Smart Growth Operational Program (2014-2020) and co-financed by the European Union through the European Structural and Investment Funds.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Chapuis, G.; Djidjev, H.; Hahn, G.; Rizk, G. Finding Maximum Cliques on the D-Wave Quantum Annealer. J. Signal Process. Syst. 2019, 91, 363–377. [Google Scholar] [CrossRef] [Green Version]
- Lucas, A. Ising formulations of many NP problems. Front. Phys. 2014, 2, 1–5. [Google Scholar] [CrossRef] [Green Version]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Pelofske, E.; Hahn, G.; Djidjev, H. Solving large Maximum Clique problems on a quantum annealer. In International Workshop on Quantum Technology and Optimization Problems; Springer: Munich, Germany, 2019; pp. 63–70. [Google Scholar]
- Cincio, L.; Subaşı, Y.; Sornborger, A.; Coles, P. Learning the quantum algorithm for state overlap. New J. Phys. 2018, 20, 113022. [Google Scholar] [CrossRef]
- Verdon, G.; Broughton, M.; McClean, J.R.; Sung, K.J.; Babbush, R.; Jiang, Z.; Neven, H.; Mohseni, M. Learning to learn with quantum neural networks via classical neural networks. arXiv 2019, arXiv:1907.05415. [Google Scholar]
- Fösel, T.; Niu, M.Y.; Marquardt, F.; Li, L. Quantum circuit optimization with deep reinforcement learning. arXiv 2021, arXiv:2103.07585. [Google Scholar]
- Magesan, E.; Gambetta, J.M.; Córcoles, A.; Chow, J.M. Machine Learning for Discriminating Quantum Measurement Trajectories and Improving Readout. Phys. Rev. Lett. 2015, 114, 200501. [Google Scholar] [CrossRef] [PubMed]
- Rivera-Dean, J.; Huembeli, P.; Acín, A.; Bowles, J. Avoiding local minima in Variational Quantum Algorithms with Neural Networks. arXiv 2021, arXiv:2104.02955. [Google Scholar]
- Farhi, E.; Goldstone, J.; Gutmann, S.; Neven, H. Quantum Algorithms for Fixed Qubit Architectures. arXiv 2017, arXiv:1703.06199. [Google Scholar]
- Wauters, M.M.; Panizon, E.; Mbeng, G.B.; Santoro, G.E. Reinforcement-learning-assisted quantum optimization. Phys. Rev. Res. 2020, 2, 033446. [Google Scholar] [CrossRef]
- Moussa, C.; Calandra, H.; Dunjko, V. To quantum or not to quantum: Towards algorithm selection in near-term quantum optimization. Quantum Sci. Technol. 2020, 5, 044009. [Google Scholar] [CrossRef]
- Pelofske, E.; Hahn, G.; Djidjev, H. Optimizing the Spin Reversal Transform on the D-Wave 2000Q. In Proceedings of the 2019 IEEE International Conference on Rebooting Computing (ICRC), San Mateo, CA, USA, 4–8 November 2019; pp. 1–8. [Google Scholar]
- Barbosa, A.; Pelofske, E.; Hahn, G.; Djidjev, H. Optimizing embedding-related quantum annealing parameters for reducing hardware bias. arXiv 2020, arXiv:2011.00719. [Google Scholar]
- Håstad, J. Clique is hard to approximate within n1−ε. Acta Math. 1999, 182, 105–142. [Google Scholar] [CrossRef]
- Chen, J.; Huang, X.; Kanj, I.A.; Xia, G. Strong computational lower bounds via parameterized complexity. J. Comput. Syst. Sci. 2006, 72, 1346–1367. [Google Scholar] [CrossRef] [Green Version]
- D-Wave Systems. D-Wave Ocearn: Minorminer. 2021. Available online: https://docs.ocean.dwavesys.com/projects/minorminer/en/latest/ (accessed on 15 May 2021).
- D-Wave Systems. D-Wave System Documentation: Uniform Torque Compensation. 2019. Available online: https://docs.ocean.dwavesys.com/projects/system/en/stable/reference/generated/dwave.embedding.chain_strength.uniform_torque_compensation.html (accessed on 15 May 2021).
- Hagberg, A.A.; Schult, D.A.; Swart, P.J. Exploring Network Structure, Dynamics, and Function using NetworkX. In Proceedings of the 7th Python in Science Conference, Pasadena, CA, USA, 19–24 August 2008; pp. 11–15. [Google Scholar]
- NetworkX. Return the Clique Number (Size of the Largest Clique) for a Graph. 2021. Available online: https://networkx.org/documentation/networkx-1.10/reference/generated/networkx.algorithms.clique.graph_clique_number.html (accessed on 15 May 2021).
- Scikit Learn. Gradient Boosting for Regression. 2021. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.ensemble.GradientBoostingRegressor.html (accessed on 15 May 2021).
- Cvetković, D.; Simić, S. The second largest eigenvalue of a graph (a survey). Filomat 1995, 9, 449–472. [Google Scholar]
- Lovász, L. Eigenvalues of Graphs. 2007. Available online: https://web.cs.elte.hu/~lovasz/eigenvals-x.pdf (accessed on 15 May 2021).
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).