Abstract
In this paper, a comparison among Particle swarm optimization (PSO), Bee Colony Optimization (BCO) and the Bat Algorithm (BA) is presented. In addition, a modification to the main parameters of each algorithm through an interval type-2 fuzzy logic system is presented. The main aim of using interval type-2 fuzzy systems is providing dynamic parameter adaptation to the algorithms. These algorithms (original and modified versions) are compared with the design of fuzzy systems used for controlling the trajectory of an autonomous mobile robot. Simulation results reveal that PSO algorithm outperforms the results of the BCO and BA algorithms.
1. Introduction
Bio-inspired optimization algorithms have proven that they are really good at numerical optimization and finding good results from a defined search space, no matter how many parameters they are looking for. In this paper, a comparison of most popular bio-inspired methods is presented in the problem of optimization of membership functions for a fuzzy controller.
In this paper, three bio-inspired methods are used for a comparison in the optimization of a fuzzy system used as a controller of an autonomous mobile robot. These methods are selected because they use the same methodology for parameter adaptation, as these three methods use a fuzzy system with the same inputs, but with different outputs, because the outputs are the parameters to be dynamically adjusted over the iterations of each algorithm.
PSO (Particle Swarm Optimization), inspired by collective intelligence, can handle complex problems and gives very good results, but lacks the ability to dynamically control its parameters, and a methodology for parameter adaptation is presented.
The Bat Algorithm is a bio-inspired metaheuristic based on the characteristics of micro-bats, essentially echolocation. This echolocation is used by a bat to locate its prey; this algorithm was formulated in 2010 by Xin-She Yang in [1], and has since been used to solve global optimization problems.
PID (Proportional-Integral-Derivative)-fuzzy controllers are tuned in [2,3] using PSO and tested on an electrical DC drive benchmark and a laboratory micro air vehicle controller, respectively. A hybrid PSO and pattern search optimized PI-fuzzy controller is applied in [4] to the automatic generation control of multi-area power systems. The Gravitational Search Algorithm (GSA) is employed in [5,6] for the optimal tuning of PI-fuzzy and PID-fuzzy controllers for DC servo systems and load frequency control in power systems. Charged System Search algorithms are applied in [7] to the optimal tuning of PI-fuzzy controllers for DC servo systems. Ant Colony Optimization is applied in [8,9] to the optimal tuning of fuzzy controllers for robots and ball and beam systems.
A hybridization of the algorithms was performed in [10]; the authors publish a hybridization between the PSO and GA algorithms to minimize the cost and materials required for the elaboration of a metal cylinder. The artificial bee colony algorithm (ABC) has been used to optimize this same problem [11]. The authors propose in [12] a novel intelligent technique for solutions in a biography system and, through a comparison, the authors conclude that the solutions of the proposed approach are better than the solutions available in the literature. In [13], the authors present a new GA-GSA hybrid algorithm to increase reliability and performance in the analysis of uncertain data and the intuitionistic fuzzy is used to determine the optimal parameters in the algorithms, intuitionistic fuzzy logic, is a powerful technique in bio-inspired algorithms. A new model for decision making is proposed in [14]; the objective of this new model is to reduce the level of uncertainty in the data to help decision making. This model uses fuzzy logic to eliminate the level of uncertainty; the use of these techniques have significantly improved timing and pressure by decision makers. In [15], with the objective of determine the level of membership of an object to another in numerical terms, a novel method that uses Type-2 fuzzy set (T2FS) is proposed, and this method significantly improves the accuracy of membership of a data set.
Recently the BCO algorithm has proven to be an efficient technique in solving complex problems, especially for fuzzy controllers; some current examples of research are the following: Amador-Angulo et al. [16], a new fuzzy bee colony optimization with dynamic adaptation of parameters using interval type-2 fuzzy logic for tuning fuzzy controllers is presented; Banu et al. [17] present an implementation of fractional order PID controller for three interacting tank process optimally tuned using Bee Colony Optimization; Chaiyatham et al. [18] propose a Bee Colony Optimization based-fuzzy logic-PID control design of electrolyzer for microgrid stabilization; Jovanovic et al. [19] present an area-wide urban traffic control: A Bee Colony Optimization approach; Rajeswari et al. [20] present a directed Bee Colony Optimization algorithm to Solve the nurse rostering problem; Sharma et al. [21] shows an efficient cooperative relaying in flying ad hoc networks using fuzzy-bee colony optimization; and, Wong et al. [22] present a novel artificial bee colony optimization strategy-based extreme learning machine algorithm. In addition, other related works can be found in [23,24,25,26]. There are several works by Garg et al. in which fuzzy logic has been used for the same metaheuristics [10,11,27,28,29,30,31].
This is why we consider, as the main contribution of this research, a comparative study based on three bio-inspired algorithms and their fuzzy version with dynamic adjustment of the important parameters using type-1 fuzzy logic systems and interval type-2 fuzzy logic systems as tools for modeling complex problems, especially for the stabilization of the trajectory in an autonomous mobile robot using these algorithms as tools to optimize the fuzzy controller, a comparison is performed.
The rest of the paper is organized as follows. Section 2 describes the state of the art with related works for each bio-inspired optimization algorithm. Section 3 contains a more detailed explanation of the internal work of each algorithm. Section 4 describes the methodology used to dynamically adjust the parameters of each method. Section 5 contains the versions of the algorithms with dynamic parameter adaptation using the proposed methodology with a type-1 and an interval type-2 fuzzy system. Section 6 describes briefly the problem statement in which all the bio-inspired optimization algorithms were tested. Section 7 shows the results of applying the bio-inspired optimization algorithms to the optimization of a fuzzy system used in control. Finally, in Section 8, the conclusion and future work of this paper are presented.
2. Related Works
Bee colony optimization (BCO) is a relatively new metaheuristic designed to deal with hard combinatorial optimization problems. It belongs to the group of nature-inspired methods that explore collective intelligence, in this case applying the behavior of honeybees during the nectar collecting, originally process, proposed by Dušan B. Teodorovic.
There are in the literature many variants and improvements of this algorithm, for example, in [32], the authors present a work, where the algorithm is combined with techniques of processing and acquisition of images and the algorithm is able to obtain fine points of a visual image obtained by infrared.
In addition, in [33], an empirical study of the Bee Colony Optimization (BCO) algorithm is presented, where authors present a comparative study between different meta-heuristics, and the obtained results are compared with the results achieved by the Artificial Bee Colony, Genetic Algorithm, Differential Evolution, and Particle Swarm Optimization.
We consider it important to mention that, in [34], an optimization of fuzzy controller design using a new bee colony algorithm with fuzzy dynamic parameter adaptations was presented, where authors propose a new variant of BCO to optimize the membership functions of a fuzzy controller.
At present the works related to the dynamic adjustment of parameters in BCO are: in [35], a Sets in Dynamic Adaptation of Parameters of a Bee Colony Optimization for Controlling the Trajectory of an Autonomous Mobile Robot is shown; in [36], an improved artificial bee colony algorithm for solving constrained optimization problems is presented; in [37], a survey of swarm intelligence for dynamic optimization: algorithms and applications is shown; and, in [21], an Efficient cooperative relaying in flying ad hoc networks using fuzzy-bee colony optimization is presented, among others.
The bat algorithm has been implemented in several problems on the optimization area; some of these applications are briefly described next.
In [38], a Type-1 and Interval Type-2 Fuzzy Systems used in BA with the final purpose of selecting the best parameters for these algorithms applied in optimization of benchmark mathematical functions is presented.
Another modification to the BA was proposed by Yang et al. in 2017, which consist in the application of a directional echolocation with the objective of improving the exploration and exploitation capabilities to avoid premature convergence in [39].
In addition, BA was used to solve engineering optimization tasks, using eight nonlinear engineering optimization problems in [40].
The idea of adapting BA in the autonomous mobile robot is based in other examples: Azar et al. [41] present a hybrid heuristic to build software quality estimation models that can be used to predict software quality attributes of new systems using Ant Colony Optimization and Simulated Annealing; Johanyak et al. [42] introduce a new hybrid search algorithm for global search; Precup et al. [43] present the performance improvement of fuzzy control systems (FCSs) for three tank systems using iterative feedback tuning (IFT); and Solos et al. [44] introduce the application of a stochastic variable neighborhood algorithm to solve a problem: optimization problem and relates to shift scheduling of tank trucks for oil company, in these articles they mentioned the abstract idea on the selection of the parameters to modify the algorithms.
PSO has been applied to a great variety of problems, such as benchmark mathematical functions [45,46], and the optimization of fuzzy systems for different types of problems, such as fuzzy classifiers [47], fuzzy controllers [48], and, in this case, the optimization of a fuzzy system for controlling the trajectory of an autonomous mobile robot.
In the literature, there are several applications of the original PSO method to the optimization of fuzzy systems, and some of these applications are mentioned below.
In 2001, Shi et al. [49] proposed a modification to PSO with a fuzzy system to adjust the inertia weight, which is compared with our proposed fuzzy PSO in [46,50].
In 2010, Castillo et al. [51] proposed a comparison between Genetic Algorithms (GA) and PSO for the optimization of a type-1 and type-2 fuzzy controllers, applied to the same problem that we consider here.
In 2010, Niknam [52] used a modified PSO in the economic dispatch problem where the modification of PSO is the use of a fuzzy system to calculate the new values for C1, C2 and the inertia weight. The main difference between our proposed fuzzy PSO method is the inputs and outputs of the fuzzy system: while Niknam uses the best fitness and the number of generations of the best unchanged fitness as inputs for the fuzzy system, our inputs are the percentage of elapsed iterations and the diversity of the population.
In 2012, Khosla et al. [53] proposed an optimization of interval type-2 fuzzy system for time series prediction using PSO as optimization method.
In 2013, Maldonado et al. [54] proposed an implementation of interval type-2 fuzzy systems for FPGA applications using PSO and GA to optimize the fuzzy systems; in this case, they used the fuzzy system to control the speed of a DC motor.
In 2016, Krzeszowski et al. [55] proposed an improvement over PSO where a fuzzy system is used to update the values of C1, C2 and inertia weight as in [52], but, in this case, these values are different for each particle, which is the main difference between our proposed fuzzy PSO method, as, in our approach, the values of C1, C2 and constriction factor are the same for all particles and is used for all the swarm.
3. Bio-Inspired Optimization Methods
Bee colony optimization is a meta-heuristic developed by Dušan B. Teodorovic and is bio-inspired method that explores based on the collective intelligence applied by the honeybees during the nectar collecting process [22,56]. This algorithm has some unique characteristics that make it interesting and efficient, for example forward pass and backward pass, and assigning roles for bee, e.g., follower bees and scout bees; for more detail please consult [22,57].
The dynamics of BCO are defined by Equations (1)–(4); Equation (1) shows the probability that a bee has located the best solution, and α and β are parameters that determine the heuristics of BCO [16]:
Equation (1) indicates the probability that bee k located on a node i selects the next node denoted by j, where Nki is the set of feasible nodes (in a neighborhood) connected to node i with respect to bee k, and β is the probability to visit the following node. dij indicates the distance of node i to node j, and for this algorithm indicates the total dance that a bee has in this moment. Finally, α is a binary variable that is used to find better solutions in the algorithm. Equation (2) represents the fact that a waggle dance will last for a certain duration, determined by a linear function, where K denotes the waggle dance scaling factor, Pfi denotes the profitability scores of bee i as defined in Equation (3) and Pfcolony denotes the bee colony’s average profitability, as in Equation (4) and is updated after each bee completes its tour.
The pseudocode of the original BCO method is illustrated in Algorithm 1:
| Algorithm 1. Bee Colony Optimization. | |
| 01. | Initialize parameters |
| 02. | Determine initial solutions |
| 03. | Evaluate the initial solutions |
| 04. | S← the best solution of the bees. |
| 05. | for each iteration do |
| 06. | for each bee do |
| 07. | Set an initial solution |
| 08. | Evaluate modified solutions generated by possible changes |
| 09. | By roulette wheel selection choose one of the modified solutions |
| 10. | Evaluate new solutions |
| 11. | Make a decision whether the bee is loyal |
| 12. | if the bee is not loyal then |
| 13. | Choice one of the loyal bees to be followed by the i-th bee. |
| 14. | if the best solution of the bees better the solution S |
| 15. | S← the best bee’s solution |
The pseudocode of the modified BCO with parameter adaptation is illustrated in Algorithm 2, where the main difference with respect to Algorithm 1 is the calculation of iteration and diversity in line 06 and the use of a fuzzy system to calculate new Alpha and Beta in line 07.
| Algorithm 2. Fuzzy Bee Colony Optimization. | |
| 01. | Initialize parameters |
| 02. | Determine initial solutions |
| 03. | Evaluate the initial solutions |
| 04. | S← the best solution of the bees. |
| 05. | for each iteration do |
| 06. | Calculate iteration and diversity using Equations (10) and (11) |
| 07. | Use a fuzzy system to calculate the new Beta and Alpha parameters |
| 08. | for each bee do |
| 09. | Set an initial solution |
| 10. | Evaluate modified solutions generated by possible changes |
| 11. | By roulette wheel selection choose one of the modified solutions |
| 12. | Evaluate new solutions |
| 13. | Make a decision whether the bee is loyal |
| 14. | if the bee is not loyal then |
| 15. | Choice one of the loyal bees to be followed by the i-th bee. |
| 16. | if the best solution of the bees better the solution S |
| 17. | S← the best bee’s solution |
Particle Swarm Optimization, an optimization algorithm first developed by Kennedy and Eberhart in 1995 [58,59], inspired by the behavior of schools of fish and flock of birds, and using the collective intelligence of these animals to maintain individuals (known as particles) in the search space. Each position represents a solution to a problem; PSO uses Equations (5) and (6) to update the position and velocity of each particle. PSO guides its particle through a multidimensional space using the collective intelligence of animals described in Equations (5) and (6).
xi(t + 1) = xi(t) + vi(t + 1)
vij(t + 1) = C[vij(t) + c1r1(t)[yij(t) − xij(t)] + c2r2j(t)[ŷj(t) − xij(t)]]
Equation (5) represents the movement of a particle i from its actual position xi(t) to the new position xi(t + 1) adding its new velocity vi(t + 1). Equation (6) represents the velocity of a particle i in its dimension j. This equation is an update of the velocity from actual velocity vij(t) to its new velocity vij(t + 1), adding the cognitive component c1r1(t)[yij(t) − xij(t)] and the social component c2r2j(t)[ŷj(t) − xij(t)]; this new velocity is also weighted with a constriction factor C.
The pseudocode of the original PSO method is illustrated in Algorithm 3.
| Algorithm 3. Particle Swarm Optimization. | |
| 01. | Initialize size of the particle swarm n, and other parameters |
| 02. | Initialize positions and velocities for all particles randomly |
| 03. | While (end criterion is not met) do |
| 04. | Increment iteration counter |
| 05. | Calculate fitness value of each particle |
| 06. | Update new local and global best particle |
| 07. | Calculate new velocity of each particle |
| 08. | Update new position of each particle |
| 09. | End While |
The pseudocode of the modified PSO with parameter adaptation is illustrated in Algorithm 4. The main difference between Algorithm 3 and Algorithm 4 is the calculation of iteration and diversity from line 07 and the use of a fuzzy system to calculate the new C1, C2 and Constriction factor from line 08.
| Algorithm 4. Fuzzy Particle Swarm Optimization. | |
| 01. | Initialize size of the particle swarm n, and other parameters |
| 02. | Initialize positions and velocities for all particles randomly |
| 03. | While (end criterion is not met) do |
| 04. | Increment iteration counter |
| 05. | Calculate fitness value of each particle |
| 06. | Update new local and global best particles |
| 07. | Calculate iteration and diversity using Equations (10) and (11) |
| 08. | Calculate new C1, C2, and Constriction factor using a fuzzy system |
| 09. | Calculate new velocity of each particle |
| 10. | Update new position of each particle |
| 11. | End While |
The Bat Algorithm uses echolocation to get the best value from the search space, all bats use echolocation and start iterations flying randomly with velocity vi at position xi, wavelength and frequency values are varied in each iteration, the BA is idealized in the pseudocode shown in Algorithm 5 [60,61].
| Algorithm 5. Bat Algorithm. | |
| 01. | Initialize the bat population xi (i = 1, 2, ..., n) and vi |
| 02. | Initialize frequency fi, pulse rates ri and the loudness Ai |
| 03. | While (t < Max numbers of iterations) |
| 04. | Generate new solutions by adjusting frequency |
| 05. | and updating velocities and locations/solutions (Equations (7)–(9)) |
| 06. | if (rand > ri) |
| 07. | Select a solution among the best solutions |
| 08. | Generate a local solution around the selected best solution |
| 09. | end if |
| 10. | Generate new solutions by flying randomly |
| 11. | if (rand < Ai&f(xi) < f(x*)) |
| 12. | Accept the new solutions |
| 13. | Increase ri and reduce Ai |
| 14. | end if |
| 15. | Rank the bats and find the current best x* |
| 16. | End While |
The pseudocode of the modified BA with parameter adaptation is shown in Algorithm 6; the main difference between Algorithms 5 and 6 is that, in the last one, we have the calculation of iteration in line 04, the calculation of diversity in line 14 and the use of a fuzzy system to calculate the new Pulse Rate and Loudness.
| Algorithm 6. Fuzzy Bat Algorithm. | |
| 01. | Initialize the bat population xi (i = 1, 2, ..., n) and vi |
| 02. | Initialize frequency fi, pulse rates ri and the loudness Ai |
| 03. | While (t < Max numbers of iterations) |
| 04. | Normalize Iterations Equation (10) |
| 05. | Generate new solutions by adjusting frequency |
| 06. | and updating velocities and locations/solutions (Equations (7) to (9)) |
| 07. | if (rand > ri) |
| 08. | Select a solution among the best solutions |
| 09. | Generate a local solution around the selected best solution |
| 10. | end if |
| 11. | Generate new solutions by flying randomly |
| 12. | if (rand < Ai&f(xi) < f(x*)) |
| 13. | Accept the new solutions |
| 14. | Size Diversity Equation (11) |
| 15. | Assign Values ri and Ai using fuzzy system |
| 16. | end if |
| 17. | Rank the bats and find the current best x* |
| 18. | End While |
To update velocities and locations of bats, Equations (7)–(9) are used: Equation (7) adjusts the frequency, while Beta is a random value in the range [0, 1]; Equation (8) updates velocities of all bats; and Equation (9) updates positions of all bats [62].
4. Methodology for Dynamic Parameter Adaptation
All bio-inspired methods used in these works use the same methodology for parameter adaptation, but adjustment is applied to each bio-inspired optimization method, because this methodology applies a fuzzy logic system to update one or more parameters during the execution of each algorithm, and on each iteration the fuzzy system is evaluated to calculate new parameters.
To perform the calculation of new parameter values, the fuzzy system uses as input the percentage of elapsed iterations and the degree of dispersion of individuals from each bio-inspired method, and these metrics are now used as inputs for the fuzzy system as defined by Equations (10) and (11), respectively.
To put the methodology in perspective, the iteration number give us a percentage of what iteration we are currently in, so we can design rules to update the parameters depending if the algorithm is in early iterations or if is in final iterations, and, based on this knowledge, update the parameters of the bio-inspired optimization algorithm accordingly.
The diversity give us a degree of how much are the individuals close to the global best individual, and with this we can control if we want that individuals get closer together or if we want that individuals move far away from the rest, in other words, we can control if the algorithm will use a global search (individual get separated for the rest) or if it use a local search (individual get close together).
Combining these two metrics we can much better control the behavior of a bio-inspired optimization algorithm by controlling its parameters, this of course based on previous knowledge of the algorithm.
5. Bio-Inspired Methods with Parameter Adaptation
The BCO algorithm has proven to be a good technique to optimize parameters [35,63], which is why we perform an automated search that allows better performance of the BCO algorithm.
For the studied case of the fuzzy controller, the fitness function in the BCO algorithm is represented with the Mean Square Error (MSE) shown in Equation (12). For each Follower Bee for N Cycles, the Type-1 FLS design for the BCO algorithm is evaluated and the objective is to minimize the error.
Therefore, for designing the fuzzy systems, which dynamically adjust the alpha and beta parameters, the iteration and diversity metrics are considered as inputs.
The distribution of membership functions in the inputs and outputs is realized in a symmetrical way. The design of input variables can be appreciated in Figure 1 for the type-1 fuzzy logic system.
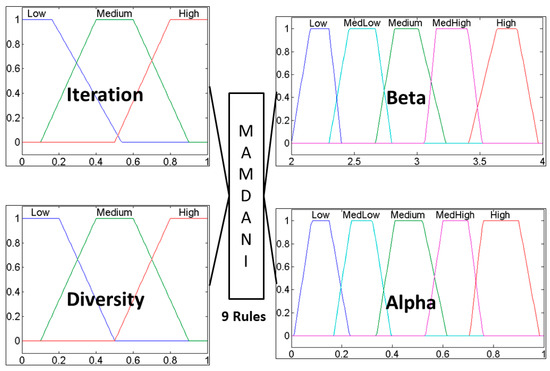
Figure 1.
Type-1 fuzzy system for dynamic parameter adaptation in BCO (Bee Colony Optimization).
The fuzzy system illustrated in Figure 1 is type-1, has iteration and diversity as inputs and has the Beta and Alpha parameters as outputs. In this case, the inputs were granulated into three trapezoidal membership functions and outputs into five trapezoidal membership functions. It contains nine rules that were designed to control the behavior of BCO.
The fuzzy system in Figure 2 is an interval type-2 system, has the same number of membership functions per input and output as the type-1 fuzzy system, but now, as type-2 trapezoidal membership functions, the fuzzy rule base is the same as in type-1 because the knowledge is not changing only the type of membership functions.
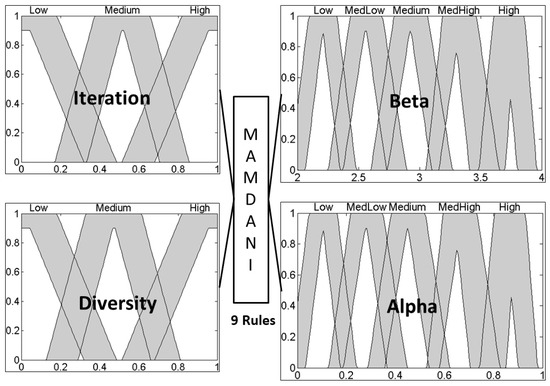
Figure 2.
Interval type-2 fuzzy system for dynamic parameter adaptation in BCO.
Table 1 contains the fuzzy rules used for both fuzzy systems in Figure 1 and Figure 2; these rules were designed based on several experiments to create knowledge from parameters of BCO and how to control its behavior or model a proper behavior.

Table 1.
Fuzzy rules for dynamic Beta and Alpha.
The distribution of membership functions from the type-1 FLS is taken as reference to design the interval type-2 FLS. In addition, membership functions from interval type-2 FLS were designed symmetrically. T1FLS and IT2FLS have the same rules and are of Mamdani style.
Using the described methodology for parameter adaptation presented in Section 4, some parameters in PSO are dynamically adjusted using a type-1 and interval type-2 fuzzy systems. Based on several experiments, the best parameters were selected to be adjusted over the iterations, in this case, C1, C2 and the constriction factor C from Equation (6), which are the most important and have a big impact in the behavior of the algorithm, so controlling these parameters allows to control the entire algorithm.
Figure 3 and Figure 4 present the type-1 fuzzy system and the interval type-2 fuzzy system used to dynamic parameter adaptation of the parameters of PSO, using as inputs metrics iteration and diversity.
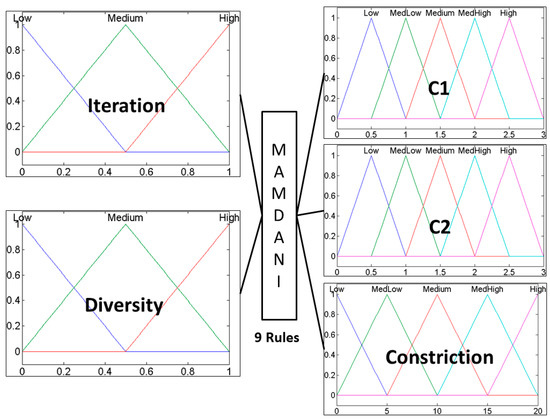
Figure 3.
Type-1 fuzzy system for dynamic parameter adaptation in PSO (Particle Swarm Optimization).
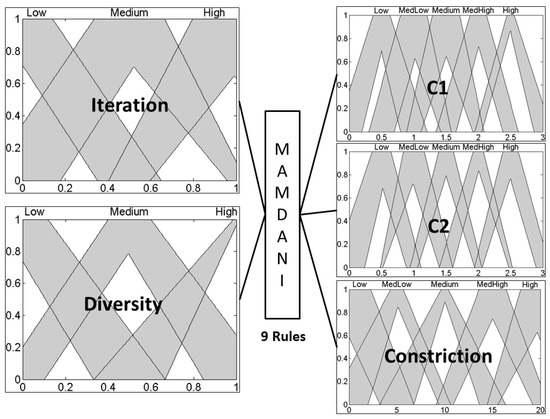
Figure 4.
Interval type-2 fuzzy system for dynamic parameter adaptation in PSO.
The fuzzy system illustrated in Figure 3 is type-1, has iteration and diversity as inputs and has the parameters C1, C2 and constriction factor as outputs. In this case, the inputs were granulated into three triangular membership functions, and the outputs into five triangular membership functions. It contains nine rules that were designed to control the behavior of PSO.
The fuzzy system in Figure 4 is an interval type-2, has the same number of membership per input and output, but now as type-2 triangular membership functions, the fuzzy rule base is the same as in the type-1 because the knowledge is not changing only the type of membership functions.
Table 2 contains the fuzzy rules used for the fuzzy systems in Figure 3 and Figure 4; these rules were designed based on several experiments to create knowledge of the parameters of PSO and how to control its behavior.

Table 2.
Fuzzy rules for dynamic parameter adaptation in PSO.
The implementation of the bat algorithm integrated with a type-1 and interval type-2 fuzzy systems, in this case fuzzy systems aim to control the Beta and Pulse Rate parameters from BA, Figure 5 and Figure 6 illustrate the fuzzy systems used for parameter adaptation, a type-1 fuzzy system and an interval type-2 fuzzy system, respectively; both fuzzy systems are Mamdani type, and the construction of these fuzzy systems is based in previous works [64].
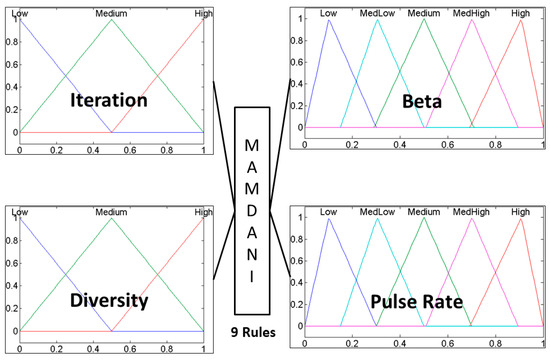
Figure 5.
Type-1 Fuzzy System.
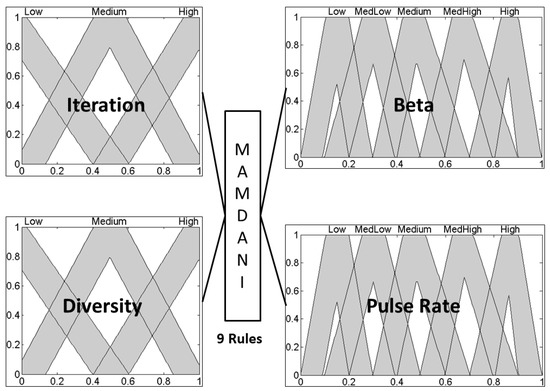
Figure 6.
Interval Type-2 Fuzzy System.
The First output in the type-1 and interval type-2 fuzzy systems is beta (β) and the second output is pulse rate (ri), both are granulated into five fuzzy sets (Low, MediumLow, Medium, MediumHigh and High).
Inputs and outputs of the two fuzzy systems use triangular membership functions; the first input variable iteration is granulated into three fuzzy sets (Low, Medium and High). The second input variable diversity is granulated into three fuzzy sets (Low, Medium and High).
Table 3 shows the fuzzy rules used in both type-1 and interval type-2 fuzzy systems.

Table 3.
Fuzzy rules for dynamic parameter adaptation in BA (Bat Algorithm).
6. Problem Statement
To test the proposed methods with dynamic parameter adaptation, a complex problem was selected. In this case, the optimization of a fuzzy system design used for controlling an autonomous mobile robot, the task of the fuzzy controller is to provide a way to control the two motors of the robot in order to minimize the trajectory error.
The robot body illustrated in Figure 7 has two wheel motors and one passive wheel for stabilization. The motion of the passive wheel can be ignored in the dynamics represented by the following set of equations from [65]:
where is the vector of the configuration coordinates; is the vector of velocities; is the vector of torques applied to the wheels of the robot, where τ1 and τ2 denote the torques of the right and left wheel, respectively; is the uniformly bounded disturbance vector; is the positive-definite inertia matrix; is the vector of centripetal and Coriolis forces; and is a diagonal positive-definite damping matrix. Equation (13) represents the kinematics of the system, where (x, y) is the position in the X–Y (world) reference frame; θ is the angle between the heading direction and the x-axis; and v and w are the linear and angular velocities, respectively.
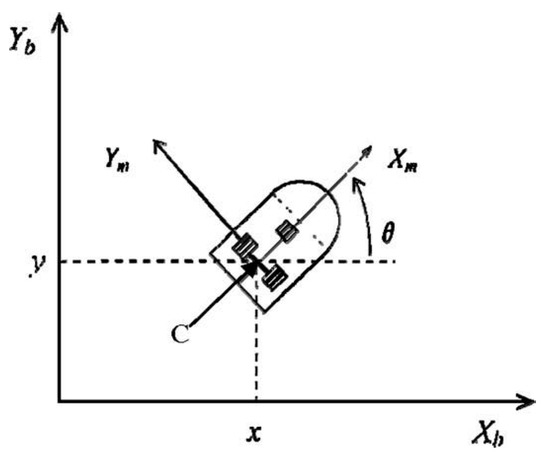
Figure 7.
Scheme of the autonomous mobile robot.
Figure 8 shows the complex plant for the autonomous mobile robot, where a fuzzy system is used to control the trajectory of a robot to follow a desired reference trajectory.
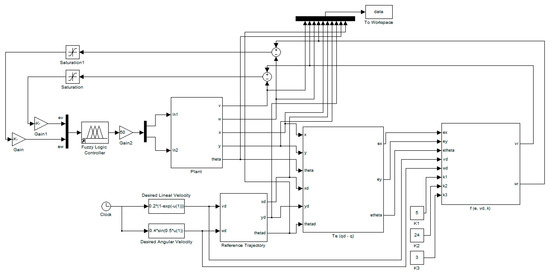
Figure 8.
Complex plant for an autonomous mobile robot.
The fuzzy system is shown in Figure 9 and is used for the complex plant to control the trajectory of the autonomous mobile robot. This is the fuzzy system that the bio-inspired optimization algorithms will optimize; in this case, only the parameters of the membership functions are optimized.
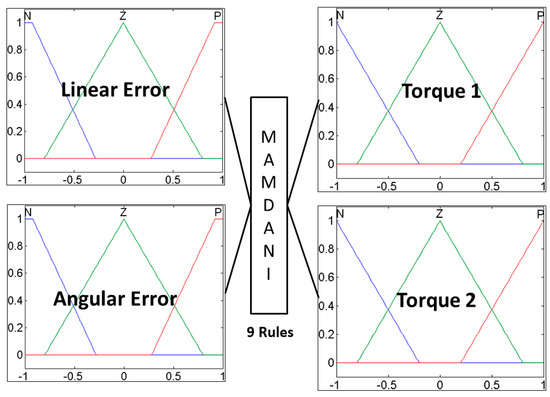
Figure 9.
Fuzzy system for control.
The fuzzy controller of Figure 9 has two inputs, the Linear error and Angular error, and two outputs, Torque 1 and Torque 2, for each motorized wheel of the robot. The inputs are granulated into two trapezoidal membership functions in the ends and one triangular membership function in the middle, the outputs are granulated into three triangular membership functions. Also this fuzzy controller uses the fuzzy rule set from Table 4.

Table 4.
Fuzzy rules for control.
The desired reference trajectory is illustrated in Figure 10, where it starts from the (0,0) point and makes turns creating that “U” shape trajectory, in order to create a complex problem.
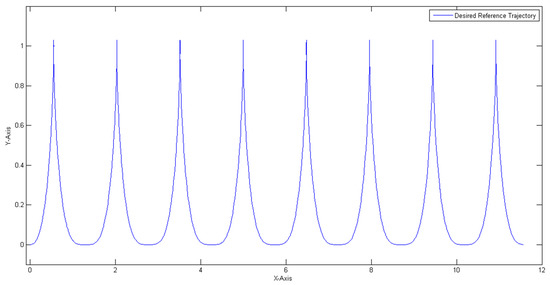
Figure 10.
Reference trajectory for the autonomous mobile robot.
The main difference between the type-1 and interval type-2 fuzzy systems is the ability of the latter to handle uncertainty, thus, to simulate this problem and to provide better tools to perform the comparison, a modification of the original plant is added, where a level of noise is added to the desired reference trajectory and the same noise added to the inputs of the fuzzy controller.
The modified plant is illustrated in Figure 11, where two random number generators were added to simulate noise; the level of noise used is 5%.
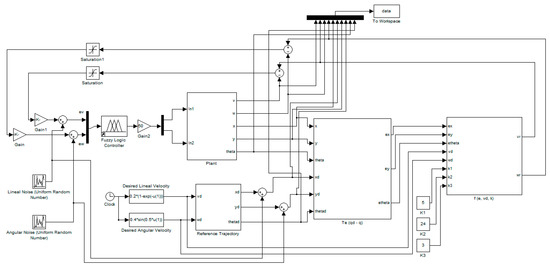
Figure 11.
Complex plant for an autonomous mobile robot with noise.
With the noise added to the plant, the desired reference trajectory is changed; the reference with noise is illustrated in Figure 12, where it can be notice the level of noise added.
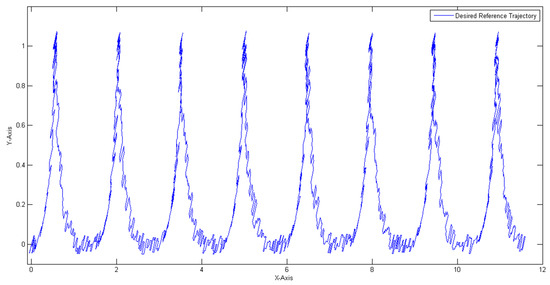
Figure 12.
Reference trajectory with noise for the autonomous mobile robot.
With these two desired reference trajectories, a comparison of proposed methods against original methods can be performed, and appreciate the difference with and without noise.
The optimization problem can be stated as follows: to optimize all the points of the membership functions of the fuzzy system used for control from Figure 9, this is illustrated in Figure 13 where for each membership function the bio-inspired methods will try to find the best values for each point. In this case, the fuzzy controller has two inputs with two trapezoidal membership functions and one input each, and two outputs with three triangular membership functions, this is for each trapezoidal membership function the bio-inspired methods need to find four values and three values for each triangular membership function, with a total of 40 points (values) for these particular fuzzy system for control as optimization problem. In this case the fuzzy rule set from Table 4 was not modified and only the membership functions were optimized.
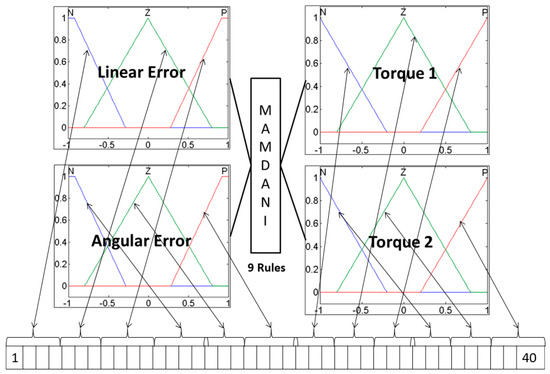
Figure 13.
Optimization problem (points of the membership functions).
The objective function is to minimize the trajectory error created by the optimized fuzzy controller using Equation (14), this means that each bio-inspired method will try to find the best values for each point of each membership function and with this the optimized fuzzy controller creates a trajectory with the lowest possible error.
7. Simulation Results
The problem described in Section 6 is now used to test the proposed bio-inspired optimization algorithms with parameter adaptation illustrated in Section 5 as well as to test original methods shown in Section 3, and a comparison with the results of traditional methods and proposed methods is presented.
The bio-inspired optimization algorithms were applied to the optimization of the fuzzy system (Figure 9) for control of the autonomous mobile robot, using the same parameters, such as population, iterations and number of experiments described in Table 5, Table 6 and Table 7 for the PSO, BCO and BA.

Table 5.
Parameters for the PSO method original/proposed.

Table 6.
Parameters for the BA method original/proposed.

Table 7.
Parameters for the BCO method original/proposed.
These parameters were selected based on several experiments with all the methods applied to the optimization of some benchmark mathematical functions, such as Rastrigin, De Jong first function, Rosenbrock, and Ackley, just to search for the best parameters, while also trying to use almost the same parameters for all the bio-inspired methods. For the BCO and BA methods, these parameters were taken from recommended values from the authors of the original methods, but, in the case of PSO, we first take the typical values for each parameter (such as the values recommended by Eberhart et al. [66]), but then changes were made to improve the results, taking into account that the constriction factor is not used in the original PSO and only in the proposed PSO method (this is why the value of the constriction in the original PSO is equal to 1, from Equation (6); if C is equal to 1, this does not affect the rest of the equation because it is a multiplier).
The metric used to evaluate the performance of all methods is the Mean Square Error described in Equation (14), calculated from the desired reference trajectory and the trajectory created by the optimized fuzzy controller. In addition, each method is applied 30 times to each problem, and presents the average, best, worst and standard deviation of those experiments.
Equation (14) is presented in the field of fuzzy control as follows; is the estimated value of the control-signal reference; is the observed value control-signal; and n represents the total number of observed samples.
With the goal of realizing a comparison, the three variants of BCO algorithm were used: Original BCO, which is the original method by Dušan B. Teodorovic; BCO + T1FS, which is the BCO algorithm with type-1 fuzzy system with dynamic adaptation parameters; and BCO + IT2FS, which is the BCO algorithm with interval type-2 fuzzy system with dynamic adaptation parameters. Results for the BCO and Fuzzy BCO algorithms are presented in Table 8 and Table 9.

Table 8.
Comparison of results of the plant without noise for the BCO.

Table 9.
Comparison of results of the plant with noise for the BCO.
For comparison purposes, there are three variations of PSO, which are described below. All of these variations use the parameters described in Table 5.
Original PSO is the original PSO method with linear decreasing inertia weight.
PSO + T1FS is the PSO method with parameter adaptation using the type-1 fuzzy system illustrated in Figure 3.
PSO + IT2FS is the PSO method with parameter adaptation using the interval type-2 fuzzy system illustrated in Figure 4.
Table 10 contains the results of applying the variations of PSO to the optimization of the membership functions from the fuzzy controller illustrated in Figure 9, using the plant without noise shown in Figure 8. In this case, results in bold are the best from all methods on each category.

Table 10.
Comparison of results from the plant without noise.
From results in Table 10, the proposed PSO + IT2FS method obtains the best results on average, best, worst and standard deviation, when compared with the original PSO and PSO + T1FS. In addition, the PSO + T1FS obtains better results than the original PSO.
Table 11 contains the results of applying the variations of PSO to the optimization of the membership functions from the fuzzy controller illustrated in Figure 9, using the plant with noise shown in Figure 11. Results highlighted in bold are the best from all methods on each category.

Table 11.
Comparison of results from the plant with noise.
From the results in Table 11 the proposed PSO + IT2FS method obtains better results than the other two methods, also PSO + T1FS obtains better results than original PSO.
For comparison, there are three variants of the bat algorithm: Original BA, which is the original method by X.S. Yang; BA + T1FS, which is the bat algorithm with type-1 fuzzy system for dynamical parameter adaptation; and BA + IT2FS, which is the bat algorithm with interval type-2 fuzzy system for dynamical parameter adaptation.
Table 12 contains the results of applying the variations of the BA to the optimization of the membership functions from the fuzzy controller illustrated in Figure 9, using the plant without noise shown in Figure 8.

Table 12.
Comparison of results of the original BA, the BA + T1FS and BA + IT2FS.
Table 13 contains the results of applying the variations of the BA algorithm to the optimization of the membership functions from the fuzzy controller illustrated in Figure 9, using the plant with noise shown in Figure 11.

Table 13.
Comparison of results of the original BA, the BA + T1FS and BA + IT2FS.
After presenting each method separately, we now present two tables to compare the best results from each of the BA, BCO and PSO methods, applied to the optimization of fuzzy controllers for a plant with and without noise.
Table 14 contains a comparison of the best methods with the plant without noise. In this case, the best method from Bat Algorithm is the original BA; from Bee Colony Optimization, it is BCO + IT2FS; and, from Particle Swarm Optimization, it is PSO + IT2FS.

Table 14.
Comparison of best methods applied to the plant without noise.
Results in Table 14 show that the PSO, which uses an interval type-2 fuzzy system for parameter adaptation, can obtain on average better results than BA and BCO as well as the lowest MSE. This is the best of all controllers; its worst results is lower on MSE than the other methods and finally also obtains the lowest standard deviation. In addition, note that original BA can obtain better results than BCO + IT2FS, but BCO can obtain a lower MSE than the original BA.
Table 15 contains a comparison of results with the best methods using the plant with noise. In this case, from the Bat Algorithm, it is BA + T1FS; from Bee Colony Optimization, it is BCO + T1FS; and, from Particle Swarm Optimization, it is PSO + IT2FS.

Table 15.
Comparison of best methods applied to the plant with noise.
Results in Table 15 show that the PSO, which uses an interval type-2 fuzzy system for parameter adaptation, can obtain the best results when compared with BA and BCO. In addition, BA + T1FS can obtain better results than BCO + T1FS, but again BCO obtains a lower MSE than BA.
The next figures illustrate the best trajectories from each method, for visual comparison purpose; note that, in each figure, all trajectories from the optimized fuzzy system used for control are very similar to desired trajectory.
Figure 14 contains the best trajectory from all variations of BA, in this case using original BA with a MSE of 4 × 10−3.
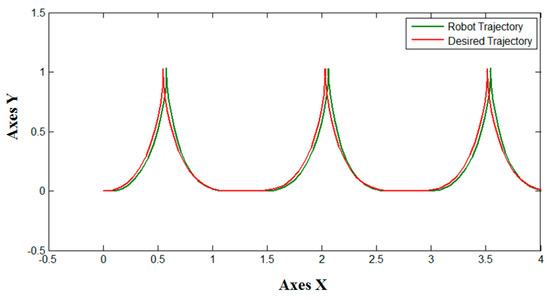
Figure 14.
Best simulation of BA algorithm.
Figure 15 shows the best trajectory from all variations of BCO, in this case, BCO + IT2FS with a MSE of 2.80 × 10−3.
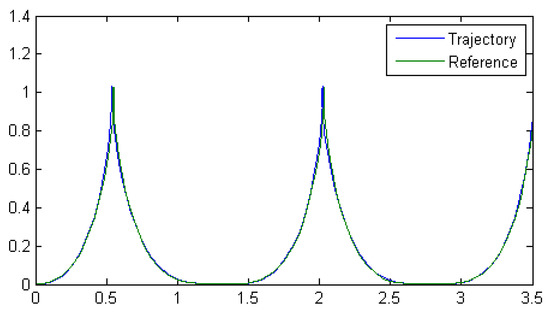
Figure 15.
Best simulation of BCO algorithm.
Figure 16 illustrates the best trajectory from all variations of PSO, in this case, this trajectory was created by the fuzzy controller optimized by the method PSO + IT2FS with a MSE of 1.9081 × 10−4, which can obtain a better fuzzy controller than compared to methods BA and BCO algorithms.
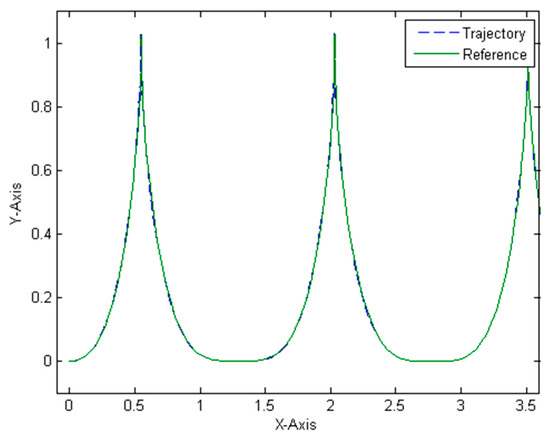
Figure 16.
Best simulation of the PSO algorithm.
The results shows that an interval type-2 fuzzy system used for parameter adaptation can help PSO to obtain better quality results than other methods such as BA and BCO, even when all these methods use the same methodology for dynamic parameter adaptation and also use a type-1 or interval type-2 fuzzy system for the same task.
Aside from the results with the autonomous mobile robot, a comparison against a fuzzy PSO is also presented. In this case, a comparison against a modified PSO proposed by Shi et al. in [49], where they proposed a PSO that is updated with a fuzzy system, using the current best performance evaluation and the current inertia weight to control or adjust the inertia weight from PSO is performed. The main difference from our proposed fuzzy PSO is that our fuzzy system updates the parameters C1, C2 and constriction factor, using iteration and diversity as inputs in an interval type-2 fuzzy system.
The following results (contained in Table 16, Table 17 and Table 18) were obtained using the same parameters and restrictions as the ones published in [49]; the only difference is the dynamic parameters and the fuzzy system used to update these parameters. In addition, results highlighted in bold are the best results.

Table 16.
Comparison against Shi et al. [49].

Table 17.
Comparison against Shi et al. [49].

Table 18.
Comparison against Shi et al. [49].
Table 16 contains the results with the Rosenbrock function using the results from [49] and our proposed PSO method with parameter adaptation using an interval type-2 fuzzy system.
From the results in Table 16, it is clear that our proposed approach obtains on average better results when compared with the results of the other method.
Table 17 illustrates the results of the comparison between the proposed PSO method against Shi et al. from [49], with the Rastrigin function.
The results in Table 17 clearly show that our proposed approach, which uses an interval type-2 fuzzy system to update the parameters of PSO, can obtain on average better results when compared with the results from [49].
Table 18 shows the results of the comparison between the methods of Shi et al. from [49] and our proposed approach with an interval type-2 fuzzy system.
The results contained in Table 16, Table 17 and Table 18 illustrate a comparison between our proposed fuzzy PSO method against the fuzzy PSO method proposed by Shi et al. in [49], where, in all experiments using the same parameters and constrictions, our proposed approach can obtain on average better results.
8. Conclusions
Particle Swarm Optimization is an excellent bio-inspired optimization algorithm, capable of handling complex problems and obtaining very good results; in this case, the optimization of membership functions from a fuzzy controller. From the results in the comparison of different variants of PSO, the PSO + IT2FS variant, which uses an interval type-2 fuzzy system for dynamic parameter adaptation, can obtain better results than all other variants of PSO and also better results than BA and BCO.
The Bee Colony Optimization algorithm is used to optimize membership functions of a fuzzy logic controller applied to track the trajectory of an autonomous mobile robot, with the objective of minimizing an error. After observing and analyzing the obtained results, we can conclude that BCO is efficient in optimization problems. In this case, it can achieve acceptable results; however, the algorithm presents stability problems, and does not always finds acceptable results, i.e., some experiments are good and some are bad.
The integration of Type-1 and Interval Type-2 fuzzy systems into the bat algorithm represents a high level of difficulty for the solution of optimization problems and, analyzing the results that the fuzzy bat algorithm obtained, the MSE is acceptable in following an established trajectory, but the results can be improved by optimizing other parameters in the original bat algorithm method or by optimizing the rules in the fuzzy systems.
The motivation for the development of this paper was to verify the improvement with our methodology for parameter adaptation through fuzzy logic, applied to different bio-inspired methods. The main contribution of this paper is a comparative study based on three bio-inspired algorithms for the design and implementation of fuzzy controllers. In addition, a comparative study of traditional methods, proposed methods with parameter adaptation using type-1 and interval type-2 fuzzy logic systems as tools for modeling complex problems in control.
For future work, we want to extend the proposed methodology for parameter adaptation to other bio-inspired methods as well as use other applications, such as the optimization of neural networks, fuzzy systems applied to other problems, or even a hybridization between two or more of the proposed modified bio-inspired methods.
Author Contributions
Frumen Olivas prepared the part of the paper related to particle swarm optimization. Leticia Amador-Angulo prepared the methods and implementation of bee colony optimization. Jonathan Perez prepared the part of the paper related to the bat algorithm. Camilo Caraveo performed the experiments of bee colony optimization and made comparative tables. Fevrier Valdez prepared the comparisons for bat algorithm and particle swarm optimization. Oscar Castillo coordinated the whole team and prepared the organization and writing of the paper.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Yang, X.S. A new metaheuristic bat-inspired algorithm. In Nature Inspired Cooperative Strategies for Optimization (NICSO 2010); Springer: Berlin/Heidelberg, Germany, 2010; pp. 65–74. [Google Scholar]
- Bouallègue, S.; Haggège, J.; Ayadi, M.; Benrejeb, M. PID-type fuzzy logic controller tuning based on particle swarm optimization. Eng. Appl. Artif. Intell. 2012, 25, 484–493. [Google Scholar] [CrossRef]
- Tran, H.-K.; Chiou, J.-S. PSO-based algorithm applied to quadcopter micro air vehicle controller design. Micromachines 2016, 7. [Google Scholar] [CrossRef]
- Sahu, R.K.; Panda, S.; Sekhar, G.C. A novel hybrid PSO-PS optimized fuzzy PI controller for AGC in multi area interconnected power systems. Int. J. Electr. Power Energy Syst. 2015, 64, 880–893. [Google Scholar] [CrossRef]
- Azadani, H.N.; Torkzadeh, R. Design of GA optimized fuzzy logic-based PID controller for the two area non-reheat thermal power system. In Proceedings of the 13th Iranian Conference on Fuzzy Systems (IFSC), Qazvin, Iran, 27–29 August 2013; pp. 1–6. [Google Scholar]
- Precup, R.E.; David, R.C.; Petriu, E.M.; Preitl, S.; Radac, M.B. Gravitational search algorithms in fuzzy control systems tuning. IFAC Proc. Vol. 2011, 44, 13624–13629. [Google Scholar] [CrossRef]
- Precup, R.E.; David, R.C.; Petriu, E.M.; Preitl, S.; Radac, M.B. Novel adaptive charged system search algorithm for optimal tuning of fuzzy controllers. Expert Syst. Appl. 2014, 41, 1168–1175. [Google Scholar] [CrossRef]
- Castillo, O.; Lizárraga, E.; Soria, J.; Melin, P.; Valdez, F. New approach using ant colony optimization with ant set partition for fuzzy control design applied to the ball and beam system. Inf. Sci. 2015, 294, 203–215. [Google Scholar] [CrossRef]
- Castillo, O.; Neyoy, H.; Soria, J.; Melin, P.; Valdez, F. A new approach for dynamic fuzzy logic parameter tuning in ant colony optimization and its application in fuzzy control of a mobile robot. Appl. Soft Comput. 2015, 28, 150–159. [Google Scholar] [CrossRef]
- Garg, H. A hybrid PSO-GA algorithm for constrained optimization problems. Appl. Math. Comput. 2016, 274, 292–305. [Google Scholar] [CrossRef]
- Garg, H. Solving structural engineering design optimization problems using an artificial bee colony algorithm. J. Ind. Manag. Optim. 2014, 10, 777–794. [Google Scholar] [CrossRef]
- Garg, H. An efficient biogeography based optimization algorithm for solving reliability optimization problems. Swarm Evolut. Comput. 2015, 24, 1–10. [Google Scholar] [CrossRef]
- Garg, H. A hybrid GA-GSA algorithm for optimizing the performance of an industrial system by utilizing uncertain data. In Handbook of Research on Artificial Intelligence Techniques and Algorithms; IGI Global: Hershey, PA, USA, 2015; pp. 620–654. [Google Scholar]
- Garg, H. Performance analysis of an industrial system using soft computing based hybridized technique. J. Braz. Soc. Mech. Sci. Eng. 2017, 39, 1441–1451. [Google Scholar] [CrossRef]
- Singh, S.; Garg, H. Distance measures between type-2 intuitionistic fuzzy sets and their application to multicriteria decision-making process. Appl. Intell. 2017, 46, 788–799. [Google Scholar] [CrossRef]
- Amador-Angulo, L.; Castillo, O. A new fuzzy bee colony optimization with dynamic adaptation of parameters using interval type-2 fuzzy logic for tuning fuzzy controllers. Soft Comput. 2016, 1–24. [Google Scholar] [CrossRef]
- Banu, U.S. Implementation of Fractional Order PID Controller for Three Interacting Tank Process Optimally Tuned Using Bee Colony Optimization. In Proceedings of the International Conference on Swarm, Evolutionary, and Memetic Computing, Chennai, India, 19–21 December 2013; Springer: Cham, Switzerland, 2013; pp. 413–423. [Google Scholar]
- Chaiyatham, T.; Ngamroo, I. A Bee Colony Optimization based-fuzzy logic-PID control design of electrolyzer for microgrid stabilization. Int. J. Innov. Comput. Inf. Control 2012, 8, 6049–6066. [Google Scholar]
- Jovanovic, A.; Nikolic, M.; Teodorovic, D. Area-wide urban traffic control: A Bee Colony Optimization approach. Transp. Res. Part C Emerg. Technol. 2017, 77, 329–350. [Google Scholar] [CrossRef]
- Rajeswari, M.; Amudhavel, J.; Pothula, S.; Dhavachelvan, P. Directed Bee Colony Optimization Algorithm to Solve the Nurse Rostering Problem. Comput. Intell. Neurosci. 2017, 2017. [Google Scholar] [CrossRef] [PubMed]
- Sharma, V.; Srinivasan, K.; Kumar, R.; Chao, H.C.; Hua, K.L. Efficient cooperative relaying in flying ad hoc networks using fuzzy-bee colony optimization. J. Supercomput. 2017, 73, 3229–3259. [Google Scholar] [CrossRef]
- Wong, L.P.; Low, M.Y.H.; Chong, C.S. A bee colony optimization algorithm for traveling salesman problem. In Proceedings of the Second Asia International Conference on Modeling Simulation, Kuala Lumpur, Malaysia, 13–15 May 2008; pp. 818–823. [Google Scholar]
- Dell’Orco, M.; Marinelli, M.; Altieri, M.G. Solving the gate assignment problem through the Fuzzy Bee Colony Optimization. Transp. Res. Part C Emerg. Technol. 2017, 80, 424–438. [Google Scholar] [CrossRef]
- Jovanovic, A.; Teodorovic, D. Pre-timed control for an under-saturated and over-saturated isolated intersection: A Bee Colony Optimization approach. Transp. Plan. Technol. 2017, 40, 556–576. [Google Scholar] [CrossRef]
- Markovic, G.Z.; Teodorovic, D.B.; Acimovic-Raspopovic, V.S. Routing and wavelength assignment in all-optical networks based on the bee colony optimization. AI Commun. 2007, 20, 273–285. [Google Scholar]
- TienBui, D.; Tuan, T.A.; Hoang, N.D.; Thanh, N.Q.; Nguyen, D.B.; Van Liem, N.; Pradhan, B. Spatial prediction of rainfall-induced landslides for the Lao Cai area (Vietnam) using a hybrid intelligent approach of least squares support vector machines inference model and artificial bee colony optimization. Landslides 2017, 14, 447–458. [Google Scholar] [CrossRef]
- Garg, H. Reliability, availability and maintainability analysis of industrial systems using PSO and fuzzy methodology. MAPAN 2014, 29, 115–129. [Google Scholar] [CrossRef]
- Garg, H. An approach for solving constrained reliability-redundancy allocation problems using cuckoo search algorithm. Beni-Suef Univ. J. Basic Appl. Sci. 2015, 4, 14–25. [Google Scholar] [CrossRef]
- Garg, H.; Sharma, S.P. Multi-objective reliability-redundancy allocation problem using particle swarm optimization. Comput. Ind. Eng. 2013, 64, 247–255. [Google Scholar] [CrossRef]
- Garg, H.; Rani, M.; Sharma, S.P. An efficient two phase approach for solving reliability–redundancy allocation problem using artificial bee colony technique. Comput. Oper. Res. 2013, 40, 2961–2969. [Google Scholar] [CrossRef]
- Garg, H.; Rani, M.; Sharma, S.P.; Vishwakarma, Y. Intuitionistic fuzzy optimization technique for solving multi-objective reliability optimization problems in interval environment. Expert Syst. Appl. 2014, 41, 3157–3167. [Google Scholar] [CrossRef]
- Chatterjee, A.; Biswas, M.; Maji, D.; Jana, D.; Brojabasi, S.; Sarkar, G.; Das, S. Discrete Wavelet Transform based VI image fusion with Artificial Bee Colony Optimization. In Proceedings of the 7th Annual Computing and Communication Workshop and Conference (CCWC), Las Vegas, NV, USA, 9–11 January 2017; pp. 1–4. [Google Scholar]
- Nikolic, M.; Teodorovic, D. Empirical study of the Bee Colony Optimization (BCO) algorithm. Expert Syst. Appl. 2013, 40, 4609–4620. [Google Scholar] [CrossRef]
- Caraveo, C.; Valdez, F.; Castillo, O. Optimization of fuzzy controller design using a new bee colony algorithm with fuzzy dynamic parameter adaptation. Appl. Soft Comput. 2016, 43, 131–142. [Google Scholar] [CrossRef]
- Amador-Angulo, L.; Mendoza, O.; Castro, J.R.; Rodríguez-Díaz, A.; Melin, P.; Castillo, O. Fuzzy sets in dynamic adaptation of parameters of a bee colony optimization for controlling the trajectory of an autonomous mobile robot. Sensors 2016, 16. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.; Wan, Z.; Fang, D. An improved artificial bee colony algorithm for solving constrained optimization problems. Int. J. Mach. Learn. Cybern. 2017, 8, 739–754. [Google Scholar] [CrossRef]
- Mavrovouniotis, M.; Li, C.; Yang, S. A survey of swarm intelligence for dynamic optimization: Algorithms and applications. Swarm Evolut. Comput. 2017, 33, 1–17. [Google Scholar] [CrossRef]
- Pérez, J.; Valdez, F.; Castillo, O. Modification of the bat algorithm using type-2 fuzzy logic for dynamical parameter adaptation. In Nature-Inspired Design of Hybrid Intelligent Systems; Springer: Cham, Switzerland, 2017; pp. 343–355. [Google Scholar]
- Chakri, A.; Khelif, R.; Benouaret, M.; Yang, X.S. New directional bat algorithm for continuous optimization problems. Expert Syst. Appl. 2017, 69, 159–175. [Google Scholar] [CrossRef]
- Yang, X.S.; Hossein Gandomi, A. Bat algorithm: A novel approach for global engineering optimization. Eng. Comput. 2012, 29, 464–483. [Google Scholar] [CrossRef]
- Azar, D.; Fayad, K.; Daoud, C. A Combined Ant Colony Optimization and Simulated Annealing Algorithm to Assess Stability and Fault-Proneness of Classes Based on Internal Software Quality Attributes. Int. J. Artif. Intell. 2016, 14, 137–156. [Google Scholar]
- Johanyák, Z.C.; Papp, O. A hybrid algorithm for parameter tuning in fuzzy model identification. Acta Polytech. Hung. 2012, 9, 153–165. [Google Scholar]
- Precup, R.E.; Tomescu, M.L.; Radac, M.B.; Petriu, E.M.; Preitl, S.; Dragos, C.A. Iterative performance improvement of fuzzy control systems for three tank systems. Expert Syst. Appl. 2012, 39, 8288–8299. [Google Scholar] [CrossRef]
- Solos, I.P.; Tassopoulos, I.X.; Beligiannis, G.N. Optimizing shift scheduling for tank trucks using an effective stochastic variable neighbourhood approach. Int. J. Artif. Intell. 2016, 14, 1–26. [Google Scholar]
- Monson, C.K.; Seppi, K.D. Adaptive diversity in PSO. In Proceedings of the 8th Annual Conference on Genetic and Evolutionary Computation, Seattle, WA, USA, 8–12 July 2006; ACM: New York, NY, USA, 2006; pp. 59–66. [Google Scholar]
- Olivas, F.; Valdez, F.; Castillo, O.; Melin, P. Dynamic parameter adaptation in particle swarm optimization using interval type-2 fuzzy logic. Soft Comput. 2016, 20, 1057–1070. [Google Scholar] [CrossRef]
- Melin, P.; Olivas, F.; Castillo, O.; Valdez, F.; Soria, J.; Garcia, J. Optimal design of fuzzy classification systems using PSO with dynamic parameter adaptation through fuzzy logic. Elsevier Exp. Syst. Appl. 2013, 40, 3196–3206. [Google Scholar] [CrossRef]
- Castillo, O.; Melin, P. A review on the design and optimization of interval type-2 fuzzy controllers. Appl. Soft Comput. 2012, 12, 1267–1278. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R.C. Fuzzy adaptive particle swarm optimization. In Proceedings of the 2001 Congress on Evolutionary Computation, Seoul, Korea, 27–30 May 2001; Volume 1, pp. 101–106. [Google Scholar]
- Olivas, F.; Valdez, F.; Castillo, O. An interval type-2 fuzzy logic system for dynamic parameter adaptation in particle swarm optimization. In Proceedings of the 2014 IEEE Conference on Norbert Wiener in the 21st Century (21CW), Boston, MA, USA, 24–26 June 2014; pp. 1–6. [Google Scholar]
- Castillo, O.; Martinez-Marroquin, R.; Melin, P.; Valdez, F.; Soria, J. Comparative study of bio inspired algorithms applied to the optimization of type-1 andtype-2 fuzzy controllers for an autonomous mobile robot. Inf. Sci. 2012, 192, 19–38. [Google Scholar] [CrossRef]
- Niknam, T. A new fuzzy adaptive hybrid particle swarm optimization algorithm for non-linear, non-smooth and non-convex economic dispatch problem. Appl. Energy 2010, 87, 327–339. [Google Scholar] [CrossRef]
- Khosla, M.; Sarin, R.K.; Uddin, M. Identification of type-2 fuzzy models for time-series forecasting using particle swarm optimization. In Proceedings of the 2012 International Conference on Communication Systems and Net-work Technologies (CSNT), Rajkot, India, 11–13 May 2012; pp. 259–264. [Google Scholar]
- Maldonado, Y.; Castillo, O.; Melin, P. Particle swarm optimization of interval type-2 fuzzy systems for FPGA applications. Appl. Soft Comput. 2013, 13, 496–508. [Google Scholar] [CrossRef]
- Krzeszowski, T.; Wiktorowicz, K. Evaluation of selected fuzzy particle swarm optimization algorithms. In Proceedings of the 2016 Federated Conference on Computer Science and Information Systems (FedCSIS), Gdansk, Poland, 11–14 September 2016; pp. 571–575. [Google Scholar]
- Basu, M. Bee colony optimization for combined heat and power economic dispatch. Expert Syst. Appl. 2011, 38, 13527–13531. [Google Scholar] [CrossRef]
- Davidovic, T.; Ramljak, D.; Šelmic, M.; Teodorovic, D. Bee colony optimization for the p-center problem. Comput. Oper. Res. 2011, 38, 1367–1376. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; IEEE Service Center: Piscataway, NJ, USA, 1995; pp. 1942–1948. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. Swarm Intelligence; Morgan Kaufmann: San Francisco, CA, USA, 2001. [Google Scholar]
- Perez, J.; Valdez, F.; Castillo, O.; Roeva, O. Bat algorithm with parameter adaptation using interval type-2 fuzzy logic for benchmark mathematical functions. In Proceedings of the 2016 IEEE 8th International Conference on Intelligent Systems (IS), Sofia, Bulgaria, 4–6 September 2016; pp. 120–127. [Google Scholar]
- Tuba, M.; Bacanin, N. Hybridized bat algorithm for multi-objective radio frequency identification (RFID) network planning. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan, 25–28 May 2015; pp. 499–506. [Google Scholar]
- Pérez, J.; Valdez, F.; Castillo, O. Modification of the bat algorithm using fuzzy logic for dynamical parameter adaptation. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan, 25–28 May 2015; pp. 464–471. [Google Scholar]
- Tiacharoen, S.; Chatchanayuenyong, T. Design and Development of an Intelligent Control by Using Bee Colony Optimization Technique. Am. J. Appl. Sci. 2012, 9, 1464–1471. [Google Scholar]
- Perez, J.; Valdez, F.; Castillo, O.; Melin, P.; Gonzalez, C.; Martinez, G. Interval type-2 fuzzy logic for dynamic parameter adaptation in the bat algorithm. Soft Comput. 2016, 3, 667–685. [Google Scholar] [CrossRef]
- Lee, T.C.; Song, K.T.; Lee, C.H.; Teng, C.C. Tracking control of unicycle-modeled mobile robots using a saturation feedback controller. IEEE Trans. Control Syst. Technol. 2001, 9, 305–318. [Google Scholar]
- Eberhart, R.C.; Shi, Y. Comparing inertia weights and constriction factors in particle swarm optimization. In Proceedings of the 2000 Congress on Evolutionary Computation, La Jolla, CA, USA, 16–19 July 2000; Volume 1, pp. 84–88. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).