1. Introduction
Fireworks Algorithm (FWA) [
1] is a new group of intelligent algorithms developed in recent years based on the natural phenomenon of simulating fireworks sparking, and can solve some optimization problems effectively. Compared with other intelligent algorithms such as particle swarm optimization and genetic algorithms, the FWA adopts a new type of explosive search mechanism, to calculate the explosion amplitude and the number of explosive sparks through the interaction mechanism between fireworks.
However, many researchers quickly find that traditional FWA has some disadvantages in solving optimization problems; the main disadvantages include slow convergence speed and low accuracy, thus, many improved algorithms have been proposed. So far, research on the FWA has concentrated on improving the operators. One of the most important improvements of the FWA is the enhanced fireworks algorithm (EFWA) [
2], where the operators of the conventional FWA were thoroughly analyzed and revised. Based on the EFWA, an adaptive fireworks algorithm (AFWA) [
3] was proposed, which was the first attempt to control the explosion amplitude without preset parameters by detecting the results of the search process. In [
4], a dynamic search fireworks algorithm (dynFWA) was proposed which divided the fireworks into core firework and non-core fireworks according to the fitness value and adaptive adjustment of the explosion amplitude for the core firework. Based on the analysis of each operator of the fireworks algorithm, an improvement of fireworks algorithm (IFWA) [
5] was proposed. Since the FWA was proposed, it has been applied to many areas [
6], including digital filter design [
7], nonnegative matrix factorization [
8], spam detection [
9], image identification [
10], mass minimization of trusses with dynamic constraints [
11], clustering [
12], power loss minimization and voltage profile enhancement [
13], etc.
The aforementioned dynFWA variants can improve the performance of FWA to some extent. However, the inhibition of premature convergence and solution accuracy improvement are still challenging issues that require further research on dynFWA.
In this paper, an adaptive mutation dynamic search fireworks algorithm (AMdynFWA) is presented. In AMdynFWA, the core firework chooses either Gaussian mutation or Levy mutation based on the mutation probability. When it chooses the Gaussian mutation, the local search ability of the algorithm will be enhanced, and by choosing Levy mutation, the ability of the algorithm to jump out of local optimization will be enhanced.
The paper is organized as follows. In
Section 2, the dynamic search fireworks algorithm is introduced. The AMdynFWA is presented in
Section 3. The simulation experiments and analysis of the results are given in detail in
Section 4. Finally, the conclusion is summarized in
Section 5.
2. Dynamic Search Fireworks Algorithm
The AMdynFWA is based on the dynFWA because it is very simple and it works stably. In this section, we will briefly introduce the framework and the operators of the dynFWA for further discussion.
Without the loss of generality, consider the following minimization problem:
The object is to find an optimal x with a minimal evaluation (fitness) value.
In dynFWA, there are two important components: the explosion operator (the sparks generated by the explosion) and the selection strategy.
2.1. Explosion Operator
Each firework explodes and generates a certain number of explosion sparks within a certain range (explosion amplitude). The numbers of explosion sparks (Equation (2)) are calculated according to the qualities of the fireworks.
For each firework
Xi, its explosion sparks’ number is calculated as follows:
where
ymax = max (
f(
Xi)),
m is a constant to control the number of explosion sparks, and
ε is the machine epsilon to avoid
Si equal to 0.
In order to limit the good fireworks that do not produce too many explosive sparks, while the poor fireworks do not produce enough sparks, its scope
Si is defined as.
where
a and
b are fixed constant parameters that confine the range of the population size.
In dynFWA, fireworks are divided into two types: non-core fireworks and core firework, and the core firework (CF) is the firework with the best fitness, and is calculated by Equation (4).
The calculations of the amplitude of the non-core fireworks and the core firework are different. The non-core fireworks’ explosion amplitudes (except for CF) are calculated just as in the previous versions of FWA:
where
ymin = min
f(
Xi),
A is a constant to control the explosion amplitude, and
ε is the machine epsilon to avoid
Ai equal to 0.
However, for the CF, its explosion amplitude is adjusted according to the search results in the last generation:
where
ACF(
t) is the explosion amplitude of the CF in generation
t. In the first generation, the CF is the best among all the randomly initialized fireworks, and its amplitude is preset to a constant number which is usually the diameter of the search space.
Algorithm 1 describes the process of the explosion operator in dynFWA.
| Algorithm 1. Generating Explosion Sparks |
| Calculate the number of explosion sparks Si |
| Calculate the non-core fireworks of explosion amplitude Ai |
| Calculate the core firework of explosion amplitude ACF |
| Set z = rand (1, d) |
| For k = 1:d do |
| If k ∈ z then |
| If Xjk is core firework then |
| Xjk = Xjk + rand (0, ACF) |
| Else |
| Xjk = Xjk + rand (0, Ai) |
| If Xjk out of bounds |
| Xjk = Xmink + |Xjk| % (Xmaxk − Xmink) |
| End if |
| End if |
| End for |
Where the operator % refers to the modulo operation, and Xmink and Xmaxk refer to the lower and upper bounds of the search space in dimension k.
2.2. Selection Strategy
In dynFWA, a selection method is applied, which is referred to as the Elitism-Random Selection method. In this selection process, the optima of the set will be selected firstly. Then, the other individuals are selected randomly.
3. Adaptive Mutation Dynamic Search Fireworks Algorithm
The mutation operation is an important step in the swarm intelligence algorithm. Different mutation schemes have different search characteristics. Zhou pointed out that the Gaussian mutation has a strong local development ability [
14]. Fei illustrated that the Levy mutation not only improves the global optimization ability of the algorithm, but also helps the algorithm jump out of the local optimal solution and keeps the diversity of the population [
15]. Thus, combining the Gaussian mutation with the Levy mutation is an effective way to improve the exploitation and exploration of dynFWA.
For the core firework, for each iteration, two mutation schemes are alternatives to be conducted based on a probability
p. The new mutation strategy is defined as:
where
p is a probability parameter,
XCF is the core firework in the current population, and the symbol
represents the dot product.
Gaussian() is a random number generated by the normal distribution with mean parameter
mu = 0 and standard deviation parameter
sigma = 1, and
Levy() is a random number generated by the Levy distribution, and it can be calculated with the parameter β = 1.5 [
16]. The value of
E varies dynamically with the evolution of the population, with reference to the annealing function of the simulated annealing algorithm, and the value of
E is expected to change exponentially, and it is calculated as follows:
where
t is the current function evaluations, and
Tmax is the maximum number of function evaluations.
To sum up, another type of sparks, the mutation sparks, are generated based on an adaptive mutation process (Algorithm 2). This algorithm is performed Nm times, each time with the core firework XCF (Nm is a constant to control the number of mutation sparks).
| Algorithm 2. Generating Mutation Sparks |
| Set the value of mutation probability p |
| Find out the core firework XCF in current population |
| Calculate the value of E by Equation (8) |
| Set z = rand (1, d) |
| For k = 1:d do |
| If k ∈ z then |
| Produce mutation spark XCF’ by Equation (7) |
| If XCF’ out of bounds |
| XCF’ = Xmin + rand * (Xmax − Xmin) |
| End if |
| End if |
| End for |
Where d is the number of dimensions, Xmin is the lower bound, and Xmax is the upper bound.
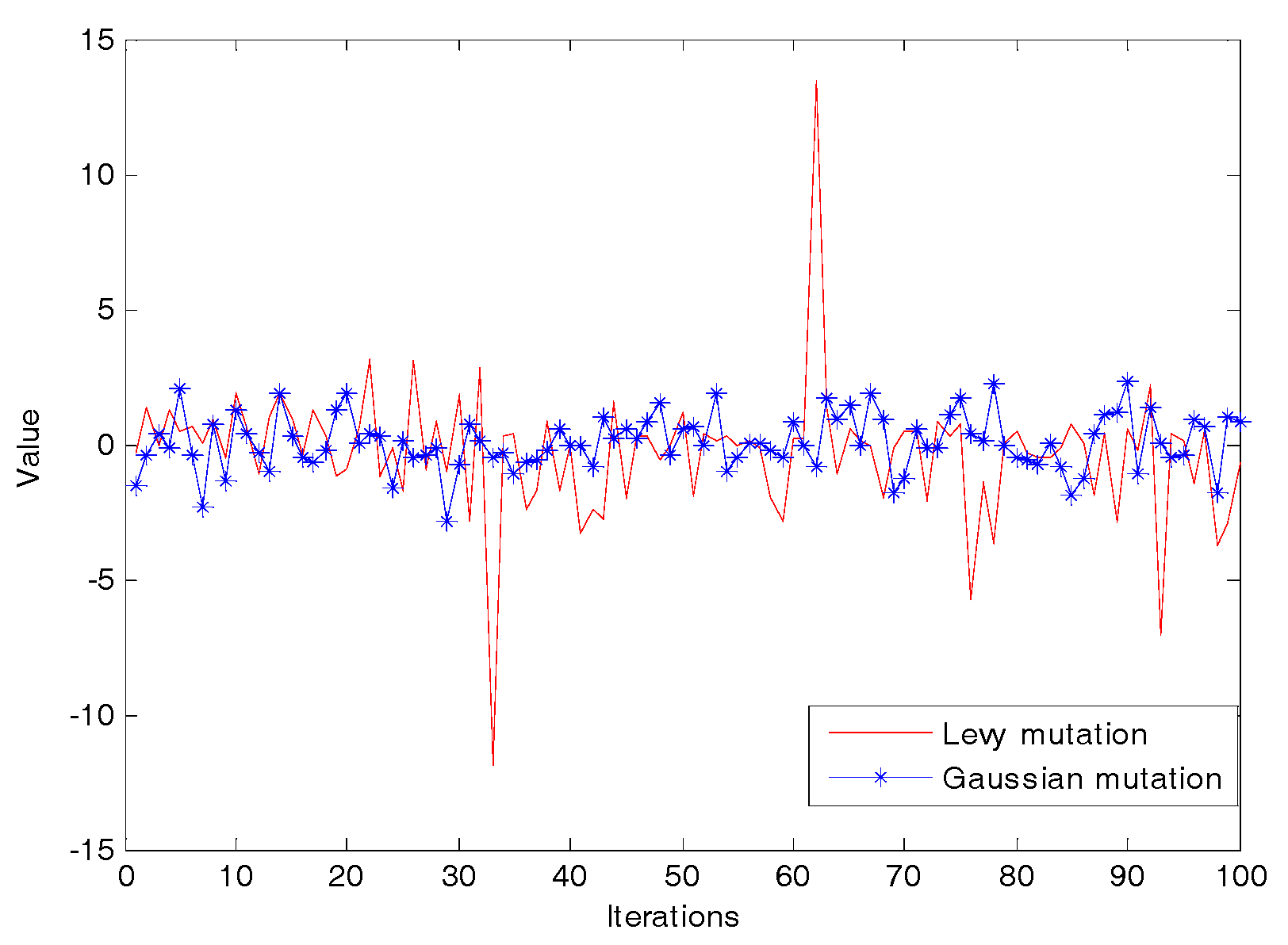
As
Figure 1 shows, the Levy mutation has a stronger perturbation effect than the Gaussian mutation. In the Levy mutation, the occasional larger values can effectively help jump out of the local optimum and keep the diversity of the population. On the contrary, the Gaussian mutation has better stability, which improves the local search ability.
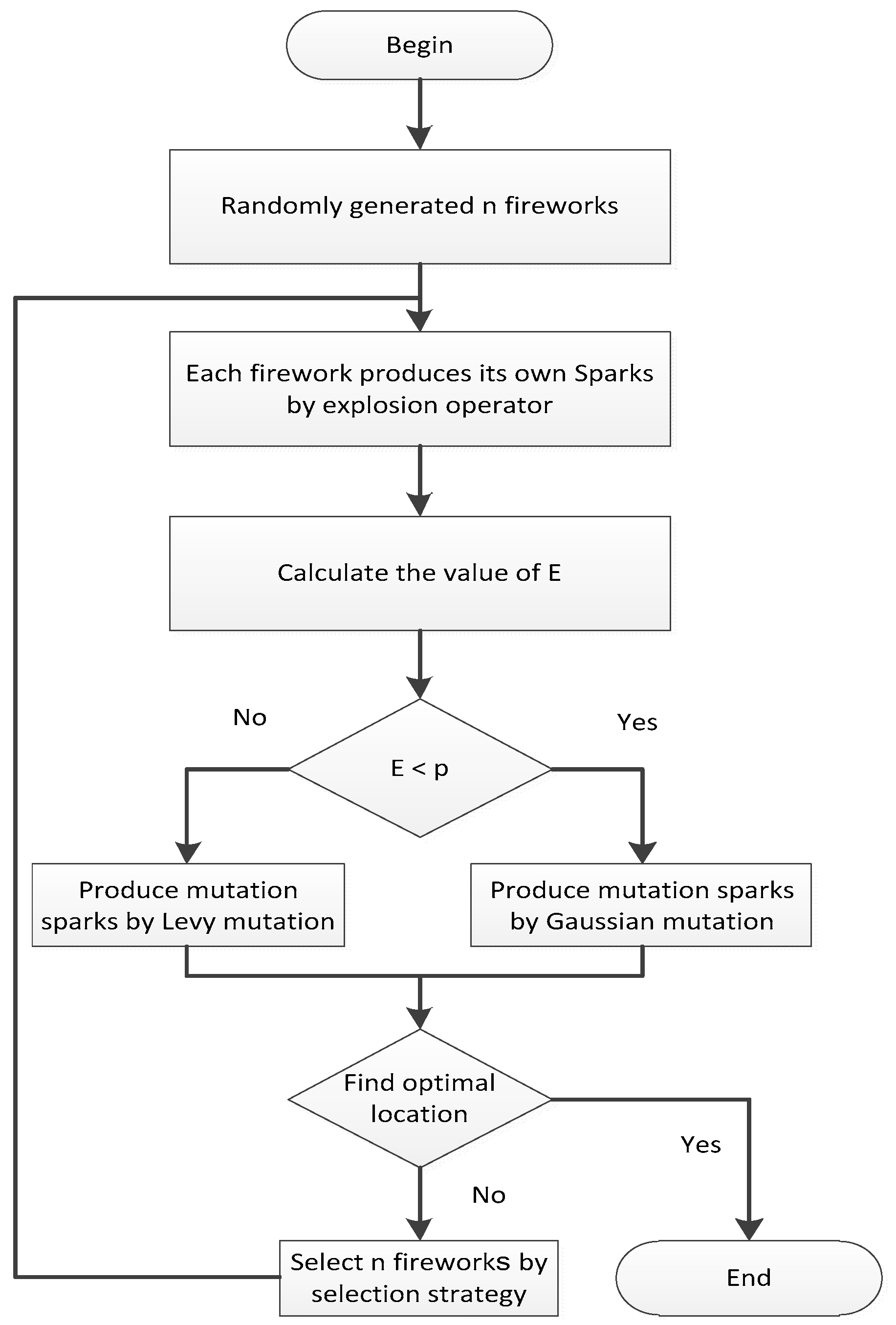
The flowchart of the adaptive mutation dynamic search fireworks algorithm (AMdynFWA) is shown in
Figure 2.
Algorithm 3 demonstrates the complete version of the AMdynFWA.
| Algorithm 3. Pseudo-Code of AMdynFWA |
| Randomly choosing m fireworks |
| Assess their fitness |
| Repeat |
| Obtain Ai (except for ACF) |
| Obtain ACF by Equation (6) |
| Obtain Si |
| Produce explosion sparks |
| Produce mutation sparks |
| Assess all sparks’ fitness |
| Retain the best spark as a firework |
| Select other m−1 fireworks randomly |
| Until termination condition is satisfied |
| Return the best fitness and a firework location |
4. Simulation Results and Analysis
4.1. Simulation Settings
Similar to dynFWA, the number of fireworks in AMdynFWA is set to five, the number of mutation sparks is also set to five, and the maximum number of sparks in each generation is set to 150.
In the experiment, the function of each algorithm is repeated 51 times, and the final results after 300,000 function evaluations are presented. In order to verify the performance of the algorithm proposed in this paper, we use the CEC2013 test set [
16], including 28 different types of test functions, which are listed in
Table 1. All experimental test function dimensions are set to 30,
d = 30.
Finally, we use the Matlab R2014a software on a PC with a 3.2 GHz CPU (Intel Core i5-3470), 4 GB RAM, and Windows 7 (64 bit).
4.2. Simulation Results and Analysis
4.2.1. Study on the Mutation Probability p
In AMdynFWA, the mutation probability p is introduced to control the probability of selecting the Gaussian and Levy mutations. To investigate the effects of the parameter, we compare the performance of AMdynFWA with different values of p. In this experiment, p is set to 0.1, 0.3, 0.5, 0.7, and 0.9, respectively.
Table 2 gives the computational results of AMdynFWA with different values of
p, where ‘Mean’ is the mean best fitness value. The best results among the comparisons are shown in bold. It can be seen that
p = 0.5 is suitable for unimodal problems f1 − f5. For f6 − f20,
p = 0.3 has a better performance than the others. When
p is set as 0.1 or 0.9, the algorithm obtains better performance on f21 − f28.
The above results demonstrate that the parameter p is problem-oriented. For different problems, different p may be required. In this paper, taking into account the average ranking, p = 0.3 is regarded as the relatively suitable value.
4.2.2. Comparison of AMdynFWA with FWA-Based Algorithms
To assess the performance of AMdynFWA, AMdynFWA is compared with enhanced fireworks algorithm (EFWA), dynamic search fireworks algorithms (dynFWA), and adaptive fireworks algorithm (AFWA), and the EFWA parameters are set in accordance with [
2], the AFWA parameters are set in accordance with [
3], and the dynFWA parameters are set in accordance with [
4].
The probability
p used in AMdynFWA is set to 0.3. For each test problem, each algorithm runs 51 times, all experimental test function dimensions are set as 30, and their mean errors and total number of rank 1 are reported in
Table 3.
The results from
Table 3 indicate that the total number of rank 1 of AMdynFWA (23) is the best of the four algorithms.
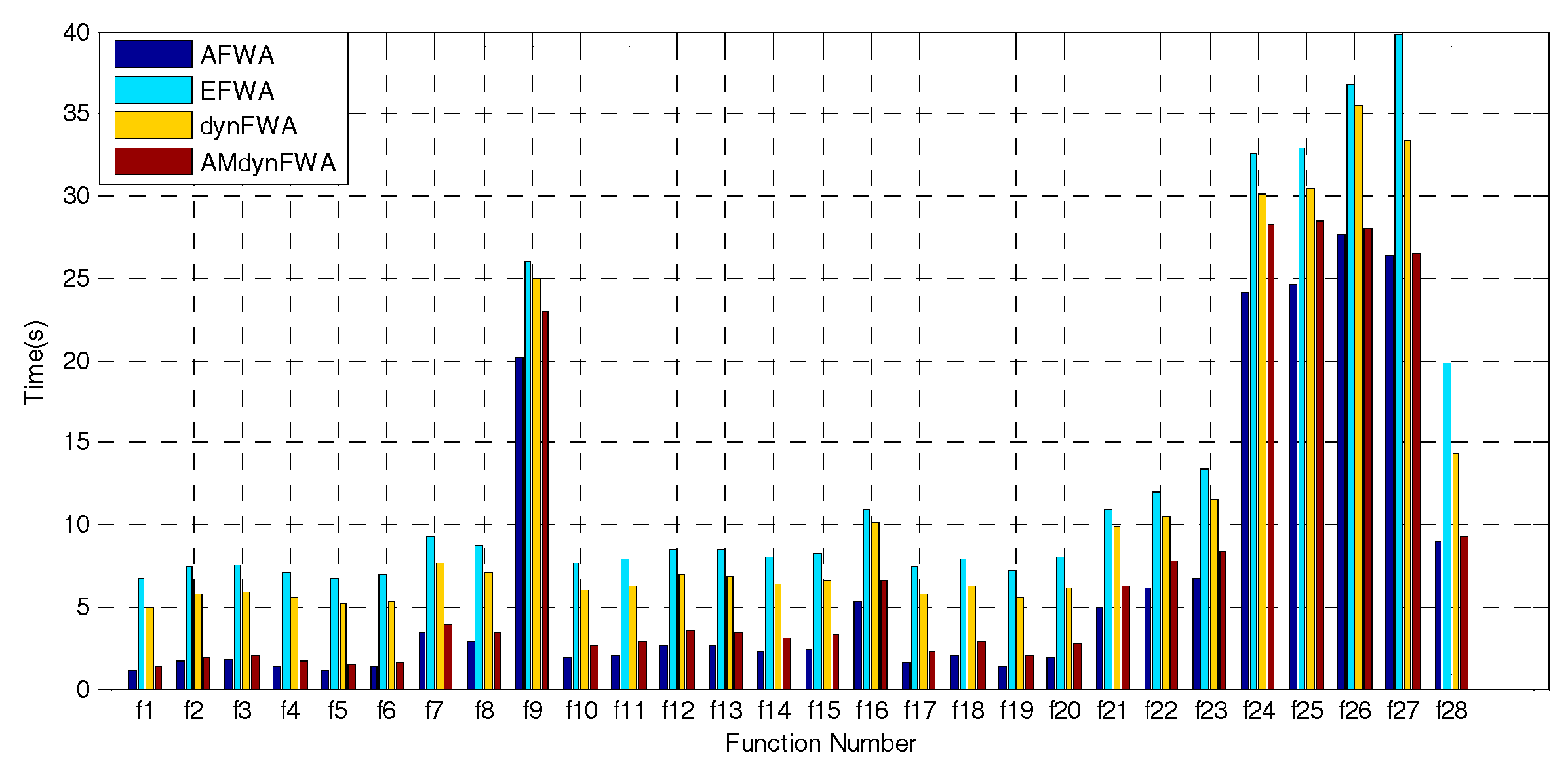
Figure 3 shows a comparison of the average run-time cost in the 28 functions for AFWA, EFWA, dynFWA, and AMdynFWA.
The results from
Figure 3 indicate that the average run-time cost of EFWA is the most expensive among the four algorithms. The time cost of AFWA is the least, but the run-time cost of AMdynFWA is almost the same compared with AFWA. The run-time cost of AMdynFWA is less than that of dynFWA. Taking into account the results from
Table 3, AMdynFWA performs significantly better than the other three algorithms.
To evaluate whether the AMdynFWA results were significantly different from those of the EFWA, AFWA, and dynFWA, the AMdynFWA mean results during the iteration for each test function were compared with those of the EFWA, AFWA, and dynFWA. The
T test [
17], which is safe and robust, was utilized at the 5% level to detect significant differences between these pairwise samples for each test function.
The
ttest2 function in Matlab R2014a was used to run the
T test, as shown in
Table 4. The null hypothesis is that the results of EFWA, AFWA, and dynFWA are derived from distributions of equal mean, and in order to avoid increases of type I errors, we correct the
p-values using the Holm’s method, and order the
p-values for the three hypotheses being tested from smallest to largest, and we then have three
T tests. Thus, the
p-value 0.05 is changed to 0.0167, 0.025, and 0.05, and then the corrected
p-values were used to compare with the calculated
p-values, respectively.
Where the p-value is the result of the T test. The ‘+’ indicates the rejection of the null hypothesis at the 5% significance level, and the ‘-’ indicates the acceptance of the null hypothesis at the 5% significance level.
Table 5 indicates that AMdynFWA showed a large improvement over EFWA in most functions. However, in Unimodal Functions, AMdynFWA is not significant when compared with AFWA and dynFWA. In Basic Multimodal Functions and Composition Functions, the AMdynFWA also showed a large improvement over AFWA and dynFWA.
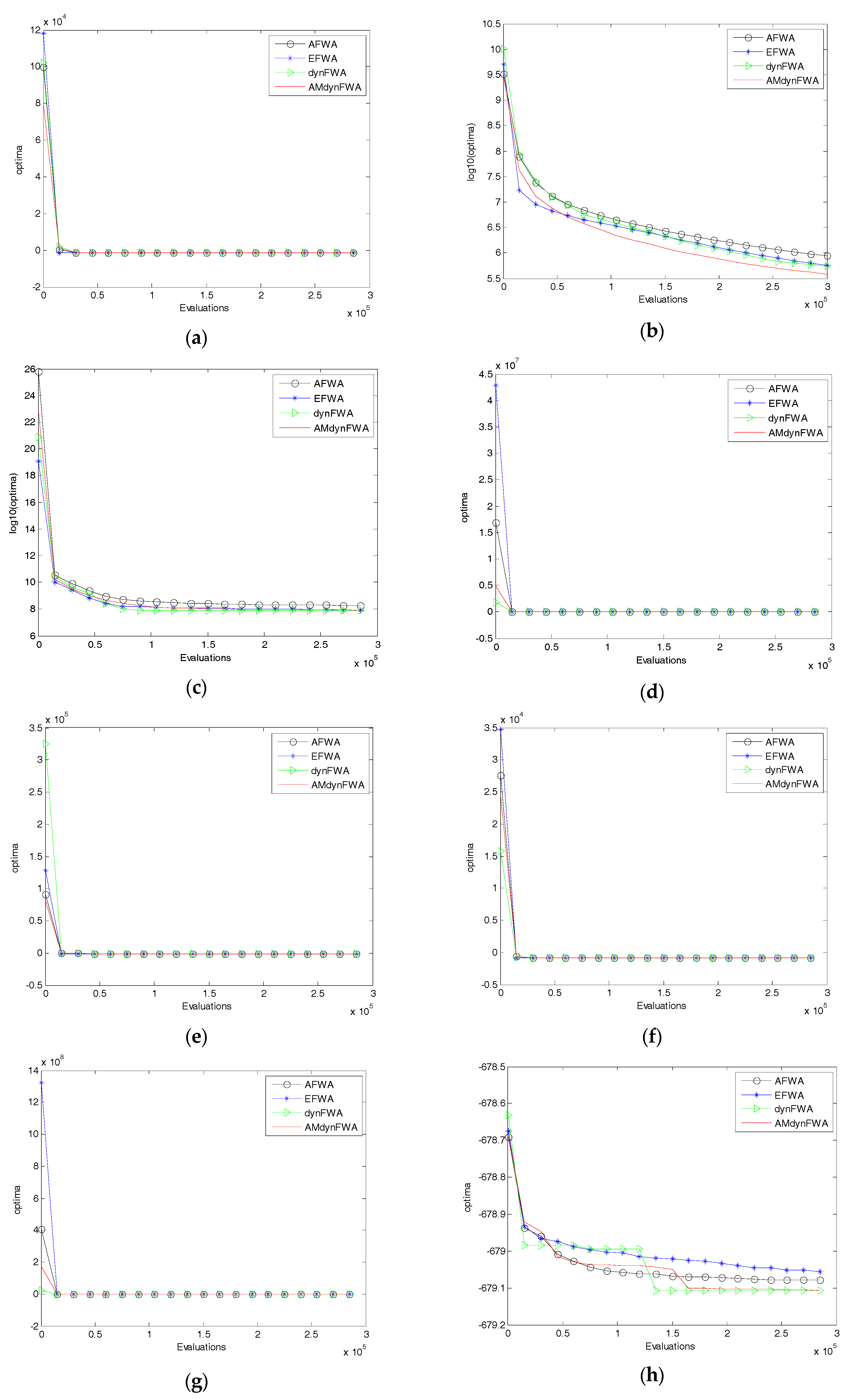
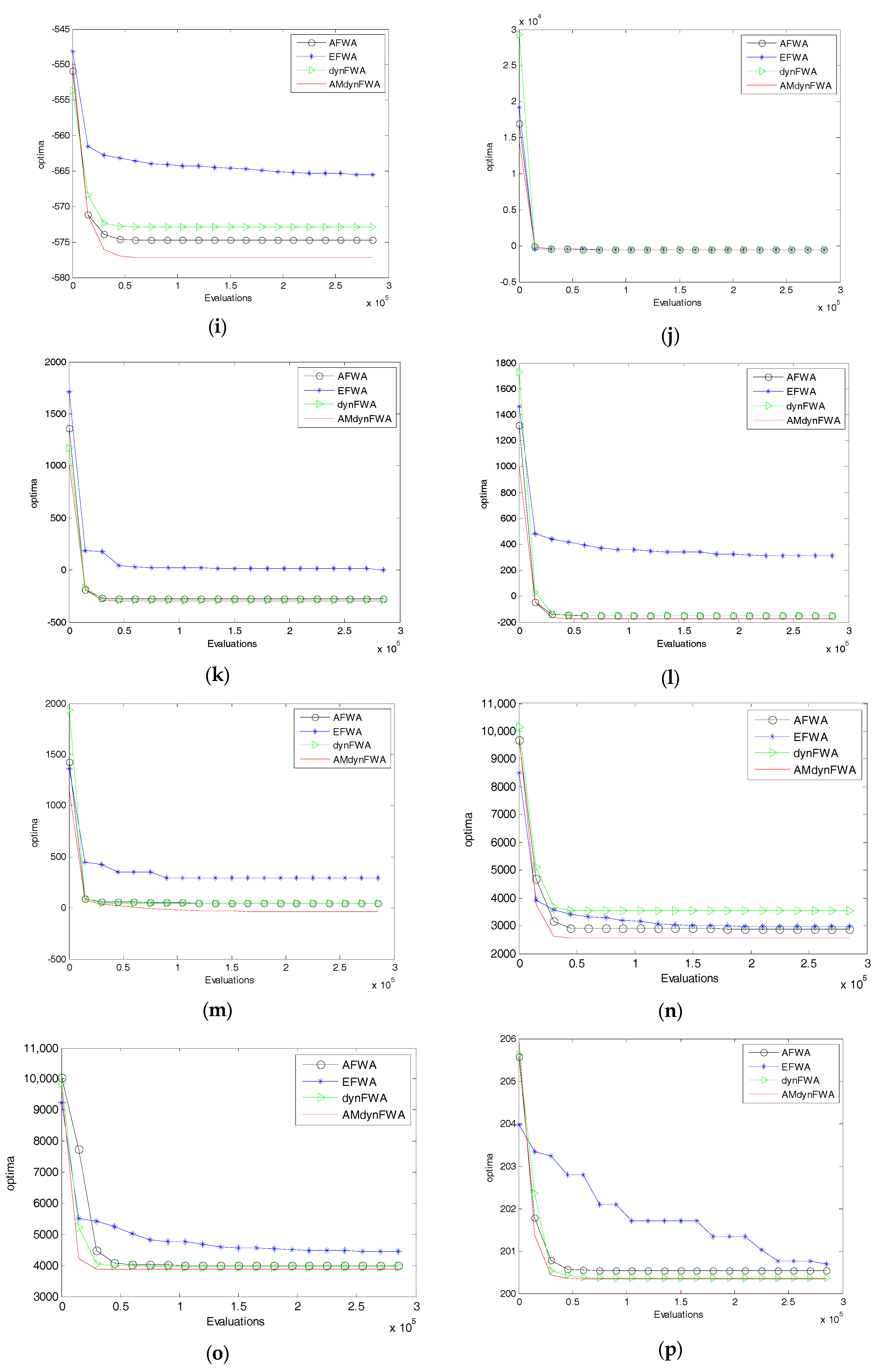
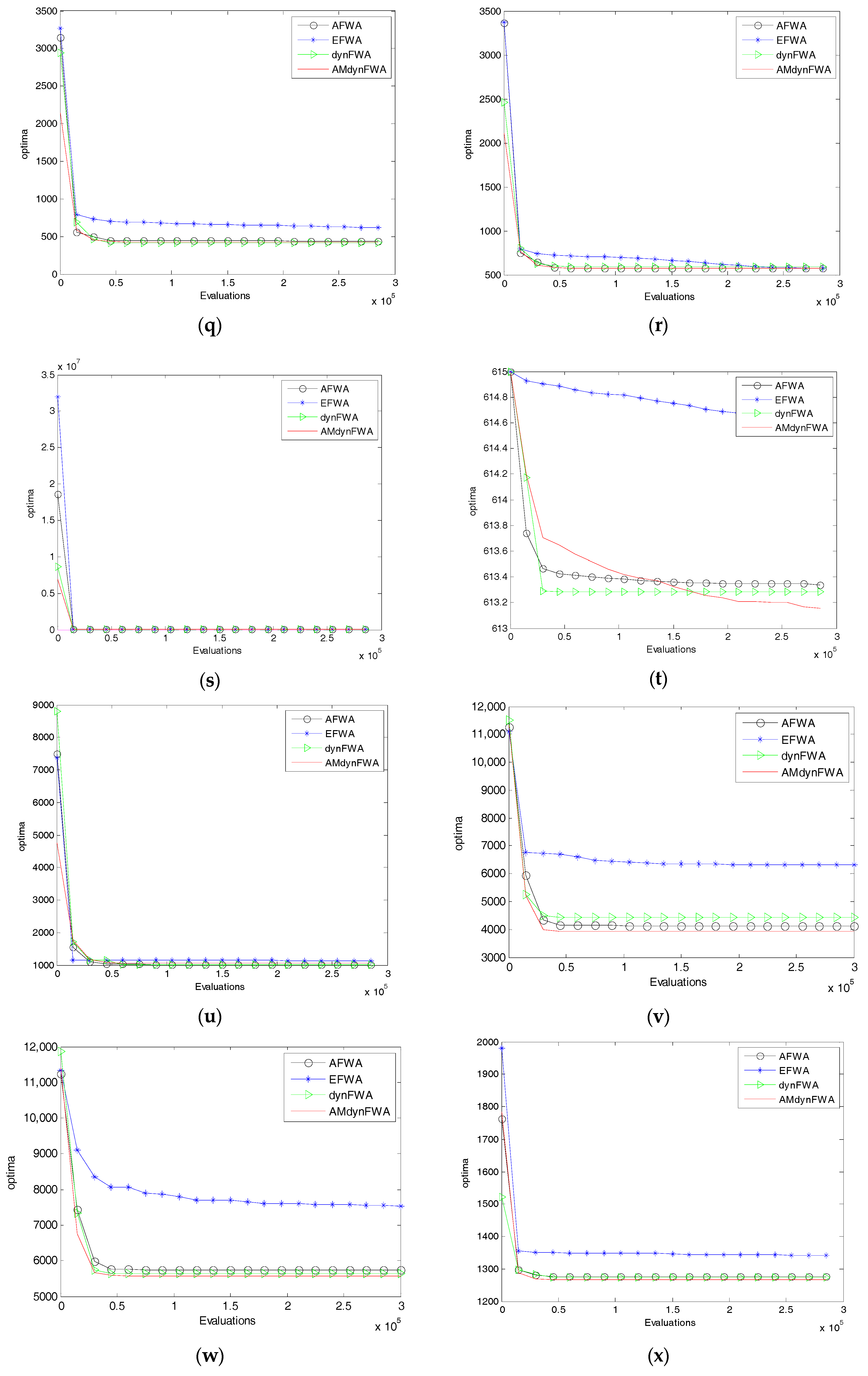
Figure 4 shows the mean fitness searching curves of the 28 functions for EFWA, AFWA, dynFWA, and AMdynFWA.
4.2.3. Comparison of AMdynFWA with Other Swarm Intelligence Algorithms
In order to measure the relative performance of the AMdynFWA, a comparison among the AMdynFWA and the other swarm intelligence algorithms is conducted on the CEC2013 single objective benchmark suite. The algorithms compared here are described as follows.
- (1)
Artificial bee colony (ABC) [
18]: A powerful swarm intelligence algorithm.
- (2)
Standard particle swarm optimization (SPSO2011) [
19]: The most recent standard version of the famous swarm intelligence algorithm PSO.
- (3)
Differential evolution (DE) [
20]: One of the best evolutionary algorithms for optimization.
- (4)
Covariance matrix adaptation evolution strategy (CMA-ES) [
21]: A developed evolutionary algorithm.
The above four algorithms use the default settings. The comparison results of ABC, DE, CMS-ES, SPSO2011, and AMdynFWA are presented in
Table 6, where the ’Mean error’ is the mean error of the best fitness value. The best results among the comparisons are shown in bold. ABC beats the other algorithms on 12 functions (some differences are not significant), which is the most, but performs poorly on the other functions. CMA-ES performs extremely well on unimodal functions, but suffers from premature convergence on some complex functions. From
Table 7, the AMdynFWA ranked the top three (22/28), which is better than the other algorithms (except the DE), and in terms of average ranking, the AMdynFWA performs the best among these five algorithms on this benchmark suite due to its stability. DE and ABC take the second place and the third place, respectively. The performances of CMS-ES and the SPSO2011 are comparable.
5. Conclusions
AMdynFWA was developed by applying two mutation methods to dynFWA. It selects the Gaussian mutation or Levy mutation according to the mutation probability. We apply the CEC2013 standard functions to examine and compare the proposed algorithm AMdynFWA with ABC, DE, SPSO2011, CMS-ES, AFWA, EFWA, and dynFWA. The results clearly indicate that AMdynFWA can perform significantly better than the other seven algorithms in terms of solution accuracy and stability. Overall, the research demonstrates that AMdynFWA performed the best for solution accuracies.
The study on the mutation probability p demonstrates that there is no constant p for all the test problems, while p = 0.3 is regarded as the relatively suitable value for the current test suite. A dynamic p may be a good choice. This will be investigated in future work.
Acknowledgments
The authors are thankful to the anonymous reviewers for their valuable comments to improve the technical content and the presentation of the paper. This paper is supported by the Liaoning Provincial Department of Education Science Foundation (Grant No. L2013064), AVIC Technology Innovation Fund (basic research) (Grant No. 2013S60109R), and the Research Project of Education Department of Liaoning Province (Grant No. L201630).
Author Contributions
Xi-Guang Li participated in the draft writing. Shou-Fei Han participated in the concept, design, and performed the experiments and commented on the manuscript. Liang Zhao, Chang-Qing Gong, and Xiao-Jing Liu participated in the data collection, and analyzed the data.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Tan, Y.; Zhu, Y. Fireworks Algorithm for Optimization. In Advances in Swarm Intelligence, Proceedings of the 2010 International Conference in Swarm Intelligence, Beijing, China, 12–15 June 2010; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Zheng, S.; Janecek, A.; Tan, Y. Enhanced fireworks algorithm. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 2069–2077. [Google Scholar]
- Zheng, S.; Li, J.; Tan, Y. Adaptive fireworks algorithm. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation, Beijing, China, 6–11 July 2014; pp. 3214–3221. [Google Scholar]
- Zheng, S.; Tan, Y. Dynamic search in fireworks algorithm. In Proceedings of the 2014 IEEE Congress on Evolutionary Computation, Beijing, China, 6–11 July 2014; pp. 3222–3229. [Google Scholar]
- Li, X.-G.; Han, S.-F.; Gong, C.-Q. Analysis and Improvement of Fireworks Algorithm. Algorithms 2017, 10, 26. [Google Scholar] [CrossRef]
- Tan, Y. Fireworks Algorithm Introduction, 1st ed.; Science Press: Beijing, China, 2015; pp. 13–136. (In Chinese) [Google Scholar]
- Gao, H.Y.; Diao, M. Cultural firework algorithm and its application for digital filters design. Int. J. Model. Identif. Control 2011, 4, 324–331. [Google Scholar] [CrossRef]
- Andreas, J.; Tan, Y. Using population based algorithms for initializing nonnegative matrix factorization. In Advances in Swarm Intelligence, Proceedings of the 2010 International Conference in Swarm Intelligence, Chongqing, China, 12–15 June 2011; Springer: Berlin/Heidelberg, Germany, 2011; pp. 307–316. [Google Scholar]
- Wen, R.; Mi, G.Y.; Tan, Y. Parameter optimization of local-concentration model for spam detection by using fireworks algorithm. In Proceedings of the 4th International Conference on Swarm Intelligence, Harbin, China, 12–15 June 2013; pp. 439–450. [Google Scholar]
- Zheng, S.; Tan, Y. A unified distance measure scheme for orientation coding in identification. In Proceedings of the 2013 IEEE Congress on Information Science and Technology, Yangzhou, China, 23–25 March 2013; pp. 979–985. [Google Scholar]
- Pholdee, N.; Bureerat, S. Comparative performance of meta-heuristic algorithms for mass minimisation of trusses with dynamic constraints. Adv. Eng. Softw. 2014, 75, 1–13. [Google Scholar] [CrossRef]
- Yang, X.; Tan, Y. Sample index based encoding for clustering using evolutionary computation. In Advances in Swarm Intelligence, Proceedings of the 2014 International Conference on Swarm Intelligence, Hefei, China, 17–20 October 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 489–498. [Google Scholar]
- Mohamed Imran, A.; Kowsalya, M. A new power system reconfiguration scheme for power loss minimization and voltage profile enhancement using fireworks algorithm. Int. J. Electr. Power Energy Syst. 2014, 62, 312–322. [Google Scholar] [CrossRef]
- Zhou, F.J.; Wang, X.J.; Zhang, M. Evolutionary Programming Using Mutations Based on the t Probability Distribution. Acta Electron. Sin. 2008, 36, 121–123. [Google Scholar]
- Fei, T.; Zhang, L.Y.; Chen, L. Improved Artificial Fish Swarm Algorithm Mixing Levy Mutation and Chaotic Mutation. Comput. Eng. 2016, 42, 146–158. [Google Scholar]
- Liang, J.; Qu, B.; Suganthan, P.; Hernandez-Diaz, A.G. Problem Definitions and Evaluation Criteria for the CEC 2013 Special Session on Real-Parameter Optimization; Technical Report 201212; Zhengzhou University: Zhengzhou, China, January 2013. [Google Scholar]
- Teng, S.Z.; Feng, J.H. Mathematical Statistics, 4th ed.; Dalian University of Technology Press: Dalian, China, 2005; pp. 34–35. (In Chinese) [Google Scholar]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Zambrano-Bigiarini, M.; Clerc, M.; Rojas, R. Standard particle swarm optimization 2011 at CEC2013: A baseline for future PSO improvements. In Proceedings of the 2013 IEEE Congress on Evolutionary Computation, Cancun, Mexico, 20–23 June 2013; pp. 2337–2344. [Google Scholar]
- Storn, R.; Price, K. Differential evolution—A simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 1997, 11, 341–359. [Google Scholar] [CrossRef]
- Hansen, N.; Ostermeier, A. Adapting arbitrary normal mutation distributions in evolution strategies: The covariance matrix adaptation. In Proceedings of the 1996 IEEE International Conference on Evolutionary Computation, Nagoya, Japan, 20–22 May 1996; pp. 312–317. [Google Scholar]
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).