Multivariate Statistical Process Control Using Enhanced Bottleneck Neural Network
Abstract
:1. Introduction
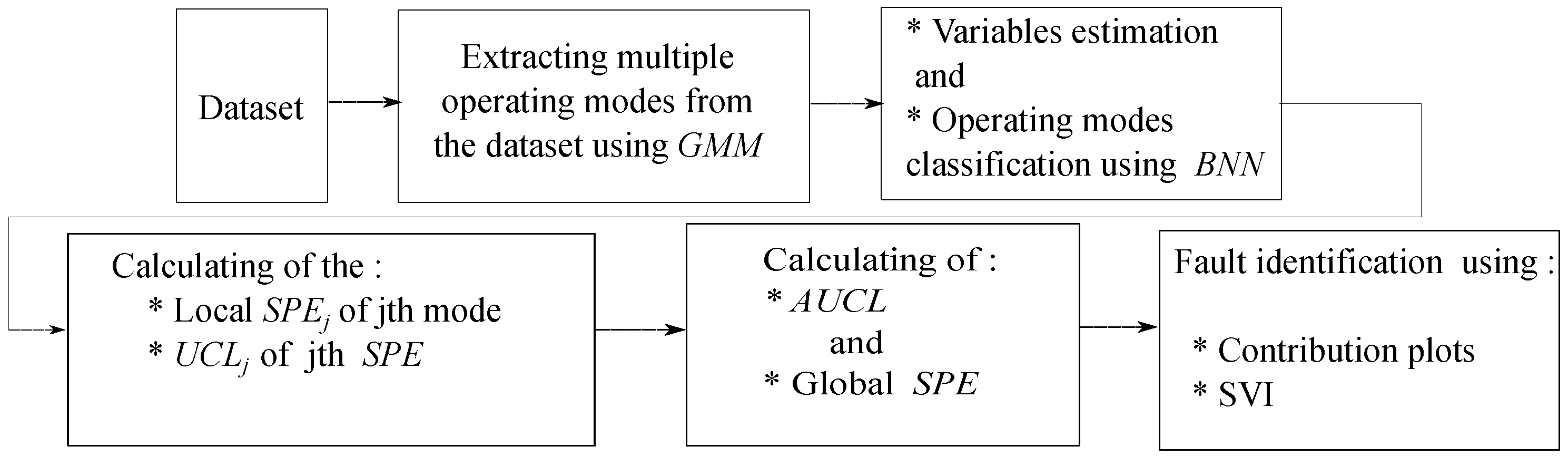
2. Materials and Methods
2.1. Multivariate Statistical Process Control
2.1.1. Gaussian Mixture Model
- E-Step: compute the posterior probability of the training sample at the iterationwhere denotes the Gaussian component.
- M-Step: update the model parameters at the iteration
2.1.2. Enhanced Bottleneck Neural Network
- Encoding process (compression): For an input vector , the encoding process (compress inputs) can be described as:When the bottleneck layer forces the EBNN to compress the inputs (variables to be monitored).
- Decoding process (decompression): The bottleneck layer produces the network outputs (estimation and classification) by decompression, which is given as:with
- -
- n is the number of neurons in the input layer.
- -
- h is the number of neurons in the mapping layer.
- -
- q is the number of neurons in the bottleneck layer.
- -
- w is the weight values of the network.
- -
- is the threshold value for the node of the mapping layer.
- -
- m is the number of neurons in the output layer of the operating modes classification part.
- -
- is the sigmoid transfer function,
where the transfer function in the mapping and de-mapping layers is sigmoid, and in bottleneck and output layers is linear. Exceptionally, in the output classification part is log-sigmoid in order to generate a posterior probability rates vary between 0 and 1.
- -
- N is the number of training samples.
- -
- n is the number of neurons in the output layer of the estimation part.
- -
- m is the number of neurons in the output layer of the modes classification part.
- -
- is the n desired values of the output neuron.
- -
- is the n actual outputs of that neuron.
- -
- is the probability rate already obtained with GMM of the mode.
- -
- is the actual output of neuron which corresponds to jth mode.
2.2. Process Monitoring and Diagnosis
2.2.1. Squared Prediction Error
2.2.2. Adaptive Upper Control Limits
- -
- m is number of Gaussian components corresponding to the normal operating modes.
- -
- is the probability rate of mode during the normal operating regime.
- -
- is the upper control limit using the kernel density estimation (KDE) of each mode during the normal operating regime.
- -
- n is the number of samples.
2.2.3. Upper Control Limit by KDE
- (1)
- a full symmetrical positive definite matrix with parameters —for example, in which = ;
- (2)
- a diagonal matrix with only l parameters, ;
- (3)
- a diagonal matrix with one parameter, , where, I is unit matrix.
2.3. Fault Isolation
2.3.1. Isolation by Contribution Plots
2.3.2. Sensor Validity Index
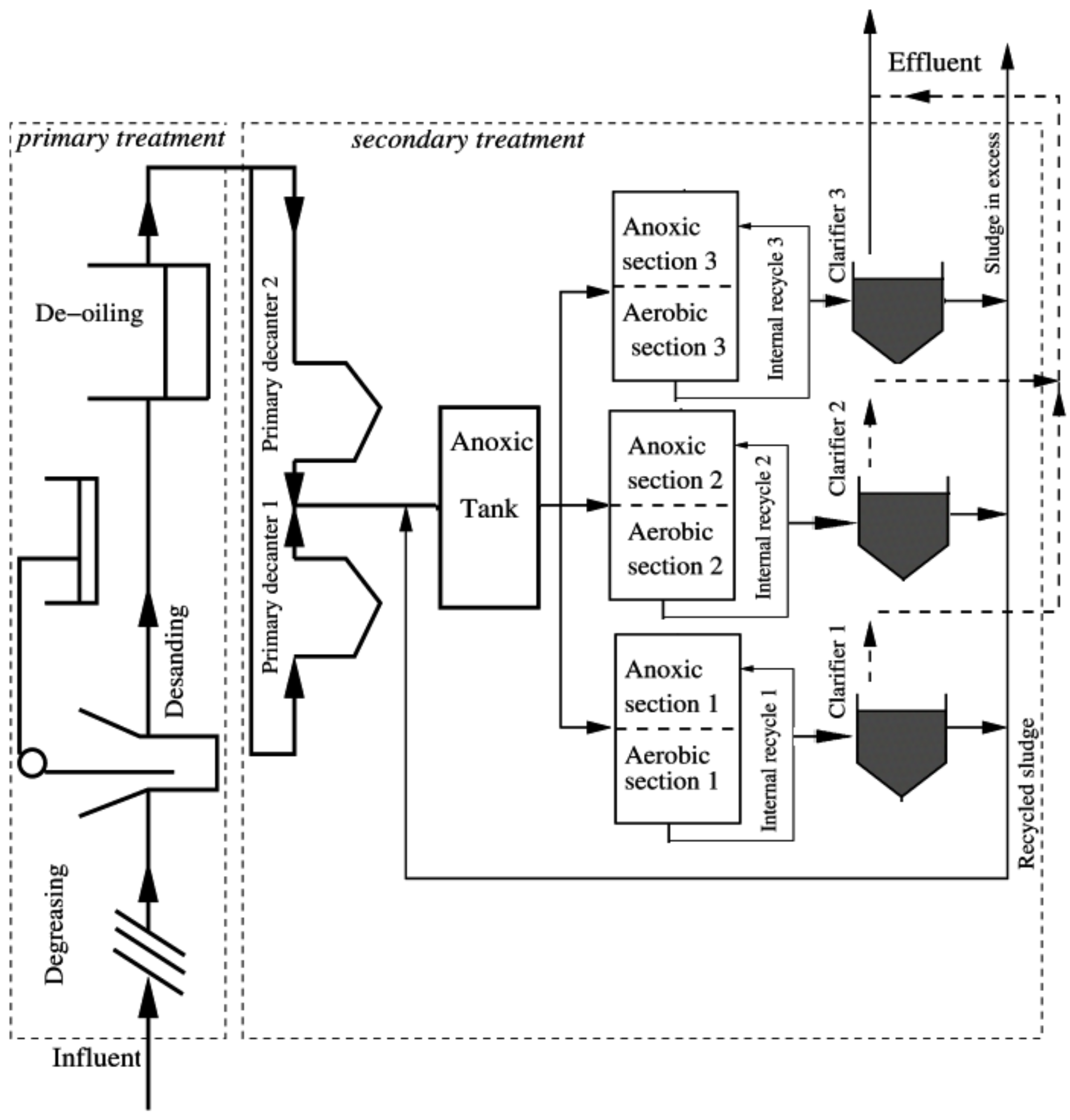
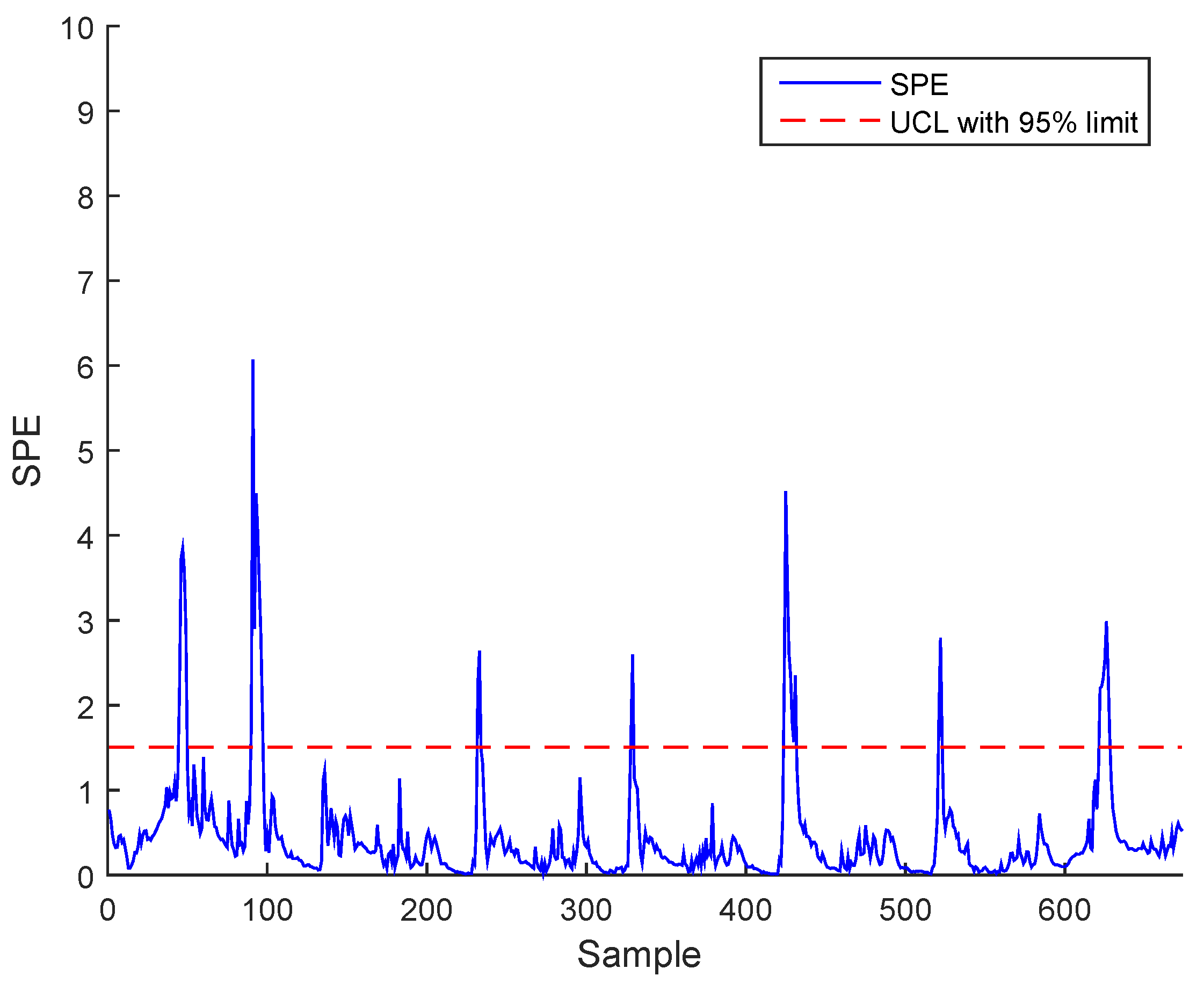
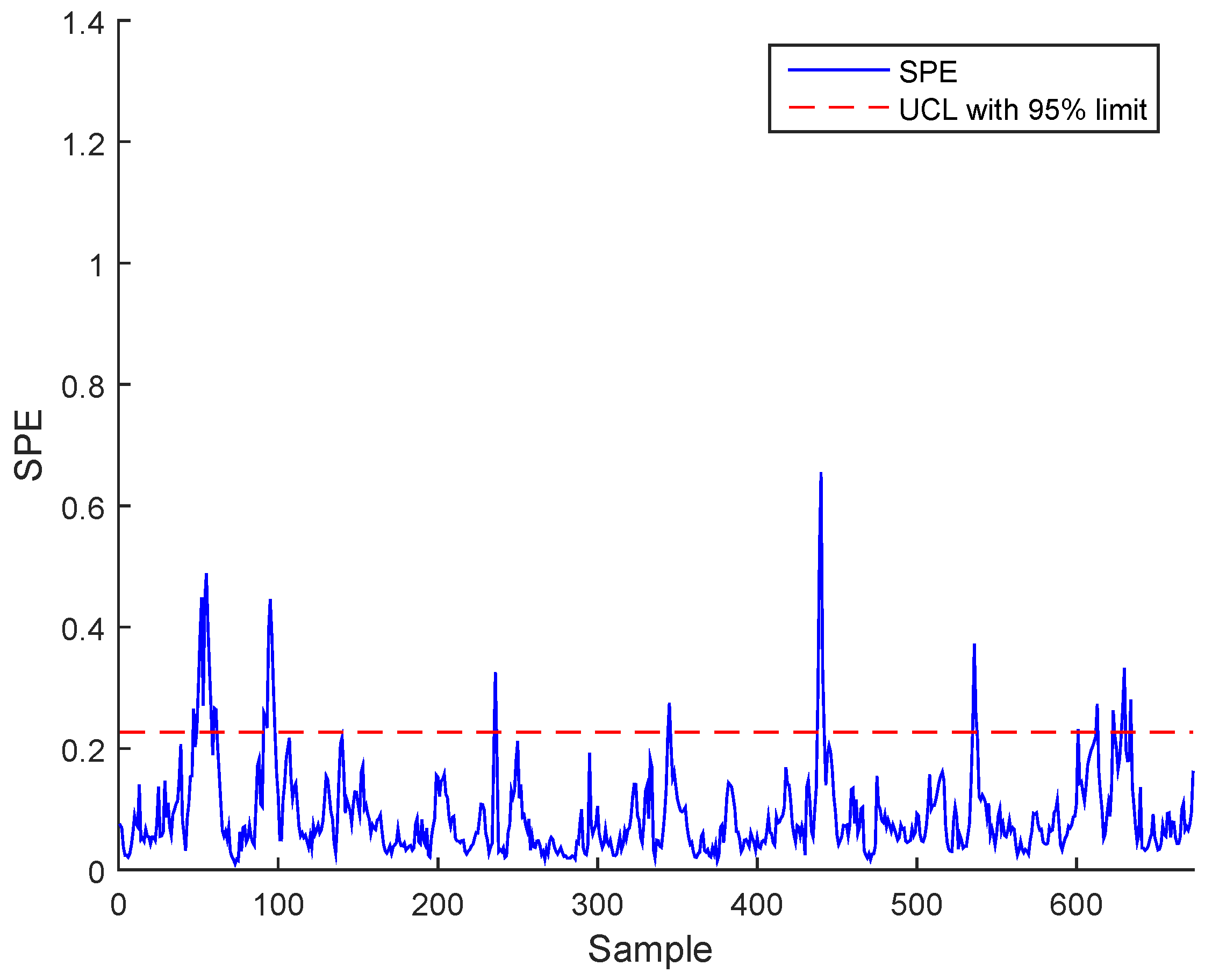
3. Case Study : Wastewater Treatment Plant (WWTP) Monitoring
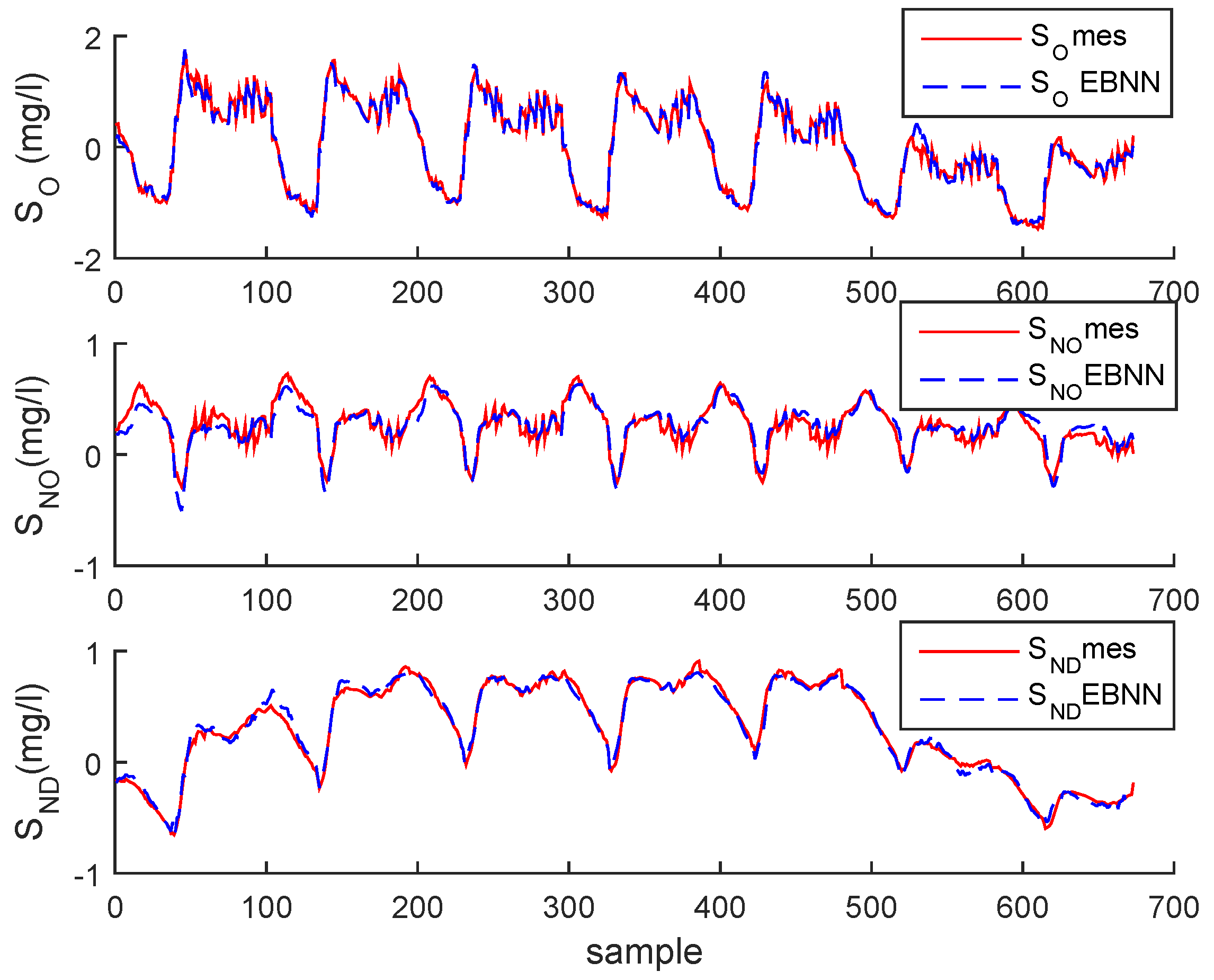
3.1. Simulated Process Case
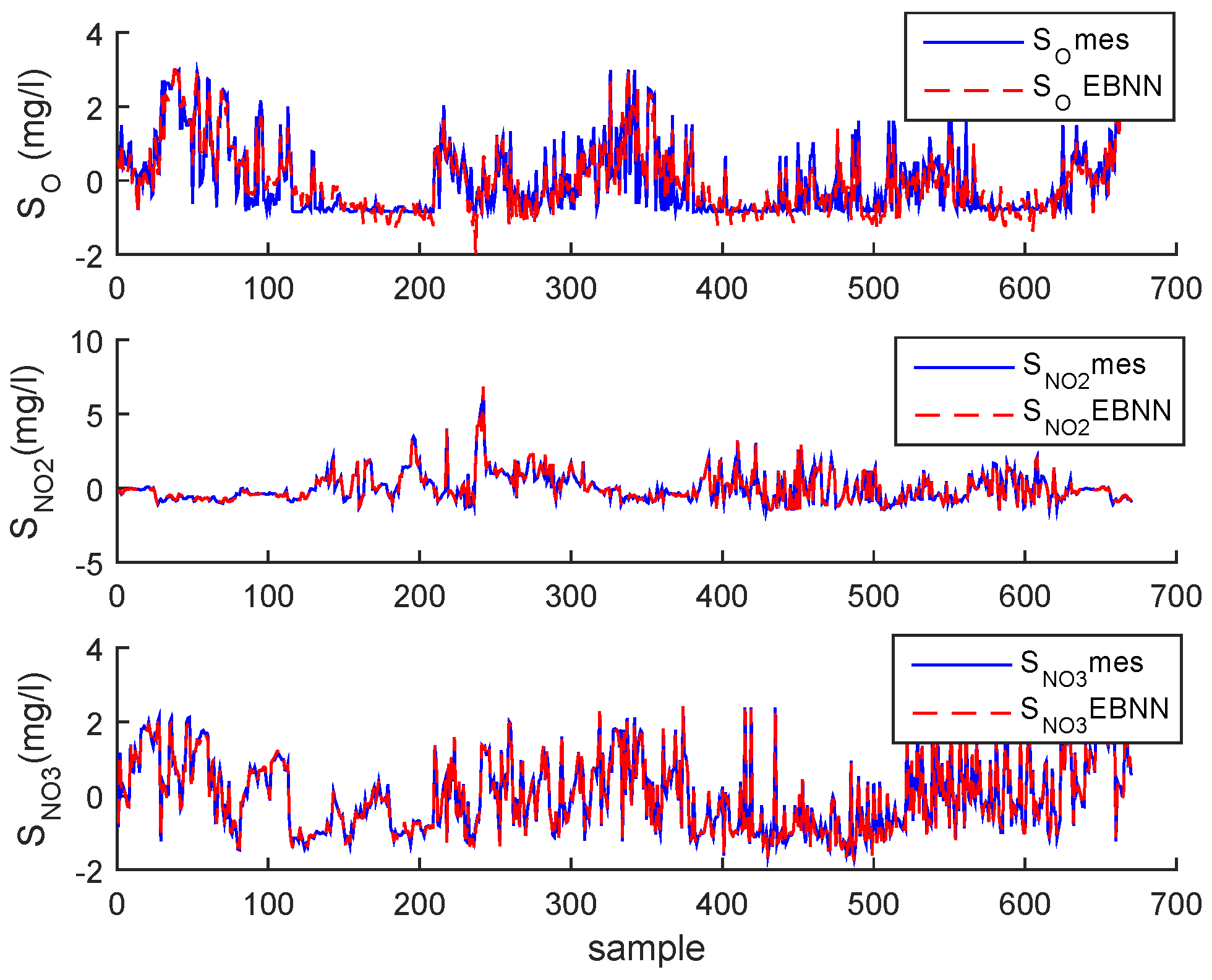
3.2. Real Process Case
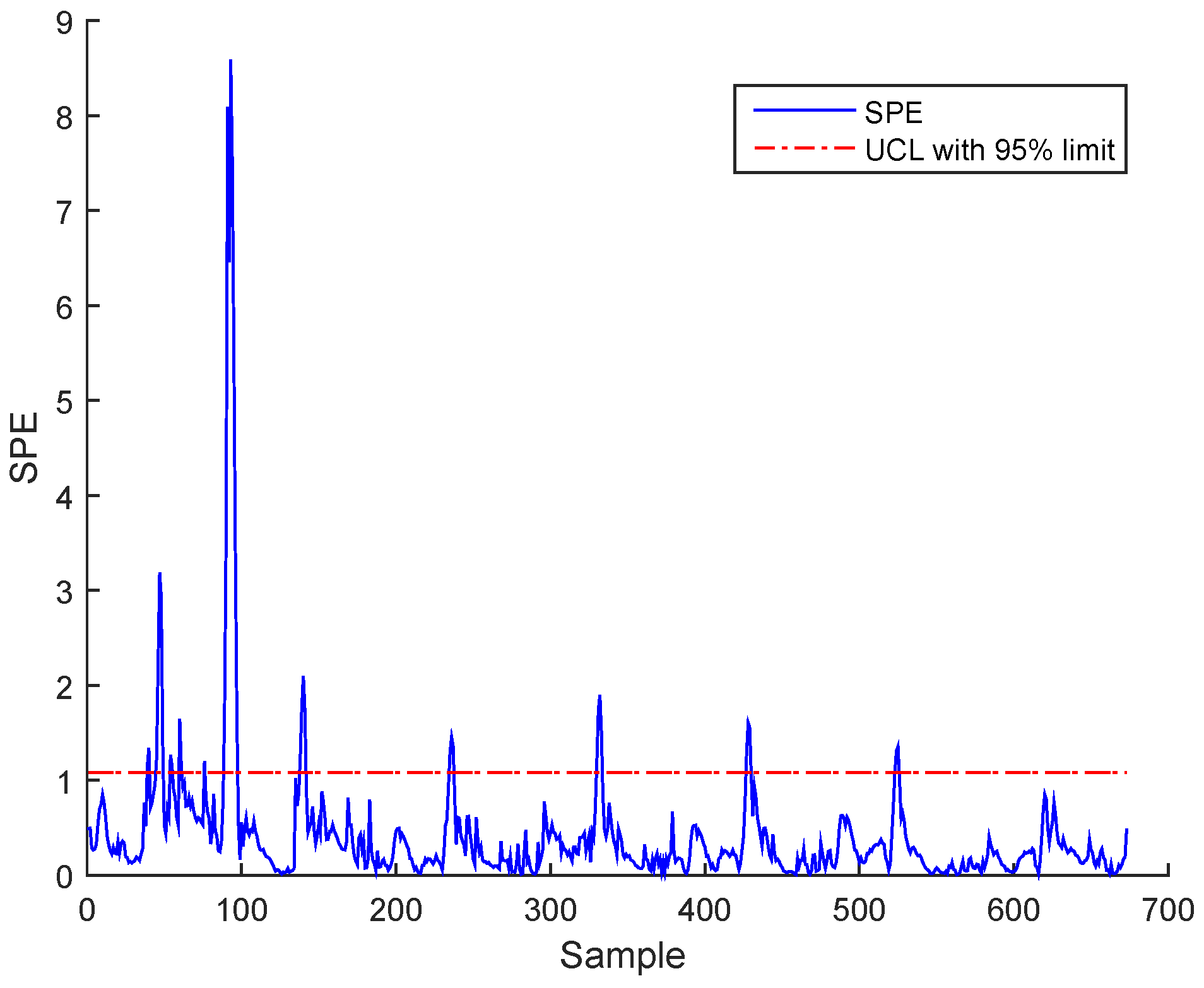
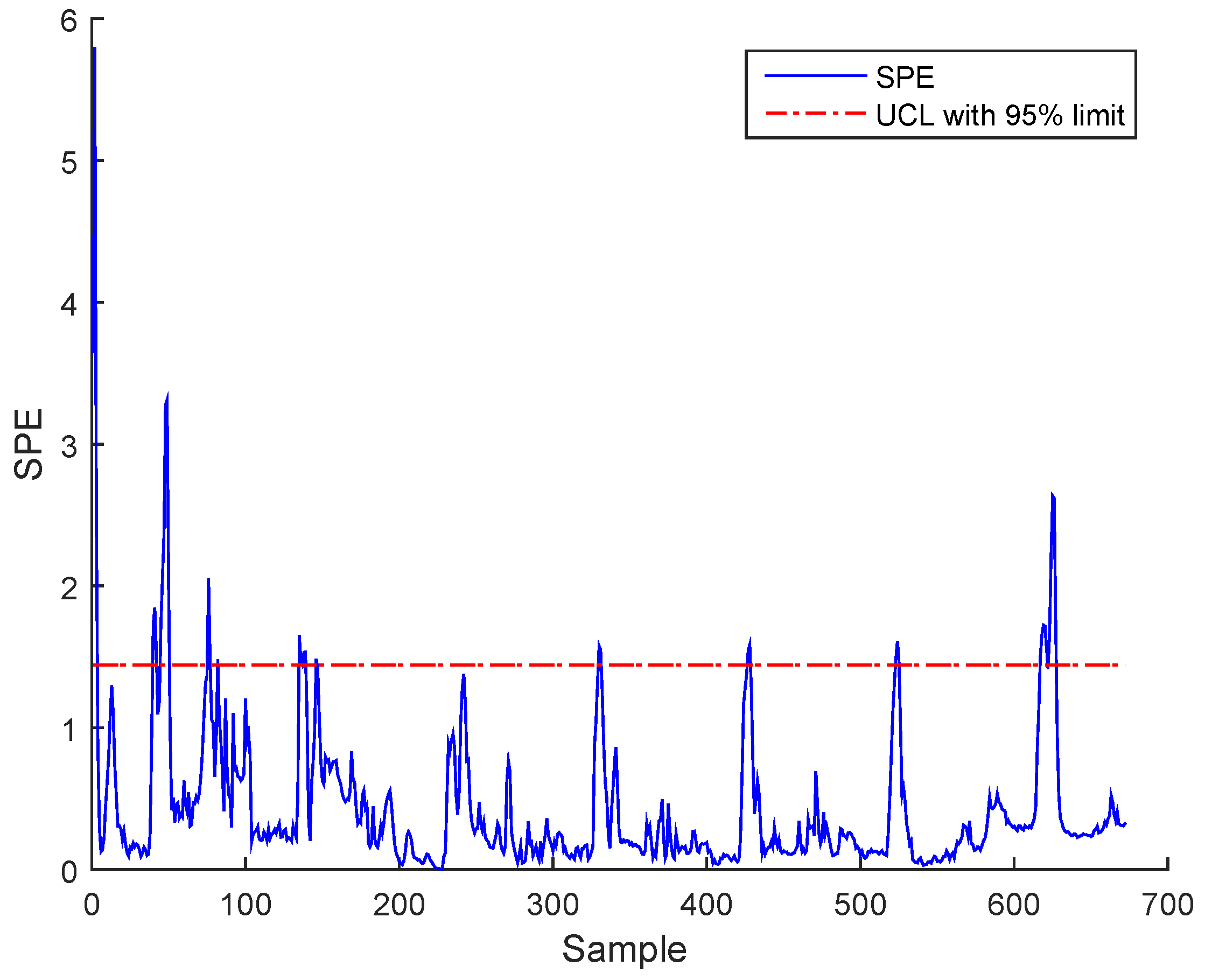
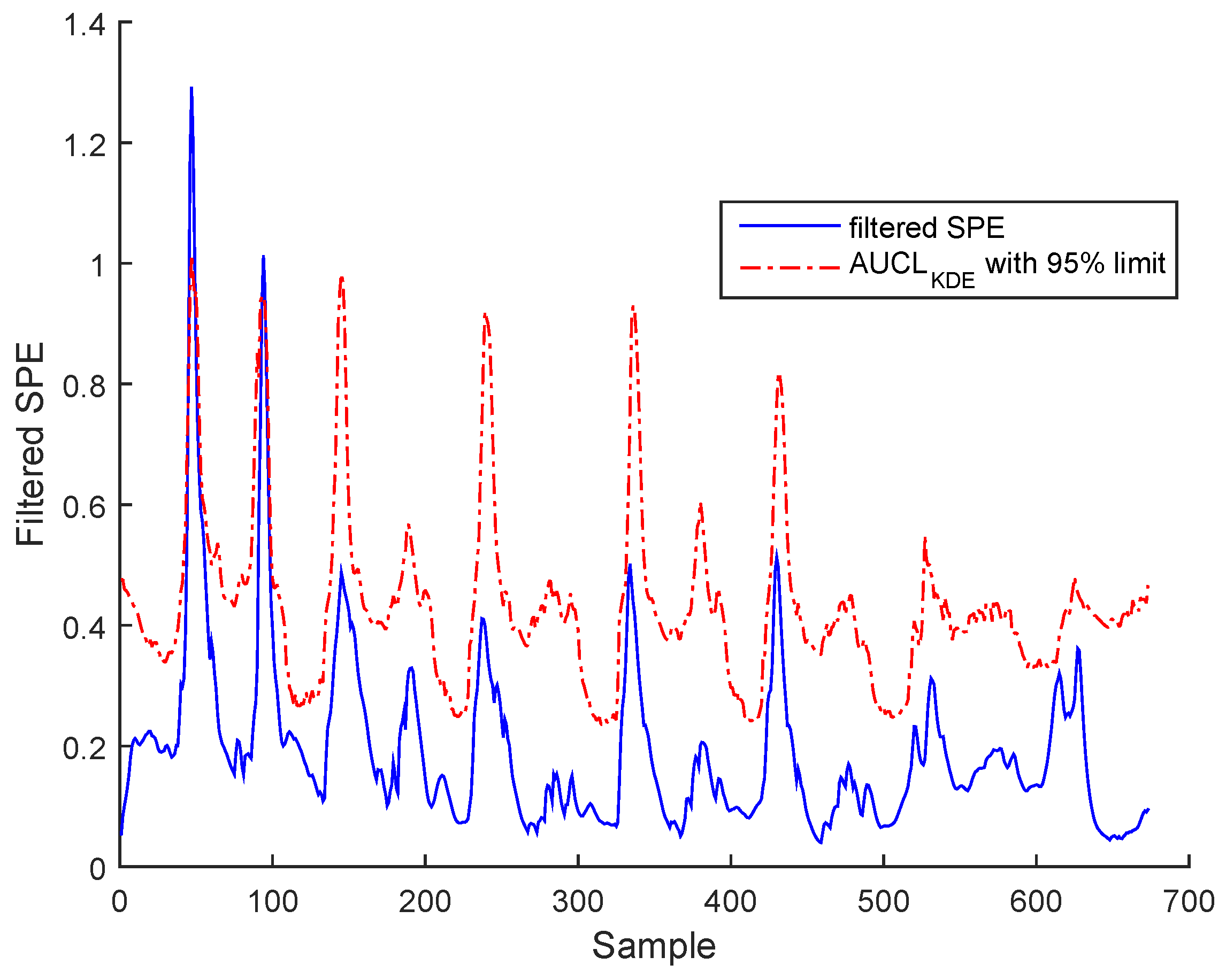
3.3. Results and Discussion
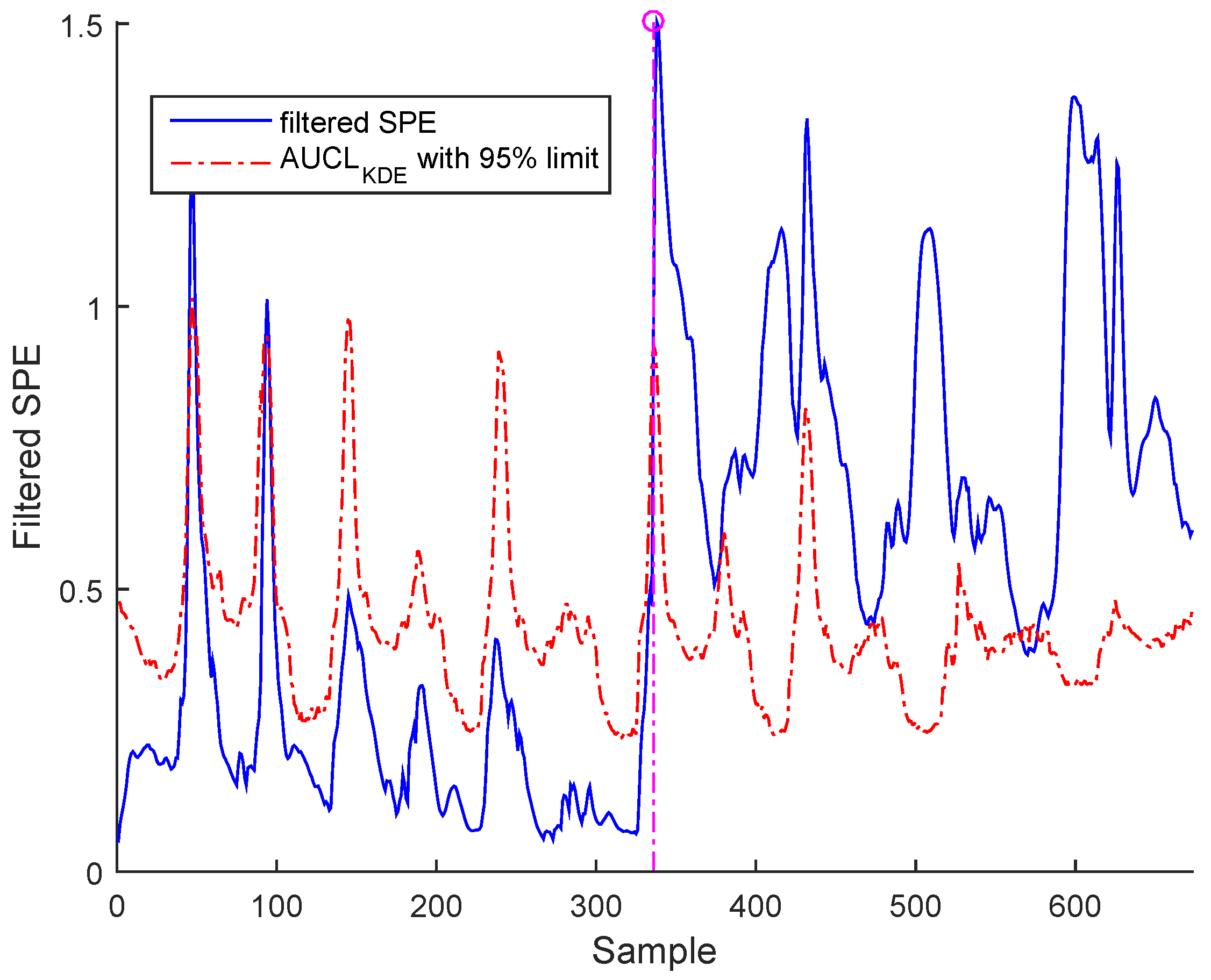
- a- Precision degradation: The precision degradation model is defined as a Gaussian random process with zero mean and unknown covariance matrix.
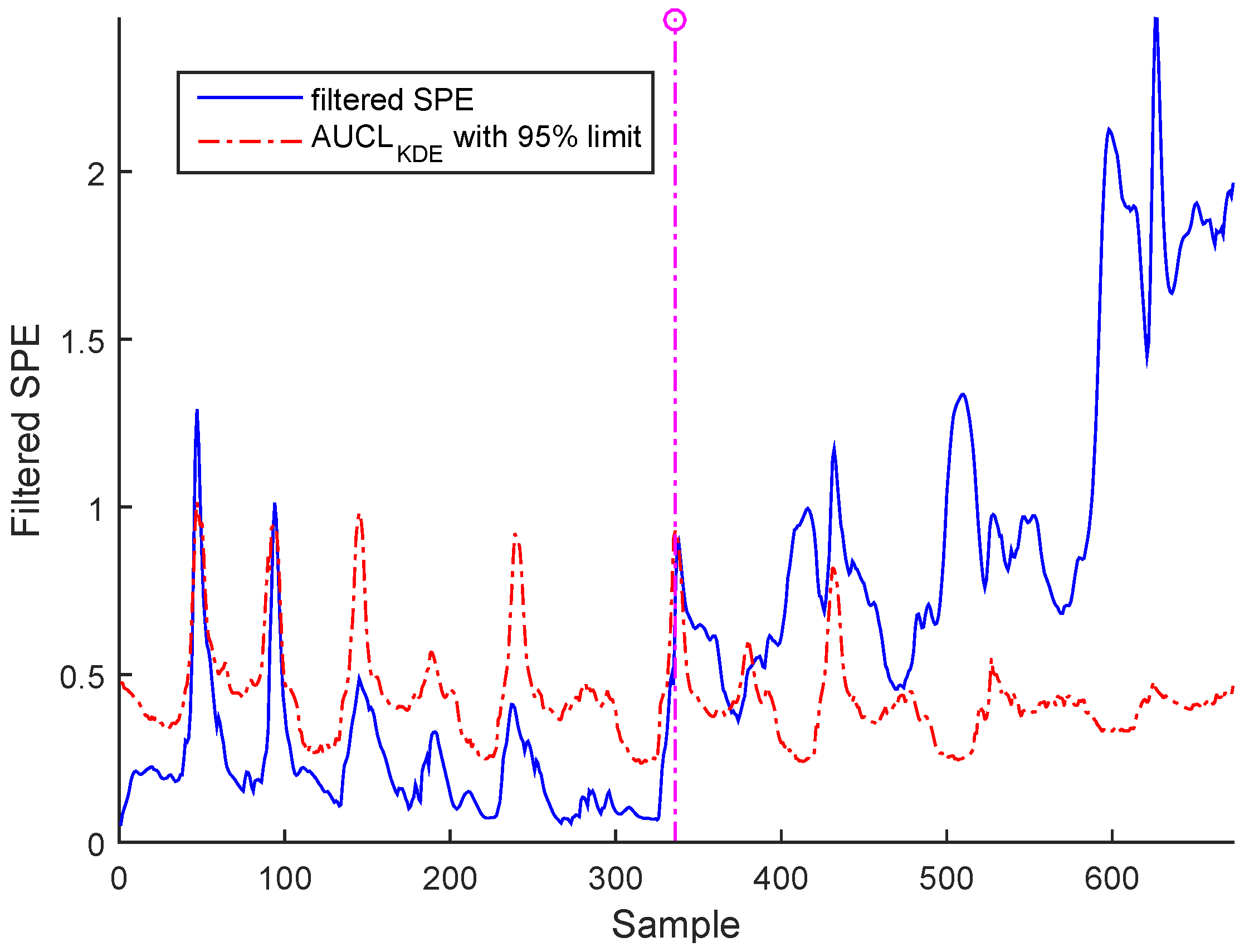
- b- Bias: The bias error evolution can be characterized by positive or negative value.
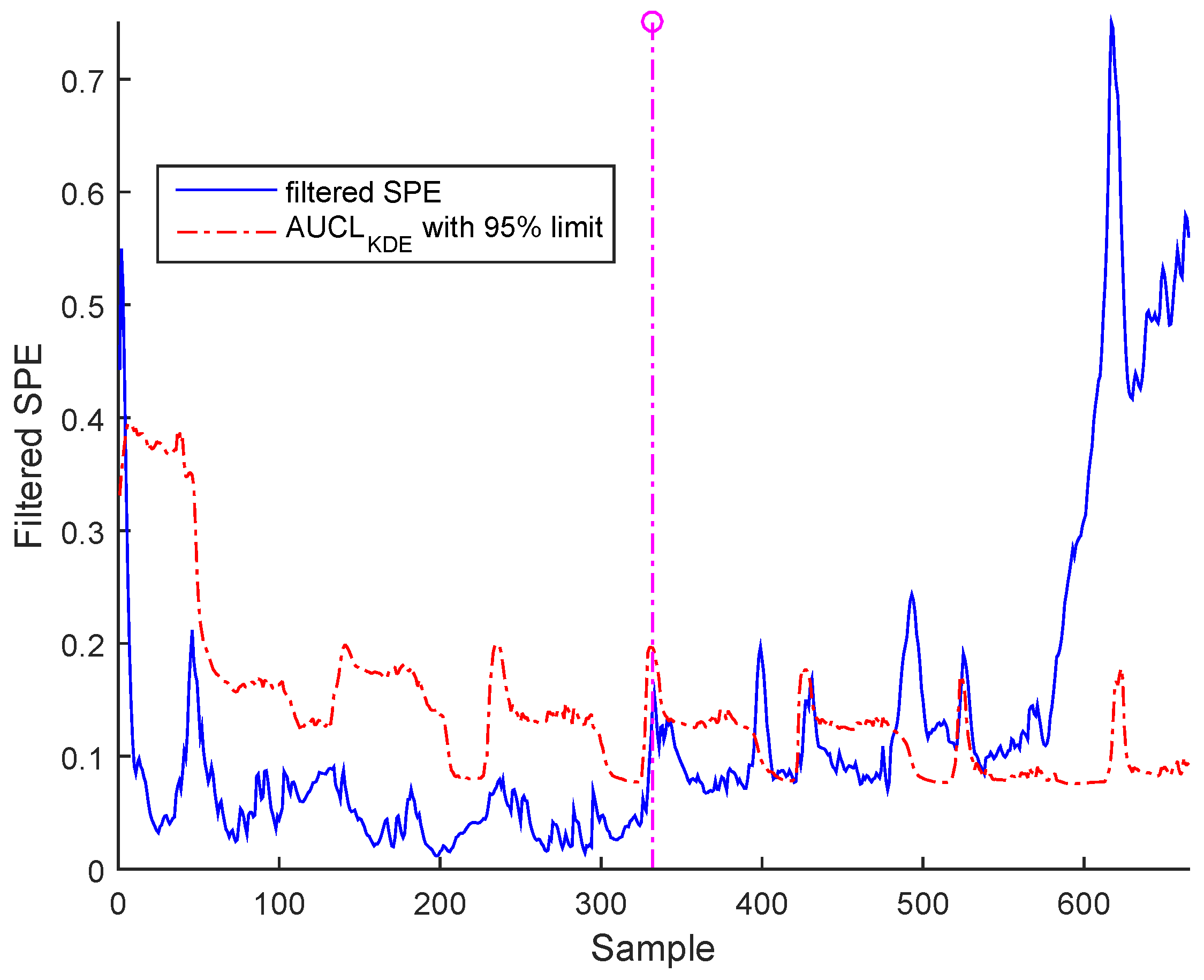
- c- Drift: This error follows an increasing deviation, such as polynomial change.
Sensor Fault Identification and Reconstruction
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| PCA | Principal Component Analysis |
| ICA | Independent Component Analysis |
| BNN | Bottleneck Neural Network |
| EBNN | Enhanced Bottleneck Neural Network |
| GMM | Gaussian Mixture Model |
| KDE | Kernel Density Estimation |
| MSPC | Multivariate Statistical Process Control |
| SVI | Sensor Validity Index |
| AUCL | Adaptive Upper Control Limit |
| UCL | Upper Control Limit |
| SPE | Squared Prediction Error |
| AANN | Auto-Associative Neural Network |
| ANNC | Artificial Neural Network Classifier |
| IWA | International Water Association |
| EWMA | Exponentially Weighted Moving Average |
| WWTP | Wastewater Treatment Plant |
| BSM1 | Benchmark Simulation Model no. 1 |
| SPM | Statistical Process Monitoring |
| SPC | Statistical Process Control |
References
- Kresta, J.V.; MacGregor, J.F.; Marlin, T.E. Multivariate statistical monitoring of process operating performance. Can. J. Chem. Eng. 1991, 69, 35–47. [Google Scholar] [CrossRef]
- McAvoy, T.J.; Ye, N. Base Control for the Tennessee Eastman Problem. Comput. Chem. Eng. 1994, 18, 383–413. [Google Scholar] [CrossRef]
- Kourti, T.; MacGregor, J.F. Recent Developments in Multivariate SPC Methods for Monitoring and Diagnosing Process and Product Performance. J. Qual. Technol. 1996, 28, 409–428. [Google Scholar]
- Dunia, R.; Qin, S.J.; Edgar, T.F.; McAvoy, T.J. Use of principal component analysis for sensor fault identification. Comput. Chem. Eng. 1996, 20, S713–S718. [Google Scholar] [CrossRef]
- MacGregor, J.F.; Kourti, T.; Nomikos, P. Anlysis, Monitoring and fault diagnosis of industrial process using multivariate statistical projection methods. In Proceedings of the 13th Triennial Word Congress (IFAC), San Francisco, CA, USA, 30 June–5 July 1996; pp. 145–150. [Google Scholar]
- Wise, B.M.; Gallagher, N.B. The process chemometrics approach to process monitoring and fault detection. J. Process Control 1996, 6, 329–348. [Google Scholar] [CrossRef]
- Bakshi, B.R. Multiscale PCA with application to multivariate statistical process monitoring. AIChE J. 1998, 44, 1596–1610. [Google Scholar] [CrossRef]
- MacGregor, J.F.; Kourti, T. Statistical process control of multivariate processes. Control Eng. Pract. 1995, 3, 403–414. [Google Scholar] [CrossRef]
- Dunia, R.; Qin, S.J.; Edgar, T.F.; McAvoy, T.J. Identification of faulty sensors using principal component analysis. AIChE J. 1996, 42, 2797–2812. [Google Scholar] [CrossRef]
- Dong, D.; McAvoy, T.J. Nonlinear principal component analysis based on principal curves and neural networks. Comput. Chem. Eng. 1996, 20, 65–78. [Google Scholar] [CrossRef]
- Martin, E.B.; Morris, A.J.; Zhang, J. Process performance monitoring using multivariate statistical process control. IEE Proc.-Control Theory Appl. 1996, 143, 132–144. [Google Scholar] [CrossRef]
- Ge, Z.; Song, Z. Process monitoring based on independent component analysis—Principal component analysis (ICA-PCA) and similarity factors. Ind. Eng. Chem. Res. 2007, 46, 2054–2063. [Google Scholar] [CrossRef]
- Kramer, M.A. Nonlinear principal component analysis using autoassociative neural networks. AIChE J. 1991, 37, 233–243. [Google Scholar] [CrossRef]
- He, Q.P.; Wang, J. Fault Detection Using the k-Nearest Neighbor Rule for Semiconductor Manufacturing Processes. IEEE Trans. Semicond. Manuf. 2007, 20, 345–354. [Google Scholar] [CrossRef]
- Yu, H. A Just-in-time Learning Approach for Sewage Treatment Process Monitoring with Deterministic Disturbances. In Proceedings of the 2015-41st Annual Conference of the IEEE Industrial Electronics Society IECON, Yokohama, Japan, 9–12 November 2015; pp. 59–64. [Google Scholar]
- Dobos, L.; Abonyi, J. On-line detection of homogeneous operation ranges by dynamic principal component analysis based time-series segmentation. Chem. Eng. Sci. 2012, 75, 96–105. [Google Scholar] [CrossRef]
- Zhao, S.; Xu, Y. Multivariate statistical process monitoring using robust nonlinear principal component analysis. Tsinghua Sci. Technol. 2005, 10, 582–586. [Google Scholar]
- Verdier, G.; Ferreira, A. Fault detection with an adaptive distance for the k-nearest neighbors rule. Preoceedings of the IEEE International Conference on Computers and Industrial Engineering CIE, Troyes, France, 6–9 July 2009; pp. 1273–1278. [Google Scholar]
- Yu, J. A particle filter driven dynamic Gaussian mixture model approach for complex process monitoring and fault diagnosis. J. Process Control 2012, 22, 778–788. [Google Scholar] [CrossRef]
- Yu, J. A nonlinear kernel Gaussian mixture model based inferential monitoring approach for fault detection and diagnosis of chemical processes. Chem. Eng. Sci. 2012, 68, 506–519. [Google Scholar] [CrossRef]
- Figueiredo, M.A.T.; Jain, A.K. Unsupervised learning of finite mixture models. IEEE Trans. Pattern Anal. Mach. Intell. 2002, 24, 381–396. [Google Scholar] [CrossRef]
- Wang, G.; Cui, Y. On line tool wear monitoring based on auto associative neural network. J. Intell. Manuf. 2013, 24, 1085–1094. [Google Scholar] [CrossRef]
- Huang, Y. Advances in artificial neural networks methodological development and application. Algorithms 2009, 2, 973–1007. [Google Scholar] [CrossRef]
- Dev, A.; Krôse, B.J.A.; and Groen, F.C.A. Recovering patch parameters from the optic flow with associative neural networks. In Proceedings of the 1995 International Conference on Intelligent Autonomous Systems. Karlsruche, Germany, March 27–30; 1995; pp. 213–216. [Google Scholar]
- Jung, C.; Ban, S.W.; Jeong, S.; Lee, M. Input and output mapping sensitive auto-associative multilayer perceptron for computer interface system based on image processing of laser pointer spot. Neural Inf. Process. Models Appl. 2010. [Google Scholar] [CrossRef]
- Box, G.E.P. Some Theorems on Quadratic Forms Applied in the Study of Analysis of Variance Problems. Ann. Math. Stat. 1954, 25, 290–302. [Google Scholar] [CrossRef]
- Chen, T.; Morris, J.; Martin, E. Probability density estimation via an infinite Gaussian mixture model: Application to statistical process monitoring. J.R. Stat. Soc. Ser. C (Appl. Stat.) 2006, 55, 699–715. [Google Scholar] [CrossRef]
- Xiong, L.; Liang, J.; Jixin, Q. Multivariate Statistical Process Monitoring of an Industrial Polypropylene Catalyzer Reactor with Component Analysis and Kernel Density Estimation. Chin. J. Chem. Eng. 2007, 15, 524–532. [Google Scholar] [CrossRef]
- Odiowei, P.E.P.; Cao, Y. Nonlinear dynamic process monitoring using canonical variate analysis and kernel density estimations. IEEE Trans. Ind. Inform. 2010, 6, 36–45. [Google Scholar] [CrossRef]
- Chen, Q.; Wynne, R. J.; Goulding, P.; Sandoz, D. The application of principal component analysis and kernel density estimation to enhance process monitoring. Control Eng. Pract. 2000, 8, 531–543. [Google Scholar] [CrossRef]
- Liang, J. Multivariate statistical process monitoring using kernel density estimation. Dev. Chem. Eng. Min. Process. 2005, 13, 185–192. [Google Scholar] [CrossRef]
- Harkat, M.F.; Mourot, G.; Ragot, J. An improved PCA scheme for sensor FDI: Application to an air quality monitoring network. J. Process Control 2006, 16, 625–634. [Google Scholar] [CrossRef]
- Bouzenad, K.; Ramdani, M.; Zermi, N.; Mendaci, K. Use of NLPCA for sensors fault detection and localization applied at WTP. In Proceedings of the 2013 World Congress on Computer and Information Technology (WCCIT), Sousse, Tunisia, 22–24 June 2013; pp. 1–6. [Google Scholar]
- Bouzenad, K.; Ramdani, M.; Chaouch, A. Sensor fault detection, localization and reconstruction applied at WWTP. In Proceedings of the 2013 Conference on Control and Fault-Tolerant Systems (SysTol), Nice, France, 9–11 October 2013; pp. 281–287. [Google Scholar]
- Chaouch, A.; Bouzenad, K.; Ramdani, M. Enhanced Multivariate Process Monitoring for Biological Wastewater Treatment Plants. Int. J. Electr. Energy 2014, 2, 131–137. [Google Scholar] [CrossRef]
- Carnero, M.; HernÁndez, J.L.; SÁnchez, M.C. Design of Sensor Networks for Chemical Plants Based on Meta-Heuristics. Algorithms 2009, 2, 259–281. [Google Scholar] [CrossRef]
- Zhao, W.; Bhushan, A.; Santamaria, A.D.; Simon, M.G.; Davis, C.E. Machine learning: A crucial tool for sensor design. Algorithms 2008, 1, 130–152. [Google Scholar] [CrossRef] [PubMed]
- Aguado, D.; Rosen, C. Multivariate statistical monitoring of continuous wastewater treatment plants. Eng. Appl. Artif. Intell. 2008, 21, 1080–1091. [Google Scholar] [CrossRef]
- Rosen, C.; Olsson, G. Disturbance detection in wastewater treatment plants. Water Sci. Technol. 1998, 37, 197–205. [Google Scholar] [CrossRef]
- Zhao, L.J.; Chai, T.Y.; Cong, Q.M. Multivariate statistical modeling and monitoring of SBR wastewater treatment using double moving window PCA. Mach. Learn. Cybern. 2004, 3, 1371–1376. [Google Scholar]
- Alex, J.; Benedetti, L.; Copp, J.; Gernaey, K.V.; Jeppsson, U.; Nopens, I.; Pons, M.N.; Rieger, L.; Rosen, C.; Steyer, J. Benchmark Simulation Model no. 1 (BSM1.). 2008. Available online: http://www.iea.lth.se/publications/Reports/LTH-IEA-7229.pdf (accessed on 28 April 2017).
- Yoo, C.K.; Villez, K.; Lee, I.B.; Van Hulle, S.; Vanrolleghem, P.A. Sensor validation and reconciliation for a partial nitrification process. Water Sci. Technol. 2006, 53, 513–521. [Google Scholar] [CrossRef] [PubMed]
- Yoo, C.K.; Villez, K.; Van Hulle, S.W.; Vanrolleghem, P.A. Enhanced process monitoring for wastewater treatment systems. Environmetrics 2008, 19, 602–617. [Google Scholar] [CrossRef]










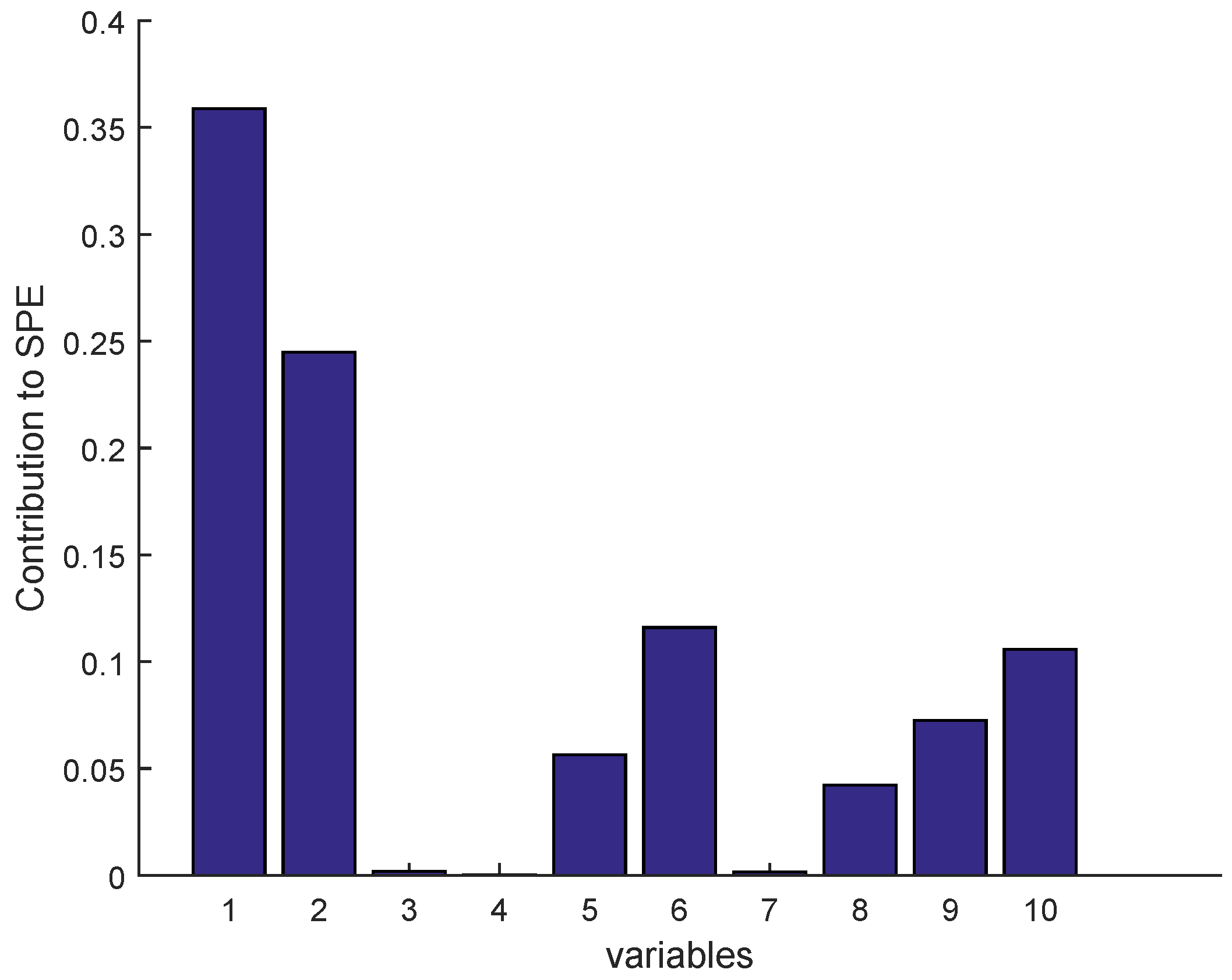
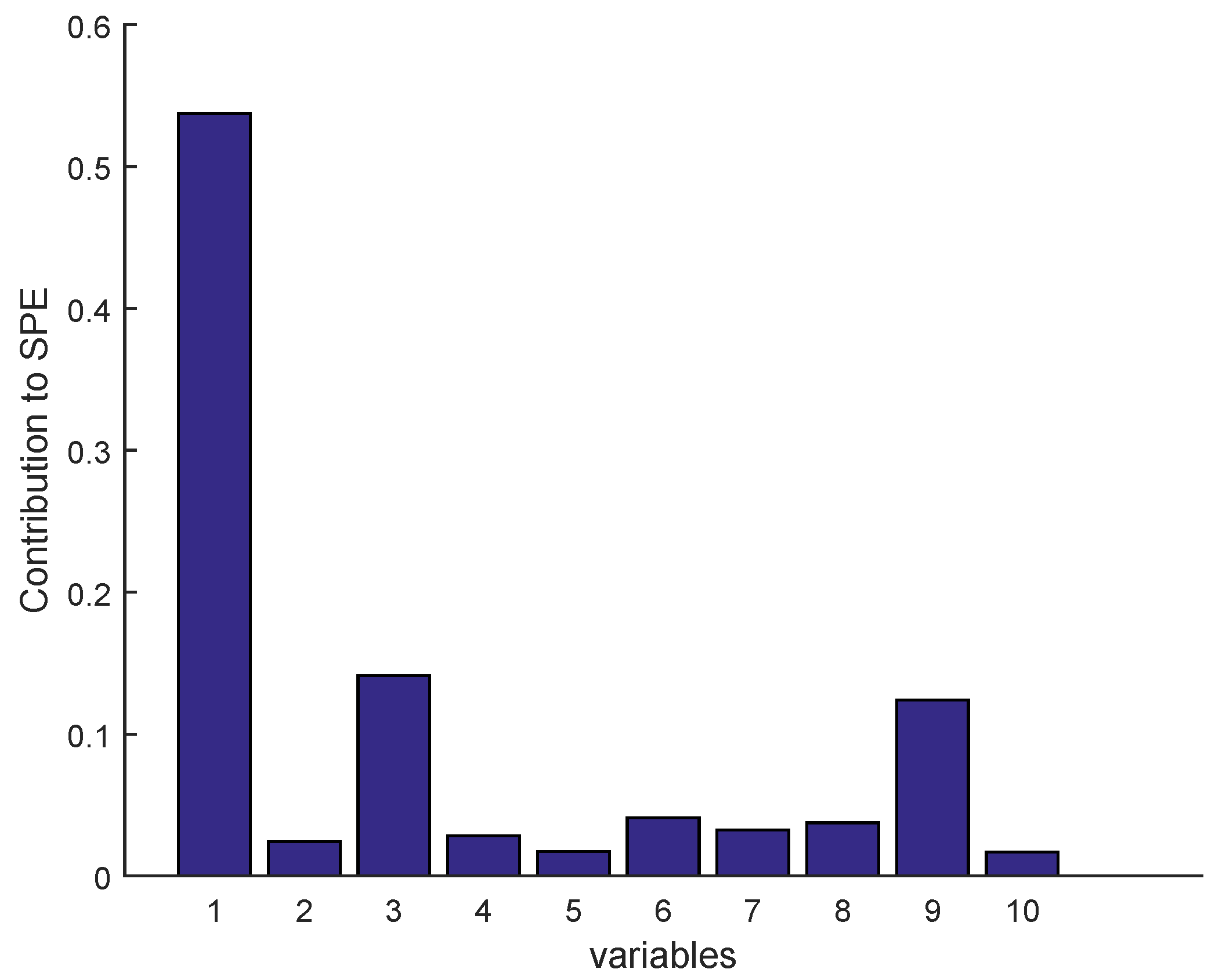
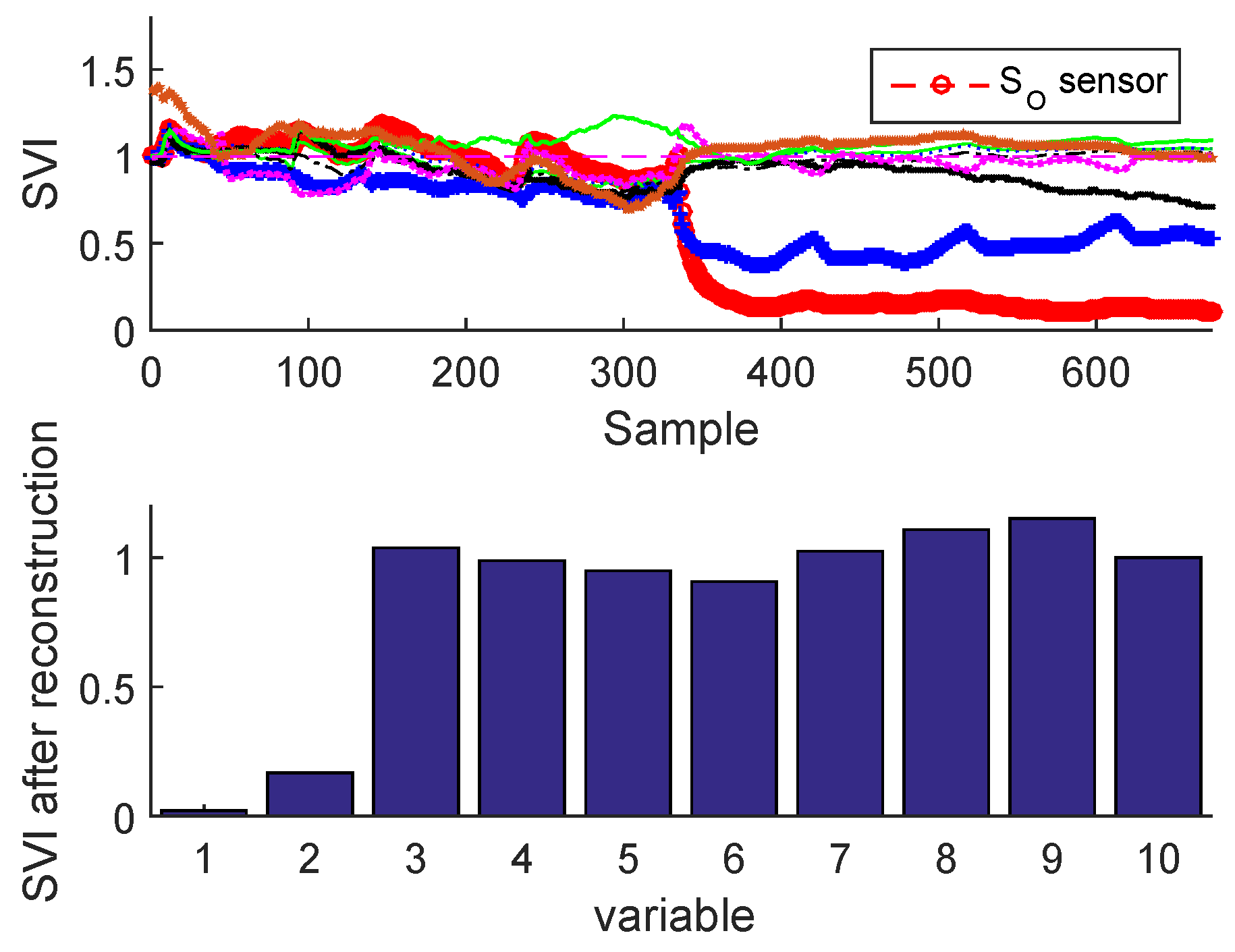
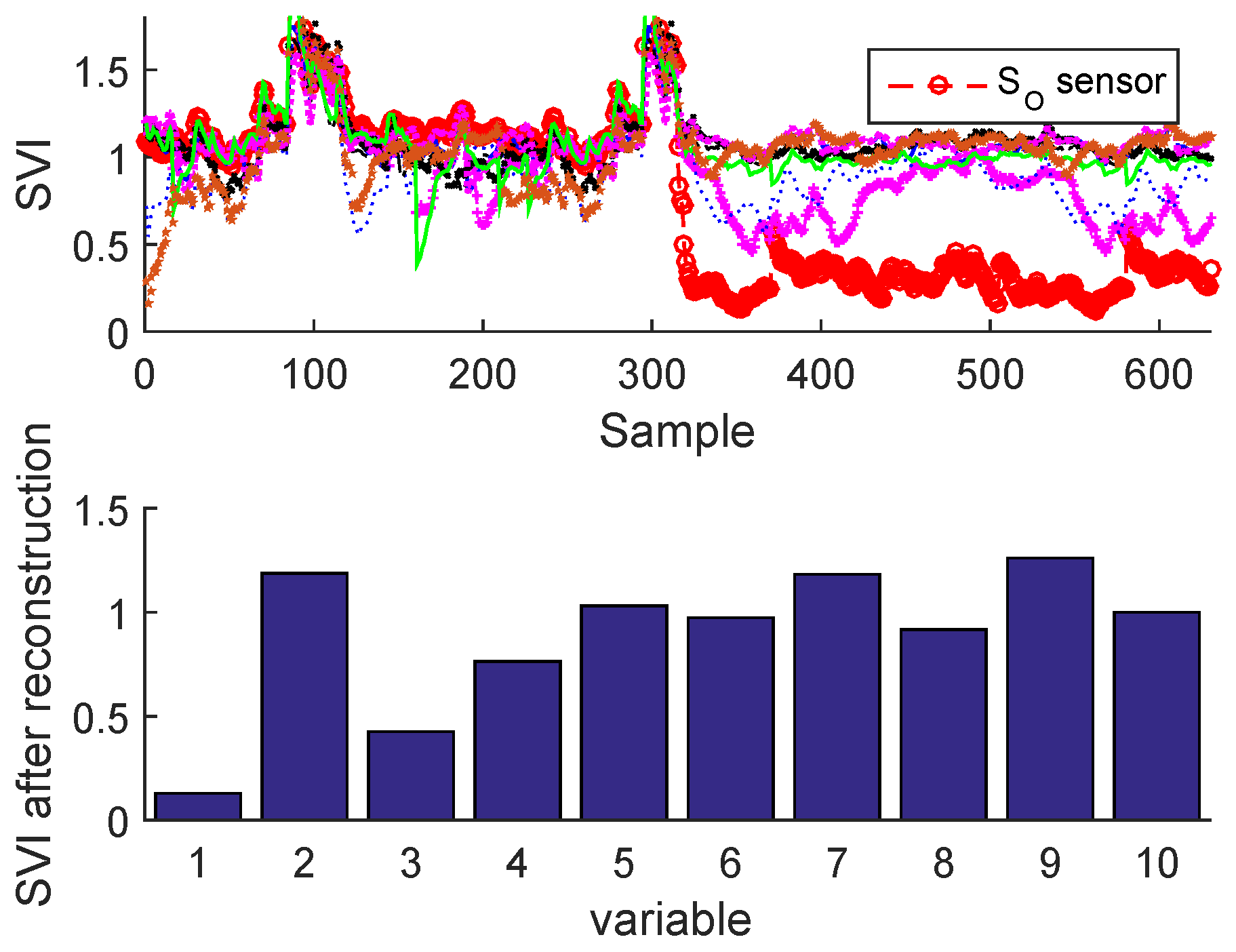
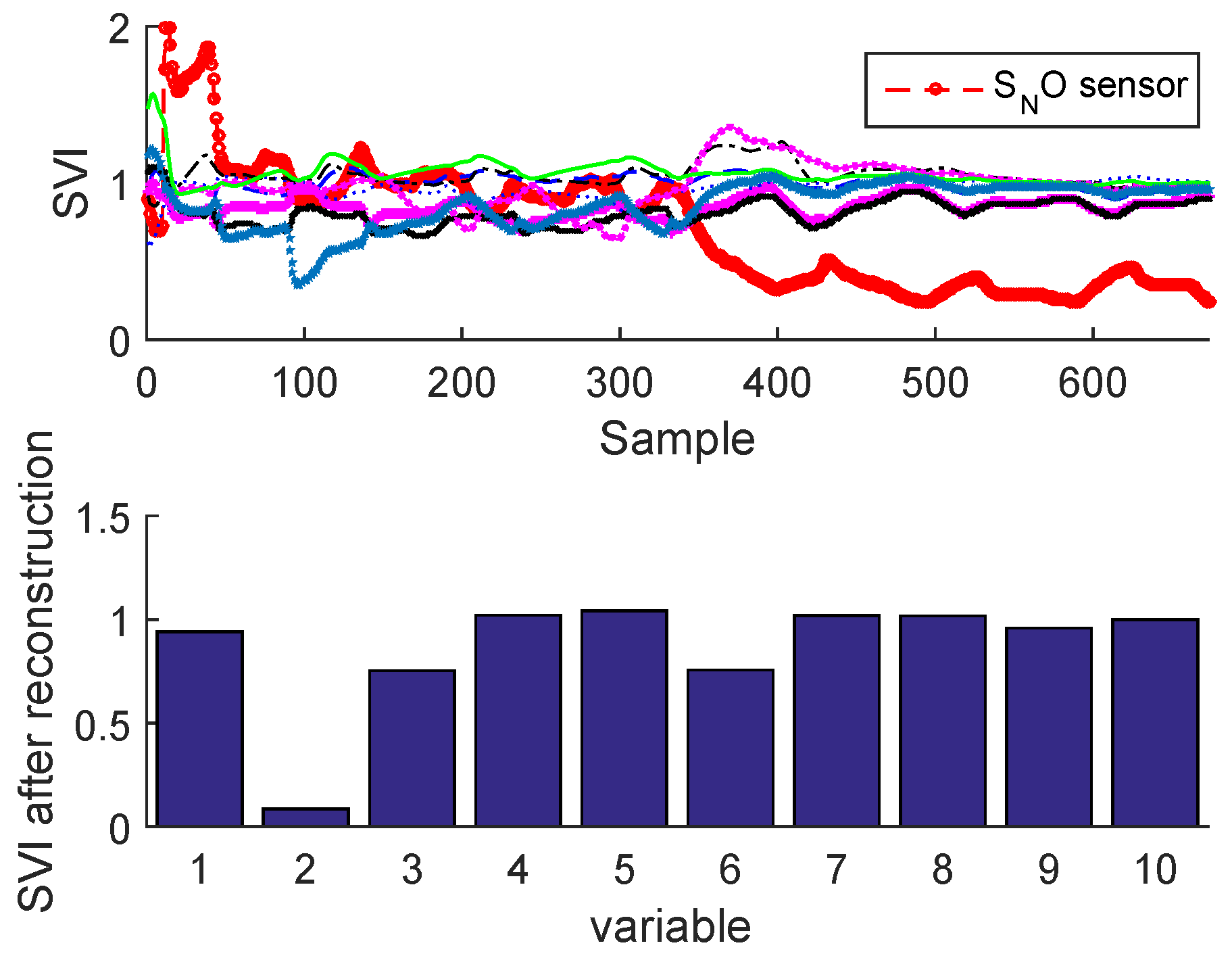
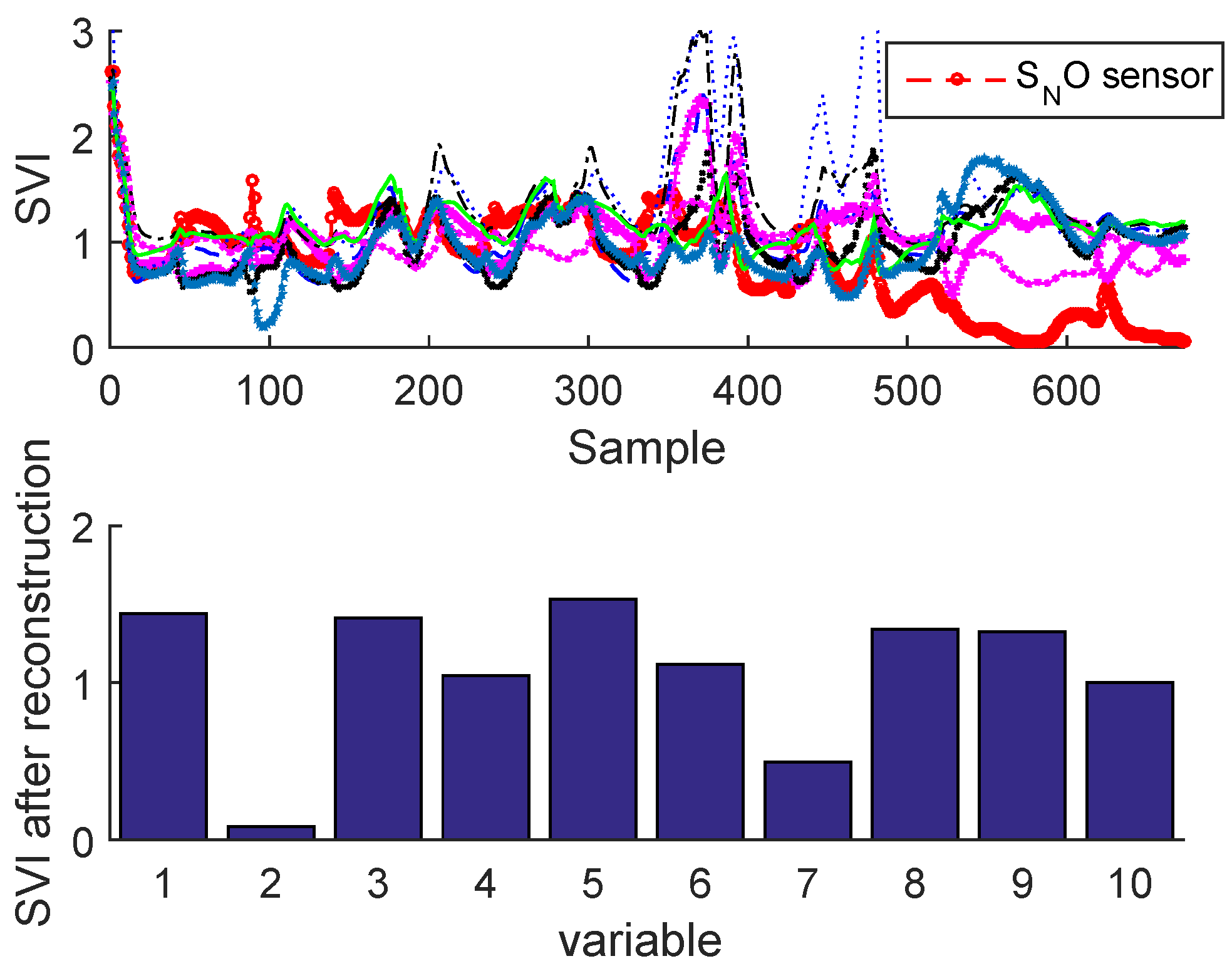
| N | Monitored Sensors | Notation |
|---|---|---|
| 1 | Dissolved oxygen in | |
| 2 | Nitrate and nitrite nitrogen in | |
| 3 | nitrogen in | |
| 4 | Soluble biodegradable organic nitrogen in | |
| 5 | Particulate biodegradable organic nitrogen in | |
| 6 | Dissolved oxygen in | |
| 7 | Nitrate and nitrite nitrogen in | |
| 8 | nitrogen in | |
| 9 | Soluble biodegradable organic nitrogen in | |
| 10 | Particulate biodegradable organic nitrogen in |
| N | Monitored Sensors | Notation |
|---|---|---|
| 1 | Dissolved oxygen in influent | |
| 2 | Nitrites in influent | |
| 3 | Nitrates in influent | |
| 4 | Ammoniacal nitrogen in influent | |
| 5 | Chemical oxygen demand in influent | |
| 6 | Dissolved oxygen in effluent | |
| 7 | Nitrites in effluent | |
| 8 | Nitrates in effluent | |
| 9 | Ammoniacal nitrogen in effluent | |
| 10 | Chemical oxygen demand in effluent |
| Fault type | Precision degradation | Bias | Drift |
|---|---|---|---|
| Fault expression | . | ||
| Faulty sensor expression | |||
| Fault time | 336 | 366 | 366 |
| 2*Detection time | 349.4 for BSM1 data and | 336.7 for BSM1 data and | 342.3 for BSM1 data and |
| 346.2 for real data | 337.2 for real data | 392.1 for real data |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouzenad, K.; Ramdani, M. Multivariate Statistical Process Control Using Enhanced Bottleneck Neural Network. Algorithms 2017, 10, 49. https://doi.org/10.3390/a10020049
Bouzenad K, Ramdani M. Multivariate Statistical Process Control Using Enhanced Bottleneck Neural Network. Algorithms. 2017; 10(2):49. https://doi.org/10.3390/a10020049
Chicago/Turabian StyleBouzenad, Khaled, and Messaoud Ramdani. 2017. "Multivariate Statistical Process Control Using Enhanced Bottleneck Neural Network" Algorithms 10, no. 2: 49. https://doi.org/10.3390/a10020049
APA StyleBouzenad, K., & Ramdani, M. (2017). Multivariate Statistical Process Control Using Enhanced Bottleneck Neural Network. Algorithms, 10(2), 49. https://doi.org/10.3390/a10020049





