A Numerical Study of the Mechanical Behavior of Jointed Soft Rocks under Triaxial Loading Using a Bonded Particle Model
Abstract
1. Introduction
2. Numerical Test Scheme
3. Strength and Deformation Characteristics
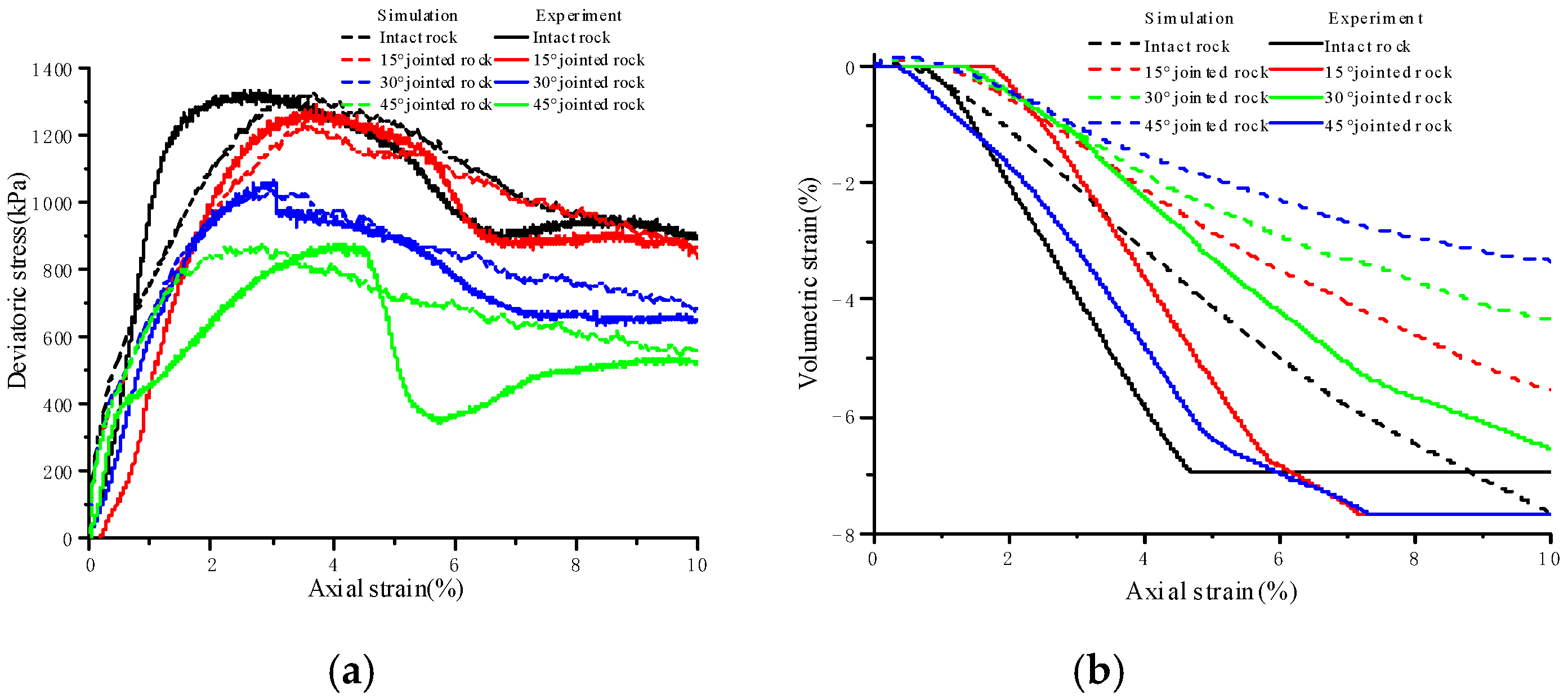
3.1. Strength Characteristics
3.2. Deformation Characteristics
4. Failure Mode, Crack Propagation, and Force Chain Distribution
4.1. Failure Mode Analysis of Jointed Soft Rock
4.2. Distribution Pattern of Cracks in Jointed Soft Rock
4.3. Evolution of Force Chains in Jointed Soft Rock
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Murakami, H.; Impelluso, T.; Hegemier, G. A continuum finite element for single-set jointed media. Int. J. Numer. Methods Eng. 1991, 31, 1169–1194. [Google Scholar] [CrossRef]
- BhaSin, R.; Hoeg, K. Numerical modelling of block size effects and influence of joint properties in multiply jointed rock. Tunn. Undergr. Space Technol. 1997, 12, 407–415. [Google Scholar] [CrossRef]
- Itasca Consulting Group, Inc. PFC3D Users’ Manual (Version5.0); Itasca Consulting Group, Inc: Minneapolis, MN, USA, 2016. [Google Scholar]
- Fan, X.; Kulatilake, P.; Chen, X. Mechanical behavior of rock-like jointed blocks with multi-non-persistent joints under uniaxial loading: A particle mechanics approach. Eng. Geol. 2015, 190, 17–32. [Google Scholar] [CrossRef]
- Cheng, C.; Cheney, X.; Zhang, S. Multi-peak deformation behavior of jointed rock mass under uniaxial compression: Insight from particle flow modeling. Eng. Geol. 2016, 213, 25–45. [Google Scholar] [CrossRef]
- Song, Z.; Konietzky, H.; Herbst, M. Bonded-particle model-based simulation of artificial rock subjected to cyclic loading. Acta Geotech. 2019, 14, 955–971. [Google Scholar] [CrossRef]
- Mehran, N.; Gholamreza, K.; Vahab, S.; Behrouz, R.; Hamid, R.N.; Mehrdad, I.; Wulf, S.; Shirin, J. An experimental and numerical study of layered sandstone’s anisotropic behaviour under compressive and tensile stress conditions. Rock Mech. Rock Eng. 2024, 57, 1451–1470. [Google Scholar]
- Cundall, P. A computer model for simulating progressive, large-scale movement in blocky rock system. In Proceedings of the Symposio of the International Society of Rock Mechanics, Nancy, France, 4–6 October 1971. [Google Scholar]
- Farahmand, K.; Diederichs, M. A calibrated synthetic rock mass (SRM) model for simulating crack growth in granitic rock considering grain scale heterogeneity of polycrystalline rock. In Proceedings of the 49th US Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 28 June–1 July 2015; pp. 9–22. [Google Scholar]
- Chiu, C.; Weng, M. Simulating interface characteristics by using a particulate interface model of a discrete element method. Comput. Geotech. 2019, 109, 1–11. [Google Scholar] [CrossRef]
- Damjanac, B.; Cundall, P. Application of distinct element methods to simulation of hydraulic fracturing in naturally fractured reservoirs. Comput. Geotech. 2016, 71, 283–294. [Google Scholar] [CrossRef]
- Liu, X.; Dong, C. Research on mechanical characteristics of the cemented sandstone based on 3Dimensional PFC numerical model. J. Chongqing Univ. 2013, 36, 37–44. [Google Scholar]
- Park, J.; Song, J. Numerical simulation of a direct shear test on a rock joint using a bonded-particle model. Int. J. Rock Mech. Min. 2009, 46, 1315–1328. [Google Scholar] [CrossRef]
- Bahaaddini, M.; Sharrock, G.; Hebblewhite, B.K. Numerical investigation of the effect of joint geometrical parameters on the mechanical properties of a non-persistent jointed rock mass under uniaxial compression. Comput. Geotech. 2013, 49, 206–225. [Google Scholar] [CrossRef]
- Kulatilake, P.; Malama, B.; Wang, J. Physical and particle flow modeling of jointed rock block behavior under uniaxial loading. J. Rock Mech. Min. 2001, 38, 641–657. [Google Scholar] [CrossRef]
- Xia, C.; Zhou, S.; Du, S.; Song, Y. Particle flow modeling for direct shear behavior of rough joints. In TC105 ISSMGE International Symposium on Geomechanics from Micro to Macro; Taylor and Francis Group: London, UK, 2015. [Google Scholar]
- Fan, X.; Li, K.; Lai, H.; Xie, Y.; Cao, R.; Zheng, J. Internal stress distribution and cracking around flaws and openings of rock block under uniaxial compression: A particle mechanics approach. Int. J. Rock Mech. Min. 2018, 102, 28–38. [Google Scholar] [CrossRef]
- Li, X.; Li, H.; Xia, X.; Liu, B.; Feng, H. Numerical simulation of mechanical properties of jointed rock in direct shear test. Rock Soil Mech. 2016, 37, 583–591. [Google Scholar]
- Sun, Q.; Jin, F.; Wang, G.; Zhang, G. Force chains in a uniaxially compressed static granular matter in 2D. Acta Phys. Sin.-Chin. Ed. 2010, 59, 30–37. [Google Scholar]
- Xu, Z.; Wang, Z.; Wang, W.; Lin, P.; Wu, J. An integrated parameter calibration method and sensitivity analysis of microparameters on mechanical behavior of transversely isotropic rocks. Comput. Geotech. 2022, 142, 104573. [Google Scholar] [CrossRef]
- Zhou, B.; Wang, H.; Zhao, W.; Li, J.; Zheng, B. Analysis of relationship between particle mesoscopic and macroscopic mechanical parameters of cohesive materials. Rock Soil Mech. 2012, 33, 3171–3175+3177–3178. [Google Scholar]
- Liu, M.; Liao, M.; Liu, E.; Zheng, Q. Experimental research on mechanical properties of jointed rock mass with different angles of inclination. J. Beijing Univ. Technol. 2018, 44, 336–343. [Google Scholar]
- Liu, M.; Liu, E. Dynamic mechanical properties of artificial jointed rock samples subjected to cyclic triaxial loading. Int. J. Rock Mech. Min. 2017, 98, 54–66. [Google Scholar] [CrossRef]
- Wang, W.; Liu, Y. The influence of macro and micro parameters of rock-like materials of parallel bonding model. Sci. Technol. Eng. 2020, 20, 9155–9162. [Google Scholar]
- Tang, J.; Yang, S.; Elsworth, D.; Tao, Y. Three-Dimensional Numerical Modeling of Grain-Scale Mechanical Behavior of Sandstone Containing an Inclined Rough Joint. Rock Mech. Rock Eng. 2021, 54, 905–919. [Google Scholar] [CrossRef]
- Abi, E.; Zheng, Y.; Feng, X.; Cong, Y. Relationship between particle micro and macro mechanical parameters of parallel-bond model. Rock Soil Mech. 2018, 39, 1289–1301. [Google Scholar]
- Chen, D.; Wang, L.; Sun, C.; Ao, Y. Particle flow study on the micro scale effects and damage evolution of sandstone creep. Comput. Geotech. 2023, 161, 105606. [Google Scholar] [CrossRef]
- Wu, L.; Zhu, Y.; Bai, H.; Feng, Y.; Li, H.; Su, C. Study on the correlation of macro and meso parameters of parallel bond model sandstone. Int. J. Min. Sci. Technol. 2023, 8, 487–501. [Google Scholar]
- Li, J.; Song, R.; Wang, S. Pore pressure and dilatancy change of rock under triaxial compression. In Abstract of Papers of the Fourth National Symposium on Structural Physics and the Second National Symposium on High Temperature and High Pressure; Chinese Society of Rock Mechanics and Engineering: Beijing, China, 1989. [Google Scholar]
- Zhao, X.; Li, P.; Ma, L.; Su, R.; Wang, J. Damage and dilation characteristics of deep granite at Beishan under cyclic loading-unloading conditions. J. Rock Mech. Eng. 2014, 33, 1740–1748. [Google Scholar]
- Sun, G. Study on dynamic elastic parameters of mudstone under cyclic load. Gansu Water Resour. Hydropower Technol. 2020, 56, 45–47. [Google Scholar]














| Particle parameters | |||||
| Minimum radius (mm) | Maximum to minimum radius ratio | Particle density (kg/m3) | Normal particle stiffness (MPa/m) | Stiffness ratio kn/ks | Frictional factor |
| 1.5 | 1.66 | 2300 | 9 | 1.0 | 0.5 |
| Particle bonding parameters | |||||
| Normal bond stiffness (GPa/m) | Tangential bond stiffness (GPa/m) | Bonding tensile strength (MPa) | Cohesion (MPa) | Friction angle (°) | Parallel bond radius multiplier |
| 4 | 12.5 | 12.35 | 5.45 | 35 | 0.5 |
| Parameters of smooth parallel joint models | |||||
| Normal stiffness (GPa/m) | Tangential stiffness (GPa/m) | Friction coefficient | Cohesion (MPa) | ||
| 45 | 24 | 0.5 | 0 | ||
| Confining pressure (kPa) | 100 | 200 | 300 | 400 |
| Peak strength (kPa) | 1097 | 1457 | 1576 | 1770 |
| Residual strength (kPa) | 870 | 1153 | 1291 | 1475 |
| Residual strength ratio | 0.7931 | 0.7914 | 0.8192 | 0.8333 |
| Number of Cracks | |||
| Tensile Crack | Shear Crack | Total Crack | |
| Intact | 157 | 316 | 473 |
| 15° | 124 | 250 | 374 |
| 30° | 116 | 196 | 312 |
| 45° | 38 | 72 | 110 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Xu, Y.; Gao, X.; Fu, J.; Liu, X.; Liu, E. A Numerical Study of the Mechanical Behavior of Jointed Soft Rocks under Triaxial Loading Using a Bonded Particle Model. Materials 2024, 17, 4842. https://doi.org/10.3390/ma17194842
Liu M, Xu Y, Gao X, Fu J, Liu X, Liu E. A Numerical Study of the Mechanical Behavior of Jointed Soft Rocks under Triaxial Loading Using a Bonded Particle Model. Materials. 2024; 17(19):4842. https://doi.org/10.3390/ma17194842
Chicago/Turabian StyleLiu, Mingxing, Yijian Xu, Xiaohu Gao, Jie Fu, Xingyan Liu, and Enlong Liu. 2024. "A Numerical Study of the Mechanical Behavior of Jointed Soft Rocks under Triaxial Loading Using a Bonded Particle Model" Materials 17, no. 19: 4842. https://doi.org/10.3390/ma17194842
APA StyleLiu, M., Xu, Y., Gao, X., Fu, J., Liu, X., & Liu, E. (2024). A Numerical Study of the Mechanical Behavior of Jointed Soft Rocks under Triaxial Loading Using a Bonded Particle Model. Materials, 17(19), 4842. https://doi.org/10.3390/ma17194842






