Optimization of the Winding Layer Structure of High-Pressure Composite Overwrapped Pressure Vessels
Abstract
1. Introduction
2. Materials and Methods
2.1. Liner Structure and Material Performance
2.2. Thickness of Composite Layer
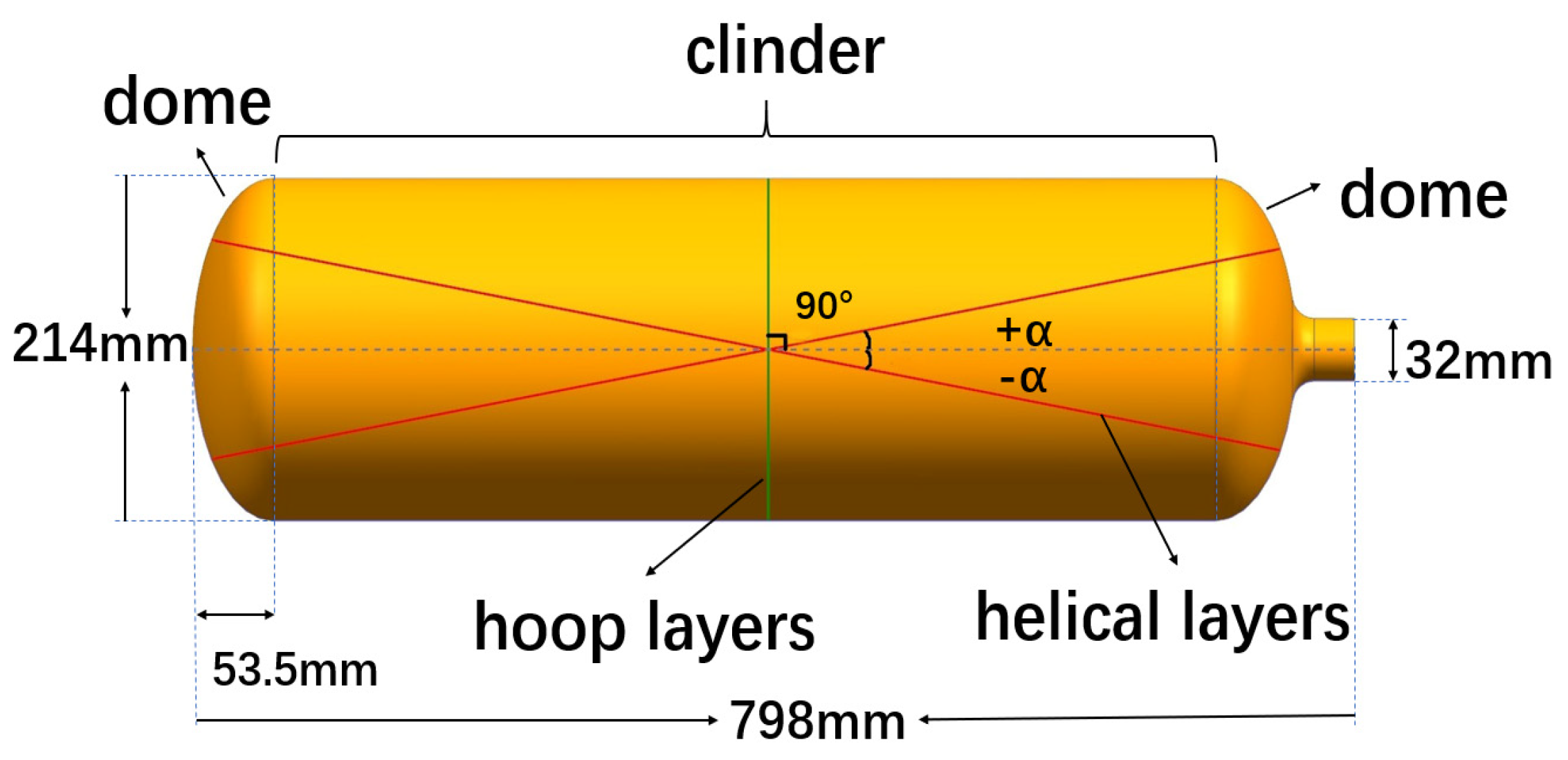
2.2.1. COPV Cylindrical Section
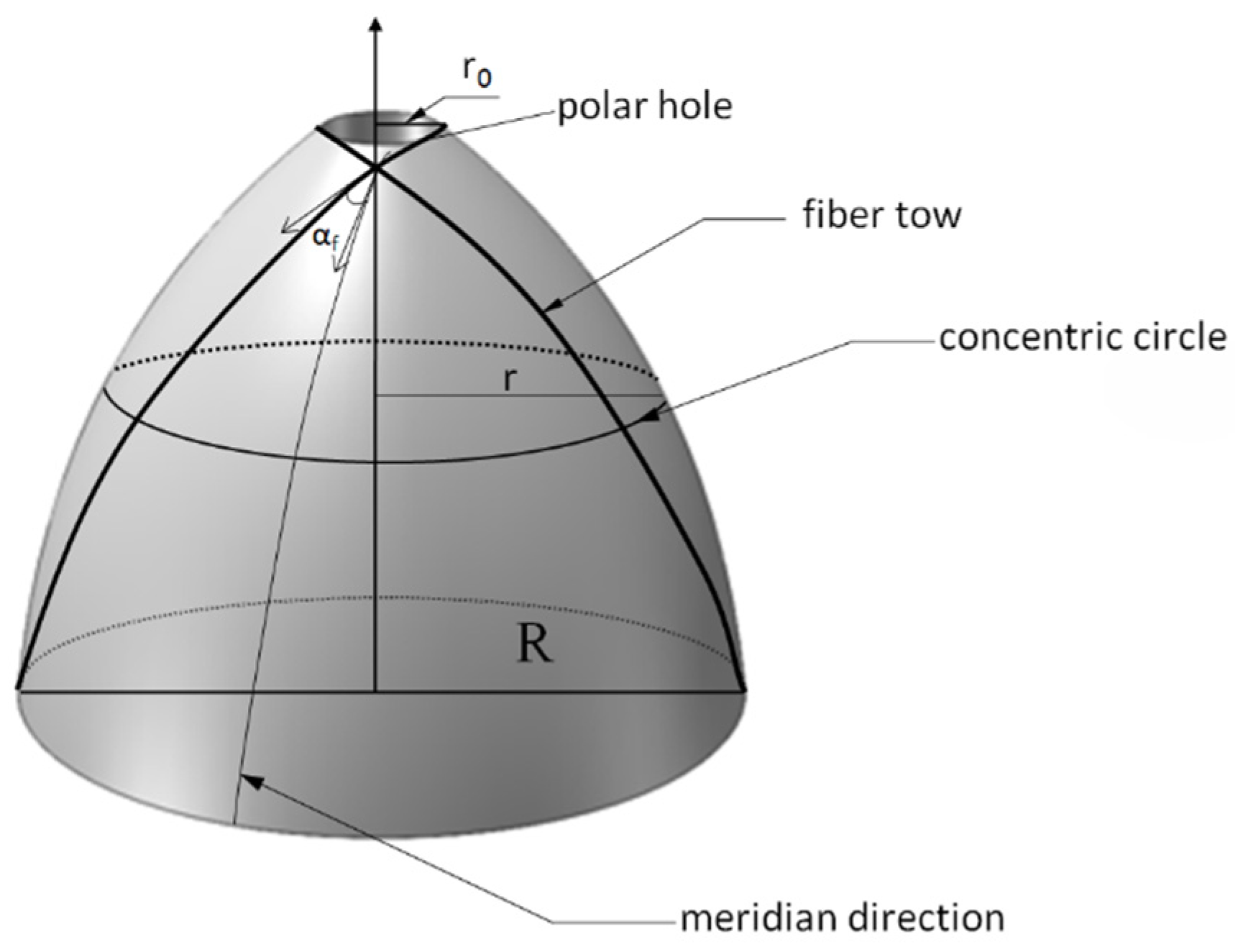
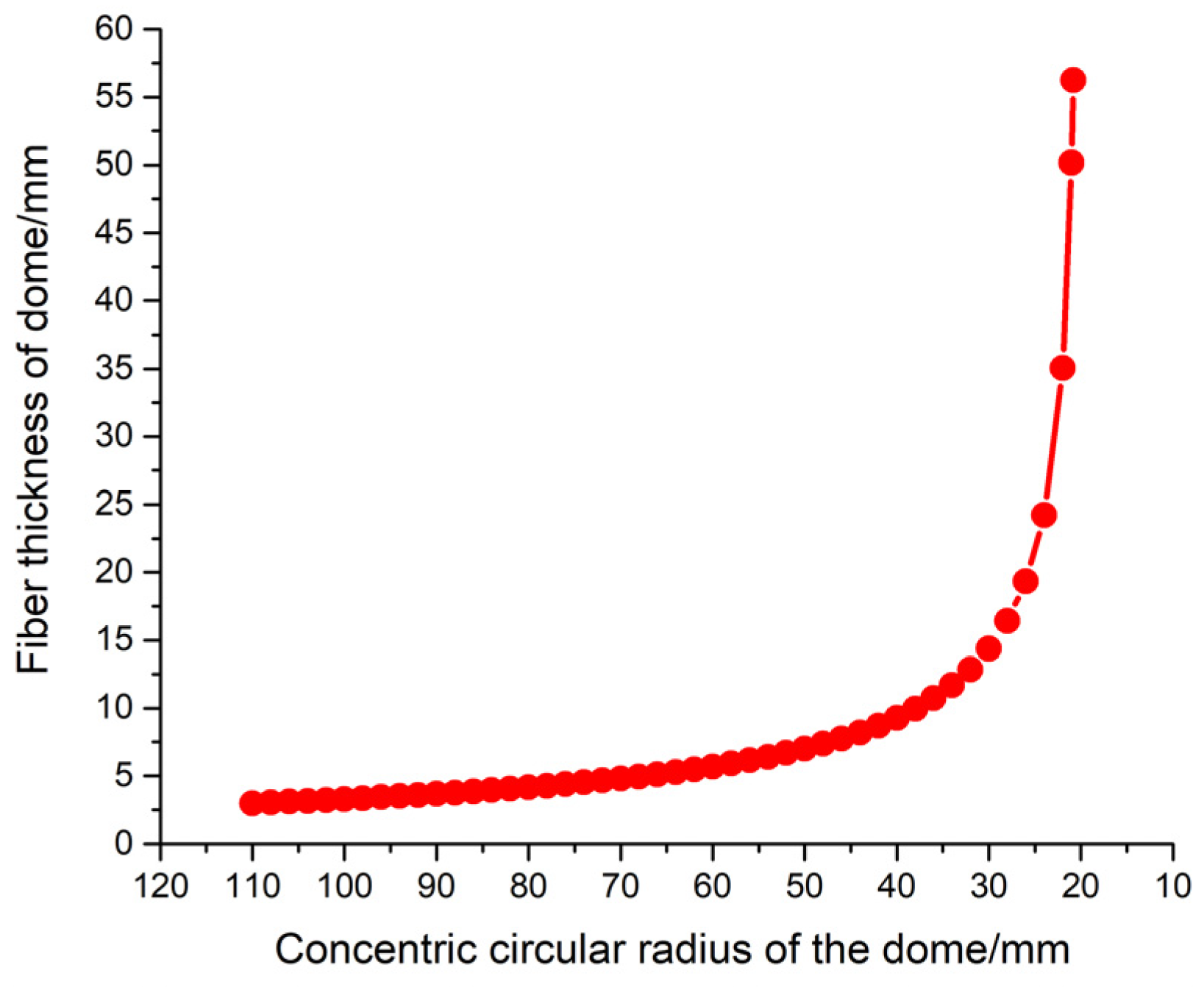
2.2.2. COPV Dome Section
2.3. Design Pressure
2.4. Manufacturing Method
2.5. Finite Element Analysis and Performance Testing
3. Results and Discussion
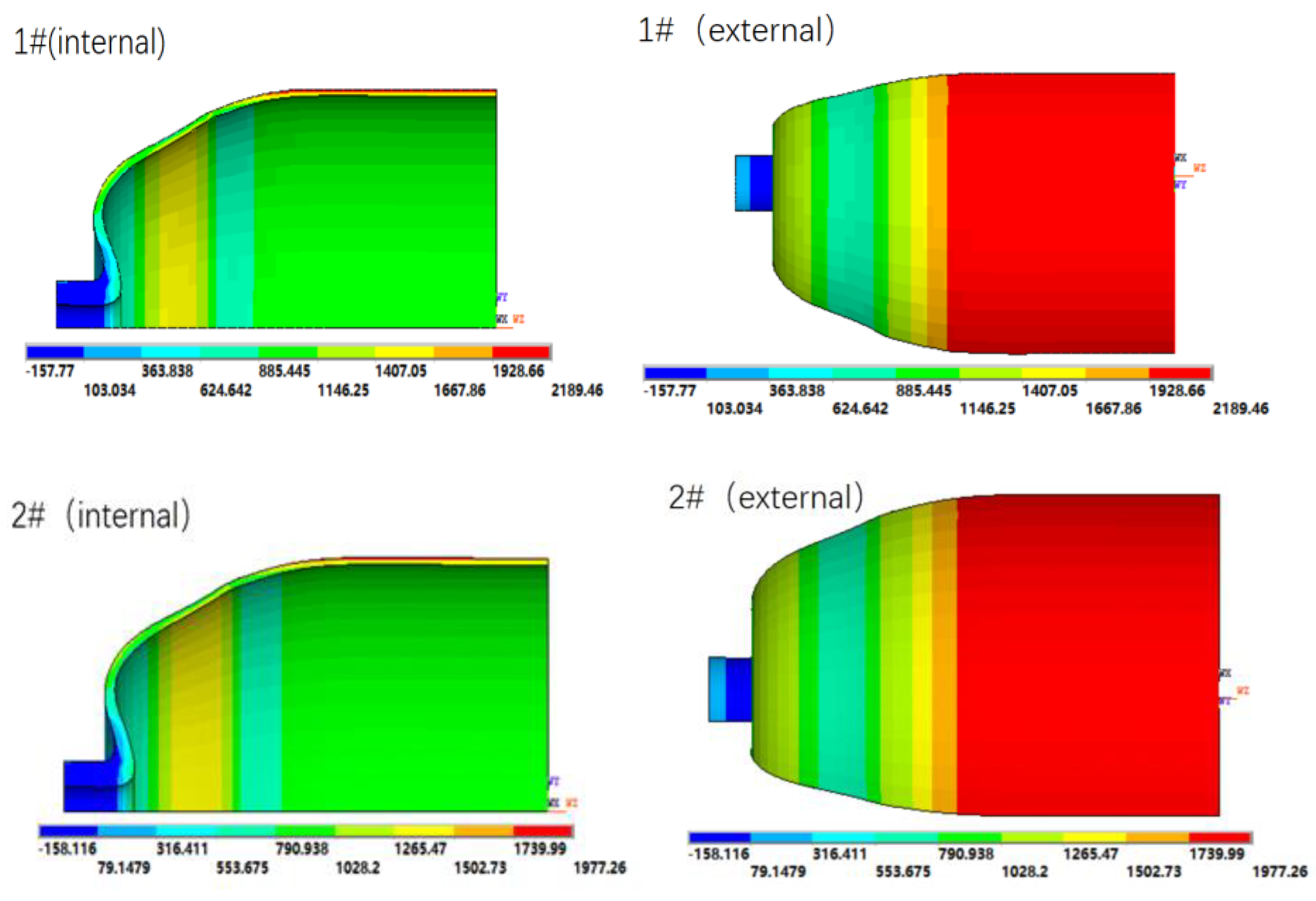
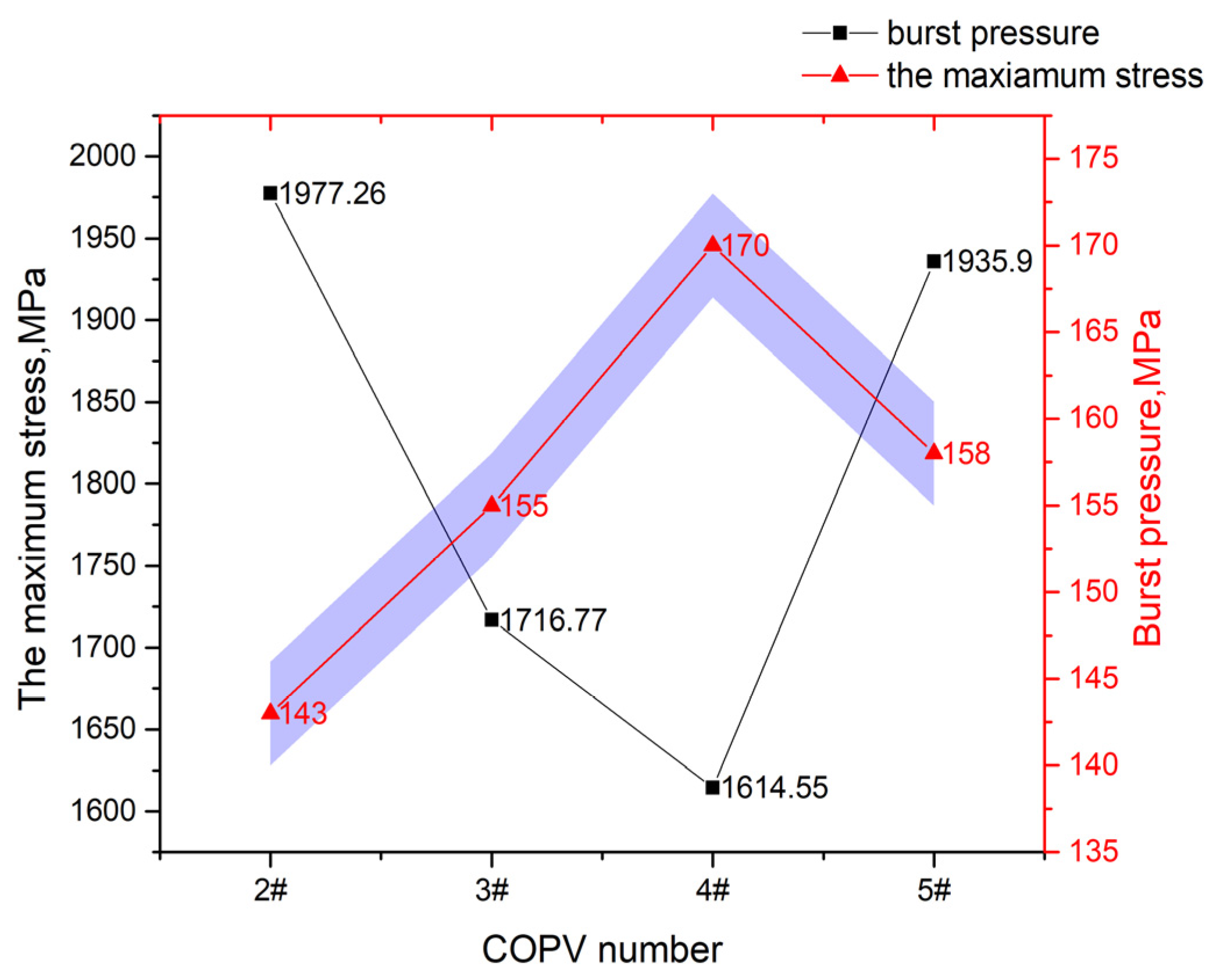
3.1. Effect of Winding Thickness on Burst Pressure
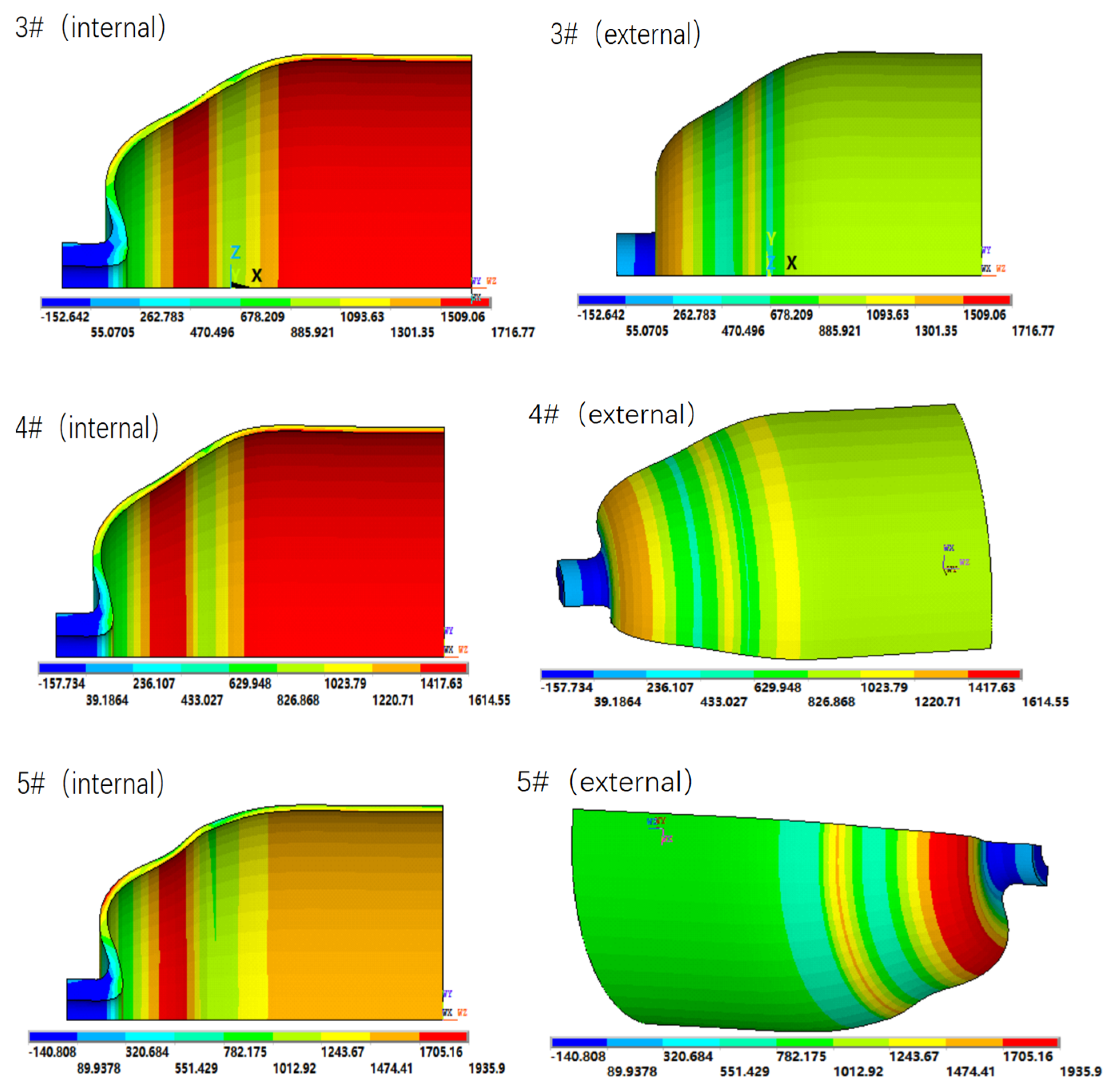
3.2. Effect of Ratio of Annular/Helical Fiber on Bursting Pressure of COPV
3.3. Effect of Ratio of Annular/Helical Fiber on Fatigue Property of COPVs
4. Conclusions
- According to the netting theory formula, the design parameters of the 70 MPa COPV were preliminarily determined and the failure location of the COPV was predicted by ANSYS finite element analysis method.
- It is found that the measured performance of the COPV is very different from the design goal, and the effect is minor when the thickness of the winding layer is increased. By analyzing the failure mode, the ratio of annular fiber to helical fiber is further adjusted, which greatly improves the bearing capacity and fatigue performance of the COPV. When the number of winding layers is 48 and the ratio of annular fiber to helical fiber is 3.0, the performance of the COPV is optimal.
- The method is validated by deducing the netting theory formula. However, further study is needed to determine how to use the finite element simulation method to further design and predict the performance of COPVs with large thickness.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Demir, I.; Sayman, O.; Dogan, A.; Arikan, V.; Arman, Y. The effects of repeated transverse impact load on the burst pressure of composite pressure vessel. Compos. Part B 2015, 68, 121–125. [Google Scholar] [CrossRef]
- Han, M.G.; Chang, S.H. Failure analysis of a type III hydrogen pressure vessel under impact loading induced by free fall. Compos. Struct. 2015, 127, 288–297. [Google Scholar] [CrossRef]
- Geng, P.; Xing, J.Z.; Chen, X.X. Winding angle optimization of filament-wound cylindrical vessel under internal pressure. Arch. Appl. Mech. 2017, 87, 365–384. [Google Scholar] [CrossRef]
- Mohammad, Z.K. Finite element analysis of composite pressure vessels with a load sharing metallic liner. Compos. Struct. 2000, 49, 247–255. [Google Scholar]
- Roy, A.K.; Tsai, S.W. Design of thick composite cylinders. J. Press. Vessel Technol. 1988, 110, 255–262. [Google Scholar] [CrossRef]
- Molavizadeh, A.; Rezaei, A. Progressive Damage Analysis and Optimization of Winding Angle and Geometry for a Composite Pressure Hull Wound Using Geodesic and Planar Patterns. Appl. Compos. Mater. 2019, 26, 1021–1040. [Google Scholar] [CrossRef]
- Son, D.S.; Chang, H.S. Evaluation of modeling techniques for a type III hydrogen pressure vessel (70 MPa) made of an aluminum liner and a thick carbon/epoxy composite for fuel cell vehicles. Int. J. Hydrogen Energy 2012, 37, 2353–2369. [Google Scholar] [CrossRef]
- Zhang, X.; Zhao, J.; Wang, Z. Burst Pressure Prediction and Structure Reliability Analysis of Composite Overwrapped Cylinder. Appl. Compos. Mater. 2018, 25, 1269–1285. [Google Scholar] [CrossRef]
- Ao, W.A.; Liu, Z.M.; Zhang, H.Y.; Huang, Y.G. Elastic limit analysls of composed thick-wall cylinder considering difference in tension-compression strength. Int. J. Innov. Comput. I 2021, 17, 919–932. [Google Scholar]
- Zu, L.; Xu, H.; Wang, H.B.; Zhang, B.; Zi, B. Design and analysis of filament-wound composite pressure vessels based on non-geodesic winding. Compos. Struct. 2019, 207, 41–52. [Google Scholar] [CrossRef]
- Di, C.R.; Yu, J.W.; Wang, B.M.; Lau AK, T.; Zhu, B.; Qiao, K. Study of hybrid nanoparticles modified epoxy resin used in filament winding composite. Materials 2019, 12, 3853. [Google Scholar] [CrossRef] [PubMed]
- Zhang, H.H.; Xiao, Y.C.; Xu, Z.Q.; Yang, M.; Zhang, L.; Yin, L.; Chai, S.; Wang, G.; Zhang, L.; Cai, X. Effects of Ni-decorated reduced graphene oxide nanosheets on the microstructural evolution and mechanical properties of Sn-3.0Ag-0.5Cu composite solders. Intermetallics 2022, 150, 107683. [Google Scholar] [CrossRef]
- Sharma, P.; Bera, T.; Semwal, K.; Badhe, R.M.; Sharma, A.; Ramakumar, S.S.V.; Neogi, S. Theoretical analysis of design of filament wound type 3 composite cylinder for the storage of compressed hydrogen gas. Int. J. Hydrogen Energy 2020, 45, 25386–25397. [Google Scholar] [CrossRef]
- Zu, L.; Xu, H.; Zhang, B. Filament-wound composite sleeves of permanent magnet motor rotors with ultra-high fiber tension. Compos. Struct. 2018, 204, 525–535. [Google Scholar] [CrossRef]
- Huang, Q.Z.; Zheng, J.Y.; Hu, J.; Reng, M.F. Research on the fatigue life prediction of composite vessel under mulita-axial loading. Fiber Reinf. Plast/Compos. 2016, 11, 39–45. [Google Scholar]
- Debski, H.; Rozylo, P.; Wysmulski, P. Stability and load-carrying capacity of short open-section composite columns under eccentric compression loading. Compos. Struct. 2020, 252, 112716.1–112716.13. [Google Scholar] [CrossRef]
- Rozylo, P.; Wysmulski, P. Failure analysis of thin-walled composite profiles subjected to axial compression using progressive failure analysis (PFA) and cohesive zone model (CZM). Compos. Struct. 2021, 262, 113597.1–113597.17. [Google Scholar] [CrossRef]
- Zhang, Q.; Xu, H.; Jia, X.L.; Zu, L.; Cheng, S.; Wang, H. Design of a 70 MPa type IV hydrogen storage vessel using accurate modeling techniques for dome thickness prediction. Compos. Struct. 2020, 236, 111915. [Google Scholar] [CrossRef]
- Hua, T.Q.; Roh, H.S.; Ahluwalia, R.K. Performance assessment of 700-bar compressed hydrogen storage for light duty fuel cell vehicles. Int. J. Hydrogen Energy 2017, 42, 25121–25129. [Google Scholar] [CrossRef]
- Magneville, B.; Gentilleau, B.; Villalonga, S.; Nony, F.; Galiano, H. Modeling, parameters identification and experimental validation of composite materials behavior law used in 700 bar type IV hydrogen high pressure storage vessel. Int. J. Hydrogen Energy 2015, 40, 13193–13205. [Google Scholar] [CrossRef]
- Ramos, I.; Park, Y.H.; Ulibarri-Sanchez, J. Analytical and Numerical Studies of a Thick Anisotropic Multilayered Fiber-Reinforced Composite Pressure Vessel. J. Press. Vessel. Technol. 2019, 141, 011203. [Google Scholar] [CrossRef]
- Hajmohammad, M.H.; Tabatabaeian, A.; Ghasemi, A.R.; Taheri-Behrooz, F. A novel detailed analytical approach for determining the optimal design of FRP pressure vessels subjected to hydrostatic loading: Analytical model with experimental validation. Compos. Part B Eng. 2020, 183, 107732. [Google Scholar] [CrossRef]



| Project | E1 (GPa) | E2 (GPa) | G12 (GPa) | V12 | V23 | Xt (MPa) |
|---|---|---|---|---|---|---|
| 6061 AL | 70 | 70 | 26.9 | 0.3 | 0.3 | 262 |
| T700SC/epoxy | 154 | 114 | 7.09 | 0.33 | 0.49 | 2300 |
| T700SC | 230 | - | - | - | - | 4900 |
| NO. | Total Number of Winding Layers | K | na | nz | λ | Maximum Stress, MPa | Mean Burst Pressure, MPa |
|---|---|---|---|---|---|---|---|
| 1# | 42 | 0.75 | 28 | 14 | 2.0 | 2189.46 | 138 |
| 2# | 48 | 0.65 | 32 | 16 | 2.0 | 1977.26 | 143 |
| NO. | Total Number of Winding Layers | K | na | nz | λ | Maximum Stress, MPa | Mean Burst Pressure, MPa |
|---|---|---|---|---|---|---|---|
| 2# | 48 | 0.65 | 32 | 16 | 2.0 | 1977.26 | 143 |
| 3# | 48 | 0.65 | 34 | 14 | 2.4 | 1716.77 | 155 |
| 4# | 48 | 0.65 | 36 | 12 | 3.0 | 1614.55 | 170 |
| 5# | 48 | 0.65 | 38 | 10 | 3.8 | 1935.90 | 158 |
| NO. | Total Number of Winding Layers | λ | Failure Location | Failure Mode | Fatigue Life Cycle |
|---|---|---|---|---|---|
| 2# | 48 | 2.0 | cylindrical section | longitudinal crack | 2852 |
| 3# | 48 | 2.4 | cylindrical section | longitudinal crack | 5520 |
| 4# | 48 | 3.0 | cylindrical section | longitudinal crack | 10,122 |
| 5# | 48 | 3.8 | cylindrical section | circular crack | 7625 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di, C.; Zhu, B.; Guo, X.; Yu, J.; Zhao, Y.; Qiao, K. Optimization of the Winding Layer Structure of High-Pressure Composite Overwrapped Pressure Vessels. Materials 2023, 16, 2713. https://doi.org/10.3390/ma16072713
Di C, Zhu B, Guo X, Yu J, Zhao Y, Qiao K. Optimization of the Winding Layer Structure of High-Pressure Composite Overwrapped Pressure Vessels. Materials. 2023; 16(7):2713. https://doi.org/10.3390/ma16072713
Chicago/Turabian StyleDi, Chengrui, Bo Zhu, Xiangji Guo, Junwei Yu, Yanbin Zhao, and Kun Qiao. 2023. "Optimization of the Winding Layer Structure of High-Pressure Composite Overwrapped Pressure Vessels" Materials 16, no. 7: 2713. https://doi.org/10.3390/ma16072713
APA StyleDi, C., Zhu, B., Guo, X., Yu, J., Zhao, Y., & Qiao, K. (2023). Optimization of the Winding Layer Structure of High-Pressure Composite Overwrapped Pressure Vessels. Materials, 16(7), 2713. https://doi.org/10.3390/ma16072713






