Abstract
When designing scaffolds for bone tissue engineering (BTE), the wall shear stress (WSS), due to the fluid flow inside the scaffold, is an important factor to consider as it influences the cellular process involved in new tissue formation. The present work analyzed the average WSS in Schwartz diamond (SD) and gyroid (SG) scaffolds with different surface topologies and mesh elements using computational fluid dynamics (CFD) analysis. It was found that scaffold meshes with a smooth surface topology with tetrahedral elements had WSS levels 35% higher than the equivalent scaffold with a non-smooth surface topology with hexahedral elements. The present work also investigated the possibility of implementing the optimization algorithm simulated annealing to aid in the design of BTE scaffolds with a specific average WSS, with the outputs showing that the algorithm was able to reach WSS levels in the vicinity of 5 mPa (physiological range) within the established limit of 100 iterations. This proved the efficacy of combining CFD and optimization methods in the design of BTE scaffolds.
1. Introduction
In bone tissue engineering (BTE), scaffolds are porous support matrixes designed as an environment to promote cell proliferation, differentiation, and growth [1]. These cellular processes are considerably influenced by several parameters, one of which is the wall shear stress (WSS) that affects the cells inside the scaffold [2,3,4,5]. WSS is caused by the relative movement between the scaffold walls and the fluidic phase inside the scaffold. Studies have shown that different levels of WSS lead to different mechanical signals for the mesenchymal stromal cells, which, in turn, cause differences to the cellular differentiation process [6,7]. This parameter is affected by various factors, with one being the scaffold geometry. In fact, small changes in the scaffold’s design parameters (such as its porosity, surface topology, or curvature) considerably alter the average WSS experienced by the cells inside the scaffolds [8,9]. Furthermore, in order to promote the desired conditions to promote bone proliferation, the average WSS experienced by the cells needs to be between 0.1 and 10 mPa [10,11].
When designing scaffolds, the multiple possible inputs for scaffold development result in a large range of possible designs. Therefore, computational simulations are normally implemented to reduce the time and cost associated with conceptualizing a new scaffold. For BTE, computational fluid dynamics (CFD) analysis is essential in understanding how changes to a scaffold’s design influence its fluidic properties (such as the WSS) and the underlying cellular processes [12,13,14].
Additionally, computational simulations can also be used to design scaffold geometry with the desired characteristics, through a structural optimization approach. Although there are several different optimization methods, most of them follow the same framework [15]. After defining the design space, the chosen objective function, and the constraints for that specific optimization process, the process starts with an initial step where the initial geometry (initial solution) is set as well as the material properties of the structure. Afterward, the state variables are computed through a proper numerical tool in order to analyze the relevant properties of the initial geometry. If the resulting properties do not reach the objective, then an optimization algorithm is utilized to obtain a new geometry, according to the predefined constraints. This process repeats itself iteratively until a new structure satisfies the objective function. However, in BTE, optimization methods have rarely focused on the fluidic properties of the scaffold [14,15,16], instead only consider the scaffold’s mechanical properties (such as their Young’s modulus [17]; compressive strength [18] and octahedral shear strain [19,20,21]).
Taking this into consideration, the objective of this work was twofold. Firstly, the difference in average WSS was analyzed for different scaffold topologies, with either smoothed (tetrahedral elements) or non-smoothed (hexahedral elements) wall surface topologies. This was in order to determine whether previously designed numerical models [22] can be used in the study of WSS, or if an additional step to correct their surface topology is required. Secondly, a simulated annealing (SA) optimization strategy was used to design scaffolds for a specific average WSS, in order to investigate the feasibility of using structural optimization methodologies combined with CFD analysis in the design of scaffolds for required fluidic properties.
2. Materials and Methods
2.1. Scaffold Design
To generate the scaffold’s mesh for the CFD analysis a computer code was used, which, given the specific design parameters, created a hexahedral mesh of the desired geometry for the analysis [22]. This mesh consists of a single cubic unit of the fluidic phase of the chosen scaffold design, with forty elements per side, seeing as previous studies have shown that 40 elements per side are the minimum in order to obtain an appropriate scaffold geometry [23]. For this study, the chosen scaffold geometries were the triply periodic minimum surfaces (TPMS) gyroid (SG) and Schwartz diamond (SD) designs. This choice was because these scaffolds were found to be the most appropriate TPMS structures for cellular growth given their high permeability and fluid tortuosity that promotes cell–scaffold interaction [22]. Additionally, an empty portion was added before and after the scaffold, which represented the empty permeability chamber that allows the fluid flow to stabilize before and after passing the scaffold (Figure 1), mimicking the experimental setup for permeability analysis [24].

Figure 1.
Example of a mesh with empty chambers before and after the scaffold.
Having designed a scaffold mesh with hexahedral elements (Figure 2a), to create the corresponding mesh with tetrahedral elements and a smooth surface, an additional design step was required. To this end, Meshlab® [25] was used to apply a three-step Laplacian smoothing process followed by a three-step isotropic explicit remeshing process to obtain the scaffold with smooth surfaces (Figure 2b).

Figure 2.
Example meshes: (a) original hexahedral scaffold mesh; (b) smoothed hexahedral scaffold mesh.
The scaffold design parameters considered for this paper were: the porosity of the scaffold and the length of the side of a single basic cubic unit (higher values result in scaffolds with larger pore sizes). In addition to these two characteristics, two other parameters that were analyzed were the length of empty chambers before and after the scaffold and, in the case of the tetrahedral meshes, the world unit parameter from Meshlab’s isotropic explicit remeshing process (which directly controls the number of elements in the final mesh). Given that these factors were constant across all scaffolds that were studied, a convergence test was carried out for each one to determine their best value. For these tests, both scaffold geometries were analyzed in regard to their average WSS and permeability with a fluid inlet velocity of 0.0001 m/s, a length of 5 mm for the cubic unit, and a 70% porosity.
2.2. Surface Topology CFD Analysis
Having defined the optimal values for the cubic unit length and the world unit parameters, the next step was to define the scaffold designs to be compared. For each of the two TPMS geometries, three different levels of porosity were considered (60%, 70%, and 80%) for a total of six different scaffold designs. A hexahedral and a tetrahedral mesh were then created for each design and their average WSS was studied using CFD analysis with the previously mentioned fluid inlet velocity of 0.0001 m/s and cubic unit length of 5 mm. For this study, the computational simulations were conducted using the commercial software Fluent® Ansys® (Ansys Inc., Canonsburg, PA, USA), which has already proven to be a useful tool for analyzing the fluidic properties of scaffolds [26,27]. In terms of the parameters for the Fluent solver, the fluid chosen for the simulations was water, in accordance with previous studies [22,28], with a density of 1000 kg/m3 and dynamic viscosity of 0.001 Pa.s. The fluid was also assumed to pass through the scaffold in a steady state laminar flow.
Three different boundary conditions need to be defined, these being the velocity inlet, the pressure outlet, and the wall boundary. For these simulations, it was considered that the fluid was traveling in the y direction through the scaffold. This meant that an exterior wall on the xz plane was the velocity inlet surface, while the opposite wall was the pressure outlet with 0 Pa, so that the pressure drop of the scaffold would be equal to the pressure at the inlet (since the pressure drop is the pressure at the inlet minus the pressure at the outlet). Additionally, interfaces with periodic boundary conditions were implemented in parallel on the remaining exterior walls in order to create an infinite scaffold in the x and z directions.
Finally, after running the simulations, the software CFD-post from Ansys was used to calculate the average WSS on the scaffold walls and, if needed, the pressure difference between the inlet and outlet of each scaffold. Afterward, the scaffold permeability could be calculated using the pressure drop and Darcy’s law (Equation (1)) [29,30]:
where K is the permeability expressed in m2; ΔP is the pressure drop expressed in Pa; L is the length of the scaffold expressed in m; v is the inlet velocity of the fluid and µ is the dynamic viscosity of the water which is 0.001 Pa*s.
K = (v·µ·L)/ΔP,
2.3. Structural Optimization Process
For this work, the created optimization algorithm was focused on the scaffold’s average WSS on both the SD and SG geometries with tetrahedral elements. More specifically, the algorithm will attempt to design a scaffold geometry with an average WSS that promotes cellular proliferation and growth. Zhao et al. (2015) [10] and Ali et al. (2019) [11] discussed how the WSS of structures meant for bone growth needed to be between 0.1 and 10 mPa. Given that the present method looks at the average WSS, a target was set at 5 mPa for the optimization program, as an average target value between the two edges of the accepted physiological levels. Additionally, seeing as the average WSS of the scaffold was dependent on the fluid velocity passing through it (unlike permeability, which is only dependent on the scaffold design), a constant inlet velocity of 0.001 m/s (similar to the parameter described in a comparable scaffold perfusion analysis [31]), was selected to allow a comparison between all scaffold geometries.
To solve the established scaffold optimization challenge, the metaheuristic optimization computational algorithm simulated annealing (SA) was chosen. This is a metaheuristic optimization approach used to solve optimization problems with a large search space. Additionally, this algorithm allows a worse solution to be accepted in the earlier iterations, which minimized the probability of the program reaching a local minimum and being unable to progress further.
SA requires the definition of an appropriate cooling schedule variable (a); the objective function; the maximum number of iterations the algorithm runs before stopping (Kmax); and the upper (Uj) and lower (Lj) boundaries of each parameter. In this work, a cooling schedule variable of 0.9 was chosen, alongside a maximum of 100 iterations. The objective function was defined as the normalized difference between the target (5 mPa) and the real average calculated WSS, and the design variables are the side length of the unit cell of the TPMS structure and the scaffold porosity. These variables are limited to the lower and upper bounds of 1 and 10 mm for the unit length and 60% and 80% for the porosity, respectively. These values were chosen to maintain pore sizes that promote cellular processes.
After defining the variables, the algorithm then calculated an initial value for each parameter (equal to the halfway point between the upper and lower boundary of each parameter), and used the process discussed in the previous section to create and study the average WSS of the scaffold.
The program then used a Matlab® (Mathworks, Natick, MA, USA) script to calculate the objective function value of the designed scaffold and recorded it as the current solution (Zc). Subsequently, the algorithm defined an initial temperature (Tj) equal to 1/5 of the current solution. The temperature was cooled after each iteration by multiplying it by the previously established cooling schedule variable (a).
Having the initialization of the SA algorithm, the iterative process started with testing the immediate neighbors of the current solution (using the current parameters and normal distribution). If a parameter went outside the predefined boundaries, then it was replaced by the closest values within the boundaries (for example, if the new porosity parameter was equal to 85%, then the code replaced it with 8’, the corresponding maximum allowed value). The program then calculated the objective function value of the new parameters, using the same method as discussed above, and recorded it as the next trial solution (Zn). If Zn was lower than or equal to Zc, then the code always accepted the new value. Otherwise, the chance of accepting the new value was equal to . The code then recorded the value of the parameters and objective function value and proceeded with the temperature cooling. Finally, when the algorithm ended, it returned the history of the optimization process.
3. Results
3.1. Scaffold Design Parameters
Figure 3 shows the results of the convergence analysis on the pressure drops and average WSS for simulations conducted on both 70% porosity test scaffolds. After obtaining these results, the relative difference between the analysis with the smallest world unit and every other simulated mesh was calculated (Table 1 and Table 2). As expected, the results showed that an increase in the number of elements in the simulation led to more accurate results. However, an increase in the number of elements also resulted in longer simulations. Therefore, a compromise had to be made between the accuracy of the results and the computational cost of the simulation. Accordingly, the world unit value 0.15 was decided as the best option seeing as it always presented a considerably low relative error (almost always around or below 1%) with considerably quicker simulations than models with a higher element count.
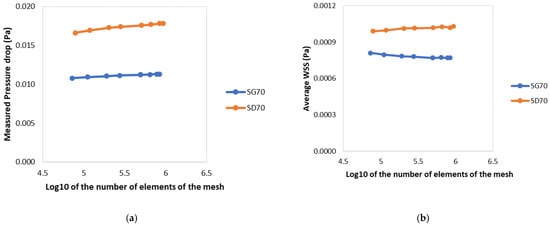
Figure 3.
Comparison between different values of the world unit parameter, resulting in tetrahedral meshes with varying element numbers, regarding the test scaffold’s: (a) pressure drop; (b) average WSS.

Table 1.
Calculated pressure drop and average WSS for the SD70 scaffold.

Table 2.
Calculated pressure drop and average WSS for the SG70 scaffold.
For the fluid flow to stabilize, the chambers before and after the scaffold must have sufficient “empty” length to allow the flow to stabilize before and after the scaffold; otherwise, this could affect the numerical simulation, namely the pressure drop measurement. However, the longer the empty chamber, the higher the computational cost of the simulations, which would in turn considerably affect the computational cost of the optimization algorithm. Therefore, the desirable empty chamber length is the shortest one that still allows the stabilization of the fluid flow. Furthermore, an additional length should be added to the minimum length to account for different scaffold configurations that require a longer chamber to stabilize, such as lower porosity scaffolds.
In order to determine a minimal length, two different scaffolds were designed: one where the length of the empty chambers, before and after the scaffold, was equal to the length of the basic cubic unit and another where the length empty chambers was equal to half the length of the basic cubic unit. As the fluid flow pressure drop measurement and the average scaffold WSS are both independent from the length of the chambers (as long as the flow is stable at both ends of the numerical model), if both CFD simulations returned similar pressure drop and average WSS values, then this meant that the model with the smaller empty chamber was enough to allow the fluid flow to stabilize.
As shown in Table 3, for both the SG and SD scaffolds, the difference between the models with varying values of h was minimal, with their difference always below 0.3%. This indicates how the shorter chamber was sufficient in allowing the flow to stabilize at the edges of the numerical model. On top of that, analyzing the fluid flow streamlines presented in Figure 4 highlights how the fluid flow is completely stable at the edges of the numerical model. However, choosing a shorter chamber could potentially risk the CFD simulations for the scaffolds with the smallest pore sizes whilst not significantly contributing to a lower computational cost. Therefore, an empty chamber length of half the length of the scaffold was chosen for all the CFD analysis.

Table 3.
Comparison of the pressure drop and average WSS between scaffolds with different length of the empty chamber before and after the scaffold.
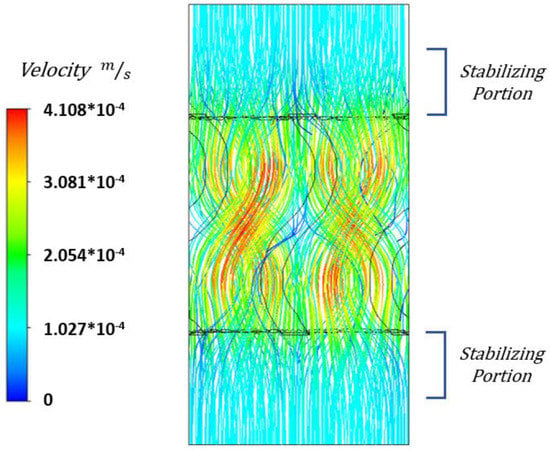
Figure 4.
Fluid flow streamlines of a 1 mm sided SG scaffold with 70% porosity.
3.2. Surface Topology CFD Analysis
Table 4 and Table 5 illustrate how the difference in the of scaffold surface topology (original jagged surfaces with hexahedral elements or smooth surfaces with tetrahedral) influences the average WSS of the six different scaffold designs. The results show that all of the smoothed scaffolds had a higher average WSS than the original scaffolds (average of 35% increase).

Table 4.
Comparison of the average WSS between SG scaffolds with and without surface topology smoothing.

Table 5.
Comparison of the average WSS between SD scaffolds with and without surface topology smoothing.
Additionally, the volumes of the original and smoothed scaffolds were compared to determine if the smoothing process would influence the porosity of the scaffolds (Table 6).

Table 6.
Volume (mm2) of various scaffolds with square size of 1 mm before and after smoothing.
3.3. Optimization Method
For each scaffold geometry, the optimization algorithm ran multiple times. Examples of one optimization run for the SD and SG geometries are shown in Table 7 and Table 8, respectively. The iterations where no new point was considered were not presented in the tables. The convergence of the results is shown in Figure 5.

Table 7.
Simulated annealing process for the SD scaffolds.

Table 8.
Simulated annealing process for the SG scaffolds.
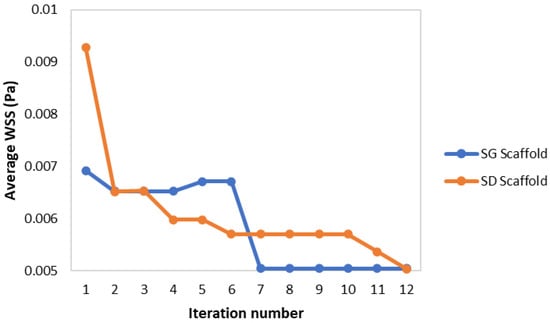
Figure 5.
Convergence of the average WSS for the SA algorithm on the SD and SG scaffolds.
4. Discussion
The comparison between the different surface topologies showed that the WSS levels in the smoothed surfaces increased by an average of 35% when compared to the original non-smoothed surfaces. A previous study has shown that in scaffolds with equal geometry but different surface roughness levels, a lower average WSS was calculated for the scaffolds with a higher roughness [32]. This corresponds to what was observed in Table 5, where the original jagged mesh, given its higher surface roughness, resulted in a lower WSS than the smoothed tetrahedral mesh. Furthermore, when fabricating scaffolds using 3D printing techniques, these methods normally create surface topologies closer to the smoothed surfaces than the original jagged ones. Therefore, the smoothed surface was chosen as the basis for the optimization algorithm of the scaffold’s average WSS. Finally, the difference between the volume before and after the smoothing is illustrated in Table 6. The difference between the two is minimal, indicating that the smoothing process can be used without it affecting the scaffold’s porosity.
In terms of the optimization algorithm, it was able to consistently reach the desired average WSS of 5 mPa taking a maximum of 12 iterations, well within the established 100-iterations limit. However, given the inherent random nature of the SA algorithm, the number of iterations and the final parameters varied between each optimization run. Nevertheless, the outputs remained similar to those reported in Table 7 and Table 8. The optimal SD scaffold was always close to the maximum limit of 10 mm for the cubic unit length and a porosity close to 70%; whilst the SG scaffolds had a cubic unit length between 7 and 8.5 mm and porosity between 63% and 73% (higher porosity corresponded with lower cubic unit length).
The resulting scaffold designs from this algorithm were able to refine the scaffold geometry in order to reach the desired average WSS of 5 mPa. This highlights how the optimization algorithm presented in this work can be combined with CFD analysis; additionally, this algorithm can enhance the design of TPMS scaffolds with a specific fluidic property such as a specific average WSS or permeability. The results also demonstrate how the SA method worked as intended, with the code accepting worse solution to the current one at earlier iterations (for example the SG optimization from the second to the fifth iteration as seen in Table 8) and only accepting strictly better solutions at higher iterations (when the temperature variable Tj of the algorithm was at its lowest).
Although the SA algorithm proved as useful to optimize and improve one specific parameter, it would not be able to simultaneously improve multiple fluidic parameters, such as both WSS and permeability. In other words, WSS and permeability are inversely correlated, with studies have shown that that increasing the average WSS leads to a decrease in the scaffold’s permeability and vice versa [33,34]. To address the limitations of the current algorithm, a multi-objective optimization approach might be implemented in future developments. Instead of focusing on a single objective function, multi-objective optimization could analyze each parameter individually and would give a set of possible solutions, organized as a Pareto front, but with a higher computational cost. This method would result in multiple possible solutions, which would need to be analyzed in terms of their suitability for BTE.
Author Contributions
Conceptualization, P.R.F.; Data curation, T.H.V.P.; Formal analysis, T.H.V.P.; Funding acquisition, P.R.F.; Investigation, T.H.V.P.; Methodology, T.H.V.P. and A.P.G.C.; Project administration, P.R.F.; Software, T.H.V.P.; Supervision, J.W.C.D., A.P.G.C. and P.R.F.; Validation, J.W.C.D. and A.P.G.C.; Visualization, J.W.C.D.; Writing—original draft, T.H.V.P.; Writing—review & editing, J.W.C.D., A.P.G.C. and P.R.F. All authors have read and agreed to the published version of the manuscript.
Funding
T.H.V.P., A.P.G.C. and P.R.F. would like to acknowledge the Portuguese Science and Technology Foundation (FCT) for the funding provided, through IDMEC, under LAETA project UIDB/50022/2020; T.H.V.P. would also like to acknowledge FCT for the PhD Grant 2020.04417.BD.
Data Availability Statement
The generated models can be made available upon reasonable request to the corresponding author.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Laubach, M.; Suresh, S.; Herath, B.; Wille, M.-L.; Delbrück, H.; Alabdulrahman, H.; Hutmacher, D.W.; Hildebrand, F. Clinical translation of a patient-specific scaffold-guided bone regeneration concept in four cases with large long bone defects. J. Orthop. Transl. 2022, 34, 73–84. [Google Scholar] [CrossRef] [PubMed]
- Perier-Metz, C.; Cipitria, A.; Hutmacher, D.W.; Duda, G.N.; Checa, S. An in silico model predicts the impact of scaffold design in large bone defect regeneration. Acta Biomater. 2022, 145, 329–341. [Google Scholar] [CrossRef] [PubMed]
- Ali, D.; Sen, S. Permeability and fluid flow-induced wall shear stress of bone tissue scaffolds: Computational fluid dynamic analysis using Newtonian and non-Newtonian blood flow models. Comput. Biol. Med. 2018, 99, 201–208. [Google Scholar] [CrossRef] [PubMed]
- Basri, H.; Nasution, J.D.; Syahrom, A.; Sulong, M.A.; Md Saad, A.P.; Prakoso, A.T.; Aminin, F. The effect to flow rate characteristic on biodegradation of bone scaffold. Malays. J. Fundam. Appl. Sci. 2017, 13, 546–552. [Google Scholar] [CrossRef]
- Yu, G.; Li, Z.; Li, S.; Zhang, Q.; Hua, Y.; Liu, H.; Zhao, X.; Dhaidhai, D.T.; Li, W.; Wang, X. The select of internal architecture for porous Ti alloy scaffold: A compromise between mechanical properties and permeability. Mater. Des. 2020, 192, 108754. [Google Scholar] [CrossRef]
- McCoy, R.J.; O’Brien, F.J. Influence of Shear Stress in Perfusion Bioreactor Cultures for the Development of Three-Dimensional Bone Tissue Constructs: A Review. Tissue Eng. Part B Rev. 2010, 16, 587–601. [Google Scholar] [CrossRef]
- Vetsch, J.R.; Betts, D.C.; Müller, R.; Hofmann, S. Flow velocity-driven differentiation of human mesenchymal stromal cells in silk fibroin scaffolds: A combined experimental and computational approach. PLoS ONE 2017, 12, e0180781. [Google Scholar] [CrossRef]
- Zhao, F.; Vaughan, T.J.; McNamara, L.M. Quantification of fluid shear stress in bone tissue engineering scaffolds with spherical and cubical pore architectures. Biomech. Model. Mechanobiol. 2016, 15, 561–577. [Google Scholar] [CrossRef]
- Zhao, F.; Rietbergen, B.; Ito, K.; Hofmann, S. Fluid flow-induced cell stimulation in bone tissue engineering changes due to interstitial tissue formation in vitro. Int. J. Numer. Methods Biomed. Eng. 2020, 36, e3342. [Google Scholar] [CrossRef]
- Zhao, F.; Vaughan, T.J.; Mcnamara, L.M. Multiscale fluid–structure interaction modelling to determine the mechanical stimulation of bone cells in a tissue engineered scaffold. Biomech. Model. Mechanobiol. 2015, 14, 231–243. [Google Scholar] [CrossRef]
- Ali, D.; Ozalp, M.; Blanquer, S.B.G.; Onel, S. Permeability and fluid flow-induced wall shear stress in bone scaffolds with TPMS and lattice architectures: A CFD analysis. Eur. J. Mech. B/Fluids 2019, 79, 376–385. [Google Scholar] [CrossRef]
- Melchels, F.P.W.; Barradas, A.M.C.; van Blitterswijk, C.A.; de Boer, J.; Feijen, J.; Grijpma, D.W. Effects of the architecture of tissue engineering scaffolds on cell seeding and culturing. Acta Biomater. 2010, 6, 4208–4217. [Google Scholar] [CrossRef] [PubMed]
- Melchels, F.P.W.; Tonnarelli, B.; Olivares, A.L.; Martin, I.; Lacroix, D.; Feijen, J.; Wendt, D.J.; Grijpma, D.W. The influence of the scaffold design on the distribution of adhering cells after perfusion cell seeding. Biomaterials 2011, 32, 2878–2884. [Google Scholar] [CrossRef] [PubMed]
- Pires, T.; Dunlop, J.W.C.; Fernandes, P.R.; Castro, A.P.G. Challenges in computational fluid dynamics applications for bone tissue engineering. Proc. R. Soc. A Math. Phys. Eng. Sci. 2022, 478. [Google Scholar] [CrossRef]
- Metz, C.; Duda, G.N.; Checa, S. Towards multi-dynamic mechano-biological optimization of 3D-printed scaffolds to foster bone regeneration. Acta Biomater. 2019, 101, 117–127. [Google Scholar] [CrossRef]
- Boccaccio, A.; Fiorentino, M.; Uva, A.E.; Laghetti, L.N.; Monno, G. Rhombicuboctahedron unit cell based scaffolds for bone regeneration: Geometry optimization with a mechanobiology—Driven algorithm. Mater. Sci. Eng. C 2018, 83, 51–66. [Google Scholar] [CrossRef]
- Vijayavenkataraman, S.; Zhang, L.; Zhang, S.; Lu, W.F.; Hsi Fuh, J.Y. Triply Periodic Minimal Surfaces Sheet Scaffolds for Tissue Engineering Applications: An Optimization Approach toward Biomimetic Scaffold Design. ACS Appl. Bio Mater. 2018, 1, 259–269. [Google Scholar] [CrossRef]
- Uth, N.; Mueller, J.; Smucker, B.; Yousefi, A.-M. Validation of scaffold design optimization in bone tissue engineering: Finite element modeling versus designed experiments. Biofabrication 2017, 9, 015023. [Google Scholar] [CrossRef]
- Boccaccio, A.; Uva, A.E.; Fiorentino, M.; Mori, G.; Monno, G. Geometry design optimization of functionally graded scaffolds for bone tissue engineering: A mechanobiological approach. PLoS ONE 2016, 11, e0146935. [Google Scholar] [CrossRef]
- Boccaccio, A.; Uva, A.E.; Fiorentino, M.; Lamberti, L.; Monno, G. A Mechanobiology-based Algorithm to Optimize the Microstructure Geometry of Bone Tissue Scaffolds. Int. J. Biol. Sci. 2016, 12, 1–17. [Google Scholar] [CrossRef]
- Rodríguez-Montaño, Ó.L.; Cortés-Rodríguez, C.J.; Uva, A.E.; Fiorentino, M.; Gattullo, M.; Monno, G.; Boccaccio, A. Comparison of the mechanobiological performance of bone tissue scaffolds based on different unit cell geometries. J. Mech. Behav. Biomed. Mater. 2018, 83, 28–45. [Google Scholar] [CrossRef] [PubMed]
- Pires, T.; Santos, J.; Ruben, R.B.; Gouveia, B.P.; Castro, A.P.G.; Fernandes, P.R. Numerical-experimental analysis of the permeability-porosity relationship in triply periodic minimal surfaces scaffolds. J. Biomech. 2021, 117, 110263. [Google Scholar] [CrossRef]
- Castro, A.P.G.; Pires, T.; Santos, J.; Gouveia, B.P.; Fernandes, P.R. Permeability versus Design in TPMS Scaffolds. Materials 2019, 12, 1313. [Google Scholar] [CrossRef] [PubMed]
- Santos, J.; Pires, T.; Gouveia, B.P.; Castro, A.P.G.; Fernandes, P.R. On the permeability of TPMS scaffolds. J. Mech. Behav. Biomed. Mater. 2020, 110, 103932. [Google Scholar] [CrossRef] [PubMed]
- Cignoni, P.; Callieri, M.; Corsini, M.; Dellepiane, M.; Ganovelli, F.; Ranzuglia, G. MeshLab: An open-source mesh processing tool. In Proceedings of the 6th Eurographics Italian Chapter Conference, Salerno, Italy, 2–4 July 2008; pp. 129–136. [Google Scholar] [CrossRef]
- Arjunan, A.; Demetriou, M.; Baroutaji, A.; Wang, C. Mechanical performance of highly permeable laser melted Ti6Al4V bone scaffolds. J. Mech. Behav. Biomed. Mater. 2019, 102, 103517. [Google Scholar] [CrossRef] [PubMed]
- Campos Marin, A.; Grossi, T.; Bianchi, E.; Dubini, G.; Lacroix, D. µ-Particle tracking velocimetry and computational fluid dynamics study of cell seeding within a 3D porous scaffold. J. Mech. Behav. Biomed. Mater. 2017, 75, 463–469. [Google Scholar] [CrossRef]
- Campos Marin, A.; Brunelli, M.; Lacroix, D. Flow perfusion rate modulates cell deposition onto scaffold substrate during cell seeding. Biomech. Model. Mechanobiol. 2017, 17, 675–687. [Google Scholar] [CrossRef]
- Chor, M.V.; Li, W. A permeability measurement system for tissue engineering scaffolds. Meas. Sci. Technol. 2007, 18, 208–216. [Google Scholar] [CrossRef]
- Ochoa, I.; García-Aznar, J.M.; Boccaccini, A.R.; Doblaré, M.; Sanz-Herrera, J.A.; Yunos, D.M. Permeability evaluation of 45S5 Bioglass®-based scaffolds for bone tissue engineering. J. Biomech. 2008, 42, 257–260. [Google Scholar] [CrossRef]
- Zhao, F.; Lacroix, D.; Ito, K.; van Rietbergen, B.; Hofmann, S. Changes in scaffold porosity during bone tissue engineering in perfusion bioreactors considerably affect cellular mechanical stimulation for mineralization. Bone Rep. 2020, 12, 100265. [Google Scholar] [CrossRef]
- Ali, D.; Sen, S. Computational Fluid Dynamics Study of the Effects of Surface Roughness on Permeability and Fluid Flow-Induced Wall Shear Stress in Scaffolds. Ann. Biomed. Eng. 2018, 46, 2023–2035. [Google Scholar] [CrossRef] [PubMed]
- Noordin, M.A.; Rahim, R.A.A.; Roslan, A.N.H.; Ali, I.A.; Syahrom, A.; Saad, A.P.M. Controllable Macroscopic Architecture of Subtractive Manufactured Porous Iron for Cancellous Bone Analogue: Computational to Experimental Validation. J. Bionic Eng. 2020, 17, 357–369. [Google Scholar] [CrossRef]
- Egan, P.F.; Gonella, V.C.; Engensperger, M.; Ferguson, S.J.; Shea, K. Computationally designed lattices with tuned properties for tissue engineering using 3D printing. PLoS ONE 2017, 12, e0182902. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).