Abstract
This paper presents an initial investment cost analysis of public transportation systems operating with wireless charging electric vehicles (EVs). There are three different types of wireless charging systems, namely, stationary wireless charging (SWC), in which charging happens only when the vehicle is parked or idle, quasi-dynamic wireless charging (QWC), in which power is transferred when a vehicle is moving slowly or in stop-and-go mode, and dynamic wireless charging (DWC), in which power can be supplied even when the vehicle is in motion. This analysis compares the initial investment costs for these three types of charging systems for a wireless charging-based public transportation system. In particular, this analysis is focused on the energy logistics cost in transportation, which is defined as the cost of transferring and storing the energy needed to operate the transportation system. Performing this initial investment analysis is complicated, because it involves considerable tradeoffs between the costs of batteries in the EV fleet and different kinds of battery-charging infrastructure. Mathematical optimization models for each type of EV and infrastructure system are used to analyze the initial costs. The optimization methods evaluate the minimum initial investment needed to deploy the public transportation system for each type of EV charging solution. To deal with the variable cost estimates for batteries and infrastructure equipment in the current market, a cost-sensitivity analysis is performed. The goal of this analysis is to identify the market cost conditions that are most favorable for each type of wireless charging solution. Furthermore, the cost analysis quantitatively verifies the qualitative comparison of the three different wireless charging types conducted in the previous research.
1. Introduction
The recent increase in concern over the environment has generated opportunities for developing alternative fuel vehicles that reduce dependency on oil. Numerous studies have reported the benefits and advantages of pure electric vehicles (EVs), which use only electric energy, compared to the conventional internal combustion(IC)-based vehicles or hybrid EVs in terms of their environmental effects, manufacturing processes and product reliability [1]. However, the advantages of pure EVs may be offset by the limited amounts of energy that can be stored in their batteries [2]. This limitation can cause “range anxiety”, the fear of being stranded due to loss of energy in the battery. Unlike IC engine vehicles, which typically have a range of more than 200 miles and can be rapidly refueled, recharging the depleted battery of a pure EV may require several hours with a home charger. Even charging with the fastest charger still requires at least 30 minutes [2,3]. To solve this range problem, wireless charging EVs that use wireless power transfer technology have been introduced. The power for these vehicles can be supplied without human intervention, and the most advanced wireless charging technology can transfer power while a vehicle is moving. Therefore, the current range problem is expected to be solved by these systems for charging vehicles without halting their operation.
There are three types of wireless charging systems: stationary wireless charging (SWC), where charging happens only when the vehicle is parked or idle, quasi-dynamic wireless charging (QWC), in which power is transferred when the vehicle is moving slowly or in stop-and-go mode, and dynamic wireless charging (DWC), in which power is supplied even when the vehicle is in motion. This classification of the systems for wireless charging EVs has been recently introduced in a number of studies and reports, including [4,5]. The SWC system was first introduced to eliminate the requirement for a connection cable to plug-in EVs. The DWC system is more advanced, and it utilizes power transmitters embedded in the road for the wireless transfer of electric power as the vehicle travels over it. DWC is also known as a move-and-charge, dynamic inductive charging, ground-electrified or road-way-powered system. Although DWC is the most advanced wireless charging solution, this does not necessarily mean that DWC will replace the SWC and QWC solutions. In particular, when wireless charging EV-based public transportation systems are designed, the costs and benefits of each system depend on the fleet size, service range and other cost factors, such as battery prices or charging installation costs. Depending on the operational conditions and costs, the SWC solution may be more competitive than DWC, or vice versa.
In this paper, we compare the initial investment costs for installing the three types of wireless charging (SWC, QWC and DWC) in a new public transportation system (“EV type”, or “solution type”, refers to the type of wireless charging). Our analysis focuses on public transit applications, as the most current wireless charging EV applications have been developed and tested for public transit rather than personal vehicles [6]. We are motivated to explore options for wireless charging EVs as an extension of our work in developing the On-Line Electric Vehicle (), which is one of the first commercially-available DWC-capable EVs. The OLEVwas first developed at the Korea Advanced Institute of Science and Technology (KAIST), and it uses an innovative inductive power transfer technology called the shaped magnetic field in resonance system [7]. The first commercial application of this technology was introduced in 2009 as the trolley in Seoul Grand Park. The second commercial version of the system was developed for the shuttle buses on the KAIST campus, which have been in operation since 2012 [8]. Figure 1 shows the OLEV currently serving as a campus shuttle on the KAIST campus and the power track installed under the road. The third commercial version has been operating as a public transit line in Gumi City, South Korea, since 2013. Although the KAIST OLEV is primarily designed as a DWC-based transportation vehicle, it can operate as SWC or QWC if the infrastructure is installed only at a base station or it allows charging only when the vehicle halts at a bus stop.

Figure 1.
KAIST OLEV: one of the dynamic wireless charging EVs (DWC-EVs), (a) under construction; (b) in operation.
From the experience gained in the development and actual operation of the OLEV system, the engineers initially found that there were clear advantages and disadvantages for each type of wireless system. They therefore presented a qualitative cost-benefit analysis for each type, as shown in Figure 2. This figure qualitatively illustrates the competitiveness of each type, depending on the costs of batteries and infrastructure. However, policy makers and investors will not make a multi-million-dollar decision based on this type of qualitative analysis. Suppose that someone asks the following very specific question: “The current battery cost in the market is $500/kWh, and the cost of the charging infrastructure is $10,000 per unit. If 10 buses will be operating on a specific route, how much investment is needed for the dynamic charging of EVs compared to the stationary charging of EVs?”. This kind of specific question cannot be answered by the qualitative estimate shown in Figure 2. The cost analysis conducted in this paper quantitatively verifies the comparison shown in this figure. The initial cost investment analysis proposed in this paper is further motivated by the following considerations.
- First, the development and commercialization of wireless-charging EVs depend on the evaluations of the new technology’s operational reliability. Once the reliability of such EVs is proven, the next step prior to mass commercialization is to analyze the startup and operating costs of these systems.
- Second, researchers and engineers involved in these initiatives claim that DWC reduces the high investment costs of conventional plug-in EVs by allowing the batteries to be substantially downsized [9]. For example, it was originally claimed that the KAIST OLEV system would have substantially reduced initial investment costs, as the technology used batteries one-fifth the size of those in conventional plug-in EVs (the supplemental file for this paper “CNN-Report-KAIST-OLEV.avi” contains the CNNreport mentioning the battery size of the KAIST-OLEV). In addition, it was also reported that DWC would be economical because it would effectively utilize the installed charging infrastructure, as a large number of vehicles would use the same road segments equipped with a charging system [6]. However, none of these claims have been yet supported by any quantitative analysis.
- Last, it is reasonable to expect that whenever a wireless charging EV-based transportation system is proposed, the policy-makers and stakeholder will request a cost analysis of the SWC, QWC and DWC options. Therefore, it is necessary to develop a method for comparing the initial investment costs for these different types of charging systems.
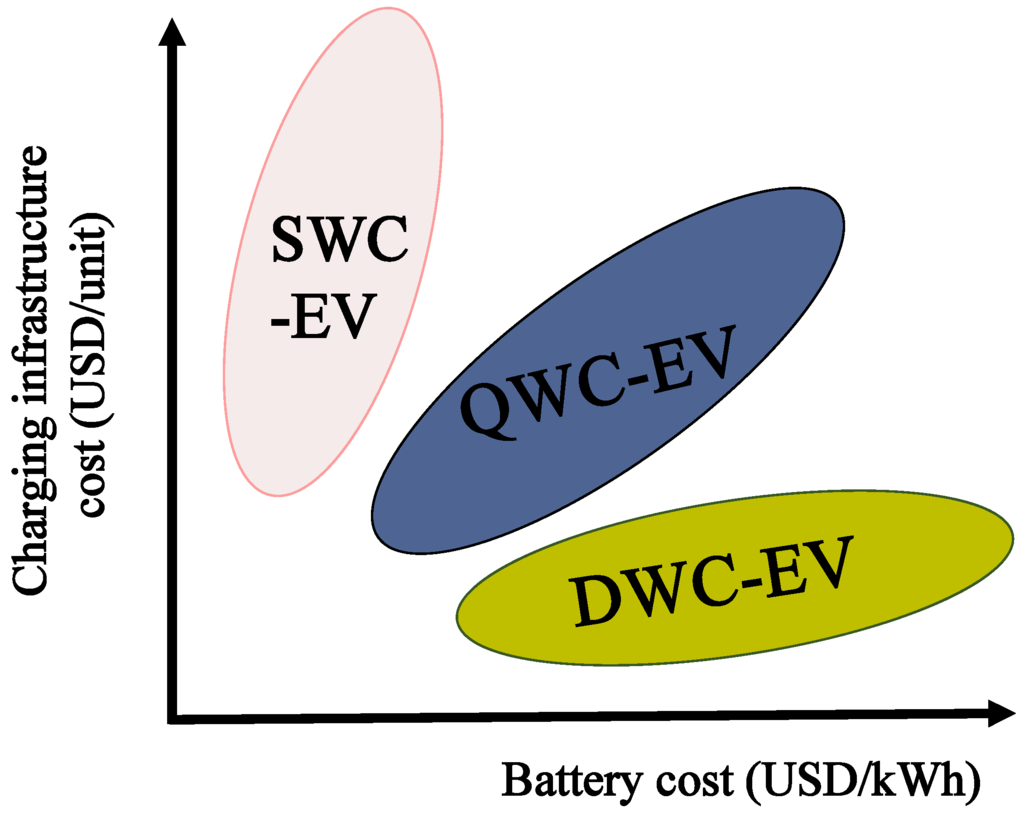
Figure 2.
Qualitative analysis of the economic benefits of different EV charging systems [6].
The cost comparison of different wireless charging systems is a significant part of the initial investment analysis. This type of comparison is important, not just because the costs of the chargers and required components are different for each type, but also because the type of charging system determines the cost of the batteries and the charging infrastructure. For example, consider a service route where 10 vehicles are circulating. Suppose that an SWC system is used for this service. Then, all 10 vehicles need a battery that is large enough to complete the required circulation. As a charger needs to be installed only at the base station for an SWC system, a larger expenditure must be made on the batteries than on the charger. Suppose that the QWC type is used instead. The cost of batteries can be reduced by installing chargers at the various bus stations. Further cost reduction on the batteries can be achieved if a DWC system is adopted. However, in these cases, the costs of the charging infrastructure will increase. This example clearly shows that depending on which type of wireless charging solution is used, the costs of the batteries and the charging infrastructure can radically change. If we consider that the combined costs of the batteries and the charging infrastructure account for a significant portion of the total investment in an EV-based transportation system, the decision on which type of wireless charging to use is critical [10].
Furthermore, analyzing the costs of QWC and DWC systems is complicated, as the tradeoff between allocations for battery capacity and infrastructure must be considered. One of the key decisions in deploying QWC or DWC EVs for a public transit system is choosing where to allocate the charging infrastructure along the bus lines. The charging infrastructure should be allocated to supply sufficient electric power to the vehicles, and the location of the charging stations determines how frequently the vehicles are charged. This allocation should also be considered relative to the battery size. It should be noted that the battery capacity determines the maximum amount of energy that can be stored. If the battery capacity is low, the per-charging distance (or the maximum distance that the EV can travel on a fully-charged battery) will be short. Consequently, more frequent charging is required for smaller batteries, and a greater density of charging stations must be distributed along the routes. Therefore, in planning for a QWC or DWC-based transit system, the issue of charging infrastructure allocation should be considered together with the size of the batteries.
To deal with the complicated nature of initial investments, we use optimization models to evaluate the minimum initial investments required for QWC- and DWC-based solutions. These optimization models evaluate the optimal allocation of the charging stations in relation to battery capacity for the minimum total investment. For our analysis, we draw on two different routing scenarios and apply actual data collected from the OLEV systems currently operating on the KAIST campus and in Gumi City. Although the OLEV at Gumi City is primarily designed for DWC, the data collected from this system, such as the amount of energy consumption, the velocity trajectories, the road gradients and other operational data, can be used for the analysis of other types of charging systems. Moreover, as the options we consider all involve commercialized wireless charging EVs, credible cost figures can be used for the analysis.
We understand that the costs of ownership, lifetime cost analyses and any other return-on-investment analyses are important. However, the initial investment cost, which is the most basic cost-related analysis, needs to be assessed before any other investment and cost analyses. Therefore, the analysis proposed in this paper can be treated as the first step toward further investment and benefit analyses. It should also be noted that comparisons of costs for other classes of vehicles (such as an IC engine, hydrogen-fuel cell engine or any other alternative fuel vehicles) are beyond the scope of this paper. The proposed analysis seeks to answer the following questions:
- What is the cost configuration by which one type of wireless charging solution is more competitive than the other solutions?
- On what economic scale is each type of transit system most cost-effective?
The remainder of this paper is organized as follows. Section 2 presents the related literature on the recent development of wireless charging technology, on the investment cost analysis of alternative fuel vehicles and on the system design issues for EV charging stations. This overview also shows how our research differs from previous studies. Section 3 explains the system boundaries of this analysis and the data used. Our analysis uses data collected from the OLEV systems in the KAIST campus and Gumi City operations. The operational conditions for these systems are provided, so that readers can better understand the basis of the initial analysis. Section 4 describes the model for determining the minimum investment cost for each type of EV and introduces the optimization models. Section 5 presents the results of the analysis, comparing the investment costs among the three types of wireless charging systems. The cost structure conditions that are beneficial for each type of wireless charging are discussed. Finally, Section 6 concludes the analysis and suggests how this research can be extended in the future.
2. Background and Literature Review
2.1. Wireless Charging of Electric Vehicles and Its Commercialization
Since the earliest concept of the wireless-charging EV was suggested by Bolger in 1978 [11], significant technological accomplishments have been made in developing the wireless EV. The progress of this technology is explored in [12,13,14]. One of the recently-commercialized wireless-charging EVs developed by KAIST is the OLEV [15]. The OLEV system is specified as a DWC type, and detailed technical descriptions of the OLEV are found in [7,16,17,18,19,20].
2.2. Current Progress in Wireless-Charging EVs
Major automotive manufacturers are also currently developing electric vehicles that utilize wireless power transfer. More detailed information on current developments can be found in [7,21]. Several metropolitan cities around the world are considering wireless charging EVs as sustainable public transportation systems. In 2013, Gumi City, South Korea, conducted a trial deployment of two DWC buses, and there are plans for expansion to more service lines in the city. Sejong City, which is the new government capital city of South Korea, plans to deploy a DWC-based public transportation system to serve existing bus lines [22]. Other commercially-available DWC-EVs include those developed at Auckland University [23] and at Utah University [24]. Furthermore, the European project UNPLUGGEDhas recently developed and constructed an inductive quick-charging station for electric vehicles. This project has investigated how the use of inductive charging in urban environments can improve the convenience and sustainability of electric mobility [25].
2.3. Charging Station Allocation for DWC
This paper deals with the optimized allocation of EV-charging infrastructure. For conventional electric vehicles, the charging infrastructure is the charging station. The problems of optimal allocation for such stations have been addressed in the context of location problems and network flow problems. Recent research on these topics can be found in [26,27]. However, the problems of allocating charging stations and of allocation for DWC infrastructure are fundamentally different. Most previous studies of the charging station allocation problem consider stations as fixed points at which vehicles halt to recharge. However, as DWC-EVs can be charged while in motion, power transmitters need to be installed where the vehicles are operating. Moreover, for a DWC system, the amount of charging required is a function of vehicle velocity. In the conventional station allocation problem, vehicle velocity is not related to the allocation. Therefore, the station allocation problem for conventional EVs has limited relevance to a DWC system.
3. Operations and Scenarios
In this section, we present the EV types and the scenarios used for our initial investment cost analysis. Note that this analysis focuses on public transportation services using EVs. For our analysis, it is assumed that all of the transportation systems operate under the following conditions:
- Identical multiple EVs serve the passengers.
- EVs circulate on a predefined service route, and one complete circulation of the route is called a service.
- EVs start and finish each service at a station called the base station.
- Once an EV completes a service, it remains idle at the base station for a certain amount of time, which we call the resting time.
- EVs follow a regulated velocity.
These conditions are not very different from the operational rules of the existing public transit systems for any urban environment. These conditions are also aligned with the rules used in the operations of the KAIST OLEVs at KAIST campus and at Gumi City, on which the analysis is based.
3.1. Characteristics of EV Types
The initial investment costs for three types of EVs are compared. Their charging methods, places and cost structures are described in Table 1. For SWC, the vehicles are charged at the base station, as shown in the first panel in Figure 3. For QWC, depicted in the second panel in Figure 3, the vehicle is charged while it is stationary or in the stop-and-go mode at bus stations. In our analysis, it is assumed that the chargers are installed only at the bus stops and the base station. Identical chargers are installed at the stations. The major investment cost of a QWC-based system consists of the cost of the batteries and the chargers embedded in the bus stations. For DWC, as illustrated in the third panel in Figure 3, charging is done while the vehicle is in motion. Therefore, the charging infrastructure involves “power tracks” that are installed anywhere on the route. The major cost consists of the expense for the batteries and the power tracks. The cost of the power track is broken down into fixed and variable costs. As the cost of the power track is determined by its length, the variable cost indicates the cost of the track per unit of length. Regardless of the track length, one inverter unit (inverter and other components connecting the inverter, power tracks and power grid) needs to be installed for each route. This cost is referred to as the fixed cost.

Table 1.
Characteristics of each EV type (based on the current OLEV system [6]).
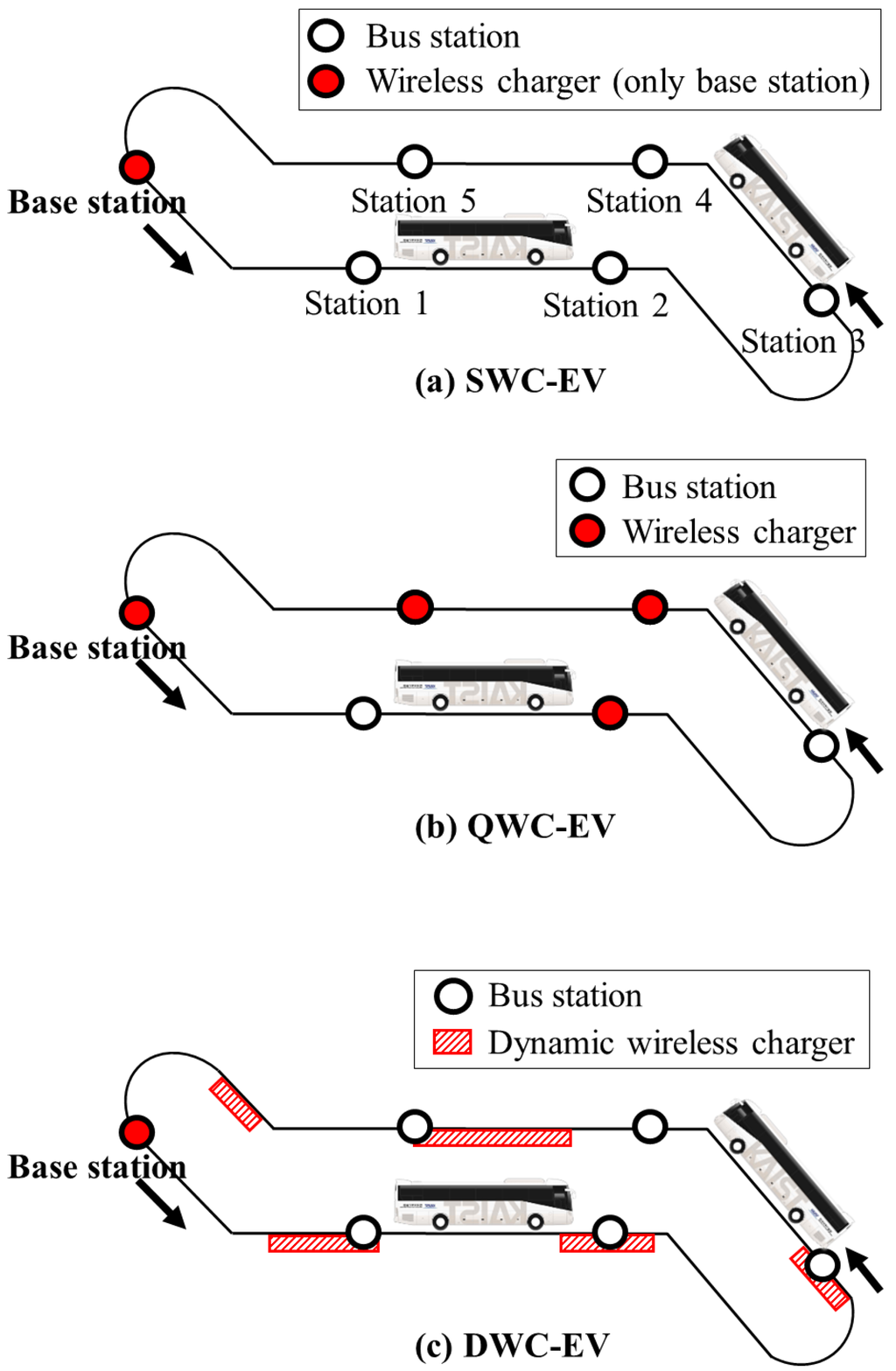
Figure 3.
Charging allocation properties for each type of EV. (a) SWC-EV; (d) QWC-EV; (c) DWC-EV.
3.2. Analysis scenarios
For the initial cost analysis, two scenarios are analyzed—the KAIST campus shuttle and Gumi City urban transit. As the KAIST OLEVs are currently operating for the KAIST campus shuttle and an urban transit route in Gumi City, realistic cost figures and actual data can be utilized in the analysis. For the sake of convenience, the KAIST campus shuttle and the Gumi City urban transit are characterized as “short” and “medium” routing services, respectively, as indicated in Table 2. The KAIST campus route illustrated in Figure 4 circulates a 3.374-km route with eight bus stops. This KAIST shuttle case may represent a transit service for short-travel distances with frequent stops within limited areas, such as theme parks, school bus routes or in-town transit services. For the Gumi City case, as shown in Figure 5, the 34.448-km service route connects the east and west ends of the city through the city center, with 23 stops and a base station.

Table 2.
Bus category according to service distance.
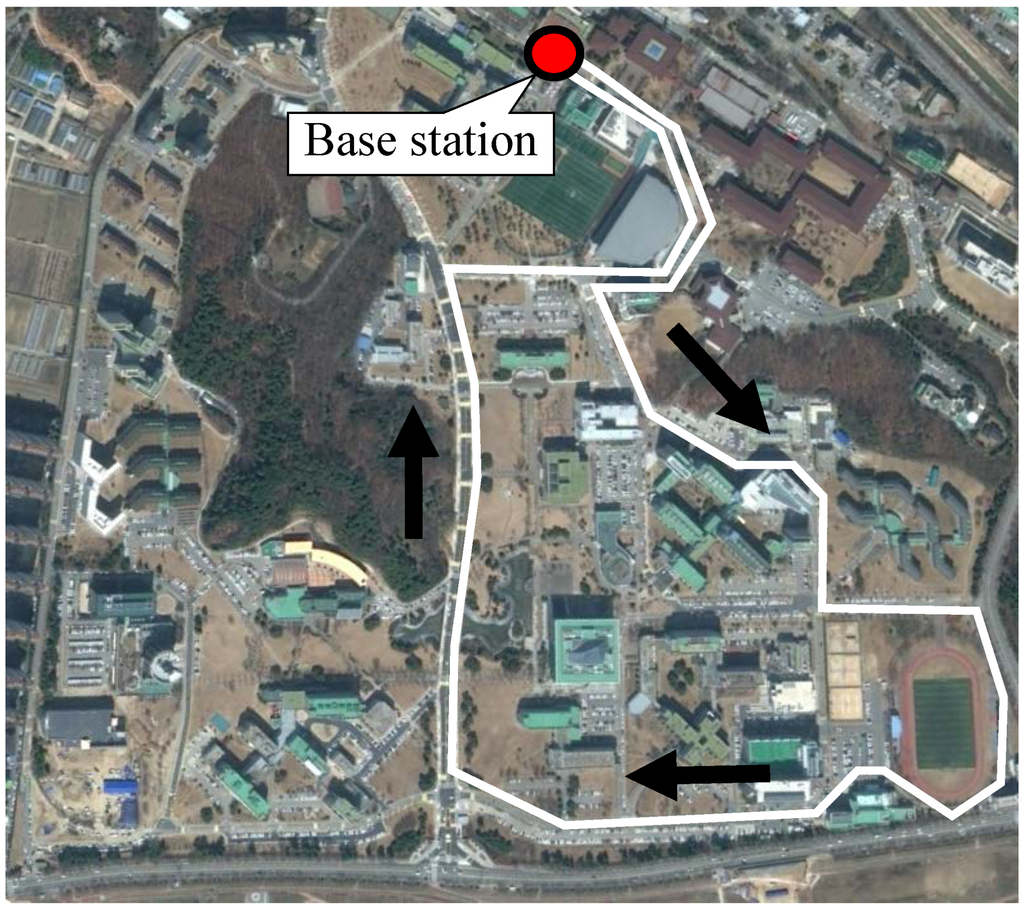
Figure 4.
The OLEV shuttle route on the KAIST campus.
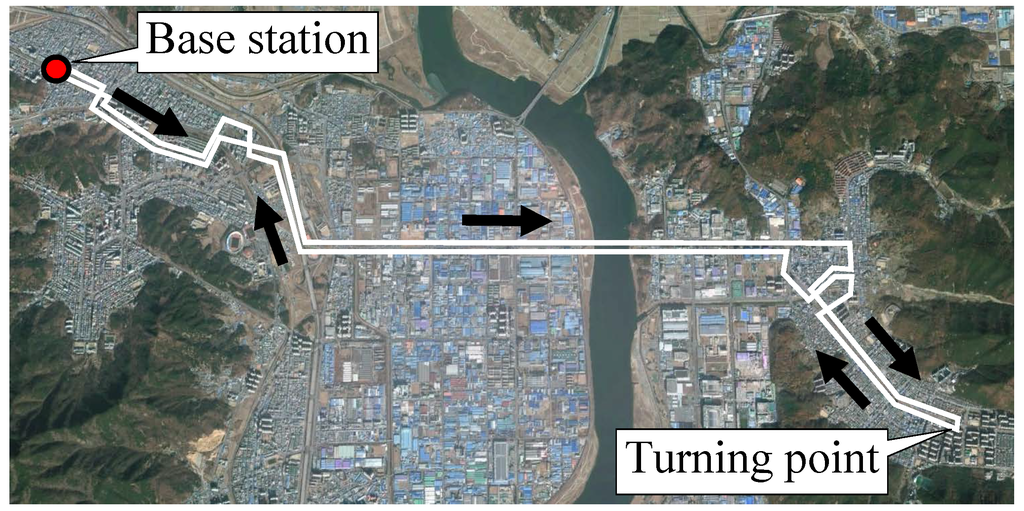
Figure 5.
The OLEV service route in Gumi City.
4. Economic System Design Method
In this section, we provide the method for analyzing the initial investment for each type of EV system. In particular, this analysis is focused on the energy logistics cost in transportation, which is defined as the cost of transferring and storing the energy needed to operate the transportation system. In the domain of EVs for public transit systems, the energy transfer and storage functions are performed by the charging infrastructure and the batteries, respectively. Therefore, the total cost includes the costs of the charging infrastructure and the batteries. In our analysis, we compare the energy logistics cost among the different types of wireless charging EV. Note that the energy logistics cost excludes the cost of generating electric energy and installing the energy grid. The system boundary of the cost analysis is described in Figure 6. We focus on the energy logistics cost in the initial cost analysis for the following reasons.
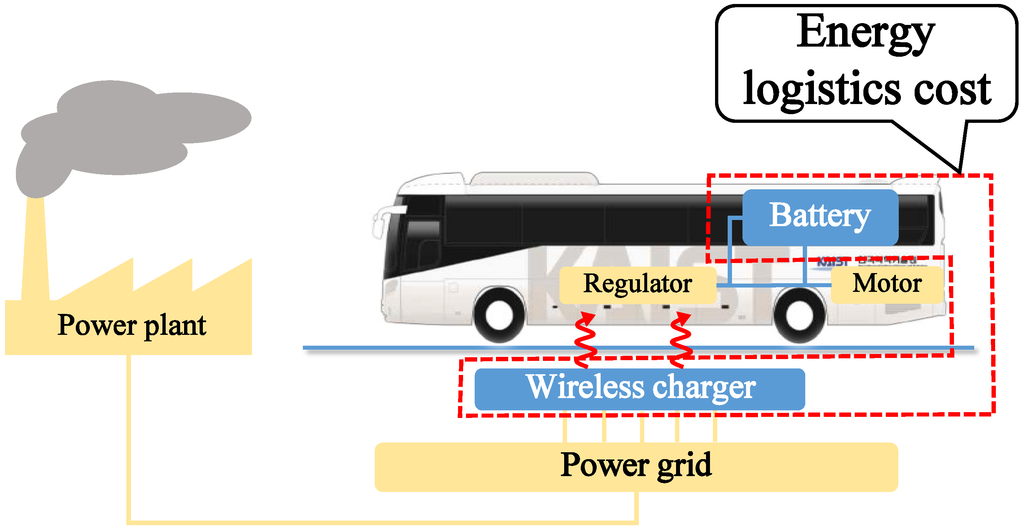
Figure 6.
System boundary of the analysis.
The initial investment cost for an EV-based transit system is mainly composed of the cost of a fleet of vehicles and the cost of the charging infrastructure. The cost of the vehicles further breaks down into the costs of the batteries, the vehicle units and the other charging components. Note that the goal of our analysis is to compare the initial costs of different EV types for each scenario, rather than to evaluate the absolute investment amount. We assume that each type of EV uses the same type of vehicle units, and therefore, we exclude the vehicle unit cost. We then characterize the costs of the batteries and the charging infrastructure as the “energy logistics cost.” Therefore, analyzing the breakdown of costs within the energy logistics cost is adequate for understanding the different investment cost structures among the different types of EVs. Moreover, we should note that the energy logistics cost (including the battery and charging infrastructure costs) accounts for more than 80% of the total cost of an EV-based transit system [6]. Therefore, understanding the cost structure of the energy logistics is critical for deciding on investments in EV-based transit systems.
We define as the total energy logistics cost for one service route operated with EVs of s type. Let be the cost function of energy storage in the vehicles for type s, where . This cost is mainly determined by the battery size in the vehicle and the number of vehicles. Let be the cost function of energy transfer for type s. This cost is mainly a function of the sum of the charging units. Then, the total energy logistics cost can be approximated as:
Our analysis is concerned with evaluating for each type of EV for a given route. That is, for each type s, we try to find the minimum cost of while satisfying the service requirement. Specifically, the service requirement is that the EVs operate with sufficient energy in their batteries. Therefore, for each type s, the cost analysis seeks the minimum investment cost needed to complete the service, such that:
That is, the optimization in Equation (2) involves finding the least amount of investment needed for a service using each type of EV.
The constraint in Equation (2) is directly related to the size of the battery. Let be the size of the battery for type s. Let and be the maximum and the minimum allowable energy levels in the battery, respectively. These limits are usually provided by the battery manufacturers to help guarantee the required battery life cycle, as the battery’s life is seriously degraded if it is overcharged or over-depleted. Therefore, the required energy levels are defined as:
where and are the proportional coefficients that present the upper and lower limits, respectively. These coefficients are provided by the battery manufacturers (in our analysis, and are used). The energy level should be within the lower and upper limits, as shown in Figure 7. We assume that the cost of the battery is linearly proportional to the energy capacity of the battery. This assumption is reasonable, as an EV battery pack consists of multiple battery cells, and the capacity is determined by the number of cells contained in the battery pack. This approach to linear cost approximation is also widely used in the industry [28].
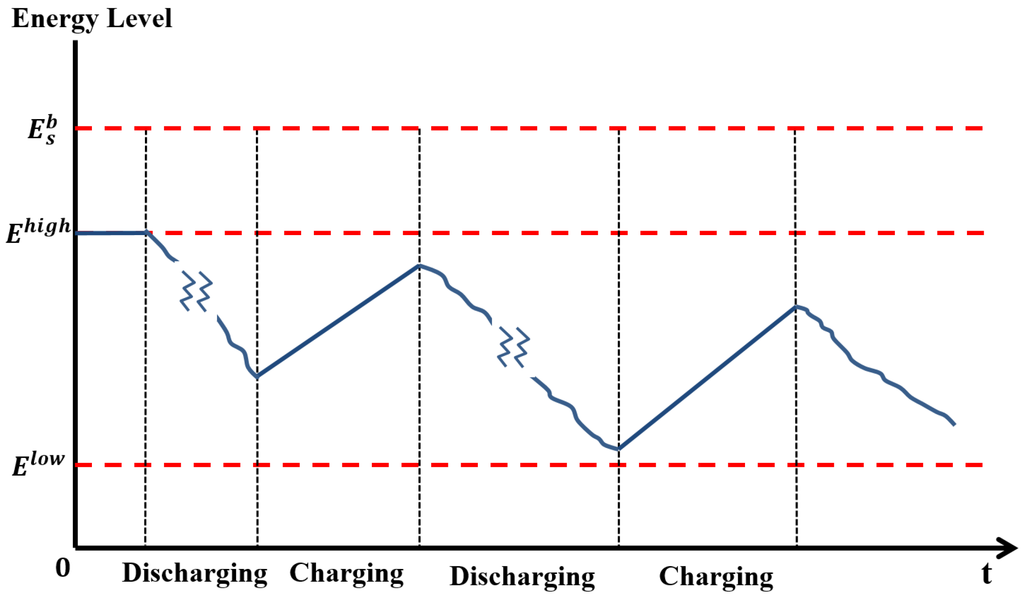
Figure 7.
Energy level of the battery and its boundaries.
4.1. Model for Stationary Wireless Charging
For the SWC, the charger can be installed only at the base station where the vehicles rest between services. Given that there is only one place that a vehicle can charge, the minimum energy logistics cost in Equation (2) can be achieved by having the minimum battery size needed to complete a service. The amount of energy needed to complete a service (which is a decision variable) is denoted by . The size of the battery for SWC is denoted by . We define k as the number of EVs in a given route and as the battery cost per unit of energy capacity (cost/kWh) for the SWC system. Let be the number of stationary wireless chargers in the base station and be the unit cost per charger. Then, the objective function becomes . Then, the optimization in Equation (2) for the SWC EV is specified as follows:
Note that once k and are given, this function monotonically increases with . Therefore, the minimum cost is achieved when .
4.2. Model for Quasi-Dynamic Wireless Charging
The QWC system charges the battery when the vehicle is stationary. In this analysis, the QWC-EVs are charged only at the bus stops and base station, where the vehicles make complete stops. Therefore, in the cost analysis of a QWC system, the primary issue is to identify where to install the wireless chargers at minimum cost. This problem is not as straightforward as in the SWC case, as the allocation of the chargers should be considered along with the amounts of energy consumption and depletion between the stations in a service. The optimization problem in Equation (2) becomes a problem of identifying the minimum number of stations that need to have a charger for satisfying the operating condition. Note that this optimization problem includes the base station as a place to install a charger. As a vehicle is idle for some time at the base station, this station is the best candidate to install the charger. We assume that a vehicle rests long enough to fully charge the battery () at the base station. Using the base station as the reference point, any other point along the route is described by its travel distance x from the base station. Let L be the total distance of the route. Then, each bus begins its trip at and completes it at . As the route is a closed loop, the starting point (where ) and the end point (where ) both indicate the base station. Let represent a station, where . The sequence of the station index i is such that , where is the distance of the i-th station from the base station. Station is the base station, which is the starting point of each trip. The bus covers this route and returns to the base station. Two types of decision variables are examined in this case. One type is , which is defined as a binary decision variable that indicates whether a charger is installed at . The other type is , which is the battery size. These decision variables are described in Figure 8. Let be the energy level of the battery at the moment when the bus leaves station . We define the amount of energy consumption from to as . We define as the amount of energy supplied at , if a charger is installed at . Then, the following energy balance equation can be constructed.
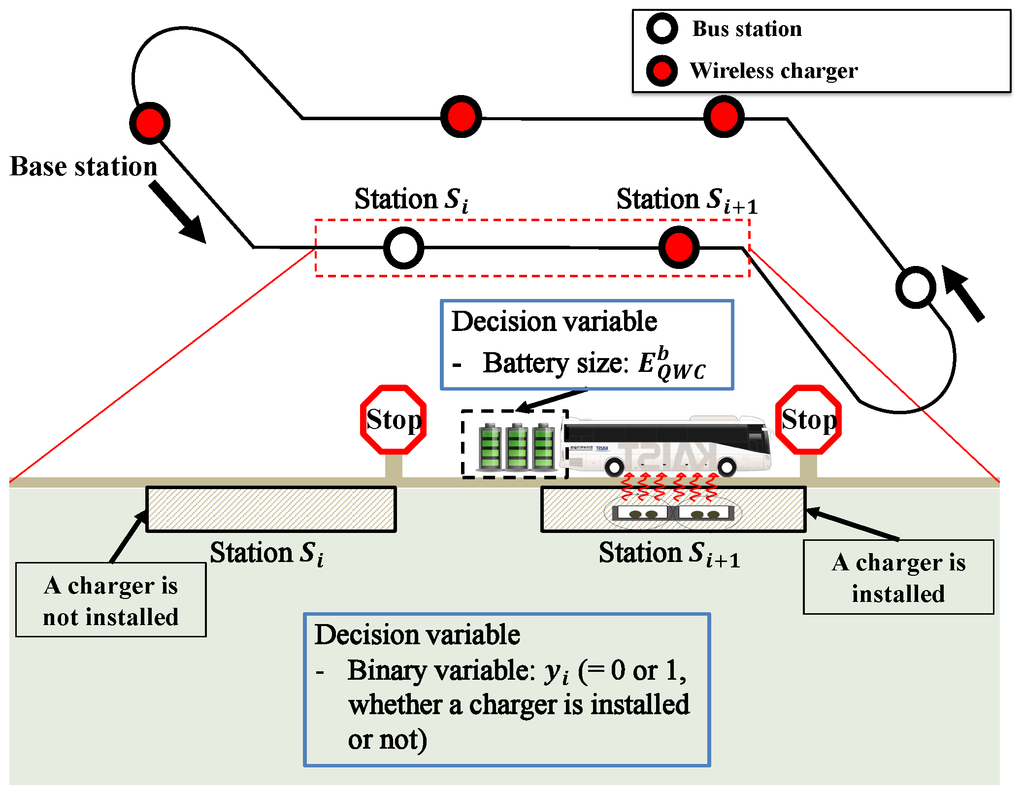
Figure 8.
Decision variables for the system design of QWC-EVs.
The energy level should be between and , such that:
Assume that there are k EVs, and let be the battery cost coefficient for QWC. Then, the energy storage cost is . Suppose that is the cost to install a charger at a bus station. Then, the optimization for QWC is constructed as:
Notice that is defined in Equation (3). Furthermore, note that the optimization problem involves a form of mixed-integer programming, and it can be solved with standard commercial software, such as IBM-CPLEX for small- and medium-sized systems, like those of the Gumi City and KAIST shuttle cases.
4.3. Model for Dynamic Wireless Charging
Notice that the cost optimization model presented for a DWC system is based on the previous study in [29]. This subsection summarizes the model described in that study. For DWC, the cost analysis is more complicated than that for the first two types. As the charging can be done while the vehicle is in motion, we should consider both the vehicle speed and the road gradient when determining the allocation of chargers along the route. Due to the behavior of dynamic charging, the parameters should be described as functions of time. We let t be the elapsed time that an EV has traveled from the base station, and let be the amount of energy at t. First we define as the energy consumption from the battery at travel time t. Over the course of a given route, the value can be estimated by the analytical vehicle dynamics model, by a simulation of a vehicle dynamic method or by experiments on the actual vehicle [1]. The detailed electromechanical configuration and power dynamics model of the EV are found in [1,30]. We define as the energy supply at time t, when the vehicle is on the power track installed along the road. In the DWC system, the vehicle will be in one of the following states:
- : moving where no power track is installed;
- : moving where a power track is installed;
In , the energy in the battery is being depleted while the vehicle operates. Therefore, the battery’s energy level, , decreases with a power demand of . In , changes with a rate of . Then, the rate of charge for each state can be expressed as follows:
In a DWC system, the battery size and power track allocation are the two sets of decision variables. Again, each vehicle in the system has an identical battery size, which is denoted by . We let the base station be the reference point, and any point can be expressed by the travel displacement x away from the base station. Then, the location of the i-th power track is represented as both its start point and end point . We denote the number of power tracks as M, which is one of the decision variables. Then, all of the power tracks can be expressed by ordered pairs of the start and end points () for . The decision variables for a DWC system are shown in Figure 9. Note that the locations of power tracks are expressed by the distance variables with their start and end points. However, the amount of charging on each power track depends on the elapsed time spent on that power track. Therefore, the relationship among the displacement variable and the temporal variable has to be defined. We define a function to represent the relation between the displacement variables and the temporal variables, such that:
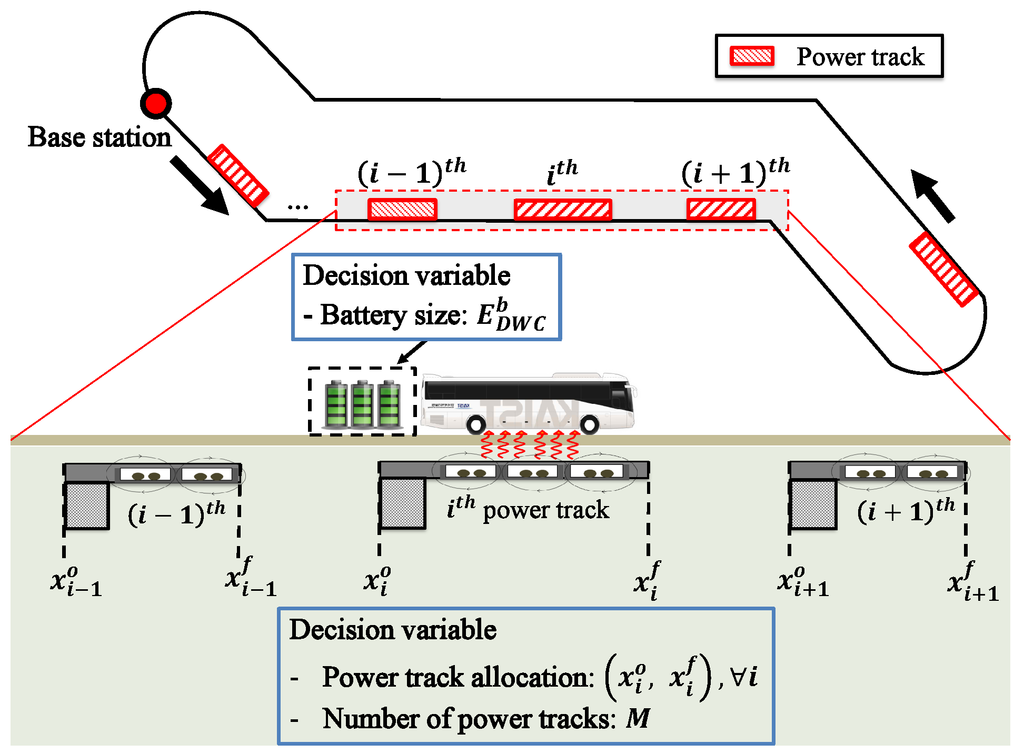
Figure 9.
Decision variables for the system design of DWC-EVs.
We expect that the vehicle will follow the regulated speed trajectory while in service. If we know the travel time starting from the base station (reference point), then we can easily evaluate the travel distance at the elapsed time. As is a monotonically-increasing function, an inverse function is presented as follows:
With Equation (14), the location of the i-th power track, (), can be restated as time variables, (, ), which indicate the times at which the vehicle enters and leaves the i-th power track. Note that the energy logistics cost for DWC includes the battery and power track installation costs. We break the power track cost into the variable and fixed costs. The variable cost is a function of the power track lengths. The fixed construction and materials costs can also vary, depending on the power track length. The length of each power track is calculated by the distance between its start and end points, . Then, the total length of the power tracks is . Regardless of the length of the power track, there is a fixed cost to install one unit of power track. This cost involves the installation of an inverter and other costs for connecting the inverter to the grid. We define this cost as the fixed cost. Suppose that there are k vehicles in the system. Then, the energy logistics cost is presented as follows:
The optimization problem aims to minimize the energy logistics cost by finding the optimal decision variables , , … and .
The relationships between and are described in Equation (3). The constraints in Equations (17)–(19) represent the battery energy state constraints. The relations between displacement and the temporal variables are presented in Equation (20). The constraints for installing the power tracks are defined in Equations (21)–(22). The decision variables and their boundary conditions are defined in Equations (23)–(26). Note that the algorithm for this problem can be found in [29]. One example result of the optimization problem is shown in Figure 10 and Table 3.
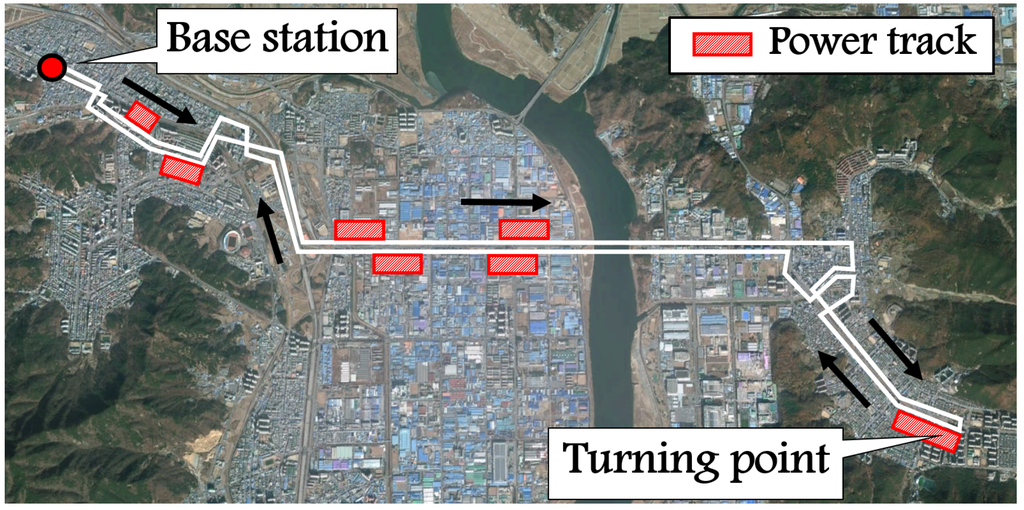
Figure 10.
An example of the optimization problem for the Gumi City case (for ).

Table 3.
Summary of the optimization results for the Gumi City case (for ).
5. Analysis and Discussion
5.1. Cost Function for Sensitivity Analysis
The first numerical analysis investigates how the initial investment cost varies as the costs of the charging infrastructure and the batteries change. The goal of this analysis is to understand which type of EV is competitive at which cost structure. The different battery and infrastructure cost scenario analyses are performed to solve the following issue. First, there are many different ranges of battery costs in the market, as shown in Table 4. The cost of the battery depends on the type of battery and the battery management/configuration system adopted in the EV. Therefore, instead of using an absolute battery cost, we use various battery cost scenarios. For the same reason, we also consider various infrastructure cost scenarios. As shown in Figure 1, the infrastructure for wireless charging requires costs for construction, which is variable depending on the geographical region concerned. In addition, most parts used in the wireless charging infrastructure are still custom-made, and therefore, their costs depend heavily on the local labor costs. If the parts are mass produced, a significant change in cost is expected. As a result, due to the anticipated cost fluctuations and variations, it is reasonable to perform various cost scenarios in this analysis. The analysis is performed by changing the parameters in the optimization models. The first parameter varied is the battery coefficient. In the optimization models, the objective functions in Equations (4), (6) and (16) have the cost coefficient . We try to understand which types of EV are cost effective as the battery cost changes by varying the battery coefficients. For this cost comparison, we assume that the same types of batteries, or batteries from the same manufacturer, are used across the different types of EVs. Therefore, the battery coefficients and can be expressed as a single battery coefficient, , such that:

Table 4.
Battery price [31,32,33,34].
Unlike the battery cost variation, it is not a straight-forward procedure to define the unified infrastructure cost. Note that the charging methods are different, and the costs of the charging infrastructure for each type of EV are determined by different parameters. Therefore, we should clarify that defining the infrastructure cost should come first. The following assumptions are made in defining a unified infrastructure cost parameter across the different types of EV:
- The costs of installing a charger at a base station for SWC and installing a wireless charger at a bus station for QWC are identical.
- For the DWC, the fixed cost of installing a power track is identical to that of installing one wireless charger unit for QWC.
- For the DWC, the variable cost coefficient of a power track is of the fixed cost.
- All of the buses follow their operation schedule, and no randomness is considered in arrival times.
- For the SWC case, is evaluated based on the following equation:which means that the battery charging time is divided by the inter-arrival time, and the result is rounded up to the nearest integer of the greater-than number.
According to the price range for each charger type described in Table 1, it is reasonable to make the above-given assumptions. For the third assumption, the variable costs of installing the power tracks are expressed in terms of the fixed cost. That is, installing a 1 m-long power track is of the fixed cost. This α value is approximated as 100 in relation to the market data. As indicated in Table 1, the power transmitter (variable cost) is between $400 and $600/m, while the inverter cost (fixed cost) is between $50,000 and $60,000 per unit. Therefore, installing a 1m-long power track is around 1/100 of the fixed cost. Then, with the charging infrastructure cost denoted by , the objective function for each EV type is redefined as follows:
For the objective functions in Equations (28)–(30), the initial investment costs for different types of EV can be evaluated with different scenarios for the battery cost coefficient () and the infrastructure cost coefficient (). For our convenience, we define , , as the minimum investment costs for the SWC, QWC and DWC systems, given and .
Cases with different numbers of EVs () are evaluated. We define the as the minimum investment cost across the different types of EV as follows.
5.2. Cost Sensitivity Analysis
Figure 11 shows the three dimensional bar graphs of for different values of and for the Gumi City case. For each graph, the x- and y-axes represent the battery cost coefficient () and the charging infrastructure cost efficiency (), respectively. The z-axis represents the minimum investment cost , which shows the most economical EV type for the corresponding battery and infrastructure cost coefficients. The numerical values presented in Figure 11 are shown in the Appendix in the supplementary document. In each graph, white bars are shown if the most economical solution is the SWC type. The gray and black bars represent cases where the most economical solutions are QWC and DWC, respectively. As illustrated, when the cost of the battery is high and the infrastructure cost is low, the DWC type is the most competitive solution. On the contrary, if the infrastructure cost is high and the battery cost is low, the SWC type is more competitive. This result is well aligned with the qualitative speculation illustrated in Figure 2. As the battery cost becomes more expensive (given that the infrastructure cost remains the same), the DWC type becomes more economical, as the DWC needs a relatively smaller battery than the SWC type. However, if the battery cost remains the same, but the infrastructure cost increases, the SWC type becomes more attractive, as SWC requires the least expensive charging infrastructure among the three types. As expected, the economical space for QWC is located between the SWC and DWC spaces. For comparison among the different k’s, as the number of EVs in the fleet gets larger, the DWC type grows more favorable. In this case, the total cost of the batteries for the vehicles increases as the cost-benefit of the charging infrastructure gets larger, because the charging infrastructure is shared with a greater number of vehicles. Figure 12 shows a similar analysis performed for the KAIST shuttle case. The numerical values are presented in the Appendix in the supplementary document. For most of the cost scenarios, the SWC type is the most economical, because the service route is short and a small battery can hold enough power to complete a service without recharging. Interestingly, the DWC type becomes cost-effective when the number of EVs is more than 19. However, the QWC type is never shown as the most competitive solution. In practice, it may not make sense to run 19 or more EVs for such a short route (note that as mentioned earlier, the KAIST OLEV on the KAIST campus was installed mainly to validate the reliability of the system). Interestingly, some researchers argue that DWC is the more economical solution for short routing services, such as those for the KAIST campus or for trolleys in theme parks [6]. However, with the results we obtain, we do not see any benefit from DWC with the current cost structure. Rather, DWC is a more economical solution for medium-range service, as in the Gumi City case. We discuss this issue in the next section.
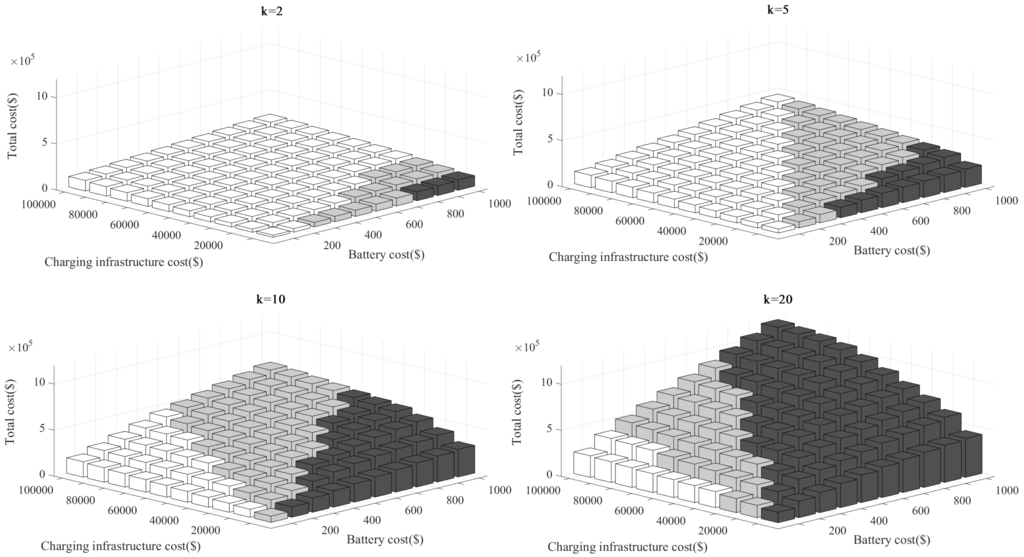
Figure 11.
Cost comparison of EV types for the Gumi case (white region: SWC is competitive; gray region: QWC is competitive; black region: DWC is competitive).
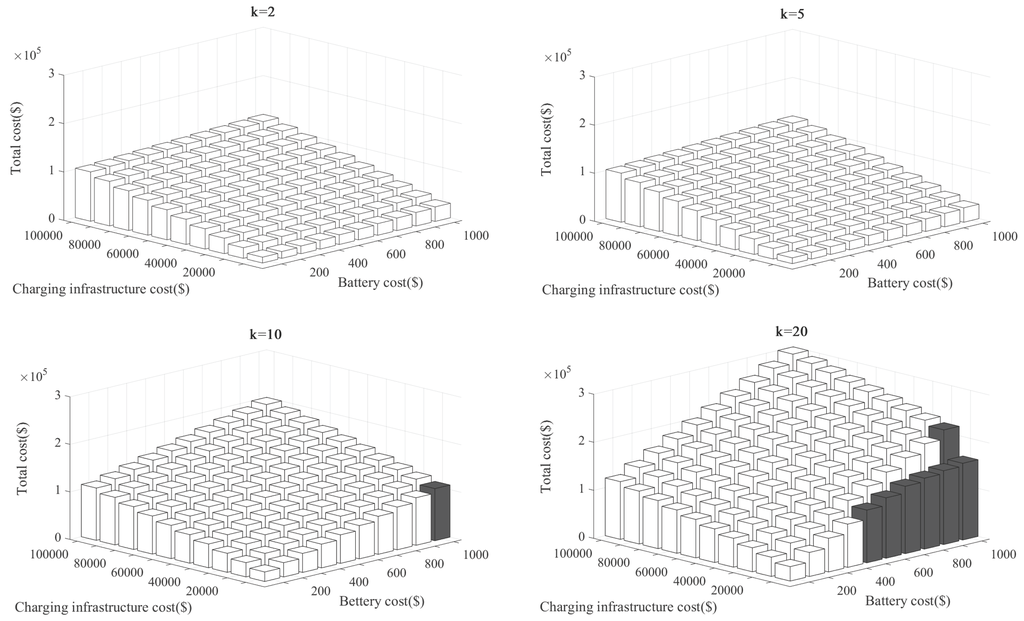
Figure 12.
Cost comparison of EV types for the KAIST case (white region: SWC is competitive; gray region: QWC is competitive; black region: DWC is competitive).
5.3. Sensitivity Analysis for k
Figure 13 analyzes the economic fleet size with the current cost structure. The x- and y-axes represent the number of vehicles and the total investment cost, respectively, for the Gumi City case. In other words, the minimum cost corresponding to k for each EV type is plotted.
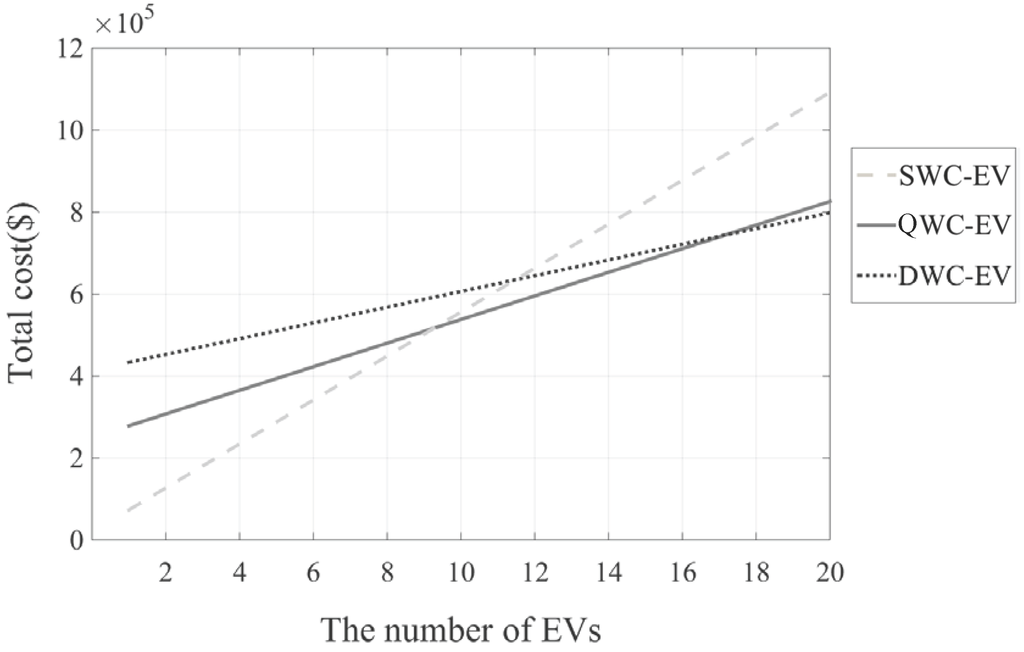
Figure 13.
Economic fleet-scale analysis for the Gumi City case.
First, the cost of SWC increases linearly. That is, the total cost of the system is proportional to the total size of the battery. For SWC under this assumption, the charger is installed only at the base station, and this cost is fixed even if the number of EVs increases. As a result, the energy logistics cost is linearly proportional to k. Note that in practice, more charging capacity needs to be added at the base station for an SWC-type system to avoid unnecessary delays as vehicles wait to be charged. Therefore, in reality, an additional charger needs to be installed for every certain number of k. However, even if this rule for additional chargers is applied in the analysis, the linear trend to k still remains.
For the DWC case in Figure 13, the rate of cost increase is relatively smaller than that for the SWC case. For a DWC system, a growing number of EVs serves to increase optimization, so that smaller batteries are more economical. Then, through using smaller batteries, the rate of change in cost against k decreases. Note that when and , the cost lines for SWC-QWC and for QWC-DWC cross, respectively. That is, if k is less than nine, SWC is competitive; if k is between nine and 17, QWC is competitive; and if k is greater than 17, DWC is the most economical. The lines with lower costs (SWC for , QWC for and DWC for ) can be considered a lower bound for the wireless charging EV regardless of the charging type.
6. Discussion and Conclusions
In this paper, we present an initial investment cost analysis of the wireless charging-based mass transportation system by comparing the costs of installing the SWC, QWC and DWC systems. To provide a creditable cost analysis for the emerging transportation system, our analysis is based on two commercialized wireless-charging public transportation systems—the KAIST shuttle and Gumi City OLEV routes. We try to use the actual cost figures from these two commercialized systems and to provide engineers and policy makers with realistic insights into the deployment and economic operations of these systems. For the initial investment analysis, we introduce optimization-based models for three types of EVs. These optimization models are developed to deal with the complex tradeoffs between the costs of battery size and of charging infrastructure. The total battery cost for a fleet of vehicles and the infrastructure cost for a route make up a significant portion of the total investment required for an EV-based transportation system. Therefore, analyzing this cost tradeoff is critical. Our optimization model estimates the minimum initial investment cost for each type of EV for a given service route. The numerical analysis, conducted with the proposed optimization models, quantitatively validates the qualitative cost-benefit analysis for each type of EV as proposed by an earlier study. In other words, we show in numeric terms that a DWC system is beneficial when the battery costs are high, but the costs of charging infrastructure are low. If the cost structure is the opposite, SWC is more beneficial. The cost-benefit outcome of a QWC system is somewhere between that of the DWC and SWC systems. We also show numerically that DWC is not economical for a short distance service, such as the KAIST shuttle system. This finding somewhat contradicts previous arguments by some DWC proponents, who claim that DWC is beneficial for short-range transportation systems. We speculate that these proponents have believed that short-range EVs do not require a significant investment for charging infrastructure. Given the fact that wireless charging infrastructure is more expensive than the conventional plug-in chargers, a short-range service that requires only a limited wireless charging infrastructure might be believed economical. However, these proponents underestimate the issue of battery cost. The benefit of DWC-type EVs is that they are able to operate with smaller batteries even for long-distance travel. This benefit cannot be utilized if the service distance is short. We also show that there is a minimum fleet size needed for DWC systems at current cost figures. For the Gumi City case, a DWC fleet needs at least 18 vehicles to be competitive against the SWC- or QWC-type EVs. We understand that the current cost figures for DWC are subject to change, as DWC is still in the early stages of commercialization. For example, most of the wireless charging components in the OLEV are custom made, as there is no standardization of the parts and components. We understand that there is an active discussion toward standardizing these parts and components. If such parts are made in a mass production process, DWC systems will become more competitive.
Figure 14 shows a qualitative analysis of the cost trend for the battery-infrastructure cost space based on the finding in the cost sensitivity analysis in the previous section. Note that DWC systems may not be competitive with the SWC or QWC types due to the currently high costs of infrastructure or may not be competitive unless the systems involve greater numbers of EVs. However, considering the past and current trends in technology development, we suggest the movements in cost as depicted in a vector of Figure 14. The rate of the cost decline in batteries has been very sluggish for the last several decades. However, there is a significant opportunity for reducing the cost of the charging infrastructure. Note that as shown in the first panel of Figure 1, the parts for the power tracks are now custom made, and the construction is all done manually. If the parts are mass-produced and if standardized construction methods are introduced, significant cost reductions are expected. As a result, the vector representing the expected cost trend in Figure 14 shows that the costs of infrastructure are expected to decline faster than the costs of batteries. In this paper we provide only qualitative figures concerning the future cost vector. However, it would be interesting to investigate these trends quantitatively. We reserve this study for the future.
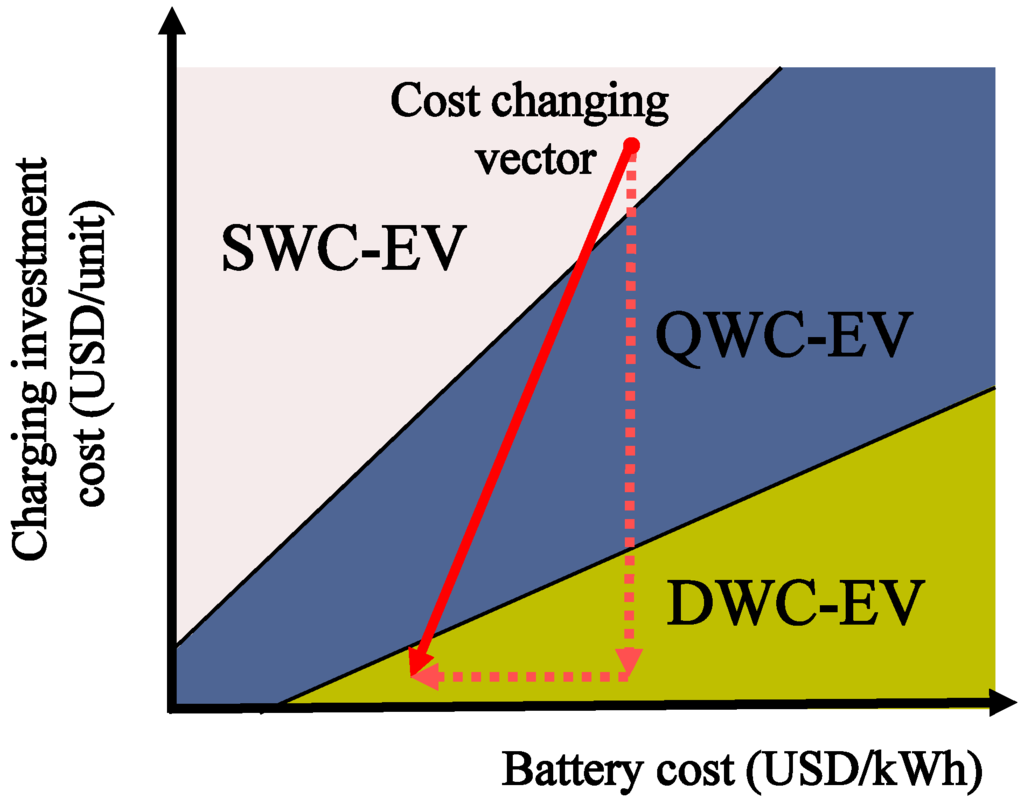
Figure 14.
Future cost trend.
This paper introduces mathematical models to analyze the initial investment costs for different types of EVs, as categorized by their methods of charging. This is the first paper to present a cost-benefit analysis comparing the DWC, QWC and SWC systems. We emphasize that the method of analysis and approach, as well as the structure and logics of the modeling used in this paper are not limited to the KAIST OLEV system and can be used for any type of charging system. The costs, which are the input values for the analysis, are the only KAIST OELV-specific figures.
We understand that there is still plenty of room for improvement in our method and analysis. First, our analysis does not consider the number of SWC chargers needed as the number of EVs increases. Due to the queue waiting issue, more chargers should be added to support additional EVs. Conventional queuing theory can be applied to determine the appropriate number of chargers for an SWC system. Furthermore, the analysis assumes that the cost of installing a QWC charger at a bus stop is identical to the fixed cost of a DWC charger. This, however, is a very broad approximation, and further investigation is needed to ascertain more accurate costs for QWC systems.
Another interesting analysis for future research is the investigation of the optimal speed profile for the DWC EV. Again, the amount of charging required directly depends on the speed of the vehicle on the charging infrastructure. We use the standard speed regulations in the analyses. Instead, it will be of interest to develop an economical speed profile for DWC. As preliminary research, we performed a sensitivity analysis of the velocity of the EV. Figure 15 shows the total cost response as the speed of the vehicle is reduced for the case when there are 20 vehicles in Gumi City under current market conditions.
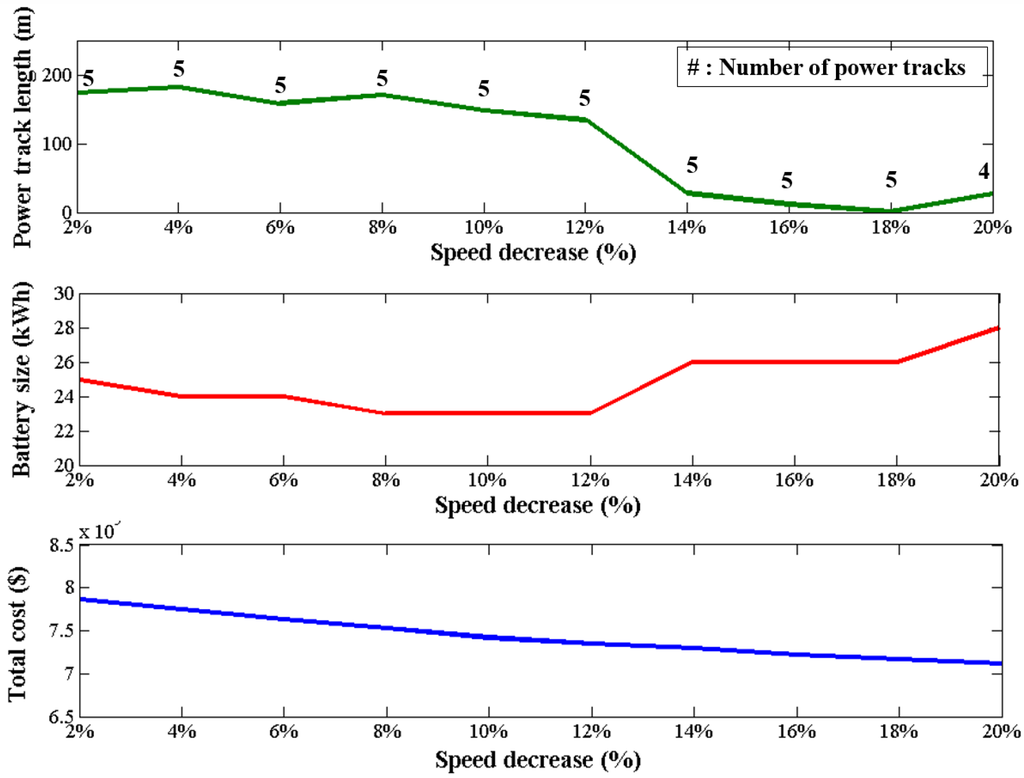
Figure 15.
Sensitivity analysis of the decrease in vehicle speed.
As the speed is reduced, the amount of charge per length is increased, and therefore, the total length of the power track is reduced, as shown in the first panel in Figure 15. Interestingly, the battery size increases slightly, as shown in the second panel. Overall, the total cost gradually drops as indicated in the third panel in Figure 15.
This analysis is intended to illustrate the idea that the total cost is sensitive to vehicle speed. With this idea, an optimal velocity profile can be developed. We reserve further investigation of this to a future study.
The level of the power supplied from the power tracks is also a critical factor in the allocation of the power track. That is, if the power level is higher, the overall power track length might be shorter. The proper power level requires extensive investigation, and we reserve this topic for future research.
There might be situations in which the battery level is lower than anticipated due to an unexpected traffic condition. One of the approaches for dealing with this type of uncertainty is to use stochastic optimization or robust optimization. However, these approaches are completely different from the optimization method proposed in this manuscript. Again, the approach provided in this paper has its own academic value, although the uncertainty is not exclusively addressed. This is the first paper to logically deal with the issue of the initial investment in different types of wireless charging EVs. As the first study in this area, the proposed deterministic optimization approach provides guidance and direction for more complicated research in the future.
Finally, in calculating the costs of DWC systems, we assume that the variable cost for one meter of power track is 1/100 of the fixed cost, which is based on the market data. However, this cost assumption could easily change if the construction operations and the manufacturing of parts are undertaken more systematically and on larger scales. A sensitivity analysis on this cost ratio might be another topic for future research. In this paper, we focus on initial cost analysis. With extensions of this method, further conventional economic analyses can be performed, such as calculations of return-on-investment, cost-benefit, cost-of-ownership and environmental impact analyses across various types of wireless charging systems. We also propose these topics for future research.
Supplementary Materials
The following are available online at www.mdpi.com/1996-1073/9/7/483/s1. Table S1: Numerical values of optimal costs for Gumi; Table S2: Numerical values of optimal costs for KAIST; Table S3: Battery size and number of power tracks for QWC case of Gumi; Table S4: Battery size, number of power tracks, and total track length for DWC case of Gumi; Table S5: Battery size and number of power tracks for QWC case of KAIST; Table S6: Battery size, number of power tracks, and total track length for DWC case of KAIST. Video S1: CNN-Report-KAIST-OLEV.
Acknowledgments
This research was supported by the Basic Science Research Program through the National Research Foundation of Korea (NRF), which is funded by the Ministry of Education, Science and Technology (NRF-2013R1A1A2009076).
Author Contributions
Young Jae Jang identified the problem and first proposed the idea for the research. Seungmin Jeong and Min Seok Lee performed the modeling analysis and analyzed the data. Young Jae Jang wrote the paper.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| SWC | stationary wireless charging |
| QWC | quasi-dynamic wireless charging |
| DWC | dynamic wireless charging |
| IC | internal combustion |
| On-Line Electric Vehicle | |
| KAIST | Korea Advanced Institute of Science and Technology |
References
- Mi, C.; Masrur, M.A.; Gao, D.W. Hybrid Electric Vehicles, Principles and Applications with Practical Perspectives; Wiley: Chichester, UK, 2011. [Google Scholar]
- Ulrich, L. State of charge. IEEE Spectrum 2012, 49, 56–59. [Google Scholar] [CrossRef]
- Kowalenko, K. Going Electric: Things to Consider. Available online: http://theinstitute.ieee.org/ technology-focus/technology-topic/going-electric-things-to-consider (accessed on 9 January 2012).
- Miller, J.M.; Jones, P.; Li, J.M.; Onar, O.C. ORNL Experience and Challenges Facing Dynamic Wireless Power Charging of EV’s. IEEE Circuits Syst. Mag. 2015, 15, 40–53. [Google Scholar] [CrossRef]
- Overview About Wireless Charging Electrified Vehicles—Basic Principles Challenges. Available online: http://content.time.com/time/specials/packages/0,28757,2029497,00.html (accessed on 26 June 2014).
- Business development and Commercialization of the On-Line Electric Vehicle OLEV, Annual Technical Report (Korean); Technical Report; Korea Advanced Institute of Science and Technology (KAIST): Daejeon, Korea, 2009.
- Shun, J.; Shin, S.; Kim, Y.; Ahn, S.; Lee, S.; Jung, G.; Jeon, S.J.; Cho, D.H. Design and Implementation of Shaped Magnetic-Resonance-Based Wireless Power Transfer System for Roadway-Powered Moving Electric Vehicles. IEEE Trans. Ind. Electron. 2013, 61, 1179–1192. [Google Scholar] [CrossRef]
- Falk, T. An Electric Bus That Wirelessly Charges at Each Stop. Available online: http://www.smartplanet.com/blog/bulletin/an-electric-bus-that-wirelessly-charges-at-each-stop/ (accessed on 30 November 2012).
- Lukic, S.; Pantic, Z. Cutting the Cord. IEEE Electr. Mag. 2013, 1, 57–64. [Google Scholar] [CrossRef]
- Du, J.; Ouyang, M.; Wang, H. Battery electric vehicle parameters design targeting to cost-benefit objective. In Proceedings of the Vehicle Power and Propulsion Conference (VPPC), Seoul, Korea, 9–12 October 2012; pp. 1160–1164.
- Bolger, J.; Kirsten, F.; Ng, L. Inductive power coupling for an electric highway system. In Proceedings of the 28th IEEE Vehicular Technology Conference, Denver, CO, USA, 22–24 March 1978; Volume 28, pp. 137–144.
- Esser, A. Contactless charging and communication for electric vehicles. IEEE Ind. Appl. Mag. 1995, 1, 4–11. [Google Scholar] [CrossRef]
- Wang, C.S.; Stielau, O.H.; Covic, G.A. Design considerations for a contactless electric vehicle battery charger. IEEE Trans. Ind. Electron. 2005, 52, 1308–1314. [Google Scholar] [CrossRef]
- Covic, G.A.; Boys, J.T.; Kissin, M.L.; Lu, H.G. A three-phase inductive power transfer system for roadway-powered vehicles. IEEE Trans. Ind. Electron. 2007, 54, 3370–3378. [Google Scholar] [CrossRef]
- Suh, N.; Cho, D.; Rim, C. Design of On-Line Electric Vehicle (OLEV). In Proceedings of the Plenary Presentation, CIRP Design Conference, Nantes, France, 19–21 April 2010.
- Huh, J.; Lee, S.; Park, C.; Cho, G.H.; Rim, C.T. High performance inductive power transfer system with narrow rail width for On-Line Electric Vehicles. In Proceedings of the 2010 IEEE Energy Conversion Congress and Exposition (ECCE), Atlanta, GA, USA, 12–16 September 2010; pp. 647–651.
- Ahn, S.; Pak, J.; Song, T.; Lee, H.; Byun, J.G.; Kang, D.; Choi, C.S.; Kim, E.; Ryu, J.; Kim, M.; et al. Low frequency electromagnetic field reduction techniques for the On-Line Electric Vehicle (OLEV). In Proceedings of the IEEE International Symposium on Electromagnetic Compatibility (EMC), Fort Lauderdale, FL, USA, 25–30 July 2010.
- Ahn, S.; Lee, J.Y.; Choi, D.H.; Kim, J. Magnetic Field Design for Low EMF and High Efficiency Wireless Power Transfer System in On-Line Electric Vehicles. In Proceedings of the CIRP Design Conference, Bochum, Germany, 11–13 March 2011.
- Huh, J.; Lee, S.; Lee, W.; Cho, G.; Rim, C. Narrow-width inductive power transfer system for online electrical vehicles. IEEE Trans. Power Electron. 2011, 26, 3666–3679. [Google Scholar] [CrossRef]
- Choi, S.; Gu, B.; Lee, S.; Lee, W.; Huh, J.; Rim, C. Generalized Active EMF Cancel Methods for Wireless Electric Vehicles. IEEE Trans. Power Electron. 2014, 29, 5770–5783. [Google Scholar] [CrossRef]
- Ahn, S.; Suh, N.P.; Cho, D.H. Charging up the road. IEEE Spectrum 2013, 50, 48–54. [Google Scholar] [CrossRef]
- Kwaak, J.S. Korean Electric Buses Go Wireless. Available online: http://blogs.wsj.com/ korearealtime/2013/08/08/korean-electric-buses-go-wireless/tab/video/ (accessed on 8 August 2013).
- Corner, S. Qualcomm Buys Auckland Uni’s Wireless Electric Car Charging Technology. Available online: http://www.itwire.com/it-industry-news/deals/51038-qualcomm-buys-auckland-unis-wireless-electric-car-charging-technology (accessed on 30 November 2011).
- Barry, K. You Could Soon Be Riding Utah? Gloriously Wireless Electric Bus. Available online: http://www.wired.com/autopia/2013/10/utah-ev-bus/ (accessed on 31 October 2013).
- CORDIS. Inductive Charging Is Already Closer to Electric Vehicle Users Thanks to the UNPLUGGED Project. Available online: http://cordis.europa.eu/news/rcn/123635_en.html (accessed on 19 May 2015).
- Kuby, M.; Lim, S. The flow-refueling location problem for alternative-fuel vehicles. Soc. Econ. Plan. Sci. 2005, 39, 125–145. [Google Scholar] [CrossRef]
- Wen, M.; Laporte, G.; Madsen, O.B.; Nørrelund, A.V.; Olsen, A. Locating replenishment stations for electric vehicles: Application to Danish traffic data. J. Oper. Res. Soc. 2013, 65, 1555–1561. [Google Scholar] [CrossRef]
- Li, J.Q. Transit bus scheduling with limited energy. Transp. Sci. 2013, 48, 521–539. [Google Scholar] [CrossRef]
- Ko, Y.D.; Jang, Y.J. The Optimal System Design of the Online Electric Vehicle Utilizing a Wireless Power Transmission Technology. IEEE Trans. Intell. Transp. Syst. 2013, 14, 1255–1265. [Google Scholar] [CrossRef]
- James, L.; John, L. Electric Vehicle Technology Explained; Wiley Online Library: Chichester, UK, 2003. [Google Scholar]
- Takeshita, H. LIB-Pack Technology Trend; Technical Report; B3 Corporation: Raleigh, NC, USA, 2015. [Google Scholar]
- Trigg, T.; Telleen, P. Global EV Outlook: Understanding the Electric Vehicle Landscape to 2020; Technical Report; International Energy Agency: Washington, DC, USA, 2013. [Google Scholar]
- Nurhaswani, A.; Ahmad Azmin, M. Advances of aqueous rechargeable lithium-ion battery: A review. J. Power Sources 2015, 274, 237–251. [Google Scholar]
- Schuyler, M.; Eric, W. Learning dependent subsidies for lithium-ion electric vehicle batteries. Technol. Forecast. Soc. Chang. 2015, 92, 322–331. [Google Scholar]
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).